 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coordination of dissolved transition metals in pristine battery electrolyte solutions determined by NMR and EPR spectroscopy†
Jennifer P.
Allen
 ab,
Conrad
Szczuka
ab,
Conrad
Szczuka
 cd,
Holly E.
Smith
cd,
Holly E.
Smith
 a,
Erlendur
Jónsson
a,
Erlendur
Jónsson
 a,
Rüdiger-A.
Eichel
cd,
Josef
Granwehr
a,
Rüdiger-A.
Eichel
cd,
Josef
Granwehr
 ce and
Clare P.
Grey
ce and
Clare P.
Grey
 *ab
*ab
aYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge, CB2 1EW, Cambridge, UK. E-mail: cpg27@cam.ac.uk
bThe Faraday Institution, Quad One, Harwell Science and Innovation Campus, Didcot OX11 0RA, UK
cInstitute of Energy and Climate Research (IEK-9), Forschungszentrum Jülich GmbH, 52425 Jülich, Germany
dInstitute of Physical Chemistry, RWTH Aachen University, 52056 Aachen, Germany
eInstitute of Technical and Macromolecular Chemistry, RWTH Aachen University, 52056 Aachen, Germany
First published on 9th July 2024
Abstract
The solvation of dissolved transition metal ions in lithium-ion battery electrolytes is not well-characterised experimentally, although it is important for battery degradation mechanisms governed by metal dissolution, deposition, and reactivity in solution. This work identifies the coordinating species in the Mn2+ and Ni2+ solvation spheres in LiPF6/LiTFSI–carbonate electrolyte solutions by examining the electron–nuclear spin interactions, which are probed by pulsed EPR and paramagnetic NMR spectroscopy. These techniques investigate solvation in frozen electrolytes and in the liquid state at ambient temperature, respectively, also probing the bound states and dynamics of the complexes involving the ions. Mn2+ and Ni2+ are shown to primarily coordinate to ethylene carbonate (EC) in the first coordination sphere, while PF6− is found primarily in the second coordination sphere, although a degree of contact ion pairing does appear to occur, particularly in electrolytes with low EC concentrations. NMR results suggest that Mn2+ coordinates more strongly to PF6− than to TFSI−, while the opposite is true for Ni2+. This work provides a framework to experimentally determine the coordination spheres of paramagnetic metals in battery electrolyte solutions.
Introduction
As lithium-ion cells degrade, transition metal ions may dissolve from cathode materials and be deposited at the anode, causing issues including degradation of the solid electrolyte interphase (SEI) at the anode, further SEI formation and increased trapping of active lithium, impedance rise, and capacity loss.1–5 While many studies have been conducted on the topic of Li+ solvation in battery electrolytes, there is far less work surrounding the solvation of dissolved transition metals. Yet an understanding of the nature and strength of coordination of the transition metal ions by the different species in both pristine (fresh) and degraded electrolyte solutions is important to understand and control both the dissolution of transition metals from the cathode and their deposition on the anode, ultimately providing chemical insights into cell degradation pathways.The picture of Li+ solvation in battery electrolyte solutions is itself complicated; however, it is understood that Li+ tends to be tetrahedrally solvated6–10 and that coordination to ethylene carbonate (EC) is preferred over coordination to linear carbonates,7,9–17 with the extent of ion pairing between Li+ and PF6− being dependent on the salt concentration.11,18,19 For transition metal solvation, a computational study of Mn2+, Ni2+, and Co2+ solvation by EC showed that the structures would likely be six-coordinate, and that Mn2+ desolvation occurs more readily than Ni2+ or Co2+ desolvation, potentially influencing the role of Mn2+ in the SEI.20 Later simulations of the Mn2+ solvation shell showed that Mn2+ interaction energies follow the order EC > PF6− > linear carbonates.21 Our previous NMR studies have suggested that dissolved transition metals may favour coordination to EC over ethyl methyl carbonate22,23 and may coordinate preferentially to PF6− degradation products over pristine electrolyte components.23,24
In addition to understanding the solvation of dissolved transition metal ions, we aim to understand the solvation of model transition metal salts, and identify whether these model species are truly representative. Most studies aiming to mimic the effects of dissolved metals from cathode materials, including this work, use commercially available M(TFSI)2 salts.21,25–34 Although it is assumed that the metal cations dissociate from the TFSI− anions, (i.e., tight M2+–TFSI− ion pairs are not formed) due to the high solubility of the metal salts, and their small concentrations within the electrolyte, the extent of coordination between dissolved metals and TFSI− is not yet clear. At these low concentrations, the TFSI− anion is not thought to alter the reduction potential of dissolved transition metals or to affect cell cycling.28 It has also been suggested that because electrolyte solutions containing LiTFSI and LiPF6 behave similarly with respect to gassing at the negative electrode,35–37 the TFSI− counterion that is added with transition metals to an LiPF6 solution should not affect the electrolyte decomposition reactions induced by those transition metals.26 However, a comparison of electrolyte solutions containing added Mn(TFSI)2 and Mn(PF6)2 produced different cycling behaviour in LiFePO4/graphite cells, even though cells were not negatively affected by the addition of LiTFSI.29 Specifically, differences were observed in the amount of Mn deposited at both electrode surfaces and in the rate of capacity loss, with rapid initial capacity loss caused by Mn(TFSI)2 and smaller, continual capacity loss with more ongoing parasitic side reactions caused by Mn(PF6)2.29 A potential explanation for this is that Mn(TFSI)2 may not dissociate completely in a typical electrolyte solution comprising LiPF6, EC, and linear carbonates; such a notion is consistent with calculations showing that the Mn2+ interaction energy with TFSI− is even stronger than with EC, PF6−, or linear carbonates.21 In a similar vein, a study of Co deposition using the additive Co(NO3)2 found deposition of Li3N, which was not present when LiNO3 was added to the electrolyte solution.38 We note that the SEIs formed in electrolytes comprising LiTFSI are very different from those formed with LiPF6, which may also play an indirect role in some of the observed experimental differences. However, if the compounds that are used to mimic the effects of transition metal dissolution are found to alter the transition metal coordination shells, such that the counterions affect the action of dissolved transition metals, then studies using transition metal salts may be non-representative and lead to flawed conclusions about the role of dissolved transition metal ions in lithium-ion cells.
Transition metals are largely believed to dissolve from cathode materials in the +2 oxidation state (e.g., Ni2+, Mn2+, Co2+).5,22,28,39–42 These species are paramagnetic, enabling the use of paramagnetic NMR spectroscopy and, in some cases, EPR spectroscopy. In NMR, the nuclei that are located near paramagnetic species undergo rapid relaxation, permitting an indirect understanding of the coordination sphere of the paramagnetic centre; in pulsed EPR, the paramagnetic centre is probed directly and the surrounding magnetic nuclei affect the resonance conditions. In EPR spectroscopy, transition metal ions are often difficult to study if they have integer spins, as is the case for the d8S = 1 Ni2+ ion, because of the zero field splittings and short relaxation times. In contrast, dilute high-spin d5 Mn2+ ions are well-suited for EPR studies, because the half-filled outer d shell ensures a small-to-zero ground-state orbital angular momentum, especially for cubic symmetry,43 and small zero field splittings for the central transitions of the S = 5/2 spin system. Consequently, anisotropies are small and electronic relaxation times are comparably long, since modulations in the spin–orbit couplings no longer drive significant relaxation effects.44 Provided electronic relaxation times T1,2e are sufficiently long, pulsed EPR techniques probing small electron–nuclear (hyperfine) interactions are particularly useful for ligand identification. These specialised techniques are necessary since inhomogeneous EPR line broadening typically exceeds the resolution limit necessary to identify hyperfine couplings in transition metal ion complexes apart from those involving the central nucleus. Measurements are performed on frozen solutions at cryogenic temperatures to ensure sufficiently long T1,2e as well as rigid and potentially well-defined complexes. Although dynamics, as probed by NMR spectroscopy, are inaccessible as a consequence, an ensemble of structural snapshots should be generated during freezing, which should capture the thermodynamic ground state.
We have previously shown that the presence of dissolved paramagnetic ions can result in differential enhancement of the NMR relaxation rates of the signals from a variety of species in both pristine and degraded battery electrolyte solutions.23,24 We have used these relaxation rates, coupled with the accompanying bulk magnetic susceptibility shifts, to quantify metal concentrations and investigate binding to different electrolyte solvents. We have also used EPR to, for example, establish the solvation shell of dissolved vanadyl ions.45,46 Here, we combine the direct observation of the paramagnetic ions by EPR with solution NMR measurements to characterise the solvation shells of both Mn2+ and Ni2+ in pristine battery electrolytes. Model Mn(TFSI)2 and Ni(TFSI)2 solutions with varying concentrations of EC, LiPF6, and LiTFSI are investigated.
Static Mn2+ complexes are examined at low temperature in frozen solutions via EPR, field-swept echo and electron nuclear double resonance (ENDOR) experiments, revealing their complex symmetry and the magnetic nuclei in surrounding molecules. In liquids, at ambient temperatures, Mn2+ and Ni2+ solvation is studied dynamically via1H and 19F longitudinal and transverse nuclear relaxation rates, and the favourability of coordination to EC vs. PF6− in pristine electrolyte solutions is probed. Interactions with PF6−vs. TFSI− are then explored to determine whether M(TFSI)2 salts, added to mimic the effects of transition metal dissolution, alter the transition metal coordination shells. While transition metals are unlikely to accumulate in the electrolyte solution of a full cell undergoing charge–discharge cycling in the concentrations used in this work (1–8 mM vs., for example, the ∼0.1 mM Ni concentrations found in electrolytes from cycled LiNi0.8Mn0.1Co0.1O2 cells),47,48 we consider the concentrations used in this work to be small enough to be representative of the solvation shell of metals dissolved at very low concentrations. That is, the metals are present in low enough concentrations that the pristine electrolyte components are still in significant excess, and no metal clustering effects or other high-concentration effects should occur. We also note that soaking of cathode materials in battery electrolytes, often used to assess dissolution, can cause Mn or Ni accumulation in the electrolyte beyond what is typically observed in cycling cells—particularly in high-temperature soaking experiments, for example, with LiMn2O4 or LiNi0.5Mn1.5O4.42,49–51 While this work centres on coordination in pristine lithium-ion battery electrolytes, the approaches developed and employed herein are suitable to probe Mn2+ dissolution in any electrolyte solution or cell chemistry.
Methods
Electrolyte solutions
Transition metal bis(trifluoromethane)sulfonimide (TFSI) salts were added to electrolytes to mimic dissolved transition metals: Mn(TFSI)2 (Solvionic, 99.5%) and Ni(TFSI)2 (Alfa Aesar, ≥97%). Ethylene carbonate (EC) and ethyl methyl carbonate (EMC) were used as electrolyte solvents. Solutions used in this work include: 1 M LiPF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (for EPR and NMR); 1 M LiTFSI in 3
EMC (for EPR and NMR); 1 M LiTFSI in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (for EPR and NMR); 1 M LiPF6 in EMC (for NMR); and 3
EMC (for EPR and NMR); 1 M LiPF6 in EMC (for NMR); and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (for NMR). All solvent ratios are given as volume ratios (v/v). Solutions were prepared in an argon glovebox. For EPR experiments: Solutions were mixed in-house, using LiPF6 (Sigma Aldrich, ≥99.99% trace metals basis), LiTFSI (Alfa Aesar, 98+%), EC (Sigma Aldrich, 99%, anhydrous), and EMC (Sigma Aldrich, 99%). Mn(TFSI)2 was dried at 110 °C under dynamic vacuum for three days. For NMR experiments: 1 M LiPF6 in 3
EMC (for NMR). All solvent ratios are given as volume ratios (v/v). Solutions were prepared in an argon glovebox. For EPR experiments: Solutions were mixed in-house, using LiPF6 (Sigma Aldrich, ≥99.99% trace metals basis), LiTFSI (Alfa Aesar, 98+%), EC (Sigma Aldrich, 99%, anhydrous), and EMC (Sigma Aldrich, 99%). Mn(TFSI)2 was dried at 110 °C under dynamic vacuum for three days. For NMR experiments: 1 M LiPF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC was sourced premixed (soulbrain MI PuriEL R&D 280); 3
EMC was sourced premixed (soulbrain MI PuriEL R&D 280); 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC was sourced premixed (soulbrain and Solvionic); 1 M LiTFSI in 3
EMC was sourced premixed (soulbrain and Solvionic); 1 M LiTFSI in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC was mixed in-house (99.95% LiTFSI, Sigma Aldrich, with premixed EC
EMC was mixed in-house (99.95% LiTFSI, Sigma Aldrich, with premixed EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC); and 1 M LiPF6 in EMC was mixed in-house (99.99% LiPF6, Solvionic; 99.9% EMC, Solvionic). Salts were dried at 100 °C under vacuum before use.
EMC); and 1 M LiPF6 in EMC was mixed in-house (99.99% LiPF6, Solvionic; 99.9% EMC, Solvionic). Salts were dried at 100 °C under vacuum before use.
EPR spectroscopy
Samples for EPR experiments were freshly prepared by dissolving 8 mM of Mn(TFSI)2 in the electrolyte stock solution. The obtained solution was transferred into a 2 mm outer diameter EPR tube (Wilmad, CFQ) for X-band and into a 0.9 mm outer diameter tube (Wilmad, Suprasil) for Q-band experiments. Tubes were sealed and transferred from the glovebox into the pre-cooled EPR resonator within 15 min after preparation.EPR experiments were conducted on a Bruker ElexSys E580 spectrometer at a temperature of 20 K, maintained within a helium cryostat (Oxford Instruments, CF935). The EPR resonator was pre-cooled before inserting the sample, to rapidly cool (flash-freeze) the sample. (It should be noted that EPR/ENDOR experiments performed by more slowly cooling the resonator over approximately 15 minutes did not yield observable differences.)
Microwave pulses were amplified using a 1 kW travelling-wave tube amplifier, radiofrequency pulses with a 150 W amplifier. Measurements were performed using an EN4118X-MD4 resonator for X-band and an EN5107-D2 resonator for Q-band microwave frequencies. Field-swept pulsed EPR spectra were obtained by integration in a window of 62 ns centred at the Hahn echo. For X-band, τ = 180 ns and the pulse durations were tπ/2 = 12 ns and tπ = 24 ns. For Q-band, τ = 160 ns and pulse durations were tπ/2 = 20 ns and tπ = 40 ns. A two-step phase cycle was applied. Davies-type electron nuclear double resonance (ENDOR) experiments were conducted at Q-band using the pulse sequence π–D–π/2–τ–π–τ-echo for the microwaves with tπ/2 = 100 ns, tπ = 200 ns, and τ = 450 ns. During the delay D, radiofrequency π-pulses (at close to the 1H Larmor frequency) lasting 10 μs were applied. ENDOR experiments were acquired at a frequency offset that corresponds to the maximum of the low-field signal, corresponding to the 55Mn nuclear spin manifold mI = −5/2.
EPR spectra simulation
EPR spectra simulations were performed by using EasySpin v6.0.0-dev.4952,53 running in Matlab v2020b (MathWorks). 1H powder Davies ENDOR spectra were simulated taking into account all specified nuclei with hyperfine tensor components as obtained from DFT calculations. Easyspin's simulation module salt was used, applying second-order perturbation theory and the product rule. The obtained spectra were multiplied with the Davies ENDOR detection function54,55 | (1) |
Field-swept echo-detected spectra were fitted using the EasySpin fitting module pepper. The fit was initialised using an electronic spin 5/2 exhibiting an isotropic g tensor and an anisotropic zero-field splitting, coupled to a 55Mn nucleus with isotropic hyperfine coupling. A convolutional Gaussian with a full width at half maximum (FWHM) of 6 MHz for X-band and 13 MHz for Q-band was used along with anisotropic Gaussian zero-field splitting parameter strain.
NMR spectroscopy
For variable temperature NMR, 1H and 19F NMR relaxation times were measured on a Bruker Avance III HD 500 MHz spectrometer using a broadband observe (BBO) probe. A sealed capillary of C6D6 was used for field locking. Longitudinal, T1, relaxation times were measured using the inversion recovery pulse sequence and transverse, T2, relaxation times were measured using the Carr–Purcell–Meiboom–Gill (CPMG) pulse sequence56,57 with 2 ms echo spacings. Experiments were performed at 0, 15, 30, 45, and 60 °C.Ambient temperature relaxation experiments were performed on a Bruker Avance III HD 300 MHz spectrometer equipped with a Bruker double-channel MicWB40 probe. No deuterated solvents were incorporated into the electrolyte samples. T1 values were measured using inversion recovery and T2 values were measured using CPMG, with 2 ms echo spacings (τ) for diamagnetic and Ni2+-containing solutions. Due to fast relaxation, for Mn2+-containing solutions τ = 0.05–2 ms was used. Use of shorter τ values did not significantly impact the T2 measurements. For all NMR experiments, J-Young NMR tubes were filled and sealed in an argon glovebox.
Viscosity measurements
Kinematic viscosities of EMC, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (v/v), 1 M LiPF6 in EMC, 1 M LiPF6 in 3
EMC (v/v), 1 M LiPF6 in EMC, 1 M LiPF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC, and 1 M LiTFSI in 3
EMC, and 1 M LiTFSI in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC were measured in an argon glovebox with a Micro-Ostwald viscometer, type 51610/1 (Xylem Analytics), with an instrument constant K = 0.01063 mm2 s−2. A volume of 2 mL of each solution was used for viscosity measurements. Temperature varied from 25.7–27.2 °C. Kinematic viscosities were converted to dynamic viscosities by multiplying by solution density; solution density was measured by weighing 1 mL of solution in an argon glovebox.
EMC were measured in an argon glovebox with a Micro-Ostwald viscometer, type 51610/1 (Xylem Analytics), with an instrument constant K = 0.01063 mm2 s−2. A volume of 2 mL of each solution was used for viscosity measurements. Temperature varied from 25.7–27.2 °C. Kinematic viscosities were converted to dynamic viscosities by multiplying by solution density; solution density was measured by weighing 1 mL of solution in an argon glovebox.
DFT calculations
The density functional theory (DFT) calculations used the software package ORCA, version 5.0.1.58 Geometry optimisation was performed on [Mn(EC)4]2+, [Mn(EC)5PF6]2+, and [Mn(EC)6]2+ (identified as being the likeliest candidate in a set of DFT calculations described in the ESI†), with the TPSSh59,60 hybrid functional, approximating the relativistic Hamiltonian with the zeroth-order regular approximation (ZORA).61 Def2-TZVP(-f) basis sets62 in their ZORA-recontracted version63 were used. Decontracted def2/J auxiliary basis sets64 were employed for the resolution-of-identity and chain-of-spheres approximation.65 Convergence was attained by a tight self-consistent-field criterion. Hyperfine coupling tensors were calculated with the hybrid functional TPSSh and the ZORA relativistic approximation, as described recently.45,46 ZORA-def2-TZVP(-f) basis sets were modified through full decontraction of s shells and adding three more Gaussians, with exponents calculated by multiplying the steepest original primitive with 2.5, 6.25, and 15.625.66 Spin–orbit coupling was taken into account with the spin–orbit mean-field approximation (SOMF).67 To increase integration accuracy, the defgrid3 setting was chosen with radial accuracy IntAcc further increased to 11 for manganese and 9 for all other atoms.NMR relaxation theory
In this work, Solomon–Bloembergen–Morgan (SBM) theory is applied to interpret measured NMR relaxation times.68–72 Within this theory, relaxation is considered to be driven by a dipolar term (the Solomon equations)70 and a contact term (the Bloembergen equations).71 The dipolar term treats the through-space coupling of the nucleus and unpaired electron as an interaction between two point dipoles, i.e., the unpaired electron is localised on the paramagnetic ion, while the isotropic Fermi contact term results from the unpaired electron density present at the nucleus.68,69 The relaxation of a nucleus bound or close to a paramagnetic metal centre, M, is described by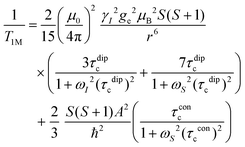 | (2) |
 | (3) |
Molecular rotation results in fluctuations arising from the orientation dependence of the anisotropic dipolar coupling tensor, thus the correlation time for the dipolar term
| (τdipc)−1 = τr−1 + τe−1 + τM−1 | (4) |
 | (5) |
| (τconc)−1 = τe−1 + τM−1 | (6) |
At the magnetic fields used in this work, the Larmor frequency of the electron spin, ωS, is very large.71,75,76 Since Mn2+ ions undergo relatively slow electronic relaxation, and thus τe is long,68 all the terms involving 1/ωS2 are expected to be small and can be ignored to a first approximation.71,75,77 For Mn2+, eqn (2) and (3) can therefore be approximated as
 | (7) |
 | (8) |
In most solutions, NMR nuclei are not statically bound to a paramagnetic centre. The measured relaxation rates R1 and R2 depend on the timescale and nature of the exchange between bound and unbound species, and whether inner or outer sphere complexes are formed.68,74 If we consider a system with rapid exchange between bound and unbound ligands, assuming only an inner sphere relaxation mechanism, then the fast-exchange limit of paramagnetic contribution to the relaxation time is given by R1p = fMR1M and R2p = fMR2M, where fM indicates the molar fraction of the species being probed that is coordinated to the transition metal. For intermediate exchange rates, τM−1, more complicated expressions can be derived. For R1, the terms are relatively simple, where R1d is the diamagnetic longitudinal relaxation rate,
 | (9) |
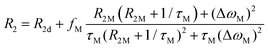 | (10) |
Results and discussion
EPR spectroscopy, 20 K
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 ratio of EC and EMC were studied at a temperature of 20 K. Fig. 1 shows field-swept echo-detected pulsed EPR spectra of the two samples at X- and Q-band. The spectra are dominated by the |−1/2〉 ↔ |1/2〉 transitions of the high-spin d5 complex. The six-fold line splitting, clearly evident at Q-band, indicates strong hyperfine coupling to the 55Mn nucleus of similar magnitude for both samples. The sets of doublets in between the central transitions are formally forbidden transitions originating from zero-field splitting interactions intermixing mI states,78 indicating deviation from perfect cubic symmetry. Their presence is more evident at X-band since the zero-field splitting is less effectively quenched by the electron Zeeman effect at this lower static magnetic field. The observation of well-resolved Mn-hyperfine splittings is clear evidence for the Mn-ions being diluted in the EC/EMC/LiTFSI/LiPF6 frozen matrix, consistent with the low concentration of this ion.79 Close Mn–Mn proximity in, for example, a precipitated Mn salt would result in exchange interactions and more broadening/disappearance of the hyperfine splittings. The broad featureless outer transitions originate from electron-spin transitions other than the |−1/2〉 ↔ |1/2〉 transitions. The two samples appear to possess very similar electronic interaction parameters, but Mn2+ in the LiTFSI electrolyte exhibits a larger line broadening, evident from the reduced relative intensity of the sextet (Fig. S1, ESI†).
7 ratio of EC and EMC were studied at a temperature of 20 K. Fig. 1 shows field-swept echo-detected pulsed EPR spectra of the two samples at X- and Q-band. The spectra are dominated by the |−1/2〉 ↔ |1/2〉 transitions of the high-spin d5 complex. The six-fold line splitting, clearly evident at Q-band, indicates strong hyperfine coupling to the 55Mn nucleus of similar magnitude for both samples. The sets of doublets in between the central transitions are formally forbidden transitions originating from zero-field splitting interactions intermixing mI states,78 indicating deviation from perfect cubic symmetry. Their presence is more evident at X-band since the zero-field splitting is less effectively quenched by the electron Zeeman effect at this lower static magnetic field. The observation of well-resolved Mn-hyperfine splittings is clear evidence for the Mn-ions being diluted in the EC/EMC/LiTFSI/LiPF6 frozen matrix, consistent with the low concentration of this ion.79 Close Mn–Mn proximity in, for example, a precipitated Mn salt would result in exchange interactions and more broadening/disappearance of the hyperfine splittings. The broad featureless outer transitions originate from electron-spin transitions other than the |−1/2〉 ↔ |1/2〉 transitions. The two samples appear to possess very similar electronic interaction parameters, but Mn2+ in the LiTFSI electrolyte exhibits a larger line broadening, evident from the reduced relative intensity of the sextet (Fig. S1, ESI†).
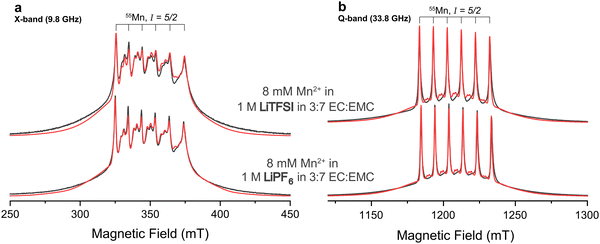 | ||
| Fig. 1 (a) X-band and (b) Q-band experimental pulsed EPR spectra recorded using field-swept Hahn-echoes (black) and spin Hamiltonian fits (red). Mn2+ is studied in premixed electrolytes with either LiPF6 (bottom) or LiTFSI (top) salts. All fits used identical interaction parameters but different line broadening (Table 1). | ||
Mn2+ in 1 M LiPF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC 7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC EMC |
Mn2+ in 1 M LiTFSI in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC 7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC EMC |
|
|---|---|---|
| a Fitted with a stretched/compressed exponential: S(t) = exp(−(t/Te)β) + y0. | ||
| From spin Hamiltonian fit | ||
| Isotropic g-value | 2.0016 ± 0.0002 | |
| |A|(55Mn)| (MHz) | 273 ± 5 | |
| |D| (MHz) | 415 ± 60 | |
| |E/D| (MHz) |

|
|
| D, E strain (MHz) | 230, 60 | 330, 120 |
| From relaxation measurementsa | ||
| T 2e (μs) | 0.37 | 0.49 |
| β T 2e | 1.26 | 1.29 |
| T 1e (μs) | 6.16 | 8.65 |
| β T 1e | 0.79 | 0.77 |
Further extractable parameters describe the zero-field splitting arising from the interaction of multiple unpaired electrons within the same (d5) ion, which can be described by the electron-spin Hamiltonian term
![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) D D![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) = D(Ŝz2 − Ŝ2/3) + E(Ŝx2 − Ŝy2) = D(Ŝz2 − Ŝ2/3) + E(Ŝx2 − Ŝy2) | (11) |
Predominantly, Mn2+ complexes are sixfold coordinated in solution, while occasionally five- or sevenfold, and fourfold coordination can occur if halogens and oxygen are directly coordinated.81,82 For sixfold coordinated Mn2+ with close to octahedral symmetry, D is often comparably small, on the order of |D| ≈ 300 MHz or smaller.43 The experimental value extracted here falls in the upper limit of that range, but is at least an order of magnitude smaller than values for known fivefold oxygen coordination or fourfold halogen/oxygen coordination.81 The exact value of D will depend on the orientation of the ligands,83i.e., degrees of freedom along dihedral angles, the composition and freezing behaviour of the solvent mixture,78 and the exact geometry, particularly the bond length between the transition metal and the first ligand atom.84 Furthermore, the experimentally determined zero-field splitting tensor exhibits large rhombicity. This rhombicity may also result from different participating ligands in the first coordination sphere. Assuming symmetric sixfold carbonate coordination of Mn2+via oxygen following the arguments above, then solvent-separated anions surrounding the complex may also be responsible for the rhombicity. One charge-compensating anion situated around the central atom would favour axial symmetry, as would two with anion–Mn2+–anion angles of 180°; two anions with 90° angles would favour rhombic symmetry. The only extractable difference from the pulsed EPR spectrum between the two samples under investigation is the estimated breadth of D and E distribution, given as strain parameters. These are significantly higher for the sample involving TFSI− anions. Again, assuming a solvent-separated ion pair, the Oh symmetry of the PF6− anion may result in a more ordered inner and outer coordination sphere compared to the TFSI− anion with lower symmetry and a flatter total energy landscape. The coordination of the anions is explored further below via double resonance EPR experiments.
 | ||
| Fig. 2 Experimental (black) and simulated (using values extracted from DFT calculations, blue) Davies ENDOR spectra at Q-band microwave frequencies. Excitation νrf was performed at the low-field maximum of the field-swept spectrum shown in Fig. 1b. The radiofrequency (rf) axis is shifted to place the 1H or 19F Larmor frequency at 0 MHz. The dashed line indicates the 19F Larmor frequency at −2.96 MHz (relative to that of 1H). Lines at −0.17 and 0.22 MHz are a guide to the eye and centred at the experimental ENDOR maxima. On the left, additional 19F Davies ENDOR measurements are shown where the rf axis is shifted to the 19F frequency. Interpolation with a cubic spline was used to extract the two local maxima and their frequency difference Δ. | ||
Given that the ENDOR experiments revealed hyperfine coupling to 1H, DFT calculations of Mn2+ coordinated to either EC or EMC in fourfold or sixfold complexes were performed, similar to the recent work of some of the authors.45,46 Coupling to 13C and 17O were ignored due to their low natural abundance. Spectra were simulated (Fig. 2, blue traces; Table S2, ESI†) using couplings extracted from the calculations, the simulations representing cumulative contributions from all involved 1H nuclei (4 per EC, 8 per EMC), where some conformational variability is intrinsically incorporated through multiple ligands and nuclei. Overall, all the simulated spectra cover a range that is of the same order of magnitude as the experimental spectra. The experimental maxima are best reproduced by EC ligands, but we cannot distinguish between fourfold or sixfold coordination. The shoulders may originate from coordinating EMC, where the flexible side chains can move closer to the central manganese, increasing the hyperfine coupling. However, the shoulders can also be caused by asymmetric strain which is not included in the simulation, other preferred conformers due to effects from outer solvation spheres, or minor impurities like H2O ligands which would give rise to intense resonances at around ±1.5 MHz.
Values for the hyperfine couplings of a directly coordinating PF6− or F− ion of larger than 10 MHz were estimated from additional DFT calculations (simulations in Fig. S5; parameters in Table S3, ESI†). Thus, the experimental spectra are not consistent with a contact ion pair and the 19F nuclei are rather located in anions in the outer solvation sphere. This means that the Fermi-contact interaction can be neglected for 19F, leaving a purely dipolar hyperfine tensor. Additional scans in the ν19F region reveal weak but distinct local maxima (Fig. 2, left panel) from which an approximate 55Mn–19F distance can be estimated using Δ = T, where T describes the diagonal hyperfine tensor A19F,diag = (−T, −T, 2T). A distance of 6.9 Å for the sample with PF6− anions and 7.8 Å for the sample with TFSI− anions is extracted from this tensor. By comparison with the DFT geometry optimised carbonate complex, this distance can be assigned to an anion in the second solvation shell – i.e., the cation–anion distance in an outer sphere complex (Fig. S6, ESI†). The presence of two or more anions in the second coordination shell may be responsible for the D/E ratio of >0 estimated above from the simulations of the EPR spectra (in Fig. 1). While there may be further, more distant 19F ions, resonances with smaller splittings will be even further attenuated, and this estimated distance is likely a good approximation for the closest 19F nuclei.
NMR spectroscopy, 0–60 °C
The EPR measurements provide compelling evidence for no inner-sphere coordination of anions in frozen Mn2+ complexes. We now use variable temperature (VT) NMR spectroscopy at 11.7 T to probe solution dynamics in the liquid state. Fig. 3 shows VT relaxation measurements for electrolyte solutions that are either diamagnetic or that contain 1 mM Mn2+. The longitudinal and transverse relaxation rates of EC (1H) and PF6− (19F) are shown at 0, 15, 30, 45, and 60 °C. The R1 and R2 values of diamagnetic solutions are labelled R1d and R2d, respectively; for paramagnetic solutions, the average R1d and R2d values are subtracted from measured R1 and R2 values to yield R1p and R2p values, i.e., isolating the relaxation enhancement.In the diamagnetic solutions, all 1H EC and 19F PF6−R1d and R2d values decrease (become slower) with increasing temperature (Fig. 3a). This decrease with increasing temperature and thus decreasing viscosity, indicates that both 1H EC and 19F PF6− relaxation occur in the fast motion regime. This is consistent with the relatively low viscosity of the electrolyte solutions that are optimised for Li+ mobility. Indeed, variable temperature relaxation measurements of a similar electrolyte solution, LiBF4 in propylene carbonate, have similarly shown that BF4− and propylene carbonate are in the fast motion regime.86 For the Mn2+-containing solutions, the 1H R1p and R2p values similarly decrease with temperature, indicating that the dynamics that drive relaxation are in the fast regime. The 19F R1p values initially increase between 0–30 °C then decrease between 30–60 °C. Therefore, at ambient temperature, the relevant mobility process for 19F relaxation appears to be in an intermediate regime, with τc of the same order of magnitude as the inverse of the 19F Larmor frequency (i.e., 3.4 × 10−10 s)87 at 11.7 T, whereas the correlation times driving 1H relaxation are shorter and in the fast regime. The PF6−τc value at the R1p maximum is consistent with values of τr and τd of ∼10−9–10−10 s estimated for low viscosity electrolytes.68T1e values of 6–9 × 10−6 s were measured for the Mn2+ spins at 20 K; while the T1e values are likely shorter at ambient temperature, τe should be the same for EC and PF6−, i.e., it should not account for the differences in the observed correlation times for 1H and 19F, suggesting that it is caused by different rotational processes or τM values arising from different binding and exchange processes.
The 19F R2p values reach a minimum at 45 °C and then increase again. This suggests that the 19F PF6− paramagnetic relaxation may be exchange-limited in the probed temperature range. Notably, as the different correlation times typically show a different temperature dependence, the dominant contribution may change as the temperature is altered, with R1p and R2p affected differently. Additionally, if exchange is in the intermediate regime, then R2M can be strongly enhanced. According to the SBM model and as discussed further below, these results imply that the R2M values likely contain both dipolar and contact terms, while R1M is dominated by the dipolar term. A more detailed analysis of the variable temperature 19F data is presented in the ESI,† since it does not unambiguously identify the driving forces for relaxation and rather motivates further relaxation experiments described in the next section.
NMR spectroscopy, ambient temperature
In this section, we separately analyse the trends in the relaxation rate of each environment as the solution composition is changed. We note that ambient temperature measurements were performed at 7.05 T, while VT NMR was performed at 11.7 T. The coordination of both Mn2+ and Ni2+ is investigated; unlike with pulsed EPR, the rapid Ni2+ electronic relaxation and its integer spin does not prevent NMR measurement. Coordination to EMC is not explored directly. We note that metal–solvent coordination is thought to primarily involve EC, because: (i) the solvent properties of EC suggest it is more coordinating than EMC, based on their respective dielectric constants88 and solvent polarity parameters (ET(30) and ENT);89 and (ii) Li+ coordination studies clearly show that EC is preferred over EMC.7,9,13,15,17 Additionally, a computational study of Mn2+ coordination has shown that EC is preferred over EMC.21 That is not to say that no coordination to EMC can occur: our previous NMR studies of 1 M LiPF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC containing dissolved Mn(TFSI)2 showed a larger 1H hyperfine shift for the EC resonance than for all EMC resonances, suggesting that while coordination to EC is likely preferred, coordination to EMC is also possible.22 Some variation likely exists among the coordination environments of paramagnetic ions, with several possible solvation environments of varying probabilities—but the fraction of Mn2+ or Ni2+ coordinated to EMC is probably small (or the fraction of time that an EMC molecule spends coordinated to a transition metal is small). Ambient temperature EMC relaxation data are, however, provided in the ESI.†
EMC containing dissolved Mn(TFSI)2 showed a larger 1H hyperfine shift for the EC resonance than for all EMC resonances, suggesting that while coordination to EC is likely preferred, coordination to EMC is also possible.22 Some variation likely exists among the coordination environments of paramagnetic ions, with several possible solvation environments of varying probabilities—but the fraction of Mn2+ or Ni2+ coordinated to EMC is probably small (or the fraction of time that an EMC molecule spends coordinated to a transition metal is small). Ambient temperature EMC relaxation data are, however, provided in the ESI.†
| Kinematic viscosity (mm2 s−1) | Density (g mL−1) | Dynamic viscosity (mPa s) | |
|---|---|---|---|
| EMC | 0.617 ± 0.003 | 1.012* | 0.62 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC 7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (v/v) EMC (v/v) |
0.940 ± 0.002 | 1.11 | 1.05 |
| 1 M LiPF6 in EMC | 1.440 ± 0.006 | 1.10 | 1.58 |
1 M LiTFSI in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC 7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC EMC |
2.183 ± 0.005 | 1.23 | 2.68 |
1 M LiPF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC 7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC EMC |
2.518 ± 0.007 | 1.20 | 3.03 |
Both the kinematic and dynamic viscosities follow the order: 1 M LiPF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (v/v) > 1 M LiTFSI in 3
EMC (v/v) > 1 M LiTFSI in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC > 1 M LiPF6 in EMC > 3
EMC > 1 M LiPF6 in EMC > 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC > EMC. The values presented here are consistent with literature values for the dynamic viscosity of EMC (0.65 cP at 25 °C), 3
EMC > EMC. The values presented here are consistent with literature values for the dynamic viscosity of EMC (0.65 cP at 25 °C), 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC w/w (1.11 cP at 20 °C), and 1 molal LiPF6 in 3
EMC w/w (1.11 cP at 20 °C), and 1 molal LiPF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC w/w (3.05 cP at 20 °C).91
EMC w/w (3.05 cP at 20 °C).91
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC + 0–1 M LiPF6 and 1 M LiPF6 in EMC + 0–1 M EC). Solutions contain either no transition metals (diamagnetic) or 1 mM Mn2+ or Ni2+ (paramagnetic).
EMC + 0–1 M LiPF6 and 1 M LiPF6 in EMC + 0–1 M EC). Solutions contain either no transition metals (diamagnetic) or 1 mM Mn2+ or Ni2+ (paramagnetic).
For solutions with varying LiPF6, in the diamagnetic solutions, 1H EC and 19F PF6− relaxation rates both increase as the PF6− concentration increases (Fig. 4a-i and ii). In the paramagnetic solutions, the 1H EC R1p values increase as the PF6− concentration increases, but the 19F PF6−R1p values decrease. As LiPF6 is added to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC, the solution becomes significantly more viscous (Table 2), increasing the rotational and diffusional correlation times of the species in solution. In the fast motion regime, longer correlation times increase the relaxation rate, until an R1 maximum (or T1 minimum) occurs.68,92 In the paramagnetic solutions, the 1H EC relaxation rates increase as the PF6− concentration increases (Fig. 4a-iii and v); this change is the same as the diamagnetic solution and again is likely a viscosity effect.
EMC, the solution becomes significantly more viscous (Table 2), increasing the rotational and diffusional correlation times of the species in solution. In the fast motion regime, longer correlation times increase the relaxation rate, until an R1 maximum (or T1 minimum) occurs.68,92 In the paramagnetic solutions, the 1H EC relaxation rates increase as the PF6− concentration increases (Fig. 4a-iii and v); this change is the same as the diamagnetic solution and again is likely a viscosity effect.
The paramagnetic contribution to the longitudinal relaxation rate, R1p, is proportional to the fraction of nuclei bound to paramagnetic ions, and it is also dependent on the length of time the nuclei are nearby paramagnetic ions (eqn (9)). The decrease in 19F PF6− relaxation rates as the PF6− concentration increases (Fig. 4a-iv and vi) is consistent with the reduction in the ratio of transition metal ions to PF6−. Assuming the total number of paramagnetic-coordinated PF6− ions remains constant, as the overall molar fraction of PF6− grows, the coordinated fraction of PF6− becomes smaller. For instance, if Mn2+ is ordinarily nearby two PF6− ions, then as the PF6− concentration changes from 0.05 M to 1 M, in a solution containing 1 mM Mn2+, the Mn2+-coordinated fraction of PF6− would decrease from 4% to 0.2%. The PF6− molecule is less likely, on average, to be bound or in close proximity to a paramagnetic ion, e.g., in a second coordination shell; hence, the overall PF6− relaxation rate is decreased. The observed trend is not linear, which is ascribed, at least in part, to the simultaneous viscosity increase as LiPF6 is added to solution. EMC relaxation rates are not discussed in detail here; however, the 1H EMC relaxation rates do increase in diamagnetic and paramagnetic solutions as LiPF6 is added, presumably due to the viscosity change (Fig. S8, ESI†).
The 1H EC and 19F PF6− relaxation rates of diamagnetic and paramagnetic solutions were also measured as the EC concentration in solution was increased from 0–1 M, with the LiPF6 concentration constant at 1 M (Fig. 4b). Increasing the EC concentration increases the solution viscosity (Table 2): thus, in the diamagnetic case, the 19F PF6− relaxation rates increase (as do the 1H EMC relaxation rates, shown in Fig. S9, ESI†). However, the diamagnetic 1H EC relaxation rate decreases as the EC concentration increases. The EC relaxation is therefore controlled by a different (non-viscosity) mechanism, which is likely related to the extent of Li+ coordination: while 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (v/v) contains 4.5 M EC, the solutions in Fig. 4b contain only 0–1 M EC. Li+ is preferentially solvated by EC over EMC,7,9,13,15,17 but in these solutions, 1 M Li+ cannot be fully (tetrahedrally) solvated by EC and there is likely no free EC. Rather, many Li+ ions are left to compete for solvation by EC, and with ≤1 EC available per Li+, the binding interaction may be stronger than in a solution with a larger EC concentration, as each Li+ does not have any other EC molecules to bind to, and the rate of EC exchange in the Li+ solvation shell is likely slower. Thus, an EC molecule in a solution of 0–1 M EC + 1 M LiPF6 on average is more likely to exist as a bound Li+–EC complex, relative to an EC molecule in a solution of 4.5 M EC + 1 M LiPF6 where free EC molecules are also present. Since the Li+–EC complex is larger than a free EC molecule, it is associated with longer rotational correlation times than free EC, even though the overall solution is less viscous.
EMC (v/v) contains 4.5 M EC, the solutions in Fig. 4b contain only 0–1 M EC. Li+ is preferentially solvated by EC over EMC,7,9,13,15,17 but in these solutions, 1 M Li+ cannot be fully (tetrahedrally) solvated by EC and there is likely no free EC. Rather, many Li+ ions are left to compete for solvation by EC, and with ≤1 EC available per Li+, the binding interaction may be stronger than in a solution with a larger EC concentration, as each Li+ does not have any other EC molecules to bind to, and the rate of EC exchange in the Li+ solvation shell is likely slower. Thus, an EC molecule in a solution of 0–1 M EC + 1 M LiPF6 on average is more likely to exist as a bound Li+–EC complex, relative to an EC molecule in a solution of 4.5 M EC + 1 M LiPF6 where free EC molecules are also present. Since the Li+–EC complex is larger than a free EC molecule, it is associated with longer rotational correlation times than free EC, even though the overall solution is less viscous.
In the paramagnetic solutions, the 1H EC and 19F PF6− relaxation rates both decrease as the EC concentration increases (Fig. 4b-iii–vi), neither being consistent with a (dominant) viscosity-driven inner sphere or an outer sphere mechanism. The decrease in 1H EC relaxation rate as EC is added to the solution is consistent with both the diamagnetic case, as well as eqn (9), which predicts slower 1H EC relaxation as the metal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC ratio changes from 1
EC ratio changes from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 to 1
100 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 (due to the smaller fM, the EC spending less time on average bound to a paramagnetic ion). The 19F PF6− relaxation time decreases as EC is added, likely because EC is preferentially adopted into the transition metal coordination sphere, and fM is thereby reduced. When EC is absent, PF6− spends more time in the transition metal inner coordination shell, resulting in the fastest PF6− relaxation rates in EC-free solution. By contrast, when the EC concentration is increased further from 1 M to 4.5 M, or 3
1000 (due to the smaller fM, the EC spending less time on average bound to a paramagnetic ion). The 19F PF6− relaxation time decreases as EC is added, likely because EC is preferentially adopted into the transition metal coordination sphere, and fM is thereby reduced. When EC is absent, PF6− spends more time in the transition metal inner coordination shell, resulting in the fastest PF6− relaxation rates in EC-free solution. By contrast, when the EC concentration is increased further from 1 M to 4.5 M, or 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (shown in Fig. 4a, highest concentration point), the 19F R1p values drop from 9.7 to 5.6 s−1 for Mn2+ and from 0.72 to 0.29 s−1 for Ni2+, consistent with the predominance of EC in the Mn2+ inner shell seen by EPR.
EMC (shown in Fig. 4a, highest concentration point), the 19F R1p values drop from 9.7 to 5.6 s−1 for Mn2+ and from 0.72 to 0.29 s−1 for Ni2+, consistent with the predominance of EC in the Mn2+ inner shell seen by EPR.
Taken together, the results in Fig. 4a and b support the EPR results, showing that Mn2+ and Ni2+ coordinate preferentially to EC over PF6−. Removal of PF6− from solution affects the EC relaxation rate only little, and it is still dominated by a viscosity effect: if PF6− coordination were preferred, removing PF6− would increase the M2+–EC fraction, which may produce a faster 1H EC relaxation rate in LiPF6-free solution. Instead, the opposite is observed (Fig. 4a-i, iii and v), due to the higher viscosity of LiPF6-containing solution. By contrast, removing EC from solution causes a dramatic increase in the PF6− relaxation rate (Fig. 4b-ii, iv and vi), which is notably opposite to what the viscosity change would predict: this indicates that M2+–PF6− coordination is favoured only in the absence of EC, and that the addition of EC reduces the M2+–PF6− fraction.
Fig. 5 shows the R2/R1 ratios for all solutions examined in Fig. 4 (an expanded view showing small R2/R1 ratios is shown in Fig. S10, ESI†). The R2/R1 ratios are small for the 1H EC resonance for all Mn2+-containing samples (1.5–2.1) and for all resonances of the Ni2+-containing solutions. In contrast, the R2/R1 ratios are consistently large for the 19F PF6− resonance in all Mn2+-containing samples. When the LiPF6 concentration is varied (Fig. 5a), the 19F PF6−R2/R1 ratio is ∼8, but when the EC concentration is varied (Fig. 5b), the 19F PF6−R2/R1 ratio decreases linearly from 63.1 to 35.3 as the EC concentration increases to 1 M; it drops further to 9.0 when EC is present at 4.5 M (Fig. 5a, highest concentration point).
 | ||
Fig. 5
R
2/R1 ratios of (a) solutions of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC 7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC (4.5 M EC) with 0–1 M LiPF6 or (b) solutions of 1 M LiPF6 in EMC with 0–1 M EC. Solutions are diamagnetic or contain Ni2+ or Mn2+; relaxation of 1H EC (circles) and 19F PF6− (triangles) is shown. Expanded view of small R2/R1 ratios is shown in ESI,† Fig. S10. Measurements were performed at a field strength of 7.05 T. EMC (4.5 M EC) with 0–1 M LiPF6 or (b) solutions of 1 M LiPF6 in EMC with 0–1 M EC. Solutions are diamagnetic or contain Ni2+ or Mn2+; relaxation of 1H EC (circles) and 19F PF6− (triangles) is shown. Expanded view of small R2/R1 ratios is shown in ESI,† Fig. S10. Measurements were performed at a field strength of 7.05 T. | ||
The ambient temperature NMR measurements were performed at a lower field strength of 7.05 T, compared to 11.7 T for VT NMR measurements. As a result, 1H relaxation rates are now more distinctly within the fast regime, while the 19F R1 rates are also shifted towards the fast regime, since R1 maxima are now expected at lower temperatures at the lower field. Assuming that the 19F relaxation is close to a maximum for 1 M LiPF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC—and in the fast regime—then if the EC concentration is decreased, which should reduce viscosity and τr, R1p is predicted to decrease. Instead R1p is seen experimentally to increase (Fig. 4), which we ascribed earlier to the decrease of EC bound to the paramagnetic ions in the inner coordination shell. Furthermore, the LiPF619F R2/R1 ratio increases noticeably from 9 in 3
EMC—and in the fast regime—then if the EC concentration is decreased, which should reduce viscosity and τr, R1p is predicted to decrease. Instead R1p is seen experimentally to increase (Fig. 4), which we ascribed earlier to the decrease of EC bound to the paramagnetic ions in the inner coordination shell. Furthermore, the LiPF619F R2/R1 ratio increases noticeably from 9 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC
7 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EMC electrolytes to 63 in EMC-only electrolytes (Fig. 5). In an outer sphere mechanism, R1 and R2 should approach each other in the fast regime. This suggests that a driving force (fluctuating field) beyond simply an outer-shell dipolar mechanism plays an increasingly important role, at least at low EC concentrations. We suggest that inner sphere mechanisms start to play a larger role; this is unsurprising because less EC is present in the Mn2+ inner shell.
EMC electrolytes to 63 in EMC-only electrolytes (Fig. 5). In an outer sphere mechanism, R1 and R2 should approach each other in the fast regime. This suggests that a driving force (fluctuating field) beyond simply an outer-shell dipolar mechanism plays an increasingly important role, at least at low EC concentrations. We suggest that inner sphere mechanisms start to play a larger role; this is unsurprising because less EC is present in the Mn2+ inner shell.
In an inner sphere complex, Mn2+ will coordinate directly to 19F, resulting in more electron density at the nucleus being studied, and a large hyperfine interaction (static average DFT value of Aiso(19F) = 2.90 MHz including Mn–F–P, Table S3, ESI†). Thus, at lower EC concentrations, at least, we tentatively suggest the large R2/R1 ratios may arise from a contact contribution to relaxation for 19F. Rotations of the coordinating PF6− anion, leading to changes in the F atoms that are coordinated to Mn2+, will also result in large fluctuations of the 19F hyperfine interactions, providing another (contact) relaxation mechanism. By contrast, with EC, Mn2+ coordinates at the carbonyl oxygen,20,21 which is located much farther away from the 1H nuclei that are being studied, resulting in a small hyperfine interaction as is seen in the EPR results (static average DFT value of Aiso(1H) = 0.03 MHz, Table S2, ESI†) and thus a small contact term for 1H. The observed small 1H R2/R1 ratios are consistent with this.
In Fig. 6a–c, the diamagnetic relaxation rates all decrease as the LiPF6 salt is replaced by LiTFSI; this is consistent with the viscosity measurements of these solutions in Table 2 showing that the LiPF6 solution is more viscous. When the solution contains 1 mM Mn2+, the 1H EC relaxation rates decrease (Fig. 6f), again matching the diamagnetic, viscosity-driven behaviour. However, the 19F PF6− and 19F TFSI− relaxation rates both increase as LiPF6 is replaced by LiTFSI (Fig. 6d and e). If Mn2+ coordination to PF6− and TFSI− are equally preferable, there should be no effect, to a first approximation, with changing the LiPF6/LiTFSI concentration, as the ratio of Mn2+-coordinated anions vs. total anions would stay the same. However, if PF6− coordination is preferred over TFSI−, then the 19F PF6−R1p and 19F TFSI−R1p values should both increase as LiTFSI replaces LiPF6, as is observed. (If PF6− coordination is preferred, further increasing the PF6− concentration only reduces the total coordinated fraction, lowering PF6−R1p values.) Notably, this result is inconsistent with previous computational work suggesting TFSI− coordination should be preferred.21 However, variable temperature NMR measurements were not performed for TFSI− solutions, and it is possible that the paramagnetic 19F TFSI−R1 is exchange-limited. If so, then increasing the TFSI− concentration may result in more rapid TFSI− chemical exchange, which could ultimately cause the relaxation rate to increase (viaeqn (9)). In outer sphere mechanisms, since the concentration of metals remains constant, the viscosity of the solutions is expected to dominate this mechanism, the results lending further support to the role that there is an inner sphere contribution to relaxation.
In the Ni2+-containing solutions (Fig. 6g–i), the 19F TFSI−, 19F PF6−, and 1H EC relaxation rates all decrease as LiPF6 is replaced by LiTFSI. While these are the same results as observed in diamagnetic solution, this is not explained entirely by viscosity effects: Fig. 4a-vi shows that in a Ni2+-containing solution, removing PF6− (without replacing it with TFSI−) does cause the 19F PF6−R1p values to increase as fM increases. The largest 19F PF6−R1p value coinciding with the smallest Ni2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PF6− ratio (1
PF6− ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000) therefore suggests that Ni2+ is only nearby PF6− when PF6− is present in substantial concentrations. Additionally, the decrease in 19F TFSI−R1p values as the TFSI− concentration increases is consistent with a decrease in fM. Fig. 6 therefore indicates that Ni2+ prefers TFSI− coordination over PF6− coordination, while Mn2+ prefers PF6− coordination over TFSI− coordination. However, in a 1 M LiPF6 electrolyte solution where 1 mM Mn(TFSI)2 or Ni(TFSI)2 is added as a model compound, the PF6− concentration is 500× larger than the TFSI− concentration and interactions with the PF6− anion may dominate for both Mn2+ and Ni2+.
1000) therefore suggests that Ni2+ is only nearby PF6− when PF6− is present in substantial concentrations. Additionally, the decrease in 19F TFSI−R1p values as the TFSI− concentration increases is consistent with a decrease in fM. Fig. 6 therefore indicates that Ni2+ prefers TFSI− coordination over PF6− coordination, while Mn2+ prefers PF6− coordination over TFSI− coordination. However, in a 1 M LiPF6 electrolyte solution where 1 mM Mn(TFSI)2 or Ni(TFSI)2 is added as a model compound, the PF6− concentration is 500× larger than the TFSI− concentration and interactions with the PF6− anion may dominate for both Mn2+ and Ni2+.
An analysis of the R2/R1 ratios for the same solutions as studied in Fig. 6 is provided in the ESI† (Fig. S11); these data are consistent with conclusions drawn from the R1p data. The idea of preferential coordination to TFSI− by Ni2+ but not Mn2+ may be rationalised on the basis of crystal field arguments. Ni2+ (d8) complexes, with larger crystal field stabilisation energies and smaller radii, are more long lived once they form, whereas Mn2+ (d5) complexes have zero crystal field stabilisation energies, larger radii, and more rapid equilibria (following the Irving–Williams order of stability), i.e., more fluctional, short-lived complexes are formed.93–95 The more rapid equilibria found for Mn2+ ions means that EC molecules will also move in and out of the Mn2+ coordination shell, allowing Mn2+–PF6− inner sphere interactions to occur, albeit short-lived, contributing to the more rapid transverse nuclear relaxation. These interactions are weak, however, so that no inner sphere binding is seen in the EPR experiments. Thermodynamically, the M2+–TFSI− interaction is likely stronger than the M2+–PF6− interaction, in accordance with computational work for Mn2+,21 but transition metals may coordinate at any F of the small, symmetric PF6− molecule, whereas TFSI− is bulkier and may be more difficult to accommodate around a metal ion. In actual electrolyte solutions containing dissolved transition metals and multiple solvent molecules, it may be that the smaller PF6− is easier to incorporate in the Mn2+ solvation shell and thus outcompete TFSI− in this respect. By contrast, the greater crystal field stabilisation of Ni2+ should result in stronger binding of TFSI− to Ni2+vs. binding to Mn2+, combined with longer lived complexes. These results indicate the importance of experimental studies to complement theoretical work. Finally, we note that the timescales in which the anions and solvation molecules move in and out of the solvation shells, and the role that metal binding has on the rotational modes of the anions themselves, will clearly have implications for the different relaxation processes, motivating further molecular dynamics simulations of these systems, coupled with more variable temperature NMR studies.
Conclusions
Electron–nuclear spin interactions have been exploited in this study to identify the solvation sphere(s) of paramagnetic transition metal ions in battery electrolytes, combining synergetic insights from EPR and NMR into ligand identity and dynamics. Pulsed EPR spectroscopy was beneficial for the direct observation of ligands using ENDOR. However, EPR is limited to systems with slow electronic relaxation rates, typically requiring cryogenic measurement temperatures, and is best suited to metals with non-integer electron spins, i.e., Mn2+. In contrast, simple T1 and T2 NMR measurements at ambient conditions can provide indirect insights into the nature of solvation shells, for a wide range of paramagnetic ions and including dynamic effects such as ligand exchange. This is due to nuclear relaxation rates of electrolyte components being highly sensitive to the presence of paramagnetic transition metals.In frozen pristine electrolyte solutions, EPR experiments identified that dissolved Mn2+ is primarily coordinated to EC in solutions of 1 M LiPF6 or LiTFSI in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 EC/EMC (v/v), with distorted Oh symmetry (sixfold coordination). In addition to EC coordination, rhombic zero-field splitting suggests an asymmetric coordination environment, influenced by EMC and/or salt anions. This is consistent with NMR experiments of Mn2+- and Ni2+-containing solutions with a variety of salt and solvent concentrations. NMR results showed that EC outcompetes PF6− in the solvation shell. At the same time, the extremely fast 19F PF6− transverse relaxation in Mn2+-containing solutions, particularly at low EC concentrations, likely arises from a contact term and indicates that some PF6− is indeed present in the first solvation shell (i.e., as contact ion pairs). In contrast, 19F ENDOR experiments do not indicate the presence of a contact ion pair, but instead a solvent-separated ion pair is found, presumably due to the sole presence of the thermodynamically more stable EC-coordinated complex at cryogenic temperature. Taken together, the results suggest that the Mn2+ and Ni2+ solvation shell in pristine electrolyte solutions comprises primarily EC, with some exchange of PF6− between the inner and outer spheres, particularly in Mn2+ solutions at low EC concentrations. NMR experiments probing coordination to TFSI− showed that TFSI− can displace PF6− in the Ni2+ solvation shell, but there is no clear evidence from either NMR or EPR that this occurs in the Mn2+ solvation shell.
7 EC/EMC (v/v), with distorted Oh symmetry (sixfold coordination). In addition to EC coordination, rhombic zero-field splitting suggests an asymmetric coordination environment, influenced by EMC and/or salt anions. This is consistent with NMR experiments of Mn2+- and Ni2+-containing solutions with a variety of salt and solvent concentrations. NMR results showed that EC outcompetes PF6− in the solvation shell. At the same time, the extremely fast 19F PF6− transverse relaxation in Mn2+-containing solutions, particularly at low EC concentrations, likely arises from a contact term and indicates that some PF6− is indeed present in the first solvation shell (i.e., as contact ion pairs). In contrast, 19F ENDOR experiments do not indicate the presence of a contact ion pair, but instead a solvent-separated ion pair is found, presumably due to the sole presence of the thermodynamically more stable EC-coordinated complex at cryogenic temperature. Taken together, the results suggest that the Mn2+ and Ni2+ solvation shell in pristine electrolyte solutions comprises primarily EC, with some exchange of PF6− between the inner and outer spheres, particularly in Mn2+ solutions at low EC concentrations. NMR experiments probing coordination to TFSI− showed that TFSI− can displace PF6− in the Ni2+ solvation shell, but there is no clear evidence from either NMR or EPR that this occurs in the Mn2+ solvation shell.
These new insights on transition metal coordination add experimental evidence to previous work, which is dominated by computational studies. A clear understanding of metal solvation may contribute to approaches adopted to prevent transition metal dissolution, deposition, and overall battery capacity fade. Finally, the presented combined EPR–NMR approach is well-suited to assess the solvation of paramagnetic transition metals and may be readily applied to any other electrolyte system or cell chemistry, including studying transition metal coordination to novel electrolyte components or electrolyte degradation species.
Data availability
Additional data supporting this article, including DFT xyz files, have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
JPA thanks the Natural Sciences and Engineering Research Council of Canada for funding; JPA and CPG acknowledge support from the Faraday Institution under grant number FIRG001 and from the Royal Society via a professorship to CPG; CS acknowledges computing resources granted by RWTH Aachen University under project rwth0701; HES thanks Prof Stuart Clarke for helpful discussions and the EPSRC for funding, award number EP/R513180/1; EJ and CPG acknowledge support from the ERC grant BATNMR no. 835073.References
- W. Choi and A. Manthiram, Comparison of Metal Ion Dissolutions from Lithium Ion Battery Cathodes, J. Electrochem. Soc., 2006, 153(9), A1760 CrossRef CAS.
- H. Zheng, Q. Sun, G. Liu, X. Song and V. S. Battaglia, Correlation between Dissolution Behavior and Electrochemical Cycling Performance for LiNi1/3Co1/3Mn1/3O2-Based Cells, J. Power Sources, 2012, 207, 134–140 CrossRef CAS.
- J. A. Gilbert, I. A. Shkrob and D. P. Abraham, Transition Metal Dissolution, Ion Migration, Electrocatalytic Reduction and Capacity Loss in Lithium-Ion Full Cells, J. Electrochem. Soc., 2017, 164(2), A389–A399 CrossRef CAS.
- C. Zhan, T. Wu, J. Lu and K. Amine, Dissolution, Migration, and Deposition of Transition Metal Ions in Li-Ion Batteries Exemplified by Mn-Based Cathodes – a Critical Review, Energy Environ. Sci., 2018, 11(2), 243–257 RSC.
- O. C. Harris, S. E. Lee, C. Lees and M. Tang, Review: Mechanisms and Consequences of Chemical Cross-Talk in Advanced Li-Ion Batteries, J. Phys. Energy, 2020, 2(3), 032002 CrossRef CAS.
- B. Klassen, R. Aroca, M. Nazri and G. A. Nazri, Raman Spectra and Transport Properties of Lithium Perchlorate in Ethylene Carbonate Based Binary Solvent Systems for Lithium Batteries, J. Phys. Chem. B, 1998, 102(24), 4795–4801 CrossRef CAS.
- S. Yanase and T. Oi, Solvation of Lithium Ion in Organic Electrolyte Solutions and Its Isotopie Reduced Partition Function Ratios Studied by Ab Initio Molecular Orbital Method, J. Nucl. Sci. Technol., 2002, 39(10), 1060–1064 CrossRef CAS.
- M. D. Bhatt, M. Cho and K. Cho, Interaction of Li+ Ions with Ethylene Carbonate (EC): Density Functional Theory Calculations, Appl. Surf. Sci., 2010, 257(5), 1463–1468 CrossRef CAS.
- M. T. Ong, O. Verners, E. W. Draeger, A. C. T. van Duin, V. Lordi and J. E. Pask, Lithium Ion Solvation and Diffusion in Bulk Organic Electrolytes from First-Principles and Classical Reactive Molecular Dynamics, J. Phys. Chem. B, 2015, 119(4), 1535–1545 CrossRef CAS PubMed.
- M. Shakourian-Fard, G. Kamath and S. K. R. S. Sankaranarayanan, Evaluating the Free Energies of Solvation and Electronic Structures of Lithium-Ion Battery Electrolytes, ChemPhysChem, 2016, 17(18), 2916–2930 CrossRef CAS PubMed.
- M. Morita, Y. Asai, N. Yoshimoto and M. Ishikawa, A Raman Spectroscopic Study of Organic Electrolyte Solutions Based on Binary Solvent Systems of Ethylene Carbonate with Low Viscosity Solvents Which Dissolve Different Lithium Salts, J. Chem. Soc., Faraday Trans., 1998, 94(23), 3451–3456 RSC.
- S.-K. Jeong, M. Inaba, Y. Iriyama, T. Abe and Z. Ogumi, Surface Film Formation on a Graphite Negative Electrode in Lithium-Ion Batteries: AFM Study on the Effects of Co-Solvents in Ethylene Carbonate-Based Solutions, Electrochim. Acta, 2002, 47(12), 1975–1982 CrossRef CAS.
- Y. Wang and P. B. Balbuena, Theoretical Studies on Cosolvation of Li Ion and Solvent Reductive Decomposition in Binary Mixtures of Aliphatic Carbonates, Int. J. Quantum Chem., 2005, 102(5), 724–733 CrossRef CAS.
- L. Yang, A. Xiao and B. L. Lucht, Investigation of Solvation in Lithium Ion Battery Electrolytes by NMR Spectroscopy, J. Mol. Liq., 2010, 154(2), 131–133 CrossRef CAS.
- A. Cresce and K. von; Xu, Preferential Solvation of Li+ Directs Formation of Interphase on Graphitic Anode, Electrochem. Solid-State Lett., 2011, 14(10), A154–A156 CrossRef.
- X. Bogle, R. Vazquez, S. Greenbaum, A. Cresce, W. von and K. Xu, Understanding Li+–Solvent Interaction in Nonaqueous Carbonate Electrolytes with 17O NMR, J. Phys. Chem. Lett., 2013, 4(10), 1664–1668 CrossRef CAS PubMed.
- C.-C. Su, M. He, R. Amine, T. Rojas, L. Cheng, A. T. Ngo and K. Amine, Solvating Power Series of Electrolyte Solvents for Lithium Batteries, Energy Environ. Sci., 2019, 12(4), 1249–1254 RSC.
- D. M. Seo, S. Reininger, M. Kutcher, K. Redmond, W. B. Euler and B. L. Lucht, Role of Mixed Solvation and Ion Pairing in the Solution Structure of Lithium Ion Battery Electrolytes, J. Phys. Chem. C, 2015, 119(25), 14038–14046 CrossRef CAS.
- S. A. Krachkovskiy, J. D. Bazak, S. Fraser, I. C. Halalay and G. R. Goward, Determination of Mass Transfer Parameters and Ionic Association of LiPF6: Organic Carbonates Solutions, J. Electrochem. Soc., 2017, 164(4), A912–A916 CrossRef CAS.
- Y.-K. Han, K. Lee, S. Kang, Y. S. Huh and H. Lee, Desolvation and Decomposition of Metal (Mn, Co and Ni)–Ethylene Carbonate Complexes: Relevance to Battery Performance, Comput. Mater. Sci., 2014, 81, 548–550 CrossRef CAS.
- C. Wang, L. Xing, J. Vatamanu, Z. Chen, G. Lan, W. Li and K. Xu, Overlooked Electrolyte Destabilization by Manganese(II) in Lithium-Ion Batteries, Nat. Commun., 2019, 10(1), 3423 CrossRef PubMed.
- J. P. Allen and C. P. Grey, Determining the Oxidation States of Dissolved Transition Metals in Battery Electrolytes from Solution NMR Spectra, Chem. Commun., 2023, 59(12), 1677–1680 RSC.
- J. P. Allen, C. A. O’Keefe and C. P. Grey, Quantifying Dissolved Transition Metals in Battery Electrolyte Solutions with NMR Paramagnetic Relaxation Enhancement, J. Phys. Chem. C, 2023, 127(20), 9509–9521 CrossRef CAS PubMed.
- J. P. Allen and C. P. Grey, Solution NMR of Battery Electrolytes: Assessing and Mitigating Spectral Broadening Caused by Transition Metal Dissolution, J. Phys. Chem. C, 2023, 127(9), 4425–4438 CrossRef CAS PubMed.
- T. Joshi, K. Eom, G. Yushin and T. F. Fuller, Effects of Dissolved Transition Metals on the Electrochemical Performance and SEI Growth in Lithium-Ion Batteries, J. Electrochem. Soc., 2014, 161(12), A1915–A1921 CrossRef.
- S. Solchenbach, G. Hong, A. T. S. Freiberg, R. Jung and H. A. Gasteiger, Electrolyte and SEI Decomposition Reactions of Transition Metal Ions Investigated by On-Line Electrochemical Mass Spectrometry, J. Electrochem. Soc., 2018, 165(14), A3304–A3312 CrossRef CAS.
- J. Betz, J.-P. Brinkmann, R. Nölle, C. Lürenbaum, M. Kolek, M. C. Stan, M. Winter and T. Placke, Cross Talk between Transition Metal Cathode and Li Metal Anode: Unraveling Its Influence on the Deposition/Dissolution Behavior and Morphology of Lithium, Adv. Energy Mater., 2019, 9(21), 1900574 CrossRef.
- R. Jung, F. Linsenmann, R. Thomas, J. Wandt, S. Solchenbach, F. Maglia, C. Stinner, M. Tromp and H. A. Gasteiger, Nickel, Manganese, and Cobalt Dissolution from Ni-Rich NMC and Their Effects on NMC622-Graphite Cells, J. Electrochem. Soc., 2019, 166(2), A378–A389 CrossRef CAS.
- A. Tornheim, J. Kirner, R. Sahore, K.-C. Lau, D. C. O’Hanlon, W. M. Dose, C.-W. Lee, C. Liao, Z. Zhang, M. Balasubramanian and J. R. Croy, Communication—Ligand-Dependent Electrochemical Activity for Mn2+ in Lithium-Ion Electrolyte Solutions, J. Electrochem. Soc., 2019, 166(10), A2264–A2266 CrossRef CAS.
- K. Wang, L. Xing, K. Xu, H. Zhou and W. Li, Understanding and Suppressing the Destructive Cobalt(II) Species in Graphite Interphase, ACS Appl. Mater. Interfaces, 2019, 11(34), 31490–31498 CrossRef CAS PubMed.
- D. Huang, C. Engtrakul, S. Nanayakkara, D. W. Mulder, S.-D. Han, M. Zhou, H. Luo and R. C. Tenent, Understanding Degradation at the Lithium-Ion Battery Cathode/Electrolyte Interface: Connecting Transition-Metal Dissolution Mechanisms to Electrolyte Composition, ACS Appl. Mater. Interfaces, 2021, 13(10), 11930–11939 CrossRef CAS PubMed.
- S. Klein, P. Bärmann, T. Beuse, K. Borzutzki, J. E. Frerichs, J. Kasnatscheew, M. Winter and T. Placke, Exploiting the Degradation Mechanism of NCM523 Graphite Lithium-Ion Full Cells Operated at High Voltage, ChemSusChem, 2021, 14(2), 595–613 CrossRef CAS PubMed.
- H. Xu, Z. Li, T. Liu, C. Han, C. Guo, H. Zhao, Q. Li, J. Lu, K. Amine and X. Qiu, Impacts of Dissolved Ni2+ on the Solid Electrolyte Interphase on a Graphite Anode, Angew. Chem., Int. Ed., 2022, 61(30), e202202894 CrossRef CAS PubMed.
- X. Zhang, Z. Cui and A. Manthiram, Insights into the Crossover Effects in Cells with High-Nickel Layered Oxide Cathodes and Silicon/Graphite Composite Anodes, Adv. Energy Mater., 2022, 2103611 CrossRef CAS.
- R. Bernhard, M. Metzger and H. A. Gasteiger, Gas Evolution at Graphite Anodes Depending on Electrolyte Water Content and SEI Quality Studied by On-Line Electrochemical Mass Spectrometry, J. Electrochem. Soc., 2015, 162(10), A1984 CrossRef CAS.
- B. Zhang, M. Metzger, S. Solchenbach, M. Payne, S. Meini, H. A. Gasteiger, A. Garsuch and B. L. Lucht, Role of 1,3-Propane Sultone and Vinylene Carbonate in Solid Electrolyte Interface Formation and Gas Generation, J. Phys. Chem. C, 2015, 119(21), 11337–11348 CrossRef CAS.
- B. Strehle, S. Solchenbach, M. Metzger, K. U. Schwenke and H. A. Gasteiger, The Effect of CO2 on Alkyl Carbonate Trans-Esterification during Formation of Graphite Electrodes in Li-Ion Batteries, J. Electrochem. Soc., 2017, 164(12), A2513 CrossRef CAS.
- B. Markovsky, A. Rodkin, G. Salitra, Y. Talyosef, D. Aurbach and H.-J. Kim, The Impact of Co2+ Ions in Solutions on the Performance of LiCoO2, Li, and Lithiated Graphite Electrodes, J. Electrochem. Soc., 2004, 151(7), A1068–A1076 CrossRef CAS.
- L. Hanf, K. Brüning, M. Winter and S. Nowak, Method Development for the Investigation of Mn2+/3+, Cu2+, Co2+, and Ni2+ with Capillary Electrophoresis Hyphenated to Inductively Coupled Plasma–Mass Spectrometry, Electrophoresis, 2023, 44(1–2), 89–95 CrossRef CAS PubMed.
- Y. Terada, Y. Nishiwaki, I. Nakai and F. Nishikawa, Study of Mn Dissolution from LiMn2O4 Spinel Electrodes Using in Situ Total Reflection X-Ray Fluorescence Analysis and Fluorescence XAFS Technique, J. Power Sources, 2001, 97–98, 420–422 CrossRef CAS.
- J. Wandt, A. Freiberg, R. Thomas, Y. Gorlin, A. Siebel, R. Jung, H. A. Gasteiger and M. Tromp, Transition Metal Dissolution and Deposition in Li-Ion Batteries Investigated by Operando X-Ray Absorption Spectroscopy, J. Mater. Chem. A, 2016, 4(47), 18300–18305 RSC.
- L. Hanf, J. Henschel, M. Diehl, M. Winter and S. Nowak, Mn2+ or Mn3+? Investigating Transition Metal Dissolution of Manganese Species in Lithium Ion Battery Electrolytes by Capillary Electrophoresis, Electrophoresis, 2020, 41(9), 697–704 CrossRef CAS PubMed.
- G. H. Reed and G. D. Markham, EPR of Mn(II) Complexes with Enzymes and Other Proteins, Biological Magnetic Resonance, Springer, US, 1984, pp. 73–142 Search PubMed.
- M. Blume and R. Orbach, Spin-Lattice Relaxation of S-State Ions: Mn2+ in a Cubic Environment, Phys. Rev., 1962, 127(5), 1587–1592 CrossRef CAS.
- C. Szczuka, P. Jakes, R.-A. Eichel and J. Granwehr, Identification of LiPF6 Decomposition Products in Li-Ion Batteries with Endogenous Vanadyl Sensors Using Pulse Electron Paramagnetic Resonance and Density Functional Theory, Adv. Energy Sustainability Res., 2021, 2(12), 2100121 CrossRef CAS.
- C. Szczuka, R.-A. Eichel and J. Granwehr, Exploring the Solvation Sphere and Spatial Accumulation of Dissolved Transition-Metal Ions in Batteries: A Case Study of Vanadyl Ions Released from V2O5 Cathodes, ACS Appl. Energy Mater., 2022, 5(1), 449–460 CrossRef CAS.
- Z. Ruff, C. Xu and C. P. Grey, Transition Metal Dissolution and Degradation in NMC811-Graphite Electrochemical Cells, J. Electrochem. Soc., 2021, 168(6), 060518 CrossRef CAS.
- W. M. Dose, I. Temprano, J. P. Allen, E. Björklund, C. A. O’Keefe, W. Li, B. L. Mehdi, R. S. Weatherup, M. F. L. De Volder and C. P. Grey, Electrolyte Reactivity at the Charged Ni-Rich Cathode Interface and Degradation in Li-Ion Batteries, ACS Appl. Mater. Interfaces, 2022, 14(11), 13206–13222 CrossRef CAS PubMed.
- T. Aoshima, K. Okahara, C. Kiyohara and K. Shizuka, Mechanisms of Manganese Spinels Dissolution and Capacity Fade at High Temperature, J. Power Sources, 2001, 97–98, 377–380 CrossRef CAS.
- Y. Shilina, B. Ziv, A. Meir, A. Banerjee, S. Ruthstein, S. Luski, D. Aurbach and I. C. Halalay, Combined Electron Paramagnetic Resonance and Atomic Absorption Spectroscopy/Inductively Coupled Plasma Analysis As Diagnostics for Soluble Manganese Species from Mn-Based Positive Electrode Materials in Li-Ion Cells, Anal. Chem., 2016, 88(8), 4440–4447 CrossRef CAS PubMed.
- C.-C. Su, M. He, R. Amine, Z. Chen, Z. Yu, T. Rojas, L. Cheng, A. T. Ngo and K. Amine, Unveiling Decaying Mechanism through Quantitative Structure-Activity Relationship in Electrolytes for Lithium-Ion Batteries, Nano Energy, 2021, 83, 105843 CrossRef CAS.
- S. Stoll and A. Schweiger, EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR, J. Magn. Reson., 2006, 178(1), 42–55 CrossRef CAS PubMed.
- S. Stoll and R. D. Britt, General and Efficient Simulation of Pulse EPR Spectra, Phys. Chem. Chem. Phys., 2009, 11(31), 6614–6625 RSC.
- C. Fan, P. E. Doan, C. E. Davoust and B. M. Hoffman, Quantitative Studies of Davies Pulsed ENDOR, J. Magn. Reson. (1969), 1992, 98(1), 62–72 CrossRef CAS.
- P. E. Doan, N. S. Lees, M. Shanmugam and B. M. Hoffman, Simulating Suppression Effects in Pulsed ENDOR, and the “hole in the Middle” of Mims and Davies ENDOR Spectra, Appl. Magn. Reson., 2010, 37(1), 763–779 CrossRef PubMed.
- H. Y. Carr and E. M. Purcell, Effects of Diffusion on Free Precession in Nuclear Magnetic Resonance Experiments, Phys. Rev., 1954, 94(3), 630–638 CrossRef CAS.
- S. Meiboom and D. Gill, Modified Spin-Echo Method for Measuring Nuclear Relaxation Times, Rev. Sci. Instrum., 1958, 29(8), 688–691 CrossRef CAS.
- F. Neese, Software Update: The ORCA Program System—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1606 Search PubMed.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes, J. Chem. Phys., 2003, 119(23), 12129–12137 CrossRef CAS.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91(14), 146401 CrossRef PubMed.
- E. Van Lenthe, E. J. Baerends and J. G. Snijders, Relativistic Regular Two-Component Hamiltonians, J. Chem. Phys., 1993, 99(6), 4597–4610 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms, J. Chem. Theory Comput., 2008, 4(6), 908–919 CrossRef CAS PubMed.
- F. Weigend, Accurate Coulomb-Fitting Basis Sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, Approximate and Parallel Hartree-Fock and Hybrid DFT Calculations. A “chain-of-Spheres” Algorithm for the Hartree-Fock Exchange, Chem. Phys., 2009, 356(1–3), 98–109 CrossRef CAS.
- F. Neese, Prediction and Interpretation of the 57Fe Isomer Shift in Mössbauer Spectra by Density Functional Theory, Inorg. Chim. Acta, 2002, 337, 181–192 CrossRef.
- F. Neese, Efficient and Accurate Approximations to the Molecular Spin-Orbit Coupling Operator and Their Use in Molecular g-Tensor Calculations, J. Chem. Phys., 2005, 122(3), 034107 CrossRef PubMed.
- I. Bertini, C. Luchinat, G. Parigi and E. Ravera, NMR of Paramagnetic Molecules: Applications to Metallobiomolecules and Models, Elsevier, 2016 Search PubMed.
- A. J. Pell, G. Pintacuda and C. P. Grey, Paramagnetic NMR in Solution and the Solid State, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271 CrossRef CAS PubMed.
- I. Solomon, Relaxation Processes in a System of Two Spins, Phys. Rev., 1955, 99(2), 559–565 CrossRef CAS.
- N. Bloembergen, Proton Relaxation Times in Paramagnetic Solutions, J. Chem. Phys., 1957, 27(2), 572–573 CrossRef CAS.
- N. Bloembergen and L. O. Morgan, Proton Relaxation Times in Paramagnetic Solutions. Effects of Electron Spin Relaxation, J. Chem. Phys., 1961, 34(3), 842–850 CrossRef CAS.
- Z. Luz, Ion Solvation in Solution, Studied by Nuclear Magnetic Resonance Spectroscopy, Isr. J. Chem., 1971, 9(3), 293–300 CrossRef CAS.
- T. J. Swift and R. E. Connick, NMR-Relaxation Mechanisms of O17 in Aqueous Solutions of Paramagnetic Cations and the Lifetime of Water Molecules in the First Coordination Sphere, J. Chem. Phys., 1962, 37(2), 307–320 CrossRef CAS.
- M. R. Jensen and J. J. Led, Determination of the Electron Relaxation Rates in Paramagnetic Metal Complexes: Applicability of Available NMR Methods, J. Magn. Reson., 2004, 167(2), 169–177 CrossRef CAS PubMed.
- EPR Spectroscopy: Fundamentals and Methods, ed. D. Goldfarb and S. Stoll, John Wiley & Sons, Chichester, UK, 2018 Search PubMed.
- P. Caravan, C. T. Farrar, L. Frullano and R. Uppal, Influence of Molecular Parameters and Increasing Magnetic Field Strength on Relaxivity of Gadolinium- and Manganese-Based T1 Contrast Agents, Contrast Media Mol. Imaging, 2009, 4(2), 89–100 CrossRef CAS PubMed.
- T. A. Stich, S. Lahiri, G. Yeagle, M. Dicus, M. Brynda, A. Gunn, C. Aznar, V. J. DeRose and R. D. Britt, Multifrequency Pulsed EPR Studies of Biologically Relevant Manganese(II) Complexes, Appl. Magn. Reson., 2007, 31(1–2), 321–341 CrossRef CAS PubMed.
- I. A. Shkrob, A. J. Kropf, T. W. Marin, Y. Li, O. G. Poluektov, J. Niklas and D. P. Abraham, Manganese in Graphite Anode and Capacity Fade in Li Ion Batteries, J. Phys. Chem. C, 2014, 118(42), 24335–24348 CrossRef CAS.
- F. Neese, Metal and Ligand Hyperfine Couplings in Transition Metal Complexes: The Effect of Spin–Orbit Coupling as Studied by Coupled Perturbed Kohn–Sham Theory, J. Chem. Phys., 2003, 118(9), 3939–3948 CrossRef CAS.
- C. Duboc, Determination and Prediction of the Magnetic Anisotropy of Mn Ions, Chem. Soc. Rev., 2016, 45(21), 5834–5847 RSC.
- H. Konieczna, D. Lundberg and I. Persson, Solvation and Coordination Chemistry of Manganese(II) in Some Solvents. A Transfer Thermodynamic, Complex Formation, EXAFS Spectroscopic and Crystallographic Study, Polyhedron, 2021, 195, 114961 CrossRef CAS.
- B. T. Allen, Zero-Field Splitting Parameter of the Mn++ Ion in Glassy and in Polycrystalline Media, J. Chem. Phys., 1965, 43(11), 3820–3826 CrossRef CAS.
- C. Duboc, M.-N. Collomb and F. Neese, Understanding the Zero-Field Splitting of Mononuclear Manganese(II) Complexes from Combined EPR Spectroscopy and Quantum Chemistry, Appl. Magn. Reson., 2010, 37(1), 229–245 CrossRef.
- S. S. Eaton and G. R. Eaton, Relaxation Mechanisms, eMagRes, 2016, 5(4), 1543–1556 CAS.
- P. M. Richardson, A. M. Voice and I. M. Ward, NMR T1 Relaxation Time Measurements and Calculations with Translational and Rotational Components for Liquid Electrolytes Containing LiBF4 and Propylene Carbonate, J. Chem. Phys., 2013, 139(21), 214501 CrossRef CAS PubMed.
- C. P. Slichter, in Principles of Magnetic Resonance, ed. M. Cardona, P. Fulde, K. Von Klitzing, H.-J. Queisser and H. K. V. Lotsch, Springer Series in Solid-State Sciences, Springer-Verlag, Berlin, Heidelberg, 3rd Enlarged and Updated edn, 1990, vol. 1 Search PubMed.
- C. Wohlfarth, Permittivity (Dielectric Constant) of Liquids, in CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, Boca Raton, 2016, pp. 6-199–6-220 Search PubMed.
- C. Reichardt and T. Welton, Solvents and Solvent Effects in Organic Chemistry, 4th edn, 2010 Search PubMed.
- CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, Boca Raton, 97th edn, 2016 Search PubMed.
- E. R. Logan, E. M. Tonita, K. L. Gering, J. Li, X. Ma, L. Y. Beaulieu and J. R. Dahn, A Study of the Physical Properties of Li-Ion Battery Electrolytes Containing Esters, J. Electrochem. Soc., 2018, 165(2), A21 CrossRef CAS.
- M. H. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, John Wiley & Sons, 2001 Search PubMed.
- H. Irving and R. J. P. Williams, The Stability of Transition-Metal Complexes, J. Chem. Soc., 1953, 3192–3210 RSC.
- S. F. A. Kettle, Coordination Compounds, Thomas Nelson and Sons, London, 1969 Search PubMed.
- J. E. Huheey, E. A. Keiter and R. L. Keiter, Inorganic Chemistry: Principles of Structure and Reactivity, HarperCollins College Publishers, New York, 4th edn, 1993 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01663g |
| This journal is © the Owner Societies 2024 |



