Dependence of lactose adsorption on the exposed crystal facets of metals: a comparative study of gold, silver and copper

Abstract

In this theoretical work, we investigated the adsorption of a lactose molecule on metal-based surfaces, with a focus on the influence of the nature of the metal and of the type of exposed crystal facet on the adsorbed structures and energetics. More precisely, we considered three flat crystallographic facets of three face-centered cubic metals (gold, silver, and copper). For the global exploration of the energy landscape, we employed a multi-stage procedure where high-throughput searches, using a stochastic method that performs global optimization by iterating local searches, are followed by a refinement of the most probable adsorption conformations of the molecule at the ab initio level. We predicted the optimal conformation of lactose on each of the nine metal-surface combinations, classified the many low-energy minima into possible adsorption modes, and analyzed the structural, electronic and energetic aspects of the lactose molecule on the surface, as well as their dependence on the type of metal and exposed crystal facet. We observed structural similarities between the various minimum-energy conformations of lactose in vacuum and on the surface, a rough correlation between adsorption and interaction energies of the molecule, and a small charge transfer between molecule and surface whose direction is metal-dependent. During adsorption, an electronic reorganization occurs at the metal–molecule interface only, without affecting the vacuum-pointing atoms of the lactose molecule. For all types of surfaces, lactose exhibits the weakest adsorption on silver substrates, while for each coinage metal the adsorption is strongest on the (110) crystal facet. This study demonstrates that the control of exposed facets can allow to modulate the interaction between metals and small saccharides.

---

1 Introduction

In recent years, numerous investigations have explored the biotic/abiotic interface from a fundamental point of view.^1–4 The influence of the exposed facets of metal-based materials on molecular adsorption and reactivity is an active field of research, particularly in the context of environmental chemistry,^5–9 biology^10–12 and catalysis.^13–15 Nevertheless, very little is known about the influence of the exposed facets of metal-based materials on the adsorption of molecules contained in dairy products.

Taking the example of milk, whose worldwide production in liquid or powder form amounts to more than 600 million tons per year (50% of the population consumes milk or milk-based products on a daily basis),¹⁶ only few studies have been devoted to the evaluation of its interaction with contact surfaces during transport, processing, packaging or use.^17–19 For most species, milk mainly contains water, proteins, fats and lactose.²⁰ The interaction between metal-based surfaces and peptides/proteins has been the subject of a number of studies.^21,22 As far as fats are concerned, there are studies of the interaction between steel and fatty acids used as lubricants,²³ or investigations involving metal nanoparticles.²⁴ Concerning lactose, this carbohydrate has been at the heart of many scientific studies for the past sixty years, due to the phenomenon of lactose maldigestion discovered in the 1960s, usually referred to as lactose intolerance,^25,26 and to its frequent use as filler or soluble diluent in pharmaceutical formulations.²⁷ However, no studies describing the interaction between a lactose molecule and a metal-based surface have been reported. The only studies dealing with the lactose–metal interaction explore its interaction with the metal cations contained in milk such as Zn^2+ 28 or the relations between its chemical properties and its efficiency as iron corrosion inhibitor.²⁹

To contribute to filling this gap, we have performed computer simulations to investigate the interaction between lactose and metal surfaces with a focus on the influence of the type of exposed crystal facet. The model systems we consider consist of a lactose molecule adsorbed in vacuum on the three most stable crystallographic facets ((111), (100), (110)) of three face-centered cubic (fcc) metals: gold (Au), silver (Ag) and copper (Cu). These metals have been chosen to establish the theoretical proof that the type of metal and facet exposed can play an important role in the adsorption of a diary molecule such as a sugar, intuitively thought to adsorb only very weakly on a surface. The three chosen metals are not frequently used in the production processes of everyday products but they allow us to investigate the effect of variation in electronic structure only and the joint effect of variation in electronic and atomic structure. Indeed, gold and silver have different electronic structure but the same bulk lattice constant (a^exp_gold = 4.0796 Å and a^exp_silver = 4.0855 Å),³⁰ while copper in addition differs from the other two in its atomic structure as its lattice constant is smaller by about 11% (a^exp_copper = 3.62 Å).³¹

To investigate the interaction between the lactose molecule and the metal surfaces without introducing any pre-conceptions or biases, it is necessary to globally explore the energy landscape of the lactose molecule on the nine different metal surfaces in order to identify stable conformations of the system.³² These predicted structures can then be classified into typical adsorption modes, followed by their detailed analysis. Ideally, this should be done on an ab initio level of theory throughout, i.e., by taking into account the electronic structure of the system at all stages of the investigation. However, the prohibitive cost of these ab initio calculations in terms of computational resources prevents an exhaustive exploration of the potential energy surface. Indeed, global energy landscape explorations can be carried out at the ab initio level only for small surface adsorbates such as single atoms or molecules containing a few atoms.^33,34 To circumvent this problem, one strategy consists in setting up a multi-stage procedure in which the global exploration stage is carried out at a lower level of theory allowing high-throughput searches, followed by a refinement of the most probable adsorption conformations of the lactose molecule at the ab initio level. With that in mind, we used a multi-stage approach that we had recently developed to study the adsorption and self-organization of two other disaccharides, sucrose³⁵ and trehalose,³⁶ on a copper surface.

The simulated models and the methodology used are presented in Section 2. Next, the most relevant lactose adsorption modes on the different metal surfaces identified by our multi-stage computational approach are described and discussed in Section 3, both from an energetic and a structural point of view. The dependence of the adsorption on the metal and on the exposed metal facet is analyzed, and the charge reorganization at the molecule–surface interface is discussed. A final section presents the conclusions and perspectives of this work.

2 Methodology and computational details

2.1 Systems

2.1.1 The metal surfaces. The model metal surfaces considered in this work consist of low energy (111), (100) and (110) surfaces of three face-centered cubic metals: gold (Au), silver (Ag) and copper (Cu). The (111) surface is very compact and flat and has a six-fold symmetry. The (100) surface, also flat, is less dense and has a four-fold symmetry. Finally, the (110) surface, which is the least compact one, differs greatly from the two others in that it is crenellated and has a two-fold symmetry.

2.1.2 The lactose molecule. Lactose (β-O-D-galactopyranosyl-(1–4)-D-glucopyranose³⁷) is a neutral molecule containing 12 carbon, 11 oxygen and 22 hydrogen atoms arranged in two six-membered rings, a D-galactose and a D-glucose, linked by a β-1,4 glycosidic linkage³⁸ (see Fig. 1). Whereas the galactose unit can only have the β-pyranose form, the glucose unit can adopt two isomeric forms, either α-pyranose or β-pyranose; thus, one speaks of α-lactose and β-lactose, respectively. The difference between the two lies in the configuration of the hydroxyl group of the anomeric hemiacetal carbon of the glucose ring. In α-lactose, this hydroxyl group is in axial position, while in β-lactose it is in equatorial position (see Fig. 1). In aqueous solution, the two forms interchange until they reach an equilibrium, with the transition from one form to the other involving a mutarotation reaction.³⁹ At room temperature, the ratio between the two forms is about 40 : 60 for α- and β-lactose, respectively.⁴⁰ In this work, we have arbitrarily chosen to deposit a lactose molecule in its anomeric α form on the metal surfaces.

Fig. 1 The lactose molecule, formed by a galactose and a glucose linked by a β-1,4 glycosidic linkage. The two pairs of dihedral angles used to characterize this linkage are depicted in red (ϕ, ψ) and pink (ϕ_H, ψ_H). The galactose unit can only have the β-pyranose form and the glucose unit can adopt two isomeric forms, either α-pyranose, in which the hydroxyl group of the anomeric hemiacetal carbon of the glucose ring is in axial position, or β-pyranose, in which it is in equatorial position. These two forms lead to α-lactose and β-lactose, respectively.

The flexibility of the two six-membered ring units allows for two low-energy forms for each unit commonly referred to as the “chair” and the “boat” conformation, respectively. The choice of the initial lactose structure for our global exploration was based on a comparison at the DFT level of the four different possible combinations of these two conformations of galactose (Gal) and glucose (Glc), i.e., a comparison of the Gal-chair/Glc-chair, Gal-chair/Glc-boat, Gal-boat/Glc-chair and Gal-boat/Glc-boat structures. The most stable structure was found to be Gal-chair/Glc-chair, in agreement with the literature.⁴¹ Moreover, we note that the glucose ring can exist in two chair conformations.⁴¹ The interconversion between these two conformers is a very fast reversible process that is extremely difficult to detect;⁴¹ thus, we arbitrarily chose one of the two conformers. To have an estimate of the stability of this lactose conformation once deposited on a metal surface, we performed an ab initio molecular dynamics simulation of 1 ps at 500 K in which the lactose molecule was initially deposited on a Cu(111) surface in this Gal-chair/Glc-chair conformation. We did not observe any significant conformational change. Furthermore, we note that the conformational transformations of the lactose molecule in the gas phase have been studied on the empirical potential level, and it was found that the chair–chair conformation is the global minimum and is the most stable conformation up to quite high energies.⁴²

2.1.3 Structural descriptors. The commonly used descriptors of the conformation of lactose are the values of two torsion angles characterizing the glycosidic linkage, for which two alternative choices are found in the literature,^43–45 denoted as (ϕ, ψ) and (ϕ_H, ψ_H) (see Fig. 1). The usual convention to define these four dihedral angles is:

• ϕ: Gal-O – Gal-C1 – O – Glc-C4′

• ψ: Gal-C1 – O – Glc-C4′ – Glc-C5′

• ϕ_H: Gal-H1 – Gal-C1 – O – Glc-C4′

• ψ_H: Gal-C1 – O – Glc-C4′ – Glc-H4′

Based on the results of our calculations, we found that low-energy conformations of lactose on metal surfaces can be classified into a number of distinct adsorption modes, which can be described using a three-component notation A–B–C. The first and the last terms concern the orientation of the galactose (A) and glucose (C) units. If the OH group linked to carbon C4 (resp. C1′) point toward the surface, the orientation unit will be denoted “D” (for down). If it points toward the vacuum side, it will be denoted “U” (for up). The middle term (B) concerns the oxygen atom of the glycosidic linkage. If it points toward the surface, the structure will be denoted “V”. If it points to the vacuum side, it will be denoted “Λ”. We note that for the case of Gal-chair/Glc-chair conformations, this description encompasses all stable low-energy adsorption modes identified on the energy landscape.

2.2 Computational methods

2.2.1 Global exploration. We applied the IGLOO (iterative global exploration and local optimization) algorithm⁴⁶ to globally explore the energy landscape of systems composed of a lactose molecule deposited on a metal surface, aiming at finding a representative set of low-energy conformations. IGLOO is a stochastic method that performs global optimization by iterating local searches. More precisely, IGLOO iterates three stages: (1) the global exploration is performed via multiple rapidly-exploring random trees^47,48 that tend to cover low-energy regions of the conformational space, (2) nodes of the trees contained in mutually exclusive volumes are selected and the corresponding conformations are subject to local minimization, (3) clustering is applied to the resulting local minima, aiming to identify a set of low-energy basins. The lowest-energy conformation in each cluster is selected as a root for the next iteration of the algorithm, which repeats these three stages until convergence. We have successfully applied IGLOO in previous work,^35,36 and an improved version of IGLOO has been recently presented by Margerit et al.,⁴⁶ showing good performance compared to other global exploration methods.

For the energy evaluation during the global exploration, we applied an in-house implementation of an AMBER-like force field⁴⁹ using parameters generated with the GLYCAM molecular modelling library (GMML)⁵⁰ for the lactose molecule. The accuracy of the parameters and coefficients of this simple molecular-mechanics-based force-field was evaluated and tuned using DFT calculations. The interaction between the molecule and the metal surface, again tuned via comparison with DFT calculations, consisted of Lennard-Jones type interactions plus electrostatic terms modelled via mirror charges. The degrees of freedom of the molecule during the global exploration phase were reduced: only the six parameters defining the pose (position and orientation) of the molecule with respect to the surface and the dihedral angles of the lactose molecule were considered as free variables as far as the global optimization was concerned. Since ab initio molecular dynamics performed at 500 K showed no change in the rings' conformation, these rings were considered as rigid bodies at this stage. Low-energy conformations resulting from this exploration were selected for further refinement at the DFT level.

2.2.2 Local refinement. DFT minimization was performed employing the Vienna ab initio simulation package (VASP^51–53) with PAW pseudopotentials,^54,55 using periodic boundary conditions. A given periodic cell is periodic both in the parallel (x and y axes) and perpendicular (z axis) directions to the surface. To avoid interactions between the molecule and the periodic images, two molecules of two adjacent periodic boxes were separated by at least 12 Å along the x and y axes, and a vacuum region was introduced along the z-axis. The thin film used to simulate the metal surfaces contained 4 metal layers, the lowest one being kept fixed and all other atoms (3 metal layers + the lactose molecule) being allowed to relax unconstrained. A conjugate-gradient algorithm was used to relax the atomic positions. Since the size of the supercell was large enough, the Brillouin zone sampling in reciprocal space restricted to the Γ point was sufficient to ensure good convergence of the total energy. A plane-wave kinetic energy cutoff of 500 eV was employed and the convergence criterion was set up so that the maximum atomic force was less than 0.01 eV Å⁻¹. For dealing with the partial occupancies around the Fermi level, a Methfessel–Paxton smearing was used with σ = 0.01 eV.⁵⁶ The DFT functional used, optB86b-vdw, belongs to the dispersion-corrected vdw-DF family, developed by Dion et al.⁵⁷ In this family, the van-der-Waals interaction is directly obtained from the electron density by adding a non-local term to the local correlation functional. For evaluating electron transfers, Bader charge analyses were performed on electron densities.^58–60

2.3 Energy definitions

The adsorption energy of the lactose molecule on a given metal surface was calculated as

E_ads = E_tot − E^surf_relax − E^lact_relax (1)

Here, E_tot is the energy of the system containing the metal slab and the lactose molecule in the periodic cell, E^surf_relax the energy of the metal slab relaxed without the lactose molecule, and E^lact_relax the energy of the most stable conformation of the lactose molecule in vacuum.

The deformation energy of the lactose molecule was calculated as

E^lact_def = E^lact_sp − E^lact_relax (2)

where E^lact_sp is the energy of the lactose molecule in its adsorbed geometry computed in vacuum.

The deformation energy of the metal slab was calculated as‡

E^surf_def = E^surf_sp − E^surf_relax (3)

with E^surf_sp being the energy of the metal slab in its grafted geometry.

Finally, the interaction energy between the molecule and the surface was calculated as

E_int = E_ads − E^lact_def − E^surf_def = E_tot − E^lact_sp − E^surf_sp (4)

3 Results and discussion

After an exploration of the accessible conformations in vacuum of the lactose molecule chosen for this study (cf. Section 2), we will present the most likely adsorption conformations on the (111), (100) and (110) crystallographic facets of gold, silver and copper predicted by our exploration method. The structure of the predicted adsorbates and the associated energetics will be discussed, together with the effect of the metal substrate and of the exposed crystal facet on lactose adsorption. Finally, the charge reorganization at the lactose–metal interface will be examined.

3.1 Lactose in vacuum

IGLOO was applied to identify a representative set of low-energy conformations of an α-lactose molecule in the Gal-chair/Glc-chair structure in vacuum. The algorithm was run 10 times with different seeds for the initialization of the random number generators. The results of these runs were consistent at finding various low-energy conformations, and in agreement with the literature.⁴² Clustering of the accumulated results of all the runs of IGLOO provided five clusters of low-energy conformations. The ϕ_H, ψ_H, ϕ, and ψ angles and the relative energies of the representative members of these clusters are presented in Table 1 together with the data relative to the DFT refinement of these structures. The energy range (0.4 eV for IGLOO and 0.5 eV for the DFT calculations), the global minimum (Min^Vac₁) and the energetic hierarchy between the conformers are the same with both energy functions. Only two noticeable differences appear: DFT calculations found an energy gap (0.34–0.37 eV) between the most stable structure (Min^Vac₁) and three almost isoenergetic conformers (Min^Vac₂, Min^Vac₃ and Min^Vac₄) whereas IGLOO found a very small first gap (0.05 eV) and conformers exhibiting more distinct energy levels. The DFT grouping into three energy levels is consistent with the number of hydrogen bonds present in the structures. As can be seen in Fig. 2, Min^Vac₁ contains three intramolecular hydrogen bonds, Min^Vac₂, Min^Vac₃ and Min^Vac₄ contain two, and Min^Vac₅ contains only one. As these intramolecular hydrogen bonds can be considered strong on the basis of the distances between the atoms involved, we can estimate that each of them stabilizes the system at a few hundred meV, which is consistent with the energy differences observed.⁶¹

Table 1 (Top) α-lactose minima in vacuum Min^Vac_X: IGLOO (resp. DFT) total energy E^IGLOO (resp. E^DFT) in eV and dihedral angles ϕ_H, ψ_H, ϕ and ψ in degrees. (Bottom) XRD and DFT structural data from the literature

Name	E ^IGLOO	ϕ ^IGLOOH	ψ ^IGLOOH	ϕ ^IGLOO	ψ ^IGLOO	E ^DFT	ϕ ^DFTH	ψ ^DFTH	ϕ ^DFT	ψ ^DFT
Min^Vac1	0.0	174.1	−3.6	55.4	−122.0	0.0	178.6	−2.1	60.5	−121.8
Min^Vac2	0.05	50.4	−13.5	−68.2	−132.0	0.34	49.6	−12.5	−70.3	−131.6
Min^Vac3	0.18	22.8	−28.8	−95.8	−147.3	0.36	26.9	−32.0	−93.3	−150.3
Min^Vac4	0.28	6.0	178.6	−112.6	60.2	0.37	10.3	179.1	−109.1	61.5
Min^Vac5	0.39	−17.5	−37.3	−136.2	−155.8	0.50	15.8	−48.8	−103.6	−165.6

---

Ref.	Method	α-Lactose	ϕ	ψ
Fries et al.^62	XRD	Monohydrate	−92.6	−143.0
Platteau et al.^63	XRD	Anhydrous	−85.9/−87.3	−160.9/−153.0
Márquez et al.^64	DFT	Anhydrous	−90.4	−157.0

---

Fig. 2 The five low-energy vacuum conformations Min^Vac_1,2,3,4,5 of α-lactose localized by the IGLOO exploration and subsequently minimized using DFT. Carbon atoms are depicted in green, oxygen in red, hydrogen in white and H-bonds using yellow dashed lines.

Concerning the dihedral angles, their values are very similar for both energy functions for conformers Min^Vac₁, Min^Vac₂, Min^Vac₃ and Min^Vac₄, with a maximum difference of 5.1° and an average variation of 2.4°. Isomer Min^Vac₅ undergoes a larger structural variation during the DFT minimisation, resulting in a modification of the four dihedral angles by 21.8° on average. If we compare our results with structural data in the literature, obtained from X-ray diffraction (XRD) measurements of molecular crystals of lactose,^62,63 we find that the experimental ϕ and ψ angles are more similar to those of Min^Vac₃ than to those of the global minimum Min^Vac₁ (see Table 1). This is not very surprising as the presence of neighbours within the crystal may have a great influence on the ranking of the minima, in particular due to the formation of intermolecular hydrogen bonds within the crystal (possibly accompanied by the breaking of intramolecular hydrogen bonds). Note that the DFT study performed by Márquez et al.⁶⁴ gave results in very good agreement with experiments; however, these authors did not perform a global optimization but started directly from the experimental structure and locally minimized it. Therefore, the results presented here are aimed to provide a more general picture of the most probable conformations of lactose in vacuum.

3.2 Lactose on metal surfaces – adsorption modes

The same global optimization procedure was applied to predict the low-energy conformations of the lactose molecule in the Gal-chair/Glc-chair structure on the nine different metal-surface combinations: (111), (100), (110) facets for each of the Au, Ag and Cu substrates. The most stable adsorbates systematically belong to four families of adsorbate orientations: U–Λ–U, D–V–D, D–Λ–U and U–V–D. These structures are shown in Fig. 3 for Au, Ag and Cu. Their corresponding energies and structural parameters are gathered in Table 2. Note that when there were several structures with very similar energies for one of the four types of deposition conformation, we chose the most stable one. In contrast, U–Λ–D and D–V–U structures were found only in rare cases and they were systematically of higher energy than the others. Finally, none of the low-energy local minimum conformations belonged to one of the two remaining feasible adsorption modes, which would be classified as D–Λ–D and U–V–U.

Fig. 3 Lactose molecule adsorbed on M(100), M(110) and M(111) with M = Au, Ag, Cu. Top and side views of the predicted local minima are shown.

Table 2 α-lactose molecule adsorbed on M(100), M(110) and M(111) with M = Au, Ag, Cu: DFT adsorption E_ads and interaction E_int energies in eV, deformation energies of the molecule E^lact_def and of the surface E^surf_def in eV, dihedral angles ϕ_H, ψ_H, ϕ and ψ in degrees, number of hydrogen N^z<3.0_H and oxygen N^z<3.0_O atoms located at less than 3.0 Å from the metal surface, number of hydrogen N^d<3.0_H or oxygen N^d<3.0_O atoms separated by less than 3 Å from a metal atom, minimal M–H d^min_M–H and M–O d^min_M–O distance in Å, charge of the lactose molecule q^lact and surface metal atoms d-band center energy ε_d with respect to the metal slab Fermi level in eV before (clean surface) and after (d-band center of the silver atom closest to an oxygen atom of the lactose molecule) adsorption

Surface	Structure	E ads	E int	E ^lactdef	E ^surfdef	ϕ H	ψ H	ϕ	ψ	N ^z<3.0H/O	N ^d<3.0H/O	d ^minM–H	d ^minM–O	q ^lact	ε d
Au(100)	Clean surf.														−3.28
	U–Λ–U	−1.531	−2.038	0.489	0.019	36.4	−25.73	−83.1	−144.1	11/2	7/1	2.490	2.798	0.03	−3.23
	D–V–D	−1.737	−2.235	0.464	0.034	43.1	−6.3	−76.0	−125.0	8/5	7/4	2.560	2.727	0.02	−3.24
	D–Λ–U	−1.354	−2.012	0.614	0.044	−173.0	2.9	69.7	−117.6	7/3	6/1	2.366	2.730	0.00	−3.31
	U–V–D	−1.276	−1.908	0.517	0.115	178.7	−3.8	61.6	−123.9	8/2	5/2	2.311	2.747	0.05	−3.23
Au(110)	Clean surf.														−3.16
	U–Λ–U	−1.957	−2.521	0.483	0.080	27.3	−28.2	−91.0	−145.1	12/5	9/3	2.321	2.490	0.09	−3.28
	D–V–D	−1.900	−2.624	0.651	0.073	41.5	−18.0	−77.8	−135.9	11/7	6/4	2.173	2.597	0.11	−3.17
	D–Λ–U	−1.554	−2.293	0.682	0.057	−176.0	−3.8	67.1	−124.1	10/5	9/4	2.466	2.764	0.04	−3.23
	U–V–D	−1.958	−2.435	0.377	0.100	−178.8	−3.4	64.6	−123.9	9/4	6/4	2.291	2.522	0.12	−3.19
Au(111)	Clean surf.														−3.35
	U–Λ–U	−1.458	−1.961	0.486	0.017	34.5	−26.9	−85.2	−145.4	8/1	6/1	2.501	2.743	0.02	−3.32
	D–V–D	−1.456	−1.883	0.407	0.020	42.7	−12.5	−76.9	−131.0	7/2	6/0	2.442	3.156	−0.05	−3.36
	D–Λ–U	−1.718	−2.177	0.410	0.049	−176.3	0.7	66.3	−119.5	6/2	4/2	2.536	2.535	0.04	−3.38
	U–V–D	−1.417	−1.873	0.425	0.032	−179.9	−4.5	63.7	−126.4	7/3	7/2	2.433	2.758	0.02	−3.32
Ag(100)	Clean surf.														−3.80
	U–Λ–U	−1.353	−1.783	0.410	0.019	34.7	−43.2	−85.5	−161.6	7/1	6/1	2.399	2.558	−0.11	−3.71
	D–V–D	−1.636	−2.246	0.572	0.038	29.2	−26.1	−90.2	−146.2	8/5	7/4	2.419	2.687	−0.15	−3.75
	D–Λ–U	−1.358	−1.954	0.555	0.041	−175.5	−0.5	68.1	−120.7	6/4	5/2	2.441	2.475	−0.06	−3.77
	U–V–D	−1.390	−1.894	0.469	0.035	−175.9	−6.3	67.7	−125.7	8/4	5/4	2.472	2.596	−0.09	−3.80
Ag(110)	Clean surf.														−3.91
	U–Λ–U	−1.829	−2.381	0.495	0.056	32.4	−42.0	−87.1	−159.7	11/5	8/3	2.300	2.484	−0.08	−3.96
	D–V–D	−1.904	−2.615	0.652	0.059	51.8	−11.2	−67.3	−129.6	10/7	8/5	2.187	2.587	−0.11	−3.86
	D–Λ–U	−1.478	−2.287	0.757	0.052	−175.6	−5.2	66.8	−124.3	9/5	6/3	2.284	2.531	−0.12	−3.89
	U–V–D	−1.290	−2.107	0.762	0.055	−172.9	3.9	71.4	−116.8	10/4	7/4	2.342	2.588	−0.08	−3.97
Ag(111)	Clean surf.														−3.91
	U–Λ–U	−1.313	−1.744	0.402	0.029	27.7	−38.8	−90.8	−156.4	6/2	6/2	2.321	2.822	−0.11	−3.86
	D–V–D	−1.349	−1.834	0.458	0.028	43.1	−12.9	−76.1	−131.6	8/4	7/1	2.543	2.972	−0.18	−3.86
	D–Λ–U	−1.013	−1.926	0.841	0.072	175.3	0.4	57.4	−119.8	6/3	5/2	2.710	2.458	−0.05	−4.00
	U–V–D	−1.274	−1.702	0.401	0.028	−178.2	−0.5	65.2	−121.7	7/3	4/3	2.281	2.683	−0.08	−3.87
Cu(100)	Clean surf.														−2.36
	U–Λ–U	−1.484	−2.219	0.687	0.047	32.5	−28.1	−86.3	−145.5	8/2	8/2	2.173	2.204	−0.09	−2.31
	D–V–D	−1.557	−2.109	0.484	0.068	44.0	−16.6	−75.9	−135.7	8/3	7/3	2.154	2.369	−0.18	−2.30
	D–Λ–U	−1.463	−2.049	0.520	0.066	−175.1	0.4	68.5	−120.6	9/2	7/2	2.182	2.318	−0.13	−2.32
	U–V–D	−1.698	−1.858	0.108	0.052	−178.4	2.7	64.3	−117.0	6/2	5/2	2.144	2.306	−0.09	−2.35
Cu(110)	Clean surf.														−2.55
	U–Λ–U	−2.054	−2.820	0.640	0.126	36.2	−40.0	−83.2	−157.2	11/4	9/3	1.968	2.146	−0.08	−2.59
	D–V–D	−1.902	−2.527	0.553	0.072	50.6	−15.2	−69.4	−134.2	9/5	7/5	2.085	2.178	−0.15	−2.60
	D–Λ–U	−1.871	−2.611	0.670	0.070	−176.3	−6.8	67.4	−126.5	8/3	6/3	2.171	2.114	−0.15	−2.59
	U–V–D	−1.812	−1.981	0.110	0.060	175.3	1.2	57.6	−118.3	9/3	7/2	2.183	2.154	−0.08	−2.66
Cu(111)	Clean surf.														−2.44
	U–Λ–U	−1.447	−1.956	0.468	0.040	43.8	−19.9	−75.5	−138.8	10/1	9/1	2.490	2.234	−0.09	−2.43
	D–V–D	−1.570	2.206	0.581	0.056	26.8	−29.1	−92.3	−146.9	7/4	7/4	2.231	2.315	−0.11	−2.38
	D–Λ–U	−1.508	−2.260	0.685	0.067	178.7	−1.5	62.3	−121.1	9/3	7/2	2.333	2.187	−0.09	−2.47
	U–V–D	−1.373	−1.926	0.508	0.045	−178.6	−2.4	64.7	−123.9	8/3	8/2	2.499	2.234	−0.07	−2.42

---

In this context, an interesting question arises: what would happen if lactose molecules were deposited on the surface directly with one of the five types of low-energy conformations in vacuum, instead of following the global optimization protocol? We find that different adsorption modes can be envisaged depending on the conformer that is adsorbed. For example, isomer Min^Vac₁ could give rise to a D–Λ–U or a U–V–D adsorption, conformers Min^Vac₂, Min^Vac₃ and Min^Vac₅ to U–Λ–U or D–V–D, and isomer Min^Vac₄ could lead to U–Λ–D or D–V–U. These observations compare well with the results of the global optimization; in particular, we will show later that the observed adsorbates of type U–Λ–U or a D–V–D have the angular characteristics of Min^Vac₂ and Min^Vac₃, and not of Min^Vac₅ – the one with the highest energy in vacuum. We note that adsorbates corresponding to the deposition of a Min^Vac₄-type isomer (U–Λ–D and D–V–U) appeared rarely during the global optimizations, and only with unfavorable energies.

The energetic ranking of the different adsorption modes for each metal-surface combination is summarized in Table 3. Interestingly, the D–V–D and U–Λ–U modes, i.e., those which would result from the deposition of conformers Min^Vac₂, Min^Vac₃ or Min^Vac₅, are found to be the most stable ones in 7 out of 9 cases and the U–V–D and the D–Λ–U modes, i.e., those which would appear for the deposition of isomer Min^Vac₁, are most stable in 3 out of 9 cases (U–V–D and U–Λ–U having essentially the same energy in the case of Au(110)). These results lead to the conclusion that there is no unanimously preferred adsorption mode, but one can note that the D–V–D mode is usually either the most stable or competitive, and the U–Λ–U mode corresponds to the most frequent lowest-energy alternative. In contrast, the two other modes (U–V–D and D–Λ–U) exhibit higher energies in the majority of cases, although this should not be considered a systematic outcome, since they correspond to the most stable conformations in a few cases.

Table 3 For each metal-surface pair, we present the adsorption modes of the lactose molecule ranked by increasing energy, together with the associated energy differences (in eV), with the global minimum taken as reference. The four colors correspond to the four adsorption modes, and serve as visual cues

---

Analyzing the shapes of the four classes of adsorbates with the lowest energies, the side views presented in Fig. 3 show that, from an overall morphological point of view, the lactose molecules adsorbed according to the U–Λ–U and D–V–D modes adopt an overall flat shape, whereas those adsorbed according to the D–Λ–U and U–V–D modes are bent, regardless of the type of metal. These two types of morphologies correspond to intervals of torsion angles (see Table 2). Indeed, for the flat molecules, the angles ϕ, ψ, ϕ_H and ψ_H lie between −92.3° and −67.3°, between −161.6° and −125.0°, between 26.8° and 51.8° and between −43.2° and −6.3°, respectively. Such torsion angles would correspond to the deposition of Min^Vac₂ and Min^Vac₃-type conformers, thus excluding Min^Vac₅. As expected, the bent molecules exhibit torsion angles that may be consistent with the deposition of Min^Vac₁-type conformers, with torsion angle values for ϕ,ψ,ϕ_H and ψ_H in the intervals 57.4° to 71.4°, −126.5° to −116.8°, 175.3° to −172.9° and −6.8° to 3.9°, respectively.

Considering the distance between the lactose molecule and the surface, we note that the molecule is generally closer in the case of the (110) surfaces. Indeed, the number of hydrogen and oxygen atoms located at a distance smaller than 3.0 Å from the metal surface (N^z<3.0_H/O) and the number of hydrogen or oxygen atoms separated by less than 3 Å from a metal atom (N^d<3.0_H/O) are systematically larger for this surface (see Table 2). This difference is due to the crenellated nature of this surface, which allows the molecule to get closer. In contrast, there is no noticeable difference between the (100) and (111) surfaces with respect to the proximity of the molecule. If we look in more detail at the interatomic distances between the metal atoms on the surface and the oxygen atoms of the lactose molecule, we can see that the distance is systematically shorter in the case of copper than in the case of gold and silver on the three types of facets. Furthermore, the Cu–O distance is shorter on the (110) surface and similar on the (100) and (111) facets. The differences between the gold–oxygen and silver–oxygen distances are less systematic: the Ag–O bond is shorter than the Au–O bond in the case of the (100) facet, but they are similar on the other two facets. The distance between the hydrogen atoms and the closest metal atoms is also generally shorter for the copper surface than for the gold and silver ones, and for all three metals, the distance is shorter on the (110) facet than on the (111) and (100) facets.

3.3 Lactose on metal surfaces – effect of deposition metal and exposed facet

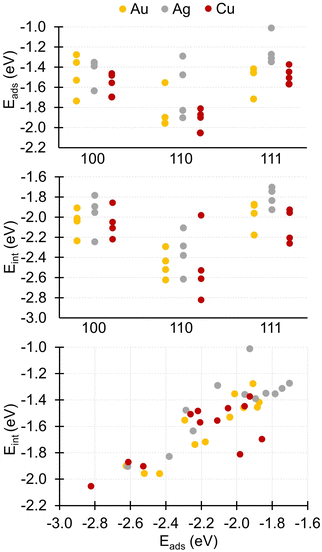
The most stable adsorbates we identified are always slightly less favorable on silver than on gold and copper, as measured by their adsorption energies (see Table 2). Concerning the competition between the two latter metals, copper wins on the (110) surfaces and gold on the other two. For each metal, the adsorption energies vary in the same way as a function of the surface, with |E⁽¹¹⁰⁾_ads| > |E⁽¹⁰⁰⁾_ads| > |E⁽¹¹¹⁾_ads|. It is interesting to note that this variation is inverse to that of the atomic density ρ^surf_atom of the metal facets, with ρ^surf_atom (111) > ρ^surf_atom (100) > ρ^surf_atom (110).

This greater stability of the adsorbate on the (110) surface can also be seen in Fig. 4, where the adsorption and interaction energies for the nine metal-surface combinations are plotted, presenting in each case the lowest energy for each of the four main adsorption modes. Furthermore, we see from the graph at the bottom of Fig. 4, which shows the variation of the interaction energy as a function of adsorption energy, that overall there appears to be a rough correlation between adsorption and interaction energies for the nine metal-surface pairs. However, we note several exceptions, for which the adsorption energy E_ads of the lactose molecule is either much lower (e.g., U–V–D on Cu(100) and on Cu(110); see Table 2) or much higher (e.g., U–V–D on Ag(110) and D–Λ–U on Ag(111); see Table 2) than the value expected from the correlation diagram. From Table 2, we see that for the conformations associated with these two groups of outliers, the deformation energies E^lact_def are either much lower or much higher than the average deformation energy (0.522 eV), respectively. Let us recall that the interaction energy equals the adsorption energy after subtracting the deformation energies of the surface (E^surf_def) and of the molecule (E^lact_def) (see eqn (4)). The surface deformation energy being systematically very low (see Table 2), an outlier value in the lactose deformation energy is directly reflected in a deviation from the adsorption vs. interaction energy correlation plot. If we focus solely on the lowest-energy structure, i.e., the global minimum, for each metal-surface pair, then the ranking of the three types of surface by the adsorption energy and by the interaction energy are the same for Ag and Au substrates, whereas for Cu the order of the two rankings is reversed for Cu(111) and Cu(100).

Fig. 4 Adsorption (top) and interaction (middle) energies of the lactose molecule on the different facets of gold (yellow), silver (grey) and copper (brown) surfaces; the correlation between the two energies is shown at the bottom.

Preferential adsorption on the (110) facet compared to the (111) and (100) ones has already been reported in the literature for DNA bases,⁶⁵ N-containing ligands⁶⁶ or ampicillin antibiotics⁶⁷ deposited on gold surfaces, and for organic contaminants adsorbed on palladium surfaces.⁶⁸ In the case of aromatic molecules, different types of interaction have been reported as a function of the metal surface, with physisorption found only on (111) facets and a partial chemisorption on (110) facets.⁶⁹ The differences between facets are sometimes more nuanced, with similar adsorption energies found for methoxy, methanethiol and methylamine radicals on Au(110) and Au(100) facets.⁴ Beyond the adsorption of molecules on pure metals, facet-dependent properties have also been reported concerning molecular adsorption or assembly on oxides^{5–7,9,10,14} and catalytic properties of metal and oxide surfaces.^{8,13,15,70–74}

Considering now the effect of the metal type on the adsorption of a given molecule, we note that while in the case of lactose we observed that the adsorbates are slightly more stable on gold and copper than on silver, this order changes for aromatic molecules, for which a more favorable binding was reported in the case of Au(111), followed by Ag(111) and then Cu(111).^69,75 Interestingly, in the case of the adsorption of atomic oxygen on cuboctahedral nanoparticles in the diameter range of 0.7–3.5 nm, the opposite is observed: the most favorable adsorption occurs on copper, a median on silver and the least favorable on gold,⁷⁶ in agreement with the well-known oxidation resistance of Au.

To explain the differences in adsorption strength of molecules on various metallic surfaces, two related arguments are frequently mentioned in the literature. The first concerns the under-coordination of the metal adsorption sites, whether in the case of extended surfaces⁷⁷ or nanoparticles.⁷⁸ The more the site is undercoordinated, the stronger the adsorption. This hypothesis is compatible with our data for lactose, where the (110) facet exhibits the most undercoordinated metal atoms among the three facets investigated. The second argument concerns the position of the d-band center of the metal with respect to the frontier orbitals (HOMO and LUMO) of the molecule, often described as a relevant factor for determining adsorption site preference.⁷⁹ In this theory, often referred to as the d-band center model, the higher the metal d-band center, the stronger the molecule-metal bonding. This assumption is based on a decrease in the filling of the antibonding states when the d-band center is higher in energy. As a corollary, the lower the d-band center, the weaker the bonding. However, in the case of lactose, the variation of the energy level of the d-band center of the metal surface atoms is not correlated with that of the adsorption energies for silver and copper (see Table 2 and Fig. 4). This lack of agreement is probably linked to the fact that the d-band model has been developed to predict the strength of a bond formed between a transition metal surface and a small molecule. Thus, the model reaches its limits of plausibility when the size of the molecule is such that the contribution of dispersive forces to the interaction, and thus to the adsorption energy, becomes non-negligible.

3.4 Lactose on metal surfaces – charge reorganization at the interface

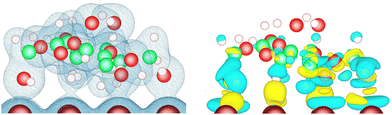
The electronic density at the lactose–metal interface is shown on the left part of (Fig. 5) for the case of the lactose molecule adsorbed on Cu(110) via the U–Λ–U mode. These isosurfaces highlight the presence of electron density between several oxygen and hydrogen atoms of the lactose molecule and the copper surface. The electronic density re-organization that occurs when depositing the molecule on the metal surface is shown as isosurfaces on the right part of this figure. This density re-organization is obtained by subtracting the electronic density of the surface and the molecule in vacuum from the one of the whole system. (Fig. 5) demonstrates that only the electronic structure of the molecule moiety facing the surface is impacted by the adsorption, with the majority of the electronic reorganisation taking place at the interface. The electronic reorganisation observed at the interface is reflected in the computed adsorption energies, which are characteristic of strong adsorption, where the highest adsorption energies found on the nine metal-surface combinations ranged from −1.349 to −2.054 eV.

Fig. 5 Isosurfaces of the electronic density (isovalue 0.03 e Å⁻³) (left), and of the electronic density difference (isovalues +0.0018 e Å⁻³ in yellow and −0.0018 e Å⁻³ in cyan) (right), for the U–Λ–U orientation of the lactose molecule adsorbed on Cu(110).

To confirm that the nature of lactose adsorption on the three studied metals is chemisorption, the atom-projected density of states were computed for the U–Λ–U orientation of the lactose molecule on the (110) surfaces. For each of them, the d-projected density of states of the metal atom and the p-projected density of states of the oxygen atom are depicted in Fig. 6 for the pair of atoms with the smallest interatomic distance (d^min_M–O). For the three metals, a hybridization between the metal d orbital and oxygen p orbital is observed, confirming chemisorption. To evaluate the influence of adsorption on the position, relative to the Fermi level, of the d-band center of the metal atom implied in d^min_M–O, its d-band center was calculated for the 36 metal-surface-adsorption structure combinations for comparison with the one of the corresponding clean metal surface (see Table 2). We can observe that the effect of lactose adsorption on the center of the metal d-band is very weak whatever the metal-surface combination, with a shift between −0.12 and +0.09 eV.

Fig. 6 p-Projected density of states for oxygen atom (red line) and d-projected density of states for gold (yellow), silver (grey) and copper (brown) surface atoms for the pair of atoms with the smallest interatomic distance (d^min_M–O, cf.Table 3) in the case of the U–Λ–U orientation of the lactose molecule adsorbed on (110) surfaces. The dotted line at E = 0 eV indicates the Fermi level.

The charge transferred between the metal and the molecule is very small, with a maximum value of 0.12e for gold and 0.18e for silver and copper (Table 2). In the case of silver and copper, the electron transfer occurs from the metal to the molecule. In the case of gold, it occurs in the opposite direction, i.e., from the molecule to the surface, except for one of the structures. Such a dependence of transfer direction on the metal constituting the surface has already been reported in the case of tetraphenylporphyrin adsorbed on Au(111), Ag(111) and Cu(111).⁷⁵ For a given metal, subtleties in the direction and magnitude of charge transfer have been described in the case of DNA bases on gold nanoparticles, for which the transfer was found to depend on the kind of exposed metal facet.⁶⁵

In summary, most of the electronic reorganization takes place at the lactose–metal interface during adsorption – the nature of which is chemisorption -, and the charge transfer direction depends on the metal. The atoms of the lactose molecule pointing towards the vacuum side are not affected by the adsorption.

4 Conclusions and perspectives

In this study, we have performed global explorations of the energy landscape of a lactose molecule, in the Gal-chair/Glc-chair structure, in vacuum or placed on the (111), (110) and (100) facets of fcc Au, Ag, and Cu substrates. Using the IGLOO algorithm, we predicted not only the global minimum but several other low-energy conformations of the lactose molecule both in vacuum and adsorbed on each of the nine metal-surface combinations. The predicted low-energy adsorbed structures cluster into four main groups, which can be related to the most likely conformations of lactose in vacuum. The most stable representatives of these four groups were found below a threshold energy located between 0.196 and 0.614 eV above the most stable minimum for each metal-surface pair. No unanimously preferred adsorption mode was found on the surfaces. However, even though this observation is not systematically true, some of those, in which the molecule adsorbs in a flat mode on the surface, seem to be favoured over those in which the molecule is bent. As expected, the distance between the molecule and the surface is shortest for the crenellated facet (110), while the (111) and (100) surfaces appear to have similar molecule–surface distances. This distance was found to be shorter for copper than for silver and gold.

The adsorption was found to be strongest on the (110) surface of the three studied coinage metals (with adsorption energies of −1.958 eV for gold, −1.904 eV for silver and −2.054 eV for copper, respectively). This is followed by the (100) one (−1.737 eV for gold, −1.636 eV for silver and −1.698 eV for copper, respectively), with the most unfavourable being the (111) in all cases (−1.718 eV for gold, −1.349 eV for silver and −1.570 eV for copper, respectively). Ag surfaces were systematically found to be the least favorable ones, despite the similarity in atomic structure between gold and silver. This finding highlights the importance of metal electronic structure in the adsorption of small saccharides on metal surfaces. Moreover, the non-applicability of the classic d-band center model in the case of lactose suggests a non-negligible contribution of the van der Waals forces to the lactose–metal surface interactions. The readjustment in the electron density of the lactose molecule when placed on the surface was investigated. The reorganization was found to be concentrated on the atoms that are in closest contact with the surface atoms, adsorption having been found to be chemical in nature. The electron density located at the outer atoms far away from the surface (facing the vacuum) essentially experienced no change during adsorption. The charge transfer occurring at the metal–molecule interface is small (with a maximal transfer of 0.18 electron) and metal-dependent.

This study demonstrates that optimal conformations of the lactose molecule on the surface can still be related to optimal conformations in vacuum. This validates many modeling approaches that rely on the simple deposition of the optimal vacuum conformations onto the surface followed by a simple local optimization. However, this work highlights that taking into account only the global minimum of the conformations of the molecule in vacuum in such a placement-based approach would have been insufficient for determining the global minimum conformation of the molecule on the surface. Furthermore, it is crucial for such a type of study to employ many different starting conformations corresponding to low energy minima in vacuum. Clearly, the predictions obtained in this work pose a great challenge and opportunity for experimentalists, who are provided with a target for deposition experiments of single lactose molecules followed by, e.g., atom-level resolved measurements of the structure of the deposited molecules. Regarding possible insights for practical applications, this study demonstrates the importance that the machining of metal parts, and therefore the control of exposed facets, can have on their interaction with everyday molecules. In future computational work, an important issue will be to quantify the contribution of dispersion forces to overall adsorption and to assess whether surface reconstruction phenomena have an effect on the facet-specificity of sugars, as has been observed in the case of peptide adsorption on gold.⁸⁰

Author contributions

Nathalie Tarrat: conceptualization, data curation, formal analysis, investigation, methodology, resources, software, validation, visualization, writing – original draft, writing – review & editing. J. Christian Schön: conceptualization, writing – original draft, writing – review & editing. Juan Cortés: conceptualization, formal analysis, investigation, methodology, software, validation, writing – original draft, writing – review & editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was granted access to the Max Planck Computing and Data Facility in Garching and the HPC resources of CALMIP supercomputing center under the allocation p19055.

Notes and references

1. C.-Y. Chiu, H. Wu, Z. Yao, F. Zhou, H. Zhang, V. Ozolins and Y. Huang, Facet-Selective Adsorption on Noble Metal Crystals Guided by Electrostatic Potential Surfaces of Aromatic Molecules, J. Am. Chem. Soc., 2013, 135, 15489–15500.
2. S. K. Ramakrishnan, M. Martin, T. Cloitre, L. Firlej and C. Gergely, Design rules for metal binding biomolecules: understanding of amino acid adsorption on platinum crystallographic facets from density functional calculations, Phys. Chem. Chem. Phys., 2015, 17, 4193–4198.
3. Z. E. Hughes, R. Kochandra and T. R. Walsh, Facet-Specific Adsorption of Tripeptides at Aqueous Au Interfaces: Open Questions in Reconciling Experiment and Simulation, Langmuir, 2017, 33, 3742–3754.
4. X. Fenouillet, M. Benoit and N. Tarrat, Methoxy radical adsorption on gold nanoparticles: a comparison with methanethiol and methylamine radicals, Adsorption, 2020, 26, 579–586.
5. S. Cao, X. Zhang, X. Huang, S. Wan, X. An, F. Jia and L. Zhang, Insights into the facet-dependent adsorption of phenylarsonic acid on hematite nanocrystals, Environ. Sci.: Nano, 2019, 6, 3280–3291.
6. Z. Shen, Z. Zhang, T. Li, Q. Yao, T. Zhang and W. Chen, Facet-Dependent Adsorption and Fractionation of Natural Organic Matter on Crystalline Metal Oxide Nanoparticles, Environ. Sci. Technol., 2020, 54, 8622–8631.
7. H. Zhai and L. Wang, Single-molecule determination of the phase- and facet-dependent adsorption of alginate on iron oxides, Environ. Sci.: Nano, 2020, 7, 954–962.
8. Z. Shen, Z. Zhang, T. Li, Q. Yao, T. Zhang and W. Chen, Facet-Dependent Adsorption and Fractionation of Natural Organic Matter on Crystalline Metal Oxide Nanoparticles, Environ. Sci. Technol., 2020, 54, 8622–8631.
9. M. Yang, X. Ren, L. Hu, H. Zhou and W. Guo, Insights into the facet-dependent adsorption of antibiotic ciprofloxacin on goethite, Environ. Sci. Pollut. Res., 2021, 28, 11486–11497.
10. L. Dong, Q. Luo, K. Cheng, H. Shi, Q. Wang, W. Weng and W.-Q. Han, Facet-Specific Assembly of Proteins on SrTiO₃ Polyhedral Nanocrystals, Sci. Rep., 2014, 4, 5084.
11. L. B. Wright, J. P. Palafox-Hernandez, P. M. Rodger, S. Corni and T. R. Walsh, Facet selectivity in gold binding peptides: exploiting interfacial water structure, Chem. Sci., 2015, 6, 5204–5214.
12. X. Fenouillet, M. Benoit and N. Tarrat, On the role of intermolecular interactions in stabilizing AuNP@Ampicillin nano-antibiotics, Materialia, 2018, 4, 297–309.
13. Q. Zhang and H. Wang, Facet-Dependent Catalytic Activities of Au Nanoparticles Enclosed by High-Index Facets, ACS Catal., 2014, 4, 4027–4033.
14. R. Rajendiran, P. K. Seelam, A. Patchaiyappan, P. Balla, H. Shankar, B. Ravi, V. Perupogu and U. Lassi, Morphologically tailored facet dependent silver nanoparticles supported α-Al₂O₃ catalysts for chemoselective reduction of aromatic nitro compounds, Chem. Eng. J., 2023, 451, 138507.
15. G. L. De Gregorio, T. Burdyny, A. Loiudice, P. Iyengar, W. A. Smith and R. Buonsanti, Facet-Dependent Selectivity of Cu Catalysts in Electrochemical CO₂ Reduction at Commercially Viable Current Densities, ACS Catal., 2020, 10, 4854–4862.
16. R. Haimov-Kochman, L. S. Shore and N. Laufer, The milk we drink, food for thought, Fertil. Steril., 2016, 106, 1310–1311.
17. A. L. Brody, Packaging Milk and Milk Products, John Wiley & Sons, Ltd, 2015, ch. 21, pp. 506–527.
18. M. Atapour, Z. Wei, H. Chaudhary, C. Lendel, I. O. Wallinder and Y. Hedberg, Metal release from stainless steel 316L in whey protein – And simulated milk solutions under static and stirring conditions, Food Control, 2019, 101, 163–172.
19. K. Hansson, T. Andersson and M. Skepö, Adhesion of fermented diary products to packaging materials. Effect of material functionality, storage time, and fat content of the product. An empirical study, J. Food Eng., 2012, 111, 318–325.
20. V. Gantner, P. Mijić, M. Baban, Z. Škrtić and A. Turalija, The overall and fat composition of milk of various species, Mljekarstvo, 2015, 65, 223–231.
21. A. Vallee, V. Humblot and C.-M. Pradier, Peptide Interactions with Metal and Oxide Surfaces, Acc. Chem. Res., 2010, 43, 1297–1306.
22. D. Costa, L. Savio and C.-M. Pradier, Adsorption of Amino Acids and Peptides on Metal and Oxide Surfaces in Water Environment: A Synthetic and Prospective Review, J. Phys. Chem. B, 2016, 120, 7039–7052.
23. S. Loehlé, C. Matta, C. Minfray, T. Mogne, R. Iovine, Y. Obara, A. Miyamoto and J. Martin, Mixed lubrication of steel by C18 fatty acids revisited. Part I: toward the formation of carboxylate, Tribol. Int., 2015, 82, 218–227.
24. N. Wu, L. Fu, M. Su, M. Aslam, K. C. Wong and V. P. Dravid, Interaction of Fatty Acid Monolayers with Cobalt Nanoparticles, Nano Lett., 2004, 4, 383–386.
25. T. H. Vesa, P. Marteau and R. Korpela, Lactose Intolerance, J. Am. Coll. Nutr., 2000, 19, 165S–175S.
26. S. Ugidos-Rodríguez, M. C. Matallana-González and M. C. Sánchez-Mata, Lactose malabsorption and intolerance: a review, Food Funct., 2018, 9, 4056–4068.
27. S. Edge, A. Kibbe and K. Kussendrager, Lactose, Pharmaceutical Press and American Pharmacists Association, 1 Lambeth High Street, London SE1 7JN, UK 100 South Atkinson Road, Suite 206, Grayslake, IL 60030-7820, USA 1 2215 Constitution Avenue, NW Washington, DC, 2005, pp. 385–398.
28. S. Angelova, V. Nikolova and T. Dudev, Divalent metal ions binding to lactose: a DFT computational study, Bulg. Chem. Commun., 2018, 50, 130–134.
29. S. M. Khalil, E. E. Ali-Shattle and N. M. Ali, A Theoretical Study of Carbohydrates as Corrosion Inhibitors of Iron, Z. Naturforsch. A, 2013, 68, 581–586.
30. Z. Fan and H. Zhang, Template Synthesis of Noble Metal Nanocrystals with Unusual Crystal Structures and Their Catalytic Applications, Acc. Chem. Res., 2016, 49, 2841–2850.
31. C. Kittel, Introduction to solid state physics, Wiley, New York, 2005.
32. J. C. Schön, C. Oligschleger and J. Cortés, Prediction and clarification of structures of (bio)molecules on surfaces, Z. Naturforsch. B, 2016, 71, 351–374.
33. D. G. Sangiovanni, R. Faccio, G. K. Gueorguiev and A. Kakanakova-Georgieva, Discovering atomistic pathways for supply of metal atoms from methyl-based precursors to graphene surface, Phys. Chem. Chem. Phys., 2023, 25, 829–837.
34. G. Sfuncia, G. Nicotra, F. Giannazzo, B. Pécz, G. K. Gueorguiev and A. Kakanakova-Georgieva, 2D graphitic-like gallium nitride and other structural selectivity in confinement at the graphene/SiC interface, CrystEngComm, 2023, 25, 5810–5817.
35. S. Abb, N. Tarrat, J. Cortés, B. Andriyevsky, L. Harnau, J. C. Schön, S. Rauschenbach and K. Kern, Carbohydrate Self-Assembly at Surfaces: STM Imaging of Sucrose Conformation and Ordering on Cu(100), Angew. Chem., Int. Ed., 2019, 58, 8336–8340.
36. S. Abb, N. Tarrat, J. Cortés, B. Andriyevsky, L. Harnau, J. C. Schön, S. Rauschenbach and K. Kern, Polymorphism in carbohydrate self-assembly at surfaces: STM imaging and theoretical modelling of trehalose on Cu(100), RSC Adv., 2019, 9, 35813–35819.
37. J. Johnson and F. Conforti, LACTOSE, Academic Press, Oxford, 2nd edn, 2003, pp. 3472–3476.
38. C. A. Beevers and H. N. Hansen, The structure of α-lactose monohydrate, Acta Crystallogr., Sect. B: Struct. Sci., 1971, 27, 1323–1325.
39. M. J. Altamimi, K. Wolff, A. Nokhodchi, G. P. Martin and P. G. Royall, Variability in the α and β anomer content of commercially available lactose, Int. J. Pharm., 2019, 555, 237–249.
40. P. Zarmpi, T. Flanagan, E. Meehan, J. Mann and N. Fotaki, Biopharmaceutical aspects and implications of excipient variability in drug product performance, Eur. J. Pharm. Biopharm., 2017, 111, 1–15.
41. R. Jawad, A. F. Drake, C. Elleman, G. P. Martin, F. J. Warren, B. B. Perston, P. R. Ellis, M. A. Hassoun and P. G. Royall, Stability of Sugar Solutions: A Novel Study of the Epimerization Kinetics of Lactose in Water, Mol. Pharmaceutics, 2014, 11, 2224–2238.
42. S. Neelamraju, C. Oligschleger and J. C. Schön, The threshold algorithm: description of the methodology and new developments, J. Chem. Phys., 2017, 147, 152713.
43. Symbols for specifying the conformation of polysaccharide chains (Recommendations 1981), Pure Appl. Chem., 1983, 55, 1269–1272.
44. R. A. Jockusch, R. T. Kroemer, F. O. Talbot, L. C. Snoek, P. Carçabal, J. P. Simons, M. Havenith, J. M. Bakker, I. Compagnon, G. Meijer and G. von Helden, Probing the Glycosidic Linkage: UV and IR Ion-Dip Spectroscopy of a Lactoside, J. Am. Chem. Soc., 2004, 126, 5709–5714.
45. R. Lefort, P. Bordat, A. Cesaro and M. Descamps, Exploring the conformational energy landscape of glassy disaccharides by cross polarization magic angle spinning C13 nuclear magnetic resonance and numerical simulations. II. Enhanced molecular flexibility in amorphous trehalose, J. Chem. Phys., 2007, 126, 014511.
46. W. Margerit, A. Charpentier, C. Maugis-Rabusseau, J. C. Schön, N. Tarrat and J. Cortés, IGLOO: An Iterative Global Exploration and Local Optimization Algorithm to Find Diverse Low-Energy Conformations of Flexible Molecules, Algorithms, 2023, 16, 476.
47. L. Jaillet, F. J. Corcho, J.-J. Pérez and J. Cortés, Randomized tree construction algorithm to explore energy landscapes, J. Comput. Chem., 2011, 32, 3464–3474.
48. D. Devaurs, K. Molloy, M. Vaisset, A. Shehu, T. Siméon and J. Cortés, Characterizing energy landscapes of peptides using a combination of stochastic algorithms, IEEE Trans. NanoBiosci., 2015, 14, 545–552.
49. R. Salomon-Ferrer, D. A. Case and R. C. Walker, An overview of the Amber biomolecular simulation package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210.
50. K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. González-Outeiriño, C. R. Daniels, B. L. Foley and R. J. Woods, GLYCAM06: a generalizable biomolecular force field. Carbohydrates, J. Comput. Chem., 2008, 29, 622–655.
51. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
52. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
53. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
54. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
55. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
56. M. Methfessel and A. T. Paxton, High-precision sampling for Brillouin-zone integration in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621.
57. J. Klimes, D. R. Bowler and A. Michaelides, Chemical accuracy for the van der Waals density functional, J. Phys.: Condens. Matter, 2010, 22, 022201.
58. G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360.
59. E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, Improved grid-based algorithm for Bader charge allocation, J. Comput. Chem., 2007, 28, 899–908.
60. W. Tang, E. Sanville and G. Henkelman, A grid-based Bader analysis algorithm without lattice bias, J. Phys.: Condens. Matter, 2009, 21, 084204.
61. D. L. Andrews, Nanostructured Surfaces, Elsevier B.V., 2011.
62. D. C. Fries, S. T. Rao and M. Sundaralingam, Structural chemistry of carbohydrates. III. Crystal and molecular structure of 4-O-[beta]-D-galactopyranosyl-[alpha]-D-glucopyranose monohydrate ([alpha]-lactose monohydrate), Acta Crystallogr., 1971, B27, 994–1005.
63. C. Platteau, J. Lefebvre, F. Affouard, J.-F. Willart, P. Derollez and F. Mallet, Structure determination of the stable anhydrous phase of α-lactose from X-ray powder diffraction, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 185–191.
64. M. J. Márquez, A. B. Brizuela, L. Davies and S. A. Brandán, Spectroscopic and structural studies on lactose species in aqueous solution combining the HATR and Raman spectra with SCRF calculations, Carbohydr. Res., 2015, 407, 34–41.
65. H. Farrokhpour, S. Abedi and H. Jouypazadeh, Directional affinity of a spherical Gold nanoparticle for the adsorption of DNA bases, Colloids Surf., B, 2019, 173, 493–503.
66. M. Domingo, M. Shahrokhi, I. Remediakis and N. Lopez, Shape Control in Gold Nanoparticles by N-Containing Ligands: Insights from Density Functional Theory and Wulff Constructions, Top. Catal., 2018, 61, 412–418.
67. N. Tarrat, M. Benoit, M. Giraud, A. Ponchet and M. J. Casanove, The gold/ampicillin interface at the atomic scale, Nanoscale, 2015, 7, 14515–14524.
68. H. Guo, E. A. Gerstein, K. C. Jha, I. Arsano, M. A. Haider, T. S. Khan and M. Tsige, Non-reactive facet specific adsorption as a route to remediation of chlorinated organic contaminants, Front. Catal., 2023, 3, 1116867.
69. A. Bilić, J. R. Reimers, N. S. Hush, R. C. Hoft and M. J. Ford, Adsorption of Benzene on Copper, Silver, and Gold Surfaces, J. Chem. Theory Comput., 2006, 2, 1093–1105.
70. Z. Zhang, S.-S. Wang, R. Song, T. Cao, L. Luo, X. Chen, Y. Gao, J. Lu, W.-X. Li and W. Huang, The most active Cu facet for low-temperature water gas shift reaction, Nat. Commun., 2017, 8, 488.
71. C. Wang, Q. Zhang, B. Yan, B. You, J. Zheng, L. Feng, C. Zhang, S. Jiang, W. Chen and S. He, Facet Engineering of Advanced Electrocatalysts Toward Hydrogen/Oxygen Evolution Reactions, Nano-Micro Lett., 2023, 15, 52.
72. Y. Ye, H. Yang, J. Qian, H. Su, K.-J. Lee, T. Cheng, H. Xiao, J. Yano and W. A. G. I. E. J. Crumlin, Dramatic differences in carbon dioxide adsorption and initial steps of reduction between silver and copper, Nat. Commun., 2019, 10, 1875.
73. L. Han, B. Tian, X. Gao, Y. Zhong, S. Wang, S. Song, Z. Wang, Y. Zhang, Y. Kuang and X. Sun, Copper nanowire with enriched high-index facets for highly selective CO₂ reduction, SmartMat, 2022, 3, 142–150.
74. D. Su, S. Dou and G. Wang, Gold nanocrystals with variable index facets as highly effective cathode catalysts for lithium-oxygen batteries, NPG Asia Mater., 2015, 7, e155.
75. H. Tang, N. Tarrat, V. Langlais and Y. Wang, Adsorption of iron tetraphenylporphyrin on (111) surfaces of coinage metals: a density functional theory study, Beilstein J. Nanotechnol., 2017, 8, 2484–2491.
76. A. H. Hakimioun, E. M. Dietze, B. D. Vandegehuchte, D. Curulla-Ferre, L. Joos, P. N. Plessow and F. Studt, Theoretical Investigation of the Size Effect on the Oxygen Adsorption Energy of Coinage Metal Nanoparticles, Catal. Lett., 2021, 151, 3165–3169.
77. D. A. Schlosser, D. Yehorova, H. Kaleem, E. M. Maxwell, J. S. Baker, M. Z. Gillum, M. C. DePonte, K. Letchworth-Weaver and A. E. Baber, Effect of undercoordinated Ag(111) defect sites on the adsorption of ethanol, J. Vac. Sci. Technol., A, 2020, 38, 033213.
78. A. Faeli Qadikolae and S. Sharma, Facet Selectivity of Cetyltrimethyl Ammonium Bromide Surfactants on Gold Nanoparticles Studied Using Molecular Simulations, J. Phys. Chem. B, 2022, 126, 10249–10255.
79. B. Hammer and J. Norskov, Why gold is the noblest of all the metals, Nature, 1995, 376, 238.
80. L. B. Wright, P. M. Rodger, T. R. Walsh and S. Corni, First-Principles-Based Force Field for the Interaction of Proteins with Au(100)(5 × 1): An Extension of GolP-CHARMM, J. Phys. Chem. C, 2013, 117, 24292–24306.

---

Footnotes

† Electronic supplementary information (ESI) available: Cartesian coordinates of all DFT structures. See DOI: https://doi.org/10.1039/d4cp01559b

‡ Note that this energy cannot be directly compared between two surfaces; it only allows to evaluate the contribution of the surface deformation to the total adsorption energy. To compare this value between two systems, it must be divided by the surface area.

---