Photoprocessing of cationic triazacoronene: dissociation characteristics of polycyclic aromatic nitrogen heterocycles in interstellar environments

Abstract

Polycyclic aromatic nitrogen heterocycles (PANHs) are present in various astronomical environments where they are subjected to intense radiation. Their photodissociation pathways give crucial insights into the cycle of matter in the universe, yet so far only the dissociation characteristics of few PANHs have been investigated. Moreover, most experiments use single photon techniques that only reveal the initial dissociation step, and are thus unsuited to replicate astronomical environments and timescales. In this work, we use the Instrument for the Photodynamics of PAHs (i-PoP) at the Laboratory for Astrophysics to simulate the interstellar photodissociation of a model PANH, cationic triazacoronene (TAC˙⁺, C₂₁H₉N₃). Comparing the observed fragments to similar PAHs such as the isoelectronic coronene can give mechanistic insight into PAH dissociation. For coronene the major photodissociation products were found to be C₉H⁺, C₁₀⁺, and C₁₁⁺. In contrast, fragmentation in TAC˙⁺ is initiated by up to three HCN losses often in combination with H- or H₂ losses. In the lower mass region, the fragments show similarities to comparable PAHs like coronene, but for TAC˙⁺ the inclusion of nitrogen atoms into the ionic fragments in the form of e.g. (di)cyanopolyynes is also observed. These nitrogen-containing species may be important tracers of regions in interstellar space where interstellar PANHs are being photodissociated.

---

1 Introduction

Polycyclic aromatic hydrocarbons (PAHs) are ubiquitous in various regions in the interstellar medium (ISM) and planetary atmospheres, such as that of Saturn's largest moon, Titan.^1–3 In the ISM, they are identified based on their characteristic mid-infrared (IR) emission bands that arise when PAHs cascade down to the ground state after getting excited by the interstellar radiation field.^4–8 The 6.2 micrometer features of PAHs are consistently red-shifted compared to the observed IR emission bands and thus homocyclic PAHs alone cannot explain the observations.^9,10 Heteroatom substitutions were proposed to account for this observed shift in position of the 6.2 micrometer emission feature.¹¹ Recent experimental studies have confirmed that incorporating nitrogen atoms into the PAH honeycomb structure indeed shifts the IR features towards shorter wavelengths,¹² but this shift is only noticeable for endoskeletal nitrogen atoms, in which a carbon atom inside the molecule is replaced by a nitrogen atom. The relative abundance of interstellar endoskeletal polycyclic aromatic nitrogen heterocycles (PANHs) has recently been estimated to be no more than 12%.¹¹ Exoskeletal substitutions, i.e. a CH/N exchange, hardly alter the IR emissions and, thus, exoskeletal PANHs may contribute significantly to the observed emission bands.

Based on the molecular heat capacity it is believed that only large PA(N)Hs with more than 50 heavy atoms survive the harsh interstellar radiation field.^1,6,13 Smaller PA(N)Hs get photoprocessed on astronomical time scales and fragment into thermodynamically more stable species. The dissociation of several model PAHs, such as dicoronylene, dibenzopyrenes,^14,15 naphthalene,¹⁶ and anthracene¹⁷ have been studied experimentally in detail. In catacondensed PAHs like dibenzopyrenes the inital dehydrogenation is always accompanied by the loss of acetylene (C₂H₂) fragments, whereas H-loss dominates for more symmetrical PAHs like coronene and dicoronylene.^18,19 Subsequently, different carbon clusters and polyyne chains are formed, which can also contain a small number of hydrogen atoms. Among those carbon clusters, C₁₁⁺ is one of the most intense and it is thus believed that it represents a thermodynamic sink.^14,15,19

Just like PAHs, PANHs may also show universal fragmentation pathways that lead to common photoproducts from different parent molecules.²⁰ Although significant efforts have been put into elucidating the dissociation characteristics of PAHs, very little is known about those for PANHs. Bouwman et al.²¹ investigated the dissociation of quinoline and isoquinoline cations by dissociative photoionization (DPI) and found nearly isoenergetic channels H-loss and HCN-loss. The dissociation barriers are almost 1 eV lower when compared to similar channels in naphthalene, signaling that nitrogen incorporation into a PAH framework lowers its stability. A similar observation was made in phenantridine and acridine (C₁₃H₉N) which exhibit the loss of a HCN fragment upon electron ionization resulting in the introduction of five-membered rings in the nascent PAH structure.²² Based on these studies it is currently believed that PANHs initially eliminate all nitrogen atoms through HCN losses and eventually turn into pure PAHs. Yet, due to the nature of these single step dissociative ionization experiments, only the initial dissociation pathways are revealed and as such they fail to give a complete picture of processing of PAHs on longer, astronomically more relevant, time scales. In addition, the investigated PANHs only contain a single nitrogen atom and are limited to a maximum of three aromatic cycles, while interstellar PAHs are believed to be larger with potentially more than one hetero atom substitution.

Here, we use the instrument for the Photodynamics of PAHs (i-PoP) to investigate the similarities and dissimilarities in the photoprocessing of PAHs and PANHs. This setup has been used in the past to study infrared spectroscopic properties of PAHs^23–27 as well as various facets of PAH photoprocessing.^{14,15,19,28–32} As a model compound for our study we chose 1,5,9-triazacoronene (TAC, C₂₁H₉N₃, illustrated in Fig. 1). TAC is a structural variation of coronene in which three equidistant CH-groups are replaced by three nitrogen atoms. Coronene is a highly symmetric pericondensed PAH, which has been studied in the past.^33,34TAC contains about twice the number of heavy atoms (C, N) compared to the previously largest investigated PANHs and is thus of larger interstellar significance. Moreover, its dissociation may result in the incorporation of one or more nitrogen atoms in the fragment ions. The isoelectronic CH/N exchange shifts their mass up by 1 atomic mass unit (amu) per nitrogen atom (i.e. 3 amu for TAC).

Fig. 1 Structure of the investigated triazacoronene.

2 Methods

The experiments on the dissociation of TAC˙⁺ were performed on i-PoP, situated in the Laboratory for Astrophysics (LfA) at Leiden Observatory. TAC was synthesized according to a procedure described in the literature.³⁵ The complete synthesis procedure, including NMR spectroscopic data can be found in the ESI.† The experimental apparatus has been described in detail elsewhere,²⁸ so only a brief description is given here.

The setup consists of two differentially pumped chambers; a source chamber that houses a commercial ion trap (Jordan C-1251), and a detection chamber which comprises a reflectron time-of-flight (re-TOF) spectrometer (Jordan D-850). The samples were placed in an oven (Heat Wave Labs) that is positioned in the source chamber next to the ion trap and heated to 150 °C to gently sublimate the TAC sample.

The neutral molecules that sublimated from the oven were ionized by electron ionization at 70 eV using an electron gun (EGUN, Jordan C-950). The formed cations were subsequently guided into the ion trap through electrostatic lenses and an ion gate that determines the fill time of the trap. The ions were captured in the 1 MHz radio frequency (RF) field of the trap and the ion cloud was confined to the center of the trap by admitting a small, continuous flow of helium gas to the ion trap assembly reaching a static pressure of 1–2 × 10⁻⁶ reached in the source chamber. The RF amplitude was set to 1500 V and resulted in trapping of ions with mass to charge ratios (m/z) down to 93. However, the signals of lowest masses from m/z 93 to 103 were found to fluctuate and were disregarded in the analysis.

The data acquisition scheme can be separated into four distinct steps that are described in this paragraph. First, the ion trap was filled for 2.7 s, after which the ion gate was closed. A Stored Waveform Inverse Fourier Transform (SWIFT) pulse of 0.25 s was applied to one of the end caps of the ion trap to filter out all of the ions but the ionic species of interest, which in our case is TAC˙⁺. After a brief re-thermalization period (0.05 s) the isolated ions inside the trap were exposed to laser light from a dye laser (LIOP-TEC, Quasar2-VN) that was pumped by a 10 Hz Nd:YAG (INDI-40-10). The dye laser was filled with the dye 4-(dicyanomethylene)-2-methyl-6-(4-dimethylaminostyryl)-4H-pyran (DCM) dissolved in ethanol and tuned to a wavelength of 630 nm. This wavelength allows to utilize a multi-photon absorption approach, which helps to probe the potential energy surface of TAC˙⁺ more gently, with respect to its dissociation barriers. It also limits secondary processes, like multiple ionization, which has been observed in experiments with VUV photons and PAHs of similar sizes, among them coronene.^36,37 The laser pulse energy measured outside the vacuum chamber after passing through the ion trap was set to 4.1 mJ and the laser pulse has a duration of 10 ns with a diameter of 1.2 ± 0.1 mm, resulting in an average fluence of 362.5 mJ cm⁻² pulse⁻¹. The number of laser pulses admitted to the ion cloud in the trap ranged from 0 to 20 and was controlled by a mechanical shutter. The exposure to laser light is expressed as fluence (number of pulses × laser pulse energy). During the irradiation period, the ions were always retained for a the same amount of time, typically two seconds, independent of the number of laser pulses that they were subjected to. In the final step, a potential of ∼−800 and ∼+800 V was applied to the end cap electrodes of the ion trap to accelerate the ions into the reflectron time-of-flight (re-TOF) tube. Ions were detected using a multichannel plate (MCP) detector and digitized using an 8-bit GaGe Cobra card. The aforementioned data acquisition sequence was programmed in a LabVIEW routine that controlled two high-precision delay generator (SRS DG535) via a GPIB interface. The measurement routine was triggered on the signal of the Q-switch of a Nd:YAG laser to ensure exposure to the correct number of laser pulses during each measurement cycle. Each mass spectrum for a certain laser exposure was taken as an average over 50 individual mass spectra.

In order to quantitatively investigate the data, each peak was fitted with a Pearson type IV distribution³⁸ to account for the asymmetry in the mass peak (see Fig. S1 for typical fit, ESI†). Subsequently, the fitted distribution was integrated numerically, giving the integrated signal intensity of the mass peak. The integrated intensities for each peak were normalized to the parent TAC˙⁺ signal at zero pulses and corrected for ¹³C contributions.

Experimental errors were determined from the fluctuations in the ion signal at each normalization measurement, which was found to fluctuate by a total of 15%. These errors can only be given on a measurement-to-measurement basis, but each peak in a mass spectrum should be equally affected by the filling of the ion trap. Errors of the fitting procedure were accounted for by introducing a random noise signal for each peak using the Markov Chain Monte Carlo (MCMC) method. Each peak was subsequently refitted, giving the total error of the fit for each peak. The total error of the fit is far below 1%, resulting in a combined relative error of 15%.

3 Results

An overview of the mass spectra range as a function of laser fluence is given in Fig. 2. The formed ionic dissociation products are discussed in the following sections for three mass ranges: high (m/z 300–320), medium (m/z 200–299) and low (m/z 103–199).

Fig. 2 Photodissociation mass spectra for TAC˙⁺ as a function of the number of applied laser pulses (fluence). A 2D mass spectrum after 8 pulses is displayed at the bottom.

3.1 Mass range m/z 300–320

The most intense peak in the mass spectrum when the ion cloud is not subjected to any laser light is observed at m/z 303 and is attributed to the parent TAC˙⁺. Weak signals are seen at 302 and 301, which correspond to hydrogen loss from the parent ion caused by electron ionization of the parent species, and have relative intensities of 11% and 6%, respectively. The signals at 304 and 305 correspond to the ¹³C isotope peaks and their relative intensities are 25% and 3%, which aligns very well with the expected isotope abundance. These weak signals observed next to the parent ion signal at zero laser pulse exposure cannot be filtered out completely using the SWIFT filtering technique.

After being subjected to an increasing number of laser pulses, a peak at m/z 320 grows in, while the parent signal is depleted. As illustrated in Fig. 3 the former is absent when the ions are not exposed to radiation, but continues to grow until the maximum number of pulses has been reached. Hence, this peak is the result of a reaction occurring inside the ion-trap and is likely initiated by photoactivation the parent ion. The most probable reactant is water which is always present in neutral background gas inside our vacuum chamber. However, the direct addition of water to TAC˙⁺ would result in a product at m/z 321. The absence of any reaction when retaining TAC˙⁺ in the ion trap without irradiation, points to a involvement of the hydrogen loss product TAC-H⁺ (at m/z 302) and water to form the species at m/z 320. Similar behavior was observed for another nitrogen-containing aromatic molecule, 3-azafluoranthene.³⁹ The loss of a hydrogen atom leads to the formation of a cationic hetero-aryne, which are known to be very reactive even towards closed–shell molecules.⁴⁰ To investigate this further we have performed experiments, where we admitted a mix of 5% acetylene in helium to the ion trap. The resulting mass spectrum is given in Fig. S2 (ESI†) and shows that almost all water addition product is replaced by an acetylene addition product (m/z 328). We recorded a mid-infrared (IR) action spectrum of the m/z 320 species to identify the structure of the water addition product, which indeed corroborates the above conclusion. The mid-IR spectra of the m/z 320 species, as well as TAC˙⁺ and protonated TAC are the subject of another manuscript.⁴¹

Fig. 3 Integrated values of all major peaks in the range of m/z 300–320 as a function of laser fluence.

Further hydrogen losses are not observed, as illustrated in Fig. S3 (ESI†), likely due to the high reactivity of TAC-H⁺.

The integrated signals of both m/z 303 and 320 in Fig. 3 show a clear trend that m/z 320 is formed at the expense of the parent TAC˙⁺. After 20 laser pulses the TAC˙⁺ signal is essentially gone, whereas the m/z 320 signal reaches its maximum at about 20% of the original TAC˙⁺ signal making it by far the strongest single product peak in the TAC˙⁺ photolysis.

3.2 Mass range m/z 200–299

In this intermediate mass range, peaks at m/z 293, m/z 294, 274–276, 247–249, and 220–222. The intensity of each peak is about ten times lower than the signal for the water addition product at m/z 320 and less than 3% of the initial TAC˙⁺ signal. With the exception of the first, all of these product ions align with loss of HCN or HCN + H/H₂ from TAC˙⁺. HCN losses are often observed as an initial and low energy decomposition pathway in cationic PANHs.^21,42

The integrated signals in this mass range are shown in Fig. 4. From this it is clear that all aforementioned species are formed within the first few laser pulses and reach their peak at ∼8 pulses after which they decline steadily. The two most intense peaks are at m/z 274 and 247, which exhibit a mass difference of 27, corresponding to the mass of a HCN fragment. Interestingly, m/z 274 can only originate from TAC˙⁺via a CNH₃ loss, which could also be a sequential loss of HCN and H₂. The signals at m/z 276, 249 and 222 correspond to the consecutive loss of HCN from TAC˙⁺. Their signals are comparable in integrated intensity for all three over the investigated laser fluences and is about half of the signals at m/z 274 or 247, indicating that the loss of CNH₃ (or HCN + H₂) followed by HCN loss is preferred over the loss of multiple HCN units from the parent TAC˙⁺. The other signals (m/z 275, 248, 221) would correspond to the loss of CNH₂ (or HCN + H) followed by HCN loss and show a similar fluence dependence and comparable intensities to signals at m/z 276, 249 and 222.

Fig. 4 Integrated values of all observed peaks in the range of m/z 200–299 as a function of laser fluence.

The only peak in the intermediate mass range that cannot be explained with the loss of CNH_n=1–3 from TAC is m/z 293. The obvious solution would be the loss of HCN from m/z 320. To confirm this, we generated and subsequently isolated m/z 320 in the ion-trap and irradiated it without any other masses present. The corresponding mass spectra in Fig. S4 (ESI†) show no visible decay upon irradiation, eliminating the possibility of such a process occurring. Hence, m/z 293 is likely a reaction product forming in the trap. If we again assume that water is the primary reactant, then a CNH₂ loss (or H-loss followed by HCN loss) from TAC˙⁺ with a subsequent water addition could explain the appearance of m/z 293 in a manner analogous to the addition of water to TAC-H⁺.

The integrated signals in this mass region indicate that either direct HCN losses from TAC may be less important than CNH₃ (or HCN + 2H) losses, or that fragment ion species formed by direct HCN loss are so unstable that they decompose more readily by also eliminating H, or H₂ fragments.

3.3 Mass range m/z 103–199

In the lowest mass range, there are not only more but also more intense signals (>5% of the initial parent signal) compared to the previous region. All detected ion masses in this range are depicted in Table 1 and their integrated signals are displayed in Fig. S5–S8 (ESI†). Table 1 also contains all reasonable molecular compositions based on the four elements C, H, N, and O, since the mass resolution of our mass spectrometer is not sufficient to disentangle isobaric species. As such, we cannot distinguish between different elemental compositions in one mass channel and only the pure carbon (C_n⁺) and C_nH⁺ species can be assigned unambiguously, whereas species of various C_AN_BO_CH_D⁺ compositions are plausible for other mass channels as well.

Table 1 Ion signals in the m/z 103–199 range detected as a result of the photodissociation of TAC˙⁺

Identified masses (m/z)	Probable compositions CANBOCHD					Group Γn	Group η	Complete notation Γn + η
108	C9					Γ 9	0	Γ 9 + 0
109	C9H						1	Γ 9 + 1
110	C9H2	C8N					2	Γ 9 + 2
111	C9H3	C8HN					3	Γ 9 + 3
112	C9H4	C8H2N	C7N2		C8O		4	Γ 9 + 4
120	C10					Γ 10	0	Γ 10 + 0
121	C10H						1	Γ 10 + 1
122	C10H2	C9N					2	Γ 10 + 2
123	C10H3	C9HN					3	Γ 10 + 3
124	C10H4	C9H2N	C8N2		C9O		4	Γ 10 + 4
125	C10H5	C9H3N	C8HN2		C9HO		5	Γ 10 + 5
126	C10H6	C9H4N	C8H2N2	C7N3	C9H2O		6	Γ 10 + 6
127	C10H7	C9H5N	C8H3N2	C7HN3	C9H3O		7	Γ 10 + 7
132	C11					Γ 11	0	Γ 11 + 0
133	C11H						1	Γ 11 + 1
134	C11H2	C10N					2	Γ 11 + 2
135	C11H3	C10HN					3	Γ 11 + 3
136	C11H4	C10H2N	C9N2		C10O		4	Γ 11 + 4
144	C12					Γ 12	0	Γ 12 + 0
145	C12H						1	Γ 12 + 1
146	C12H2	C11N					2	Γ 12 + 2
147	C12H3	C11HN					3	Γ 12 + 3
148	C12H4	C11H2N	C10N2		C11O		4	Γ 12 + 4

---

The possible inclusion of nitrogen atoms in the fragment ions, as well as the reactivity of fragment ions towards background water (i.e. the inclusion of O-atoms in the molecule), complicate the analysis of the data. Hence, to facilitate the discussion on the evolution of species, we refer to the observed ionic species using the Γ_n + η notation, where n signifies the number of heavy atoms in the ion (C_AN_BO_CH_D⁺, n = A + B + C, Γ = C,N,O) and η the number of hydrogen equivalents in the ion. E.g. m/z 122, 123, and 124 will be referred to as Γ₁₀ + 2, Γ₁₀ + 3, Γ₁₀ + 4, respectively. The pure carbon ions are used as reference points, with η = 0. The assignment of two independent variables to one mass channel allows us to group each observed mass peak in two different ways. To probe the stability of the fragments with respect to their size, we grouped the appearing fragments based on the number of heavy atoms (Γ_n). This method allows for a comparison of individual contributions within one Γ_n group. Moreover, it enables a cross comparison of the integrated signals of each Γ_n cluster (e.g. comparing intensities in Γ₉ and Γ₁₀). However, Γ_n alone does not allow us to probe how mass distributions change for different values of n. Fragments where a carbon atom is exchanged by a nitrogen atom shift their mass by two amu. Visualizing this shift highlights how the potential incorporation of heteroatoms changes with the cluster size Γ_n. To facilitate such a comparison we group the appearing masses according to their η-value. Each added amu raises its value by one until the next higher carbon mass is reached, allowing us to intuitively group mass peaks that have similar composition but a different number of heavy atoms.

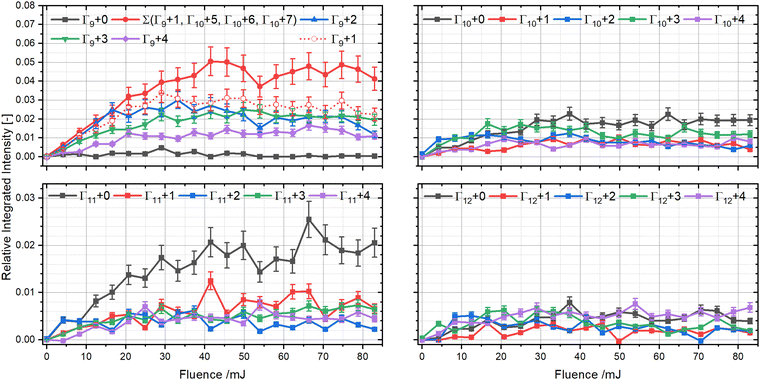
The RF setting of our ion trap allows for a complete analysis down to the Γ₉ region and all the way up to the Γ₁₂ region. To investigate the distribution of individual mass channels within the same cluster size as a function of fluence, we first grouped them based on their Γ_n-value, as illustrated in Fig. 5. The different groups show contrasting signals, demonstrating that the number of heavy atoms significantly influences the product distributions.

Fig. 5 Photon flux dependence of individual mass peaks for Γ₉ (top left), Γ₁₀ (top right), Γ₁₁ (bottom left), and Γ₁₂ (bottom right). Due to the reaction of Γ₉ + 1 with water, its original signal (empty red dots) was modified by adding the Γ₁₀ + 5, Γ₁₀ + 6, and Γ₁₀ + 7 signals.

The Γ₉ group shows almost no signal for Γ₉ + 0 (which can only be the bare C₉⁺ species) over the investigated range, whereas Γ₉ + 1 (C₉H⁺) rises fast and is the most intense signal. Γ₉ + 2 has a similar intensity as Γ₉ + 1, but after peaking at around 8 pulses, it shows a significant decline by almost 60%, indicating that it is either being processed further at higher fluence or that its production is impeded due to other channels becoming more important. In contrast Γ₉ + 3 and Γ₉ + 4 are produced slightly slower and are less intense than the other two, but show no decline within our investigated region, which suggests that these correspond to more stable structures.

For Γ₁₀ we observe fragments from η = 0–7, which is a clear deviation from all other groups. The appearance of fragments with η-values between 5 and 7 are only observed in significant quantities in this group, which can be explained by either retaining up to 7 hydrogen atoms in the fragment structure, by incorporating up to three nitrogen atoms, or by oxygen inclusion. The first two options would require unreasonable amounts of hydrogen and nitrogen atoms, that are in conflict with the observations in the previously discussed mass ranges. The high reactivity of TAC-H⁺ to form m/z 320 shows that reactions with water can happen readily in our ion trap, rendering the water addition reaction as the most likely candidate to explain these peaks.

We tried to prove the above hypothesis by gently raising the RF value so that the Γ₉ + 1 channel is no longer retained in the trap. As soon as retention of Γ₉ + 1 is no longer possible, the Γ₁₀ + 5–Γ₁₀ + 7 peaks also disappear, which indicates that they are formed by chemistry involving Γ₉ + 1. This interpretation is also in line with similar findings in the literature during the dissociation of coronene.¹⁹ Likely reaction candidates are C₉H, which can initially form m/z 127 (C₉H₃O) by reaction with water and lose up to two hydrogen atoms through photoprocessing forming masses m/z 125 (C₉HO). The potential loss of a hydrogen atom in C₉HO to form m/z 124 is not observed in the coronene measurements.¹⁹ This reaction in the ion trap also masks the true Γ₉ + 1 signal. If we assume that Γ₁₀ + 5–Γ₁₀ + 7 arise exclusively from the C₉H + H₂ O reaction, their combined intensities show a clear dominance of the Γ₉ + 1 channel in its group. Its overall fluence dependence does not change and only it maximum is pushed to slightly higher laser fluences.

The remaining signals in the Γ₁₀ group show that Γ₁₀ + 0 is dominant at high fluences, but grows in somewhat slower than Γ₁₀ + 3, which is the second most intense channel. The three other channels, Γ₁₀ + 1, Γ₁₀ + 2, and Γ₁₀ + 4 exhibit similar intensities but Γ₁₀ + 2 is produced instantly, while Γ₁₀ + 1 and Γ₁₀ + 4 grow in around 5 pulses. Γ₁₁ and Γ₁₂ show very similar behavior, with similar intensities for all mass channels except for Γ₁₁ + 0, which is the dominant signal within its group. All other masses from η = 1–4 are non-zero, but are significantly less intense than comparable signals from other Γ_n groups.

To quantify the stabilities of the various observed ionic fragments, we integrated ion signals in the respective groups and cross compared their intensities as a function of photon fluence. Fig. 6 shows that Γ₉ clearly dominates, while Γ₁₀ and Γ₁₁ exhibit equal intensities, and Γ₁₂ being the least intense of all. The intensities of Γ₉ are more than twice as high as Γ₁₀ and Γ₁₁, which underlines the general trend that smaller fragments with fewer heavy atoms tend to be produced more efficiently than bigger ones. While all groups exhibit a rise within the first 8 pulses, Γ₁₀, Γ₁₁, and Γ₁₂ plateau afterwards. In contrast Γ₉ begins to decline after reaching its maximum intensity. As such, even though Γ₉ is produced more efficiently it is processed further, whereas Γ_10–12 seem to be more stable, due to their plateau.

Fig. 6 Integrated values of all observed peaks in the respective Γ_n sections. The original signal of Γ₉ + 1 (empty purple squares) was modified by adding the signals from Γ₁₀ + 5, Γ₁₀ + 6, and Γ₁₀ + 7 due to the reaction of Γ₉ + 1 with water. Similarly, the original signal of Γ₁₀ (empty orange dots) was modified by subtracting Γ₁₀ + 5, Γ₁₀ + 6, and Γ₁₀ + 7.

Even though the Γ-value gives insight into the contributions of each mass in a group with the same number of heavy atoms as well as the fluence dependence of individual groups with different Γ_n, it is hard to determine how the product distribution changes depending on the cluster size. We therefore used the η-value to group signals with similar compositions but different number of heavy atoms and displayed their relative intensities as a function of laser fluence, as shown in Fig. 7. Pure carbon fragments (η = 0) do not appear with Γ₉ but only form for Γ₁₀ and higher. Here, Γ₁₀ + 0 and Γ₁₁ + 0 follow identical trends and exhibit the same intensities whereas Γ₁₂ + 0 is less intense. For η = 1, corresponding to the monohydrogenated carbon cluster (C_nH⁺), the dominant signal is found for Γ₉ + 1, while the others are six times less abundant. The dominance of the Γ₉ region is also shown for η = 2, 3, although it is less pronounced there. In both groups the Γ₁₀ fragments are (slightly) more intense than Γ₁₁ and Γ₁₂, which are equally intense. This trend continues for η = 4 where all four mass channels exhibit very similar intensities and Γ₉ is only marginally more intense. As a result, while species with η ≤ 3 do show some preference for smaller species with less heavy atoms, there is almost no preference for the size of a species when η = 4. The fluence dependence of each mass channel has already been described in detail for the Γ groups and no notable discrepancies arise within the new grouping.

Fig. 7 Photon flux dependence of individual mass peaks for η = 0–4. The original signal of Γ₉ + 1 (empty purple squares, dotted line) was modified by adding the signals from Γ₁₀ + 5, Γ₁₀ + 6, and Γ₁₀ + 7 due to the reaction of Γ₉ + 1 with water.

To complete our analysis we cross compared the different η groups by integrating over all mass channels with the same η-value. Fig. 8 shows that Γ_n + 1 signals exhibit the highest intensities, with Γ_n + 0, Γ_n + 2, and Γ_n + 3 having comparable intensities over large portions of the investigated laser fluences. Γ_n + 4 has the slowest rise and least intensity at lower photon fluxes, yet the decay of the Γ_n + 2 group in the second half of our investigated range shows that both groups have comparable intensities. Contrary to Fig. 6 and 8 shows that the fragments in the TAC˙⁺ dissociation are distributed almost equally up to η = 4, and only due to the intense Γ₉ + 1 signal is the respective η = 1 channel slightly more intense.

Fig. 8 Integrated values of all observed peaks with the same η-value from Γ₉ to Γ₁₂ for TAC˙⁺. The original signal of Γ₉ + 1 (empty orange circles, dotted line) was modified by adding the signals from Γ₁₀ + 5, Γ₁₀ + 6, and Γ₁₀ + 7 due to the reaction of Γ₉ + 1 with water.

4 Discussion

4.1 Differences between coronene and TAC

Coronene and TAC are isoelectronic and the only difference between the two structures is that three equidistant CH units in coronene are substituted with nitrogen atoms. The similarity allows us to gain insight into the dissociation mechanism as well as investigate the role that the exoskeletal ring plays in the formation of main fragment ions as compared to coronene. Before we can discuss these adequately, we need to first understand which photodissociation fragments are formed in the TAC˙⁺ and coronene radical cation (Cor˙⁺), respectively.

In Cor˙⁺ dissociation the lower mass section is exclusively dominated by carbon clusters like C_10–14⁺ or singly hydrogenated polyynes (C₉H⁺), while in TAC˙⁺ many more peaks are observed that cannot be attributed to these species. To better illustrate this behavior, Fig. 9 shows the relative integrated peak intensities of all observed Γ₉ fragments for Cor˙⁺ (top) and TAC˙⁺ (bottom). In both, the Γ₉ + 1 fragments are clearly dominating, while Γ₉ + 2, Γ₉ + 3 and Γ₉ + 0 exhibit smaller values. However, the relative strength of the Γ₉ + 1 channel with respect to the other channels is significantly higher in Cor˙⁺ than in TAC˙⁺, which suggests a more equal distribution of the observed fragments for Γ₉ in the latter. The fourth mass, Γ₉ + 4, is completely absent in Cor˙⁺ dissociation, but visible in TAC˙⁺. Its presence is one of the major differences between Cor˙⁺ and TAC˙⁺ and similar trends can be observed for Γ_10–12, as illustrated in Fig. S9–S11 (ESI†).

Fig. 9 Comparison of the fragment ions formed in the dissociation of Cor˙⁺ (top) and TAC˙⁺ (bottom) in the mass range spanning m/z 108 to 112. The Γ₉ + 1 channels in both molecules are comprised of the initial Γ₉ + 1 signal as well as the Γ₁₀ + 5–7 channels.

Before we interpret this difference, we also want to point out that fragments in the Γ_9–12 region appear to reach their maxima at lower pulse numbers for TAC˙⁺, which is expected since the incorporation of nitrogen atoms into a PAH structure is associated with a reduced stability of the aromatic structure.²¹ The latter conclusion needs to be treated with care, as laser alignment differences between the two experiments may also induce slight differences.

The shift in the TAC˙⁺ photoproducts towards higher η-values can be either attributed to the incorporation of nitrogen atoms forming C_AN_B=1,2 cations or by more hydrogen atoms leading to C_AH_D=2–4. The complete absence of any C_AH₄ ions in the Cor˙⁺ experiments as well as the lower number of hydrogen atoms available in TAC˙⁺ compared to Cor˙⁺ (12 in Cor˙⁺ and 9 in TAC˙⁺) both point to nitrogen atom incorporation rather than the formation of carbon structures with extra hydrogen atoms. The nitrogen incorporation into Cor˙⁺ therefore expresses itself by lowering the propensity to form pure carbonaceous fragments, while raising the availability of mixed C/N/H-bearing fragments. In this context it is also interesting to mention that there is no experimental evidence supporting the formation of cationic fragments with three nitrogen atoms, suggesting that at least one nitrogen-atom is contained in the neutral co-fragment, or that structures with three nitrogen atoms are too high in energy and cannot be accessed.

The formation of nitrogenated cationic fragments seems obvious at first glance, considering that TAC has a C/N ratio of 7, and nitrogen atoms are distributed evenly over the molecular structure. Yet, previous studies showed that HCN elimination dominates for all investigated smaller PANHs,^21,42 and the only channel that has been shown to be able to compete with the HCN loss is hydrogen atom elimination.²¹ Consequently, literature data^21,42 currently predict the exclusive appearance of completely carbonaceous fragments for TAC˙⁺. The latter are still detected as major products in our experiments with TAC˙⁺, which simultaneously highlights their stability and provides experimental evidence that multiple nitrogen atoms can be efficiently eliminated from larger PANH structures.

Now that we established which fragments appear in the TAC˙⁺ case, we aim to deduce a possible dissociation mechanism. The photoprocessing of TAC˙⁺ is initiated in two different ways, by either losing a hydrogen atom and forming TAC-H⁺ or by loss of H_1–3 CN. The former channel reacts to m/z 320 on the time scale of our experiment, while the latter leads to m/z 274–276 from where two possibilities exist for further decays. One can eliminate another HCN fragment to form m/z 247 leading to mono nitrogenated or even pure carbonaceous species and the other towards dicyanopolyynes (Γ_n + 4), by expulsion of these as the charge-bearing fragments. The fact that masses corresponding to just three H_1–3 CN losses have only minor intensities indicates that this pathway is unfavorable and structures resulting from three HCN eliminations cannot be formed easily, ultimately resulting in the appearance of cyanopolyyne fragments (Γ_n + 2, Γ_n + 3).

From the data, it is inferred that the masses between m/z 220 and m/z 276 represent major branching points where nitrogen inclusion into cationic fragments is decided. We can try to visualize this mechanism by extrapolating from the dissociation mechanism of smaller PANHs. Recently, Subramani et al.²⁰ showed that the dissociation of the quinoline cation exhibits its lowest energy pathway towards pentalene via elimination of a neutral HCN fragment. If one considers TAC˙⁺ to be three separate quinoline units, all three nitrogen atoms may be eliminated via HCN fragments, resulting in a open bowl structure, due to the introduction of five-membered rings in the outside rings of the initially planar TAC˙⁺ structure. Such a dissociation mechanism is depicted schematically in Fig. 10. However, to agree with the less intense signals from m/z 220–222, the third HCN fragment has to have a lower propensity to be eliminated. One possible explanation for this observation is increasing geometrical strain in the molecule with each HCN loss step. As a result, the energies of the transition states likely increases as well, which may also be why nitrogen elimination is not exclusively observed. Pure carbon fragments, like C₁₁⁺, are then formed from either m/z 247–249 or m/z 220–222 in accordance with the previously established PAH dissociation mechanisms. Based on these findings we come to the conclusion that once PANHs reach a low nitrogen content, their dissociation characteristics become very similar to regular PAHs. Contrary, a higher nitrogen content can lead to incorporation of nitrogen atoms into cationic photoproducts. Furthermore, the introduction of nitrogen atoms in the coronene framework leads to an increased reactivity of key intermediates and different dissociation channels become more relevant.

Fig. 10 Possible HCN loss mechanisms for TAC.

The initial molecular transformations in PAH and PANH dissociation begin on the periphery of the molecule and so their shape and hetero atom substitution alter the dissociation mechanisms. In PAHs these effects have been investigated to some extend using experimental and computational techniques.^{16,18,43–46} Ekern et al.¹⁸ categorized PAHs when photodissociated using a Xenon arc lamp in four different groups: photostable, H-losses, H- and C-loss and completely photodestroyed. The main conclusion from their work is, that individual “exposed” aromatic rings are required in PAHs to see combined H- and C-losses. As such, highly symmetric PAHs, like the pericondensed coronene, show different dissociation patterns than irregular PAHs, like dibenzopyrenes. Our investigation of TAC˙⁺ offers the possibility to extend this phenomenological description to exoskeletal PANHs. Since the size of the PA(N)H can also affect its dissociation, we will only compare similar sized PAHs, like coronene and different dibenzopyrene (C₂₄H₁₄) isomers, to TAC˙⁺.

Even though TAC˙⁺ is a highly symmetrical PANH, the loss of small carbon fragments, like H_1–3 CN is akin to the C₂/C₂H₂ losses in irregular PAHs. Hence, its dissociation pattern aligns best with that of an irregular, catacondensed PAHs like the dibenzopyrenes (DBPs). This observation can be best explained by considering that “exposed” aromatic rings in PAHs have a low photostability and are easily cleaved off.^14,18 Similarly, nitrogen atom incorporation reduces the stability of aromatic rings,²¹ by acting as a breaking point in the molecular structure and facilitating the elimination of small carbonaceous fragments like HCN. As such, nitrogen containing rings, even in highly symmetric PANHs like TAC˙⁺, dissociate just like exposed rings in irregular PAHs resulting in their destruction and the occurrence of similar fragmentation patterns for both. However, these parallels reach their limits when looking at other photoproducts, like carbon clusters, the two differ substantially.

Further similarities between TAC˙⁺ and DBPs arise in their fragmentation mechanisms. Akin to our proposed formation of five-membered rings during the dissociation of TAC˙⁺ (see Fig. 10), Rodriguez Castillo et al.⁴⁴ observed the formation of a five-membered ring species after molecular hydrogen loss in dibenzo[a,l]pyrene. This supports our proposed reaction mechanism in Fig. 10 and suggests that exoskeletal PANHs and irregular PAHs both favor connected structures, instead of “exposed” aromatic rings during their photoprocessing.

4.2 Astrophysical implications

Nitrogen containing polyynes like HC_nN, C_nN, and NC_nN chains have already been detected in the atmosphere of Titan as well as in the coma of the comet 67P/Churyumov-Gerasimenko.^47–49 They are also suggested to be abundant in interstellar objects,^50,51 but the absence of a dipole moment makes it hard to identify dicyanopolyynes. Recently M. Agúndez et al.⁵² proposed the presence of NC₄N in the dark molecular cloud TMC-1, based on the detection of its protonated derivative NC₄NH⁺, providing first observational prove of their existence in the ISM. Another congener HC₅NH⁺ has been detected tentatively⁵³ and even though no cationic (di)cyanopolyyne has been detected yet, their presence is expected as their neutral counterparts have been detected. So far the origin of these molecules is thought to be from bottom-up chemistry.^54–56 The results presented here show that, among others, cyanopolyynes and dicyanopolyyne cations are likely created in the top-down photoprocessing of a PANH species.

In this context, their presence could help to evaluate the current predictions on nitrogen atom incorporation in PAHs. Based on current observations and shifts of the aromatic IR (AIR) bands, the amount of endoskeletal nitrogen atoms incorporated into the PAH framework has been suggested to be no more than 12%.¹¹ This estimate originates from the fact that endoskeletal PANHs exhibit an intense 11 μm band, which acts as a limiting factor. This feature is significantly reduced in regular PAHs as well as exoskeletal PANHs. Furthermore, exoskeletal CH/N substitutions alter the IR emission properties only marginally, if at all, making it almost impossible to discern between the two by IR observations alone. The number of nitrogen atoms that could be incorporated is also unclear and can hardly be identified by the aforementioned observational techniques. Photoproduct analysis could act as a more robust metric to determine the degree of nitrogen incorporation, independent from the AIR bands. Of course the difficulty to detect dicyanopolyynes also excludes them from being suitable tracers. However, our experiments show that the photoprocessing of TAC˙⁺ generates equal amounts of Γ_n + 0 and Γ_n + 3, while Γ_n + 1 is about 30% higher and Γ_n + 2 as well as Γ_n + 4, i.e. dicyanopolyynes, are approximately 30% less abundant (see Fig. 8). Although we cannot distinguish between nitrogen incorporation and additional hydrogen atoms in the detected fragments, it is likely that nitrogen atoms are also incorporated in the Γ_n + 2 and Γ_n + 3 channels. The resulting presence of cyano- (NC_n) and hydrocyanopolyynes (NC_nH), which both exhibit dipole moments, could potentially serve as a suitable tracer to estimate the degree of nitrogen incorporation in interstellar PAHs. This should lead to an upper limit, since the bottom-up production of these species represents a competing pathway. Future observations could actively search for cationic cyanopolyynes in the boundary layers between photon dominated regions and dark molecular clouds and determine their column densities to get a more reliable picture as to how common nitrogen atom incorporation in PAHs actually is.

5 Conclusion

We have investigated the photodissociation of a model PANH, TAC˙⁺ by simulating the continued photodissociation that occurs in photon dominated regions in space. The cations were retained in a Paul-Type ion-trap and irradiated using 630 nm photons from a dye laser. The photoproducts were subsequently ejected into a time-of-flight mass spectrometer and mass analyzed. TAC˙⁺ initially loses hydrogen atoms as well as up to three H_1–3CN fragments, while at lower m/z-values carbon based fragments appear that are accompanied by peaks with up to four hydrogen equivalents. Even though our setup cannot discriminate isobaric fragments, the presence of masses with three and four hydrogen equivalents in TAC˙⁺ and their complete absence in coronene demonstrates, that nitrogen atoms are also incorporated into these fragments. The size stability of the fragments suggests that masses below 10 heavy atoms are favored in the dissociation and double nitrogen incorporation is slightly less intense than single nitrogen or even pure carbon fragments. The dissociation mechanism is best described by a curl up of the planar PANH sheet from which cationic fragments are consequently ejected. The increasing rigidity of the intermediates likely impedes the elimination of the second and third HCN fragments, which may be the reason why nitrogen incorporation into lower mass fragments is observed. The dissociation characteristics of TAC˙⁺ can be best compared to that of an irregular PAH and consequently nitrogen-containing rings can be viewed similarly to “exposed” carbon rings in catacondensed PAHs. Both structural elements can be considered prominent breaking points in the molecular structure during their respective dissociation. The appearance of carbon fragments with one or two nitrogen atoms, shows that these species are formed in the dissociation of PANHs, which can ultimately help to determine the total nitrogen content in extraterrestrial PANHs.

Author contributions

Domenik Schleier: conceptualization, project administration, resources, investigation, formal analysis, writing – original draft, writing – review and editing, funding acquisition. Jerry Kamer: investigation, resources, writing – review and editing. Andy Jiao: resources, writing – review and editing. Grégory Schneider: resources, writing – review and editing. Harold Linnartz: writing – review and editing. Jordy Bouwman: conceptualization, funding acquisition, project administration, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

JB acknowledges the Netherlands Organisation for Scientific Research (Nederlandse Organisatie voor Wetenschappelijk Onderzoek, NWO) for a Vidi grant (grant number 723.016.006). This work was supported in part by NASAs Solar System Exploration Research Virtual Institute (SSERVI): Institute for Modeling Plasma, Atmosphere, and Cosmic Dust (IMPACT). DS acknowledges support by the PRIME programme of the German Academic Exchange Service (DAAD) with funds from the German Federal Ministry of Education and Research (BMBF). DS ackowledges a grant for computing time at the Paderborn Center for Parallel Computing PC² under the project PEPICON. DS gratefully acknowledges continued support by Prof. Tina Kasper and funding from DFG under project number KA 3871/3-2 and 270672969.

References

1. A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337.
2. M. López-Puertas, B. M. Dinelli, A. Adriani, B. Funke, M. García-Comas, M. L. Moriconi, E. DAversa, C. Boersma and L. J. Allamandola, Astrophys. J., 2013, 770, 132.
3. M. Delitsky and C. McKay, Icarus, 2010, 207, 477–484.
4. L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., 1985, 290, L25–L28.
5. A. Leger and J. L. Puget, Astron. Astrophys., 1984, 137, L5–L8.
6. L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., 1989, 71, 733.
7. D. A. Dale, M. Boquien, A. T. Barnes, F. Belfiore, F. Bigiel, Y. Cao, R. Chandar, J. Chastenet, M. Chevance, S. Deger, O. V. Egorov, K. Grasha, B. Groves, H. Hassani, K. F. Henny, R. S. Klessen, K. Kreckel, J. M. D. Kruijssen, K. L. Larson, J. C. Lee, A. K. Leroy, D. Liu, E. J. Murphy, E. Rosolowsky, K. Sandstrom, E. Schinnerer, J. Sutter, D. A. Thilker, E. J. Watkins, B. C. Whitmore and T. G. Williams, Astrophys. J., Lett., 2023, 944, L23.
8. R. Chown, A. Sidhu, E. Peeters, A. G. G. M. Tielens, J. Cami, O. Berné and E. Habart, Astron. Astrophys., 2023 DOI:10.1051/0004-6361/202346662.
9. E. Peeters, S. Hony, C. Van Kerckhoven, A. G. G. M. Tielens, L. J. Allamandola, D. M. Hudgins and C. W. Bauschlicher, Astron. Astrophys., 2002, 390, 1089–1113.
10. D. M. Hudgins, J. Charles, W. Bauschlicher and L. J. Allamandola, Astrophys. J., 2005, 632, 316–332.
11. A. Ricca, C. Boersma and E. Peeters, Astophys. J., 2021, 923, 202.
12. D. B. Rap, J. G. M. Schrauwen, A. N. Marimuthu, B. Redlich and S. Brünken, Nat. Astron., 2022, 6, 1059–1067.
13. T. Allain, S. Leach and E. Sedlmayr, Astron. Astrophys., 1996, 305, 616.
14. H. R. Hrodmarsson, J. Bouwman, A. G. M. Tielens and H. Linnartz, Int. J. Mass Spectrom., 2022, 476, 116834.
15. H. R. Hrodmarsson, J. Bouwman, A. G. Tielens and H. Linnartz, Int. J. Mass Spectrom., 2023, 485, 116996.
16. J. Bouwman, A. J. de Haas and J. Oomens, Chem. Commun., 2016, 52, 2636–2638.
17. S. Banhatti, D. B. Rap, A. Simon, H. Leboucher, G. Wenzel, C. Joblin, B. Redlich, S. Schlemmer and S. Brünken, Phys. Chem. Chem. Phys., 2022, 24, 27343–27354.
18. S. P. Ekern, A. G. Marshall, J. Szczepanski and M. Vala, J. Phys. Chem. A, 1998, 102, 3498–3504.
19. S. Panchagnula, J. Kamer, A. Candian, H. R. Hrodmarsson, H. Linnartz, J. Bouwman and A. Tielens, Phys. Chem. Chem. Phys., 2024 , accepted.
20. A. Subramani, K. Ramanathan, M. Selvaraj, M. Cautero, R. Richter, N. Pal, J. Chiarinelli, P. Bolognesi, L. Avaldi, M. V. Vinitha, C. S. Jureddy and U. R. Kadhane, J. Chem. Phys., 2023, 159, 104308.
21. J. Bouwman, B. Sztáray, J. Oomens, P. Hemberger and A. Bodi, J. Phys. Chem. A, 2015, 119, 1127–1136.
22. A. J. de Haas, J. Oomens and J. Bouwman, Phys. Chem. Chem. Phys., 2017, 19, 2974–2980.
23. J. Zhen, P. Castellanos, J. Bouwman, H. Linnartz and A. G. G. M. Tielens, Astrophys. J., 2017, 836, 28.
24. J. Zhen, A. Candian, P. Castellanos, J. Bouwman, H. Linnartz and A. G. G. M. Tielens, Astrophys. J., 2018, 854, 27.
25. J. Bouwman, P. Castellanos, M. Bulak, J. Terwisscha van Scheltinga, J. Cami, H. Linnartz and A. G. G. M. Tielens, Astron. Astrophys., 2019, 621, A80.
26. J. Bouwman, C. Boersma, M. Bulak, J. Kamer, P. Castellanos, A. G. G. M. Tielens and H. Linnartz, Astron. Astrophys., 2020, 636, A57.
27. J. Bouwman, H. Linnartz and A. G. Tielens, J. Mol. Spectrosc., 2021, 378, 111458.
28. J. Zhen, D. Paardekooper, A. Candian, H. Linnartz and A. Tielens, Chem. Phys. Lett., 2014, 592, 211–216.
29. J. Zhen, P. Castellanos, D. M. Paardekooper, H. Linnartz and A. G. G. M. Tielens, Astrophys. J., Lett., 2014, 797, L30.
30. P. Castellanos, A. Candian, J. Zhen, H. Linnartz and A. G. G. M. Tielens, Astron. Astrophys., 2018, 616, A166.
31. W. Zhang, Y. Si, J. Zhen, T. Chen, H. Linnartz and A. G. G. M. Tielens, Astrophys. J., 2019, 872, 38.
32. C. Zhang, X. Hu, Y. Ge, Z. Dong, Y. Yang, Jia Liu, Y. Chen, J. Zhen and L. Qin, Astron. Astrophys., 2023, 669, A41.
33. A. Simon, M. Rapacioli, G. Rouaut, G. Trinquier and F. X. Gadéa, Philos. Trans. R. Soc., A, 2017, 375, 20160195.
34. Tao Chen, Yi Luo and Aigen Li, Astron. Astrophys., 2020, 633, A103.
35. Q. Tan, H. Chen, H. Xia, B. Liu and B. Xu, Chem. Commun., 2016, 52, 537–540.
36. J. Zhen, S. R. Castillo, C. Joblin, G. Mulas, H. Sabbah, A. Giuliani, L. Nahon, S. Martin, J.-P. Champeaux and P. M. Mayer, Astrophys. J., 2016, 822, 113.
37. G. Wenzel, C. Joblin, A. Giuliani, S. Rodriguez Castillo, G. Mulas, M. Ji, H. Sabbah, S. Quiroga, D. Peña and L. Nahon, Astron. Astrophys., 2020, 641, A98.
38. K. Pearson and O. M. F. E. Henrici, Philos. Trans. R. Soc. London, 1895, 186, 343–414.
39. D. Schleier, J. Kamer, J. Martens, G. Berden, J. Oomens and J. Bouwman, ChemPhysChem, 2024 , accepted.
40. R. Sparrapan, M. A. Mendes, M. Carvalho and M. N. Eberlin, Chem. – Eur. J., 2000, 6, 321–326.
41. J. Kamer, D. Schleier, A. Jiao, G. Schneider, J. Martens, G. Berden and J. Bouwman, Phys. Chem. Chem. Phys. , in preparation.
42. A. J. de Haas, J. Oomens and J. Bouwman, Phys. Chem. Chem. Phys., 2017, 19, 2974–2980.
43. P. Pla, C. Dubosq, M. Rapacioli, E. Posenitskiy, M. Alcamí and A. Simon, J. Phys. Chem. A, 2021, 125, 5273–5288.
44. S. Rodriguez Castillo, A. Simon and C. Joblin, Int. J. Mass Spectrom., 2018, 429, 189–197.
45. O. Berné and A. G. G. M. Tielens, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 401–406.
46. G. Trinquier, A. Simon, M. Rapacioli and F. X. Gadéa, Mol. Astrophys., 2017, 7, 37–59.
47. M. B. Bell, P. A. Feldman, M. J. Travers, M. C. McCarthy, C. A. Gottlieb and P. Thaddeus, Astrophys. J., 1997, 483, L61.
48. C. Mathé, T. Gautier, M. G. Trainer and N. Carrasco, Astrophys. J., Lett., 2018, 861, L25.
49. N. Hänni, K. Altwegg, H. Balsiger, M. Combi, S. A. Fuselier, J. De Keyser, B. Pestoni, M. Rubin and S. F. Wampfler, Astron. Astrophys., 2021, 647, A22.
50. R. Khanna, M. Perera-Jarmer and M. Ospina, Spectrochim. Acta, Part A, 1987, 43, 421–425.
51. S. Petrie, T. J. Millar and A. J. Markwick, Mon. Not. R. Astron. Soc., 2003, 341, 609–616.
52. M. Agúndez, C. Cabezas, N. Marcelino, R. Fuentetaja, B. Tercero, P. de Vicente and J. Cernicharo, Astron. Astrophys., 2023, 669, L1.
53. N. Marcelino, M. Agúndez, B. Tercero, C. Cabezas, C. Bermúdez, J. D. Gallego, P. deVicente and J. Cernicharo, Astron. Astrophys., 2020, 643, L6.
54. O. Kostko, J. Zhou, B. J. Sun, J. S. Lie, A. H. Chang, R. I. Kaiser and M. Ahmed, Astrophys. J., 2010, 717, 674.
55. T. Grösser and A. Hirsch, Angew. Chem., Int. Ed. Engl., 1993, 32, 1340–1342.
56. I. Cherchneff, A. E. Glassgold and G. A. Mamon, Astrophys. J., 1993, 410, 188.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01387e

‡ These authors contributed equally to this work.

§ Present address: Institut für Optik und Atomare Physik, Technische Universität Berlin, Hardenbergstr. 36, Berlin 10623, Germany.

---