Can we quantitatively evaluate the mutual impacts of intramolecular metal–ligand bonds the same as intermolecular noncovalent bonds?†
Received
31st March 2024
, Accepted 30th April 2024
First published on 30th April 2024
Abstract
In this paper, we have reviewed several equations for calculating the cooperative energy of two chemical bonds between three fragments/species, regardless of whether they are atoms, ions or molecules, and whether the bonds between them are intra- or intermolecular. It is emphasized that two chemical bonds upon cooperation in a new compound change the bond dissociation energy of each other exactly by the same quantitative value, their cooperative energy, regardless of the nature of the bonds or whether one bond is very weak and another one is very strong. However, the final benefit/drawback of weak bonds from this cooperation can be considerably larger than that of strong bonds. The above statements are supported by a computational study on the various types of inter- and intramolecular chemical bonds.
1. Introduction
Understanding the possible effects of chemical bonds on each other and the total stability of a system of bonds will help us to design the desired molecular and supramolecular systems rationally. Among all types of chemical bonds, only the mutual impact of intermolecular noncovalent bonds on the strength of each other, named the cooperativity of bonds, has been extensively studied during the last six decades.1 There are some well-known methodologies for the evaluation of the cooperativity of noncovalent bonds and the calculation of related cooperative energies. The following equations have been frequently used for the evaluation of the cooperativity of coinage-metal bonds with other types of interactions2–13 and also that of intermolecular noncovalent bonds, especially those including hydrogen bonds,14–25 dihydrogen bonds,26–28 beryllium bonds,29,30 lithium bonds,31–34 lithium–π,35 halogen bonds,36–48 chalcogen bonds,49–51 pnicogen bonds,52–56 cation–π interactions,57–60 anion–π interactions,61–63 π⋯π interactions,64σ-hole65,66 and π-hole67–70 interactions in ternary systems.| | | ΔABC = IEtotalABC − (IEABCA–B + IEABCB–C + IEABCA–C) | (1) |
| | | Ecoop = SEABC − (SEAB + SEBC + SEABCAC) | (2) |
| | | Ecoop = SEABC − (SEAB + SEBC) | (3) |
In the above equations, ΔABC and Ecoop correspond to the three-body term71–77 and cooperative energy, respectively. The term IEtotalABC is used for the value of the total interaction energy of the ABC system, and the terms IEABCAB, IEABCBC and IEABCAC are used for pairwise interaction energies in the structure of the ABC system. Also, the term SEABC is used for the total stabilization energy of a ternary system, and the terms SEAB and SEBC are used for the stabilization energy of the corresponding isolated AB and BC systems in their optimized geometries, respectively. The term SEABCAC also represents the stabilization energy of the AC pair frozen into the geometry of the ABC system. To the best of our knowledge, still, two following important questions have never been clearly answered:
(I) Can we quantitatively evaluate the cooperative energies of all types of chemical bonds?
(II) Do chemical bonds have the same impacts on the values of bond dissociation energies of each other?
The main aim of this paper is to answer both the above important questions. Herein, we show that in agreement with the law of conservation of energy and Hess's law, two A–B and B–C chemical bonds upon cooperation in a new ABC compound change the energy of each other exactly by the same quantitative value, even when one bond is very strong and the other one is very weak. One can arbitrarily name such a phenomenon the “intrinsic cooperativity of bonds”, and evaluate it for all types of chemical bonds using the equations recommended here. Several equations are proposed and used for calculating the total stabilization and interaction energies of ABC systems and the cooperativity of bonds in such systems. All equations are tested in different ABC systems with intermolecular noncovalent bonds or intramolecular metal–ligand bonds.
2. Theoretical methods
The geometries of all systems of intermolecular bonds (compounds 1 to 6) were fully optimized at the DFT level with the BP86-D3(BJ)78 functional (a DFT function and D3 version of Grimme's dispersion with Becke–Johnson damping for dispersion correction) and also the MP279–82 method in combination with aug-cc-pVTZ83,84 and def2-TZVP85,86 basis sets using the GAUSSIAN-0987 program without any symmetry restrictions for all the above compounds. For compounds 1 to 6, the data at BP86-D3(BJ)/def2-TZVP and MP2/def2-TZVP levels of theory are given in the ESI.† Similarly, the geometries of all systems of intramolecular metal–ligand bonds (compounds 7 to 12) were fully optimized at the DFT level with the BP86-D3(BJ) functional and also MP2 method in combination with the def2-TZVP basis set. In the case of molybdenum, gold, mercury and lead metal ions, the inner shell electrons were modelled by effective core potentials (ECPs), which reduce the required basis set size and account for scalar relativistic effects.85,86,88 In the case of compound 8, exceptionally, the geometry of the complex was optimized at the MP2/def2-SVP level of theory. In all cases, vibrational frequency analysis, calculated at the above levels of theory, indicates that the optimized structures are at the stationary points corresponding to local minima without any imaginary frequency. Herein, we use the terms stabilization energy (SE), bond dissociation energy (BDE), and interaction energy (IE) when we refer to how much a system is energetically more stable than its isolated components, how much the required energy for dissociation of a defined bond, and how much is the attractive/repulsive energy between some species frozen into the geometry of a system, respectively (see also Fig. 1). The energy required for the probable deformation of a species upon interaction with other species is also shown as Es. Indeed, the deformation or strain energy (Es) is the difference between the values of stabilization or bond dissociation energies and interaction energies. The larger positive value of Es is a reason for a larger difference between SE (or –BDE) and IE values (see Fig. 1).89–97 The following equations, for instance, show how we calculate the total stabilization of an ABC system (SEABC), the bond dissociation energy of an A–BC bond (BDEA–BC) and also its interaction energy (IEABCA–BC):| | | SEABC = EABC − (EA + EB + EC) | (4) |
| | | –BDEA–BC = EABC − (EA + EBC) | (5) |
| | | IEABCA–BC = EABC − (EABCA + EABCBC) | (6) |
In the above equations, the EABC, EBC, EA, EB and EC are the electronic energies of ABC, BC, A, B and C, respectively, in their optimized geometries. On the other hand, EABCA and EABCBC are the electronic energies of A and BC frozen in the optimized geometry of ABC. All calculated SE, IE and BDE values are corrected for the basis set superposition error (BSSE), which was estimated with the counterpoise (CP) method proposed by Boys and Bernardi.98 The corrected data are given here, and uncorrected data are given in the ESI† of the paper. However, the BSSE correction can be ignored for standard chemical bonds because it can be significantly overestimated. In this work, only in the case of compound 8, at the MP2/def2-SVP level of theory, the BSSE corrections have large values.
 |
| | Fig. 1 Typical energy profile for the formation of AB, BC and ABC systems, along with the definition of stabilization energies (SEs) and bond dissociation energies (BDEs), as well as total deformation (strain) energy (Es) and total interaction energy (IEABCtotal) in the ABC system. As can be seen, it is arbitrarily assumed that the AB system is more stable than the BC system, and the bond dissociation energies (BDEs) of A–BC and AB–C bonds are larger than those of A–B and B–C bonds. | |
3. Results and discussion
When we want to compare the strength of two chemical bonds, we must be aware of the difference between the bond dissociation energy of a bond and its interaction energy. It is revealed that for some metastable compounds, the BDE values may even be negative.99–101 It has been shown that when the positive value of strain (deformation) energies (Es) of species involved in the bond are larger than the negative value of their intrinsic interaction energy (IE), the BDE value (–BDE = IE + Es) will be negative.102 Thus, in order to accurately evaluate the impact of bonds on each other, in addition to comparing the BDE values of the bonds, we have to compare their IEs. Thus, in this work, the mutual impacts of chemical bonds are studied with the comparison of both bond dissociation energies and interaction energies. Using the following equation one can show that the difference between the BDEs of the A–B and A–BC bonds, regardless of the type and nature of bonds, always is the same as that of B–C and AB–C bonds.| | | BDEA–B − BDEA–BC = BDEB–C − BDEAB–C | (7) |
Let us name the left and right sides of the above equation as ΔBDEA–B and ΔBDEB–C, respectively. Using eqn (8), it can be shown that the above differences in bond dissociation energies of A–B and A–BC bonds (ΔBDEA–B) or of B–C and AB–C bonds (ΔBDEB–C) are equal to Ecoop calculated using eqn (3):| | | Ecoop = ΔBDEA–B = ΔBDEB–C | (8) |
Obviously, we can correct the calculated ΔBDEA–B and ΔBDEB–C values, and therefore the Ecoop values, for A⋯C stabilization energy (SEAC).
As explained above, in this work, the mutual impact of chemical bonds is also studied with the comparison of interaction energies. However, the comparison of interaction energies of A–B and B–C bonds in AB and BC systems with those in the resulting noncyclic ABC systems usually leads to a wrong conclusion. As has been explained previously, in some cases even where the system has a negative cooperative energy (having the intrinsic positive cooperativity), the values of interaction energies for A–B and B–C bonds in the ABC system are even slightly smaller than those in the AB and BC systems, respectively.103 Thus, in this work, in the ABC geometry, four A–B, B–C, A–BC and AB–C interaction energies are calculated and compared. Interestingly, the following useful and meaningful equation shows that, in the ABC geometry, the difference between the values of A–BC and A–B interactions is the same as that of AB–C and B–C interactions.
| | | IEABCA–BC − IEABCA–B = IEABCAB–C − IEABCB–C | (9) |
We name the left and right sides of the above equation as ΔIE
A–B and ΔIE
B–C, respectively. Thus, an interaction-based cooperative energy (ΔIE
coop) that represents the impact of two bonding interactions on the value of each other can be calculated as below:
| | | ΔIEcoop = ΔIEA–B = ΔIEB–C | (10) |
Once again, we can correct the calculated ΔIE
A–B and ΔIE
B–C values, and therefore the ΔIE
coop values, for the A⋯C interaction energy (IE
ABCA–C). The most important benefit of
eqn (10) is that even where we have no information about AB and BC systems (for example when both or one of them is not a stable system), still in the structure of the ABC system, we can evaluate the impact of A–B and B–C interactions on each other. Obviously, with considering the data derived from both
eqn (8) and (10) one can better evaluate the impact of bonds on the strength of each other.
3.1. Cooperativity in some systems of intermolecular bonds
Different types of intermolecular bonds, including the hydrogen bond, cation–π bond, chalcogen bond, halogen bond and lithium bond, were selected for the present study. The A, B and C species are defined in Fig. 2, and the optimized structures of related ABC systems are given in Fig. 3. The calculated stabilization-based and interaction-based cooperative energies are presented in Tables 1 and 2, respectively.
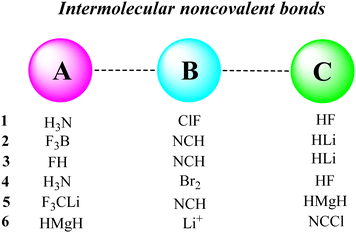 |
| | Fig. 2 Species A, B and C in the triads studied in this work. | |
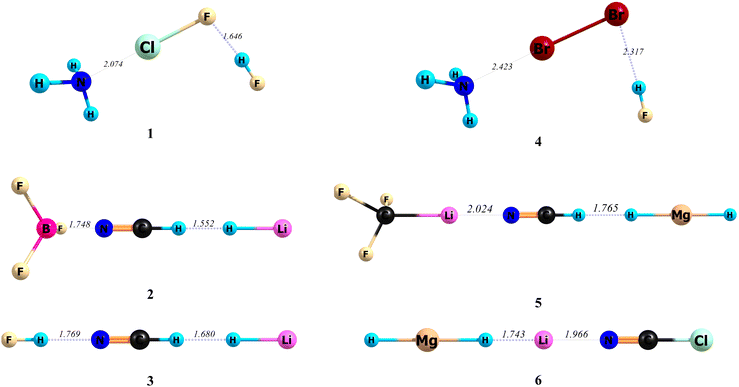 |
| | Fig. 3 The optimized structures and related A–B and B–C bond lengths (Å) of the triads studied here, at the MP2/aug-cc-pVTZ level of theory. | |
Table 1 Correcteda bond dissociation energies, cooperative energies (kcal mol−1) and the percentages of changes in the bond dissociation energies of A–B and B–C bonds upon the formation of triads studied hereb
| Compound |
–BDEA–B |
–BDEA–BC |
–BDEB–C |
–BDEAB–C |
SEABCc |
E
coop
|
%ΔBDEA–Be |
%ΔBDEB–Ce |
Corrected for basis set superposition errors (BSSEs).
The data calculated at the BP86-D3(BJ)/aug-cc-pVTZ level of theory are given as plain text and those at the MP2/aug-cc-pVTZ level are in bold.
See eqn (4) and eqn (S2)–(S5) (ESI), all of which give the same value.
See eqn (3) and (8), both of which give the same value.
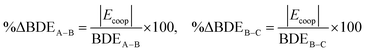 .
Corrected for SEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3). .
Corrected for SEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
|
|
1
|
−17.84 |
−25.65 |
−1.65 |
−9.46 |
−27.30 |
−7.81(−8.06)f |
44% |
473% |
| −10.94 |
−16.94 |
−2.00 |
−8.00 |
−18.94 |
−6.00(−5.70) |
55%
|
300%
|
|
|
|
2
|
−4.30 |
−10.14 |
−8.83 |
−14.67 |
−18.97 |
−5.84(−23.05) |
136% |
66% |
| −5.17 |
−9.18 |
−8.58 |
−12.59 |
−17.76 |
−4.01(−20.22) |
78%
|
47%
|
|
|
|
3
|
−7.69 |
−11.10 |
−8.83 |
−12.24 |
−19.93 |
−3.41(−2.94) |
44% |
39% |
| −7.35 |
−10.06 |
−8.58 |
−11.29 |
−18.64 |
−2.71(−1.99) |
37%
|
32%
|
|
|
|
4
|
−12.18 |
−15.83 |
−2.60 |
−6.25 |
−18.43 |
−3.65(−3.81) |
30% |
140% |
| −6.81 |
−9.14 |
−1.78 |
−4.11 |
−10.92 |
−2.33(−2.03) |
34%
|
131%
|
|
|
|
5
|
−17.96 |
−21.24 |
−3.85 |
−7.13 |
−25.09 |
−3.28(−2.46) |
18% |
85% |
| −17.94 |
−20.91 |
−3.68 |
−6.65 |
−24.59 |
−2.97(−2.09) |
17%
|
81%
|
|
|
|
6
|
−31.42 |
−24.56 |
−38.74 |
−31.88 |
−63.30 |
6.86(8.59) |
22% |
18% |
| −31.17 |
−25.16 |
−36.36 |
−30.35 |
−61.52 |
6.01(7.57)
|
19%
|
17%
|
Table 2 Correcteda calculated values for interaction energies (IE, kcal mol−1) between the defined fragments frozen in the optimized geometry of the triads studied here, and related IEABCtotal, %ΔIECoop, %ΔIEA–B and %ΔIEB–C valuesb
| Compound |
IEABCA–B |
IEABCA–BC |
IEABCB–C |
IEABCAB–C |
IEABCtotal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
ΔIEcoopd |
%ΔIEA–Be |
%ΔIEB–Ce |
Corrected for basis set superposition errors (BSSEs).
The data calculated at the BP86-D3(BJ)/aug-cc-pVTZ level of theory are given as plain text and those at the MP2/aug-cc-pVTZ level are in bold.
See eqn (S8)–(S11) (ESI), all of which give the same value.
See eqn (10).
 .
Corrected for IEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3). .
Corrected for IEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
|
|
1
|
−24.28 |
−33.23 |
−1.94 |
−10.89 |
−35.17 |
−8.95(−8.23)f |
37% |
461% |
| −15.24 |
−23.23 |
−1.77 |
−9.76 |
−25.00 |
−7.99(−7.18) |
52%
|
451%
|
|
|
|
2
|
−20.83 |
−29.87 |
−9.95 |
−18.99 |
−39.82 |
−9.04(−7.70) |
43% |
91% |
| −20.25 |
−27.74 |
−8.58 |
−16.07 |
−36.32 |
−7.49(−6.05) |
37%
|
87%
|
|
|
|
3
|
−8.05 |
−11.78 |
−9.52 |
−13.25 |
−21.30 |
−3.73(−2.78) |
46% |
39% |
| −7.48 |
−10.46 |
−8.76 |
−11.74 |
−19.22 |
−2.98(−2.02) |
40%
|
34%
|
|
|
|
4
|
−14.34 |
−18.43 |
−2.61 |
−6.70 |
−21.04 |
−4.09(−3.68) |
29% |
157% |
| −7.47 |
−10.69 |
−1.55 |
−4.77 |
−12.24 |
−3.22(−2.74) |
43%
|
208%
|
|
|
|
5
|
−18.11 |
−21.73 |
−3.89 |
−7.51 |
−25.62 |
−3.62(−2.64) |
20% |
93% |
| −18.08 |
−21.18 |
−3.71 |
−6.81 |
−24.89 |
−3.10(−2.09) |
17%
|
84%
|
|
|
|
6
|
−31.64 |
−24.94 |
−38.93 |
−32.23 |
−63.87 |
6.70(7.85) |
21% |
17% |
| −31.44 |
−25.56 |
−36.52 |
−30.64 |
−62.08 |
5.88(6.89)
|
19%
|
16%
|
In all cases, the data in Table 1 confirm that the difference between the BDEs of A–B and A–BC bonds is the same as that between B–C and AB–C bonds, and can be equal to the cooperative energy of the bonds. Among the triads studied in this work, the largest percentage of changes in the value of a bond dissociation energy was observed in triad 1, where a very weak ClF⋯HF (B–C) hydrogen bond upon the formation of this triad converts into the much stronger {H3N⋯ClF}⋯HF (AB–C) hydrogen bond. The percentages of changes for the above bond are 473 and 300% at BP86-D3(BJ)/aug-cc-pVTZ and MP2/aug-cc-pVTZ levels of theory, respectively. It should be noted that HF⋯ClF is an alternative possible complex between the ClF and HF molecules. The HF⋯ClF and ClF⋯HF dyads upon the interaction with the NH3 molecule form the H3N⋯HF⋯ClF and H3N⋯ClF⋯HF triads, respectively. While the HF⋯ClF dyad, having the halogen bond instead of a hydrogen bond (initially called antihydrogen bonding),104–107 is more stable than the ClF⋯HF dyad, the H3N⋯HF⋯ClF triad is less stable than the H3N⋯ClF⋯HF triad. Indeed, the larger strength of the H3N⋯ClF bond, compared to the H3N⋯HF bond, and the larger cooperative energy of the bonds in the H3N⋯ClF⋯HF triad, compared to the H3N⋯HF⋯ClF triad, are two important reasons that H3N⋯ClF⋯HF is the more stable triad (see Tables S1 and S2, ESI†). As can be seen in Table 1, only in the case of triad 6, there is an intrinsic negative cooperativity (anticooperativity), where the HMgH⋯{Li+⋯NCCl} (A–BC) and {HMgH⋯Li+}⋯NCCl (AB–C) bonds are weaker than initial HMgH⋯Li+ (A–B) and Li+⋯NCCl (B–C) bonds, respectively. For a typical example, let us review the data for triad 5 (F3CLi⋯NCH⋯HMgH). The BDEs of A–BC and AB–C bonds at the MP2/aug-cc-pVTZ level of theory are 20.91 and 6.65 kcal mol−1 and both of them, by a value of 2.97 kcal mol−1, are larger than the corresponding values of 17.94 and 3.68 kcal mol−1 for BDEs of A–B and B–C bonds, respectively. Thus, according to eqn (1), the stabilization-based cooperative energy of the above bonds is −2.97 kcal mol−1. Indeed, the net changes in the BDEs of the F3CLi⋯NCH (A–B) and NCH⋯HMgH (B–C) bonds upon the formation of the F3CLi⋯NCH⋯HMgH (ABC) triad and converting into F3CLi⋯{NCH⋯HMgH} (A–BC) and {F3CLi⋯NCH}⋯HMgH (AB–C) bonds, respectively, are the same. However, the related percentages of the changes are 17 and 81%, respectively. Thus, the percentage of the change, as expected, is larger for the weaker bond (NCH⋯HMgH). Interaction-based cooperative energies were also calculated using eqn (9) and (10). For example, for triad 5 discussed above, the values of A–B, A–BC, B–C, and AB–C interaction energies are −18.08, −21.18, −3.71, and −6.81 kcal mol−1, respectively. Thus the IEABCA–BC and IEABCAB–C values are larger than the corresponding IEABCA–B and IEABCB–C values, respectively, by a value of −3.10 kcal mol−1. In conclusion, according to eqn (10) the interaction-based cooperative energy of F3CLi⋯NCH (A–B) and NCH⋯HMgH (B–C) bonds in the F3CLi⋯NCH⋯HMgH triad is −3.10 kcal mol−1. The comparison of data in Tables 1 and 2 shows that in all cases, except triad 2 (F3B⋯NCH⋯HLi), the interaction-based cooperative energies (ΔIEcoop) do not differ significantly from the stabilization-based cooperative energies (Ecoop).
However, in triad 2, the values of Ecoop at BP86-D3(BJ)/aug-cc-pVTZ and MP2/aug-cc-pVTZ levels of theory are −5.84 and −4.01 kcal mol−1, but ΔIEcoop values are −9.04 and −7.49 kcal mol−1, respectively. Interestingly, this difference arises from the fact that the IE and BDE values only in the case of triad 2 differ significantly. The values of –BDE and IE at the MP2/aug-cc-pVTZ level of theory for the F3B⋯NCH bond are −5.17 and −6.75 kcal mol−1, respectively, and do not differ significantly (see Fig. 4a). In contrast, as shown in Fig. 4b, the values of –BDE and IE for the F3B⋯{NCH⋯HLi} bond at the same level of theory are −9.18 and −27.74 kcal mol−1, respectively, and there is a large difference between them. We note that the planar structure of the BF3 molecule, upon the interaction with the NCH molecule, only in the case of triad 2 changes significantly. Thus, the deformation energy of the BF3 molecule in triad 2 is considerably larger than that in the related F3B⋯NCH dyad. In fact, from the total deformation energies (18.56 kcal mol−1) of interacted species in triad 2, an amount of 17.66 kcal mol−1 belongs to the BF3 molecule. Obviously, the calculated interaction energies do not depend only on the strength of interactions, and they increase with increasing the amount of deformation energies. In conclusion, as can be seen in Fig. 4a and b, both the IEABCA–B and IEABCA–BC interaction energies have a large value, and the difference between them is also relatively large. Therefore, the difference between IEs of F3B⋯NCH (A–B) and F3B⋯{NCH⋯HLi} (A–BC) bonds (ΔIEcoop = −7.49 kcal mol−1) is considerably larger than that between BDEs of these bonds (Ecoop = −4.01 kcal mol−1).
 |
| | Fig. 4 Comparison of the BDEs and IEs of the A–B bond in the optimized geometry of the F3B⋯NCH (AB) dyad and also the IE of the A–B bond in the F3B⋯NCH (AB) dyad frozen into the optimized geometry of the F3B⋯NCH⋯HLi (ABC) triad (a), and comparison of the BDEs and IEs of the A–BC bond in the optimized geometry of the F3B⋯NCH⋯HLi triad (b). | |
On the other hand, the comparison of the values of %ΔBDEA–B and %ΔIEA–B in Tables 1 and 2, respectively, show that the percentage of change in the BDE of the F3B⋯NCH bond (78%) is larger than that of its IE (37%). Furthermore, the data show that the F3B⋯{NCH⋯HLi} bond with a length of 1.748 Å, is considerably shorter than the F3B⋯NCH bond, having a length of 2.361 Å (see Fig. 3 and Fig. S1, and also Table S3, ESI†). Thus, we can conclude that only the ΔIEcoop and %ΔBDEA–B values clearly explain why the change in the length of the F3B⋯NCH bond is very large. In conclusion, the data for triad 2 clearly show that where the deformation energies of interacted species are very large, the comparison of the ΔIEcoop values and/or the percentage of change in the BDE values (%ΔBDEA–B) are more reliable than the comparison of Ecoop values. On the other hand, one may be interested in comparing the A–B and B–C interaction energies in AB and BC systems with A–BC and AB–C interaction energies in the ABC system, respectively. However, nobody has proved that the related differences are the same (i.e. ).
).
Furthermore, such comparisons sometimes will lead us to wrong conclusions. For example, in the case of triad 2, the values of IEABCA–BC and IEABCAB–C at the MP2/aug-cc-pVTZ level of theory are −27.74 and −16.07 kcal mol−1, while those of IEA–B and IEB–C for corresponding F3B⋯NCH and NCH⋯HLi dyads are −6.75 and −8.76 kcal mol−1, respectively. Thus, the difference between IEABCA–BC and IEA–B is −20.99 kcal mol−1, while that between IEABCAB–C and IEB–C is −7.31 kcal mol−1. Therefore, the above differences differ significantly, and in contrast to the concept of cooperativity of bonds are not the same. However, when we compare the IEABCA–BC and IEABCA–B values in the F3B⋯NCH⋯HLi triad, because the large deformation energy of the BF3 molecule has the same effect on their values, the difference between them is not too large and is the same as that between the IEABCAB–C and IEABCB–C values (ΔIEcoop = −7.49 kcal mol−1).
3.2. Cooperativity in some systems of intramolecular bonds
Herein, we report the quantitative evaluation of some intramolecular metal–ligand bonds. The various types of metal complexes are selected and considered as an ABC system having two A–B and B–C bonds. The A, B and C fragments are defined in Fig. 5 and the optimized structure of complexes is presented in Fig. 6. The optimized structures of the complexes are all very similar to their available solid-state molecular structures108–111 determined by X-ray crystallography (see also Table S12, ESI†). The data for calculating the stabilization-based and interaction-based cooperative energies are presented in Tables 3 and 4, respectively.
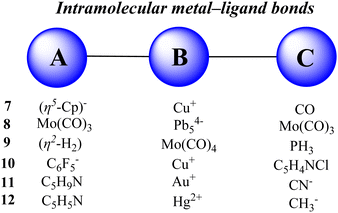 |
| | Fig. 5 Fragments A, B and C in the metal complexes studied here. | |
 |
| | Fig. 6 The optimized structures and related A–B and B–C bond lengths (Å) for the metal complexes studied here, at the MP2/def2-TZVP level of theory for compounds 7, 9–12, and at the MP2/def2-SVP level in the case of compound 8. | |
Table 3 Correcteda bond dissociation energies, cooperative energies (kcal mol−1) and the percentages of changes in the bond dissociation energies of A–B and B–C bonds upon the formation of metal complexes studied hereb
| Compound |
–BDEA–B |
–BDEA–BC |
–BDEB–C |
–BDEAB–C |
SEABCc |
E
coop
|
%ΔBDEA–Be |
%ΔBDEB–Ce |
Corrected for basis set superposition errors (BSSEs).
The data calculated at the BP86-D3(BJ)/aug-cc-pVTZ level of theory are given as plain text and those at the MP2/aug-cc-pVTZ level are in bold.
See eqn (4) and eqn (S2)–(S5) (ESI), all of which give the same value.
See eqn (3) and (8) both of which give the same value.
 .
Corrected for SEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
MP2 calculations for this compound were performed using the def2-SVP basis set. .
Corrected for SEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
MP2 calculations for this compound were performed using the def2-SVP basis set.
|
|
7
|
−198.26 |
−207.49 |
−47.50 |
−56.73 |
−249.99 |
−9.23(−7.03)f |
5% |
19% |
| −184.81 |
−202.74 |
−32.70 |
−50.63 |
−235.44 |
−17.93(−17.92) |
10%
|
55%
|
|
|
|
8
|
— |
— |
— |
— |
−303.77 |
— |
— |
— |
| — |
— |
— |
— |
−352.21
|
— |
— |
— |
|
|
|
9
|
−34.99 |
−19.91 |
−57.64 |
−42.56 |
−77.55 |
15.08(11.61) |
43% |
26% |
| −34.03 |
−21.98 |
−60.98 |
−48.93 |
−82.96 |
12.05(8.84)
|
35%
|
20%
|
|
|
|
10
|
−198.57 |
−167.15 |
−74.98 |
−43.56 |
−242.13 |
31.42(24.71) |
16% |
42% |
| −178.54 |
−162.86 |
−57.32 |
−41.64 |
−220.18 |
15.68(9.29)
|
9%
|
27%
|
|
|
|
11
|
−94.23 |
−51.76 |
−227.78 |
−185.31 |
−279.54 |
42.47(35.47) |
45% |
19% |
| −81.30 |
−55.76 |
−214.63 |
−189.09 |
−270.39 |
25.54(17.71)
|
31%
|
12%
|
|
|
|
12
|
−198.50 |
−62.58 |
−518.47 |
−382.55 |
−581.05 |
135.92(134.38) |
68% |
26% |
| −172.87 |
−60.78 |
−507.09 |
−395.00 |
−567.87 |
112.09(101.30)
|
65%
|
22%
|
Table 4 Correcteda calculated values for interaction energies (IE, kcal mol−1) between the defined fragments frozen in the optimized geometry of metal complexes studied here, and related IEABCtotal, ΔIEcoop, %ΔIEA–B and %ΔIEB–C valuesb
| Compound |
IEABCA–B |
IEABCA–BC |
IEABCB–C |
IEABCAB–C |
IEABCtotal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
ΔIEcoopd |
%ΔIEA–Be |
%ΔIEB–Ce |
Corrected for basis set superposition errors (BSSEs).
The data calculated at the BP86-D3(BJ)/aug-cc-pVTZ level of theory are given as plain text and those at the MP2/aug-cc-pVTZ level are in bold.
See eqn (S8)–(S11) (ESI), all of which give the same value.
See eqn (10).
 .
Corrected for IEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
The MP2 calculations for this compound were performed using the def2-SVP basis set. .
Corrected for IEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
The MP2 calculations for this compound were performed using the def2-SVP basis set.
|
|
7
|
−198.37 |
−209.81 |
−45.88 |
−57.32 |
−255.69 |
−11.44(−8.54)f |
6% |
25% |
| −184.72 |
−203.15 |
−32.98 |
−51.41 |
−236.13 |
−18.43(−17.73) |
10%
|
56%
|
|
|
|
8
|
−136.15 |
−190.22 |
−152.13 |
−206.20 |
−342.35 |
−54.07(−59.71) |
40% |
35% |
| −184.14 |
−218.13 |
−187.00 |
−220.99 |
−405.13 |
−33.99(−39.94) |
18%
|
18%
|
|
|
|
9
|
−35.61 |
−23.46 |
−57.57 |
−45.42 |
−81.03 |
12.15(12.02) |
34% |
21% |
| −34.24 |
−25.35 |
−61.24 |
−52.35 |
−86.59 |
8.89(8.77)
|
26%
|
14%
|
|
|
|
10
|
−200.84 |
−169.89 |
−75.17 |
−44.22 |
−245.06 |
30.95(27.17) |
15% |
41% |
|
−180.27
|
−164.82 |
−57.50 |
−42.05 |
−222.32 |
15.45(11.20)
|
9%
|
27%
|
|
|
|
11
|
−93.87 |
−52.80 |
−227.76 |
−186.69 |
−280.56 |
41.07(35.09) |
44% |
18% |
| −81.45 |
−56.59 |
−214.77 |
−189.91 |
−271.36 |
24.86(18.00)
|
30%
|
12%
|
|
|
|
12
|
−197.13 |
−64.40 |
−519.04 |
−386.31 |
−583.44 |
132.73(133.57) |
67% |
26% |
| −171.42 |
−63.86 |
−505.94 |
−398.38 |
−569.80 |
107.56(98.70)
|
63%
|
21%
|
The data show that in complex 7 there is an intrinsic positive cooperativity, while in complexes 9 to 12 an intrinsic negative cooperativity (anticooperativity) exists. For complex 7, the calculated Ecoop values at BP86-D3(BJ)/def2-TZVP and MP2/def2-TZVP levels of theory are −9.23 and −17.93 kcal mol−1, respectively. Thus, the BDEs of (η5-Cp)–AuCO and (η5-Cp)Au–CO bonds are larger than the initial (η5-Cp)–Au and Au–CO bonds, respectively. On the other hand, the percentages of changes in the value of initial bonds at the BP86-D3(BJ)/def2-TZVP and MP2/def2-TZVP levels of theory are 5 and 10% for the (η5-Cp)–Au bond, and 19 and 55% of the Au–CO bond, respectively. Thus, while the BDEs of both the initial bonds, upon the formation of the [(η5-Cp)AuCO] complex, change by the same quantitative value, the percentage of change for the weaker Au–CO bond is larger than that for the stronger (η5-Cp)–Au bond. Among the complexes studied here, the largest change in the bond dissociation energies occurs in the formation of the [(C5H5N)Hg(CH3)]+ complex, where the value of Ecoop is +135.92 kcal mol−1 at the BP86-D3(BJ)/def2-TZVP level of theory, which is a good indication of the strong anticooperativity of bonds. Indeed, the BDEs of the new bonds C5H5N–Hg(CH3) and (C5H5N)Hg–CH3 are smaller than the initial C5H5N–Hg and Hg–CH3 bonds by a value of 135.92 kcal mol. However, the percentages of changes are different and at the above level of theory are about 68 and 26% for the C5H5N–Hg and Hg–CH3 bonds, upon converting into new C5H5N–Hg(CH3) and (C5H5N)Hg–CH3 bonds, respectively. We note that in the case of compound 8, [Pb5{Mo(CO)3}2]4−, the BDEs of A–B, B–C, A–BC and AB–C bonds have not been calculated, as the [Pb5Mo(CO)3]4− system (AB or BC) is not a stable anion and does not exist. Indeed, it has been previously shown that the isolated [Pb5]4− anion has a square pyramidal geometry, but into the geometry of the [Pb5{Mo(CO)3}2]4− anion, due to the strong interactions with two M(CO)3 fragments, it can be deformed into a five-membered ring with a planar geometry.112 Therefore, in the case of the [Pb5{Mo(CO)3}2]4− anion, one cannot evaluate the stabilization-based cooperative energies of bonds. However, we can quantitatively evaluate the interaction-based cooperative energies of bonds using eqn (10) and by calculating the interaction energies in the geometry of the above anion complex. As can be seen in Table 4, the value of ΔIEcoop for the above complex is −54.07 kcal mol−1, which is a good indication of the intrinsic positive cooperativity of bonds between the [Pb5]4− anion and two M(CO)3 fragments. As can be seen, in all cases the differences between the IEABCA–B and IEABCA–BC values are the same as those between the IEABCB–C and IEABCAB–C ones. On the other hand, the values of interaction-based cooperative energies (ΔIEcoop) do not differ significantly from those of stabilization-based cooperative energies (Ecoop). For the present complexes, similar to the triads 1 to 6 (except triad 2), there is an excellent correlation between the calculated ΔIEcoop and Ecoop values (see Fig. S5 and S6, ESI†), indicating that both the Ecoop and ΔIEcoop values are good evidence for the comparison of the degree of the cooperativity of bonds in a series of metal complexes.
3.3. The effect of A⋯C interaction on cooperative energies
We remember that in a cyclic ABC system the A⋯C interaction cannot be ignored and one cannot use eqn (3) and (8) for calculating the synergetic effects of the bonds. However, in this work, the cooperative energies for the present noncyclic systems have been calculated and compared with and without considering the A⋯C interaction (see Tables 1–4). Fortunately, as the data in Tables 1–4 show, the correction of cooperative energies for SEABCAC or IEABCAC (see Tables S17 and S18 for their calculated values, ESI†) in all cases do not change the type of the cooperativities/anticooperativities and in most cases do not change significantly the value of cooperative energies. Herein, we prefer ignoring the A⋯C interaction in the noncyclic ABC systems and naming the difference between the BDEs of A–B and A–BC bonds (or B–C and AB–C bonds) as the cooperative energy of the bonds in the ABC system. In this type of nomenclature, we assume that in a noncyclic ABC system, the whole impact of A on the B–C bond and C on the A–B bond can be named the cooperative energy of A–B and B–C bonds, apart from the fact that whether A or C only change the nature of B to AB or BC, respectively, or they have also a possible interaction with each other. However, a literature review shows that most authors have not ignored the A⋯C interaction and used eqn (1) and/or (2) for calculating the cooperative energy in noncyclic ABC systems.
On the other hand, many authors have ignored the A⋯C interaction and used only eqn (3) (for example see ref. 22, 23, 30–32, 35, 40, 43, 45, 49, 55, 69 and 103). Also, some other authors have used both eqn (1) and (3) at the same time (for example see ref. 14, 16, 17, 21, 36–38, 44 and 65). We note that when species A and C have a very weak interaction but their deformation energies due to a strong interaction with B are very large, the calculated value of SEABCAC may have a large positive value. Thus, under such conditions, eqn (2) will give us the misleading values for the cooperative energy of the A–B and B–C bonds. Triad 2 is a good example of the above situation and the fact that previously known eqn (2) in some cases can give us misleading data. Surprisingly, due to the large Es of the BF3 molecule in the triad 2 (see Table S19 and its footnote, ESI†), the value of the term SEABAC at the MP2/aug-cc-pVTZ level of theory is +16.22 kcal mol−1. Thus, as can be seen in Table 1, eqn (2) will give a value of −20.22 kcal mol−1 (more than 80 kJ mol−1) for the Ecoop value of triad 2 which is surprisingly larger than the total stabilization energy (SEABC) of this molecule (−17.76 kcal mol−1) and also much larger than both initial bond dissociation energies (−5.17 and −8.58 kcal mol for F3B⋯NCH and NCH⋯HLi bonds, respectively). Obviously, the above result is not logical and clearly proves that the previously known eqn (2) gives the misleading data for the cooperative energy of the F3B⋯NCH and NCH⋯HLi bonds in triad 2. On the other hand, eqn (3) and (8) give a value of −4.01 kcal mol−1 for the Ecoop value of the above bonds in triad 2, which is quite logical for a triad with a total stabilization energy of −17.76 kcal mol−1. We note that the relatively small value of −4.01 kcal mol−1 (−16.78 kJ mol−1) still is much larger than most of the cooperative energies found in the literature.
4. Conclusions
In this work, it is emphasized that the quantitative evaluation of the impact of chemical bonds on the strength of each other is not restricted to the intermolecular noncovalent bonds. The data showed that in agreement with the law of conservation of energy and also Hess's law the difference between the BDEs of the A–B bond in the AB system and the A–BC bond in the ABC one, is identical to that of B–C and AB–C bonds in BC and ABC systems, respectively. Interestingly, the above energy difference is identical to the energy known in the literature as cooperative energy (Ecoop) in noncyclic ABC systems. Thus, it is shown that the intrinsic cooperativity of two chemical bonds changes their bond dissociation energies by the same value. The data also showed that in all ABC systems studied in this work, the difference between the energies of A–B and A–BC interactions is identical to that of B–C and AB–C interactions. Thus, we can similarly name the above difference as an interaction-based cooperative energy (ΔIEcoop). The above quantitative value is very useful for evaluating the degree of the cooperativity of bonds in an ABC system when we have no information about the corresponding free AB and BC systems. The negative and positive values of ΔIEcoop indicate how much the attractive interaction energies are increased or decreased upon the intrinsic positive cooperativity and intrinsic negative cooperativity of bonds, respectively. The above statements were supported by a computational study on the various types of chemical bonds. Indeed, the quantitative evaluation of cooperative energies of two intramolecular bonds, similar to some systems of intermolecular noncovalent bonds, has been reported. The results showed that while, interestingly, the net changes in the bond dissociation energies of A–B and B–C bonds upon formation of an ABC system and converting into A–BC and AB–C bonds, respectively, are the same, the percentages of the above changes are different and, as expected, are larger for weaker bonds. Fortunately, an excellent correlation was observed between the values of Ecoop and ΔIEcoop for both systems of inter- and intramolecular bonds, where the deformation energies of interacted species were low. The data also showed that ignoring the A⋯C interaction in noncyclic systems does not change the result of our evaluation of the type of cooperativity in most cases.
Author contributions
Samaneh Sanei Movafagh: investigation, data curation, validation, and writing – original draft. Sadegh Salehzadeh: supervision, conceptualization, methodology, validation, and writing – review & editing.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
We are grateful to the Bu-Ali Sina University for financial support.
References
- A. S. Mahadevi and G. N. Sastry, Cooperativity in Noncovalent Interactions, Chem. Rev., 2016, 116, 2775–2825 CrossRef CAS PubMed.
- Q. Li, H. Li, R. Li, B. Jing, Z. Liu, W. Li, F. Luan, J. Cheng, B. Gong and J. Sun, Influence of Hybridization and Cooperativity on the Properties of Au-Bonding Interaction: Comparison with Hydrogen Bonds, J. Phys. Chem. A, 2011, 115, 2853–2858 CrossRef CAS PubMed.
- M. Gao, X. Yang, J. Cheng, Q. Li, W. Li and R. E. Loffredo, Interplay between Metal⋯p Interactions and Hydrogen Bonds: Some Unusual Synergetic Effects of Coinage Metals and Substituents, Chem. Phys. Chem., 2013, 14, 3341–3347 CrossRef CAS PubMed.
- H. Lv, H. Y. Zhuo, Q. Li, X. Yang, W. Z. Li and J. B. Cheng, Mutual influence between covalent and noncovalent interactions in H3N–MCN–XF(X = H, Li, Cl, Br; M = Ag, Cu, Au), Mol. Phys., 2014, 112, 1081–1088 CrossRef CAS.
- M. Gao, J. Cheng, X. Yang, W. Li, B. Xiao and Q. Li, Influence of substituents on the nature of metal⋯π interaction and its cooperativity with halogen bond, J. Chem. Phys., 2015, 143, 054308 CrossRef PubMed.
- M. Gao, Q. Li, J. Cheng, W. Lia and H. B. Li, Complicated synergistic effects between metal–p interaction and halogen bonding involving MCCX, RSC Adv., 2015, 5, 105160 RSC.
- M. Gao, G. Gao, G. Li, X. Yang, W. Li and J. Cheng, Theoretical study on synergistic effects between anion–π and metal–Lp interactions, RSC Adv., 2015, 5, 76912–76918 RSC.
- M. Gao, Q. Li, W. Li and J. Cheng, Interplay between Cation–p and Coinage-Metal–Oxygen Interactions: An Ab Initio Study and Cambridge Structural Database Survey, ChemPhysChem., 2015, 16, 1008–1016 CrossRef CAS PubMed.
- X. Guo, Y. P. Yang, Q. Li, Z. Li and H. B. Li, Origin of selenium–gold interaction in F2CSe⋯AuY (Y = CN, F, Cl, Br, OH, and CH3): Synergistic effects, J. Chem. Phys., 2016, 144, 114306 CrossRef PubMed.
- Y. Wei, J. Cheng, W. Li and Q. Li, Regulation of coin metal substituents and cooperativity on the strength and nature of tetrel bonds, RSC Adv., 2017, 7, 46321 RSC.
- J. Zhang, Zh Wang, Zh Liu, J. Cheng, W. Li and Q. Li, Synergistic and diminutive effects between triel bond and regium bond: Attractive interactions between π-hole and σ-hole, Appl. Organomet. Chem., 2019, 33, e4806 CrossRef.
- R. Wang, Sh Yang and Q. Li, Coinage-Metal Bond between [1.1.1]Propellane and M2/MCl/MCH3 (M = Cu, Ag, and Au): Cooperativity and Substituents, Molecules, 2019, 24, 2601–2612 CrossRef PubMed.
- R. Wang, Zh Wang, X. Yu and Q. Li, Synergistic and Diminutive Effects between Regium and Aerogen Bonds, ChemPhysChem, 2020, 21, 2426–2431 CrossRef CAS PubMed.
- R. Rivelino, P. Chaudhuri and S. Canuto, Quantifying multiple-body interaction terms in H-bonded HCN chains with many-body perturbation/coupled-cluster theories, J. Chem. Phys., 2003, 118, 10593 CrossRef CAS.
- O. Mó, M. Yáñez, J. E. Del Bene, I. Alkorta and J. Elguero, Cooperativity and Proton Transfer in Hydrogen-Bonded Triads, ChemPhysChem, 2005, 6, 1411–1418 CrossRef PubMed.
- Q. Li, Zh Liu, J. Cheng, W. Li, B. Gong and J. Sun, Theoretical study on the cooperativity of hydrogen bonds in (HNC)2⋯HF complexes, J. Mol. Struct., 2009, 896, 112–115 CrossRef CAS.
- Q. Li, X. An, J. Cheng, B. Gong and J. Sun, Ab initio study of the structure, cooperativity, and vibrational
properties of HNC ternary complexes with two HF molecules, Mol. Phys., 2009, 107, 1649–1654 CrossRef CAS.
- I. Alkorta, F. Blanco and J. Elguero, Simultaneous Interaction of Tetrafluoroethene with Anions and Hydrogen-Bond Donors: A Cooperativity Study, J. Chem. Theory Comput., 2009, 5, 1186–1194 CrossRef CAS PubMed.
- I. Alkorta, F. Blanco, P. M. Deya, J. Elguero, C. Estarellas, A. Frontera and D. Quiñonero, Cooperativity in multiple unusual weak bonds, Theor. Chem. Acc., 2010, 126, 1–14 Search PubMed.
- B. Gong, B. Jing, Q. Li, Z. Liu, W. Li, J. Cheng, Q. Zheng and J. Sun, Ab initio study of the cooperativity between NH⋯N and NH⋯C hydrogen bonds in H3N–HNC–HNC complex, Theor. Chem. Acc., 2010, 127, 303–309 Search PubMed.
- M. Solimannejad, M. Malekani and I. Alkorta, Cooperativity between the hydrogen bonding and halogen bonding in F3CX⋯NCH(CNH)⋯NCH(CNH) complexes (X = Cl, Br), Mol. Phys., 2011, 109, 1641–1648 CrossRef CAS.
- J. E. Del Bene, I. Alkorta and J. Elguero, An ab initio study of cooperative effects in ternary complexes X:CNH:Z with X, Z = CNH, FH, ClH, FCl, and HLi: structures, binding energies, and spin–spin coupling constants across intermolecular bonds, Phys. Chem. Chem. Phys., 2011, 13, 13951–13961 RSC.
- J. E. Del Bene, I. Alkorta and J. Elguero, Ab Initio Study of Ternary Complexes X:(HCNH):Z with X, Z = NCH, CNH, FH, ClH, and FCl: Diminutive Cooperative Effects on Structures, Binding Energies, and Spin–Spin Coupling Constants Across Hydrogen Bonds, J. Phys. Chem. A, 2011, 115, 12677–12687 CrossRef CAS PubMed.
- M. Solimannejad and S. Ghafari, Ab initio study of ternary radical–molecule complexes between HCN(HNC) and HO(HS) species, Struct. Chem., 2013, 24, 1493–1498 CrossRef CAS.
- H. Zhuo, Q. Li, W. Li and J. Cheng, Non-additivity between substitution and cooperative effects in enhancing hydrogen bonds, J. Chem. Phys., 2014, 141, 244305 CrossRef PubMed.
- C. Estarellas, A. Frontera, D. Quiñ, I. Alkorta, P. M. Deyà and J. Elguero, Energetic vs Synergetic Stability: A Theoretical Study, J. Phys. Chem. A, 2009, 113, 3266–3273 CrossRef CAS PubMed.
- M. Solimannejad, Cooperative and Diminutive Interplay Between Lithium and Dihydrogen Bonding in F3YLi⋯NCH⋯HMH and F3YLi⋯HMH⋯HCN Triads (Y = C, Si; M = Be, Mg), ChemPhysChem, 2012, 13, 3158–3162 CrossRef CAS PubMed.
- M. Solimannejad, M. Rabbani, A. Ahmadi and M. D. Esrafili, Cooperative and diminutive interplay between the sodium bonding with hydrogen and dihydrogen bondings in ternary complexes of NaC3N with HMgH and HCN (HNC), Mol. Phys., 2014, 112, 2017–2022 CrossRef CAS.
- L. Albrecht, R. J. Boyd, O. Mó and M. Yáñez, Changing Weak Halogen Bonds into Strong Ones Through Cooperativity with Beryllium Bonds, J. Phys. Chem. A, 2014, 118, 4205–4213 CrossRef CAS PubMed.
- I. Alkorta, J. Elguero, J. E. Del Bene, O. M. Romero, M. M. Montero-Campillo and M. Yáñez, Mutual Influence of Pnicogen Bonds and Beryllium Bonds: Energies and Structures in the Spotlight, J. Phys. Chem. A, 2020, 124, 5871–5878 CrossRef CAS PubMed.
- X. Liu, Q. Li, J. Cheng and W. Li, Influence of cooperativity on the frequency shift of the Ar–H stretch vibration in HArF complexes, Mol. Phys., 2012, 111, 497–504 CrossRef.
- J. E. Del Bene, I. Alkorta, G. Sanchez-Sanz and J. Elguero, Ab Initio Study of Cooperative Effects in Complexes X:HBO:Z, with X, Z = LiH, HNC, HF, HCN, HCl, ClF, and HBO: Structures, Binding Energies, and Spin-Spin Coupling Constants across Intermolecular Bonds, Z. Phys. Chem., 2013, 227, 821–839 CrossRef CAS.
- S. A. C. McDowell, Significant cooperative effects in model FLi⋯CH3X⋯F− (X = Cl, Br, H) and FLi⋯Kr⋯F− complexes, Chem. Phys. Lett., 2018, 708, 17–20 CrossRef CAS.
- S. A. C. McDowell, R. Wang and Q. Li, Interactions in Model Ionic Dyads and Triads Containing Tetrel Atoms, Molecules, 2020, 25, 4197 CrossRef CAS PubMed.
- M. D. Esrafili, P. Esmailpour, F. Mohammadian-Sabet and M. Solimannejad, Theoretical study of the interplay between halogen bond and lithium–π interactions: cooperative and diminutive effects, Chem. Phys. Lett., 2013, 588, 47–50 CrossRef CAS.
- Q. Li, Q. Lin, W. Li, J. Cheng, B. Gong and J. Sun, Cooperativity between the Halogen Bond and the Hydrogen Bond in H3N⋯XY⋯HF Complexes (X, Y = F, Cl, Br), ChemPhysChem, 2008, 9, 2256–2269 Search PubMed.
- M. Solimannejad, M. Malekani and I. Alkorta, Cooperative and Diminutive Unusual Weak Bonding In F3CX⋯HMgH⋯Y and F3CX⋯Y⋯HMgH Trimers (X = Cl, Br; Y) HCN, and (HNC), J. Phys. Chem. A, 2010, 114, 12106–12111 CrossRef CAS PubMed.
- Q. Li, R. Li, Z. Liu, W. Li and J. Cheng, Interplay Between Halogen Bond and Lithium Bond in MCN–LiCN–XCCH (M = H, Li, and Na; X = Cl, Br, and I) Complex: The Enhancement of Halogen Bond by a Lithium Bond, J. Comput. Chem., 2011, 32, 3296–3303 CrossRef CAS PubMed.
- Q. Zhao, D. Feng and J. Hao, The cooperativity between hydrogen and halogen bond in the XY⋯HNC⋯XY (X,Y= F, Cl, Br) complexes, J. Mol. Model., 2011, 17, 2817–2823 CrossRef CAS PubMed.
- Q. Li, R. Li, Z. Zhou, W. Li and J. Cheng, S⋯X halogen bonds and H⋯X hydrogen bonds in H2CS–XY (XY = FF, ClF, ClCl, BrF, BrCl, and BrBr) complexes: Cooperativity and solvent effect, J. Chem. Phys., 2012, 136, 014302 CrossRef PubMed.
- S. J. Grabowski, Cooperativity of hydrogen and halogen bond interactions, Theor. Chem. Acc., 2013, 132, 1347 Search PubMed.
- M. Solimannejad and M. Malekani, Substituent Effects on the Cooperativity of Halogen Bonding, J. Phys. Chem. A, 2013, 117, 5551–5557 CrossRef CAS PubMed.
- W. Wu, Y. Zeng, X. Li, X. Zhang, S. Zheng and L. Meng, Interplay between halogen bonds and hydrogen bonds in OH/SH⋯HOX⋯HY (X = Cl, Br; Y= F, Cl, Br) complexes, J. Mol. Model., 2013, 19, 1069–1077 CrossRef CAS PubMed.
- M. Vatanparast, E. Parvini and A. Bahadori, Computational study of the cooperative effects between tetrel bond and halogen bond in XCN⋯F2CO⋯YCN complexes (X = H, F, Cl, Br; Y = F, Cl, Br), Mol. Phys., 2016, 114, 1478–1484 CrossRef CAS.
- H. Xu, J. Cheng, X. Yang, Z. Liu, X. Bo and Q. Li, Interplay between the s-tetrel bond and s-halogen bond in PhSiF3/4-iodopyridine/N-base, RSC Adv., 2017, 7, 21713 RSC.
- G. Ciancaleoni, Cooperativity between hydrogen- and halogen bonds: the case of selenourea, Phys. Chem. Chem. Phys., 2018, 20, 8506–8514 RSC.
- B. Zheng, Y. Liu, L. Huang, Z. Wang, H. Liu and Y. Liu, Cooperative effects between F⋯Ag bonded and X⋯Br (Cl) halogen-bonded interaction in BrF(ClF)⋯AgX⋯BrF(ClF) (X = F, Cl, Br) complexes: a theoretical study, Mol. Phys., 2018, 116, 1834–1843 CrossRef CAS.
- Z. Li and X. An, Strengthening of halogen bond in XCl⋯FH⋯F− through cooperativity with a strong hydrogen bond and proton transfer, J. Mol. Graphics Modell., 2020, 100, 107673 CrossRef CAS PubMed.
- X. Guo, Y. W. Liu, Q. Z. Li, W. Z. Li and J. B. Cheng, Competition and cooperativity between tetrel bond and chalcogen bond in complexes involving F2CX (X = Se and Te), Chem. Phys. Lett., 2015, 620, 7–12 CrossRef CAS.
- O. Mó, M. M. Montero-Campillo, I. Alkorta, J. Elguero and M. Yáñez, Ternary complexes stabilized by chalcogen and alkaline-earth bonds. Crucial role of cooperativity and secondary noncovalent interactions, Eur. J. Chem., 2019, 25, 11688–11695 CrossRef PubMed.
- P. V. Bijina and Ch. H. Suresh, Molecular Electrostatic Potential Reorganization Theory to Describe Positive Cooperativity in Noncovalent Trimer Complexes, J. Phys. Chem. A, 2020, 124, 2231–2241 CrossRef CAS PubMed.
- I. Alkorta, G. Sanchez-Sanz and J. Elguero, Influence of Hydrogen Bonds on the P⋯P Pnicogen Bond, J. Chem. Theory Comput., 2012, 8, 2320–2327 CrossRef CAS PubMed.
- J. E. Del Bene, I. Alkorta, G. Sanchez-Sanz and J. Elguero, Interplay of F–H⋯F Hydrogen Bonds and P⋯N Pnicogen Bonds, J. Phys. Chem. A, 2012, 116, 9205–9213 CrossRef CAS PubMed.
- Q. Li, R. Li, X. F. Liu, W. Li and J. Cheng, Concerted Interaction between Pnicogen and Halogen Bonds in XCl–FH2P–NH3 (X = F, OH, CN, NC, and FCC), ChemPhysChem, 2012, 13, 1205–1212 CrossRef CAS PubMed.
- M. D. Esrafili, P. Fatehi and M. Solimannejad, Comput. Mutual interplay between pnicogen bond and dihydrogen bond in HMH⋯HCN⋯PH2X complexes (M = Be, Mg, Zn; X = H, F, Cl), Theor. Chem., 2014, 1034, 1–6 CAS.
- Q. Zhao, Cooperative effects between halogen bonds and pnicogen bonds in XBr⋯OFH2P⋯NH3 (X = F, Cl, CN, NC, OH, and NO2) complexes, J. Mol. Model., 2016, 22, 1–7 CrossRef CAS PubMed.
- Q. Li, W. Li, J. Cheng, B. Gong and J. Sun, Effect of methyl group on the cooperativity between cation–p interaction and NH⋯O hydrogen bonding, J. Mol. Struct., 2008, 867, 107–110 CrossRef CAS.
- R. Li, Q. Li, J. Cheng, Z. Liu and W. Li, The Prominent Enhancing Effect of the Cation–p Interaction on the Halogen–Hydride Halogen Bond in M1⋯C6H5X⋯HM2, ChemPhysChem, 2011, 12, 2289–2295 CrossRef CAS PubMed.
- A. S. Mahadevi and G. N. Sastry, Cation–π Interaction: Its Role and Relevance in Chemistry, Biology, and Material Science, Chem. Rev., 2013, 113, 2100–2138 CrossRef CAS PubMed.
- M. Saberinasab, S. Salehzadeh and M. Solimannejad, The effect of a strong cation⋯π interaction on a weak selenium⋯π interaction: a theoretical study, Comput. Theor. Chem., 2016, 1092, 41–46 CrossRef CAS.
- X. Lucas, C. Estarellas, D. Escudero, A. Frontera, D. QuiÇonero and P. M. Deyá, Very Long-Range Effects: Cooperativity between Anion–p and Hydrogen-Bonding Interaction, ChemPhysChem, 2009, 10, 2256–2264 CrossRef CAS PubMed.
- C. Estarellas, A. Frontera, D. QuiÇonero and P. M. Deyá, Theoretical Study on Cooperativity Effects between Anion–p and Halogen-Bonding Interactions, ChemPhysChem, 2011, 12, 2742–2750 CrossRef CAS PubMed.
- Y. Lu, Y. Liu, H. Li, Zhu, H. Liu and W. Zhu, Energetic Effects between Halogen Bonds and Anion–π or Lone Pair-π Interactions: A Theoretical Study, J. Phys. Chem. A, 2012, 116, 2591–2597 CrossRef CAS PubMed.
- T. P. Tauer and C. D. Sherrill, Beyond the Benzene Dimer: An Investigation of the Additivity of π–π Interactions, J. Phys. Chem. A, 2005, 109, 10475–10478 CrossRef CAS PubMed.
- Q. Li, B. Jing, Z. Liu, W. Li, J. Cheng, B. Gong and J. Sun, Competition and cooperativity between hydrogen bond and σ-hole bond in SCS–(HF)n (n = 1 and 2) systems, J. Mol. Struct., 2010, 952, 90–95 CrossRef CAS.
- S. A. C. McDowell, Sigma-hole cooperativity in anionic [FX⋯CH3⋯YF]− (X, Y = Cl, Br) complexes, Chem. Phys. Lett., 2014, 598, 1–4 CrossRef CAS.
- M. D. Esrafili, Z. Amiri and F. Shankal, Strong cooperative effects between π-hole and dihydrogen bonds interactions: a computational study, Mol. Phys., 2016, 114, 2315–2324 CrossRef CAS.
- Y. Wang, Y. Zeng, X. Li, L. Meng and X. Zhang, The mutual influence between p-hole pnicogen bonds and r-hole halogen bonds in complexes of PO2Cl and XCN/C6H6 (X = F, Cl, Br), Struct. Chem., 2016, 27, 1427–1437 CrossRef CAS.
- Y. Wang, X. Li, Y. Zeng, L. Meng and X. Zhang, Theoretical insights into the p-hole interactions in the complexes containing triphosphorus hydride (P3H3) and its derivatives, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 195–202 CrossRef CAS PubMed.
- S. Shen, X. Jing, X. Zhang, X. Li and Y. Zeng, The competition and cooperativity of hydrogen/halogen bond and π-hole bond involving the heteronuclear ethylene analogues, J. Comput. Chem., 2021, 42, 908–916 CrossRef CAS PubMed.
- A. Beyer, A. Karpfen and P. Schuster, On the origin of three-body potentials in clusters of polar molecules and ions, Chem. Phys. Lett., 1979, 67, 369–373 CrossRef CAS.
- L. Ojamie and K. Hermansson, Ab Initio Study of Cooperativity in Water Chains: Binding Energies and Anharmonic Frequencies, J. Phys. Chem., 1994, 98, 4271–4282 CrossRef.
- W. Chen and M. S. Gordon, Energy Decomposition Analyses for Many-Body Interaction and Applications to Water Complexes, J. Phys. Chem., 1996, 100, 14316–14328 CrossRef CAS.
- S. S. Xantheas, Cooperativity and hydrogen bonding network in water clusters, Chem. Phys., 2000, 258, 225–231 CrossRef CAS.
- L. RincÓn, R. Almeida and D. G. Aldea, Many-Body Energy Decomposition Analysis of Cooperativity in Hydrogen Fluoride Clusters, Int. J. Quantum Chem., 2005, 102, 443–453 CrossRef.
- J. Řezać, Y. Huang, P. Hobza and G. J. O. Beran, Benchmark Calculations of Three-Body Intermolecular Interactions and the Performance of Low-Cost Electronic Structure Methods, J. Chem. Theory Comput., 2015, 11, 3065–3079 CrossRef PubMed.
- K. Low, M. L. Coote and E. I. Izgorodina, Accurate Prediction of Three-Body Intermolecular Interactions via Electron Deformation Density-Based Machine Learning, J. Chem. Theory Comput., 2023, 19, 1466–1475 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, MP2 energy evaluation by direct methods, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- M. J. Frisch, Semi-direct algorithms for the MP2 energy and gradient, Chem. Phys. Lett., 1990, 166, 275–280 CrossRef CAS.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, A direct MP2 gradient method, Chem. Phys. Lett., 1990, 166, 281–289 CrossRef CAS.
- M. Head-Gordon and T. Head-Gordon, Analytic MP2 frequencies without fifth-order storage. Theory and application to bifurcated hydrogen bonds in the water hexamer, Chem. Phys. Lett., 1994, 220, 122–128 CrossRef CAS.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, Klene, M. J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision A 01), Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, A New Basis Set Exchange: An Open, Up-to-date Resource for the Molecular Sciences Community, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- G. Theodoor, d Jong, R. Visser and F. M. Bickelhaupt, Oxidative addition to main group versus transition metals: Insights from the Activation Strain model, J. Org. Chem., 2006, 691, 4341–4349 CrossRef.
- W. J. van Zeist and F. M. Bickelhaupt, The activation strain model of chemical reactivity, Org. Biomol. Chem., 2010, 8, 3118–3127 RSC.
- L. P. Wolters, P. Schyman, M. J. Pavan, W. L. Jorgensen, F. M. Bickelhaupt and S. Kozuch, The many faces of halogen bonding: a review of theoretical models and methods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 523–540 CAS.
- L. P. Wolters and F. M. Bickelhaupt, The activation strain model and molecular orbital theory, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324–343 CAS.
- I. Fernández and F. M. Bickelhaupt, Deeper Insight into the Diels–Alder Reaction through the Activation Strain Model, Chem. – Asian J., 2016, 11, 3297–3304 CrossRef PubMed.
- F. M. Bickelhaupt and K. N. Houk, Analyzing Reaction Rates with the Distortion/Interaction–Activation Strain Model, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed.
- F. Maleki and S. Salehzadeh, Extension of the atom by atom scheme of counterpoise method and presentation of its new advantages, J. Chem. Phys., 2018, 149, 064116 CrossRef PubMed.
- S. Yu, P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, How Oriented External Electric Fields Modulate Reactivity, Chem. – Eur. J., 2021, 27, 5683–5693 CrossRef CAS PubMed.
- L. A. Santos, T. A. Hamlin, T. C. Ramalho and F. M. Bickelhaupt, The pnictogen bond: a quantitative molecular orbital picture, Phys. Chem. Chem. Phys., 2021, 23, 13842 RSC.
- S. F. Boys and F. D. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- B. Liang and L. Andrews, Reactions of Laser-Ablated Ag and Au Atoms with Carbon Monoxide: Matrix Infrared Spectra and Density Functional Calculations on Ag(CO)n (n = 2, 3), Au(CO)n (n = 1, 2) and M(CO)n+ (n = 1–4; M = Ag, Au), J. Phys. Chem. A, 2000, 104, 9156–9164 CrossRef CAS.
- T. Yang, D. M. Andrad and G. Frenking, Dative versus electron sharing bonding in Nimides and phosphane imides R3ENX and relative energies of the R2EN(X)R isomers (E = N, P; R = H, Cl, Me, Ph; X = H, F, Cl), Phys. Chem. Chem. Phys., 2018, 20, 11856–11866 RSC.
- T. Yang, D. M. Andrad and G. Frenking, Dative versus Electron Sharing Bonding in N-Oxides and Phosphane Oxides R3EO and Relative Energies of the R2EOR Isomers (E = N, P; R = H, F, Cl, Me, Ph). A Theoretical Study, Mol. Phys., 2018, 117, 1306–1314 CrossRef.
- C. Loschen, L. Voigt, J. Frunzke, A. Diefenbach, M. Diedenhofen and G. Frenking, Theoretical Studies of Inorganic Compounds. (191) Quantum Chemical Investigations of the Phosphane Complexes X3B-PY3 and X3Al-PY3 (X = H, F, Cl; Y = F, Cl, Me, CN), Z. Anorg. Allg. Chem., 2002, 628, 1294–1304 CrossRef CAS.
- S. Salehzadeh and F. Maleki, New Equation for Calculating Total Interaction Energy in One Noncyclic ABC Triad and New Insights into Cooperativity of Noncovalent Bonds, J. Comput. Chem., 2016, 37, 2799–2805 CrossRef CAS PubMed.
- S. E. Novick, K. C. Janda and W. Klemperer, HFClF: Structure and Bonding, J. Chem. Phys., 1976, 65, 5115 CrossRef CAS.
- P. L. Alistair, G. Rendell, B. Bacskay and N. S. Hush, An ab initio quantum chemical study of the hydrogen- and “anti”-hydrogen-bonded HF/CIF and HF/CI2 dimers, Chem. Phys., 1987, 87, 535–544 Search PubMed.
- B. Wagner, A. De, D. A. Barker and A. Hinchliffe, Ab initio molecular orbital study of the potential energy surface for the HF⋯ClF binary complex, Chem. Phys., 1993, 99, 5917–5923 Search PubMed.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, The Halogen Bond, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- R. T. C. Brownlee, A. J. Canty and M. F. Mackay, The Crystal Structure of [MeHg(py)]+[NO3]−, a Complex with Linear Geometry for Methylmercury(II), Aust. J. Chem., 1978, 31, 1933–1936 CrossRef CAS.
- L. Yong, S. D. Hoffmann, T. F. Fässler, S. Riedel, M. Kaupp, S. Riedel and M. Kaupp, [Pb5{Mo(CO)3}2]4−: A Complex Containing a Planar Pb5 Unit, Angew. Chem., Int. Ed., 2005, 44, 2092–2096 CrossRef CAS PubMed.
- A. Doshi, A. Sundararaman, K. Venkatasubbaiah, L. N. Zakharov, A. L. Rheingold, M. Myahkostupov, P. Piotrowiak and F. Jakle, Pentafluorophenyl Copper–Pyridine Complexes: Synthesis, Supramolecular Structures via Cuprophilic and π-Stacking Interactions, and Solid-State Luminescence, Organometallics, 2012, 31, 1546–1558 CrossRef CAS.
- C. Döring and P. G. Jones, Aminkomplexe des Golds, Teil 8: Zwei Pyridinderivate des Gold(I)-thiocyanats[1], Z. Naturforsch., B: J. Chem. Sci., 2014, 68, 474–491 CrossRef.
- Y. Gholiee, S. Salehzadeh and S. Khodaveisi, Electronic structure, nature of bond and carbonyl vibrational frequency analysis of half-sandwich complexes [(η6-arene)M(CO)3] (arene= hexafluorobenzene, 1,3,5-trifluorobenzene, benzene, 1,3,5-trimethylbenzene, hexamethylbenzene; M = Cr, Mo, W); a theoretical study, New J. Chem., 2019, 43, 7797–7805 RSC.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  *
*

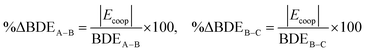 .
f Corrected for SEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
.
f Corrected for SEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c
c .
f Corrected for IEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
.
f Corrected for IEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
 ).
). .
f Corrected for SEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
g MP2 calculations for this compound were performed using the def2-SVP basis set.
.
f Corrected for SEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
g MP2 calculations for this compound were performed using the def2-SVP basis set.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c
c .
f Corrected for IEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
g The MP2 calculations for this compound were performed using the def2-SVP basis set.
.
f Corrected for IEABCA–C, but we do not recommend it for the above noncyclic systems (see Section 3.3).
g The MP2 calculations for this compound were performed using the def2-SVP basis set.





