 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The thermodynamics of self-assembled monolayer formation: a computational and experimental study of thiols on a flat gold surface†
Alberto
Zoccante
 *a,
Eleonora
Cara
*a,
Eleonora
Cara
 b,
Federico
Ferrarese Lupi
b,
Federico
Ferrarese Lupi
 b,
Philipp
Hönicke
ce,
Yves
Kayser
cf,
Burkhard
Beckhoff
c,
Petr
Klapetek
d,
Davide
Marchi
a and
Maurizio
Cossi
b,
Philipp
Hönicke
ce,
Yves
Kayser
cf,
Burkhard
Beckhoff
c,
Petr
Klapetek
d,
Davide
Marchi
a and
Maurizio
Cossi
 a
a
aDipartimento di Scienze e Innovazione Tecnologica (DISIT), Università del Piemonte Orientale, via T. Michel 11, I-15121 Alessandria, Italy. E-mail: alberto.zoccante@uniupo.it
bIstituto Nazionale di Ricerca Metrologica (INRiM), Strada delle Cacce, 91, 10135 Torino, Italy
cPhysikalisch-Technische Bundesanstalt (PTB), Abbestr. 2-12, 10587 Berlin, Germany
dDepartment of Nanometrology, Czech Metrology Institute (CMI), Okružní 31, 638 00 Brno, Czech Republic
eHelmholtz-Zentrum Berlin, Hahn-Meitner Platz 1, 14109 Berlin, Germany
fMax-Planck-Institut für chemische Energiekonversion Mulheim an der Ruhr, Nordrhein-Westfalen, DE, Germany
First published on 12th June 2024
Abstract
A methodology based on molecular dynamics simulations is presented to determine the chemical potential of thiol self-assembled monolayers on a gold surface. The thiol de-solvation and then the monolayer formation are described by thermodynamic integration with a gradual decoupling of one molecule from the environment, with the necessary corrections to account for standard state changes. The procedure is applied both to physisorbed undissociated thiol molecules and to chemisorbed dissociated thiyl radicals, considering in the latter case the possible chemical potential of the produced hydrogen. We considered monolayers formed by either 7-mercapto-4-methylcoumarin (MMC) or 3-mercapto-propanoic acid (MPA) on a flat gold surface: the free energy profiles with respect to the monolayer density are consistent with a transition from a very stable lying-down phase at low densities to a standing-up phase at higher densities, as expected. The maximum densities of thermodynamically stable monolayers are compared to experimental measures performed with reference-free grazing-incidence X-ray fluorescence (RF-GIXRF) on the same systems, finding a better agreement in the case of chemisorbed thiyl radicals.
1 Introduction
Self-assembled monolayers (SAMs) represent a good example of the spontaneous formation of complex nanometer-sized structures from simpler subunits. SAMs are typically constituted by molecules adsorbed on a solid surface, and many chemical headgroups are suitable for the preparation of such ordered layers. Thiols, dithiols and other sulfur compounds are particularly popular for nanotechnological applications owing to their ability to readily form SAMs over oxide-free metal surfaces.Thiol self-assembled monolayers (SAMs) on gold and, to a lesser extent, silver surfaces have been intensively studied for their important applications in nanotechnology. Specific applications include their use as inks or resists in lithography,1–6 as passive or active components in molecular electronics,7–12 and in sensors or biosensors13–16 (see ref. 17 for a comprehensive review).
While the kinetics of thiol SAM formation has been deeply studied over the years, some uncertainty remains about its actual mechanism.17–19 Most investigations assume chemical interactions, i.e. the formation of a S–Au covalent bond (chemisorption), to be at the base of the stability of thiol SAMs. In particular, it is assumed that the thiol hydrogen atoms react upon adsorption to evolve as H2, hence facilitating the formation of a strong S–Au bond. However, other recent studies suggest that non-dissociative adsorption (physisorption), which preserves the S–H bond in SAMs, may also occur. For instance, programmed temperature desorption experiments failed to detect the formation of disulfides (as one would expect from desorption in the absence of remaining S–H bonds).20 Single molecule conductance measurements also seem to detect physisorbed molecules rather than chemisorbed ones.19 While different studies have attempted to clarify this issue, and at least in one case21 some indication of the formation of free hydrogen has been provided, to our knowledge a deep understanding of the SAM formation mechanism and energetics is still lacking.
Thiol SAMs have been extensively studied from a computational perspective too:22–26 most calculations dealt with possible chemisorption mechanisms and energetics, whereas the works on SAM thermodynamic stability are rarer.27,28 In particular, a detailed comparison of the thermodynamics of physisorbed and chemisorbed SAMs has not been presented yet, though this information could provide very useful insights about the nature of the monolayers. In the present work, we propose such a detailed analysis by computing the chemical potentials of physisorbed and chemisorbed SAMs at different layer densities, considering non-crystalline SAMs, in a similar fashion as in a recent study about the relative stability of SAM polymorphs.27
Classical molecular dynamics (MD) has been long used for the computation of free energy differences in biophysics: for instance, binding free energies have been computed for ligand–enzyme complexes with MD simulations since the beginning of the 1980s,29–33 as well as more recently for protein–protein or protein–nucleic acid complexes.34 So-called “alchemical” techniques have also been applied to the computation to molecular crystal solubilities,35–37 as well as to the calculation of the adsorption free energies of catalytic species on metal surfaces.38
We applied a similar approach to compute the chemical potentials of SAMs formed by two different thiols, namely, 7-mercapto-4-methylcoumarin (MMC) and 3-mercapto-propanoic acid (MPA), either by physisorption (i.e. keeping the thiol S–H bond) or by chemisorption (breaking the S–H bond) at various densities: the molecular structures are illustrated in Fig. 1. The goal is to determine at which layer density the various SAMs become thermodynamically unstable (that is, their chemical potential becomes positive) and to compare these maximum theoretical densities with the density measured experimentally. If physisorbed/chemisorbed simulated layers have different maximum densities, such a comparison will provide an indication about the SAM nature.
 | ||
| Fig. 1 Molecular structure of 7-mercapto-4-methylcoumarin (MMC) and 3-mercapto-propanoic acid (MPA). Radical thiyls are obtained by homolytic cleavage of the S–H bond. | ||
Early studies of the structure of alkanethiol SAMs on flat gold surfaces proposed a 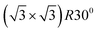 structure relative to the underlying Au(111) substrate,39 corresponding to 4.6 molecules per nm2. Other values, however, were found with various experimental techniques, reaching, for instance, for MPA 6.3 ± 0.640 and 7.8 ± 1.241 molecules per nm2. Such a variety of data calls for more elaborated theoretical models, not based on simple ordered lattices, but including thermal, steric and entropic effects as well, like the approach proposed in this work.
structure relative to the underlying Au(111) substrate,39 corresponding to 4.6 molecules per nm2. Other values, however, were found with various experimental techniques, reaching, for instance, for MPA 6.3 ± 0.640 and 7.8 ± 1.241 molecules per nm2. Such a variety of data calls for more elaborated theoretical models, not based on simple ordered lattices, but including thermal, steric and entropic effects as well, like the approach proposed in this work.
In the first part of the paper, we first review the thermodynamics of SAM formation and then proceed to describe a double-decoupling procedure to compute the chemical potentials of SAMs (Section 2). In Section 3, we describe the models and computational details, while in Section 4 we discuss the results of our investigation. Section 5 deals with conclusion and discusses directions for further work.
2 SAM formation thermodynamics
2.1 SAM formation thermodynamics
We consider two reactions in which one thiol molecule, originally in ethanol solution, enters into a pre-existing SAM:| R-SH(sol) + Au·(R-SH)n−1 → Au·(R-SH)n; μSH(n) | (1) |
 | (2) |
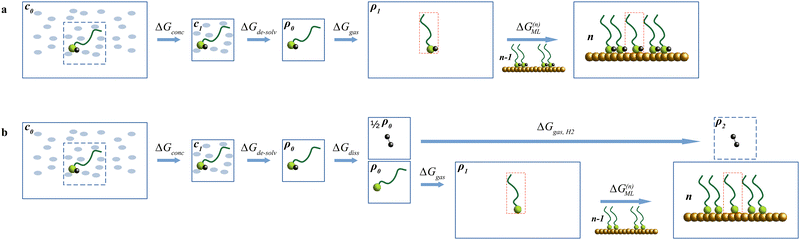
Reaction (1) (Fig. 2(a)) describes the physisorption of one more thiol in a monolayer already containing (n − 1) thiol molecules; in reaction (2) (Fig. 2(b)) the S–H bond is broken generating a thiyl radical – which enters the chemisorbed SAM originally containing (n − 1) radicals – along with a hydrogen atom, eventually leading to gaseous H2. In both cases, the free energy difference between the reactants and products corresponds to the chemical potential (μSH and μS, respectively) at the surface density of n molecules or radicals per surface unit.
 | ||
| Fig. 2 Graphical representation of reaction (1) (a) and reaction (2) (b). | ||
Note that, following the terminology adopted in ref. 42, we consider the dissociated species as a thiyl radical rather than a thiolate ion, unlike many other studies. In fact, the S–H bond dissociates homolytically, and whether the R-S unit should be considered a radical or an ion depends on the charge distribution in the S–Au bond, which is of little importance for our purposes.
Classical statistical mechanics provides the starting point for the computation of (Helmholtz) free energy differences in terms of the configurational partition functions of reagents and products.
For the case of physisorbed SAMs, the chemical potential can be computed as
 | (3) |
Following the double decoupling scheme, the logarithm in eqn (3) can be rewritten as
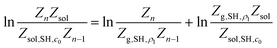 | (4) |
That is
| μSH(n) = ΔGde-solv(c0,ρ1) + ΔG(n)SAM | (5) |
These terms can be computed with MD techniques, as explained below, but some corrections are needed to take into account the changes in translational volumes: typically, the experimental concentration (c0) is not suited to a MD simulation (as it would require a very large simulation box), so a different, larger concentration (c1) is used to calculate the de-solvation free energy. Hence, a correction term is added, accounting for the reduction of the accessible translational volume:
ΔGconc = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(c1/c0) ln(c1/c0) | (6) |
Moreover, in our setup the simulation boxes for the de-solvation and the insertion steps differ. Hence, a second volume term is needed to account for the difference between the density ρ1 of the ideal gas phase coming from the de-solvation and the density ρ2 required for the insertion step:
ΔGgas = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ρ2/ρ1) ln(ρ2/ρ1) | (7) |
Summarizing, reaction (1) is split into the following steps, whose ΔG values are computed separately.
| R-SH(sol)(c0) → R-SH(sol)(c1); ΔGconc | (8) |
| R-SH(sol)(c1) → R-SH(g)(ρ1); ΔGde-solv | (9) |
| R-SH(g)(ρ1) → R-SH(g)(ρ2); ΔGgas | (10) |
| R-SH(g)(ρ2) + Au·(R-SH)n−1 → Au·(R-SH)n; ΔG(n)SAM | (11) |
| μSH(n) = ΔGconc + ΔGde-solv + ΔGgas + ΔG(n)SAM | (12) |
A visual representation of the setup is given in Fig. 3(a).
 | ||
| Fig. 3 Thermodynamic cycle for the double-decoupling calculations of the chemical potentials of the physisorbed (a) and chemisorbed (b) monolayers. | ||
On the other hand, the chemical potential of chemisorbed SAMs can be written as
 | (13) |
The process can be split into successive steps following the same scheme as above, with an additional contribution accounting for the thiol dissociation in thiyl and hydrogen, ΔGdiss. Thiol dissociation produces molecular hydrogen at half the concentration of the thiyl (ρ1); then, H2 is expected to evolve from the reaction site to a final density ρH2, so that another concentration term is needed,  .
.
Reaction (2) can hence be split into the following steps:
| R-SH(sol)(c0) → R-SH(sol)(c1); ΔGconc | (14) |
| R-SH(sol)(c1) → R-SH(g)(ρ1); ΔGde-solv | (15) |
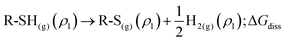 | (16) |
| R-S(g)(ρ1) → R-S(g)(ρ2); ΔGgas | (17) |
 | (18) |
 | (19) |
 | (20) |
The graphical summary for the chemisorption steps is given in Fig. 3(b).
3 Models and computational and experimental details
3.1 Model systems
The SAM models were composed of three-atom-thick Au(111) slabs covered by a variable number of physisorbed thiol molecules or chemisorbed thiyl radicals.The gold slab model was obtained by optimizing a periodic three-layer-thick surface using CRYSTAL17 at the DFT/PW91 level; the cc-PVDz basis set was chosen, and Hay and Wadt's pseudopotentials were used for S and Au core electrons. The periodic slab for MD, containing 2187 gold atoms (27 × 27 × 3), was cut out of the optimized surface and kept frozen during all the simulations.
We investigated SAMs formed either by 7-mercapto-4-methylcoumarin (MMC) and 3-mercapto-propanoic acid (MPA) or by the corresponding radical thiyls, indicated as MMCr and MPAr.
Structures, atomic partial charges and slightly modified GROMOS 54A7 force field parameters for the two thiols were obtained from the ATB website.43,44 Atomic partial charges for thiyls were generated using the QEq equilibration method (with a 10−6e convergence). Initial geometries for molecular dynamics simulations were obtained by packing either molecules or radicals on the gold slab using the PACKMOL code:45 a number of different initial densities were defined for the various species, as summarized in Table 1.
| SAM units | Adsorption process | Density range (molecules per nm2) |
|---|---|---|
| MMC | Physisorbed | 0.56–5.03 |
| Chemisorbed | 0.5–4.84 | |
| MPA | Physisorbed | 0.56–7.45 |
| Chemisorbed | 0.5–7.24 |
The calculation of ΔGde-solv was performed with MD simulations of a single thiol molecule with 2342 ethanol molecules in a cubic box of 198.3 nm3 volume, ensuring the proper solvent density at 298 K, using the GROMOS 54A7 force field.
3.2 Gold–molecule interactions
While interactions between molecules in the monolayer can be expected to be accurately reproduced by GROMOS 54A7 force field parameters, the same cannot be granted for surface–molecule interactions. Hence, force field parameters for thiol/thiyl–gold interactions were optimized against DFT calculations on small model systems following the procedure described in ref. 46 (see in particular the ESI† of that publication for more details).3.3 MD simulations
All the MD calculations were performed using the GROMACS software suite. The model systems were first minimized and then equilibrated for 200 ps at 300 K. The molecules to be decoupled from the environment to compute free energies (see below) were selected randomly from this pre-equilibrated system. Further minimization and equilibration for 200 ps at 300 K with a time step of 0.5 fs were then performed for each value of the decoupling parameter λ. Finally, for each λ, data were collected from a 1 ns simulation at 300 K with a timestep of 1 fs.Both MMC and MPA in their undissociated (thiol) form showed dynamic instability at high SAM densities, leading some molecules to leave the monolayer, forming a sort of the “second layer” above the SAM. This would prevent the calculation of ΔG(n)SAM with the method described below for some of the highest densities, so a mono-dimensional restraint was added in all the MD for thiols to limit the vertical motion with respect to the slab.
3.4 De-solvation and insertion free energies
The insertion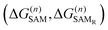 and de-solvation (ΔGde-solv) free energies were computed numerically from MD simulations, following the Bennet acceptance ratio (BAR) method.47 Free energy differences are calculated by “switching off” the interactions between a single thiol molecule or thiyl radical and its environment, being a SAM on gold or a liquid solution (decoupling). As the accuracy of such free energy estimates depends on the overlap of the initial and final states,48 the decoupling is commonly obtained as the succession of small steps where the interactions are slowly reduced.
and de-solvation (ΔGde-solv) free energies were computed numerically from MD simulations, following the Bennet acceptance ratio (BAR) method.47 Free energy differences are calculated by “switching off” the interactions between a single thiol molecule or thiyl radical and its environment, being a SAM on gold or a liquid solution (decoupling). As the accuracy of such free energy estimates depends on the overlap of the initial and final states,48 the decoupling is commonly obtained as the succession of small steps where the interactions are slowly reduced.
In our setup, Coulomb interactions were switched off first, followed by Lennard–Jones interactions (using soft LJ potential energy functions to prevent divergence); in both cases, 20 steps were performed starting from the fully-interacting to the fully-decoupled system: considering the initial state, then a total of 41 MD simulations were required for each ΔG calculation.
This procedure was performed once for each molecule in solution, while for SAMs it was replicated for each monolayer density. Furthermore, to take into account the effects of SAM inhomogeneity, in each monolayer the calculation was repeated for 5 randomly chosen molecules/radicals, and the insertion ΔG was computed as the mean of the 5 values.
3.5 Concentration free energy terms
As explained above, the calculation of SAM formation free energies includes two terms due to translational volume changes (ΔGconc, ΔGgas): they depend on the concentrations of thiol in ethanol (c0, c1) and on the gaseous densities (ρ1, ρ2).We use c0 = 0.1 mmol L−1 as a typical concentration found in SAM synthesis, allowing a direct comparison with the experiments; the values of c1, ρ1 and ρ2 are derived from the MD simulation box volume. In the de-solvation process, a box of 198.3 nm3 is used, containing one thiol molecule (along with a suitable number of ethanol molecules in the condensed phase), so that c1 = ρ1 = 8.4 mmol L−1.
In steps (11) and (19), the simulation box volume is 386.8 nm3, and a single molecule is decoupled from the monolayer, leading to ρ2 = 4.3 mmol L−1. Then at T = 298 K we have
ΔGconc = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(c1/c0) = 11.0 kJ mol−1 ln(c1/c0) = 11.0 kJ mol−1 | (21) |
ΔGgas = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ρ2/ρ1) = −1.7 kJ mol−1 ln(ρ2/ρ1) = −1.7 kJ mol−1 | (22) |
3.6 Dissociation free energy
We computed the bond dissociation energies in the gas phase, treating all the species as ideal gases at thermodynamic equilibrium. The dissociation free energy, ΔGdiss, can be obtained with the Gaussian program: the dissociation energy is computed at the DFT level, setting the suitable functional and basis sets; enthalpies and free energies are then obtained by adding vibrational, rotational and translational contributions for reagents and products. For (harmonic) vibrational terms, the second derivatives of the DFT energies are also computed at the same level as the energies. By default, the statistical thermodynamics is performed at 298 K and 1 atm (1.01325 bar), corresponding to a gas density of ρ3 = 4.08 × 10−2 mol L−1.While experimental dissociation free energies are not available for the molecules of interest, their dissociation enthalpies are known better: so, as detailed in the ESI,† we used some experimental ΔHdiss to set the best combination of density functional and basis set, and then compute at the same level ΔGdiss for MMC and MPA.
Since ρ3 ≠ ρ1, the latter being the density at which the de-solvation term is computed (see eqn (15) and Fig. 3), a further volume correction term should be added. However, the contributions from R-SH (ρ1 → ρ3) and from R-S (ρ3 → ρ1) before and after the dissociation, respectively, cancel out; on the other hand, the molecular hydrogen produced in the reaction does provide a density term, ΔGgas,H2, discussed below.
3.7 H2 concentration term
Under the experimental conditions, the radical formation does not occur in a closed system, and molecular hydrogen can evolve and leave the reaction. We assume that during the SAM formation a small concentration of H2 remains constant in the reaction environment, considering that the process occurs close to the gold surface, in the presence of denser and denser molecular layers and in contact with the solvent, all conditions that could hamper the gas evolution (but also making less and less reliable the ideal gas approximation!). In this model, ρH2 can be assigned a (presumably very low) constant value until the SAM growth stops at the maximum density. Assuming the ideal gas behaviour for H2 and using PH2 for the “steady state” hydrogen partial pressure (in bar), the correction term to be added to ΔGdiss is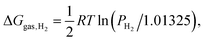 | (23) |
As we are not aware of any experimental determination of the hydrogen concentration at the monolayer level, we are left with the issue of estimating PH2.
The extreme case is ρH2 → 0, PH2 → 0, i.e. all the produced hydrogen leaves the reaction surroundings immediately, and this formally prevents the definition of a free energy change for the bond dissociation.
Avoiding this divergence, we restrict the model to two well-defined limiting cases, assuming that realistic scenarios should fall within these limits: in the first one, ΔGH2,gas = 0, i.e. the hydrogen is produced in the standard state, with 1 bar partial pressure. In the second limit, ΔGH2,gas = −ΔGdiss, i.e. the concentration term balances the dissociation free energy completely, which corresponds to extremely low concentrations/partial pressures (anticipating the results illustrated in the next section, the H2 pressure should be around 10−23 bar, i.e. about 13 orders of magnitude lower than the partial pressure of hydrogen in the atmosphere).
Both these limits appear unrealistic: most likely, in real experiments H2 will be produced at some intermediate concentration, with effects on the SAM chemical potential discussed below.
3.8 Helmholtz and Gibbs free energies
To improve the simulation stability, we adopted NVT ensembles in the calculation with the BAR method of free energy changes for reactions (11) and (19). This provides Helmholtz (ΔA), rather than Gibbs (ΔG) free energies: the latter can be obtained by evaluating the factor PV for products and reactants. The correction can be likely neglected for the monolayers (which are condensed phases) but it has to be included for the (ideal) gaseous thiol/thiyl molecule, leading to| ΔGSAM = ΔASAM − RT = ΔASAM − 2.5 kJ mol−1 | (24) |
3.9 Experimental MMC and MPA surface densities
As previously presented,42 the quantitative determination of the surface density of SAMs can be conducted through reference-free grazing-incidence X-ray fluorescence (RF-GIXRF).49 This method allows the mass per area of a given target element to be derived from the detected X-ray fluorescence signal employing physically calibrated instrumentation50 and tabulated51 or experimentally determined atomic fundamental parameters.52 To determine the density of MMC and MPA, we used sulfur as the target atom to find its mass density σS through eqn (25).53 | (25) |
4 Results and discussion
4.1 Experimental MMC and MPA surface densities
The RF-GIXRF quantification yielded a surface density value of (4.1 ± 0.6) MMC molecules per nm2 and (7.6 ± 1.1) MPA molecules per nm2. The uncertainties are due to the propagation of uncertainties for independent measurements. The density measured for MPA is quite high compared to the regular geometrical model mentioned in the Introduction section: this value, however, is comparable within the uncertainty to the densities found with inductively coupled plasma mass spectrometry40,41 (see above). A part of the recorded signal could be ascribed to thiol molecules adsorbed on top of the monolayer, held by van der Waals interactions and H-bonds despite the accurate ethanol rinsing applied to the samples. In a previous work,42 we investigated the oxidation state of MMC SAM sulfur atoms through X-ray photoelectron spectroscopy (XPS), finding a minor component in the XPS spectra compatible with unbound undissociated thiols, along with a major contribution from chemisorbed thiyls: the former could be due to MMC molecules lying on top of the SAM, and a similar hypothesis is possible for MPA, whose acid group could form even stronger intermolecular interactions. In this case, the measured densities have to be considered as upper bounds when compared with the simulations.4.2 Common concentration terms
The chemical potentials for (physisorbed) thiol and (chemisorbed) thiyl SAMs at various surface densities were computed with eqn (12) and (20), respectively.The concentration terms are common to all the simulated systems with the values ΔGconc = 11.0 kJ mol−1 and ΔGgas = −1.7 kJ mol−1, as reported in the previous section; the other contributions have to be computed for MMC and MPA separately.
4.3 MMC
The MMC thiol de-solvation energy, from ethanol to the gas phase, was computed with the BAR method, obtaining ΔGde-solv = 17.9 kJ mol−1. The MMC dissociation energy was computed using the Gaussian program at the DFT level, with the B3P86 functional and cc-pVTZ basis set, as described in the ESI:† the best estimate is ΔGdiss = 130 kJ mol−1.The remaining contributions, ΔG(n)SAM or 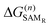 , due to MMC insertion into an existing SAM of density n were evaluated with the BAR method as the negative of the free energy of removal of one molecule/radical from the SAM. To account for possible layer inhomogeneities, 5 molecules or radicals were chosen randomly in each SAM and decoupled from the system, averaging the corresponding removal free energies. All the results are reported in the ESI.†
, due to MMC insertion into an existing SAM of density n were evaluated with the BAR method as the negative of the free energy of removal of one molecule/radical from the SAM. To account for possible layer inhomogeneities, 5 molecules or radicals were chosen randomly in each SAM and decoupled from the system, averaging the corresponding removal free energies. All the results are reported in the ESI.†
The resulting chemical potentials are illustrated in Fig. 4. As noted in the previous section, the potential for chemisorbed thiyls contains a term that depends on the (unknown) concentration of H2 produced in the dissociation reaction: two limiting cases are shown in Fig. 4, namely H2 at standard pressure (leading to ΔGH2,gas = 0) or at extremely low pressure, so that ΔGdiss + ΔGH2,gas = 0: likely, the real value falls between these extremes.
For both chemisorbed and physisorbed SAMs, the chemical potential grows slowly at low densities, corresponding to the striped (lying down) phase, until about 3.5 molecules per nm2. Above this density, the (physisorbed) thiol SAM chemical potential rises steeply as the “standing up” phase appears and spreads. The same happens for the chemisorbed thiyl SAMs, whose chemical potential rises even more sharply: the two curves corresponding to the limiting cases mentioned above are parallel, with a distance equal to the dissociation free energy. Crossing of the μ = 0 line, indicating thermodynamic instability for very dense layers, occurs at about 4 molecules per nm2 for physisorbed SAMs; chemisorbed monolayers become unstable between 4 and 4.5 molecules per nm2 depending on the pressure of H2 in the dissociation reaction. All these values are compatible with the measured MMC SAM density reported above: the calculated chemical potentials, however, appear to favor the chemisorbed thiyl SAMs in the whole range of the monolayer thermodynamic stability.
4.4 MPA
The same approach as above was applied to MPA SAMs: the de-solvation free energy, ΔGde-solv = 55.8 kJ mol−1, is much larger than that for MMC, since the thiol is polar and able to form hydrogen bonds with the solvent. The dissociation free energy was computed at the DFT level with B3P86/cc-pVTZ again, obtaining ΔGdiss = 120 kJ mol−1. Insertion free energies were computed as above by averaging the results for 5 molecules or radicals from each SAM.The chemical potentials of physisorbed and chemisorbed MPA monolayers are reported for various densities in Fig. 5: as in MMC, the potentials show a plateau for densities below 3 molecules per nm2, though in this case with a very small negative slope, probably because the striped phase is more and more stabilized by hydrogen bonds between neighboring molecules or radicals.
At higher densities, the chemical potential rises, as the standing up phase appears and spreads: for physisorbed molecules, the free energy becomes positive around 3.8 molecules per nm2, while chemisorbed radical monolayers become unstable between 3.8 and 5.8 molecules per nm2. Chemical potentials rise less steeply for MPA than for MMC, so the crossing of the μ = 0 line occurs over a larger density range: unlike the MMC case, for MPA only the (chemisorbed) thiyl SAMs are compatible with the experimental density (provided that the equilibrium H2 concentration is very small, so the real curve approaches the limit of ΔGdiss + ΔGH2,gas = 0).
This is a significant result, indeed, since the debate on the chemical nature of the monolayers is still intense as noted in the Introduction section: at least for MPA, the present chemical potential calculations clearly show that the density can reach values close to the experimental measures only in the case of radical thiyl SAMs.
Then, the chemisorbed SAMs formed by radical thiyls are found to be thermodynamically favored with respect to the undissociated physisorbed phase: for MMC this result does not change, qualitatively, even considering very different values for the S–H dissociation energy; for MPA it holds assuming a low concentration for the evolved gaseous hydrogen, but it is reinforced by the comparison with the experimental density. We noted above that the experimental uncertainty can be larger than the instrumental contribution shown in Fig. 4 and 5 for the possible presence of some molecules lying on top of the SAMs. Anyway, even considering the smaller density reported in the literature for MPA monolayers, around 4.6 molecules per nm2 as recalled in the Introduction section, the comparison with the theoretical values in Fig. 5 suggests that MPA monolayers are formed by radical thiyls, with a steady concentration of gaseous hydrogen intermediate between the two considered extreme cases.
Since in our approach the SAM formation process is split into successive steps, computing the free energy changes separately, one can see that the prevalence of the chemisorbed phase is due to the interaction with the gold atoms, much larger for radical sulfur than for the thiol group, despite the large dissociation energy required. Desolvation free energies and molecule–molecule side interactions, on the other hand, do not affect the balance between physisorbed and chemisorbed phases significantly.
A further comment can be useful about the transferability of the present model. The main source of uncertainty in the computed chemical potentials comes from the dissociation process, whose ΔG depends dramatically on the assumed equilibrium concentration of H2: this is expected to hold for any other thiol/thiyl couple under the same conditions, so the physisorbed/chemisorbed balance will always be determined with such a large uncertainty. On the other hand, we have shown that all the other thermodynamic contributions can be effectively computed with our method, and this led us to conclude that both MMC and MPA SAM are likely to be formed by radical thiyls rather than undissociated thiols. Other systems will differ for the entity of sulfur/gold and especially intermolecular interactions, and we believe that the approach described here is well suited to compute the chemical potentials for these terms with the same accuracy as in the present case.
5 Conclusions and outlook
We described a computational procedure to evaluate the chemical potential of thiol/thiyl SAMs based on the analysis of molecular dynamics data. Compared to the models based on electronic structure calculations, the present approach includes a much larger description of thermal contributions to enthalpies and entropies, and it allows the simulation of large monolayers, so formation free energies can be computed as a function of SAM densities, with accuracy mostly dependent on the force field quality.This procedure was applied to 7-mercapto-4-methylcoumarin (MMC) and 3-mercapto-propanoic acid (MPA) on a flat (111) Au surface at various monolayer densities; both thiol and thiyl SAMs were considered to investigate whether the maximum attainable densities differ for molecules (R-SH) and radicals (R-S), thus contributing to the debate on the chemical nature of these systems.
The chemical potential is defined as the free energy change when a thiol molecule leaves a 0.1 mmol L−1 ethanol solution and enters a pre-formed monolayer on a flat Au surface, possibly dissociating the S–H bond in the case of radical thiyl SAMs. Since this quantity depends on the layer density, one can find how many molecules or radicals can be added to the SAM before the chemical potential becomes positive, and the layer growth is thermodynamically unfavored.
The results can be compared with the experimental measure of MMC and MPA monolayer densities, performed with the RF-GIXRF method. For MMC, the maximum theoretical densities of both thiol and thiyl SAMs agree with the experimental data; for MPA, on the other hand, only the radical thiyl model is compatible with the experimental density, though the calculation provides a slightly lower density.
Our calculations of thermodynamic stability, then, suggest that the monolayers are formed by thiyl radicals, rather than undissociated thiols, contributing to clarifying the debated chemical nature of these SAMs.
Author contributions
A. Z., M. C. and D. M. performed theoretical calculations; P. K. performed AFM measurements; E. C. and F. F. L. performed sample preparation; P. H. and Y. K. performed GIXRF measurements; P. H. and E. C. performed data analysis; F. F. L., B. B. and M. C. provided funding; A. Z., M. C. and E. C. wrote the paper.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. Z., D. M. and M. C. acknowledge the financial support by Università del Piemonte Orientale (through the FAR funding program). E. C., F. F. L., P. H. and B. B. acknowledge the project 21GRD01 OpMetBat. The project has received funding from the European Partnership on Metrology, cofinanced by the European Union's Horizon Europe Research and Innovation Programme and by Participating States.References
- J. L. Wilbur and G. M. Whitesides, Nanotechnology, Springer, 1999, pp. 331–369 Search PubMed.
- B. D. Gates, Q. Xu, M. Stewart, D. Ryan, C. G. Willson and G. M. Whitesides, Chem. Rev., 2005, 105, 1171–1196 CrossRef CAS PubMed.
- J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103–1170 CrossRef CAS PubMed.
- J. A. Rogers and R. G. Nuzzo, Mater. Today, 2005, 8, 50–56 CrossRef CAS.
- B. Ziaie, A. Baldi and M. Z. Atashbar, Springer Handb. Nanotechnol., 2010, 231–269 Search PubMed.
- A. Terfort and M. Zharnikov, Adv. Mater. Interfaces, 2021, 8, 2100148 CrossRef CAS.
- J. M. Tour, Acc. Chem. Res., 2000, 33, 791–804 CrossRef CAS PubMed.
- D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440 CrossRef CAS PubMed.
- B. Chen and K. Xu, NANO, 2019, 14, 1–19 Search PubMed.
- G. Kong, S. Byeon, S. Park, H. Song, S.-Y. Kim and H. Yoon, Adv. Electron. Mater., 2020, 6, 1901157 CrossRef CAS.
- Y. Liu, X. Qiu, S. Soni and R. C. Chiechi, Chem. Phys. Rev., 2021, 2, 021303 CrossRef.
- R. Gupta, J. A. Fereiro, A. Bayat, A. Pritam, M. Zharnikov and P. C. Mondal, Nat. Rev. Chem., 2023, 7, 106–122 CrossRef CAS PubMed.
- B. Bonanni, A. R. Bizzarri and S. Cannistraro, J. Phys. Chem. B, 2006, 110, 14574–14580 CrossRef CAS PubMed.
- E. T. Castellana and P. S. Cremer, Surf. Sci. Rep., 2006, 61, 429–444 CrossRef CAS PubMed.
- D. Samanta and A. Sarkar, Chem. Soc. Rev., 2011, 40, 2567–2592 RSC.
- T. Zeng, R. P. Gautam, D. H. Ko, H.-L. Wu, A. Hosseini, Y. Li, C. J. Barile and E. C. Tse, Nat. Rev. Chem., 2022, 6, 862–880 CrossRef CAS PubMed.
- C. Vericat, M. Vela, G. Benitez, P. Carro and R. Salvarezza, Chem. Soc. Rev., 2010, 39, 1805–1834 RSC.
- E. Pensa, E. Cortés, G. Corthey, P. Carro, C. Vericat, M. H. Fonticelli, G. Benítez, A. A. Rubert and R. C. Salvarezza, Acc. Chem. Res., 2012, 45, 1183–1192 CrossRef CAS PubMed.
- M. Inkpen, Z.-F. Liu, H. Li, L. Campos, J. Neaton and L. Venkataraman, Nat. Chem., 2019, 11, 351–358 CrossRef CAS PubMed.
- I. I. Rzeźnicka, J. Lee, P. Maksymovych and J. T. Yates, J. Phys. Chem. B, 2005, 109, 15992–15996 CrossRef PubMed.
- L. Kankate, A. Turchanin and A. Gölzhäuser, Langmuir, 2009, 25, 10435–10438 CrossRef CAS PubMed.
- N. B. Luque, E. Santos, J. Andres and F. Tielens, Langmuir, 2011, 27, 14514–14521 CrossRef CAS PubMed.
- F. Tielens and E. Santos, J. Phys. Chem. C, 2010, 114, 9444–9452 CrossRef CAS.
- G. Rajaraman, A. Caneschi, D. Gatteschi and F. Totti, Phys. Chem. Chem. Phys., 2011, 13, 3886–3895 RSC.
- H. Guesmi, N. B. Luque, E. Santos and F. Tielens, Chem. – Eur. J., 2017, 23, 1402–1408 CrossRef CAS PubMed.
- J. K. Roy, E. S. Vasquez, H. P. Pinto, S. Kumari, K. B. Walters and J. Leszczynski, Phys. Chem. Chem. Phys., 2019, 21, 23320–23328 RSC.
- J. R. Reimers, D. Panduwinata, J. Visser, Y. Chin, C. Tang, L. Goerigk, M. J. Ford, M. Sintic, T. J. Sum, M. J. Coenen, B. L. Hendriksen, J. A. Elemans, N. S. Hush and M. J. Crossley, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E6101–E6110 CrossRef CAS PubMed.
- E. Pensa, L. M. Azofra, T. Albrecht, R. C. Salvarezza and P. Carro, J. Phys. Chem. C, 2020, 124, 26748–26758 CrossRef CAS.
- M. K. Gilson, J. A. Given, B. L. Bush and J. A. McCammon, Biophys. J., 1997, 72, 1047–1069 CrossRef CAS PubMed.
- J. Wang, Y. Deng and B. Roux, Biophys. J., 2006, 91, 2798–2814 CrossRef CAS PubMed.
- Y. Deng and B. Roux, J. Chem. Theory Comput., 2006, 2, 1255–1273 CrossRef CAS PubMed.
- Y. Deng and B. Roux, J. Phys. Chem. B, 2009, 113, 2234–2246 CrossRef CAS PubMed.
- R. Salari, T. Joseph, R. Lohia, J. Hénin and G. Brannigan, J. Chem. Theory Comput., 2018, 14, 6560–6573 CrossRef CAS PubMed.
- E. Duboué-Dijon and J. Hénin, J. Chem. Phys., 2021, 154, 204101 CrossRef PubMed.
- L. Li, T. Totton and D. Frenkel, J. Chem. Phys., 2017, 146, 214110 CrossRef PubMed.
- G. Gobbo, G. Ciccotti and B. L. Trout, J. Chem. Phys., 2019, 150, 201104 CrossRef PubMed.
- D. L. Mobley and G. Duarte Ramos Matos, F1000Research, 2018, 7, 1–22 Search PubMed.
- X. Zhang, R. S. Defever, S. Sarupria and R. B. Getman, J. Chem. Inf. Model., 2019, 59, 2190–2198 CrossRef CAS PubMed.
- F. Schreiber, Prog. Surf. Sci., 2000, 65, 151–257 CrossRef CAS.
- H. Hinterwirth, S. Kappel, T. Waitz, T. Prohaska, W. Lindner and M. Lämmerhofer, ACS Nano, 2013, 7, 1129–1136 CrossRef CAS PubMed.
- S. Elzey, D.-H. Tsai, S. A. Rabb, L. L. Yu, M. R. Winchester and V. A. Hackley, Anal. Bioanal. Chem., 2012, 403, 145–149 CrossRef CAS PubMed.
- D. Marchi, E. Cara, F. F. Lupi, P. Hönicke, Y. Kayser, B. Beckhof, M. Castellino, P. Klapetek, A. Zoccante, M. Laus and M. Cossi, Phys. Chem. Chem. Phys., 2022, 24, 22083–22090 RSC.
- A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, J. Chem. Theory Comput., 2011, 7, 4026–4037 CrossRef CAS PubMed.
- M. Stroet, B. Caron, K. M. Visscher, D. P. Geerke, A. K. Malde and A. E. Mark, J. Chem. Theory Comput., 2018, 14, 5834–5845 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- E. Cara, L. Mandrile, A. Sacco, A. M. Giovannozzi, A. M. Rossi, F. Celegato, N. De Leo, P. Hönicke, Y. Kayser, B. Beckhoff, D. Marchi, A. Zoccante, M. Cossi, M. Laus, L. Boarino and F. Ferrarese Lupi, J. Mater. Chem. C, 2020, 8, 16513–16519 RSC.
- C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268 CrossRef.
- A. Pohorille, C. Jarzynski and C. Chipot, J. Phys. Chem. B, 2010, 114, 10235–10253 CrossRef CAS PubMed.
- P. Hönicke, B. Detlefs, E. Nolot, Y. Kayser, U. Mühle, B. Pollakowski and B. Beckhoff, J. Vac. Sci. Technol., A, 2019, 37, 041502 CrossRef.
- J. Lubeck, B. Beckhoff, R. Fliegauf, I. Holfelder, P. Hönicke, M. Müller, B. Pollakowski, F. Reinhardt and J. Weser, Rev. Sci. Instrum., 2013, 84, 045106 CrossRef CAS PubMed.
- T. Schoonjans, A. Brunetti, B. Golosio, M. S. Del Rio, V. A. Solé, C. Ferrero and L. Vincze, Spectrochim. Acta, Part B, 2011, 66, 776–784 CrossRef CAS.
- P. Hönicke, R. Unterumsberger, N. Wauschkuhn, M. Krämer, B. Beckhoff, P. Indelicato, J. Sampaio, J. P. Marques, M. Guerra, F. Parente and J. P. Santos, Radiat. Phys. Chem., 2023, 202, 110501 CrossRef.
- B. Beckhoff, J. Anal. At. Spectrom., 2008, 23, 845–853 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01322k |
| This journal is © the Owner Societies 2024 |


