 Open Access Article
Open Access ArticleDesigning potentially singlet fission materials with an anti-Kasha behaviour†
Ricardo
Pino-Rios
 *ab,
Rodrigo
Báez-Grez
*ab,
Rodrigo
Báez-Grez
 c,
Dariusz W.
Szczepanik
c,
Dariusz W.
Szczepanik
 d and
Miquel
Solá
d and
Miquel
Solá
 *e
*e
aCentro de Investigación Medicina de Altura – CEIMA, Universidad Arturo Prat. Casilla 121, Iquique 1100000, Chile. E-mail: rpinorios@unap.cl
bQuímica y Farmacia, Facultad de Ciencias de la Salud, Universidad Arturo Prat, Casilla 121, Iquique 1100000, Chile
cFacultad de Ciencias, Universidad Arturo Prat, Casilla 121, Iquique 1100000, Chile
dK. Guminski Department of Theoretical Chemistry, Faculty of Chemistry, Jagiellonian University, Poland
eInstitut de Química Computacional i Catàlisi (IQCC) and Departament de Química, Universitat de Girona, C/ Maria Aurèlia Capmany 69, 17003 Girona, Catalonia, Spain. E-mail: miquel.sola@udg.edu
First published on 3rd May 2024
Abstract
Singlet fission (SF) compounds offer a promising avenue for improving the performance of solar cells. Using TD-DFT methods, anti-Kasha azulene derivatives that could carry out SF have been designed. For this purpose, substituted azulenes with a donor (–OH) and/or an acceptor group (–CN) have been systematically studied using the S2 ≥ 2T1 formula. We have found that –CN (–OH) substituents on electrophilic (nucleophilic) carbons result in improved SF properties when compared to azulene.
Introduction
Singlet fission (SF) is a process in which, from light absorption, a chromophore passes from its fundamental state to a singlet excited state, and later, it can collide by diffusion and share its excitation energy with a neighbouring ground state chromophore generating two triplet excited states in a spin-allowed process.1–4 As a result, from a single photon one can generate two excitons. This phenomenon is exploited in designing new organic compounds with technological, medical, and other applications, the most important being the development of the new generation of solar cells. One of the characteristics that a compound must have in order to be able to perform SF is that it should fulfil the following relation:5| S1 ≥ 2T1 | (1) |
Additionally, the aromatic character of these PAHs confers stability in the ground state (S0) and, depending on their delocalization pattern,12,13 also in the final lowest-lying triplet (T1) or singlet (S1) excited state.14 In this latter group of compounds, stabilization of T1 explains the low S0–T1 gap values of some of these compounds. The S1 state is involved in photochemical processes only in compounds where Kasha's rule is fulfilled. This rule indicates that the photoelectronic properties, such as fluorescence/phosphorescence, occur in the lowest energy excited state.15
A compound well known for its photoelectronic properties is azulene,16 a naphthalene isomer with a low S0–T1 gap and a dipole moment of 1.08 Debye in the ground state.17 This compound also possesses ten π electrons and, therefore, the compound is globally aromatic according to Platt's perimeter model.18 Additionally, a local aromatic behaviour is explained in terms of the coexistence of two fused charged rings and the Glidewell–Lloyd rule:19–21 the tropylium cation and the cyclopentadienyl anion (Scheme 1). Because of this, the negative charge is concentrated on the five-membered ring, allowing it to explain this compound's direction and high dipole moment value.
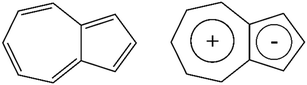 | ||
| Scheme 1 Proposed covalent (global aromaticity) and ionic (local aromaticity) resonance forms for the ground state of Azulene. | ||
Another interesting feature of this compound is that it emits through the S2 excited state in complete violation of Kasha's rule. It is worth mentioning that this was reported by Michael Kasha himself in his original 1950 paper.15 Recently, this anomaly has been explained by considering two properties of azulene: first, the excited S2 state is globally aromatic, giving it stability and a long lifetime allowing the emission from S2, and, second, there is an easily accessible antiaromaticity relief pathway of the S1 state.22
Research on azulene-containing compounds has once again received considerable attention,23 with recent work by Casanova et al. who integrated two antiparallel azulene units bridged with one heptalene all inserted into a polycyclic conjugated hydrocarbon to design anti-Kasha organic emitters from high excited states.24
Moreover, a very detailed study reported by Nickel and Klemp indicates that fluorescence is not the only form of azulene emission since triplet states may also be involved in photochemical processes. The authors indicate that processes such as thermally activated delayed fluorescence (TADF) and SF can take place, with smaller lifetimes and quantum yields, but significant enough to be detected.25,26
Computational methods
The construction of the studied compounds was carried out through the systematic substitution of the azulene hydrogens with –OH (π-electron donor) and –CN (π-electron acceptor) groups avoiding the substitution of two rings at the same time in order to understand the influence of the substituents on each of the aromatic rings. A total of 60 systems were designed and optimized to B3LYP27,28/6-311G(d,p)29 in the gas phase, checking that they are local minima on their respective potential energy surfaces. All calculations were performed using the Gaussian 16 program.30Additionally, excited state energies have been studied at the time-dependent density functional theory approach (TD-DFT)31 level using the same basis set. Since studying the excited states of azulene is not a simple task,32–34 to obtain reliable energies, a total of 16 functionals were tested, including pure, hybrid, long-range corrected functionals and the Tamm–Dancoff approximation, which is known to correct the triplet instability problems of standard TD-DFT.35,36 The data obtained were compared with gas-phase experimental data and with DFT/MRCI37 and CASSCF-NEVPT222 calculations reported in the literature. The selection criterion is based not only on the accuracy of the calculations performed with respect to the available data, but also the fact that eqn (2) (S2–2T1) presents values greater than zero. Another important reason in the selection of the best functional is that the electronic transitions are correctly assigned. For example, experimental reports in conjunction with computational calculations at the DFT/MRCI level indicate that the excited states of interest in this study: T1, S1, and S2 correspond to H → L, H → L, and H−1 → L & H → L+1 transitions, respectively.38
The chosen functional (see Table 1) for the calculation of the designed systems is LC-ωHPBE using regular TD-DFT. This functional not only presents reasonable values compared to the experimental data, but also presents a positive value for eqn (2) (1245 cm−1) in full agreement with the experimental results (1000 cm−1). In this case, the values using the Tamm–Dancoff approximation35 present less accurate values as can be seen in Table S1 in the ESI.†
| Regular TD-DFT | T1 | S1 | S2 | S2–2T1 |
|---|---|---|---|---|
| H → L | H → L | H−1 → L; H → L+1 | (Eqn (2)) | |
| Experimental37 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
1000 |
| DFT/MRCI38 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
−460 |
| CASSCF-NEVPT239 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 383 383 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 450 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 446 446 |
680 |
| B3LYP27,28 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 090 090 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 452 452 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418 418 |
−2762 |
| BH and HLYP28,40 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696 696 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512 512 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 690 690 |
−2701 |
| CAM-B3LYP41 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 885 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 516 516 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 456 456 |
−1314 |
| M0642 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 146 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 156 156 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 611 611 |
−3682 |
| M06-2X42 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 405 405 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 448 448 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 313 313 |
−1496 |
| M06-HF43,44 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129 129 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 991 991 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544 544 |
286 |
| M11L45 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 997 997 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 747 747 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640 640 |
−6353 |
| BP8640,46 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 730 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 885 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195 195 |
−3266 |
| TPSS47 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032 032 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 355 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 667 667 |
−3396 |
| WB97XD48 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 048 048 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517 517 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 407 407 |
−1689 |
| B97D49 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 736 736 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 938 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 067 067 |
−3404 |
| PBE50 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712 712 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885 885 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 263 263 |
−3160 |
| PBE051 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 029 029 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 691 691 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 976 976 |
−2083 |
| HSEH1PBE52–54 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 033 033 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 689 689 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 872 872 |
−2195 |
| LC-BLYP55 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220 220 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 223 223 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191 191 |
750 |
| LC-ωHPBE56 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 982 982 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 164 164 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 208 208 |
1245 |
Results and discussion
The purpose of this article is to take advantage of the characteristics of azulene to design compounds that can carry out SF. For this purpose, we have modified the electronic structure of azulene by systematically replacing hydrogen atoms by π-electron donor groups (–OH) and π-electron acceptor groups (–CN) in positions 1 to 8 (see Fig. 1) obtaining a total of 60 systems that are labelled OH and CN depending on the substituted group followed by the numbers of C atoms to which these substituents are attached (e.g. CN4678 means that C atoms number 4, 6, 7, and 8 have a CN substituent and the rest have no substituents). The design of the systems has been carried out systematically, avoiding the substitution of the two rings at the same time in order to evaluate the effect of the substituent per ring.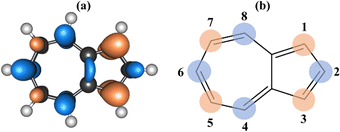 | ||
| Fig. 1 Dual descriptor (a) and experimental reactivity (b) reported for azulene, including atomic numbering. Orange/blue areas indicate areas susceptible to electrophilic/nucleophilic attack. | ||
Since the initial formula given for the design of compounds that can carry out the SF process applies only to those that comply with Kasha's rule, we have used the following formula to characterize SF chromophores in azulene derivatives:25
| S2 ≥ 2T1 | (2) |
The excitation energies of all studied compounds are shown in Table S2 (ESI†). The analysis will be carried out with respect to the unsubstituted compound since it allows understanding the effect of the substituent with respect to the type of carbon and the corresponding ring in which it has been substituted. We have checked that the nature of the excited states and the frontier molecular orbitals remain the same after substitution (Fig. S1, ESI†). We observe that for the case of the compounds substituted with the –CN group, the effect on the excited states T1, S1, and S2 is mostly stabilizing except for the cases of substitutions in C1 and C2 and those where these two atoms are involved (CN12 and CN123), for which the excited states tend to destabilize when compared to azulene. These exceptions correspond to the five-membered ring atoms.
For the case of those compounds substituted with –OH, the effect of the substituent in the T1 state is stabilizing on the C1 (C3) and C5 (C7) carbons, which are nucleophilic carbons, while for the case of the electrophilic carbons the effect is clearly destabilizing. With respect to the S2 state the effect of the substituent is stabilizing only in C1 while, for the other cases, the energies remain practically the same (this is determined by setting a range of ±1300 cm−1 or 0.16 eV).
When we apply eqn (2), it is possible to identify trends that allow us to design SF compounds. In the case of the experimental values reported for azulene, the difference S2–2T1 has a value of 1000 cm−1, while our results at the TD-LC-ωHPBE/6-311G(d,p)//B3LYP/6-311G(d,p) level give 1245 cm−1 in clear agreement with the experimental value, following the same trend, indicating that azulene can act as an SF system. If we apply the formula to literature results obtained at the DFT/MRCI level,38 we obtain a value of −1700 cm−1, which is clearly underestimated. On the other hand, the values at the CASSCF-NEVPT2 level deviate a little more from the experimental values, however they are in agreement with respect to eqn (2). The value obtained at our level for azulene will serve as a basis for comparison with the results of the substituted systems (see Fig. S2, ESI†).
Fig. 2 shows the results of the application of eqn (2) to the compounds studied. As can be seen, the compounds substituted with –CN are more likely to have positive S2–2T1 energy gaps, fulfilling the requirements for a SF process to occur. We can note that positive values occur when substitutions have been made on electrophilic carbons (even numbered carbons) and that this influence is maintained in mixed compounds (where both electrophilic and nucleophilic carbons have been replaced). Additionally, it is necessary to mention that the highest values occur when substitutions are made on the 7-membered ring.
 | ||
| Fig. 2 Computed S2 ≥ 2T1 values for azulene derivatives (a) for substituted –CN compounds and (b) for substituted –OH compounds. The red line corresponds to the value of azulene taken as a reference. | ||
Although for both the T1 and S2 states the effect of the substituent is similarly stabilizing in almost all cases, the effect in T1 is more decisive than that of S2 for the fulfilment of eqn (2). Indeed, compounds that have T1, S1, and S2 stabilized states are more prone to show SF behaviour.
A qualitative explanation of the observed changes can be derived from the dipole moments of the S0, T1, S1, and S2 states that are 1.04, −0.50, −0.43, and −0.60 Debye, respectively at the B3LYP/6-311G(d,p) level (values for LC-ωHPBE vertical and adiabatic states can be seen in Table S3, ESI†). The direction of the dipole moment in S0 is justified from Hückel's rule59,60 and that of T1 and S1 by Baird's rule.61 Therefore, the S0, and T1, S1, and S2 states have different polarity (Scheme 2). Then, electron acceptor substituents attached to the 7-MR stabilize the T1, S1, and S2 states and destabilize S0.
 | ||
| Scheme 2 The different polarity of states S0, T1, S1, and S2 of azulene. The arrows represent the direction of the dipole moment. | ||
Regarding the –OH substituted compounds, although it does not have the same number of systems with positive S2–2T1, it is the one with the highest value, for example the case of the OH13 (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 216 cm−1) and OH57 (10
216 cm−1) and OH57 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 996 cm−1) systems. It is also worth mentioning that the effect of the substitution is the inverse of that of –CN. In this case, the positive values occur when the nucleophilic carbons have been substituted.
996 cm−1) systems. It is also worth mentioning that the effect of the substitution is the inverse of that of –CN. In this case, the positive values occur when the nucleophilic carbons have been substituted.
On the other hand, it is possible to predict the behaviour of the polysubstituted compounds from the values of eqn (2) relative to the azulene of the monosubstituted compounds (see Table 2). The reason for using the relative values concerning azulene is that this compound, although it can perform a SF process, is of very low intensity, so we consider that those that could have a practical effect are those that have values much higher than those of azulene, so that high and positive values relative to this compound will have a greater probability of performing SF.
| Compound | Eqn (2) | Additive app. | Compound | Eqn (2) | Additive app. |
|---|---|---|---|---|---|
| a Values relative to azulene following: S2,X–2T1,X–S2,azulene–2T1,azulene, where Sx and Tx represent the respective excited state values for the X designed compound. | |||||
| CN12 | −831 | −1240 | CN458 | 2686 | 2761 |
| CN13 | −4348 | −5047 | CN467 | 4217 | 3972 |
| CN47 | 1146 | 535 | CN468 | 6470 | 7890 |
| CN48 | 4337 | 4452 | CN567 | 1179 | 55 |
| CN57 | −3077 | −3383 | CN678 | 3250 | 3972 |
| CN67 | 2332 | 1746 | CN4578 | 1378 | 2281 |
| CN68 | 4882 | 5664 | CN4678 | 5243 | 6198 |
| CN78 | 148 | 535 | CN5678 | 2670 | 2281 |
| CN123 | −2237 | −3764 | CN45678 | 4155 | 4507 |
| CN457 | −607 | −1157 | |||
For example, the S2–2T1 values relative to the azulene of CN1 and CN2 are −2524 and 1283 cm−1, respectively, while for the case of CN12 it is −831. The sum of the two monosubstituted compounds gives −1240 cm−1, quite close to the calculated value. Additionally, for CN6, CN7, and CN8 the values obtained are 3438, −1691, and 2226 cm−1, respectively. For the case of CN67, CN78, and CN68 the values are 2332, 148, and 4882 cm−1, respectively, very similar to the sum of the values obtained for the monosubstituted compounds. The correlation factor (r2) between the results obtained from the TD-DFT scheme and those calculated from the sum of the monosubstituted compounds with –CN is 0.97, thus allowing to predict results of polysubstituted compounds from those monosubstituted ones (see Fig. S3 and S4 in ESI†).
For those substituted with –OH, the correlation is lower but still significant (r2 = 0.92, see Table S4 and Fig. S5 and S6 in ESI†). This lower correlation may be due to the formation of intramolecular hydrogen bonds at S0 thus affecting the values that could be obtained in the vertical excited states.
For the experimental realization of these compounds, it is possible to take advantage of the nucleophilic/electrophilic nature of the azulene carbons and to react them with electrophiles/nucleophiles through aromatic substitution processes. Ideally, the electrophiles/nucleophiles used should be in excess to obtain the polysubstituted compounds.62,63
Conclusions
In summary, we have taken advantage of the electronic characteristics of azulene to design anti-Kasha compounds that can carry out singlet fission (SF) processes. For this, we have performed systematic substitutions including π-electron acceptor (–CN) and π-electron donor (–OH) groups and calculations of vertical excited states have been carried out. The formula S2–2T1 has been used to determine whether a compound can (or cannot) carry out SF processes allowing its application in light harvesting and/or photovoltaics technology. The results obtained indicate that the electron acceptor group (–CN) offers the largest S2–2T1 values when substitutions were performed on the electrophilic carbons. In the case of monosubstituted compounds, values >4 times higher than azulene were obtained, while in the case of polysubstituted compounds up to >7 times higher. Additionally, it was found that the compounds substituted with the CN group on the electrophilic atoms in the seven-membered ring are the ones that present the best values. On the other hand, the substitutions with the electron donor group (–OH) offer higher values than those of azulene when the substitutions are performed on the nucleophilic carbon atoms regardless of the type of ring.Finally, it was shown that there is an additive character which would allow predicting the values of S2–2T1 relative to the azulene of polysubstituted compounds from those of monosubstituted ones. The formula used could obey a more general rule Sm ≥ 2Tn, where Sm is the relevant singlet state in the process, while Tn is the closest triplet state to it, thus allowing us to predict in a general way compounds that can carry out SF independently of whether or not they fulfil Kasha's rule.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the financial support of the National Agency for Research and Development (ANID) through FONDECYT project 1230571 (R. P.-R.). Powered@NLHPC: this research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02) of the Universidad de Chile. M. S. is grateful for the financial support from the Ministerio de Ciencia e Innovación (Project PID2020-113711GB-I00 MCIN/AEI/10.13039/50110001103) and the Generalitat de Catalunya (Project 2021-SGR-623). D.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W.
W.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S. acknowledges financial support from the National Science Centre, Poland (2021/42/E/ST4/00332). Open access funding provided by the University of Girona.
S. acknowledges financial support from the National Science Centre, Poland (2021/42/E/ST4/00332). Open access funding provided by the University of Girona.
References
- M. B. Smith and J. Michl, Singlet Fission, Chem. Rev., 2010, 110, 6891–6936 Search PubMed.
- D. Casanova, Theoretical Modeling of Singlet Fission, Chem. Rev., 2018, 118, 7164–7207 Search PubMed.
- K. Miyata, F. S. Conrad-Burton, F. L. Geyer and X.-Y. Zhu, Triplet Pair States in Singlet Fission, Chem. Rev., 2019, 119, 4261–4292 Search PubMed.
- T. Ullrich, D. Munz and D. M. Guldi, Unconventional singlet fission materials, Chem. Soc. Rev., 2021, 50, 3485–3518 Search PubMed.
- A. Japahuge and T. Zeng, Theoretical Studies of Singlet Fission: Searching for Materials and Exploring Mechanisms, ChemPlusChem, 2018, 83, 146–182 Search PubMed.
- A. M. Berghuis, A. Halpin, Q. Le-Van, M. Ramezani, S. Wang, S. Murai and J. Gómez Rivas, Enhanced Delayed Fluorescence in Tetracene Crystals by Strong Light-Matter Coupling, Adv. Funct. Mater., 2019, 29, 1901317 Search PubMed.
- M. Einzinger, T. Wu, J. F. Kompalla, H. L. Smith, C. F. Perkinson, L. Nienhaus, S. Wieghold, D. N. Congreve, A. Kahn, M. G. Bawendi and M. A. Baldo, Sensitization of silicon by singlet exciton fission in tetracene, Nature, 2019, 571, 90–94 Search PubMed.
- J. Zirzlmeier, D. Lehnherr, P. B. Coto, E. T. Chernick, R. Casillas, B. S. Basel, M. Thoss, R. R. Tykwinski and D. M. Guldi, Singlet fission in pentacene dimers, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5325–5330 Search PubMed.
- M. Dvořák, S. K. K. Prasad, C. B. Dover, C. R. Forest, A. Kaleem, R. W. MacQueen, A. J. I. I. Petty, R. Forecast, J. E. Beves, J. E. Anthony, M. J. Y. Tayebjee, A. Widmer-Cooper, P. Thordarson and T. W. Schmidt, Singlet Fission in Concentrated TIPS-Pentacene Solutions: The Role of Excimers and Aggregates, J. Am. Chem. Soc., 2021, 143, 13749–13758 Search PubMed.
- C. Zeiser, L. Moretti, F. Reicherter, H. F. Bettinger, M. Maiuri, G. Cerullo and K. Broch, Singlet Fission in Dideuterated Tetracene and Pentacene, ChemPhotoChem, 2021, 5, 758–763 Search PubMed.
- R. Zhang, Y. Guan, Z. Zhu, H. Lv, F. Li, S. Sun and J. Li, Multifunctional Tetracene/Pentacene Host/Guest Nanorods for Enhanced Upconversion Photodynamic Tumor Therapy, ACS Appl. Mater. Interfaces, 2019, 11, 37479–37490 Search PubMed.
- J. Poater, R. Visser, M. Solà and F. M. Bickelhaupt, Polycyclic Benzenoids:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Why Kinked is More Stable than Straight, J. Org. Chem., 2007, 72, 1134–1142 Search PubMed.
Why Kinked is More Stable than Straight, J. Org. Chem., 2007, 72, 1134–1142 Search PubMed. - J. Poater, M. Duran and M. Solà, Aromaticity Determines the Relative Stability of Kinked vs. Straight Topologies in Polycyclic Aromatic Hydrocarbons, Front. Chem., 2018, 6, 561 Search PubMed.
- R. Pino-Rios, R. Báez-Grez and M. Solà, Acenes and phenacenes in their lowest-lying triplet states. Does kinked remain more stable than straight?, Phys. Chem. Chem. Phys., 2021, 23, 13574–13582 Search PubMed.
- M. Kasha, Characterization of electronic transitions in complex molecules, Discuss. Faraday Soc., 1950, 9, 14–19 Search PubMed.
- H. Xin, B. Hou and X. Gao, Azulene-Based π-Functional Materials: Design, Synthesis, and Applications, Acc. Chem. Res., 2021, 54, 1737–1753 Search PubMed.
- T. Kühne, K. H. Au-Yeung, F. Eisenhut, O. Aiboudi, D. A. Ryndyk, G. Cuniberti, F. Lissel and F. Moresco, STM induced manipulation of azulene-based molecules and nanostructures: the role of the dipole moment, Nanoscale, 2020, 12, 24471–24476 Search PubMed.
- J. R. Platt, Classification of Spectra of Cata-Condensed Hydrocarbons, J. Chem. Phys., 2004, 17, 484–495 Search PubMed.
- C. Glidewell and D. Lloyd, MNDO study of bond orders in some conjugated bi- and tri-cyclic hydrocarbons, Tetrahedron, 1984, 40, 4455–4472 Search PubMed.
- R. Báez-Grez and R. Pino-Rios, Is azulene’s local aromaticity and relative stability driven by the Glidewell–Lloyd rule?, Phys. Chem. Chem. Phys., 2024, 26, 12162–12167 Search PubMed.
- O. El Bakouri, J. Poater, F. Feixas and M. Solà, Exploring the validity of the Glidewell–Lloyd extension of Clar's π-sextet rule: assessment from polycyclic conjugated hydrocarbons, Theor. Chem. Acc., 2016, 135, 205 Search PubMed.
- D. Dunlop, L. Ludvíková, A. Banerjee, H. Ottosson and T. Slanina, Excited-State (Anti)Aromaticity Explains Why Azulene Disobeys Kasha's Rule, J. Am. Chem. Soc., 2023, 145, 21569–21575 Search PubMed.
- A. Konishi and M. Yasuda, Breathing New Life into Nonalternant Hydrocarbon Chemistry: Syntheses and Properties of Polycyclic Hydrocarbons Containing Azulene, Pentalene, and Heptalene Frameworks, Chem. Lett., 2021, 50, 195–212 Search PubMed.
- A. Diaz-Andres, J. Marín-Beloqui, J. Wang, J. Liu, J. Casado and D. Casanova, Rational design of anti-Kasha photoemission from a biazulene core embedded in an antiaromatic/aromatic hybrid, Chem. Sci., 2023, 14, 6420–6429 Search PubMed.
- B. Nickel and D. Klemp, The lowest triplet state of azulene-h8 and azulene-d8 in liquid solution. I. Survey, kinetic considerations, experimental technique, and temperature dependence of triplet decay, Chem. Phys., 1993, 174, 297–318 Search PubMed.
- B. Nickel and D. Klemp, The lowest triplet state of azulene-h8 and azulene-d8 in liquid solution.: II. Phosphorescence and E-type delayed fluorescence, Chem. Phys., 1993, 174, 319–330 Search PubMed.
- A. D. Becke, Becke's three parameter hybrid method using the LYP correlation functional, J. Chem. Phys., 1993, 98, 5648–5652 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 Search PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules, J. Chem. Phys., 1971, 54, 724–728 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- C. Ullrich, Time-Dependent Density-Functional Theory: Concepts and Applications, OUP, Oxford, 2012 Search PubMed.
- K. Veys and D. Escudero, Computational Protocol To Predict Anti-Kasha Emissions: The Case of Azulene Derivatives, J. Phys. Chem. A, 2020, 124, 7228–7237 Search PubMed.
- A. Murakami, T. Kobayashi, A. Goldberg and S. Nakamura, CASSCF and CASPT2 studies on the structures, transition energies, and dipole moments of ground and excited states for azulene, J. Chem. Phys., 2004, 120, 1245–1252 Search PubMed.
- K. Veys and D. Escudero, Anti-Kasha Fluorescence in Molecular Entities: Central Role of Electron–Vibrational Coupling, Acc. Chem. Res., 2022, 55, 2698–2707 Search PubMed.
- S. Hirata and M. Head-Gordon, Time-dependent density functional theory within the Tamm–Dancoff approximation, Chem. Phys. Lett., 1999, 314, 291–299 Search PubMed.
- M. J. G. Peach, M. J. Williamson and D. J. Tozer, Influence of Triplet Instabilities in TDDFT, J. Chem. Theory Comput., 2011, 7, 3578–3585 Search PubMed.
- R. P. Steer, Photophysics of molecules containing multiples of the azulene carbon framework, J. Photochem. Photobiol., C, 2019, 40, 68–80 Search PubMed.
- S. Vosskötter, P. Konieczny, C. M. Marian and R. Weinkauf, Towards an understanding of the singlet–triplet splittings in conjugated hydrocarbons: Azulene investigated by anion photoelectron spectroscopy and theoretical calculations, Phys. Chem. Chem. Phys., 2015, 17, 23573–23581 Search PubMed.
- Y. Guo, K. Sivalingam, E. F. Valeev and F. Neese, SparseMaps—A systematic infrastructure for reduced-scaling electronic structure methods. III. Linear-scaling multireference domain-based pair natural orbital N-electron valence perturbation theory, J. Chem. Phys., 2016, 144, 94111 Search PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 Search PubMed.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- Y. Zhao and D. G. Truhlar, Comparative DFT Study of van der Waals Complexes:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rare-Gas Dimers, Alkaline-Earth Dimers, Zinc Dimer, and Zinc-Rare-Gas Dimers, J. Phys. Chem. A, 2006, 110, 5121–5129 Search PubMed.
Rare-Gas Dimers, Alkaline-Earth Dimers, Zinc Dimer, and Zinc-Rare-Gas Dimers, J. Phys. Chem. A, 2006, 110, 5121–5129 Search PubMed. - Y. Zhao and D. G. Truhlar, Density Functional for Spectroscopy: No Long-Range Self-Interaction Error, Good Performance for Rydberg and Charge-Transfer States, and Better Performance on Average than B3LYP for Ground States, J. Phys. Chem. A, 2006, 110, 13126–13130 Search PubMed.
- R. Peverati and D. G. Truhlar, M11-L: A Local Density Functional That Provides Improved Accuracy for Electronic Structure Calculations in Chemistry and Physics, J. Phys. Chem. Lett., 2012, 3, 117–124 Search PubMed.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 Search PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta – Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91, 146401 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 Search PubMed.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 Search PubMed.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 Search PubMed.
- J. Heyd and G. E. Scuseria, Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional, J. Chem. Phys., 2004, 121, 1187–1192 Search PubMed.
- J. Heyd and G. E. Scuseria, Assessment and validation of a screened Coulomb hybrid density functional, J. Chem. Phys., 2004, 120, 7274–7280 Search PubMed.
- J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, Energy band gaps and lattice parameters evaluated with the Heyd-Scuseria-Ernzerhof screened hybrid functional, J. Chem. Phys., 2005, 123, 174101 Search PubMed.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, A long-range correction scheme for generalized-gradient-approximation exchange functionals, J. Chem. Phys., 2001, 115, 3540–3544 Search PubMed.
- T. M. Henderson, A. F. Izmaylov, G. Scalmani and G. E. Scuseria, Can short-range hybrids describe long-range-dependent properties?, J. Chem. Phys., 2009, 131, 44108 Search PubMed.
- C. Morell, A. Grand and A. Toro-Labbé, New Dual Descriptor for Chemical Reactivity, J. Phys. Chem. A, 2005, 109, 205–212 Search PubMed.
- R. Pino-Rios, D. Inostroza, G. Cárdenas-Jirón and W. Tiznado, Orbital-Weighted Dual Descriptor for the Study of Local Reactivity of Systems with (Quasi-) Degenerate States, J. Phys. Chem. A, 2019, 123, 10556–10562 Search PubMed.
- E. Hückel, Quanstentheoretische Beiträge zum Benzolproblem, Z. Phys., 1931, 72, 310–337 Search PubMed.
- H. Möllerstedt, M. C. Piqueras, R. Crespo and H. Ottosson, Fulvenes, Fulvalenes, and Azulene:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Are They Aromatic Chameleons?, J. Am. Chem. Soc., 2004, 126, 13938–13939 Search PubMed.
Are They Aromatic Chameleons?, J. Am. Chem. Soc., 2004, 126, 13938–13939 Search PubMed. - N. C. Baird, Quantum organic photochemistry. II. Resonance and aromaticity in the lowest 3.pi..pi.* state of cyclic hydrocarbons, J. Am. Chem. Soc., 1972, 94, 4941–4948 Search PubMed.
- A. C. Razus, Azulene, Reactivity, and Scientific Interest Inversely Proportional to Ring Size; Part 1: The Five-Membered Ring, Symmetry, 2023, 15, 310 Search PubMed.
- A. C. Razus, Azulene, Reactivity, and Scientific Interest Inversely Proportional to Ring Size; Part 2: The Seven-Membered Ring, Symmetry, 2023, 15, 1391 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01284d |
| This journal is © the Owner Societies 2024 |
