Pentacycloundecanylidene and pentacycloundecanone – hyperconjugatively stabilized carbene and ketone

Abstract

Pentacycloundecanylidene was spectroscopically identified during the photolysis of the corresponding aziridine and its aerial oxidation results in the corresponding ketone. Here we report the role of hyperconjugative interactions in stabilizing the singlet pentacycloundecanylidene and its corresponding ketone pentacycloundecanone. The pentacycloundecanylidene possesses a singlet ground state with two possible geometrical isomers based on the orientation of the carbene bridge (U1 and U2). The energy difference between U1 and U2 is minimal (0.9 kcal mol⁻¹) and the triplet state is 5.6 kcal mol⁻¹ energetically higher than the more stable singlet state U1. The proximal C–C bonds of the carbene bridge in the singlet state are significantly elongated as compared to the distal C–C bonds. The bending of the carbene bridge in the triplet state and the carbonyl group in the ketone are minimal as compared to the parent pentacycloundecane. The molecular orbital (MO), natural bond orbital (NBO) and energy decomposition analysis (EDA) show that both Cieplak-type hyperconjugation viz. donation of electrons from the proximal C–C σ bonds to the empty p-orbital on the carbene centre and Felkin–Anh type hyperconjugation viz. donation of the lone pair of carbene carbon to the distal C–C σ* orbitals exist in carbene systems. The bending of the carbene bridge in singlet carbene is to enhance the Cieplak-type hyperconjugative interaction. The ketone is also stabilized by Cieplak-type hyperconjugative interaction but to a lower extent as compared to the singlet carbene. The reactivity study suggests that the singlet pentacycloundecanylidene is ambiphilic in nature.

---

Introduction

Carbenes are of immense interest to experimental and theoretical chemists due to their divalent nature that violates the natural tetravalency of classical compounds.^1,2 The advancement of synthetic strategies and the development of deeper insight into chemical bonding have played a pivotal role in the growth of carbene chemistry.³ Carbenes generally exist in either the low-spin singlet state or the high-spin triplet state, even though there are other excited state possibilities.⁴ Since the singlet carbene features a σ-lone pair and a formally empty p-orbital, the ideal singlet carbene is expected to show ambiphilic reactivity.⁵ However, one type of philicity of singlet carbene was found to be predominant over the other. Singlet carbenes can be stabilized by placing hetero group-15 and group-16 main group elements adjacent to the carbenic centre.^6–8 Similarly, stabilization of singlet carbene by transition metal coordinations adjacent to the carbenic centre was also reported.^9,10 The electron-rich hetero main group atoms or transition metal fragments stabilize the vacant p-orbital of a carbene carbon atom by donating a lone pair of electrons from the former. Hence, these types of carbenes are expected to show predominantly nucleophilic character.

Apart from the electron-rich hetero main group/transition metal fragment substituted carbenes, singlet dialkyl carbenes such as 2-adamantylidene, norbornen-7-ylidene, cyclobutylidene, tricyclooct-8-ylidene, etc. are reported experimentally or computationally.^11–17 They are normally classified in the category of foiled carbenes.^18,19 The stability of these carbenes was explained by through-space interaction, non-classical bonding and hyperconjugative interaction. It has been reported that the stability of norbornen-7-ylidene is attributed to the through-space donation of electrons from the C–C π MO to the empty p-orbital on the carbene centre (Scheme 1a). Brinker and co-workers theoretically reported a cyclobutyl carbene and established that the stability of the singlet carbene is attributed to the nonclassical three-centre two-electron bond (Scheme 1b).²⁰ In another report, Brinker and co-workers computationally analyzed a caged carbene tricyclopentylidene (Scheme 1c). They reported that it is a nucleophilic carbene having a bridge flapping, resulting from a nonclassical interaction.²¹ We have established the role of hyperconjugative interactions in stabilizing caged carbene singlet 2-adamantylidene. Our studies proposed that the Cieplak-type hyperconjugation plays a major role in stabilizing the singlet 2-adamantylidene (Scheme 1d).^22,23 Since the hyperconjugative interactions are second-order interactions, both the lone pair and empty p-orbital on the carbene centre are susceptible to protonation and hydride adduct formation. Hence, the singlet 2-adamantylidene behaves as an ambiphilic carbene. The cage constraints of 2-adamantylidene enhance the hyperconjugative interactions.

Scheme 1 The schematic diagrams of the molecules (a) norbornene-7-ylidene, (b) cyclobutylcarbene, (c) tricyclopentylidene, (d) 2-adamantylidene and (e) pentacycloundecanylidene and pentacycloundecanone, and reactions for the formation of (f) pentacycloundecanylidene and (g) pentacycloundecanone.

Another caged type carbene recently isolated was pentacycloundecanylidene. It has been reported as an intermediate during the photolysis of the corresponding diaziridine by Marchand and coworkers (Scheme 1f).²⁴ Later it was spectroscopically identified by Basarić and coworkers.²⁵ It was found to be highly reactive and the aerial oxidation results in a ketone (Scheme 1g). Note that the 2-adamantylidene consists of only six membered cyclohexyl rings in the chair conformer. On the other hand, the pentacycloundecanylidene consists of one four-membered ring, four five-membered rings and one six-membered ring in the boat conformation. The more strained 4–6 membered rings in the pentacycloundecanylidene are expected to show variation in the hyperconjugative interactions as compared to the 2-adamantylidene. To understand the nature and the extent of hyperconjugative interactions, we have carried out comprehensive quantum computational analyses of the structure, bonding, reactivity, and stability of pentacycloundecanylidene. We have also analyzed how these hyperconjugative interactions varied when the carbene changes to the corresponding ketone.

Computational methodology

All calculations were carried out using the Gaussian09 and ADF2020.102. program packages.^26–28 All the geometries were optimized in the framework of DFT using the generalized gradient approximation with Becke's exchange functional included with the correlation functional of Perdew (BP86).^29–31 The basis set used has triple ζ-quality, augmented with a double polarization function (def2-TZVPP).³² This is represented as BP86/def2-TZVPP. The nature of the minimum was characterized by calculating the Hessian matrix analytically. Single point calculations were done using the meta hybrid-GGA M06 functional with a triple ζ-quality double polarization basis set (M06/def2-TZVPP).³³ Reaction energies were refined by taking electronic energy at the M06/def2-TZVPP level with zero point correction from the BP86/def2-TZVPP level. Gibbs free energies were calculated by taking electronic energy at the M06/def2-TZVPP level with thermal correction to the Gibbs free energy from the BP86/def2-TZVPP level. Natural Bond Orbital (NBO) and Natural Population Analysis (NPA) were done using the NBO 6.0 program package at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory.³⁴ NBO/NPA analysis gives the natural charge, second-order interaction, and Wiberg Bond Index (WBI). The WBI gives the average electron pairs shared between atoms, which can be taken as a measure of the bond order. Multi-reference calculations were carried out at the CASPT2(2,2)/cc-pVTZ level of theory using MOLPRO2012.1 program package.^35–37 The active orbitals used for calculation are σ-lone pair type orbitals and the vacant p-type orbitals on the carbene carbon atom. The Energy Decomposition Analysis coupled with Natural Orbital for Chemical Valence (EDA-NOCV) was carried out at the BP86/TZ2P level of theory using the ADF2020.102 program package.^38–45 Scalar relativistic correction using the zeroth order regular approximation (ZORA) was incorporated and the core electrons were treated with the frozen-core approximation.^46–50 The TZ2P basis set with a small frozen core was employed for the calculations. The frozen core orbitals considered for carbon is 1 s.

EDA calculates the intrinsic interaction energy (ΔE_int) (1) between fragments A and B in molecule A–B. The interaction energy can be considered as an indicator of the bond strength between the two fragments under consideration. This interaction energy can be correlated to a physical observable, the bond dissociation energy (D_e) by eqn (1). This makes the EDA scheme a powerful tool for interpreting data regarding molecular structure, bonding, and reactivity. Here, the ΔE_prep is the deformation energy required for fragments A and B from their respective ground and electronic states to the state where the electronic and geometric state of the fragments is as that in molecule A–B. It can be calculated using eqn (2).

ΔE_int = −D_e + ΔE_prep (1)

where,

ΔE_prep = (E^GS_A + E^GS_B) − (E_A + E_B) (2)

The terms E^GS_A and E^GS_B represent the electronic energy of the fragments A and B in their respective ground states, while E_A and E_B refer to the electronic energy of the corresponding fragments in their frozen geometries of the molecule.

The instantaneous interaction energy of a bond A–B, which is an indicator of the bond strength, is partitioned into chemically meaningful components (eqn (3)). In the EDA scheme given by Morokuma, this partitioning is as follows

ΔE_int = ΔE_elect + ΔE_Pauli + ΔE_orb + ΔE_disp (3)

The term ΔE_elect corresponds to the quasi-classical electrostatic interactions between the frozen electron density and the nuclei on the fragments in the geometry. ΔE_Pauli represents the repulsive interactions between the fragments with the same spin as they interact. ΔE_orb represents the energy stabilization of orbitals through the bond formation and is an attractive component.

The ΔE_orb term can be again classified into contributions from each symmetry-adapted interacting system. The natural orbitals for chemical valence (NOCV) give an understanding of the various orbital interactions between the fragments and the contribution of each pair of the interacting orbitals (Ψ_−n/Ψ_n) to the total orbital stabilization energy (eqn (4)).

In the EDA-NOCV scheme, the ΔE_orb is expressed in terms of NOCVs as

−F^TS_−n,−n and F^TS_n,n are the elements of the Kohn Sham matrix that correspond to the NOCV pairs having eigenvalues ν_n and ν_−n in the transition state electron densities. The orbitals possess a negative value that indicates an antibonding nature, and those with a positive value indicate a bonding nature. The strength of these pairwise interactions can provide a deep insight about the bonding interactions and the corresponding deformation densities can give the direction of electron flow.

Results and discussion

The equilibrium geometries of pentacycloundecane, and singlet and triplet states of pentacycloundecanylidene and pentacycloundecanone were analyzed at the BP86/def2-TZVPP level of theory (Fig. 1). The undecane consists of fused cyclic alkyl rings viz. one four membered ring, four five membered rings and one six membered ring. The six membered ring is in a boat conformation. The flagpole hydrogens are the hydrogens attached to the carbons, which are at the stern and bow of a boat conformer of cyclohexane. These Hs point upwards like a flagpole in a boat and cause steric repulsion. The corresponding flagpole H–H distance is 2.149 Å, which is longer than that of the cyclohexane in the boat conformer (1.830 Å) and shorter than in the twisted boat conformation (2.340 Å). Pentacycloundecane and its various derivatives were experimentally isolated.^51,52 The removal of two hydrogen atoms of one of the –CH₂ groups of the cyclohexyl ring results in the corresponding carbene. The carbene, U1 and U2 are in the singlet state whereas the U3 is in the triplet state. The orientation of the carbene bridge is different in U1–U3. These types of bent carbene systems such as singlet 2-adamantylidene, norbornene-7-ylidene, etc. are normally classified as foiled carbenes. The foiling of these reported systems is established as the consequence of an extra stabilization attained in the particular geometry. We have calculated the deviation of the carbene bridge for the corresponding –CH₂ group in undecane (U) (Scheme 2). The carbene bridge in singlet isomer U1 is bent towards the cyclohexyl –CH₂ group (θ_b = −17.1°) whereas the carbene bridge in the other singlet isomer U2 is bent away from the cyclohexyl –CH₂ group (θ_b = 27.5°). U1 is more stable than U2 by 0.9 kcal mol⁻¹. The triplet state is 5.6 kcal mol⁻¹ higher in energy than that of the most stable singlet U1. The carbene bridge in the triplet state is not bent significantly with respect to the undecane (θ_b = −0.7°). Note that the 2-adamantylidene was experimentally isolated by Bally and coworkers. The singlet–triplet gap in 2-adamntylidene is only 3.1 kcal mol⁻¹. We have also calculated the transition state for the interconversion of U1 and U2 (U_TS, Fig. S1, ESI†). The corresponding energy barrier is quite less (ΔE^‡ = 1.3 kcal mol⁻¹ and ΔG^‡ = 0.4 kcal mol⁻¹). Since the energy difference between the isomers U1 and U2 is minimal and the transition state barrier is less, we have calculated these isomers and transition states in a multi-reference level at the CASPT2/cc-pVTZ level of theory. The active orbitals used for calculation are σ-lone pair type orbitals and the vacant p-type orbitals on the carbene carbon atom. It was found that the energy differences between U1 and U2 are the same (0.9 kcal mol⁻¹) as the difference at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory. The transition state barrier (1.7 kcal mol⁻¹) is found to be slightly higher than at the M06/def2-TZVPP//BP86-def2-TZVPP level of theory (1.3 kcal mol⁻¹) (Fig. S6, ESI†). Since the singlet carbene has one vacant orbital (LUMO) and one sp-hybridized lone pair (HOMO), we have used [2,2]-CASSCF calculation. Here, two electrons and two orbitals are used in the active space. All other unoccupied orbitals are high-lying C–C and C–H σ* orbitals. The CI vectors obtained from [2,2]-CASSCF calculation for U1 and U2 are as follows,

Ψ_CI = c₁Φ₁ + c₂Φ₂

Φ₁ and Φ₂ represent the slater determinant having active space configuration as σ² π⁰ and σ⁰ π² respectively, where σ indicates the valence sp-hybrid orbital on the carbene carbon atom and π represents the valence p-type orbital on the carbene carbon atom. The contributions from the other possible slater determinants are negligible and hence are not given in the above equation. The coefficients c₁ and c₂ for U1 are 0.98 and −0.18 respectively and the corresponding coefficients for U2 are 0.99 and −0.16 respectively indicating that the ground state has a major contribution from the σ² π⁰ configuration. We have identified the normal modes of vibration corresponding to carbene bridge bending in U1 and U2. The anharmonic vibrational frequencies were calculated at the BP86/def2-TZVPP level using the Gaussian 09 programme. 332 cm⁻¹ and 230 cm⁻¹ are anharmonic vibrational frequencies corresponding to the bending vibration of the bridging carbene carbon atom of U1 and U2 respectively. The corresponding harmonic vibrational frequencies are 361 cm⁻¹ and 237 cm⁻¹ respectively. The zero-point energy calculated using anharmonic vibrational frequencies for U1 and U2 are 166 cm⁻¹ (7.6 × 10⁻⁴ a.u.) and 115 (5.3 × 10⁻⁴ a.u.) cm⁻¹ respectively. The vibrational energies of these normal modes of vibration are well below (1.1 kcal mol⁻¹ for U1 and 0.4 kcal mol⁻¹ for U2) that of the electronic energy level of the transition state (Fig. S7, ESI†). Hence, the possibility of co-existence of both isomers is likely. Accordingly, we have considered both isomers of the singlet carbene U1 and U2 for further bonding analysis. As per the experimental reports, the oxidation of the pentacycloundecanylidene results in a ketone, where the oxygen atom is added to the carbene carbon. The reaction energy was calculated and found to be highly exothermic and exergonic (2U1 + O₂ → 2U-CO, ΔE = −241.3 kcal mol⁻¹ and ΔG = −230.2 kcal mol⁻¹). Even though there are two possible geometries for the singlet state, we could locate only one minimum geometry for the undecanone (U-CO). The cyclohexanone ring in the undecanone, U-CO, is also in the boat conformation with a slight bending of the CO group (θ_b = −3.0°).

Fig. 1 Equilibrium geometries of pentacycloundecane (U), singlet pentacycloundecanylidenes (U1 and U2), triplet pentacycloundecanylidene (U3) and the undecanone (U-CO) at the BP86/def2-TZVPP level of theory. θ_b is the bending angle in degrees, the −ve sign indicates that the bending is towards the cyclohexyl –CH₂ group and the +ve sign indicates that the bending is away from the cyclohexyl –CH₂ group (Scheme 2). Bond distances are given in Angstrom and bond angles in degrees. Relative energies (in kcal mol⁻¹) of the carbenes at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory are given in parentheses.

Apart from the bending angle, other structural parameters have also significant differences between carbene and ketone. The C1–C2 and C1–C5 bonds of carbene and ketone are shorter than the corresponding bonds in undecane as well as other C–C bonds of the corresponding molecule. Among carbene and ketone, the carbene has the shortest C1–C2 and C1–C5 bonds. On the other hand, the proximal C2–C8 and C5–C6 bonds of U1, U3, and U-CO are longer than those in the undecane. The corresponding bond lengths in U2 are slightly shorter than the other C–C bonds in the molecule. The C2–C3 and C5–C4 bonds in U2 are longer than the corresponding bonds in other molecules as well as other C–C bonds in U2. There are significant differences in the bending as well as the other geometrical parameters when the undecanylidene changes to undecanone.

Scheme 2 Schematic representation of the bending angle of the carbene/CO bridge, θ_b, in carbene and ketone. The bending angle is calculated using the expression θ_b = ∠(A–B–C₁H₂) of U – of UX, X = 1, 2, 3 or –CO.

The important frontier molecular orbitals (MO) of carbene and ketone are given in Fig. 2. The LUMO and HOMO of carbene U1 and U2 and singly occupied orbitals of U3 are similar. The LUMOs of U1 and U2 are majorly p-orbital on the carbene carbon atom with slight contribution from the one set of vicinal C–C bonds viz. C2–C8 and C5–C6 in U1 and C2–C3 and C5–C4 in U2. The HOMO of singlet carbene is a σ-type lone pair orbital on the carbene carbon with contribution from the second set of vicinal C–C bonds. On the other hand, the corresponding singly occupied orbital SOMOs in the triplet carbene U3 have contributions from both sets of vicinal C–C bonds. The lone pair orbital in singlet carbene is an spⁿ hybrid orbital having 47% s character and 53% p character in U1 and 44% s character and 56% p character in U2. Even though U1 is more stable than U2, the HOMO–LUMO (H–L) gap of U2 (4.02 eV) is more than that of U1 (4.46 eV). Hoffmann proposed that a value of at least 2 eV for the H–L gap is sufficient to impose a singlet ground state indicating the stability of both the singlet states U1 and U2.⁵³

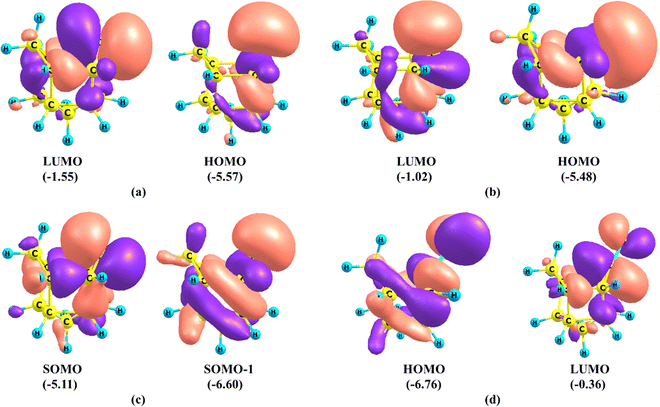Fig. 2 Important frontier molecular orbitals of (a) U1, (b) U2, (c) U3 and (d) U-CO. Eigenvalues are given in parentheses in eV. The isosurface value is 0.03.

We also analyzed the frontier MOs of the undecanone U-CO. The HOMO of the ketone is mainly a lone pair orbital on the oxygen atom having antibonding interaction with C1–C2 and C1–C5 σ bonds. The LUMO of the ketone is a π* orbital centered on the C–O bond with a major contribution on the C atom and a slight contribution from the one set of vicinal C–C bonds. The H–L gap in the undecanone is 6.40 eV, which is higher than that of the singlet carbene (4.02 eV for U1 and 4.46 eV for U2).

The numerical data obtained from the natural bond order (NBO) and natural population analyses are correlated well with the geometrical and molecular orbital data for the carbene and ketone (Table 1). In corroboration with the geometrical data, the C2–C8 and C5–C6 bond orders of U1 (0.93 and 0.88) and U-CO (0.95 and 0.95), as well as C2–C3 and C4–C5 bond orders of U2 (0.91 and 0.89), are slightly lower than those of other bonds. Note that the vacant p-orbitals of the carbene carbon atoms are significantly populated in the singlet carbenes (0.21e in U1 and 0.25e in U2) indicating that electron deficiency of the carbene bridge is reduced by the second-order interaction. On the other hand, the population of the C–O π* orbital in ketone (0.09e) is much less than that of the population of the p-orbital in the singlet carbene. This suggests that the electrophilic nature of the carbene carbon atom is much higher than that of the carbonyl carbon atom in the ketone. The lone pair occupancies are in the range of 1.87e–1.90e for the singlet carbenes suggesting that they are stabilized by second-order interaction. The natural charge on the carbonyl carbon in U-CO (0.63) is significantly positive as compared to the carbene carbon atom in singlet (0.14–0.18) and triplet carbenes (0.23). Note that the charge on the carbon atom in undecane is negative.

Table 1 Wiberg bond indices of important bonds (WBI), natural charge on the carbene/carbonyl carbon C1 (q), orbital occupancy of important orbitals in undecane U, singlet carbenes U1, U2, triplet carbene U3 and the ketone U-CO obtained from natural bond order (NBO) analysis at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory

	WBI				q(C1)	Occupancy
	C2–C3	C4–C5	C2–C8	C5–C6		C1(LP)	C1(p)/C–O π*	C2–C3/C4–C5	C2–C8/C5–C6
U	0.98	0.98	0.97	0.98	−0.40	—	—	1.97/1.98	1.97/1.98
U1	0.96	0.95	0.91	0.89	0.18	1.90	0.21	1.97/1.97	1.92/1.89
U2	0.93	0.88	0.95	0.95	0.14	1.87	0.25	1.91/1.86	1.97/1.97
U3	0.95	0.94	0.93	0.93	0.23	0.97	1.03	1.96/1.95	1.95/1.95
U-CO	0.98	0.98	0.95	0.95	0.63	—	0.09	1.96/1.97	1.95/1.95

---

We have analyzed the nature of the second-order interaction to explain the population of electron density in the empty orbital of the carbene carbon atom in U1 and U2, and the C–O π* orbital on ketone U-CO as well as the low value of the lone pair occupancy in U1 and U2 (Table 2). The second-order interaction data suggest two different types of hyperconjugative interactions responsible for the stability of the system. The first type is Cieplak-type hyperconjugation where the empty p-orbital on the carbene carbon atom and C–O π* orbital of ketone are stabilized by accepting electrons from the C–C σ orbitals. The second type is Felkin–Anh type hyperconjugation where the lone pair orbital is stabilized by donating electrons to the C–C σ* orbitals. Similar hyperconjugative interactions were proposed for the stability of singlet 2-adamantylidene. The Cieplak-type hyperconjugative stabilization energy of U1 resulting from the donation of C2–C8 and C5–C6 σ bonding electrons to the empty p-orbital on the carbene carbon atom is 33.7 kcal mol⁻¹. The corresponding value for U2 resulting from the donation of C2–C3 and C4–C5 σ bonding electrons to the empty p-orbital on the carbene carbon atom is 65.9 kcal mol⁻¹. Note that, the Cieplak-type hyperconjugative stabilization energy of U-CO (12.7 kcal mol⁻¹) and the triplet carbene U3 (9.9 kcal mol⁻¹) are quite less. On the other hand, the Felkin–Anh type hyperconjugative energies are much less than that of the Cieplak-type hyperconjugation values. The overall Felkin–Anh type hyperconjugation energy of U2 and that for U3 is in the range of 20.9–22.8 kcal mol⁻¹. The corresponding value for U1 is relatively low (13.7 kcal mol⁻¹). Note that the Felkin–Anh hyperconjugation is absent in the ketone.

Table 2 Important second-order hyperconjugative interactions of U1, U2, U3 and U-CO calculated using natural bond order (NBO) analysis at the M06/Def2-TZVPP//BP86/def2-TZVPP level of theory

Second-order interaction energy (kcal mol^−1)
	C2–C3 to C1 (p)/CO	C4–C5 to C1 (p)/CO	C2–C8 to C1 (p)/CO	C5–C6 to C1 (p)/CO	C1 (LP) to C2–C3*	C1 (LP) to C4–C5*	C1 (LP) to C2–C8*	C1 (LP) to C5–C6*
U1	—	—	13.5	20.2	6.1	7.6	—	—
U2	27.3	38.6	—	—	—	—	10.2	10.7
U3	5.0	4.9	—	—	7.6	8.8	3.4	3.0
U-CO	3.1	—	4.3	5.3	—	—	—	—

---

To get a deep insight into the bonding and hyperconjugation present in the undecanylidenes and undecanone, we have carried out an EDA-NOCV analysis at the BP86/TZ2P (ZORA) level of theory by considering carbene carbon atom/CO groups as one fragment and the rest of the cage as a second fragment. The bonding possibility considered here is the classic electron-sharing bonds between the carbene/ketonic carbon and the cage fragment (Scheme 3).

Scheme 3 Schematic representation of the bonding possibility considered for EDA-NOCV analysis for (a) singlet carbene (U1 and U2), (b) triplet carbene (U3) and (c) ketone (U-CO) by taking the carbene carbon/CO group as one fragment and the rest of the alkyl cage as another fragment.

The various energy components obtained from the EDA-NOCV analysis are given in Table 3. In corroboration with the relative energy difference between U1 and U2, the ΔE_int for U1 (−198.9 kcal mol⁻¹) is slightly higher than that of U2 (−189.7 kcal mol⁻¹). The C–C bonds of U1 and U2 have more contribution from the covalent interaction (61–64%) as compared to the electrostatic interaction (36–39%). The electrostatic stabilization energy of U1 (−302.0 kcal mol⁻¹) is slightly higher than that of U2 (−275.1 kcal mol⁻¹). Similar to the U1 and U2, the covalent contributions of the C–C bonds in the triplet carbene U3 (55%) and the ketone U-CO (61%) are high compared to the electrostatic stabilization (45% and 39%). ΔE_σ1 and ΔE_σ2 are the orbital stabilization energy corresponding to the two σ bonding interactions between the carbene/ketone and cage fragments (Fig. S2–S5, ESI†). ΔE_σ1 represents the interaction between the bonding combination of sp-hybrid orbitals on the cage carbons and 2p_z orbital on the carbene/ketone fragment, whereas the ΔE_σ2 represents the interaction between the antibonding combination of sp-hybrid orbitals on the cage carbons and the 2p_x (carbene carbon)/π* (ketone carbon) orbitals. These interactions constitute the major part of the total orbital stabilization energy (85–90%) in all molecules. There are two more important energy components contributing to the orbital stabilization energy in the carbenes, viz. ΔE_h1 and ΔE_h2. The ΔE_h1 corresponds to a Cieplak-type hyperconjugation whereas the ΔE_h2 represents a Felkin–Anh type hyperconjugation. The deformation density plots for ΔE_h1 and ΔE_h2 are given in Fig. 3a–c. The stabilization energy corresponding to the Cieplak-type hyperconjugation is most contributing in all carbene systems as compared to Felkin–Anh type hyperconjugation. Note that the extent of Felkin–Anh-type hyperconjugation is moreover the same in all carbene systems (−12 to −15 kcal mol⁻¹). Even though the Cieplak-type conjugation is higher for U2, U1 is slightly more stable than U2. This can be attributed to the extra stabilization energy obtained through electrostatic interaction in U2. This is also evident from the slightly higher NBO positive charge on the carbene carbon atom in U1 as compared to that in molecule U2. On the other hand, the extent of Cieplak-type hyperconjugation energy in the triplet carbene U3 is much lower (−20.4 kcal mol⁻¹) than that of the singlet carbenes (−30.1 kcal mol⁻¹ for U1 and −38.3 kcal mol⁻¹ for U2). Note that the magnitude of orbital stabilization energy is much lower in the triplet carbene than the singlet carbenes. However, the interaction energy of the triplet carbene is found to be more than that of the singlet carbene, which can be attributed to the lower values of Pauli's repulsion in the former. The Cieplak-type hyperconjugation is also present in the ketone (Fig. 3d) by the donation of C2–C8 and C5–C6 σ bonding molecular orbitals to the C–O π* molecular orbital. The extent of stabilization due to the Cieplak-type hyperconjugation (−13.0 kcal mol⁻¹) is less than half of those present in the singlet carbenes. The ΔE_h2 present in the ketone is not the Felkin–Anh type hyperconjugation present in the carbenes, rather it is a hyperconjugative interaction by the donation of the oxygen lone pair to the C1–C2 and C1–C5 σ* orbitals. The extent of this hyperconjugation is comparatively lower (−9.6 kcal mol⁻¹) than that of the Cieplak-type of hyperconjugation (−13.0 kcal mol⁻¹).

Table 3 EDA-NOCV results of singlet carbenes U1 and U2, triplet carbene U3, and the ketone U-CO at the BP86/TZ2P level of theory. Energies are in kcal mol⁻¹

	U1	U2	U3	U-CO
a Values in parentheses give the percentage contribution to the total attractive interactions ΔEele + ΔEorb. b Values in parentheses give the percentage contribution to the total orbital interaction ΔEorb. ΔErest = ΔEorb − (ΔEσ1 + ΔEσ2 + ΔEh1 + ΔEh2). ΔEprep and De represent the preparatory and dissociation energy, respectively.
ΔEint	−198.9	−189.7	−289.6	−245.3
ΔEPauli	580.6	573.6	339.9	369.7
ΔEele^a	−302.0 (38.74%)	−275.1 (36.04%)	−283.4 (45.02%)	−237.6 (38.63%)
ΔEorb^a	−477.5 (61.26%)	−488.2 (63.96%)	−346.1 (54.98%)	−377.4 (61.37%)
ΔEσ1^b	−237.2 (49.67%)	−227.5 (46.60%)	−157.3 (45.46%)	−186.8 (49.50%)
ΔEσ2^b	−186.5 (39.06%)	−195.1 (39.96%)	−143.2 (41.36%)	−150.7 (39.93%)
ΔEh1^b	−30.1 (6.30%)	−38.3 (7.85%)	−20.4 (5.89%)	−13.8 (3.66%)
ΔEh2^b	−12.3 (2.57%)	−14.8 (3.03%)	−13.0 (3.76%)	−9.6 (2.54%)
ΔErest^b	−11.4 (2.39%)	−12.5 (2.56%)	−12.2 (3.52%)	−16.5 (4.34%)
ΔEprep	33.3	25.3	127.1	156.5
–De	−165.6	−164.4	−162.5	−88.8

---

Fig. 3 Deformation density plots corresponding to the hyperconjugative interactions present in (a) U1, (b) U2, (c) U3 and (d) U-CO. Isosurface value is 0.003. The charge flow is from red to blue. Corresponding energies in kcal mol⁻¹ are given in parentheses.

Reactivity of the singlet carbenes (U1 and U2) and ketone (U-CO)

To explore the reactivity of the singlet carbenes and ketone, we have calculated proton and hydride affinities. The protonated adducts and the hydride adducts are given in Fig. 4. The calculated proton affinities are 262.6 kcal mol⁻¹ for U1 and 262.9 kcal mol⁻¹ for U2. These PA values are quite high and comparable with the PA of NHCs (250–254 kcal mol⁻¹), norbornene-7-ylidene (263 kcal mol⁻¹) and 2-adamantylidene (261.6 kcal mol⁻¹). The C5–C6 bond is quite elongated (1.957 Å) as compared to the C2–C8 bond (1.615 Å) in U1-H⁺. On the other hand, the C5–C4 bond is elongated significantly (1.907 Å) compared to the C2–C3 bond (1.565 Å) in U2-H⁺. This can be attributed to enhanced Cieplak-type hyperconjugatuve interaction in the protonated structure. The corresponding values from the NBO analysis are −206.9 kcal mol⁻¹ for the donation of C5–C6 and −10.8 kcal mol⁻¹ for the donation of C2–C8 bonds to the empty p-type orbital on the formal carbocationic centre in U1. The corresponding value for the donation of the C5–C4 bond is −464.3 kcal mol⁻¹ and for the donation of C2–C3 is −19.0 kcal mol⁻¹ to the empty p-type orbital on the formal carbocationic centre in U2. The Cieplak-type hyperconjugative interaction values of the protonated structure from the EDA-NOCV analysis are −85.0 kcal mol⁻¹ for U1-H⁺ and −84.0 kcal mol⁻¹ for U2-H⁺ (Table 4 and Table S1, ESI†). The Felkin–Anh hyperconjugation is absent in the protonated structures.

Fig. 4 Equilibrium geometries and important parameters of the protonated adduct and hydride adduct of U1, U2 and U-CO at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory. θ_b is the bending angle in degrees, and θ_p is the pyramidalization angle around C1, calculated as 360 – (∠C5–C1–H + ∠C2–C1–C5 + ∠C2–C1–H). Distances are given in angstroms, and angles are given in degrees. Corresponding PA or HA values in kcal mol⁻¹ are given in parentheses.

Table 4 The hyperconjugation values obtained for the proton adducts of singlet carbenes U1 and U2 (U1-H⁺, U2-H⁺), hydride adducts of the singlet carbenes U1 and U2 the ketone U-CO (U1-H⁻, U2-H⁻ and U-CO-H⁻) from the EDA-NOCV analysis at the BP86/TZ2P level of theory. Energies are in kcal mol⁻¹

	U1-H^+	U2-H^+	U1-H^−	U2-H^−	U-CO-H^−
ΔEh1	−85.0	−84.0	—	—	—
ΔEh2	—	—	−29.1	−32.0	—

---

We have also calculated the hydride affinity values to check the electrophilicity of the singlet carbene carbon atom. The HA values are 98.4 kcal mol⁻¹ for U1 and 99.5 kcal mol⁻¹ for U2. The HA values are also high as compared to the electrophilic BH₃ (73.1 kcal mol⁻¹) and the NHCs (8.0 kcal mol⁻¹) and comparable to 2-adamntylidene (97.6 kcal mol⁻¹). The addition of hydride into the empty p-orbital on the carbene carbon atom induces pyramidalization around the carbene centre. The corresponding angles in U1-H⁻ and U2-H⁻ are 28.2° and 28.6°, respectively. The hydride addition enhances the Felkin–Anh type hyperconjugative interactions as compared to those of singlet carbenes. The corresponding values from the NBO are −24.0 kcal mol⁻¹ for U1-H⁻ and −38.2 kcal mol⁻¹ for U2-H⁻. The corresponding EDA-NOCV analysis values are −29.1 kcal mol⁻¹ for U1-H⁻ and −32.0 kcal mol⁻¹ for U2-H⁻ (Table 4 and Table S1, ESI†). It is noteworthy that the bending of C1 is reduced in both molecules (−3.2° for U1-H⁻ and 6.5° for U2-H⁻). This can be attributed to the absence of Cieplak hyperconjugation due to the unavailability of a vacant p-orbital. So, it is established that both the structural isomers of undecanylidene are ambiphilic in nature. We have also calculated the hydride affinity of the undecanone. The hydride is added to the C–O π* orbital, which has a major contribution on the ketonic carbon atom. However, the hydride affinity value of U-CO is much lower (53.0 kcal mol⁻¹) compared to the carbene systems (98–99 kcal mol⁻¹).

Conclusions

We have carried out a detailed computational quantum mechanical study of pentacycloundecanylidene (U1, U2 and U3) and its ketone derivative pentacycloundecanone (U-CO). The spectroscopically identified pentacycloundecanylidene possesses a singlet ground state with a singlet–triplet gap of 5.6 kcal mol⁻¹. The singlet state exhibits two geometrical isomers (U1 and U2), which have different orientations of the carbene bridge. The energy gap between these isomers is minimal (0.9 kcal mol⁻¹). The cyclohexane ring in which the carbene bridge is a part possesses a boat conformation. The geometrical analysis established that the carbene bridge shows a bending compared to the saturated undecane. The bending is significant in the case of singlet isomers (−17.1° for U1 and 27.5° for U2) compared to the almost non-bent triplet analogue (−0.7°). So, the singlet isomers can be classified as foiled carbenes. The MO analysis suggests that the singlet pentacycloundecanylidene could display ambiphilic reactivity due to the presence of σ-type lone pair and p-type vacant orbitals. The second-order perturbation analysis using NBO shows two significant types of hyperconjugative interactions in U1 and U2, viz. Cieplak-type hyperconjugation and Felkin–Anh hyperconjugation. The Cieplak-type hyperconjugation is more in magnitude compared to the Felkin–Anh type. On the other hand, in the triplet U3, the hyperconjugative interactions are very minimal as compared to the singlet states. The detailed bonding analysis using the EDA-NOCV method also bolstered the presence of hyperconjugative interactions where the Cieplak-type interaction is major in singlet systems. This emphasizes that the Cieplak-type hyperconjugative interaction stabilizes the singlet isomer. The high proton and hydride affinities of U1 and U2 indicate the ambiphilic reactivity. The oxidation of the carbene results in the undecanone U-CO, the reaction energy calculations show that this reaction is highly exothermic and exergonic. The undecanone possesses a singlet ground state (U-CO). The bending of the CO bridge in the ketone is much less (−3.0°) compared to the bending of the carbene bridge in the singlet pentacycloundecanylidene. The MO analysis suggested the presence of a low-lying C–O π* orbital in U-CO. The NBO and EDA-NOCV analysis indicated the existence of Cieplak-type hyperconjugation in U-CO, but less in magnitude compared to the carbene systems. The undecanone also shows hydride affinity but comparatively less than that of the singlet isomers. This study reveals that the singlet pentacycloundecanylidene is a foiled carbene stabilized by the Cieplak-type hyperconjugation and can show ambiphilic reactivity. Also, the oxidized product, undecanone, exhibits less bending than the singlet carbenes and the extent of Cieplak-type hyperconjugation is also less. The undecanone possesses electrophilic reactivity, but less than that of singlet carbene systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

PP thanks SERB, India, for the financial support. JS thanks UGC for providing the fellowship. PP and JS also thank the Centre for Computational Modelling and Simulation (CCMS) and Central Computer Center (CCC) at NITC for the computational facilities.

References

1. A. Igau, H. Grutzmacher, A. Baceiredo and G. Bertrand, J. Am. Chem. Soc., 1988, 110, 6463–6466.
2. F. E. Hahn, Chem. Rev., 2018, 118, 9455–9456.
3. C. Boehme and G. Frenking, J. Am. Chem. Soc., 1996, 118, 2039–2046.
4. B. Chen, A. Yu Rogachev, D. A. Hrovat, R. Hoffmann and W. T. Borden, J. Am. Chem. Soc., 2013, 135, 13954–13964.
5. S. N. Khan, A. Kalemos and E. Miliordos, J. Phys. Chem. C, 2019, 123, 21548–21553.
6. A. J. Arduengo, R. L. Harlow and M. Kline, J. Am. Chem. Soc., 1991, 113, 361–363.
7. J. Vignolle, X. Cattoën and D. Bourissou, Chem. Rev., 2009, 109, 3333–3384.
8. P. Bellotti, M. Koy, M. N. Hopkinson and F. Glorius, Nat. Rev. Chem., 2021, 5, 711–725.
9. M. Gómez-Gallego, M. J. Mancheño and M. A. Sierra, Acc. Chem. Res., 2005, 38, 44–53.
10. S. Zhou, J. Li, M. Schlangen and H. Schwarz, Acc. Chem. Res., 2016, 49, 494–502.
11. T. Bally, S. Matzinger, L. Truttmann, M. S. Platz and S. Morgan, Angew. Chem., Int. Ed. Engl., 1994, 33, 1964–1966.
12. K. J. Szabo, E. Kraka and D. Cremer, J. Org. Chem., 1996, 61, 2783–2800.
13. J.-L. Mieusset and U. H. Brinker, J. Am. Chem. Soc., 2006, 128, 15843–15850.
14. M. G. Rosenberg and U. H. Brinker, Eur. J. Org. Chem., 2006, 5423–5440.
15. K.-J. Su, M. Pačar, J.-L. Mieusset, V. B. Arion and U. H. Brinker, J. Org. Chem., 2011, 76, 7491–7496.
16. U. H. Brinker, A. A. Bespokoev, H. P. Reisenauer and P. R. Schreiner, J. Org. Chem., 2012, 77, 3800–3807.
17. I. M. Apeland, M. G. Rosenberg, V. B. Arion, H. Kählig and U. H. Brinker, J. Org. Chem., 2015, 80, 11877–11887.
18. R. Gleiter and R. Hoffmann, J. Am. Chem. Soc., 1968, 90, 5457–5460.
19. R. Hoffmann, J. Am. Chem. Soc., 1968, 90, 1475–1485.
20. M. G. Rosenberg and U. H. Brinker, J. Org. Chem., 2019, 84, 11873–11884.
21. M. G. Rosenberg and U. H. Brinker, J. Org. Chem., 2021, 86, 878–891.
22. V. C. Rojisha, K. Nijesh, S. De and P. Parameswaran, Chem. Commun., 2013, 49, 8465–8467.
23. K. Nijesh, V. C. Rojisha, S. De and P. Parameswaran, Dalton Trans., 2015, 44, 4693–4706.
24. A. P. Marchand, K. A. Kumar, K. Mlinarić-Majerski and J. Veljković, Tetrahedron, 1998, 54, 15105–15112.
25. T. Šumanovac, M. Alešković, M. Šekutor, M. Matković, T. Baron, K. Mlinarić-Majerski, C. Bohne and N. Basarić, Photochem. Photobiol. Sci., 2019, 18, 1806–1822.
26. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, Jr., J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09 Revision E.01, Gaussian Inc., Wallingford CT, 2016.
27. SCM and V. U. Theoretical Chemistry.
28. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
29. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
30. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
31. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406.
32. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
33. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
34. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
35. P. Celani and H.-J. Werner, J. Chem. Phys., 2000, 112, 5546–5557.
36. A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, J. Chem. Phys., 1999, 110, 7667–7676.
37. H. Werner, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(2), 242–253.
38. K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244.
39. T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755–1759.
40. T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565.
41. L. Zhao, M. Hermann, W. H. E. Schwarz and G. Frenking, Nat. Rev. Chem., 2019, 3, 48–63.
42. M. Mitoraj and A. Michalak, J. Mol. Model., 2008, 14, 681–687.
43. M. Mitoraj and A. Michalak, J. Mol. Model., 2007, 13, 347–355.
44. A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933–1939.
45. M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576–6580.
46. C. Chang, M. Pelissier and P. Durand, Phys. Scr., 1986, 34, 394–404.
47. J.-L. Heully, I. Lindgren, E. Lindroth, S. Lundqvist and A.-M. Martensson-Pendrill, J. Phys. B: At. Mol. Phys., 1986, 19, 2799–2815.
48. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
49. E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516.
50. E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
51. G. J. Kabo, A. A. Kozyro, V. V. Diky, V. V. Simirsky, L. S. Ivashkevich, A. P. Krasulin, V. M. Sevruk, A. P. Marchand and M. Frenkel, J. Chem. Thermodyn., 1995, 27, 707–720.
52. M. T. Kelani, H. G. Kruger, T. Govender, G. E. M. Maguire, T. Naicker and O. K. Onajole, J. Mol. Struct., 2020, 1204, 127497.
53. R. Hoffmann, G. D. Zeiss and G. W. Van Dine, J. Am. Chem. Soc., 1968, 90, 1485–1499.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01248h

---