Exploring flat-band properties in two-dimensional M₃QX₇ compounds

Abstract

We present a computational study of the M₃QX₇ family of two-dimensional compounds, focusing specifically on their flat-band properties. We use a high-throughput search methodology, accelerated by machine learning, to explore the vast chemical space spawned by this family. In this way, we identify numerous stable 2D compounds within the M₃QX₇ family. We investigate how the chemical composition can be manipulated to modulate the position and dispersion of the flat bands. By employing a tight-binding model we explain the formation of flat bands as a result of a relatively loose connection between triangular M₃QX₃ clusters via bridges of X atoms. The model provides an understanding of the residual interactions that can impact the band dispersion. The same loose connection between clusters not only leads to strongly localized electronic states and thus flat electronic bands but also leads to localized phonon modes and flat bands in the phonon dispersion.

---

I. Introduction

Many materials can be well described by assuming parabolic electronic bands, however, there are instances where the band structure deviates from this simplified model. Such non-parabolic band structures give rise to a series of unique characteristics. For example, in graphene¹ the linear band crossing, known as a Dirac point, enables high electron mobility and unconventional quantum transport phenomena. Similarly, in topological insulators,^2,3 the surface states, topologically protected by time-reversal symmetry, possess unique electronic properties, such as robust spin-polarized currents and immunity to backscattering. Another example of non-parabolic bands is found in materials that exhibit a fractional quantum Hall effect.^4,5

In recent years, there has been growing interest in materials that exhibit quasi-dispersionless (flat) bands at or close to the Fermi energy. These materials hold promise for hosting a range of intriguing emergent phenomena. Flat-band states can be viewed as strongly localized electronic states whose extension is considerably smaller than the unit cell. Such flat bands have been shown to give rise to correlated phenomena, such as ferromagnetism,⁶ superconductivity,⁷ Wigner crystals,⁸ and more, as summarized in ref. 9.

The concept of flat bands was initially studied by Landau in 1930 in the context of Landau levels of free electrons in magnetic fields.¹⁰ Since then, topological flat bands (TFB) have been found in simple artificial models such as Kagome⁶ and Lieb¹¹ lattices and their variants. Moreover, recent experimental advancements have enabled the realization of TFB in actual materials, such as twisted bilayer graphene.¹² Flat bands in twisted bilayer graphene have been linked to the emergence of unconventional superconductivity, correlated insulating states, and other intriguing phenomena. This unique platform allows for studying strongly correlated electron systems in a controlled and tunable environment. This also leads to a large effort to search for TFBs in other Moiré superlattices¹³ of stacked van der Waals heterostructures, for example, in small angle twisted bilayer WSe₂,¹⁴ and even in a honeycomb In_0.53Ga_0.47 As/InP heterostructure.¹⁵ These flat bands were observed in the first Brillouin zone of the Moiré superlattice. In momentum space, the area occupied by the flat band is inversely proportional to the square of the superlattice lattice constant, which is usually very large for Moiré superlattices. This limits the practical applications of the flat bands in these systems. For example, the critical superconducting temperature is only a few Kelvin for twisted bilayer graphene.^16,17 Consequently, it is crucial to explore systems capable of hosting more extended flat bands over larger portions of momentum space.

In addition to the studies mentioned above, ref. 18 explored bipartite crystalline lattices in the quest for TFBs. The bipartite lattice can be divided into two sublattices with no intrasublattice interaction, which offers a versatile framework to understand and design flat bands in actual materials. This lattice has been applied in high-throughput searches of electronic flat bands in real three-dimensional¹⁹ and two-dimensional materials.^20,21 The TFBs found in those studies could always be explained by mapping the ab initio band structures onto the simple tight-binding lattice models.

Recently,²² TFBs were studied in Nb₃Cl₈, a compound hosting a breathing Kagome lattice (see Fig. 1). The band structure of this compound exhibits a gap due to the absence of inversion symmetry, but the flat bands remain intact due to the protection by mirror reflection symmetry. The existence of TFBs in Nb₃Cl₈ has been directly observed through angle-resolved photoemission spectroscopy measurements, and corroborated by first-principles calculations.²² The calculations also indicate that the monolayer Nb₃Cl₈ exhibits a magnetic ground state, which opens up opportunities for studying the intriguing interplay among geometry, topology, and magnetism.²²

Fig. 1 Views of the crystal structure of M₃QX₇ along the a, b, and c axis. X atoms are shown in cyan, Q in gold, and X in red. The underlying breathing Kagome lattice is shown as dashed lines.

In addition to Nb₃Cl₈, another closely related compound that shares a similar breathing Kagome lattice is Nb₃TeCl₇.^20,21,23 Other stable, experimentally-known compounds of the same M₃QX₇ family, are Nb₃SBr₇,²⁴ Nb₃TeI₇,²⁵ Ta₃TeI₇,²⁶ and Ta₃SeI₇.²⁶ Due to the nature of the weak inter-layer van der Waals interaction, these compounds can in principle be exfoliated to monolayers exhibiting TFBs.^20,21 Interestingly, bilayers of Nb₃SBr₇ and Ta₃SBr₇ have also been studied recently in the context of photocatalysis as they might possess ultrahigh solar-to-hydrogen efficiency.²⁷

In this work, we perform a broad study of the two-dimensional M₃QX₇ family, and in particular, of their flat-band properties. To gain insights into the electronic properties of these compounds, we start in Section II analyzing the band structure of a specific example using a tight-binding model. This approach allows us to understand the formation of TFBs and identify the residual interactions that can influence the dispersion. Next, in Section III, we explore the vast chemical space of the M₃QX₇ family by employing a machine-learning accelerated high-throughput search method.^28–30 This approach allows us to systematically screen a large number of possible compositions, leading to the identification of numerous new stable two-dimensional M₃QX₇ compounds. Finally, in Section IV, we discuss how the chemical composition can tune the position and dispersion of the flat bands. The final Section V is devoted to conclusions.

II. Example material: Nb₃SBr₇

To gain deeper insights into the electronic structure of the M₃QX₇ family of compounds, we now study the Nb₃SBr₇ compound in detail. However, it is essential to note that the findings and conclusions from our investigation can be extended to other members of this family, including the properties of flat bands.

The crystal structure of Nb₃SBr₇ depicted in Fig. 1 has 11 atoms in the trigonal unit cell and belongs to the space group P3m1 (#156). The Nb atoms are in the Wyckoff position 3d, forming an equilateral triangle with side of 2.91 Å. In contrast, the S atom is below the plane at position 1c, forming the fourth vertex of the tetrahedron with the three Nb atoms (with S–Nb distance of 2.41 Å). Per unit cell, there are three nonequivalent Br sites: (1) the 1a position with one Br sits above the plane, having three Nb neighbors (with Br–Nb distance 2.85 Å); (2) the 3d position with three Br atoms above the plane, bonding two nearest neighboring Nb atoms (with Br–Nb distance 2.58 Å); and (3) the other 3d position with three Br atoms below the plane, bonding two Nb second nearest neighbors (with Br–Nb distance 2.72 Å).

We can readily see that the standard oxidation state of Nb (+V) is incompatible with the chemical composition of this compound. However, it is known that Nb can adopt a series of other oxidation states, mainly if the compound includes Nb–Nb bonds. Knowing that the Nb–Nb bond length in the elemental Nb metal is 2.88 Å (calculated in the same conditions as here), we can expect Nb–Nb bonds in Nb₃SBr₇. A +III state for Nb would lead to charge neutrality assuming the standard oxidation states: −I for Br and −II for S. This is confirmed by Bader charge analysis that yields respectively +1.4 for Nb, −0.8 for S, as well as −0.56, −0.50, and −0.46 for the three nonequivalent Br sites. This result is also supported by the fact that other cations – such as Sc, V, Zr, or Ti – also stabilize the M₃QX₇ structure (see Section III), as all these metals can exist in the +III oxidation state (although it is not the most common one for some of them).

The electronic band structure of the Nb₃SBr₇ monolayer is depicted in Fig. 2a. The states between −6 and −1 eV are dispersive and exhibit mainly Br-p character with some admixture of S-p and Nb-d states. The next manifold of states, composed of the first valence (doubly degenerate at Γ), the second valence, the first conduction, and the second conduction (doubly degenerate at Γ), all show a significantly reduced dispersion across the whole 2D Brillouin zone. For example, the two bands at the top of the valence have a dispersion smaller than 0.08 eV. In comparison, the lowest conduction band has a dispersion smaller than 0.05 eV.

Fig. 2 (a) Electronic band structure of monolayer Nb₃SBr₇. Iso-surfaces of the (b) second conduction band, (c) first conduction band, and (d) highest valence band, all depicted at Γ, where cyan represents negative values and yellow positive ones. (e) Electronic band structure of bulk Nb₃SBr₇.

An exciting question regards what happens to the flat bands by adding further layers into the three-dimensional bulk limit. To answer that question, we plot in Fig. 2(e) the electronic band structure and density of states of the bulk Nb₃SBr₇ (calculated at the experimental geometry). Overall, the bands and density of states of the monolayer are very similar to the ones of the bulk, as expected from the weak coupling between the layers. However, we observe a significant increase in the dispersion of the flat bands, particularly along the perpendicular direction. For example, the total dispersion of the top valence band in the bulk compound is now 0.23 eV and of the bottom conduction band 0.35 eV, while in-plane (along the M–Γ–K direction), the dispersions are 0.10 eV and 0.07 eV for the valence and the conduction, respectively. As such, we can see that interaction between the layers destroys considerably the bands’ flatness.

Looking at the frontier states depicted in Fig. 2(b)–(d), the flat bands of Nb₃SBr₇ have considerable contributions from several atoms in the unit cell. The situation is further complicated because some bands degenerate in symmetry lines of the Brillouin zone. The analysis of the lowest conduction orbital (Fig. 2(c)) (the one with the most negligible dispersion) reveals a curious behavior. We can see a metallic bonding along the sides of the triangle formed by the Nb₃ cluster (and composed of Nb-d orbitals) that hybridizes with the S-p_z state at the top of the tetrahedron. The Br-p orbitals are slightly tilted towards the star's center and are substantially polarized. They do not seem to hybridize with the orbitals of the cluster.

Further insight into the origin of the very flat bands can be obtained by constructing an effective tight-binding model on the Wannier functions basis. In Fig. 3, we plot the dependence of the magnitude of the real-space Hamiltonian matrix elements (hoppings) on the distance between the basis wavefunctions. Nonzero hoppings around 0 Å indicate that wavefunctions located at individual Nb atoms are not orthogonal to each other, which is a common assumption when constructing TB models by hand. Further most significant hoppings can be found for the distances around 2.91 Å and 4.28 Å, corresponding to the Nb–Nb distances inside the small triangles (intra-triangle) and between the second nearest Nb neighbors from two different triangles (inter-triangle), respectively, as shown in Fig. 1. In our model of Nb₃SBr₇, the intra-triangle hoppings are much stronger than inter-triangle ones. Therefore, the Nb-d orbitals can be understood as forming relatively isolated triangular molecular orbitals, which lead to the very flat bands of this breathing Kagome lattice.

Fig. 3 Magnitude of the real-space Hamiltonian matrix elements vs. the distance between the basis wavefunctions.

III. High-throughput

The experimentally synthesized compounds of the 2D M₃QX₇ family contain M = Nb, Ta, Q = S, Se, Te, and X = Br, I. There are a few apparent substitutions within these groups of the periodic table that can be further explored, specifically for X = Cl. However, the substitution of X by F and Q-elements by O is less likely due to the specificity of oxygen and fluorine compared to their heavier counterparts (this fact is known as the first-row anomaly). Substitutions of the cation M are less obvious, besides perhaps V. Unfortunately, it is known that such simple arguments often offer a somewhat incomplete view of the chemistry of the elements, and relying on them may introduce a strong bias in the predictions.

To have a more resilient view, we use a systematic computational approach based on machine-learning-assisted prototype searching instead to determine which chemical compositions stabilize the M₃QX₇ structure. This method was developed in previous studies of the two- and three-dimensional compound space,^28–30 where universal neural-network force-field³¹ and crystal-graph attention networks²⁸ were used to predict the stability of materials. We use the model to explore the stability of 2D M₃QX₇ compounds where M, Q, and X can be any chemical element from Li to Bi, excluding rare gases (He, Ne, Ar, Kr, Xe, and Rn). Compounds predicted by the machine model to be within 200 meV per atom from the convex hull are selected and the full list is included in the ESI.† We can see that the machine model predicted a variety of elements filling the M and Q positions. The majority of compositions have a halogen as X, although there are some exceptions, e.g. Rb₈Na₃, Tl₈Se₃, K₈Ag₃, In₈Ge₃, etc. Further DFT validation, as described in Section VI, has been applied to all the compounds, with the results of the distance to the convex hull (E_hull) also included in the ESI.† Interestingly, those systems with X not being a halogen have much greater E_hull, the closest to the hull being Rb₈Cd₃ (101 meV per atom) which still lies beyond our (meta-)stability threshold of 50 meV per atom. Therefore, in the subsequent discussion, we only include compounds with X being F, Cl, Br, or I, including the case Q = X (leading to the M₃X₈ family of compounds).

To illustrate the stability of the M₃QX₇ family, we present a heatmap in Fig. 4 that shows the number of stable compounds as a function of M and Q. It is worth noting that in the low energy range, X is exclusively a halogen, and in most cases a heavy halogen. The only exception to this rule is Cu₃F₈, showing again the effect of the first-row anomaly. The Q site anions, as expected, are primarily chalcogens and halogens. Interestingly, we found that Q anions with larger radii, such as Te and I, tend to lead to more stable compounds than those with smaller radii. This information is crucial for designing and synthesizing stable two-dimensional M₃QX₇ compounds. The distortion of the corner-shared octahedra could probably explain the stability trend with the Q anion radius. As the size mismatch between X and Q increases, the distortion of the octahedra increases, which could lead to lower stability.

Fig. 4 Heat map showing the number of (meta-)stable M₃QX₇ compounds (E_hull ≤ 50 meV per atom) as a function of the chemical elements M and Q. Note that all (meta-)stable compounds have X being a halogen. Other choices of X elements lead to rather unstable compounds, as shown in the ESI.† A value of 3 for a given M and Q means that three halogens (specifically Cl, Br, and I) for X stabilize the structure. The only meta-stable X = F compound is CuF₈.

The heatmap also reveals some interesting trends for different M cations. The first thing worth noticing is that the (meta-)stable compositions are not limited to the experimentally known group-V metals, such as V, Nb, and Ta. Instead, a wide range of M cations can form (meta-)stable M₃QX₇ compounds, including Sc and Y from group III, Ti, Zr, and Hf from group IV, and even some rare earth elements. This expansion of potential metal candidates for stable compounds dramatically broadens the scope of materials that can be explored. Moreover, this discovery is fascinating because these metals have different valences, which suggests that they will exhibit significant variations in the electronic structure compared to the group-V compounds. In Section IV, we will discuss the chemical trends and how these enable the tailoring of electronic properties.

It is worth noting that when Q is a chalcogen, our calculations show that Ti₃TeCl₇ is the most stable compound. Additionally, compounds such as V₃TeCl₇, Zr₃TeCl₇, Sc₃TeCl₇, and Sc₃IBr₇ also have distances to the convex hull comparable to experimentally known Nb and Ta compounds, indicating their potential synthesizability. However, it is essential to note that while the distance to the convex hull provides a valuable assessment of thermodynamic stability, it does not guarantee synthesizability. Other factors, such as the synthesis conditions, may also have a crucial impact. Nonetheless, given that the experimentally known 2D Nb₃SBr₇, has a small E_hull (7 meV per atom), it is reasonable to expect that other systems with similarly low E_hull values, such as those shown in Fig. 4, may also be synthesizable. As such, our prediction provides a valuable guide for future experimental explorations. Moreover, the exfoliation energy indicates the binding strength between 2D layers within their 3D counterparts and can serve as a valuable metric for assessing the synthesizability of 2D materials from bulk forms through physical exfoliation.³² The typical compound Nb₃SBr₇ exhibits an exfoliation energy of approximately 20 meV Å⁻²,²⁷ comparable to graphene (about 26 meV Å⁻²).³³ Most of the systems identified in the present paper do not have known 3D parent structures, thus further theoretical investigation of the stacking order and the exfoliation energy could also provide valuable insight into the synthesizability of the 2D M₃QX₇ family.

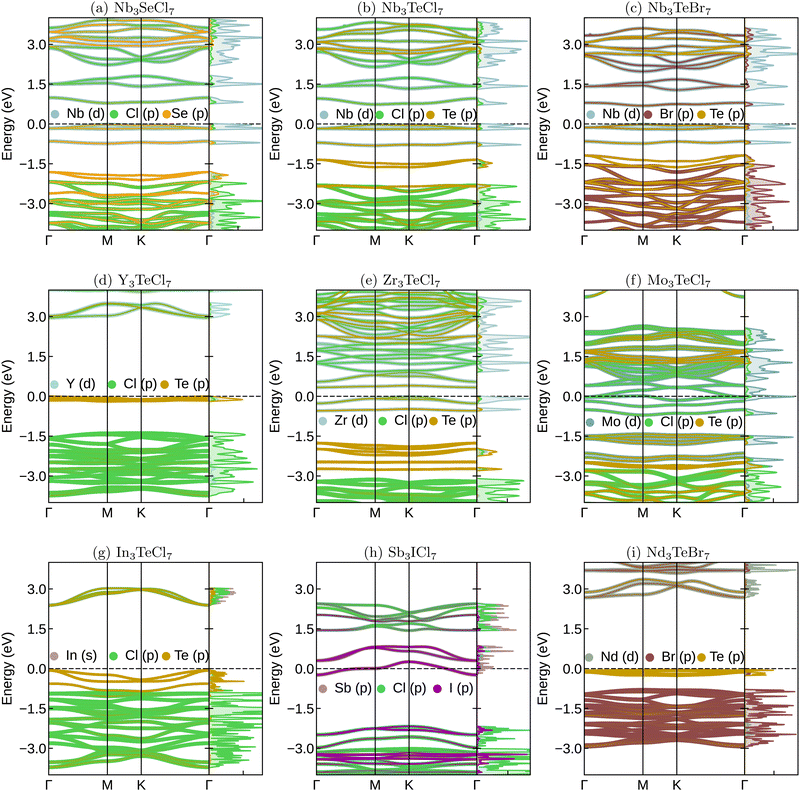
IV. Physical properties

We selected several systems (see Fig. 5) to show how physical properties could vary crossing a diverse range of chemistries within the M₃QX₇ family. The first three systems, Nb₃SeCl₇, Nb₃TeCl₇, and Nb₃TeBr share common M-elements while the Q and X elements are chalcogens and halogens, respectively. These systems represent experimentally known Nb-compounds in this family. The subsequent three systems, Y₃TeCl₇, Zr₃TeCl₇, and Mo₃TeCl₇, demonstrate how the band structures change when other transition metals besides Nb occupy the M-position. The last three exhibit further differences when the M-atoms are p-block (In, Sb) or f-block (Nd) elements. Additionally, the Sb₃ICl₇ system is an example of halogens occupying both X and Q positions.

Fig. 5 Electronic band-structure and state resolved density of states of a few selected members of the M₃QX₇ family. The spin-up bands are represented by solid lines while the spin-down bands are depicted as dotted lines. The colors represent the main character of the band.

These electronic bands can be divided into three regions. Firstly, the higher energy region corresponds to the high-lying conduction bands, which mainly arise from the empty orbitals of the M atoms. Next are the bands around the Fermi level (−1.5 to 1.5 eV), which primarily consist of M-d bands (if M is a transition metal) and X–Q hybridized bands. This region exhibits, in some cases, flat bands. Finally, the low energy valence bands mainly originate from the p-bands of the halogen X.

When M is Nb or Ta (in a +III oxidation state), X is a halogen, and Q is Te or Se, the resulting systems are spin-unpolarized and semiconducting, exhibiting band gaps of approximately 1 eV. The orbitals around the Fermi energy and in the conduction of Nb₃SeCl₇ do not change considerably with the substitutions of Se by another chalcogen and of Cl by another halogen (see Fig. 5(a)–(c)). The main effect of such substitutions can be observed in the lower valence states around −1.5 eV. The more significant the mismatch between the X and Q atoms’ radii, the farther the states are separated with an intense halogen or chalcogen character.

Semiconducting or insulating behavior is also observed for other +III metals such as Y (Fig. 5(d)) and Nd (Fig. 5(i)). However, if the M atoms are Zr (with one fewer valence electron compared to Nb) or Mo (with one additional valence electron), and despite their ability to adopt a +III oxidation state, the systems are metallic. In the case of Zr₃TeCl₇ shown in Fig. 5(e), it behaves as a half metal, with spin-asymmetric d-bands around the Fermi level, where one spin channel is filled, and the other is empty. Similarly, in the case of Mo₃TeCl₇ shown in Fig. 5(f), the system is spin-polarized, but the Fermi level lies within the conduction bands, and both spin channels have fully occupied d-bands. This result raises exciting possibilities of creating isolated spins in the Nb compounds by substituting the group V elements with either group IV or VI.

When the M atoms belong to the p-block elements, such as In (Fig. 5(g)) and Sb (Fig. 5(h)), the X–Q hybridization bands now appear at the Fermi level and are strongly dispersive.

We see that the flat bands from the breathing Kagome lattice only appear close to the Fermi energy if the M atom is a specific metal supporting a +III oxidation state. The flatness of the bands is also controlled by chemistry, as well as the distance in energy to the dispersive chalcogen and halogen bands. This observation makes the M₃QX₇ an ideal playground for studying flat bands and their interaction with dispersive bands, for example by tuning the position of flat bands through chemical doping or alloying. Another key factor for 2D systems is mechanical stability.³⁴ The elastic constants of the above systems (see Table S2 in the ESI†) show that all systems, with the exception of Sb₃ICl₇ and Mo₃TeCl₇, are mechanically stable (i.e., C₁₁ > C₁₂ > 0, C₂₂ > 0, C₆₆ > 0). Note moreover, that since some lattice mismatch between substrates and the 2D layer is to be expected, the interplay between strain and the electronic properties might be crucial for the application of these materials.

We also note that this family has potential for photocatalytic applications.²⁷ With their variable compositions and structural characteristics, they could be designed to have optimal band gaps for absorbing visible light. Moreover, flat bands can lead to high densities of electronic states, improving light absorption per volume. By forming bilayer structures with an internal electric field, the charge separation can be further enhanced,²⁷ with the electron–hole pairs bound in the flat bands with a high level of spatial confinement.^35,36 These localized excitons can contribute to more efficient photocatalytic processes due to limited charge recombination.

As we saw before, several systems of the M₃QX₇ can exhibit spin-polarized ground-state configurations depending on the chemical composition. This result is interesting, as the breathing Kagome lattice is frustrated and can not support an anti-ferromagnetic configuration of the metal atoms. Furthermore, heavy atoms, such as Te and I, further complicate the situation that may lead to strong spin–orbit coupling (SOC). To investigate such effects, we computed the energy in three different magnetic configurations (see Fig. 6). Specifically, we used the Z (ferromagnetic) arrangement, where all spins point out of the plane. Fig. 6(b) corresponds to a circular configuration, where the spins are in the plane and point along the sides of the triangles formed by the M-atoms, and Fig. 6(c) shows a radial configuration, where the spins point along the triangle's vertices. The circular configuration is chiral, while the other two are not.

Fig. 6 The different configurations for magnetic moments are located on A atoms in the A₃BC₇ motif.

In Table 1, we list the energies of the three configurations, calculated with the inclusion of SOC, relative to the non-magnetic spin state. Some configurations, marked by a “—” sign, become unstable and relax into one of the other spin arrangements. Most systems prefer to remain in a ferromagnetic configuration in their ground state, while the two planar configurations are 10–20 meV per atom higher in energy and nearly degenerate. The exception is Mo₃TeCl₇, where the ferromagnetic arrangement is unstable, and the ground energy state is the chiral circular configuration. Unfortunately, as we can see from Fig. 5(f), this compound does not exhibit a flat band around the Fermi level. We also calculated the band structures of Nb₃SBr₇, Nb₃TeBr₇, and Nb₃SBr₇ including the effects of SOC. The corresponding results are illustrated in Fig. S2 in the ESI.† We can see that the SOC has a limited effect on the dispersion and the positions of the flat bands. This observation suggests that for those M₃QX₇ compounds, SOC effects do not significantly alter their fundamental flat-band properties.

Table 1 Energies of different magnetic configurations (meV per atom) relative to the non-magnetic state, and the energy difference between with and without SOC for ferromagnetic configuration (ΔE^ferro_soc). Corresponding ordering is shown in Fig. 6

Formula	ΔEferro	ΔEcircular	ΔEradial	ΔE^ferrosoc
Zr3TeBr7	−21	−5	−6	−42
Nb3IBr7	−3	—	—	−44
Ti3TeCl7	−43	−16	−18	−12
La3IBr7	−9	—	—	−107
Hf3TeBr7	−5	−1	−1	−211
Hf3BrCl7	−23	−4	−4	−185
Mo3TeCl7	—	−18	−15	—
V3TeCl7	−119	−90	−90	−8
Zr3SbCl7	−9	−1	0	−23

---

We further calculated the phonon dispersions of this family. In Fig. 7 we show Nb₃SBr₇ as an example. As expected, the dispersion of some of the optical modes is mostly flat. In Fig. 7(c)–(e) we show the eigenvectors of the three highest modes. The highest mode is non-degenerate with A₁ symmetry, where the S-atoms vibrate up and down perpendicularly to the 2D plane. In the second highest, doubly degenerate E mode, it is again the lighter S-atoms contributing, but now they vibrate parallel to the plane. Due to the large distance between the S-atoms, the dispersion of this mode is obviously quite flat. The third highest mode (again a non-degenerate A₁ mode) can be seen as a breathing mode of the Nb₃SBr₃-islands where the Br atoms are moving outwards (and downwards) while the SBr₃-cluster is moving upwards. This mode is also rather flat because the islands are relatively loosely connected by the Br-bridges.

Fig. 7 (a) Phonon band structure, (b) Raman spectrum, (c) Raman active mode A₁ at 227 cm⁻¹, (d) Raman active mode E at 306 cm⁻¹, (e) Raman active mode A₁ at 396 cm⁻¹ of Nb₃SBr₇.

Due to the rather low point-group symmetry, C_3v, almost all modes (except the A₂ modes) are both Raman and infrared (IR) active. The three modes corresponding to the three flat phonon bands are labeled by their irreducible representation in Fig. 7(b). Among them, the lower A₁ mode is the dominant peak of the spectrum. Its position depends on the mass of the M atoms and serves thus as an important fingerprint of the material.

As for the vibrational properties of other systems, we present in the ESI† the phonon dispersion relations of the 9 compounds for which we have presented the electronic band structures in Fig. 5. Almost all dispersions display positive phonon frequencies throughout the Brillouin zone, indicating the dynamic stability of these materials. Only Sb₃ICl₇ (Fig. S3h, ESI†) has imaginary phonon branches (drawn as negative frequencies) throughout the Brillouin zone. Indeed, upon breaking the symmetry of this material by randomly displacing some of its atoms and performing a geometry optimization, the system disintegrates, while for the other 8 compounds, the system relaxes back to the C_3v symmetry. We expect most of the materials presented in Table S1 (ESI†) to be dynamically stable. However, before further investigating one of the compounds, its dynamical stability should be checked via a calculation of its phonon dispersion.

V. Conclusion

In conclusion, we studied the M₃QX₇ family of 2D compounds, revealing a diverse range of thermodynamic, electronic, magnetic, and vibrational properties. While the experimentally known van der Waals solids are limited to seven materials constructed from M₃X₈ and M₃QX₇ layers, we have identified numerous other stable compounds that lie close to the convex hull of stability. Interestingly, X is consistently a halogen, while Q is a chalcogen. In contrast, the M site exhibits remarkable chemical diversity, encompassing group V elements and elements from groups III, IV, VI, and rare earths. Unsurprisingly, this chemical diversity manifests in various electronic and magnetic properties.

Our investigations have revealed that, in many cases, the d-states of the M metal combine to form a manifold of bands reminiscent of the breathing Kagome lattice, featuring prominent flat bands. Notably, these flat bands are often located at or near the Fermi level, enabling the creation of electrons and holes of very high mass through charge transfer from a substrate, doping, gating, etc. Moreover, our findings indicate that most magnetic compounds in this family adopt a ferromagnetic configuration, with the spins oriented perpendicularly to the plane. However, an intriguing exception is observed in Mo₃TeCl₇, where the spin ground state exhibits chirality.

The M₃QX₇ family presents an ideal platform for investigating flat bands in 2D compounds. Many compositions are near thermodynamic stability and should be readily accessible through experimental synthesis. Furthermore, this family offers control over the relative position and dispersion of flat bands concerning other states by tuning the compound's chemistry within a broad composition space. Additionally, the choice of metal atoms allows for the switching between spin-unpolarized and magnetic configurations. This interplay between different properties provides a fertile ground for further experimental investigations and potential applications in electronic and magnetic devices.

While, in this paper, we have focused on the appearance of flat electron bands, we have also demonstrated that some of the reported materials have flat phonon bands. Therefore, electron–phonon interactions are expected to be worth exploring, as they can lead to novel superconducting or insulating phases. Similarly, pronounced light–matter interaction which leads to strongly localized excitons can be expected. Lastly, the co-existence of flat phonon and electron bands could offer a new range of unexpected functionalities.

Our machine learning model involved several assumptions and simplifications to manage the computational complexity and to focus on specific aspects of the M₃QX₇ family. As common in high-throughput search, we assumed idealized crystal structures without defects, disorder, or impurities, which might not fully reflect real-world materials. Additional studies need to be done to understand the effect of impurities on the electronic states. Furthermore, the model and DFT calculations only provide thermodynamic stability at zero temperature, neglecting lattice vibrations or temperature variations. Moreover, we have to note that the thermodynamic stability does not guarantee the synthesizability which remains a challenge to predict. Therefore, we look forward to further experimental validations. Meanwhile, the impact of temperature and lattice vibrations on stability can also be theoretically investigated via molecular dynamics.

VI. Methods

We performed all geometry optimizations and total energy calculations using the code VASP.^37,38 Uniform Γ-centered k-point grids sampled the 2D Brillouin zones with a density of 6 k-points per Å⁻². We performed spin-polarized calculations starting from a ferromagnetic state and used the projector augmented wave setups^39,40 of vasp version 5.2 with a cutoff of 520 eV. We converged the calculations to forces smaller than 0.005 eV Å⁻¹. As exchange–correlation functional, we used the Perdew–Burke–Ernzerhof⁴¹ functional with on-site corrections for oxides, fluorides containing Co, Cr, Fe, Mn, Mo, Ni, V, and W. The Hubbard-type effective on-site Coulomb correction to the d-states were, respectively 3.32, 3.7, 5.3, 3.9, 4.38, 6.2, 3.25, and 6.2 eV. These parameters were chosen to be compatible with the Materials Project database.⁴² We imposed a vacuum region of 15 Å.

Distances to the convex hull were evaluated using PYMATGEN⁴³ using the large complex hull of ref. 29 corresponding to the dataset available in the Materials Cloud repository.⁴⁴

The phonon properties were calculated using density-functional perturbation theory (DFPT) as implemented in QUANTUM ESPRESSO.^45,46 We use the norm-conserving pseudopotentials from the PseudoDojo project.^47,48 Total energy differences and optimized structures are almost identical in calculations with the VASP and QUANTUM ESPRESSO codes. We used an 8 × 8 Γ centered k-point grid and a cut-off of 90 Ry to converge the ground state charge density. We applied a vacuum distance of 18.5 Å and a 2D Coulomb cutoff⁴⁹ to prevent the interaction between periodic images and thus removed the weak longitudinal optical/transverse optical splitting at the Γ point.⁵⁰ We computed dynamical matrices on a uniform 4 × 4 Γ-centered coarse grid, and through a Fourier transform we then obtained the force constants to calculate the phonon dispersions. We calculated the Raman spectrum using the implementation of Lazzeri and Mauri for the Raman tensor.⁵¹ This implementation is currently only for the local-density approximation, so we used this approximation to calculate the Raman tensor but kept the phonon frequencies and eigenvectors calculated with the PBE functional.

Data availability

All crystal structures from this work are available at Materials Cloud (https://doi.org/10.24435/materialscloud:sb-cy). The database, including structures, distances to the hull, and other basic properties, can be accessed at https://tddft.org/bmg/physics/2D/ through a simple web-based interface.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work used Bridges2 and Expanse at the Pittsburgh Supercomputer (Bridges2) and the San Diego Supercomputer Center (Expanse) through allocation DMR140031 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which National Science Foundation supports grants 2138259, 2138286, 2138307, 2137603, and 2138296. AHR and LW were funded, in part, by the Luxembourg National Research Fund (FNR), Inter Mobility 2DOPMA, grant reference 15627293. AHR also recognizes the support of the WV-HEPC RCG Award 2023 and NASA EPSCoR Award 80NSSC22M0173. MALM acknowledges the computing time on the high-performance computer Noctua 2 at the NHR Center PC² through the project hpc-prf-ecsm and hpc-prf-vibff and the Gauss Centre for Supercomputing e.V. (https://www.gauss-centre.eu/) for providing computing time on the GCS Supercomputer SUPERMUC-NG at Leibniz Supercomputing Centre (https://www.lrz.de) under the project pn25co.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
2. C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2005, 95, 146802.
3. L. Fu, C. Kane and E. Mele, Phys. Rev. Lett., 2007, 98, 106803.
4. D. C. Tsui, H. L. Stormer and A. C. Gossard, Phys. Rev. Lett., 1982, 48, 1559.
5. R. B. Laughlin, Phys. Rev. Lett., 1983, 50, 1395.
6. A. Mielke, J. Phys. A: Math. Gen., 1991, 24, L73.
7. S. Miyahara, S. Kusuta and N. Furukawa, Phys. C, 2007, 460–462, 1145–1146.
8. C. Wu, D. Bergman, L. Balents and S. Das Sarma, Phys. Rev. Lett., 2007, 99, 070401.
9. L. Zheng, L. Feng and W. Yong-Shi, Chin. Phys. B, 2014, 23, 077308.
10. L. Landau, Z. Phys., 1930, 64, 629–637.
11. E. H. Lieb, Phys. Rev. Lett., 1989, 62, 1201–1204.
12. R. Bistritzer and A. H. MacDonald, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 12233–12237.
13. M. H. Naik and M. Jain, Phys. Rev. Lett., 2018, 121, 266401.
14. Z. Zhang, Y. Wang, K. Watanabe, T. Taniguchi, K. Ueno, E. Tutuc and B. J. LeRoy, Nat. Phys., 2020, 16, 1093–1096.
15. N. A. Franchina Vergel, L. C. Post, D. Sciacca, M. Berthe, F. Vaurette, Y. Lambert, D. Yarekha, D. Troadec, C. Coinon, G. Fleury, G. Patriarche, T. Xu, L. Desplanque, X. Wallart, D. Vanmaekelbergh, C. Delerue and B. Grandidier, Nano Lett., 2020, 21, 680–685.
16. Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50.
17. M. Oh, K. P. Nuckolls, D. Wong, R. L. Lee, X. Liu, K. Watanabe, T. Taniguchi and A. Yazdani, Nature, 2021, 600, 240–245.
18. D. Cǎalugǎru, A. Chew, L. Elcoro, Y. Xu, N. Regnault, Z.-D. Song and B. A. Bernevig, Nat. Phys., 2022, 18, 185–189.
19. N. Regnault, Y. Xu, M.-R. Li, D.-S. Ma, M. Jovanovic, A. Yazdani, S. S. P. Parkin, C. Felser, L. M. Schoop, N. P. Ong, R. J. Cava, L. Elcoro, Z.-D. Song and B. A. Bernevig, Nature, 2022, 603, 824–828.
20. H. Liu, S. Meng and F. Liu, Phys. Rev. Mater., 2021, 5, 084203.
21. J. Duan, D. Ma, R. Zhang, W. Jiang, Z. Zhang, C. Cui, Z. Yu and Y. Yao, Adv. Funct. Mater., 2024, 34, 2313067.
22. Z. Sun, H. Zhou, C. Wang, S. Kumar, D. Geng, S. Yue, X. Han, Y. Haraguchi, K. Shimada, P. Cheng, L. Chen, Y. Shi, K. Wu, S. Meng and B. Feng, Nano Lett., 2022, 22, 4596–4602.
23. G. J. Miller, J. Alloys Compd., 1995, 217, 5–12.
24. G. V. Khvorykh, A. V. Shevelkov, V. A. Dolgikh and B. A. Popovkin, J. Solid State Chem., 1995, 120, 311–315.
25. M. D. Smith and G. J. Miller, J. Alloys Compd., 1998, 281, 202–205.
26. M. D. Smith and G. J. Miller, J. Am. Chem. Soc., 1996, 118, 12238–12239.
27. Y. Zhou, L. Zhou and J. He, ACS Appl. Mater. Interfaces, 2021, 14, 1643–1651.
28. J. Schmidt, L. Pettersson, C. Verdozzi, S. Botti and M. A. L. Marques, Sci. Adv., 2021, 7, eabi7948.
29. J. Schmidt, N. Hoffmann, H.-C. Wang, P. Borlido, P. J. M. A. Carriço, T. F. T. Cerqueira, S. Botti and M. A. L. Marques, Adv. Mater., 2023, 2210788.
30. H.-C. Wang, J. Schmidt, M. A. L. Marques, L. Wirtz and A. H. Romero, 2D Mater., 2023, 10, 035007.
31. C. Chen and S. P. Ong, Nat. Comput. Sci., 2022, 2, 718–728.
32. J. H. Jung, C.-H. Park and J. Ihm, Nano Lett., 2018, 18, 2759–2765.
33. Y. Han, K. C. Lai, A. Lii-Rosales, M. C. Tringides, J. W. Evans and P. A. Thiel, Surf. Sci., 2019, 685, 48–58.
34. D. C. Hvazdouski, M. S. Baranava, E. A. Korznikova, A. A. Kistanov and V. R. Stempitsky, 2D Mater., 2024, 11, 025022.
35. N. Tilak, X. Lai, S. Wu, Z. Zhang, M. Xu, R. D. A. Ribeiro, P. C. Canfield and E. Y. Andrei, Nat. Commun., 2021, 12, 4180.
36. X. Sun, M. Suriyage, A. R. Khan, M. Gao, J. Zhao, B. Liu, M. M. Hasan, S. Rahman, R.-S. Chen, P. K. Lam and Y. Lu, Chem. Rev., 2024, 124, 1992–2079.
37. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
38. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
39. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
40. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
42. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
43. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
44. J. Schmidt, N. Hoffmann, H.-C. Wang, P. Borlido, P. J. M. A. Carriço, T. F. T. Cerqueira, S. Botti and M. A. L. Marques, Large-scale machine-learning-assisted exploration of the whole materials space, Materials Cloud Archive 2022.126, 2022 , https://doi.org/10.24435/materialscloud:m7-50.
45. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
46. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
47. M. van Setten, M. Giantomassi, E. Bousquet, M. Verstraete, D. Hamann, X. Gonze and G.-M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54.
48. M. Schlipf and F. Gygi, Comput. Phys. Commun., 2015, 196, 36–44.
49. T. Sohier, M. Calandra and F. Mauri, Phys. Rev. B, 2017, 96, 075448.
50. T. Sohier, M. Gibertini, M. Calandra, F. Mauri and N. Marzari, Nano Lett., 2017, 17, 3758–3763.
51. M. Lazzeri and F. Mauri, Phys. Rev. Lett., 2003, 90, 036401.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01196a

---