Excited-state dynamics of 3-hydroxychromone in gas phase

Abstract

In recent years, 3-hydroxychromone (3-HC) and its derivatives have attracted much interest for their applications as molecular photoswitches and fluorescent probes. A clear understanding of their excited-state dynamics is essential for their applications and further development of new functional 3-HC derivatives. However, the deactivation mechanism of the photoexcited 3-HC family is still puzzling as their spectral properties are sensitive to the surrounding medium and substituents. The excited-state relaxation channels of 3-HC have been a matter of intense debate. In the current work, we thoroughly investigated the excited-state decay process of the 3-HC system in the gas phase using high-level electronic structure calculations and on-the-fly excited-state dynamic simulations intending to provide insight into the intrinsic photochemical properties of the 3-HC system. A new deactivation mechanism is proposed in the gas phase, which is different from that in solvents. The excited-state intramolecular proton transfer (ESIPT) process that occurs in solutions is not preferred in the gas phase due to the existence of a sizable energy barrier (∼0.8 eV), and thus, no dual fluorescence is found. On the contrary, the non-radiative decay process is the dominant decay channel, which is driven by photoisomerization combined with ring-puckering and ring-opening processes. The results coincide with the observations of an experiment performed in a supersonic jet by Itoh (M. Itoh, Pure Appl. Chem., 1993, 65(8), 1629–1634). The current work indicates that the solution environment plays an important role in regulating the excited-state dynamic behaviour of the 3-HC system. This study thus provides theoretical guidance for the rational design and improvement of the photochemical properties of the 3-HC system and paves the way for further investigation into its photochemical properties in complex environments.

---

Introduction

In recent years, 3-hydroxychromone (3-HC) and its derivatives with dual-band fluorescence have attracted considerable research interest for their use in applications such as molecular photoswitches,^1–5 fluorescent molecular probes,^6–10 and photochromic materials.^11–15 Their dual-band fluorescence originates from their ability to undergo excited-state intramolecular proton transfer (ESIPT) and form intramolecular hydrogen bonds. Upon photoexcitation, the most stable isomer of 3-HC in the ground state (S₀), termed cis-enol (Fig. 1), is excited to the first excited state (S₁), where it can either relax from the Franck–Condon state to the most stable cis-enol form in S₁, or can undergo an ESIPT process to generate a new cis-keto isomer in S₁. The cis-enol and cis-keto isomers in S₁ can emit fluorescence with well-separated emission bands. After emission, the cis-keto isomer (in S₀) subsequently undergoes relaxation and structural reorganization to return to the cis-enol form and complete the photoreaction cycle. This process can be influenced by the solvent polarity^16,17 and the type and position of substitutions.^13,18 Consequently, the fluorescence peak position and intensity are different under different conditions. A thorough investigation of their excited-state dynamics can provide guidance for further development of 3-HC and its derivatives for advanced applications.

Fig. 1 The three stable tautomers of 3-HC in S₀ and S₁ with the general conversion scheme between them after photoexcitation.

A number of experimental and theoretical studies have been undertaken to investigate the photochemical and photophysical properties of 3-HC and its derivatives.^11–37 Especially, 3-HC, as the basic unit of its derivatives, is a good model system to study the excited-state dynamics because it can provide elementary information without perturbation from substituents. Clevalier et al.¹⁷ found that the photoinduced excited-state dynamics of 3-HC are solvent dependent. In pure water (pH = 7), the dissociation and formation of the short-lived anionic state (deprotonated) is favoured, and this phenomenon has been observed in several 3-HC derivatives.¹⁶ However, in organic solvents, the formation of the tautomer excited state (cis-keto and trans-enol) is the main pathway. Nevertheless, the reason for the slow ESIPT process (5.5 ps) in organic solvents remains unclear. Two possible processes have been proposed by Chevalier et al.:¹⁷ the intramolecular vibrational relaxation and cis–trans photoisomerization (caused by hydrogen-torsion) processes. Furthermore, to understand them, Perveaux et al.²³ carried out a theoretical study to investigate the deactivation process of the 3-HC system. They located a conical intersection within the FC region between the dark S₂ (nπ* character) and the bright S₁, which opens a channel for the system to re-populate to S₂. The new reaction pathway is unreactive with respect to the ESIPT process, and thus a new explanation for the slower ESIPT process has been proposed. Vennapusa et al.³⁰ further investigated the nonadiabatic dynamics of 3-HC using the multiconfiguration time-dependent Hartree (MCTDH) method. A similar deactivation mechanism scheme was proposed. They predicted an average timescale of 84 fs for the fast ESIPT process, and a much slower ESIPT process in S₂ with about 19% of the trajectories are remaining in S₂ at the end of the simulation (300 fs). Although the above-mentioned theoretical studies were performed in the gas phase, their results support the presence of the ESIPT process, which is observed in the solution phase. However, the experimental results obtained in the gas phase, reported by Itoh,³⁶ concluded that the photoinduced excited-state dynamics of 3-HC are dominated by non-radiative processes instead of involving fluorescent excited-state species generated by the ESIPT process. Hence, the excited-state relaxation pathways of 3-HC in the gas phase remain unclear.

Herein, we employed high-level electronic structure calculations based on the CASPT2//CASSCF method and on-the-fly excited-state dynamic simulations to investigate the intrinsic photoinduced excited-state dynamics of 3-HC in the gas phase. We found that the dark-state S₂ has a negligible influence on the deactivation of 3-HC, which can directly transfer to S₁ within an ultrafast timescale (∼50 fs), and no “S₁ → S₂ up-transfer” trajectories were found. The system decays to S₀ mainly by a non-radiative process, and two coordinates driven by the cis–trans photoisomerization process and ring-opening motion were found to be the dominant channels in the S₁ to S₀ relaxation process. The ESIPT process is not preferred due to the presence of a sizable energy barrier (∼0.8 eV), and thus dual fluorescence is not supported. This study provides a detailed understanding of the excited-state dynamics of 3-HC in the gas phase, which can provide theoretical guidance for the further modification of chemical structures to achieve the desired functions.

Calculation details

All CASSCF and CASPT2 calculations were performed using the OpenMolcas suite.³⁸ All DFT and TDDFT calculations were executed in the Gaussian 09 program package.³⁹ The geometry optimization of S₀ and the two lowest excited state (S₁, S₂) minima and the minimum energy conical intersections (MECIs) were performed using the complete active space self-consistent field (CASSCF) method. The higher excited states were not included given that they have little influence on the decay process (lying > 1.0 eV above S₂, as shown in Table S1, ESI†). Initially, the active space was chosen as sixteen electrons distributed in thirty orbitals, including seven doubly occupied π orbitals, one doubly occupied n orbital and five unoccupied π* orbitals. By eliminating the orbitals with occupations close to 2.00 or 0.00, the active space was then reduced to 12 electrons distributed in 10 orbitals. More information about the included orbitals is provided in Fig. S1 (ESI†). The reaction pathways were constructed using the linearly interpolated internal coordinate (LIIC) method between the Franck–Condon point (FC) and MECIs. Considering that the CASSCF method is unable to provide accurate energy information due to the lack of dynamic electron correlation, all energies (including the vertical excitation energies of the critical points and potential energy profiles) were calculated again using the complete active space perturbation theory to second order (CASPT2) method. An imaginary shift of 0.2 a.u. was employed to avoid intruder-state issues.⁴⁰ The 6-31G* basis set was employed throughout this work. All CASSCF and CASPT2 calculations were performed using a three-state-average with equal weights for each state. We tested different basis sets, including cc-pVTZ, cc-pVDZ, 6-31G** and 6-31G, and different active spaces, such as (16,13), (10,8), (8,8) and (6,6), to confirm the reliability of the method employed in the static electronic structure calculations. This helps to find an appropriate calculation level for the following dynamics simulations. In addition, the DFT//B3LYP//6-31G** and TDDFT//B3LYP//6-31G** methods were also employed to optimize the stable structures and calculate the vertical excitation energies, respectively.

The photoinduced deactivation dynamics of 3-HC were followed by performing the on-the-fly surface hopping dynamics simulation procedure NAIMD-DICP, which has been successfully employed to study the deactivation process of many different molecular systems.^41–46 The nuclear trajectory propagation was integrated with the velocity Verlet algorithm.⁴⁷ The transition probability between different electronic states was estimated based on the Zhu–Nakamura theory,^48–51 which was compared with a random number generated between 0 and 1 to determine whether to hop or not. The velocity adjustment was immediately executed to maintain the energy conservation after a success hop. Considering that S₂ is nearly degenerate with S₁, we initiated 50 dynamics simulation trajectories from S₂. The maximum simulation time was about 1 ps with a step of 0.5 fs, which decreased to 0.1 fs when approaching the conical intersection region. The decreased step size caused the total simulation time of the trajectories, which experienced non-adiabatic transitions, to be less than 1 ps. The adiabatic energies, gradients and non-adiabatic couplings were computed using the SA3-CASSCF(8,8)//6-31G* method, which has been confirmed to be suitable for dynamics simulations by balancing the accuracy and computational cost (Table S3, ESI†). Furthermore, 35 additional trajectories starting from S₁ were simulated to avoid any potential bias or influence from the initial state on the dynamics simulation results. The S₀ → S₁ and S₁ → S₂ processes were allowed in both dynamics simulations (S₁ or S₂ as the initial state). The initial conditions were generated at 0 K based on the harmonic Wigner distribution,^52,53 with the frequencies and normal modes in the ground state calculated using SA3-CASSCF(12,10)//6-31G* method. The reliability of the CASSCF method for dynamic simulations has also been confirmed. As shown in Fig. S4 (ESI†), the relative energy information for the various critical points obtained by the CASSCF method agreed with that obtained by the CASPT2 method. Additionally, the topological structures of the potential energy curves constructed between the FC point and the conical intersection points obtained by the CASSCF method (Fig. S12, ESI†) agreed with those obtained by the CASPT2 method (Fig. 2b). Moreover, to compare the effect of the calculation methods on the dynamic results, we further ran five additional trajectories using the Newton-X package⁵⁴ combined with TDDFT calculations. The time step and the maximum simulation time were set to 0.5 fs and 1 ps, respectively.

Fig. 2 (a) S₀-cis-enol and five MECIs between two adjacent electronic states optimized with the SA3-CASSCF(12,10)//6-31G* method and (b) energies of the MECIs relative to the ground state energy of S₀-cis-enol.

Results and discussion

Stationary points and energies

The three stable tautomers of 3-HC are in S₀, which are termed trans-enol, cis-enol and cis-keto, as shown in Fig. 1. All the optimized tautomers in S₀ are planar with the absolute dihedral angle values of O₃C₈C₉H₅ and C₇C₉O₂H₆ equal to 180° and 0°, respectively. Our calculations match well with previous theoretical work as they share similar values for most of the related geometrical parameters (Table 1). The most stable tautomer in S₀ is the cis-enol tautomer with an intramolecular hydrogen bond O₁H₆ (2.199 Å) between the hydroxyl and carbonyl group. Upon photoexcitation, the hydrogen bond is strengthened with a decrease in the bond length to 2.147 Å. The strengthening of the hydrogen bond has been reported based on DFT and TDDFT calculations.^{8,11,20,23,32} The cis-keto tautomer (S₀) is generated by the ESIPT process of the cis-enol form, with the breaking of the O₂H₆ bond and formation of the O₁H₆ bond, which is located 0.64 eV above the S₀-cis-enol tautomer.

Table 1 Key geometrical parameters (bond lengths in Å and angles in degree) of the stable tautomers of the 3-HC system optimized at the SA3-CASSCF(12,10)//6-31G* level and their vertical excitation energies (eV) calculated at the CASPT2//SA3-CASSCF(12,10)//6-31G* level, together with previous theoretical^20,23,32 and experimental data^17,19,36

Geo.	C9O2	O2H6	O1H6	C7O1	C7C9O2H6	O3C8C9H5	S0 → S1	S0 → S2
^20TDDFT//DFT//B3LYP//TZVP; ^23TDDFT//DFT//PBE0//cc-PVDZ; ^32TDDFT//DFT//B3LYP//6-31G*a DFT//B3LYP//6-31G**.b TDDFT//B3LYP//6-31G**; and f means the transition oscillator strength.
S0-cis-enol	1.349	0.952	2.199	1.235	0.0	180.0	4.09	4.18
S0-cis-enol^a	1.351	0.983	2.044	1.238	0.0	180.0	4.14 (f = 0.08)^b	4.20 (f = 0.00)^b
							Exp. 3.96;^17 3.81;^19 3.77^36
S0-cis-enol^20	1.351	0.976	2.097	1.232	0.0	180.0	—	—
S0-cis-enol^23	1.341	0.982	2.000	1.233	0.0	180.0	4.11	4.23
S0-cis-enol^32	1.351	0.983	2.043	1.238	0.0	180.0	4.02	4.12
S1-cis-enol	1.344	0.953	2.147	1.248	0.0	180.0	3.78 (0.12) ^b	—
S1-cis-enol^20	1.319	1.002	1.871	1.248	0.0	180.0	—	—
S1-cis-enol^23	1.309	1.026	1.695	1.251	0.0	180.0	—	—
S1-cis-enol^32	1.368	0.969	2.370	1.334	19.8	180.0	—	—
S0-cis-keto	1.212	2.153	0.957	1.323	0.0	180.0	2.98	3.77
S0-cis-keto^20	1.265	1.812	1.008	1.312	0.0	180.0	—	—
S1-cis-keto	1.384	2.349	0.949	1.347	0.0	180.0	1.63	—
S1-cis-keto^20	1.335	2.143	0.975	1.341	0.0	180.0	—	—
S1-cis-keto^32	1.344	2.083	0.982	1.342	0.0	180.0	—	—
S0-trans-enol	1.350	0.947	3.655	1.209	180.0	180.0	3.98	4.27
S0-trans-enol^20	1.359	0.965	3.684	1.220	180.0	180.0	—	—
S1-trans-enol	1.356	0.947	3.666	1.359	180.0	180.0	2.73	—
S1-trans-enol^20	1.370	0.964	3.649	1.313	180.0	180.0	—	—
S1-trans-enol^23	1.356	0.965	3.655	1.312	180.0	180.0	—	—

---

For the minimum in S₁, compared to that in S₀, the main changes in the cis-enol tautomer are the elongation of the C₇O₁ bond by 0.01 Å and shortening of the O₁H₆ bond by about 0.02 Å. The fluorescence energy is 3.78 eV. Consequently, the cis-keto form becomes the most stable tautomer, which is termed as S₁-cis-keto. The most obvious change in S₁-cis-keto compared with S₀-cis-keto is the bond length of the C₉O₂ carbonyl group, which is extended from 1.212 Å (in S₀) to 1.384 Å (in S₁). The geometrical changing trend agrees with previous reports.^20,32 The trans-enol is generated from the twisting motion of the C₉O₂ bond in cis-enol. The intramolecular hydrogen bond breaks as the O₁H₆ bond length increases to 3.655 Å. After photoexcitation, the C₇O₁ bond length increases by about 0.15 Å, which is longer than that in previous reports.^20,32

The calculated vertical excitation energies from S₀ to S₁ and S₂ are listed in Table 1 and displayed in Fig. 1. These results are highly consistent with those obtained with the CASPT2//SA3-CASSCF(16,13)//6-31G**, CASPT2//SA3-CASSCF(12,10)//cc-pVDZ, and CASPT2//SA3-CASSCF(12,10)//cc-pVTZ methods, as shown in Table S2 (ESI†). The most relevant molecular orbitals are provided in Fig. S2 (ESI†). The S₁ state is a “bright” state with ππ* character, with the transition oscillator strength of 0.08 calculated using the TDDFT method. The vertical excitation energy of S₀-cis-enol to S₁ is 4.09 eV, which agrees well with the value of 4.11 eV obtained using the TDDFT method^23,32 and experimental values of 3.77–3.96 eV.^17,19,36 The S₂ state of S₀-cis-enol is “dark” with nπ* character and the transition oscillator strength of 0.00. The vertical excitation energy to S₂ is 4.18 eV, which is consistent with the reported value of 4.23 eV.²³ At the FC point, the S₁ and S₂ states are degenerate with an energy gap of less than 0.1 eV.³² This degeneracy (∼0.3 eV) is present in the results calculated using the CASSCF method (Table S2, ESI†). Thus, the good agreement between our calculation results and previous theoretical and experimental values indicates the reliability of the employed calculation methods and models. The vertical excitation energy of S₀-cis-keto from S₀ to S₁ and S₂ is 2.98 eV and 3.77 eV, respectively. For the S₀-trans-enol tautomer, the excitation energy to the S₁ and S₂ states is 3.98 and 4.27 eV, respectively.

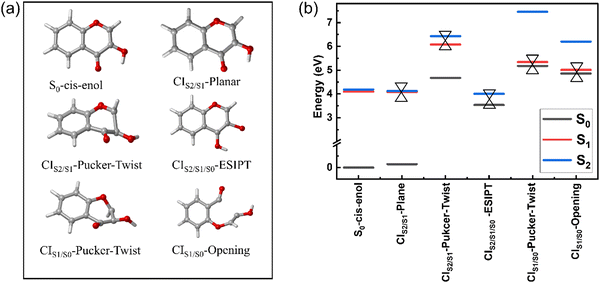
Minimum energy conical intersections (MECIs)

Fig. 2 displays the five MECIs located between two adjacent electronic states and their energies relative to the energy of S₀-cis-enol, which are in line with those calculated using the CASPT2//CASSCF(16,13)//6-31G**, CASPT2//SA3-CASSCF(12,10)//cc-pVDZ and CASPT2//SA3-CASSCF(12,10)//cc-pVTZ methods (Fig. S3, ESI†). The key geometrical parameters and specific energy information are summarized in Table 2. All MECIs were confirmed by the CASPT2 method with an energy gap less than 0.4 eV. Herein, we employed CI_m/n-X to describe their features, where m and n indicate the two adjacent electronic states and X describes the structural feature (e.g. planar, pucker, ESIPT and twist). CI_S2/S1-planar is located at 4.08 eV above the ground state minimum. The structure of CI_S2/S1-planar is similar to that of S₀-cis-enol, except that the bond lengths of C₉O₂ and C₇O₁ are shorter in CI_S2/S1-planar. Perveaux et al.²³ and Vennapusa et al.³² identified a similar structure in their TDDFT study, which was proposed as the channel for the re-population to S₂. CI_S2/S1-pucker-twist is located at 6.07 eV above S₀-cis-enol, featuring a strongly twisted C₉O₂ bond and puckering motion of the ring. The related dihedral angle of C₇C₉O₂H₆ changes to −174.2° and the C₈H₅ bond is almost perpendicular to the heterocyclic ring. However, its high energy makes it difficult to reach. CI_S2/S1/S0-ESIPT is a three-state CI, characterized by an intramolecular proton transfer process from O₂ to O₁. Its energy gap for S₁/S₀ and S₂/S₀ is 0.4 eV and 0.55 eV, respectively. In terms of geometry, the C₉O₂ and C₇O₁ bonds show obvious elongation, changing from a double bond character to a single bond character, which is similar to the keto-type MECI.³² CI_S1/S0-pucker-twist was found at 5.33 eV above S₀-cis-enol. Similar to the case of CI_S2/S1-pucker-twist, it is characterized with strong out-of-plane deformation of the C₈H₅ bond and rotation around the C₉O₂ bond. The related dihedral angle of O₃C₈C₉H₅ and C₇C₉O₂H₆ is 133.3° and 130.9°, respectively. CI_S1/S0-opening is 5.01 eV above S₀-cis-enol. It is mainly characterized by bond breakage between the C₇ and C₉ atoms, with an increase in their distance to 2.625 Å. Furthermore, it contains a pronounced twisting motion around the C₉O₂ bond, with the dihedral angle C₇C₉O₂H₆ of −69°. For the first time, we located the last four MECIs here, which may play important roles in the deactivation of 3-HC in the gas phase.

Table 2 Key geometrical parameters (bond lengths in Å and angles in degree) of the five MECIs optimized at the SA3-CASSCF(12,10)//6-31G* level and their energy information (eV) calculated at the CASPT2//SA3-CASSCF(12,10)//6-31G* level, together with previous reported results^23,32

Geo.	C9O2	O2H6	O1H6	C7C9	C7O1	C7C9O2H6	O3C8C9H5	RE^a	ΔS1−S0	ΔS2−S1
a The relative energy (RE) between listed geometries and the energy of S0-cis-enol.
CIS2/S1-Plane	1.333	0.956	2.101	1.495	1.220	0.0	180.0	4.08	3.94	0.05
CoIn^23	1.349	0.970	2.077	1.448	1.228	0.0	180.0	—	—	—
Enol-MECI^32	1.347	0.982	2.088	1.466	1.287	0.0	180.0	3.90	—	—
CIS2/S1/S0-ESIPT	1.554	2.638	0.943	1.361	1.381	0.0	180.0	3.99	0.40	0.15
Keto-MECI^32	1.352	2.274	0.968	1.408	1.362	0.0	180.0	3.26	—	—
CIS2/S1-Pucker-Twist	1.352	0.948	3.800	1.371	1.502	−174.2	−145.7	6.07	1.40	0.35
CIS1/S0-Pucker-Twist	1.393	0.946	3.676	1.310	1.378	133.3	130.9	5.33	0.16	2.11
CIS1/S0-Opening	1.331	0.948	3.834	2.625	1.183	−69.0	−177.2	5.01	0.15	1.19

---

Excited-state nonadiabatic dynamics

To gain insight about the specific roles of the MECIs in the deactivation process of photoexcited 3-HC, we carried out the excited-state dynamic simulations starting from S₂. Fig. 3(a) shows the time-dependent fractional occupations of S₀, S₁ and S₂, where 49 out of 50 trajectories were used for the following data analysis. We ruled out one trajectory with the non-conservation of total energy. Within the first 100 fs, more than 60% of the trajectories decayed to S₁. All trajectories depopulated completely from S₂ after 600 fs. We did not observe any “S₁ → S₂ up transfer” process during the whole simulation. Moreover, the S₁ → S₂ up transfer process was not present in the dynamic simulations starting from S₁ (see sections below). At 150 fs, some trajectories approached the conical intersection region and the S₁ → S₀ decay process started. At the end of the simulation, the population of S₀ reached 40% and about 60% of the trajectories remained in S₁. This implies that there are additional decay channels with longer lifetimes and 800 fs is not enough for simulating these channels.

Fig. 3 (a) Time-dependent occupation of S₂, S₁ and S₀ of the 3-HC system; (b) key bond lengths of the S₂ → S₁ hopping points; and (c) key bond lengths of the S₁ → S₀ hopping points. The green, orange and purple stars represent the C₉O₂, O₁H₆ and C₇O₁ bond lengths at the FC point, respectively.

The excited-state lifetime of S₁ and S₂ can be estimated by fitting their time-dependent population with exponential decay functions. Based on the above-mentioned discussion, S₁ and S₂ are two degenerate states. The decay channel of S₂ most likely is via fast the S₂ → S₁ internal conversion process. Hence, we used a monoexponential decay function to fit the time-dependent population of S₂ (fitted up to 800 fs). We determined the lifetime of S₂ to be 118 fs, which is within the typical timescale of the internal conversion process.^8,55,56 We then applied bootstrapping to extract 10 000 sets of data, each containing 1701 values. Subsequently, we fitted each set and obtained a 95% confidence interval of [118.90685135, 119.00291629], which is consistent with our fitting results. A plateau is present in the S₂ population (Fig. 3a), which is attributed to the molecular structure undergoing a slight torsion in the C₉O₂ bond at the beginning of the simulation. Subsequently, this torsion returned to a planar configuration, which is a process that takes some time. The population of S₁ builds up in the first ∼200 fs due to the S₂ → S₁ relaxation. The build-up process should have the same time constant as the lifetime of S₂. There are several channels that can contribute to the decay process of S₁ including isomerization, ESIPT and radiative processes. These processes are different in terms of energy and molecular configuration. Most likely, they will have different decay time constants, which causes S₁ to show multiple lifetimes. Thus, to obtain this information quantitatively, we fitted the time-dependent population of S₁ (P₁(t)) with the sum of an exponential growth function (build-up process of S₁) and a bi-exponential decay function.

P ₁(t) = −A₁ exp(t − t₀/τ₁) + A₂ exp(t − t₀/τ₂)+ A₃ exp(t − t₀/τ₃), where A₁, A₂ and A₃ represent the amplitude for different processes, t₀ is time zero, and τ₁, τ₂, and τ₃ are the fitted lifetimes. Here, we fixed the growth lifetime of S₁ to be 118 fs, which is the same as the decay lifetime of S₂. We obtained τ₂ = 110 fs, τ₃ ≫ 800 fs, which indicates that there are at least two different decay processes for S₁. As illustrated in Fig. 1 and the calculated multiple MECIs (Fig. 2), this is straightforward for the presence of multiple decay channels for S₁. However, it is rather unusual for the lifetimes of the different decay channels to show such a big difference.

Thus, to understand the different decay channels, initially we analyzed the structural change for the fast decay processes, i.e., the hopping events of S₂ → S₁ and S₁ → S₀, as shown in Fig. 3(b) and (c), respectively. Here, we focus on the key bond lengths, where in the case of both S₂ → S₁ and S₁ → S₀, the C₇O₁ and C₉O₂ bond lengths show a clear elongation (from 1.204 Å and 1.347 Å at FC to over 1.400 Å at the hoping events, respectively). The most obvious change was the elongation of the hydrogen bond between the H₆ and O₁ atoms (from 2.199 Å at FC to over 2.200 Å at the hoping events). These geometrical changes indicate that a twisting motion of the C₉O₂ bond is present in the hopping events.

The time-dependent key geometrical parameters (Fig. 4) provide information about the structural changes during the hopping events. They offer the possibility to examine whether the ESIPT process occurs during the simulation, given that the ESPIT process is characterized by the breaking of the O₂H₆ bond and the formation of the O₁H₆ bond. However, we did not observe this change, as shown in Fig. 4(a); instead, the O₂H₆ bond remained constant at around 1 Å and the O₁H₆ distance increased due to the twisting motion of the C₉O₂ bond. Hence, we can conclude that the ESIPT process was absent within the simulation time range. To provide a clear picture of the roles played by the twisting motion in the deactivation processes, we plotted the dihedral angles of C₇C₉O₂H₆ and O₃C₈C₉H₅ from all 49 trajectories (Fig. 4(b) and (c), respectively) with the S₂ → S₁ and S₁ → S₀ hopping events. All the S₂ → S₁ hopping events occur around the dihedral angles of C₇C₉O₂H₆ of 0° and O₃C₈C₉H₅ of ±180°, indicating that the twisting motion of the C₉O₂ bond does not play an important role in the relaxation process of S₂. Alternatively, the S₁ → S₀ hopping events occur around the dihedral angles of C₇C₉O₂H₆ of ±100° and O₃C₈C₉H₅ of ±140°, suggesting that the S₁ → S₀ decay process is characterized by a twisting motion of the C₉O₂ bond and clear deformation of the heterocyclic ring around the C₈ atom.

Fig. 4 Variation in (a) O₂H₆ and O₁H₆ bond lengths and (b) dihedral angle of C₇C₉O₂H₆ and (c) O₃C₈C₉H₅ as a function of the simulation time. The blue and rosy balls represent the S₂ → S₁ and S₁ → S₀ hopping events, respectively.

Moreover, we summarized the changes in the bond lengths of C₇C₉ and C₇O₁ during the simulation time in Fig. S5 (ESI†). The C₇O₁ bond length fluctuated around 1.3 Å throughout the simulation period, while the C₇C₉ bond length showed a larger range of variation, mostly above 1.45 Å. Moreover, two trajectories of C₇C₉ bond cleavage were observed. These hopping events are directly linked with or went through the relevant MECIs. To visualize this, we summarized the key parameters of the S₂ → S₁ and S₁ → S₀ hopping events together with the five MECIs in Fig. 5. Almost all the S₂ → S₁ hopping points are located around CI_S2/S1-plane, but far away from CI_S2/S1-pucker-twist. This suggests that only CI_S2/S1-plane will be easily accessible during the S₂ → S₁ relaxation dynamics, which is in good agreement with the fact that the two states are degenerate and the fast internal conversion process. The S₁ → S₀ hopping points are scattered around the two S₁/S₀ MECI points related with the pucker-twisting and ring-opening motion, which accounts for the ultrafast decay process of the S₁ population. These hopping events are far away from CI_S2/S1/S0-ESIPT, indicating that the bond twisting and ring-opening motion rather than the ESIPT process play important roles in the deactivation process of S₁. Our results from the simulations using the Newton-X package combined with TDDFT methods indicate that the 3-HC molecule tends to undergo deactivation through C₉O₂ bond torsion, as shown in Fig. S6 (ESI†).

Fig. 5 Diagram of the dihedral angles of C₇C₉O₂H₆ (ordinate) and O₁H₆ (abscissa) (a) and C₃C₈O₉H₅ (ordinate) and O₁H₆ (abscissa) (b) of the S₂ → S₁ and S₁ → S₀ hopping events. The stars with different colours represent the five MECIs.

To avoid introducing any bias by using S₂ as the starting point for the simulation, we performed dynamics simulation using S₁ as the starting point. Specifically, 35 trajectories were employed for the simulation, among which one was discarded due to a violation of energy conservation. Note that 20 trajectories completed deactivation back to S₀, and the remaining 14 trajectories were still in S₁ at the end of the simulation (Fig. S7, ESI†). The results of the dynamics simulations initiated from S₁ (Fig. S8, ESI†) are similar to the findings from the simulations initiated from S₂, except that the S₂ → S₁ internal conversion process was absent. Neither S₁ → S₂ up-transfer nor ESIPT was observed during the dynamic simulations. Hence, the dynamics of S₁ is independent of the initial state.

Deactivation mechanism and comparison with experiments

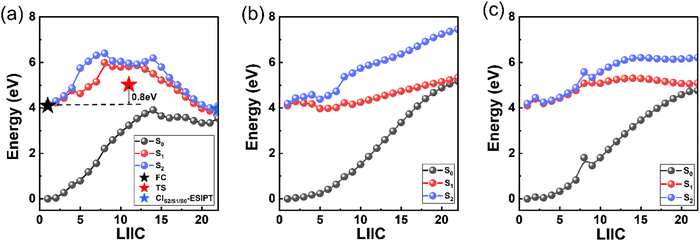
Based on the excited-state dynamic simulations, we found that the ESIPT process did not show a direct contribution to the S₁ → S₀ relaxation of 3-HC within the simulation time. Thus, to understand the reason for this, we constructed the energy profiles with the LIIC method connecting the FC point and three S₁/S₀ MECIs (Fig. 6). These energy profiles were then confirmed using the CASPT2//SA3-CASSCF(16,13)//6-31G**, CASPT2//SA3-CASSCF(12,10)//cc-pVDZ and CASPT2//SA3-CASSCF(12,10)//cc-pVTZ methods, as shown in Fig. S9–S11 (ESI†). A large energy barrier (∼1.63 eV) is present along the ESIPT pathway, which prevented the ESIPT process from occurring in our simulation timescale. However, the energy barrier may be overestimated with the LIIC method, and thus we re-optimized the excited-state transition state by picking the highest energy point on the LIIC path, as displayed by the red star in Fig. 6(a). The energy barrier decreased to 0.8 eV, which is still too high to overcome. Thus, to validate the high energy barrier for ESIPT, we employed a scan of the bond length of O₁H₆ to obtain the potential energy curve for S₁, as shown in Fig. S13(a) (ESI†). This approach corroborated our previous findings, with the energy barrier for ESIPT estimated to be approximately 0.7 eV, which aligns closely with the revised barrier obtained from the excited-state transition-state re-optimization. Different from CI_S2/S1/S0-ESIPT, there is a potential well along the other two paths (CI_S1/S0-pucker-twist and CI_S1/S0-opening, Fig. 6(b) and (c), respectively). The existence of the potential well can cause the system to be easily trapped in it during the relaxation process in S₁, and the photoisomerization pathway from the cis-enol to trans-enol form is about 0.08 eV, which was obtained by scanning the C₇C₉O₂H₆ dihedral angle change from 0° to 180°, as shown in Fig. S13(b) (ESI†). At the end of our simulation, about 57% of all the trajectories remained in S₁. This means the lifetime of S₁ can be much longer than our simulation time (800 fs), as indicated by the fitted second lifetime of ≫ 800 fs. These trajectories can be categorised into two branches based on their geometrical information (Fig. S14, ESI†). One part remains a semi-planar configuration with the O₁H₆ bond length shorter than 2.75 Å and the dihedral angle of C₇C₉O₂H₆ smaller than 30°. The other part displays a torsion of the C₉O₂ bond, which is trapped in the potential well along the twisting motion-driven deactivation channel, as shown in Fig. 6(b). Apart from the two branches showing difference in geometry, all structures of the remaining trajectories have lower energy than the FC point in S₁ and MECIs between S₁ and S₀ (Fig. S15, ESI† and Fig. 2(b)), which means that these trajectories can be activated via thermal energy and decay back to S₀ (e.g. via ESIPT process) on a longer timescale. Furthermore, the energy barrier presented at the ESIPT pathway may be lowered by the surrounding solvent molecules, which makes the ESIPT process possible in the solution phase, as observed experimentally.^16,17

Fig. 6 Energy profiles constructed using the LIIC method connecting the Franck–Condon geometry and (a) CI_S2/S1/S0-ESIPT, black star: S₁ energy of the FC point, red star: S₁ energy of the transition state between cis-enol and CI_S2/S1/S0-ESIPT, blue star: CI_S2/S1/S0-ESIPT; (b) CI_S1/S0-pucker-twist; and (c) CI_S1/S0-opening computed at the CASPT2//SA3-CASSCF(12,10)//6-31G* level.

A schematic overview of the excited-state dynamics of the 3-HC system is presented in Fig. 7. Upon photoexcitation to S₂, the system relaxes to S₁via a barrierless bond alternation process. Within our simulation time, 39% and 4% of the total simulated trajectories from S₁ decay to the ground state via CI_S1/S0-pucker-twist, and CI_S1/S0-opening, respectively, and about 26% of these trajectories finally generate the trans-enol product in S₀. The presence of a large energy barrier hinders the ESIPT process. Hence, the nonradiative deactivation of the photoexcited 3-HC system in the gas phase is mainly induced by bond twisting motion and ring-opening motion. However, these motions may be restricted in solvents due to the steric hindrance effect, forcing the system to relax via the ESIPT process. As discussed above, a large energy barrier is present in the ESIPT pathway, and thus thermal activation can enable this process to occur at a slow speed, e.g., on the picosecond timescale, which has been observed experimentally in the solution phase. However, the destruction of intramolecular hydrogen bonding due to torsional motion may slowdown the ESIPT process. Thus, the two ESIPT time constants observed in solution can be explained. Previous experiments mainly focused on studying the influence of protonic and polarity on the behavior of the excited-state dynamics of the 3-HC system. Alternatively, we suggest that future experimental studies pay more attention to the effect of solution viscosity on the deactivation mechanism of the 3-HC system.

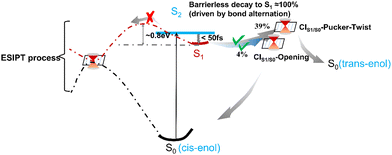Fig. 7 Schematic overview of the excited-state dynamics of the 3-HC system following excitation to the S₂ state.

Conclusion

In the current work, we investigated the excited-state deactivation process of the 3-HC system in the gas phase using high-level electronic structure calculations and on-the-fly excited-state dynamic simulations. Based on the calculations, we found that the 3-HC system prefers decaying to S₀ by a nonradiative process rather than fluorescence. The results coincide with the experimental observations. The non-radiative process is mainly driven by the twisting of the C₉O₂ bond and the deformation of the heterocyclic ring. We did not observe the ESIPT process in our dynamic simulations due to the presence of a large energy barrier in this pathway. Alternatively, the ESIPT process of 3-HC has been observed in solvent. This difference is partly because the twisting motion and the ring deformation would be restricted due to the steric-hindrance effect from solvent molecules. In addition, the energy barrier for ESIPT may decrease and the 3-HC system would gain enough thermal energy under the experimental condition (room temperature) to overcome the energy barrier. This ESIPT process would happen at a slow speed, while the destruction of intramolecular hydrogen bonding due to torsional motion may further slowdown the ESIPT process. This could explain the fact that two ESIPT reaction constants were observed in the solution phase. The present work proposes a comprehensive description of the intrinsic photophysical and photochemical properties of 3-HC, which not only provides a foundation for the further investigation of the effect of environment, but also theoretical guidance for the rational design of molecular photoswitches. Furthermore, given that the photoinduced dynamic behaviour of 3-HC and its derivatives shows strong dependence on the environment, it is worthwhile to further explore their solute–solvent hydrogen-bonding interactions in different solvents.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 21803077), the Fundamental Research Funds for the Central Universities (No. 24CX03009A, and 23CX03016A) and Novo Nordisk Foundation (NNF22OC0073582).

References

1. A. D. Dunkelberger, R. D. Kieda, J. Y. Shin, R. Rossi Paccani, S. Fusi, M. Olivucci and F. F. Crim, J. Phys. Chem. A, 2012, 116, 3527.
2. M. Andresen, M. C. Wahl, A. C. Stiel, F. Grater, L. V. Schafer, S. Trowitzsch, G. Weber, C. Eggeling, H. Grubmuller, S. W. Hell and S. Jakobs, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13070.
3. R. Mitric, U. Werner and V. Bonacic-Koutecky, J. Chem. Phys., 2008, 129, 164118.
4. C. J. Xia, D. S. Liu and H. C. Liu, Optik, 2012, 123, 1307.
5. T. Wendler, C. Schutt, C. Nather and R. Herges, J. Org. Chem., 2012, 77, 3284.
6. J. S. Chen, M. H. Yuan, J. P. Wang, Y. Yang and T. S. Chu, J. Phys. Chem. A, 2014, 118, 8986.
7. J. S. Chen, P. W. Zhou, S. Q. Yang, A. P. Fu and T. S. Chu, Phys. Chem. Chem. Phys., 2013, 15, 16183.
8. W. Zhang, L. Zhao, B. W. Laursen and J. Chen, Phys. Chem. Chem. Phys., 2022, 24, 26731.
9. J. S. Chen, T. S. Chu, R. Z. Liu and Y. Yang, Theor. Chem. Acc., 2014, 133, 1411.
10. L. Zhao, S. Jiang, Y. He, L. Wu, T. D. James and J. Chen, Phys. Chem. Chem. Phys., 2024, 26, 13506.
11. S. Basu, S. Mondal and D. Mandal, J. Chem. Phys., 2010, 132, 034701.
12. S. Chaudhuri, K. Basu, B. Sengupta, A. Banerjee and P. K. Sengupta, Luminescence, 2008, 23, 397.
13. A. P. Demchenko, K. C. Tang and P. T. Chou, Chem. Soc. Rev., 2013, 42, 1379.
14. C. Dyrager, A. Friberg, K. Dahlén, M. Fridén-Saxin, K. Börjesson, L. M. Wilhelmsson, M. Smedh, M. Grøtli and K. Luthman, Chem. – Eur. J., 2009, 15, 9417.
15. A. S. Klymchenko, C. Kenfack, G. Duportail and Y. Mely, J. Chem. Sci., 2007, 119, 83.
16. R. Das, A. S. Klymchenko, G. Duportail and Y. Mely, Photochem. Photobiol. Sci., 2009, 8, 1583.
17. K. Chevalier, A. Grun, A. Stamm, Y. Schmitt, M. Gerhards and R. Diller, J. Phys. Chem. A, 2013, 117, 11233.
18. C. Sun, X. Su, Q. Zhou and Y. Shi, Org. Chem. Front., 2019, 6, 3093.
19. G. A. Brucker and D. F. Kelley, J. Phys. Chem., 1987, 91, 2862.
20. A. Stamm, M. Weiler, A. Bracher, K. Schwing and M. Gerhards, Phys. Chem. Chem. Phys., 2014, 16, 21795.
21. J. D. Huang, J. Zhang, D. Chen and H. Ma, Org. Chem. Front., 2017, 4, 1812.
22. K. R. Nandipati, Z. Lan, H. Singh and S. Mahapatra, J. Chem. Phys., 2017, 146, 214304.
23. A. Perveaux, M. Lorphelin, B. Lasorne and D. Lauvergnat, Phys. Chem. Chem. Phys., 2017, 19, 6579.
24. Y. Yang, Z. Tang, P. Zhou, Y. Qi, Y. Wang and H. Wang, J. Mol. Liq., 2018, 260, 447.
25. J. Liu, X. Chen, Y. Zhang, G. Gao, Z. Xueyan, S. Hou and Y. Hou, New J. Chem., 2018, 42, 12918.
26. G. A. Ndongo, M. O. Boyomo and P. A. Owono, J. Mol. Model., 2018, 24, 92.
27. K. R. Nandipati, A. K. Kanakati, H. Singhb and S. Mahapatra, Phys. Chem. Chem. Phys., 2019, 21, 20018.
28. K. Kaur, J. Tomar and M. Bansal, Can. J. Chem., 2019, 97, 584.
29. J. S. Lim, H. S. You, S.-Y. Kim, J. Kim, Y. C. Park and S. K. Kim, J. Chem. Phys., 2019, 151, 244305.
30. N. Anand, S. V. K. Isukapalli and S. R. Vennapusa, J. Comput. Chem., 2020, 41, 1068.
31. P. Nag and S. R. Vennapusa, J. Chem. Phys., 2020, 153, 084306.
32. P. Nag, N. Anand and S. R. Vennapusa, J. Chem. Phys., 2021, 155, 094301.
33. P. Nag and S. R. Vennapusa, J. Photochem. Photobiol., A, 2022, 431, 114024.
34. P. Nag and S. R. Vennapusa, J. Photochem. Photobiol., A, 2022, 427, 113767.
35. P. K. Sengupta and M. Kasha, Chem. Phys. Lett., 1979, 68, 382.
36. M. Itoh, Pure Appl. Chem., 1993, 65, 1629.
37. S. Ash, S. P. De, H. Beg and A. Misra, Mol. Simul., 2011, 37, 914.
38. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. D. Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. L. Manni, H. Lischka, D. X. Ma, P. Å. Malmqvist, T. Muller, A. Nenov, M. Olivucci, T. B. Pedersen, D. L. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. S. Segarra-Martí, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506.
39. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision C.01, Gaussian, Inc., Wallingford, CT, 2009.
40. C. Angeli, J. Comput. Chem., 2009, 30, 1319.
41. L. Zhao, G. Xu, Y. Guo, H. Zheng, P. Dong and J. Chen, J. Photochem. Photobiol., A, 2023, 434, 114255.
42. L. Zhao, P. Zhou, X. Liu, H. Zheng, K. Zhan, J. Luo and B. Liu, Spectrochim. Acta, Part A, 2021, 244, 118884.
43. L. Zhao, H. Zheng, K. Zhan, Y. Guo, B. Liu and G. Xu, J. Phys. Chem. A, 2021, 125, 165–174.
44. L. Zhao, J. Liu and P. Zhou, J. Chem. Phys., 2018, 149, 034309.
45. L. Zhao, P. W. Zhou, B. Li, A. H. Gao and K. L. Han, J. Chem. Phys., 2014, 141, 235101.
46. A. H. Gao, B. Li, P. Y. Zhang and K. L. Han, J. Chem. Phys., 2012, 137, 204305.
47. W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637.
48. C. Zhu and H. Nakamura, J. Chem. Phys., 1992, 97, 8497.
49. C. Zhu and H. Nakamura, J. Chem. Phys., 1993, 98, 6208.
50. C. Zhu and H. Nakamura, J. Chem. Phys., 1994, 101, 10630.
51. C. Zhu and H. Nakamura, J. Chem. Phys., 1995, 102, 7448.
52. L. Sun and W. L. Hase, J. Chem. Phys., 2010, 133, 044313.
53. S. Kube, C. Lasser and M. Weber, J. Comput. Phys., 2009, 228, 1947.
54. M. Barbatti, M. Ruckenbauer and F. Plasser, et al., Newton-X: a surface-hopping; program for nonadiabatic molecular dynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 26–33.
55. M. Bixon and J. Jortner, J. Chem. Phys., 1968, 48, 715.
56. S. Jiang, Y. He, J. H. Brandt, L. Zhao and J. Chen, J. Phys. Chem. Lett., 2023, 14, 10482.

---

Footnote

† Electronic supplementary information (ESI) available: Further information regarding the orbitals included in the active spaces, the orbitals involved in forming the first three excited singlet states, the comparison of key geometrical parameters among different calculation methods, and the Cartesian coordinates about the stable structures and MECIs are provided. See DOI: https://doi.org/10.1039/d4cp01190b

---