 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coupled-cluster treatment of complex open-shell systems: the case of single-molecule magnets†
Maristella
Alessio
 *ab,
Garrette Pauley
Paran
*ab,
Garrette Pauley
Paran
 a,
Cansu
Utku
a,
Cansu
Utku
 a,
Andreas
Grüneis
b and
Thomas-C.
Jagau
a,
Andreas
Grüneis
b and
Thomas-C.
Jagau
 a
a
aDepartment of Chemistry, KU Leuven, Celestijnenlaan 200F, B-3001 Leuven, Belgium. E-mail: maristella.alessio@kuleuven.be
bInstitute for Theoretical Physics, TU Wien, Wiedner Hauptstraße 8-10/136, 1040 Vienna, Austria
First published on 27th May 2024
Abstract
We investigate the reliability of two cost-effective coupled-cluster methods for computing spin-state energetics and spin-related properties of a set of open-shell transition-metal complexes. Specifically, we employ the second-order approximate coupled-cluster singles and doubles (CC2) method and projection-based embedding that combines equation-of-motion coupled-cluster singles and doubles (EOM-CCSD) with density functional theory (DFT). The performance of CC2 and EOM-CCSD-in-DFT is assessed against EOM-CCSD. The chosen test set includes two hexaaqua transition-metal complexes containing Fe(II) and Fe(III), and a large Co(II)-based single-molecule magnet with a non-aufbau ground state. We find that CC2 describes the excited states more accurately, reproducing EOM-CCSD excitation energies within 0.05 eV. However, EOM-CCSD-in-DFT excels in describing transition orbital angular momenta and spin–orbit couplings. Moreover, for the Co(II) molecular magnet, using EOM-CCSD-in-DFT eigenstates and spin–orbit couplings, we compute spin-reversal energy barriers, as well as temperature-dependent and field-dependent magnetizations and magnetic susceptibilities that closely match experimental values within spectroscopic accuracy. These results underscore the efficiency of CC2 in computing state energies of multi-configurational, open-shell systems and highlight the utility of the more cost-efficient EOM-CCSD-in-DFT for computing spin–orbit couplings and magnetic properties of complex and large molecular magnets.
I. Introduction
The application of quantum chemical methods to investigate electronic states and properties of transition-metal complexes and related materials is a crucial research area, finding applications in catalysis,1–4 car-battery design,5–7 molecular magnetism8–10 and many other fields. In the design of single-molecule magnets (SMMs) with desired behavior, meaning slow magnetic relaxation, the target quantity is the spin-reversal energy barrier.11 This barrier influences how effectively a system can be magnetized by an applied magnetic field, as measured by its magnetic susceptibility, and governs the rate of magnetization switching. To maximize this barrier, a rational tuning of the ground state spin S and orbital angular momentum L, which gives rise to spin–orbit coupling (SOC), is key.12 In transition-metal SMMs, the ligand field typically removes molecular-orbital degeneracy, thereby suppressing the orbital angular momentum. However, compounds with a weak ligand field and an odd number of unpaired electrons for each d shell may have unquenched orbital angular momentum, substantial SOC, and high spin-reversal barrier. This phenomenon has been observed in a set of linear SMMs with twofold-coordinated Fe(II),13 Fe(I),14 and Co(II)15 metal centers. Among them, the Co(C(SiMe2ONaph)3)2 complex stands out with the highest barrier, reaching 450 cm−1.15 However, building such linear coordination environment necessitates bulky naphthyl (Naph) groups as ligands. Furthermore, the development of molecular quantum devices involves designing relatively large and complex systems, obtained by deposition of molecular magnets on a surface or their self-assembly.16 Alongside the structural complexity of these magnetic systems, the small energy gaps, from tens to hundreds of wavenumbers, call for spectroscopic accuracy rather than chemical accuracy. As the focus in molecular magnetism turns toward transition metals coordinated by increasingly large ligands, often binding with various environments, there is a growing demand for quantum chemical methods that are both efficient and reliable in characterizing these systems.17,18Describing open-shell electronic states is typically more challenging compared to closed-shell electronic states, and standard single-reference methods, such as density functional theory (DFT), are often qualitatively incorrect. Traditionally, multi-reference methods, e.g., complete active space perturbation theory (CASPT2)19 and n-electron valence-state perturbation theory (NEVPT2),20 are employed to approximate the exact multi-configurational wave functions of these systems, extracting magnetic properties through phenomenological spin Hamiltonians.9,10,21 For example, NEVPT2 calculations on the Co(C(SiMe2ONaph)3)2 SMM predicted a non-aufbau ground state with S = 3/2, L = 3, and total angular momentum J = S + L = 9/2, also providing accurate estimates of its magnetic properties.15 An alternative approach to treating transition-metal SMMs is offered by the equation-of-motion coupled-cluster (EOM-CC) method,22–24 which extends the hierarchy of black-box single-reference coupled-cluster methods to strongly correlated systems. Recently, Alessio and Krylov introduced a computational protocol for describing transition-metal molecular magnets based on the EOM-CC framework.25 The approach is implemented in the ezMagnet software.25 It allows for the computation of spin properties such as spin–orbit splittings, magnetizations, and susceptibilities based on EOM-CC eigenstates. The performance of the computational approach has been tested against experiments and NEVPT2 calculations for a set of Fe(III), Fe(II) and Ni(II) molecular magnets, illustrating its reliability in computing magnetic exchange interactions, energy barriers, and magnetizations and susceptibilities.18,25,26 However, the computational cost of EOM-CC methods scales steeply with the system size, rendering their application to large molecular magnets impractical.
In this work, we tackle this challenge by assessing the performance of two more computationally efficient CC methods: the second-order approximate coupled-cluster singles and doubles (CC2)27 method, and projection-based embedding,28 which combines EOM-CC singles and doubles (EOM-CCSD) with DFT, to treat open-shell transition-metal complexes. The computational efficiency gain of CC2, which scales as N5 compared to N6 for EOM-CCSD where N is the system size, is achieved through a perturbative analysis of the double amplitude equations. Typically, CC2 is paired with either the resolution-of-the-identity (RI) approximation29 or Cholesky-decomposition (CD)30 of the electron repulsion integrals, thereby enabling its application to even larger molecules. Although CC2 has been extensively applied in the study of excited states,23,27,29–35 its application to multi-configurational wave functions is scarce.
Recently, some of us introduced a spin–flip (SF) variant36 of the CC2 method. In SF approaches,37–39 multi-configurational lower-spin states are obtained by spin–flipping excitations using a single-determinant high-spin state as reference. The advantage of the SF approach lies in its capability to provide a balanced treatment of all relevant spin states, capturing both dynamical and non-dynamical correlation within a single computational step. Besides the original excitation energy (EE)-CC2 method and its SF-CC2 variant, further CC2 methods are also available. These include the ionization potential40–42 (IP) and the electron attachment42–44 (EA) variants, where the number of electrons in the target state is decreased or increased by one compared to that of the reference wave function. These EE, SF, IP, and EA variants36,44 of the CC2 method are available in the Q-Chem software45 for restricted (RHF), unrestricted (UHF), and restricted open-shell (ROHF) reference wave functions, providing access to a wide range of electronic structure patterns.
Alternatively, quantum embedding theories28,46–49 afford a reduction in computational effort by exploiting the locality of the chemical phenomenon under study. These theories combine different levels of quantum chemical calculations, a more accurate high-level treatment for the active region and a more approximate low-level one for the environment. Among these approaches, projection-based embedding28,48,50,51 has emerged as a popular choice for studying both ground and excited states52 in isolated molecules as well as periodic systems.53 In projection-based embedding, the electron density of the high-level fragment is optimized in the presence of an external embedding potential, built from the electron density of the low-level region. This embedding scheme enforces orthogonality between fragment orbitals via a projection technique, removing the need for non-additive kinetic energy potentials. By keeping the electron density of the environment frozen, the approach assumes that the chemical phenomenon of interest is localized in a restricted region, which is often the case for transition-metal complexes whose unpaired electrons are localized on the metal center.9 Recently, projection-based embedded EOM-CCSD has been shown to describe very well ionization and valence excitations in small organic molecules microsolvated by water.54 Similarly, other embedding schemes have emerged, employing the pair coupled-cluster doubles (pCCD) ansatz55,56 as high-level method for addressing excited states in large molecules.57 To treat relativistic effects in heavier elements, methods based on four-component Hamiltonians, have also been proposed.58 Moreover, projection-based embedding has been extended to describe open-shell electronic states of transition-metal compounds,59 but its applications are still somewhat limited. This method is available in the Q-Chem software within an unrestricted formalism, which closely follows the original formulation presented in ref. 59. One advantage of this projection-based embedding is its seamless integration into the EOM-CC framework. Computing the respective electronic states entails no further coding or development work, provided that the high-level fragment's orbitals are re-optimized in a self-consistent manner in the presence of the external embedding potential. Consequently, most functionalities inherent to EOM-CC are also readily accessible for embedded EOM-CC. This includes spin-state analysis, as well as the calculation and analysis of the spin properties using reduced quantities, i.e., the one-particle density matrix and corresponding natural orbitals (NO).60–67
To evaluate the performance of CC2 and EOM-CCSD-in-DFT, we compute state energies and spin-related properties of a set of transition-metal complexes, exhibiting various electron configurations, specifically, d5, d6, and d7. Our test set comprises: (i) two iron aqua complexes, [Fe(H2O)6]3+ and [Fe(H2O)6]2+, (II) a single-center cobalt-based SMM, Co(C(SiMe2ONaph)3)2,15 and (iii) its simplified model, Co(C(SiH3)3)2. The [Fe(H2O)6]2+ and [Fe(H2O)6]3+ complexes are commonly used as benchmarks for investigating spin-state splittings in transition-metal complexes and oxide materials;68–70 however, this is the first study reporting SOCs. On the other hand, the Co(C(SiMe2ONaph)3)2 SMM poses great computational challenges due to its unconventional non-aufbau filling of the d orbitals15 and large number of electrons (681). In addition to state energies and SOCs, we derive spin–orbit splittings, magnetizations, and susceptibilities using the protocol implemented in the ezMagnet software. The performance of CC2 and EOM-CCSD-in-DFT is assessed through a comparison with results from EOM-CCSD calculations and experiments.15 In addition to CC2 and EOM-CCSD-in-DFT, we also consider the combination of the SF approach with time-dependent DFT (SF-TD-DFT),71,72 which has proven to be an efficient yet reliable alternative to EOM-CCSD for transition-metal molecular magnets.18,25,26,73 This work also marks the first application of EOM-CC methods to non-aufbau electron configurations of 3d transition-metal compounds. Furthermore, it provides guidelines for determining where one variant (EE, SF, EA, or IP) of CC2 or EOM-CCSD-in-DFT is more suitable than another, and serves as inspiration for further implementation efforts aimed at improving the generality and efficiency of these methods.
II. Theoretical and computational details
A. Molecular structures
The structural models of the systems under study are depicted in Fig. 1. [Fe(H2O)6]2+ and [Fe(H2O)6]3+ are sufficiently small to be treated as a whole by EOM-CCSD. These compounds exhibit Th point group symmetry, which is commonly handled through its Abelian subgroup D2h. For [Fe(H2O)6]2+, the degeneracy of two eg orbitals (ag in D2h) results in an electronically excited doubly-degenerate 5Eg state, which corresponds to two degenerate 5Ag states in D2h. There exists no subgroup of Th where Eg can split into two distinct irreducible representations (irreps). Therefore, the two degenerate states belong to the same irrep, rendering them indistinguishable in an EOM-CCSD calculation based on real algebra and the D2h point group symmetry. Using complex algebra and the Th point group, there would be no problem as the two Eg states then had different complex-valued characters. However, here we adopted a slightly distorted structure for [Fe(H2O)6]2+ to overcome these issues, following the strategy outlined in ref. 74. This structure is optimized with ωB97X-D/cc-pVDZ, whereas for [Fe(H2O)6]3+, we exploited symmetry and used its Th geometry, optimized with ωB97X-D/cc-pVDZ.The calculation of spin states and properties of Co(C(SiMe2ONaph)3)2 was computationally feasible only using EOM-CCSD-in-DFT. The structure of Co(C(SiMe2ONaph)3)2 was taken from ref. 15 (C1 point group symmetry). We also considered a model system, i.e., Co(C(SiH3)3)2, representing Co(C(SiMe2ONaph)3)2, which is derived from the original complex by replacing methyl and naphthyl groups in the ligands with hydrogen atoms. Co(C(SiH3)3)2 has D3d symmetry; however, our calculations were carried out in the C2h point group. The molecular structure of Co(C(SiH3)3)2 was optimized with ωB97X-D/cc-pVDZ. By making use of symmetry, both EOM-CCSD and CC2 calculations for Co(C(SiH3)3)2 were feasible. All relevant Cartesian coordinates are given in the ESI.†
B. Electronic structures
Fig. 2 summarizes the electronic structure of the Fe and Co complexes and illustrates which variants of the EOM-CCSD, CC2, and EOM-CCSD-in-DFT methods are used to access the target states. Note, however, that the electronic structure of the iron complexes is simplified in Fig. 2 as there are actually two eg shells that result from bonding and antibonding interaction of the metal d-orbitals with the ligand orbitals. Additionally, for the Co(II)-SMM, Table 1 presents the electron configurations of its states. To facilitate the discussion, a numerical labeling is used for all states. However, for the Fe(II) and Fe(III) complexes, Fig. 2 provides term symbols for Th symmetry and its subgroup D2h as well. For the linear and twofold-coordinated Co(II) molecular magnet, we also included term symbols for the D3d and C2h point groups. Moreover, in ref. 15, NEVPT2 states of the Co(II)-SMM were classified using the C∞v point group notation. Therefore, to facilitate comparison with these NEVPT2 results, term symbols for C∞v symmetry are also included in Table 1.| State | Term (C∞v) | Configuration | 〈Lz〉 |
|---|---|---|---|
| |Ref1〉 | 4Σ− | (dxy, dx2−y2)4 (dxz, dyz)2 (dz2)1 | |
| |1〉, |2〉 | 4Φ | (dxy, dx2−y2)3 (dxz, dyz)3 (dz2)1 | 〈1|Lz|2〉 = 2.98i |
| |3〉, |4〉 | 4Δ | (dxy, dx2−y2)3 (dxz, dyz)2 (dz2)2 | 〈3|Lz|4〉 = 1.99i |
| |Ref2〉 | 4Σ− | (dxy, dx2−y2)2 (dxz, dyz)4 (dz2)1 | |
| |1〉, |2〉 | 4Φ | (dxy, dx2−y2)3 (dxz, dyz)3 (dz2)1 | 〈1|Lz|2〉 = 2.98i |
| |3′〉, |4′〉 | 4Π | (dxy, dx2−y2)3 (dxz, dyz)3 (dz2)1 | 〈3′|Lz|4′〉 = 1.00i |
| |5′〉, |6′〉 | 4Π | (dxy, dx2−y2)2 (dxz, dyz)3 (dz2)2 | 〈5′|Lz|6′〉 = 0.99i |
For [Fe(H2O)6]2+ and [Fe(H2O)6]3+, we computed the excitation energy between the ground state and the first electronically excited state at the equilibrium structure of the [Fe(H2O)6]3+ high-spin sextet ground state. The ground state of [Fe(H2O)6]2+ is a triply-degenerate quintet state (the states |1〉, |2〉, and |3〉 in Fig. 2), with a low-lying doubly-degenerate quintet excited state (states |4〉 and |5〉). [Fe(H2O)6]3+ has a spatially non-degenerate ground state (the state |1〉) and a triply-degenerate quartet excited state (states |2〉, |3〉, and |4〉). To treat the quintet d6 target states of [Fe(H2O)6]2+, we used the EA variant of the CC methods with a d5 high-spin sextet reference. On the contrary, for the sextet and quartet d5 states of [Fe(H2O)6]3+, we used the SF approach with the same d5 high-spin sextet reference. For the Co(II)-SMM, we computed four doubly-degenerate quartet states: states |1〉 and |2〉, states |3〉 and |4〉, states |3′〉 and |4′〉, and states |5′〉 and |6′〉. These states are treated using the EE approach, in which a β-electron is excited from the fully occupied and degenerate d-orbital shells, either (dxy, dx2−y2)4 or (dxz, dyz)4, of the reference states, |Ref1〉 and |Ref2〉 in Fig. 2, respectively.
C. Details of the electronic-structure calculations
Fig. 1 shows the partitioning scheme adopted in all embedded EOM-CCSD calculations. The [Fe(H2O)6]2+ and [Fe(H2O)6]3+ complexes have 84 and 83 electrons, respectively. Within our partitioning, the electrons associated with the metal center, 24 for [Fe(H2O)6]2+ and 23 for [Fe(H2O)6]3+, constitute the high-level EOM-CCSD fragment (orange in Fig. 1), while the remaining 60 electrons of the water molecules form the low-level DFT fragment (blue in Fig. 1). For Co(C(SiMe2ONaph)3)2, this partitioning is even more accentuated with only 25 electrons ascribed to the high-level EOM-CCSD fragment (magenta in Fig. 1) and 656 to the low-level DFT fragment (blue in Fig. 1). Fig. S1 (ESI†) illustrates the spin difference density computed using the α and β charge densities. The excess spin density is localized on the metal center, supporting the partitioning we chose. A similar partitioning scheme was previously employed in a CCSD-in-DFT study exploring the dissociation curve of hexaaquairon(II) cations.59 Additionally, to be able to perform embedded EOM-CCSD calculations on the large Co(II)-SMM, it was critical to truncate the virtual orbital space. This was done using concentric localization.75 On the other hand, for the smaller systems, [Fe(H2O)6]2+, [Fe(H2O)6]3+, and Co(C(SiH3)3)2, EOM-CCSD-in-DFT calculations were also feasible without truncation of the virtual space.Moreover, in the case of [Fe(H2O)6]2+ and [Fe(H2O)6]3+, we investigated the dependence on the density functional in EOM-CCSD-in-DFT calculations, as well as for the SF-TD-DFT calculations, using the hybrid functionals PBE0,76 B3LYP,77 and B5050LYP,71 along with CAM-B3LYP,78ωB97X-D,79 and LRC-ωPBEh80 as range-separated hybrid functionals. Following previous SF studies of SMMs,26,73 we employed the non-collinear formulation of SF-TD-DFT72,81 to calculate spin states and spin-related properties. For Co(C(SiH3)3)2 and Co(C(SiMe2ONaph)3)2, we used LRC-ωPBEh as low-level method. However, replacing LRC-ωPBEh by CAM-B3LYP for Co(C(SiH3)3)2 does not affect the spin-state ordering (see Table S8, ESI†). The differences observed between EOM-CCSD-in-LRC-ωPBEh and EOM-CCSD-in-CAM-B3LYP results are less than 500 cm−1 for state energies and within 50 cm−1 for the SOCs.
In our CC2 implementation, all CC2 variants36,44 can be combined with either the resolution-of-the-identity (RI) approximation29 or Cholesky decomposition (CD)30 of the electron repulsion integrals. For the Fe(II) and Fe(III) complexes, we carried out RI-EA-CC2 and RI-SF-CC2 calculations, respectively, while we employed CD-EE-CC2 for the Co(II)-SMM. Table S3 (ESI†) shows that using either the RI or CD approximation has a negligible impact on the excitation energies of the Fe(II) and Fe(III) compounds. In addition, RI-EA-CC2 calculations for Fe(II) were performed using the spin-component-scaled (SCS) analogue.82 This spin-scaled version of CC2 has exhibited superior performance to standard CC2 in computing vertical ionization potentials and electron affinities when benchmarked against EOM-CCSD and CCSD(T).42,44 Our present work represents the first application of spin-scaled CC2 to open-shell systems.
In all calculations, the cc-pVTZ basis set83–85 was employed unless for the SOC calculations of the actual Co(II)-SMM where we used the 6-31G* basis set. The corresponding auxiliary basis set86 was used for the RI-CC2 calculations, while we used a threshold of 10−3 for the Cholesky decomposition. The core electrons were frozen in all calculations. Open-shell reference states were computed using unrestricted Hartree–Fock (UHF). However, the level of spin contamination in the reference and target states is minimal: the corresponding 〈S2〉 values are between 6.00 and 6.19 for the quintet states of Fe(II), between 8.75 and 8.20 for the sextet states of Fe(III), between 3.77 and 3.82 for the quartet states of Fe(III), and between 3.75 and 3.92 for the quartet states of Co(II) (Tables S1, S2 and S4 in the ESI†). All electronic-structure and spin–property calculations were carried out using the Q-Chem program package, version 6.0.45
D Wave function analysis and magnetic properties
To characterize the nature of the electronic states of the Fe and Co complexes, we employed density-based analysis using natural orbitals (NOs) and natural-transition orbitals (NTOs), i.e., eigenvectors of the one-particle state- and transition-density matrices, respectively, along with their corresponding eigenvalues.60–66 For the state analysis, these eigenvalues can be interpreted as the occupation numbers of each NO. On the other hand, when analyzing NTOs, the eigenvalues of the transition density matrix are the weights of each NTO hole–particle pair describing the electronic excitation between the states. This type of analysis has been extensively applied in a set of transition-metal complexes including Fe(III), Fe(II), and Ni(II) with varying numbers of unpaired electrons and diverse electronic structure patterns (d5, d6, d8), using methods such as EOM-CCSD and SF-TD-DFT.18,25,26,67 Building upon these previous works, we extended our density-based analysis to include EOM-CCSD-in-DFT and the non-aufbau ground state of the Co(II)-SMM.In addition to computing state energies, we focused on orbital angular momenta and spin–orbit coupling constants (SOCCs), which are given by the following expression:
 | (1) |
 of the spin–orbit coupled states Ψ and Ψ′. The SOCs entering eqn (1) are expressed as matrix elements of the Breit-Pauli spin–orbit Hamiltonian87,88 evaluated for non-relativistic EOM-CC wave functions, as implemented in the Q-Chem software by Krylov and co-workers.74,89,90 This procedure has been demonstrated to accurately treat SOC in 3d transition-metal systems.18,25,26,74 Within this implementation, transition properties are computed as contraction of the corresponding integrals with reduced transition density matrices, therefore their calculation is general and can be interfaced with any method providing density matrices, e.g., EOM-CCSD, SF-TD-DFT, and EOM-CCSD-in-DFT.74,89,90 To evaluate the reliability of EOM-CCSD-in-DFT for spin properties, we computed SOCCs for [Fe(H2O)6]2+ and [Fe(H2O)6]3+, for which full EOM-CCSD calculations on the whole systems are viable as references. In the case of [Fe(H2O)6]2+, we computed the SOCC between the three degenerate states |1〉, |2〉, and |3〉. For [Fe(H2O)6]3+, we computed the SOCC between the ground state (state |1〉) and the triply-degenerate excited state (states |2〉, |3〉, and |4〉). In addition, we evaluated the SOCC for the doubly-degenerate ground state of Co(C(SiH3)3)2 (states |1〉 and |2〉) using both EOM-CCSD and EOM-CCSD-in-DFT. On the contrary, in the case of Co(C(SiMe2ONaph)3)2, SOCC calculations were only possible using EOM-CCSD-in-DFT with a smaller basis set, 6-31G*. However, energy calculations for Co(C(SiMe2ONaph)3)2 using EOM-CCSD-in-DFT were also performed with the cc-pVTZ basis set (see Table S10, ESI†). Using the larger cc-pVTZ basis set, the ordering of the states remains unchanged, with relative changes ranging from 200 cm−1 for the low-lying excited states to up to 1000 cm−1 for the highest excited states |5′〉 and |6′〉.
of the spin–orbit coupled states Ψ and Ψ′. The SOCs entering eqn (1) are expressed as matrix elements of the Breit-Pauli spin–orbit Hamiltonian87,88 evaluated for non-relativistic EOM-CC wave functions, as implemented in the Q-Chem software by Krylov and co-workers.74,89,90 This procedure has been demonstrated to accurately treat SOC in 3d transition-metal systems.18,25,26,74 Within this implementation, transition properties are computed as contraction of the corresponding integrals with reduced transition density matrices, therefore their calculation is general and can be interfaced with any method providing density matrices, e.g., EOM-CCSD, SF-TD-DFT, and EOM-CCSD-in-DFT.74,89,90 To evaluate the reliability of EOM-CCSD-in-DFT for spin properties, we computed SOCCs for [Fe(H2O)6]2+ and [Fe(H2O)6]3+, for which full EOM-CCSD calculations on the whole systems are viable as references. In the case of [Fe(H2O)6]2+, we computed the SOCC between the three degenerate states |1〉, |2〉, and |3〉. For [Fe(H2O)6]3+, we computed the SOCC between the ground state (state |1〉) and the triply-degenerate excited state (states |2〉, |3〉, and |4〉). In addition, we evaluated the SOCC for the doubly-degenerate ground state of Co(C(SiH3)3)2 (states |1〉 and |2〉) using both EOM-CCSD and EOM-CCSD-in-DFT. On the contrary, in the case of Co(C(SiMe2ONaph)3)2, SOCC calculations were only possible using EOM-CCSD-in-DFT with a smaller basis set, 6-31G*. However, energy calculations for Co(C(SiMe2ONaph)3)2 using EOM-CCSD-in-DFT were also performed with the cc-pVTZ basis set (see Table S10, ESI†). Using the larger cc-pVTZ basis set, the ordering of the states remains unchanged, with relative changes ranging from 200 cm−1 for the low-lying excited states to up to 1000 cm−1 for the highest excited states |5′〉 and |6′〉.
Furthermore, using the ezMagnet software,25 we computed magnetic properties of the Co(II)-SMM, i.e., the spin-reversal energy barrier, magnetization, and susceptibility, allowing for the direct comparison with the experiment. Magnetic properties arise from spin–orbit and Zeeman interactions. To account for these effects, we employed a two-step state-interaction scheme:91–93 first we computed EOM-CCSD or EOM-CCSD-in-DFT states and then used these states to evaluate matrix elements of the spin–orbit (ĤSO) and Zeeman (ĤZ) operators. Magnetic sublevels are then obtained by diagonalizing the perturbed Hamiltonian, i.e., Ĥ = Ĥ0 + ĤSO + ĤZ, where Ĥ0 is the Born–Oppenheimer Hamiltonian in the basis of EOM-CC states. Subsequently, by applying Boltzmann statistics, the magnetization and susceptibility are obtained from the resulting partition function. Following this protocol, we computed the spin–orbit levels of the Co(II)-SMM by accounting for the SOC between states |1〉 and |2〉. Due to SOC, the doubly-degenerate ground state (states |1〉 and |2〉) of the Co(II)-SMM splits into four Kramers doublets,15 as shown in Fig. 3. This, in turn, allowed us to quantify the spin-reversal barrier as the energy separation between the ground MJ = ±9/2 state and the first excited MJ = ±7/2 state, where MJ is the projection of J along the magnetic axis. This strategy has been already employed in a number of studies15,94 assuming that magnetic relaxation occurs by a combination of the Orbach mechanism95,96 and quantum tunnelling from the first excited state.
 | ||
| Fig. 3 Spin–orbit splitting of the J = 9/2 ground state (states |1〉 and |2〉) of Co(C(SiH3)3)2 and Co(C(SiMe2ONaph)3)2. The energy barrier for spin-inversion is shown in red. | ||
III. Results and discussion
A. Fe(II) and Fe(III) complexes
Fig. 4 and 5 depict excitation energies (left panels) of [Fe(H2O)6]2+ and [Fe(H2O)6]3+, respectively, computed using EOM-CCSD, CC2, and EOM-CCSD-in-DFT. The right panels show absolute errors of CC2 and EOM-CCSD-in-DFT as compared to EOM-CCSD. For [Fe(H2O)6]2+, the SCS-RI-EA-CC2 excitation energy closely agrees with the EOM-EA-CCSD value, with an error of less than 0.05 eV. Furthermore, EOM-EA-CCSD-in-DFT performs relatively well, with errors within 0.1 eV, only when the PBE-based functionals, PBE0 and LRC-ωPBEh, are employed as low-level methods. On the contrary, the absolute error increases to 0.4 eV for B3LYP, B5050LYP, and CAM-B3LYP, and to 0.5 eV for ωB97X-D. For [Fe(H2O)6]3+, RI-SF-CC2 outperforms again EOM-SF-CCSD-in-DFT in computing excitation energies. Both EOM-SF-CCSD-in-DFT and SF-TD-DFT, regardless of the selected density functional, exhibit poor performance compared to EOM-SF-CCSD, with errors as large as 1 eV. Interestingly, while EOM-SF-CCSD-in-DFT tends to overestimate the excitation energy, SF-TD-DFT underestimates it, both by a similar magnitude, on average +0.9 eV for EOM-SF-CCSD-in-DFT and −0.7 eV for SF-TD-DFT. In all SF calculations, only the MS = 3/2 state (state |1〉) is used to compute excitation energies and SOCCs, with the high-spin state (MS = 5/2) serving solely as reference.18,37,39,97 However, while the energy difference between the reference state and state |1〉 of [Fe(H2O)6]3+ is 0.05 eV for EOM-CCSD, this difference further deviates from zero for more approximate methods, ranging from 0.1 eV for SF-CC2 to 0.2 eV for SF-TD-DFT, and up to 1 eV for EOM-CCSD-in-DFT. As this difference vanishes in the full CC limit, these numbers illustrate the decreasing quality of the SF target states.For correlated many-body theories, NOs and NTOs provide valuable insights into the nature of the wave functions and electron excitations, facilitating the interpretation of the computed properties based on the orbitals involved. In the case of [Fe(H2O)6]2+, transitions between the spin states under study involve a single NTO pair consisting of d-like orbitals, indicating the single-determinantal character of the corresponding electronic states. Fig. 6 illustrates the EOM-CCSD-in-DFT NTOs describing the transitions between the triply-degenerate ground state (|1〉, |2〉, and |3〉) and the doubly-degenerate excited state (|4〉 and |5〉) of [Fe(H2O)6]2+. Specifically, transitions between states |1〉 and |4〉 and between states |1〉 and |5〉 correspond to transitions from dyz to dz2 and from dyz to dx2−y2, respectively. Additional NTO pairs for the remaining electronic transitions in [Fe(H2O)6]2+ can be found in Fig. S2 (ESI†). However, for the excitation between the ground state (|1〉) and the excited state (|2〉, |3〉 and |4〉) of [Fe(H2O)6]3+, the squared norm of the one-particle transition density matrix, which is considered a measure of one-electron excitation character,62,98,99 is significantly smaller than one (about 0.4), indicative of a substantial two-electron character. As a result, for [Fe(H2O)6]3+, our analysis of states and excitations in terms of NOs and NTOs becomes less meaningful100 and is not reported herein.
We also calculate SOCCs using EOM-CCSD, EOM-CCSD-in-DFT, and SF-TD-DFT eigenstates, see eqn (1). Fig. 7 illustrates the results. For [Fe(H2O)6]3+, given the two-electron character of the transition between the state |1〉 and states |2〉, |3〉 and |4〉, and also considering the mean-field treatment of the SOCs in terms of one-particle transition density matrices only,74 the absolute magnitude of the corresponding SOCCs should be considered with caution. However, in this case, the spin-flipping excitation between the reference wave function and states |2〉, |3〉 and |4〉 is a one-electron process with SOCC = 817 cm−1, which deviates only by 20 cm−1 from the SOCC between the state |1〉 and states |2〉, |3〉, and |4〉.
In the case of SOCCs, EOM-CCSD-in-DFT is less sensitive to the choice of the low-level DFT method compared to what we observed for energies. EOM-CCSD-in-DFT underestimates the SOCC of [Fe(H2O)6]2+, while it overestimates the SOCC of [Fe(H2O)6]3+, both by a similar magnitude, on average by about 50 cm−1 compared to EOM-CCSD. For [Fe(H2O)6]3+, SF-TD-DFT performs relatively poorly with errors three times as large as those of EOM-SF-CCSD-in-DFT. Similar to what we reported for energies, SOCCs computed with EOM-CCSD-in-DFT and SF-TD-DFT follow opposite trends: EOM-CCSD-in-DFT overestimates the SOCC, whereas SF-TD-DFT underestimates it when compared to EOM-SF-CCSD.
For both [Fe(H2O)6]2+ and [Fe(H2O)6]3+, we also explore the effect of truncating the virtual orbital space on the performance of EOM-CCSD-in-DFT. Table 2 presents the results for EOM-CCSD-in-LRC-ωPBEh. We observe that the excitation energies of [Fe(H2O)6]2+, computed with EOM-EA-CCSD-in-DFT, where an additional electron is attached to one of the virtual orbitals, are more sensitive to truncation of the virtual orbital space compared to those of [Fe(H2O)6]3+ computed using SF excitation operators. For [Fe(H2O)6]2+, concentric localization leads to a difference of 0.16 eV in the excitation energy. In contrast, for [Fe(H2O)6]3+, the difference between truncated and non-truncated excitation energies is 2 meV only. Furthermore, the impact of truncating the virtual orbital space on the SOCCs is much smaller compared to what we observed for the energies, with only a 10 cm−1 difference for [Fe(H2O)6]2+.
| [Fe(H2O)6]2+ | ||||
|---|---|---|---|---|
| EOM-EA-CCSD | SCS-RI-EA-CC2 | EOM-EA-CCSD-in-LRC-ωPBEh | ||
| Truncated | Full | |||
| ΔE | 1.35 | 1.32 | 1.57 | 1.41 |
| SOCC | 282 | 252 | 242 | |
| [Fe(H2O)6]3+ | ||||
|---|---|---|---|---|
| EOM-SF-CCSD | RI-SF-CC2 | EOM-SF-CCSD-in-LRC-ωPBEh | ||
| Truncated | Full | |||
| ΔE | 2.52 | 2.48 | 3.37 | 3.38 |
| SOCC | 839 | 890 | 890 | |
Experimental excitation energies are available for [Fe(H2O)6]2+ and [Fe(H2O)6]3+ in aqueous solution: these are 1.1469,101 and 1.56102 eV, respectively. The value of 1.14 eV was obtained by averaging over the energies of the two observed optical transitions at 0.99 and 1.29 eV that result from a Jahn–Teller splitting.69,101 These experimental data have been frequently used as a reference for evaluating the performance of explicit or implicit solvent models.68–70 From these experimental values, our EOM-CCSD excitation energies deviate by 0.21 eV for [Fe(H2O)6]2+ and 0.96 eV for [Fe(H2O)6]3+. However, solvation effects, which are not considered in the present work, are expected to contribute up to 0.5 eV to the excitation energies.68 Furthermore, Reimann and Kaupp70 have recently shown that the observed lowest-energy excitation of [Fe(H2O)6]3+ at 1.56 eV must be attributed to the deprotonated [Fe(H2O)5 OH]2+, rather than to the iron(III) hexaaqua complex in solution. Also, CASPT2 excitation energies69 of 1.02 and 2.39 eV were recently reported for isolated [Fe(H2O)6]2+ and [Fe(H2O)6]3+, which deviate from our EOM-CCSD results by 0.13 eV and 0.33 eV, respectively.
Our findings indicate that CC2 yields better excitation energies than EOM-CCSD-in-DFT. On the other hand, EOM-CCSD-in-DFT, independent of the chosen density functional, yields relatively accurate SOCCs. For the energies of [Fe(H2O)6]2+, EOM-EA-CCSD-in-PBE0 and EOM-EA-CCSD-in-LRC-ωPBEh afford the best agreement with EOM-EA-CCSD, while for the spin–flip methods both EOM-SF-CCSD-in-DFT and SF-TD-DFT show poor performance and no significant dependence on the density functional. Based on these results, we employ the long-range corrected hybrid functional LRC-ωPBEh as low-level method to describe a single-center Co(II)-SMM with EOM-CCSD-in-DFT. Recently, EOM-EE-CCSD-in-DFT calculations of excited states of small organic molecules microsolvated by water also showed that long-range corrected hybrid functionals, specifically CAM-B3LYP, consistently yield smaller errors compared to GGA or hybrid-GGA functionals,54 further supporting our chosen computational settings for the cobalt molecular magnet.
B. Co(II) single-molecule magnet
For the Co(C(SiMe2ONaph)3)2 molecular magnet, NEVPT2 calculations15 revealed that electron configurations following the aufbau principle, such as (dxy, dx2−y2)4 (dxz, dyz)2 (dz2)1, are less favourable than non-aufbau configurations, i.e., (dxy, dx2−y2)3 (dxz, dyz)3 (dz2)1, the latter minimizing electron–electron repulsion. The interplay between a weak ligand field and inter-electronic repulsion results in a non-aufbau ground state of maximum orbital angular momentum (L = 3) and large spin-reversal energy barrier. Table 3 and Fig. 8 report the energies of the six spin states under study for Co(C(SiH3)3)2 and Co(C(SiMe2ONaph)3)2. All computational methods employed, i.e., EOM-CCSD, CC2, and EOM-CCSD-in-DFT, consistently yield a doubly-degenerate ground state (|1〉 and |2〉) characterized by four main non-aufbau configurations as shown in Fig. 2, which is in agreement with NEVPT2 findings.15 According to our NO analysis, the two β electrons residing in the d orbitals occupy exclusively the four dxy, dx2−y2, dxz, and dyz NOs, each with an occupation number of 0.5 (see Table S5, ESI†). Four NTO pairs contribute to the SOC between states |1〉 and |2〉. These four leading contributions involve a change in orbital orientation from dxy to dx2−y2, as well as from dxz to dyz, as illustrated in Fig. 9 for Co(C(SiH3)3)2 and Fig. S4 (ESI†) for Co(C(SiMe2ONaph)3)2.| Co(C(SiH3)3)2 | Co(C(SiMe2ONaph)3)2 | ||||
|---|---|---|---|---|---|
| EOM-CCSDa | CD-CC2a | EOM-CCSD-in-DFTab | EOM-CCSD-in-DFTbc | ||
| Truncated | Full | Truncated | |||
| a cc-pVTZ basis set. b The density functional is LRC-ωPBEh. c 6-31G* basis set. d The SOCC was computed between states |1〉 and |2〉. | |||||
| |Ref1〉 | 3903 | 3690 | 1009 | 1128 | 4489 |
| |1〉 | 0 | 0 | 0 | 0 | 0 |
| |2〉 | 11 | 4 | 46 | 39 | 20 |
| |3〉 | 803 | 258 | 3225 | 3287 | 3556 |
| |4〉 | 803 | 261 | 3226 | 3288 | 3556 |
| |Ref2〉 | 4427 | 4964 | 2400 | 2412 | 2492 |
| |1〉 | 0 | 0 | 0 | 0 | 0 |
| |2〉 | 10 | 1 | 22 | 22 | 45 |
| |3′〉 | 1855 | 1645 | 3187 | 3184 | 2721 |
| |4′〉 | 1855 | 1657 | 3187 | 3184 | 2722 |
| |5′〉 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 609 609 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 911 911 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 406 406 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 384 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
| |6′〉 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 609 609 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 914 914 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 407 407 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384 384 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184 184 |
| 〈1|Lz|2〉 | 2.98i | 3.02i | 3.01i | 2.99i | |
| SOCCd | 1126 | 1114 | 1107 | 1059 | |
| U | 504 | 497 | 495 | 469 | |
Due to a weak ligand field, the five lowest states of Co(C(SiH3)3)2 are confined to a narrow energy range of only 5000 cm−1, while the sixth state is higher in energy at 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. Both EOM-CCSD and CC2 yield the same ordering of the energies, with a deviation of CC2 from EOM-CCSD energies of at most 200 cm−1 for the low-lying states. However, this deviation increases to 700 cm−1 for the fifth and the sixth state. State |Ref1〉 is more stable than state |Ref2〉 by 500 cm−1 with EOM-CCSD and by 1300 cm−1 with CC2. When using EOM-CCSD-in-DFT, |Ref1〉 is again found to be more stable than |Ref2〉, by a similar magnitude. However, by employing EOM-CCSD-in-DFT, |Ref1〉 and |Ref2〉 become more stable than the two doubly-degenerate states |3〉/|4〉 and |3′〉/|4′〉, with the latter two states being almost degenerate. Additionally, states |5′〉 and |6′〉 are higher by 4000 cm−1 when computed with EOM-CCSD-in-DFT compared to EOM-CCSD and CC2. For the actual Co(C(SiMe2ONaph)3)2 molecular magnet, |Ref2〉 is more stable than |Ref1〉 by 2000 cm−1, contrary to what we observe for the model system Co(C(SiH3)3)2. Furthermore, the states |3〉/|4〉 and |3′〉/|4′〉 are flipped in energy with respect to Co(C(SiH3)3)2. Overall, the ground and first excited states are separated by 2500 cm−1 for the actual SMM, whereas the energy gap is much smaller for the model system, namely 800 cm−1 and 250 cm−1 with EOM-CCSD and CC2, respectively. Yet, in the case of the actual Co(II)-SMM, where CC2 and EOM-CCSD calculations are not feasible, EOM-CCSD-in-DFT and NEVPT2 agree about the energetic ordering of all states (see Table S11, ESI†).
000 cm−1. Both EOM-CCSD and CC2 yield the same ordering of the energies, with a deviation of CC2 from EOM-CCSD energies of at most 200 cm−1 for the low-lying states. However, this deviation increases to 700 cm−1 for the fifth and the sixth state. State |Ref1〉 is more stable than state |Ref2〉 by 500 cm−1 with EOM-CCSD and by 1300 cm−1 with CC2. When using EOM-CCSD-in-DFT, |Ref1〉 is again found to be more stable than |Ref2〉, by a similar magnitude. However, by employing EOM-CCSD-in-DFT, |Ref1〉 and |Ref2〉 become more stable than the two doubly-degenerate states |3〉/|4〉 and |3′〉/|4′〉, with the latter two states being almost degenerate. Additionally, states |5′〉 and |6′〉 are higher by 4000 cm−1 when computed with EOM-CCSD-in-DFT compared to EOM-CCSD and CC2. For the actual Co(C(SiMe2ONaph)3)2 molecular magnet, |Ref2〉 is more stable than |Ref1〉 by 2000 cm−1, contrary to what we observe for the model system Co(C(SiH3)3)2. Furthermore, the states |3〉/|4〉 and |3′〉/|4′〉 are flipped in energy with respect to Co(C(SiH3)3)2. Overall, the ground and first excited states are separated by 2500 cm−1 for the actual SMM, whereas the energy gap is much smaller for the model system, namely 800 cm−1 and 250 cm−1 with EOM-CCSD and CC2, respectively. Yet, in the case of the actual Co(II)-SMM, where CC2 and EOM-CCSD calculations are not feasible, EOM-CCSD-in-DFT and NEVPT2 agree about the energetic ordering of all states (see Table S11, ESI†).
With EOM-CCSD, we compute an orbital angular momentum of 〈Lz〉 ≈ 3i and a large SOCC of 1126 cm−1 between states |1〉 and |2〉. This is in agreement with the El-Sayed rule103 that predicts large SOCs between states with different orbital orientation, i.e., from dxy to dx2−y2, as well as from dxz to dyz (Fig. 9). Due to the SOC between states |1〉 and |2〉, the ground state splits into eight pairwise degenerate levels (Fig. 3). The corresponding energies are reported in Table S12 (ESI†). Using these levels, we computed an energy separation of 504 cm−1 between the ground and first-excited states, which is an estimate for the spin-reversal energy barrier.15,94 The agreement between EOM-CCSD and EOM-CCSD-in-DFT is very good with a deviation of 20 cm−1 for both the SOCC and spin–orbit splitting.
For Co(C(SiH3)3), truncation of the virtual orbital space only has a minor impact on the EOM-CCSD-in-DFT results. The energy differences are less than 100 cm−1 and the impact on the orbital angular momentum, SOCC, and spin-reversal barrier is negligible.
For Co(C(SiMe2ONaph)3)2, we computed an SOCC of 1059 cm−1, corresponding to an energy splitting between the ground and first excited state of 469 cm−1, which agrees very well with the value extracted from an FIR experiment15 (450 cm−1) and a value of 476 cm−1 from NEVPT2 calculations15 (see Table S12, ESI†). The differences in the computed SOCC and energy barrier between Co(C(SiH3)3)2 and Co(C(SiMe2ONaph)3)2 amount to only 50 cm−1. These results underscore that extending the electron correlation treatment from the Co2+ ion only in EOM-CCSD-in-DFT calculations to the entire complex with EOM-CCSD, or improving the structural model by incorporating naphthyl groups, does not alter the calculated properties associated with the SOC, as SOC is a local property.
Furthermore, using the magnetic sublevels of Co(C(SiH3)3)2 and Co(C(SiMe2ONaph)3)2, we computed temperature- and field-dependent susceptibilities (χT vs. T) and magnetizations (M vs. H/T). The results are illustrated in Fig. 10. The averaged data (“av”) reproduce the magnetic behavior of a powder sample and are determined through numerical integration, following the procedure presented in ref. 25. Our calculated curves exhibit excellent agreement with experiment15 and are nearly independent of the complex (Co(C(SiH3)3)2 or Co(C(SiMe2ONaph)3)2) and level of electron correlation (EOM-CCSD or EOM-CCSD-in-DFT). From the experiment at 300 K, the product of χT is 4.89 cm3 K mol−1, closely matching the computed χavT of 4.80 cm3 K mol−1. These values are much higher than the spin-only value of 1.876 cm3 K mol−1 for an isotropic S = 3/2 ion, suggesting a large contribution of L to the magnetic behavior of the SMM. The agreement between theory and experiment is less good in the low-temperature regime; however, both curves show a significant deviation from the Curie law, that can again be interpreted as a consequence of the large orbital angular momentum. At 12 K and 7 T, we computed a saturation value of the magnetization of 3.01 μB, also in agreement with the experimental value of 3.00 μB. Furthermore, we did not observe a separation of the isofield magnetization curves (at 1, 4, and 7 T), which also confirms experimental observations. Overall, the calculated magnetization and susceptibility data are consistent with the magnetic behavior of a system with S = 3/2 and a sizeable contribution of the orbital angular momentum L = 3.
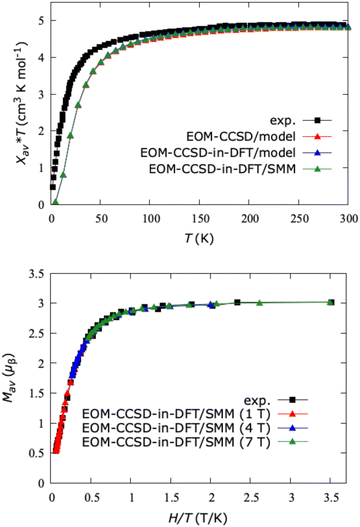 | ||
| Fig. 10 Top: Calculated susceptibility curves of the model system Co(C(SiH3)3)2 and actual SMM Co(C(SiMe2ONaph)3)2 between 5 and 300 K under an applied field of 7 T. Bottom: Calculated magnetizations for Co(C(SiMe2ONaph)3)2 at temperatures from 2 to 15 K under magnetic fields of 1, 4, and 7 T. “av” stands for isotropic powder averaging. Experimental data for Co(C(SiMe2ONaph)3)2 were taken from ref. 15. The density functional is LRC-ωPBEh. | ||
IV. Conclusions
In this work, we assessed the performance of CC2 and EOM-CCSD-in-DFT for open-shell transition-metal complexes. Our test set included the [Fe(H2O)6]2+ and [Fe(H2O)6]3+ complexes, which were treated with the SF and EA variants of the CC methods. We also considered a Co(II) single-molecule magnet, Co(C(SiMe2ONaph)3)2, and its simplified model system, Co(C(SiH3)3)2, for which we employed the EE variants of the methods. Our results show that CC2 outperforms EOM-CCSD-in-DFT for excitation energies. Also, we observe a substantial dependence of embedded EOM-CCSD energies on the density functional. Furthermore, truncating the virtual orbital space has only minimal impact on the energies of embedded EOM-SF-CCSD and EOM-EE-CCSD states, but a more pronounced effect on EOM-EA-CCSD energies. However, our results indicate that SOCCs, spin-reversal energy barriers, and macroscopic magnetic properties are insensitive to the choice of correlation scheme, EOM-CCSD or EOM-CCSD-in-DFT, and low-level DFT method, effectively reproducing experiment within spectroscopic accuracy. The adopted structural model, Co(C(SiMe2ONaph)3)2 or Co(C(SiH3)3)2, has no effect on the spin properties either. As a result, we conclude that using simpler structural models and employing an embedding potential for the interactions between the magnetic center and its environment have little effects on local properties such as the SOC.The computed spin-reversal barrier for the Co(II)-SMM ranges from 504 cm−1 for Co(C(SiH3)3)2 to 469 cm−1 for Co(C(SiMe2ONaph)3)2, representing a record value among transition-metal SMMs. This can be explained in terms of the El-Sayed rule103 and natural transition orbitals25,67 both of which predict large SOC in conjunction with a change of orbital orientation between the spin–orbit coupled states. Our calculated magnetizations and susceptibilities for Co(C(SiMe2ONaph)3)2 match experimental spectra well,15 consistently indicating a non-aufbau ground state with J = 9/2. These results do not depend on the electronic-structure method and are similar for the two cobalt complexes.
In sum, whereas embedded EOM-CCSD is less accurate than CC2 for excitation energies, our work illustrates its usefulness for spin-related properties. The embedding approach is versatile because the high-level fragment can be adapted to various properties of local character. Specifically, our results indicate that for molecular magnets whit spin density localized on the metal, ligand field effects—responsible for non-aufbau ground states and single-molecule magnetic behavior—can be adequately addressed by confining the high-level region solely to the metal ion. Additionally, different EOM-CCSD variants can be chosen for different electron configurations, which is particularly important for transition metals. Furthermore, with the integration of a periodic embedding potential, we envision that the resultant EOM-CCSD-in-DFT methods, in combination with the ezMagnet software, will find applications in the design of molecular magnetic materials, such as metal complexes adsorbed on a support or molecular self-assemblies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Marie Skłodowska-Curie Actions fellowship to M. A. (Grant Agreement No. 101062717). T.-C. J. gratefully acknowledges funding from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (Grant Agreement No. 851766) and the KU Leuven internal funds (Grant No. C14/22/083).References
- R. Poli and J. N. Harvey, Chem. Soc. Rev., 2003, 32, 1–8 RSC.
- G. Baryshnikov, B. Minaev and H. Ågren, Chem. Rev., 2017, 117, 6500–6537 CrossRef CAS PubMed.
- A. E. Rudenko, N. E. Clayman, K. L. Walker, J. K. Maclaren, P. M. Zimmerman and R. M. Waymouth, J. Am. Chem. Soc., 2018, 140, 11408–11415 CrossRef CAS PubMed.
- K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Chem. Rev., 2019, 119, 2453–2523 CrossRef CAS PubMed.
- Y. S. Meng and M. E. Arroyo-de Dompablo, Acc. Chem. Res., 2013, 46, 1171–1180 CrossRef CAS PubMed.
- M. S. Islam and C. A. J. Fisher, Chem. Soc. Rev., 2014, 43, 185–204 RSC.
- A. Urban, D.-H. Seo and G. Ceder, npj Comput. Mater., 2016, 2, 16002 CrossRef CAS.
- S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010–7018 CrossRef CAS PubMed.
- J. P. Malrieu, R. Caballol, C. J. Calzado, C. de Graaf and N. Guihéry, Chem. Rev., 2014, 114, 429–492 CrossRef CAS PubMed.
- M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, Coord. Chem. Rev., 2015, 289, 177–214 CrossRef.
- J. M. Frost, K. L. M. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491 RSC.
- F. Neese and D. A. Pantazis, Faraday Discuss., 2011, 148, 229–238 RSC.
- J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138 RSC.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581 CrossRef CAS PubMed.
- P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, 2146–2149 CrossRef PubMed.
- M. Atzori and R. Sessoli, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS PubMed.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Nat. Rev. Chem., 2020, 4, 490–504 CrossRef CAS PubMed.
- M. Alessio, S. Kotaru, G. Giudetti and A. I. Krylov, J. Phys. Chem. C, 2023, 127, 3647–3659 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- L. F. Chibotaru, Theoretical Understanding of Anisotropy in Molecular Nanomagnets, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015, pp. 185–229 Search PubMed.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- K. Sneskov and O. Christiansen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 566–584 CAS.
- R. J. Bartlett, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 126–138 CAS.
- M. Alessio and A. I. Krylov, J. Chem. Theory Comput., 2021, 17, 4225–4241 CrossRef CAS PubMed.
- S. Kotaru, S. Kähler, M. Alessio and A. I. Krylov, J. Comput. Chem., 2023, 44, 367–380 CrossRef CAS PubMed.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS.
- F. R. Manby, M. Stella, J. D. Goodpaster and T. F. Miller, J. Chem. Theory Comput., 2012, 8, 2564–2568 CrossRef CAS PubMed.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- T. B. Pedersen, A. M. J. Sánchez de Merás and H. Koch, J. Chem. Phys., 2004, 120, 8887–8897 CrossRef CAS PubMed.
- O. Christiansen, H. Koch, P. Jørgensen and T. Helgaker, Chem. Phys. Lett., 1996, 263, 530–539 CrossRef CAS.
- C. Hättig and A. Köhn, J. Chem. Phys., 2002, 117, 6939–6951 CrossRef.
- C. Hättig, J. Chem. Phys., 2003, 118, 7751–7761 CrossRef.
- A. Köhn and C. Hättig, J. Chem. Phys., 2003, 119, 5021–5036 CrossRef.
- R. Izsák, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1445 Search PubMed.
- G. P. Paran, C. Utku and T.-C. Jagau, Phys. Chem. Chem. Phys., 2022, 24, 27146–27156 RSC.
- A. I. Krylov, Chem. Phys. Lett., 2001, 338, 375–384 CrossRef CAS.
- A. I. Krylov, Acc. Chem. Res., 2006, 39, 83–91 CrossRef CAS PubMed.
- D. Casanova and A. I. Krylov, Phys. Chem. Chem. Phys., 2020, 22, 4326–4342 RSC.
- G. Wälz, D. Usvyat, T. Korona and M. Schütz, J. Chem. Phys., 2016, 144, 084117 CrossRef PubMed.
- A. K. Dutta, N. Vaval and S. Pal, Int. J. Quantum Chem., 2018, 118, e25594 CrossRef.
- A. Shaalan Alag, D. P. Jelenfi, A. Tajti and P. G. Szalay, J. Chem. Theory Comput., 2022, 18, 6794–6801 CrossRef CAS PubMed.
- F. Ma, Z. Wang, M. Guo and F. Wang, J. Chem. Phys., 2020, 152, 124111 CrossRef CAS PubMed.
- G. P. Paran, C. Utku and T.-C. Jagau, Phys. Chem. Chem. Phys., 2024, 26, 1809–1818 RSC.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- K. Gerald and C. Garnet, Phys. Rev. Lett., 2012, 109, 186404 CrossRef PubMed.
- F. Libisch, C. Huang and E. A. Carter, Acc. Chem. Res., 2014, 47, 2768–2775 CrossRef CAS PubMed.
- S. J. R. Lee, M. Welborn, F. R. Manby and T. F. Miller, Acc. Chem. Res., 2019, 52, 1359–1368 CrossRef CAS PubMed.
- L. O. Jones, M. A. Mosquera, G. C. Schatz and M. A. Ratner, J. Am. Chem. Soc., 2020, 142, 3281–3295 CrossRef CAS PubMed.
- S. J. R. Lee, F. Ding, F. R. Manby and T. F. Miller, J. Chem. Phys., 2019, 151, 064112 CrossRef.
- M. Welborn, F. R. Manby and T. F. Miller, J. Chem. Phys., 2018, 149, 144101 CrossRef PubMed.
- S. J. Bennie, B. F. E. Curchod, F. R. Manby and D. R. Glowacki, J. Phys. Chem. Lett., 2017, 8, 5559–5565 CrossRef CAS PubMed.
- D. V. Chulhai and J. D. Goodpaster, J. Chem. Theory Comput., 2018, 14, 1928–1942 CrossRef CAS PubMed.
- V. Parravicini and T.-C. Jagau, Mol. Phys., 2021, 119, e1943029 CrossRef.
- K. Boguslawski, J. Chem. Phys., 2016, 145, 234105 CrossRef PubMed.
- K. Boguslawski, J. Chem. Theory Comput., 2019, 15, 18–24 CrossRef CAS PubMed.
- R. Chakraborty, K. Boguslawski and P. Tecmer, Phys. Chem. Chem. Phys., 2023, 25, 25377–25388 RSC.
- Y. Bouchafra, A. Shee, F. Réal, V. Vallet and A. Severo Pereira Gomes, Phys. Rev. Lett., 2018, 121, 266001 CrossRef CAS PubMed.
- J. D. Goodpaster, T. A. Barnes, F. R. Manby and T. F. Miller, J. Chem. Phys., 2012, 137, 224113 CrossRef PubMed.
- A. V. Luzanov, A. A. Sukhorukov and V. E. Umanskii, Theor. Exp. Chem., 1976, 10, 354–361 CrossRef.
- A. V. Luzanov and V. F. Pedash, Theor. Exp. Chem., 1979, 15, 338–341 CrossRef.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106 CrossRef PubMed.
- F. Plasser, S. A. Bäppler, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024107 CrossRef PubMed.
- A. I. Krylov, J. Chem. Phys., 2020, 153, 080901 CrossRef CAS PubMed.
- F. Plasser, A. I. Krylov and A. Dreuw, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1595 CAS.
- S. A. Mewes, F. Plasser, A. Krylov and A. Dreuw, J. Chem. Theory Comput., 2018, 14, 710–725 CrossRef CAS PubMed.
- P. Pokhilko and A. I. Krylov, J. Phys. Chem. Lett., 2019, 10, 4857–4862 CrossRef CAS PubMed.
- M. Radoń, K. Gassowska, J. Szklarzewicz and E. Broclawik, J. Chem. Theory Comput., 2016, 12, 1592–1605 CrossRef PubMed.
- M. Radoń and G. Drabik, J. Chem. Theory Comput., 2018, 14, 4010–4027 CrossRef PubMed.
- M. Reimann and M. Kaupp, J. Chem. Theory Comput., 2023, 19, 97–108 CrossRef CAS PubMed.
- Y. Shao, M. Head-Gordon and A. I. Krylov, J. Chem. Phys., 2003, 118, 4807–4818 CrossRef CAS.
- Y. A. Bernard, Y. Shao and A. I. Krylov, J. Chem. Phys., 2012, 136, 204103 CrossRef PubMed.
- N. Orms and A. I. Krylov, Phys. Chem. Chem. Phys., 2018, 20, 13127–13144 RSC.
- P. Pokhilko, E. Epifanovsky and A. I. Krylov, J. Chem. Phys., 2019, 151, 034106 CrossRef PubMed.
- D. Claudino and N. J. Mayhall, J. Chem. Theory Comput., 2019, 15, 1053–1064 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- A. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- J. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- M. Rohrdanz, K. Martins and J. Herbert, J. Chem. Phys., 2009, 130, 054112 CrossRef PubMed.
- F. Wang and T. Ziegler, J. Phys. Chem., 2004, 121, 12191–12196 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102 CrossRef CAS.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107 CrossRef PubMed.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- H. A. Bethe and E. E. Salpeter, Quantum mechanics of one and two electron atoms, Plenum, New York, 1977 Search PubMed.
- Relativistic Electronic Structure Theory, ed. P. Schwerdtfeger, Elsevier, Amsterdam, 2002 Search PubMed.
- A. Carreras, H. Jiang, P. Pokhilko, A. Krylov, P. M. Zimmerman and D. Casanova, J. Chem. Phys., 2020, 153, 214107 CrossRef CAS PubMed.
- S. Kotaru, P. Pokhilko and A. I. Krylov, J. Chem. Phys., 2022, 157, 224110 CrossRef CAS PubMed.
- A. Berning, M. Schweizer, H.-J. Werner, P. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823–1833 CrossRef CAS.
- D. G. Fedorov, S. Koseki, M. W. Schmidt and M. S. Gordon, Int. Rev. Phys. Chem., 2003, 22, 551–592 Search PubMed.
- C. M. Marian, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 187–203 Search PubMed.
- M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, Chem. Sci., 2013, 4, 139–156 RSC.
- R. Orbach and B. Bleaney, Proc. R. Soc. London, Ser. A, 1961, 264, 458–484 CAS.
- R. Orbach, Proc. R. Soc. London, Ser. A, 1961, 264, 485–495 CAS.
- A. I. Krylov and C. D. Sherrill, J. Chem. Phys., 2002, 116, 3194–3203 CrossRef CAS.
- L. Blancafort and A. A. Voityuk, J. Chem. Phys., 2014, 140, 095102 CrossRef PubMed.
- S. Matsika, X. Feng, A. V. Luzanov and A. I. Krylov, J. Phys. Chem. A, 2014, 118, 11943–11955 CrossRef CAS PubMed.
- F. Plasser, J. Chem. Phys., 2016, 144, 194107 CrossRef PubMed.
- C. K. Jørgensen, Absorption Spectra and Chemical Bonding in Complexes, Pergamon Press, 1962 Search PubMed.
- F. A. Cotton and M. D. Meyers, J. Am. Chem. Soc., 1960, 82, 5023–5026 CrossRef CAS.
- M. A. El-Sayed, Acc. Chem. Res., 1968, 1, 8–16 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Spin density, wave function analysis of Fe-based systems, additional CC2 results, wave function analysis of Co-based systems, effects of the low-level DFT method, basis set effects, comparison with additional benchmark data. See DOI: https://doi.org/10.1039/d4cp01129e |
| This journal is © the Owner Societies 2024 |








