An NMR crystallographic characterisation of solid (+)-usnic acid

Abstract

We use a combination of one- and two-dimensional solid-state nuclear magnetic resonance (NMR) spectroscopy and density functional theory (DFT) calculations to obtain a full assignment of the ¹H and ¹³C signals for solid (+)-usnic acid, which contains two molecules in the asymmetric unit. By combining through-space ¹H–¹H correlation data with computation it is possible to assign signals not just to the same molecules (relative assignment) but to assign the signals to specific crystallographic molecules (absolute assignment). Variable-temperature measurements reveal that there is some variation in many of the ¹³C chemical shifts with temperature, likely arising from varying populations of different tautomeric forms of the molecule. The NMR spectrum of crystalline (+)-usnic acid is then compared with that of ground Usnea dasopoga lichen (the source material of the usnic acid). The abundance of usnic acid is so great in the lichen that this natural product can be observed directly in the NMR spectrum without further purification. This natural sample of usnic acid appears to have the same crystalline form as that in the pure commercial sample.

---

Introduction

Usnic acid 1 (Fig. 1) has been extensively studied since it was first isolated in 1843 by Rochleder and Heldt.^1,2 The (+) and (−) stereoisomers of 1 have been extracted and purified from lichens for investigation in various contexts including for chemical transformations and for its biological activity (including toxicity towards a range of organisms, and its ability to absorb ultraviolet light).^3,4 However, its structure was open to debate for over a century. Prior to the 1950s several structures were proposed based on exhaustive degradation studies of products derived from natural samples of 1.² The correct structure was first proposed in 1937 by Robertson and Curd,⁵ and was subsequently validated by the first total synthesis of a racemic sample by Barton, Deflorin and Edwards in 1956.⁶ With the development and use of modern analytical methods such as nuclear magnetic resonance (NMR) spectroscopy, the molecular structure of 1 is now well established.^4,7 However, the crystal structure of solid 1 was only reported much more recently in 2006¹¹ and to date the solid form has not been characterised spectroscopically.

Fig. 1 Molecular structure of 1 and numbering scheme used throughout.

Small-molecule solid-state NMR spectroscopy is often more challenging than its liquid-state counterpart, owing to the fact that crystal packing can lead to the number of crystallographically distinct molecules in the unit cell (Z′) being greater than one, necessitating assignment of the resulting spectroscopic signals to not only their corresponding chemical sites within the molecule, but also to the correct crystallographically distinct (but chemically identical) molecule within the cell. This can be particularly problematic where Z′ is large: for example, Webber et al. characterised campho[2,3-c]pyrazole, for which Z′ = 6 and the signal for each of the 11 chemical sites was split into six by the crystallographic inequivalences.⁹ Absolute crystallographic assignment is typically assisted by density functional theory (DFT) calculations although, as demonstrated below, care must be taken to use experiment to verify DFT-based assignments wherever possible, as the errors are often on the order of the small splitting of the signals arising from crystallographic inequivalences. In such cases, it can be advantageous to use advanced NMR methodology to identify the signals from adjacent H–H, H–C and C–C pairs and confirm (or refute) the DFT-based assignments. However, such an approach requires access to specialist hardware (such as a probe capable of achieving magic angle spinning (MAS) rates ≥60 kHz for ¹H–¹H correlations with usefully high resolution) and experimental times can be very long (multiple days for ¹³C–¹³C correlations at natural abundance). Despite these practical challenges, such experiments can prove invaluable. As an early and illustrative example, Harris and co-workers were able to assign all 38 ¹³C signals observed for the β-form of testosterone (Z′ = 2) using a ¹³C–¹³C Incredible Natural Abundance DoublE Quantum Experiment (INADEQUATE) correlation spectrum at natural abundance.¹⁰

The present work combines one- and two-dimensional ¹H and ¹³C solid-state NMR spectroscopy with periodic DFT calculations to characterise the pure solid form of (+)-1 (with Z′ = 2) and achieve an experimentally verified absolute assignment of signals to the crystal structure, as well as demonstrating the observation of signals from crystalline 1 in a sample of wild lichen (Usnea dasopoga¹¹).

Methods

Sample preparation

Crystalline (+)-1 (98%, CAS: 7562-61-0) was purchased from Alfa Aesar and used as supplied. Samples of wild U. dasopoga (Fig. 2) were collected with permission from a location in Northern Scotland. The lichen was air dried at room temperature and then ground to obtain the powdery coating containing natural usnic acid, while the softer but more resilient skeleton remained intact and was discarded. The powdered lichen was packed directly into a MAS rotor with no further treatment.

Fig. 2 Photograph of a representative sample of wild U. dasopoga collected for this work. See the ESI† for a larger reproduction of this figure.

Solution-phase NMR spectroscopy

The solution-phase NMR spectra were recorded using a Bruker AV 400 spectrometer equipped with a 9.4 T superconducting magnet (respective ¹H and ¹³C Larmor frequencies of 400.3 and 100.7 MHz). The sample was dissolved in CDCl₃. The ¹H spectrum was recorded at room temperature with signal averaging of 8 transients with a recycle interval of 1 s. The ¹³C spectrum was recorded using the multiplicity-edited DEPTQ pulse sequence,¹² and processed such that CH₃ and CH signals are positive and CH₂ and quaternary C are negative. Signal averaging was carried out for 800 transients with a recycle interval of 2 s. Chemical shifts are reported in ppm relative to TMS using the signals from the solvent (δ_H = 7.26 ppm, δ_C = 77.16 ppm) as a secondary reference.¹³

Solid-state NMR spectroscopy

Solid-state NMR experiments were recorded using Bruker Avance III spectrometers equipped with 9.4 T or 14.1 T wide-bore superconducting magnets (¹H Larmor frequencies of 400.1 and 600.1 MHz, respectively). Samples were packed into standard 4 mm or 1.3 mm zirconia MAS rotors. For the variable-temperature experiments, the sample temperature was controlled using a Bruker BVT control unit, BVTB-3000 heater booster and BCU-II chiller. Full experimental parameters are given in the ESI.† Chemical shifts are reported in ppm relative to TMS using L-alanine (δ(CH₃) = 20.5 ppm, δ(NH₃) = 8.5 ppm) as a secondary solid reference.

Calculations

The crystal structure of (+)-1 was taken from literature⁸ and optimised using version 19.11 of the CASTEP DFT code,¹⁴ employing the GIPAW algorithm,¹⁵ to reconstruct the all-electron wavefunction in the presence of a magnetic field for the calculation of NMR parameters. Calculations used the GGA PBE functional, with core-valence interactions described by ultrasoft pseudopotentials,¹⁶ which were generated on the fly accounting for scalar relativistic effects using ZORA.¹⁷ A planewave cut-off energy of 60 Ry was used, and integrals over the Brillouin zone were performed using a Monkhorst–Pack grid with a k-point spacing of 0.04 2 π Å⁻¹. Dispersion interactions were introduced using the scheme of Tkatchenko and Scheffler, as implemented by McNellis et al.^18,19

Calculations generate the shielding tensor in the crystal frame, σ, from which the calculated isotropic shielding is given by σ_iso = (1/3)Tr{σ}, and the isotropic chemical shift by σ_iso = –(σ_iso – σ_ref)/m, where σ_ref is a reference shielding and m is a scaling factor. In this work, values of m = 1.015 and σ_ref = 172.07 for ¹³C and m = 1.102 and σ_ref = 30.55 for ¹H were obtained as described below.

Results and discussion

Commercial (+)-usnic acid

The crystal structure of (+)-1 contains two distinct molecules in the asymmetric unit,⁸ as shown in Fig. 3a. However, particularly for molecular crystals, the positions of H atoms often require modification before yielding reasonable calculated NMR parameters.^10,20–25 As such, prior to any DFT calculations it is common to optimise the structure by minimizing the computed atomic forces. The optimised structure is that shown in Fig. 3 and, in this case, the unit cell lengths varied only slightly (by around 1%) from the experimental structure.

Fig. 3 (a) Molecular asymmetric unit of solid (+)-1. Atoms are coloured H = pale grey, C = black, O = red, with intramolecular hydrogen bonds indicated in cyan. (b) Molecular packing in the unit cell of (+)-1, viewed down the a axis with C and O coloured to denote each type of crystallographically distinct molecule and H omitted for clarity. O atoms are shown as spheres and bonds, whereas only bonds are shown for C. The structure shown has been optimised by DFT as described in the text. The molecule at the top of the dimer as shown in (a) is coloured red in (b), and the molecule at the bottom in blue.

Fig. 4 shows the ¹³C DEPTQ NMR spectrum of (+)-1 in CDCl₃ solution, and the corresponding ¹³C cross polarization (CP) MAS NMR spectrum of solid (+)-1. As the solid form contains two crystallographically (and, hence magnetically) inequivalent molecules (shown in red and blue in Fig. 3b), one might expect twice the number of signals to be observed for the solid. On initial count, only 33 signals are observed, compared to the expected 36, suggesting that some signals from the two distinct molecules are overlapped. The assignment of the solution-state spectrum is known and is indicated in Fig. 4.⁷ Given the similarity of the peak positions in the solid-state spectrum, it is reasonable to take this order of assignments as a starting point for assigning the signals for the solid. Three pairs of signals for the solid appear to be overlapped: those of carbons C2 (106.8 ppm), CA (30.6 ppm) and CB (29.8 ppm). The challenge of assigning the ¹³C NMR spectrum in the solid phase is not one simply of chemistry, but of assigning signals, from chemically identical species to the correct magnetically distinct molecules. Harris et al. demonstrated a strategy to address this problem for β-testosterone, which, like (+)-1 contains two distinct molecules in the unit cell.¹⁰ Using a combination of the two-dimensional ¹³C INADEQUATE and DFT calculations, the authors were able to observe and assign all 38 ¹³C signals. INADEQUATE requires adjacent pairs of ¹³C nuclei, which, at natural abundance (ca. 1%), gives low overall sensitivity and leads to experimental times on the order of days, even with signal enhancement by CP.

Fig. 4 Expansions of the overlaid ¹³C CP MAS NMR spectrum of solid (+)-1 (black) and the ¹³C DEPTQ NMR spectrum of (+)-1 in CDCl₃ solution (CH₃ and CH positive, CH₂ and C negative). Assignments of the solution-phase spectrum are shown in red. The signal at 28.9 ppm indicated with a dagger (†) arises from an unidentified impurity. For the complete spectra, see the ESI.†

Fig. 5 shows expansions of the ¹³C CP INADEQUATE NMR spectrum of (+)-1, and several observations can be made at this stage. First, the assumption that the signals for CA are overlapped is incorrect, as correlations between CA and C6a are observed for the methyl signals at 31.9 and 30.5 ppm, whereas correlations between CD and C9b are observed for the methyl signals at 32.5 and 30.8 ppm. Second, with the mixing time chosen for this experiment (3.84 ms) cross peaks for the C4a signals (at 176.7 and 179.8 ppm) are very weak and this may hinder full assignment (additional experiments with mixing times of 3.2 and 4.48 ms, shown in the ESI†, did not yield further correlations for C4a). Finally, to have a sweep width in the indirect dimension spanning δ₁ = 115.6 ppm (the lowest anticipated shift for CC and C8) to δ₁ = 312.0 ppm (the highest anticipated shift for C2 and C2a), a rotor-synchronised t₁ increment of τ_r/2 = 40 μs was used, resulting in spinning sidebands being observed for some signals, which clutter the spectrum but do not interfere with assignment.

Fig. 5 Expansions of the ¹³C CP INADEQUATE NMR spectrum of (+)-1 (9.4 T, 12.5 kHz MAS). Positive contours are shown in black and negative contours in red. Spinning sidebands are coloured grey and marked with asterisks (*). The ¹³C CP MAS NMR spectrum from Fig. 4 is shown along δ₂ as a guide to the eye. The correlations between CA and C6a are highlighted in blue and those between CD and C9b in green.

In principle, assignment of signals in an INADEQUATE spectrum is trivial, with pairs of peaks at the same δ₁ corresponding to carbon atoms in the same molecule. In practice, for (+)-1 some assignments were more challenging. In particular, C2, C9b, C9a and C6 have shift differences of 0.20, 0.35, 0.33 and 0.31 ppm between the two molecules, respectively, which is less than the limiting resolution in the indirect dimension. For these signals, close inspection of the lineshapes in the INADEQUATE spectrum allowed tentative assignments to be determined, and these assignments were internally consistent with other unambiguous assignments. As such, two larger fragments of the molecules could be identified from the INADEQUATE experiment, comprising C4a, C4, C3 and C2 in the first fragment and C6, C7, C8, C9, C9a and CC in the second fragment. Additionally, cross peaks linking C6a and CA could be identified, but it was not possible to unambiguously include these in the second large fragment. Closer inspection of the signal for C2 allowed identification of correlations between C2 and C2a to be added to the first fragment, which also adds CB to this fragment, since it has not proven possible to distinguish more than one signal for CB in any of the experiments in this work. Owing to the shift difference between the two CD signals, the fragment containing CD and C9b could be identified but not connected to either of the large fragments, as a result of the small shift differences for both C9a and C9b, the fact that the correlation between C9b and C4a was not observed. The resolution was also insufficient to identify the C9b-C1 pairs. This left two large fragments, the acyl group C6a-CA, the C9b-CD pair with two isolated carbons, C1 and C5 unassigned. Further connection of these fragments was not possible from the INADEQUATE spectrum alone.

Owing to the presence of strong homonuclear dipolar couplings, solid-state ¹H NMR spectra are typically of much poorer resolution than ¹³C. Fig. 6a shows the ¹H MAS NMR spectrum of (+)-1, recorded at a spinning rate of 60 kHz. Even at this rapid rotation rate, resolution of the signals for the two distinct molecules is not possible, with the exception of the hydrogen-bonded H between C7(OH) and C6(=O), which has shifts of 12.0 and 12.4 ppm. Processing with exponential weighting of −200 Hz (shown in the ESI†) further reveals that the signal for the hydrogen-bonded proton between C9(OH) and C1(=O) has contributions at 11.0 and 10.8 ppm. The CH₃ region of the spectrum clearly contains multiple signals, but these are too overlapped to yield useful information. A ¹H–¹³C INEPT experiment, shown in Fig. 6b, reveals pairs of spins that interact via the J coupling (note that the delay in the INEPT experiment is τ = 1/4J and here, τ = 0.33 ms, indicating J = 750 Hz, i.e., there is a small residual dipolar contribution to the coupling). This experiment allows assignment of the ¹H signals from the CH₃ groups and shows that although the two signals from C4 have a shift difference of 1.9 ppm, their attached protons have the same chemical shift.

Fig. 6 (a) ¹H (14.1 T, 60 kHz MAS) NMR spectrum of (+)-1 (black) and ¹H (9.4 T, CDCl₃) NMR spectrum of (+)-1 with peak assignments (red, s = solvent, † = impurity). (b) Expansions of the ¹H–¹³C (14.1 T, 60 kHz MAS) INEPT NMR spectrum of (+)-1 with the ¹³C CP MAS NMR spectrum from Fig. 4 shown along the top as a guide to the eye. (c) Expansions of the ¹H–¹³C (9.4 T, 12.5 kHz MAS) CP-HETCOR spectrum of (+)-1. Signals from nuclei near the C9(OH)–C1(=O) hydrogen bond are indicated in red, those from nuclei near the C3(OH)–C2a(=O) hydrogen bond in gold, and those from nuclei near the C7(OH)–C6(=O) hydrogen bond in green.

To gain further insight into longer-range ¹H–¹³C interactions, a heteronuclear correlation (HETCOR) experiment was recorded, with magnetization transfer by CP, using the through-space dipolar interaction. By using a short contact time of 0.35 ms, the spin–spin interactions observed are largely intramolecular rather than intermolecular. Fig. 6c shows the CP-HETCOR spectrum and despite the dramatic broadening of signals in the ¹H dimension (as a consequence of the lower MAS rate of 12.5 kHz), the spectrum reveals valuable information about the carbon spins near to the O–H⋯O hydrogen bonds. The signals highlighted in green in Fig. 6c correspond to C6a, C6 and C7, which are adjacent to the C7(OH)–C6a(=O) hydrogen bond with δ_H = 12.0 and 12.4 ppm. By noting that the ¹H signal with higher chemical shift correlates to C6a at 200.69 ppm and to C7 at 162.16 ppm, it is possible to join the fragment containing C6a and CA to the larger molecular fragment. The signals highlighted in red in Fig. 6c correspond to the carbons adjacent to the C9(OH)–C1(=O) hydrogen bond (with δ_H = 10.8 and 11.0 ppm): C9, C9a, C9b and C1. Although the difference in ¹H chemical shifts here is small, it is still possible to use these correlations to extend the large molecular fragment to include both C1 and the fragment containing C9b and CD. The signals highlighted in gold in Fig. 6c correspond to C2a, C2 and C3, which are adjacent to the C3(OH)–C2a(=O) hydrogen bond (δ_H = 18.9 ppm). However, these signals provide no additional information since there is no resolution of the ¹H chemical shifts and the ¹³C signals were assigned fully by analysis of the INADEQUATE spectrum. At this stage, as shown in the ESI,† there are two large fragments of the molecule for which assignment of all ¹H and ¹³C signals has been possible. The first fragment contains C2, C2a, CB, C3, C4 and C4a. The second contains C6, C6a, CA, C7, C8, C9, C9a, C9b, CD and C1. Only C5a cannot be assigned to either fragment and it was not possible to connect either C4a to C9b or C1 to C2.

One further relatively routine experiment presents itself in the solid-state NMR toolkit for small organic molecules; the ¹H–¹H single-quantum–double-quantum (SQ–DQ) correlation experiment. In this work, double quantum coherences were excited and converted using the BAck-to-BAck sequence,²⁶ which uses the dipolar interaction and can, therefore, show both intramolecular and intermolecular ¹H–¹H interactions. Indeed, given the sparse ¹H network within the structure of 1, many of the shortest H–H distances (i.e., those giving rise to the strongest dipolar couplings) in the solid are intermolecular. Given that the two molecules within the asymmetric unit are arranged such that some H–H distances are notably different, the ¹H SQ–DQ correlation experiment provides a means of absolute assignment of the signals to their crystallographic sites, rather than simply the relative assignment to molecular fragments that has been discussed so far.

Fig. 7a shows the ¹H SQ–DQ correlation spectrum of (+)-1. The resolution of the CH₃ region of the spectrum is not sufficient to allow unambiguous information to be extracted and many of the more obvious correlations observed do not add any new information to the spectroscopic assignment discussed above.

Fig. 7 (a) Expansions of the ¹H (14.1 T, 60 kHz MAS) SQ–DQ correlation spectrum of (+)-1. The δ₁ = 2δ₂ autocorrelation diagonal is indicated with a grey dashed line, the signals corresponding to H4–C9(OH) are indicated with a pink box and the signals corresponding to correlations with C7(OH) (discussed in more detail in the text) are indicated with blue boxes. (b and c) The local environment (in the DFT-optimised structure) around the C9(OH)–C1(=O) hydrogen bond in (b) the lower molecule in the dimer in Fig. 3(a) and (c) the upper molecule in the dimer in Fig. 3a. Atoms are coloured C = black, O = red, H = pale grey, with all H apart from C9(OH) and H4 being omitted for clarity. The short intermolecular H–H distance is indicated in (b) and the C9(OH) with no nearby H4 is indicated in (c).

However, the pair of signals at (δ₂ = 5.7 ppm, δ₁ = 16.8 ppm) and (11.1 ppm, 16.8 ppm), corresponding to H4 (5.7 ppm) and one of the C9(OH) (11.1 ppm) distinguish unambiguously between the two molecules in the crystal structure. As shown in Fig. 7b, for the optimised structure of (+)-1, H4 in one molecule (the lower, as presented in Fig. 3a) is 3.17 Å from the nearest H4 (in a different dimer) and, as shown in Fig. 7c, the other C9(OH) has no nearby H4. Similar information is also provided from the correlations observed for the C7(OH) signals at 12.4 and 12.0 ppm, highlighted in pink in Fig. 7a. For the C7(OH) in the upper molecule in Fig. 3a, the closest C3(OH) is 3.5 Å, the closest H4 is 3.8 Å and there are no nearby C9(OH), whereas for the lower molecule, there is a C9(OH) within 4 Å and the C3(OH) and C4 are further away at 3.8 and 4.4 Å, respectively. This is consistent with the observed cross peaks (note that additional signals might be expected for all H–H distances of around 4 Å, and there is some limited evidence of these just above the baseline of the spectrum, not shown in Fig. 7a). By combining the evidence from the ¹H SQ–DQ correlation experiment with the assignments of the ¹H and ¹³C signals discussed above, it is possible to achieve an absolute crystallographic assignment for the largest molecular fragment, which contains both C9(OH) and C7(OH). However, there remains no unambiguous experimental means of connecting these fragments to C5a or the smaller fragment.

As there is a fragment of the molecule for which the ¹H and ¹³C chemical shifts are known, as discussed above, this information was used to provide “internal referencing” of the DFT-calculated magnetic shielding. In this method, calculated σ_iso values are plotted against experimental δ_iso, with the slope and intercept used to determine m and σ_ref (as described in the experimental details). For the fragment of the structure for which experimental shifts were known, this resulted in σ_ref and m of 30.55 ppm and 1.102, respectively for ¹H, and 172.07 ppm and 1.015, respectively, for ¹³C (note that for ¹H, data for C3(OH) and H4 were also included because these have the same experimental δ_iso in both molecules). A small error of around 1–2% of the chemical shift range of a nucleus is typical of periodic DFT calculations and, indeed, in this case mean absolute errors (MAEs) of 0.62 and 1.77 ppm were obtained for ¹H and ¹³C (around 3% and 0.7% of the respective shift ranges), allowing confident assignment of ¹³C signals from the second fragment of the molecule that are separated by at least 1.77 ppm. The second part of the molecule contains C4 and C4a, which have shift differences of 1.9 and 3.1 ppm, respectively. This allows absolute crystallographic assignment of the signals from C2, C2a, C3, C4 and C4a (and CB) and gives an overall MAE for the ¹³C shifts of 1.52 ppm. Assuming the alternative assignment of this second fragment to the molecule gives a slightly larger MAE of 1.60 ppm. However, we note that there is around a 6 ppm error in the calculated values of δ_iso for C4a, which may make this an unreliable indicator. C5a has an experimental shift difference of 0.97 ppm between the two molecules, allowing tentative assignment of its signals and completing the absolute assignment of the ¹³C NMR spectrum. For ¹H, H4 and C3(OH) have the same experimental δ_iso in both molecules, with means that the only ¹H signals to assign are those of methyl group B. These have experimental shifts of 2.8 and 2.6 ppm, and calculated shifts of 2.7 and 2.1 ppm for the two separate molecules, which allows a tentative assignment to be made.

Table 1 summarises the ¹³C chemical shifts for (+)-1 in the solid and solution and compares these with the periodic DFT calculation for the solid. Table 2 provides a similar summary for the ¹H spectroscopic data, although the lower resolution of the CH₃ region of the spectrum leads to lower confidence in assignment of the experimental shifts, especially for methyl group B. Note that the calculated shifts for the CH₃ groups are the average of the three H within the group, each of which is magnetically distinct in the static structure, but which will rapidly interconvert owing to unhindered rotation about the C–CH₃ bond at room temperature. This approximation further adds to the error in the computed ¹H δ_iso.

Table 1 Summary of the calculated and experimental ¹³C chemical shifts of (+)-1 in CDCl₃ solution and in the solid form at room temperature

C	δ (CDCl3)	Molecule 1 δ (ppm)		Molecule 2 δ (ppm)
		Exp.	DFT.	Exp.	DFT
2a	201.8	205.1	206.7	204.3	205.0
6a	200.3	200.7	198.9	199.5	197.6
1	198.1	197.3	195.2	196.9	194.2
3	191.7	192.5	188.7	193.3	188.8
4a	179.4	176.7	182.3	179.8	184.9
7	163.9	162.2	163.6	164.3	165.7
9	157.5	159.8	159.8	157.8	157.3
5a	155.2	155.9	156.4	154.9	154.5
8	109.4	108.5	108.9	110.3	111.4
2	105.2	106.7	106.7	106.9	107.3
9a	104.0	104.9	104.9	104.5	104.4
6	101.5	100.6	100.2	100.9	100.5
4	98.4	100.2	99.3	98.3	97.7
9b	59.1	58.7	62.2	58.6	61.3
D	32.1	30.6	31.2	32.5	32.8
A	31.3	31.9	30.3	30.5	28.5
B	27.9	29.8	30.9	29.8	29.7
C	7.5	7.1	5.5	8.1	5.5

---

Table 2 Summary of the calculated and experimental ¹H chemical shifts of (+)-1 in CDCl₃ solution and in the solid form at room temperature

H	δ (CDCl3)	Molecule 1 δ (ppm)		Molecule 2 δ (ppm)
		Exp.	DFT.	Exp.	DFT
3(OH)	18.86	18.9	18.5	18.9	17.9
7(OH)	13.33	12.0	13.7	12.4	12.8
9(OH)	11.04	11.0	11.0	10.8	11.4
4	6.00	5.6	5.4	5.6	5.5
A	2.70	1.9	2.3	2.5	2.2
B	2.68	3.0	2.7	2.5	2.1
C	2.12	2.3	0.7	0.8	2.0
D	1.78	1.6	1.7	1.8	1.5

---

Despite the overall reasonable MAE values quoted above, it is worth looking in more detail at the calculated δ_iso for ¹³C. Fig. 8a shows a plot of the calculated chemical shifts against the experimental values and, on the scale of the whole spectrum, the agreement is reasonable (R² = 0.999). However, when the calculated peak positions are superimposed on the CP MAS NMR spectrum (as in Fig. 8b) or the INADEQUATE spectrum (shown in the ESI†), it is clear that the calculated shifts do not adequately describe certain regions of the spectrum, especially for C4a and the methyl region. A possible source of the apparent inaccuracy of the DFT calculations could be dynamics, particularly of the CH₃ groups in this case. The DFT calculation has an inherent temperature of 0 K and, hence, neglects thermal effects such as dynamics. Various computational strategies can be undertaken to more accurately model dynamic behaviour of molecules, although these approaches are more limited and often computationally costly for periodic calculations.²⁴ An alternative experimental approach is to carry out variable-temperature (VT) NMR experiments, in which temperature-dependent changes in chemical shift can indicate the presence of dynamics.

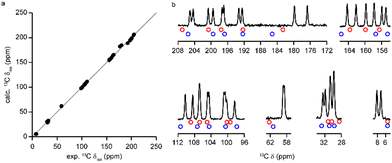Fig. 8 (a) Plot of DFT calculated ¹³C δ_iso against the experimental values for (+)-1. The ideal 1 : 1 correlation is indicated in grey. (b) The ¹³C CP MAS NMR spectrum from Fig. 4, with the calculated δ_iso for the two molecules indicated by blue and red circles, with the colours corresponding to those used in Fig. 3b.

Fig. 9 shows the change in peak positions, δδ, for ¹³C signals from (+)-1 as a function of temperature (from 260 K to 330 K). All of the signals display a small temperature dependence, but some show a much larger effect. In particular, the acyl group comprising CB and C2a, and backbone carbon C2 exhibit larger δδ than other carbons in the molecule with comparable chemical environments. While these shift differences may arise from molecular motion, this part of the molecule also exhibits tautomerism in the solution phase, as shown in Fig. 10, which has been explored by molecular DFT calculations.²⁷ Given that the two tautomers A and B are very close in energy in the molecule, it seems reasonable to assume that they will both also be present in the solid state. As different sets of signals are not observed for the different tautomers, it can be suggested that rapid interconversion between tautomers A and B occurs on the NMR timescale, (i.e., a low energy barrier between the tautomers). As such, it is likely that the changes observed experimentally arise from variation in the populations of tautomers A and B, rather than from increasing the population of C, which would require reorientation of the acyl group within the sterically confined environment of the solid crystal. This proposal is consistent with the observation that tautomers C, C′ and D do not appear to contribute to the room-temperature solution-phase NMR spectra.²⁷ The tautomerism of 1 could also explain some of the discrepancies between the calculation (only tautomer A) and experiment (an interconverting mixture of tautomers A and B).

Fig. 9 Plots of change in ¹³C peak position (δδ) as a function of temperature for (+)-1. The 35 signals are grouped by chemical shift and, for the more crowded regions of the spectrum, separated by molecule. (a) CH₃ signals, (b) carbon 9b, (c and d) δ between 96 and 112 ppm, (e and f) δ between 154 and 182 ppm, (g and h) δ between 190 and 208 ppm.

Fig. 10 Proposed tautomers of 1, with the relative gas-phase energies calculated by Galasso²⁷ indicated. The region of the molecule undergoing changes between the various tautomers is highlighted in red.

Usnic acid in lichen

Since the early days of the discovery of usnic acid, the literature has commented on the high concentration of this molecule in Usnea lichens. For this work, we prepared a sample of “natural” 1 by grinding a sample of lichen (U. dasopoga, Fig. 2) and packing the powdered material directly into an NMR rotor. Fig. 11 shows the ¹³C CP MAS NMR spectrum of this sample, and the signals from 1 are clearly visible (see the ESI† for an expansion). Owing to the non-quantitative nature of CP MAS, we make no comment on the precise concentration of 1 in this material, but the ease with which this spectrum could be collected is remarkable for a natural product. Of particular interest is that, as for the commercial solid (+)-1, the 1 in the lichen gives rise to two sets of signals with chemical shifts very similar to those of the pure compound. This indicates that the material is in the same crystalline form in the pure compound and in the lichen.

Fig. 11 ¹³C CP MAS NMR spectra (9.4 T, 12.5 kHz MAS) of ground lichen (black) and commercial (+)-1 (red).

Conclusions

In the present work we demonstrate the power of an NMR crystallographic approach, combining experimental NMR spectroscopy, DFT and crystallographic information to characterise (+)-usnic acid, which has Z′ = 2. To facilitate spectral assignment, a range of two-dimensional NMR experiments were carried out to reveal through-bond and through-space proximities. This allowed nearly full relative assignments of the signals to molecular fragments, and absolute assignment of the larger fragment to the correct crystallographic molecules. Assignment was also ambiguous when using DFT calculated chemical shifts in isolation, since the mean error in the calculations was significantly larger than some of the smaller experimental shift differences (and specific errors were sometimes surprisingly high). However, by combining the experimental assignment with the calculated shifts, it was possible to achieve a complete absolute assignment with reasonable confidence.

Variable-temperature ¹³C CP MAS NMR experiments showed that the region of the molecule capable of exhibiting tautomerism (carbons 2, 2a and B) gives rise to the largest temperature-dependent chemical shifts. However, a detailed investigation of the effects of tautomerism in the solid form of (+)-usnic acid is beyond the scope of the present work.

Finally, a sample of powdered lichen was characterised by ¹³C CP MAS NMR. This experiment presents a rare observation of a natural product in its parent tissue (facilitated by the high concentration of usnic acid in many lichen species) and allowed confirmation that the usnic acid is present in the same crystalline form in the lichen as in the pure solid.

Author contributions

I. A. S. collected the samples. S. E. A. carried out the DFT calculation D. M. D. carried out the NMR experiments and spectral analysis. All authors contributed to the writing process.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank EaStCHEM and the School of Chemistry for support. This work was supported by the EPSRC through the Collaborative Computational Project on NMR Crystallography (CCP-NC), via EP/T026642/1. In order to meet institutional and research funder open access requirements, any accepted manuscript arising shall be open access under a Creative Commons Attribution (CC-BY) reuse license with zero embargo. Research data supporting this publication are available in ref. 28.

References

1. F. Rochleder and W. Heldt, Liebigs Ann. Chem., 1843, 48, 1–18.
2. F. M. Dean, Sci. Prog., 1952, 40, 635–644.
3. M. Cocchietto, N. Skert, P. Nimis and G. Sava, Sci. Nat., 2002, 89, 137–146.
4. D. N. Solokov, O. A. Luzina and N. F. Salakhutdinov, Russ. Chem. Rev., 2012, 81, 747–768.
5. F. H. Curd and A. Robertson, J. Chem. Soc., 1937, 894–901.
6. D. H. R. Barton, A. M. Deflorin and O. E. Edwards, J. Chem. Soc., 1956, 530–534.
7. S. Forsén, M. Nilsson and C. A. Wachtmeister, Acta Chem. Scand., 1962, 16, 583–590.
8. F. R. Fronczek and N. H. Fischer, CCDC 297381: Experimental Crystal Structure Determination, 2006 DOI:10.5517/cc9zfym.
9. A. L. Webber, L. Emsley, R. M. Claramunt and S. P. Brown, J. Phys. Chem. A, 2010, 114, 10435–10442.
10. R. K. Harris, S. A. Joyce, C. J. Pickard, S. Cadars and L. Emsley, Phys. Chem. Chem. Phys., 2006, 8, 137–143.
11. There are various synonyms for U. dasopoga; however, here we use here the more “correct” name of U. dasopoga after: L. Arcadia, Taxon, 2013, 62, 604–605.
12. R. Burger and P. Bigler, J. Magn. Reson., 1998, 135, 529–534.
13. H. E. Gottlieb, V. Kotlyar and A. Nudelman, J. Org. Chem., 1997, 62, 7512–7515.
14. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
15. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
16. J. R. Yates, C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401.
17. T. F. G. Green and J. R. Yates, J. Chem. Phys., 2014, 140, 234106.
18. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
19. E. R. McNellis, J. Meyer and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205414.
20. C. M. Widdifield, J. D. Farrell, J. C. Cole, J. A. K. Howard and P. Hodgkinson, Chem. Sci., 2020, 11, 2987–2992.
21. C. M. Widdifield, H. Robson and P. Hodgkinson, Chem. Commun., 2016, 52, 6685–6688.
22. X. Filip, G. Borodi and C. Filip, Phys. Chem. Chem. Phys., 2011, 13, 17978–17986.
23. M. Baias, C. M. Widdifield, J.-N. Dumez, H. P. G. Thompson, T. G. Cooper, E. Salager, S. Bassil, R. S. Stein, A. Lesage, G. M. Day and L. Emsley, Phys. Chem. Chem. Phys., 2013, 15, 8069–8080.
24. P. Hodgkinson, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 118–119, 10–53.
25. S. E. Ashbrook and D. McKay, Chem. Commun., 2016, 52, 7186–7204.
26. M. Feike, D. E. Demco, R. Graf, J. Gottwald, S. Hafner and H. W. Speiss, J. Magn. Reson., Ser. A, 1996, 122, 214–221.
27. V. Galasso, Chem. Phys., 2010, 374, 138–145.
28. D. M. Dawson, I. A. Smellie and S. E. Ashbrook, An NMR Crystallographic Characterisation of Solid (+)-Usnic Acid. Dataset, University of St Andrews Research Portal, 2024.

---

Footnote

† Electronic supplementary information (ESI) available: further details of solid-state NMR experiments, complete one-dimensional ¹³C NMR spectra, additional ¹³C INADEQUATE NMR spectra and more detailed interpretation, and further comparison of ¹³C NMR spectra of solid (+)-usnic acid and U. dasopoga powder. See DOI: https://doi.org/10.1039/d4cp01127a

---