 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ion molecule reactions in the HBr+ + CH4 system: a combined experimental and theoretical study†
Dominik
Plamper‡
a,
Allen
Vincent‡
 b,
Kazuumi
Fujioka‡
b,
Rui
Sun
b,
Kazuumi
Fujioka‡
b,
Rui
Sun
 *b and
Karl-Michael
Weitzel
*b and
Karl-Michael
Weitzel
 *a
*a
aPhilipps-Universität Marburg, Fachbereich Chemie, 35032 Marburg, Germany. E-mail: weitzel@chemie.uni-marburg.de
bDepartment of Chemistry, University of Hawai‘i at Manoa, Honolulu, Hawaii 96822, USA. E-mail: ruisun@hawaii.edu
First published on 10th May 2024
Abstract
Reactions in the system HBr+ + CH4 have been investigated inside a guided ion-beam apparatus under single-collision conditions. The HBr+ is vibrational and rotational state selected in the electronic X2Π1/2 state created by (2+1)-REMPI. Due to the exitation scheme employed different rotational states of the HBr+ are accessible. Four reaction channels have been observed. The cross section, σ, for the exothermic proton transfer channel (PT) decreases with increasing collision energy, steeper than predicted by the Langevin model. The cross section also decreases with increasing rotational energy in the HBr+, with the effect of the rotational energy being stronger than that of translational energy. The cross section for the endothermic charge transfer (CT) increased with increasing collision energy. The energy dependence is well reproduced by a simple line of center (loc) model. Although the bromine transfer (BT) is exothermic the observed cross section increased with increasing collision energy due to an activation barrier on the potential energy surface (PES). Analysis by a modified loc model suggest the relevance of an angle dependence of σ. The cross section for the endothermic hydrogen atom abstraction (HA) exhibits a maximum at 2 eV Ecm. The measured cross sections are rationalized by means of reaction dynamics simulations which show good agreement with the experimental cross sections. The dynamics simulations are carried out with a machine learning potential that is developed and benchmarked with ab initio molecular dynamics simulation. The absolute cross sections predicted by reaction dynamics simulations are well within the same order of magnitude while reproducing the trends over three different collision energies for all four reaction channels. Furthermore, the simulations demonstrate various reaction mechanisms for these reaction channels, including a very interesting HBr+ orientation selectivity for the BT reaction channel.
Introduction
Methane is an abundant chemical species influencing earth's atmosphere as well as extra-terrestrial atmospheres. Earth's atmosphere contains an amount of methane in the order of 2000 ppb. In the last four decades the methane concentration in the atmosphere increased dramatically.1,2 Li et al. investigated the influence of halogen species on the CH4 loss and lifetime of the CH4 in the atmosphere by simulations. This led to the conclusion that the rate of CH4 loss will decrease and therefore the total lifetime of CH4 in the atmosphere will increase until the end of the century.3 Methane is also detected in the interstellar medium,4 in the atmosphere of Jupiter,5 on the Saturn moon Titan,5 on Enceladus6 and Mars.7 The atmospheres of Uranus and Neptune also contain CH4.8 HBr has been detected in the upper troposphere of Jupiter and Saturn with upper limits of 3 ppb respectively 1.6 ppb.9Since activation barriers in ion–molecule reactions are in general small, these reactions play a major role in the interstellar medium and in planetary ionospheres. Additionally long-range interactions like Coulomb or ion induced dipole interactions favor reactions of this type.10 Ion–molecule reactions (IMR) were essential in successfully describing the particle densities observed in interstellar clouds.11 The chemistry of the interstellar medium is characterized by low particle densities and low temperatures ranging from 10 K to 100 K.12,13 Due to the often barrierless IMRs small changes in the energetics of such systems can influence the outcome of this reaction type sensitively.12
IMR also form the basis for chemical ionization (CI) mass spectrometry. Munson and Field exploited the formation of CH5+ from methane and its subsequent proton transfer reactions for analyzing unknown compounds.14,15 Ultimately, this led to the development of the proton transfer reaction mass spectrometry (PTR MS) for on-line trace analysis down to the ppb level.16
The CH5+ ion is an intriguing chemical species and was subject of interest in numerous studies. Under laboratory conditions CH5+ ions can be formed by radiative association of CH3+ with H2 or by hydrogen atom abstraction in the reaction CH4+ + H2.12,17 Clearly, the CH5+ ion is a rather flexible molecular ion exhibiting a potential energy surface with shallow minima.
In fact, laboratory studies have been vital in reaching the current understanding of interstellar ion chemistry. Many studies aimed at measuring cross sections or rate constants either as a function of the temperature (in thermal ensembles) or as a function of the center of mass collision energy (typically in energy selected ensembles).18,19
Rather few studies have focused on the influence of the rotational quantum state of the reactants on the reaction dynamics. As a prominent example we mention the investigation of the reaction H2+ (v = 0,1 j = 0,4) + H2 with a single and merged beam approach.20 The observed cross section decreased with increasing vibrational and rotational excitation of the H2+ ions, with the effect of the rotation exceeding that of the vibration.20 Viggiano et al. analyzed the Kr+ + HCl system in a SIFT apparatus. Here, the increase of the rotational temperature of the neutral target, HCl, increased the rate constant for charge transfer considerably.21
The role of ion rotation in IMR has been studied in a number of cases focusing on hydrogen halide ions, HX+ with x = Cl and Br, for which the rotational constants are large allowing to address rotational selectivity in ion preparation. Conceptually, rotational effects may be expected to be large in reactions involving hydrogen halide ions. It has been argued that there is potential relevance of the hydrogen halide ions in the upper atmosphere of earth as well as other astronomical objects.22 Among the previous reaction systems investigated were the self-reactions of HCl23,24 and HBr.25 The authors groups also recently reported a combined experimental and theoretical study of the cross reaction system HBr+ + HCl.26
In the current work the study of rotational effects is extended to the system HBr+ + CH4. Here, four reaction channels are accessible, these are namely:
| HBr+ + CH4 → Br + CH5+ (PT) |
| HBr+ + CH4 → HBr + CH4+ (CT) |
| HBr+ + CH4 → CH3 + H2Br+ (HA) |
| HBr+ + CH4 → H + CH4Br+ (BT) |
Experiment and simulation
Experimental approach
The measured cross sections are analyzed using a guided ion beam setup. This was described in detail in earlier studies.27 Here, the apparatus was improved by implementing a second linear octopole stage to inhibit undesired side reactions.26 The setup is shown in Fig. 1. The ions are created by a Laser as described below, then accelerated and by a focusing stage introduced into the first new linear octopole ion guide. The collisions occur in the second linear octopole ion guide.Behind the second linear octopole ion guide the ions are transferred into a quadrupole mass spectrometer (QMS) with the help of 2 lens assemblies and a conical octopole ion guide.28
HBr+ was created in the X2Π1/2 electronic state by (2+1) resonance enhanced multiphoton ionization (REMPI) in its vibrational ground state.29,30 The REMPI transitions for ion creation were addressed with a tunable dye laser (CobraStrech, Sirah) which was pumped by a 20 Hz ND:YAG laser (INDI, Spectra Physics). The ion rotational energy was varied from 3.4 meV up to 46.8 meV. Experiments have been performed on the R(1), R(3), R(4), R(5), R(6) transition. The R(2) transition was not addressed since it overlaps with the S(0) transition. Ultimately, the REMPI excitation scheme allows to prepare HBr+ ions with narrow rotational state distribution dominated by few rotational states. The measured rotational distribution of the ions prepared on the pump lines has been reported by Penno et al.31
The collision energy in the center of mass frame was varied in the range from 0.25 eV up to 3 eV. The neutral reaction partner CH4 was introduced at room temperature with a dosing valve. The ions were analyzed by their mass to charge ration (m/z) with a Quadrupole Mass Spectrometer (QMS) and detected by a Channeltron. The signals were recorded with a multichannel scaler card (FAST ComTec, P7888). The HBr pressure was set to 5 × 10−6 mbar and the CH4 pressure to 3.5 × 10−5 mbar ensuring single collision conditions. The purity of the HBr gas was 3.5, that of the methane 4.5. The kinetic data in this study are based on the analysis of the ion species CH4+, CH5+, HBr+, H2Br+ and CH4Br+.
The second-order rate constant ki, where i indicates the reaction channel, is given in eqn (1) for the general case.
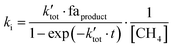 | (1) |
 is the pseudo-first order rate constant of the total reaction, faproduct is the fractional abundance of the respective product and [CH4] is the particle density of the neutral. Further details have been elaborated in the supplement by Plamper et al.26
is the pseudo-first order rate constant of the total reaction, faproduct is the fractional abundance of the respective product and [CH4] is the particle density of the neutral. Further details have been elaborated in the supplement by Plamper et al.26
Rate constants can either be transformed into cross sections employing eqn (2) assuming the velocity of the neutral target is negligible compared to that of the ion under the conditions chosen, or directly via the approach described by Armentrout.32 Here, the fact that the neutral target molecules are not at rest but exhibit an isotropic velocity distribution in laboratory space does not affect the value of the center of mass collision energy but its distribution.33,34 This corresponds to an uncertainty in Ecm as discussed by Plamper et al.26 As a consequence, reaction barriers may effectively be overcome at an Ecm nominally below that barrier. In the Ecm domain this uncertainty is on the order of ±130 meV.
 | (2) |
Experimental cross sections are complemented by theoretical data, in part derived from analytical models, but ultimately also from sophisticated molecular dynamics calculations.
For the exothermic reaction channels the experimental data are compared to the Langevin-model. According to the Langevin-model, the cross section of an exothermic ion–molecule reaction is given by35,36
 | (3) |
For target molecules with non-zero permanent dipole moment Su and Bowers developed a modified Langevin theory, the approximate dipole orientation (ADO) theory.37 Since the permanent dipole moment of the CH4 is very small (approx. 10−6 Db at room temperature),38 its justified to stay with the classical Langevin model of eqn (3). Empirically, the energy dependence of cross sections for exothermic reaction channels often deviates from the (1/Ecm)0.5 characteristic. To reflect this, the experimental data are modeled by eqn (4).
 | (4) |
For endothermic reaction channels, exhibiting an energetic threshold or a barrier to be overcome before reaction can proceed,40 the cross section can be modeled by eqn (5)41
 | (5) |
Throughout this work we will fix the value of n to n = 1. The classical loc model would be expected to apply for e.g. atom–atom reactions but also to reactions dominated by the center mass of two reactants.
For more complex reactions it may be necessary to account for sterical effects. In the simplest case one can define two line of centers and the angle between these two lines. In the reaction system investigated in this work one loc is the HBr+ axis, the second loc can be chosen to be the Br–C axis. For such a situation Levine and Bernstein suggested eqn (6) which takes into account this effect of relative orientation in a parameterized form.40,43,45 Here, D is the critical separation, which can be smaller than the hard-sphere separation,  is the negative derivative of the reaction energy profile with respect to the cosine of the angle between the two axis mentioned above.43eqn (6) will be applied to the bromine transfer channel.
is the negative derivative of the reaction energy profile with respect to the cosine of the angle between the two axis mentioned above.43eqn (6) will be applied to the bromine transfer channel.
 | (6) |
Alternative models for describing cross sections for endothermic reactions have been elaborated in the literature.18,19,40,43,45,47
Potential energy profile calculation
Although there have been studies on ion–molecule reaction involving HBr+,26,48–51 a detailed potential energy profile of the CH4 + HBr+ reaction has not been reported. The relativistic effects experienced by the core electrons of Br could be accounted for by an appropriate basis set with an effective core potential (ECP),52 which replaces the explicit treatment of these electrons. Hundreds of combinations of computationally efficient methods (DFT and MP2) and basis sets with different ECPs were performed on a similar reaction (HBr+ + HCl), where the frozen core MP2 (fc-MP2)53 in general is more accurate in representing the benchmark potential energy profile computed at the CCSD(T)/cc-pVDZ//CCSD(T)/CBS level of theory.48 Therefore, fc-MP2 with five different ECPs for the bromine atoms (pseudopotential (PP),54 LANL2DZ,55 LANL2DZdp,55,56 CRENBL,57 Stuttgart RLC58) and cc-pVTZ59,60 for carbon and hydrogen atoms have been examined to find an appropriate method for the stationary point geometry search. The heat of potential reactions is summarized in Table 1 and compared with experimental values. The latter are available for the PT, the CT and the HA reaction channels based on the 0 K heat of formation for HBr+ (2Π3/2) (1097.83 kJ mol−1),61 Br (2P3/2) (117.91 kJ mol−1),61 CH4 (−66.55 kJ mol−1) CH5+ (921.98 kJ mol−1), CH3 (149.87 kJ mol−1), CH4+ (1150.68 kJ mol−1), H2Br+ (924.20 kJ mol−1), HBr (−27.85 kJ mol−1). It is important to note that neither fc-MP2 nor CCSD(T) accounts for spin–orbit (SO) coupling effect in HBr+ or Br, whereas the experimental heat of formation of these species are measured at ground SO state. Therefore, the SO coupling energies reported by Fujioka et al.,48 are used to calibrate the experimental heat of formation of HBr+ (2Π3/2) or Br (2P3/2) to obtain the “spin-free” experimental heat of reaction. For HBr+, the four-fold degenerate spin free 2Π state splits into two double-degenerate (2Π1/2 and2Π3/2) states, thus the spin free energy state lies halfway between the two SO states. Hence, half of the SO coupling energy (31.65 kJ mol−1)62,63 is added to the experimental heat of formation of HBr+ (2Π3/2) to obtain the 2Π spin free energy of HBr+. For Br, the six-fold degenerate SO states split into double degenerate 2P1/2 state and quadruple degenerate 2P3/2 state. The SO states are split in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio and hence, the spin free energy state 2P is obtained by adding one-thirds of the SO coupling energy (43.64 kJ mol−1) to the experimental heat of formation of Br (2P3/2). This protocol offers a fair comparison of the heats of reaction obtained between calculations and experiments.24,48,49 Among the five ECPs tested, only PP gives good agreement (RMSE = 6.32 kJ mol−1) with the experimental heat of the reaction. Note the calculation without any ECP on Br gives a comparable result (RMSE = 7.44 kJ mol−1) as PP, but it is 5 times slower. Therefore, PP is selected as the ECP and fc-MP2/cc-pVTZ-PP is employed to explore the potential energy surface of the reaction. The transition states search is carried out with nudged elastic band (NEB)64 calculations and their connections to intermediates are confirmed with intrinsic reaction co-ordinate (IRC)65 calculations. The identity of critical points is confirmed by harmonic frequency calculations with 3N-6 (N is the number of atoms in the system) positive frequencies for the intermediates, and 3N-7 positive frequencies for the transition states with one imaginary frequency along the reaction coordinate. The critical points identified at the fc-MP2/cc-pVTZ-PP level of theory is reoptimized with coupled cluster with single and double excitations and perturbative triples with explicitly correlated F12 method (CCSD(T)-F12)66–68 for better accuracy. As shown in Table 1, the RMSE associated with the CCSD(T)-F12/cc-pVDZ-PP-F12 level of theory is only 6.65 kJ mol−1. The CCSD(T)-F12/cc-pVDZ-PP-F12 potential energy profile is used as the benchmark to screen computationally efficient method for dynamics simulations.
2 ratio and hence, the spin free energy state 2P is obtained by adding one-thirds of the SO coupling energy (43.64 kJ mol−1) to the experimental heat of formation of Br (2P3/2). This protocol offers a fair comparison of the heats of reaction obtained between calculations and experiments.24,48,49 Among the five ECPs tested, only PP gives good agreement (RMSE = 6.32 kJ mol−1) with the experimental heat of the reaction. Note the calculation without any ECP on Br gives a comparable result (RMSE = 7.44 kJ mol−1) as PP, but it is 5 times slower. Therefore, PP is selected as the ECP and fc-MP2/cc-pVTZ-PP is employed to explore the potential energy surface of the reaction. The transition states search is carried out with nudged elastic band (NEB)64 calculations and their connections to intermediates are confirmed with intrinsic reaction co-ordinate (IRC)65 calculations. The identity of critical points is confirmed by harmonic frequency calculations with 3N-6 (N is the number of atoms in the system) positive frequencies for the intermediates, and 3N-7 positive frequencies for the transition states with one imaginary frequency along the reaction coordinate. The critical points identified at the fc-MP2/cc-pVTZ-PP level of theory is reoptimized with coupled cluster with single and double excitations and perturbative triples with explicitly correlated F12 method (CCSD(T)-F12)66–68 for better accuracy. As shown in Table 1, the RMSE associated with the CCSD(T)-F12/cc-pVDZ-PP-F12 level of theory is only 6.65 kJ mol−1. The CCSD(T)-F12/cc-pVDZ-PP-F12 potential energy profile is used as the benchmark to screen computationally efficient method for dynamics simulations.
| Method | PT (p1): CH5+ + Br | HA (p2): CH3 + H2Br+ | CT (p3): CH4+ + HBr | BT (p4): CH4Br+ + H | RMSE | |
|---|---|---|---|---|---|---|
| Experimental at 0 K, SO ground state | 8.61 (0.089) | 42.79 (0.443) | 91.55 (0.949) | — | — | |
| “spin free” experimental | 7.09 | 27.83 | 75.74 | — | — | |
| CCSD(T)-F12/cc-pVDZ-F12 | 5.08 | 30.71 | 86.71 | 25.75 | 6.65 | |
| fc-MP2/cc-pVTZ- | — | 15.63 | 27.62 | 82.61 | 8.08 | 7.44 |
| PP | 17.34 | 26.85 | 83.49 | 16.30 | 6.32 | |
| LANL2DZ | 67.42 | 30.74 | 142.74 | 37.50 | 52.08 | |
| LANL2DZdp | 38.19 | 38.01 | 112.20 | 21.44 | 28.28 | |
| CRENBL | 110.40 | −10.92 | 133.10 | 1.55 | 71.79 | |
| Stuttgart RLC | 60.91 | 32.78 | 133.64 | 40.54 | 45.72 | |
Reaction dynamics simulation
The bimolecular reactions of interest are also studied using ab initio molecular dynamics (AIMD) simulations, in which the trajectories are propagated classically using the energy gradients computed on the fly with the fc-MP2/6-311G(d,p)53,69 level of theory. fc-MP2/6-311G(d,p) has been shown to accurately represent the dynamics of similar reactions24,26 and its accuracy is further justified in this reaction system (see Results). Separated by 8.0 Å (center of mass distance) with random orientations, HBr+ is fixed at its ground rotational and vibrational state and the rotational and vibrational states of CH4 are selected from a Boltzmann distribution at 298 K to mimic the experimental conditions. Three out of the five collision energies studied in the experiments have been simulated with AIMD, e.g., 0.5, 2.0 and 3.0 eV. A chemical dynamics software VENUS70 is employed to sample the initial conditions and to propagate the trajectory, which is interfaced with NWChem71 for ab initio energy gradients. Velocity verlet72 with a time step of 0.15 fs is used to propagate the trajectories, and for those having energy jumps greater than 1 kcal mol−1, the time step is reduced and restarted with the same initial conditions. The simulation is stopped when the two molecules (either reactive or unreactive) are separated by a center of mass distance of 12 Å. The impact parameter (b) is sampled discretely with a fixed stride (Δb). Firstly, bmax (maximum impact parameter beyond which no reactive trajectories are observed) is identified by sampling 100 trajectories at each b with Δb of 0.5 Å from 0 to 6 Å. For collisions energies of 0.5 eV, 2.0 and 3.0 eV, the bmax are 4.5 Å, 4 Å and 4 Å respectively. After detecting bmax, 50 (for 0.5 eV collision energy) or 60 (2.0 and 3.0 eV collision energy) AIMD trajectories are carried out at impact parameters separated by Δb of 0.25 Å between 0 and the bmax at each collision energy, yielding a total of 950, 1020 and 1020 trajectories for collision energies of 0.5, 2.0, and 3.0 eV, respectively.The AIMD trajectories are further used as the training set to develop a machine learning (ML) potential to carry out simulations at a much faster rate. 171![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 955 unique geometries (selected by comparing distance matrices, made of the reverse of pairwise distances between all atoms in the system, of configurations from AIMD trajectories with a threshold of 0.001 Å−1) and their energy and gradients are employed as the initial training (75%) and validation (25%) set. Several iterations of active learning were carried out – a preliminary trained ML-PES was used to propagate MLMD trajectories to potentially obtain novel geometries, which (along with their energy and gradients) were added to the training set and produce a new ML-PES. Schnetpack73,74 v1.0 is used for all ML-PES training and predictions. The MLMD trajectories are simulated using ASE's velocity Verlet integrator with a timestep of 0.15 fs and stopped when any two atoms are more than 20 Å apart. The MLMD trajectories are simulated starting from b = 0 with fixed increment Δb of 0.1 Å to bmax. The estimated bmax is 4.5, 3.8 and 3.8 Å for 0.5, 2.0 and 3.0 eV collision energies. Trajectories are rejected and restarted if the vibrational energy is lower than the zero-point energy for any species. The number of trajectories simulated at collision energies of 0.5, 2.0, and 3.0 eV, are 10
955 unique geometries (selected by comparing distance matrices, made of the reverse of pairwise distances between all atoms in the system, of configurations from AIMD trajectories with a threshold of 0.001 Å−1) and their energy and gradients are employed as the initial training (75%) and validation (25%) set. Several iterations of active learning were carried out – a preliminary trained ML-PES was used to propagate MLMD trajectories to potentially obtain novel geometries, which (along with their energy and gradients) were added to the training set and produce a new ML-PES. Schnetpack73,74 v1.0 is used for all ML-PES training and predictions. The MLMD trajectories are simulated using ASE's velocity Verlet integrator with a timestep of 0.15 fs and stopped when any two atoms are more than 20 Å apart. The MLMD trajectories are simulated starting from b = 0 with fixed increment Δb of 0.1 Å to bmax. The estimated bmax is 4.5, 3.8 and 3.8 Å for 0.5, 2.0 and 3.0 eV collision energies. Trajectories are rejected and restarted if the vibrational energy is lower than the zero-point energy for any species. The number of trajectories simulated at collision energies of 0.5, 2.0, and 3.0 eV, are 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 350, 8200 and 8200, respectively.
350, 8200 and 8200, respectively.
Results
Experimental results
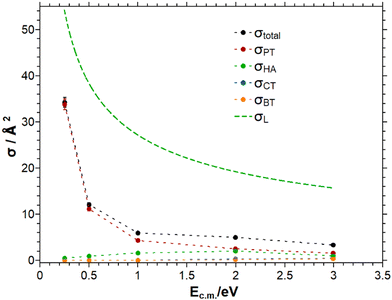
Experiments have been performed with HBr+ prepared in the upper SO state. The question whether the SO energy (0.328 eV62,63) is available to the reaction coordinate, will be discussed below.The analysis of the mass spectra results in the observation of four different reaction channels. These are namely the proton transfer (PT), the hydrogen abstraction (HA), the charge transfer (CT) and the bromine transfer (BT). The mass spectra is provided in the ESI.† In Fig. 2 the cross section of the total reaction and all observable reaction channels is shown as a function of the collision energy for an ion rotational energy of 3.4 meV.
The total cross section decreases with increasing collision energy as does the PT reaction cross section, which dominates the total cross section for collision energies below 2 eV. At collision energies above 2 eV the HA reaction becomes comparable to the PT reaction. The CT and BT reactions are the least efficient reactions and both of the same order of magnitude. Below 1 eV collision energy the latter channels do not proceed to a measurable extent. The total cross section is significantly below the Langevin prediction indicating that approximately every 4th collision leads to a reactive process.
Tichy et al. studied the reaction of HBr+ with CH4 in a SIFDT apparatus. The cross sections measured by Tichy et al. are larger than the numbers measured in this work, but in the same order of magnitude.75 One difference between the work of Tichy et al. and this work concerns the ion preparation: in this work the HBr+ is prepared in selected rovibronic states, whereas Tichy et al. employed electron impact ionization, presumably leading to a broader distribution of ionic states. In both studies, the PT reaction is the most efficient reaction at low collision energies. At collision energies around 1 to 2 eV center of mass the PT channel becomes comparable to the HA channel. The CT reaction is in both studies the least efficient reaction. In the present study this reaction channel has a threshold of around 0.5 eV, comparable to the earlier study by Tichy et al.75
In Fig. 3 the collision energy dependence of the PT reaction is presented. The different traces correspond to different ion rotational energies. The cross section decreases with increasing collision energy. Table 1 indicates a slightly positive heat of reaction for the PT channel referenced to the SO ground state of the HBr+. Here, the experimental observation of a cross section significantly decreasing with increasing collision energy suggests that the SO energy of the HBr+ ion prepared in the X2Π1/2 electronic state is available to the reaction, turning it effectively into an exothermic channel.
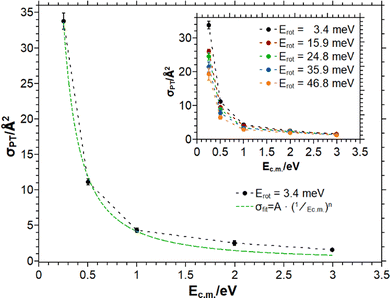 | ||
| Fig. 3 σ PT as a function of the collision energy Ecm for different ion rotational energies. The green dotted curve is the Langevin fit to the data for Erot = 3.4 meV according to eqn (4). | ||
In Table 2 the fit parameters for the PT reaction are assembled. Within the error margins the exponent n emerges constant. The decrease is much steeper than predicted by the Langevin model. With increasing rotational energy, the cross section decreases significantly, which is recognizable in Fig. 4 and indicated by the parameter A.
| E rot/meV | A/(Å2·eVn) | n |
|---|---|---|
| 3.4 | 4.16 ± 0.47 | −1.52 ± 0.09 |
| 15.9 | 3.93 ± 0.38 | −1.37 ± 0.07 |
| 24.8 | 3.55 ± 0.39 | −1.4 ± 0.09 |
| 35.9 | 3.3 ± 0.39 | −1.36 ± 0.09 |
| 46.8 | 2.68 ± 0.43 | −1.43 ± 0.12 |
Fig. 4 illustrates σPT as a function of the ion rotational energy. The cross section is highly dependent on this degree of freedom. By using the Langevin fit for the rotational energy of 3.4 meV the cross section decreases by the same amount in collision energy by 8.4 Å2 over 50 meV, whereas the same amount of rotational energy at 0.25 eV collision energy leads to a decrease of 13 Å2. Thus, the rotational motion of the ion has a larger influence on the reaction dynamics than the center of mass collision energy and is not only an additive contribution to the total excess energy.
As indicated in Fig. 5 the cross section of the HA reaction increases with increasing collision energy as expected for an endothermic reaction channel. The threshold behavior of σHA is modelled by eqn (5) fixing n = 1 in the range from Ecm = 0.25 eV up to 2 eV (i.e., the maximum of σHA). The fit parameters A, E0 and m are summarized in Table 3.
 | ||
| Fig. 5 σ HA as a function of the collision energy shown for the investigated ion rotational energies. The applied fit model is discussed in the text below and summarized in eqn (5). | ||
| E rot/meV | A/Å2 eVm−1 | E 0/eV | m |
|---|---|---|---|
| 3.4 | 1.81 ± 0.16 | 0.16 ± 0.04 | 0.70 ± 0.12 |
| 15.9 | 2.03 ± 0.19 | 0.18 ± 0.04 | 0.83 ± 0.14 |
| 24.8 | 1.95 ± 0.01 | 0.15 ± 0.01 | 0.72 ± 0.01 |
| 35.9 | 2.11 ± 0.41 | 0.06 ± 0.12 | 0.60 ± 0.23 |
| 46.8 | 1.92 ± 0.04 | 0.09 ± 0.01 | 0.62 ± 0.03 |
Note, that the center of mass collisional energy as well as the rotational energy may help in overcoming the chemical threshold for the reaction. This fact is reflected in the observation, that the effective E0 fitted to the data decreases with increasing rotational energy (cf.Table 3). The decrease in E0 is in fact comparable to the concomitant increase in the rotational energy. The reaction barrier E0 derived (ca. 0.16 eV) matches well the heat of reaction assuming the SO energy of HBr+ is available to the reaction (0.443–0.328 eV).
At 2 eV Ecm the cross section has a distinct maximum. At even higher collision energies the cross section decreases significantly. The increase up to 2 eV can be modelled by the classical loc model suggesting that no angle dependence of the HA reaction is operative. This appears in line with the intuitive expectation, because the transition state for the HA reaction should not involve steric requirements. As complementation, a plot of the cross section for HA as a function of the rotational energy is presented in the ESI.†
In Fig. 6 the collision energy dependence of the CT reaction is presented. The green dotted line is a fit to the data for Erot = 3.4 meV according to eqn (5) with n and m equaling unity and a scaling factor A which reflects the line of centers (loc) model. All parameters obtained in the analysis of the CT reaction channel are listed in Table 4.
| E rot/meV | A/Å2 | E 0/eV |
|---|---|---|
| 3.4 | 0.63 ± 0.05 | 0.98 ± 0.06 |
| 15.9 | 0.63 ± 0.03 | 0.96 ± 0.03 |
| 24.8 | 0.55 ± 0.06 | 0.92 ± 0.08 |
| 35.9 | 0.52 ± 0.03 | 0.93 ± 0.05 |
| 46.8 | 0.52 ± 0.04 | 0.98 ± 0.06 |
The model fits the experimental data quite well. The threshold of the reaction, E0, is found to be 0.95 ± 0.03 eV for all investigated rotational energies. The almost exact agreement between this threshold and the experimental heat of reaction given in Table 1 is fortuitous. In principle the true molecular threshold could be higher than the numbers given in Table 1 due to the smearing out of center of mass collision energies.34 For a step like model for the cross section this could lead to observing products some 0.25 eV below the true threshold. For the rather shallow increase of σ with Ecm as operative in the loc model (and also in the modified loc model), convolution with the thermal velocity distribution of the neutral target reveals an effective additional smearing out which is below 50 meV. Given the limited number of data points we would be reluctant to overinterpret the threshold values. On the other hand, it suggests that the SO energy deposited in the HBr+ ion upon preparation is not available for the reaction in this channel. Evaluating the PES of the CT reaction (cf.Fig. 8(c)) there is no indication of additional activation barriers. As complementation, a plot of the cross section for CT as a function of the rotational energy is presented in the ESI.†
In Fig. 7 the collision energy dependence of the BT reaction is presented. Overall, the efficiency of the BT reaction is comparable to that of the CT reaction. However, the characteristics of the variation of σ with Ecm is distinctly different.
Below 1 eV collision energy no reaction is observable. Above this threshold, the cross section for BT has been fitted both by the simple loc model and the modified loc model. Quite obviously the modified loc model fits significantly better to the experimental data shown in Fig. 7. We conclude that the BT channel must be subject to sterical restriction. Note, that in the modeling, the critical distance D was chosen to be 2.53 Å using the covalent radii of H, Br and C. An overview over the fit parameter obtained for all rotational energies of the HBr+ is given in Table 5. As complementation, a plot of the cross section for BT as a function of the rotational energy is presented in the ESI.†
The data shows the typical behavior of a reaction with a threshold. The ab initio potential energy surface (cf.Fig. 8(d)) shows an activation barrier for the spin-free BT reaction channel lying around 0.54 eV. Since the calculation of that PES is based on a spin-free Hamiltonian, the true spin–orbit energies for HBr+ in the 2Π3/2 and 2Π1/2 would correlate with barriers being approximately 0.16 eV higher or lower respectively. The experimental finding of an effective threshold around 1 eV possibly indicates that the spin orbit energy of the HBr+ is not available for the BT reaction coordinate, similar to the CT.
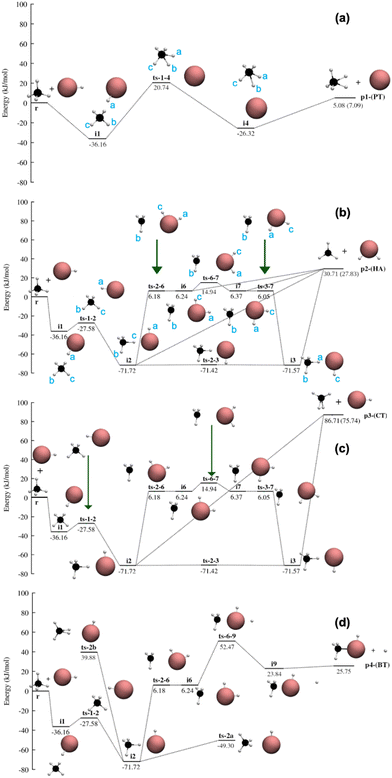 | ||
| Fig. 8 Potential energy profile of PT (a), HA (b), CT (c) and BT (d) reaction channels at CCSD(T)-F12/cc-pVDZ-PP-F12 level of theory with ZPE included. The atoms are represented as black (C), maroon (Br) and white (H). The energies in parentheses are experimental heats of reaction. The coordinates of these stationary points are given in the ESI.† | ||
As mentioned above the collision energy dependence of CT and BT reaction channels exhibits a characteristic difference. While σCT shows a right-curved characteristic above the threshold, well represented by the classical loc model, σBT shows a left-curved characteristic above the threshold only represented by the modified loc model. As a consequence, it is concluded that the BT reaction channel is angle-dependent in contrast to the CT reaction channel, where sterical orientation does not appear to play a role.
The potential energy profile
The potential energy profile of the proton transfer (PT) pathway is shown in Fig. 8(a), where the proton from HBr+ is transferred to CH4 forming Br (2P) atom and CH5+ (carbonium ion). The barrierless association between CH4 and HBr+ (r) forms a van der Waals (vdW) complex i1 (−36.16 kJ mol−1 with respect to separated reactant, r) where the proton from HBr+ (Ha) is pointing towards the CH4 molecule. i1 isomerizes to another vdW complex i4 (−26.32 kJ mol−1) via a transition state ts-1-4 that is 20.74 kJ mol−1 above r. Following the IRC of ts-1-4, Br pivots around CH5+ and moves from coordinating with Ha in i1 to Hb (∠C–Hb–Br = 180°) in i4. This pivoting mechanism is a result of the 3 centered 2 electron bond of Ha–C–Hb where Ha and Hb possess most of the partial positive charges. Cs symmetry is maintained throughout the path where Br–Ha–C–Hb–Hc are in the same plane. i4 can dissociate without a transition state to form p1 (Br (2P) + CH5+). The PT reaction is endothermic by 5.08 kJ mol−1 with an overall barrier of 20.74 kJ mol−1 (ts-1-4). The structure and reactivity of CH5+ has been extensively studied in the literature76–86 since its discovery in the 1950s which show that CH5+ is highly fluxional with many different local minimum structures.87 But the global minimum among them is the Cs(I) structure88 as depicted in the Fig. 8(a). It is important to note that experimental and previous dynamics study of CH5+ have shown its tendency to dissociate into CH3+ and H2 molecule,77 which is out of the scope of the present work.The potential energy profile of the hydrogen abstraction (HA) pathway is shown in Fig. 8(b), where HBr+ abstracts one hydrogen atom from CH4 to form planar CH3 radical (D3h) and H2Br+ (C2v). The vdW complex i1 (−36.16 kJ mol−1, see the PT pathway) is connected to a submerged barrier ts-1-2 (−27.58 kJ mol−1), where HBr+ (instead of just Br as seen in the PT pathway) pivots around CH4 to form i2 (−71.72 kJ mol−1). i2, stabilized by the hydrogen bond between Hc and Br, possesses a ‘staggered’ conformation where the dihedral angle of Ha–Br–C–Hb is 180°. ts-2a (−49.30 kJ mol−1) (Fig. 8(d)) is a self-isomerization transition state of i2, where CH4 tumbles, but does not lead to the products. CH4 in i2 could also rotate with respect to C–Hc–Br axis to form the ‘eclipsed’ conformer i3 (−71.57 kJ mol−1), where the dihedral angle of Ha–Br–C–Hb is 0°. The corresponding transition state of this rotation, ts-2-3 (−71.42 kJ mol−1), is well less than 1 kJ mol−1 compared to i2 and i3. The H atom in the CH4 group of i2 and i3 can transfer to Br, forming p2 without a transition state. p2 could also be formed without a transition state via vdW complexes i6 (6.24 kJ mol−1) and i7 (6.37 kJ mol−1), where the H has already transferred from CH4 to HBr, but the newly formed H2Br+ has not dissociated. i6 (‘staggered’) and i7 (‘eclipsed’) are roaming complexes formed from its corresponding H-bond complex i2 and i3, which can also isomerize to one another via transition state ts-6-7 (14.94 kJ mol−1). The C–Br distance changes from 2.92 Å (i6) → 3.21 Å (ts-6-7) → 2.92 Å (i7) in this process on a relative flat potential energy profile. The HA reaction is endothermic by 30.71 kJ mol−1.
The potential energy profile of the charge transfer (CT) pathway is shown in Fig. 8(c), where an electron is transferred from CH4 to HBr+. The CT reaction pathway is very similar to the HA pathway, except p3 is only formed via a barrierless dissociation of i2 and i3 (not i6 and i7). CH4 changes from Td point group to C2v point group after losing an electron, while the H–Br bond length decreased from 1.43 Å to 1.40 Å after gaining an electron. The CT reaction is the most endothermic (86.71 kJ mol−1) among all the reaction pathways.
The potential energy profile of the bromine transfer (BT) is shown in Fig. 8 (d), which forms CH4Br+ (Cs) and H. As noted in the method section, although the experimental heat of formation of CH4Br+ is not known to date, there is one ion-beam experiment tentatively speculating its formation.89 Theoretical investigation by Chistyakov et al.90 reported the geometries and energies of CH4Br+ as intermediates of the CH4 + Br+ → BrH + CH3+ reaction. While the level of the theory (MNDO/PM3) in Chistyakov et al. is not considered as state of the art anymore, its reported structure (Fig. 8(d)) agrees with CCSD(T)-F12/cc-pVDZ-PP-F12 geometry optimization in this study. Electron density analysis shows that the net positive charge is mostly concentrated on Br. The BT reaction pathway follows the reaction pathways of HA and CT until i6. The H2Br in i6 could recombine with CH3 and form a vdW complex, i9 (23.84 kJ mol−1), after crossing a barrier (ts-6-9) of 52.74 kJ mol−1. According to fc-MP2/cc-pVTZ-PP, several vdW complexes similar to i9 have been identified with the H atoms at different positions with respect to CH4Br+, suggesting a roaming region in the potential energy surface. However, these stationary points could not be confirmed with CCSD(T)-F12/cc-pVDZ-PP-F12 level of theory, thus they are not reported in Fig. 8. Further i9 dissociates to p4 without a transition state. The BT reaction is endothermic (25.75 kJ mol−1) with an overall barrier of 52.47 kJ mol−1 (ts-6-9).
Computationally efficient method for AIMD simulations
The potential energy profile is informative for a conceptual understanding of the mechanism of the reaction, but it relies on the assumptions that the reaction behaves statistically (sufficient lifetime of each intermediate) and strictly follows the IRC. Numerous examples have shown that these assumptions are not necessarily true in bimolecular reactions,24,26,49,91–94 thus ab initio molecular dynamics (AIMD) simulations are carried out. In AIMD, the positions of the atoms are propagated by the classical equations of motion with the potential energy gradients computed using quantum chemistry on the fly. AIMD demands an enormous number of gradient calculations, often in the order of millions to sample an ensemble of trajectories (of different orientations, impact parameters, etc.) that represent the experimental conditions. Therefore, it is imperative to screen different computationally efficient methods for one that can accurately characterize the potential energy profile. In the current study of CH4 + HBr+ bimolecular reaction, the collision energies in the experiments range from 48.25 kJ mol−1 (0.5 eV) to 289.46 kJ mol−1 (3.0 eV). According to the CCSD(T)-F12/cc-pVDZ-PP-F12 potential energy profile, all stationary points reported in Fig. 8 are within the energy range thus should be included in selecting the quantum chemistry method for AIMD.Both frozen core and non-frozen core MP2 has been screened in this study due to our previous experiences with similar reaction systems.26,49 15 different basis sets, including 6-311G(d,p),95,96 aug-cc-pVTZ-PP,59,60,97 aug-cc-pVTZ,59,60,97 pc-1,98,99 pc-2,98,99 aug-pc-1,98,99 aug-pc-2,98,99 cc-pVDZ,59,60 cc-pVDZ-PP,59,60 cc-pVTZ,59,60 cc-pVTZ-PP,59,60 def2-SVP,100 def2-SVPD,100 def2-TZVP100 and def2-TZVPD,100 are screened. Each method/basis set attempts to identify the stationary points found by CCSD(T)-F12/cc-pVDZ-PP-F12. An appropriate method/basis set for AIMD simulation should be able to identify all stationary points in Fig. 8 and have a small root mean square deviation (RMSD) with the benchmark PES. The RMSD of a candidate method/basis set (A) is computed as:
 | (7) |
 | (8) |
 ) and CCSD(T)-F12/cc-pVTZ-PP-F12 (
) and CCSD(T)-F12/cc-pVTZ-PP-F12 ( ). i is the index of stationary points. Table 6 contains the RMSD of the screened candidate method/basis set for AIMD simulations. It is important to note that Table 6 only assesses the performance of these methods on the CH4 + HBr+ bimolecular collision and should not be taken as a comparison of their general performance. The same convergence criteria such as maximum (1.5 × 10−5 hartree bohr−1) and RMSD (1.0 × 10−5 hartree bohr−1) change in energy gradient, maximum (6.0 × 10−5 bohr) and RMSD (4.0 × 10−5 bohr) change in coordinates are applied to all candidate methods. fc-MP2/def2-SVPD, MP2/aug-cc-pVTZ, MP2/aug-cc-pVTZ-PP, and MP2/cc-pVTZ fail to optimize i6, i7, and i9, hence their RMSDs are marked as n/a and are not considered further. The results show that both fc-MP2 and MP2 have fairly low RMSD with all tested basis set, with the lowest (9.1 kJ mol−1) and largest (16.1 kJ mol−1) RMSD found in fc-MP2/cc-pVTZ-PP and MP2/pc-1, respectively. Considering the cost of MP2 method scales as N5
). i is the index of stationary points. Table 6 contains the RMSD of the screened candidate method/basis set for AIMD simulations. It is important to note that Table 6 only assesses the performance of these methods on the CH4 + HBr+ bimolecular collision and should not be taken as a comparison of their general performance. The same convergence criteria such as maximum (1.5 × 10−5 hartree bohr−1) and RMSD (1.0 × 10−5 hartree bohr−1) change in energy gradient, maximum (6.0 × 10−5 bohr) and RMSD (4.0 × 10−5 bohr) change in coordinates are applied to all candidate methods. fc-MP2/def2-SVPD, MP2/aug-cc-pVTZ, MP2/aug-cc-pVTZ-PP, and MP2/cc-pVTZ fail to optimize i6, i7, and i9, hence their RMSDs are marked as n/a and are not considered further. The results show that both fc-MP2 and MP2 have fairly low RMSD with all tested basis set, with the lowest (9.1 kJ mol−1) and largest (16.1 kJ mol−1) RMSD found in fc-MP2/cc-pVTZ-PP and MP2/pc-1, respectively. Considering the cost of MP2 method scales as N5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48 where N is the number of basis functions which ranges between 52 (fc-MP2/cc-pVDZ-PP) and 220 (MP2/aug-pc-2), the cost of these candidate method/basis sets varies dramatically. Generally speaking, the level of theory with an RMSE of ∼10 kJ mol−1 or smaller could be used for trial runs, where the energy conservation of the trajectory, the stability of molecular orbital, and the converging speed will be used to further select a quantum chemistry method for AIMD simulations.
48 where N is the number of basis functions which ranges between 52 (fc-MP2/cc-pVDZ-PP) and 220 (MP2/aug-pc-2), the cost of these candidate method/basis sets varies dramatically. Generally speaking, the level of theory with an RMSE of ∼10 kJ mol−1 or smaller could be used for trial runs, where the energy conservation of the trajectory, the stability of molecular orbital, and the converging speed will be used to further select a quantum chemistry method for AIMD simulations.
| fc-MP2 | RMSD (kJ mol−1) | MP2 | RMSD (kJ mol−1) |
|---|---|---|---|
| 6-311G(d,p) | 10.7 | 6-311G(d,p) | 11.2 |
| aug-cc-pVTZ | 9.9 | aug-cc-pVTZ | n/a |
| aug-cc-pVTZ-PP | 10.5 | aug-cc-pVTZ-PP | n/a |
| aug-pc-1 | 15.1 | aug-pc-1 | 15.1 |
| aug-pc-2 | 10.3 | aug-pc-2 | 10.9 |
| cc-pVDZ | 11.4 | cc-pVDZ | 11.0 |
| cc-pVDZ-PP | 10.8 | cc-pVDZ-PP | 10.9 |
| cc-pVTZ | 9.4 | cc-pVTZ | n/a |
| cc-pVTZ-PP | 9.1 | cc-pVTZ-PP | 9.3 |
| pc-1 | 15.6 | pc-1 | 16.1 |
| pc-2 | 12.4 | pc-2 | 13.5 |
| def2-SVP | 12.4 | def2-SVP | 13.9 |
| def2-SVPD | n/a | def2-SVPD | 10.4 |
| def2-TZVP | 11.2 | def2-TZVP | 13.0 |
| def2-TZVPD | 11.5 | def2-TZVPD | 11.2 |
Simulation results
All four reaction channels observed in experiments are detected in simulations and their cross sections are compared in Fig. 9. First, it is interesting to note that trace amount of hydrogen exchange (HE, hydrogen from HBr+ ion is exchanged with one of the hydrogens from neutral CH4 molecule) reactions is detected in the simulation (e.g., cross section ∼0.01 Å2), which cannot be distinguished from the non-reactive collisions in the guided-ion beam experiments. Second, for the PT (proton from HBr+ ion is transferred to CH4 molecule, forming neutral Br atom and CH5+ carbonium ion) reaction, the cross section obtained from the simulation agrees well with the experiment. While the simulations in general overestimate the cross section of HA (hydrogen from CH4 is transferred to HBr+ ion, forming H2Br+ ion and neutral CH3 radical), BT (the Br from HBr+ is transferred to CH4 molecule, forming CH4Br+ ion and hydrogen atom), and CT (single electron is transferred from neutral CH4 molecule to HBr+ ion, forming neutral HBr molecule and CH4+ ion) reactions, they qualitatively reproduce the trend observed in the experiment, including the local maximum observed in the HA reaction at 2.0 eV collision energy. The simulations also reproduce the relative branching ratios of the products, for example, at 0.5 eV collision energy, nearly 88 ± 10% of the reactive trajectories yield PT products and the remaining 12 ± 2% are HA products; no CT or BT products are observed. This is in good agreement with the experiment where the reaction cross section of CT and BT products are negligible, while the cross section of HA is about one order of magnitude smaller than the PT. At higher collision energies (i.e., 2.0 eV and 3.0 eV), the agreement becomes only qualitative due to the overestimate of the cross section for HA, BT, and CT reactions. Nonetheless, the simulations agree with the experiments that PT is the most predominant reaction, followed by HA.Ion–molecule collisions yield products via direct and indirect mechanism26,48,49,93,94,101–105 with their scattering angle measured according to the illustration in Fig. 10. Reactive trajectories which do not form long-lived intermediates are classified as direct reactions. Following the convention of other ion–molecule reactions, direct reactions are classified as direct rebound (DR) and direct stripping (DS), where DR is mostly observed at small impact parameters and direct stripping (DS) is mostly observed at large impact parameters. The scattering angle distribution of direct reactions of each reaction will be discussed in detail later in the manuscript. Reactive trajectories with significant lifetime of the collision complex are classified as indirect reactions, whose collision complex is long-lived (e.g., longer than the time for intramolecular vibrational energy redistribution) before dissociating into products, and as a result, yielding a near isotropic scattering angle distribution.
Snapshots of representative trajectories of different reaction mechanisms in all pathways are provided in Fig. 10. Taking the dynamics of the reaction in the case of 2.0 eV collision energy as an example, a strong correlation between the reaction pathway and the scattering angle is observed. Fig. 11 shows the scattering angle distributions for all four reaction pathways. As noted earlier, PT and HA are the predominant reactions. The PT reaction shows large scattering angles, where the product ion leaves in the opposite direction as the reactant ion, indicating the dominance of the DS mechanism (Fig. S6(b), ESI†). The DS mechanism is also the dominating mechanism for the HA reaction (Fig. S6(c), ESI†), but in this case, resulting in small scattering angle, where the product ion leaves in the same direction as the reactant ion. Overall, the dynamics of the PT and HA reactants are in accordance with what have been reported in similar ion–molecule bimolecular collisions, e.g., HBr+ + HCl and HCl+ + HCl.24,26
 | ||
| Fig. 11 The scattering angle distribution (overall, gray; PT, green; HA, blue; BT, red; and pink, CT) from the simulation for 2.0 eV. | ||
CT and BT are two minor reaction pathways observed in this reaction (Fig. 9). CT reaction takes place only via direct mechanism across all impact parameters. This result is similar to what Luo et al.24 reported in the study of the HCl+ + HCl bimolecular collision, although the strong selectivity of the entrance channel complex (e.g., only those trajectories where chlorine collides with chlorine result in CT) is absent in the current system. More than 70% of the CT trajectories follow the DS mechanism (Fig. S6(a), ESI†), leading to large scattering angles. Similar to CT, all the BT products are formed via direct mechanism and the initial contact determines the reaction mechanism (Fig. 10): (1) the bridging H loss: if the hydrogen in CH4 is directly colliding onto the bromine of HBr+, it acts as a bridging atom between the C and Br, which is squeezed out immediately by these two heavy atoms to form the C–Br bond in CH4Br+. In this case, the hydrogen atom (and the accompanying CH4Br+) traverses perpendicular to the C–Br axis, resulting in a scattering angle of near 90 degrees. This is evident from the scattering angle distribution in Fig. S6(d) (ESI†). (2) the “SN2” H loss: if the CH4 is orientated in a direction that allows for the bromine to directly form a bond with carbon, the H atom of CH4 on the opposite side of the bromine will pop away. In this case, the hydrogen atom (and the accompanying CH4Br+) traverses parallel along the C–Br axis, resulting in a near 180-degree scattering angle Fig. S6(d) (ESI†). Combining the scattering angles from all reactions, the overall scattering angle of the HBr+ + CH4 is shown in Fig. 11.
Discussion
In this section, the results presented are put into the context of previous work. Four different reaction channels have been observed for the reaction system HBr+ + CH4, proton transfer (PT), hydrogen atom abstraction (HA), charge transfer (CT) and bromine cation transfer (BT).The PT reaction shows a monotonically decreasing cross section with increasing collision energies implying that no significant barrier is operative on that reaction coordinate. The SO energy seems to be available to the reaction coordinate. The cross section for PT also decreases with increasing rotational energy. A similar trend was observed in earlier studies HBr+ + HBr25 and HBr+ + HCl.26 In the reaction system HBr+ + HCl the influence of the rotational energy on the PT cross section was more pronounced than that of collision energy.26 The data presented in this work exhibit the same trend.
The cross section for the endothermic hydrogen abstraction can be fitted to the simple loc model up to Ecm = 2 eV. Beyond this collision energy the cross section decreases significantly. This can be rationalized by the switching-on of competing reactions, in particular the CT and the BT channel, which is observed also in the AIMD simulations. The PES prompt similar reaction pathways for the HA and BT channels with identical transition state followed by splitting up into different pathways. In the experiment the BT pathway appears significantly enhanced at the largest collision energies employed, while the HA channel appears suppressed at the largest collision energies. This observation comes along with the finding that the BT channel is the only channel exhibiting a quadratic increase of the cross section with increasing Ecm, which can be modelled by the modified loc model suggesting an angle-dependence of the reaction, which is in line with the simulation results qualitatively.
In contrast, the cross section for CT can be fitted by the simple loc model which implies no angle dependence. The thermochemical threshold for the CT reaction pathway, as obtained from the calculated PES, is higher than the corresponding activation barrier of the BT reaction. This observation is consistent with experimental results, which also indicate a lower threshold for the BT reaction channel.
The cross sections for BT as well as CT are basically independent of the rotational energy of the ion, the cross section for HA has only a minor dependence on the ion rotation. In contrast, the cross section for PT markedly decreases with rotational energy of the ion, at least for the smallest Ecm investigated. To be effective, the PT channel requires the hydrogen atom pointing in the direction of the CH4. A higher rotational velocity will likely disfavor the passage through the transition state geometry.
For the HA and the CT reaction orientational requirements do not appear to pose a major restriction to the efficiency of those reaction channels. Consequently, the cross sections appear less affected by the rotational motion. However, the BT channel requires the Br atom of HBr+ ion oriented towards CH4 for the reaction to proceed.
Finally, the threshold for the respective reaction channels suggests that the spin–orbit energy of HBr+ employed in the experiment may not automatically be available to the reaction. The SO energy in the HBr+ ion appears to be available for the reaction for the PT and the HA channel, but not for the CT channel. We note, that earlier studies by Paetow et al. clearly showed that the spin orbit energy of the X2Π1/2 state is also available for the PT reaction in HBr+ + CO2.27,106
It is of interest to note the behavior of the cross section of the PT reaction in AIMD simulations, which is slightly endothermic (5.08 kJ mol−1) and has a non-negligible barrier (20.74 kJ mol−1). Normally one would expect its cross section to increase as the collision energy increases but the simulation shows that the cross section decreases monotonically from 0.5 eV to 3.0 eV. We currently do not have a thorough explanation to this phenomenon, but we note the previous statement relies on maintaining a statistical ensemble that follows the intrinsic reaction coordinate. In the current system, the excess energy overwhelms the barrier and the heat of the reaction – the lowest collision energy simulated is 48.24 kJ mol−1 (0.5 eV). As a result, 47% percent of PT and 7% of HA trajectories are direct, as they simply glide over the intermediates and barrier reported in the potential energy profile (Fig. 8) and directly form the product (cf. Table 7). The ratio of direct reaction increases to over 90% when the collision energy is 289.44 kJ mol−1 (3.0 eV). In these cases, an increase in the collision energy results in the reactants having even less time to interact with each other, thus the reaction probability decreases. A thought experiment can be laid out to make the point – even for an exothermic reaction, if the collision energy is infinite, the molecules would simply be passing through each other and no reaction can be observed. We note, that a similar observation has been arrived at with the HBr+ + CO2 reaction system.49 Considering a well-benchmarked ML potential has been developed in this work, more AIMD simulations below 0.5 eV will be conducted to verify the impact of the collision energy when it is below the barrier of the reaction and detect the turning point after which the cross section decreases with the increase of collision energy.
| Collision energy (eV) | Direct PT trajectories | Direct HA trajectories |
|---|---|---|
| 0.5 | 47% | 7% |
| 2.0 | 84% | 77% |
| 3.0 | 87% | 91% |
The agreement between the simulations and experiments is qualitative, as shown in Fig. 9. The disagreement can be attributed to the lack of SO-coupling effect in the simulations and the differences between the SO-free PES used in the simulation and the true SO-free PES. However, it is important to realize that (1) the true SO-free PES is not accessible except for the heat of the reaction and (2) the PES for the simulations is selected from the benchmark, which only mimics the true PES. As shown in Table 6, there is a finite difference between the PES of the simulation and the benchmark thus only qualitative agreement can be expected. Nonetheless, it is our opinion that the level of agreement reported in this manuscript is better than other AIMD simulations of similar reactions, where only the trend of the cross section (e.g., normalized cross section) vs. collision energy is compared to the experiment.24,26,49,107,108 In other cases where the absolute cross sections are reported, they are off by one order of magnitude from the experiment.109,110 In particular there is almost quantitative agreement between the experimental and AIMD calculated cross sections for the dominating PT channel. The fact that both are lower by a factor of 3 compared to Langevin theory consistently indicates that on the average every third collision is reactive.
Summary
Four reaction channels in the system HBr+ + CH4 were investigated experimentally and analyzed. The PT exhibits characteristics of an exothermic reaction taking into account the SO energy in the HBr+. The HA and the CT are endothermic reaction with no dominant activation barriers observed in the PES. The BT pathway is dominated by an intermediate barrier. All measured cross sections are below the Langevin limit. The absolute values are observed between 34 Å2 and 0.1 Å2.The cross section of the PT reaction decreases with increasing collision energy as expected but steeper than predicted by the Langevin model. The monotonic decrease of σPT suggests that no effective barrier is operative in the PT reaction. σPT decreases with increasing rotational energy.
The HA cross section exhibits a maximum at 2 eV collision energy and decreases beyond this to the primal cross section value. The HA cross section is independent of the ion rotation with the exception at the point of similar angular speed of the reactants, where there is a maximum.
The CT reaction exhibits characteristics of a typical endothermic reaction. Experimentally the thermodynamic threshold was determined to be 0.95 ± 0.03 eV.
The cross section of the BT reaction fit quite well with a modified loc model, suggesting an angle-dependence to be operative. In contrast no angle-dependence appears operative for the CT reaction. For both reaction channels the cross sections are independent of the ion rotational motion in the range of collision energies investigated.
A machine learning potential for the title reaction system has been devised, which allowed the successful rationalization of experimentally measured cross sections as well as prediction of mechanistic aspects not directly accessible to the experiment.
Associated content
There is ESI† available which contains the discussion of single collision conditions, the mass spectra and the data treatment.Author contributions
The experiments discussed have been conducted by D. P., the AIMD calculations and machine-learning potential have been worked out by K. F. and A. V. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Parts of this work have been supported by a grant from the Deutsche Forschungsgemeinschaft (We 1330-11). DP has been supported by a scholarship from the Fonds der Chemischen Industrie (FCI). Parts of this work has been supported by the National Science Foundation (USA) under grant no. 2144031. The authors appreciate the information technology service (ITS) from the University of Hawai‘i, Manoa for the computational resources.References
- K. Thoning, E. Dlugokencky, X. Lan and NOAA Global Monitoring Laboratory, Trends in globally-averaged CH4, N2O, and SF6, NOAA GML, 2022.
- United Nations Environment Programmeand Climate and Clean Air Coalition (2021). Global Methane Assessment: Benefits and Costs of Mitigating Methane Emissions. Nairobi: United Nations Environment Programme.
- Q. Li, R. P. Fernandez, R. Hossaini, F. Iglesias-Suarez, C. A. Cuevas, E. C. Apel, D. E. Kinnison, J.-F. Lamarque and A. Saiz-Lopez, Nat. Commun., 2022, 13(1), 2768 CrossRef CAS PubMed.
- Interstellar molecules: Their laboratory and interstellar habitat, Springer, ed. K. Yamada, W. Gisbert and K. M. T. Yamada, Springer tracts in modern physics, Berlin, Heidelberg, vol. 241, 2011 Search PubMed.
- A. Hanslmeier, Einführung in Astronomie und Astrophysik, Springer Spektrum, Berlin, Heidelberg, Lehrbuch, 4th edn, 2020 Search PubMed.
- J. H. Waite, M. R. Combi, W.-H. Ip, T. E. Cravens, R. L. McNutt, W. Kasprzak, R. Yelle, J. Luhmann, H. Niemann, D. Gell, B. Magee, G. Fletcher, J. Lunine and W.-L. Tseng, Science, 2006, 311(5766), 1419 CrossRef CAS PubMed.
- M. J. Mumma, G. L. Villanueva, R. E. Novak, T. Hewagama, B. P. Bonev, M. A. Disanti, A. M. Mandell and M. D. Smith, Science, 2009, 323(5917), 1041 CrossRef CAS PubMed.
- J. I. Lunine, Annu. Rev. Astron. Astrophys., 1993, 31(1), 217 CrossRef CAS.
- K. S. Noll, Icarus, 1996, 124(2), 608 CrossRef CAS.
- M. Larsson, W. D. Geppert and G. Nyman, Rep. Prog. Phys., 2012, 75(6), 66901 CrossRef CAS PubMed.
- E. Herbst and W. Klemperer, Astrophys. J., 1973, 185, 505 CrossRef CAS.
- D. Gerlich and S. Schlemmer, Planet. Space Sci., 2002, 50(12–13), 1287 CrossRef CAS.
- E. Herbst, Chem. Soc. Rev., 2001, 30(3), 168 RSC.
- F. H. Field and M. S. B. Munson, J. Am. Chem. Soc., 1965, 87(15), 3289 CrossRef CAS.
- M. S. B. Munson and F. H. Field, J. Am. Chem. Soc., 1966, 88(12), 2621 CrossRef CAS.
- A. Hansel, A. Jordan, R. Holzinger, P. Prazeller, W. Vogel and W. Lindinger, Int. J. Mass Spectrom. Ion Processes, 1995, 149–150, 609 CrossRef.
- D. Gerlich, Phys. Chem. Chem. Phys., 2005, 7(7), 1583 RSC.
- P. B. Armentrout, J. Am. Soc. Mass Spectrom., 2002, 13(5), 419 CrossRef CAS PubMed.
- P. Armentrout, Int. J. Mass Spectrom., 2000, 200(1–3), 219 CrossRef CAS.
- T. Glenewinkel-Meyer and D. Gerlich, Isr. J. Chem., 1997, 37(4), 343 CrossRef CAS.
- A. A. Viggiano, R. A. Morris, F. Dale, J. F. Paulson, K. Giles, D. Smith and T. Su, J. Chem. Phys., 1990, 93(2), 1149 CrossRef CAS.
- K. G. Lubic, D. Ray, D. C. Hovde, L. Veseth and R. J. Saykally, J. Mol. Spectrosc., 1989, 134(1), 1 CrossRef CAS.
- T. Uhlemann, J. Wallauer and K.-M. Weitzel, Phys. Chem. Chem. Phys., 2015, 17(25), 16454 RSC.
- Y. Luo, T. Kreuscher, C. Kang, W. L. Hase, K.-M. Weitzel and R. Sun, Int. J. Mass Spectrom., 2021, 462, 116515 CrossRef CAS.
- S. Schmidt, D. Plamper, J. Jekkel and K.-M. Weitzel, J. Phys. Chem. A, 2020, 124(41), 8461 CrossRef CAS PubMed.
- D. Plamper, K. Fujioka, S. Schmidt, R. Sun and K.-M. Weitzel, Phys. Chem. Chem. Phys., 2023, 25(3), 2629 RSC.
- L. Paetow, F. Unger, W. Beichel, G. Frenking and K.-M. Weitzel, J. Chem. Phys., 2010, 132(17), 174305 CrossRef PubMed.
- M. A. Röttgen, K. Judai, J.-M. Antonietti, U. Heiz, S. Rauschenbach and K. Kern, Rev. Sci. Instrum., 2006, 77, 013302 CrossRef.
- J. Xie and R. N. Zare, Chem. Phys. Lett., 1989, 159(5–6), 399 CrossRef CAS.
- M. Penno, A. Holzwarth and K.-M. Weitzel, J. Phys. Chem. A, 1998, 102(11), 1927 CrossRef CAS.
- M. Penno and K.-M. Weitzel, Z. Phys. Chem., 2004, 218(3), 311 CrossRef CAS.
- P. B. Armentrout, J. Anal. At. Spectrom., 2004, 19(5), 571 RSC.
- P. J. Chantry, J. Chem. Phys., 1971, 55(6), 2746 CrossRef CAS.
- P. Armentrout, Int. J. Mass Spectrom., 2000, 200(1–3), 219 CrossRef CAS.
- M. P. Langevin, Ann. Chim. Phys., 1905, 5, 245 Search PubMed.
- G. Gioumousis and D. P. Stevenson, J. Chem. Phys., 1958, 29(2), 294 CrossRef CAS.
- T. Su, J. Chem. Phys., 1973, 58(7), 3027 CrossRef.
- I. Ozier, Phys. Rev. Lett., 1971, 27(20), 1329 CrossRef CAS.
- A. Tsikritea, J. A. Diprose, T. P. Softley and B. R. Heazlewood, J. Chem. Phys., 2022, 157(6), 60901 CrossRef CAS PubMed.
- R. B. Bernstein and R. D. Levine, Molecular reaction dynamics and chemical reactivity, Oxford University Press, New York, 1987 Search PubMed.
- P. B. Armentrout and J. L. Beauchamp, J. Chem. Phys., 1981, 74(5), 2819 CrossRef CAS.
- R. D. Levine and R. B. Bernstein, Chem. Phys. Lett., 1984, 105(5), 467 CrossRef CAS.
- I. W. M. Smith, J. Chem. Educ., 1982, 59(1), 9 CrossRef CAS.
- M. A. Eliason and J. O. Hirschfelder, J. Chem. Phys., 1959, 30(6), 1426 CrossRef CAS.
- P. L. Houston, Chemical Kinetics and Reaction Dynamics, Dover Books on Chemistry, Dover Publications, Newburyport, 2012 Search PubMed.
- Line-of-centres model, inThe IUPAC Compendium of Chemical Terminology, ed. V. Gold, International Union of Pure and Applied Chemistry (IUPAC), Research Triangle Park, NC, 2019 Search PubMed.
- N. Aristov and P. B. Armentrout, J. Am. Chem. Soc., 1986, 108(8), 1806 CrossRef CAS.
- K. Fujioka, K.-M. Weitzel and R. Sun, J. Phys. Chem. A, 2022, 126(9), 1465 CrossRef CAS PubMed.
- Y. Luo, K. Fujioka, A. Shoji, W. L. Hase, K.-M. Weitzel and R. Sun, J. Phys. Chem. A, 2020, 124(44), 9119 CrossRef CAS PubMed.
- A. E. Belikov and M. A. Smith, Russ. J. Phys. Chem. A, 2008, 82(5), 789 CrossRef CAS.
- A. E. Belikov, C. Mullen and M. A. Smith, J. Chem. Phys., 2001, 114(15), 6625 CrossRef CAS.
- M. Dolg, Chapter 14 Relativistic effective core potentials, Relativistic Electronic Structure Theory. Theoretical and Computational Chemistry, Elsevier, 2002. pp.793–862 Search PubMed.
- M. Häser, Theoret. Chim. Acta, 1993, 87(1–2), 147 CrossRef.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119(21), 11113 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82(1), 284 CrossRef CAS.
- C. E. Check, T. O. Faust, J. M. Bailey, B. J. Wright, T. M. Gilbert and L. S. Sunderlin, J. Phys. Chem. A, 2001, 105(34), 8111 CrossRef CAS.
- M. M. Hurley, L. F. Pacios, P. A. Christiansen, R. B. Ross and W. C. Ermler, J. Chem. Phys., 1986, 84(12), 6840 CrossRef CAS.
- A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuß, Mol. Phys., 1993, 80(6), 1431 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90(2), 1007 CrossRef CAS.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, J. Chem. Phys., 1999, 110(16), 7667 CrossRef CAS.
- B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108(45), 9979 CrossRef CAS.
- A. Kramida and Y. Ralchenko, NIST Atomic Spectra Database, NIST Standard Reference Database 78, National Institute of Standards and Technology, 1999.
- W. J. Orville-Thomas, J. Mol. Struct., 1980, 64, 299 CrossRef.
- D. Sheppard and G. Henkelman, J. Comput. Chem., 2011, 32(8), 1769–1771 CrossRef CAS PubMed ; author reply 1772-3.
- K. Fukui, J. Phys. Chem., 1970, 74(23), 4161 CrossRef CAS.
- C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112(1), 4 CrossRef PubMed.
- L. Kong, F. A. Bischoff and E. F. Valeev, Chem. Rev., 2012, 112(1), 75 CrossRef CAS PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157(6), 479 CrossRef CAS.
- B. Nagy and F. Jensen, Basis Sets in Quantum Chemistry, in Reviews in Computational Chemistry. Reviews in Computational Chemistry, ed. A. L. Parrill and K. B. Lipkowitz, Wiley, 2017. pp.93–149 Search PubMed.
- X. Hu, W. L. Hase and T. Pirraglia, J. Comput. Chem., 1991, 12(8), 1014 CrossRef CAS.
- U. Lourderaj, R. Sun, S. C. Kohale, G. L. Barnes, W. A. de Jong, T. L. Windus and W. L. Hase, Comput. Phys. Commun., 2014, 185(3), 1074 CrossRef CAS.
- P. M. Rodger, Mol. Simul., 1989, 3(5–6), 263 CrossRef.
- K. T. Schütt, P. Kessel, M. Gastegger, K. A. Nicoli, A. Tkatchenko and K.-R. Müller, J. Chem. Theory Comput., 2019, 15(1), 448 CrossRef PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148(24), 241722 CrossRef PubMed.
- M. Tichy, G. Javahery, N. D. Twiddy and E. E. Ferguson, Int. J. Mass Spectrom. Ion Processes, 1990, 97(2), 211 CrossRef CAS.
- O. Asvany, P. K. P, B. Redlich, I. Hegemann, S. Schlemmer and D. Marx, Science, 2005, 309(5738), 1219 CrossRef CAS PubMed.
- Z. Jin, B. J. Braams and J. M. Bowman, J. Phys. Chem. A, 2006, 110(4), 1569 CrossRef CAS PubMed.
- A. L. Kaledin, S. D. Kunikeev and H. S. Taylor, J. Phys. Chem. A, 2004, 108(23), 4995 CrossRef CAS.
- J. E. Mann, Z. Xie, J. D. Savee, J. M. Bowman and R. E. Continetti, J. Phys. Chem. A, 2010, 114(43), 11408 CrossRef CAS PubMed.
- D. Marx and M. Parrinello, Nature, 1995, 375(6528), 216 CrossRef CAS.
- D. Marx and M. Parrinello, Science, 1999, 284(5411), 59 CrossRef CAS.
- A. B. McCoy, B. J. Braams, A. Brown, X. Huang, Z. Jin and J. M. Bowman, J. Phys. Chem. A, 2004, 108(23), 4991 CrossRef CAS.
- P. R. Schreiner, S.-J. Kim, H. F. Schaefer and P. von Ragué Schleyer, J. Chem. Phys., 1993, 99(5), 3716 CrossRef CAS.
- K. C. Thompson, D. L. Crittenden and M. J. T. Jordan, J. Am. Chem. Soc., 2005, 127(13), 4954 CrossRef CAS PubMed.
- H. Tachikawa and A. J. Orr-Ewing, J. Phys. Chem. A, 2008, 112(46), 11575 CrossRef CAS PubMed.
- E. T. White, J. Tang and T. Oka, Science, 1999, 284(5411), 135 CrossRef CAS PubMed.
- G. A. Olah, Angew. Chem., Int. Ed. Engl., 1973, 12(3), 173 CrossRef.
- L. M. Johnson and A. B. McCoy, J. Phys. Chem. A, 2006, 110(26), 8213 CrossRef CAS PubMed.
- H. P. Watkins and W. S. Koski, Radiochim. Acta, 1982, 30(2), 95 CrossRef CAS.
- A. L. Chistyakov, I. V. Stankevich, N. P. Gambaryan and I. S. Akhrem, Russ. Chem. Bull., 1998, 47(9), 1666 CrossRef CAS.
- P. Manikandan, J. Zhang and W. L. Hase, J. Phys. Chem. A, 2012, 116(12), 3061 CrossRef CAS PubMed.
- R. Sun, M. R. Siebert, L. Xu, S. D. Chambreau, G. L. Vaghjiani, H. Lischka, J. Liu and W. L. Hase, J. Phys. Chem. A, 2014, 118(12), 2228 CrossRef CAS PubMed.
- R. Sun, C. J. Davda, J. Zhang and W. L. Hase, Phys. Chem. Chem. Phys., 2015, 17(4), 2589 RSC.
- R. Sun, J. Xie, J. Zhang and W. L. Hase, Int. J. Mass Spectrom., 2015, 377, 222 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72(1), 650 CrossRef CAS.
- L. A. Curtiss, M. P. McGrath, J.-P. Blaudeau, N. E. Davis, R. C. Binning and L. Radom, J. Chem. Phys., 1995, 103(14), 6104 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96(9), 6796 CrossRef CAS.
- F. Jensen, J. Chem. Phys., 2001, 115(20), 9113 CrossRef CAS.
- F. Jensen, J. Chem. Phys., 2012, 136(11), 114107 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7(18), 3297 RSC.
- C. He, G. R. Galimova, Y. Luo, L. Zhao, A. K. Eckhardt, R. Sun, A. M. Mebel and R. I. Kaiser, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(48), 30142 CrossRef CAS PubMed.
- S. Doddipatla, C. He, R. I. Kaiser, Y. Luo, R. Sun, G. R. Galimova, A. M. Mebel and T. J. Millar, Proc. Natl. Acad. Sci. U. S. A., 2020, 117(37), 22712 CrossRef CAS PubMed.
- X. Liu, J. Zhang, L. Yang and R. Sun, J. Phys. Chem. A, 2016, 120(20), 3740 CrossRef CAS PubMed.
- J. Zhang, U. Lourderaj, R. Sun, J. Mikosch, R. Wester and W. L. Hase, J. Chem. Phys., 2013, 138(11), 114309 CrossRef PubMed.
- J. Xie, M. McClellan, R. Sun, S. C. Kohale, N. Govind and W. L. Hase, J. Phys. Chem. A, 2015, 119(5), 817 CrossRef CAS PubMed.
- L. Paetow, F. Unger, B. Beutel and K.-M. Weitzel, J. Chem. Phys., 2010, 133(23), 234301 CrossRef PubMed.
- L. A. Angel and K. M. Ervin, J. Am. Chem. Soc., 2003, 125(4), 1014 CrossRef CAS PubMed.
- A. J. C. Varandas, J. Chem. Phys., 1993, 99(2), 1076 CrossRef CAS.
- J. Li, C. Xie, J. Ma, Y. Wang, R. Dawes, D. Xie, J. M. Bowman and H. Guo, J. Phys. Chem. A, 2012, 116(21), 5057 CrossRef CAS PubMed.
- F. J. Aoiz, L. Bañares, T. Bohm, A. Hanf, V. J. Herrero, K.-H. Jung, A. Läuter, K. W. Lee, M. Menéndez, V. Sáez Rábanos, I. Tanarro, H.-R. Volpp and J. Wolfrum, J. Phys. Chem. A, 2000, 104(45), 10452 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01121j |
| ‡ Contributed equally to this work. |
| This journal is © the Owner Societies 2024 |








![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif)