Ab initio molecular dynamics investigation of the Pt(111)–water interface structure in an alkaline environment with high surface OH-coverages

Abstract

In this study, we investigate the structure of the Pt(111)–water interface in an alkaline environment with large OH coverages of 1/3, 2/3 and 1 monolayer using a large well-equilibrated system. We observe that the OH coverage influences both the orientational distribution of the water molecules and their density, with more structure associated with higher coverage. At the same time, there is evidence of a highly dynamic hydrogen bond network on the lower coverage systems with substantial exchange of water between the surface and the solvent. In addition to OH and H₂O species, which are preferentially located at the top sites, the 1/3 and 2/3 monolayer surfaces also contain O atoms, which are relatively stable and prefer the hollow sites. In contrast, the 1 monolayer surface shows none of these dynamics, and is unlikely to be active. The dynamic coexistence of O, OH and H₂O on Pt(111) electrodes in alkaline conditions necessitates the investigation of several possible reaction paths for processess like ORR and water splitting. Finally, the exchange processes observed between the solvent and the interface underscore the need to explicitly include liquid water in simulations of systems similar to Pt(111).

---

1 Introduction

The hydroxide ion is a common electrolyte for electrode reactions occuring in alkaline media, such as in alkaline fuel cells.¹ At the same time, the surface adsorbed OH plays a key role in many chemical reactions such as the oxygen reduction reaction (ORR)² and water splitting.³ For example, in the hydrogen oxidation reaction OH can act both as a bystander that blocks surface sites or as an active participant through the recombination with adsorbed hydrogen to form water.⁴

Adsorbates like OH can alter the electrode–electrolyte interface in two ways:⁵ For one, the interactions between the adsorbate and the surrounding electrolyte can influence the energetics of the adsorbates and the electrochemical reactions they participate in. This phenomenon is evidenced by the way the energetics of adsorbed OH sensitively depend on the aqueous solvation for the ORR,^6–11 the hydrogen evolution reaction (HER)^12–14 and the CO oxidation reaction.^15–18 Conversely, the adsorbate can reciprocally impact the surrounding solvent molecules – an effect that is often lost when one employs a simplistic model to describe the solvent.

Platinum-based compounds constitute some of the most powerful catalysts for both the HER and ORR reactions.^6,19–21 Since Fisher and Sexton²² demonstrated the formation of adsorbed hydroxyl species on the Pt(111) surface, several experimental articles have looked into the complex roles OH can play on the surface.²³ At the same time, the electronic structure and adsorbtion energetics of OH on Pt(111)-surfaces have been extensively investigated through computational studies.^6,24–31 The calculated reversible potentials of OH formation agree reasonably well with the experimental results^32–35 and show that OH is substantially (more than 0.5 eV) stabilised by the solvation.^27–31

Even though DFT calculations have greatly advanced our understanding of the Pt(111)-surface, a key issue in the vast majority of these studies is that they do not explicitly include liquid water as part of the aqueous electrolyte–electrode interface:³⁶ While some studies choose to ignore water altogether,³⁷ others include it implicitly through a dielectric continuum^38,39 or as a static layer.^27,40–42 One way to accurately model the liquid water–electrode interface is through ab initio molecular dynamics (AIMD).⁴³ Despite the relatively high computational cost associated with AIMD, several studies have investigated OH adsorption on Pt(111), including its free energy surface,⁴⁴ formation energetics⁴⁵ and desorption mechanisms.⁴⁶

Recently, Zhu et al.⁵ provided a detailed look at the effects of adsorbed OH on the Pt(100)/water interfacial structures. Even though Kristoffersen et al.⁴⁵ investigated some aspects of the Pt(111) interfacial structure, no similar exhaustive analysis has yet been performed for the Pt(111) surface. Consequently, in this study, we perform a detailed investigation of the structure of the Pt(111)–water interface in an alkaline environment using a large-scale well-equilibrated AIMD system under zero charge conditions. As previous studies have mostly focused on OH coverages at and below 1/3 monolayer (ML),^5,27,28,47 our focus is on the higher coverages of 1/3, 2/3 and 1 ML. Our main goal is to understand the prevalence of different surface species at different OH coverages and their interactions with the solvent water molecules.

2 Computational details

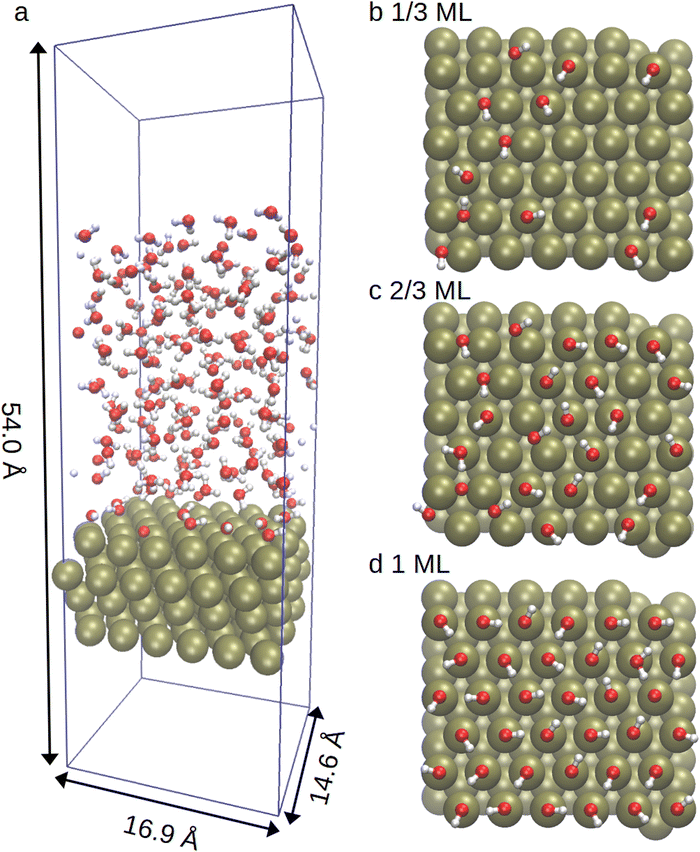
The computational procedure in this article closely paralleled the methodology of our previous Pt(111) hydrogen adsorption study.⁴⁸ Our DFT calculations utilised the CP2K/quickstep molecular dynamics and electronic structure software package,^49,50 with the hybrid Gaussian and plane wave (GPW) method.⁵¹ A 400 Ry cutoff was used for the auxiliary plane wave basis. Meanwhile, the 1s electron of hydrogen, the 2s and 2p electrons of oxygen as well as the 5s, 5p, 5d and 6s electrons of platinum were represented through molecularly optimised double-ζ plus polarisation Gaussian basis sets (MOLOPT-SR-DZVP).⁵² The resulting ionic cores were represented with norm-conserving Goedecker–Teter–Hutter (GTH) pseudopotentials.^53–55 The revised Perdew–Burke–Ernzerhof (RPBE)⁵⁶ density functional approximation was employed for the molecular dynamics simulations as recommended by Sung et al.³⁸ While dispersion corrections were included using the DFT-D3 scheme of Grimme et al.,⁵⁷ the dispersion interaction between platinum–platinum pairs was excluded due to the incorrect screening within Pt.^38,58–60 The Kohn–Sham equations were solved using a matrix diagonalisation scheme, with Fermi–Dirac smearing applied using an electronic temperature of 1000 K. The convergence criteria for the energy was set at 2.7 × 10⁻⁵ eV and at 2.3 × 10⁻² eV Å⁻¹ for the forces.

Platinum slabs consisting of 144 atoms were constructed using a (6 × 6 × 4) supercell for Pt(111) with an optimised (PBE) lattice constant of 3.98 Å. This value agrees well with accurate full-potential (linearised) augmented plane wave and local orbital (FP-(L)APW + lo) calculations (3.985 Å) and experimental measurements (3.92 Å).⁶¹ The Pt surface was covered with OH with a subsequent 20 Å water film (160 water molecules) added on top. This was followed by a 20 Å vacuum layer to decouple periodic images in the direction of the surface normal. The simulated system is illustrated in graph a of Fig. 1.

Fig. 1 Representation of the investigated system and the initial surface configurations for different OH coverages. Graph a shows the simulation system and its dimensions for the 1/3 OH ML coverage. The blue lines mark the boundaries of the simulation cell. The red, white and ochre spheres represent oxygen, hydrogen and platinum atoms, respectively. Graphs b–d show the initial surface configurations for the investigated 1/3, 2/3 and 1 ML systems.

We chose to investigate 1/3, 2/3 and 1 ML OH coverages. For the 1 ML surface, the OH groups were initially placed on the top sites. The initial OH positions for the 1/3 and 2/3 ML surfaces were then determined by randomly removing a suitable number of OH groups from the 1 ML system, followed by a geometry optimisation of all three systems. The resulting initial surface configurations are shown in graphs b–d of Fig. 1. The 1/3 ML case has been identified as the most stable surface structure in past RPBE exchange correlational studies looking at OH formation on a static water bilayer-Pt(111) surface.^30,42 This surface model is founded on experimental observations of a single water layer on Pt(111) under ultrahigh vacuum and low temperature conditions.⁶² On the other hand, the 2/3 ML coverage was identified as particularly stable in the recent AIMD simulations of Kristoffersen et al. in a highly dynamic liquid water environment at 350 K.⁴⁵ It was also identified as the emerging coverage from two different OH forming reactions in the scanning tunneling and high-resolution energy loss spectroscopy study of Bedürftig et al.,⁶³ again at ultrahigh vacuum and low temperature. According to the experimental results of Li et al.,⁶⁴ in a 0.1 M OH solution at pH > 11.3 the increasing electrode potential increases the OH-coverage of the Pt(111) electrode so that a 1/3 ML coverage is reached with an approximately 0.77 V electrode potential vs. RHE. Meanwhile, a 2/3 ML coverage requires potentials above 0.87 V. The alkaline HER also starts to increase at approximately 0.8 V under these conditions, making both coverages electrochemically interesting.

Each system was equilibrated for a minimum of 20 ps followed by a production run of approximately 20 ps. A canonical (NVT) ensemble at 300 K was chosen for these Born–Oppenheimer molecular dynamics simulations with the temperature maintained using a CSVR thermostat.⁶⁵ Following Groß et al.,^38,66,67 we employed a time step of 1.0 fs, with the lowest Pt layer frozen to mimic bulk behavior. This relatively large time step was used to compensate for the slow convergence of the calculations due to charge sloshing while securing an efficient sampling of the phase space. During the relatively long equilibration period, diffusion of OH along the surface, O-formation together with water exchange to and from the surface were observed for the 1/3 and 2/3 ML surfaces. While both the 1/3 and 2/3 ML systems showed oxygen formation after the first 3 ps of the equilibration period, most of the surface adsorbed oxygen atoms in the 2/3 ML system formed within the first 0.5 ps. Due to the strong cohesive interaction, no evaporation of water molecules was observed in any of the simulated trajectories. The data was analysed using Wolfram Mathematica 14⁶⁸ together with the Seaborn⁶⁹ and Matplotlib⁷⁰ Python libraries.

3 Results and discussion

3.1 Density profiles

Fig. 2 represents the laterally averaged number density profiles for hydrogen and oxygen at different OH-coverages. The full graph for the 1 ML coverage is displayed in the inset. Looking at the figure, we see that the oxygen density has two peaks near the edge of the slab, with the exception of the 1 ML structure. The peak closer to the slab surface indicates the occupation of hollow surface sites, while the second peak corresponds to oxygen located at the top or bridge sites of the Pt surface based on the O–Pt distance.^26,71 Surprisingly, there is no hydrogen peak below 2 Å for the 1/3 and 2/3 ML coverages, which implies that the hollow sites are occupied by oxygen atoms in contrast to OH. This is interesting, as the review by Gottesfeld⁷² argues that for potentials greater than 0.6 V vs. RHE the Pt surface is partially covered by a mixture of adsorbed OH and O during ORR. The Pt adsorbed oxygen is throught to form by deprotonation of OH at defects or at increased cathode potential.^2,64,73,74 Pt oxidation has also been experimentally observed under near ambient conditions through a PtO-like surface oxide phase⁷⁵ which may also play a role in the electrochemical oxidation of Pt(111) that is associated with a substantial activation barrier for the ORR.⁷⁶ In contrast, the fact that only one oxygen peak is observed at around 2 Å in the 1 ML graph shows that all the oxygen atoms at 1 ML coverage remain on the top or bridge sites of the surface. Curiously, there is little increase in the ∼2 Å oxygen density when moving from 1/3 ML to 2/3 ML coverage. Instead, only the O-coverage seems to increase markedly. The 1 ML system also exhibits a large gap in the oxygen density after the surface adsorbed OH-groups, indicating a clearer separation between the surface adsorbed species and the water phase compared to the other two systems.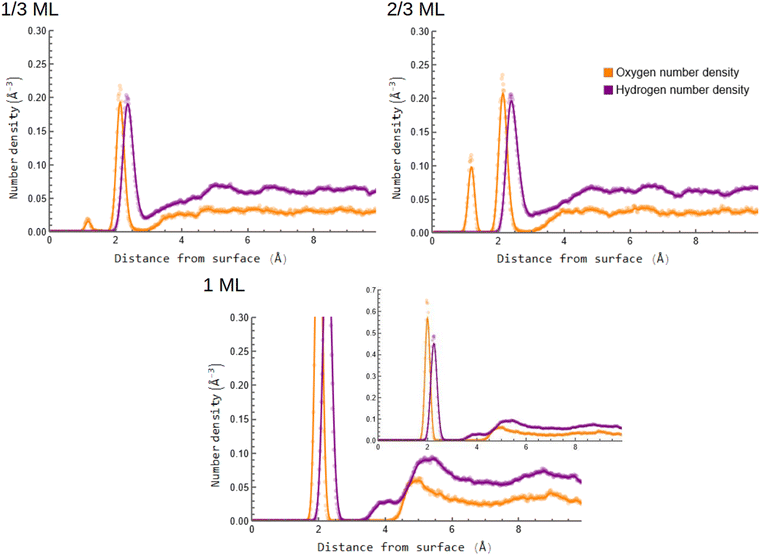

Fig. 2 Laterally averaged oxygen and hydrogen number density profiles for the 1/3, 2/3 and 1 ML OH coverages. The uncut graph for the 1 ML coverage is displayed in the inset.

In the 1 ML density profiles in Fig. 2, the surface adsorbed top site hydrogen density peak is smaller than the oxygen one, which might point to the presence of O atoms on top sites of the fully covered Pt surface. The hydrogen density profile in this system also rises before the oxygen one when moving farther from the surface, indicating the presence of donor hydrogen bonds from the water molecules to the surface adsorbates. It further appears that the oscillations in solvent density become pronounced as one moves to higher OH coverages, as does the gap in density between the surface adsorbed species and the solvating waters – both in qualitative agreement with the findings of Kristoffersen et al.⁴⁵ Indeed, the 1 ML system shows substantial structure, with both O and H densities first rising at around 5 Å and then decreasing to a minimum at around 7 Å. However, it should be borne in mind that the RPBE-D3 functional results in a clearly weaker platinum-water interaction compared to, for example, the PBE one, leading to a weaker water restructuring due to the surface.⁴⁸ One should also note that the lack of ions in our simulations is an assumption, and the results might potentially differ at high ionic strengths.

3.2 Orientation distributions

To further investigate the structure of the interfacial surface and its effects on the solvent water, we studied both the water dipole and OH vector orientations. The resulting angle distributions are shown in Fig. 3 as a function of the surface separation. In the figure, graphs a–c display the OH vector angles for the different surface coverages while graphs d–f contain the water dipole moment angles. The angle is calculated with respect to the surface normal so that a value of 0° for the OH vector corresponds to it pointing away from the surface, a value of 90° corresponds to an OH vector parallel to the surface and a value of 180° corresponds to OH pointing towards the surface as illustrated in the insets of Fig. 3. Note that in addition to the surface OH species, each water molecule contains two OH vectors.

Fig. 3 OH vector and H₂O dipole moment angles with respect to the surface normal. Graphs a–c display the OH vector angles (φ) for the different surface coverages. Note that each water molecule contains two OH vectors. Graphs d–f contain the water dipole moment angles (ω). These graphs display only water, not surface OH. The insets on each row illustrate the angle definitions.

In graphs a–c of Fig. 3, the surface adsorbed OH molecules can be seen as a bright red region at around 2–3 Å from the Pt surface. The angle these OH vectors form with the surface normal is limited to a range of about 45–95°. Upon further analysis, most of the OH-groups have angles in the 65–75° range. Consequently, while most OH-groups tilt slightly upward from the surface plane, some are more directed toward the solvent waters, especially at the 2/3 ML coverage in graph b. This upward tilt of the OH-groups is also evident in the offset of the O and H number density plots in Fig. 2. The least angular variation is observed in the 1 ML surface, where the OH groups might be more strongly hydrogen bonded to other surface OH.

Focusing on the solvent OH-vectors in graphs a–c of Fig. 3, one sees that the gap between the surface adsorbed and solvent vectors becomes larger as one moves from the 1/3 ML to the 1 ML system, in line with the number density distributions seen in Fig. 2. The solvent density oscillations also become evident as the coverage increases. Furthermore, when comparing graphs a and b with graph c, there appears to be an increasing number of OH vectors with larger angle values above the surface for the 1 ML system. These OH vectors are pointing towards the surface, likely forming donor hydrogen bonds with the surface adsorbed species, as predicted from Fig. 2.

With regards to the water dipole moment angles shown in graphs d–f of Fig. 3, one clearly sees the presence of water molecules on the surface from the pronounced dipole density at 2–3 Å in graphs d and e. Note that graphs d–f show only the water molecules, not surface OH. Based on graphs d and e, surface adsorbed water appears to be present both in the 1/3 ML and 2/3 ML systems while no water exists on the 1 ML surface in graph f. Judging from the distance from the surface, all waters are located at top or bridge sites. Meanwhile, the angular distribution of the surface adsorbed H₂O is similar to the ones for the OH vector observed in graphs a–c with most dipoles pointing slightly up from the surface at angles around 70°. These findings align with the results observed for Pt(100) by Zhe et al.,⁵ and correspond to the well-known nearly planar water adsorption orientation with hydrogens symmetrically tilted slightly away from the surface.^77–80 It is ascribed to the coupling of the metal d-band with the 1b1 orbital of water, which results in a relatively immobile adsorbed state.

For the solvent, we see some increase in the dipole angles above 100° a short distance above the surface as one moves from 1/3 to 2/3 ML coverage. As for the OH vectors, this could indicate downward pointing water molecules forming hydrogen bonds with the surface species. However, at the 1 ML surface in graph f, all dipole orientations from 50 to 140° appear common, with the general increase in dipoles reflecting the bump in the hydrogen and oxygen number density functions observed at around 5–5.5 Å in Fig. 2.

3.3 Interface structure

To understand the nature of the interface, we first looked at the amounts of different surface species. Based on Fig. 2, oxygen atoms were considered adsorbed if they were within 2.8 Å of the top Pt layer. Meanwhile, hydrogens that were less than 1.2 Å from an oxygen were considered bonded. The cumulative amounts of O, OH and H₂O species on the surface are shown in Fig. 4 as a function of time, while sample surface snapshots are displayed in Fig. 5 for the different OH coverages.

Fig. 4 Cumulative amounts of different surface species as a function of time. The coloured areas represent the relative amounts of different species while the lines indicate the cumulative amounts of the species up to that point, i.e., the green line represents the number of surface oxygens, the orange line indicates the sum of surface waters and oxygens and the blue line the sum of all surface species.

Fig. 5 Sample interface adsorption patterns for the 1/3, 2/3 and 1 ML OH coverages. The red, white and ochre represent oxygen, hydrogen and platinum atoms, respectively.

It can be immediately confirmed from Fig. 4 and 5 that only OH is present in the 1 ML system, whereas all three species are encountered in the other two systems despite all systems starting the geometry optimisation preceding equilibration with only OH on the surface and water in the solvent phase. For the 1/3 ML system, one of the initial OH species has formed oxygen, which remains stable throughout the simulation. On the other hand, several waters have been adsorbed on the surface from the solvent phase so that the total number of surface species fluctuates around 16. A different trend is observed in the 2/3 ML system where six stable oxygen atoms have formed on the surface and, on average, there are a total of 23 surface species, implying that one of the formed water molecules has escaped to the solvent.

The jagged shape of the orange line in the 1/3 and 2/3 ML systems indicates the presence of Zundel structures as protons transfer between two oxygens. Indeed, the numbers of surface adsorbed OH and H₂O fluctuate rapidly, pointing to proton transfer reactions occurring within the <1 ps timescale, as observed by Kristoffersen et al.⁴⁵ The rapidly occurring proton transfer is illustrated in graph a of Fig. 6 which follows the O–H distance for four OH groups from the start of the 1/3 ML simulation as a function of time: the r1 OH group (red) remains intact throughout the simulation while the hydrogen for the r2 (orange) OH group jumps back and forth between two oxygens. Meanwhile, the hydrogens in r3 and r4 (green and blue) quickly diffuse further away from their original oxygens via the Grotthus-mechanism.^81,82

Fig. 6 Sample distance comparisons for the 1/3 ML OH coverage simulation as a function of time. Graph a shows four O–H distances for surface adsorped OH groups and graph b shows the distance between the surface and two oxygen atoms, one starting on the surface (O1) and the other in the solution (O2).

Graph b of Fig. 6 displays the surface distances for two oxygen atoms in the 1/3 ML simulation as a function of time. Although not indicated in the figure, both oxygens are bonded to two hydrogen atoms forming H₂O when not on the surface. Interestingly, the findings of Kristoffersen et al.⁴⁵ indicated rapid H₂O adsorption/desorption on the 5 ps timescale for OH coverages below 0.17 ML, but much more rarely for systems with higher coverages. Our results, as evidenced by graph b in Fig. 6, seem to demonstrate that H₂O adsorption and desorption readily occur at 1/3 and 2/3 ML coverages. Indeed, in both of our 20 ps simulations for these systems we observed exchange processes where one water detaches from the surface followed by readsorption or the adsorption of another H₂O molecule. The presence of chemisorbed water on the equilibrated Pt(111) surface can be crucial as it has been recently identified as a potential mediator in a competitive ORR mechanism compared to the typical associative and dissociative mechanisms in alkaline conditions.⁴⁷

To understand the adsorption sites of the surface species, we also looked at the surface distributions of the O atoms as a function of the adsorbant type, i.e. O, OH or H₂O. The results are displayed in Fig. 7. In this figure, the presence of the highly dynamic hydrogen-bond network is seen in the substantial overlap of the H₂O and OH density plots in the 1/3 and 2/3 ML interfaces, reinforcing the idea of rapid interconversions occurring between these species. In contrast, the 1 ML interface shows evidence of only surface OH, in agreement with Fig. 2–4.

Fig. 7 Surface distributions of the adsorbed oxygen atoms for the 1/3, 2/3 and 1 ML systems. The different colours indicate the type of the adsorbed oxygen with blue corresponding to atomic O, orange to OH and green to H₂O. Only oxygen atoms that were less than 2.8 Å from the top Pt layer were considered. The top layers of the surface Pt atoms are shown in gray in all the figures.

Comparing the 1/3 and 2/3 ML densities in Fig. 7 with the locations of the Pt atoms in Fig. 5, we see that the OH and H₂O species mostly favour top sites over the bridge and the hcp and fcc hollow sites. The difference between the two hollow sites is that the hcp has a Pt atom under the site, whereas the fcc does not. Interestingly, according to our solvent-free individual OH adsorbtion energies shown in Table 1, the hollow, bridge and top sites are almost identical in energy. This means that the observed differences likely arise from the energetic stabilisation of the top sites by the solvent, coverage, or entropic effects. Specifically, according to Garcia-Araez³⁵ it's the enthalpy effects that are the driving force behind OH adsorption. The observed OH adsorption patterns are also in broad agreement with previous results, where some calculations show a preference for the bridge site⁸³ and others for the top^26,71,84 at various coverages below 1/3 ML. The recent AIMD results of Zhu et al.⁵ found that as the OH coverage for Pt(100) increased from 1/16 to 1/4 ML the proportion of top site OH compared to bridge site increased from 1 : 1 to more than 3 : 1. They attributed this effect to the stronger solvation of top site OH. It should be noted that the locations of the Pt atoms also naturally fluctuate during the simulation, which is not captured in Fig. 7.

Table 1 Relative adsorption energies for O, OH and H₂O compared to top-site adsorption energy in eV

	Top	Bridge	Hollow (fcc)	Hollow (hcp)
O	0	—	−0.80	−1.15
OH	0	0.05	0.01	0.07
H2O	0	0.07	0.07	0.06

---

According to both Table 1 and previous studies,^26,83,85 the top site is energetically favoured for water in Pt(111). Furthermore, the experimental results of Bedürftig et al.⁶³ and Schiros et al.⁸⁶ point to the top site as being preferred for both water and OH adsorption on the Pt(111) surface with a hexagonal surface structure corresponding to a 2/3 ML coverage. Zhu et al.⁵ also argued that the strong attractive interaction between the top site OH and solvent water molecules compared to the bridge OH could help pull down water molecules from the solvent phase onto the surface, which could help explain the large number of adsorbed water on our 1/3 ML surface. Meanwhile, steric effects could play a larger role on the 2/3 ML surface, explaining the small average decrease in oxygens compared to the initial state. According to the experimental results of Garcia-Araez, the coadsorped water molecules we see in both simulations play an important role in the interactions between the surface adsorped OH species as well as the interactions between the platinum and the surface OH.³⁵ Finally, the OHs are exclusively located on the top sites in our 1 ML system, in line with the predictions of Michaelides and Hu⁷¹ that at high coverages the H-bonding between adjacent hydroxyls causes a strong preference for OH adsorption at top sites and the formation of OH networks.

In contrast to the OH and H₂O, surface adsorbed oxygens clearly prefer the hollow sites in Fig. 5 and 7 and show little diffusion across the surface. According to Table 1 and previous experimental⁸⁷ and computational studies,⁸⁸ the hollow sites are strongly preferred for O. This also agrees with the oxygen number density peaks seen below 1.5 Å for both the 1/3 and 2/3 ML systems in Fig. 2. Furthermore, there is little overlap between the O densities and the OH and H₂O ones in Fig. 7, underscoring the stability of the O species on the surface.

During equilibration, the OH reactivity to form surface adsorbed oxygen was closely tied to the occupation of bridge sites. In fact, all O atoms in the simulation were formed from OH groups located on bridge sites. This phenomenon can be seen, for example, by comparing the initial surface configurations in Fig. 1 to the snapshots taken during the production run in Fig. 5 where the oxygen atoms are already present. It also helps to explain why no O formation was observed in the 1 ML system: each OH group was locked to the top site by the hydrogen bond network with the other surface OH species which resulted in longer hydrogen bonds.

3.4 Surface bonding patterns

We also investigated the hydrogen bonding patterns of the various surface species, and the results are shown in Tables 2–4. In these tables, the number of donor hydrogen bonds is indicated by the column and the number of acceptor hydrogen bonds by the row. For example, according to Table 2, 15.7% of the surface oxygens in the 1/3 ML surface accepted one hydrogen bond while donating none, which was one of the two hydrogen bond configurations observed for this species. The overwhelmingly more popular bonding pattern was the one where the surface oxygens did not participate in hydrogen bonds. In this study, a hydrogen bond was defined by the typical criteria of a 2.27 Å distance cutoff between the oxygen acceptor and hydrogen donor atoms and an O–H⋯O angle greater than 140°.^89,90

Table 2 Surface bonding patterns for the 1/3 ML OH covered Pt(111) surface. For each species, the horizontal direction tells the number of donor (D) hydrogen bonds and the vertical direction the number of acceptor (A) hydrogen bonds

	O			OH			H2O
	—	D	DD	—	D	DD	—	D	DD
—	84.3%			1.2%	2.9%		0.4%	12.1%	64.1%
A	15.7%			11.2%	29.4%		0.2%	3.9%	19.2%
AA				14.0%	39.2%			0.1%	0.2%
AAA				0.4%	1.8%

---

Table 3 Surface bonding patterns for the 2/3 ML OH covered Pt(111) surface. For each species, the horizontal direction tells the number of donor (D) hydrogen bonds and the vertical direction the number of acceptor (A) hydrogen bonds

	O			OH			H2O
	—	D	DD	—	D	DD	—	D	DD
—	93.4%			4.3%	8.4%		3.6%	26.7%	51.5%
A	6.6%			13.9%	33.9%		0.4%	4.2%	12.8%
AA				12.0%	26.0%			0.2%	0.8%
AAA				0.5%	0.9%

---

Table 4 Surface bonding patterns for the 1 ML OH covered Pt(111) surface. For each species, the horizontal direction tells the number of donor (D) hydrogen bonds and the vertical direction the number of acceptor (A) hydrogen bonds

	OH
	—	D	DD
—	5.2%	31.3%
A	7.3%	36.0%
AA	3.7%	15.9%
AAA	0.1%	0.4%

---

In all three surfaces, the clear majority of the OH species donated one hydrogen bond, with the AAD configuration most prevalent in the 1/3 ML surface and the AD in the other two. These results agree with previous findings on Pt (100), where the AAD configuration was the most common one for surface coverages below 1/4 ML.⁵ Overall, there is a clear shift towards lower numbers of acceptor bonds as one moves from 1/3 to 1 ML, as indicated by the increase in the D hydrogen bond configuration from 2.9% in the 1/3 ML to 31.3% in the 1 ML system. This could be explained by the decrease in surface rigidity as one moves from a high coverage to a low one, where there are less hydrogen bonds between the surface species and they are more free to move about and accept hydrogen bonds. On the other hand, there is a larger solvent to surface species ratio in the 1/3 ML case, and the gap between the surface species and the solvating water molecules is smaller as evidenced by Fig. 2. Hydrogen bond formation between solvent and the surface OH species is also visible in that the 1/3 and 2/3 ML surfaces have small subpopulations of surface OH that accept three hydrogen bonds. Interestingly, the ratio between acceptor and donor hydrogen bonds is roughly one for the 1 ML system, indicating that the surface OH groups form hydrogen bonds almost exclusively with other surface OH groups. This helps to further clarify the gap observed in Fig. 2, for the 1 ML system as well as the lack of water exchange.

For the surface water molecules in both 1/3 and 2/3 ML surfaces, the DD hydrogen bond configuration was the most common, constituting more than 50% of water molecules in both systems, followed by the D and ADD configurations. Indeed, over 70% of the surface water molecules did not accept hydrogen bonds, in line with previous findings indicating the presence of a special HO⋯HOH complex with OH as acceptor and surface adsorbed water as donor.⁵ This results in the previously discussed parallel water orientation with hydrogens tilted only slightly from the surface.^77–80

4 Conclusions

In this study, we have investigated the structure of the Pt(111)–water interface in an alkaline environment with large OH coverages of 1/3, 2/3 and 1 ML. Our simulations combine a relatively long 20 ps equilibration period with a large system size. We see that the OH coverage clearly influences both the orientational distribution of the water molecules and their density, with more structure associated with higher coverage. At the same time, there is evidence of a highly dynamic hydrogen bond network on the lower coverage systems with substantial exchange of water between surface and the solvent. In addition to OH and H₂O species, which were preferentially located at the top sites, the 1/3 and 2/3 ML surfaces also contained O atoms, which were relatively stable and preferred the hollow sites. In contrast, the 1 ML surface showed none of these dynamics, and is unlikely to be active. Consequently, future studies should account for the presence of O, OH and H₂O even at low to moderate coverages. The dynamic coexistence of all three species on Pt(111) electrodes in alkaline conditions necessitates the investigation of several possible reaction paths for processess like ORR and water splitting. Finally, the exchange processes observed between the solvent and the interface underscore the crucial need to explicitly include liquid water in simulations of the Pt(111) and similar systems.

Author contributions

Both authors participated in the conceptualisation of the study. Lauri Partanen performed the calculations and the analysis of the results. He also wrote the original draft of the manuscript and made the corrections based on the referees’ suggestions. Kari Laasonen acquired the computational resources for the study, provided supervision during the research project and provided critical commentary on both the original and edited versions of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Rasmus Kronberg for providing his input files for the Pt(111)–water interface system with hydrogen adsorbtion. These inputs served as the starting point for the calculations in this article.

Notes and references

1. T. B. Ferriday and P. H. Middleton, Int. J. Hydrogen Energy, 2021, 46, 18489–18510.
2. N. Markovic, H. Gasteiger and P. N. Ross, J. Electrochem. Soc., 1997, 144, 1591–1597.
3. A. Yamakata, T. Ishibashi and H. Onishi, J. Mol. Catal. A: Chem., 2003, 199, 85–94.
4. D. Strmcnik, M. Uchimura, C. Wang, R. Subbaraman, N. Danilovic, D. van der Vliet, A. P. Paulikas, V. R. Stamenkovic and N. M. Markovic, Nat. Chem., 2013, 5, 300–306.
5. J.-X. Zhu, J.-B. Le, M. T. M. Koper, K. Doblhoff-Dier and J. Cheng, J. Phys. Chem. C, 2021, 125, 21571–21579.
6. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892.
7. M. P. Hyman and J. W. Medlin, J. Phys. Chem. B, 2005, 109, 6304–6310.
8. G. S. Karlberg, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 5158–5161.
9. D. Strmcnik, K. Kodama, D. van der Vliet, J. Greeley, V. R. Stamenkovic and N. M. Marković, Nat. Chem., 2009, 1, 466–472.
10. D. Strmcnik, D. F. van der Vliet, K.-C. Chang, V. Komanicky, K. Kodama, H. You, V. R. Stamenkovic and N. M. Marković, J. Phys. Chem. Lett., 2011, 2, 2733–2736.
11. J.-C. Dong, X.-G. Zhang, V. Briega-Martos, X. Jin, J. Yang, S. Chen, Z.-L. Yang, D.-Y. Wu, J. M. Feliu, C. T. Williams, Z.-Q. Tian and J.-F. Li, Nat. Energy, 2019, 4, 60–67.
12. X. Chen, I. T. McCrum, K. A. Schwarz, M. J. Janik and M. T. M. Koper, Angew. Chem., Int. Ed. Engl., 2017, 56, 15025–15029.
13. I. T. McCrum, X. Chen, K. A. Schwarz, M. J. Janik and M. T. M. Koper, J. Phys. Chem. C, 2018, 122, 16756–16764.
14. I. T. McCrum and M. T. M. Koper, Nat. Energy, 2020, 5, 891–899.
15. S. Gilman, J. Phys. Chem., 1964, 68, 70–80.
16. X.-Q. Gong, P. Hu and R. Raval, J. Chem. Phys., 2003, 119, 6324–6334.
17. S. Desai and M. Neurock, Electrochim. Acta, 2003, 48, 3759–3773.
18. A. Tiwari, H. H. Heenen, A. S. Bjørnlund, D. Hochfilzer, K. Chan and S. Horch, ACS Energy Lett., 2020, 5, 3437–3442.
19. P. Strasser, Science, 2015, 349, 379–380.
20. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998.
21. P. Wang, Q. Shao and X. Huang, Joule, 2018, 2, 2514–2516.
22. G. B. Fisher and B. A. Sexton, Phys. Rev. Lett., 1980, 44, 683–686.
23. A. Hodgson and S. Haq, Surf. Sci. Rep., 2009, 64, 381–451.
24. A. B. Anderson and T. V. Albu, J. Electrochem. Soc., 2000, 147, 4229–4238.
25. A. B. Anderson, N. M. Neshev, R. A. Sidik and P. Shiller, Electrochim. Acta, 2002, 47, 2999–3008.
26. J. Roques and A. B. Anderson, J. Electrochem. Soc., 2004, 151, E85–E91.
27. J. Rossmeisl, J. K. Nørskov, C. D. Taylor, M. J. Janik and M. Neurock, J. Phys. Chem. B, 2006, 110, 21833–21839.
28. C. D. Taylor, R. G. Kelly and M. Neurock, J. Electrochem. Soc., 2007, 154, F217–F221.
29. R. Jinnouchi and A. B. Anderson, J. Phys. Chem. C, 2008, 112, 8747–8750.
30. V. Tripković, E. Skúlason, S. Siahrostami, J. K. Nørskov and J. Rossmeisl, Electrochim. Acta, 2010, 55, 7975–7981.
31. A. S. Bondarenko, I. E. L. Stephens, H. A. Hansen, F. J. Pérez-Alonso, V. Tripković, T. P. Johansson, J. Rossmeisl, J. K. Nørskov and I. Chorkendorff, Langmuir, 2011, 27, 2058–2066.
32. N. M. Marković, T. J. Schmidt, B. N. Grgur, H. A. Gasteiger, R. J. Behm and P. N. Ross, J. Phys. Chem. B, 1999, 103, 8568–8577.
33. V. Climent, R. Gómez, J. M. Orts and J. M. Feliu, J. Phys. Chem. B, 2006, 110, 11344–11351.
34. V. R. Stamenkovic, B. Fowler, B. S. Mun, G. Wang, P. N. Ross, C. A. Lucas and N. M. Marković, Science, 2007, 315, 493–497.
35. N. Garcia-Araez, J. Phys. Chem. C, 2011, 115, 501–510.
36. J. Carrasco, A. Hodgson and A. Michaelides, Nat. Mater., 2012, 11, 667–674.
37. J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5, 909–913.
38. S. Sakong, K. Forster-Tonigold and A. Groß, J. Chem. Phys., 2016, 144, 194701.
39. S. K. Iyemperumal and N. A. Deskins, ChemPhysChem, 2017, 18, 2171–2190.
40. E. Skúlason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250.
41. J. Hussain, H. Jónsson and E. Skúlason, Faraday Discuss., 2016, 195, 619–636.
42. V. Tripković and T. Vegge, J. Phys. Chem. C, 2017, 121, 26785–26793.
43. H. H. Heenen, J. A. Gauthier, H. H. Kristoffersen, T. Ludwig and K. Chan, J. Chem. Phys., 2020, 152, 144703.
44. L. M. C. Pinto, P. Quaino, M. D. Arce, E. Santos and W. Schmickler, ChemPhysChem, 2014, 15, 2003–2009.
45. H. H. Kristoffersen, T. Vegge and H. A. Hansen, Chem. Sci., 2018, 9, 6912–6921.
46. Y. Li and Z.-F. Liu, J. Phys. Chem. Lett., 2021, 12, 6448–6456.
47. S. Liu, M. G. White and P. Liu, J. Phys. Chem. C, 2016, 120, 15288–15298.
48. R. Kronberg and K. Laasonen, J. Phys. Chem. C, 2020, 124, 13706–13714.
49. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
50. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
51. G. Lippert, J. Hutter and M. Parrinello, Mol. Phys., 1997, 92, 477–488.
52. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
53. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
54. C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662.
55. M. Krack, Theor. Chem. Acc., 2005, 114, 145–152.
56. B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
57. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
58. E. R. McNellis, J. Meyer and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205414.
59. G. Mercurio, E. R. McNellis, I. Martin, S. Hagen, F. Leyssner, S. Soubatch, J. Meyer, M. Wolf, P. Tegeder, F. S. Tautz and K. Reuter, Phys. Rev. Lett., 2010, 104, 036102.
60. J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901.
61. P. Haas, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085104.
62. H. Ogasawara, B. Brena, D. Nordlund, M. Nyberg, A. Pelmenschikov, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2002, 89, 276102.
63. K. Bedürftig, S. Völkening, Y. Wang, J. Wintterlin, K. Jacobi and G. Ertl, J. Chem. Phys., 1999, 111, 11147–11154.
64. M. F. Li, L. W. Liao, D. F. Yuan, D. Mei and Y.-X. Chen, Electrochim. Acta, 2013, 110, 780–789.
65. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
66. T. Roman and A. Groß, Catal. Today, 2013, 202, 183–190.
67. S. Sakong and A. Groß, J. Chem. Phys., 2018, 149, 084705.
68. W. R. Inc, Mathematica, Version 14.0, Champaign, IL, 2024, https://www.wolfram.com/mathematica.
69. M. L. Waskom, J. Open Source Softw., 2021, 6, 3021.
70. J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95.
71. A. Michaelides and P. Hu, J. Chem. Phys., 2001, 114, 513–519.
72. S. Gottesfeld, Fuel Cell Catalysis: A surface Science Approach, John Wiley & Sons, Ltd, 2009, ch. 1, pp. 1–30.
73. M. T. M. Koper and J. J. Lukkien, J. Electroanal. Chem., 2000, 485, 161–165.
74. N. Ramaswamy and S. Mukerjee, J. Phys. Chem. C, 2011, 115, 18015–18026.
75. D. J. Miller, H. Öberg, S. Kaya, H. Sanchez Casalongue, D. Friebel, T. Anniyev, H. Ogasawara, H. Bluhm, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2011, 107, 195502.
76. D. Friebel, D. J. Miller, C. P. O’Grady, T. Anniyev, J. Bargar, U. Bergmann, H. Ogasawara, K. T. Wikfeldt, L. G. M. Pettersson and A. Nilsson, Phys. Chem. Chem. Phys., 2011, 13, 262–266.
77. S. Meng, E. G. Wang and S. Gao, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 195404.
78. J. Le, M. Iannuzzi, A. Cuesta and J. Cheng, Phys. Rev. Lett., 2017, 119, 016801.
79. J. Le, A. Cuesta and J. Cheng, J. Electroanal. Chem., 2018, 819, 87–94.
80. S. Sakong and A. Groß, Phys. Chem. Chem. Phys., 2020, 22, 10431–10437.
81. S. Cukierman, Biochim. Biophys. Acta, Bioenerg., 2006, 1757, 876–885.
82. D. Marx, ChemPhysChem, 2006, 7, 1848–1870.
83. G. S. Karlberg, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 153414.
84. M. D. Arce, P. Quaino and E. Santos, Catal. Today, 2013, 202, 120–127.
85. M. J. Ungerer, D. Santos-Carballal, A. Cadi-Essadek, C. G. C. E. van Sittert and N. H. de Leeuw, J. Phys. Chem. C, 2019, 123, 27465–27476.
86. T. Schiros, L.-Å. Näslund, K. Andersson, J. Gyllenpalm, G. S. Karlberg, M. Odelius, H. Ogasawara, L. G. M. Pettersson and A. Nilsson, J. Phys. Chem. C, 2007, 111, 15003–15012.
87. N. Materer, U. Starke, A. Barbieri, R. Döll, K. Heinz, M. A. Van Hove and G. A. Somorjai, Surf. Sci., 1995, 325, 207–222.
88. Z. Gu and P. B. Balbuena, J. Phys. Chem. C, 2007, 111, 9877–9883.
89. I.-F. W. Kuo, C. J. Mundy, B. L. Eggimann, M. J. McGrath, J. I. Siepmann, B. Chen, J. Vieceli and D. J. Tobias, J. Phys. Chem. B, 2006, 110, 3738–3746.
90. L. Partanen, G. Murdachaew, R. B. Gerber and L. Halonen, Phys. Chem. Chem. Phys., 2016, 18, 13432–13442.

---