 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning the work function of graphite nanoparticles via edge termination†
Michael P.
Mercer
 *abc,
Arihant
Bhandari
*abc,
Arihant
Bhandari
 cd,
Chao
Peng
cd,
Chao
Peng
 e,
Jacek
Dziedzic
e,
Jacek
Dziedzic
 cdf,
Chris K.
Skylaris
cdf,
Chris K.
Skylaris
 *cd and
Denis
Kramer
*cd and
Denis
Kramer
 b
b
aDepartment of Chemistry, Lancaster University, Bailrigg, Lancaster LA1 4YB, UK. E-mail: m.mercer1@lancaster.ac.uk
bFaculty of Mechanical Engineering, Helmut-Schmidt University, Holstenhofweg 85, 22043 Hamburg, Germany
cThe Faraday Institution, Quad One, Harwell Science and Innovation Campus, Didcot, UK
dSchool of Chemistry, University of Southampton, Highfield, Southampton SO17 1BJ, UK. E-mail: C.Skylaris@soton.ac.uk
eMultiscale Crystal Materials Research Center, Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Shenzhen, 518055, China
fFaculty of Applied Physics and Mathematics, Gdansk University of Technology, Gdansk 80-233, Poland
First published on 14th May 2024
Abstract
Graphite nanoparticles are important in energy materials applications such as lithium-ion batteries (LIBs), supercapacitors and as catalyst supports. Tuning the work function of the nanoparticles allows local control of lithiation behaviour in LIBs, and the potential of zero charge of electrocatalysts and supercapacitors. Using large scale density functional theory (DFT) calculations, we find that the surface termination of multilayer graphene nanoparticles can substantially modify the work function. Calculations in vacuum and in electrolyte show that manipulating the edge termination substantially modifies the potential not only around the edge, but also on the basal plane. Termination with hydrogen or oxygen completely reverses the potential distribution surrounding the basal plane and edges. The trends can be explained based on the work function differences of the edges dependent on termination, and that of the basal plane. Electronic equilibration between different surfaces at the nanoscale allows manipulation of the work function. We demonstrate a link between the area of the graphite basal plane via changing the nanoparticle size, and the work function. We expect that these insights can be utilised for local control of electrochemical functions of graphite nanoparticles prepared under oxidising or reducing conditions.
1 Introduction
Graphite is ubiquitous as the anode material of choice in lithium ion (Li-ion) cells. Ordered lithium–graphite stages affect the cell voltage1–4 and limit the rate of insertion of lithium into/deinsertion out of graphite.5–7 The rate of insertion and removal of lithium from graphite at the edges of the particles is an additional major performance bottleneck and is related to the electronic behaviour at those edges,8 where lithium insertion initially occurs, motivating a detailed study of the effect of different graphite edges. It is expected that graphite nanoparticles show different behaviour dependent on the nature of the graphite edge termination. In particular, the potential distribution around the particle is expected to be different dependent on the termination, and this effect needs to be understood in detail to systematically understand and control the electrochemical behaviour of graphite nanoparticles at a local level. Despite the apparent importance of the graphite edges to the electronic and electrochemical behaviour of graphite, only a handful of works have systematically investigated the influence of edge morphology of graphite on lithium (de)insertion through experiment.9,10 It would be highly advantageous to develop more systematic understanding of edge termination and its effects on the work function.Additionally, graphite (and graphene) nanoparticles have applications in supercapacitors11,12 and as electrocatalysts.13,14 In these applications it is also important to locally control the electronic properties in the immediate vicinity of the particles. As an example, the effect of varying the work function on the oxygen reduction reaction (ORR) has been explored.13 Previous work found a link between the activity for vanadium oxidation and the work function of different graphite felt electrodes, dependent on edge termination.15 For these applications it is also important to achieve local control of the potential distribution surrounding the particles. Although much attention has been dedicated to the effect of different adsorbates on the basal plane and their associated effects on electronic behaviour,16–19 there has so far been little exploration of the effect of different edge terminations and in particular, the effect of varying the nanoparticle size to locally adjust the electronic properties.
The edges of graphite nanoparticles can be terminated by different groups. In the present work, we focus on termination either by hydrogen- or oxygen-containing groups, representing models of the termination dependent on the precise nature of the synthesis environment.9 The nature of the termination (H– or O–) could affect the surrounding potential distribution around a graphite nanoparticle. This effect needs to be understood in detail to locally manipulate the electrochemical behaviour of graphite in lithium-ion batteries, supercapacitors, and electrocatalysts. It is expected that graphite nanoparticles will show a dependence of the work function on particle size, since the exposed area of the basal plane with respect to the edge group varies with size, providing an important means to locally tune electrochemical performance by varying the particle size.
The dependence of the work function on particle size has been explored in spherical systems,20–22 in which the work function is found to scale inversely with the particle radius.23 It is not obvious how the work function of a particle surrounded by two or more types of surface, such as graphite or graphene nanoparticles, would scale with particle size. Such particles are bounded by different surfaces, each of which may have a different work function. To tune and optimise graphene nanoparticles in the above application areas, it is necessary to model the potential distribution dependent on particle size and termination and to correlate these trends with the work function.
The present work investigates from first principles calculations, the effect of the edge termination and size of graphite nanoparticles on the work function. We exploit and showcase recent developments in the linear scaling DFT code ONETEP, to perform calculations on graphite nanoparticle systems that would be impractical using conventional DFT. In particular, the implications of edge of termination on the surrounding potential distribution are explored and explained. Following on from this, the effect of the graphene nanoparticle size on the work function is determined. Finally, we discuss the implications of these trends for electrochemical energy materials applications.
2 Computational methods
2.1 Electronic structure calculations
Calculations were performed using the ONETEP DFT program, which has a linear-scaling computational cost with the number of atoms, allowing quantum mechanical simulations of large nanoparticles.24–26 The basis set consists of psinc functions which are equivalent to plane waves.27 The kinetic energy cutoff for the basis set is 1000.0 eV. A radius of 8.0a0 is used for the localized orbitals (which are non-orthogonal generalized Wannier functions).28 An ensemble DFT method with Fermi–Dirac smearing was used with spin-polarisation enabled for all calculations.29 To model the point charges of ionic cores in DFT, we use norm-conserving pseudopotentials,30,31 generated using CASTEP.32 The DFT-D2 method was employed to describe van der Waals interactions.33DFT simulations in an electrolyte environment were performed using a Poisson–Boltzmann electrolyte model.34,35 The electrolyte is 1.0 M LiPF6 in ethylene carbonate solvent (EC), which is commonly used in Li-ion batteries. The non-homogeneous Poisson–Boltzmann equation,
| ∇·[ε(r)∇ϕ(r)] = −4πρ(r), | (1) |
 | (2) |
Slabs were cut from fully relaxed bulk graphite with an AB-stacking to construct periodic models of the armchair edges. Calculations were performed with H– or O-termination of armchair graphite edges. Pristine armchair edges were modelled using cells with a = 60.0 Å, b = 12.784 Å, c = 8.532 Å, as basis vectors, with 352 carbon atoms and 32 H/O atoms in the cell. Both cells were constructed with orthogonal basis vectors. While a minimum of two layers of graphene is required to replicate the AB-stacking of pristine graphite found experimentally, edge cells comprised four AB-stacked graphene layers in each cell to ensure accurate calculations with a single k-point as implemented within ONETEP. For all edge calculations, a vacuum layer of 23 Å along the [100]-direction was used to minimise interactions between periodic images. Cell geometries are shown in Fig. 2.
Atomic distances and cell geometry were obtained using the relaxed AB graphite cell geometry obtained from DFT. The volume and shape of the cell were kept fixed, but all the ions were allowed to relax until reaching the default force and energy convergence criteria.
 | ||
| Fig. 3 Fully relaxed unit cells of (a) and (b): H-terminated nanoparticles and (c) and (d): O-terminated nanoparticles. Geometries correspond to those obtained in vacuum; geometries obtained in electrolyte are shown in the ESI,† Fig. S1. The line in (a) shows the position of the cross-sectional plane that was used for determination of the potential and charge distributions; the cross-sectional plane is perpendicular to the plane of the page. The graphene nanoparticles are surrounded by either vacuum or implicit solvent, in all three directions. | ||
Additionally, the effect of nanoparticle size was examined. Particles with H-termination were constructed with 2728, 5600 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 148 total atoms in the unit cell. The diameter of these particles, measured along the [110]-direction, was 5.0 nm, 7.5 nm and 10.0 nm, respectively. These calculations were only performed in vacuum, within a 158.75× 158.75 × 158.75 Å3 unit cell. Calculation results were compared with the 712 atom cell, recalculated within the 158.75 × 158.75 × 158.75 Å3 unit cell. The relaxed geometries for these nanoparticles are provided in the ESI,† Fig. S2.
148 total atoms in the unit cell. The diameter of these particles, measured along the [110]-direction, was 5.0 nm, 7.5 nm and 10.0 nm, respectively. These calculations were only performed in vacuum, within a 158.75× 158.75 × 158.75 Å3 unit cell. Calculation results were compared with the 712 atom cell, recalculated within the 158.75 × 158.75 × 158.75 Å3 unit cell. The relaxed geometries for these nanoparticles are provided in the ESI,† Fig. S2.
3 Results
3.1 Potential distributions around edged nanoparticles
Cross-sections of the potential distribution around graphite nanoparticles are shown in vacuum (Fig. 4) and in electrolyte (Fig. 5a–c). In the presented figures, the potential was obtained by taking a cross-section through the mid-point of the [110]-axis. As such, the plane shown in the figures intersects mid-way through the graphite nanoparticle, with the [100]-axis perpendicular to two of the armchair edges of the nanoparticles, and the [001]-axis perpendicular to the graphite basal planes. For the vacuum calculations, the reference potential infinitely far away from the nanoparticle is zero. | ||
| Fig. 4 Cross sectional potential profiles of armchair-edged graphite nanoparticles in vacuum. (a) H-Terminated nanoparticle; (b) O-termination. The nanoparticle geometries correspond to those shown in Fig. 3. Numerical values of the potential (in V) are indicated in the key on the right. | ||
 | ||
| Fig. 5 Cross-sectional potential profiles (a) and (b) and charge densities (c) and (d) of graphite nanoparticles in 1 M LiPF6 in EC. Potential profiles of nanoparticles with: (a) H-termination; (b) O-termination. The nanoparticle geometries correspond to those shown in the ESI,† Fig. S1. Numerical values of the potential (in V) are indicated in the key on the left. Total charge densities of (c) H-armchair; (d) O-armchair, where the charge density (units × 10−3 e Å−3) is as indicated in the scale along the right. | ||
In vacuum, there is a marked difference in the surrounding potential distribution for a H-terminated particle, Fig. 4a, and an O-terminated particle, Fig. 4b. Following the [001]-direction from the top to the centre of Fig. 4a, the electrostatic potential becomes more negative as the basal plane of graphite is approached, until reaching the carbon ionic cores. However, the potential just to the right of the H-terminated armchair edge is slightly positive, and moving away from the nanoparticle edge along the [100]-direction, the potential decays towards zero. Consequently, there is a negative potential on the surface of the basal plane, but a positive one close to the edge. On the other hand, for the O-terminated particle, the potential distribution follows the opposite tendency: it is positive close to the surface of the basal plane, while being slightly negative close to the oxygen terminated edge.
The trend in the potential distributions in electrolyte, shown in Fig. 5a–c, is qualitatively similar to the one obtained in vacuum. The most notable difference results from electrostatic screening by the electrochemical double layer in the electrolyte. Consequently, considering the potential variation from the basal plane and edged surfaces of graphite, the potential decays towards zero over a much shorter length scale than in vacuum. Because all electrolyte calculations were performed without an externally applied potential, the reference potential is the potential of zero charge (pzc). Therefore, similarly to the vacuum calculations, the reference potential infinitely far away from the nanoparticle is zero.
Plots of the total charge density in electrolyte are shown in Fig. 5c and d. The charge in the electrolyte double layer electrostatically screens the charge on the electrode surface. The figures indicate that positive electrolyte charge density accumulates around the basal plane when the edges are H-terminated (Fig. 5c). Conversely, negative charge accumulates in the electrolyte around the basal plane when the edges are O-terminated (Fig. 5d).
3.2 Mulliken charge analysis
To gain more insight into the charge distribution inside the graphite nanoparticles, Mulliken analysis of the charge density distribution was performed. This enables the charge density on the atoms of the nanoparticles to be evaluated without the additional screening from the electrolyte. The analysis is shown in Fig. 6. | ||
| Fig. 6 Mulliken charge analysis of edged graphite nanoparticles. The nanoparticle geometries correspond to those shown in Fig. 3 (in vacuum) and Fig. S1 (ESI†) (in electrolyte). As shown in the key on the right, red indicates accumulation of positive charge while blue indicates negative charge accumulation. (a) and (b) Calculations in vacuum for (a) H-armchair; (b) O-armchair. (c) and (d) Calculations in electrolyte, as labelled at the top of the figure. | ||
Firstly, we observe that the charge on the surface atoms (H or O) has the opposite sign compared with the electrolyte charge distributions around the edges (cf.Fig. 5c and d), because the surface charge is electrostatically screened by the electrochemical double layer when the nanoparticle is embedded in electrolyte.
For the H-armchair nanoparticle, electrons are transferred from the H atoms to the nearest neighbour carbon atoms, resulting in the surface H atoms being uniformly positively charged (Fig. 6a).
The O-armchair edge shows the opposite tendency in vacuum, with electron transfer from the outer carbon atoms to the surface oxygen atoms (Fig. 6b). In vacuum, slightly more electrons accumulate at the corners of the nanoparticle compared with the edges, resulting in some dependence of the charge density on angle.
Qualitatively similar behaviour is observed for the O-armchair edges in electrolyte (Fig. 6d), but some differences are observed compared with the results in vacuum. The contrast between the charge on the corner and edge oxygen atoms is more pronounced compared with vacuum due to higher charge polarization in electrolyte. Additionally, there is a slightly different bonding arrangement of the surface oxygen atoms in electrolyte.
Differences between the charge distribution near the atoms in vacuum and in electrolyte also lead to differences in the potential and charge density in these two environments, as shown in the ESI,† Fig. S3 and S4.
3.3 Effect of particle size on the potential
Results for the H-armchair particle are shown, in vacuum, dependent on the particle size in Fig. 7. As in the previous sections, the figures represent a cross-section of the potential taken perpendicular to the basal planes of the nanoparticles.Results indicate that the potential becomes more negative near the basal plane as the particle size increases in diameter between 2.5 nm to 10.0 nm. The potential decays towards the vacuum level over a longer length scale along the [001] direction with increasing particle size. It can also be observed that the potential in the vicinity of the edge becomes less positive with increasing particle size, and decays towards the vacuum level along the [100] direction with a shorter length scale. It is therefore expected that the work function will vary with the particle size, as presented in the next section.
3.4 Determination of the work function
To interpret the potential distributions and charge densities of the nanoparticles presented in the previous sections, it is helpful to consider two periodic planar systems: the edged graphite systems already introduced above, and 4 graphene layers separated by vacuum.Values of ψ(r) are plotted below in Fig. 8 in vacuum, where
| ψ(r) = −eϕ(r) − EF. | (3) |
In eqn (3), ϕ(r) is the planar averaged potential as a function of the distance, r, through the slab and EF is the Fermi level. Therefore, in the vacuum region, ψ(r) is equivalent to the work function. Results for the graphite edged system are shown in Fig. 8a; results for the basal plane are in Fig. 8b.
Comparing the two pristine edges in Fig. 8a, it is found that the O-terminated edge has a much higher value of ψ(r) in the vacuum region than the H-terminated edge. As for the basal plane shown in Fig. 8b, ψ(r) lies midway between the pristine H-armchair and O-armchair edges, implying that the work function of the basal plane lies in between the H-terminated and O-terminated edges, with the H-terminated edge having the lowest value for the work function.
In principle, for the nanoparticle systems, the potential would tend to zero infinitely far away from the nanoparticle, and the work function of these systems in vacuum could be approximated by
| ψ(r → ∞) = −EF, | (4) |
All work function values obtained from the work are tabulated in the ESI,† Table S1.
3.5 Variation of work function with particle size
Work function values of the planar systems, obtained from eqn (3) in the vacuum region, are shown in Fig. 9.The results in Fig. 9 indicate that the work function of the H-armchair nanoparticles lies between that determined for the basal plane (ψ = 4.15 eV) and the planar H-armchair edge (ψ = 2.89 eV). Furthermore, as the particle size increases the work function tends towards that of the basal plane.
Different potential values were determined in vacuum and in electrolyte, which arose due to approximating the ionic cores in the electrolyte simulations with smeared ions of smearing width, σ.38 The effect of the value of σ on the electrostatic potential is discussed in the ESI.† As σ decreases, the electrostatic potential becomes steeper. In the limit of σ approaching the width of the pseudopotential cores, the work function due to smeared ions approaches the same value as the one resulting from pseudopotentials. The difference between the work functions determined in vacuum and in electrolyte was found to be insignificant (further details are in the ESI,† Fig. S6–S8).
4 Discussion
4.1 Trends in potential distribution and work function
If there are two surfaces of potentials ϕ1 and ϕ2, and work functions ψ1 and ψ2 such that ψ1 > ψ2, we can write
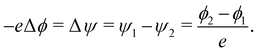 | (5) |
That is, we expect the potential, ϕ1 near the surface with higher work function to be lower in value, exactly as observed in Fig. 4a. Given the additional constraint for the potential to go to zero far away from the particle, this leads to the observed negative ϕ value in the neighbourhood of the basal plane and the positive value near the H-armchair edges. The same effect also explains the dependence of the work function on particle size for the H-armchair nanoparticles, in which the potential becomes more negative close to the basal planes as the basal plane area increases. The basal plane area on both sides of the particle scales approximately with the square of the particle radius, while the area of the H-terminated edges scales linearly with the radius. Therefore, while the increasing area of both features has an effect on the potential far away from the particle, the increasing area of the basal plane predominates for larger particles and thus the work function tends towards that of the basal plane. Therefore, the work function value tends towards that of the basal plane with increasing particle size.
The O-armchair nanoparticle shows a greater work function (ψ = 6.26 eV) than either the planar O-armchair edge or the basal plane, which were ψ = 5.26 eV and ψ = 4.15 eV, respectively. In this case, the presence of edge sites at the corner of the nanoparticle results in some disruption to the bonding arrangement compared with the planar edge (cf.Fig. 3e and 2f), as also exemplified in the Mulliken charge analysis in Fig. 6. Therefore, in the case of the O-armchair particle, finite size effects appear to be important to the value of the work function obtained. It is expected that the influence of the corners would become less significant with increasing particle size, possibly leading to a non-monotonic change in work function that eventually tends to that of the basal plane as the particle size increases.
4.2 Implications for experimental measurements
Calculations show a pronounced difference in the potential distribution near hydrogen terminated particles compared with oxygen terminated particles. The work function of the planar O-armchair edge is greater than that of the basal plane of graphite, which in turn is greater than the work function of the H-armchair edge. As a result of electronic equilibration between particle facets, the potential and charge density distribution is reversed for the two non-basal plane terminations. Additionally, the potential and charge density distribution on the basal plane is also reversed dependent on the edge termination. The same trend is observed in vacuum (Fig. 4) and in electrolyte (Fig. 5). In electrolyte, however, electrostatic screening by the solvent leads to decay of the potential over a much shorter length scale than in vacuum. It can be expected, therefore, that the effect of different edge termination would be more significant and potentially easier to detect in the gas phase than in electrolyte, with more noticeable implications in gas phase catalysis than electrocatalysis.Nevertheless, the calculated differences in potential in electrolyte, on the order of 100 mV, in the neighbourhood of the basal plane and the different edges could potentially lead to applications in various electrochemical energy storage applications. A local probe such as scanning electrochemical cell microscopy (SECCM) could be utilised to detect these differences,45,46 where it might be expected to see differences in redox activity on the basal plane dependent on edge termination. The previously demonstrated sensitivity of vanadium redox processes to graphite edge morphology and the link between termination and the work function15 suggests that precise tuning of activity through varying the particle size is a possibility, with applications in areas such as redox-flow batteries. The work could also lead to strategies to design highly active oxygen reduction reaction (ORR) electrocatalysts47 dependent on particle size.
It is also anticipated that this work will influence strategies to manipulate metal–support interactions48,49via tuning of the work function. It would be worthwhile to examine the effect of systematic particle size variation by advanced electron microscopy techniques such as scanning transmission electron microscopy (STEM).50 Changes to the local potential distribution might also be detectable by operando Kelvin probe force microscopy (KPFM) measurements.51
In the battery area, it is anticipated that these local variations in potential distribution could affect the nucleation potential of lithium on the basal plane and on the edges, with the potential to to precisely tune the nucleation behaviour of Li and other metals utilised in battery applications dependent on edge morphology, termination, and particle size.52–54 This will be investigated further in a follow-on work.
5 Summary and conclusions
The key findings of the work can be summarised as:1. The termination, either H or O, around graphite nanoparticles makes a pronounced difference to the surrounding potential distribution.
2. The potential around the edge and around the basal plane has opposite sign.
3. The trend can be related to the work function differences between the different edged systems and that of the basal plane. For planar systems, the work function goes as O-armchair > basal plane > H-armchair.
4. Atomic charge partitioning suggests electron transfer from H to carbon for the H-armchair edge. For the O-armchair, the electron transfer goes in the opposite direction.
5. A consequence of the difference of the work function of the graphite edges with respect to the basal plane is a particle size dependence on the work function around the particle.
We anticipate that the variation on the order of 100 mV in potential, in electrolyte, could influence the nucleation potential of lithium on the basal plane versus the different graphite edges. Equally, local manipulation of potential at a single particle level could have important implications for control of local activity for electrocatalytic reactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof. Magda Titirici from Imperial College London and her group for discussions on CVD doping of carbon structures with boron and nitrogen. We thank the Faraday Institution (faraday.ac.uk; EP/S003053/1), grant number FIRG025 and FIRG059, for funding. Additionally, we are grateful to the Chinesisch-Deutsches Zentrum für Wissenschaftsförderung for a Sino-German Mobility grant “Intelligent design of negative electrode for the next generation of high safety and high energy density battery”, No. M-0755. We are grateful for computational support from the Michael Supercomputer of the Faraday Institution. The HPC cluster HSUper has been provided by the project hpc.bw, funded by dtec.bw—Digitalization and Technology Research Center of the Bundeswehr. dtec.bw is funded by the European Union – NextGenerationEU. We likewise acknowledge funding through the dtec.bw project “Digital Materials Foundry”. We also thank the International Partnership Program of the Chinese Academy of Sciences (321GJHZ2023189FN) and the Shenzhen International Cooperation Program (GJHZ20220913142812025). Special thanks to Hauke Preuß at HSU for help testing ONETEP on the HSUper cluster. MPM also thanks Prof. Harry Hoster (Universität Duisburg-Essen) for some discussions early in the project on modifying graphite edges for Li-ion battery applications.Notes and references
- M. P. Mercer, M. Otero, M. Ferrer-Huerta, A. Sigal, D. E. Barraco, H. E. Hoster and E. P. Leiva, Electrochim. Acta, 2019, 324, 134774 CrossRef CAS.
- M. P. Mercer, C. Peng, C. Soares, H. E. Hoster and D. Kramer, J. Mater. Chem. A, 2021, 9, 492–504 RSC.
- J. Asenbauer, T. Eisenmann, M. Kuenzel, A. Kazzazi, Z. Chen and D. Bresser, Sustainable Energy Fuels, 2020, 4, 5387–5416 RSC.
- C. Didier, W. K. Pang, Z. Guo, S. Schmid and V. K. Peterson, Chem. Mater., 2020, 32, 2518–2531 CrossRef CAS.
- C. Schmitt, A. Kube, N. Wagner and K. A. Friedrich, ChemElectroChem, 2022, 9, e202101342 CrossRef CAS.
- E. M. Gavilán-Arriazu, M. P. Mercer, O. A. Pinto, O. A. Oviedo, D. E. Barraco, H. E. Hoster and E. P. M. Leiva, J. Electrochem. Soc., 2020, 167, 013533 CrossRef.
- E. M. Gavilán-Arriazu, M. P. Mercer, D. E. Barraco, H. E. Hoster and E. P. M. Leiva, Prog. Energy, 2021, 3, 042001 CrossRef.
- C. Peng, M. P. Mercer, C.-K. Skylaris and D. Kramer, J. Mater. Chem. A, 2020, 8, 7947–7955 RSC.
- P. Bernardo, J.-M. Le Meins, L. Vidal, J. Dentzer, R. Gadiou, W. Märkle, P. Novák, M. Spahr and C. Vix-Guterl, Carbon, 2015, 91, 458–467 CrossRef CAS.
- P. Bernardo, J. Dentzer, R. Gadiou, W. Märkle, D. Goers, P. Novák, M. Spahr and C. Vix-Guterl, Carbon, 2011, 49, 4867–4876 CrossRef CAS.
- Y. Zhou, X. Xu, B. Shan, Y. Wen, T. Jiang, J. Lu, S. Zhang, D. P. Wilkinson, J. Zhang and Y. Huang, Energy Storage Mater., 2015, 1, 103–111 CrossRef.
- L. Hu, X. Peng, Y. Li, L. Wang, K. Huo, L. Y. S. Lee, K. Wong and P. K. Chu, Nano Energy, 2017, 34, 515–523 CrossRef CAS.
- J. Y. Cheon, J. H. Kim, J. H. Kim, K. C. Goddeti, J. Y. Park and S. H. Joo, J. Am. Chem. Soc., 2014, 136, 8875–8878 CrossRef CAS PubMed.
- J. Benson, Q. Xu, P. Wang, Y. Shen, L. Sun, T. Wang, M. Li and P. Papakonstantinou, ACS Appl. Mater. Interfaces, 2014, 6, 19726–19736 CrossRef CAS.
- H. Radinger, V. Trouillet, F. Bauer and F. Scheiba, ACS Catal., 2022, 12, 6007–6015 CrossRef CAS.
- R. Garg, N. K. Dutta and N. Roy Choudhury, Nanomaterials, 2014, 4, 267–300 CrossRef.
- Y. Shi, K. K. Kim, A. Reina, M. Hofmann, L.-J. Li and J. Kong, ACS Nano, 2010, 4, 2689–2694 CrossRef CAS PubMed.
- J. Vatamanu, X. Ni, F. Liu and D. Bedrov, Nanotechnology, 2015, 26, 464001 CrossRef.
- M. Legesse, F. E. Mellouhi, E. T. Bentria, M. E. Madjet, T. S. Fisher, S. Kais and F. H. Alharbi, Appl. Surf. Sci., 2017, 394, 98–107 CrossRef CAS.
- L. Zhou and M. R. Zachariah, Chem. Phys. Lett., 2012, 525–526, 77–81 CrossRef CAS.
- C. Q. Sun, Prog. Solid State Chem., 2007, 35, 1–159 CrossRef CAS.
- M. M. Kappes, M. Schär, P. Radi and E. Schumacher, J. Chem. Phys., 1986, 84, 1863–1875 CrossRef CAS.
- J. Kaur and R. Kant, J. Phys. Chem. Lett., 2015, 6, 2870–2874 CrossRef CAS PubMed.
- J. C. A. Prentice, J. Aarons, J. C. Womack, A. E. A. Allen, L. Andrinopoulos, L. Anton, R. A. Bell, A. Bhandari, G. A. Bramley, R. J. Charlton, R. J. Clements, D. J. Cole, G. Constantinescu, F. Corsetti, S. M.-M. Dubois, K. K. B. Duff, J. M. Escartín, A. Greco, Q. Hill, L. P. Lee, E. Linscott, D. D. ORegan, M. J. S. Phipps, L. E. Ratcliff, A. R. Serrano, E. W. Tait, G. Teobaldi, V. Vitale, N. Yeung, T. J. Zuehlsdorff, J. Dziedzic, P. D. Haynes, N. D. M. Hine, A. A. Mostofi, M. C. Payne and C.-K. Skylaris, J. Chem. Phys., 2020, 152, 174111 CrossRef CAS PubMed.
- C.-K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, J. Chem. Phys., 2005, 122, 084119 CrossRef PubMed.
- L. M. Morgan, M. P. Mercer, A. Bhandari, C. Peng, M. M. Islam, H. Yang, J. Holland, S. W. Coles, R. Sharpe, A. Walsh, B. J. Morgan, D. Kramer, M. S. Islam, H. E. Hoster, J. S. Edge and C.-K. Skylaris, Prog. Energy, 2021, 4, 012002 CrossRef.
- A. A. Mostofi, P. D. Haynes, C.-K. Skylaris and M. C. Payne, J. Chem. Phys., 2003, 119, 8842–8848 CrossRef CAS.
- C.-K. Skylaris, A. A. Mostofi, P. D. Haynes, O. Diéguez and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035119 CrossRef.
- A. Ruiz-Serrano and C.-K. Skylaris, J. Chem. Phys., 2013, 139, 054107 CrossRef PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. Bhandari, L. Anton, J. Dziedzic, C. Peng, D. Kramer and C.-K. Skylaris, J. Chem. Phys., 2020, 153, 124101 CrossRef CAS.
- J. Dziedzic, A. Bhandari, L. Anton, C. Peng, J. C. Womack, M. Famili, D. Kramer and C.-K. Skylaris, J. Phys. Chem. C, 2020, 124, 7860–7872 CrossRef CAS.
- J. C. Womack, L. Anton, J. Dziedzic, P. J. Hasnip, M. I. J. Probert and C.-K. Skylaris, J. Chem. Theory Comput., 2018, 14, 1412–1432 CrossRef CAS.
- https://www.dlmg.org .
- J. Dziedzic, S. J. Fox, T. Fox, C. S. Tautermann and C.-K. Skylaris, Int. J. Quantum Chem., 2013, 113, 771–785 CrossRef CAS.
- G. Bramley, M.-T. Nguyen, V.-A. Glezakou, R. Rousseau and C.-K. Skylaris, J. Chem. Theory Comput., 2020, 16, 2703–2715 CrossRef CAS PubMed.
- J. Dziedzic, H. H. Helal, C.-K. Skylaris, A. A. Mostofi and M. C. Payne, EPL, 2011, 95, 43001 CrossRef.
- D. S. Hall, J. Self and J. R. Dahn, J. Phys. Chem. C, 2015, 119, 22322–22330 CrossRef CAS.
- R. Naejus, C. Damas, D. Lemordant, R. Coudert and P. Willmann, J. Chem. Thermodyn., 2002, 34, 795–806 CrossRef CAS.
- A. Bhandari, C. Peng, J. Dziedzic, L. Anton, J. R. Owen, D. Kramer and C.-K. Skylaris, J. Chem. Phys., 2021, 155, 024114 CrossRef CAS.
- G. Soldano, M. Juarez, B. Teo and E. Santos, Carbon, 2014, 78, 181–189 CrossRef CAS.
- C. L. Bentley, Electrochem. Sci. Adv., 2022, 2, e2100081 CrossRef CAS.
- A. G. Güell, A. S. Cuharuc, Y.-R. Kim, G. Zhang, S.-Y. Tan, N. Ebejer and P. R. Unwin, ACS Nano, 2015, 9, 3558–3571 CrossRef.
- J. Qulez-Bermejo, M. Melle-Franco, E. San-Fabián, E. Morallón and D. Cazorla-Amorós, J. Mater. Chem. A, 2019, 7, 24239–24250 RSC.
- C. Jackson, G. T. Smith, D. W. Inwood, A. S. Leach, P. S. Whalley, M. Callisti, T. Polcar, A. E. Russell, P. Levecque and D. Kramer, Nat. Commun., 2017, 8, 15802 CrossRef CAS PubMed.
- T. Binninger, T. J. Schmidt and D. Kramer, Phys. Rev. B, 2017, 96, 165405 CrossRef.
- J. J. Liu, ChemCatChem, 2011, 3, 934–948 CrossRef CAS.
- H. Masuda, K. Matsushita, D. Ito, D. Fujita and N. Ishida, Commun. Chem., 2019, 2, 140 CrossRef.
- C. Peng, A. Bhandari, J. Dziedzic, J. R. Owen, C.-K. Skylaris and D. Kramer, J. Mater. Chem. A, 2021, 9, 16798–16804 RSC.
- A. Bhandari, C. Peng, J. Dziedzic, J. R. Owen, D. Kramer and C.-K. Skylaris, J. Mater. Chem. A, 2022, 10, 11426–11436 RSC.
- J. Holland, A. Bhandari, D. Kramer, V. Milman, F. Hanke and C.-K. Skylaris, Mater. Adv., 2022, 3, 8469–8484 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01079e |
| This journal is © the Owner Societies 2024 |






