Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Valence-to-core X-ray emission spectroscopy of transition metal tetrahalides: mechanisms governing intensities†
Christina
Roemelt
 a,
Sergey
Peredkov
a,
Frank
Neese
b,
Michael
Roemelt
a,
Sergey
Peredkov
a,
Frank
Neese
b,
Michael
Roemelt
 *c and
Serena
DeBeer
*c and
Serena
DeBeer
 *a
*a
aMax Planck Institute for Chemical Energy Conversion, Stiftstr. 34-36, 45470 Mülheim an der Ruhr, Germany. E-mail: serena.debeer@cec.mpg.de
bMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany
cHumboldt University Berlin, Brook-Taylor-Str. 2, 12489 Berlin, Germany. E-mail: michael.roemelt@hu-berlin.de
First published on 24th June 2024
Abstract
Valence-to-core (VtC) X-ray emission spectroscopy offers the opportunity to probe the valence electronic structure of a system filtered by selection rules. From this, the nature of its ligands can be inferred. While a preceding 1s ionization creates a core hole, in VtC XES this core hole is filled with electrons from mainly ligand based orbitals. In this work, we investigated the trends in the observed VtC intensities for a series of transition metal halides, which spans the first row transition metals from manganese to copper. Further, with the aid of computational studies, we corroborated these trends and identified the mechanisms and factors that dictate the observed intensity trends. Small amounts of metal p contribution to the ligand orbitals are known to give rise to intensity of a VtC transition. By employing an LCAO (linear combination of atomic orbitals) approach, we were able to assess the amount of metal p contribution to the ligand molecular orbitals, as well as the role of the transition dipole moment and correlate these factors to the experimentally observed intensities. Finally, by employing an ano (atomic natural orbital) basis set within the calculations, the nature of the metal p contribution (3p vs. 4p) was qualitatively assessed and their trends discussed within the same transition metal halide series.
Introduction
Transition metals play key structural and functional roles in biological processes,1–4 catalytic transformations,5 as well as in environmental6 and material science.7 Understanding the geometric and electronic structure changes that occur at transition metals during various processes is thus of broad general interest. To this end, a wide variety of spectroscopic methods (e.g. EPR, vibrational and optical spectroscopy) have been utilized by the broader scientific community and in recent years there has been increasing interest in the element selective manifold of spectroscopy. In this regard, X-ray absorption (XAS) and X-ray emission spectroscopy (XES) provide insight into the geometric and electronic structure of the metal center.8–16 XES, in particular, has seen increased applications in recent years due to the availability of both synchrotron and laboratory setups to perform these measurements.17 Submitting a sample to high incident energy leads to ionization of a 1s electron of a nucleus (in this context, a transition metal) and an excited state featuring a 1s core hole. This excited state can undergo several decay processes where the 1s core hole is filled with electrons from higher shells, accompanied by the emission of energy in form of X-ray photons or photoelectrons. In the case of a 1s core hole the intensity of the observed emission spectra are dominated by electric dipole allowed np to 1s transitions.11Fig. 1 shows the Kβ mainline XES of a Mn complex in which the intense feature results from a 3p → 1s transition, which is split by 3p–3d exchange in the final state. As such, Kβ mainline XES is indicative of the spin state of a system, with the Kβ1,3 and Kβ′′ peaks moving closer together with a decreasing number of unpaired spins at the metal center.9To higher energy and with much weaker intensity are the so-called valence-to-core (VtC) XES features (Fig. 1, enhanced inlet). VtC XES corresponds to transitions from mainly ligand based ns and np orbitals into the metal 1s orbital, which gain intensity from a small amount of metal np mixing, imparting dipole allowed character to these transitions.18,19 The VtC spectra are often comprised of two main features, the low intensity Kβ′′ peak, corresponding to ligand ns → metal 1s transitions, and the more intense Kβ2,5 peak, corresponding to ligand np → metal 1s transitions.9,20 The number, intensities and shifts of the VtC features are sensitive to metal ligand bond length (and hence indirectly metal spin state), as well as the identity, ionization state and protonation state of the bound ligands.19 Previous studies show that these transitions gain intensity by admixture of metal 3p and 4p orbitals to the filled ligand orbitals.9,11,19–27 Several studies have addressed the nature of p contribution (metal 3p vs. metal 4p). However, orbitals are not physical observables but mathematical constructs which were designed to describe the probabilities of where the electrons of a system are located. Therefore, any quantitative assessment is obstructed: the description of orbitals (for example their principal quantum numbers) via computational methods always depends on the level of theory that is chosen. Thus, determination of the amount of metal 3p vs. metal 4p contribution will always be a function of the theory that was applied. In a previous study by our group,19 a clear dependence between intensity and metal–ligand bond distance was observed when systematically elongating the Fe–Cl bond lengths of an otherwise identical iron complex. Elongation of the Fe–Cl bond leads to a decrease in orbital overlap and thus, to a decrease in p admixture and VtC intensity. The amount of 3p and 4p contribution was assessed with the aid of calculations employing an ano (atomic natural orbital) basis set, where it was found that both 3p and 4p orbitals contribute to the VtC MO's.
In a previous report from our research group21 on a series of Fe complexes, it was corroborated that the intensities associated with the VtC transitions are governed by the overlap between metal and ligand orbitals, as well as the symmetry of this overlap, since only transitions with orbitals of the same symmetry exhibit spectral intensity. The amount of metal p contribution was determined via Loewdin population analysis. It was postulated that the total p contribution to all occupied orbitals should sum up to a total of 1200% if only 2p and 3p orbitals (spin up and spin down) contribute. However, the obtained values for the total p contribution were found to be well above 1200% and metal p admixture to the VtC transition MO's is thus attributed to 4p orbitals. In further studies, not only the amount of p admixture but also the transition dipole moment was taken into consideration when investigating the mechanisms contributing to intensity.22 A detailed analysis of Mn and Fe VtC areas was performed, since it was found that the calculated VtC areas for Mn are always larger than those for Fe at a given bond length. The role of the transition dipole moment was assessed by decomposition into a local (metal np to metal 1s) and nonlocal (ligand orbitals to metal 1s) part. The local part of the transition dipole moment was here obtained by atomic calculations for the respective M2+ atoms but no clear assignment of 3p vs. 4p contributions was made. It was found that the reason for higher Mn VtC areas than Fe VtC areas is a subtle interplay of different values for the local transition dipole moments, different amounts of np contribution, as well as a distortion of the metal p orbitals in molecular environment as compared to the atomic calculations.
In a subsequent study23 the valence molecular orbitals were treated as a linear combination of metal 4p and ligand MO's. It was found that no simple linear relationship can be found when correlating metal 4p contribution in combination with the respective transition dipole moment (4p → 1s) to the observed oscillator strengths of the transitions. When taking into consideration metal 3p admixture, it was determined that while it is mostly the 4p orbitals contributing to the shape of the VtC MO's, it seems to be the 3p orbitals in combination with their transition dipole moments (3p → 1s) which contribute mostly to the observed intensities.
Despite several previous investigations on the intensity contributions to the VtC XES, to our knowledge, these trends have never been investigated across a systematic series that spans the first row transition metals. Within this project, our research focuses on gaining insight in the experimentally observed trends in intensities within the Mn–Cu halide series [MX4][NEt4]2, providing experimental data on the two series featuring varying metal/constant halide and constant metal/varying halide. Further, computational studies were conducted in order to corroborate the observed trends and to investigate in detail the role of metal p contribution, as well as the transition dipole moments contributing to the mechanisms which govern the VtC intensities across these series.
Experimental section
Sample preparation
All investigated compounds ([MnCl4][NEt4]2, [MnBr4][NEt4]2, [MnI4][NEt4]2, [FeCl4][NEt4]2, [FeBr4][NEt4]2, [CoCl4][NEt4]2, [CoBr4][NEt4]2, [NiCl4][NEt4]2, [NiBr4][NEt4]2, [CuCl4][NEt4]2 and [CuBr4][NEt4]2) were synthesized according to literature procedure.28 XES data were obtained on solid state samples (without any dilution) which were ground to fine powder and sealed into 1 mm aluminum samples holders using 38 μm Kapton tape.XES data collection
XES data were collected at the PINK tender X-ray beamline at BESSY II.29 The beam size of all measurements was 30 × 500 μm FWHM (V × H). The incoming photon flux was about 1013 ph s−1. The FWHM values of the excitation energies decrease from 120 eV to 110 eV to 100 eV for excitation energies of 7.3 keV to 8.0 keV to 9.5 keV, respectively. The spectra were recorded by the use of a dispersive von Hamos spectrometer (bending radius R = 250 mm) equipped with an Eiger2 R 500 K (75 μm × 75 μm pixel size, 512 × 1030 pixels) detector. The dispersive spectrometer records the entire energy range of an XES spectrum simultaneously. Hence no energy scanning is needed. The beam was scanned over the sample and the signal was averaged. For all samples scan speeds of 50 or 100 μm s−1 were utilized for which no time dependent changes in the spectra were observed. Calibration of the energy scale was done by measuring suitable reference foils for each transition metal (see Table 1). The PINK beamline in high-flux mode uses a multilayer monochromator with a large passing energy band (≈100 eV) without access to monochromatic light.| Measured element | Excitation energy, keV | FWHM (excitation energy), eV | Analyzer reflection | Estimated spectral broadening, eV | Energy calibrationa | |
|---|---|---|---|---|---|---|
| Emission line | Energy, eV/Bragg angle | |||||
| a Energy calibration for Mn, Fe and Co was performed using energies, asymmetry and FWHM values from Hölzer et al.30 Calibration for Ni and Cu was performed using the X-ray data booklet. b The Tb Lα and Ho Lα spectra were collected from Si(333) reflection of the same crystal without any rearrangements of the photon beam or the spectrometer. | ||||||
| Mn | 7.3 | 120 | Ge(440) | 1.4 | Fe Kα1 | 6404.01/75.45° |
| 70.5°–78.8° | Fe Kα2 | 6391.03/75.89° | ||||
| Fe | 8 | 110 | Si(440) | 1.4 | Co Kα1 | 6930.38/68.71° |
| 62.0°–69.6° | Co Kα2 | 6915.54/69.03° | ||||
| Fe Kβ | 7058.18/66.19° | |||||
| Co | 9.5 | 100 | Si(620) | 1.7 | Ni Kα1 | 7478.26/74.89° |
| 68.1°–76.3° | Ni Kα2 | 7461.04/75.38° | ||||
| Co Kβ | 7649.45/70.7° | |||||
| Ni | 9.5 | 100 | Si(444) | 1.7 | Ta Lα1 | 8146.1/76.13° |
| 68.8°–76.8° | Ni Kβ | 8264.66/73.12° | ||||
| Tb Lα1 Si(333)b | 6272.8/71.01° | |||||
| Tb Lα2 Si(333)b | 6238.0/71.96° | |||||
| Cu | 9.5 | 100 | Si(444) | 1.8 | Cu Kβ | 8905.42/62.63° |
| 60.7°–68° | Zn Kα1 | 8638.86/66.27° | ||||
| Zn Kα2 | 8615.78/66.62° | |||||
| Ho Lα1 Si(333)b | 6719.8/61.97° | |||||
Therefore, emission lines from reference samples are used for calibration. For the energy calibration procedure two or more emission lines visible by a detector under steady state conditions are needed. The calibration procedure is described in more detail elsewhere.29 Energies were translated into Bragg angles and a fit with tangential function was applied. The samples were continuously scanned within the X-ray beam in order to reduce and evenly distribute the absorbed dose. The samples were scanned at different rates depending on the rate of sample damage. For all samples a scan speed was utilized for which no time dependent changes in the spectra were observed. The estimated total spectral broadening is calculated via where Klevelwidth is the natural broadening of K shell spectral features.31
where Klevelwidth is the natural broadening of K shell spectral features.31
Data processing
The raw data obtained at the PINK beamline were processed using an in-house developed Python script. First, the spectra were preliminarily normalized to the same total to simplify the handling of fitting values during the fit process. Then, a baseline correction is performed where the baseline is fit with one or two broad Pearson functions. In addition, impurities, if present, are also fit with Pearson functions. Fits were performed using the Lmfit package in Python.32 During the fit, the mainline and VtC region are masked (Fig. 2, left, masked region is highlighted in grey) and only the region before the mainline and the last 10 eV of the spectrum are used as fit points. In order to achieve consistency among all investigated species, the masking area is kept constant within a given metal series. | ||
| Fig. 2 Fit of the baseline and impurities (background traces from energy calibration with Fe foil, see Table 1) for [MnCl4]2− where mainline and VtC features are masked. Right: Spectrum after baseline subtraction and renormalization. | ||
As introduced vide supra, the mainline peak corresponds to metal 3p to 1s transitions and is, for our investigated compounds, around two orders of magnitude more intense than the VtC features which gain intensity only by small amounts of metal np admixture. With the total area normalized to 1000 units, the observed VtC areas range from ∼4–8 units. Therefore, in order to compare absolute areas, it is crucial to define the peak regions in a consistent fashion, especially when comparing the areas of different metal series to each other. Therefore, the mainline onset (that is, the beginning of the mask region) is defined as that position on the energy axis where the intensity of the mainline feature of a normalized spectrum rises above an intensity of I > 0.05. Everything before that position is baselined to a value of zero while everything that is masked maintains intensity. The baseline and, if present, impurities are then subtracted from the spectrum and the spectra were renormalized to a total area of 1000, so that only the mainline and VtC features contribute to the total area (Fig. 2, right). In order to separate the mainline and VtC areas, the mainline tail is subtracted from the VtC region. To achieve this, now the VtC area is masked during fit (Fig. 3, left, marked in grey). The masking area is kept constant within a given metal series to achieve consistency. The mainline tail is then fit with several Pearson functions. In order to ensure consistency among all investigated species, the fit curve (Fig. 3, left: “Mainline Tail Fit”) must not deviate from the normalized data by a value of more than 2% of the most intense VtC peak intensity. Further, the fit curve must not cross the unmasked data (that is, overestimate the data) to give negative fit values (no zero-crossing). Since only a part of the mainline was used for fitting the tail, the need for additional, physically rather irrelevant fit functions (one broad fit with a maximum between mainline and VtC region) was needed in order to fit the data within the boundaries presented. Then, the mainline tail is subtracted from the VtC region and the resulting VtC area is fit with several Pearson functions (Fig. 3, right). For all obtained spectra, 5–8 Pearson functions are needed to sufficiently describe mainline and VtC data. The FWHMs of the main Kβ2,5 peaks increase from Mn to Cu (2.2 eV to 4.7 eV), in agreement with increasing core hole lifetime broadenings in the same direction. Fits of all mainline tails and VtC peaks can be found in the ESI.† Within the VtC region, the areas of all required fit functions are summed up to yield the total VtC area. Since the total area of mainline and VtC features is set to 1000, the numbers obtained via this procedure give the total VtC area as a fraction out of 1000.
Results and discussion
Experimental and calculated trends
Experimental and computational data were obtained for a series of transition metal halides [Net4]2[MX4] (Table 2) with M = Mn, Fe, Co, Ni, Cu and X = Cl, Br and I. In the case of the tetraiodides, only the Mn species was experimentally accessible owing to the instability of other iodides or a lack of starting material MI2.| a Calculated areas are scaled such that experimental and calculated values of the compound with the highest area (MnCl42−) tally. All calculated values are then scaled by this value (areacalc *0.751). |
|---|

|
All experimentally obtained VtC spectra (Fig. 4 showing the metal chloride series) show the most intense Kβ2,5 peak with shoulders to both sides, originating from transitions from ligand-based np orbitals into the metal 1s orbital. In addition, the Kβ′′ features can be found on the lower energy side of the spectrum, originating from transitions from ligand-based ns orbitals into the metal 1s orbital, with the Kβ′′ peaks becoming less resolved with increasing nuclear charge of the metal center and decreasing overall intensity of the VtC features. The position of both features on the energy axis depends strongly on the ns/np ionization energies of the respective ligands and move to higher energies for the respective bromides and iodides (see Fig. 1 for the exemplary [MnCl4]2−). When all experimentally observed peak maxima of the metal chlorides are aligned at 0 eV (Fig. 5), an overall decrease in intensity is observed with increasing Z. Although the Kβ′′ peaks become less resolved due to a rather low signal-to-noise ratio and are clearly distinguishable only for manganese and iron, intensity seems to be present for all compounds at roughly the same position relative to their 0 eV Kβ2,5 maximum. Thus, the nature of the transition metal center influences the intensity, but not the relative position of both peak regions. This observation is consistent with the energy of the VtC features correlating with the ligand ionization energies.19
 | ||
| Fig. 4 Experimental (black, smoothed by savgol filter) and calculated (blue, broadening 2.5 eV (Mn, Fe)/3 eV (Co, Ni)/4 eV (Cu)) spectra of the [MX4]2− series. The areas assigned to double excitation features are hatched in grey and are not considered when determining the VtC area. The calculated spectra were preliminary normalized to a total area of 1000. For optimal visualization the calculated spectra were further scaled by 0.5. We note this is in contrast to the numerical correlations in Table 2, which utilize a scaling factor of 0.751. | ||
Further, additional peaks on the high energy side of the VtC region are found, which gain in intensity with increasing nuclear charge of the metal and obscure the shape of the Kβ2,5 peaks. As seen in Fig. 4 (the region hatched in grey), these high energy features are located in a region on the energy axis where X-ray absorption pre-edge features for the respective M2+ species are typically found. Their observed intensities correlate with the higher incident energies when changing the metal Mn → Cu. Therefore, and in accordance with other studies,59–61 these high energy features may be attributed to either vertical or adiabatic double excitation features59 (KL or even KM double excitations in case of Cu) and are not considered during the determination of experimental VtC areas. During the fit process, peaks that maximize before they grey area are taken into account when determining the VtC area while peaks which exhibit a maximum within the grey area are neglected.
When changing the halide for a given transition metal, a decrease in the overall intensity (area) accompanied by a shift of the VtC features to higher energies is observed in the chloride → bromide → iodide direction (see Fig. 1 for the exemplary Mn series). These observations can be rationalized with an elongation of bond lengths (influencing the intensities, vide infra) and higher ns/np ionization energies (influencing the energies) in the same direction.
When the experimental and calculated spectra are compared (Fig. 4 representing the chlorides), the relative position of the Kβ′′ peaks, where experimentally identifiable, is reasonably well described. The shoulders to the right side of the Kβ2,5 peaks are visibly reproduced by calculations only for the manganese chloride. For all other [MCl4]2−, the calculated transitions associated with this shoulder merge together with the most intense transitions and cannot be visualized with the applied broadenings. The shoulders on the left side of the Kβ2,5 peaks were not visibly reproduced by the calculations which is consistent with previous studies on Fe chlorides and likely arise from charge transfer processes that are not captured in the one-electron DFT approach utilized here.19 Although this approach does not capture multi excitation or charge transfer processes, it was used here because of its previously established ability to reliably compute VtC features (as referenced in the introduction), its computational feasibility as well as the opportunity to directly assess the relationship between metal p contribution, transition dipole moment and intensity of a transition. When all calculated spectra are aligned at 0 eV (Fig. 6), a decrease in intensity is observed with increasing Z. Further, the relative position of both peak regions stays constant. Both of these findings agree with the experimentally observed trends (Fig. 5). Lastly, when changing the halide (chloride to bromide to iodide), the calculated decrease in intensity and shift to higher energies also correlates to the experimentally observed findings. Thus, experimentally obtained and calculated values for all VtC areas show excellent correlation (Fig. 7). The observed slight deviations from linearity can mostly be attributed to manual fluctuations in the fit procedure and the rather low signal-to-noise ratio for VtC transitions as compared to other transitions.
 | ||
| Fig. 6 Calculated spectra (broadening as stated in Fig. 4) with all Kβ2,5 peak maxima aligned at 0 eV. | ||
For all obtained VtC areas, the previously discussed observations can be summarized as two separate trends: (1) constant metal, varying halide: bond lengths increase and VtC areas decrease (Table 2, marked with dashed arrows); (2) constant halide, varying metal: bond lengths decrease and VtC areas decrease (Table 2, marked with solid arrow). These two trends are discussed in further detail in the following paragraphs. As introduced vide supra it has been established that VtC transitions (ligand ns/np to metal 1s) gain intensity by admixture of metal np character into the ligand-based orbitals from which the transitions originate. Therefore, the amount of p contribution to the VtC transitions was quantitatively assessed for all examined complexes by means of computational studies.
Assessment of metal p contribution to the VtC transitions with the aid of DFT
Within this study, we chose an LCAO (linear combination of atomic orbitals) approach to determine the metal p contributions to the VtC transitions. Prior to any qualitative and quantitative analysis, it is instructive to reiterate that all observed transitions are modeled as transitions between single-determinantal initial and final states as described originally by Lee et al.19 This means that every transition is associated with a single pair of valence donor and Mn 1s acceptor orbital. Although any state couplings are neglected within this model, it has been successfully applied in many instances.22,23,59,62–65The amount of p contribution to any molecular orbital can be determined by Loewdin population analysis, as has been done previously as described vide supra. However, while Loewdin population analysis provides molecular orbital compositions in terms of atomic orbitals with different angular momenta, e.g. s-, p- or d-type orbitals it does not differ between principal quantum numbers, e.g. between 3p and 4p contributions. Following an approach presented by Pollock et al.21 (vide supra), the total metal p contribution to all occupied orbitals can be determined by summing up their metal p contributions as obtained from the Loewdin population. Completely filled metal 2p and 3p orbitals result in a total of 1200% p character (consistent with a total of 12 p-electrons in the 2p and 3p shells). Our values for the total p orbital character of the exemplary [MnX4]2− series exceed 1200% by almost the exact value which was determined to be the Loewdin p contribution within the VtC transitions (Table 3), thus suggesting that the 4p orbitals contribute to the observed intensity of VtC transitions.
| Substrate | Mn p contribution to VtC transitions (%) | Total Mn p character (%) |
|---|---|---|
| [MnCl4]2− | 74.9 | 1273.2 |
| [MnBr4]2− | 72.3 | 1271.2 |
| [MnI4]2− | 69.7 | 1269.3 |
In order to more quantitatively assess the transition metal p contribution to the valence donor orbitals in all VtC transitions, we have applied the LCAO approach, in which it is assumed that any molecular orbital is composed of atomic orbitals, i.e.
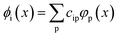 | (1) |
 | (2) |
 | (3) |
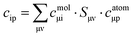 | (4) |
| C = Cmol,TSCatom | (5) |
 are overlap integrals between the GTO basis functions that are gathered in the overlap matrix S. The matrices in eqn (5) have been extracted from the ORCA output files with the aid of the orca_2json program. With matrix C at hand, the contribution of a given atomic orbital φp to molecular orbital ϕi is quantified by taking the square of the corresponding matrix element cip.
are overlap integrals between the GTO basis functions that are gathered in the overlap matrix S. The matrices in eqn (5) have been extracted from the ORCA output files with the aid of the orca_2json program. With matrix C at hand, the contribution of a given atomic orbital φp to molecular orbital ϕi is quantified by taking the square of the corresponding matrix element cip.
Following this LCAO approach, the molecular orbitals of an exemplary [MnCl4]2− molecule that are most relevant in terms of VtC intensity comprise only traces of Mn 3p character (10−3%) but considerable contributions from Mn 4p orbitals (3–20%, exact values for all orbitals can be found in the ESI†). By construction, this approach renders 4p contribution as main component because of a clear separation into 3p (occupied) and 4p (unoccupied) orbitals within the atomic calculations. In the following projection of the atomic orbitals onto the molecular orbitals (see eqn (5)), this partitioning is maintained, leaving only 4p contribution to significantly modulate the intensity of the VtC peaks.
Correlation of p contribution and the observed trends
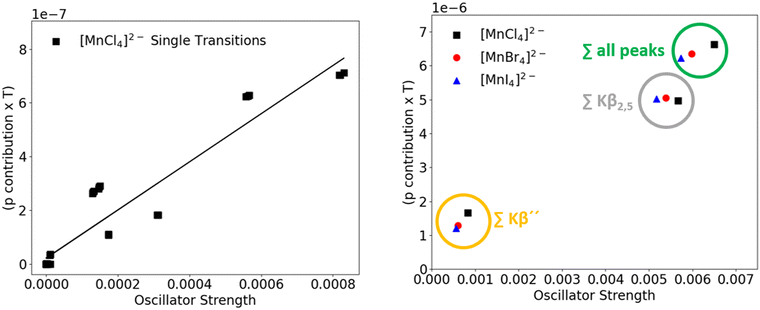
With the amount of metal p contribution determined for all transitions of all compounds, the correlation between p contribution and the intensity of a transition was further investigated.However, when plotting the oscillator strength of the single VtC transitions vs. the p contribution determined via the LCAO approach, there does not seem to be a clear linear dependence between the intensity of the transition and the amount of metal p contribution. In Fig. 9, we examine the correlation between the oscillator strength and p contributions for both single transitions (left) and for different spectral regions (right). The left panel visualizes the non-linear behavior through a plot of the predicted VtC oscillator strengths of [MnCl4]2−vs. the corresponding metal p contributions. Particularly the transitions in the Kβ′′ region (six clustered transitions marked with a star) feature a significant amount of Mn p contribution while exhibiting comparably low intensities. A very similar distribution pattern was also observed for the single transitions when the amount of p admixture was determined by Loewdin population analysis (for comparison, see ESI†).
Notwithstanding the lack of linear correlation, a few noteworthy observations can be made when the transitions of the Kβ′′ and Kβ2,5 regions of the [MnX4]2− series are considered separately and compared to the sum of all transitions (Fig. 9, right panel). In the Kβ′′ region (marked in yellow), oscillator strength as well as p contribution decrease in the series chloride → bromide → iodide. In contrast, the total Mn p contribution to donor orbitals associated with transitions in the Kβ2,5 region (marked in grey) increases with decreasing intensity. These opposing trends can be rationalized by looking at the shape of the participating orbitals. In agreement with experimental evidence,45–47 the calculated Mn–X bond length increases from chloride to bromide to iodide by an average of 1.48 Å and 2.0 Å, respectively. However, the character of the donor orbitals corresponding to the transitions in the two aforementioned spectral regions differ (halide ns for the Kβ′′ peaks, halide np for the Kβ2,5 peaks). The overlap between ligand ns vs. ligand np orbitals with Mn 3p and 4p orbitals was quantified according to eqn (1)–(5). The overlap of both ligand ns and np orbitals with the manganese 3p orbitals (Table 4, first column) was found to decrease upon bond elongation.
| Mn 3p–L s/p | Mn 4p–L s/p | |||
|---|---|---|---|---|
| MnCl4 | Cl-3s | 0.05 | Cl-3s | 11.5 |
| Cl-3p | 0.36 | Cl-3p | 17.0 | |
| MnBr4 | Br-4s | 0.04 | Br-4s | 10.0 |
| Br-4p | 0.34 | Br-4p | 18.1 | |
| MnI4 | I-5s | 0.03 | I-5s | 9.3 |
| I-5p | 0.28 | I-5p | 18.8 | |
As described above though, the Mn 3p orbitals were found to contribute only marginally to the total Mn p admixture. The overlap between the Mn 4p and ligand ns orbitals (Table 4, second column) was also found to decrease, as expected from Fig. 9. Interestingly, the Mn 4p/ligand np overlap was now found to increase with increasing bond length, again as assumed from Fig. 9. Thus, due to the nodal plane inherent to the p orbitals, the overlap of the more diffuse Mn 4p orbitals with the ligand np orbitals seems to maximize at a longer bond length rather than the shortest.
Finally, the total p contribution obtained by our LCAO analysis to all VtC transitions (Fig. 9, right, marked in green) increases from [MnCl4]2− to [MnI4]2−, opposing the expected trend and the trend obtained via Loewdin population analysis. Before elaborating on these observations in more detail, the correlation of p contribution and oscillator strength for the series with other metal centers is assessed.
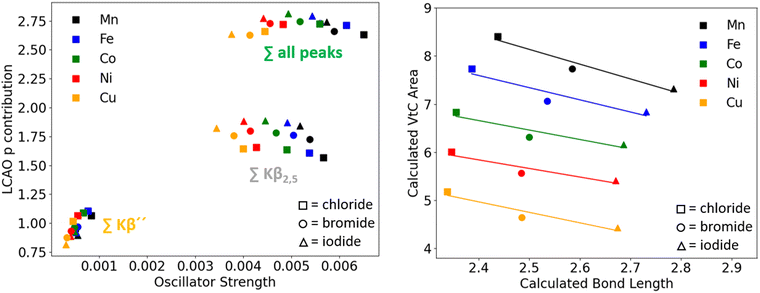 | ||
| Fig. 10 Left: LCAO p contribution vs. oscillator strength for all investigated compounds. Right: Correlation of calculated bond lengths and calculated VtC areas for all compounds. | ||
| Orbital | I total | I 2p (%2p) | I 3p (%3p) | I 4p (%4p) | I other (%other) |
|---|---|---|---|---|---|
| a Every orbital carries a spin function, i.e. either α or β spin. | |||||
| 6αa | 6.94 × 10−4 | 6.94 × 10−4 (100.0) | 8.13 × 10−9 (0.0) | 3.1 × 10−10 (0.0) | −3.1 × 10−9 (−0.0) |
| 7α | 6.94 × 10−4 | 6.94 × 10−4 (100.0) | 8.1 × 10−9 (0.0) | 3.0 × 10−10 (0.0) | −3.1 × 10−9 (−0.0) |
| 8α | 6.94 × 10−4 | 6.94 × 10−4 (100.0) | 8.1 × 10−9 (0.0) | 2.9 × 10−10 (0.0) | −3.0 × 10−0 (−0.0) |
| 26α | 6.06 × 10−5 | −8.1 × 10−9 (−0.0) | 6.08 × 10−5 (100.2) | −1.15 × 10−7 (−0.2) | 9.68 × 10−9 (0.0) |
| 27α | 6.07 × 10−5 | −8.1 × 10−9 (−0.0) | 6.08 × 10−5 (100.2) | −1.15 × 10−7 (−0.2) | 1.04 × 10−8 (0.0) |
| 28α | 6.06 × 10−5 | −8.1 × 10−9 (−0.0) | 6.08 × 10−5 (100.2) | −1.15 × 10−7 (−0.2) | 1.16 × 10−8 (0.0) |
| 31β | 9.46 × 10−8 | 1.5 × 10−11 (0.0) | 1.45 × 10−8 (15.3) | 2.73 × 10−7 (288.0) | −1.92 × 10−7 (−203.3) |
| 34β | 5.22 × 10−7 | 1.68 × 10−10 (0.0) | 3.5 × 10−8 (6.7) | 6.77 × 10−7 (129.7) | −1.9 × 10−7 (−36.5) |
Assessment of the role of the transition dipole moment
Due to the observed non-linear behavior of p contribution and intensity and following previously performed studies, the influence of the transition dipole moment was evaluated in more detail (for definition, see ESI†). However, we do not focus solely on the metal p orbitals and their respective transition dipole moments, but take into consideration all atomic orbitals that comprise a molecular orbital. According to Fermi's golden rule the intensity of a given electronic transition from orbital ϕi to the Mn 1s orbital is proportional to the square of the corresponding transition dipole moment, i.e. | (6) |
 | (7) |
 | (8) |
 | (9) |
 | (10) |
The calculated intensities show a perfectly linear correlation within the applied numerical accuracy to the oscillator strengths obtained within the XES output files.
Through eqn (10) the intensity of every transition can be deconvoluted into atomic orbital contributions. We have divided Ii according to
 | (11) |
However, these large contributions are partially canceled due to negative interference with “other” orbitals, as indicated by large negative contributions to the intensity from Iother. This finding can be interpreted in terms of antiparallel orientation of transition dipole moments for these transitions (vide infra). What also becomes apparent is that the intensity originating from Mn 3p/4p orbital contributions for MO 34β is calculated to be about 2.5 times higher than the corresponding intensity for MO 31β, but at the same time the values for negative interference are similar. This observation rationalizes the differences in total intensity as well as the non-linearity previously observed for pure p contribution vs. intensity plots. With these findings, the correlation between metal np contribution combined with the respective transition dipole moment (p*T) and the calculated oscillator strength is revisited. Fig. 12 (left panel) shows the correlation of (p*T) vs. oscillator strength for the [MnCl4]2− single transitions. Now, a clear linear correlation can be found, where the oscillator strength increases with increasing (p*T) values. Deviation from total linearity is here accounted for by the negligence of interference with “other” orbitals, as obtained according to Table 5. When the interplay of all orbital contributions (np plus “other”) is plotted, a perfectly linear correlation is obtained.
 | ||
| Fig. 12 Correlation of (p*T) and oscillator strength for the [MnCl4]2− single transitions (left) as well as for the total intensities of the manganese halide series (right). | ||
Further, when assessing the trend within the manganese halide series (Fig. 12, right panel), a decrease in total oscillator strength (sum over all peaks) is accompanied by a decrease in the total (p*T) values, thus highlighting the importance of taking the transition dipole moment into consideration here.
Finally, when changing the metal center (Mn → Fe → Co → Ni → Cu), the orbitals close to the core of the transition metal center experience an increase in orbital contraction due to an increase in nuclear charge. Thus, it is expected that the respective 1s orbitals (the XES acceptor orbitals) are more contracted and therefore exhibit smaller intrinsic transition dipole moments (M np → M 1s) in the same direction. Fig. 13 shows the correlation between the total (p*T) and the total oscillator strengths for all transitions for the metal chloride series, where the (p*T) value decreases in an almost perfectly linear fashion with decreasing oscillator strength.
The origin of negative interference
To assess the nature and origin of the “other” orbitals contributing to the intensity of the VtC transitions in terms of negative (or sometimes even positive) interference, the composition of molecular orbital 31β was analyzed in detail in terms of atomic orbitals according to eqn (1). Moreover, the contribution of every atomic orbital to I31β is computed through eqn (12): | (12) |
The nature of this interaction is captured by the shape of the corresponding molecular orbital 31β, whose shape is also constituted by the antibonding combination of ligand s and metal p orbitals. Thus, negative values for Iother as shown in Table 5 can be interpreted in terms of antibonding interactions of the ligand and metal orbitals and might even be used as a means to measure the degree of antibonding character between np and all “other” AO's within any molecular orbital. For a small number of transitions, positive interference between metal np and “other” contributions is observed. This, consequently, is accompanied by bonding interactions between the participating atomic orbitals.
To conclude, bonding interaction between orbitals leads to positive interference between metal p and “other” orbitals and thus positive contribution to the intensity. Accordingly, antibonding interaction leads to negative interference between metal p and “other” orbitals and therefore to a negative contribution to intensity. When metal p contribution and all “other” contributions are quantitatively combined as a sum of their single components, the (T*c) values for the combined 4p (red) and combined “other” contributions (blue) are shown in Fig. 15, again depicting the antiparallel orientation of both transition dipole moment vectors. Further, combination of the transition dipole moment vectors of both contributions as calculated by this approach adds up to exactly the value of the transition dipole moment of molecular orbital 31β (Fig. 15, magenta) as obtained within the DFT XES calculation output.
It thus becomes apparent that the total intensity of a calculated transition is an interplay of contributions from several atomic orbitals to a molecular orbital and the direction of their respective transition dipole moments.
Revisiting the p contribution: 3p or 4p?
Although the LCAO approach for metal p contribution provided us with an explanation on the non-linear behavior between intensity and metal p contribution of a transition, as well as a means to assess the nature and extent of atomic orbital interactions within a molecular orbital, it is not designed for assessing the ratio of metal 3p and metal 4p contribution (vide supra). Therefore, for the exemplary [MnCl4]2− molecule, the metal p contribution was determined by employing an ano (Atomic Natural Orbital) basis set (ANO-RCC-TZP66) according to previously published results,19 where 3p and 4p orbitals can be identified in the basis set and therefore also within the molecular orbitals.The total manganese p contribution (Fig. 16, blue) was found to be dominated by 3p contribution (Fig. 16, black) when, within a molecular orbital, ligand and metal orbitals interact via sigma bonding interactions (peak region B). The more diffuse 4p orbitals (Fig. 16, red) were found to dominate the amount of p contribution in molecular orbitals where metal and ligands interact via pi bonding (peak region A). Further, when changing the halide (chloride → bromide → iodide), metal 4p contributions gain in importance even for those MO's which exhibit sigma interaction between metal and ligand orbitals, which can be rationalized by the more diffuse p orbital character of the heavier halides and thus better interactions with metal 4p orbitals. When the nature of the transition metal center is varied, 4p contributions again increase with increasing effective nuclear charge of the metal center, irrespective of the type of interaction. This is due to the fact that the energetics of the interacting orbitals changes drastically. For the metal chloride series, the energies of ligand s and p orbitals, as well as metal 4 p orbitals was found to maintain rather constant, while the energies of the 3p orbitals decrease linearly with increasing Z, thus promoting 4p contribution.
It has to be noted however that, due to the fact that orbitals are not physical observables, a quantitative analysis of the nature of p contribution is always a function of the employed level of theory and can vary with different sets of unitary transformed molecular orbitals. However, employment of the ano basis set renders a good qualitative picture to assess the nature and trends of the dominating interactions within our transition metal halide series.
Conclusions
Herein a systematic VtC XES study of the first-row transition metal tetrahalides has been performed. The VtC features were investigated with respect to the experimentally observed intensities and changes thereof. The experimentally observed trends with (a) varying halide and (b) varying metal center were corroborated with the aid of computations. Further, employing an LCAO (linear combination of atomic orbitals) approach, the mechanisms which govern these intensities were identified. It was found that there are two main factors whose interplay determines the intensity of each transition within a VtC region. Metal p admixture to the ligand ns and np orbitals, from which these transitions originate, gives intensity to these transitions, and the amount of metal p contribution gives a rough estimate of the intensity of a transition. However, the total intensity of a transition was found to be an interplay of the metal p admixture and the directions of the transition dipole moment vectors of all atomic orbitals that comprise a molecular orbital from which a given transition originates. While for constant metal and varying halide, the amount of metal p contribution roughly dictates the trend of calculated intensities, the effect of the transition dipole moment gains in importance and dictates the general trends in intensities when investigating transition metal complexes with varying metal center. Due to the increasing effective nuclear charge when going from manganese to copper, the metal 1s orbital experiences a greater increase in orbital contraction than the valence orbitals, thus leading to a decrease in the intrinsic transition dipole moment and therefore to reduced intensities. In contrast to previous studies on this topic, we have not considered metal np orbital contributions and ligand orbital contributions with their transition dipole moments separately, but instead investigated the interplay of all atomic orbitals within a molecular orbital by also considering the cross terms. With the introduction of negative interference (or, in other words, a means to determine the extent of antibonding interaction) between np and other orbitals, we were able to assess and explain the non-linearity previously observed for the correlation of p contribution and intensity of a given transition. Lastly, by employing an atomic natural orbital basis set, we were able to qualitatively address the question of metal 3p versus metal 4p contribution and their trends within our transition metal tetrahalide series. It was found that the amount 3p and 4p contributions in [MnCl4]2− depends on the type of bonding interactions between ligand and metal center. In case of sigma bonding interactions, 3p contributions dominate, while 4p contributions are the dominating factor for pi interactions. When changing the halide, 4p contributions gain in importance due to more diffuse halide np orbitals. With varying metal center, 4p contributions again gain in importance due to a linear decrease of the energies of the metal 3p orbitals with increasing nuclear charge.Data availability
All XES raw data, input and xyz files for reproduction of calculations as well as the data necessary for reproduction of the figures within this manuscript can be found online: https://doi.org/10.17617/3.JECRGR.Conflicts of interest
There are no conflicts to declare.Acknowledgements
CR, SP, FN and SD thank the Max Planck Society for funding. CR thanks the HZBP PINK beamline for the opportunity to measure the samples.Open Access funding provided by the Max Planck Society.
Notes and references
- C. Van Stappen, L. Decamps, G. E. Cutsail, III, R. Bjornsson, J. T. Henthorn, J. A. Birrell and S. DeBeer, Chem. Rev., 2020, 120, 5005–5081 CrossRef CAS PubMed.
- C.-H. Wang and S. DeBeer, Chem. Soc. Rev., 2021, 50, 8743–8761 RSC.
- P. Gandeepan, T. Müller, D. Zell, G. Cera, S. Warratz and L. Ackermann, Chem. Rev., 2019, 119, 2192–2452 CrossRef CAS PubMed.
- B. M. Hoffman, D. R. Dean and L. C. Seefeldt, Acc. Chem. Res., 2009, 42, 609–619 CrossRef CAS PubMed.
- M. Inoue, H. Tsurugi and K. Mashima, Coord. Chem. Rev., 2022, 473, 214810 CrossRef CAS.
- J. J. Soldevila-Barreda and N. Metzler-Nolte, Chem. Rev., 2019, 119, 829–869 CrossRef CAS PubMed.
- M. M. Montemore, M. A. van Spronsen, R. J. Madix and C. M. Friend, Chem. Rev., 2018, 118, 2816–2862 CrossRef CAS PubMed.
- M. Bauer, Phys. Chem. Chem. Phys., 2014, 16, 13827–13837 RSC.
- C. J. Pollock and S. DeBeer, Acc. Chem. Res., 2015, 48, 2967–2975 CrossRef CAS PubMed.
- G. E. Cutsail III and S. DeBeer, ACS Catal., 2022, 12, 5864–5886 CrossRef CAS.
- P. Glatzel and U. Bergmann, Coord. Chem. Rev., 2005, 249, 65–95 CrossRef CAS.
- L. Cao, X. Liu, X. Shen, D. Wu and T. Yao, Acc. Chem. Res., 2022, 55, 2594–2603 CrossRef CAS PubMed.
- E. Lundgren, C. Zhang, L. R. Merte, M. Shipilin, S. Blomberg, U. Hejral, J. Zhou, J. Zetterberg and J. Gustafson, Acc. Chem. Res., 2017, 50, 2326–2333 CrossRef CAS PubMed.
- M. L. Baker, M. W. Mara, J. J. Yan, K. O. Hodgson, B. Hedman and E. I. Solomon, Coord. Chem. Rev., 2017, 345, 182–208 CrossRef CAS PubMed.
- C. J. Milne, T. J. Penfold and M. Chergui, Coord. Chem. Rev., 2014, 277–278, 44–68 CrossRef CAS.
- C. Garino, E. Borfecchia, R. Gobetto, J. A. van Bokhoven and C. Lamberti, Coord. Chem. Rev., 2014, 277–278, 130–186 CrossRef CAS.
- P. Zimmermann, S. Peredkov, P. M. Abdala, S. DeBeer, M. Tromp, C. Müller and J. A. van Bokhoven, Coord. Chem. Rev., 2020, 423, 213466 CrossRef CAS.
- G. Smolentsev, A. V. Soldatov, J. Messinger, K. Merz, T. Weyhermüller, U. Bergmann, Y. Pushkar, J. Yano, V. K. Yachandra and P. Glatzel, J. Am. Chem. Soc., 2009, 131, 13161–13167 CrossRef CAS PubMed.
- N. Lee, T. Petrenko, U. Bergmann, F. Neese and S. DeBeer, J. Am. Chem. Soc., 2010, 132, 9715–9727 CrossRef CAS PubMed.
- E. Gallo and P. Glatzel, Adv. Mater., 2014, 26, 7730–7746 CrossRef CAS PubMed.
- C. J. Pollock and S. DeBeer, J. Am. Chem. Soc., 2011, 133, 5594–5601 CrossRef CAS PubMed.
- M. A. Beckwith, M. Roemelt, M. N. Collomb, C. DuBoc, T. C. Weng, U. Bergmann, P. Glatzel, F. Neese and S. DeBeer, Inorg. Chem., 2011, 50, 8397–8409 CrossRef CAS PubMed.
- M. U. Delgado-Jaime, S. DeBeer and M. Bauer, Chemistry, 2013, 19, 15888–15897 CrossRef CAS PubMed.
- P. Chandrasekaran, K. P. Chiang, D. Nordlund, U. Bergmann, P. L. Holland and S. DeBeer, Inorg. Chem., 2013, 52, 6286–6298 CrossRef CAS PubMed.
- S. N. MacMillan, R. C. Walroth, D. M. Perry, T. J. Morsing and K. M. Lancaster, Inorg. Chem., 2015, 54, 205–214 CrossRef CAS PubMed.
- M. Torres Deluigi, F. M. F. de Groot, G. López-Díaz, G. Tirao, G. Stutz and J. Riveros de la Vega, J. Phys. Chem. C, 2014, 118, 22202–22210 CrossRef CAS.
- K. P. Schwalenstocker, J. Paudel, A. Kohn, C. Dong, K. van Heuvelen, E. Farquhar and F. Li, Dalton Trans., 2016, 45, 14191–14202 RSC.
- N. Gill and F. B. Taylor, Inorg. Synth., 1967, IX, 136–142 CrossRef.
- S. Peredkov, N. Pereira, D. Grötzsch, S. Hendel, D. Wallacher and S. DeBeer, J. Synchrotron Radiat., 2024, 31, 622–634 CrossRef CAS PubMed.
- G. Hölzer, M. Fritsch, M. Deutsch, J. Härtwig and E. Förster, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 56, 4554–4568 CrossRef.
- M. O. Krause and J. H. Oliver, J. Phys. Chem. Ref. Data, 1979, 8, 329–338 CrossRef CAS.
- M. Newville, T. Stensitzki, D. B. Allen, M. Rawlik, A. Ingargiola and A. Nelson, Lmfit: Non-Linear Least-Square Minimization and Curve-Fitting for Python, 2016 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- J. D. Rolfes, F. Neese and D. A. Pantazis, J. Comput. Chem., 2020, 41, 1842–1849 CrossRef CAS PubMed.
- Y. J. Franzke, R. Treß, T. M. Pazdera and F. Weigend, Phys. Chem. Chem. Phys., 2019, 21, 16658–16664 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612 CrossRef CAS PubMed.
- I. Dhouib, A. Ouasri and Z. Elaoud, J. Saudi Chem. Soc., 2020, 24, 567–583 CrossRef CAS.
- F. A. Cotton, L. M. Daniels and P. Huang, Inorg. Chem., 2001, 40, 3576–3578 CrossRef CAS PubMed.
- M. Daub, I. Ketterer and H. Hillebrecht, Zeitschrift für anorganische und allgemeine Chemie, 2018, 644, 280–287 CrossRef CAS.
- S. I. P. I. G. Gusakovskaya, N. S. Ovanesyan, N. I. Golovina, R. F. Trofimova, G. V. Shilov and E. A. Lavrent'eva, Zhurnal Obshchei Khimii, 1998 Search PubMed.
- U. Flörke, E. Akin and G. Henkel, CCDC 1033638: Experimental Crystal Structure Determination, 2014 DOI:10.5517/cc13pl5k.
- U. Flörke and A. Ahmida, CCDC 1571757: Experimental Crystal Structure Determination, 2017 DOI:10.5517/ccdc.csd.cc1prjvt.
- E. Styczeń, Z. Warnke, D. Wyrzykowski, J. Kłak, J. Mroziński and A. Sikorski, Struct. Chem., 2010, 21, 269–276 CrossRef.
- A. L. Rheingold, L. Doerrer and S. Neville, CCDC 1503773: Experimental Crystal Structure Determination, 2016 DOI:10.5517/ccdc.csd.cc1mgstp.
- G. D. Stucky, J. B. Folkers and T. J. Kistenmacher, Acta Crystallogr., 1967, 23, 1064–1070 CrossRef CAS.
- P. G. Jones and H. Thonnessen, CCDC 611801: Experimental Crystal Structure Determination, 2006 DOI:10.5517/ccnjmj9.
- J. A. Golen, A. L. Rheingold, G. Wang and L. Doerrer, CCDC 781132: Experimental Crystal Structure Determination, 2014 DOI:10.5517/ccv6ttn.
- T. Kawata, T. Aoyama and S. Ohba, Acta Crystallogr., Sect. C: Struct. Chem., 1993, 49, 137–139 CrossRef.
- G. L. Starova, M. Y. Skripkin and I. M. Gusev, Russ. J. Gen. Chem., 2010, 80, 1236–1241 CrossRef CAS.
- R.-Y. Wang, X. Zhang, J.-H. Yu and J.-Q. Xu, J. Solid State Chem., 2019, 269, 239–245 CrossRef CAS.
- O. McCubbin Stepanic, J. Ward, J. E. Penner-Hahn, A. Deb, U. Bergmann and S. DeBeer, Inorg. Chem., 2020, 59, 13551–13560 CrossRef PubMed.
- H. Lim, M. L. Baker, R. E. Cowley, S. Kim, M. Bhadra, M. A. Siegler, T. Kroll, D. Sokaras, T.-C. Weng, D. R. Biswas, D. M. Dooley, K. D. Karlin, B. Hedman, K. O. Hodgson and E. I. Solomon, Inorg. Chem., 2020, 59, 16567–16581 CrossRef CAS PubMed.
- R. A. Valenza, E. P. Jahrman, J. J. Kas and G. T. Seidler, Phys. Rev. A, 2017, 96, 032504 CrossRef.
- M. U. Delgado-Jaime, B. R. Dible, K. P. Chiang, W. W. Brennessel, U. Bergmann, P. L. Holland and S. DeBeer, Inorg. Chem., 2011, 50, 10709–10717 CrossRef CAS PubMed.
- J. K. Kowalska, A. W. Hahn, A. Albers, C. E. Schiewer, R. Bjornsson, F. A. Lima, F. Meyer and S. DeBeer, Inorg. Chem., 2016, 55, 4485–4497 CrossRef CAS PubMed.
- K. M. Lancaster, K. D. Finkelstein and S. DeBeer, Inorg. Chem., 2011, 50, 6767–6774 CrossRef CAS PubMed.
- K. M. Lancaster, M. Roemelt, P. Ettenhuber, Y. Hu, M. W. Ribbe, F. Neese, U. Bergmann and S. DeBeer, Science, 2011, 334, 974–977 CrossRef CAS PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6575–6579 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Mainline and VtC fits of experimental spectra, comparison between Loewdin and LCAO p contribution, comparison of LCAO 3p and 4p contribution. See DOI: https://doi.org/10.1039/d4cp00967c |
| This journal is © the Owner Societies 2024 |