Open Access Article
Open Access ArticleUnexpected concentration dependence of the mass accommodation coefficient of water on aqueous triethylene glycol droplets†
Michael J.
Gleichweit
 ,
Mercede
Azizbaig Mohajer
,
Mercede
Azizbaig Mohajer
 ,
Dominique P.
Borgeaud dit Avocat
,
Dominique P.
Borgeaud dit Avocat
 ,
Matúš E.
Divéky
,
Matúš E.
Divéky
 ,
Grégory
David
,
Grégory
David
 and
Ruth
Signorell
and
Ruth
Signorell
 *
*
Department of Chemistry and Applied Biosciences, ETH Zurich, CH-8093 Zurich, Switzerland. E-mail: ruth.signorell@phys.chem.ethz.ch
First published on 20th May 2024
Abstract
The mass accommodation coefficient αM of water on aqueous triethylene glycol droplets was determined for water mole fractions in the range xmol = 0.1–0.93 and temperatures between 21 and 26 °C from modulated Mie scattering measurement on single optically-trapped droplets in combination with a kinetic multilayer model. αM reaches minimum values around 0.005 at a critical water concentration of xmol = 0.38, and increases with decreasing water content to a value of ≈0.1 for almost pure triethylene glycol droplets, essentially independent of the temperature. Above xmol = 0.38, αM first increases with increasing water content and then stabilises at a value of ≈0.1 at the lowest temperatures, while at the highest temperature its value remains around 0.005. We analysed the unexpected concentration and temperature dependence with a previously proposed two-step model for mass accommodation which provides concentration and temperature-dependent activation enthalpies and entropies. We suggest that the unexpected minimum in αM at intermediate water concentrations might arise from a more or less saturated hydrogen-bond network that forms at the droplet surface.
1 Introduction
Introduced as a concept already by Maxwell in 1859,1 the mass accommodation coefficient (αM) still plays a key role in the quantitative description of mass transport from the gas to the condensed phase (liquid, solid).2–5 It represents the fraction of gas phase molecules that remain in the condensed phase after colliding with the surface (0 ≤ αM ≤ 1). | (1) |
Even though many different experimental approaches have been invented to measure αM, the determination of accurate experimental accommodation coefficients has been challenging.2,4–7 The reasons are diverse, mainly concerning various experimental but also conceptual aspects.5,7–10 Theoretical approaches to retrieve αM, such as molecular dynamics simulations, provide an alternative option to the experiment.11–18 But they have their own challenges, and direct comparison with experimental data remains demanding.
This is partly because in theoretical studies the mass accommodation process has often been divided into a surface accommodation step and a subsequent transfer to bulk. However, distinguishing the two steps is rarely possible in experiments.7 The first step is described by an accommodation coefficient αS defined as “the number of gas phase molecules accommodated at the surface divided by the total number of molecules colliding with the surface”.5 The bulk accommodation coefficient αB is “the number of molecules incorporated into the particle bulk divided by the total number of molecules colliding with the surface”.5 In our experiment, we cannot distinguish between surface accommodated molecules and bulk accommodated molecules. Therefore, we use the symbol αM for the accommodation coefficient determined in our experiments (see Section 3). Assuming that most molecules that accommodate at the surface either desorb or are subsequently accommodated into the bulk, αM would approach αB as defined above.5,19 Another coefficient that is closely related to αM is the uptake coefficient γ. It describes the ratio of the number of molecules removed from the gas phase divided by the total number of molecules colliding with the surface.5,19 In the absence of chemical reactions, if diffusion is fast and if the system stays close to equilibrium,3,5,7,20–22γ is equal to αM.5,23 Our experiment closely appraoches these conditions.
As a consequence, consensus does not even exist on the value of the accommodation coefficient for water vapour on liquid water, i.e. for one of the most important systems.4,24–28 Over the last two decades there has been increasing evidence that the value for water on water might be larger than 0.6, possibly close to unity.9,26,27,29 Because of the omnipresence of water, water-containing multi-component systems are of particular interest.2,3,7,22,30–35 The knowledge of αM for these systems is relevant for cloud activation by atmospheric aerosols and cloud formation, and questions concerning the delivery of aerosolised pharmaceutics to the lungs and their effectiveness. The accommodation coefficient of multi-component systems does not only vary with the composition of the condensed phase but also with temperature. For surface-active and water-immiscible compounds, a non-trivial dependence of αM on temperature and composition is expected, similar to what has been reported for the temperature dependence in ref. 33, 34 and 36.
Here, we report experimental values of αM for aqueous triethylene glycol (TREG) droplets over a wide concentration range from essentially pure TREG droplets (<2% water by volume) to water-rich droplets (<60% water by volume) at temperatures between 21 °C and 26 °C. Note that although these droplets are rich in water, they are not comparable to almost pure water droplets. TREG is a colourless, odourless, viscous liquid that is commonly used for humidity control of room air, air and surface disinfection, dehydration during natural gas production, as working fluid in fog machines and for moisture control of tobacco products.37–41 For the determination of αM, we combined our newly developed Photothermal Single-Particle Spectroscopy (PSPS)7,30,42–46 with our recently developed multilayer heat and mass flux model for photoacoustic spectroscopy on single aerosol particles (MHM-PA).47
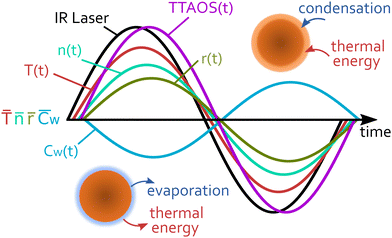
PSPS consists of an optical trap (not shown in Fig. 1) that immobilises a single droplet in a gas environment of controlled gas composition, relative humidity, pressure and temperature. Once trapped, the droplet and gas phase are in equilibrium. A small but fast, periodic perturbation is then applied to the droplet by excitation with a sinusoidally intensity-modulated infrared (IR) laser that is absorbed by the droplet. The light energy deposited in the droplet results in periodic heat (thermal energy) and mass exchange (condensation and evaporation) between droplet and surrounding gas phase (Fig. 1). Heat flux is exchange of thermal energy between the particle surface and ambient gas phase molecules through ballistic collisions. Mass flux describes the transport of molecules across the interface, with an energy transfer characterised by the associated latent heat. This is accompanied by periodic changes of the droplet temperature (T(t)) and the droplet radius (r(t)) caused by water evaporation and condensation, and by thermal expansion and contraction. For aqueous TREG droplets, only water contributes to the mass exchange because of the very low vapour pressure of TREG (<1 Pa). The change in temperature and composition (evaporation and condensation, here given by the water concentration Cw(t)) also results in a periodic change of the refractive index (n(t)).
In our previous studies using PSPS, we have shown that αM can be retrieved simultaneously from the measurement of three independent signals, which are the photoacoustic amplitude (PAA), the photoacoustic phase (PAP) and modulated Mie scattering (MMS).43,45 The PAA and PAP are recorded with a microphone or other acoustic transducers,42 while MMS relies on optical detection, where the periodic change in the droplet size and refractive index is measured by collecting the light (usually from the trapping laser) elastically scattered by the droplet. In the present study, we only employed MMS because it had the best signal quality and, compared with PA, it is a calibration free method (see Section 2.2). Important advantages of PSPS are its high sensitivity and the fact that the measurements are performed under near equilibrium conditions (small perturbation). In addition, the single droplet approach circumvents issues with unwanted ensemble averaging, and it guarantees optimal control of droplet properties (size, composition, temperature) and environmental conditions.
TREG and water are miscible. In contrast to multi-component systems containing surface-active or water-immiscible compounds,33,34 one would rather expect to observe a monotonic concentration and temperature behaviour for αM. However, as we show in this study this is not the case for the concentration dependence, which actually exhibits an unexpected minimum in αM at intermediate water concentrations. The temperature dependence of droplets with intermediate to high water content, by contrast, follows the systematic trend that was expected based on our previous study of water accommodation on aqueous tetraethylene glycol (TEG) droplets;43,45i.e. a systematic decrease of αM with increasing temperature. We analyse the observed trends in αM with the two-step model proposed in previous studies by Nathanson et al. and Davidovits et al.20,48 which provides values for the activation Gibbs free energy ΔGobs, and the activation enthalpy ΔHobs and entropy ΔSobs.
2 Experimental
2.1 Single droplet optical trap
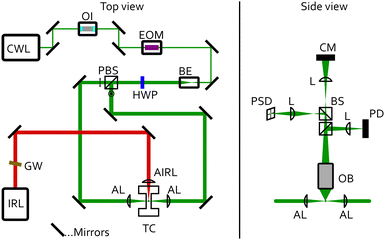
A sketch of the experimental setup is shown in Fig. 2. Single aqueous triethylene glycol (C6H14O4) droplets were immobilised in a humidified nitrogen atmosphere by counter-propagating optical tweezers (CPT). The CPT optical trap was built from a continuous wave laser (trapping laser) with a wavelength of 532 nm (CWL, Laser Quantum Opus 532, 220 mW), which was protected against unwanted backreflections by an optical isolator (OI, Thorlabs IO-5-532-HP). The trapping laser passed through an electro-optic modulator (EOM, Conoptics 350-50-01) that enabled dynamic rotation of its polarisation state, before being expanded to a diameter of 7.4 mm using a beam expander (BE, Edmund Optics #37-053). The single beam passed through a half-wave plate (HWP) before being split into two beams of orthogonal polarisation by a polarisation beamsplitter cube (PBS). The HWP after the EOM was used to fine-tune the neutral point of the power-splitting to create a stable counter-propagating trap. Each of the two beams was directed onto an aspherical lens (AL, 75 mm, Thorlabs ASL10142), which focused them in the centre of a custom-built photoacoustic trapping cell (TC). The benefit of this CPT setup is a tight droplet confinement perpendicular to the directions of the trapping beams combined with long working distances. To also maintain a high confinement of the droplets along the trapping laser directions, we implemented a feedback system in which the particle's position is continuously monitored by projecting light elastically scattered by the droplet onto a position sensitive photodiode (PSD, lateral effect sensor, Thorlabs PDP90A; Fig. 2 right). The PSD sensor was connected to a proportional-integral-derivative controller (PID, Thorlabs KPA101), which regulated the voltage applied to the EOM and thus the polarisation state of the trapping beam before passing the PBS. This closed-loop control circuit rapidly adjusted the power ratio of the two counter-propagating beams at a time scale of up to 20 kHz (limited by the PID controller). It thereby applies static and dynamic corrections to the particle's position and ensures stable trapping during the measurement.The TC is described in more detail in ref. 42. It is made of stainless steel and holds a relative humidity and temperature sensor (Sensirion SHT35). It can also be used for photoacoustic measurements at a resonance frequency of 3540 Hz.49 Aqueous TREG droplets generated by a medical nebuliser were trapped by the CPT. The relative humidity (RH), and with this the composition of the particle,50,51 was set by a humidified nitrogen gas flow of 30 sccm. The RH was controlled by a PID controller implemented in LabVIEW, which regulates the mixing ratio of a dry and a humidified nitrogen gas flow prior to the cell inlet.
2.2 Modulated Mie scattering
The particle radius r and αM were retrieved from the trapping laser light that was elastically scattered by the droplet using Mie theory.52 The light scattering patterns depend on r and on the refractive index (droplet composition). The elastically scattered light was collected over an angular range of 49.0° around a scattering angle of 90° (Fig. 3) using a microscope objective (Mitutoyo, M Plan Apo 20×, slightly de-collimated operation). The collected scattered light was divided up by non-polarising beam splitter cubes (BS) (Fig. 2, right), and directed onto a photodiode (PD, Hamamatsu S2506-02) for the determination of r and αM, onto the CMOS camera (CM) for observation of the particle in the trap,53 and onto the PSD for feedback stabilisation (see above).Fig. 3 illustrates the angle-dependent scattering intensity of a droplet for cross-polarised, counter-propagating optical tweezers, viewed in the same plane as in Fig. 2 (right). The red lines indicate the collection angle of the microscope objective. The blue and purple trace illustrate the scattering intensity profiles of the p- and s-polarised trapping beams, respectively. The PD records the integrals over the collected angular range, visualised by the corresponding blue- and purple-shaded areas.
To determine αM, a small fast periodic (3540 Hz) perturbation was induced in the droplet by exposing the droplet to an intensity modulated infrared (IR) laser (IRL, AdTech Optics, λ = 9456 nm, TEC controlled), which was focused onto the trapping position using a ZnSe lens (AIRL, 75.0 mm, Thorlabs, LA7660-G)(Fig. 2).30 An angled Germanium Longpass filter (GW, Edmund Optics, #36-151) protects the IR laser against unwanted reflections. The IR light was absorbed by TREG and resulted in periodic changes of the droplet temperature and concentration (and therefore the refractive index), and the droplet radius. These changes are the result of periodic heat (expansion/contraction) and mass flux (evaporation/condensation of water) away and towards the droplet (Fig. 1). The very small changes in refractive index (Δnr < 0.06) and radius (Δr < 2 nm) manifested themselves as periodic changes in the scattering patterns (Fig. 3), and hence characteristic changes of the recorded PD signal. Demodulating the PD signal at the modulation frequency of the IR laser yields a complex signal MMS = X + iY, referred to as modulated Mie scattering (MMS). We refer to the absolute value of this signal as the experimental MMS amplitude  (Fig. 4(a) and (b), blue trace). The phase shift of the MMS signal in our experiments is measured with respect to the IR laser, and is referred to as the experimental MMS phase MMSexpϕ = atan2(Y,X) (Fig. 4(b), red trace).30
(Fig. 4(a) and (b), blue trace). The phase shift of the MMS signal in our experiments is measured with respect to the IR laser, and is referred to as the experimental MMS phase MMSexpϕ = atan2(Y,X) (Fig. 4(b), red trace).30
Aqueous TREG droplets evaporate very slowly on a time scale (minutes to hours) much slower than the modulation period (∼250 μs) of the IR laser; i.e. the decrease of the droplet size caused by slow evaporation is negligible for the MMS measurements. The slow shrinking of the droplets over time enabled the determination of the average absolute droplet radius ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) and normalisation of the MMS signals (eqn (2)). The droplet shrinking is contained in the DC signal of the PD, which is referred to as Total Two-dimensional Angular Optical Scattering, TTAOSexp.53Fig. 5 (brown trace) shows the theoretical TTAOS signal as a function of the average droplet radius
and normalisation of the MMS signals (eqn (2)). The droplet shrinking is contained in the DC signal of the PD, which is referred to as Total Two-dimensional Angular Optical Scattering, TTAOSexp.53Fig. 5 (brown trace) shows the theoretical TTAOS signal as a function of the average droplet radius ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) and the average real part of the refractive index
and the average real part of the refractive index ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) r (droplet composition).
r (droplet composition). ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) was determined from the analysis of Mie resonances (maxima), resulting in an uncertainty in
was determined from the analysis of Mie resonances (maxima), resulting in an uncertainty in ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) of less than ±2 nm for sizes in the sub-micrometre to micrometre range.53 The size of the droplets was also exploited to adjust the average droplet temperatures
of less than ±2 nm for sizes in the sub-micrometre to micrometre range.53 The size of the droplets was also exploited to adjust the average droplet temperatures ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) between 21 °C and 26 °C. Larger droplets have a higher IR absorption cross section and a reduced surface-to-volume ratio compared with smaller droplets. As a result, larger droplets equilibrate at a higher
between 21 °C and 26 °C. Larger droplets have a higher IR absorption cross section and a reduced surface-to-volume ratio compared with smaller droplets. As a result, larger droplets equilibrate at a higher ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) during modulated IR excitation.
during modulated IR excitation.
The signal from the PD was recorded and evaluated by a lock-in amplifier (Zürich Instruments MFLI, 500 kHz), which also controlled the IR laser modulation. This lock-in amplifier provided the amplitude and phase response at the IR modulation frequency (MMS signals) as well as the TTAOSexp signal. To compare the MMSexpA with the simulated amplitude MMSsim,normA (eqn (9), section Modelling), the former was normalised by the total experimental scattering intensity TTAOSexp.
 | (2) |
Eqn (2) represents a dimensionless MMS amplitude that can be directly compared with simulations because it is independent of the power from the trapping laser beam of which the elastically scattered light is collected.
In principle, the modulation frequency of the IR laser can be chosen arbitrarily. However, there are certain physical limitations to consider. To be able to observe processes such as evaporation and condensation through damping of the amplitude and the phase delay, the period of the driving laser 1/ω and the relaxation time τ of the system should be of roughly the same order of magnitude:
| ω·τ ≈ 1 | (3) |
Depending on the choice of RH and r, our experiments operated in the range ω·τ = 0.3–4 (15 μs < τ < 180 μs).
3 Modelling
For the simulation of the MMS signals, we combined Mie theory for light scattering with Fourier's law of thermal conduction and Fick's first law of diffusion to describe heat and mass flux, respectively. External fluxes according to eqn (4) and (5) (heat and water mass exchange of the liquid surface of the particles with the surrounding gas phase) and internal diffusion of heat and water according to eqn (7) were calculated as a function of time t during photothermal cycles using our recently reported multi-layer heat and mass transfer model MHM-PA.47 MHM-PA is a numerical approach to solve Fick's first law of diffusion, and hence allows us to simulate heat and mass flux away from and towards the droplet and the temporal evolution of the water concentration and temperature inside the droplet at conditions close to equilibrium. In contrast to the multi-layer model reported by Shiraiwa et al.,21,54 we do neither assume a sorption layer nor a quasi-static surface layer to model the cyclic heat and water exchange with the ambient gas phase. Instead, we use eqn (4) and (5) based on the work by Kulmala et al., Murphy and Winkler et al.55–57 This is conceptually similar to the resistor model often used. In our model, the surface is not at strict equilibrium with the ambient gas phase. In fact, we assume that during a cycle, there is a slight difference (ΔT in eqn (4) and (5)) between the temperature of the surrounding gas phase and the temperature at the droplet surface (![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) + ΔT).7,49
+ ΔT).7,49
The heat flux ΔQ away from or towards the droplet during a photothermal cycle can be expressed as:
ΔQ = 4πrβTK(![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) )ΔT )ΔT | (4) |
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) the average particle temperature and ΔT is the maximum change of the temperature at the droplet's surface from
the average particle temperature and ΔT is the maximum change of the temperature at the droplet's surface from ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) during a photothermal cycle. The mass flux ΔI of water molecules away from or toward the droplet surface is given by Fick's law combined with the Clausius–Clapeyron equation, assuming an ideal gas:
during a photothermal cycle. The mass flux ΔI of water molecules away from or toward the droplet surface is given by Fick's law combined with the Clausius–Clapeyron equation, assuming an ideal gas: | (5) |
 | (6) |
The MHM-PA model does not explicitly treat surface and bulk mass accommodation separately. This is consistent with the fact that the experimental data do not provide any information on the individual processes, but only on the entire process. Consistent with the experimental information we have, we thus incorporate the mass transfer process into the model via the transition regime correction factor βM (eqn (6)).7,47,55–57 This approach works well for the measurements presented here because TREG particles even when they are dry remain moderately viscous (<0.049 Pa s50). Hence the viscosity is not limiting the mass accommodation of water in our droplets, unlike what has been observed with highly viscous particles.22,61 For highly viscous or reactive particles, a sorption layer or quasi-static surface layer would need to be implemented in the model.
During a photothermal cycle, small gradients in the temperature and water concentration establish inside the droplet. The temporal evolution of these gradients can be described by Fick's first law of diffusion:
 | (7) |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) is the heat or mass flux vector, D is the corresponding heat or mass diffusion coefficient,
is the heat or mass flux vector, D is the corresponding heat or mass diffusion coefficient,  is the gradient operator, and C is the temperature or the water concentration.
is the gradient operator, and C is the temperature or the water concentration.
The MHM-PA model divides the droplet into a discrete number of radial layers. Each layer has a particular time-dependent temperature, water concentration (refractive index) and volume. The flux F of either heat or mass from one layer i to the adjacent layers i ± 1 can be expressed as
| Fi,i±1(t) = k(T,xmol)δCw,i,i±1(t), | (8) |
An MHM-PA simulation provides the temporal evolution of r, T, n and Cw during a cycle, which is schematically illustrated in Fig. 1. From these quantities, the time-dependent scattering intensity TTAOS(t) (Fig. 1, purple trace) was calculated for all experimental ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) and RH. Fig. 1 also schematically shows that r, T, n and Cw have individual phase delays. Thus, the resulting TTAOS signal is no longer strictly sinusoidal as it contains small higher frequency components. In the experiment, the lock-in amplifier filters out all unwanted frequency components. To account for this, the simulated signals were also digitally filtered, which provides TTAOS(t) at the modulation frequency. The MMS amplitude MMSsim,normA was then calculated according to eqn (9). This procedure can be considered equivalent to the amplitude-demodulation during the experiment.
and RH. Fig. 1 also schematically shows that r, T, n and Cw have individual phase delays. Thus, the resulting TTAOS signal is no longer strictly sinusoidal as it contains small higher frequency components. In the experiment, the lock-in amplifier filters out all unwanted frequency components. To account for this, the simulated signals were also digitally filtered, which provides TTAOS(t) at the modulation frequency. The MMS amplitude MMSsim,normA was then calculated according to eqn (9). This procedure can be considered equivalent to the amplitude-demodulation during the experiment.
 | (9) |
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) is the average particle radius,
is the average particle radius,  the average scattering intensity over a full excitation cycle, and max(TTAOS(t)) and min(TTAOS(t)) are the maximal and minimal scattering intensity within one cycle, respectively. Because the lock-in amplifier provides root-mean-square data for a sinusoidal signal and the simulations determine peak-peak amplitudes, an additional factor of
the average scattering intensity over a full excitation cycle, and max(TTAOS(t)) and min(TTAOS(t)) are the maximal and minimal scattering intensity within one cycle, respectively. Because the lock-in amplifier provides root-mean-square data for a sinusoidal signal and the simulations determine peak-peak amplitudes, an additional factor of  is necessary to compare the MMS simulations with the experimental MMS signal. Eqn (9) normalises the calculated MMS amplitude by the average scattering intensity (
is necessary to compare the MMS simulations with the experimental MMS signal. Eqn (9) normalises the calculated MMS amplitude by the average scattering intensity (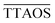 ). After normalisation, this calculated signal is directly comparable with the normalised experimental MMS signal amplitude (eqn (2)), without any calibration.
). After normalisation, this calculated signal is directly comparable with the normalised experimental MMS signal amplitude (eqn (2)), without any calibration.
The MMS phase, MMSϕ, was calculated from the time difference between the IR laser maximum tIR,max, and the first maximum in TTAOS(t), tMMS,max, according to eqn (10):
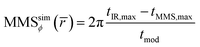 | (10) |
Fig. 5 shows a typical TTAOS simulation (brown trace) as a function of the average droplet radius ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) and the average real part of the refractive index
and the average real part of the refractive index ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) r. The cyan trace visualises how a typical MMS signal amplitude looks like when a droplet shrinks over time from
r. The cyan trace visualises how a typical MMS signal amplitude looks like when a droplet shrinks over time from ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 1.7 to 1.5 μm. Double-peak features appear in the MMS signals in the vicinity of the maxima of Mie resonances (maxima brown trace). A more comprehensive description of the MMS signal generation is given in ref. 62.
= 1.7 to 1.5 μm. Double-peak features appear in the MMS signals in the vicinity of the maxima of Mie resonances (maxima brown trace). A more comprehensive description of the MMS signal generation is given in ref. 62.
Fig. 4(a) shows an experimentally recorded MMS amplitude trace that is compared to four simulated MMS amplitudes for different values of αM between 0.01–1. At smaller droplet radii, MMSexpA overlaps best with the orange trace. Towards higher radii, MMSexpA agrees better with the purple trace, indicating a reduction of αM with increasing radius. This is due to the fact that in our experiments larger droplets reach equilibrium at higher average particle temperatures.
The double-peak features are the essential features for the determination of the mass accommodation coefficient. αM (fit parameter) is determined from a fit of the calculated MMS trace (eqn (9); light blue trace in Fig. 4(b)) of one double-peak to the experimental trace (eqn (2), dark blue trace in Fig. 4(b)) by minimising the normalised sum of squared residuals SSR (for more information, see ESI†):
 | (11) |
Fig. 4(b) compares a typical experimental MMS trace (dark blue) with a calculated trace (light blue). The two traces show excellent agreement. For completeness, the red and the magenta trace show the experimental (MMSexpϕ) and calculated MMS phase (MMSsimϕ, Eqn 10), respectively. Note that the phase was not used to determine αM. Considering that no calibration was performed on the phase measurements, the agreement between the simulated and experimental phase is very good.
4 Results and discussion
The MMS signal responses for 176 individual droplets were recorded for droplet sizes in the range between![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 0.7 and 2 μm at different temperatures between
= 0.7 and 2 μm at different temperatures between ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 21 °C and 26 °C and different RHs between 8 and 96% RH (1.5% relative error). The RH determines the droplet composition.50,51 The examined RH range corresponds to water mole fractions xmol between 0.1 and 0.93, covering a broad range of different droplet compositions from almost pure TREG droplets (<2% water by volume) to water-rich droplets (<60% water by volume), and we exclude data obtained above xmol = 0.78 (≳35% water by volume) because of measurement artefacts (see below). We note that the presented results cannot be used to obtain αM for water on water. In total, more than 3100 MMS double-peak features (Fig. 5) were fitted to retrieve αM over this xmol and
= 21 °C and 26 °C and different RHs between 8 and 96% RH (1.5% relative error). The RH determines the droplet composition.50,51 The examined RH range corresponds to water mole fractions xmol between 0.1 and 0.93, covering a broad range of different droplet compositions from almost pure TREG droplets (<2% water by volume) to water-rich droplets (<60% water by volume), and we exclude data obtained above xmol = 0.78 (≳35% water by volume) because of measurement artefacts (see below). We note that the presented results cannot be used to obtain αM for water on water. In total, more than 3100 MMS double-peak features (Fig. 5) were fitted to retrieve αM over this xmol and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) range.
range.
In the following, we indicate the average (averaged over a modulation cycle) water mole fraction xmol, the average water volume fraction xvol and the average droplet temperature T of the top layer of the droplet (thickness ≈50 nm), obtained from the MHM-PA simulations. Even though all these values deviate only by a few percent from the values averaged over the whole droplet, they represent conditions close to the surface best.
4.1 Observed trends
Fig. 6(a) and (b) show αM of aqueous TREG droplets as a function of![[T with combining overline]](https://www.rsc.org/images/entities/char_0054_0305.gif) (colour code) and xmol (left) and xvol (right), respectively. The volume fraction was calculated using the densities of bulk TREG and water.50,63 Two general trends are visible:
(colour code) and xmol (left) and xvol (right), respectively. The volume fraction was calculated using the densities of bulk TREG and water.50,63 Two general trends are visible:
(i) αM has a comparatively high value around 0.1 for almost pure TREG droplets (xmol ≈ 0.1, xvol ≈ 0.015). With increasing water content, αM then quickly decreases, reaching minimum values around 0.005 at xmol ≈ 0.38 (xvol ≈ 0.075). A further increase of the water content in the droplet reverses the behaviour and results in a temperature-dependent increase of αM, again reaching a value of ≈0.1 for water rich droplets with xmol ≈ 0.6 (xvol ≈ 0.17) at the lowest temperatures. Above xmol ≈ 0.78 (xvol ≈ 0.33), αM appears to slightly decrease again. We believe, however, that this apparent decrease is a measurement artefact. These data points were retrieved from measurements at very high RH (>90%). At such high relative humidities, condensation of water on the cell windows can easily build up. This can cause distortions of the IR laser beam resulting in a reduction of the overall light intensity, and hence a reduced MMS response and thus αM values that are slightly too low.
(ii) A temperature-dependence that is correlated with the water content in the droplet. For mole fractions between 0.38 and 0.6 and the lowest temperatures, the αM values show a distinct increase with increasing water content. The extent of this increase decreases as the temperature rises, and disappears for the highest temperatures. The data also show that αM does not strongly depend on the water concentration above xmol ≈ 0.6. At mole fractions below xmol ≈ 0.38 (xvol ≈ 0.075), where αM is minimal, αM is essentially temperature independent – the data points recorded at different temperatures more or less overlap here, except for outliers.
4.2 Unexpected concentration dependence
How can these two trends be explained? The pronounced minimum in αM at intermediate water concentrations (xmol ≈ 0.38) is unexpected and seems rather unusual (case (i) in Section 4.1). At first sight, one would expect to observe a more or less monotonous trend of αM with increasing water content because water and TREG are fully miscible. The most likely behaviour would be an increase in αM with changing water content, simply because water is expected to interact more strongly with water than with TREG. However, for the aqueous TREG droplets this trend is only found above xmol ≈ 0.38 (xvol ≈ 0.075), but not below that value. We observed the same trend also for water accommodation on aqueous tetraethylene glycol (TEG) droplets above xmol ≈ 0.5.7,43 This more or less expected trend can be explained by a continuous increase of the number of H2O molecules at the droplet's surface and thus likely an increase of free OH groups of H2O surface molecules that facilitate water accommodation at the surface. That αM reaches a minimum at xmol ≈ 0.38, would indicate that at this composition only a few free OH groups are available to accommodate incoming H2O gas phase molecules because the TREG and H2O molecules at the surface form a common more or less saturated hydrogen-bond network. When xmol is reduced below ≈0.38, αM again increases pronouncedly. The increasing lack of water molecules in this concentration range renders the formation of a saturated TREG–H2O hydrogen-bond network less and less likely. This in turn could result in an increased number of free OH groups from TREG at the droplet's surface, which again would facilitate water accommodation from the gas phase and thus result in an increased αM value. At the lowest water mole fraction, αM can be interpreted as water mass accommodation on an almost pure TREG surface.The observed minimum of αM at xmol ≈ 0.38 seems consistent with a special behaviour previously observed for other quantities. Begum et al. found a pronounced maximum in excess viscosity at xmol ≈ 0.3–0.4: they argue that this might be caused by a strengthening of the hydrogen bond network in the water–TREG solution at this composition.64 Klimaszewski et al. measured the speed of sound in aqueous TREG solutions and found a distinct kink in their data at xmol ≈ 0.3–0.4. They proposed that this could be caused by progressive replacement of water–water bonds with newly formed water–TREG bonds when going from water rich solutions to xmol ≈ 0.3–0.4.65 Their data also suggest that the temperature dependence for the excess sound velocity almost vanishes below xmol ≈ 0.3 (see the following subsection). Both the viscosity and speed of sound are related to the mutual diffusion coefficient of aqueous TREG, which can influence the net water mass accommodation.27,33
Shinyashiki et al. and Sudo et al. performed broadband dielectric measurements on aq. TREG and other ethylene glycol oligomers.66–68 They drew conclusions about the molecular interactions and the cooperative motion of water and solute molecules. They proposed that the water molecules in mixtures with high water content have the ability to move cooperatively, which is primarily facilitated by the formation of hydrogen bonds and small clusters with surrounding water molecules. Shinyashiki et al. argued that ethylene glycol and diethylene glycol are small enough to efficiently form clusters with water molecules, but TREG molecules are already too large to facilitate cooperative motions, and actually act as a constraint in the water binding network.66,68 This might explain why the values of αM at higher water content (xmol ≈ 0.4–0.8, xvol ≈ 0.08–0.33) are lower than the value of αM of water on pure water, which is assumed to be >0.6.9,26,27,29 For aqueous TREG mixtures with lower water content, by contrast, they argue that the water molecules lack the ability to move cooperatively because the large TREG molecules impose a global geometric constraint on the movement of the water molecules. In this case, the (cooperative) motion of TREG molecules becomes important for transport inside the liquid.67 These dynamics and associated structural changes might support our explanation regarding the formation of a minimum in αM provided above.
Note that the studies mentioned above consider bulk mixtures, and can only serve as indications of how the surface and near-surface structure may be organised. The molecular interpretations suggested in this article and in the referenced publications are hypothetical scenarios that could explain the unusual concentration dependence of αM. Molecular dynamics simulations (MD) of water accommodation at surfaces might provide more insight into the molecular origin. What is crucial, however, is that these simulations apply to the specific system under consideration. To the best of our knowledge, there are no such studies on the accommodation of water on TREG, nor are there any other simulations representative (e.g. (poly-)ethylene glycol water surfaces) of the system studied here. MD simulations for water accommodation are available for surfactants or molecules with low solubility in water,13,14,61,69–72 which however, differ greatly from our water TREG system.
4.3 Temperature dependence
The temperature trend (see (ii) in Section 4.1) and its correlation with the water content are again visualised in Fig. 7 in a slightly different way than in Fig. 6. Fig. 7 shows αM as a function of temperature and xvol (dichotomous colour code). For water contents below the critical value where αM reaches a minimum (xvol < 0.075; light brown to black colours), αM is temperature independent within uncertainties. For larger water contents (light to dark green), by contrast, an inverse temperature dependence is visible for the higher volume fractions (darker green) at all temperatures and for the lower volume fractions (lighter green) at the lower temperatures (see also Fig. 8 and Table 1). | ||
| Fig. 8 Arrhenius type plot of αM according to eqn (16) for six defined classes of volume fraction. To guide the eye, the colours of the data points in the respective panels are chosen according to the colour scale in Fig. 7. Panel (a) shows the class below and panels (b) to (e) show the classes above the critical water concentration of xvol = 0.075 (xmol = 0.38). The black lines show the linear fits according to eqn (16). Panel (f) shows the class of excluded data points (measurement artefacts). | ||
| Class | T-range | x vol | x mol | ΔHobs | ΔSobs | ΔGobs (21 °C) | ΔGobs (26 °C) |
|---|---|---|---|---|---|---|---|
| °C | kJ mol−1 | J mol−1 K−1 | kJ mol−1 | kJ mol−1 | |||
| (a) | 21–26 | 0.015–0.075 | 0.1–0.38 | 0 | −38 ± 5 | 11.2 | 11.4 |
| (b) | 21–22.5 | 0.075–0.13 | 0.38–0.50 | −834 ± 230 | −2858 ± 782 | 6.8 | — |
| 22.5–26 | 0.075–0.13 | 0.38–0.50 | 0 | −44 ± 5 | — | 13.2 | |
| (c) | 21–24 | 0.13–0.18 | 0.50–0.62 | −706 ± 70 | −2417 ± 235 | 5.3 | — |
| 24–26 | 0.13–0.18 | 0.50–0.62 | 0 | −42 ± 1 | — | 12.7 | |
| (d) | 21–26 | 0.18–0.24 | 0.62–0.70 | −661 ± 21 | −2260 ± 72 | 3.7 | 14.9 |
| (e) | 21–26 | 0.24–0.33 | 0.70–0.78 | −674 ± 27 | −2302 ± 90 | 3.2 | 14.7 |
| (f) | 21–26 | 0.33–0.64 | 0.78–93 | −420 ± 40 | −1447 ± 136 | 5.8 | 13.0 |
To analyse the temperature dependence, Davidovits et al.48 proposed to describe mass accommodation as a two-step process, resulting in a Gibbs energy of the transition state between the gas phase and the solvated molecule ΔGobs = ΔHobs − TΔSobs (ESI,† Section 2 and Fig. S4). The first step is the adsorption of a gas phase molecule at the surface (kads) and the second step is either the solvation of this molecule (ksol) or the desorption of the molecule back into the gas phase (kdes).
 | (12) |
The subscripts g indicate gas phase water molecules, s surface adsorbed molecules and l liquid phase molecules. Assuming that the collision rate of gas phase water molecules with the surface is equal to the adsorption rate, the mass accommodation coefficient is
 | (13) |
Note that this assumption is in agreement with ref. 48 and 73, and also consistent with molecular dynamics simulations.14,74 Assuming quasi-stationarity for surface adsorbed molecules
 | (14) |
 | (15) |
This provides the following linear inverse temperature dependence of the logarithm of 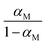 :
:
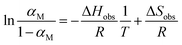 | (16) |
ΔHobs and ΔSobs were retrieved from the experimental data in Fig. 7 using eqn (16). To account for the correlation between temperature dependence and water content, we first divided the data in six classes with similar water content, with one class below the critical xvol < 0.075 where αM is minimal (Fig. 8(a)) and five classes above this threshold (Fig. 8(b)–(f)). Table 1 lists for all classes the enthalpy of activation ΔHobs, the entropy of activation ΔSobs, and the activation Gibbs energies ΔGobs for the two limiting temperatures of the experiment.
The data in Fig. 8(a) does not show indications for a systematic temperature dependence, suggesting that the formation of the transition state on TREG-rich surfaces is enthalpically neutral (ΔHobs ≈ 0, Table 1 (a)) within the uncertainty. The energy gain by forming new interactions with the incoming gas phase water molecule is more or less balanced by the loss of energy that is required to disturb the surface. For ΔHobs ≈ 0, ΔSobs is negative, indicating that the formation of the transition state is entropically hindered. The reduction in entropy can be rationalised by the fact that the number of degrees of freedom reduces as a molecule transitions from the gas phase to a more restricted surface bound molecule. The value of ΔSobs indicated in Table 1 (a) corresponds to the value averaged over the entire concentration range below the critical concentration xvol < 0.075, assuming that ΔHobs = 0. This averaging neglects any concentration dependence. To identify potential concentration trends, we grouped the data into three subclasses as indicated by the colour scheme in panel (a). We calculated ΔSobs at different concentrations for ΔHobs = 0, and we found that ΔSobs becomes more negative with increasing water content (by less than factor of two). This increase in the entropic barrier might explain the observed decrease in αM for increasing water content in the region xvol < 0.075 (Fig. 6), suggesting that a higher content of surface water increasingly hinders the formation of the transition state in this concentration range. However, because of the measurement uncertainties and because ΔSobs and ΔHobs are correlated, the interpretation that the observed decrease in αM is purely entropic is only tentative.
The next two concentration classes in Fig. 8(b) and (c) show a strong temperature dependence of ΔHobs which is given by the negative of the slope of 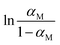 with respect to the inverse temperature (Gibbs–Helmholtz equation). Within the accuracy of our measurements, we can distinguish two regions: above a certain temperature (22.5 °C and 24 °C in Fig. 8(b) and (c), respectively) ΔHobs ≈ 0. Below this temperature, ΔHobs is finite and we approximate it as temperature independent (approximately linear behaviour in Fig. 8(b) and (c)). The corresponding values of ΔHobs and ΔSobs resulting from eqn (16) are given in Table 1. The formation of the transition state is entropically hindered (negative activation entropy) for both concentration classes, and either enthalpically neutral (no activation enthalpy) or enthalpically favoured (negative activation enthalpy) depending on the temperature. Interestingly, in the concentration range represented by Fig. 8(b) and (c), the temperature region where ΔHobs = 0 correlates with an αM that is approximately concentration independent (Fig. 6), while the temperature region where ΔHobs is finite correlates with the range where αM increases linearly with increasing water content.
with respect to the inverse temperature (Gibbs–Helmholtz equation). Within the accuracy of our measurements, we can distinguish two regions: above a certain temperature (22.5 °C and 24 °C in Fig. 8(b) and (c), respectively) ΔHobs ≈ 0. Below this temperature, ΔHobs is finite and we approximate it as temperature independent (approximately linear behaviour in Fig. 8(b) and (c)). The corresponding values of ΔHobs and ΔSobs resulting from eqn (16) are given in Table 1. The formation of the transition state is entropically hindered (negative activation entropy) for both concentration classes, and either enthalpically neutral (no activation enthalpy) or enthalpically favoured (negative activation enthalpy) depending on the temperature. Interestingly, in the concentration range represented by Fig. 8(b) and (c), the temperature region where ΔHobs = 0 correlates with an αM that is approximately concentration independent (Fig. 6), while the temperature region where ΔHobs is finite correlates with the range where αM increases linearly with increasing water content.
In the concentration range xvol = 0.18–0.33, αM strongly depends on the temperature but is essentially independent of the water content (Fig. 6). This concentration range corresponds to the two concentration classes shown in Fig. 8(d) and (e). As for the lower temperatures in classes (b) and (c), an inverse temperature dependence is observed, which again can be well approximated by a temperature-independent, finite ΔHobs. The data in Table 1 (d) to (e) show that in this concentration range the formation of the transition state is enthalpically favoured and entropically hindered. The fact that the water accommodation is enthalpically favoured is not surprising for systems that are considered to be miscible, such as TREG–water solutions. As mentioned further above, the apparent slight decrease of αM for the highest water concentration (xvol = 0.33–0.64, Fig. 6) is likely not real but caused by a measurement artefact. Thus, we also anticipate this measurement artefact to be the reason for the apparent change of the values of ΔHobs and ΔSobs (Fig. 8(f) and Table 1 (f)) compared with those in the classes (d) and (e).
The (non-zero) ΔHobs values, the ΔSobs values and ΔGobs values in the classes (b) to (e) are essentially indistinguishable within uncertainties (Table 1 (b)–(e)). This hints that there is no pronounced concentration-dependence of ΔHobs and ΔSobs above the critical concentration xvol > 0.075 for the lower temperatures where ΔHobs is non-zero. Potentially, there might be a slight trend towards less negative ΔHobs and ΔSobs values with increasing water content (Table 1 (b)–(e)), but again this is difficult to say given the quality of the data. The stability in the thermodynamic quantities with respect to the concentration might be related to the almost constant surface tension of aqueous TREG at water concentrations below xvol < 0.33 (xmol ≈ 0.8), which changes by less than 8%.50
5 Conclusion
It has previously been reported that αM of water on aqueous systems containing surface-active or immiscible compounds show a complex dependence of αM on the composition and temperature. The present work reveals that pronounced non-trivial dependencies on composition and temperature can also occur for water miscible compounds (here TREG). This behaviour was rather unexpected. This result might be relevant for questions concerning aerosolised pharmaceutics as well as cloud activation by atmospheric aerosols, e.g. hinting at a generally very sensitive and complex temperature and concentration dependence of the cloud activation potential of aerosols.We investigated the behaviour of αM on aqueous TREG droplets from almost pure TREG droplets to almost pure water droplets over a comparatively small temperature range from 21 °C to 26 °C. Single optically-trapped droplets were excited by an intensity-modulated infrared laser resulting in minor oscillatory changes of the droplet radius, composition, and Mie scattering pattern (MMS). αM was retrieved from the analysis of the MMS patterns with a kinetic multilayer model.
We observed a composition-dependent variation of αM by almost two orders of magnitude, covering the range from less than 0.005 to more than 0.1. Surprisingly, for the lower temperatures the values of αM lie close to 0.1 for TREG-rich and water-rich droplets, while the minimum value of αM is reached at intermediate concentrations (water mole fractions of 0.38). The minimum of αM might be explained by the formation of a more or less saturated hydrogen-bond network between TREG and water forming at the surface at intermediate concentrations, minimising the sites (e.g. free OH groups) where gas phase water molecules can accommodate. The high values of αM for TREG-rich and water-rich droplets could be the result of an increase in the number of free OH-groups at the surface facilitating water accommodation from the gas phase. At concentrations below the minimum of αM, αM is essentially temperature independent. Above the minimum, however, αM decreases systematically from 0.1 to 0.005 with increasing temperature.
An Arrhenius type analysis reveals that the formation of the transition state is entropically hindered at all conditions studied, in agreement with the fact that the number of degrees of freedom reduce when a molecule transitions from the gas phase to a more restricted surface-bound molecule. Our analysis suggests that the formation of the transition state is enthalpically neutral at concentrations below the minimum of αM and enthalpically favoured at higher water concentrations. In the intermediate concentration range, the enthalpy of activation is strongly temperature-dependent. These findings underscore the sensitivity of αM to moderate changes in conditions even for miscible systems. The present results for the supposedly simple, miscible TREG–water system further highlight the complexity of the interplay between different factors governing mass accommodation.
Data availability
The data repository related to this article can be found at https://doi.org/10.3929/ethz-b-000673390.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr. Tanya L. Myers from the Pacific Northwest National Laboratory for providing the complex refractive index data of TREG, Dr. Pablo Corral Arroyo who developed the original version of the MHM-PA model, and Markus Steger and David Stapfer for technical support. This work was financially supported by the Swiss National Science Foundation (SNSF grant. no. 200020-200306) and ETH Zurich. The authors declare no competing financial interest.Notes and references
- J. C. Maxwell, Phil. Trans. Royal Society, 1859, 1, 49–88 Search PubMed.
- P. Davidovits, C. E. Kolb, L. R. Williams, J. T. Jayne and D. R. Worsnop, Chem. Rev., 2006, 106, 1323–1354 CrossRef CAS PubMed.
- P. Davidovits, C. E. Kolb, L. R. Williams, J. T. Jayne and D. R. Worsnop, Chem. Rev., 2011, 111, PR76–PR109 CrossRef CAS PubMed.
- E. Davis, Atmos. Res., 2006, 82, 561–578 CrossRef CAS.
- C. E. Kolb, R. A. Cox, J. P. D. Abbatt, M. Ammann, E. J. Davis, D. J. Donaldson, B. C. Garrett, C. George, P. T. Griffiths, D. R. Hanson, M. Kulmala, G. McFiggans, U. Pöschl, I. Riipinen, M. J. Rossi, Y. Rudich, P. E. Wagner, P. M. Winkler, D. R. Worsnop and C. D. O’Dowd, Atmos. Chem. Phys., 2010, 10, 10561–10605 CrossRef CAS.
- J. P. D. Abbatt, A. K. Y. Lee and J. A. Thornton, Chem. Soc. Rev., 2012, 41, 6555–6581 RSC.
- M. E. Diveky, M. J. Gleichweit, S. Roy and R. Signorell, J. Phys. Chem. A, 2021, 125, 3528–3548 CrossRef CAS PubMed.
- A. H. Persad and C. A. Ward, Chem. Rev., 2016, 116, 7727–7767 CrossRef CAS PubMed.
- A. Laaksonen, T. Vesala, M. Kulmala, P. M. Winkler and P. E. Wagner, Atmos. Chem. Phys., 2005, 5, 461–464 CrossRef CAS.
- A. P. Kryukov and V. Y. Levashov, Int. J. Heat Mass Transfer, 2011, 54, 3042–3048 CrossRef CAS.
- A. Morita, M. Sugiyama, H. Kameda, S. Koda and D. R. Hanson, J. Phys. Chem. B, 2004, 108, 9111–9120 CrossRef CAS.
- A. Morita and B. C. Garrett, Fluid Dyn. Res., 2008, 40, 459 CrossRef.
- W. Li, C. Y. Pak, X. Wang and Y.-L. S. Tse, J. Phys. Chem. C, 2019, 123, 18924–18931 CrossRef CAS.
- M. von Domaros, P. S. J. Lakey, M. Shiraiwa and D. J. Tobias, J. Phys. Chem. B, 2020, 124, 3836–3843 CrossRef CAS PubMed.
- X. Li and I. C. Bourg, Environ. Sci. Technol., 2023, 57, 13092–13103 CrossRef CAS PubMed.
- S. M. Johansson, J. Lovrić, X. Kong, E. S. Thomson, P. Papagiannakopoulos, S. Briquez, C. Toubin and J. B. C. Pettersson, Phys. Chem. Chem. Phys., 2019, 21, 1141–1151 RSC.
- J. Julin, P. M. Winkler, N. M. Donahue, P. E. Wagner and I. Riipinen, Environ. Sci. Technol., 2014, 48, 12083–12089 CrossRef CAS PubMed.
- P. Varilly and D. Chandler, J. Phys. Chem. B, 2013, 117, 1419–1428 CrossRef CAS PubMed.
- U. Pöschl, Y. Rudich and M. Ammann, Atmos. Chem. Phys., 2007, 7, 5989–6023 CrossRef.
- G. M. Nathanson, P. Davidovits, D. R. Worsnop and C. E. Kolb, J. Phys. Chem., 1996, 100, 13007–13020 CrossRef CAS.
- M. Shiraiwa, C. Pfrang and U. Pöschl, Atmos. Chem. Phys., 2010, 10, 3673–3691 CrossRef CAS.
- M. Shiraiwa and U. Pöschl, Atmos. Chem. Phys., 2021, 21, 1565–1580 CrossRef CAS.
- M. Kulmala and P. E. Wagner, J. Aerosol Sci., 2001, 32, 833–841 CrossRef CAS.
- R. Marek and J. Straub, Int. J. Heat Mass Transfer, 2001, 44, 39–53 CrossRef CAS.
- I. Eames, N. Marr and H. Sabir, Int. J. Heat Mass Transfer, 1997, 40, 2963–2973 CrossRef CAS.
- D. Jakubczyk, M. Zientara, K. Kolwas and M. Kolwas, J. Atmos. Sci., 2007, 64, 996–1004 CrossRef.
- R. E. H. Miles, J. P. Reid and I. Riipinen, J. Phys. Chem. A, 2012, 116, 10810–10825 CrossRef CAS PubMed.
- P. Davidovits, D. R. Worsnop, J. T. Jayne, C. E. Kolb, P. Winkler, A. Vrtala, P. E. Wagner, M. Kulmala, K. E. J. Lehtinen, T. Vesala and M. Mozurkewich, Geophys. Res. Lett., 2004, 31, L22111 CrossRef.
- J. D. Smith, C. D. Cappa, W. S. Drisdell, R. C. Cohen and R. J. Saykally, J. Am. Chem. Soc., 2006, 128, 12892–12898 CrossRef CAS PubMed.
- M. E. Diveky, S. Roy, J. W. Cremer, G. David and R. Signorell, Phys. Chem. Chem. Phys., 2019, 21, 4721–4731 RSC.
- S. T. Govoni and G. M. Nathanson, J. Am. Chem. Soc., 1994, 116, 779–780 CrossRef CAS.
- G. M. Nathanson, Annu. Rev. Phys. Chem., 2004, 55, 231–255 CrossRef CAS PubMed.
- R. E. H. Miles, J. F. Davies and J. P. Reid, Phys. Chem. Chem. Phys., 2016, 18, 19847–19858 RSC.
- J. F. Davies, R. E. H. Miles, A. E. Haddrell and J. P. Reid, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8807–8812 CrossRef CAS PubMed.
- J. M. Langridge, M. S. Richardson, D. A. Lack, C. A. Brock and D. M. Murphy, Aerosol Sci. Technol., 2013, 47, 1163–1173 CrossRef CAS.
- X. Kong, E. S. Thomson, P. Papagiannakopoulos, S. M. Johansson and J. B. C. Pettersson, J. Phys. Chem. B, 2014, 118, 13378–13386 CrossRef CAS PubMed.
- W. Lester Jr, S. Kaye, O. Robertson and E. W. Dunklin, Am. J. Public Health, 1950, 40, 813–820 CrossRef CAS PubMed.
- P. Gandhidasan, Energy Sources, 2003, 25, 189–201 CrossRef CAS.
- B. Ballantyne and W. M. Snellings, J. Appl. Toxicol., 2007, 27, 291–299 CrossRef CAS PubMed.
- X. Guo, T. Ehindero, C. Lau and R. Zhao, Indoor Air, 2022, 32, e13100 CAS.
- C. Rainey, J. Shifflett, J. Goodpaster and D. Bezabeh, Nicotine Tob. Res., 2013, 25, 576–585 CAS.
- J. W. Cremer, K. M. Thaler, C. Haisch and R. Signorell, Nat. Commun., 2016, 7, 10941 CrossRef CAS PubMed.
- S. Roy, M. E. Diveky and R. Signorell, J. Phys. Chem. C, 2020, 124, 2481–2489 CrossRef.
- S. Roy, M. E. Diveky and R. Signorell, J. Phys. Chem. C, 2020, 124, 17848–17849 CrossRef CAS.
- M. E. Diveky, S. Roy, G. David, J. W. Cremer and R. Signorell, Photoacoustics, 2020, 18, 100170 CrossRef PubMed.
- M. E. Diveky, S. Roy, J. W. Cremer, G. David and R. Signorell, Phys. Chem. Chem. Phys., 2020, 22, 15770–15771 RSC.
- P. Corral Arroyo, M. J. Gleichweit, M. E. Diveky and R. Signorell, Aerosol Sci. Technol., 2023, 57, 742–757 CrossRef CAS.
- P. Davidovits, J. T. Jayne, S. X. Duan, D. R. Worsnop, M. S. Zahniser and C. E. Kolb, J. Phys. Chem., 1991, 95, 6337–6340 CrossRef CAS.
- M. E. Diveky, M. J. Gleichweit, S. Roy, E. Bartalucci and R. Signorell, Proc. SPIE 11463, OTOM XVII, 2020, pp. 115-131.
- The Dow Chemical Company, Triethylene Glycol, Dow techreport XXX-0207X CRCG, 2007.
- U. K. Krieger, F. Siegrist, C. Marcolli, E. U. Emanuelsson, F. M. Gøbel, M. Bilde, A. Marsh, J. P. Reid, A. J. Huisman, I. Riipinen, N. Hyttinen, N. Myllys, T. Kurtén, T. Bannan, C. J. Percival and D. Topping, Atmos. Meas. Tech., 2018, 11, 49–63 CrossRef.
- C. F. Bohren and D. R. Huffman, Absorption and Scattering of Light by Small Particles, John Wiley & Sons, Ltd, 1998 Search PubMed.
- G. David, O. Reich, M. E. Divéky, S. Roy, E. A. Parmentier, J. W. Cremer, K. Esat and R. Signorell, Proc. SPIE11083, OTOM XVI, 2019, p. 1108322.
- M. Shiraiwa, C. Pfrang, T. Koop and U. Pöschl, Atmos. Chem. Phys., 2012, 12, 2777–2794 CrossRef CAS.
- M. Kulmala, T. Vesala and P. E. Wagner, Proc. R. Soc. London, Ser. A, 1993, 441, 589–605 CrossRef CAS.
- D. M. Murphy, Aerosol Sci. Technol., 2009, 43, 356–363 CrossRef CAS.
- P. M. Winkler, A. Vrtala, R. Rudolf, P. E. Wagner, I. Riipinen, T. Vesala, K. E. J. Lehtinen, Y. Viisanen and M. Kulmala, J. Geophys. Res., 2006, 111, D19202 CrossRef.
- N. A. Fuchs and A. G. Sutugin, Topics in Current Aerosol Research, Pergamon, 1971, vol. 2, ch. Properties of HDAs, pp.29–37 Search PubMed.
- Y. Q. Li, P. Davidovits, C. E. Kolb and D. R. Worsnop, J. Phys. Chem. A, 2001, 105, 10627–10634 CrossRef CAS.
- I. Riipinen, B. Svenningsson, M. Bilde, A. Gaman, K. Lehtinen and M. Kulmala, Atmos. Res., 2006, 82, 579–590 CrossRef CAS.
- P. S. J. Lakey, B. E. Cummings, M. S. Waring, G. C. Morrison and M. Shiraiwa, Environ. Sci.: Processes Impacts, 2023, 25, 1464–1478 RSC.
- M. J. Gleichweit, M. Azizbaig Mohajer, D. Borgeaud, M. E. Diveky, G. David and R. Signorell, Proc. SPIE 12198, OTOM XIX 2022, p. 1219805.
- J. Rumble, CRC Handbook of Chemistry and Physics, CRC Press/Taylor & Francis Group, 99th edn, 2018 Search PubMed.
- S. K. Begum, R. J. Clarke, M. S. Ahmed, S. Begum and M. A. Saleh, J. Mol. Liq., 2013, 177, 11–18 CrossRef CAS.
- K. Klimaszewski, E. Stronka-Lewkowska, K. Abramczyk and A. Bald, J. Chem. Thermodyn., 2015, 89, 212–222 CrossRef CAS.
- N. Shinyashiki, S. Sudo, W. Abe and S. Yagihara, J. Chem. Phys., 1998, 109, 9843–9847 CrossRef CAS.
- S. Sudo, N. Shinyashiki, Y. Arima and S. Yagihara, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 011501 CrossRef PubMed.
- S. Sudo, S. Tsubotani, M. Shimomura, N. Shinyashiki and S. Yagihara, J. Chem. Phys., 2004, 121, 7332–7340 CrossRef CAS PubMed.
- P. Chakraborty and M. R. Zachariah, J. Phys. Chem. A, 2008, 112, 966–972 CrossRef CAS PubMed.
- X. Ma, P. Chakraborty, B. J. Henz and M. R. Zachariah, Phys. Chem. Chem. Phys., 2011, 13, 9374–9384 RSC.
- S. Takahama and L. M. Russell, J. Geophys. Res., 2011, 116, D02203 CrossRef.
- G. Ergin and S. Takahama, J. Phys. Chem. A, 2016, 120, 2885–2893 CrossRef CAS PubMed.
- J. T. Jayne, S. X. Duan, P. Davidovits, D. R. Worsnop, M. S. Zahniser and C. E. Kolb, J. Phys. Chem., 1991, 95, 6329–6336 CrossRef CAS.
- B. C. Garrett, G. K. Schenter and A. Morita, Chem. Rev., 2006, 106, 1355–1374 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00966e |
| This journal is © the Owner Societies 2024 |