Field-dependent THz transport nonlinearities in semiconductor nano structures†
Received
4th March 2024
, Accepted 22nd April 2024
First published on 22nd April 2024
Abstract
Charge transport nonlinearities in semiconductor quantum dots and nanorods are studied. Using a density matrix formalism, we retrieve the field-dependent nonlinear mobility and show the possibility of intra-pulse gain. We further demonstrate that the dynamics of master equations can be captured in an analytical formula for the field-dependent charge carrier mobility, e.g. for two-level systems. This equation extends the linear response theory based Kubo–Greenwood result to nonlinear processes at elevated field strength, easily reached in THz transport spectroscopy. With these tools we analyze the field strength, chirp, temperature and dephasing dependence of the charge carrier mobility in the model system of CdSe quantum dots and wires. Stark broadening and Rabi splitting result in strong alterations of the mobility spectra, pronounced at low temperatures. The mobility spectra are strongly temperature and pulse shape dependent in the nonlinear regime. The findings are of immediate interest e.g. for nonlinear THz generation, conversion and amplification in 6G technology and nano electronics. Our results further enable experimentalists to fit and understand measured charge transport nonlinearities with analytical expressions and to design nanosystems with engineered material properties.
1 Introduction
Charge transport in nanostructures and materials is a highly active research field. These systems promise to optimize and facilitate processes e.g. for hydrogen generation, solar energy harvesting or electronics at a nano scale, nano photonics as well as high frequency THz generation and detection by nanomaterials in emerging 6G technology.1–6 THz time-domain and pump–probe spectroscopy have proven to be an efficient tool to investigate charge mobility and exciton polarizability in low dimensional systems like semiconductor quantum wells, nanowires and dots.7–22 Nonlinear transport phenomena in bulk and nano semiconductors occur at elevated field strengths, giving rise to high harmonics generation (e.g. in graphene23) and Bloch oscillations24 (at very high fields) as well as THz generation by rectification25 for example. These phenomena show great promise for upcoming technologies like 6G telecommunication in the THz range as they allow efficient frequency generation and conversion. Although there is in-depth understanding of linear transport in bulk and nano semiconductors based on Drude, Drude-Smith and Kubo–Greenwood based models,26–32 understanding of nonlinear transport and charge carrier mobility remains scarce.33–36 Recent density matrix calculations show strong THz transport nonlinearity in nanowires as well as a yet unexplored equilibration current, suppressing the low-frequency charge (or exciton) mobility.32,34,37,38 The latter can be understood in the frame of a generalized Kubo–Greenwood theory including charge carrier relaxation and dephasing.
In this paper, we study the field-dependent nonlinear mobility based on master equations and demonstrate that it can be understood with an analytical equation, e.g. for two-level systems, extending the linear response theory based Kubo–Greenwood result to nonlinear processes, which occur at elevated field strength, e.g. in THz spectroscopy of transport phenomena. Using master equations for the density matrix, we analyze the full field strength, chirp, temperature dependence of the charge carrier mobility as well as dephasing by phonon scattering, exemplified with CdSe wires and quantum dots. The obtained frequency-dependent mobility spectra are shown to be strongly temperature and THz pulse shape dependent, especially in the nonlinear regime. Our results are of direct interest e.g. for nano electronics or nonlinear THz generation and conversion (e.g. from the high, electronically accessible GHz range to THz frequencies) as well as amplification via gain in 6G technology. There nonlinear currents are the basis for efficient frequency mixing, harmonics generation and amplification, seen as re-radiation in the spectrum emitted by the nanostructure. We remark that our paper is focused on introducing the methodology of nonlinear charge transport simulation on a quantum mechanical basis and identifying the relevant parameters that govern the resultant system properties, while detailed analysis of experimental findings is not the focus.
2 Theoretical foundations
2.1 Density matrix formalism
We describe the mobility of a charge carrier on a semiconductor quantum dot or rod (represented by cuboids) within the frame of density matrix theory. Starting point of our discussion is a photogenerated electron in the conduction band (CB) or hole left in the valence band (VB). The time-dependent dynamics of this charged particle is given by action of the Hamiltonian H on the density matrix ρ through the Liouville–von Neumann equation.34,39 Subjecting the system to a time-varying perturbation, e.g. a THz-pulse, we write| | 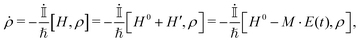 | (1) |
where we divided the system into an unperturbed system Hamiltonian H0 and a perturbation H′ = −M·E(t), with E(t) a THz field and M the transition dipole moment. The energy transferred between THz field and nanosystem relates to a relative charge displacement, so that we write in the 1D case M = qe(x − L/2). We assume parallel orientation of THz field and rod axis. Eqn (1) is the short-hand notation for a set of coupled differential equations – the density matrix master equations.40 The corresponding elements of ρ related to the quantized electron (hole) states k can be selected by ρij = 〈i|ρ|j〉, so that we expand eqn (1) above| |  | (2) |
We introduced a decay contribution Rij reflecting population i = j and polarization i ≠ j decay. The way these phenomena are addressed differs from many modeling approaches. We consider the nanorods and dots we are dealing with as 4-level systems. Our intention is to model coupling between energetic states within the relaxation-time approximation. We write| |  | (3) |
where Γik is the population decay rate coefficient from |k〉 → |i〉. On the other hand, population shifting among the energetic states can only destroy phase coherence, prior imposed onto the system by coherent coupling to a (THz) electric field. For that reason, every single population distribution process is translating into a loss of phase relation information, the decoherence. For the off-diagonal elements, we write| |  | (4) |
and, referring to polarization among states |i〉 and |j〉, sum over all terms that either populate or deplete i (first sum) as well as j (second sum). The last term γpure is the so-called pure dephasing, a term corresponding to random resonance frequency fluctuations41,42 or inelastic scattering.43 Due to the pronounced presence of (acoustic) phonons in nanoparticles, we assume the dephasing to be governed by phonon mediated relaxation. The corresponding population redistribution and polarization decay processes are indicated in Fig. 1a.
 |
| | Fig. 1 (a) 1D Quantum well with relaxation and dephasing channels for the electron populations and polarization exemplified for the |2〉 and |3〉 state pair. (b) Illustration of an electron being driven and excited by an electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) inside a 1D nanorod including electron–phonon interactions. Population (c) and polarization (ρ12(t)) (d) dynamics for a 20 nm length CdSe rod at E0 = 20 kV cm−1 and 10 K. inside a 1D nanorod including electron–phonon interactions. Population (c) and polarization (ρ12(t)) (d) dynamics for a 20 nm length CdSe rod at E0 = 20 kV cm−1 and 10 K. | |
2.2 Relaxation rate coefficients
After intraband excitation of charge carriers, e.g. by THz photons of a pump beam, a hot, non-thermalized charge carrier distribution arises, which cools predominantly by the emission of phonons.44–47 The charge carrier dynamics can then be probed by THz photons. The rate of electron or hole scattering from initial state i to the final state f under assistance of a phonon with wave vector  is given by Fermi's golden rule:
is given by Fermi's golden rule:| |  | (5) |
Here ν = e, h stands for electron or hole respectively. Ψi(f)ν is the initial (final) state, λ is the phonon mode. The δ function represents energy conservation, ΔEν = Efν − Eiν is the energy separation between the initial and final state, Eλ(q) is the phonon energy. 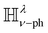 is the electron/hole phonon interaction Hamiltonian. The upper sign corresponds to emission and the lower sign to the absorption of a phonon. In non-centrosymmetric materials, the coupling to acoustic phonons arises from both the deformation potential and the piezoelectric coupling mechanisms.48,49 However, different studies on CdSe nanomaterials have shown that the acoustic phonon scattering mechanisms are dominated by deformation potential interaction rather than piezoelectric coupling.48–52 As we focus on dot-like and short rod-like CdSe quantum structures treated as quantum boxes characterized by discrete densities of state, we will omit the consideration of optical phonons in our investigation. In fact, in contrast to acoustic phonons, optical phonons have no continuous-energy spectrum in our dispersionless approach. For a OD system, the discrete electron and LO phonon energies don't have any first-order (Frohlich) interaction, except for the special cases Ef − Ei = ELO, so that the scattering rates are low and we do not consider them. Hence, we will consider only the electron-longitudinal acoustic (LA) phonon scattering. We remark that the intention of this paper is to study the basics of nonlinear charge transport physics and not a refined model for all kinds of phonon related processes in the considered nanostructures. Within our acoustic deformation potential approach eqn (5) turns into
is the electron/hole phonon interaction Hamiltonian. The upper sign corresponds to emission and the lower sign to the absorption of a phonon. In non-centrosymmetric materials, the coupling to acoustic phonons arises from both the deformation potential and the piezoelectric coupling mechanisms.48,49 However, different studies on CdSe nanomaterials have shown that the acoustic phonon scattering mechanisms are dominated by deformation potential interaction rather than piezoelectric coupling.48–52 As we focus on dot-like and short rod-like CdSe quantum structures treated as quantum boxes characterized by discrete densities of state, we will omit the consideration of optical phonons in our investigation. In fact, in contrast to acoustic phonons, optical phonons have no continuous-energy spectrum in our dispersionless approach. For a OD system, the discrete electron and LO phonon energies don't have any first-order (Frohlich) interaction, except for the special cases Ef − Ei = ELO, so that the scattering rates are low and we do not consider them. Hence, we will consider only the electron-longitudinal acoustic (LA) phonon scattering. We remark that the intention of this paper is to study the basics of nonlinear charge transport physics and not a refined model for all kinds of phonon related processes in the considered nanostructures. Within our acoustic deformation potential approach eqn (5) turns into| |  | (6) |
where Nq stands for the Bose distribution function,  is the overlap integral in η = x, y, z direction, ni(f)η is the initial(final) state quantum number in η direction. We will consider in our work an infinitely deep, rectangular quantum box. α(q)2 = Dν2ħωq/2ρdcs2V, where V = LxLyLz is the principal volume of the nanocrystal, Dν is the acoustic deformation potential, ρd is the mass density, ωq = csq is the long wave approximation of the acoustic phonon dispersion, and cs is the sound velocity in the material. See (ESI,† Section S1) for further details. Tables S1–S6 (ESI†) display the calculated electron (hole) acoustic phonon scattering rates for three different CdSe nanoparticle sizes (6 × 6 × 6 nm3, 20 × 6 × 6 nm3 and 40 × 6 × 6 nm3) for several transitions and three different temperatures T = 10, 70 and 300 K. We approximate our nanosystems as four-level systems in the THz range, since the relevant transitions fall in the typically observed range in (broadband) THz probe experiments. Tables S1–S6 (ESI†) show the size and transition energy dependence of scattering rates. The coupling to acoustic phonons decreases with the nanoparticles size and increases with decreasing transition energy for fixed size. The calculated scattering rates are then implemented in our master equation description. Fig. 1c and d shows the results for the dynamics of populations ρii and polarizations ρij as obtained for 20 nm CdSe rods at 10 K. With these results the charge carrier mobility on semiconductor nanoparticles is obtained in the following.
is the overlap integral in η = x, y, z direction, ni(f)η is the initial(final) state quantum number in η direction. We will consider in our work an infinitely deep, rectangular quantum box. α(q)2 = Dν2ħωq/2ρdcs2V, where V = LxLyLz is the principal volume of the nanocrystal, Dν is the acoustic deformation potential, ρd is the mass density, ωq = csq is the long wave approximation of the acoustic phonon dispersion, and cs is the sound velocity in the material. See (ESI,† Section S1) for further details. Tables S1–S6 (ESI†) display the calculated electron (hole) acoustic phonon scattering rates for three different CdSe nanoparticle sizes (6 × 6 × 6 nm3, 20 × 6 × 6 nm3 and 40 × 6 × 6 nm3) for several transitions and three different temperatures T = 10, 70 and 300 K. We approximate our nanosystems as four-level systems in the THz range, since the relevant transitions fall in the typically observed range in (broadband) THz probe experiments. Tables S1–S6 (ESI†) show the size and transition energy dependence of scattering rates. The coupling to acoustic phonons decreases with the nanoparticles size and increases with decreasing transition energy for fixed size. The calculated scattering rates are then implemented in our master equation description. Fig. 1c and d shows the results for the dynamics of populations ρii and polarizations ρij as obtained for 20 nm CdSe rods at 10 K. With these results the charge carrier mobility on semiconductor nanoparticles is obtained in the following.
2.3 Charge carrier mobility
With the Liouville–von Neumann equation fully set up, we can solve numerically for all population and polarization elements.34 In the next step, we can calculate observables, which represent the microscopic properties of our system. Aiming to determine the frequency-dependent mobility μ(ω) of charge carriers, we write53–56| | 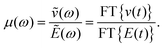 | (7) |
Making use of the fundamental property of Fourier transformation| |  | (8) |
we have reduced the calculation of mobility to evaluation of charge carrier position x on a 1D nanorod| |  | (9) |
so that the final measured (complex) mobility spectrum is given by| |  | (10) |
Inspecting eqn (10) as well as revisiting eqn (2), we see that the numerical modeling is going to depend on the choice of the electric field E(t). In accordance to experiment, we describe the field of our THz (probe) pulse as| |  | (11) |
with E0 the electric field strength, ω0 the carrier frequency, a the chirp parameter (negative a equals up-chirp)53 and τ the 1/e width of the Gaussian envelope, which relates to the full width at half maximum by 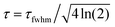 .
.
Before delving into the discussion of results, we should differentiate between possible size and temperature effects on the electronic structure of the charge carrier itself vs. its surrounding, e.g. phonons in the semiconductor. Charge carrier states, described in the infinite-well approximation, populated according to Fermi–Dirac statistics,37,57 follow a 1/L2 energy scaling. For that reason, smaller systems (with larger energy differences) accumulate more population close to ground state, from where transitions are going to dominate. At the same time, transition matrix elements 〈i|M|j〉 shrink with increasing j, but grow, when looking at elements 〈j|M|j + 1〉 corresponding to absorption between neighboring states. Similarly, for a fixed size but lowered temperature, the population accumulates close to ground state, as well, implying the same effect.31 At room temperature (RT), however, the Fermi energy is elevated and the Fermi-edge smeared, so that states in energetic proximity are gradually populated.31
Inspecting eqn (5), size effects on electronic energies and wavefunctions, impact the coupling rate to phonons as well. The phonon coupling Hamiltonian matrix elements 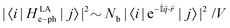 can be expanded for small wave vectors
can be expanded for small wave vectors ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , so that we see for a transition i ≠ j
, so that we see for a transition i ≠ j
| |  | (12) |
An indirect length scaling is the result, which becomes obvious when
Lx >
Ly,
Lz. Hence, the
L2 influence from the squared matrix element is countered by the 1/
V = 1/(
LxLyLz) dependence, so that roughly a proportional scaling with increasing nanorod length is observed (see ESI
†).
Temperature, on the other hand, affects the phonon-coupling rate solely through the LA phonon occupation number Nb. Given a certain energy (or wave vector, respectively) of LA phonons, this number grows strictly with rise of temperature – linearly for very small LA phonon energies. The dephasing rate coefficient is translating into the FWHM wL by wL = 2γ of the transition between states 〈i| and |j〉. Using eqn (4) omitting γpure as discussed, we find
| |  | (13) |
Each of the pairs in parentheses refers to an up- and down-scattering transition rate constant proportional to either
Nb or
Nb + 1, respectively. Only at higher temperatures we can expect a clear linear growth dependence of linewidth (where
Nb ≈
Nb + 1 ∝
kBT). Although its precise behavior might not be immediately clear, we reasonably expect the number of phonons and thus the linewidth through
eqn (13) to shrink towards cryogenic temperatures.
3 Results and discussion
Fig. 2 shows the comprised results for temperature dependent complex linear mobility spectra of three different sizes of CdSe nanoparticles (6 × 6 × 6 nm3Fig. 2(a) and (d), 20 × 6 × 6 nm3Fig. 2(b) and (e) and 40 × 6 × 6 nm3Fig. 2(c) and (f)). If not specified otherwise, for modeling purposes of linear mobility spectra our standard E-field parameters are E0 = 0.1 kV cm−1, ω0 = 2π × 1 THz, a = −3, ϕ = 0 and τfwhm = 0.5 ps.
 |
| | Fig. 2 Size dependence of real (a)–(c) and imaginary (d)–(f) electron mobility for 6 × 6 × 6 nm3, 20 × 6 × 6 nm3 and 40 × 6 × 6 nm3 CdSe quantum dots and wires at 10 K, 70 K and 300 K and a weak THz field with E0 = 0.1 kV cm−1, ω0 = 2π × 1 THz, a = −3, ϕ = 0 and τfwhm = 0.5 ps. Results are obtained with eqn (10) from 4-level master equation approach. Insets in (b) and (c) display the room temperature case in a zoomed version. | |
Starting with the special case of the 6 × 6 × 6 nanocrystal structure (Fig. 2a and d), it is striking that regardless of temperature seemingly no real part is present (compare axis scale), while the imaginary contribution is small, but non-negligible and decreasing linearly. Commonly, such feature is attributed to excitons, whose polarizability is claimed to merely cause a THz field phase lag.58,59 While this is true at low temperature, where the exciton ground state is solely populated,17,60 it has been shown recently to render an incomplete picture at room temperature.38 Here, however, the behavior of an electron can be fully explained given the eigenenergy scaling by ∼1/L2. At an effective mass of  the first resonance occurs at 42 THz outside of the THz window any common experimental setup can provide. With that in mind, even at RT only the ground state is populated, so that the single line of width wL = 2.37 ps−1 leaves no detectable real part in the 0–8 THz window, while the initial slope of the pole function in the imaginary part appears to be linear.
the first resonance occurs at 42 THz outside of the THz window any common experimental setup can provide. With that in mind, even at RT only the ground state is populated, so that the single line of width wL = 2.37 ps−1 leaves no detectable real part in the 0–8 THz window, while the initial slope of the pole function in the imaginary part appears to be linear.
This scenario is educational for the case of larger nanorod species, as it renders the contribution of short orthogonal extensions to total THz mobility negligible. An electron on the 20 nm rod being more resonant within the 0–8 THz window, shows pronounced peak and pole functions Fig. 2(b) and (e) up to 4000 cm2 V−1 s−1 (10 K) decreasing with temperature down to still >50 cm2 V−1 s−1 (inset Fig. 2(b)) for the larger spectral range at room temperature. However, this amplitude decrease is not directly proportional to temperature, because (i) at the same time total population is distributing among the 4-level system and (ii) the width of (multiple somewhat overlaying) transition lines is growing non-linearly with temperature between 10–300 K. This effect is amplified, when the nanorod is lengthened even further to 40 nm Fig. 2(c) and (f). Here, two additional effects become apparent, best seen at cryogenic level: (i) the total dephasing rate is increasing with the growth of respective up- and down-scattering rates as discussed with eqn (12) and (ii) the 1/L2 dependence of the energy levels is driving the resonance frequencies close to the DC limit. The sharp mobility drop towards 0 THz is reflecting a purely quantum mechanic equilibration current contribution,34 coming from non-unitarian system dynamics (i.e. dephasing and relaxation).32 For such nanowire like structures, the familiar Drude-Smith response shape emerges for long wires, however for completely different reasons than assumed backscattering at domain boundaries.16,30 Approaching room temperature, we are confronted with another exception: the particularly small mobility (Fig. 2(c) inset) is an unrealistic byproduct of our 4-level modeling. Due to the Fermi-distribution reaching out to many higher states for large L, modeling of more than 10 levels deems necessary. As the computational effort is growing (N2 − N − 2)/2 with the number of states N,34 we choose the 20 nm nanorod for our nonlinear discussion in the following. Fig. 3 displays the field strength dependent real and imaginary parts of mobility spectra from a 20 nm CdSe nanorod in case of 3 different temperatures. For reference the linear case (E0 = 0.1 kV cm−1) is always plotted as start of the series. The ESI,† Section S4 contains our results for the hole transport in the CdSe nanoparticles, in analogy to Fig. 2 as well as the total mobility.
 |
| | Fig. 3 Field strength dependence (a–f) of the electron mobility on a 20 × 6 × 6 nm3 CdSe nanorod for different temperatures using ω0 = 2π × 1 THz, a = −3, ϕ = 0 and τfwhm = 0.5 ps, obtained from 4-level master equation approach together with eqn (10). | |
In order to understand the underlying physics, we expand the time-dependent velocity v(t) into a linear and third order nonlinear contribution (omitting even order terms for symmetry reasons)33,61,62
| | | v(t) = v(1)(t) + v(3)(t) | (14) |
We realize that in combination to
eqn (7) two distinct contributions to the measured spectrum arise
| | 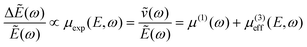 | (15) |
We intentionally write
μeff for the third order related contribution, as it will become clear that an experimental measurement, as performed by
eqn (15), renders the term
μ(3)eff itself field dependent. Expanding the quantum mechanical expression for the mobility from
eqn (10) by means of a perturbation series and defining
ρ(
t) =
ρ(0)(
t) +
ρ(1)(
t) +
ρ(3)(
t), we find
| |  | (16) |
Since we ask for the relative displacement, only off-diagonal elements are going to add to the total mobility. Hence, all graphs in
Fig. 3 will derive from the corresponding linear spectra given in
Fig. 2b and e and contain dynamic information according to
ρ(3)ij in the second term of
eqn (16) above. For that reason, we revisit the generalized Liouville–von Neumann
eqn (1) and (2) to apply the common perturbation assumptions
ρij =
ρ(0)ij +
λρ(1)ij +
λ2ρ(2)ij +
λ3ρ(3)ij and

for the perturbative regime of interaction.
63 Further, we expand the decay contribution in the same manner
Rij =
R(0)ij +
λR(1)ij +
λ2R(2)ij +
λ3R(3)ij. Sorting the respective terms by orders of
λ, we find the
q-th order off-diagonal elements to evolve according to
| |  | (17) |
This approach might seem similar to conventional perturbation theory, but bears significantly different implications due to the way relaxation among population elements is implemented. Often the assumption of an overarching relaxation rate coefficient by means of −
Γi(
ρii −
ρeqii) is applied, which is identical to the way dephasing is treated here. Within such an approximation, we could easily derive nonlinear evolution of population according to
eqn (17) above (by setting
i =
j). Instead, however, we need to define another evolution equation
| |  | (18) |
As we can see, the first order polarization evolution (
eqn (17),
q = 1) can easily be integrated, while this is not possible for the first order population differential equation (DEQ) ((
eqn (18),
q = 1)). Still, the relaxation terms enforce coupled DEQs we can not disentangle. The shape of the perturbation equations, however, teaches us that a polarization element of third order
q = 3 depends on population and polarization accumulated by preceding order 2. In contrast, a population element is depending on even earlier installed polarization by order 1 only. Nonlinear interaction is governed by the principle of polarization generation out of population and in turn, generating a nonlinear population distribution
etc.
Inspecting Fig. 3, generally speaking, we can see stronger spectral alterations for lower temperatures. This observation is rooted in the more pronounced accumulation of population (in the ground state) at low temperatures. By iteratively inserting eqn (17) and (18) into themselves, we can trace ρeqjj − ρeqii = fj(T) − fi(T) up to ![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) (3)ij. The less distributed a population is among states prior to perturbation, the more scattered it can become among all relevant levels during heavy excitation. This constitutes a new situation, which is then immediately probed by the same THz field. At 10 K (Fig. 3a and d) we can approach best, what is seen. Ignoring the lineshape for a moment, we crudely recognize the light curves (constituting the lone |1〉 → |2〉 resonance at 3.8 THz) decrease, while another is emerging at ∼6.3 THz – the |2〉 → |3〉 transition. The same phenomenon, however in a weakened form, can be observed for higher temperatures: low-frequency absorption and dispersion bands are weakened and resonances occur at higher energies (Fig. 3b and e and c and f). Elevated temperatures also include higher levels, which brings the system closer and closer to the state of equal occupation of individual levels. The graphs in Fig. 3(c) and (f) describe the same finding, but over a frequency range outside 0–8 THz.
(3)ij. The less distributed a population is among states prior to perturbation, the more scattered it can become among all relevant levels during heavy excitation. This constitutes a new situation, which is then immediately probed by the same THz field. At 10 K (Fig. 3a and d) we can approach best, what is seen. Ignoring the lineshape for a moment, we crudely recognize the light curves (constituting the lone |1〉 → |2〉 resonance at 3.8 THz) decrease, while another is emerging at ∼6.3 THz – the |2〉 → |3〉 transition. The same phenomenon, however in a weakened form, can be observed for higher temperatures: low-frequency absorption and dispersion bands are weakened and resonances occur at higher energies (Fig. 3b and e and c and f). Elevated temperatures also include higher levels, which brings the system closer and closer to the state of equal occupation of individual levels. The graphs in Fig. 3(c) and (f) describe the same finding, but over a frequency range outside 0–8 THz.
In order to understand the lineshapes themselves, we are going to look at several limiting cases of strong field coupling. We bring the discussion down to a two-level system, where we can easiest recognize phenomena known from optical spectroscopy. We adapt eqn (2) to write the closed two level DEQs as
| |  | (19) |
| |  | (20) |
where we introduced the Rabi-frequency
Ω =
M21E0/
ħ, leaving the normalized field
Ē(
t) =
E(
t)/
E0 behind and made use of the closure relation
ρ11 +
ρ22 = 1. Typically, from here one introduces multiple constraints: (i) the electric field is monochromatic, (ii) the excitation is quasi-resonant (rotating wave approximation) at
ωk, hence (iii) polarization is separable into envelope and carrier
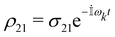
and (iv) up-scattering is non-existent
Γ21 (due to
ρ11 being the ground state), while (v)
Γ12 is slow. Many of these approximations can not be applied rigorously in the THz regime, hence the matrix master equations remain coupled at all times. However, at low temperature, where relaxation and dephasing become increasingly lower we can ask for the steady-state solution of the system (
eqn (19) and (20) above) under quasi-resonant excitation
E(
t) ∼
E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos(
ωt). This allows to deduce general properties expected upon growing coupling strength. Making use of ref.
43, we find
| |  | (21) |
for the of the 2-level mobility, containing resonant and antiresonant contributions already. We want to highlight the term
G =
γ21/(
Γ21 +
Γ12), representing the ratio of dephasing to relaxation, which is scaling the impact of the Rabi-frequency
Ω and thus the field-dependence itself. The result from
eqn (21) is quite similar to what is known from optical spectroscopy for the susceptibility.
41 We recognize two emerging effects upon larger Rabi-frequency affecting the real part: (i) the decrease of peak maximum (decline of mobility amplitude due to reduced energy transfer form the THz field to the charge carrier analogous to absorption saturation in two-level systems). Setting

, we find
| |  | (22) |
and (ii) linewidth growths due to power broadening. It is worth mentioning that the equilibration current
32,34 causing the DC mobility to vanish in nanosystems is the origin of rather complicated amplitude and especially linewidth functions, see ESI,
† Section S2. This is, because the Lorentzian line is highly asymmetric when the transition frequency
ω21 is low (due to the antiresonant contribution). Likewise, for the linewidth (full width at half maximum) we obtain:
| |  | (23) |
While the change in amplitude is undoubtedly present in all spectra from
Fig. 3a and f, the broadening of linewidth is especially difficult to discern in superposition with another very prominent spectral feature: the energy shifting. Before entering this discussion, though, we want to find a generalized solution to the nonlinear two-level polarization (
eqn (19) and (20)) valid for any field form and especially room-temperature. Applying the rules of perturbation expansion discussed prior, we write for third order of two-level polarization
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (3)21
(3)21 in the frequency domain
| |  | (24) |
According to
eqn (16), we can understand the complicated total spectral lineshape, see ESI,
† Section S3 for further details. For simplification we introduce the third order lineshape distortion function

by the double integral term above. Further, the evaluation of the velocity expectation value is carried out by reinterpreting the relative displacement
xij from
eqn (16) through
xij = −
Mij/
qe. Again, being reminded that FT{
E(
t)} =
E0FT{
Ē(
t)} =
E0Ẽ(
ω), we finally write
| |  | (25) |
where a.r. denotes the antiresonant part,
i.e. μ12(
ω) and
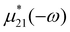
denote the resonant and antiresonant contribution to
μexp(
ω). Closely inspecting the resulting complex mobility function reveals several properties that could easily be overlooked. Firstly, as we would expect, the overall spectrum is build from a linear spectrum that is successively diminished by a growing nonlinear contribution scaling with the squared Rabi frequency
Ω2. Usually, in the optical regime large electric field strengths deem necessary to introduce nonlinearities to the measurement. In the THz regime, especially for nanostructures, the large transition dipole moments (often corresponding to several nm of charge displacement) impact the measurements already at low
E0, as seen in
Fig. 3. With
eqn (25) we have a new equation for the frequency-dependent mobility in nanosystems including nonlinear third order interaction being present at elevated field strength. Our finding reproduces the linear extended Kubo–Greenwood equation recently discovered,
32 in the weak field limit of linear response theory (
Ω → 0)
| |  | (26) |
containing both resonant and antiresonant contributions. As expected, reducing the interaction strength leads to the weak-field (Lorentzian and pole like) lineshapes we observed in
e.g.Fig. 2b and e for the low temperature limit (where the pure two-level approximation is expected to hold). Extending the rod length from 20 to 40 nm
Fig. 2(c) and (f) results in an assymetric lineshape due to the antiresonant contribution (at negative frequency) in
eqn (26), having increased relevance once the resonance shifts towards zero frequency, as well as an increasing contribution of thermally populated higher states. Finally, to fully set the stage for field-dependency discussions of the electron mobility in nanorods, we shortly want to address the energy level shifting and Rabi splitting. From diagonalization of the total Hamiltonian

(in the 2-level approximation), we can determine the eigenvalues, reading
| | 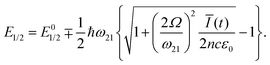 | (27) |
This immediately shows that the strength of the electric field is having an influence on the energy level positioning of the eigenstates, as the perturbation field strength is entering the eigenenergy expressions thorugh
Ω. Starting from here, three different cases can be distinguished: (i) either in case of vanishingly low fields (
Ω ≈ 0) or large detuning (
ω21 ≫
Ω) the eigenenergies of
H0 are recovered. If the field intensity is increasing, first (ii) the energy levels start to split further as the coupling strength grows with
Ω. The levels then oscillate according to the temporal profile of
Ī(
t) = 2
nc0ε0|
Ē(
t)|
2, with
n, the refractive index and
c0 the speed of light. There is a regime in which the increase of energy level distance becomes noticeable in absorption, the states, however, still evolve almost unperturbed.
When the coupling strength becomes very large (as in the THz regime) (iii), Rabi splitting occurs, as the evolution of states is now coupled to the strong Rabi oscillation frequency as well. This phenomenon is described for semiclassical light fields, too.41,64,65 The latter is especially relevant for the occurrence of gain in the THz regime as seen very prominently in Fig. 3a around 4.4 THz. At strong fields, the system is no longer resonating solely at the system eigenfrequency ω21 (Rayleigh resonance), but at the Rabi sidebands ω21 ± Ω, which correspond to resonances among the so called dressed states. The latter constitute the AC Stark effect shifted resonances. It is a core finding of dressed state theory that these strong light–matter interaction related states contain their own population and dynamics. Depending on the excitation field profile,41,43 and especially the detuning from resonance absorption and amplification can be obtained. It is extremely important to realize that we are dealing with a polychromatic excitation, so that some frequency components will be more resonant than others and – at the same time – interact with the system at different points in real time.
Rabi splitting is apparent predominantly at cryogenic temperatures, where line broadening is smaller (see Fig. 3a, d, b and e). While we clearly observe large splitting and gain at 10 K, the superposed broadening and population effects at 70 K are resulting in a strong lineshape asymmetrization only. Hence, we find the possibility of THz gain in eqn (25), where the strong driving via Ω can make the third order contribution overcome the linear absorption leading to an amplification, as seen in the negative real mobility around 4.4 THz in Fig. 3a. We remark that this gain is related to intra-pulse frequency conversion via third-order nonlinearity of our nanosystem and note that with the absorption coefficient α = Re(σ)/(n·c·ε0) for the intrinsic conductivity σ∝μ, with n the refractive index, speed of light c and vacuum permittivity, ε0 the amount of stimulated emission and gain can be calculated. α becomes negative in this case. The occurrence of nonlinear intra-pulse frequency conversion paves the way for efficient frequency conversion and amplification in the THz regime, useful for many applications, e.g. in 6G technology. Our master equation model is suitable to investigate these processes and make predictions, while eqn (25) and (21) allow an interpretation of the results or are prospective for fits to experimental results.
In order to shed more light on the role of the perturbing field we investigate in Fig. 4 the chirp and carrier-envelope dependence of the electron mobility calculated using the 4-level master equation approach together with eqn (10). We remark that depending on the chirp and envelope phase the pulses have a different degree of unipolarity.66 Unipolar pulses can also propagate in the far field once a lens or mirror system is used,67 so that e.g. the waveform is recovered with inverted amplitude in the image focus. We consider the nonlinear transport regime, where the mobility becomes field strength and pulse shape dependent, leaving linear response theory. In panel (a) we see a pronounced dependence of the induced charge velocity on the pulse chirp. Interestingly the electron acquires less velocity amplitude in the case of an unchirped pulse (with zero carrier-envelope phase). The reason is that the unchirped pulse is strongly sub-resonant to the first electronic transition at about 3.8 THz in 20 nm rods and has nearly no field strength at this frequency, see Fig. 4e. The chirped pulses have a much larger spectral amplitude resonant to the first transition and hence induce a higher charge velocity, see Fig. 4f. Altering the THz pulse carrier-envelope phase in Fig. 4b leads to strong changes in the waveform while there is a less pronounced effect on the acquired electron velocity. Only at early times there are considerable differences, which result in line width (and amplitude) changes of the frequency-dependent velocity (Fig. 4f) around the lowest 3.8 THz system resonance in 20 nm CdSe rods. Apart from that, the sub resonant regime is strongly altered.
 |
| | Fig. 4 THz time-domain waveforms and resultant electron velocity (a) and (b) as well as THz field and charge velocity in the frequency domain (e) and (f) for different chirp and carrier-envelope phase values, as obtained from 4-level master equation approach together with eqn (10) at 10 K. (First column for ϕ = 0, second column for a = −3.) For all curves E0 = 10 kV cm−1, ω0 = 2π × 1 THz and τfwhm = 0.5 ps. The resultant real and imaginary electron mobility spectra for 20 nm CdSe nanorods at 10 K are displayed for different chirp (with ϕ = 0) (c) and (g) and carrier envelope phase (d) and (h) (with a = −3). The a = 0 case delivers values in a 0–3 THz window only (overlaid by the other curves) due to finite pulse spectral bandwidth and center frequency. | |
These findings translate in strong alterations of the frequency-dependent (nonlinear) mobility spectra in Fig. 4c, d, g and h. Near the resonances, strong alterations occur, indicative for the discussed AC Stark effect causing non-Lorentzian broadening and level splitting Fig. 4(c) and (g). However, due to the broad pulse spectra, cf.Fig. 4(e), the alterations of the resonances are complex. Interesting to see is that an alteration of the pulse chirp from a = −3 to a = 3 results in considerable optical gain near 5.5 and 6.5 THz (Fig. 4c), an effect of the occurring strong nonlinearities in the CdSe rods. This means that in the latter (down chirped) pulse the parametric interaction of the THz field with population and polarization (captured in the Liouville–von Neumann evolution of the density matrix of eqn (2)) creates a transient inversion, causing intra pulse gain and frequency conversion at the expense of other frequency components in the pulse. According to dressed state theory for strong coupling41,43 gain occurs above the electronic resonance at about ω = ω21 + Ω for strong fields, while there is induced absorption in the opposite case. However, for spectrally broad pulses with respect to ω21 the situation gets more complicated and results in the seen complex spectral shapes.
In Fig. 4g and h we visualize the effect of different carrier-envelope phases from Fig. 4(b). We see that the phase changes the nonlinear mobility spectrum especially by amplitude alteration at the second transition. Hence it is important to notice, that in contrast to linear mobility measurements at low field strength, pulse carrier-envelope phase (CEP) is important. This impacts e.g. the necessity of CEP-stabilization of pulsed THz sources. E.g. in THz generation by Four Wave Mixing68 CEP is imprinted from a IR-pulse, while for optical rectification and difference frequency generation69 this is not the case.
4 Conclusions
Transport nonlinearities in semiconductor quantum dots and nanorods were investigated using a density matrix formalism for the field-dependent nonlinear mobility. The charge dynamics represented by the resultant master equations can be cast in an analytical formula for the field-dependent charge carrier mobility, e.g. for two-level systems. Our equation extends the Kubo–Greenwood result of linear response theory to nonlinear processes at elevated field strength. We have demonstrated strong field strength, chirp, temperature and dephasing dependence of the charge carrier mobility on CdSe quantum dots and wires, especially in the nonlinear regime. Stark broadening and Rabi splitting result in pronounced alterations of the mobility spectra. We have found the possibility of THz gain in the semiconductor nanostructures based on intra pulse frequency mixing by third order nonlinearities. The nonlinear changes are strongest for strongly chirped pulses at low temperatures and depend weaker on the THz pulse carrier-envelope phase. The findings are of immediate interest e.g. for nonlinear THz generation and conversion in 6G technology and nano electronics. Tunable and intense THz sources e.g. from laser difference frequency mixing,70,71 plasms,72 on chip nonlinear mixing73 or quantum cascade lasers74 are interesting for implementation into future 6G communication systems with carrier frequencies operating in frequency ranges of ∼300 GHz to 10 THz.75,76 Nonlinear frequency conversion and gain in semiconductor nanostructures, like demonstrated in this paper may provide the needed functionalities for signal mixing and amplification. As we have shown, selective gain regions within the pulse spectrum can occur so that intra-pulse amplification of THz signals at moderate THz field strength in a finite spectral region and potentially lasing may be feasible, an aspect potentially usable for amplifiers or signal recovery in data links. Ultrafast, nonlinear THz imaging techniques77 may benefit from particles with high THz nonlinarities, like the presented dots and wires, and the gained understanding of how to model and tune their properties. Furthermore, the presented formalism and simple analytical expressions offer experimentalists the ability to analyze nonlinear transport phenomena35 and interpret the frequency-dependent conductivity of nano systems in the THz regime to obtain microscopic system parameters as well as design nanosystems with desired material properties.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
A. A. acknowledges support by DFG Grant AC290-2/2.
Notes and references
- J. D. Meindl, Q. Chen and J. A. Davis, Science, 2001, 293, 2044–2049 CrossRef CAS PubMed.
- J. J. Yoo, G. Seo, M. R. Chua, T. G. Park, Y. Lu, F. Rotermund, Y.-K. Kim, C. S. Moon, N. J. Jeon, J.-P. Correa-Baena, V. Bulović, S. S. Shin, M. G. Bawendi and J. Seo, Nature, 2021, 590, 587–593 CrossRef CAS PubMed.
- J. Y. Kim, J.-W. Lee, H. S. Jung, H. Shin and N.-G. Park, Chem. Rev., 2020, 120, 7867–7918 CrossRef CAS PubMed.
- M. Mittendorff, S. Winnerl and T. E. Murphy, Adv. Opt. Mater., 2021, 9, 2001500 CrossRef CAS.
- K. Sengupta, T. Nagatsuma and D. M. Mittleman, Nat. Electron., 2018, 1, 622–635 CrossRef.
- M. Pelton, Nat. Photonics, 2015, 9, 427–435 CrossRef CAS.
- L. T. Kunneman, J. M. Schins, S. Pedetti, H. Heuclin, F. C. Grozema, A. J. Houtepen, B. Dubertret and L. D. A. Siebbeles, Nano Lett., 2014, 14, 7039–7045 CrossRef CAS PubMed.
- H. Liu, J. Lu, Z. Yang, J. Teng, L. Ke, X. Zhang, L. Tong and C. H. Sow, Sci. Rep., 2016, 6, 27387 CrossRef CAS PubMed.
- M. C. Beard, G. M. Turner and C. A. Schmuttenmaer, Nano Lett., 2002, 2, 983–987 CrossRef CAS.
- C. He, L. Zhu, Q. Zhao, Y. Huang, Z. Yao, W. Du, Y. He, S. Zhang and X. Xu, Adv. Opt. Mater., 2018, 6, 1800290 CrossRef.
- M. Helm, T. Fromherz, B. N. Murdin, C. R. Pidgeon, K. K. Geerinck, N. J. Hovenyer, W. T. Wenckebach, A. F. G. van der Meer and P. W. van Amersfoort, Appl. Phys. Lett., 1993, 63, 3315–3317 CrossRef CAS.
- D. Zhao and E. E. M. Chia, Adv. Opt. Mater., 2020, 8, 1900783 CrossRef CAS.
- X. Zou, J. Luo, D. Lee, C. Cheng, D. Springer, S. K. Nair, S. A. Cheong, H. J. Fan and E. E. M. Chia, J. Phys. D: Appl. Phys., 2012, 45, 465101 CrossRef.
- J. B. Baxter and C. A. Schmuttenmaer, J. Phys. Chem. B, 2006, 110, 25229–25239 CrossRef CAS PubMed.
- J. Lauth, A. Kulkarni, F. C. M. Spoor, N. Renaud, F. C. Grozema, A. J. Houtepen, J. M. Schins, S. Kinge and L. D. A. Siebbeles, J. Phys. Chem. Lett., 2016, 7, 4191–4196 CrossRef CAS PubMed.
- H. J. Joyce, J. L. Boland, C. L. Davies, S. A. Baig and M. B. Johnston, Semicond. Sci. Technol., 2016, 31, 103003 CrossRef.
- R. A. Kaindl, D. Hägele, M. A. Carnahan and D. S. Chemla, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 045320 CrossRef.
- G. Folpini, L. Gatto, D. Cortecchia, M. Devetta, G. Crippa, C. Vozzi, S. Stagira, A. Petrozza and E. Cinquanta, J. Chem. Phys., 2020, 152, 214705 CrossRef CAS PubMed.
- P. Han, X. Wang and Y. Zhang, Adv. Opt. Mater., 2021, 8, 1900533 CrossRef.
- P. Parkinson, J. Lloyd-Hughes, Q. Gao, H. H. Tan, C. Jagadish, M. B. Johnston and L. M. Herz, Nano Lett., 2007, 7, 2162–2165 CrossRef CAS.
- G. R. Yettapu, D. Talukdar, S. Sarkar, A. Swarnkar, A. Nag, P. Ghosh and P. Mandal, Nano Lett., 2016, 16, 4838–4848 CrossRef CAS PubMed.
- H. Hempel, T. J. Savenjie, M. Stolterfoht, J. Neu, M. Failla, V. C. Paingad, P. Kužel, E. J. Heilweil, J. A. Spies, M. Schleuning, J. Zhao, D. Friedrich, K. Schwarzburg, L. D. Siebbeles, P. Dörflinger, V. Dyakonov, R. Katoh, M. J. Hong, J. G. Labram, M. Monti, E. Butler-Caddle, J. Lloyd-Hughes, M. M. Taheri, J. B. Baxter, T. J. Magnanelli, S. Luo, J. M. Cardon, S. Ardo and T. Unold, Adv. Energy Mater., 2022, 12, 2102776 CrossRef CAS.
- H. A. Hafez, S. Kovalev, J.-C. Deinert, Z. Mics, B. Green, N. Awari, M. Chen, S. Germanskiy, U. Lehnert, J. Teichert, Z. Wang, K.-J. Tielrooij, Z. Liu, Z. Chen, A. Narita, K. Müllen, M. Bonn, M. Gensch and D. Turchinovich, Nature, 2018, 561, 507–511 CrossRef CAS PubMed.
- O. Schubert, M. Hohenleutner, F. Langer, B. Urbanek, C. Lange, U. Huttner, D. Golde, T. Meier, M. Kira, S. W. Koch and R. Huber, Nat. Photonics, 2014, 8, 119–123 CrossRef CAS.
- U. Arregui Leon, L. Carletti, D. Rocco, C. De Angelis and G. Della Valle, Laser Photonics Rev., 2023, 2300669 Search PubMed.
- R. Ulbricht, E. Hendry, J. Shan, T. F. Heinz and M. Bonn, Rev. Mod. Phys., 2011, 83, 543–586 CrossRef CAS.
- J. Lloyd-Hughes and T.-I. Jeon, J. Infrared Millim. Terahertz Waves, 2012, 33, 871–925 CrossRef CAS.
- W. H. Evers, J. M. Schins, M. Aerts, A. Kulkarni, P. Capiod, M. Berthe, B. Grandidier, C. Delerue, H. S. J. van der Zant, C. van Overbeek, J. L. Peters, D. Vanmaekelbergh and L. D. A. Siebbeles, Nat. Commun., 2015, 6, 8195 CrossRef CAS PubMed.
- P. Kužel and H. Němec, Adv. Opt. Mater., 2020, 8, 1900623 CrossRef.
- T. L. Cocker, D. Baillie, M. Buruma, L. V. Titova, R. D. Sydora, F. Marsiglio and F. A. Hegmann, Phys. Rev. B, 2017, 96, 205439 CrossRef.
- A. W. Achtstein, N. Owschimikow and M. T. Quick, Nanoscale, 2022, 14, 19–25 RSC.
- M. T. Quick and A. W. Achtstein, J. Phys. Chem. C, 2023, 127, 24591–24597 CrossRef CAS.
- J. Kucharik and J. Nemec, Phys. Rev. B, 2021, 103, 205426 CrossRef CAS.
- M. T. Quick, Q. Wach, N. Owschimikow and A. W. Achtstein, Adv.
Photonics Res., 2023, 4, 2200243 CrossRef CAS.
- R. Rana, L. Balaghi, I. Fotev, H. Schneider, M. Helm, E. Dimakis and A. Pashkin, Nano Lett., 2020, 20, 3225–3231 CrossRef CAS PubMed.
- Z. Mics, K.-J. Tielrooij, K. Parvez, S. A. Jensen, I. Ivanov, X. Feng, K. Müllen, M. Bonn and D. Turchinovich, Nat. Commun., 2015, 6, 7655 CrossRef CAS PubMed.
- M. T. Quick, S. Ayari, N. Owschimikow, S. Jaziri and A. W. Achtstein, ACS Appl. Nano Mater., 2022, 5, 8306–8313 CrossRef CAS.
- M. T. Quick, S. Ayari, N. Owschimikow, S. Jaziri and A. W. Achtstein, Phys. Chem. Chem. Phys., 2023, 25, 3354–3360 RSC.
- T. Ostatnický, V. Pushkarev, H. Němec and P. Kužel, Phys. Rev. B, 2018, 97, 085426 CrossRef.
-
S. Mukamel, Principles of Nonlinear Optical Spectroscopy, Oxford University Press, 1995 Search PubMed.
-
S. C. Rand, Lectures on Light, Oxford University Press, 2nd edn, 2016 Search PubMed.
-
B. Kramer, Advances in Solid State Physics, Springer, 2003 Search PubMed.
-
R. W. Boyd, Nonlinear Optics, Academic Press, 2008 Search PubMed.
- U. Bockelmann and G. Bastard, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 8947 CrossRef CAS PubMed.
- A. Alcalde, G. Marques, G. Weber and T. Reinecke, Solid State Commun., 2000, 116, 247–252 CrossRef CAS.
- S. Arshia Khatoon, M. Ansari, S. Ashraf and M. Obaidurrahman, J. Appl. Phys., 2021, 129, 014308 CrossRef CAS.
- M. Makkar, L. Moretti, M. Maiuri, G. Cerullo and R. Viswanatha, J. Phys. Mater., 2021, 4, 034005 CrossRef CAS.
-
G. D. Mahan, Many-particle physics, Springer Science & Business Media, 2000 Search PubMed.
-
G. Mahan, Proc. 1971 Antwerp Advanced Study Inst., 1972, pp. 553–657.
- A. W. Achtstein, S. Ayari, S. Helmrich, M. T. Quick, N. Owschimikow, S. Jaziri and U. Woggon, Nanoscale, 2020, 12, 23521–23531 RSC.
- M. Pugnet, J. Collet and A. Cornet, Solid State Commun., 1981, 38, 531–536 CrossRef CAS.
- P. Zhao and D. L. Woolard, Phys. Lett. A, 2008, 372, 1666–1670 CrossRef CAS.
-
J.-C. Diels and W. Rudolph, Ultrashort Laser Pulse Phenomena, Academic Press, 2006 Search PubMed.
- C. Maes, Aip Conf. Proc., 2020, 8, 2296–424X Search PubMed.
-
R. Zwanzig, Nonequilibrium Statistical Mechanics, Oxford University Press, 2001 Search PubMed.
-
C. Lang and N. Pucker, Mathematische Methoden in der Physik, Spektrum Verlag, 2005 Search PubMed.
- M. T. Quick, N. Owschimikow and A. W. Achtstein, J. Phys. Chem. Lett., 2021, 12, 7688–7695 CrossRef CAS PubMed.
- J. Lauth, S. Kinge and L. D. Siebbeles, Z. Phys. Chem., 2017, 231, 107–119 CrossRef CAS.
- R. Tomar, A. Kulkarni, K. Chen, S. Singh, D. van Thourhout, J. M. Hodgkiss, L. D. Siebbeles, Z. Hens and P. Geiregat, J. Phys. Chem. C, 2019, 123, 9640–9650 CrossRef CAS.
- R. Kaindl, D. Haegele, M. Carnahan, R. Loevenich and D. Chemla, Phys. Status Solidi B, 2003, 238, 451–454 CrossRef CAS.
-
J. P. Dahl, Introduction to the Quantum World of Atoms and Molecules, World Scientific, 2001 Search PubMed.
-
I. R. Afnan, Quantum Mechanics with Applications, Bentham Science Publishers, 2018 Search PubMed.
-
D. J. Griffiths, Introduction to Quantum Mechanics, Pearson Prentice Hall, 2nd edn, 2004 Search PubMed.
- I. G. Koprinkov, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 3679 CrossRef CAS.
- A. Santana, J. M. G. Llorente and V. Delgado, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 2371 CrossRef CAS.
- A. V. Bogatskaya, E. A. Volkova and A. M. Popov, Phys. Rev. E, 2021, 104, 025202 CrossRef CAS PubMed.
- D. You and P. H. Bucksbaum, J. Opt. Soc. Am. B, 1997, 14, 1651–1655 CrossRef CAS.
- Z. Wang, H. Liu, N. Huang, Q. Sun and J. Wen, Opt. Express, 2012, 20, 8920–8928 CrossRef CAS PubMed.
- B. Liu, H. Bromberger, A. Cartella, T. Gebert, M. Först and A. Cavalleri, Opt. Lett., 2017, 42, 129–131 CrossRef CAS PubMed.
- Y. Liu, K. Zhong, A. Wang, M. Zhou, S. Li, L. Gao and Z. Zhang, Crystals, 2022, 12, 936 CrossRef CAS.
- S. Y. Tochitsky, C. Sung, S. E. Trubnick, C. Joshi and K. L. Vodopyanov, J. Opt. Soc. Am. B, 2007, 24, 2509–2516 CrossRef CAS.
- M. Kumar, K. Lee, S. Hee Park, Y. Uk Jeong and N. Vinokurov, Phys. Plasmas, 2017, 24, 033104 CrossRef.
- J. Bravo-Abad, A. W. Rodriguez, J. D. Joannopoulos, P. T. Rakich, S. G. Johnson and M. Soljačić, Appl. Phys. Lett., 2010, 96, 101110 CrossRef.
- L. Gao, C. Feng and X. Zhao, Nanotechnol. Rev., 2023, 12, 20230115 CrossRef CAS.
- A. Leitenstorfer, A. S. Moskalenko, T. Kampfrath, J. Kono, E. Castro-Camus, K. Peng, N. Qureshi, D. Turchinovich, K. Tanaka, A. G. Markelz, M. Havenith, C. Hough, H. J. Joyce, W. J. Padilla, B. Zhou, K.-Y. Kim, X.-C. Zhang, P. U. Jepsen, S. Dhillon, M. Vitiello, E. Linfield, A. G. Davies, M. C. Hoffmann, R. Lewis, M. Tonouchi, P. Klarskov, T. S. Seifert, Y. A. Gerasimenko, D. Mihailovic, R. Huber, J. L. Boland, O. Mitrofanov, P. Dean, B. N. Ellison, P. G. Huggard, S. P. Rea, C. Walker, D. T. Leisawitz, J. R. Gao, C. Li, Q. Chen, G. Valušis, V. P. Wallace, E. Pickwell-MacPherson, X. Shang, J. Hesler, N. Ridler, C. C. Renaud, I. Kallfass, T. Nagatsuma, J. A. Zeitler, D. Arnone, M. B. Johnston and J. Cunningham, J. Phys. D: Appl. Phys., 2023, 56, 223001 CrossRef.
- W. Jiang, Q. Zhou, J. He, M. A. Habibi, S. Melnyk, M. El-Absi, B. Han, M. D. Renzo, H. D. Schotten, F.-L. Luo, T. S. El-Bawab, M. Juntti, M. Debbah and V. C. M. Leung, IEEE Commun. Surveys Tutorials, 2024, 1 Search PubMed.
- L. Olivieri, J. S. Totero Gongora, A. Pasquazi and M. Peccianti, ACS Photonics, 2018, 5, 3379–3388 CrossRef CAS.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Michael T.
Quick
a,
Sabrine
Ayari
b and
Alexander W.
Achtstein
a,
Michael T.
Quick
a,
Sabrine
Ayari
b and
Alexander W.
Achtstein
 *ac
*ac
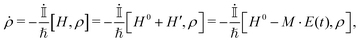



 is given by Fermi's golden rule:
is given by Fermi's golden rule:
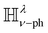 is the electron/hole phonon interaction Hamiltonian. The upper sign corresponds to emission and the lower sign to the absorption of a phonon. In non-centrosymmetric materials, the coupling to acoustic phonons arises from both the deformation potential and the piezoelectric coupling mechanisms.48,49 However, different studies on CdSe nanomaterials have shown that the acoustic phonon scattering mechanisms are dominated by deformation potential interaction rather than piezoelectric coupling.48–52 As we focus on dot-like and short rod-like CdSe quantum structures treated as quantum boxes characterized by discrete densities of state, we will omit the consideration of optical phonons in our investigation. In fact, in contrast to acoustic phonons, optical phonons have no continuous-energy spectrum in our dispersionless approach. For a OD system, the discrete electron and LO phonon energies don't have any first-order (Frohlich) interaction, except for the special cases Ef − Ei = ELO, so that the scattering rates are low and we do not consider them. Hence, we will consider only the electron-longitudinal acoustic (LA) phonon scattering. We remark that the intention of this paper is to study the basics of nonlinear charge transport physics and not a refined model for all kinds of phonon related processes in the considered nanostructures. Within our acoustic deformation potential approach eqn (5) turns into
is the electron/hole phonon interaction Hamiltonian. The upper sign corresponds to emission and the lower sign to the absorption of a phonon. In non-centrosymmetric materials, the coupling to acoustic phonons arises from both the deformation potential and the piezoelectric coupling mechanisms.48,49 However, different studies on CdSe nanomaterials have shown that the acoustic phonon scattering mechanisms are dominated by deformation potential interaction rather than piezoelectric coupling.48–52 As we focus on dot-like and short rod-like CdSe quantum structures treated as quantum boxes characterized by discrete densities of state, we will omit the consideration of optical phonons in our investigation. In fact, in contrast to acoustic phonons, optical phonons have no continuous-energy spectrum in our dispersionless approach. For a OD system, the discrete electron and LO phonon energies don't have any first-order (Frohlich) interaction, except for the special cases Ef − Ei = ELO, so that the scattering rates are low and we do not consider them. Hence, we will consider only the electron-longitudinal acoustic (LA) phonon scattering. We remark that the intention of this paper is to study the basics of nonlinear charge transport physics and not a refined model for all kinds of phonon related processes in the considered nanostructures. Within our acoustic deformation potential approach eqn (5) turns into
 is the overlap integral in η = x, y, z direction, ni(f)η is the initial(final) state quantum number in η direction. We will consider in our work an infinitely deep, rectangular quantum box. α(q)2 = Dν2ħωq/2ρdcs2V, where V = LxLyLz is the principal volume of the nanocrystal, Dν is the acoustic deformation potential, ρd is the mass density, ωq = csq is the long wave approximation of the acoustic phonon dispersion, and cs is the sound velocity in the material. See (ESI,† Section S1) for further details. Tables S1–S6 (ESI†) display the calculated electron (hole) acoustic phonon scattering rates for three different CdSe nanoparticle sizes (6 × 6 × 6 nm3, 20 × 6 × 6 nm3 and 40 × 6 × 6 nm3) for several transitions and three different temperatures T = 10, 70 and 300 K. We approximate our nanosystems as four-level systems in the THz range, since the relevant transitions fall in the typically observed range in (broadband) THz probe experiments. Tables S1–S6 (ESI†) show the size and transition energy dependence of scattering rates. The coupling to acoustic phonons decreases with the nanoparticles size and increases with decreasing transition energy for fixed size. The calculated scattering rates are then implemented in our master equation description. Fig. 1c and d shows the results for the dynamics of populations ρii and polarizations ρij as obtained for 20 nm CdSe rods at 10 K. With these results the charge carrier mobility on semiconductor nanoparticles is obtained in the following.
is the overlap integral in η = x, y, z direction, ni(f)η is the initial(final) state quantum number in η direction. We will consider in our work an infinitely deep, rectangular quantum box. α(q)2 = Dν2ħωq/2ρdcs2V, where V = LxLyLz is the principal volume of the nanocrystal, Dν is the acoustic deformation potential, ρd is the mass density, ωq = csq is the long wave approximation of the acoustic phonon dispersion, and cs is the sound velocity in the material. See (ESI,† Section S1) for further details. Tables S1–S6 (ESI†) display the calculated electron (hole) acoustic phonon scattering rates for three different CdSe nanoparticle sizes (6 × 6 × 6 nm3, 20 × 6 × 6 nm3 and 40 × 6 × 6 nm3) for several transitions and three different temperatures T = 10, 70 and 300 K. We approximate our nanosystems as four-level systems in the THz range, since the relevant transitions fall in the typically observed range in (broadband) THz probe experiments. Tables S1–S6 (ESI†) show the size and transition energy dependence of scattering rates. The coupling to acoustic phonons decreases with the nanoparticles size and increases with decreasing transition energy for fixed size. The calculated scattering rates are then implemented in our master equation description. Fig. 1c and d shows the results for the dynamics of populations ρii and polarizations ρij as obtained for 20 nm CdSe rods at 10 K. With these results the charge carrier mobility on semiconductor nanoparticles is obtained in the following.




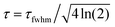 .
.
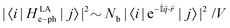 can be expanded for small wave vectors
can be expanded for small wave vectors ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) , so that we see for a transition i ≠ j
, so that we see for a transition i ≠ j


 the first resonance occurs at 42 THz outside of the THz window any common experimental setup can provide. With that in mind, even at RT only the ground state is populated, so that the single line of width wL = 2.37 ps−1 leaves no detectable real part in the 0–8 THz window, while the initial slope of the pole function in the imaginary part appears to be linear.
the first resonance occurs at 42 THz outside of the THz window any common experimental setup can provide. With that in mind, even at RT only the ground state is populated, so that the single line of width wL = 2.37 ps−1 leaves no detectable real part in the 0–8 THz window, while the initial slope of the pole function in the imaginary part appears to be linear.
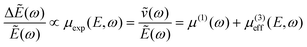

 for the perturbative regime of interaction.63 Further, we expand the decay contribution in the same manner Rij = R(0)ij + λR(1)ij + λ2R(2)ij + λ3R(3)ij. Sorting the respective terms by orders of λ, we find the q-th order off-diagonal elements to evolve according to
for the perturbative regime of interaction.63 Further, we expand the decay contribution in the same manner Rij = R(0)ij + λR(1)ij + λ2R(2)ij + λ3R(3)ij. Sorting the respective terms by orders of λ, we find the q-th order off-diagonal elements to evolve according to

![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) (3)ij. The less distributed a population is among states prior to perturbation, the more scattered it can become among all relevant levels during heavy excitation. This constitutes a new situation, which is then immediately probed by the same THz field. At 10 K (Fig. 3a and d) we can approach best, what is seen. Ignoring the lineshape for a moment, we crudely recognize the light curves (constituting the lone |1〉 → |2〉 resonance at 3.8 THz) decrease, while another is emerging at ∼6.3 THz – the |2〉 → |3〉 transition. The same phenomenon, however in a weakened form, can be observed for higher temperatures: low-frequency absorption and dispersion bands are weakened and resonances occur at higher energies (Fig. 3b and e and c and f). Elevated temperatures also include higher levels, which brings the system closer and closer to the state of equal occupation of individual levels. The graphs in Fig. 3(c) and (f) describe the same finding, but over a frequency range outside 0–8 THz.
(3)ij. The less distributed a population is among states prior to perturbation, the more scattered it can become among all relevant levels during heavy excitation. This constitutes a new situation, which is then immediately probed by the same THz field. At 10 K (Fig. 3a and d) we can approach best, what is seen. Ignoring the lineshape for a moment, we crudely recognize the light curves (constituting the lone |1〉 → |2〉 resonance at 3.8 THz) decrease, while another is emerging at ∼6.3 THz – the |2〉 → |3〉 transition. The same phenomenon, however in a weakened form, can be observed for higher temperatures: low-frequency absorption and dispersion bands are weakened and resonances occur at higher energies (Fig. 3b and e and c and f). Elevated temperatures also include higher levels, which brings the system closer and closer to the state of equal occupation of individual levels. The graphs in Fig. 3(c) and (f) describe the same finding, but over a frequency range outside 0–8 THz.

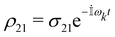 and (iv) up-scattering is non-existent Γ21 (due to ρ11 being the ground state), while (v) Γ12 is slow. Many of these approximations can not be applied rigorously in the THz regime, hence the matrix master equations remain coupled at all times. However, at low temperature, where relaxation and dephasing become increasingly lower we can ask for the steady-state solution of the system (eqn (19) and (20) above) under quasi-resonant excitation E(t) ∼ E0
and (iv) up-scattering is non-existent Γ21 (due to ρ11 being the ground state), while (v) Γ12 is slow. Many of these approximations can not be applied rigorously in the THz regime, hence the matrix master equations remain coupled at all times. However, at low temperature, where relaxation and dephasing become increasingly lower we can ask for the steady-state solution of the system (eqn (19) and (20) above) under quasi-resonant excitation E(t) ∼ E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt). This allows to deduce general properties expected upon growing coupling strength. Making use of ref. 43, we find
cos(ωt). This allows to deduce general properties expected upon growing coupling strength. Making use of ref. 43, we find
 , we find
, we find

![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (3)21 in the frequency domain
(3)21 in the frequency domain
 by the double integral term above. Further, the evaluation of the velocity expectation value is carried out by reinterpreting the relative displacement xij from eqn (16) through xij = −Mij/qe. Again, being reminded that FT{E(t)} = E0FT{Ē(t)} = E0Ẽ(ω), we finally write
by the double integral term above. Further, the evaluation of the velocity expectation value is carried out by reinterpreting the relative displacement xij from eqn (16) through xij = −Mij/qe. Again, being reminded that FT{E(t)} = E0FT{Ē(t)} = E0Ẽ(ω), we finally write
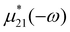 denote the resonant and antiresonant contribution to μexp(ω). Closely inspecting the resulting complex mobility function reveals several properties that could easily be overlooked. Firstly, as we would expect, the overall spectrum is build from a linear spectrum that is successively diminished by a growing nonlinear contribution scaling with the squared Rabi frequency Ω2. Usually, in the optical regime large electric field strengths deem necessary to introduce nonlinearities to the measurement. In the THz regime, especially for nanostructures, the large transition dipole moments (often corresponding to several nm of charge displacement) impact the measurements already at low E0, as seen in Fig. 3. With eqn (25) we have a new equation for the frequency-dependent mobility in nanosystems including nonlinear third order interaction being present at elevated field strength. Our finding reproduces the linear extended Kubo–Greenwood equation recently discovered,32 in the weak field limit of linear response theory (Ω → 0)
denote the resonant and antiresonant contribution to μexp(ω). Closely inspecting the resulting complex mobility function reveals several properties that could easily be overlooked. Firstly, as we would expect, the overall spectrum is build from a linear spectrum that is successively diminished by a growing nonlinear contribution scaling with the squared Rabi frequency Ω2. Usually, in the optical regime large electric field strengths deem necessary to introduce nonlinearities to the measurement. In the THz regime, especially for nanostructures, the large transition dipole moments (often corresponding to several nm of charge displacement) impact the measurements already at low E0, as seen in Fig. 3. With eqn (25) we have a new equation for the frequency-dependent mobility in nanosystems including nonlinear third order interaction being present at elevated field strength. Our finding reproduces the linear extended Kubo–Greenwood equation recently discovered,32 in the weak field limit of linear response theory (Ω → 0)
 (in the 2-level approximation), we can determine the eigenvalues, reading
(in the 2-level approximation), we can determine the eigenvalues, reading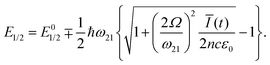



![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif)