 Open Access Article
Open Access ArticleUnexpected longer T1 lifetime of 6-sulfur guanine than 6-selenium guanine: the solvent effect of hydrogen bonds to brake the triplet decay†
Shaoting
Liu
ab,
Yuhsuan
Lee
bc,
Lingfang
Chen
bc,
Jingheng
Deng
b,
Tongmei
Ma
*a,
Mario
Barbatti
 *de and
Shuming
Bai
*de and
Shuming
Bai
 *bc
*bc
aSchool of Chemistry and Chemical Engineering, South China University of Technology, Guangzhou 510641, China. E-mail: tongmei@scut.edu.cn
bBeijing National Laboratory for Molecular Sciences, State Key Laboratory for Structural Chemistry of Unstable and Stable Species, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China. E-mail: baishuming@iccas.ac.cn
cUniversity of Chinese Academy of Sciences, Beijing 100049, China
dAix Marseille University, CNRS, ICR, 13397 Marseille, France. E-mail: mario.barbatti@univ-amu.fr
eInstitut Universitaire de France, Paris 75231, France
First published on 15th April 2024
Abstract
The decay of the T1 state to the ground state is an essential property of photosensitizers because it decides the lifetime of excited states and, thus, the time window for sensitization. The sulfur/selenium substitution of carbonyl groups can red-shift absorption spectra and enhance the triplet yield because of the large spin–orbit coupling, modifying nucleobases to potential photosensitizers for various applications. However, replacing sulfur with selenium will also cause a much shorter T1 lifetime. Experimental studies found that the triplet decay rate of 6-seleno guanine (6SeGua) is 835 times faster than that of 6-thio guanine (6tGua) in aqueous solution. In this work, we reveal the mechanism of the T1 decay difference between 6SeGua and 6tGua by computing the activation energy and spin–orbit coupling for rate calculation. The solvent effect of water is treated with explicit microsolvation and implicit solvent models. We find that the hydrogen bond between the sulfur atom of 6tGua and the water molecule can brake the triplet decay, which is weaker in 6SeGua. This difference is crucial to explain the relatively long T1 lifetime of 6tGua in an aqueous solution. This insight emphasizes the role of solvents in modulating the excited state dynamics and the efficiency of photosensitizers, particularly in aqueous environments.
Introduction
For many photochemical applications such as photodynamic therapy (PDT), photosensitizers (PS) harness specific light wavelengths to form reactive excited states and generate reactive oxygen species (ROS), such as superoxide anions and singlet oxygen (1O2).1 The active products of the process of molecular excited-state dynamics can selectively destroy targeted aberrant cells, offering an effective therapeutic modality. A potential photosensitizer should strongly absorb in the 600–900 nm therapeutic window for deep penetration. It should also have enough energy to produce ROS, a high quantum yield of the reactive T1 state, a long lifetime of the T1 state, and low biotoxicity.2–4 The natural nucleobases have ultrafast excitation relaxation processes because of the barrierless conical intersection between the excited and the ground states,5,6 and this fast decaying to the ground state prevents photodamage. It protects life under light but excludes these canonical biomolecules from photosensitizer candidates. Through a simple chemical modification by replacing the oxygen atom with a sulfur atom, the derivative thiobases become potential photosensitizers with near-unity triplet yields. Starting from the photoexcited bright state, a typical “S2 → S1 → T2 → T1” ultrafast process as a mixture of internal conversion and intersystem crossing has been discovered as the dominant relaxation pathway for thionucleobases.7 The ultrafast S1 → T2/T1 intersystem crossing among bio-organic molecules comes from the near-degeneracy state energies and the enhanced spin–orbit couplings in thiobases.8,9With the yield of the triplet state near unity, the performance of thiobases as a photosensitizer is mainly determined by the subsequent steps starting from the T1 state. Among them, the T1 decay to the singlet ground state is the dominant competing pathway of photosensitization. In our previous work, we have developed high-level quantum chemical modeling of the T1 decay dynamics of thionucleobases using a two-step model, and the theoretical results quantitatively agree with experiments very well.10,11 The featured double-well topography of the T1 state of thionucleobases was theoretically found and soon confirmed by a specifically designed experiment and other theoretical studies.12,13
Beyond the substitution with sulfur, incorporating selenium into nucleobases has recently been explored for photosensitization.14,15 Leveraging the heavier atom effect and lower electronegativity of the selenium atom, selenonucleobases are expected to have larger spin–orbit couplings with higher triplet yield, and red-shifted absorption, aiming for better photosensitizers. Although experimental and theoretical research has confirmed these advantages, Crespo-Hernandez et al. found that 6-selenoguanine has a much shorter T1 lifetime than 6-thioguanine by 835 times in aqueous solution.14 This factor may cripple their performance as photosensitizers.
Recently, there have been theoretical studies on simulating the excited dynamics after photoexcitation of selenonucleobases such as 6-selenoguanine and 2-selenouracil.16–18 Similar to the thionucleobases, “S2 → S1 → T2 → T1” is still the main pathway for the excitation relaxation process.19,20 T1 decay dynamics was involved, and the difference between the thio- and seleno-derivatives was qualitatively explained. However, there is still a lack of theoretical research focusing on the triplet decay dynamics, especially tackling the solvent effect with an explicit solvent model. The solvent effect is a potential factor affecting photoinduced excited-state spectroscopy and dynamics, especially when the charge transfer is involved.21–23 Although during the intersystem crossing, the molecule remains charge-neutral, both experimental and theoretical studies have found that the solvent effect appears when singlet–triplet energy gaps and reorganization energies are changed.24–26
In this work, we focus on the difference between the T1 decay dynamics of 6tGua and 6SeGua, whose structures are shown in Fig. 1. Based on the quantum chemical calculations, we first obtained the triplet decay pathways of these two molecules. Then, we investigated the solvent effect with explicit microsolvation and implicit solvent models. It is confirmed that both 6tGua and 6SeGua have similar deactivation channels, and the calculation of the decay rate quantitatively reveals the roles of spin–orbit coupling (SOC) and activation energy in the rate difference. An interesting finding is that the hydrogen bond between the water and the 6tGua, which is much stronger than that of 6SeGua, is essential to causing the different T1 decay between them.
Computational details
Geometry optimizations of the ground and excited states were computed with density functional theory (DFT), Tamm–Dancoff approximation density functional theory (TDA-DFT),27 and the algebraic diagrammatic construction to second order (ADC(2)).28 ADC(2)/aug-cc-pVDZ calculations were done for T1 optimizations and the energy profiles between two T1 minima in the gas phase using the Turbomole program.29 The results are taken as the reference for the unrestricted DFT and TDA-DFT calculations. DFT and TDA-DFT calculations were done using the B3LYP30 functional, the aug-cc-pVDZ basis set for excited energies and the cc-pVDZ basis set for geometry optimization,31,32 all of which are carried out using the Gaussian 09 program.33 The implicit solvent model was executed using the polarizable continuum model (PCM).34 Structures of crossing points were optimized using an in-house modified version of the CIOpt program35 at the DFT and TDA-DFT levels, with the energy gap smaller than 0.02 eV. Cartesian coordinates of all optimized structures are given in the ESI† (Section S1).The matrix elements of spin–orbit couplings (SOCs) were calculated using the Breit-Pauli spin–orbit Hamiltonian with effective charge approximation, as implemented in the PySOC program interfaced using the Gaussian 09 program.36,37 The effective SOCs are given as follows:
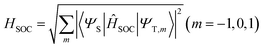 | (1) |
The rate of ISC was calculated using the following quasi-Marcus formula:10,38
 | (2) |
Results and discussion
Double-well structure of T1 states
We first optimized the structures of the T1 state of 6tGua and 6SeGua molecules. As found before, the ADC(2) method provides nearly the same description of the T1 state of thionucleobases compared to the MS-CASPT2 method, and 6tGua has a double-well T1 topography.10 Here, we employed ADC(2) to optimize the T1 state for 6tGua and 6SeGua and obtained two T1 minimum structures for each, as shown in Fig. 2. In the first minimum structure, the sulfur/selenium atom exhibits a significant displacement out of the pyrimidine ring plane (op–S and op–Se). The dihedral angle of op–Se is 10° larger than that of op–S. The second minimum structure has a ring-distorted conformation, with N1 moving downward and C6 shifting slightly upward.For both 6tGua and 6SeGua, the op–S/Se T1 minimum has a lower energy than the ring distorted (Fig. 3 top), and the energy gap between them is 0.36 eV in 6tGua and 0.55 eV in 6SeGua. Given the tiny Boltzmann factor of the ring distorted minimum, we can take the op–S/Se structures as the starting point for the T1 decay. Besides, we found in previous studies that the ring-distorted structures of thionucleobases have much higher T1/S0 crossing points and much smaller SOCs than the op–S structure.10 We computed the SOCs at the op–Se/S and ring distorted structures; the latter has much smaller magnitudes (see Table S8 in the ESI†). Thus, we do not need to consider the transition between these two minima and the decay through the ring-distorted structure, and the intersystem crossing from the op–S/Se minima alone determines the triplet decay.
 | ||
| Fig. 3 Potential energy profiles for the lowest triplet states for (a) 6tGua and (b) 6SeGua from ADC(2), TDA-DFT, and DFT calculations. | ||
The energy curves for the S1 state were also computed. They lie above the T1 curves with nearly parallel energy shifts. The T1–S1 shift at op–S structures is narrowed from 0.3 eV for 6tGua to around 0.1 eV for 6SeGua. Considering that most of the excitation will be relaxed to the T1 population and that Fang et al. have shown that the S1–T1 shift increased to about 0.5 eV at the T1/S0 crossing point for 6SeGua,16,18 the S1 state should not play any essential role at this point of the process. However, the possibility of more complicated triplet decay pathways involving the T2 and S1 states for 6SeGua could be further studied in the future. In this study, we still focus on the direct triplet pathway for 6SeGua, the same as for 6tGua.
We then optimized the structures using DFT and TDA-DFT calculations and reproduced the energy profiles. The energy profiles of different quantum chemical methods are shown in Fig. 3 and Fig. S2 in the ESI.† TDA-DFT has been found to describe triplet states better than TD-DFT because the latter suffers from the problem of triplet instability.39–41 The result demonstrates that TDA-DFT calculations with different functionals agree with ADC(2), reproducing the state energies of the ground state and the two lowest triplet excited states very well. The B3LYP and PBE0 functionals perform better than the CAM-B3LYP and ωB97XD functionals. The accuracy for S1 energies from TDA-DFT calculations is not as good as for the triplet energies, especially in the middle between the two minima. Unrestricted DFT calculations show reasonable results for the T1 energies. However, it can only deliver the lowest triplet excited state, and there is a discontinuity point for the triplet energy of 6SeGua at the middle range. Here, the B3LYP functional works better than PBE0, and we will primarily use the former functional for the upcoming DFT calculations.
For the points near op–S of 6tGua, T1 and T2 are nearly parallel with a small gap of ∼0.2 eV. These two states originate from the very close 3ππ* state and the 3nπ* state as found for thiothymine.10 When sulfur is replaced with selenium, this gap decreases to nearly zero. Because of the weaker double-bond between Se and C atoms, the 3nπ* and 3ππ* characters in 6SeGua are less different. Such a small energy gap in 6SeGua was also observed in previous MS-CASPT216,18 and TD-DFT calculations.42,43
Compared to the reference energy profiles of ADC(2), the accuracy of the TDA-DFT and DFT methods is entirely satisfactory. Thus, we will mainly use the TDA-DFT and unrestricted DFT in the subsequent calculations to study the solvent effect with the explicit microsolvation model and profit from their reduced computational cost.
Non-radiative decay of triplet state
For thionucleobases and selenonucleobases with their large spin–orbit couplings, the primary decay of the T1 state is the non-radiative transition of intersystem crossing to their ground states. Using the T1 optimized structure as the initial point, we further optimized the T1/S0 crossing point. Then, we calculated the energy profiles between them by linearly interpolating internal coordinates (LIIC). The results of calculations with distinct solvent models were compared to study the solvent effects on triplet decay dynamics.Energy profiles in Fig. 3 and 4 exhibit that 6tGua and 6SeGua have nearly the same relaxation dynamics from photoexcitation to triplet decay. Similar results have been obtained in previous theoretical work with MS-CASPT2, where the solvent effect was considered under an implicit solvent model.44 The solvent effect does not change the non-radiative decay pathway, including the S1 → T1 intersystem crossing and the T1 → S0 triplet decay. For the latter, the T1 state reaches the T1/S0 crossing point with a low energy barrier, and the large spin–orbit coupling contributes to the occurrence of the intersystem crossing.
During the decay process, the conformation of 6tGua and 6SeGua changes similarly: The structures of the S0 minima are planar. The T1 structures have the sulfur/selenium atom out of the plane at an angle of 158.2°/152.9°. Then, the dihedral angle decreases to 94.5°/103.6° at the T1/S0 crossing point.
We applied the quasi-Marcus theory described in eqn (2) to calculate the decay rate and investigate the effects of heavier atom replacement with sulfur and selenium and the solvent effect. These rates depend on three critical factors, the reorganization energy λ, SOC, and the activation energy ΔE*.
We can write the ratio between the rates for 6SeGua and 6tGua given by eqn (2) as:
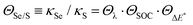 | (3) |
 | (4) |
ΘSOC ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) H2SOC(Se)/H2SOC(S) H2SOC(Se)/H2SOC(S) | (5) |
 | (6) |
Each of these factors is discussed next.
Reorganization energy
The reorganization energy λ is computed as the S0 energy difference between its value at the T1 and the S0 minimum geometries. The S0 energy value is taken instead of the T1 energy because more than one diabatic state (3nπ* and 3ππ* excitation) is involved in the T1 potential energy surface, which may cause anharmonic effects. We computed λ using DFT and TDA-DFT in the gas phase and with implicit PCM. The results are shown in Fig. 5. For 6tGua, λPCM calculated with the PCM model is reduced compared to λgas in the gas phase because the geometry change between the optimized structures of S0 and T1 states is smaller when the solvent effect is involved. On the other hand, λPCM for 6SeGua remains nearly the same, with only a little increase when considering the implicit solvent. When we take one explicit water into the calculation (mono-hydrated complex, as mentioned later), the obtained λ are nearly the same as the ones with the implicit solvent model (see Section S4 of the ESI†). | ||
| Fig. 5 Reorganization energy in the non-radiative triplet decay of (a) 6tGua and (b) 6SeGua at the DFT/B3LYP and TDA-DFT/B3LYP level. Details are showed in ESI† (Section S3). | ||
Considering the solvent effect with the PCM model, the result shows that λPCM of 6SeGua is larger than λPCM of 6tGua. According to eqn (2), the decay rate is affected by λ as 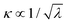 . Substituting Se for S will decrease the rate, with all other things being equal. However, because the λ for thio- and selenobases are in the same order, the impact of the reorganization energy should be limited to a factor Θλ between 0.9 (gas phase) and 0.5 (PCM). Even explicit water inclusion (discussed below) does not change it, delivering Θλ ≈ 0.6. As such, reorganization energy is not among the main origins of the much-enhanced decay rate of 6SeGua compared to 6tGua.
. Substituting Se for S will decrease the rate, with all other things being equal. However, because the λ for thio- and selenobases are in the same order, the impact of the reorganization energy should be limited to a factor Θλ between 0.9 (gas phase) and 0.5 (PCM). Even explicit water inclusion (discussed below) does not change it, delivering Θλ ≈ 0.6. As such, reorganization energy is not among the main origins of the much-enhanced decay rate of 6SeGua compared to 6tGua.
Enhanced spin–orbit coupling
Because of selenium's heavier atomic effect, its larger spin–orbit coupling must enhance the triplet decay rate. We computed SOCs at T1/S0 crossing points with and without solvent effect, and the values of 6tGua and 6SeGua are in the range of 91–112-cm−1 and 496–611 cm−1, respectively (Table 1). No matter whether or not the solvent effect is considered, the Se/S SOC ratio boost is nearly constant at 5.2–5.5. For nonadiabatic coupling calculation, it is known that the Tamm–Dancoff approximation may need extra treatment to maintain accuracy.45,46 Bearing that in mind, we also computed the SOCs at the TD-B3LYP level (see Section S5 in the ESI†). The couplings at the TDA-B3LYP level are systematically about 20% higher than those at the TD-B3LYP level for both 6tGua and 6SeGua, so the ratios remain nearly the same. It is reasonable since spin–orbit coupling originates from the relativistic effect of heavy atoms, and the solvent effect plays a little role there.| T1/S0 crossing | B3LYP | TDA-B3LYP | ||
|---|---|---|---|---|
| SOCs/cm−1 | Gas phase | PCM | Gas phase | PCM |
| 6tGua | 110.5 | 91.5 | 112.2 | 94.2 |
| 6SeGua | 575.7 | 496.1 | 611.0 | 518.7 |
| SOC ratio | 5.2 | 5.4 | 5.4 | 5.5 |
According to eqn (2) (which stems from Fermi's Golden rule), the non-radiative triplet decay is determined by the square of SOCs: κ ∝ H2SOC. Then, the 5.3–5.5 times enhanced SOC of 6SeGua will only cause the decay rate to increase by about a factor of ΘSOC ≈ 29, much less than the experimentally observed rate ratio ΘSe/S = 835. We conclude that the change in SOC contributes to the enhanced triplet decay of 6SeGua, but it must not be the only reason.
Difference in activation energy
All these previous points considered, the difference in activation energy should contribute a factor of to eqn (3) at T = 300 K. Thus, the difference in activation energies ΔE* should be about δΔE* = −0.1 eV.
to eqn (3) at T = 300 K. Thus, the difference in activation energies ΔE* should be about δΔE* = −0.1 eV.
The activation energies were calculated as the T1 energy difference between the optimized structure and the crossing point, and the results are summarized in Table 2. Without the solvent effect, the activation energy from the DFT calculation is 0.32 and 0.28 eV for 6tGua and 6SeGua, respectively. The result of the TDA-DFT calculation is 0.37 and 0.32 eV, respectively.
| Activation energy ΔE*/eV | δΔE*(Se–S)/eV | |||
|---|---|---|---|---|
| 6tGua | 6SeGua | |||
| DFT/B3LYP | Gas phase | 0.32 | 0.28 | −0.04 |
| PCM | 0.33 | 0.29 | −0.04 | |
| Mono-hydrated | 0.44 | 0.36 | −0.08 | |
| TDA-DFT/B3LYP | Gas phase | 0.37 | 0.32 | −0.05 |
| PCM | 0.41 | 0.33 | −0.08 | |
| Mono-hydrated | 0.52 | 0.40 | −0.12 | |
Although the ΔE* values of the two methods are slightly different, the difference between the two molecules, δΔE*, is nearly the same. 6SeGua has smaller activation energy; however, δΔE* = −0.04 or −0.05 eV is not enough to introduce the expected ratio of 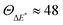 .
.
We first added the solvent effect using an implicit PCM model. ΔE* computed with PCM is 0.33 and 0.29 eV for 6tGua and 6SeGua from DFT calculations, respectively, rendering δΔE* = −0.04 eV, just like in the gas phase. Results from TDA-DFT calculations are 0.41 and 0.33 eV, yielding δΔE* = −0.08 eV, an increase of 0.03 eV from the data in the gas phase.
Finally, we utilized an explicit microsolvation model by introducing a water molecule into the calculation. Although a single water molecule is not representative of bulk water, it has been noticed before that local microsolvation interactions may capture crucial features of the environmental effect when it is dominated by changes in the local electronic structure.47,48
Because the out-of-plane sulfur/selenium motion is mainly involved during triplet decay, we put the water molecule around the S/Se atom in different positions to form a mono-hydrated complex. Two optimized structures are obtained, with water approaching S/Se from two sides (see Section S4 in ESI†). The optimized structures with the lower energies in T1 states are shown in Fig. 6, and they have shorter S–H bond lengths than the other ones. Then, we computed the activation energy with these geometries. The results are listed in Table 2.
Now we see a more significant change in the activation energy difference between 6tGua and 6SeGua, as the DFT calculation gives δΔE* = 0.44 − 0.36 = −0.08 eV, doubly increased from −0.04 eV with implicit model. The TDA-DFT calculation gives δΔE* = 0.52 − 0.40 = −0.12 eV, which is even slightly bigger than the δΔE* = −0.1 eV as we expected to justify the rate change. These results show that explicit microsolvation can provide a bigger activation energy difference than the implicit PCM method, evidencing the crucial effect of the water molecule local interactions.
It is worth noting that the calculated absolute activation energy difference of 6SeGua between PCM (0.29/0.33 eV) and explicit water (0.36/0.40 eV) is 0.07 eV. This same absolute difference in 6tGua is significantly larger, 0.11 eV. It implies that the explicit microsolvation effect originates from local intermolecular interaction between 6tGua and the water molecule, which is weaker or absent in 6SeGua. Thus, this local single-water solvent effect contributes to the higher activation energy of 6tGua, which acts as a brake on triplet decay.
Hydrogen bond between 6tGua and water
The difference in solvent effect originates from the intermolecular interactions with water molecules. Fig. 6 shows a hydrogen atom from the water molecule near the sulfur/selenium atom in hydrated 6tGua/6SeGua, forming a S/Se–H–O structure. This specific structure could form a hydrogen bond. The bond length for S and Se is different. The Se–H bond in hydrated 6SeGua is longer than S–H in hydrated 6tGua, which may be because of the large atom radius of Se or because of the weaker interaction between atoms in the former case.We analyzed the weak intermolecular interactions by employing the independent gradient model based on the Hirschfield partition (IGMH)49 method in conjunction with the wavefunction analysis program Multiwfn,50 as depicted in Fig. 6. The isosurface color signifies the type and strength of interactions, with blue indicating stronger attractive interactions corresponding to hydrogen bond interaction. In contrast, the green color means a regular van der Waals interaction. The hydrogen bond of N1–H–O, clearly signaled with a dark blue color, exists for both 6tGua and 6SeGua.
The light blue surface between S and H for hydrated 6tGua means that a weak S–H–O hydrogen bond exists at the T1 minimum. The bond length of H–S is 2.35 Å, in the range of hydrogen bonds for sulfur atoms.51 Meanwhile, for the structure of the crossing point, the H–S bond is increased to 2.50 Å, and the surface between S and H is just green colored, indicating that the hydrogen bond disappears. Thus, the hydrogen bond interaction stabilizes 6tGua at the initial point of the triplet decay (T1 optimized structure) but not at the crossing point. Consequently, this increases the energy barrier to the T1/S0 crossing point, explaining the further increase of activation energy of 6tGua with an explicit microsolvation model.
For 6SeGua, however, this hydrogen bond effect is much dimmer even at the T1 minimum. Although the Se–H–O structure is formed, the IGMH surface between Se and H is dominated by van der Waals interactions, not a hydrogen bond. The weaker intermolecular interaction with water leads to a smaller ΔE* increase in the microsolvated 6SeGua.
The weaker Se–H–O bond in 6SeGua compared with the S–H–O hydrogen bond stems from the lower electronegativity of the selenium atom.52 This phenomenon has also been found in previous studies, as the pairwise radial distribution function between Sesolute–Hsolvent in the ground and excited states revealed the disruption of hydrogen bonds to the selenium atom upon excitation.20
This analysis shows that hydrogen bond with the S/Se atom contributes less to the triplet decay activation energy in 6SeGua than in 6tGua. This effect of braking the triplet decay contributes to the long triplet lifetime of 6tGua in water. It can only be described well within an explicit solvation model.
To further confirm the role of this hydrogen bond, we have also computed the hydrated complexes with one or two more water molecules (see Section S7 of the ESI†). With the additional water molecules interacting with the ring core of 6tGua/6SeGua, although the N–H hydrogen bond can be formed, the computed activation energies remain nearly the same as those of the corresponding homo-hydrated complexes. We can conclude that only the intermolecular interaction at the sulfur/selenium part changes the triplet decay effectively.
Conclusions
In this work, we have investigated the triplet decay dynamics of 6tGua and 6SeGua, quantitatively explaining the difference in decay rates by calculating the corresponding reorganization energies, spin–orbit couplings, and activation energies. The origin of the marked enhancement of the triplet decay from sulfur to selenium, ΘSe/S = 835, is factorized into three contributions: reorganization energies, the SOCs, and the activation energies, . Reorganization energy plays a minor role (Θλ ≈ 0.6) and most of the effect is dominated by the other two variables. 6SeGua has a large SOC for T1/S0 intersystem crossing than 6tGua by a factor 5.5, resulting in ΘSOC ≈ 29. The remaining rate enhancement is due to the activation energy variation, corresponding to the order of δΔE* = −0.1 eV.
. Reorganization energy plays a minor role (Θλ ≈ 0.6) and most of the effect is dominated by the other two variables. 6SeGua has a large SOC for T1/S0 intersystem crossing than 6tGua by a factor 5.5, resulting in ΘSOC ≈ 29. The remaining rate enhancement is due to the activation energy variation, corresponding to the order of δΔE* = −0.1 eV.
From the calculations in the gas phase and with the implicit solvent effect, the obtained difference in activation energy (0.04–0.08 eV) is insufficient to explain the experimental result. However, when we utilize an explicit microsolvation model by introducing a water molecule to form the mono-hydrated complexes of 6tGua and 6SeGua, the difference in activation energy increases significantly, reaching 0.08–0.12 eV. After analyzing the structure of the hydrated complex, we found that the difference is due to the hydrogen bond between the sulfur atom and the water molecule in 6tGua, which is weaker for the selenium atom in 6SeGua. Hence, the stronger intermolecular interaction from the solvent effect can brake the triplet decay of 6tGua more effectively than 6SeGua.
Our study has contributed to the understanding of the mechanism of enhanced triplet decay caused by selenium replacing sulfur in thioguanine by considering the role of the solvent effect with quantum chemical calculations. Addressing this issue is beneficial for refining the excited state properties of chalcogen-substituted guanines and other nucleobases as photosensitizers. Hydrogen bond interactions with solvents can be essential to affect triplet decay, and an explicit solvent model is required to describe it well. Starting from this point, first, we can predict that in an aprotic solvent where no hydrogen bond can form, the difference of triplet decay between 6SeGua and 6tGua would be smaller than in aqueous solution. Upcoming experiments can verify this prediction directly. Second, the solvent effect provides an extra variable to control the performance of photosensitizers besides the design of the molecule itself. The interplay between these parameters may be a promising strategy to regulate the triplet decay dynamics more effectively.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support from the National Key R & D Program of China (No. 2022YFA1505400) and the National Natural Science Foundation of China (22203098). T. Ma thanks the support from the Guangdong Basic and Applied Basic Research Foundation (No. 2022A1515010334). MB thanks the European Research Council (ERC) Advanced grant SubNano (grant agreement 832237).Notes and references
- D. E. J. G. J. Dolmans, D. Fukumura and R. K. Jain, Nat. Rev. Cancer, 2003, 3, 380–387 CrossRef CAS PubMed.
- T. C. Pham, V.-N. Nguyen, Y. Choi, S. Lee and J. Yoon, Chem. Rev., 2021, 121, 13454–13619 CrossRef CAS PubMed.
- X. Li, S. Lee and J. Yoon, Chem. Soc. Rev., 2018, 47, 1174–1188 RSC.
- S. Kwiatkowski, B. Knap, D. Przystupski, J. Saczko, E. Kędzierska, K. Knap-Czop, J. Kotlińska, O. Michel, K. Kotowski and J. Kulbacka, Biomed. Pharmacother., 2018, 106, 1098–1107 CrossRef PubMed.
- L. Serrano-Andrés and M. Merchán, J. Photochem. Photobiol., C, 2009, 10, 21–32 CrossRef.
- M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallová, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21453–21458 CrossRef CAS PubMed.
- S. Mai, P. Marquetand and L. González, J. Phys. Chem. Lett., 2016, 7, 1978–1983 CrossRef CAS PubMed.
- S. Mai, M. Pollum, L. Martínez-Fernández, N. Dunn, P. Marquetand, I. Corral, C. E. Crespo-Hernández and L. González, Nat. Commun., 2016, 7, 13077 CrossRef CAS PubMed.
- M. Pollum, S. Jockusch and C. E. Crespo-Hernández, J. Am. Chem. Soc., 2014, 136, 17930–17933 CrossRef CAS PubMed.
- S. Bai and M. Barbatti, Phys. Chem. Chem. Phys., 2017, 19, 12674–12682 RSC.
- S. Bai and M. Barbatti, Phys. Chem. Chem. Phys., 2018, 20, 16428–16436 RSC.
- D. Koyama, M. J. Milner and A. J. Orr-Ewing, J. Phys. Chem. B, 2017, 121, 9274–9280 CrossRef CAS PubMed.
- J. A. Sanchez-Rodriguez, A. Mohamadzade, S. Mai, B. Ashwood, M. Pollum, P. Marquetand, L. Gonzalez, C. E. Crespo-Hernandez and S. Ullrich, Phys. Chem. Chem. Phys., 2017, 19, 19756–19766 RSC.
- K. M. Farrell, M. M. Brister, M. Pittelkow, T. I. Sølling and C. E. Crespo-Hernández, J. Am. Chem. Soc., 2018, 140, 11214–11218 CrossRef CAS PubMed.
- M. Prejanò, M. E. Alberto, B. C. De Simone, T. Marino, M. Toscano and N. Russo, Molecules, 2023, 28, 3153 CrossRef PubMed.
- Y.-G. Fang, D. Valverde, S. Mai, S. Canuto, A. C. Borin, G. Cui and L. González, J. Phys. Chem. B, 2021, 125, 1778–1789 CrossRef CAS PubMed.
- M. Xie, S.-x Ren, D. Hu, J.-m Zhong, J. Luo, Y. Tan, Y.-p Li, L.-p Si and J. Cao, Phys. Chem. Chem. Phys., 2023, 25, 27756–27765 RSC.
- Y.-G. Fang, Q. Peng, Q. Fang, W. Fang and G. Cui, ACS Omega, 2019, 4, 9769–9777 CrossRef CAS PubMed.
- S. Mai, A.-P. Wolf and L. González, J. Chem. Theory Comput., 2019, 15, 3730–3742 CrossRef CAS PubMed.
- D. Valverde, S. Mai, S. Canuto, A. C. Borin and L. González, JACS Au, 2022, 2, 1699–1711 CrossRef CAS PubMed.
- A. Petrone, F. Perrella, F. Coppola, L. Crisci, G. Donati, P. Cimino and N. Rega, Chem. Phys. Rev., 2022, 3, 021307 CrossRef CAS.
- G. Kohler and K. Rechthaler, Pure Appl. Chem., 1993, 65, 1647–1652 CrossRef.
- J. Cerezo, A. Petrone, F. J. A. Ferrer, G. Donati, F. Santoro, R. Improta and N. Rega, Theor. Chem. Acc., 2016, 135, 263 Search PubMed.
- Ó. Guzmán-Méndez, M. M. Reza, B. Meza, J. Jara-Cortés and J. Peón, J. Phys. Chem. B, 2023, 127, 5655–5667 CrossRef PubMed.
- A. Muñoz Losa, I. Fdez Galván, M. L. Sánchez, M. E. Martín and M. A. Aguilar, J. Phys. Chem. B, 2008, 112, 877–884 CrossRef PubMed.
- C. M. Marian, Annu. Rev. Phys. Chem., 2021, 72, 617–640 CrossRef CAS PubMed.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- C. Hättig, in Advances in Quantum Chemistry, ed. H. J. Å. Jensen, Academic Press, 2005, vol. 50, pp. 37–60 Search PubMed.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- R. A. Kendall, T. H. Dunning, Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, Jr., J. Chem. Phys., 1999, 110, 7667–7676 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, 2013 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- B. G. Levine, J. D. Coe and T. J. Martínez, J. Phys. Chem. B, 2008, 112, 405–413 CrossRef CAS PubMed.
- S. G. Chiodo and N. Russo, J. Comput. Chem., 2009, 30, 832–839 CrossRef CAS PubMed.
- X. Gao, S. Bai, D. Fazzi, T. Niehaus, M. Barbatti and W. Thiel, J. Chem. Theory Comput., 2017, 13, 515–524 CrossRef CAS PubMed.
- Q. Ou and J. E. Subotnik, J. Phys. Chem. C, 2013, 117, 19839–19849 CrossRef CAS.
- C. Y. Cheng, M. S. Ryley, M. J. G. Peach, D. J. Tozer, T. Helgaker and A. M. Teale, Mol. Phys., 2015, 113, 1937–1951 CrossRef CAS.
- M. J. G. Peach, M. J. Williamson and D. J. Tozer, J. Chem. Theory Comput., 2011, 7, 3578–3585 CrossRef CAS PubMed.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- J. Pirillo, G. Mazzone, N. Russo and L. Bertini, J. Chem. Inf. Model., 2017, 57, 234–242 CrossRef CAS PubMed.
- J. Pirillo, B. C. De Simone and N. Russo, Theor. Chem. Acc., 2015, 135, 8 Search PubMed.
- L. Martínez-Fernández, I. Corral, G. Granucci and M. Persico, Chem. Sci., 2014, 5, 1336–1347 RSC.
- Q. Ou, S. Fatehi, E. Alguire, Y. Shao and J. E. Subotnik, J. Chem. Phys., 2014, 141, 024114 CrossRef PubMed.
- C. Hu, O. Sugino and K. Watanabe, J. Chem. Phys., 2014, 140, 054106 CrossRef PubMed.
- S. Lobsiger, S. Blaser, R. K. Sinha, H.-M. Frey and S. Leutwyler, Nat. Chem., 2014, 6, 989–993 CrossRef CAS PubMed.
- M. Barbatti and H. Lischka, Phys. Chem. Chem. Phys., 2015, 17, 15452–15459 RSC.
- T. Lu and Q. Chen, J. Comput. Chem., 2022, 43, 539–555 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- M. Karthika, L. Senthilkumar and R. Kanakaraju, Struct. Chem., 2012, 23, 1203–1218 CrossRef CAS.
- M. Karthika, L. Senthilkumar and R. Kanakaraju, Struct. Chem., 2014, 25, 197–213 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of optimized structures and definitions of parameters used in eqn (2). See DOI: https://doi.org/10.1039/d4cp00875h |
| This journal is © the Owner Societies 2024 |




