OH-Formation following vibrationally induced reaction dynamics of H₂COO

Abstract

The reaction dynamics of H₂COO to form HCOOH and dioxirane as first steps for OH-elimination is quantitatively investigated. Using a machine learned potential energy surface (PES) at the CASPT2/aug-cc-pVTZ level of theory vibrational excitation along the CH-normal mode ν_CH with energies up to 40.0 kcal mol⁻¹ (∼5ν_CH) leads almost exclusively to HCOOH which further decomposes into OH + HCO. Although the barrier to form dioxirane is only 21.4 kcal mol⁻¹ the reaction probability to form dioxirane is two orders of magnitude lower if the CH-stretch mode is excited. Following the dioxirane-formation pathway is facile, however, if the COO-bend vibration is excited together with energies equivalent to ∼2ν_CH or ∼3ν_COO. For OH-formation in the atmosphere the pathway through HCOOH is probably most relevant because the alternative pathways (through dioxirane or formic acid) involve several intermediates that can de-excite through collisions, relax via internal vibrational relaxation (IVR), or pass through loose and vulnerable transition states (formic acid). This work demonstrates how, by selectively exciting particular vibrational modes, it is possible to dial into desired reaction channels with a high degree of specificity.

---

I. Introduction

The photodissociation dynamics of small molecules is of fundamental interest in atmospheric chemistry. One of the chemically most relevant agents is the hydroxyl radical (OH)¹ which was also referred to as the “detergent of the troposphere”.^2,3 The radical triggers degradation of pollutants including volatile organic compounds (VOCs) and is an important chain initiator in most oxidation processes in the atmosphere. The amount of OH generated from alkene ozonolysis is an important determinant required for chemical models of the lower atmosphere. Field studies have suggested that ozonolysis of alkenes is responsible for the production of about one third of the atmospheric OH radicals during daytime, and is the predominant source of OH radicals at night.^4,5 Alkene ozonolysis proceeds through a 1,3-cycloaddition of ozone across the C=C bond to form a primary ozonide which then decomposes into carbonyl compounds and energized carbonyl oxides, known as Criegee Intermediates (CIs).⁶ These energized intermediates rapidly undergo either unimolecular decay to hydroxyl radicals⁷ or collisional stabilization.⁸ Stabilized CIs can isomerize and decompose into products including the OH radical, or undergo bimolecular reactions with water vapor, SO₂, NO₂ and acids.^9,10

The smallest CI is formaldehyde oxide (H₂COO). Laboratory studies required for a more detailed understanding of the spectroscopy and reaction dynamics¹¹ became possible following successful in situ generation of H₂COO using photolysis of CH₂I₂ in O₂.¹² Earlier computations^13–15 proposed that energized H₂COO can decompose to HCO + OH and H₂CO + O(³P) or isomerize to dioxirane. Access to the HCO + OH channel requires H-transfer to form the HCOOH isomer. The dioxirane and H-transfer pathways are shown in Fig. 1.

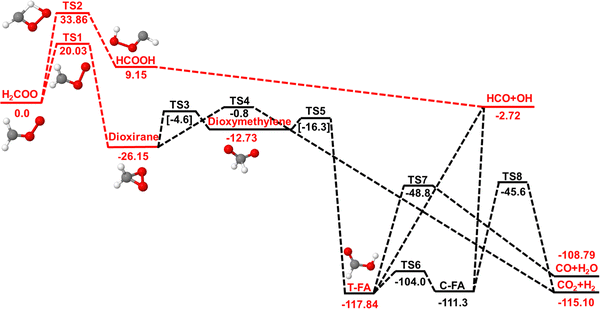Fig. 1 Decomposition pathways for H₂COO on the singlet PES at the CCSD(T)-F12a/aVTZ level of theory (red). Two reaction channels (red line) were considered in the present work (dashed red lines): The H-transfer channel leading to HCOOH which further decays to HCO + OH and the dioxirane channel which leads to formic acid (FA) and three different final product channels (the H-production channels are omitted for clarity). The remaining data (black line, energies in black from CCSD(T)/aVTZ//B3LYP/aVTZ calculations, and in square brackets determined at the CCSD(T)/aVTZ//CASSCF(8,8)/cc-pVTZ level) were those from ref. 20. Note that for TS3 and TS5 the structures were optimized at the CASSCF(8,8) level as optimization with B3LYP was not possible.²⁰ The present work investigates the first reactive step along the two pathways. Barriers for formation of the CO + CH₂O and CO₂ +H₂ are ∼70 kcal mol⁻¹. A third possible pathway involving oxygen-atom insertion into one of the CH-bonds to yield formic acid is not shown in this chart.²⁰

Vibrationally induced reactivity has been found to initiate a sequence of chemical transformations in the next-larger CI, syn-CH₃CHOO. Direct time-domain experimental rates for appearance of OH from unimolecular dissociation of syn-CH₃CHOO under collision free conditions were obtained by vibrationally activating the molecules with energies equivalent to approximately two quanta in the CH-stretch vibration^16,17 which is close to the barrier for formation of H₂CCHOOH and subsequent OH-elimination. Computationally, the entire reaction pathway from energized syn-CH₃CHOO to OH(X²Π) elimination was followed using neural network (NN) representations of the potential energy surfaces (PESs).¹⁸ In addition to OH-elimination, OH-roaming and formation of glycolaldehyde was found as an alternative reaction pathway.¹⁹

Excitation of internal vibrational modes was also proposed as a means for OH-elimination in species relevant to atmosphere chemistry, including HONO, HONO₂, or HO₂NO₂. These species can absorb visible radiation and induce vibrational overtone transitions to states with several quanta in the OH stretching vibration.²¹ For H₂SO₄ (sulfuric acid) vibrationally induced reactivity by exciting the OH-stretch mode was implicated in photodissociation dynamics forming SO₃ and water.²² Subsequent molecular dynamics (MD) simulations at various levels of sophistication confirmed that excitation of the OH-stretch with 4 to 5 quanta drives the decomposition of H₂SO₄.^23–25 However, although cavity ring-down spectroscopy successfully probed the asymmetric OH stretching vibration with ν₉ = 4 and ν₉ = 5, vibrationally induced photodissociation dynamics has as yet not been observed directly.²⁶

In the present work, the reaction dynamics of the smallest CI, H₂COO, following vibrational excitation of internal vibrational modes is considered in order to characterize two competing, low-energy pathways. Excitation of the CH-stretch mode was demonstrated to initiate chemical processing for syn-CH₃CHOO both, from experiments²⁷ and atomistic simulations.^18,19 For H₂COO oxygen-atom elimination requires up to 50 kcal mol⁻¹ whereas the H-transfer and dioxirane channels feature approximate barrier heights of 34 and 20 kcal mol⁻¹, respectively. Following the H-transfer pathway directly yields OH + HCO whereas the dioxirane pathway leads to formic acid which may stabilize through collisions or follow further chemical processing, see Fig. 1. First, the methods are presented, followed by a description of the intermolecular interactions and the dynamics and rates of the photodissociation reaction. At the end, conclusions are drawn.

II. Methods

This section describes the reference electronic structure calculations and the construction of the reactive, multidimensional PESs. Two representations are considered in the following: a neural network-based approach using the PhysNet architecture and a more empirical but computationally considerably more efficient multi-state adiabatic reactive MD (MS-ARMD) representation. One important difference between these two representations is that MS-ARMD requires a dedicated model to follow one reaction pathway at a time whereas the NN-based representation is capable of describing the dynamics along both pathways at the same time.

A. Electronic structure calculations

Reference energies were first determined at the explicitly correlated (F12) coupled cluster method with singles, doubles, and perturbative triples^28,29 with the augmented correlation-consistent polarized valence triple-ζ basis set (CCSD(T)-F12a/aVTZ). For transfer learning (TL), vide infra, additional CASPT2/aVTZ calculations were carried out. All electronic structure calculations used the Molpro2019 suite of codes.³⁰

Initially, ∼6000 structures for each H₂COO and Dioxirane were selected from two existing datasets that were used to construct two PESs based on permutationally invariant polynomial neural networks (PIP-NN) from reference calculations at the CCSD(T)-F12a/aVTZ level.^31,32 Additional reference structures were generated around the two TSs and all the minima considered in the present work by scanning a regular grid in internal coordinates. Subsequently, the “base model” was trained (see below) using energies and forces at this level of theory. The “base model” was further improved from several rounds of adaptive sampling. This lead to a total of 29 612 structures covering a wide configurational space covering the H-transfer and dioxirane formation channels.

To explore whether alternative feasible reaction channels at the conditions considered in the dynamics simulations exist, one-dimensional scans along the O–O and C–H bonds starting from the minimum energy structure of H₂COO were carried out at the CASPT2 level of theory. The barriers for O–O and C–H dissociation are ∼55.0 and 131.0 kcal mol⁻¹, respectively – are significantly higher than the barriers for H-transfer (35.47 kcal mol⁻¹) and dioxirane formation (21.39 kcal mol⁻¹). Hence, for exploring the two channels of interest here reference structures for the O + CH₂O and H + CHOO channels are not required. The potential energy curve along the O–O bond, shown in Fig. S1 (ESI†), is consistent with results at the MRCI-F12 level of theory.¹⁴ The minimum energy paths for both reaction channels from different computational levels are shown in Fig. S2 (ESI†). Both, CCSD(T)-F12a and CASPT2 methods are reliable for developing PESs for the title reaction in this work. Conversely, with MRCI(12,11) the barrier for H-transfer is lower compared with CCSD(T)-F12a and CASPT2 calculations and the dioxirane product is overstabilized. Hence, CASPT2 is preferred for the present application.

B. Training of the neural network and transfer learning

Machine-learned PESs were trained based on the PhysNet architecture,³³ which is designed to predict energies, forces, dipole moments, and partial charges. The overall translational and rotational invariance are maintained, and permutation invariance is also ensured. The technical background for PhysNet has been detailed in ref. 33. For the base model, energies, forces and dipole moments for 29 612 structures were determined at the CCSD(T)-F12a/aVTZ level of theory. For this data set, four independent PhysNet models were generated, using 80% of the data as the training set whereas test and validation sets each contained 10% of the data. The performance on the test data is reported in Fig. S3 (ESI†) and the best of the four base models was selected for subsequent simulations.

Some of the structural rearrangements are likely to require multi-reference descriptions of the electronic structure. To this end, TL from the CCSD(T)-F12a/aVTZ to the CASPT2/aVTZ level of theory was used to improve the PES in regions where multi reference effects may become relevant, for example for O–O bond breaking after H-transfer. Transfer learning has been shown to be a valuable and resource-efficient technique for developing global PESs starting from models based on different initial calculations.^34–38 Here, energies and forces for 2000 structures along the intrinsic reaction coordinates (IRCs) were used together with several hundred structures around the minima and transition states for both pathways (Fig. 1) from which a preliminary TL-PES was trained. Next, adaptive sampling was employed to refine the dataset for the TL-PES. For this, diffusion Monte Carlo (DMC) and short MD simulations with 40.0 kcal mol⁻¹ excess energy along the CH-stretch mode were run to validate the TL-PES and identify deficiencies. The final data set contained 5162 structures for which energies and forces at the CASPT2/aug-cc-pVTZ level were used to train 4 independent models. For TL, the data was split into training (90%), validation (5%), and test set (5%). After that, the best of the four models was chosen for production simulations.

C. Fitting the MS-ARMD PES

MS-ARMD is a computationally efficient means to investigate chemical reactions based on empirical force fields.³⁹ The initial parameters for the reactant (H₂COO) and products (HCOOH and dioxirane) were taken from SwissParam.⁴⁰ First, representative structures were sampled from 500 ps MD simulations at 1000 K, and energies were determined at the CCSD(T)-F12a/aug-cc-pVTZ level of theory. The force fields for reactant and products were separately parametrized using a downhill simplex algorithm.⁴¹ Several rounds of parameter refinements followed and the final root mean squared deviation (RMSD) between the target (ab initio) and the fitted energies for H₂COO, HCOOH and dioxirane reached 0.8, 1.0, and 1.5 kcal mol⁻¹, respectively. Next, Gaussian and polynomial (GAPO) functions³⁹ were used to connect reactant and product force fields to yield a continuous, reactive PES along the reaction paths. The RMSDs for the final, reactive MS-ARMD PESs were 1.5 and 1.7 kcal mol⁻¹ for H₂COO and dioxirane along the dioxirane-channel and 0.9 and 1.1 kcal mol⁻¹ for H₂COO and HCOOH along the H-transfer channel. The decreased performance for the H₂COO reactant along the dioxirane pathway is due to the more pronounced stretch/bend-couplings that arise as the hydrogen atoms move out of the plane for dioxirane formation. The transition states for hydrogen transfer and dioxirane formation were 33.83 and 20.33 kcal mol⁻¹, respectively, which compare well with reference energies of 33.86 and 20.03 kcal mol⁻¹. All parameters for the MS-ARMD PESs are given in the ESI,† see Tables S1–S4.

D. Molecular dynamics simulations and analysis

All reactive MD simulations were carried out using the CHARMM molecular simulation program⁴² including provisions for reactive MD (MS-ARMD) simulations^39,43 and pyCHARMM/PhysNet for the ML/MD simulations.^44,45 Simulations were run in the NVE ensemble for 1 ns and with a time step Δt = 0.1 fs to conserve total energy as the bonds involving hydrogen atoms were flexible.

For simulations using the TL-PES the protocol for obtaining initial coordinates and velocities was as follows. First, the system was heated to 300 K for 200 ps, followed by equilibration during 50 ps, and a 1 ns production simulation in the microcanonical (NVE) ensemble, from which coordinates and velocities were extracted at intervals of 100 fs. This was repeated for 10 independent trajectories. The coordinates and velocities were then utilized as initial conditions for subsequent extensive simulations conducted at various excitation energies.

Following the experiments and previous simulations for syn-CH₃CHOO,^18,19,46 vibrational excitation along particular internal modes was used to energize the reactant. Experimentally, an ensemble of low-temperature syn-CH₃CHOO structures is generated. Subsequently, the alkyl CH-stretching vibration is excited by a laser pulse for syn-CH₃CHOO.⁴⁶ Such a preparation is mimicked in the simulations by starting non-equilibrium trajectories from structures sampled from a thermal distribution. The laser pulse exciting the alkyl CH-stretch amounts to scaling the velocities along the relevant mode such that the energy corresponds to the experimental photon energy. Perturbing the positions in addition to the velocities was not considered because experimentally, the energy is primarily provided as kinetic energy⁴⁶ and it was found that a short (ps) simulation may be required to avoid artifacts after the perturbing the positions.⁴⁷

For the excitation along the CH-stretch normal mode the instantaneous velocity vector was scaled along the normal mode of the CH-stretch vibration such as to yield the desired excitation energy. For the H-transfer channel, excitation energies ranged from 16 to 40 kcal mol⁻¹, corresponding to ∼2 to ∼5 quanta along the CH-stretch vibration, for which 1000 (∼2ν_CH), 1000 (∼3ν_CH), 6000 (∼4ν_CH) and 3000 (∼5ν_CH) independent trajectories were propagated for 1 ns each. The number of quanta considered for the excitation was guided by the barrier heights for the H-transfer and dioxirane channels which are 35.5 and 21.4 kcal mol⁻¹, respectively, at the CASPT2/aVTZ level of theory.

Because excitation along the CH-stretch vibration leads to very small numbers of crossings along the dioxirane channel even for the highest excitation energy (46/3000 crossings with 40.0 kcal mol⁻¹ excitation for a barrier height of 21.4 kcal mol⁻¹), different vibrational modes were considered for this pathway. Guided by the minimum dynamic path, discussed further below, excitation along the combination of the CH-stretch and the CO_AO_B bending mode (ν_COO) was used. In this case, the instantaneous velocity vector was first scaled such as to excite the CH-stretch vibration with the desired energies which were 16.0 and 24.0 kcal mol⁻¹, respectively, corresponding to ∼2ν_CH and ∼3ν_CH. Next, the resulting velocity vector was scaled along the ν_COO normal mode to reach total excitation energies of 22.0 and 25.5 kcal mol⁻¹, respectively, equivalent to exciting ∼(2ν_CH + 4ν_COO) and ∼(3ν_CH + 1ν_COO).

Using MS-ARMD the reactant was heated to 300 K and equilibrated for 50 ps followed by free NVE dynamics for 1 ns. Again, coordinates and velocities were saved to obtain 5000 initial conditions for each of the excitation energies. Vibrational excitation was accomplished through the same procedure as for the simulations using the NN-PES described above and 2000 independent trajectories for each excitation energy were run for 1 ns each.

III. Results

First, the representations of the PESs are validated with respect to the reference data, followed by a characterization of the reaction dynamics and the rates for formation of HCOOH and dioxirane.

A. Validation of the PESs

NN-base model. The performance metrics of the base model on energies and forces for the test set are summarized in Fig. S4 (ESI†). The MAE_train(E) and MAE_test(E) are 0.007, 0.009 kcal mol⁻¹, and the corresponding RMSE_train(E) and RMSE_test(E) are 0.019, 0.062 kcal mol⁻¹. For the forces the MAE_train(F) and MAE_test(F) are 0.022, 0.063 kcal (mol Å)⁻¹, and the corresponding RMSE_train(F) and RMSE_test(F) are 0.251, 0.597 kcal (mol Å)⁻¹, respectively. Optimized structures for H₂COO, dioxirane, HCOOH and the TSs connecting them agree to within better than an RMSD of 10⁻³ Å with optimized structures from CCSD(T)-F12a calculations and their energies agree to within better than 10⁻² kcal mol⁻¹, see Table S5 (ESI†). For the harmonic frequencies, the absolute deviations between the predictions for the 5 stationary points and the corresponding ab initio values are all smaller than 6 cm⁻¹, see Fig. S5 (ESI†).

It is also of interest to report the minimum energy path and compare the performance of the base model with reference calculations at the CCSD(T)-F12a level, see Fig. S6 (ESI†). The RMSD between the reference and NN-PES energies for the test set is 0.063 kcal mol⁻¹. Finally, DMC simulations were carried out to further validate the PES. Previous work established that due to their extensive sampling of configurational space, DMC simulations are particularly effective in locating irregularities of PESs, such as “holes”.^45,48 Propagating 30 000 walkers for 50 000 steps did not detect a single hole which illustrates the robustness of the PES.

Transfer learned model to CASPT2. The quality of the TL-PES is reported in Fig. 2. The RMSE(E) and MAE(E) between reference calculations and inference of the NN are 0.85 kcal mol⁻¹ and 0.41 kcal mol⁻¹, respectively. Fig. S7 (ESI†) provides additional performance metrics. On energies for the TL model, the MAE_train(E) and MAE_test(E) are 0.43, 0.41 kcal mol⁻¹, and the corresponding RMSE_train(E) and RMSE_test(E) are 0.91, 0.85 kcal mol⁻¹. The MAE_train(F) and MAE_test(F) on forces for the TL model are 0.39, 0.75 kcal (mol Å)⁻¹, and the corresponding RMSE_train(F) and RMSE_test(F) are 1.46, 3.54 kcal (mol Å)⁻¹. Optimized structures at the CASPT2 level and from using the TL-PES agree to within a RMSD of 0.01 Å. Finally, the barrier heights (21.4 and 35.5 kcal mol⁻¹ for the dioxirane and HCOOH pathways) from CASPT2 calculations and from using the TL-PES differ by 0.81 and 0.22 kcal mol⁻¹ and the minimum energy paths are reported in Fig. 3.

Fig. 2 Panel A: Correlation of 259 (5%) ab initio reference energies and predicted energies for the test set from the TL-PES. Panel B: Correlation of the ab initio reference energies and the fitted MS-ARMD force field for the dioxirane channel. For H₂COO (black) and dioxirane (red) the RMSEs are 1.5 and 1.7 kcal mol⁻¹, respectively. Inset: ab initio IRC (red circles) and fitted MS-ARMD (black curve, after GAPOs fitting). Panel C: Correlation of the ab initio reference energies and the fitted MS-ARMD force field for the H-transfer channel. For H₂COO (black) and HCOOH (blue) the RMSEs are 0.9 and 1.1 kcal mol⁻¹, respectively. Inset: ab initio IRC (red circles) and fitted MS-ARMD (black curve, after GAPOs fitting).

Fig. 3 Energy profiles of the H-transfer channel (left panel) and the dioxirane formation channel (right panel). Here, the black solid line represents the energies from the TL-PES, and the red open circles are the reference (CASPT2) energies.

For a more comprehensive evaluation of the TL model's performance, a limited set of simulations involving the excitation of the CH stretch mode with 32.0 kcal mol⁻¹ was run. For a single reactive trajectory for the H-transfer channel structures were extracted at regular intervals between reactant and product. Energies for these structures from CASPT2/aVTZ calculations (red circles) and from the TL-PES (black line) are compared in Fig. 4. With respect to the trained NN-PES all these geometries are off-grid and the agreement between reference and model energies is rather encouraging with R² = 0.96 and RMSE = 1.58 kcal mol⁻¹, respectively.

Fig. 4 Main view: Comparison of reference CASPT2 energies (red circles) and predictions from the TL-PES (black line) for a reactive H-transfer trajectory with an excitation energy of 32.0 kcal mol⁻¹ from reactant to product. The inset shows the corresponding correlation of reference CASPT2 energies and predictions. R² and RMSE are 0.96 and 1.58 kcal mol⁻¹, respectively.

MS-ARMD. The quality of the MS-ARMD representations of the reactive PESs is reported in Fig. 2. The fitted PESs feature a RMSE ≈ 1.0 kcal mol⁻¹ and the IRC closely follows the reference calculations (see insets). Preliminary simulations were run to establish energy conservation along the H-transfer and dioxirane channels. Contrary to the machine-learned PESs which allows to simultaneously follow both reaction pathways, MS-ARMD representations can only be used for either H-transfer or dioxirane formation.

B. Reaction dynamics

For a first impression of the reaction dynamics the minimum dynamic path (MDP) was determined for the two pathways and using the TL-PES. Such simulations start from the TS separating two neighboring minima.⁴⁹ The excess energies were ΔE = 0.03 and 0.11 kcal mol⁻¹, respectively, and variations of important internal coordinates along the downhill pathway towards reactant and product for both pathways are reported in Fig. 5 for the TL-PES.

Fig. 5 CH_A, CO_A and O_AO_B separations, and change of CO_AO_B angle, and H_ACO_AO_B and H_BCO_AO_B dihedrals along the minimum dynamic path from the TL-PES. Panel A: The H-transfer channel from H₂COO to HCOOH and then dissociation to OH + HCO. Panel B: Dioxirane formation. Structures A to E and F to J illustrate geometrical arrangements along the pathways. The black arrows indicate the location of the transition states for the H-transfer (structure C) and dioxirane (structure H) route.

For H-transfer the most important participating internal degree of freedom for the reactant → TS step as judged from the MDP is the CH_A stretch (solid black). The CO_A and O_AO_B separations (solid red and blue) only change insignificantly as the TS is approached. Similarly, the two dihedral angles (dashed red and blue) do not vary and the chemical transformation occurs in a planar arrangement. There is, however, a readjustment of the CO_AO_B angle (dashed black) from 118° to 100°. These geometrical changes imply that vibrational excitation along the CH-stretch normal mode will be most effective to promote reactivity of H₂COO towards the TS leading to the HCOOH product and beyond. On the product side it is interesting to note that the O_AO_B distance starts to increase after passing the TS which facilitates breakup towards OH-elimination.

Contrary to that, the dioxirane channel is characterized by an insignificant change along the CH_A bond, some variation of the CO_A separation, and an increase of the O_AO_B bond length by 0.1 Å when moving towards the TS. At the same time, all three angles considered decrease in concert. Specifically, the CO_AO_B angle changes from 117° to 92°. Taken together, this suggests that sole excitation along the CH_A stretch mode is not expected to be particularly effective for dioxirane formation but a combination mode involving the CO_AO_B bend may be a good and productive reaction coordinate.

Consequently, two types of vibrational excitations were considered. One used exclusively the CH_A normal mode for which excitation energies of 16 kcal mol⁻¹ to 40 kcal mol⁻¹ along this vibration were investigated (∼2ν_CH to ∼5ν_CH quanta). This is akin to previous experimental⁴⁶ and computational^18,19 work which also did not employ resonant excitation and the precise number of quanta in a particular degree of freedom is not decisive. The second scheme used excitation energies of 22.0 kcal mol⁻¹ and 25.5 kcal mol⁻¹ along two CH-stretch/COO-bend combinations: ∼(3ν_CH + ν_COO) and ∼(2ν_CH + 4ν_COO).

Time series for typical atom–atom separations along the H-transfer channel are reported in Fig. 6. Panel A illustrates an example reactive trajectory using the TL-PES with excitation energy 32.0 kcal mol⁻¹ (∼4ν_CH). The CH_A (black), O_AO_B (blue), and O_BH_A (pink) separations are shown. Initially, the CH_A and O_AO_B distances fluctuate around their equilibrium bond length, while the O_BH_A varies more widely from 2.3 to 2.7 Å due to the bending of CH and the excited CH_A-stretch. HCOOH forms at t ≈ 0.9 ns accompanied by a sudden increase of the CH_A separation. Notably, HCOOH rapidly decomposes into HCO + OH as this is a barrierless reaction. Fig. 6B reports a similar reactive trajectory from MS-ARMD. The amplitudes for the O_AO_B and O_BH_A separations are comparable whereas for the CH_A bond the TL-PES is softer. The varying amplitudes in both sets of time series indicate that energy exchange between the mode occurs.

Fig. 6 Time series for CH_A (black), O_AO_B (blue), and O_BH_A (pink) separations for a reactive trajectory along the H-transfer channel with ∼4ν_CH (32.0 kcal mol⁻¹). Panel A: Using the TL-PES, HCOOH is formed at t ≈ 0.9 ns (see also Fig. S8, ESI†). Panel B: Using the MS-ARMD PES HCOOH forms at t ≈ 0.5 ns. The amplitudes for the O_AO_B and O_BH_A separations are comparable whereas for the CH_A bond the TL-PES is softer.

Fig. 7A reports the distribution of CO_AO_B angles following excitation with 40.0 kcal mol⁻¹ (∼5ν_CH) and the ensuing dynamics. Excitation along the CH-normal mode yields almost entirely the HCOOH isomer. The distribution functions for the reactant (black) and the TS (red) towards HCOOH clarify that the geometry of the TS towards dioxirane (green dashed line) is virtually never sampled. The maximum of the probability distribution function for the reactant is centered at 120° and extends from ∼90° to ∼150°. For the transition state towards HCOOH the maximum shifts to 100° and the distribution narrows considerably, extending only between ∼90° and ∼110°. The positions of the two maxima are also consistent with the MDP, see Fig. 5A. Analysis of these trajectories, (vide infra) indicates that all of them develop towards the TS leading to the isomer and dioxirane formation is unlikely despite the fact that the excitation energy of ∼40 kcal mol⁻¹ is considerably larger than the barrier towards dioxirane (21.4 kcal mol⁻¹, see Fig. 1). One important reason for this is that the TS leading to dioxirane is characterized by a CO_AO_B angle of ∼90° (green dashed line in Fig. 7) which is not sampled for trajectories in which vibrational excitation occurs along the CH-stretch normal mode only. This also means that energy transfer between the CH-stretching and the COO-bending motion is ineffective on the time scale of the present simulations (1 ns).

Fig. 7 Panel A: Distribution of CO_AO_B angle for 2000 reactive trajectories from the simulations with ∼5ν_CH (40.0 kcal mol⁻¹) on the TL-PES for the reactant (black) and the transition state (red) for the pathway. The dashed green line indicates the CO_AO_B angle at the TS for accessing the dioxirane pathway. As trajectories with excitation exclusively along the CH_A bond do not sample values ≤90° for the CO_AO_B angle only the pathway leading to HCOOH is followed; see text for discussion. Panel B: Distribution of CO_AO_B angle for 1400 reactive trajectories from the simulations with excitation ∼3ν_CH + ν_COO (25.5 kcal mol⁻¹) on the TL-PES for the reactant (black) and the transition state (red) for the dioxirane channel. The dashed green line indicates the CO_AO_B angle at the TS.

Because the MDP for the pathway (see Fig. 5A) indicated that the CH_A-stretch changes appreciably and the CO_AO_B-bend also varies in approaching the TS, it is of interest to characterize their correlated motion along the reaction pathway. For this, ∼10⁷ geometries sampled in the reactant, TS, and product states were analyzed (see ESI†) following excitation with 40.0 kcal mol⁻¹. Fig. 8 reports black (reactant), red (TS), and blue (HCOOH) point clouds which provide a comprehensive description of the motions that are followed for the H-transfer reaction path. This clarifies that the transition region has finite width, both along the CH_A-stretch and the CO_AO_B-bend coordinates, extending well beyond the transition state (yellow cross).

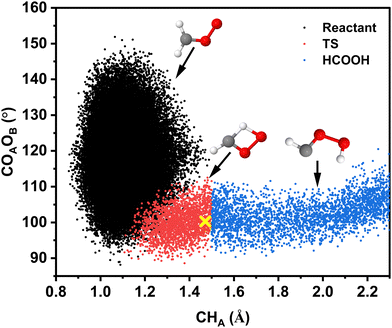Fig. 8 Geometry changes along the HCOOH-pathway: correlation between the CO_AO_B angle and the CH_A separation for 2500 reactive trajectories from the simulations with 40.0 kcal mol⁻¹ (∼5ν_CH) for the H-transfer channel on the TL-PES. A total of ∼10⁷ structures was analyzed, see ESI.† The width of the transition seam along the O_AO_B-separation is 0.4 Å. The yellow cross is at the TS geometry from the CASPT2/aVTZ calculations.

Excitation of the combination mode with 25.5 kcal mol⁻¹ (∼(3ν_CH + ν_COO)) only leads to following the dioxirane pathway. The CO_AO_B-distribution functions P(θ_COO) for the reactant (black) and the TS-geometries (red) are reported in Fig. 7B together with the CO_AO_B angle for the TS from the electronic structure calculations (green dashed line). Evidently, the dynamics samples the TS-geometry extensively and the widths of the distributions decrease in going from the reactant to the TS. The correlation between O_AO_B-stretch and the CO_AO_B-bend coordinates for this pathway is shown in Fig. 9. It is interesting to note that product state geometries for the O_AO_B-bond lengths are already sampled in the reactant state but the decisive coordinate along the dioxirane-pathway is the CO_AO_B-bend.

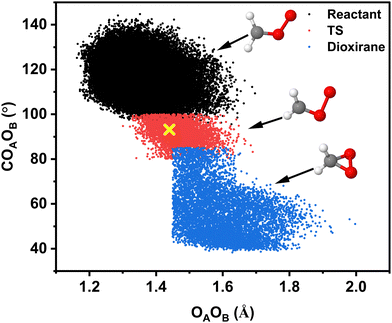Fig. 9 Geometry changes along the dioxirane-pathway: distribution of CO_AO_B angle as a function of the O_AO_B distance for 1400 reactive trajectories from simulations with 25.5 kcal mol⁻¹ (∼3ν_CH + ν_COO) for the dioxirane channel on the TL-PES. A total of ∼10⁷ structures was analyzed. Each of the 3 states (reactant, TS, product) was approximately identified through specific geometric criteria, see ESI.†

C. Reaction probabilities

The excitation schemes considered in the present work are chosen to follow the H-transfer or dioxirane-formation pathways. Excitation along the CH-stretch normal mode yields predominantly HCOOH and only minor amounts of dioxirane even for the highest excitation energy of 40.0 kcal mol⁻¹ despite a barrier height of only 21.4 kcal mol⁻¹ to form dioxirane. Conversely, excitation of the CH-stretch/COO-bend combination mode leads exclusively to dioxirane primarily because energies of 22.0 to 25.5 kcal mol⁻¹ are not sufficient to reach the TS energy towards HCOOH of 33.9 kcal mol⁻¹.

Table 1 shows that for excitation energies below or close to the barrier height for H-transfer (33.9 kcal mol⁻¹ at CCSD(T)-F12a/aVTZ and 35.5 kcal mol⁻¹ at CASPT2/aVTZ) the reaction probability is 0 or a few percent. Excitation with 40.0 kcal mol⁻¹ (∼5ν_CH) leads to formation of HCOOH in almost all cases. Both, the reaction probabilities and the distribution of reaction times agree well for simulations using MS-ARMD and the TL-PES. Because excitation is close to the barrier height with 32.0 kcal mol⁻¹ (∼4ν_CH) the reaction times τ are widely distributed, see Fig. 10a, and converging them would require a considerably larger number of trajectories. Contrary to that, exciting the CH-stretch normal mode with 40.0 kcal mol⁻¹ shifts the maximum of the reaction times to short τ (Fig. 10c).

Table 1 Reaction probability for H-transfer channel from simulations by exciting the CH stretch mode with the NN-TL-PES and the MS-ARMD force field

Excitation energy (kcal mol^−1)	∼2 quanta (16.0)	∼3 quanta (24.0)	∼4 quanta (32.0) (%)	∼5 quanta (40.0) (%)
NN-TL (E^CASPT2TS = 35.5 kcal mol^−1)	0	0	0.7	98.4
MS-ARMD (E^CCSD(T)TS = 33.9 kcal mol^−1)	0	0	3.0	96.0

---

Fig. 10 Normalized reaction time distribution from the MD simulations for the H-transfer (left column) and dioxirane (right column) pathways using the TL-PES (red) and MS-ARMD (blue). Excitation energies in panels a to d are 32.0 kcal mol⁻¹ (∼4ν_CH), 22.0 kcal mol⁻¹ (∼(2ν_CH + 4ν_COO)), 40.0 kcal mol⁻¹ (∼5ν_CH), and 25.5 kcal mol⁻¹ (∼(3ν_CH + 1ν_COO)), respectively.

Following the dioxirane-formation channel features a barrier height of 20.0 and 21.4 kcal mol⁻¹ at the CCSD(T)-F12a/aVTZ and CASPT2/aVTZ levels of theory, respectively, and requires excitation of the CH-stretch/COO-bend combination band. With an excitation energy of 22.0 kcal mol⁻¹ (∼(2ν_CH + 4ν_COO)) 96.0% of the trajectories yield dioxirane if the MS-ARMD PES is used compared with 8.3% when running the simulations with the TL-PES. Excitation with 25.5 kcal mol⁻¹ features 99.0% compared with 70.3% of reactive trajectories, see Table 2. The reaction time distributions from using the two PESs can differ quite substantially. With the MS-ARMD PES, P(τ) for excitation with 22.0 kcal mol⁻¹ peaks at 50.5 ps (blue trace in Fig. 10b compared with ∼400 ps with the TL-PES (red trace in Fig. 10b). Excitation with 25.5 kcal mol⁻¹ (see Fig. 10d) features a pronounced peak at early reaction times for simulations using MS-ARMD whereas with the TL-PES the maximum is shifted to ∼150 ps and the entire distribution is considerably wider. Part of the differences between both PESs for dioxirane is due to the lower barrier height (by 1.4 kcal mol⁻¹) and the coarse representation of stretch/bend-couplings in MS-ARMD.

Table 2 Reaction probability for dioxirane channel from simulations by exciting the CH stretch mode and the COO bending mode with the NN-base PES, the NN-TL-PES and the MS-ARMD force field

Excitation energy (kcal mol^−1)	∼(2νCH + 4νCOO) (22.0)	∼(3νCH + 1νCOO) (25.5)
NN-base (E^CCSD(T)TS = 20.0 kcal mol^−1)	20.3%	67.1%
NN-TL (E^CASPT2TS = 21.4 kcal mol^−1)	8.3%	70.3%
MS-ARMD (E^CCSD(T)TS = 20.0 kcal mol^−1)	96.0%	99.0%

---

IV. Discussion and conclusion

The present work reports on the reactive dynamics following vibrational excitation of the smallest Criegee intermediate, H₂COO. Excitation of vibrations to drive OH-formation relevant to atmospheric chemistry has been used for syn-CH₃CHOO^18,19,46 and considered for species such as HSO₃ X (X = F, Cl, OH).^26,50 Contrary to this, for H₂COO two reaction pathways were considered which lead to different product channels. Importantly, the present work suggests that depending on the vibrational modes that are excited, the two pathways are almost selectively followed from simulations using the TL-PES which allows to access both pathways in the same simulation.

If the CH-stretch is excited with ∼5ν_CH (40.0 kcal mol⁻¹), the probability for H-transfer to give HCOOH is two orders of magnitude larger than dioxirane formation. This is despite the fact that the barrier height for formation of dioxirane is only 21.4 kcal mol⁻¹ at the CASPT2/aVTZ level of theory. Conversely, excitation of the COO-bend with energy equivalent to 1 quantum in the ν_COO mode is sufficient to yield appreciable amounts of dioxirane using both PESs considered. Notably, excitation with 5ν_CH on the TL-PES leads to ∼98% HCOOH as the product (see Table 1) whereas including the COO-bend (5ν_CH + ν_COO) yields the alternative product – dioxirane – with ∼99% probability on the 1 ns time scale. And excitation of the 3ν_CH + ν_HACOAOB combination mode (∼26 kcal mol⁻¹), including the H_ACO_AO_B-torsion, results in a probability for dioxirane formation of ∼80% compared with ∼70% from excitation of (3ν_CH + ν_COO). This is consistent with the MDP for the dioxirane channel, see Fig. 5B. Hence, excitation of stretch-bend/torsion combination bands is decisive to steer the reaction towards dioxirane. All this underscores that mode selective chemistry is observed for H₂COO.

The possibility to deposit energy corresponding to multiple quanta in stretch modes was demonstrated for H₂SO₄ for which the 4ν₉ and 5ν₉ O–H stretching overtones were excited.²⁶ Similarly, vibrational “ladder climbing” was used to deposit up to 4 quanta of vibrational energy in nitrile (–CN) functionalized phenol.⁵¹ Finally, excitation of high vibrational states (v ≥ 7) of CO-ligands in Cr(CO)₆ was found to lead to CO-dissociation from the parent molecule.⁵² These findings illustrate that excitation of highly excited vibrational states is possible to probe the spectroscopy and even induce reactivity. Reactivity on the 10 to 100 ps time scale was already observed for vibrationally excited H₂SO₄, HSO₃ Cl, and syn-Criegee in the gas phase.^18,24,53 Although IVR does take place, the fraction of products formed on the 100 ps time scale range from a few % to 100% depending on the level of vibrational excitation and the species considered.

Reactive MD simulations were also run using the NN-base model determined from CCSD(T)-F12a/aVTZ reference calculations. Although the quality of the NN-representation is excellent (see e.g. Table S5, ESI†), excitation along the CH-stretch normal mode often features problems: for example, C–O bond breaking to form CH₂ + O₂ is found which should not occur at such low excitation energies. In search for a reason it was found that the CCSD(T)-F12a/aVTZ reference data on the singlet PES feature a local minimum for elongations along the C–O stretch coordinate at 1.75 Å, corresponding to an energy of ∼30 kcal mol⁻¹. Although the NN-base model reliably captures this feature, breaking of the CO bond along the singlet-PES at such low energies is not realistic. The reason for this spurious feature is the proximity of the triplet-PES which complicates the electronic structure calculations in this region of configuration space and single-reference methods are not sufficiently reliable.

Using the TL-PES at the CASPT2/aVTZ level improves the situation in that the spurious minimum is shifted to longer CO-separations and to ∼85 kcal mol⁻¹ which is considerably higher than the transition state towards H-transfer at 33.8 kcal mol⁻¹. This allows to run meaningful simulations for the processes of interest in the present work. Nevertheless, no globally valid PES is yet available and the CASPT2/aVTZ level of theory does not provide reference data to sufficiently high energies for developing such a PES. For the dioxirane pathway the situation is better and meaningful simulations using the base model are possible.

From the perspective of atmospheric chemistry, OH-formation from vibrational excitation of H₂COO is most relevant. The present work suggests that excitation of the CH-stretch with ∼4 to ∼5ν_CH is most likely to yield OH after H-transfer to form HCOOH. The pathway through dioxirane involves barriers that are comparable to the stabilization energy of dioxirane itself, hence IVR will limit productive OH-generation, see Fig. 1. Finally, the pathway through FA – which was not considered here – first involves a very loose transition state (with O-separations of ∼4 Å from the H₂CO-core at the CASSCF level). Such a TS is very “vulnerable” in an atmospheric environment. Secondly, although the insertion product (c-FA) is highly stabilized by −120 kcal mol⁻¹, subsequent barriers are still of the order of 60 to 80 kcal mol⁻¹. Thermodynamically, surmounting such barriers is feasible. However, again, IVR and collisional de-excitation limit this process as has, e.g., been shown for acetaldehyde to form vinoxy-radical.⁵⁴

Earlier simulations for syn-CH₃CHOO explicitly considered in- and exclusion of zero-point vibrational energy. This aspect⁵⁵ is intensely debated, primarily because vibrational energy can leak from one mode to other modes on the time scale of the simulation which may affect computed observables. However, as of now no satisfactory and universally accepted treatment of this issue exists. For syn-CH₃CHOO no significant differences were found for the reaction rates whether or not zero-point vibrational energy was included.¹⁹ However, when analyzing the products formed at a state-specific level – which is not done in the present work – including zero-point vibrational effects was found to be important.

In summary, the present work explores the reactive dynamics following vibrational excitation of the smallest Criegee intermediate H₂COO at the CCSD(T)-F12a and CASPT2 levels of theory. Two different excitation schemes almost exclusively lead to reactive dynamics along the H-transfer and dioxirane-formation pathways. The most promising route for OH-formation involves excitation of the CH-stretch normal mode with energies equivalent to between 4 and 5 quanta to yield HCOOH with subsequent breaking of the O–O bond. Although the molecule only contains 5 atoms its electronic structure is challenging and despite the considerable effort in the present and previous work no globally valid, reactive PES is available as of now.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Prof. Jun Li for providing the datasets for H₂COO and dioxirane. Valuable discussions with Dr Silvan Käser and Dr Cangtao Yin are acknowledged. We also thank Prof R. Dawes for providing raw data and Prof. H. Guo for exchange on the work. This work was supported by China Scholarship Council (to KS), the Swiss National Science Foundation through grants 200020_219779 and 200021_215088 and the University of Basel.

References

1. D. Stone, L. K. Whalley and D. E. Heard, Chem. Soc. Rev., 2012, 41, 6348–6404.
2. S. Gligorovski, R. Strekowski, S. Barbati and D. Vione, Chem. Rev., 2015, 115, 13051–13092.
3. H. Levy, Science, 1971, 173, 141–143.
4. K. Emmerson and N. Carslaw, Atmos. Environ., 2009, 43, 3220–3226.
5. M. Khan, C. Percival, R. Caravan, C. Taatjes and D. Shallcross, Environ. Sci.: Process. Impacts, 2018, 20, 437–453.
6. R. Criegee and G. Wenner, Justus Liebigs Ann. Chem., 1949, 564, 9–15.
7. M. S. Alam, M. Camredon, A. R. Rickard, T. Carr, K. P. Wyche, K. E. Hornsby, P. S. Monks and W. J. Bloss, Phys. Chem. Chem. Phys., 2011, 13, 11002–11015.
8. A. Novelli, L. Vereecken, J. Lelieveld and H. Harder, Phys. Chem. Chem. Phys., 2014, 16, 19941–19951.
9. C. A. Taatjes, Annu. Rev. Phys. Chem., 2017, 68, 183–207.
10. R. Mauldin Iii, T. Berndt, M. Sipilä, P. Paasonen, T. Petäjä, S. Kim, T. Kurtén, F. Stratmann, V.-M. Kerminen and M. Kulmala, Nature, 2012, 488, 193–196.
11. Y.-P. Lee, J. Chem. Phys., 2015, 143, 020901.
12. O. Welz, J. D. Savee, D. L. Osborn, S. S. Vasu, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Science, 2012, 335, 204–207.
13. K. Samanta, J. M. Beames, M. I. Lester and J. E. Subotnik, J. Chem. Phys., 2014, 141, 134303.
14. R. Dawes, B. Jiang and H. Guo, J. Am. Chem. Soc., 2015, 137, 50–53.
15. Y.-T. Su, Y.-H. Huang, H. A. Witek and Y.-P. Lee, Science, 2013, 340, 174–176.
16. Y. Fang, F. Liu, V. P. Barber, S. J. Klippenstein, A. B. McCoy and M. I. Lester, J. Chem. Phys., 2016, 144, 061102.
17. Y. Fang, F. Liu, V. P. Barber, S. J. Klippenstein, A. B. McCoy and M. I. Lester, J. Chem. Phys., 2016, 145, 234308.
18. M. Upadhyay and M. Meuwly, ACS Earth Space Chem., 2021, 5, 3396–3406.
19. M. Upadhyay, K. Topfer and M. Meuwly, J. Phys. Chem. Lett., 2023, 15, 90–96.
20. T.-N. Nguyen, R. Putikam and M.-C. Lin, J. Chem. Phys., 2015, 142, 124312.
21. D. Donaldson, G. Frost, K. Rosenlof, V. Tuck and A. F. Vaida, Geophys. Res. Lett., 1997, 24, 2651–2654.
22. V. Vaida, H. G. Kjaergaard, P. E. Hintze and D. J. Donaldson, Science, 2003, 299, 1566–1568.
23. Y. Miller and R. B. Gerber, J. Am. Chem. Soc., 2006, 128, 9594–9595.
24. J. Yosa Reyes and M. Meuwly, J. Phys. Chem. A, 2011, 115, 14350–14360.
25. J. Yosa Reyes, T. Nagy and M. Meuwly, Phys. Chem. Chem. Phys., 2014, 16, 18533–18544.
26. K. J. Feierabend, D. K. Havey, S. S. Brown and V. Vaida, Chem. Phys. Lett., 2006, 420, 438–442.
27. F. Liu, J. M. Beames, A. S. Petit, A. B. McCoy and M. I. Lester, Science, 2014, 345, 1596–1598.
28. T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106.
29. G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104.
30. H.-J. Werner, P. J. Knowles, P. Celani, W. Györffy, A. Hesselmann, D. Kats, G. Knizia, A. Köhn, T. Korona, D. Kreplin, R. Lindh, Q. Ma, F. R. Manby, A. Mitrushenkov, G. Rauhut, M. Schütz, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, J. A. Black, P. J. Bygrave, R. Cimiraglia, D. L. Cooper, D. Coughtrie, M. J. O. Deegan, A. J. Dobbyn, K. Doll, M. Dornbach, F. Eckert, S. Erfort, E. Goll, C. Hampel, G. Hetzer, J. G. Hill, M. Hodges, T. Hrenar, G. Jansen, C. Köppl, C. Kollmar, S. J. R. Lee, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, B. Mussard, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. A. Peterson, K. Pflüger, R. Pitzer, I. Polyak, M. Reiher, J. O. Richardson, J. B. Robinson, B. Schröder, M. Schwilk, T. Shiozaki, M. Sibaev, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, J. Toulouse, M. Wang, M. Welborn and B. Ziegler, MOLPRO, 2019.1, a package of ab initio programs, https://www.molpro.net/.
31. J. Li, S. Carter, J. M. Bowman, R. Dawes, D. Xie and H. Guo, J. Phys. Chem. Lett., 2014, 5, 2364–2369.
32. J. Li and H. Guo, J. Phys. Chem. A, 2016, 120, 2991–2998.
33. O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693.
34. S. Käser, J. O. Richardson and M. Meuwly, J. Chem. Theory Comput., 2022, 18, 6840–6850.
35. S. Käser and M. Meuwly, J. Chem. Phys., 2023, 158, 214301.
36. S. Käser, L. I. Vazquez-Salazar, M. Meuwly and K. Töpfer, Digital Discovery, 2023, 2, 28–58.
37. S. Käser and M. Meuwly, Phys. Chem. Chem. Phys., 2022, 24, 5269–5281.
38. J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Nat. Commun., 2019, 10, 2903.
39. T. Nagy, J. Yosa Reyes and M. Meuwly, J. Chem. Theory Comput., 2014, 10, 1366–1375.
40. V. Zoete, M. A. Cuendet, A. Grosdidier and O. Michielin, J. Comput. Chem., 2011, 32, 2359–2368.
41. J. A. Nelder and R. Mead, Comput. J., 1965, 7, 308–313.
42. B. R. Brooks, C. L. Brooks, III, A. D. Mackerell, Jr., L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614.
43. J. Danielsson and M. Meuwly, J. Chem. Theory Comput., 2008, 4, 1083.
44. K. Song, S. Käser, K. Töpfer, L. I. Vazquez-Salazar and M. Meuwly, J. Chem. Phys., 2023, 159, 024125.
45. J. Buckner, X. Liu, A. Chakravorty, Y. Wu, L. F. Cervantes, T. T. Lai and C. L. Brooks III, J. Chem. Theory Comput., 2023, 3752–3762.
46. N. M. Kidwell, H. Li, X. Wang, J. M. Bowman and M. I. Lester, Nat. Chem., 2016, 8, 509–514.
47. P. H. Nguyen and G. Stock, J. Chem. Phys., 2003, 119, 11350–11358.
48. J. Li, C. Qu and J. M. Bowman, Mol. Phys., 2021, 119, e1976426.
49. O. T. Unke, S. Brickel and M. Meuwly, J. Chem. Phys., 2019, 150, 074107.
50. S. Brickel and M. Meuwly, J. Phys. Chem. A, 2017, 121, 5079–5087.
51. J. P. Kraack and P. Hamm, Phys. Chem. Chem. Phys., 2016, 18, 16088–16093.
52. T. Witte, T. Hornung, L. Windhorn, D. Proch, R. de Vivie-Riedle, M. Motzkus and K.-L. Kompa, J. Chem. Phys., 2003, 118, 2021–2024.
53. J. Yosa Reyes, S. Brickel, O. T. Unke and M. Meuwly, Phys. Chem. Chem. Phys., 2016, 18, 6780–6788.
54. S. Käser, O. T. Unke and M. Meuwly, J. Chem. Phys., 2020, 152, 214304.
55. S. Mukherjee, M. Pinheiro Jr, B. Demoulin and M. Barbatti, Philos. Trans. R. Soc., A, 2022, 380, 20200382.

---

Footnote

† Electronic supplementary information (ESI) available: https://github.com/MMunibas/PhysNet, and the PhysNet PESs and the data sets containing the reference data can be obtained from https://github.com/MMunibas/H2COO-PhysNet. See DOI: https://doi.org/10.1039/d4cp00739e

---