Vibrational anisotropy decay resolves rare earth binding induced conformational change in DTPA

Abstract

Elucidating the relationship between metal–ligand interactions and the associated conformational change of the ligand is critical for understanding the separation of lanthanides via ion binding. Here we examine DTPA, a multidentate ligand that binds lanthanides, in its free and metal bound conformations using ultrafast polarization dependent vibrational spectroscopy. The polarization dependent pump–probe spectra were analyzed to extract the isotropic and anisotropic response of DTPA's carbonyl groups in the 1550–1650 cm⁻¹ spectral region. The isotropic response reports on the population relaxation of the carbonyl stretching modes. We find that the isotropic response is influenced by the identity of the metal ion. The anisotropy decay of the carbonyl stretching modes reveals a faster decay in the lanthanide–DTPA complexes than in the free DTPA ligand. We attribute the anisotropy decay to energy transfer among the different carbonyl sites – where the conformational change results in an increased coupling between the carbonyl sites of metal-bound DTPA complexes. DFT calculations and theoretical simulations of energy transfer suggest that the carbonyl sites are more strongly coupled in the metal-bound conformations compared to the free DTPA. The stronger coupling in the metal bound DTPA conformation leads to efficient energy transfer among the different carbonyl sites. Comparing the rate of anisotropy decay across the series of metal bound DTPA complexes we find that the anisotropy is sensitive to the charge density of the central metal ion, and thus can serve as a molecular scale reporter for lanthanide ion binding.

---

Introduction

The sustainable and energy efficient separation of rare earth elements (REE) is critical for meeting the rising demand of REE required by modern technologies.^1–6 Of the REE, the lanthanides pose a significant challenge for efficient separations because of their similar physicochemical properties.^6–9 While developing green chemical routes for extracting lanthanides from minerals and ores is an active area of research,^3,5,6,10,11 additional research effort has focused on finding alternative recycling strategies for end-of-life products in order to extract lanthanides^1–4,8,12 Solvent extraction using chelating ligands has been ubiquitous in industrial scale chemical processes for lanthanide separations (TALKSPEAK, PUREX, ALPES).^6,9,11,13 During these processes, polyaminocarboxylate (PAC) ligands can act as aqueous phase holdback reagents where they bind with the lanthanides through electrostatic interactions.^13–16 With the rise of green and sustainable lanthanide recycling, these biologically relevant PAC ligands^12,17 have regained attention for their ability to separate lanthanides from spent nuclear fuel and electronic waste.^3,5 Upon metal encapsulation the PAC ligands undergo large scale conformational distortions^18–20 in addition to smaller picometer structural changes associated with the ionic radii (∼19 picometer reduction from La³⁺ to Lu³⁺).²¹ The conformational distortion and structural changes can impact the strain and the overall thermodynamic stability of the metal complexes.^9,19,22,23 A better understanding of the conformational and structural changes associated with lanthanide–ligand binding could provide critical benchmarking information for computational modelling that is important for optimizing separations.^6,24

Diethylenetriaminepentaacetic acid (DTPA) is a member of the PAC ligand family that is commonly used for the separation of lanthanides during the TALKSPEAK process.^{9,10,13,15,16} Being an octa-dentate ligand, DTPA can bind to the metal ion via 5 carboxylate groups, forming a coordination complex with a square anti-prism geometry.^25–27 The distorted geometry of the ligand is stabilized by strong electrostatic interactions between the central metal ion and the negatively charged carboxylate binding arms.^17,19 For the metal bound conformations, the thermodynamic properties can be related to the strength of ionic interaction between the metal ion and DTPA's five carboxylate groups.⁹ As the charge density of the metal ion increases across the lanthanide series, this could lead to slight structural changes of the metal bound DTPA conformation due to increased electrostatic interactions. Understanding how the charge density of the metal center impacts the conformational and structural changes of DTPA is essential for strategizing efficient lanthanide separation using next generation chelating ligands.^6,24 To this end, we investigate the conformational and structural changes of DTPA in free and lanthanide bound forms using ultrafast polarization dependent mid-IR pump probe spectroscopy.

Previous work has demonstrated that the high frequency vibrational modes of carboxylate groups can be used to probe conformational and structural changes in the condensed phase.^28–35 In the context of previous PAC ligands, the ultrafast vibrational dynamics of EDTA's carboxylate groups have been extensively studied by the Baiz group³¹ and the Garret-Roe group.³⁰ Using mid-IR pump–probe spectroscopy, the Baiz group measured the vibrational lifetime of the carboxylate groups in free and metal bound EDTA.³¹ They observed a net slowdown in the relaxation dynamics of the asymmetric stretching modes for metal bound EDTAs, which was attributed to poor coupling between the asymmetric and the symmetric stretch of the carboxylates.³¹ The Garret-Roe group found that metal binding to EDTA influences the mixing of the carboxylate symmetric stretching modes to terminal C–H bending modes of EDTA, and that ion binding induces geometric distortions giving rise to new cross-peak and diagonal peak features in the 2DIR spectra.³⁰ These previous studies on EDTA highlight the role of ultrafast IR spectroscopy in resolving conformational and picometer scale structural changes of the PAC ligands during ion binding in the solution phase.

Building on these studies, we use ultrafast polarization dependent mid-IR pump probe spectroscopy to monitor the carbonyl vibrations (ν_C=O) of DTPA to probe the conformational and structural changes of the DTPA ligand due to ion binding. DTPA differs from EDTA as DTPA has five carboxylate groups that bind with the metal ion, thus leading to much higher thermodynamic stability of the metal–DTPA complexes.⁹ As DTPA binds with the metal ions, the carboxylates are brought into closer proximity of one another which can lead to an increase in vibrational coupling among the carbonyl vibrations of the different carboxylate groups. Previous work on oxalate has shown that the vibrational anisotropy can report on the vibrational delocalization across different carboxylate groups as well the energy transfer timescale among the asymmetric stretching modes of the carboxylates,^34,35 where the changes in the delocalization and energy transfer can be governed by changes in vibrational coupling. By applying polarization dependent mid-IR pump probe spectroscopy to DTPA in free and lanthanide bound form, we can extract the vibrational anisotropy and relate changes in the anisotropy decay to changes in vibrational coupling among the carbonyl vibrations of different carboxylate groups of DTPA as a function of ion binding.

In this work, we study a series of lanthanide DTPA complexes (La³⁺, Nd³⁺, Gd³⁺, Tb³⁺, Er³⁺, and Lu³⁺) and free DTPA using polarization dependent mid-IR pump–probe spectroscopy to monitor the DTPA's ν_C=O vibrations. Through analysis of the spectra, we extract the ultrafast population relaxation and anisotropy decay of the carbonyl vibrations in the 1550–1650 cm⁻¹ across the series of lanthanide–DTPA complexes and free DTPA. We find that the population relaxation of the carbonyl stretching modes in the metal bound DTPA complexes is biexponential – with a ∼300 fs IVR component followed by a >1 ps component assigned to energy dissipation to the solvent. In addition, we extract the anisotropy decay and find faster decay time constants in the metal bound DTPA complexes (fastest for Lu³⁺–DTPA with 280 fs ± 60 fs) when compared to the free DTPA ligand (940 fs ±110 fs). To understand the origin of the sub-ps anisotropy decay, we estimate the coupling between the 5 local carbonyl sites in metal free and metal bound DTPA from the results of density functional theory (DFT) calculations. The magnitude of inter-site coupling is larger (by a factor of ∼10) in the metal bound DTPA as compared to free DTPA. The larger coupling leads to delocalized ligand vibrations strictly originating from the conformational change and geometric distortion of DTPA during ion binding. To help interpret the experimental observations we build a simple model to describe the carbonyl vibrations by their site energies and intersite couplings and solve the time dependent Schrödinger equation where we include bath induced fluctuations. From the simulations, we can gain insight into the ultrafast vibrational energy transfer (VET) among the 5 local carbonyl sites in the free and metal bound DTPA ligands. We find that the large-scale conformational change of DTPA upon binding to a metal ion can lead to ultrafast VET. The ultrafast VET results in an ultrafast decay in the anisotropy, consistent with our experimental observations of the anisotropy decays of metal free and metal bound DTPA ligands. In addition, we observe a trend in anisotropy decay timescales across the series of metal complexes where the metal ions with larger charge density show faster anisotropy decay. Through our calculations, we attribute the change in anisotropy to changes in the coupling among the 5 local carbonyl sites that arises from structural changes to the ligand induced by changes in the charge density of the metal ions. Taken all together, our results show that the anisotropy decay of the of DTPA's carbonyl stretching modes can report on the conformational and structural changes of DTPA upon binding a metal ion.

Experimental

Synthetic procedure

All aqueous solutions were prepared from reagent grade materials using 18 MΩ distilled de-ionized water. Diethylenetriaminepentaacetic acid (DTPA), Fluka Analytical, >99.0%, was used as received. Deuterium oxide, Cambridge Isotope Laboratories Inc., D 99.9%, was used as received. High purity HNO₃ was used for conversion of the metal oxide to metal nitrate. The metal nitrate solutions were prepared by conversion from the solid oxide (99.999% from Arris International Co.) to the soluble nitrate by evaporating the dissolved oxide down and redissolving in HNO₃ multiple times. The metal nitrate solutions were converted to metal chloride solutions by evaporating the nitrate down and redissolving in 1.5 mol L⁻¹ HCl multiple times. The solutions were standardized to determine metal concentration and H⁺ concentration using ion-exchange chromatography (Dowex 50x beads, H⁺ form). From these stock solutions 0.08 mol L⁻¹ solutions of LnCl₃ were made in 18 MΩ distilled de-ionized water with 0.08 mol L⁻¹ DTPA pH adjusted to 4.0 using HCl or NaOH depending on the initial pH. A pH of 4 was chosen for all the samples as all the metal bound DTPA complexes are stable at pH ∼ 4, while the metal hydroxide precipitate forms at mildly basic pH. Therefore, the steady state and ultrafast experiments have been performed at pH ∼ 4. The solutions were converted to a D₂O matrix by 4 successive evaporations under vacuum and redissolution in D₂O.

Linear spectroscopy

Steady state FTIR spectra were collected on a JASCO FTIR-4600 spectrometer with a spectral resolution of 4 cm⁻¹ and averaging 10 accumulations per spectrum. The FTIR spectra were obtained in a Harrick transmission cell with 2 mm thick CaF₂ windows with a 25 μm spacer. The same sample cell was used for the ultrafast measurements.

Pump–probe spectroscopy

A detailed description of our mid-IR pump–probe spectrometer is given in our previous work.^36,37 Briefly, 60% of the 800 nm output (100 fs duration, 1 kHz repetition rate) from a commercial Ti:Sapphire laser was used to generate mid-IR pulse at 6250 nm (TOPAS two stage optical parametric amplifier, TOPAS DFG-1). The mid-IR output was split into a pump (>90% of the total power) and a probe pulse (<10% of the total power). A PhaseTech Pulse shaper was used to compress and chop the pump pulse. Polarization Gated Frequency Resolved Optical Gating (PG-FROG) measurements were performed to characterize the temporal width of the incoming pump and probe pulses where the temporal width of the cross correlation was measured to be 107 fs (Section S1, ESI†). Delay time dependent pump–probe spectra were collected by changing the delay time between the pump and the probe pulse with a computer-controlled delay stage. The pump–probe spectra were taken under parallel and perpendicular polarization conditions by setting the relative polarization between the pump and the probe pulse to be 0 or 90° respectively with respect to the probe pulse. The ultrafast mid-IR spectrometer was contained in a box and nitrogen gas was used to purge the spectrometer to maintain a RH of 5–8% at 26 °C within the box.

Computational methods

All electronic structure calculations on neutral and metal bound DTPA were performed using the ORCA 4.1.0 program and additional calculations on the deprotonated forms of free DTPA were performed using the ORCA 4.2.1 program.^38,39 Structure optimizations and analytical frequency analyses of free DTPA, La³⁺–DTPA, and Lu³⁺–DTPA were calculated using Density Functional Theory (DFT) with the Perdew–Burke–Ernzerhof (PBE)⁴⁰ functional together with Grimme's van der Waals corrections with Becke–Johnson damping (D3BJ),^41,42 as has been reported to work well with lanthanide-containing systems.^43–45 In order to take the solvent effect into account, a CPCM solvent continuum model is used in the calculations.

Ahlrich's double zeta basis set with a polarization function (Def2-SVP) and electron-core potentials (Def2-ECPs) were used for La³⁺ and Lu³⁺.^46–48 Since relativistic effects are important for lanthanides, we use the second generation (SARC2-QZVP)⁴⁹ basis set with polarization functions and zero-order regular approximation (ZORA)^50–54 Hamiltonians that have worked well with similar lanthanide complexes. In addition, the tight convergence (TightSCF) and the standard exchange–correlation functional integration grids (grid2 and finalgrid6) and the resolution of identity (RI) integral approximation were employed for all systems.^38–45

Results and discussion

Linear spectroscopy

The normalized FTIR spectrum of free DTPA shown in Fig. 1(A) (blue), exhibits two transitions with a main peak at 1626 cm⁻¹ and a shoulder at 1588 cm⁻¹. These transitions are assigned to the carbonyl stretching (ν_C=O) vibrations of the carboxylate groups of the lanthanide bound DTPA complexes, and a mixture of carboxylate and carboxylic acid groups of the free DTPA ligand consistent with previous studies.^20,31 The FTIR spectra of the lanthanide–DTPA complexes are also displayed in Fig. 1(A). Compared to free DTPA, the lanthanide DTPA complexes exhibit a skewed vibrational band in the 1550–1600 cm⁻¹ region. From the FTIR, the maximum frequency of the main peak (ν_max) for La³⁺, Nd³⁺, Gd³⁺, Tb³⁺, Er³⁺ and Lu³⁺ is at 1590 cm⁻¹, 1592 cm⁻¹, 1595 cm⁻¹, 1596 cm⁻¹, 1599 cm⁻¹, 1602 cm⁻¹ respectively.

Fig. 1 (A) Normalized FTIR spectra for free-DTPA (blue), and the lanthanide—DTPA complexes in D₂O with a pH of ∼4; (B) plot of the main peak frequency (ν_max) versus the inverse of ionic volume of the metal ions.

For the different metal complexes, the maximum frequency of the main peak increases with the atomic number of the metal. To further examine the trend in the frequency, Fig. 1(B) plots the main peak frequency (ν_max) versus the inverse of the ionic volume of the metal ion. To generate the plot, the ionic radii (r_Ln) of the lanthanides in the +3-oxidation state were taken from the literature.⁵⁵ From a linear fitting, we extract a slope of 6.3 × 10⁷ (±0.6 × 10⁷) cm⁻¹ pm⁻³. This indicates that the vibrational frequency of the carboxylate's carbonyl stretch is linearly proportional to the charge density of the metal ion where the charge density is the charge (Z) of the ion divided by the ionic volume (4πr³_Ln/3).

Assignment of vibrational transitions

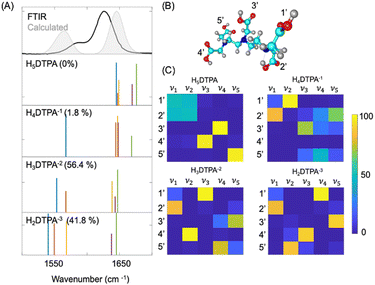
To assign the FTIR spectra, DFT calculations were performed on free DTPA, La³⁺–DTPA and Lu³⁺–DTPA. La and Lu were chosen as they are respectively the largest and smallest elements in the lanthanide series studied, and their FTIR spectra in the 1540–1660 cm⁻¹ region are the most different among the series.

At a pH of ∼4, the FTIR spectrum of free DTPA has contributions from three different species with the following relative concentrations: 1.8% of H₄DTPA⁻¹, 56.4% of H₃DTPA⁻², and 41.8% of H₂DTPA⁻³ (see Section S4, ESI† for details regarding the estimation of the relative populations of the different species). To better understand how the different species impact the FTIR spectra, we performed DFT calculations on the lowest energy deprotonated species to optimize the ground electronic states and determine their vibrational spectra. The detailed description of the energy optimization of differently deprotonated species is provided in Section S4 of the ESI.† The optimized geometries and cartesian coordinates of H₄DTPA⁻¹, H₃DTPA⁻², and H₂DTPA⁻³ are reported in the ESI† along with the fully protonated H₅DTPA. Fig. 2 displays the calculated vibrational frequencies of the carbonyl stretches for H₅DTPA, H₄DTPA⁻¹, H₃DTPA⁻², and H₂DTPA⁻³ (scaling factor of 0.9369). We find that the vibrational frequency is sensitive to the deprotonation state. According to the calculations, there are five normal modes that involve the stretching motions of carbonyl groups and these modes are labelled ν₁, ν₂, ν₃, ν₄, and ν₅ in Fig. 2. The nuclear displacements associated with the normal modes are reported in the ESI.† Our calculation suggests that the carbonyl stretching frequencies of the deprotonated carboxylate groups are significantly red shifted when compared to the stretching frequencies of the carboxylic acid groups of DTPA. The carboxylic acid groups of DTPA absorb at ∼1650 cm⁻¹, and H₅DTPA (having 5 carboxylic acid groups) has 5 transitions in this region. The carboxylate groups absorb at ∼1550 cm⁻¹, and with each deprotonation, the frequency associated with the carbonyl transitions of the deprotonated groups is shifted to 1550 cm⁻¹.

Fig. 2 (A) (top) The simulated spectrum of free DTPA (grey) at pH ∼ 4 along with the experimental FTIR of free DTPA (black), (bottom) DFT calculated stick spectra (ν₁-blue, ν₂-orange, ν₃-yellow, ν₄-purple, ν₅-green) of differently deprotonated DTPA species (H₅DTPA, H₄DTPA⁻¹, H₃DTPA⁻² and H₂DTPA⁻³) with their relative fractions at pH ∼ 4 reported as percentages; (B) DFT optimized structure of free H₅DTPA with the assignment of different carbonyl group sites for percent contribution calculations; (C) percent contribution of different carbonyl group sites (1′, 2′, 3′, 4′, and 5′) to the normal mode displacements of the carbonyl stretching modes (ν₁, ν₂, ν₃, ν₄, and ν₅).

To compare the experimental FTIR and the calculated spectra we first broadened the stick spectra of the differently deprotonated species with Gaussian functions (∼width 15 cm⁻¹) and weighted each spectrum by the relative concentration of the corresponding deprotonated species (denoted as a percentage on the calculated spectra in Fig. 2). We added the weighted spectra together to yield the calculated spectrum that is plotted in shaded grey in Fig. 2 along with the experimental spectrum of free DTPA at a pH ∼ 4. The calculated spectrum of free DTPA shows a larger splitting between the carboxylate and carboxylic acid peaks of 81 cm⁻¹, compared to the experimental value of 38 cm⁻¹ obtained from the FTIR. Such a larger splitting could be attributed to the lack of explicit hydrogen bonding interactions between DTPA and D₂O in the DFT calculations. Both the carboxylic acid and carboxylate groups can act as hydrogen bond donors and acceptors respectively, resulting in the spectral shift of the carbonyl stretching modes. However, incorporation of explicit solvation by D₂O and the quantum mechanical description of the hydrogen bonding interactions (which would also require incorporating anharmonic effects in determining the vibrational spectra) is beyond the scope of this work. From the comparison of the calculated spectra and FTIR spectra, we assign the shoulder peak at 1588 cm⁻¹ to the deprotonated carbonyl groups and the peak at 1626 cm⁻¹ to the protonated carbonyl groups.

Next, we characterized the nuclear motion associated with the normal modes of the different species by determining the percent contribution of the different carbonyl groups denoted with a number in Fig. 2(C) (summation over the constituting C and O atoms) corresponding to the normal mode displacements associated with the stretching modes (ν₁, ν₂, ν₃, ν₄, and ν₅). The method is described in Section S11 of the ESI† and the percent contributions are reported in Fig. 2(C). The matrices represent the contribution of the different carbonyl sites, 1′, 2′, 3′, 4′, and 5′ to the carbonyl stretching normal modes (ν₁, ν₂, ν₃, ν₄, and ν₅) for different free DTPA species. For all the species, the total contribution of these sites to the mass weighted displacements of the carbonyl stretching modes is higher than 50%. This suggests that the C=O stretching motions in the 1540–1700 cm⁻¹ region mostly involve the motion of the 5 carbonyl group sites and have minimal contributions from C–H bending and waging motions of the DTPA ligand. As observed in Fig. 2(C), the normal mode displacements of carbonyl stretch mostly arise from a single carbonyl site for all the species, except for neutral H₅DTPA, where ν₁ and ν₂ are equally shared between 1′ and 2′. Therefore, the normal modes of the predominant species of free DTPA at pH ∼ 4, have carbonyl stretches that are highly localized on the 5 different sites.

The optimized geometries of La and Lu bound DTPA are provided in Fig. 3(B). Comparison between the optimized geometries of the free DTPA (Fig. 2(B)) and the metal bound DTPA (Fig. 3(B)) shows a large-scale conformational change of the ligand structure after binding to the lanthanide ion. To determine how the large-scale conformational change impacts the vibrational modes of DTPA, we compare the DFT calculated frequencies of the carbonyl vibrations of the carboxylate groups for the metal bound DTPA. The DFT calculated vibrational stick spectra (scaling factors of 0.9522 and 0.9547 for La³⁺–DTPA and Lu³⁺–DTPA) in the 1540–1700 cm⁻¹ region are plotted in Fig. 3(A) along with the experimental FTIR spectra (in black). Both the La³⁺–DTPA and Lu³⁺–DTPA complexes exhibit a narrower distribution in normal mode frequencies when compared to free DTPA. Unlike free DTPA, the carbonyl stretches in the metal bound DTPA belong to carboxylate groups that bind to the metal (COO–M). The single vibrational band for the metal bound DTPA complexes has a skewed intensity distribution which we attribute to the differences in oscillator strengths for each vibrational mode. We note that the DFT calculations predict a blue shift in the unscaled frequencies of the carbonyl stretching modes from La³⁺–DTPA to Lu³⁺–DTPA. The blue shift is consistent with the experimental spectra where ν_max increases with the charge density of the metal ion. We also characterized the nuclear motion associated with the normal modes of the metal bound DTPA complexes by determining the percent contribution of the different carbonyl groups to the normal mode displacements. Fig. 3(C) reports the percent contribution of the carbonyl sites (1′, 2′, 3′, 4′, and 5′) to the normal mode displacements of ν₁, ν₂, ν₃, ν₄, and ν₅. As compared to free DTPA, we observe that the normal mode displacements for the metal bound DTPA are shared by all the different sites, indicating a delocalized nature of these modes across the different sites.

Fig. 3 (A) DFT calculated vibrational stick spectra for La³⁺–DTPA and Lu³⁺–DTPA are shown as dashed colored sticks (ν₁-blue, ν₂-orange, ν₃-yellow, ν₄-purple, ν₅-green) along with the experimental FTIR spectra (black); (B) the DFT optimized structures for La³⁺–DTPA and Lu³⁺–DTPA and, (C) the percent contribution of the different carbonyl groups (1′, 2′, 3′, 4′, and 5′) to the displacement of the carbonyl stretching normal modes (ν₁, ν₂, ν₃, ν₄, and ν₅).

Polarization dependent mid-IR pump–probe spectroscopy

To characterize the ultrafast vibrational dynamics of the carbonyl stretches in free DTPA and the lanthanide–DTPA complexes, we performed mid-IR pump probe spectroscopy under parallel and perpendicular polarization conditions. The parallel and perpendicular pump probe spectra are plotted as a function of delay time (t) between the pump and the probe pulses for free DTPA and Gd³⁺–DTPA in Fig. 4(A), (B) and (D), (E) respectively. For each spectrum, a negative amplitude feature corresponds to the ground state bleach (GSB) and stimulated emission (SE) processes. A positive amplitude feature arises from excited state absorption (ESA) and is red shifted with respect to the GSB due to the vibrational anharmonicity. Pump–probe spectra of free DTPA, (Fig. 4(A) and (B)) reveals strong GSB and ESA features at ω_probe = 1631 cm⁻¹ and ω_probe = 1604 cm⁻¹ respectively. A second weaker ESA peak is observed at ω_probe = 1565 cm⁻¹ which corresponds to the ESA associated with the GSB of the shoulder peak that absorbs at 1588 cm⁻¹ in the FTIR spectra. We note that we do not observe a GSB associated with the 1588 cm⁻¹ transition as it overlaps with the ESA feature at ω_probe = 1604 cm⁻¹. The Gd³⁺–DTPA pump probe spectra are shown in Fig. 4(D) and (E). We observe a GSB and ESA feature at ω_probe = 1603 cm⁻¹ and ω_probe = 1573 cm⁻¹ respectively. We note that the pump probe spectra of Gd³⁺–DTPA are representative of the other metal–DTPA complexes, where similar features are observed at slightly different frequencies as expected based on the frequency shifts in the FTIR (Fig. 1(A) and (B)). The pump probe spectra of the other metal–DTPA complexes are reported in the ESI.† For all the spectra, both the GSB and ESA absorption lineshapes are affected by the interaction of the pump and the probe pulses with residual water vapor present in the purged ultrafast spectrometer. These water vapor absorption peaks could also be recorded in the pump and the probe channel separately, by collecting spectra of the incoming pump and probe pulses.

Fig. 4 DTPA: (A) and (B) pump–probe spectra and (C) ESA ΔI traces versus delay time between the pump and the probe pulses for parallel (circles) and perpendicular (squares) polarizations; Gd³⁺–DTPA: (D) and (E) pump–probe spectra and (F) ESA ΔI traces versus delay time between the pump and the probe pulses for parallel (circles) and perpendicular (squares) polarizations.

To extract the vibrational population relaxation and the anisotropy decay, we focus on the time dependence of the ESA feature associated with main band in the FTIR. The GSB decays are reported in the ESI.† For the ESA feature, traces were taken from the parallel (I_‖) and perpendicular (I_⊥) polarized pump probe spectra across the series of lanthanide DTPA complexes and free DTPA where representative spectra of free and metal bound DTPA are plotted in Fig. 4(C) for free DTPA and Fig. 4(F) for Gd³⁺–DTPA. The following linear combinations of I_‖ and I_⊥ are used to extract the vibrational population relaxation, P(t), and the vibrational anisotropy decay, r(t).^35,56,57

Fig. 5 plots normalized population and anisotropy decays for the free DTPA ligand and the Gd³⁺–DTPA complex. The Gd³⁺–DTPA complex serves as a representative for the metal bound DTPA complexes where the metal–DTPA complexes all have the same general trends as the Gd³⁺–DTPA complex but decay with different timescales. As shown in Fig. S12 of the ESI,† all the population decays can be fit well with a biexponential function, P(t) = A₁ exp(−(t/t₁)) + A₂ exp(−(t/t₂)) while the anisotropy decays were fit with a single exponential decay and a constant offset, r(t) = A₁ exp(−(t/τ)) + A₂. For the fitting procedure we exclude data points from early waiting times and begin fitting data points after 200 fs to avoid contributions from pulse overlap and the coherent artifact. Table 1 reports the extracted parameters associated with the population relaxations and the anisotropy decays. Comparing the time constants of the population relaxation for free and metal bound species, we observe an overall slowdown of the energy relaxation of the excited carbonyl modes of the metal–DTPA complexes compared to free DTPA. Further, as shown in Table 1, both t₁ and t₂ are sensitive to the change in ionic radii of the central metal ion. In the following paragraphs we provide an explanation for this observation. We assign the slower timescale component (t₂) of the population relaxation to energy dissipation to the low frequency solvent modes. We find that the population relaxation is faster for free DTPA with a time constant of 980 fs ± 50 fs when compared to that of metal bound DTPA (∼1250–1870 fs). The faster relaxation for free DTPA is expected due to the direct exposure of the COO⁻/COOH groups to the solvent. For the metal bound DTPA complexes, the metal binding shields the carboxylate groups from the solvent molecules and thus extends the vibrational lifetime to 1250–1870 fs. This is consistent with previous work on oxalates, where contact ion-pair formation with metal ions leads to slower bath dissipation of the oxalate asymmetric stretching vibrations.^33,34 We also find the t₂ time constant is highly sensitive to the identity of the central metal ion, with the slowest time constant extracted for Nd³⁺.

Fig. 5 (A) Normalized population decay plotted as a function of delay time (t) for free DTPA and Gd³⁺–DTPA (representative of all the lanthanide DTPA complexes). (B) Normalized anisotropy decay plotted as a function of delay time (t) for free DTPA and Gd³⁺–DTPA (representative of all the lanthanide DTPA complexes). The fits associated with the optimized parameters reported in Table 1 are plotted as solid lines.

Table 1 Population lifetimes and anisotropy decay time constants. Error bars for the metal complexes represent the standard error measured over five experiments

Sample	Population relaxation				Anisotropy decay
	A 1	t 1 (ps)	A 2	t 2 (ps)	A 1	τ (ps)	A 2
Free-DTPA	0.63 ± 0.03	0.19 ± 0.01	0.39 ± 0.02	0.98 ± 0.05	0.36 ± 0.02	0.94 ± 0.11	0
La^3+–DTPA	0.91 ± 0.02	0.34 ± 0.01	0.21 ± 0.03	1.48 ± 0.11	0.33 ± 0.04	0.41 ± 0.12	0.1 ± 0.03
Nd^3+–DTPA	0.93 ± 0.02	0.39 ± 0.02	0.19 ± 0.03	1.87 ± 0.14	0.33 ± 0.04	0.39 ± 0.1	0.02 ± 0.02
Gd^3+–DTPA	0.80 ± 0.02	0.4 ± 0.02	0.19 ± 0.02	1.68 ± 0.16	0.27 ± 0.03	0.35 ± 0.1	0.01 ± 0.01
Tb^3+–DTPA	1.02 ± 0.02	0.35 ± 0.01	0.25 ± 0.03	1.44 ± 0.08	0.34 ± 0.03	0.39 ± 0.07	0.08 ± 0.01
Er^3+–DTPA	0.84 ± 0.01	0.33 ± 0.01	0.21 ± 0.02	1.47 ± 0.09	0.31 ± 0.03	0.39 ± 0.1	0.16 ± 0.02
Lu^3+–DTPA	0.98 ± 0.04	0.33 ± 0.02	0.32 ± 0.05	1.25 ± 0.11	0.4 ± 0.04	0.28 ± 0.06	0.03 ± 0.02

---

To compare the relaxation times between the free and metal bound DTPA, we first want to determine if the different protonation states of free DTPA impact the extracted time constants. Since spectral congestion from different species present at pH ∼ 4 leads to cancellation of peaks in the pump–probe spectra of free DTPA, we analyze the 2DIR spectrum of free DTPA obtained under the same experimental conditions. Section S7 in the ESI† reports the 2DIR spectra of free DTPA at different waiting times, along with the waiting time dependent ESA amplitude for both the main peak associated with the carboxylic acids groups and shoulder peak associated with the carboxylate groups (Fig. S13, ESI†). The comparison of excited state lifetimes between the main and the shoulder peak suggests that the population relaxation is not sensitive to the deprotonation state of DTPA species (Table S3, ESI†).

As shown in Table 1, the faster relaxation (t₁) extracted from the main band (1604 cm⁻¹) occurs with a time constant of 190 ± 10 fs for free DTPA, whereas it is increased up to 330 ± 20 fs–400 ± 20 fs for the metal bound DTPA conformations. Typically, the ultrafast relaxation processes can be attributed to intramolecular vibrational energy redistribution (IVR). Previous studies on lanthanide–EDTA complexes have shown that the ion binding impedes the IVR mechanism by altering the intramolecular coupling with the lower frequency modes of the ligand in the EDTA complexes.³¹ The slower t₁ timescales for lanthanide DTPA complexes compared to the free DTPA ligand are consistent with the previous EDTA studies. However, owing to the proximity of the carboxylates in metal bound DTPA, we also need to consider the impact of vibrational energy transfer (VET) among the different carbonyl stretching modes in the 1560–1660 cm⁻¹ region. If vibrational energy transfer occurs within a few hundreds of femtoseconds, it may also contribute to the measured t₁ timescales. To better understand the different processes contributing to the ultrafast decay of the excited states of DTPA we analyze the vibrational anisotropy where previous work has demonstrated that the vibrational anisotropy can be sensitive to energy transfer processes.^34,58,59 As will be discussed below, we find that the anisotropy decay reveals ultrafast population transfer among the carbonyl stretching modes of the lanthanide–DTPA complexes.

The timescales and amplitudes extracted from fitting the vibrational anisotropy decays for free and metal bound DTPA complexes are reported in Table 1. These time constants differ significantly for the free and metal bound conformations. For free DTPA, the anisotropy decays with a time constant of 940 fs ± 110 fs. Further, Fig. S14 (ESI†) shows that the ESA of the shoulder peak in the pump probe spectra of free DTPA has longer time constant (1530 fs ± 450 fs) as compared to that of the main peak. The time constants are provided in Section S7 of the ESI† (Table S4, ESI†). In comparison to free DTPA, anisotropy decay is faster for the metal bound DTPA complexes with time constants ranging from 280 fs ± 60 fs extracted for Lu³⁺–DTPA to 410 fs ± 120 fs extracted for La³⁺–DTPA. The time dependence of the vibrational anisotropy of the transient signal could originate from different molecular processes. For example, molecular reorientation in the solution during the vibrational dephasing can lead to anisotropy decay.^36,37,56,60 However, given the molecular volume of the free DTPA and metal bound DTPA complexes, the ∼300 fs decay of the anisotropy is much faster than that predicted for overall molecular reorientation based on the Stokes–Einstein Debye equation (see Section S8 of the ESI† for more details). In addition to molecular reorientation, the carbonyl groups may undergo a “wobbling in a cone motion”, a more local rotation in a cone shaped space.^37,56 However, such motion will be highly restricted in the metal bound conformations compared to the free DTPA ligands.²⁶ Thus, the wobbling in a cone motion cannot fully account for the sub-ps loss of vibrational anisotropy. Another mechanism resulting in ultrafast anisotropy decay is vibrational energy transfer (VET) among the near degenerate vibrational states, which induces an angular jump in the vibrational transition dipole moments and subsequent loss of anisotropy.^57–59 We attribute the ultrafast anisotropy decay to VET among the carbonyl stretching modes of DTPA for both the metal free and metal bound conformations. This assignment can explain the difference in anisotropy decay between free and metal bound DTPA, where the metal bound complexes can access faster VET channels due to the conformational change of DTPA upon metal binding. As the carboxylate groups interact with the metal ion, the coupling among the different carbonyl sites can be altered and additional vibrational energy transfer pathways can be accessed on much faster timescales. To further test this assignment and determine if the structural changes upon metal binding can lead to ultrafast population transfer, we use a simple model to describe VET in free DTPA, La³⁺–DTPA, and Lu³⁺–DTPA.

Theoretical modelling

To investigate the impact of structural changes associated with metal complexation, we focus on the vibrational energy transfer in free DTPA, La³⁺–DTPA, and Lu³⁺–DTPA, where La³⁺ and Lu³⁺ lie at the ends of the lanthanide series. As discussed earlier, all the free DTPA species with variable deprotonation states (H₄DTPA⁻¹, H₃DTPA⁻², and H₂DTPA⁻³) are similar to neutral DTPA (H₅DTPA) in terms of structural conformation and the delocalization of the ν_C=O normal modes. Thus, we choose neutral DTPA as a model for the free DTPA species and compare its energy transfer dynamics with that of metal bound DTPAs. Both the neutral DTPA and metal bound DTPA have five C=O bonds, one at each site, that have comparable bond lengths (see ESI†), where the C=O bonds are the main contributor to the normal mode displacements in this spectral region (see ESI†). We note that the C–O–H bonds of the free DTPA complex and the C–O–M ionic bonds of the metal bound DTPA complexes are both longer than the C=O bonds for a given site. Thus, we will focus on comparing the energy transfer between the C=O bonds to characterize the effect of ion binding induced conformational change of the ligand on the vibrational dynamics. For the simulation, we build a simple model to account for energy transfer among the carbonyl stretching modes of the metal free and metal bound DTPA species using the DFT optimized structures. We then use this model to predict the population transfer among the different carbonyl sites following the procedure laid out by the Stock and Hochstrasser groups for polypeptides and carboxylate model systems.^34,61

To build the model we first extract the Hamiltonian in the local site basis from the DFT calculations, where the individual sites are located on different carbonyl groups that we treat as harmonic oscillators. The off-diagonal coupling elements of the Hamiltonian represent the inter-site coupling between the local carbonyl sites. We then use the extracted site energies and couplings to solve the time dependent Schrödinger equation in the local site basis. From the modelling, we gain insight into the role of site energy fluctuations and the magnitude of the inter-site couplings on the timescale of energy transfer among the carbonyl sites, and we compare the energy transfer for the free and metal bound conformations of DTPA.

Wavefunction demixing (WFD) analysis

To extract the local site energies and inter-site couplings, we perform a wavefunction demixing (WFD) analysis following the procedure (Section S12, ESI†) introduced by the Cho and Wang groups.^62,63 In the past, this method has been shown to efficiently estimate the inter-site coupling among the local carbonyl sites for amide-I and amide-II vibrations of α-helix and β-sheet structures. For DTPA, 5 C=O bonds, one bond for COO–M/COOH group, are considered as local sites as they participate in the carbonyl stretching normal modes obtained from the DFT calculations (see Fig. 2 and 3). Fig. 6 displays the Hamiltonian in the local site basis, {ϕ_i}, for free H₅DTPA (Fig. 6(A)), La³⁺–DTPA (Fig. 6(B)) and Lu³⁺–DTPA (Fig. 6(C)). We note that the local sites are color coded for each of the Hamiltonians where the color coding for each molecule is unique. The diagonal elements of the Hamiltonian report the vibrational frequencies (ω_i) of the local sites in cm⁻¹, where the off-diagonal elements report the inter-site couplings (β_ij) between the different local sites, i and j (eqn (3)).As expected, the off-diagonal elements are closely symmetric (β_ij = β_ji) for both metal free and metal bound conformations. However, the magnitude of coupling is larger for the metal bound cases (La³⁺–DTPA and Lu³⁺–DTPA) as compared to the free H₅DTPA ligand. We attribute the change in coupling to the conformational change of the ligand that accompanies the metal ion binding. To compare the couplings, we look at the average of the absolute values of the coupling over all sites, 〈|β_ij|〉. 〈|β_ij|〉 in La³⁺–DTPA and Lu³⁺–DTPA is 4.0 ± 1.6 cm⁻¹ and 5.2 ± 2.2 cm⁻¹ respectively. In comparison, the 〈|β_ij|〉 for the free DTPA ligand is 0.23 ± 0.34 cm⁻¹. Thus, the average couplings for the metal DTPA complexes, are larger than that of free DTPA, and are sensitive to the central metal ion. This indicates that the conformational changes associated with DTPA complexation impacts the coupling between the carbonyl stretches.

Fig. 6 The results of wavefunction demixing analysis for the carbonyl stretching modes in the 1540–1700 cm⁻¹ region of (A) free H₅DTPA, (B) La³⁺–DTPA, and (C) Lu³⁺–DTPA. The sites are color coded: site 1 (blue), site 2 (orange), site 3 (yellow), site 4 (green), site 5 (purple); the diagonal matrix elements are the vibrational local site frequencies, {ω_i}, and the off-diagonal matrix elements are the associated inter-site couplings, {β_ij}. All the site frequencies and couplings are reported in cm⁻¹.

Time dependent fluctuations to local site Hamiltonian

Before modeling energy transfer in the local site basis, we add fluctuations to the site frequencies (δω) as a function of time according to the following expression.⁶⁴

ω_i(t) = ω_i0 + δω^inh_i(t) + δω^homo_i(t) (4)

The method for simulating the time dependent Gaussian fluctuations (〈δω_i(t)〉 = 0) is provided in the ESI,† Section S9. In eqn (4), the homogeneous contribution is completely decorrelated, where the inhomogeneous contribution has a bath correlation time, τ_c characterized by eqn (5).

With this model we assume that the transition dipole moment and structure is static, so we only consider fluctuations in the site energies and not the couplings. We note that structural changes will occur in solution which will impact the energy transfer rates through altering the β_ij terms (Sections S9 and S10, ESI†). However, for the simple model here we only consider fluctuations in the site energy terms.

For the simulations, we have chosen values of the inhomogeneous and homogeneous contributions for site frequencies with a standard deviation of 10 cm⁻¹ respectively. These values are consistent with previous work by Hochstrasser et al. focusing on the oxalate ion.^34,35 The bath correlation time for the frequency fluctuations was set to be τ_c = 0.5 ps, consistent with previous 2DIR spectroscopy studies of carboxylates in D₂O.^33–35

Energy transfer in local site basis

Modelling the evolution of the vibrational wavefunction with the time dependent Hamiltonian gives the energy transfer rate in the local site basis. This method has previously been used by the Stock and Hochstrasser groups.^34,35,61 After producing the time dependent Hamiltonian in the local site basis for multiple trajectories, we solve the Schrödinger equation using a fourth order Runge–Kutta method (RKM) following the previous methods. The accuracy of the simulation is strongly dependent on the step size used in the RKM. In our simulation, we generate 5000 trajectories of 2 ps duration with a time step of 0.5 fs starting from the local site Hamiltonian of free DTPA, La³⁺–DTPA, or Lu³⁺–DTPA obtained from the WFD analysis. Eqn (6) represents the time dependent Schrödinger equation, where c_i, and ω_i are the coefficient and the site frequency of the local site i.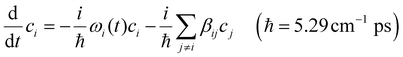From the coefficients obtained by solving eqn (6), we can obtain the elements of the density matrix (eqn (7)) and the population for site i if i = j. During the simulations, we compute the time dependent population of different local sites according to eqn (7) where we take the average over 5000 trajectories (N = 5000).

Population transfer mediated anisotropy decay

The results of the simulations are plotted in Fig. 7 with a schematic description of the energy level diagram depicting the local and normal modes for metal free and metal bound DTPA (Fig. 7(A)). As described above, the high frequency carbonyl stretching manifold of free DTPA lies in the weak coupling regime (〈|β_ij|〉 = 0.23 ± 0.34 cm⁻¹). Metal binding induces a conformational change that results in stronger coupling between the carbonyl groups for the metal bound DTPA complexes with 〈|β_ij|〉 = 4.0 ± 1.6 cm⁻¹ for La³⁺–DTPA and 〈|β_ij|〉 = 5.2 ± 2.2 cm⁻¹ for Lu³⁺–DTPA. The larger inter-site coupling for the metal complexes results in a faster timescale for population transfer among the carbonyl groups compared to free DPTA. Further, decreasing the size of the metal ion (from La³⁺ to Lu³⁺) significantly alters the coupling which subsequently results in the faster population transfer for Lu³⁺–DTPA. As discussed above, we assume that the fluctuations in the inter-site coupling are insignificant owing to the rigid conformation of bound carboxylates around the metal ion. The results of the simulation are presented in Fig. 7(B), (C) and(D) for free DTPA, La³⁺–DTPA and Lu³⁺–DTPA respectively. For ease of discussion, we only consider two of the representative sites, site 3 and site 5, in the main text. For each of the species we start the simulation assuming that the system is initially populated to either site 3 or site 5. Simulation outcomes of initial populations at sites 1, 2, and 4 are presented in the ESI† for free DTPA, La³⁺–DTPA and Lu³⁺–DTPA. We find that there is a slow population transfer among the local sites for free DTPA (Fig. 7(B) and Fig. S16 top row, ESI†). In contrast, La³⁺–DTPA and Lu³⁺–DTPA exhibit ultrafast population transfer, with the population decaying more rapidly over the first 1 ps, owing to the larger magnitude of inter-site coupling for the metal bound carboxylate groups (Fig. 7(C), (D) and Fig. S16 middle, and bottom row, ESI†). Comparing the two metal complexes, we find that energy transfer in Lu³⁺–DTPA is slightly faster than in La³⁺–DTPA, consistent with larger couplings for the Lu³⁺–DTPA complex. The faster energy transfer in Lu³⁺–DTPA is in qualitative agreement with the experimental anisotropy decay of ∼280 fs for Lu³⁺–DTPA and 410 fs for La³⁺–DTPA. Thus, the simulations support the assignment of the anisotropy decay to VET among the different carbonyl sites, and the simple model captures the importance of metal binding induced structural reorganization on the vibrational dynamics of the high frequency carbonyl stretching modes of DTPA.

Fig. 7 (A) Schematic of local and normal modes for weak (left) and strong (right) vibrational inter-site coupling among the carbonyl stretching modes in the 1540–1700 cm⁻¹ region; (B)–(D) time dependent population of the local sites in free-DTPA, La³⁺–DTPA, Lu³⁺–DTPA with initial population at site 3 (left) and site 5 (right) respectively.

We note that though the simulations can predict the general behavior, the simulation for free DTPA approaches equilibrium beyond the 2 ps time window. For free DTPA, conformational fluctuation in the solution can also lead to fluctuations in the inter-site coupling and associated vibrational dynamics. To determine whether this scenario gives rise to faster energy transfer timescales, which would be more consistent with the experimental timescale for anisotropy decay, we added fluctuations to the inter-site couplings for both free and metal bound DTPA (ESI,† Section S10). However, the coupling fluctuations added here are generated based on a correlated Gaussian fluctuation model as shown in the ESI.† Thus, these time dependent couplings are only representative of possible structural fluctuations of free DTPA in solution and not extracted from molecular dynamics simulation. However, from our simulations, we find that fluctuations in the inter-site couplings result in a faster population transfer among the carbonyl sites of free DTPA, which roughly matches with the experimental anisotropy decay timescale. The qualitative agreement between the simulations and experimental results indicates that vibrational energy transfer (VET) among the high frequency carbonyl stretching modes of the different sites is one of the primary mechanisms for anisotropy decay in DTPA. As the DTPA undergoes significant ligand reorganization during lanthanide binding, the metal electric field induces a conformational change leading to an increase in inter-site coupling among the carboxylate groups. The increase in inter-site coupling leads to faster population transfer among the different sites which results in a faster reorientation of the transition dipole vector of the carbonyl stretching modes. Thus, the anisotropy decay is very sensitive to ion binding induced vibrational delocalization.

Competing population relaxation: free DTPA vs. metal bound DTPA

Fig. 8 summarizes the energy relaxation pathways in metal free and metal bound DTPA. In free DTPA, the IVR to lower energy stretching and bending modes is faster than the VET among the different carbonyl stretching modes for each COO⁻/COOH group. This is primarily caused by poor inter-site coupling as suggested by the DFT calculations and the energy transfer simulations. For metal bound DTPA, the lanthanide binding leads to a large-scale conformational change of the ligand. Such structural change affects the vibrational relaxation in two main ways. (1) As discussed in previous work on EDTA complexes,^30,31 the IVR process to lower energy modes becomes slower. (2) In addition, the conformation change associated with metal bound DTPA leads to an increase in the inter-site coupling as the carboxylate groups approach each other. The increase in inter-site coupling facilitates ultrafast VET among the carbonyl stretching modes of the different carboxylate groups. The assignment of this pathway is supported by the complete decay of the anisotropy signal on the ultrafast timescale.

Fig. 8 (A) and (B) A Jablonski diagram denoting the vibrational dynamics of the high frequency carbonyl stretching manifold in metal free DTPA and metal bound DTPA complexes.

In the metal bound DTPA complexes, we find that both the ultrafast VET and IVR pathways contribute to the shorter lifetime (t₁) extracted from the population relaxation for the metal bound DTPA complexes. By combining a lifetime analysis with vibrational anisotropy decay measurements and simulations we are able to resolve the complicated ultrafast vibrational dynamics in metal–DTPA complexes.

Conclusion

In this work, we used polarization dependent mid-IR pump–probe spectroscopy to investigate the impact of lanthanide binding on the vibrational dynamics of DTPA. Lanthanide binding to DTPA causes large structural rearrangement in the ligand, which gives rise to two distinct conformations for metal free and metal bound DTPA in solution. We characterized the different conformations by the isotropic and anisotropic vibrational response of the high frequency carbonyl modes of DTPA. In addition, we found that the dynamics obtained from the vibrational response of the carbonyl stretches are very sensitive to picometer scale change in the size of the metal ion within the binding pocket. By comparing the vibrational lifetime of the free and metal bound conformations, we extract a slower energy relaxation for DTPA in metal bound conformations (Fig. 8(B)). Comparing the population decay across the series of lanthanide complexes shows that the vibrational lifetime of DTPA is sensitive to the identity of the metal ions, consistent with previous work on EDTA.^30,31 In addition to population relaxation, we characterized vibrational energy transfer among the high frequency near resonant carbonyl stretching modes of DTPA by using the anisotropic vibrational response. We find that an energy transfer among the carbonyl stretching modes is faster in the metal bound conformations, with a strong dependency on the identity of the metal ion (Fig. 8(A) and (B)). Quantum mechanical calculations and theoretical modeling of the vibrational energy transfer in metal free and metal bound conformations reveals the crucial role of inter-site vibrational coupling among the different carbonyl sites in the VET process. We conclude that the increase in inter-site coupling leads to efficient VET pathways in the metal bound conformations, which corresponds to metal ion binding induced conformational change of DTPA. Thus, the anisotropy decay reports on the metal induced structural distortion of DTPA, which is a key step in lanthanide separation.

Author contributions

J. A. J., and J. C. S. have synthesized and purified the compounds. T. S., and G. C. S. have conducted the DFT calculations. R. B., and J. M. A. have collected all the ultrafast IR spectra, and analyzed them. R. B., and J. M. A. have done the theoretical simulation with inhouse codes. All authors contributed to discussing the results and writing the manuscript. All authors gave approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Center for Sustainable Separations of Metals (CSSM), a National Science Foundation Center for Chemical Innovation (CHE-1925708) for supporting this work. DFT work was supported by the Department of Energy grant DE-SC0022231. RB acknowledges Wei Weng and Phoebe Askelson for training and discussion on spectroscopic tools.

References

1. D. Kim, L. E. Powell, L. H. Delmau, E. S. Peterson, J. Herchenroeder and R. R. Bhave, Environ. Sci. Technol., 2015, 49, 9452–9459.
2. Y. Fujita, S. K. McCall and D. Ginosar, MRS Bull., 2022, 47, 283–288.
3. K. De Jesus, R. Rodriguez, D. L. Baek, R. V. Fox, S. Pashikanti and K. Sharma, J. Mol. Liq., 2021, 336, 116006.
4. K. Binnemans, P. T. Jones, B. Blanpain, T. Van Gerven, Y. Yang, A. Walton and M. Buchert, J. Cleaner Prod., 2013, 51, 1–22.
5. E. Alonso, A. M. Sherman, T. J. Wallington, M. P. Everson, F. R. Field, R. Roth and R. E. Kirchain, Environ. Sci. Technol., 2012, 46, 3406–3414.
6. T. Cheisson and E. J. Schelter, Science, 2019, 363, 489–493.
7. M. Regueiro-Figueroa, D. Esteban-Gómez, A. de Blas, T. Rodríguez-Blas and C. Platas-Iglesias, Chem. – Eur. J., 2014, 20, 3974–3981.
8. J. A. Mattocks, J. J. Jung, C.-Y. Lin, Z. Dong, N. H. Yennawar, E. R. Featherston, C. S. Kang-Yun, T. A. Hamilton, D. M. Park, A. K. Boal and J. A. Cotruvo, Nature, 2023, 618, 87–93.
9. K. L. Nash, D. Brigham, T. C. Shehee and A. Martin, Dalton Trans., 2012, 41, 14547–14556.
10. J. C. Braley, T. S. Grimes and K. L. Nash, Ind. Eng. Chem. Res., 2011, 51, 629–638.
11. A. V. Gelis, P. Kozak, A. T. Breshears, M. A. Brown, C. Launiere, E. L. Campbell, G. B. Hall, T. G. Levitskaia, V. E. Holfeltz and G. J. Lumetta, Sci. Rep., 2019, 9, 12842.
12. J. A. Jackson, V. Linero, N. P. Bessen, K. L. Nash and J. C. Shafer, Sep. Purif. Technol., 2021, 274, 118919.
13. M. Nilsson and K. L. Nash, Solvent Extr. Ion Exch., 2007, 25, 665–701.
14. N. E. F. Uhnak and K. L. Nash, Solvent Extr. Ion Exch., 2020, 38, 401–416.
15. J. Dehaudt, N. J. Williams, H. Luo and S. Dai, Solvent Extr. Ion Exch., 2018, 36, 574–582.
16. T. S. Grimes, C. R. Heathman, S. Jansone-Popova, V. S. Bryantsev, S. Goverapet Srinivasan, M. Nakase and P. R. Zalupski, Inorg. Chem., 2017, 56, 1722–1733.
17. T. J. Clough, L. Jiang, K. L. Wong and N. J. Long, Nat. Commun., 2019, 10, 1–14.
18. C. A. Chang, Y. L. Liu, C. Y. Chen and X. M. Chou, Inorg. Chem., 2001, 40, 3448–3455.
19. R. J. Ellis, D. M. Brigham, L. Delmau, A. S. Ivanov, N. J. Williams, M. N. Vo, B. Reinhart, B. A. Moyer and V. S. Bryantsev, Inorg. Chem., 2017, 56, 1152–1160.
20. M. M. Foreman and J. Mathias Weber, J. Phys. Chem. Lett., 2022, 13, 8558–8563.
21. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
22. A. G. Baldwin, A. S. Ivanov, N. J. Williams, R. J. Ellis, B. A. Moyer, V. S. Bryantsev and J. C. Shafer, ACS Cent. Sci., 2018, 4, 739–747.
23. P. Thakur, J. L. Conca, C. J. Dodge, A. J. Francis and G. R. Choppin, Radiochim. Acta, 2013, 101, 221–232.
24. T. Liu, K. R. Johnson, S. Jansone-Popova and D. Jiang, JACS Au, 2022, 2, 1428–1434.
25. Y.-M. Chen, C.-Z. Wang, Q.-Y. Wu, J.-H. Lan, Z.-F. Chai, C.-M. Nie and W.-Q. Shi, J. Mol. Liq., 2020, 299, 112174.
26. L. Fusaro, F. Mocci, R. N. Muller and M. Luhmer, Inorg. Chem., 2012, 51, 8455–8461.
27. G. Tian, L. R. Martin, Z. Zhang and L. Rao, Inorg. Chem., 2011, 50, 3087–3096.
28. S. C. Edington, A. Gonzalez, T. R. Middendorf, D. B. Halling, R. W. Aldrich and C. R. Baiz, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E3126–E3134.
29. A. A. Korotkevich and H. J. Bakker, J. Chem. Phys., 2022, 156, 094501.
30. S. Mitra, K. Werling, E. J. Berquist, D. S. Lambrecht and S. Garrett-Roe, J. Phys. Chem. A, 2021, 125, 4867–4881.
31. S. C. Edington and C. R. Baiz, J. Phys. Chem. A, 2018, 122, 6585–6592.
32. C. R. Baiz, B. Błasiak, J. Bredenbeck, M. Cho, J.-H. Choi, S. A. Corcelli, A. G. Dijkstra, C.-J. Feng, S. Garrett-Roe, N.-H. Ge, M. W. D. Hanson-Heine, J. D. Hirst, T. L. C. Jansen, K. Kwac, K. J. Kubarych, C. H. Londergan, H. Maekawa, M. Reppert, S. Saito, S. Roy, J. L. Skinner, G. Stock, J. E. Straub, M. C. Thielges, K. Tominaga, A. Tokmakoff, H. Torii, L. Wang, L. J. Webb and M. T. Zanni, Chem. Rev., 2020, 120, 7152–7218.
33. D. G. Kuroda and R. M. Hochstrasser, Phys. Chem. Chem. Phys., 2012, 14, 6219–6224.
34. D. G. Kuroda and R. M. Hochstrasser, J. Chem. Phys., 2011, 135, 204502.
35. D. G. Kuroda, M. Abdo, L. Chuntonov, A. B. Smith III and R. M. Hochstrasser, J. Chem. Phys., 2013, 139, 164514.
36. W. Weng, A. B. Weberg, R. Gera, N. C. Tomson and J. M. Anna, J. Phys. Chem. B, 2021, 125, 12228–12241.
37. R. Gera, S. L. Meloni and J. M. Anna, J. Phys. Chem. Lett., 2019, 10, 413–418.
38. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
39. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
41. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
42. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
43. D. Panthi, O. Adeyiga, N. K. Dandu and S. O. Odoh, Inorg. Chem., 2019, 58, 6731–6741.
44. W. Mao, L. Xiang, L. Maron, X. Leng and Y. Chen, J. Am. Chem. Soc., 2017, 139, 17759–17762.
45. X. Pan, C. Wu, H. Fang and C. Yan, Inorg. Chem., 2022, 61, 14288–14296.
46. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
47. M. Dolg, H. Stoll, A. Savin and H. Preuss, Theor. Chim. Acta, 1989, 75, 173–194.
48. X. Cao and M. Dolg, J. Chem. Phys., 2001, 115, 7348–7355.
49. D. Aravena, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2016, 12, 1148–1156.
50. T. Nakajima and K. Hirao, Chem. Rev., 2011, 112, 385–402.
51. M. Reiher, Theor. Chem. Acc., 2006, 116, 241–252.
52. T. Saue, ChemPhysChem, 2011, 12, 3077–3094.
53. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792.
54. E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281–293.
55. J. B. Lansman, J. Gen. Physiol., 1990, 95, 679–696.
56. H.-S. Tan, I. R. Piletic and M. D. Fayer, J. Chem. Phys., 2005, 122, 174501.
57. N. E. Levinger and L. A. Swafford, Annu. Rev. Phys. Chem., 2009, 60, 385–406.
58. D. G. Kuroda, P. K. Singh and R. M. Hochstrasser, J. Phys. Chem. B, 2012, 117, 4354–4364.
59. D. Yu. Vorobyev, C.-H. Kuo, D. G. Kuroda, J. Nathan Scott, J. M. Vanderkooi and R. M. Hochstrasser, J. Phys. Chem. B, 2010, 114, 2944–2953.
60. G. M. Sando, Q. Zhong and J. C. Owrutsky, J. Chem. Phys., 2004, 121, 2158–2168.
61. M. Kobus, P. H. Nguyen and G. Stock, J. Chem. Phys., 2011, 134, 124518.
62. S. Ham, S. Cha, J.-H. Choi and M. Cho, J. Chem. Phys., 2003, 119, 1451–1461.
63. J. Zhao and J. Wang, J. Phys. Chem. B, 2015, 119, 14831–14839.
64. R. Fernández-Terán and P. Hamm, J. Chem. Phys., 2020, 153, 154706.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00673a

---