Data-driven stabilization of NimPdn–m nanoalloys: a study using density functional theory and data mining approaches†
Tiago M.
Souza
a,
Lucas B.
Pena
a,
Juarez L. F.
Da Silva
 b and
Breno R. L.
Galvão
b and
Breno R. L.
Galvão
 *ac
*ac
aCentro Federal de Educação Tecnológica de Minas Gerais, CEFET-MG, Av. Amazonas 5253, 30421-169 Belo Horizonte, Minas Gerais, Brazil. E-mail: brenogalvao@gmail.com
bSão Carlos Institute of Chemistry, University of São Paulo, P.O. Box 780, 13560-970 São Carlos, SP, Brazil
cDepartment of Chemistry and Chemical Biology, University of New Mexico, Albuquerque 87131, New Mexico, USA
First published on 20th May 2024
Abstract
Green hydrogen, generated through the electrolysis of water, is a viable alternative to fossil fuels, although its adoption is hindered by the high costs associated with the catalysts. Among a wide variety of potential materials, binary nickel-palladium (NiPd) systems have garnered significant attention, particularly at the nanoscale, for their efficacious roles in catalyzing hydrogen and oxygen evolution reactions. However, our atom-level understanding of the descriptors that drive their energetic stability at the nanoscale remains largely incomplete. Here, we investigate by density functional theory calculations the descriptors that drives the stability of the NimPdn–m clusters for different sizes (n = 13, 27, 41) and compositions. To achieve our goals, a large number of trial configurations were generated and selected using data mining algorithms (k-means, t-SNE) and genetic algorithms, while the most important physical–chemical descriptors were identified using Spearman correlation analysis. We have found that core–shell formation, with the smaller Ni atoms lying in the center of the particle, plays a major role in the stabilization of the nanoalloys, and this effect causes the alloys to assume a icosahedral-fragment configuration (as the unary nickel cluster) instead of a fcc fragment (as the unary palladium cluster). However, the core–shell formation in this alloy is unique in that Pd poor compositions exhibit scattered Pd atoms on the surface. As the palladium content increases, this gives rise to the complete Pd shell. This stabilization mechanism is quantitatively supported by the different correlations observed in the number of Ni–Ni and Pd–Pd bonds with energy, in which the latter tends to decrease alloy stability. Furthermore, a notable trend is the correlation between the coordination number of Ni atoms with alloy stabilization, while the coordination of Pd atoms shows an inverse correlation.
1 Introduction
The escalating concerns regarding environmental pollution driven by the consumption of fossil fuels, in conjunction with energy security issues, have catalyzed an increased interest in alternative energy sources, notably the generation of molecular hydrogen (H2) through the electrolysis of water using renewable energy sources (e.g. photovoltaics, wind).1 To date, the feasibility of this process has been constrained to the use of costly catalysts such as Pt and Ru/Ir oxides,1–3 which hinder the large-scale production of H2.1,2 A potential resolution to this challenge may involve the employment of particles with about one nanometer (cluster) composed of noble elements in conjunction with economically viable and abundantly available metals.1,2Nanoparticles are known to have physical–chemical properties very different in comparison to their bulk counterparts, and hence their properties can be investigated for a wide range of applications. For instance, it has been demonstrated that a low activation barrier for H2 production from water is obtained using the unary Aln (with n = 12 and n = 17) cluster as a catalyst.4 Small Nin and Pdn clusters have been assessed for oxygen evolution reaction (OER), presenting considerable catalytic activity.3 It is well known that the properties of such particles can be modulated by changes of their size, charge state, etc.3,5–7 In fact, it has been experimentally shown that water oxidation in alkaline conditions does not occur on Pd4, while Pd6 and Pd17 are active,8 that is, a strong dependence on the cluster size.
In addition to size, the physical–chemical properties of metallic nanoparticles can also be tuned by composition.3,5–7 For example, the hydrogen evolution reaction (HER) and OER are viable on surfaces of Cr-doped FeNi nanoparticles encapsulated into N-doped carbon nanotubes and NiCo2Te2.9,10 The mixture of different metals may help overcome difficulties of water electrolysis, such as the low pH range currently required for this procedure and the stability of materials used for large-scale production.3,10 Furthermore, these materials may have poisoning tolerance when in a harsh acid environment, which improves the electrolytic process.11
Given that water shows significant dissociation on Ni surfaces,12 nanoalloys combining this earth-abundant material with Pd, a noble transition metal used to obtain H2 by water splitting, could have potential applications for H2 production.3 In bulk phase, the Ni and Pd species are miscible for a wide range of compositions;13,14 however, for nanoparticles the solubility varies considerably with the size,13 and hence, affects its properties.
Segregated core–shell NiPd nanoparticles have in fact been synthesized15,16 with sizes below 5 nm. It has been shown15 that NiPd nanoalloys with a Pd-rich shell showed much improved catalytic activity than Pd nanoparticles of similar sizes, for Sonogashira coupling reactions.15 Furthermore, the catalytic activities of such nanoalloys for the oxidation of CO are similar to the case of pure Pd clusters, thus showcasing the possibility of a cost reduction by the introduction of the more accessible metal (Ni).16
From a computational standpoint, the investigation of these nanoalloys presents significant challenges because of the vast array of potential geometric configurations and number of isomers generated by permutations among the species. For example, even small unary clusters, namely Nin17,18 and Pdn,18,19 can display several geometrical arrangements. Among these, certain nickel clusters, such as Ni4, Ni13, and Ni19, have demonstrated improved energetic stability.20–23 Furthermore, Pd13 and the tetrahedral cationic Pd4+ clusters are also remarkably stable.24,25 For larger cluster sizes, it has been shown26 that surface reconstruction can have important effects on the NiPd nanoalloy properties, which was exemplified for its hydrogen adsorption capabilities.
For small NiPd clusters, previous computational results indicate the tendency of Ni to concentrate toward the center of the cluster, while most of Pd occupy surface positions.7,27,28 This is possibly due to the fact that Pd has a slightly larger radius, while Ni possesses a higher surface energy,29–33 which explains this spatial distribution of atoms. However, our fundamental understanding of the mechanisms underlying the stabilization of such nanoparticles and their operational dynamics remains significantly limited.
Given their potential as catalysts for HER and OER, in this work, we perform density functional theory (DFT) calculations for several binary NimPdn−m clusters in order to understand the key features (physical–chemical properties) that drive their stabilization. To analyze how the properties and stabilities vary with different particle sizes, we have considered clusters with n = 13, 27 and 41 atoms. To map both Ni-rich and Pd-rich clusters and achieve a homogeneous range of compositions, we have chosen m to yield a percentage of Ni atoms of 12.5%, 25.0%, 37.5%, 50.0%, 62.5%, 75.0%, and 87.5%. Thus, using DFT calculations combined with data mining techniques and correlation analyzes, we have revealed that the unique segregation of the core and shell NiPd is driven by the preferences of the two elements for different coordination environments and the number of homogeneous bonds.
2 Theoretical approach and computational details
2.1 Total energy calculations
Our calculations were based on the DFT34,35 framework, within the semilocal Perdew–Burke–Ernzerhof formulation for the exchange–correlation energy functional (PBE),36 as implemented in the Vienna ab initio simulation package (VASP),37 which uses the projected augmented wave (PAW) method.38,39 All calculations are spin-polarized and, as default in VASP, the initial on-site magnetic moment for each atom is set to 1.0μB, which is then allowed to relax along the electron density self-consistence. The contribution of each Ni atom to the magnetic moment is close to one, and thus this is a reasonable starting point.The search for local minimum structures requires a substantial quantity of DFT-PBE computations for various trial structures, leading to an escalation in computational cost proportional to the growth in the number of structures. Therefore, to reduce computational cost, we separated our calculations into two stages: (i) screening DFT-PBE calculations using lower computational parameters and (ii) final optimization using accurate computational parameters. For example, in the screening stage, we used a plane wave cutoff energy of 340.939 eV, which is 12.5% lower than the recommended maximum value of the selected PAW projectors (ENMAXmax). For the final geometric optimizations and property calculations, we used a 12.5 higher cutoff energy than ENMAXmax (i.e. 438.351 eV).
We smeared the partial occupancy with a smearing width of 0.100 eV and 0.010 eV for the screening and final calculations, respectively. Geometry optimizations were performed until the forces fell below 0.250 eV Å−1 for all atoms in the screening calculations and 0.050 eV Å−1 for the final calculations. Finally, to avoid the interaction between the cluster and its periodic images, we scaled the unit cell to maintain the 10 Å vacuum (distance between the surface of the cluster and the surface of the periodic images) for the screening calculations and 15 Å of the vacuum for the final ones, that is, we used different cubic box sizes for clusters with different numbers of atoms. Given the large cell size, no dispersion occurs in the electronic states within the Brillouin zone (BZ), and hence we used only the Γ-point for the BZ integration.
2.2 Structure generation
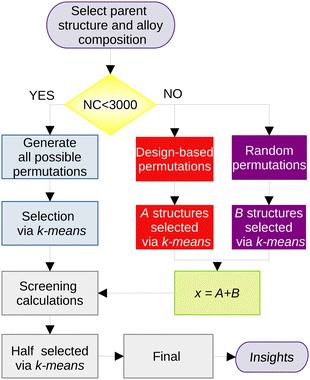
The generation of the trial configurations was divided into two subsections, which combine different strategies.The empirical potential coupled to the GA was employed simply to generate a large number of reasonable trial structures for the unary clusters, which must be further re-optimized using our DFT-PBE calculations in order to propose a putative global minimum configuration (pGMC). For unary clusters with n atoms, we have selected the 2n lowest energy structure from the empirical potential to screen the DFT-PBE calculations and after that the n structures for the final optimizations. The lowest-energy configuration is assumed to be pGMC for the unary clusters. Note that the above procedure is used to generate geometries for the unary clusters only. The alloy structure generation (described in the next section) is not based on the Gupta potential and does not use the GA.
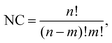 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random permutations and 200
000 random permutations and 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 design-based permutations for each parent, totaling 1 million structures for each NimPd41−m stoichiometry. If NC is smaller than 3000 (applicable to all clusters of 13 atoms and to Ni3Pd24 and Ni24Pd3), all possible permutations are included.
000 design-based permutations for each parent, totaling 1 million structures for each NimPd41−m stoichiometry. If NC is smaller than 3000 (applicable to all clusters of 13 atoms and to Ni3Pd24 and Ni24Pd3), all possible permutations are included.
The most representative structures within this very large set are then selected based on a protocol that is, briefly, based on the following steps: (i) representation of each structure as the eigenvalues of its Coulomb matrix,54 (ii) dimensionality reduction of the problem using the t-SNE algorithm,55 (iii) selection of the x most representative structures by using the k-means approach, (iv) geometry optimization at the screening DFT level in all x selected structures, (v) selection of x/2 structures from this set for a re-optimization at the final DFT level. A more in-depth description of the protocol, together with a flow diagram of its procedures, is provided in the ESI† and in the original work.53
The number of structures selected for the DFT calculations (x) depends on the size of the cluster, and were chosen as x = 30, 40 and 50 for the cluster sizes of n = 13, 27 and 41, respectively. Given that this procedure is repeated for each of the seven compositions selected for each size of the cluster, the number of DFT optimizations only in the screening part is 840.
2.3 Physical–chemical properties
To improve our understanding of the stability of those unary and binary clusters, we calculated several physical–chemical properties, which will be used as descriptors for our correlation Spearman analysis.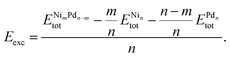 | (2) |
In this equation, 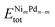 is the total energy of the binary cluster,
is the total energy of the binary cluster, 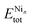 and
and 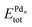 are the total energy of the unary clusters, while n and m were defined at the end of the introduction. Negative values indicate that the alloy is energetically favored, whereas positive values indicate that the two species tend not to mix at the specific particle size.
are the total energy of the unary clusters, while n and m were defined at the end of the introduction. Negative values indicate that the alloy is energetically favored, whereas positive values indicate that the two species tend not to mix at the specific particle size.
The binding energy per atom (Eb) is also a relevant parameter that measures how much energy is necessary to break the particle into its isolated atoms. It is also normalized by the total number of atoms, and calculated as
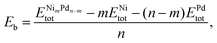 | (3) |
To further characterize the NimPdn−m system, we also analyze the total magnetic moment (mtot) to understand how its magnetism behaves when size and compositions are changed. Another relevant property to evaluate is the system's energy HOMO–LUMO gap, since clusters with a small gap tend to present higher chemical reactivity. The HOMO–LUMO gap is given as
| Eigap = EiLUMO − EiHOMO, | (4) |
Volume and density. In order to obtain the cluster's density and volume, we applied the methodology described in ref. 56, in which the volume of the cluster is estimated using a Monte Carlo integration within the surface of the particle.56 In this work, we employed the van der Waals radius of nickel and palladium atoms provided by Batsanov.29
Root mean square deviation. In order to measure the deformation from the parent structure caused by the atom permutations that generate the alloys, we calculate the root mean square deviation (RMSD) of the atomic positions, which is defined as
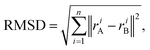 | (5) |
Effective coordination number. For each structure, we also calculate the effective coordination number (ECN) and the average weighted bond length (dav) to provide information on the chemical environment around each atom. The ECN of the atom i is calculated using the following equation.52,58,59
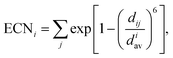 | (6) |
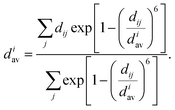 | (7) |
A self-consistent method can be used to obtain the final values of diav.58,59 We also calculate the average values of all atoms as
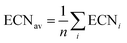 | (8) |
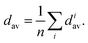 | (9) |
Average radial distance and cluster radius. The average radial distance Dav is the average of the atomic distances from each atom to the geometric center of the cluster. Another variable related to cluster size is the average radius (Rav), which is given by the following equation,
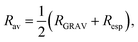 | (10) |
Under coordination number. The under coordination number for an element A (UCA), is the ratio between the number of atoms of this element on the surface of the particle and the total number of atoms of this element in the structure.52,60 This property indicates the tendency of a given element to occupy the surface of the structure: if UCA is close to 1, it tends to occupy the surface, while if closer to zero the majority of these atoms are in core positions.52
Chemical order parameter. The chemical order parameter (σ) provides information on how the different atoms are bonded in an alloy. It is calculated as,59,61
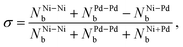 | (11) |
2.4 Spearman's rank correlation
Upon completion of the geometry optimization for each designated isomer of the specified NimPdn−m cluster, the properties defined in the preceding section are evaluated and characterized to ascertain potential correlations between the property in question and the excess energy, which defines the cluster energetic stability in comparison with separated species. The objective is to discern electronic and structural properties that exhibit a correlation with a reduction in excess energy, implying that augmentation of such properties enhances the stability of the alloy. Consequently, this analysis was performed by computing the Spearman rank correlation coefficient (ρs).Starting with two vectors containing the values of the two properties (x and y), these are first rank transformed to values between 1 and M, with M being the number of elements in the sample.62 The strength of the association of these variables can be measured by ρs, which is defined from the ratio between the covariance of x and y and the product of their standard deviations (σxσy) as,62,63
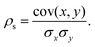 | (12) |
The results range from −1.00 and 1.00, with extreme values indicating perfect inverse correlation or perfect direct correlation. Weak correlations below <0.25 are considered too low and are not reported.
3 Results and discussion
All screening calculations using lower computational parameters are reported within the ESI,† while the results obtained by larger computational parameters (final) for all calculated configurations will be reported and discussed in the following. To reach our goals, this section is separated into few subsections, namely (i) discussion of the structural features of the pGMC unary clusters, which is expected to drive several features of the alloys; (ii) discussion of the size-dependent structural preferences in binary NiPd clusters, which will help to understand and explain the descriptors that drive the stability of those binary clusters; (iii) stability analysis via electronic properties of the binary clusters; (iv) discussion of the structural descriptors that drives the stability of those binary systems; (v) finally, the discussion of Spearman correlation analysis.3.1 Structure features of putative global minima unary clusters
As mentioned above, several DFT optimizations were performed, which yields the lowest energy configurations for the unary cluster. The molecular configurations are shown in Fig. 2. Furthermore, the group symmetry and number of atoms in the core region are summarized in Table 1. The Ni13 and Pd13 clusters do not show icosahedral symmetry, which is in agreement with previous studies.17,18 We found a truncated triangular bipyramid for Ni13, whereas Pd13 shows a less symmetric configuration that can be described as two pentagonal bipyramids that share Pd atoms on the side. Neither of these structures has a central atom that would constitute a core (as in the perfect icosahedron structure with 13 atoms).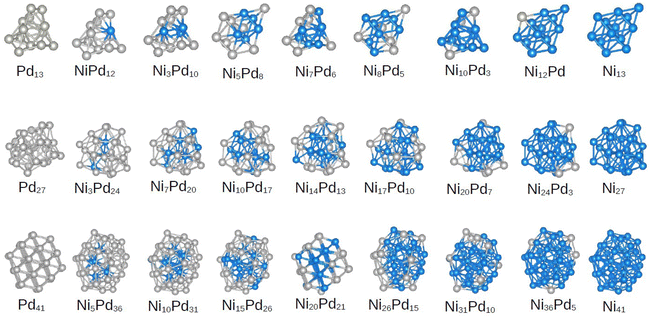 | ||
| Fig. 2 Putative global minima configurations for all compositions and sizes assessed. From top to bottom, clusters and alloys of 13, 27 and 41 atoms. The nickel content increases from left to right. | ||
| Cluster | Symmetry | Core size |
|---|---|---|
| Ni13 | C 3v | 0 |
| Ni27 | C 1 | 3 |
| Ni41 | C s | 7 |
| Pd13 | C 2 | 0 |
| Pd27 | C 1 | 2 |
| Pd41 | C 3v | 7 |
For unary clusters of 27 atoms, we obtained structures approaching more spherical-like shapes without symmetry elements for both Pd27 and Ni27, with a more prolate structure achieved by Pd27. At this intermediate cluster size, we already have atoms in the core, which will be interesting for the study of the core–shell segregation of the alloys as a function of size.
Interestingly, the Pd41 clusters can be described as a fragment of a face-centered cubic (fcc) structure, as also occurs for the Pd55 cluster.42 This fragment has 4 layers in the shortest dimension and 5 layers in the largest. The top layer in the largest dimenstion has only 3 atoms, and these can also be though as the three atoms capping a truncated octahedron of size 38. The fragment of the 41-atom cluster belongs to the C3v point group and has 7 atoms at its core.
On the other hand, Ni41 maintains a more spherical shape as observed in Ni27. This structure is a fragment of the perfect icosahedral of the Ni55 cluster. Coincidentally, this structure also shows a core composed of 7 atoms. This core is composed of a pentagonal bipyramid, and the atoms on the surface form a second bipyramid around the core, with extra atoms capping the whole structure. This configuration belongs to the Cs point group, which agrees with ref. 23. It is interesting to note that at the 41 atoms size we already have fragments of both the icosahedral (Ni41) and fcc (Pd41) structures, which are very common arrangements for larger nanoparticles.64,65
3.2 Size-dependent structural preferences in binary NiPd clusters
In this section, we focus on the discussion of the obtained geometries only for the lowest energy configuration of the alloys, while leaving the properties of all other calculated structures to the next sections. We must emphasize at this point that we did not consider binary cluster structures that did not originate from the unary parents. However, the presence of a different atom may alter the energetic order, and the real global minimum may not follow the unary preferred structure. However, we emphasize that the focus of this work is on sampling a diverse set of structures for NimPdn−m clusters to understand and extract correlations between their characteristics and stability. However, analyzing the pGMCs obtained here can aid in the subsequent discussions.As seen in Fig. 2, the NimPd13−m clusters can be seen to follow the structure of the parent Pd13 at m = 1, 3, 7 and 10, and thus even on nickel rich compositions. A pattern of Ni atoms bonded to each other with homogeneous bonds can be observed even in compositions with a low Ni content, whereas palladium atoms tend to be more spread around all parts of the cluster, favoring heterogeneous bonds. This may be explained by bond energies following the Ni–Ni > Ni–Pd > Pd–Pd order. The results of a previous computational investigation of 13 atom NiPd clusters27 focused only on icosahedral configurations also showed this tendency. In this work, Chutia et al. rationalize the stability of these clusters from the interaction between the orbitals Ni (4s,3p) and Pd (4s,4p).27
On the other hand, the pGMCs for all compositions of the 27-atom alloys were obtained from the parent structure Ni27. The three atomic positions in the core are always occupied by Ni atoms, except for the case Ni3Pd24. In addition to finding Pd atoms on the surface, we can see that they tend not to be grouped in the same regions of the shell, giving rise to more heterogeneous bonds (as in the case of 13 atoms). This is in contrast to the behavior of Ni, which tends to be clumped together. This effect has been discussed for 26-atom NiPd clusters,28 where the authors describe it as the formation of “islands” on the surface, which occurs for all compositions until the number of Pd atoms on the surface is so large that it leads to a core–shell configuration.
Observing the pGMCs of the structures with 41 atoms, we again see a clear preference for the unary parent structure of nickel (icosahedral fragment), with the exception of the composition Ni20Pd21, which shows the fcc fragment structure of the parent Pd. The fcc-to-icosahedron transformation in bimetallic alloys has been extensively discussed by Nelli et al.,66 and the driving-force is believed to be the relaxation of local stress in the icosahedron, after the inclusion of an element with different radius.
This cluster size continues the trend of Pd atoms spreading over the surface and favoring heterogeneous bonds, while Ni atoms are grouped together in the center of the particle whenever possible. It is important to note here that core–shell NiPd nanoparticles have in fact been synthesized.15
As core–shell segregation has been shown to be a preferential organization motif in minimum energy structures (which also extends to the 55-atom alloys7), we would like to highlight that this phenomenon has received considerable attention in the literature. In particular, it has been noticed that Ni atoms tend to segregate to the surface in the NiFe, NiRu and NiIr alloys,67,68 while tending to internal sites in systems such as NiCu, NiAg, NiAu and NiPt, and showing mixed arrangements in NiCo the nanoalloys.67–69 All such results can be expected from the fact that elements tend to occupy the surface if they have lower surface energy and larger atomic radius than the other metal.67 It has also been argued that if there is a large difference in the electronegativity between the two metals, further stabilization may occur from a charge transfer mechanism leading to a cationic core and anionic surface, increasing the strain on the core and further favoring segregation of large species to the surface region.50 Specifically for the binary NiPd clusters studied in this work, we note that palladium has a larger radius than Ni,29–31 and a lower surface energy,70 which explains the segregation presented in Fig. 2.
3.3 Stability analysis via electronic properties
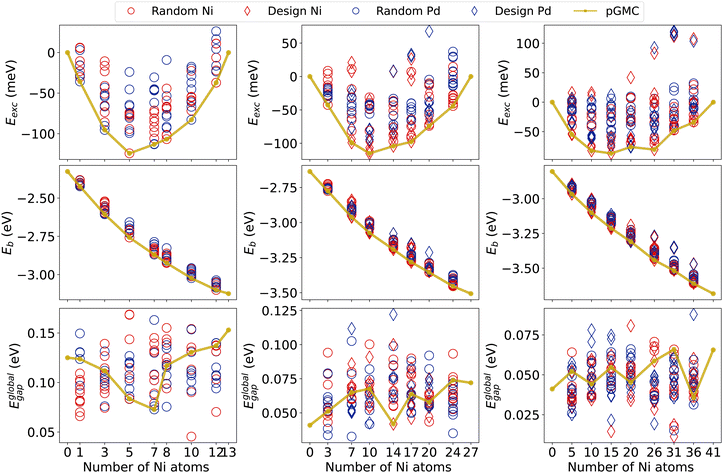
We now analyze the most relevant electronic properties (Eexc, Eb, and Egap) of all optimized structures using the results of our final DFT calculations. The results are summarized in Fig. 3, while other electronic properties are also presented in the ESI.†For all cluster sizes, the Eexc minimum deviates from the 50% compositions and tends to favor slightly Ni-poor ones at around 37.5% in nickel. This shift towards Pd-rich composition is in agreement with previous work for NiPd clusters of 26 and 55 atoms.7,28 The lowest Eexc is observed for the Ni5Pd8 cluster, which is about −124 meV per atom. Most of the other structures fall above −115 meV for alloys of 13- and 27-atoms. The tendency to decrease the magnitude of the excess energy per atom can be seen as a function of the size of the cluster, with clusters of 41 atoms showing Eexc of only −87 meV. We also note that the formation of binary NiPd clusters is energetically favorable for the vast majority of generated structures (which include both random and design-based structures), as shown by the small number of structures with positive excess energies in all compositions and sizes.
Fig. 3 also allows us to compare the stability of randomly generated structures with those generated by the principles of physical–chemical design for the 27- and 41-atom clusters. Recall that for all 13-atom clusters and for Ni3Pd24 and Ni24Pd3, the reduced number of possible permutations allowed us to generate all configurations and therefore this figure does not differentiate design and random in these cases. We see that for systems of 41 atoms, design structures were observed in both the lowest and the largest excess energy obtained for each composition. This is related to opposing core–shell designs, where nickel atoms are in the core (favorable) or in the shell (unfavorable).
Regarding the binding energies per atom, in Fig. 3, we see that its magnitude increases as a function of the Ni content. This is in agreement with the fact that the bulk cohesive energy of palladium is lower (3.89 eV per atom) than that of nickel (4.44 eV per atom).71 For all sizes, Eb shows a fairly linear behavior as a function of composition. Furthermore, we notice that the magnitude of Eb tends to increase with increasing cluster size.21,23,72,73
For the global HOMO–LUMO gap, we see a decrease in the average of Eglobalgap with an increase in size, as also observed in other nanoalloys with similar numbers of atoms.74 However, a clear trend of larger gaps for Ni- or Pd-rich compositions cannot be observed, and the values for the different minima for all compositions of fixed size show a similar range.
We observe that pGMCs (golden line) appear mainly in intermediate Eglobalgap values, suggesting that there is no correlation between the increasing HOMO–LUMO gaps (which generally indicate lower reactivity) with energetic stability. Exceptions to this are compositions Ni7Pd6, Ni14Pd13, and Ni36Pd5 that have pGMCs with the lowest Eglobalgap. We also see that some design-based structures have higher (or lower) values for Eglobalgap, especially in 41-atom alloys, again showing the influence of surface segregation on electronic properties.
3.4 Structural descriptors of NiPd alloys: clues to energetic stability
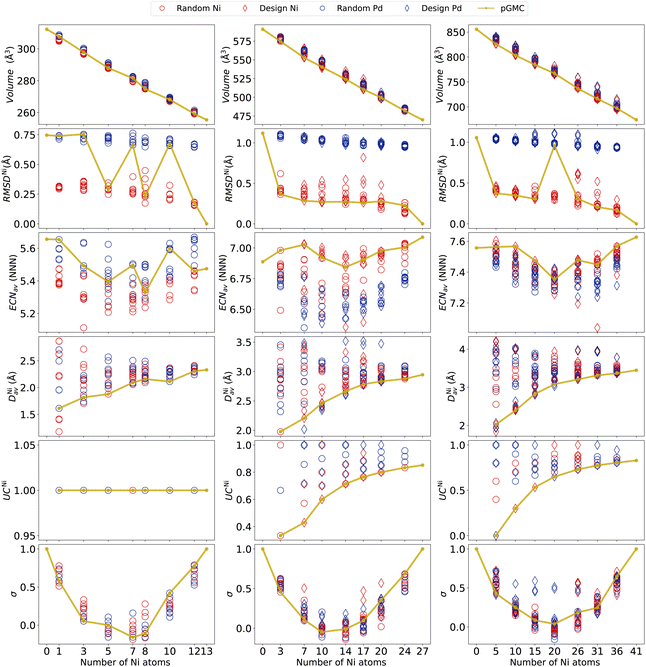
A better understanding of the alloy structures obtained can be achieved by analyzing structural descriptors such as those presented in Fig. 4 (for other properties not included here, see the ESI†). Starting with the volume, we observe a linear decrease as a function of Ni content, as expected from its lower atomic radius (Zen's law75). At this scale, only moderate variability in volumes can be observed in each composition (caused by different geometrical arrangements of the cluster).To measure the deformations of the parent structure caused by the replacement of a dopant atom at different sites in the unary cluster, we calculate RMSD. Here, we focus on the deviation of each structure from the unary nickel parent, RMSDNi. The deviations from the palladium unary cluster are given in the ESI† and provide analogous information. Note that, as the points in Fig. 4 are colored according to which of the two parent structures they were obtained from, a clear separation is seen, with alloys originating from the parent Pd naturally showing larger RMSDNi. We can see a tendency of the pGMCs to be correlated to a smaller geometrical deviation from the unary cluster, meaning that large distortions from the initial structures lead to unfavorable energies.
An outlier can be seen in Ni17Pd10, where the higher RMSDNi is caused by a significant change in geometry caused by the dopant atoms, leading the system to escape the basin of geometry of the Ni27 parent cluster. This figure also allows an easy visualization of the fact that all pGMCs of the n = 27 and 41 clusters originate from the parent structure of nickel, with the exception of Ni20Pd21.
The coordination around each chemical species is quantified (on average) using ECNav, as shown in Fig. 4. We can see that, for the 13-atom clusters, the unary Pd structure is more coordinated than the unary Ni structure, and the alloys generated from the former also tend to have higher coordination. In the cases where the pGMCs were obtained from the parent Ni13, it is possible to observe a tendency for the lowest energy structure to present a high ECNav. For n = 27, we see an inverted situation in which Ni27 has greater coordination than Pd27, which is also reflected in the values ECNav presented by the alloys of each parent. The pGMCs tend to follow more coordinated structures. For n = 41, both parent structures have similar ECNav, and a clear separation between alloys obtained from different parents cannot be observed. In general, it seems that the alloys will follow the trend of the unary parents and that, in the cases where the pGMC originates from the parent Ni27 structure, it seems that larger ECNav values are energetically favored. A clearer picture of the dependence of energy on coordination will be presented in the next section using Spearman's rank correlation.
To quantitatively assess the occupation of Ni atoms in the center of the clusters, we now discuss the average radial distance DNiav (how far on average the Ni atoms are from the geometric center of the cluster) and the undercoordination number UCNi (ratio between the number of Ni atoms in the surface and the total number of Ni atoms). Both variables clearly indicate that the lowest energy structures occur when Ni atoms are located closer to the center, even if the structure does not possess a core region (13-atoms case).
For compositions with a lower nickel content, we obtain very low DNiav and UCNi, which naturally tend to increase with increasing Ni percentages. Here we again see the importance of including design-based structures in the analysis, as much lower DNiav and UCNi values can be obtained from them, compared to the random ones. The graphs for DPdav and UCPd are given in the ESI† and reveal similar conclusions.
Concerning the chemical order parameter σ, the parabolic shape observed in Fig. 4 is typical in nanoalloys,28,52,53 and the fact that the NiPd alloys do not reach substantially negative values is due to the fact that the number of heterogeneous bonds is generally lower than or equal to the number of homogeneous ones. It can be seen that pGMCs do not consistently correspond to higher or lower values of σ. The reason why σ does not capture the lowest energy structures is that it accounts for both NNi–Nib and NPd–Pdb on an equal footing, while what we observed in Section 3.2 is that NNi–Nib and NPd–Pdb have different tendencies: nickel tends to clump together (favoring homogeneous bonds), while the palladium atoms tend to spread around the surface far from each other until the previously described “islands”28 are formed (not favoring homogeneous bonds). For this reason, homogeneous and heterogeneous bonds must be considered separately to explain the energetic stability. This is performed in the following section.
3.5 Spearman's correlation analysis unveils key trends
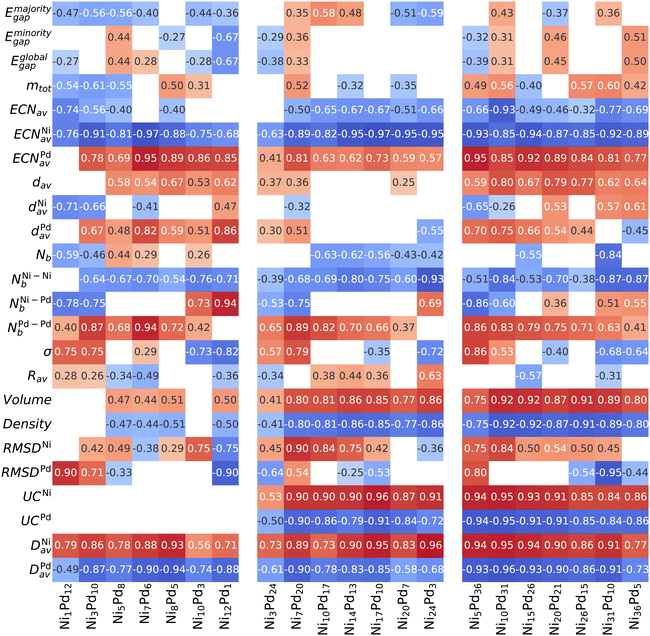
The Spearman correlation coefficient ρs evaluates how well one arbitrary monotonic function can describe the relationship between two variables and, therefore, is not restricted to linear correlations.62,63 Following previous works,50–53 we establish the correlation of several physical–chemical parameters with excess energy to search for properties that can influence alloy stabilization. All such parameters are plotted against the excess energies to show an overall picture, which can be seen in the ESI.† Here, we focus only on the values of the correlation coefficient, which is shown in Fig. 5. Positive correlations (red) indicate that the excess energy increases with the property (unfavorable), and negative correlations (blue) indicate that the excess energy decreases with the property increment (the property is correlated with energy stabilization). Weak correlations below <0.25 are not shown.Firstly, we can see that the electronic properties (Eigap and mtot) are only weakly correlated to energy stabilization. On the other hand, an intimate relationship is observed between the coordination numbers and excess energy. For all compositions and sizes, high values of ECNNiav make the energy more negative (thereby stabilizing the alloy), while ECNPdav increase the energy. This is consistent with the tendency of nickel atoms to occupy central positions (more coordinated) even when a core is not available (13-atom clusters) and Pd atoms to occupy positions in the vertices of the polyhedron formed by the atoms, thus being more isolated (even from each other), leading to the formation of Pd “islands” and eventually Pd shells, when the palladium content is high enough.
Although the bond distances are necessary to calculate the number of nearest neighbors (and thus provide the coordination number), we can see that their magnitude itself, given by the weighted bond lengths dav, presents only small correlations with energy. This correlation is not consistent among different compositions and sizes, and thus dav is not an important descriptor of stability in alloys NiPd.
The particular pattern in which the bonds are arranged in the cluster is revealed by the correlation analysis to be a crucial factor and strongly influences the energy. Although the total number of bonds (Nb) and the number of heterogeneous bonds (NNi–Pdb) do not show consistent patterns through different cluster sizes and compositions, the number of homogeneous bonds is strongly correlated with energy stabilization, as shown in Fig. 5. It can be clearly seen that increasing the number of Ni–Ni bonds leads to a decrease in energy (increasing stabilization), while those of Pd–Pd lead to destabilization.
Note that this is not a necessary feature of core–shell segregation, as the formation of a stable Pd shell could favor the number of Pd–Pd bonds on the surface. In fact, in our recent investigation of four different gold nanoalloys,53 in which gold always preferred surface positions, we found that the number of homogeneous Au–Au bonds was not correlated with energy stabilization. In such gold nanoalloys, only the number of homogenous bonds of the element in the core enhanced the stability. In summary, while the core formation stabilizes the structures in all such examples, the organization pattern of the shell atoms mattered only in the NiPd case.
The NiPd is a special case of shell formation, in which the Pd shell on top of Ni begins with isolated “islands” on Pd-poor compositions that only tend to a proper shell on Pd-rich ones, as first described for Ni26−xPdx by Aguilera-Granja et al.28 In the same work, the authors studied NiPt alloys, showing that this presents a different pattern of Pt layer instead of “islands”. Our analyzes show that this structure organization pattern is not restricted to 26-atom NiPd alloys and not only to pGMCs, and further sheds light on the underlying impact on energy.
As argued in the previous section, the chemical order parameter takes both types of homogeneous bonds on equal footing and therefore cannot capture the organization patterns that are correlated with the stabilization of the alloy NiPd (opposite trends for NNi–Nib and NPd–Pdb). For this reason, σ is not consistently correlated with stabilization. Increasing the radius of the cluster (as shown by Rav) within a fixed number of atoms and composition is also not particularly relevant, showing only small correlations of varying signs.
As for the volume (and consequently the density, with an identical correlation magnitude but opposite sign), we see a significant correlation with energy where a smaller volume tends to be energetically favorable. The correlation is strong for n = 27 and 41, but small for n = 13 (which does not have a core). Together, these two observations indicate that stabilization occurs by compressing the inner core sites of the structure, caused by the presence of the smaller Ni atoms. Therefore, our correlation analysis for these small clusters is in agreement with what has been obtained for much larger clusters.66
The analysis of RMSDNi was performed considering only the structures coming from the unary Nin clusters, and thus uses fewer data points (this is also is performed for RMSDPd). The reason is that we want to measure how a deformation from the original parent structure correlates with energy decrease, and including the RMSD between a structure coming from one parent to a completely different unary would not allow that. What we obtain generally is that the structures based on the parent Ni that show a large deformation tend to be more destabilized, whereas the structures coming from the parent Pd tend to deviate from their parent to become more stable. However, the correlations are not strong and do not occur for the 13-atom case.
The two final variables analyzed, UCX and DXav, can be seen in Fig. 5 to be strongly correlated with energy. Recall that UCX gives the fraction of element X that lies on the surface of the particle, while DXav express (on average) how far the element X is distributed away from the geometric center. Both variables are descriptive of core–shell segregation, with large values indicating that element X occupy the surface, even though DXav is meaningful even when the particle does not present a core region, such as n = 13. As can be seen, the numerical values of the correlation coefficient for both variables are very similar (except the n = 13 case where UCX cannot be defined). This analysis again captures the fact that Ni atoms tend to be in the center of the particle, while Pd tends to be located in the outer regions.
In summary, we see that the energy stabilization of arrangements with a core based on Ni is well described by the variables ECNav, UC, and Dav. However, core–shell segregation is not the only motif of stabilization by a structural organization, as there is also a particular type of Pd atom arrangement on the surface of the particle, which could only be captured quantitatively by analyzing the number of homogeneous bonds of each type. By analyzing a representative set of structures, instead of relying solely on the pGMC, it is possible to affirm that such properties can describe driving forces for particle stabilization rather than being a feature of the pGMC alone.
4 Conclusions
In this work, we have generated a very large number of structures for several compositions and sizes for the binary NimPdn−m clusters. Data mining techniques were used to sample the most representative structures, which were then optimized using DFT calculations. The results of the DFT optimizations were used to calculate several electronic and structural properties for all such structures, which were subsequently analyzed to check for correlations between alloy stabilization and the properties.We have shown that NiPd represents a special case of core–shell formation, in which the Pd shell shows “islands” in Pd-poor compositions that evolve to a proper shell on Pd-rich ones. This can be seen by visual inspection of the structures, but it finds quantitative support with the opposite correlations that the number of Ni–Ni and Pd–Pd bonds shows with stabilization (while the number of heterogeneous bonds is not correlated with stabilization or destabilization). A further indication of this stabilization pattern is that the coordination number of Ni atoms is correlated with alloy stabilization, while the coordination of the Pd ones is inversely correlated.
Our analyses show that, for structures containing a core region, an important feature is that the presence of the smaller nickel atoms in the core compresses the overall size of the particle, which enhances stabilization. The techniques and protocol employed in this study are shown to yield both quantitative and qualitative explanations of nanoalloy stabilization.
Data and software availability
The authors declare that they have no competing financial interest. As mentioned, all DFT calculations were performed using the Vienna ab initio simulation package, which can be used under a non-free academic license. Additional details can be obtained from the link https://www.vasp.at. Furthermore, additional details are provided within the ESI,† while additional crude data can be obtained directly with the authors upon request.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work is supported by Fundação de Amparo à Pesquisa do estado de Minas Gerais (FAPEMIG), grants APQ-00597-22 and APQ-03705-23, and Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), grant 311508-2021-9. The authors also gratefully acknowledge support from FAPESP (São Paulo Research Foundation) and Shell, projects no. 2017/11631-2 and 2018/21401-7, and the strategic importance of the support given by ANP (Brazil's National Oil, Natural Gas and Biofuels Agency) through the R&D levy regulation. This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001. The authors are also thankful for the infrastructure provided to our computer cluster by the Department of Information Technology – Campus São Carlos. Research was developed with the help of HPC resources provided by the Information Technology Superintendence of the University of São Paulo.References
- J. Wang, X. Yue, Y. Yang, S. Sirisomboonchai, P. Wang, X. Ma, A. Abudula and G. Guan, Earth-Abundant Transition-Metal-Based Bifunctional Catalysts for Overall Electrochemical Water Splitting: A Review, J. Alloys Compd., 2020, 819, 153346, DOI:10.1016/j.jallcom.2019.153346.
- J. Zhang, T. Wang, D. Pohl, B. Rellinghaus, R. Dong, S. Liu, X. Zhuang and X. Feng, Interface Engineering of MoS2/Ni3S2 Heterostructures for Highly Enhanced Electrochemical Overall-Water-Splitting Activity, Angew. Chem., 2016, 128, 6814–6819, DOI:10.1002/ange.201602237.
- A. Munir, K. S. Joya, T. Ul Haq, N.-U.-A. Babar, S. Z. Hussain, A. Qurashi, N. Ullah and I. Hussain, Metal Nanoclusters: New Paradigm in Catalysis for Water Splitting, Solar and Chemical Energy Conversion, ChemSusChem, 2019, 12, 1517, DOI:10.1002/cssc.201802069.
- F. Shimojo, S. Ohmura, R. K. Kalia, A. Nakano and P. Vashishta, Molecular dynamics simulations of rapid hydrogen production from water using aluminum clusters as catalyzers, Phys. Rev. Lett., 2010, 104, 126102, DOI:10.1103/PhysRevLett.104.126102.
- R. L. Johnston, Atomic and molecular clusters, Taylor & Francis, London, 1st edn, 2002, p. 256 Search PubMed.
- R. Ferrando, J. Jellinek and R. L. Johnston, Nanoalloys: From Theory to Applications of Alloy Clusters and Nanoparticles, Chem. Rev., 2008, 108, 845–910, DOI:10.1021/cr040090g.
- J. Zhu, P. Cheng, N. Wang and S. Huang, Insight into the structural and electronic properties of Pd55−nNin (n = 0–55) clusters: A density functional theory study, Comput. Theor. Chem., 2015, 1071, 9–17, DOI:10.1016/j.comptc.2015.08.010.
- G. Kwon, G. A. Ferguson, C. J. Heard, E. C. Tyo, C. Yin, J. DeBartolo, S. Seifert, R. E. Winans, A. J. Kropf and J. Greeley, et al., Size-dependent subnanometer Pd cluster (Pd4, Pd6, and Pd17) water oxidation electrocatalysis, ACS Nano, 2013, 7, 5808–5817, DOI:10.1021/nn400772s.
- Y. Wu, X. Tao, Y. Qing, H. Xu, F. Yang, S. Luo, C. Tian, M. Liu and X. Lu, Cr-Doped FeNi–P Nanoparticles Encapsulated into N-Doped Carbon Nanotube as a Robust Bifunctional Catalyst for Efficient Overall Water Splitting, Adv. Mater., 2019, 31, 1900178, DOI:10.1002/adma.201900178.
- L. Tao, M. Huang, S. Guo, Q. Wang, M. Li, X. Xiao, G. Cao, Y. Shao, Y. Shen and Y. Fu, et al., Surface Modification of NiCo2Te4 Nanoclusters: a Highly Efficient Electrocatalyst for Overall Water-Splitting in Neutral Solution, Appl. Catal., B, 2019, 254, 424–431, DOI:10.1016/j.apcatb.2019.05.010.
- Y. Li, Y. Sun, Y. Qin, W. Zhang, L. Wang, M. Luo, H. Yang and S. Guo, Recent Advances on Water-Splitting Electrocatalysis Mediated by Noble-Metal-Based Nanostructured Materials, Adv. Energy Mater., 2020, 10, 1903120, DOI:10.1002/aenm.201903120.
- L. Zhu, C. Liu, X. Wen, Y.-W. Li and H. Jiao, Coverage-Dependent Water Dissociative Adsorption Properties on Nickel Surfaces, J. Phys. Chem. C, 2020, 124, 25835–25845, DOI:10.1021/acs.jpcc.0c07528.
- G. Guisbiers, R. Mendoza-Pérez, L. Bazán-Daz, R. Mendoza-Cruz, J. J. Velázquez-Salazar and M. José-Yacamán, Size and shape effects on the phase diagrams of nickel-based bimetallic nanoalloys, J. Phys. Chem. C, 2017, 121, 6930–6939, DOI:10.1021/acs.jpcc.6b09115.
- Y. Liu, Q. Song, L. Zhang and Z. Xu, Novel approach of in-situ nickel capture technology to recycle silver and palladium from waste nickel-rich multilayer ceramic capacitors, J. Cleaner Prod., 2021, 290, 125650, DOI:10.1016/j.jclepro.2020.125650.
- S. U. Son, Y. Jang, J. Park, H. B. Na, H. M. Park, H. J. Yun, J. Lee and T. Hyeon, Designed Synthesis of Atom-Economical Pd/Ni Bimetallic Nanoparticle-Based Catalysts for Sonogashira Coupling Reactions, J. Am. Chem. Soc., 2004, 126, 5026–5027 CrossRef CAS PubMed.
- S. Sao-Joao, S. Giorgio, J.-M. Pénisson, C. Chapon, S. Bourgeois and C. Henry, Structure and deformations of Pd–Ni core-shell nanoparticles, J. Phys. Chem. B, 2005, 109, 342–347, DOI:10.1021/jp040473i.
- Q. L. Lu, Q. Q. Luo, L. L. Chen and J. G. Wan, Structural and Magnetic Properties of Nin(n = 2–21) Clusters, Eur. Phys. J. D, 2011, 61, 389–396, DOI:10.1140/epjd/e2010-10129-8.
- A. S. Chaves, M. J. Piotrowski and J. L. F. Da Silva, Evolution of the Structural, Energetic, and Electronic Properties of the 3d, 4d, and 5d Transition-metal Clusters (30 TMn Systems for n = 2–15): A Density Functional Theory Investigation, Phys. Chem. Chem. Phys., 2017, 19, 15484–15502, 10.1039/c7cp02240a.
- P. Nava, M. Sierka and R. Ahlrichs, Density Functional Study of Palladium Clusters, Phys. Chem. Chem. Phys., 2003, 5, 3372–3381, 10.1039/b303347c.
- M. J. López and J. Jellinek, Fragmentation of Atomic Clusters: A Theoretical Study, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 50, 1445, DOI:10.1103/PhysRevA.50.1445.
- J. M. Montejano-Carrizales, M. P. Iniguez, J. A. Alonso and M. J. López, Theoretical Study of Icosahedral Ni Clusters within the Embedded-Atom Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 5961, DOI:10.1103/PhysRevB.54.5961.
- N. N. Lathiotakis, A. N. Andriotis, M. Menon and J. Connolly, Tight Binding Molecular Dynamics Study of Ni Clusters, J. Chem. Phys., 1996, 104, 992–1003, DOI:10.1063/1.470823.
- V. G. Grigoryan and M. Springborg, Structural and Energetic Properties of Nickel Clusters: 2 < N < 150, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205415, DOI:10.1103/physrevb.70.205415.
- J. Rogan, G. García, J. A. Valdivia, W. Orellana, A. H. Romero, R. Ramírez and M. Kiwi, Small Pd Clusters: A Comparison of Phenomenological and Ab Initio Approaches, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 115421, DOI:10.1103/physrevb.72.115421.
- X. Xing, A. Hermann, X. Kuang, M. Ju, C. Lu, Y. Jin, X. Xia and G. Maroulis, Insights into the geometries, electronic and magnetic properties of neutral and charged palladium clusters, Sci. Rep., 2016, 6, 1–11, DOI:10.1038/srep19656.
- E. Panizon and R. Ferrando, Strain-induced restructuring of the surface in core@shell nanoalloys, Nanoscale, 2016, 8, 15911–15919, 10.1039/c6nr03560d.
- A. Chutia and M. Tokuyama, Orbital interaction and local stability of Ni substituted Pd nanoalloys, Chem. Phys. Lett., 2011, 515, 96–101, DOI:10.1016/j.cplett.2011.08.092.
- F. Aguilera-Granja and L. J. Gallego, Structural and electronic properties of Ni26−pXp clusters (X = Pd, Pt): A density-functional-theoretic study, J. Appl. Phys., 2013, 114, 054311, DOI:10.1063/1.4817501?ver=pdfcov.
- S. S. Batsanov, van der Waals radii of elements, Inorg. Mater., 2001, 37, 871–885, DOI:10.1023/A:1011625728803.
- S.-Z. Hu, Z.-H. Zhou and B. Robertson, Consistent approaches to van der Waals radii for the metallic elements, Z. Kristallogr., 2009, 224, 375–383 CrossRef CAS.
- M. Rahm, R. Hoffmann and N. W. Ashcroft, Atomic and ionic radii of elements 1–96, Chem. Ber., 2016, 22, 14625–14632, DOI:10.1002/chem.201602949.
- O. M. Løvvik, Surface segregation in palladium based alloys from density-functional calculations, Surf. Sci., 2005, 583, 100–106, DOI:10.1016/j.susc.2005.03.028.
- B. D. Todd and R. M. Lynden-Bell, Surface and bulk properties of metals modelled with Sutton-Chen potentials, Surf. Sci., 1993, 281, 191–206 CrossRef CAS.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, B864–B871, DOI:10.1103/physrev.136.b864.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138, DOI:10.1103/physrev.140.a1133.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868, DOI:10.1103/physrevlett.77.3865.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for ab initio Total-energy Calculations Using a Plane-wave Basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186, DOI:10.1103/physrevb.54.11169.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979, DOI:10.1103/physrevb.50.17953.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775, DOI:10.1103/physrevb.59.1758.
- Z. Lu, Z. Yang and K. Hermansson, The adsorption properties of Cu and Ni on the ceria(111) surface, Adv. Mater. Res., 2011, 213, 166 CAS.
- M. J. Piotrowski, P. Piquini and J. L. F. Da Silva, Density Functional Theory Investigation of 3d, 4d, and 5d 13-atom Metal Clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155446, DOI:10.1103/physrevb.81.155446.
- M. J. Piotrowski, C. G. Ungureanu, P. Tereshchuk, K. E. A. Batista, A. S. Chaves, D. Guedes-Sobrinho and J. L. F. Da Silva, Theoretical Study of the Structural, Energetic, and Electronic Properties of 55-atom Metal Nanoclusters: A DFT Investigation Within van der Waals Corrections, Spin-orbit Coupling, and PBE+U of 42 Metal Systems, J. Phys. Chem. C, 2016, 120, 28844–28856, DOI:10.1021/acs.jpcc.6b10404.
- M. Blanco-Rey, J. I. Juaristi, M. Alducin, M. J. López and J. A. Alonso, Is spillover relevant for hydrogen adsorption and storage in porous carbons doped with palladium nanoparticles?, J. Phys. Chem. C, 2016, 120, 17357–17364, DOI:10.1021/acs.jpcc.6b04006.
- F. F. Guimarães, J. C. Belchior, R. L. Johnston and C. Roberts, Global optimization analysis of water clusters H2On (11 ≤ n ≥ 13)through a genetic evolutionary approach, J. Chem. Phys., 2002, 116, 8327–8333, DOI:10.1063/1.1471240.
- M. X. Silva, B. R. L. Galvão and J. C. Belchior, Growth analysis of sodium-potassium alloy clusters from 7 to 55 atoms through a genetic algorithm approach, J. Mol. Model., 2014, 20, 1–9, DOI:10.1007/s00894-014-2421-3.
- D. Guedes-Sobrinho, R. K. Nomiyama, A. S. Chaves, M. J. Piotrowski and J. L. F. Da Silva, Structure, Electronic, and Magnetic Properties of Binary PtnTM55−n (TM = Fe, Co, Ni, Cu, Zn) Nanoclusters: A Density Functional Theory Investigation, J. Phys. Chem. C, 2015, 119, 15669–15679, DOI:10.1021/acs.jpcc.5b02242.
- K. E. A. Batista, M. J. Piotrowski, A. S. Chaves and J. L. F. Da Silva, A Theoretical Investigation of the Structural and Electronic Properties of 55-atom Nanoclusters: The Examples of Y-Tc and Pt, J. Chem. Phys., 2016, 144, 054310, DOI:10.1063/1.4941295.
- K. E. A. Batista, J. L. F. Da Silva and M. J. Piotrowski, Ab initio Investigation of the Role of Atomic Radius in the Structural Formation of PtnTM55−n (TM = Y, Zr, Nb, Mo, and Tc) Nanoclusters, J. Phys. Chem. C, 2018, 122, 7444–7454, DOI:10.1021/acs.jpcc.7b05714.
- K. E. A. Batista, J. L. F. Da Silva and M. J. Piotrowski, Adsorption of CO, NO and H2 on the PdnAu55−n Nanoclusters: A Density Functional Theory Investigation Within the van der Waals D3 Corrections, J. Phys. Chem. C, 2019, 123, 7431–7439, DOI:10.1021/acs.jpcc.8b12219.
- P. C. D. Mendes, S. G. Justo, J. Mucelini, M. D. Soares, K. E. A. Batista, M. G. Quiles, M. J. Piotrowski and J. L. F. Da Silva, Ab initio Insights into the Formation Mechanisms of 55-atom Pt-Based Core-shell Nanoalloys, J. Phys. Chem. C, 2020, 124, 1158–1164, DOI:10.1021/acs.jpcc.9b09561.
- F. O. Morais, K. F. Andriani and J. L. F. Da Silva, Investigation of the Stability Mechanisms of Eight-atom Binary Metal Clusters Using DFT Calculations and k-means Clustering Algorithm, J. Chem. Inf. Model., 2021, 61, 3411–3420, DOI:10.1021/acs.jcim.1c00253.
- L. R. da Silva, F. O. Morais, J. P. A. de Mendonça, B. R. L. Galvão and J. L. F. Da Silva, Theoretical investigation of the stability of A55−nBn nanoalloys (A, B = Al, Cu, Zn, Ag), Comput. Mater. Sci., 2022, 215, 111805, DOI:10.1016/j.commatsci.2022.111805.
- L. B. Pena, L. R. Da Silva, J. L. F. Da Silva and B. R. L. Galvão, Underlying Mechanisms of Gold Nanoalloys Stabilization, J. Chem. Phys., 2023, 159, 244310, DOI:10.1063/5.0180906.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Fast and Accurate Modeling of Molecular Atomization Energies With Machine Learning, Phys. Rev. Lett., 2012, 108, 058301, DOI:10.1103/physrevlett.108.058301.
- L. vd Maaten and G. Hinton, Visualizing data using t-sne, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- J. P. A. de Mendonça, T. C. Lourenço, L. P. M. Freitas, A. A. E. Santo, G. T. Feliciano and J. L. F. Da Silva, Molecular Dynamics Investigation of the Structural and Energetic Properties of CeO2–MOx (M = Gd, La, Ce, Zr) Nanoparticles, Mater. Adv., 2021, 2, 7759–7772, 10.1039/d1ma00543j.
- J. M. C. Marques and F. B. Pereira, An evolutionary algorithm for global minimum search of binary atomic clusters, Chem. Phys. Lett., 2010, 485, 211 CrossRef CAS.
- J. L. F. Da Silva, Effective Coordination Concept Applied for Phase Change (GeTe)m(Sb2Te3)n Compounds, J. Appl. Phys., 2011, 109, 023502, DOI:10.1063/1.3533422.
- A. S. Chaves, G. G. Rondina, M. J. Piotrowski and J. L. F. Da Silva, Structural Formation of Binary PtCu Clusters: A Density Functional Theory Investigation, Comput. Mater. Sci., 2015, 98, 278–286, DOI:10.1016/j.commatsci.2014.11.022.
- H. Zhen, L. Liu, Z. Lin, S. Gao, X. Li and X. Zhang, Physically Compatible Machine Learning Study on the Pt–Ni Nanoclusters, J. Phys. Chem. Lett., 2021, 12, 1573–1580 CrossRef CAS PubMed.
- D. Guedes-Sobrinho, R. L. H. Freire, A. S. Chaves and J. L. F. Da Silva, Ab initio Investigation of the Role of CO Adsorption on the Physical Properties of 55-atom PtCo Nanoalloys, J. Phys. Chem. C, 2017, 121, 27721–27732, DOI:10.1021/acs.jpcc.7b09243.
- J. C. De Winter, S. D. Gosling and J. Potter, Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: A tutorial using simulations and empirical data, Psychol. Methods, 2016, 21, 273, DOI:10.1037/met0000079.
- J. Hauke and T. Kossowski, Comparison of values of Pearson's and Spearman's correlation coefficients on the same sets of data, Quaest. Geogr., 2011, 30, 87–93, DOI:10.2478/v10117-011-0021-1.
- T. Rapps, R. Ahlrichs, E. Waldt, M. M. Kappes and D. Schooss, On the Structures of 55-Atom Transition-Metal Clusters and Their Relationship to the Crystalline Bulk, Angew. Chem., Int. Ed., 2013, 52, 6102–6105, DOI:10.1002/anie.201302165.
- D. Nelli, C. Roncaglia, R. Ferrando and C. Minnai, Shape changes in AuPd alloy nanoparticles controlled by anisotropic surface stress relaxation, J. Phys. Chem. Lett., 2021, 12, 4609–4615, DOI:10.1021/acs.jpclett.1c00787.
- D. Nelli, C. Roncaglia and C. Minnai, Strain engineering in alloy nanoparticles, Adv. Phys.: X, 2023, 8, 2127330, DOI:10.1080/23746149.2022.2127330.
- Z. Zhao, F.-H. Wang, A. Fisher, Y. Shen and D. Cheng, Phase stability and segregation behavior of nickel-based nanoalloys based on theory and simulation, J. Alloys Compd., 2017, 708, 1150–1160, DOI:10.1016/j.jallcom.2017.03.027.
- P. Cui, J.-H. Choi, W. Chen, J. Zeng, C.-K. Shih, Z. Li and Z. Zhang, Contrasting Structural Reconstructions, Electronic Properties, and Magnetic Orderings Along Different Edges of Zigzag Transition Metal Dichalcogenide Nanoribbons, Nano Lett., 2017, 17, 1097–1101, DOI:10.1021/acs.nanolett.6b04638.
- A. Radillo-Díaz, Y. Coronado, L. A. Pérez and I. L. Garzón, Structural and electronic properties of PtPd and PtNi nanoalloys, Eur. Phys. J. D, 2009, 52, 127–130, DOI:10.1140/epjd/e2009-00053-5.
- W. R. Tyson and W. A. Miller, Surface free energies of solid metals: Estimation from liquid surface tension measurements, Surf. Sci., 1977, 62, 267–276, DOI:10.1016/0039-6028(77)90442-3.
- C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, New York, 7th edn, 1996 Search PubMed.
- V. G. Grigoryan and M. Springborg, A Theoretical Study of the Structure of Ni Clusters (NiN, Phys. Chem. Chem. Phys., 2001, 3, 5135–5139, 10.1039/B105831M.
- J. Rogan, G. Garca, M. Ramrez, V. Munoz, J. A. Valdivia, X. Andrade, R. Ramrez and M. Kiwi, The structure and properties of small Pd clusters, Nanotechnology, 2008, 19, 205701, DOI:10.1088/0957-4484/19/20/205701.
- M. A. M. Paiva, B. M. T. C. Peluzo, J. C. Belchior and B. R. L. Galvão, Structure and stability of neutral Al–Mg nanoclusters up to 55 atoms, Phys. Chem. Chem. Phys., 2016, 18, 31579–31585, 10.1039/C6CP05605A.
- E.-A. Zen, Validity of “Vegard's law”, Am. Mineral., 1956, 41, 523–524 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00672k |
| This journal is © the Owner Societies 2024 |