Unveiling the photophysical and excited state properties of multi-resonant OLED emitters using combined DFT and CCSD method†
Received
13th February 2024
, Accepted 11th June 2024
First published on 23rd July 2024
Abstract
Multi-resonance thermally-activated delayed fluorescence (MR-TADF) is predominantly observed in organoboron heteroatom-embedded molecules, featuring enhanced performance in organic light-emitting diodes (OLEDs) with high color purity, chemical stability, and excellent photoluminescence quantum yields. However, predicting the impact of any chemical change remains a challenge. Computational methods including density functional theory (DFT) still require accurate descriptions of photophysical properties of MR-TADF emitters. To circumvent this drawback, we explored recent investigations on the CzBX (Cz = carbazole, X = O, S, or Se) molecule as a central building block. We constructed a series of MR-TADF molecules by controlling chalcogen atom embedding, employing a combined approach of DFT and coupled-cluster (CCSD) methods. Our predicted results for MR-TADF emitter molecules align with the reported experimental data in the literature. The variation in the positions of chalcogen atoms embedded within the CzBX2X framework imparts unique photophysical properties.
1. Introduction
In recent years, pure organoboron molecules with heteroatoms are attractive candidates that are receiving considerable attention and are a hot topic of research because of their narrowband emissive property, purity of color, and versatile applications in fields such as optoelectronic devices, photocatalytic synthesis, quantum information technologies, and organic light-emitting diodes (OLEDs).1–8 Researchers are particularly focused on the characteristics of triplet excited states to enhance the luminescence efficiency.9–16 The conversion between singlet and triplet states occurs through intersystem crossing (ISC) and reverse intersystem crossing (RISC), respectively, with these processes playing a pivotal role in achieving a high quantum yield for the luminescence process.17–19 Efficient ISC and RISC processes efficiently occur for low energy gap (ΔEST) between the lowest excited singlet (S1) and the lowest excited triplet energy (T1) states. ΔEST < ∼0.3 eV promotes the molecule's role as a thermally-activated delayed fluorescence (TADF) emitter. The TADF mechanism involves the thermal up-conversion of triplet excitons into singlets via RISC.19–23 Conversely, if ΔEST exceeds ∼0.4 eV, delayed luminescence at room temperature is most likely due to the room temperature phosphorescence (RTP) and triplet–triplet annihilation (TTA).24–29 Rate constants for RISC (kRISC) and ISC (kISC) are intrinsic characteristics dependent on their electronic structure and configuration of molecules. The interplay between the lowest energy gap (ΔEST) and high spin–orbit coupling (SOC) between the singlet and triplet excited states are two important factors that determine the path for the RISC and ISC processes. To harvest the lowest excited states (i.e., ISC for S1 → Tn and RISC for T1 → S1 conversion), a strong SOC matrix element (SOCME) is essential. In the case of MR-TADF, the rate of RISC is a key factor for efficiently harvesting triplet excitons and thereby converting them into radiative singlet excitons to achieve an internal quantum efficiency (IQE) of ∼100%.30,31 In some rare cases of MR-TADF molecules, where the S1 state energy is close to the energies of two triplets (T1 and T2) with a low ΔES1–Tn < 0.25 eV, the T1 exciton can also be harvested via RISC from S1 ← T2.32 Hatakeyama et al. observed MR-TADF features in DABNA derivatives containing boron and nitrogen atoms.33 Although the kRISC was initially slow, it was improved significantly in recently developed MR-TADF materials.9,34–37 A narrow full-width at half-maximum (FWHM) of less than 35 nm is beneficial for enhancing the spectral purity.38–40 Extending the molecule (donor–acceptor) or introducing substitution (heavy atoms) gradually increases the performance and reduces the FWHM value.38–40 Recent studies by Park et al. explored organoboron emitters doped with chalcogens to enhance the MR-TADF property for achieving excellent color purity and high luminescence efficiency.41 Using the design concept by Hatakeyama et al., featuring the MR effects as a new approach to the development of narrowband TADF emitters, MR-TADF molecules used polyaromatic compounds based on organoboron.33 Hatakeyama and others have introduced a new strategy for the design of embedding methods in organoboron-based polyaromatic molecules.42–45 Organoboron-based polyaromatic adjacent phenyl units have two hydrogen bonds converted to a heavy atom or chalcogen atom bond in MR-TADF molecules, and this type of embedded molecule shows excellent performance in OLEDs.34,44–46 Moreover, Park et al. identified a novel ideal superimposed fluorescence mechanism for the CzBSe molecule, exhibiting a high kRISC up to ∼108 s−1. The kRISC significantly increases with an upsurge in the chalcogen atomic number (9.0 × 103, 4 × 105 and 1.5 × 108 s−1 for O, S and Se, respectively) in toluene solvent.41 In this article, we unravel the photophysical properties of the recently published CzBX (X = O, S, or Se) molecules and successfully reproduced the experimental data with the combined DFT and CCSD approach results.47,48 The chalcogen-embedded framework for CzBX2X molecules significantly improved the narrowband emission and optical properties. In addition to that, we investigated a comparative study of the MR-TADF CzBX skeleton molecules: CzBO (5-oxa-8b-aza-15b-borabenzo[a]naphtho[1,2,3-hi]aceanthrylene), CzBS (5-thia-8b-aza-15b-borabenzo[a]naphtho[1,2,3-hi]aceanthrylene) and CzBSe (5-selena-8b-aza-15b-borabenzo[a]naphtho[1,2,3-hi]aceanthrylene). We also proposed and calculated the photophysical and excited properties of a series of CzBX2X-type MR-TADF molecules by controlling chalcogen atom embedding: CzBO2O (6,10,13-trioxa-3a2-aza-5a2-boraindeno[1,2,3,4-pqra]naphtho[3,2,1,8-ghij]perylene), CzBO2S (10-oxa-6,13-dithia-3a2-aza-5a2-boraindeno[1,2,3,4-pqra]naphtho[3,2,1,8-ghij]perylene), CzBO2Se (10-oxa-6,13-diselena-3a2-aza-5a2-boraindeno[1,2,3,4-pqra]naphtho[3,2,1,8-ghij]perylene), CzBS2O (6,13-dioxa-10-thia-3a2-aza-5a2-boraindeno[1,2,3,4-pqra]naphtho[3,2,1,8-ghij]perylene), CzBS2S (6,10,13-trithia-3a2-aza-5a2-boraindeno[1,2,3,4-pqra]naphtho[3,2,1,8-ghij]perylene), CzBS2Se (10-thia-6,13-diselena-3a2-aza-5a2-boraindeno[1,2,3,4-pqra]naphtho[3,2,1,8-ghij]perylene), CzBSe2O (6,13-dioxa-10-selena-3a2-aza-5a2-boraindeno[1,2,3,4-pqra]naphtho[3,2,1,8-ghij]perylene), CzBS2S (6,13-dithia-10-selena-3a2-aza-5a2-boraindeno[1,2,3,4-pqra]naphtho[3,2,1,8-ghij]perylene) and CzBSe2Se (6,10,13-triselena-3a2-aza-5a2-boraindeno[1,2,3,4-pqra]naphtho[3,2,1,8-ghij]perylene) (see Fig. 1).
 |
| | Fig. 1 Chemical structures of the CzBX and CzBX2X series are investigated in this work where X = O, S and Se. CzBX molecules are experimentally reported before, and CzBX2X molecules are proposed in this work. | |
2. Theoretical methodology and computational details
2.1 Geometries optimization and optical absorption
Ground state (S0) optimizations were carried out using density functional theory (DFT) employing the optimally tuned screened range-separated hybrid (OT-SRSH)15,49,50 ωB97XD functional (ω values are listed in Table S1a, ESI†) and 6-31G(d) basis set for H, B, C, N, O and S atoms except for Se atom, for which the ECP (effective core potential) type basis set LANL2DZ was used. Excited state geometry optimizations were performed using time-dependent DFT (TDDFT) method with OT-SRSH-ωB97XD functional with the abovementioned basis set. The toluene solvent was modeled with polarizable continuum model (PCM) with dielectric constant (ε) = 2.3741 to compare with the reported experimental data available in the literature.51 For TDDFT calculations, Tamm–Dancoff approximation (TDA) were considered to avoid triplet instability.49 The range-separation parameter, ω for OT-SRSH-ωB97XD functional was determined by minimizing J2 as follows.52–54| |  | (1) |
where IP and εH denote the ionization potential and HOMO (highest occupied molecular orbital) energy of a given molecule, respectively, and N is the number of electrons in the molecule. All the DFT and TDDFT calculations mentioned above were carried out with the Gaussian 16 software.55 In a previous study, Olivier and coworkers showed that linear-response DFT approaches consistently overestimate the ΔEST gaps in MR-TADF molecules.56 We carried out similarity transformed equation-of-motion coupled-cluster (with single and double excitations) method augmented with domain-based on local pair natural orbitals (STEOM-DLPNO-CCSD), which is a highly correlated wave function-based approach. It offers an accurate treatment for the excited state characteristics of various molecules, including MR-TADF molecules. These wavefunction-based calculations were performed with def2-TZVP basis set, as implemented in the ORCA V5.0.3 package.57,58 To avoid prohibitive computational costs, the energies of the singlet and triplet states and the related ΔEST values were calculated using STEOM-DLPNO-CCSD/def2-TZVP on the basis of the excited-state geometries (for S1, T1 and T2) obtained using the OT-SRSH-ωB97XD/6-31G(d)/LANL2DZ level of theory. This protocol provides manageable computational costs, while accurately reproducing the experimental data reported for known MR-type molecules.59,60 Thus, in our combined DFT and CCSD method, we used the OT-SRSH-ωB97XD/6-31G(d)/LANL2DZ level of theory for geometry optimization and STEOM-DLPNO-CCSD/def2-TZVP level of theory for single-point energy calculation. Vertical excitation calculation of STEOM-DLPNO-CCSD configuration details is provided in the ESI.†
2.2 Intersystem crossing (ISC) rate
The rate constant for the ISC process from S1 → Tn conversions and RISC process from T1 or T2 → S1 conversions were calculated using the Fermi's Golden Rule61,62| |  | (2) |
where 〈S1|ĤSOC|Tn〉 and ρFC denote the spin–orbit coupling matrix element (SOCME) between the S1 and Tn state and Franck–Condon weighted density of states, respectively. We used optimized excited state geometry (T1, T2-state optimized geometry for RISC and S1 state optimized geometry for ISC) obtained using OT-SRSH-ωB97XD/6-31G(d)/LANL2DZ//STEOM-DLPNO-CCSD/def2-TZVP (DFT-CCSD) for the calculation of the SOCME between the S1, T1 and T2 states. According to the Franck–Condon principle, electronic transition happens first and then relaxation of the geometry occurs. Thus, we considered the T1, T2-state optimized geometry for the calculation of the SOCME between the S1 and T1, and S1 and T2 states as we studied the transition (i.e., ISC and RISC) from the T1, T2 state to S1 state (RISC), and S1 state to T1, T2 state (ISC). The ρFC was estimated using the Marcus–Levich–Jortner theory.63| |  | (3) |
where λM is the reorganization energy, kB is the Boltzmann constant, T is the absolute temperature, S is the effective Huang–Rhys factor (S) associated with non-classical high-frequency intramolecular vibrational modes, and we found that S is less than 0.05 and the RMSD is less than 0.04 Å between the S1 and T1 optimized geometries. Thus, the reorganization energy between the S1 and T1 optimized geometries tends to zero (see Table S1b, ESI†). Thus, the S values were considered to be zero. The total reorganization energy has two components: the intramolecular reorganization energy is ∼0.006 eV (see Table S1c, ESI†) and the contribution of reorganization energy from the surroundings and solvent effect approximated to 0.2 eV. It is worthy to note that ΔEST = ΔES1–Tn for the ISC process whereas ΔEST = ΔETn–S1 for the RISC process. We used our own FORTRAN code to calculate kRISC/ISC using eqn (2) and (3) (available on https://Github.Com/Pralok87/Fortran-Code-for-ISC (https://Github.Com/Pralok87/Fortran-Code-for-ISC)). The overall intersystem crossing rate constant (kISC) from the excited S1 state to the triplet manifold (Tm) is given by63| |  | (4) |
2.3 Fluorescence and phosphorescence rate
The fluorescence and phosphorescence calculations were done based on excited state geometries optimized using the OT-SRSH-ωB97XD/6-31G(d)/LANL2DZ method. In order to account for the solvent effect, the toluene conductor-like polarizable continuum model (CPCM) was used. The fluorescence rate constants (kr) were calculated using Einstein A coefficient63,64| |  | (5) |
where Ef and Ei are the energies of the excited (f) and ground states (i), respectively, and f|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |i is the corresponding transition–dipole moment.
|i is the corresponding transition–dipole moment.
The phosphorescence rate constant, kph and radiative lifetime τph from each sublevel i (i = I, II, III) of the T1 state to the ground S0 state were calculated by making use of the transition energy ΔEi and the transition dipole moment Mi, as defined in eqn (6)65,66
| |  | (6) |
where
t0 = (4π
ε0)
2ħ3/
mee4.
ε0,
ħ,
me,
e and
α0 are the vacuum permittivity, reduced Planck constant, electron mass, electron charge and the fine structure constant, respectively. The contribution to the transition moment was calculated from the first-order (higher order is neglected in this study) corrected wave functions. The sublevels of the triplet state are considered to be energy degenerate; thus, the final expression for
Miα is
| |  | (7) |
The transition dipole moment operator
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif)
can be expanded in terms of vibrational normal modes.
67,68| |  | (8) |
The first order correction term (
i.e., the Herzberg–Teller (HT) term) was taken into account in
eqn (8) as it can significantly impact the spectra and rate constant calculations.
69 For the calculation of
kF and
kph, we considered the adiabatic hessian (HESSFLAG AH) method along with the Cartesian coordinate systems using the excited state dynamics (ESD) module of the ORCA package.
68,70 A broadening parameter of 200 cm
−1 was used. Both the emission calculations were done using the OT-SRSH-ωB97XD and def2-TZVP basis set as implemented in the ORCA V5.0.3 package.
58
We note that the computational methodology used here works relatively well as we compared our calculated results with the available experimentally reported data. The harmonic approximation to the vibrational normal modes works well for the calculation of radiative rate constant, but it is more prone to errors for the calculation of non-radiative rate constants.68 However, the approximation works well for present molecules due to the less structural relaxation of their ground and excited states optimized geometries. Also, the PCM solvent (toluene) model was used to mimic the surrounding environment effect in the bulk. As the properties of any thin film depends on its thickness, it is difficult to mimic the properties of thin films in reality.
3. Results and discussion
3.1 Structural and electronic properties
The optimized geometrical parameter of the ground-state (S0) shows the accuracy of the experimental molecule nature. The bond lengths and angles of CzBX (X = O, S, or Se) molecules well match with that of the experimental single crystal structure (CIF).41 The bond lengths of carbon and chalcogen atoms (C–X, X = O, S, Se) are 1.37, 1.75 and 1.90 Å, as reported in the experimental study, and are well comparable with our predicted results of 1.36, 1.77 and 1.89 Å, respectively. The bond lengths between the boron and carbon (C–B) bonds are ∼1.54–1.56 Å. The distance between the carbon and nitrogen (C–N) atoms are ∼1.40–1.43 Å and are well comparable with the reported experimental data (see Table 1 and Fig. 2). The angle of CXC, CBC and CNC decreased correspondingly to the chalcogen atoms.
Table 1 Comparison data from the experimental single crystal structure and theoretically optimized (OT-SRSH-ωB97XD/6-31G(d)/LANL2DZ) geometry
| Molecules |
C–Xa |
C–Xb |
C–Bc |
C–Bd |
C–Ne |
C–Nf |
CXCg |
CBCh |
CBCi |
CNCj |
CNCk |
|
Carbon and chalcogen atom distance.
Carbon and chalcogen atom distance.
Carbon and boron atom distance.
Carbon and boron atom distance.
Carbon and nitrogen atom distance.
Carbon and nitrogen atom distance.
Angle of carbon, chalcogen and carbon atoms.
Angle of carbon, boron and carbon atoms.
Angle of carbon, boron and carbon atoms.
Angle of carbon, nitrogen and carbon atoms.
Angle of carbon, nitrogen and carbon atoms.Distances are given in Å and angles are given in degrees. See Fig. 2 for angles and distances mentioned in footnotes a–k. |
| Expt.41 |
|
CzBO
|
1.37 |
1.38 |
1.54 |
1.55 |
1.41 |
1.43 |
122.2 |
114.7 |
130.6 |
121.5 |
130.5 |
|
CzBS
|
1.75 |
1.75 |
1.55 |
1.56 |
1.41 |
1.42 |
106.8 |
114.1 |
125.6 |
121.2 |
130.6 |
|
CzBSe
|
1.90 |
1.90 |
1.54 |
1.54 |
1.41 |
1.43 |
101.8 |
113.9 |
123.9 |
120.7 |
129.9 |
|
|
| Calculated results |
|
CzBO
|
1.36 |
1.37 |
1.53 |
1.55 |
1.40 |
1.41 |
122.7 |
114.6 |
130.7 |
121.6 |
130.2 |
|
CzBS
|
1.77 |
1.77 |
1.55 |
1.55 |
1.40 |
1.41 |
106.0 |
114.4 |
125.7 |
121.2 |
130.3 |
|
CzBSe
|
1.89 |
1.89 |
1.55 |
1.55 |
1.40 |
1.41 |
102.6 |
114.2 |
124.2 |
121 |
130.4 |
 |
| | Fig. 2 Chemical structures of the CzBX: left distances, middle angles of CzBX, and right substitution of chalcogen (CzBX2X) atoms (X = O, S, or Se), see Table 1. | |
The HOMO and LUMO (lowest unoccupied molecular orbital) energy levels and their associated ΔEH–L help to explain the origins of the energy shifts of the singlet and triplet states upon the substitution of O, S and Se. In CzBX-type molecules, both the HOMO and LUMO energies decrease in the order O, S and Se (EHOMO = −7.537, −7.421 and −7.408 eV; ELUMO = 1.183, 1.111 and 1.081 eV, respectively, see Table S2, ESI†). The HOMO and LUMO gap (ΔEH–L) decreases in the same order (8.720, 8.532 and 8.489 eV for O, S and Se, respectively). It is the reason behind the red shift in the S1 and T1 energies going from O to S and Se for CzBX molecules (see Fig. 3). The results can be explained from the electronegativity of the chalcogen atoms. A similar observation was found for doubly substituted chalcogens CzBX2X series, following the same trend (see Table S2, ESI†).
 |
| | Fig. 3 HOMO and LUMO of CzBX (X = O, S, or Se) molecule (isosurface value is 0.02 a.u.). HOMO (EH), LUMO (EL) and energy gap (ΔEH–L) energies are given in eV (obtained from the combined DFT-CCSD method). | |
3.2 Excited state optical properties
The calculated photophysical properties of the CzBX molecules are compared with the available experimental data (see Table 2). The UV-visible absorption spectrum calculated for the CzBX molecules exhibits a characteristic spectral signature with the lowest energy absorption maximum (λmaxabs) in the range of 422–450 nm. For the CzBO molecule, the calculated λabs is 422 nm (f = 0.3415), which is well comparable with the experimental results (λabs is 426 nm). On the other hand, the calculated λmaxabs for S and Se substituted for the CzBS molecules are 441.8 nm (f = 0.3169) and 450.0 nm (f = 0.2881), respectively. This result is well comparable to the reported experimental values for CzBX (447 nm and 451 nm for S and Se substitution, respectively). These results show the importance of the combined DFT and CCSD method used in this work (see Table 2). Orbital configurations of the transitions are provided in Table S3 (ESI†). The combined DFT and CCSD method effectively reproduces the fluorescence data of the CzBX molecules. The calculated (experimental) fluorescence energies are 446.4 (445) nm, 468.3 (471) nm, and 476 (477) nm, respectively for O, S and Se substituted CzBX molecules, respectively (see Table 3).
Table 2 Calculated low energy optical absorption (in eV) spectra compared with different functionals and the experimental reported results (ref. 41)
| Molecules |
Expt.41 |
B3LYP |
BHandHLYP |
CAM-B3LYP |
M062X |
PBE0 |
ωb97xD |
ω*B97XD |
Combined DFT and CCSD |
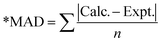 . . |
|
CzBO
|
2.910 |
3.036 |
3.625 |
3.520 |
3.489 |
3.138 |
3.580 |
3.427 |
2.938 |
|
f = 0.330 |
f = 0.488 |
f = 0.488 |
f = 0.476 |
f = 0.357 |
f = 0.507 |
f = 0.455 |
f = 0.342 |
|
CzBS
|
2.774 |
2.887 |
3.476 |
3.375 |
3.334 |
2.986 |
3.435 |
3.272 |
2.806 |
|
f = 0.301 |
f = 0.442 |
f = 0.413 |
f = 0.394 |
f = 0.324 |
f = 0.463 |
f = 0.413 |
f = 0.317 |
|
CzBSe
|
2.749 |
2.810 |
3.418 |
3.318 |
3.270 |
2.910 |
3.380 |
3.210 |
2.755 |
|
f = 0.274 |
f = 0.412 |
f = 0.444 |
f = 0.429 |
f = 0.296 |
f = 0.432 |
f = 0.383 |
f = 0.288 |
| MAD* |
0 |
0.100 |
0.695 |
0.593 |
0.554 |
0.200 |
0.654 |
0.492 |
0.022
|
Table 3 Comparison data of experimental (ref. 41) and theoretical absorption, emission profile data using the DFT-CCSD level of theory. f is the oscillator strength
| Molecules |
λ
abs (S0 → S1) in nm |
λ
F (S1 → S0) in nm |
| Expt. |
Cal. |
Expt. |
Cal. |
|
CzBO
|
426 |
422.0 (f = 0.3415) |
445 |
446.4 (f = 0.2985) |
|
CzBS
|
447 |
441.8 (f = 0.3169) |
471 |
468.3 (f = 0.2803) |
|
CzBSe
|
451 |
450.0 (f = 0.2881) |
477 |
476.0 (f = 0.2666) |
3.3 Intersystem crossing and reverse intersystem crossing process
3.3.1 Origin of SOC and intersystem crossing (ISC).
The interesting thing about light sources is that SOC depends on the structure, shape of the molecules and heavy atom effect, which will have a significant impact. Nowadays, organic molecule-based MR emitters are mostly constructed with heavy atoms (S, Se, Te and Br) and twisted-shape structures to achieve faster RISC rate constants for fluorescence. Additionally, the ΔEST plays a crucial role in fluorescence-based emitters. Both ΔEST and SOCME are important components in the overall TADF process. In this work, we explored a series of CzBX (X = O, S, Se) and substituted series of CzBX2X-based emitters. In the CzBX series of molecules, the fluorescence emission and delayed emission are purely dependent upon the puckered shape of the structure, heavy atoms and low ΔEST. The ΔES1–T1 values decrease with an increase in the atomic number of the chalcogen atoms (0.155, 0.113 and 0.095 eV for O, S and Se-substituted CzBX, respectively). On the other hand, the experimentally reported ΔES1–T1 values are 0.15, 0.11 and 0.12 eV for O, S and Se-substituted CzBX, respectively. The calculated ΔES1–T1 values are well comparable with the reported experimental results (Table 4).
Table 4 Calculated and experimental (ref. 41) ΔES1–T1 (in eV) with different DFT functionals and CCSD methods
| Molecules |
Expt. |
B3LYP |
BHandHLYP |
CAM-B3LYP |
M062X |
PBE0 |
ωb97xD |
ω*B97XD |
Combined DFT and CCSD |
|
Experimental values are measured in toluene.
Experimental values are measured in film state.The MAD value is calculated with respect to the experimental values obtained in toluene solvent. The tuned ω for ω*B97XD are provided in Table S1 (ESI). |
|
CzBO
|
0.15a, 0.16b |
0.46 |
0.87 |
0.73 |
0.60 |
0.51 |
0.67 |
0.55 |
0.155 |
|
CzBS
|
0.11a, 0.14b |
0.46 |
0.73 |
0.63 |
0.57 |
0.50 |
0.63 |
0.51 |
0.113 |
|
CzBSe
|
0.12a, 0.15b |
0.45 |
0.62 |
0.61 |
0.54 |
0.49 |
0.61 |
0.50 |
0.095 |
| MAD |
0
|
0.330 |
0.616 |
0.528 |
0.442 |
0.373 |
0.512 |
0.393 |
0.011
|
On the other hand, the ΔES1–T2 increases with the chalcogen atom decreasing order (−0.054, −0.146 and −0.173 eV for O, S and Se-substituted CzBX, respectively). The negative ΔES1–T2 value indicates that the T2 state is higher in energy than the S1 state. The ΔES1–Tn energies between the S1 and Tn (n = 1, 2) states and SOCME are reported in Tables 5 and 6 for the CzBX series. Based on the above ΔEST gap, we have calculated the rate constants of two possible transition ISC and RISC processes. Both the ISC and RISC process of MR-TADF emitters are greatly connected with the strength of SOC between the singlet and triplet states. In this study, for both CzBX and CzBX2X series, the strength of SOCME strongly depends on the excited state geometry and the presence of chalcogen atoms. Fig. 4 illustrates the top and side views, depicting the puckered shape for the CzBX series, the umbrella curve shape (UCS) for a few molecules, and the planar shape structure in the CzBX2X series (X = O, S, or Se). Also, the bond lengths (see Table S5, ESI†) increase in the same chalcogen order (O → S → Se). CzBO (d(C–O) is ∼1.36–1.37 Å), CzBS (d(C–S) is ∼1.75–1.76 Å), and CzBSe (d(C–Se) ∼1.87–1.89 Å) greatly increased this puckered shape structure, which helps to achieve the higher value of SOC matrix elements. For the ISC rate (kISC), SOCME is calculated in the geometry of S1 for the ISC from S1 → Tn (n = 1, 2) states. The SOCME between the S1 and T1 states increases with an increase in the atomic number of chalcogen atoms (0.086, 0.381 and 2.495 cm−1 for O, S, and Se-substituted CzBX, respectively). A similar observation was noted for the SOCME between the S1 and T2 states for CzBX molecules (0.099, 0.527 and 3.833 cm−1, respectively). For the calculation of the RISC rate constants (kRISC), the SOCMEs were calculated in the T1 state optimized geometry for the T1 → S1 RISC process and the T2 state optimized geometry for the T2 → S1 state RISC process. Similar to the SOCME for the ISC process, the SOCME for the RISC process increases with an increase in the atomic number of chalcogen atoms (viz., 0.077, 0.438 and 2.209 cm−1, respectively, between the S1 and T1 states, see Table 6 and Table S5, ESI†). The ISC rate for the CzBX series is calculated using eqn (2)–(4) and compared with the available experimental data.41 In this CzBX series of molecules, intramolecular H⋯H steric repulsions between the phenyl rings progressively increases, leading to the geometries becoming more puckered. This results in a twisted shape with heavy Se atoms, enhancing the spin–orbit coupling (SOC) and intersystem crossing rate (ISC and RISC) constants. The calculated ISC rate constants of CzBO and CzBS molecules are 4.0 × 106 s−1 and 6.0 × 107 s−1, respectively. The same for the heavy chalcogen atom Se substituted in the CzBSe molecule is 2.11 × 109 s−1 and the corresponding reported experimental data is 1.28 × 109 s−1. RISC is mostly favorable for this type of pure organic MR-TADF molecules. The kRISC values were calculated by taking into account the RISC not only directly from T1 to S1 but also from T1 to S1via the T2 states. The relative population in the T2 state with respect to that in the T1 state was obtained by considering thermal equilibrium.15
Table 5 Calculated singlet–triplet energy difference (ΔEST), spin–orbit coupling matrix element (SOCME), and ISC rate constants (kISC) for the CzBX series
| Molecule |
ΔESTa (eV) |
SOCMEa (cm−1) |
k
ISC (s−1) |
Expt. [ref. 41] kISC (s−1) |
| S1 ↔ T1 |
S1 ↔ T2 |
S1 → T2 |
S1 → T2 |
S1 → T1 |
S1 → T2 |
Total kISC |
Tolueneb/filmc |
|
ΔEST and SOCME were calculated using the combined DFT-CCSD method considering PCM (toluene) solvent.
Experimental ISC rate in toluene.
Experimental ISC rate in film.
|
|
CzBO
|
0.155 |
−0.054 |
0.086 |
0.099 |
3.86 × 106 |
2.45 × 105 |
0.4 × 107 |
—/2.5 × 107 |
|
CzBS
|
0.113 |
−0.146 |
0.381 |
0.527 |
5.79 × 107 |
4.74 × 105 |
0.6 × 108 |
2.1 × 108/1.9 × 108 |
|
CzBSe
|
0.095 |
−0.173 |
2.495 |
3.833 |
2.10 × 109 |
9.75 × 106 |
2.11 × 109 |
1.28 × 109/1.10 × 109 |
Table 6 Calculated singlet–triplet energy difference (ΔEST), spin–orbit coupling matrix element (SOCME), and RISC rate constants (kRISC) for the CzBX series
| Molecules |
ΔESTa (eV) |
SOCMEa (cm−1) |
k
RISC (s−1) |
Expt. [ref. 41] kRISC (s−1) |
| S1 ↔ T1 |
S1 ↔ T2 |
S1 ← T1 |
S1 ← T2 |
S1 ← T1 |
S1 ← T2 ← T1d |
Total kRISC |
Tolueneb/filmc |
|
ΔEST and SOCME were calculated using the combined DFT-CCSD method considering the PCM (toluene) solvent.
Experimental ISC rate in toluene.
Experimental ISC rate in film.
The kRISC values were calculated by taking into account the RISC from T1via T2 to S1; the relative population in the T2 state with respect to that in the T1 state was obtained by considering the thermal equilibrium (ref. 15).
|
|
CzBO
|
0.155 |
−0.054 |
0.077 |
0.286 |
7.44 × 103 |
5.11 × 103 |
1.26 × 104 |
—/9 × 103 |
|
CzBS
|
0.113 |
−0.146 |
0.438 |
0.496 |
9.43 × 105 |
5.17 × 103 |
9.48 × 105 |
4 × 105/2.2 × 105 |
|
CzBSe
|
0.095 |
−0.173 |
2.209 |
4.054 |
4.08 × 107 |
2.6 × 105 |
0.41 × 108 |
1.5 × 108/1.8 × 108 |
 |
| | Fig. 4 The S1 excited state structures of CzBX and CzBX2X. Excited state (S1/T1/T2) different chalcogens bond distances with carbon atom (d(X–C) when X = O, S, or Se), collected in Table S6 (ESI†). | |
The calculated rate constant of RISC for the CzBO molecule is 1.26 × 104 s−1, while the reported experimental value is 9.0 × 103 s−1 (in film). For the CzBS molecule, the calculated and experimentally reported RISC rate constants are 9.48 × 105 s−1 and 4.0 × 105 s−1, respectively. The heavy chalcogen atom Se substituted in the CzBSe molecule results in RISC rate constants of 0.41 × 108 s−1 (calc.) and 1.50 × 108 s−1 (exp.), respectively (see Table 6), which is the experimentally recorded high kRISC in recent times.41 The presence of heavy atoms gradually increased the kRISC due to an increase in SOCME. In the CzBX2X series, the molecules are categorized into two types, i.e., planar and UCS shape. The excited state geometry of these planar shapes has a 0° to 1.2° dihedral angle for CzBO2S (1.2°), CzBO2Se (0.4°), CzBS2S (0.1°), CzBS2Se, CzBSe2S and CzBSe2Se. The planar emitters have a very low SOCME, and in the presence of doubly substituted Se molecules with a high SOCME of above 0.088 cm−1 compared to other (non-Se atom and single substituted Se) SOCME of less than 0.009 cm−1 (except for CzBSe2S, 0.073 cm−1). Similarly, the excited state geometry of UCS molecules is significantly increased (>0.09 cm−1 due to the curve moiety). The dihedral angles of 20.8° (CzBO2O), 13.1° (CzBS2O), and 5.5° (CzBSe2Se) make the USC construction feasible, and the O atom has a shorter bond length with the nearest C atom distance (d(C–O) is ∼1.37–1.4 Å), chalcogen has a longer bond length with the nearest C atom (C–O ∼1.37–1.4 Å, C–S ∼1.76 – 1.82 Å and C–Se ∼1.92–1.99 Å), as shown in Table S6 (ESI†).
The UCS-shaped CzBO2O in the CzBO2X series has lower ΔES1–T1 (= 0.043 eV) and comparatively higher SOCME (0.082 cm−1) with a total ISC rate constant of 1.17 × 106 s−1. Similarly, for RISC, CzBO2O has a higher value of SOCME (S1 ← T1 is 0.091 and S1 ← T2 is 0.213 cm−1) and less energy gap (ΔES1–T1 = 0.043, ES1–T2 = −0.36 eV), and the conversional total RISC rate constant is 2.70 × 105 s−1. The other two CzBO2S and CzBO2Se molecules are planar in nature due to the high S and Se atom distances, and the RMSD is also less than ∼0.02 Å. The CzBO2S molecule has a lesser SOCME of 0.009 cm−1 and a smaller energy gap (ΔES1–T1 = 0.028, ΔES1–T2 = −0.075 eV), and the rate of RISC is 1.13 × 103 s−1. The doubly substituted Se-based CzBO2Se molecule has a high SOCME (0.012 cm−1 in S1 ← T1 and 0.085 cm−1 in S1 ← T2) and increased the total kRISC of 9.35 × 103 s−1. In comparison, the CzBO2X series of rate ISC and RISC in CzBO2O, CzBO2O and CzBO2Se have high kISC (see Tables 7 and 8). In the CzBS2X series, the CzBS2O molecule, with a UCS, has less ΔES1–Tn (ΔES1–T1 is 0.137, ΔES1–T2 is −0.196 eV) and high (in CzBS2X series only) SOCMEs (S1 → T1 is 0.137 cm−1 and S1 → T2 is 0.233 cm−1); the conversional total ISC rate reached 4.22 × 106 s−1. Similarly, for RISC, CzBS2O has a high SOCMEs (S1 ← T1 is 0.094 cm−1 and S1 ← T2 is 0.196 cm−1) and less (ΔES1–T1 = 0.137, ΔES1–T2= −0.196 eV) energy gap, and the total kRISC reached 2.04 × 104 s−1. The other two CzBS2S and CzBS2Se molecules are planar in nature. Also, these two molecules have low ΔES1–Tn and SOCMEs; hence, their kISC becomes low as well as that of ∼105 s−1. The CzBS2S molecule has low SOC matrix elements (S1 ← T1 is 0.003 cm−1 and S1 ← T2 is 0.007 cm−1), a smaller energy gap (ΔES1–T1 = 0.086, ΔES1–T2 = −0.129 eV), and the rate of RISC is 1.02 × 102 s−1. For the CzBS2Se molecule, the heavy Se atom has a high SOCMEs (S1 ← T1 is 0.088 cm−1 and S1 ← T2 is 0.246 cm−1), which increased the kRISC up to 2.41 × 105 s−1.
Table 7 Calculated singlet–triplet energy difference (ΔEST), spin–orbit coupling matrix element (SOCME), and ISC rate constants (kISC) for CzBX2X molecules
| Molecules |
Calc. ΔEST (eV) |
Calc. SOCME (cm−1) |
k
ISC (s−1) |
Tot. kISC (s−1) |
| S1 ↔ T1 |
S1 ↔ T2 |
S1 → T1 |
S1 → T2 |
S1 → T1 |
S1 → T2 |
|
CzBO2O
|
0.043 |
−0.360 |
0.082 |
0.236 |
1.17 × 106 |
7.60 × 100 |
1.17 × 106 |
|
CzBO2S
|
0.028 |
−0.075 |
0.009 |
0.008 |
1.11 × 104 |
9.32 × 102 |
1.20 × 104 |
|
CzBO2Se
|
0.013 |
−0.239 |
0.018 |
0.050 |
3.41 × 104 |
1.22 × 102 |
3.42 × 104 |
|
CzBS2O
|
0.137 |
−0.196 |
0.094 |
0.233 |
4.20 × 106 |
1.52 × 104 |
4.22 × 106 |
|
CzBS2S
|
0.086 |
−0.129 |
0.004 |
0.009 |
4.90 × 103 |
2.42 × 102 |
5.14 × 103 |
|
CzBS2Se
|
0.045 |
−0.275 |
0.071 |
0.109 |
9.03 × 105 |
1.17 × 102 |
9.04 × 105 |
|
CzBSe2O
|
0.207 |
−0.085 |
0.463 |
2.448 |
1.23 × 108 |
6.65 × 107 |
1.90 × 108 |
|
CzBSe2S
|
0.090 |
−0.208 |
0.008 |
0.046 |
2.05 × 104 |
3.72 × 102 |
2.09 × 104 |
|
CzBSe2Se
|
0.058 |
−0.240 |
0.080 |
0.788 |
1.38 × 106 |
2.91 × 104 |
1.41 × 106 |
Table 8 Calculated singlet–triplet energy difference (ΔEST), spin–orbit coupling matrix element (SOCME), and RISC rate constants (kRISC) for CzBX2X molecules
| Molecules |
Calc. ΔEST (eV) |
Calc. SOCME (cm−1) |
k
RISC (s−1) |
Tot. kRISC (s−1) |
| S1 ↔ T1 |
S1 ↔ T2 |
S1 ← T1 |
S1 ← T2 |
S1 ← T1 |
S1 ← T2 ← T1 |
|
CzBO2O
|
0.043 |
−0.360 |
0.091 |
0.213 |
2.70 × 105 |
1.17 |
2.70 × 105 |
|
CzBO2S
|
0.028 |
−0.075 |
0.004 |
0.009 |
7.36 × 102 |
3.97 × 102 |
1.13 × 103 |
|
CzBO2Se
|
0.013 |
−0.239 |
0.012 |
0.085 |
9.14 × 103 |
2.13 × 102 |
9.35 × 103 |
|
CzBS2O
|
0.137 |
−0.196 |
0.094 |
0.196 |
2.03 × 104 |
5.43 × 101 |
2.04 × 104 |
|
CzBS2S
|
0.086 |
−0.129 |
0.003 |
0.007 |
9.71 × 101 |
4.95 |
1.02 × 102 |
|
CzBS2Se
|
0.045 |
−0.275 |
0.088 |
0.246 |
2.41 × 105 |
1.04 × 102 |
2.41 × 105 |
|
CzBSe2O
|
0.207 |
−0.085 |
1.485 |
0.917 |
4.03 × 105 |
2.96 × 103 |
4.06 × 105 |
|
CzBSe2S
|
0.090 |
−0.208 |
0.007 |
0.073 |
4.73 × 102 |
2.93 × 101 |
5.02 × 102 |
|
CzBSe2Se
|
0.058 |
−0.240 |
0.089 |
0.106 |
1.79 × 105 |
5.52 × 101 |
1.79 × 105 |
The ISC and RISC rates went up a lot because of the heavy Se atoms in the CzBSe2X series and the molecule CzBSe2O, which has both UCS and heavy Se atoms. Among the CzBX2X series, CzBSe2O exhibited a high ISC rate due to its higher SOCMEs (S1 → T1 is 0.463 cm−1 and S1 → T2 is 2.448 cm−1) value and the lowest energy gap (ΔES1–T1 = 0.207 eV and ΔES1–T2 = −0.085 eV). It reached a very high ISC rate constant of 1.9 × 108 s−1. The RISC rate of CzBSe2O is the highest in the CzBX2O series, with a kRISC of 4.06 × 105 s−1 due to its low energy gap and high SOC matrix elements (S1 ← T1 is 1.485 cm−1 and S1 ← T2 is 0.917 cm−1). The other two molecules are planar with the heavy Se atom of CzBSe2S as the low energy gap and a low SOCMEs (S1 → T1 is 0.008 cm−1 and S1 → T2 is 0.046 cm−1) value to reach kISC of 2.09 × 104 s−1. But the RISC rate in CzBSe2S (single Se and double S atom) is low SOCMEs (in S1 ← T1 is 0.007 cm−1 and S1 ← T2 is 0.073 cm−1) value to achieve 5.02 × 102 s−1. The CzBSe2Se molecule with three Se atoms and planar geometry has lower rate (ISC and RISC) constants (see Tables 7 and 8). The CzBSe2Se molecule has a low energy gap (ΔES1–T1 = 0.058, ΔES1–T2 = −0.240 eV) and good SOC matrix elements (S1 → T2 is 0.788 cm−1) to increase the kISC up to 1.41 × 106 s−1. The rate of RISC also had good SOCMEs (S1 ← T1 is 0.089 and S1 ← T2 is 0.106 cm−1) to achieve the kRISC up to 1.79 × 105 s−1. The highest RISC rate constant for the CzBSe2Se molecule, as reported in a previous work by Pratik et al.,47,48 showed that increasing the chalcogen heavy Se atom greatly increases the RISC rate constants for non-planar molecules, but in our study, due to the planar geometry (0° dihedral angle) with triple Se heavy atoms, the kRISC becomes ∼105 s−1.
The RISC values are higher for doubly substituted chalcogen atoms: 2.7 × 105 s−1, 2.04 × 104 s−1 and 4.06 × 105 s−1 for CzBO2O, CzBS2O and CzBSe2O, respectively, due to the UCS shape (high bond distance in C–Se and less bond distance in C–O, see Table S5 for the UCS, ESI†) moiety. The majority of heavy atom compounds in MR-TADF reached the kRISC, which is approximately 104–7 s−1.71–73 This study shows the lightest atom with UCS, resulting in a kRISC ∼105 s−1 for the CzBX2O series. The natural transition orbitals (NTOs) presented in Fig. S2 (ESI†) shows the intramolecular charge transfer nature. The rate of emission can decide the path; taking a deep look into the kF and kP decides the best way of converting the exciton energy of S1 ⇄ Tn (ISC and RISC) to reach ∼100% of IQE.
3.3.2 Dihedral angle vs. RISC rate constants.
The dihedral angles of CzBX and CzBX2X series are calculated in the C–N–B–C middle part (see Fig. 4). The dihedral angle and SOCME are the major phenomena that enhance the RISC rate constants plotted in Fig. 5. The shapes of molecules are described using different layer colours. The planar (unsubstituted Se atom) structure, having lower SOCME values ∼0.009 cm−1 (in S1 ← T1 and S1 ← T2), reached the RISC rate constants lower than 103 s−1. Similarly, the similar planar structure with Se atom molecules reached the highest RISC rate up to 103–105 s−1 (CzBO2Se, CzBS2Se and CzBSe2Se), and the dihedral angle is 1.2° for CzBO2S (due to the O distance, see Table S5, ESI†) while CzBS2S is planar (see Fig. 4). The UCS structure has a high RISC rate constant due to the non-planar shape and dihedral angle of 20.8° for CzBO2O (triple O atom high dihedral angle in CzBX2X series), 13.1° for CzBS2O and 5.5° for CzBSe2O. These dihedral angles boosted the SOCME values and hence increased the RISC rate constants up to 104–105 s−1. The main series of CzBX has a puckered shape and is twisted in the excited state; the dihedral angle also greatly increases in the 62°–76° range. High dihedral angle increases the SOCME and RISC rate constants up to 1.26 × 104 s−1 (CzBO), 9.48 × 105 s−1 (CzBS), and 0.41 × 108 s−1(CzBSe). The presence of heavy or metal atoms will significantly increase the intersystem rate constants (ISC and RISC), and SOCME always plays an important role in the twisted or bent shape of the structure.
 |
| | Fig. 5 The effect of dihedral angle in MR-TADF and how it affects the RISC rate constants in different shapes (planar (brown), UCS (grey) and puckered (turquoise)). Here, blue and red circles denote the molecules with and without Se atoms in both CzBX and CzBX2X. | |
The different rate constants of fluorescence (kF), ISC (kISC) and RISC (kRISC) are compared in Table 9 (and Table S7, ESI†). Because of the higher rate constant for RISC compared to that of phosphorescence, these molecules show TADF features (see Fig. 6).
Table 9 Comparison of the calculated rate constant for fluorescence (kF), ISC (kISC) and RISC (kRISC) processes in s−1 (here, ϕ is the dihedral angle in degrees)
| Molecules |
ϕ (°) |
O |
ϕ (°) |
S |
ϕ (°) |
Se |
|
k
F (107) |
k
ISC (107) |
k
RISC (104) |
k
F (107) |
k
ISC (107) |
k
RISC (104) |
k
F (107) |
k
ISC (107) |
k
RISC (105) |
|
CzBX (expt.) |
— |
15/13 |
—/2.5 |
—/0.9 |
— |
1.5/3.3 |
21/19 |
40/22 |
— |
0.05 |
128/110 |
1500/1800 |
|
CzBX
|
62.2 |
17.4 |
0.41 |
1.26 |
75.9 |
15 |
5.84 |
94.8 |
67.4 |
14.6 |
211 |
411 |
|
CzBO2X
|
20.8 |
11.4 |
0.17 |
27 |
1.2 |
9 |
1.2 × 104 |
0.13 |
0.4 |
9.13 |
3.42 × 104 |
0.093 |
|
CzBS2X
|
13.1 |
12.2 |
0.42 |
2.04 |
0.1 |
9.24 |
5.1 × 103 |
1.02 × 102 |
0 |
8.51 |
0.09 |
2.41 |
|
CzBSe2X
|
5.5 |
14.2 |
19 |
4.06 |
0 |
8.62 |
2.1 × 104 |
5.02 × 102 |
0 |
8.33 |
0.14 |
6.21 × 102 |
 |
| | Fig. 6 MR-TADF mechanism in harvesting triplet excitons. Here B. RISC is T1 to S1 conversion via the T2 state. The relative population in the T2 state compared with the T1 state was obtained by considering thermal equilibrium (using the Boltzmann factor). | |
4. Conclusions
In conclusion, we investigated how chalcogens (O → S → Se) affect the MR-TADF features and properties for a series of CzBX and CzBX2X molecules obtained either by the substitution of O atoms with S or Se in CzBX or by fusing intramolecular H⋯H bond with chalcogen atoms, the CzBX adjacent phenyl position to create the new MR-TADF CzBX2X series. The results of calculations based on highly correlated wave functions show the following.
(i) The CzBX and CzBX2X series of MR-TADF emitters have high radiative (fluorescence) rate constants (kF) of about ∼107–8 s−1.
(ii) The ISC and RISC rate constants that follow are significantly influenced by the molecules electronic structure and geometry. While the CzBX series has the same chemical compositions, the ISC and RISC rate constants are found to be much larger due to the increasing chalcogen molecular size order (O → S → Se) compared to the CzBX2X series, which has lower SOCME values due to the planer and puckered geometry. UCS structures have higher SOCMEs.
(iii) The selenium-containing (CzBX) molecules exhibit higher ISC and RISC rate values (kISC ∼ 109 s−1 and kRISC ∼ 108 s−1), which is due to the higher spin–orbit coupling interactions. The higher RISC rate constants in the CzBX2X series for both types of planar and UCS geometries reach ∼105 s−1.
(iv) The phosphorescence rate constants (kP) are in the range from ∼101 to 104 s−1 (calculated). Due to faster RISC and fluorescence rate constants, these CzBX and CzBX2X series of MR-TADF emitters show bright fluorescence (kF ∼107–8 s−1).
(v) This CzBX series of molecules has a unique deep-sky blue luminescence with sharp narrow band emission peaks and CzBX2X as bright bluish emitters.
Overall, we demonstrated that the chemical nature of the chalcogen atoms, as well as their changing position(s), have a significant influence on the optical and electronic features of the CzBX and CzBX2X-based MR-TADF emitters and their accurate prediction using combined DFT and CCSD methods. We compared our calculated results with available experimentally reported data to validate our computational methodology used in this study. We used PCM solvent (toluene) model to mimic the surrounding environment effect in the bulk. In reality, it is difficult to mimic the properties of thin films as the properties of any thin-film depend on its thickness. Here in, we explained the origins of MR-TADF properties in organoboron heteroatom-embedded molecules from the molecular point of view. We believe that the present methodology and findings will aid in the development of narrow-band blue OLED emitters with a high level of efficiency.
Author contributions
P. S.: conceptualization of the total work, computation and analysis of the works done, writing the original manuscript. P. K. S.: overall supervision, analysis and writing the manuscript.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
P. S. thanks BITS-Pilani for the “Institute Research Fellowship”. P. K. S. thanks Department of Science and Technology-Science and Engineering Research Board (DST-SERB), Government of India (grant number: CRG/2021/002706) for the partial financial support. We acknowledge the support for high-performance computing and storage resources at GITAM and BITS-Pilani (Hyderabad Campus).
References
- T. Wang, Y. Zou, Z. Huang, N. Li, J. Miao and C. Yang, Angew. Chem., Int. Ed., 2022, 61, 1–7 Search PubMed
 .
.
- H. Gao, S. Shen, Y. Qin, G. Liu, T. Gao, X. Dong, Z. Pang, X. Xie, P. Wang and Y. Wang, J. Phys. Chem. Lett., 2022, 13, 7561–7567 CrossRef CAS
 .
.
- S. Lin, Z. Pei, B. Zhang, H. Ma and W. Z. Liang, J. Phys. Chem. A, 2022, 126, 239–248 CrossRef CAS PubMed
 .
.
- P. Jiang, J. Miao, X. Cao, H. Xia, K. Pan, T. Hua, X. Lv, Z. Huang, Y. Zou and C. Yang, Adv. Mater., 2022, 34, 1–7 CAS
 .
.
- Y. C. Cheng, X. C. Fan, F. Huang, X. Xiong, J. Yu, K. Wang, C. S. Lee and X. H. Zhang, Angew. Chem., Int. Ed., 2022, 61, 1–6 Search PubMed
 .
.
- X. Wu, J. Huang, B. Su, S. Wang, L. Yuan, W. Zheng, H. Zhang, Y. Zheng, W. Zhu and P. Chou, Adv. Mater., 2022, 34, 2270006 CrossRef
 .
.
- G. Zhao, D. Liu, P. Wang, X. Huang, H. Chen, Y. Zhang, D. Zhang, W. Jiang, Y. Sun and L. Duan, Angew. Chem., Int. Ed., 2022, 61, e202212861 CrossRef CAS
 .
.
- J. Park, J. Lim, J. H. Lee, B. Jang, J. H. Han, S. S. Yoon and J. Y. Lee, ACS Appl. Mater. Interfaces, 2021, 13, 45798–45805 CrossRef CAS
 .
.
- Y. Liu, X. Xiao, Z. Huang, D. Yang, D. Ma, J. Liu, B. Lei, Z. Bin and J. You, Angew. Chem., Int. Ed., 2022, 134, e202210210 CrossRef
 .
.
- N. Ikeda, S. Oda, R. Matsumoto, M. Yoshioka, D. Fukushima, K. Yoshiura, N. Yasuda and T. Hatakeyama, Adv. Mater., 2020, 32, 1–6 CrossRef
 .
.
- W. Sotoyama, J. Phys. Chem. A, 2021, 125, 10373–10378 CrossRef CAS PubMed
 .
.
- S. Wu, W. Li, K. Yoshida, D. Hall, S. Madayanad Suresh, T. Sayner, J. Gong, D. Beljonne, Y. Olivier, I. D. W. Samuel and E. Zysman-Colman, ACS Appl. Mater. Interfaces, 2022, 14, 22314–22352 Search PubMed
 .
.
- H. Cheon, S. Woo, S. Baek, J. Lee and Y. Kim, Adv. Mater., 2022, 34, 2207416 CrossRef CAS
 .
.
- P. K. Samanta and N. J. English, J. Phys. Chem. C, 2020, 124, 8178–8185 CrossRef CAS
 .
.
- P. K. Samanta, D. Kim, V. Coropceanu and J. L. Brédas, J. Am. Chem. Soc., 2017, 139, 4042–4051 CrossRef CAS PubMed
 .
.
- B. C. Garain, P. K. Samanta and S. K. Pati, J. Phys. Chem. A, 2021, 125, 6674–6680 CrossRef CAS
 .
.
- S. Kuila, A. Ghorai, P. K. Samanta, R. B. K. Siram, S. K. Pati, K. S. Narayan and S. J. George, Chem. – Eur. J., 2019, 25, 16007–16011 CrossRef CAS
 .
.
- H. Shu, L. Chen, X. Wu, T. Wang, S. Wang, H. Tong and L. Wang, J. Mater. Chem. C, 2022, 10, 1833–1838 RSC
 .
.
- B. Li, Z. Yang, W. Gong, X. Chen, D. W. Bruce, S. Wang, H. Ma, Y. Liu, W. Zhu, Z. Chi and Y. Wang, Adv. Opt. Mater., 2021, 9, 1–10 RSC
 .
.
- P. Sivasakthi, J. M. Jacob, M. K. Ravva and P. K. Samanta, J. Phys. Chem. A, 2022, 124, 886–893 Search PubMed
 .
.
- A. Arjona-Esteban, S. Barbara and O. Julian, Lumin. OLED Technol. Appl., 2019, 1–18 Search PubMed
 .
.
- D. K. A. Phan Huu, S. Saseendran, R. Dhali, L. G. Franca, K. Stavrou, A. Monkman and A. Painelli, J. Am. Chem. Soc., 2022, 144, 15211–15222 CrossRef CAS PubMed
 .
.
- R. Dhali, D. K. A. Phan Huu, F. Terenziani, C. Sissa and A. Painelli, J. Chem. Phys., 2021, 154, 134112 CrossRef CAS PubMed
 .
.
- M. Li, W. Xie, X. Cai, X. Peng, K. Liu, Q. Gu, J. Zhou, W. Qiu, Z. Chen, Y. Gan and S. J. Su, Angew. Chem., Int. Ed., 2022, 61, e202209343 CrossRef CAS PubMed
 .
.
- A. Chatterjee, J. Chatterjee, S. Sappati, T. Sheikh, R. M. Umesh, M. D. Ambhore, M. Lahiri and P. Hazra, J. Phys. Chem. B, 2021, 125, 12832–12846 CrossRef CAS
 .
.
- Kenry, C. Chen and B. Liu, Nat. Commun., 2019, 10, 1–15 CrossRef CAS
 .
.
- J. Yu, H. Ma, W. Huang, Z. Liang, K. Zhou, A. Lv, X.-G. Li and Z. He, JACS Au, 2021, 1, 1694–1699 CAS
 .
.
- P. K. Samanta and S. K. Pati, J. Mol. Model., 2018, 24, 1–11 CrossRef CAS
 .
.
- N. Liang, G. Liu, D. Hu, K. Wang, Y. Li, T. Zhai, X. Zhang, Z. Shuai, H. Yan, J. Hou and Z. Wang, Adv. Sci., 2022, 9, 2103975 CrossRef CAS
 .
.
- R. K. Konidena and K. R. Naveen, Adv. Photonics Res., 2022, 3, 2200201 CrossRef CAS
 .
.
- K. R. Naveen, P. Palanisamy, M. Y. Chae and J. H. Kwon, Chem. Commun., 2023, 59, 3685–3702 RSC
 .
.
- T. Wang, A. K. Gupta, D. B. Cordes, A. M. Z. Slawin and E. Zysman-Colman, Adv. Opt. Mater., 2023, 11, 2300114 CrossRef CAS
 .
.
- T. Hatakeyama, K. Shiren, K. Nakajima, S. Nomura, S. Nakatsuka, K. Kinoshita, J. Ni, Y. Ono and T. Ikuta, Adv. Mater., 2016, 28, 2777–2781 CrossRef CAS
 .
.
- S. Madayanad Suresh, D. Hall, D. Beljonne, Y. Olivier and E. Zysman-Colman, Adv. Funct. Mater., 2020, 30, 1908677 CAS
 .
.
- S. Oda, W. Kumano, T. Hama, R. Kawasumi, K. Yoshiura and T. Hatakeyama, Angew. Chem., 2021, 133, 2918–2922 CrossRef
 .
.
- K. R. Naveen, H. I. Yang and J. H. Kwon, Commun. Chem., 2022, 5, 149 CrossRef CAS PubMed
 .
.
- S. Oda, T. Sugitani, H. Tanaka, K. Tabata, R. Kawasumi and T. Hatakeyama, Adv. Mater., 2022, 34, 1–6 CrossRef
 .
.
- K. R. Naveen, H. Lee, L. H. Seung, Y. H. Jung, C. P. Keshavananda Prabhu, S. Muruganantham and J. H. Kwon, Chem. Eng. J., 2023, 451, 138498 CrossRef CAS
 .
.
- P. Palanisamy, O. P. Kumar, H. U. Kim, K. R. Naveen, J. Y. Kim, J. H. Baek, M. Y. Chae and J. H. Kwon, Chem. Eng. J., 2024, 481, 148781 CrossRef CAS
 .
.
- H. X. Ni, X. F. Luo, L. Yuan, J. J. Hu, W. W. Zhang and Y. X. Zheng, J. Mater. Chem. C, 2024, 12, 2578–2584 RSC
 .
.
- I. S. Park, H. Min and T. Yasuda, Angew. Chem., Int. Ed., 2022, 134, e202205684 CrossRef
 .
.
- M. Yang, I. S. Park and T. Yasuda, J. Am. Chem. Soc., 2020, 142, 19468–19472 CrossRef CAS
 .
.
- Y. Zhang, D. Zhang, J. Wei, Z. Liu, Y. Lu and L. Duan, Angew. Chem., Int. Ed., 2019, 58, 16912–16917 CrossRef CAS
 .
.
- K. Matsui, S. Oda, K. Yoshiura, K. Nakajima, N. Yasuda and T. Hatakeyama, J. Am. Chem. Soc., 2018, 140, 1195–1198 CAS
 .
.
- H. Hirai, K. Nakajima, S. Nakatsuka, K. Shiren, J. Ni, S. Nomura, T. Ikuta and T. Hatakeyama, Angew. Chem., Int. Ed., 2015, 54, 13581–13585 CAS
 .
.
- H. Jiang, Y. Cao, Q. Yang, L. Xian, Y. Tao, R. Chen and W. Huang, J. Phys. Chem. Lett., 2020, 11, 7739–7754 CrossRef CAS
 .
.
- S. M. Pratik, V. Coropceanu and J. L. Brédas, Chem. Mater., 2022, 34, 8022–8030 CrossRef CAS
 .
.
- S. M. Pratik, V. Coropceanu and J. L. Brédas, ACS Mater. Lett., 2022, 4, 440–447 CrossRef CAS
 .
.
- H. Sun, C. Zhong and J. L. Brédas, J. Chem. Theory Comput., 2015, 11, 3851–3858 CrossRef CAS PubMed
 .
.
- M. Rubešová, E. Muchová and P. Slavíček, J. Chem. Theory Comput., 2017, 13, 4972–4983 CrossRef
 .
.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 Search PubMed
 .
.
- S. Rohman and R. Kar, J. Phys. Chem. A, 2022, 126, 3452–3462 CrossRef CAS
 .
.
- O. S. Bokareva, G. Grell, S. I. Bokarev and O. Kühn, J. Chem. Theory Comput., 2015, 11, 1700–1709 CAS
 .
.
- L. Kronik, T. Stein, S. Refaely-Abramson and R. Baer, J. Chem. Theory Comput., 2012, 8, 1515–1531 CrossRef CAS
 .
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed
 .
.
- A. Pershin, D. Hall, V. Lemaur, J. C. Sancho-Garcia, L. Muccioli, E. Zysman-Colman, D. Beljonne and Y. Olivier, Nat. Commun., 2019, 10, 597 CrossRef CAS
 .
.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CAS
 .
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed
 .
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
 .
.
- A. K. Dutta, M. Nooijen, F. Neese and R. Izsák, J. Chem. Phys., 2017, 146, 074103 CrossRef
 .
.
- V. Lawetz, G. Orlandi and W. Siebrand, J. Chem. Phys., 1972, 56, 4058–4072 CrossRef CAS
 .
.
- G. W. Robinson and R. P. Frosch, J. Chem. Phys., 1963, 38, 1187–1203 CrossRef CAS
 .
.
- K. Schmidt, S. Brovelli, V. Coropceanu, D. Beljonne, J. Cornil, C. Bazzini, T. Caronna, R. Tubino, F. Meinardi, Z. Shuai and J. L. Brédas, J. Phys. Chem. A, 2007, 111, 10490–10499 CrossRef CAS
 .
.
- R. C. Hilborn, Am. J. Phys., 1982, 50, 982–986 CrossRef CAS
 .
.
- E. Jansson, B. Minaev, S. Schrader and H. Ågren, Chem. Phys., 2007, 333, 157–167 CrossRef CAS
 .
.
- Q. Zhang, X. Wang, Y. Zhang, L. Wang, J. Li and J. Zhang, J. Phys. Chem. C, 2016, 120, 27523–27532 CrossRef CAS
 .
.
- Z. Shuai and Q. Peng, Phys. Rep., 2014, 537, 123–156 CAS
 .
.
- M. T. do Casal, K. Veys, M. H. E. Bousquet, D. Escudero and D. Jacquemin, J. Phys. Chem. A, 2023, 127, 10033–10053 CrossRef CAS PubMed
 .
.
- A. Manian and S. P. Russo, Sci. Rep., 2022, 12, 21481 CrossRef CAS PubMed
 .
.
- M. H. E. Bousquet, T. V. Papineau, K. Veys, D. Escudero and D. Jacquemin, J. Chem. Theory
Comput., 2023, 19, 5525–5547 CAS
 .
.
- X. Cao, K. Pan, J. Miao, X. Lv, Z. Huang, F. Ni, X. Yin, Y. Wei and C. Yang, J. Am. Chem. Soc., 2022, 144, 22976–22984 CrossRef CAS
 .
.
- S. Wu, L. Zhang, J. Wang, A. Kumar Gupta, I. D. W. Samuel and E. Zysman-Colman, Angew. Chem., Int. Ed., 2023, 62, e202305182 CrossRef CAS PubMed
 .
.
- T. Wang, A. K. Gupta, D. B. Cordes, A. M. Z. Slawin and E. Zysman-Colman, Adv. Opt. Mater., 2023, 11, 2300114 CrossRef CAS
 .
.
Footnote |
| † Electronic supplementary information (ESI) available: STEOM-DLPNO-CCSD computational details, structural details, excited state energy using different DFT functional, HOMO, LUMO, ΔEH–L, configurations percentage, and calculated fluorescence and phosphorescence rate constants (pdf). See DOI: https://doi.org/10.1039/d4cp00637b |
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab and
Pralok K.
Samanta
ab and
Pralok K.
Samanta
 *ab
*ab





![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |i is the corresponding transition–dipole moment.
|i is the corresponding transition–dipole moment.


![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) can be expanded in terms of vibrational normal modes.67,68
can be expanded in terms of vibrational normal modes.67,68

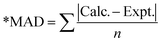 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.




