Ab initio calculation of magnetic anisotropy and thermal spin transition in the variable temperature crystal conformations of [Co(terpy)2]2+†
Moromi
Nath
,
Shalini
Joshi
and
Sabyashachi
Mishra
 *
*
Department of Chemistry, Indian Institute of Technology Kharagpur, Kharagpur, India. E-mail: mishra@chem.iitkgp.ac.in
First published on 3rd May 2024
Abstract
The structure–property correlation of [Co(terpy)2]2+, which shows a spin crossover at 270 K, has been computationally investigated based on its variable temperature crystal structures. Among the employed DFT functionals, only the re-parametrized hybrid B3LYP* functional could describe the correct spin transition temperature. Explicit consideration of metal–ligand sigma bonding with dynamic electron correlation is found to be necessary for an accurate determination of the SCO temperature with multi-reference calculations. The metal–ligand axial bond distances are found to be the most significant internal coordinates in deciding SCO. A small structural change along the axial distance causes a change in the t2g orbital splitting pattern and a reorientation of the magnetization axes at the SCO temperature. The complex shows an unusual triaxial magnetic anisotropy, with an easy axis of magnetization developing at higher temperatures. The strong coupling of low-frequency wagging motion of the two terpyridine ligands with the spin states of the complex provides an effective pathway for the relaxation of magnetization, resulting in a small magnetic anisotropy barrier.
1 Introduction
The spin crossover (SCO) phenomenon describes the change in the spin state between the low-spin (LS) and the high-spin (HS) states of a suitable transition metal ion, typically triggered by temperature, but they can also be induced by irradiation, the application of pressure, or a magnetic field.1–4 Since the pioneering work of Cambi and Szegö 90 years ago,5 SCO coordination compounds have attracted consistent attention.6–9 The octahedral complexes of the first-row transition metal ions with electronic configurations from d4 to d7 can exist in HS and LS states. The HS ↔ LS conversion has potential for use in spintronic devices, molecular switches, and sensors under the right conditions, such as abrupt magnetic behaviour, the presence of a hysteresis loop and an appropriate transition temperature range.9,10Crystallography coupled with various magnetic measurement studies have been regularly employed to obtain a correlation between molecular structure and magnetic properties, including the SCO characteristics.11–15 The importance of crystal packing and the role of ligand substitution in determining the SCO properties of Fe(II) complexes have been studied by Park et al., in which they focus on a series of isostructural Fe(II) complexes with different ligand substitutions and investigate the electronic effects of these substitutions on the SCO behaviour.16 Their crystallographic analysis reveals that the complexes are well-separated from each other in the solid state due to the presence of bulky tetra(aryl)borate counteranions, indicating that the SCO is not significantly affected by intermolecular interactions in those complexes due to the bigger size of the associated ligands. The crystallographic analysis in a dinuclear iron(II) complex, containing a pyridyl bridging ligand, reveals that the spin-state change occurs independently at each iron(II) site, with no role of intramolecular coupling between the metal centres in determining the SCO behavior of the complex.17 Instead, the crystal packing has been found to have a dominating influence on the SCO properties. Further, the influence of solvent molecules on the crystal packing and SCO properties of a mononuclear iron(II) complex has been studied by Sun et al.,18 where the presence of different solvent molecules is shown to subtly change the molecular packing structures and intermolecular interactions in these complexes, leading to different SCO behaviour.
While a large number of studies have focussed on SCO in iron(II) complexes, the SCO studies on Co(II) complexes are rather limited. In Co(II) complexes, the SCO occurs between spin states S = 1/2 and 3/2. Unlike Fe(II) or Fe(III) SCO complexes, the SCO in Co(II) transfers one electron from the t2g to the eg orbitals. Cobalt(II) complexes usually show a gradual SCO as the molecular volume changes with SCO. The (spin) entropy change during SCO, expressed as ΔS = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln[(2S + 1)HS/(2S + 1)LS], is much smaller in Co(II) (5.8 J K−1 mol−1) compared to the same in Fe(III) or Fe(II) (13.4 and 9.1 J K−1 mol−1, respectively). Thus, Co(II) complexes can show SCO with weaker external stimuli. Since the first report of the SCO in [Co(terpy)2][BF4]2 (terpy = 2,2′:6′,2′′ terpyridine), various derivatives of the terpy ligand have been employed to investigate S = 1/2 ↔ 3/2 SCO.9,19–26 The SCO behaviour of [Co(terpy)2]2+ is strongly influenced by the counter-anions and solvents present. The Co(II) complexes [Co(terpy)2]X2·nH2O (X = Br−, Cl−, I-, F−, ClO4−, NCS−, NO3−, [Co(CN)4]2−, SO42−, BPh4− and n = 0–6) exhibit different SCO behaviour, resulting in incomplete or gradual SCO curves.20,22,24,25,27–31 Kilner and Halcrow have reported a crystallographic study of [Co(terpy)2][BF4]2 at nine temperatures between 30–375 K. The complex shows a gradual thermal spin-transition with SCO temperature near 270 K.32 Long alkyl chains in SCO cobalt(II) complexes can result in new physical properties due to the interaction between SCO and response to external stimuli, as well as the coordination of spin-state transitions and crystal-liquid-crystal phase transitions.10,28 A range of Co(II) complexes have been studied for their spin-crossover behavior, with some showing very high transition temperatures. Sun et al. (2021) reported two such complexes, demonstrating their hysteretic spin crossover at high temperatures. This finding is consistent with previous research27,33,34 showing high transition temperatures for Co(II) SCO complexes. The synthesis of dinuclear cobalt(II) compounds with complementary terpyridine ligands has been a recent research focus. Some of these compounds display solvent-modulated behavior and thermal hysteresis loops.15
ln[(2S + 1)HS/(2S + 1)LS], is much smaller in Co(II) (5.8 J K−1 mol−1) compared to the same in Fe(III) or Fe(II) (13.4 and 9.1 J K−1 mol−1, respectively). Thus, Co(II) complexes can show SCO with weaker external stimuli. Since the first report of the SCO in [Co(terpy)2][BF4]2 (terpy = 2,2′:6′,2′′ terpyridine), various derivatives of the terpy ligand have been employed to investigate S = 1/2 ↔ 3/2 SCO.9,19–26 The SCO behaviour of [Co(terpy)2]2+ is strongly influenced by the counter-anions and solvents present. The Co(II) complexes [Co(terpy)2]X2·nH2O (X = Br−, Cl−, I-, F−, ClO4−, NCS−, NO3−, [Co(CN)4]2−, SO42−, BPh4− and n = 0–6) exhibit different SCO behaviour, resulting in incomplete or gradual SCO curves.20,22,24,25,27–31 Kilner and Halcrow have reported a crystallographic study of [Co(terpy)2][BF4]2 at nine temperatures between 30–375 K. The complex shows a gradual thermal spin-transition with SCO temperature near 270 K.32 Long alkyl chains in SCO cobalt(II) complexes can result in new physical properties due to the interaction between SCO and response to external stimuli, as well as the coordination of spin-state transitions and crystal-liquid-crystal phase transitions.10,28 A range of Co(II) complexes have been studied for their spin-crossover behavior, with some showing very high transition temperatures. Sun et al. (2021) reported two such complexes, demonstrating their hysteretic spin crossover at high temperatures. This finding is consistent with previous research27,33,34 showing high transition temperatures for Co(II) SCO complexes. The synthesis of dinuclear cobalt(II) compounds with complementary terpyridine ligands has been a recent research focus. Some of these compounds display solvent-modulated behavior and thermal hysteresis loops.15
Practical applications of an SCO complex in magnetic switching, data storage, and nanophotonic devices are further enhanced when the complex shows a large magnetic anisotropy barrier for the reversal of magnetization.6 Magnetic anisotropy is the property that presents the direction of spin of a system that may not be aligned with an external magnetic field in a preferred direction, as promoted by the Zeeman effect. If there is a preferred direction, the systems are classified as easy axis; however, if the spin remains contained within a plane, the systems are referred to as easy plane.35 Consequently, molecules with a high degree of magnetic anisotropy can behave as individual nanomagnets in the absence of a magnetic field due to their propensity to maintain their inherent spin direction.36–38 In recent decades, synthetic chemists have exerted significant efforts to develop new transition metal complexes capable of behaving as single-ion magnets.39–41 The conventional spin Hamiltonian for addressing such effects contains zero-field splitting (ZFS) terms42,43
 | (1) |
Spin-vibration coupling plays a crucial role in the relaxation and decoherence of spins in magnetically anisotropic complexes. Molecular vibrations can modify the spin relaxation dynamics. Detailed studies have been conducted to understand the nature of spin-vibration coupling in transition metal complexes with slow magnetic relaxation.44–47 This coupling has been shown to be responsible for under-barrier spin relaxation in single-molecule magnets at high temperatures.48 It is, therefore important to consider spin-vibration coupling as a strategy for engineering room-temperature SMMs with large magnetic anisotropy to protect them from low-barrier relaxation processes.49
In addition to experimental studies, the computational studies involving ab initio electronic structure calculations of electronic properties, spin state energetics, and magnetic properties bring unique clarity and insight to the magnetic and SCO behaviour of transition metal complexes.50 Accurate modelling of spin-state energetics is crucial for understanding the magnetic properties, reactivity, and functional properties of SCO complexes. Several theoretical studies have been reported on SCO energetics using different levels of theory, which includes DFT and wave-function based single and multi-reference methods.51–53 The coupled cluster-based method (CCSD(T)) with different correlation diagnostics, iterative triples corrections, and different extents of PNO thresholds have been successful for treating small to moderate-sized molecules. However, for large systems and systems with significant static correlation, the accuracy of these methods decreases. DFT calculations, when combined with appropriate functionals and methodologies,54 can provide reasonable predictions for spin-state energetics and magnetic properties.55 DFT and ab initio calculations have been employed to investigate the effects of ligand substitution, solvent interactions, and crystal packing on the SCO behaviour of the complexes.56 Additionally, DFT and ab initio methods are valuable for studying spin-dependent properties beyond SCO, such as spin–spin coupling, zero-field splittings, and magnetic anisotropy.57,58 Since they offer a good balance between accuracy and computational efficiency, DFT calculations are widely used to investigate SCO systems, although accurate estimation of the multi-configurational characters of the electronic states of a transition metal complex often demands more accurate treatment of static and dynamic electron correlations that are nicely captured by complete active space self-consistent field (CASSCF) and its perturbation corrected CASPT2 or NEVPT2 methods.59–61
Our aim here is to understand the structure–property correlation of the [Co(terpy)2]2+ complex based on the variable temperature crystal structures of this complex obtained at temperatures ranging from 30 K to 375 K.32 We have employed DFT calculations with different functionals to correctly describe the spin-transition temperature in this complex. For magnetic and SCO properties, we have used the CASSCF/NEVPT2 method to show the effect of metal–ligand interaction on zero-field splitting parameters and magnetic anisotropy and the effect of spin-vibration coupling on the relaxation of magnetization.
2 Computational methods
The crystal structures of the Co(II) complex obtained at different temperatures by Kilner and Halcrow32 were taken as the starting geometries for our calculations. Since we are interested in investigating the molecular properties of the variable temperature geometries at the lattice structure level, so to retain the essence of the lattice, the crystal structures were partially optimized with the B3LYP functional and def2-TZVP basis set for Co and TZVP for C, N and H in both the HS and LS states in Gaussian 1662 by freezing the first coordination site of the metal centre (Co and the six N atoms coordinated to it). The partial optimizations retain the characteristics of the most dominant coordination site. Their effect on structure and energetics are discussed in Fig. S1 and S2 in the ESI.† The counterion was not explicitly considered in our calculations, as the crystal structures we use are already influenced by the counterion present in the experiment, and the molecular properties calculated from these structures, therefore, have implicit dependence on the counterion. The root-mean-squared deviation (RMSD) between the reported crystal structure and the (constrained) optimized geometries is less than 0.1 Å (Fig. S1 in ESI†). With these geometries, single-point energy calculations were performed for both LS and HS with eight different functionals viz. CAM-B3LYP,63 B3LYP,64 B3LYP*,65 B3PW91,66 PBE,67 M062X,62 BLYP64,68 and BP8668 with the same basis as used for the geometry optimization. The goal is to find the functionals that best describe the experimental observation.To account for the multi-configuration characters of the electronic state of the transition metal complexes and to include the dynamic correlation, complete active space self-consistent field69 (CASSCF) and N-electron valence perturbation theory70 (NEVPT2) calculations were performed on all the structures using ORCA 5.0.1.71–73 For the CASSCF/NEVPT2 calculations, the Douglas–Kroll–Hess (DKH) def2-TZVP basis set74 for Co and N and DKH-def2-SVP for C and H were used. The automatic generation of an auxiliary basis set facility of ORCA was used via the AUTOAUX module.75 For all calculations, tight SCF convergence criteria (10−10 au) were used. In the quasi-degenerate perturbation theory (QDPT), both the spin–orbit and Zeeman interactions were taken into account.76,77 The effective Hamiltonian approach,78 as implemented in ORCA 5.0.1, was used to calculate the magnetic parameters (D, E/D, and the g-tensors). The SINGLE_ ANISO module was used to calculate ab initio blocking barriers for relaxation mechanisms.79,80 The ab initio ligand field theory (AILFT) was used to investigate the splitting of the d-orbitals.81,82 Three different active spaces were chosen to determine the role of the active space in the correct description of the spin-state switch. The first active space CAS(7,5) contains seven electrons of Co(II) distributed among the five 3d orbitals. To consider the double d-shell effect, the active space CAS(7,10) was chosen. The double shell 3d′ Co orbitals were found automatically in the CASSCF calculations by using the “extorbs doubleshell” option, and they were rotated to be the initial virtual orbitals. The third active space CAS(11,7) contains eleven electrons distributed among seven orbitals: five 3d Co orbitals and two σ-bonding ligand orbitals. This active space ensures a balanced description of two important effects, i.e., the dynamical electron correlation associated with the Co 3d electrons and the non-dynamical correlation effects associated with covalent metal–ligand interactions.83,84 This active space allows both metal-centered d–d states and the LMCT configurations to be properly described. For all the active spaces, 40 roots for LS and 10 roots for HS were considered. For the evaluation of the spin-phonon coupling constants, the gz component of the g-tensor and the axial ZFS parameter D were calculated at geometries distorted along the low-frequency normal modes of vibration starting from the optimized geometry of the HS state. The distortion along the (dimensionless) normal coordinate (Q) was carried out between Q = ±1, in the step of 0.2.
3 Results and discussion
3.1 Structural analysis of the X-ray crystal structures
The variable temperature magnetic susceptibility studies of [Co(terpy)2]2+ by Kilner and Halcrow provide X-ray crystal structure and magnetic measurements of the complex at nine different temperature between 30 K and 375 K. The complex shows low-spin at low temperature and undergoes a gradual thermal spin transition upon further warming with T1/2 = 270 ± 2 K. The crystal structures at different temperatures, when aligned with respect to each other, show marginal overall structural changes (Fig. S1 in ESI†). The structure of the complex at 30 K is shown in Fig. 1. | ||
| Fig. 1 The crystal structure of [Co(terpy)2]2+ at 30 K.32 The hydrogen atoms are not shown for clarity. The axial bonds (Rax) are shown in red and equatorial bonds (Req) are shown in green and blue. | ||
The metal–ligand bonds and angles at different temperatures are compared in Fig. 2(a)–(c). The bonds along the x-axis are termed axial bonds (Co–N1 and Co–N2), while those along the y- and z-axes are termed equatorial bonds. The complex forms three bite-angles (N1–Co–N2, N3–Co–N4, and N5–Co–N6), see Fig. 1. With the increase in temperature, as the electronic configuration of the metal centre changes from LS to HS, the two axial bonds elongate, and at around 220 K, they become equal (Fig. 2(a)). At 30 K, two equatorial bonds are shorter than the other two. This structure shows the signature of a pronounced pseudo Jahn–Teller distortion along the two equatorial bond lengths, as expected for a low-spin d7 metal centre. With an increase in temperature, all four become similar in length, particularly after 225 K. In the case of the three bite angles, two of them show a decrease with an increase in temperature, while the third remains nearly unchanged over temperature change (Fig. 2(c)). The two changing bite angles become equal at around 325 K.
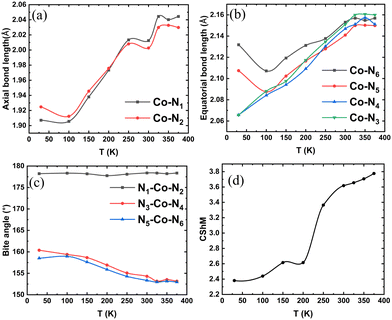 | ||
| Fig. 2 (a)–(c) The variation of the axial and equatorial bonds and the bite angles in the X-ray crystal structure of [Co(terpy)2]2+ at different temperatures.32 (d) The continuous shape measure (CShM) map of the crystal structures at different temperatures with reference to an ideal octahedron. | ||
To quantify the deviation of the coordination sphere of the Co(II) complex from ideal polyhedra, we have used the continuous shape measure (CShM) to evaluate the closest ideal geometry for the crystal structures at different temperatures. The CShM of a molecular fragment is defined as its distance from an ideal shape, regardless of its size and orientation.85 For molecules (or molecular fragments) that can be described approximately by a polyhedron, the deviation between the molecular structure and the perfect polyhedron is then given by a dimensionless quantity Sq(p), defined as85
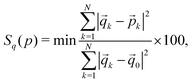 | (2) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) k (k = 1,…,N), while their coordinates for the perfect polyhedron closest in size and orientation are given by the vectors
k (k = 1,…,N), while their coordinates for the perfect polyhedron closest in size and orientation are given by the vectors ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) k and
k and ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) 0 is the coordinate vector of the geometrical centre of the investigated structure. In the present case, we examined the deviation of the crystal structure of the hexa-coordinated Co(II) complex with respect to different ideal polyhedra, such as octahedral, hexagon, pentagonal pyramid, trigonal prism, and Johnson pentagonal pyramid (Fig. S3 in ESI†). The crystal structures are found to have the closest similarity with the octahedral complexes. Fig. 2(d) shows the CShM of the complex at different temperatures with respect to an ideal octahedral polyhedron. At low temperatures, we can observe that the crystal structures are closer to an octahedron with a CShM of 2.4 compared to the higher temperature ones with a CShM of 3.7, indicating greater deviation. This CShM trend is dominated by the distortion in the bite angles. While one bite angle remains linear, the other two deviate by 20° to 27.5° as the temperature increases, and the structure becomes rather distorted. The CShM are much less affected by bond length than by angular distortions, a fact that is related to the much wider variation found in bond- and torsion-angles compared to those in bond distances.86
0 is the coordinate vector of the geometrical centre of the investigated structure. In the present case, we examined the deviation of the crystal structure of the hexa-coordinated Co(II) complex with respect to different ideal polyhedra, such as octahedral, hexagon, pentagonal pyramid, trigonal prism, and Johnson pentagonal pyramid (Fig. S3 in ESI†). The crystal structures are found to have the closest similarity with the octahedral complexes. Fig. 2(d) shows the CShM of the complex at different temperatures with respect to an ideal octahedral polyhedron. At low temperatures, we can observe that the crystal structures are closer to an octahedron with a CShM of 2.4 compared to the higher temperature ones with a CShM of 3.7, indicating greater deviation. This CShM trend is dominated by the distortion in the bite angles. While one bite angle remains linear, the other two deviate by 20° to 27.5° as the temperature increases, and the structure becomes rather distorted. The CShM are much less affected by bond length than by angular distortions, a fact that is related to the much wider variation found in bond- and torsion-angles compared to those in bond distances.86
3.2 DFT single-point energy analysis with different functionals
To explore the SCO behaviour in this complex, single-point DFT calculations are performed on the partially optimized crystal structures at different temperatures for both the HS and LS states using eight different functionals. The single-point energies (with reference to the LS energy of the 30 K structure) are compared in Fig. 3.With the BP86, PBE and BLYP functionals, the HS state is found to be higher in energy than the LS state at all temperatures. The remaining five functionals (B3LYP, B3LYP*, M06, CAMB3LYP, B3PW91) could reproduce the correct energy ordering, i.e., the LS state is more stable at lower temperatures while the HS state is more stable at higher temperatures, in agreement with the results from the variable temperature magnetic susceptibility study.32 From Fig. 3, we can also observe the point where the energy becomes equal for both the spin states. The spin-state switch occurs at around 200 K with the B3PW91, CAM-B3LYP, and M06 functionals, while it appears at a higher temperature (between 250 to 300 K) with B3LYP*. The latter is in better agreement with the experimental results, where the SCO appears at 270 K.32
The GGA functionals, commonly referred to as “pure”, tend to excessively stabilise the LS (low-spin) states, whereas the hybrid functionals tend to prefer the HS (high-spin) states. The terms pure and hybrid in this context pertain to the extent of HF exchange integrated within the functional itself, typically falling within the range of 0 to 30%. The re-parametrization of the B3LYP functional by incorporating a moderate value of 15% exact exchange instead of 20% exact exchange leads to correct predictions of the SCO energetics by the B3LYP* functional (Fig. 3).
The Gibbs free energies, taking into consideration the entropy corrections to the electronic energy, are compared in Fig. 4. The lowest temperature and highest temperature crystal structures are globally optimised at LS and HS, respectively. The thermal energy corrections and entropy are evaluated from these geometries. The details of calculating various entropy contributions are discussed in the ESI.† After including the entropy corrections to the electronic energies, the spin transition temperatures are found to decrease by around 10–25 K for different functionals. The B3LYP* functional estimates a thermal spin transition temperature very close to the experimental value of 270 K (Fig. 4).
3.3 Scanning of internal coordinates
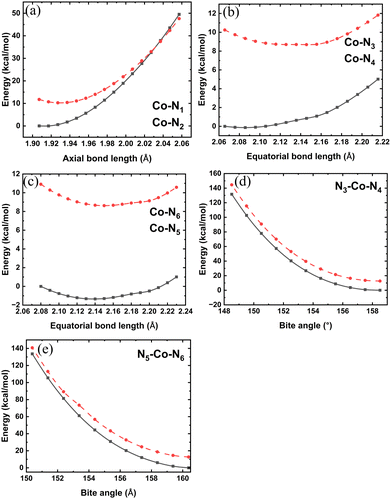
Since structural parameters in a transition-metal complex have a significant role in its SCO potential, we wanted to investigate which structural parameter plays a dominant role in the SCO process. To that end, we carried out (rigid) scans of the potential energy surface along four different internal coordinates (Fig. 5). We started from the structure of 30 K and varied the selected internal coordinate (bond distances in the step of 0.01 Å and bond angles in the step of 1°) until it reached its value in the 375 K crystal structure while leaving the other coordinates unchanged.The axial bond distances vary between 1.9 Å and 2.04 Å (Fig. 2(a)) in the LS and HS crystal structures. The potential-energy curves along the axial distance show the LS state as more stable at smaller axial distances, and at around 2.05 Å, the HS state attains more stability (Fig. 5(a)). It should be noted that apart from the axial distance, the rest of the internal coordinates are still in their LS conformation. This indicates that the axial distance has a significant role in the SCO process.
As is evident from Fig. 2(b), there are two pairs of equatorial bond lengths, one which is shorter (2.06 Å) and the other which is longer (2.12 Å and 2.13 Å). Both the pairs of unequal bond lengths at the LS state, however, become equal in the HS state, with a bond length of 2.15 Å. Hence, the LS state should be more stable at a smaller equatorial bond length, whereas at a longer equatorial bond length range, the HS state should be more stable. We scanned the four equatorial bonds, taking the shorter pair and the longer pair as two separate variables. The shorter pair of the equatorial bond lengths varied between 2.06 Å and 2.21 Å, while the longer pair varied between 2.08 and 2.23 Å. According to the rigid scan plots shown in Fig. 5(b) and (c), we observe that at both small and long equatorial bond lengths, the LS state is more stable than the HS state. This indicates that the equatorial bond lengths are not the dominant SCO coordinate by themselves since they fail to show SCO as the rest of the geometry is in the internal coordinates of the LS state (30 K structure). Unlike the scanning along the axial distance, the potential-energy curve along the equatorial distance is largely a flat surface (note the small change in the energy in Fig. 5(b) and (c) in contrast to Fig. 5(a)).
Among the three bite angles, one barely changes its value (178°) from the LS to HS state, while the other two decrease from about 160° in the LS state to 152.5° in the HS state (Fig. 2(c)). Hence, at around 160°, the LS state should be more stable and at around 152.5°, the HS state should be more stable. However, according to the potential energy scan (Fig. 5(d) and (e)), the LS state is always more stable. This result is similar to what we obtained from the equatorial distance scan. This analysis concludes that the axial bonds are the most significant internal coordinates in deciding SCO. Therefore, in the search for suitable SCO candidates, attempts must be made to tune this parameter.
We have further carried out a relaxed potential energy scan along the axial distance from its smallest to largest observed values. In the relaxed scan, the variable temperature crystal structure geometries were optimized by keeping the axial distance of the crystal structures frozen. The relaxed scan energy profiles of the HS and LS structures are shown in Fig. 6, where they are compared with the single-point energy at the corresponding crystal structures. The relaxed PE scans show a spin-transition temperature at an axial bond length of around 2.01 Å, which is similar to what is observed in the variable-temperature crystal structures (Fig. 6). The agreement between the results from the relaxed PE scan and the variable temperature crystal structures shows that the latter represents a reasonable choice for studying the SCO process in this complex.
 | ||
| Fig. 6 The potential energies of the relaxed scan and the single-point energies of the variable temperature crystal structures for the HS and LS states. | ||
3.4 Electronic structure of [Co(terpy)2]2+ with multi-configuration methods
A free Co(II) ion with d7 electrons exists in the 4F ground state, which splits in an octahedral environment of the ligands into the 4T1g ground state, and 4T2g and 4A2g excited states. The three-fold degeneracy of the ground 4T1g state is further lifted due to structural distortion (Jahn–Teller distortion), resulting in the 4E and 4B1 states, although this splitting is rather small. The LS configuration of Co(II) forms the 2G ground state, which splits in an octahedral ligand environment into a 2Eg LS ground term and 2T1g, 2T2g, and 2A1g as the first three LS excited states. Again, further structural distortion of the high-symmetric octahedral structure lifts the two-fold degeneracy of the 2Eg state to 2A1 and 2B2. But unlike the HS state, the splitting in the LS 2Eg due to structural distortion is significant. The subtle distortions in the HS ground state occur because the two eg -like orbitals, which have strong anti-bonding character, are filled by only one electron each, limiting them from causing distortion. The uneven occupation of the t2g -like orbitals does cause some distortion, however, the impact is minimal as these orbitals are primarily non-bonding. On the contrary, the dominating electronic structure of the LS ground state consists of only one electron in the eg-like orbitals, which is the typical configuration for substantial Jahn–Teller distortion. Due to this inherent multi-configurational character of the ground states in the HS and LS configurations of the Co(II) complexes, it is necessary to investigate these systems with multi-configurational ab initio methods.To examine the electronic structure of the nine different structures of [Co(terpy)2]2+ at different temperatures, ab initio wave-function-based multi-reference calculations were performed using the complete active space self-consistent field (CASSCF) method on the DFT partially-optimized geometries for both the HS and LS configurations. The CASSCF reference wavefunctions are widely acknowledged for their consistent reliability as qualitative electronic structure descriptors, provided that appropriate active space is selected. The minimal active space that can be chosen for the Co2+ complex is CAS(7,5) with seven d-electrons in five 3d orbitals having an electronic configuration of t62ge1g in LS and t52ge2g in HS. This active space generates 40 LS and 10 HS electronic states that form the closely spaced low-lying HS and LS excited states arising from the ground HS and LS term of the parent ion (Co2+).
For transition metal ions with more than a half-filled configuration, a second set of d-orbitals (the so-called double d-shell effect) is often found important in the electronic structure of the low-lying states. For this reason, we considered the active space of CAS(7,10). However, as the results would show, we observed very little effect of the double d-shell in our calculations. In octahedral transition metal complexes, metal–ligand σ orbitals are energetically proximate to the d-orbitals. The inclusion of the ligand-based doubly degenerate bonding eg orbitals in the active space is necessary in order to generate a wave function that allows effective mixing of metal–ligand orbitals. This leads to an active space of CAS(11,7). To take into account dynamic correlation, NEVPT2 calculations were done on top of the CASSCF wavefunctions in all three active spaces.
Fig. 7 shows the energy of the lowest (quasi-degenerate) LS and (quasi-degenerate) HS state (data given in Table S2 in ESI†). In [Co(terpy)2]2+, the structural distortion from ideal octahedral geometry is due to steric distortion (associated with two strained terpyridine ligands and due to Jahn–Teller distortion), and the orbital degeneracy of the ground HS and LS states is partially lifted. While this splitting is marginal for the HS state (4T1g), it is more pronounced in the case of the LS state, where the splitting between the two orbital components of the 2Eg state ranges from 12–20 kcal mol−1 (Fig. 7). With the increase in temperature, the separation between the two states steadily decreases to 7–9 kcal mol−1 at 375 K. The reduced splitting at high-temperature structures can be rationalized from the structural analysis shown in Fig. 2, where the two axial distances and the four equatorial distances are found to be rather symmetric at high temperatures. The restoration of symmetry at higher temperatures quenches the Jahn–Teller splitting. Unlike the LS state, the ground state 4T1g maintains its (quasi)-degeneracy at all temperatures.
CASSCF calculations with all three active spaces are found to overestimate the HS state at all temperatures, as can be seen in Fig. 7(a), (c) and (e), where the HS states are always lower in energy than the LS states. Thus, the static correlation alone cannot predict the correct spin-state energy ordering of the electronic states at different temperatures. The situation improves significantly after including the dynamic correlation (Fig. 7(b), (d) and (f)). All NEVPT2 calculations found the LS ground state at low temperature and HS ground state at high temperature, in good agreement with the experimental result, where the spin-transition is reported to occur at 270 K.32 NEVPT2 calculations on the minimal active space CAS(7,5) predict a spin transition around 180 K. The inclusion of double d-shell (CAS(7,10)/NEVPT2) lowers it further to around 160 K. In contrast, including the ligand orbitals in the active space, i.e., CAS(11,7)/NEVPT2, improves the spin-transition temperature to around 240 K (Fig. 7(f)).
The metal–ligand sigma bonding plays a crucial role in the electronic structure and, hence in the magnetic properties of the metal complexes.87–89 In the present case, the explicit inclusion of metal–ligand orbital interactions and dynamic electron correlation are found to be necessary for a correct description of the spin transition. This observation supports the fact that increased covalency is often associated with greater multiconfigurational behaviour, necessitating the use of larger active spaces.90 On the other hand, the inclusion of a double d-shell in CAS(7,5) does not play a deciding role in spin transition.
The ordering of the d-orbitals from ab initio ligand field theory (AILFT)91 is shown in Fig. 8. The t2g orbitals preserve their orbital degeneracy, while the two anti-bonding eg orbitals show large splitting. The gap between the t2g and eg orbitals decreases in the high-temperature structures, which stabilizes the HS state at high temperature (Fig. 8(b)). Among the t2g set of orbitals, at low-temperature structures, the dzx and dxy orbitals lie lower in energy than dyz while an orbital reordering occurs after the spin-transition temperature, where the dyz appears at lower energy than the other two (Fig. 8(b)). These changes are due to the fact that the bond lengths along the x axis increase to the greatest extent from low-temperature to high-temperature structures, which is also the deciding parameter for SCO and this is nicely reflected in the d-orbital energy ordering.
3.5 Zero field splitting parameters
In molecules with more than one unpaired electron, the inter-electron interactions mediated by the spin–orbit coupling lift the electronic degeneracy, even in the absence of an external magnetic field, via the so-called zero-field splitting. This splitting is characterised by two parameters: the axial (D) and the rhombic (E) ZFS, calculated from the effective spin-Hamiltonian Ĥ defined in eqn (1).42,43 In the present case, we focus on the HS system where the lowest three quartet states arising from the 4T1g manifold are well-separated from the other HS states (Fig. 7). The ZFS parameters for the HS state of the complex were calculated with a pseudo-spin of S = 3/2 for the Kramers pairs.In the HS complex of all the structures, we observe a unique triaxial anisotropy (where the g-tensors follow the order gx < gy < gz, see Fig. 9(a)), as opposed to the more common easy-plane and easy-axis anisotropy.92 By convention, gx, gy, and gz are arranged in ascending order. The selection of the z-axis is conventionally made to maximise the value of |D|, while the x- and y-axes are oriented in a manner that ensures E > 0. D values can be positive or negative: positive D corresponds to easy-plane (or hard axis) magnetic anisotropy, while negative D corresponds to easy-axis type magnetic anisotropy. In the limit of pure d-orbitals, the eigenvectors of the g and D-matrices are collinear with the molecular axes.
In the present case, we observe different magnitudes of magnetization along the three axes, representing a totally unsymmetric anisotropy. At lower temperatures, gy and gz are comparable and distinct from the small value of gx. At higher temperatures, the g-tensors tend to develop an easy axis as the gx and gy-values become similar and the gz-value increases substantially. We can thus infer that the structures become less distorted and more symmetric at higher temperatures, with the anisotropy developing an easy axis (Fig. 9(a) and Table 1).
| Structure | g x | g y | g z | D | E/D | KD1 |
|---|---|---|---|---|---|---|
| 30 K | 2.46 | 4.41 | 5.47 | 83.45 | 0.06 | 167.79 |
| 100 K | 2.37 | 4.42 | 5.48 | 78.70 | 0.06 | 158.26 |
| 150 K | 2.48 | 4.39 | 5.55 | 86.01 | 0.06 | 173.10 |
| 200 K | 2.56 | 4.17 | 5.79 | 94.19 | 0.09 | 190.62 |
| 250 K | 2.67 | 4.02 | 5.97 | 103.77 | 0.10 | 210.91 |
| 300 K | 2.72 | 3.88 | 6.10 | 109.11 | 0.11 | 222.55 |
| 325 K | 2.78 | 3.96 | 6.01 | 111.98 | 0.11 | 223.60 |
| 350 K | 2.84 | 3.91 | 6.04 | 115.99 | 0.10 | 236.02 |
| 375 K | 2.83 | 3.83 | 6.12 | 116.17 | 0.10 | 236.97 |
We now rationalize the magnetic anisotropy with the help of AILFT d-orbital splitting (Fig. 8b). The use of d-orbitals in predicting the sign and magnitude of magnetic anisotropy has already been proved previously in various cases.91,93,94 In order to measure the degree of anisotropy, the task at hand involves assessing the potential connections between the d-orbitals that are doubly occupied and singly occupied, utilizing the various Li (i = x, y, z) operators. The operators coupling various doubly occupied and singly occupied d-orbitals according to symmetry arguments are provided in Table S3 in the ESI.† The magnitudes of the interaction of the Li operators are inversely related to the energy difference of the d-orbitals, which are coupled through the operators.
At low temperatures, the electronic configuration for the HS ground state is given by dxy2dzx2dyz1dz21dx2−y21. The Ly operator couples dxy with dyz and Lz couples dzx with dyz (Fig. 9(b)). Since the dzx → dyz is the lowest energy excitation and that the Lz couples these two orbitals, we can infer that the easy-axis is along the z-direction. An intermediate magnetic axis lies along the y-direction. Since no doubly and singly occupied orbitals are coupled through the Lx operator, the x-axis is the hard axis. This is in agreement with the calculated values of the g and D-tensors (Table 2). At lower temperatures, gx has the largest contribution along the x-direction, gy along the y-direction and gz along the z-direction of the complex (see the eigenvector composition in Table 2). At low temperatures, since Dzz (= 2D/3) is positive, it must be along the hard axis (x-axis). Dyy has the largest negative value, and hence it is along the easy-axis (z-axis), see Table 2. Thus, we can conclude that the anisotropy increases with the order x < y < z.
| 30 K structure | 375 K structure | |||||||
|---|---|---|---|---|---|---|---|---|
| Eigenvalues | X | y | z | Eigenvalues | x | y | z | |
| g x | 2.46 | −0.83 | −0.18 | 0.52 | 2.83 | −0.42 | −0.81 | 0.39 |
| g y | 4.41 | 0.13 | −0.98 | −0.12 | 3.84 | 0.08 | −0.47 | −0.87 |
| g z | 5.47 | 0.54 | −0.03 | 0.84 | 6.11 | 0.90 | −0.35 | 0.28 |
| D xx | −22.87 | 0.14 | −0.98 | −0.12 | −25.36 | −0.07 | 0.48 | 0.87 |
| D yy | −32.73 | 0.51 | −0.03 | 0.86 | −51.90 | 0.85 | −0.41 | 0.30 |
| D zz | 55.60 | 0.85 | 0.18 | −0.49 | 77.27 | −0.51 | −0.77 | 0.38 |
| E/D | 0.05 | 0.10 | ||||||
At higher temperatures (beyond the spin-transition temperature), the electronic configuration for the HS ground state is given by dyz2dxy2dzx1dz21dx2−y21. The Lx operator couples the closely spaced doubly-occupied dxy with the singly-occupied dzx orbital. Hence, the x-axis is the easy axis here. The intermediate magnetic axis lies along the z-direction since dyz and dzx are coupled through Lz. Also, the y-axis is the hard axis since no doubly and singly occupied orbitals are coupled through the Ly operator. This is seen from the direction of the gx, which is now along the y-direction, while gy is along the z-direction and gz is along the x-direction of the molecule (Table 2). Even at high temperatures, the Dzz eigenvalue is positive, which is along the hard axis (y-axis). Dyy which has the largest negative value is also along the x-axis (the easy axis). Hence, at high temperatures, the magnetic anisotropy changes the order to y < z < x.
3.6 Relaxation of magnetization
To understand the magnetic relaxation pathway of half-integer total spin, S = 3/2 systems, we have estimated the effective anisotropy barrier from the matrix elements of the transition magnetic moment between pairs of spin–orbit states (Kramers doublets, KD) with opposite magnetic moments for the different structures under investigation (Fig. 10). The process of magnetization relaxation can be primarily achieved through three different pathways: (a) quantum tunnelling of magnetization (QTM) within the ground spin–orbit pairs, (b) thermally assisted quantum tunnelling of magnetization (TA-QTM) across excited Kramers doublets, and (c) the Orbach process involving direct or Raman transitions.95 The structure at high temperature (with HS ground state) shows a large transition magnetic moment matrix element between the ground state KD pair (1.1μB). Therefore, it is apparent that the magnetic relaxation occurs through ground state QTM, thereby effectively quenching the magnetic anisotropy barrier. | ||
| Fig. 9 (a) Variation in the magnitude of g-tensors with temperature. (b) The angular momentum operators L coupling the t2g orbitals at 30 K (left) and 375 (right). | ||
To probe the ground state QTM in terms of the vibrational quantum states via spin-vibrational coupling, we looked closer at the vibrational modes of the HS ground state of [Co(terpy)2]2+. Spin-vibrational or spin-phonon coupling refers to the interaction of the spin state of a system with its vibrational or phonon modes. Spin-phonon coupling is a significant factor in the spin relaxation process and has been extensively investigated using various methodologies.96–98 The extent of spin-vibrational coupling in a complex with N atoms can be assessed by monitoring any magnetic property B, as a function of its normal mode of vibration, i.e., B = B(Qk), with k = 1,…,3N−6. A Taylor series expansion of B around the equilibrium geometry results,
 | (3) |
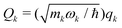 for a mass-weighted normal mode (qk) with reduced mass mk and harmonic frequency ωk.
for a mass-weighted normal mode (qk) with reduced mass mk and harmonic frequency ωk.
Here, we study the effect of spin-vibrational coupling on two magnetic properties: the gz component of the g-tensor and the axial ZFS parameter D. Their variation along normal modes of vibration is shown in Fig. S7 in the ESI.† The second derivatives of gz and D, denoted by 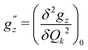 and
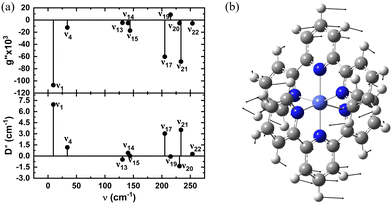
and 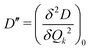 , along with a few selected normal modes are shown in Fig. 11(a). We have selected low-frequency vibrational modes (energy lower than the energy of the first excited KD, 237 cm−1) with strong IR absorption. This led to a total of ten vibrational modes, and the spin-vibrational properties were calculated (Fig. 11(a)). A large value of
, along with a few selected normal modes are shown in Fig. 11(a). We have selected low-frequency vibrational modes (energy lower than the energy of the first excited KD, 237 cm−1) with strong IR absorption. This led to a total of ten vibrational modes, and the spin-vibrational properties were calculated (Fig. 11(a)). A large value of 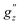 and D′′ indicates a strong spin-vibrational coupling, which is seen for modes 1, 17 and 21. The vibrational motion along modes 17 and 21 shows distortion involving the metal centre and its immediate coordination environment (Fig. S6 in ESI†). However, the strongest coupling is provided by mode 1, which involves a wagging motion of the two terpyridine ligands (Fig. 11(b)). Furthermore, this low-frequency mode is expected to be thermally more populated than the other two modes. Thus, we can conclude that the relaxation of magnetization in the complex is facilitated by mode 1. This mode corresponds to a harmonic frequency of 9.36 cm−1, which is in good agreement with the observed small effective anisotropy barrier of 2.5–2.9 cm−1 for the relaxation process.99
and D′′ indicates a strong spin-vibrational coupling, which is seen for modes 1, 17 and 21. The vibrational motion along modes 17 and 21 shows distortion involving the metal centre and its immediate coordination environment (Fig. S6 in ESI†). However, the strongest coupling is provided by mode 1, which involves a wagging motion of the two terpyridine ligands (Fig. 11(b)). Furthermore, this low-frequency mode is expected to be thermally more populated than the other two modes. Thus, we can conclude that the relaxation of magnetization in the complex is facilitated by mode 1. This mode corresponds to a harmonic frequency of 9.36 cm−1, which is in good agreement with the observed small effective anisotropy barrier of 2.5–2.9 cm−1 for the relaxation process.99
4 Conclusions
We have provided a comprehensive account of the relationship between the structure and magnetic properties of [Co(terpy)2]2+ on the basis of its temperature-dependent crystal structures. The structural comparison shows that the complex undergoes SCO with a very small change in the geometry. Among the structural parameters, the axial bond length is found to influence the SCO property the most. Our DFT calculation shows that while the GGA functionals fail to explain the SCO behavior, the hybrid and meta-hybrid functionals correctly reproduce the relative spin-state stability at both low and high temperatures. However, an accurate spin-transition temperature could be predicted by the re-parametrized B3LYP* functional. For the multi-configurational methods, the correct description of the spin transition requires an explicit treatment of static and dynamic correlation of the metal–ligand bonding, although the double d-shell effect is not found to be essential.The metal–ligand axial distances are found to be largely responsible for SCO, whereas the equatorial distances and bite angles play a less significant role. The elongation of the axial bonds (along x-axis) with temperature leads to a subtle change in the d-orbital splitting pattern at the SCO temperature, where the low-lying dxy and dzx orbitals are destabilized with respect to the dyz orbital. This reordering causes a realignment of the magnetic axes, wherein the easy-axis of magnetization changes from z to x at the SCO. The complex shows unusual triaxial magnetic anisotropy at lower temperatures, while an easy axis of magnetization begins to develop at higher temperatures. The spin-vibration analysis reveals a strong coupling of low-frequency wagging motion of the two terpyridine ligands with the spin states of the complex, allowing an effective relaxation of magnetization that yields a small magnetic anisotropy barrier. While the present study focusses on the static aspects of the parent [Co(terpy)2]2+ complex, the effect of substituted terpyridine ligands on the SCO behaviour and the dynamical aspects of SCO are hoped to be undertaken in future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
MN and SJ acknowledge IIT Kharagpur and UGC, New Delhi, respectively, for research fellowships. SM acknowledges the support from SERB, DST, Government of India (CRG/2022/004088 and SR/FST/CSII-026/2013) and CSIR, New Delhi, India (01(2987)/19/EMR-II). This work used the resources of the Paramshakti supercomputing facility of IIT Kharagpur, established under the National Supercomputing Mission of the Government of India and supported by CDAC, Pune.References
- P. Gütlich, Y. Garcia and H. A. Goodwin, Chem. Soc. Rev., 2000, 29, 419–427 RSC.
- O. Sato, J. Tao and Y.-Z. Zhang, Angew. Chem., Int. Ed., 2007, 46, 2152–2187 CrossRef CAS PubMed.
- M. A. Halcrow, Chem. Soc. Rev., 2008, 37, 278–289 RSC.
- P. Gütlich, V. Ksenofontov and A. B. Gaspar, Coord. Chem. Rev., 2005, 249, 1811–1829 CrossRef.
- L. Cambi and L. Szegö, Ber. Dtsch. Chem. Ges., 1933, 66, 656–661 CrossRef.
- A. Bousseksou, G. Molnár, L. Salmon and W. Nicolazzi, Chem. Soc. Rev., 2011, 40, 3313 RSC.
- Spin-Crossover Materials, ed. M. A. Halcrow, Wiley, 2013 Search PubMed.
- A. W. Hauser, Top. Curr. Chem., 2004, 234, 155–198 CrossRef CAS.
- P. Gütlich and H. A. Goodwin, Spin Crossover–An Overall Perspective, Springer, Berlin, Heidelberg, 2004, pp. 1–47 Search PubMed.
- S. Hayami, M. R. Karim and Y. H. Lee, Eur. J. Inorg. Chem., 2013, 683–696 CrossRef CAS.
- M. Mikami, M. Konno and Y. Saito, Chem. Phys. Lett., 1979, 63, 566–569 CrossRef CAS.
- D. Chernyshov, M. Hostettler, K. W. Törnroos and H.-B. Bürgi, Angew. Chem., Int. Ed., 2003, 42, 3825–3830 CrossRef CAS PubMed.
- M. A. Halcrow, Crystals, 2016, 6, 58 CrossRef.
- C. T. Kelly, M. Griffin, K. Esien, S. Felton, H. Müller-Bunz and G. G. Morgan, Cryst. Growth Des., 2022, 22, 6429–6439 CrossRef CAS PubMed.
- S.-Y. Zhang, H.-Y. Sun, R.-G. Wang, Y.-S. Meng, T. Liu and Y.-Y. Zhu, Dalton Trans., 2022, 51, 9888–9893 RSC.
- J. G. Park, I.-R. Jeon and T. D. Harris, Inorg. Chem., 2015, 54, 359–369 CrossRef CAS PubMed.
- J. J. Amoore, C. J. Kepert, J. D. Cashion, B. Moubaraki, S. M. Neville and K. S. Murray, Chem. – Eur. J., 2006, 12, 8220–8227 CrossRef CAS PubMed.
- X.-P. Sun, R.-J. Wei, Z.-S. Yao and J. Tao, Cryst. Growth Des., 2018, 18, 6853–6862 CrossRef CAS.
- R. Hogg and R. Wilkins, J. Chem. Soc., 1962, 341–350 RSC.
- S. Kremer, W. Henke and D. Reinen, Inorg. Chem., 1982, 21, 3013–3022 CrossRef CAS.
- C. Harris, T. Lockyer, R. Martin, H. Patil and E. Sinn, Aust. J. Chem., 1969, 22, 2105–2116 CrossRef CAS.
- J. S. Judge and W. A. Baker Jr., Inorg. Chim. Acta, 1967, 1, 68–72 CrossRef CAS.
- E. N. Maslen, C. L. Raston and A. H. White, J. Chem. Soc., Dalton Trans., 1974, 1803–1807 RSC.
- R. C. Stoufer, D. W. Smith, E. A. Clevenger and T. E. Norris, Inorg. Chem., 1966, 5, 1167–1171 CrossRef CAS.
- H. Oshio, H. Spiering, V. Ksenofontov, F. Renz and P. Gütlich, Inorg. Chem., 2001, 40, 1143–1150 CrossRef CAS PubMed.
- Y.-C. Sun, F.-L. Chen, K.-J. Wang, Y. Zhao, H.-Y. Wei and X.-Y. Wang, Inorg. Chem., 2023, 62, 14863–14872 CrossRef CAS PubMed.
- C. Enachescu, I. Krivokapic, M. Zerara, J. A. Real, N. Amstutz and A. Hauser, Inorg. Chim. Acta, 2007, 360, 3945–3950 CrossRef CAS.
- S. Hayami, Y. Komatsu, T. Shimizu, H. Kamihata and Y. H. Lee, Coord. Chem. Rev., 2011, 255, 1981–1990 CrossRef CAS.
- V. García-López, N. Giaconi, L. Poggini, J. Calbo, A. Juhin, B. Cortigiani, J. Herrero-Martín, E. Ortí, M. Mannini, M. Clemente-León and E. Coronado, Adv. Funct. Mater., 2023, 33, 2300351 CrossRef.
- M. Nakaya, R. Ohtani, K. Sugimoto, M. Nakamura, L. F. Lindoy and S. Hayami, Chem. – Eur. J., 2017, 23, 7232–7237 CrossRef CAS PubMed.
- S. Hayami, D. Urakami, Y. Kojima, H. Yoshizaki, Y. Yamamoto, K. Kato, A. Fuyuhiro, S. Kawata and K. Inoue, Inorg. Chem., 2010, 49, 1428–1432 CrossRef CAS PubMed.
- C. A. Kilner and M. A. Halcrow, Dalton Trans., 2010, 39, 9008–9012 RSC.
- S. Hayami, Y. Kojima and K. Inoue, Mol. Cryst. Liq. Cryst., 2009, 509, 309–316 Search PubMed.
- J. Palion-Gazda, A. Switlicka Olszewska, B. Machura, T. Grancha, E. Pardo, F. Lloret and M. Julve, Inorg. Chem., 2014, 53, 10009–10011 CrossRef CAS PubMed.
- R. Skomski, Simple Models of Magnetism, Oxford university press, 2008 Search PubMed.
- J. R. Friedman and M. P. Sarachik, Annu. Rev. Condens. Matter Phys., 2010, 1, 109–128 CrossRef CAS.
- D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268–297 CrossRef CAS PubMed.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006, vol. 5 Search PubMed.
- J. Lu, M. Guo and J. Tang, Chem. – Asian J., 2017, 12, 2772–2779 CrossRef CAS PubMed.
- X.-N. Yao, J.-Z. Du, Y.-Q. Zhang, X.-B. Leng, M.-W. Yang, S.-D. Jiang, Z.-X. Wang, Z.-W. Ouyang, L. Deng, B.-W. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373–380 CrossRef CAS PubMed.
- A. K. Bar, C. Pichon and J.-P. Sutter, Coord. Chem. Rev., 2016, 308, 346–380 CrossRef CAS.
- R. Boca, Theoretical Foundations of Molecular Magnetism, Elsevier, 1999 Search PubMed.
- R. Boca, Coord. Chem. Rev., 2004, 248, 757–815 CrossRef CAS.
- A. Albino, S. Benci, M. Atzori, L. Chelazzi, S. Ciattini, A. Taschin, P. Bartolini, A. Lunghi, R. Righini, R. Torre, F. Totti and R. Sessoli, J. Phys. Chem. C, 2021, 125, 22100–22110 CrossRef CAS PubMed.
- F. A. Mautner, F. Bierbaumer, R. C. Fischer, À. Tubau, S. Speed, E. Ruiz, S. S. Massoud, R. Vicente and S. Gómez-Coca, Inorg. Chem., 2022, 61, 11124–11136 CrossRef CAS PubMed.
- A. Lunghi and S. Sanvito, Sci. Adv., 2019, 5, eaax7163 CrossRef CAS PubMed.
- Z. Hu, A. Ullah, H. Prima-Garcia, S.-H. Chin, Y. Wang, J. Aragó, Z. Shi, A. Gaita-Ariño and E. Coronado, Chem. – Eur. J., 2021, 27, 13242–13248 CrossRef CAS PubMed.
- P. Gargiani, R. Cuadrado, H. B. Vasili, M. Pruneda and M. Valvidares, Nat. Commun., 2017, 8, 699 CrossRef CAS PubMed.
- A. Lunghi and S. Sanvito, J. Chem. Phys., 2020, 153, 174113 CrossRef CAS PubMed.
- M. Reiher, Inorg. Chem., 2002, 41, 6928–6935 CrossRef CAS PubMed.
- M. Radon, Adv. Inorg. Chem., Elsevier, 2019, vol. 73, pp. 221–264 Search PubMed.
- Q. M. Phung, M. Feldt, J. N. Harvey and K. Pierloot, J. Chem. Theory Comput., 2018, 14, 2446–2455 CrossRef CAS PubMed.
- M. Drosou, C. A. Mitsopoulou and D. A. Pantazis, J. Chem. Theory Comput., 2022, 18, 3538–3548 CrossRef CAS PubMed.
- S. Ye and F. Neese, Inorg. Chem., 2010, 49, 772–774 CrossRef CAS PubMed.
- M. Radon, K. Gassowska, J. Szklarzewicz and E. Broclawik, J. Chem. Theory Comput., 2016, 12, 1592–1605 CrossRef CAS PubMed.
- S. Song, M.-C. Kim, E. Sim, A. Benali, O. Heinonen and K. Burke, J. Chem. Theory Comput., 2018, 14, 2304–2311 CrossRef CAS PubMed.
- F. Neese, J. Am. Chem. Soc., 2006, 128, 10213–10222 CrossRef CAS PubMed.
- R. Khurana, S. Gupta and M. E. Ali, J. Phys. Chem. A, 2021, 125, 2197–2207 CrossRef CAS PubMed.
- M. Radon, E. Broclawik and K. Pierloot, J. Phys. Chem. B, 2010, 114, 1518–1528 CrossRef CAS PubMed.
- T. Helgaker, M. Watson and N. C. Handy, J. Chem. Phys., 2000, 113, 9402–9409 CrossRef CAS.
- S. Takahashi, S. Iuchi, S. Hiraoka and H. Sato, Phys. Chem. Chem. Phys., 2023, 25, 14659–14671 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, 2016 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55 Search PubMed.
- J. P. Perdew, Electron. Struct. Solids, 1991, 11, 11–20 Search PubMed.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- P.-Å. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- S. Pathak, L. Lang and F. Neese, J. Chem. Phys., 2017, 147, 234109 CrossRef PubMed.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554–562 CrossRef CAS PubMed.
- B. A. Hess, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef CAS.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- R. Maurice, R. Bastardis, C. D. Graaf, N. Suaud, T. Mallah and N. Guihery, J. Chem. Theory Comput., 2009, 5, 2977–2984 CrossRef CAS PubMed.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Chem. – Eur. J., 2017, 23, 3708–3718 CrossRef CAS PubMed.
- S. K. Singh, J. Eng, M. Atanasov and F. Neese, Coord. Chem. Rev., 2017, 344, 2–25 CrossRef CAS.
- D. M. P. Mingos, P. Day and J. P. Dahl, Molecular electronic structures of transition metal complexes II, Springer Science & Business Media, 2012, vol. 2 Search PubMed.
- K. Pierloot and S. Vancoillie, J. Chem. Phys., 2006, 125, 124303 CrossRef PubMed.
- B. Ordejon, C. de Graaf and C. Sousa, J. Am. Chem. Soc., 2008, 130, 13961–13968 CrossRef CAS PubMed.
- J. Cirera, E. Ruiz and S. Alvarez, Organometallics, 2005, 24, 1556–1562 CrossRef CAS.
- S. Alvarez and M. Llunell, J. Chem. Soc., Dalton Trans., 2000, 3288–3303 RSC.
- W. Hieringer, K. Flechtner, A. Kretschmann, K. Seufert, W. Auwärter, J. V. Barth, A. Görling, H.-P. Steinrück and J. M. Gottfried, J. Am. Chem. Soc., 2011, 133, 6206–6222 CrossRef CAS PubMed.
- M. J. Hartmann, J. E. Millstone and H. Hakkinen, J. Phys. Chem. C, 2016, 120, 20822–20827 CrossRef CAS.
- F. Ma, Q. Chen, J. Xiong, H.-L. Sun, Y.-Q. Zhang and S. Gao, Inorg. Chem., 2017, 56, 13430–13436 CrossRef CAS PubMed.
- R. J. Deeth, J. Organomet. Chem., 2001, 631, 194 CrossRef CAS.
- E. Damgaard-Møller, L. Krause, H. Lassen, L. A. Malaspina, S. Grabowsky, H. Bamberger, J. McGuire, H. N. Miras, S. Sproules and J. Overgaard, Inorg. Chem., 2020, 59, 13190–13200 CrossRef PubMed.
- Z. Tian, S. Moorthy, H. Xiang, P. Peng, M. You, Q. Zhang, S.-Y. Yang, Y.-L. Zhang, D.-Q. Wu, S. K. Singh and D. Shao, CrystEngComm, 2022, 24, 3928–3937 RSC.
- R. Ruamps, L. J. Batchelor, R. Maurice, N. Gogoi, P. Jiménez-Lozano, N. Guihéry, C. de Graaf, A.-L. Barra, J.-P. Sutter and T. Mallah, Chem. – Eur. J., 2013, 19, 950–956 CrossRef CAS PubMed.
- S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010–7018 CrossRef CAS PubMed.
- J. M. Frost, K. L. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470–2491 RSC.
- L. Escalera-Moreno, N. Suaud, A. Gaita-Arino and E. Coronado, J. Phys. Chem. Lett., 2017, 8, 1695–1700 CrossRef CAS PubMed.
- A. Lunghi, F. Totti, S. Sanvito and R. Sessoli, Chem. Sci., 2017, 8, 6051–6059 RSC.
- L. T. A. Ho and L. F. Chibotaru, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 024427 CrossRef CAS.
- F. Kobayashi, Y. Komatsumaru, R. Akiyoshi, M. Nakamura, Y. Zhang, L. F. Lindoy and S. Hayami, Inorg. Chem., 2020, 59, 16843–16852 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00591k |
| This journal is © the Owner Societies 2024 |