Open Access Article
Open Access ArticleElectronic structure and thermodynamic approaches to the prospect of super abundant vacancies in δ-Pu
Alexander
Muñoz
 *,
Ivana
Matanovic
*,
Ivana
Matanovic
 ,
Brendan
Gifford
,
Sven
Rudin
,
Troy
Holland
and
Travis
Jones
*
,
Brendan
Gifford
,
Sven
Rudin
,
Troy
Holland
and
Travis
Jones
*
T-1: Physics and Chemistry of Materials, Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA. E-mail: alexmunoz@lanl.gov; tejones@lanl.gov
First published on 10th April 2024
Abstract
Super abundant vacancies (SAVs) have been suggested to form in the fcc phase of plutonium, δ-Pu, under a low-pressure hydrogen environment. Under these conditions, the vacancy concentration is proposed to reach 10−3 at% due to H trapping in vacancies lowering the effective vacancy formation energy. Previous density functional theory (DFT) results suggest that seven H atoms can be trapped in a single vacancy when a collinear special quasirandom magnetic structure is used to stabilize the δ phase, suggesting SAVs are a possible source of H stored in plutonium. In this report, we present DFT results for δ-Pu in the noncollinear 3Q magnetic state to study the formation of SAVs in mechanically stable δ-Pu. Together with these new simulations, we use publicly available computational and experimental data to provide further constraints on the physical conditions needed to thermodynamically stabilize SAVs in δ-Pu. Using several thermodynamic models, we estimate the vacancy concentrations in δ-Pu and discuss the limits of hydrogen driven formation of vacancies in δ-Pu. We find that, when hydrogen in the lattice is equilibrated with gaseous H2, the formation of SAVs in δ-Pu is unlikely and any excess vacancy concentration beyond thermal vacancies would need to occur by a different mechanism.
1 Introduction
The super abundant vacancies (SAV) model posits metal vacancy concentrations reach 10−3 at% in metal hydrides because of H trapping in vacancies.1 While the occurrence of SAVs in metal hydrides has been observed,2 it typically requires high H chemical potentials, often requiring GPa pressures, to stabilize the hydride phase at temperatures sufficient to drive vacancy formation and the appearance of an ordered vacancy phase. Electrodeposition has also been employed to grow metal hydride with SAVs.3 In many cases, vacancy ordered L12 SAV phases are thermodynamically favored in fcc metal hydrides because metal vacancy formation is exothermic.4,5 For instance, in PdH, the stable phase at room temperature is a Cu3 Au-type (L12) structure with a Pd3 Vac-H4 stoichiometry rather than NaCl-type PdH, as observed through X-ray diffraction.2 While this behavior commonly occurs in metal hydrides, SAVs do not typically form in metals with dissolved hydrogen owing to differences in the electronic structures of metal hydrides and metals.4 However, in the case of the fcc allotrope of plutonium (δ-Pu), anomalous hydrogen solubility data has been interpreted as suggesting that 1–2 at% dissolved hydrogen may induce SAVs in the metal because the dissolved H lowers the vacancy formation energy.6 To date, however, it is unclear if the SAV mechanism operates in δ-Pu and whether SAVs form at low H chemical potentials before hydride (PuH2) formation occurs.Previous experimental work aimed to determine whether SAVs are present in δ-Pu with a low concentration of dissolved H. Experimental observations of lattice contractions when ca. 2 at% H is dissolved into δ-Pu at room temperature have been interpreted as evidence of SAVs in the metal because vacancy formation tends to reduce a metals lattice constant (a).8,9 While a vacancy concentration (xV) of ca. 10−3 at% was estimated using such data, unfortunately, accurate estimation of xV requires both  and the macroscopic strain (
and the macroscopic strain ( ).10 However, the hydride radius is greater than the radius of the Pu atom, so, on H adsorption into the Pu complex, one should not expect a lattice contraction. Beyond such indirect measurements, however, vacancy concentrations in δ-Pu have also been measured by way of positron annihilation, which suggest xV can reach as high as 0.1 at%. The same measurements indicate that these vacancies are filled with helium generated through α decay rather than H-induced SAVs.11–13 Beyond efforts to measure xV, H diffusivity measurements show a concentration dependence in the dilute regime (<1 at%) that has been posited to demonstrate SAV formation in δ-Pu. The SAVs are assumed to trap dissolved H and therefore change the observed diffusivity. However, in all cases where SAV formation in δ-Pu is proposed, the dissolved H concentrations are far in excess of the solubility limit of ca. 10−7 at% found by extrapolating high temperature data with concentrations of ca. 1 at% known to precipitate the hydride.14,15 The experimental challenges associated with investigating SAV formation in δ-Pu have prompted researchers to perform computational investigations of possible SAV formation.
).10 However, the hydride radius is greater than the radius of the Pu atom, so, on H adsorption into the Pu complex, one should not expect a lattice contraction. Beyond such indirect measurements, however, vacancy concentrations in δ-Pu have also been measured by way of positron annihilation, which suggest xV can reach as high as 0.1 at%. The same measurements indicate that these vacancies are filled with helium generated through α decay rather than H-induced SAVs.11–13 Beyond efforts to measure xV, H diffusivity measurements show a concentration dependence in the dilute regime (<1 at%) that has been posited to demonstrate SAV formation in δ-Pu. The SAVs are assumed to trap dissolved H and therefore change the observed diffusivity. However, in all cases where SAV formation in δ-Pu is proposed, the dissolved H concentrations are far in excess of the solubility limit of ca. 10−7 at% found by extrapolating high temperature data with concentrations of ca. 1 at% known to precipitate the hydride.14,15 The experimental challenges associated with investigating SAV formation in δ-Pu have prompted researchers to perform computational investigations of possible SAV formation.
Using density functional theory (DFT), Taylor et al. showed multiple H can bind exothermically to vacancies in δ-Pu, with respect to gas phase H2.16 They went on to develop a statistical mechanical model to predict the hydrogen chemical potential, μH2(T,pH2), at which SAVs form based on their computed energetics. SAVs were found to become metastable at H chemical potentials sufficient to stabilize bulk PuH2 showing there is no thermodynamic driving force for SAV formation in δ-Pu, though the authors speculated hydride formation may be slow enough to allow metastable SAV formation. However, this work employed a collinear special quasirandom magnetic structure to stabilize the δ phase of Pu, which may impact the computed energetics.17 While collinear antiferromagnetism results in a symmetry lowering of δ-Pu and mechanical instability, hence the common use of quasirandom magnetic structures, a newly proposed noncollinear 3Q structure restores the correct symmetry and eliminates mechanical instabilities.18 It is important to determine whether the mechanically stable 3Q magnetic structure will significantly change the DFT energetics of vacancy formation and H adsorption in δ-Pu, which is the subject of this effort. In this paper, we focus on the thermodynamic driving force for SAV formation, rather than the kinetic model. To do this, we develop thermodynamic models to establish whether H atoms drive SAV formation in δ-Pu and if vacancies can effectively trap dissolved H. These models are then parametrized using energetics computed for the 3Q magnetic structure. We go on to set bounds on the energetics and chemical potentials required for SAV formation and test if published experimental and computational data fit within these bounds to demonstrate hydrogen does not induce SAV formation in δ-Pu.
2 DFT results
Computational results were obtained using DFT in the projector augmented wave method as implemented in the VASP package.19–21 We study δ-Pu with a noncollinear 3Q spin structure in which all structurally equivalent bonds have identical spin character in their bonding. This structure has been shown to remove the mechanical instability observed in previous collinear models of δ-Pu.18 Furthermore, elastic constants and phonons of δ-Pu calculated with the 3Q spin structure show the correct symmetry and lead to better agreement with experiment. Additionally, the DFT calculations with the noncollinear 3Q spin structure show a unique stiffening of most transverse phonon modes at contracted volumes, which leads to a negative thermal expansion as observed in experiment. The results in this work were obtained using the experimental lattice constant of 4.64 Å22 We used a 2 × 2 × 2 conventional supercell with 32 atoms and the 3Q spin structure of δ-Pu. In this supercell, the distance between a defect and its mirror image is 9.28 Å. The 4 × 4 × 4 k-point mesh for this cell results in energy converged to less than 1 meV per atom and was used throughout this work. The electronic states were treated in the generalized gradient approximation using the exchange–correlation functional of Perdew et al. with first-order Methfessel–Paxton smearing and smearing width set to 0.2 eV.23,24 The cutoff energy for the plane wave basis was set to 500 eV.To study the energetics of SAV formation, we began by computing the vacancy formation energy in δ-Pu with the undistorted octahedral symmetry as well as in the presence of a monoclinic distortion around the vacancy. For the monoclinic distortion, our initial geometry included displacing Pu atoms around the vacancy site. Four nearest neighbor atoms above (+z or [001] direction) the vacancy were compressed along the z-axis ([001] direction) and displaced along the x-axis (+x or [100] direction), while four atoms below (−z or [00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction) the vacancy were compressed along the z-axis with the same distortion along the x as the top atoms but in the opposite direction (−x or [
] direction) the vacancy were compressed along the z-axis with the same distortion along the x as the top atoms but in the opposite direction (−x or [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00] direction), Fig. 1. The 3Q spin structure was initialized on all Pu atoms in the cell and allowed to relax. The monoclinic distortion affects the magnetic ground state as the bond equivalent directions in the lattice have shifted away from the Pu–Pu bond directions, Fig. 2. Distortions have been suggested to reduce the vacancy formation energy in δ-Pu, making the formation of SAVs more likely.17 We found that the monoclinic distortion does affect the vacancy formation energy but does not significantly affect the hydrogen adsorption energy (less than 0.05 eV). As a consequence, we compute the H adsorption using undistorted δ-Pu in the 3Q state for computational efficiency.
00] direction), Fig. 1. The 3Q spin structure was initialized on all Pu atoms in the cell and allowed to relax. The monoclinic distortion affects the magnetic ground state as the bond equivalent directions in the lattice have shifted away from the Pu–Pu bond directions, Fig. 2. Distortions have been suggested to reduce the vacancy formation energy in δ-Pu, making the formation of SAVs more likely.17 We found that the monoclinic distortion does affect the vacancy formation energy but does not significantly affect the hydrogen adsorption energy (less than 0.05 eV). As a consequence, we compute the H adsorption using undistorted δ-Pu in the 3Q state for computational efficiency.
 | ||
| Fig. 1 Visualization in VESTA of the lattice centered on a vacancy in δ-Pu and the monoclinically distorted cell.7 Blue sites represent Pu atoms, and the black site is the vacancy in the center of the complex. Left panel: The original cell with labeled interatomic distances d1 and d2. Right panels: View of the monoclinically distorted cell on the three faces of the complex. The (100) plane shows the compression in the [001] direction, or z direction in the figure, and the changes in the interatomic distances. The (010) plane shows the effect of the shearing in the [100] direction, x-direction in figure, and the compression in the [001] or z-direction. The shearing in the x-direction involves a displacement of five percent of the lattice constants. The (001) plane in the last panel shows the effect of the shearing. | ||
 | ||
| Fig. 2 The magnetic structure of δ-Pu and its undistorted and distorted vacancy complexes visualized in VESTA.7 Left: The 3Q magnetic state of δ-Pu where the blue spheres are Pu atoms, and the blue arrows are the directions of the magnetic moments on the Pu atoms. The 3Q state is identified by the noncollinear alignment of four Pu magnetic moments toward tetrahedral interstitial sites. Middle: The vacancy complex with the 3Q structure shows the vacancy in black in the center of the complex. The black arrow is the magnetic moment direction in the vacancy-free δ-Pu cell, preserved for visualization. Right: The monoclinically distorted cell relaxes the spins away from the 3Q structure. This relaxation of the spins reduces the vacancy formation energy. | ||
We compute the vacancy formation energy, the formation energy of hydrogen-vacancy complexes, and the binding energy per H atom in the noncollinear 3Q Pu structure using DFT. The binding energy of hydrogen atoms in an interstitial site of the pristine lattice is calculated as:
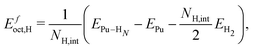 | (1) |
 | (2) |
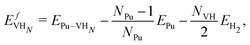 | (3) |
 | (4) |
 | (5) |
The values of the vacancy formation energies and binding energy per H atom as a function of hydrogen occupancy, NVH, are reported in Table 1 and Fig. 3.
 ), the formation energy of the hydrogen vacancy complex (
), the formation energy of the hydrogen vacancy complex ( ), the 95% confidence interval on the vacancy formation energy (
), the 95% confidence interval on the vacancy formation energy (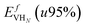 ), and the average binding energy per hydrogen atom (EbnH) in eV evaluated for hydrogen occupancy n = 0–14 using a noncollinear 3Q spin structure of δ-Pu. We have included the 95% confidence interval as an estimate of our errors based on data accumulated by Medasani et al.26,27 Binding to the bulk interstitial sites in the noncollinear 3Q structure of δ-Pu yields adsorption energies of −0.20 eV and −0.47 eV for the tetrahedral and octahedral interstitial, respectively
), and the average binding energy per hydrogen atom (EbnH) in eV evaluated for hydrogen occupancy n = 0–14 using a noncollinear 3Q spin structure of δ-Pu. We have included the 95% confidence interval as an estimate of our errors based on data accumulated by Medasani et al.26,27 Binding to the bulk interstitial sites in the noncollinear 3Q structure of δ-Pu yields adsorption energies of −0.20 eV and −0.47 eV for the tetrahedral and octahedral interstitial, respectively
 | ||
| Fig. 3 The formation energy of vacancy-hydrogen complexes plotted against the H occupancy, NVH, as calculated using the noncollinear 3Q structure of δ-Pu. The circles show the results of Table 1 with the black dots showing H going to octahedral interstitials around the vacancy and the red dots show the H entering tetrahedral interstitials. | ||
In running calculations with an fcc structure, with constrained magnetism, without constrained magnetism and with the distorted structure, we found that the vacancy formation energy ranges from 1.65–1.95 eV. The vacancy formation energy reported in Table 1 is the lowest value we obtained. This value comes from the use of the distorted cell with relaxed magnetic moment magnitudes and directions. The higher end of vacancy formation energy, 1.95 eV, comes from using the undistorted cell, creating a vacancy and constraining the remaining magnetic moments to the original 3Q structure. Our results in Table 1 show that Pu can accommodate 14 H atoms around a Pu vacancy where the first six H atoms enter the octahedral interstitial sites around the vacancy, and the next eight H atoms enter the tetrahedral interstitial sites as shown in Fig. 4. On optimization of the geometry, we found that these H positions yield the minimum energy for the H-vacancy complexes. The formation of hydrogen-vacancy complexes become exothermic with four H atoms.
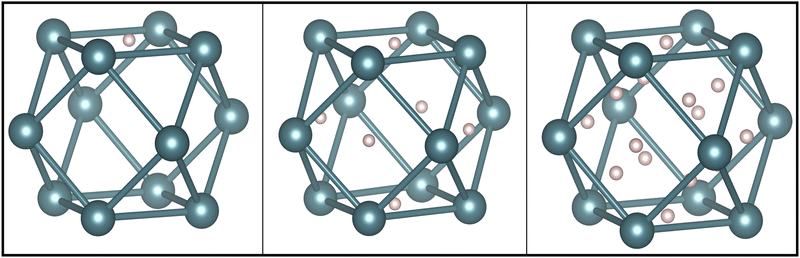 | ||
| Fig. 4 Positions of H atoms adsorbed in the vacancy complex for one H atom, six H atoms, and 14 H atoms, visualized in VESTA.7 Left: The lowest energy configuration for one H atom is in an octahedral interstitial site neighboring the vacancy. Middle: The lowest energy configuration for six H atoms is for each H to occupy an octahedral interstitial. Right: After the first six H atoms, the H atoms will occupy the tetrahedral interstitials surrounding the vacancy. | ||
Successive placement of H atoms in the octahedral interstitial sites yields an adsorption energy of −0.55 eV, but on introducing H to the tetrahedral sites, the adsorption energy of H decreases with each additional H atom. In comparison, binding to the bulk interstitials in the noncollinear 3Q structure of δ-Pu, yields adsorption energies of −0.20 eV and −0.47 eV for the tetrahedral and octahedral interstitial, respectively. This demonstrates an enthalpic driving force for H atoms to bind around pre-existing vacancy sites until there are eight H atoms, at which point the eighth H atom will prefer to bind to the bulk octahedral interstitial sites.
The influence of the magnetic state on the vacancy formation energy and H adsorption is an open question in the literature.28,29 The interplay of magnetic degrees of freedom and structural degrees of freedom creates a state space that makes a priori determination of the magnetic ground state difficult.17 As a test of this effect, we also computed the vacancy formation energy, and H adsorption energy using a collinear antiferromagnetic state with the monoclinically distorted cell. The vacancy formation energy is computed as 1.78 eV, and the H adsorption energy into the vacancy is computed as −0.48 eV. This indicates that further investigation into the magnetic structures effect on vacancy formation is necessary.
3 Thermodynamic analysis
In this report, we seek to develop simple statistical models to identify whether SAV formation is expected with slow hydride formation at 298 K in δ-Pu. We employ DFT total energies and assume dissolved H is mobile.30 In Model 1, we compare dissolved and interstitial H with H trapped in vacancies to draw comparison to the H-charged Pu under vacuum measured in XRD. In model 2, we extend this analysis to study H-driven vacancy formation. The primary differences with the model proposed by Taylor et al. are the inclusion of configurational entropy for dissolved and interstitial H, and the study of metastable states by allowing high dissolved H concentrations. We compare phases at fixed H content to determine conditions where dissolved H can drive vacancy formation. In other words, we will determine the H partitioning, and whether SAV formation is possible in Pu that has been charged with NH% H like in the experiments reported by Schwartz et al.8 This analysis is intended to discern between H free vacancy concentrations and the proposed SAVs at room temperature. In Model 3, we extend the model to include gas-phase H2.3.1 Model 1
To develop this model, we begin by expressing the Helmholtz free energy in terms of energies from Table 1:| F(T,V,NPu,NH) = E(V,NPu,NH) + Fvib.(T,V,NPu,NH) + Fconf.(T,V,NPu,NH), | (6) |
| Fvib.(T,V,NPu,NH) = Evib.(T,V,NPu,NH) − TSvib.(T,V,NPu,NH), | (7) |
Experimentally, we are concerned with constant pressure, so we can define the Gibbs free energy from the Helmholtz free energy:
| Gvib.(T,p,NPu,NH) = Fvib.(T,V,NPu,NH) + pV(T,p,NPu,NH). | (8) |
Dimensional analysis shows the pV can be ignored since we are concerned with volumetric energies. The pV term contributes an energy per volume of:
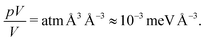 | (9) |
A Pu atom is approximately 25 Å3, which gives a pV contribution of 0.025 meV, significantly less than the hundreds of meV associated with H adsorption. Therefore, at pressures around 100 atm., the enthalpy in the solid can be approximated by the total energy, which allows us to work directly with the data in Table 1.
With the free energy defined, we can determine if SAVs form with a given concentration of H in Pu by comparing the free energy of a phase with interstitial H and a phase with H decorated vacancies. This model is illustrated in Fig. 5, where we can see that the problem amounts to identifying concentrations where the chemical potentials (μH) of various forms of stored H. Fig. 5 shows the case where interstitial H is equilibrated with 1H and 3H vacancy clusters.
From Table 1, the total energy of H can be reduced by 0.08 eV by migrating from an interstitial site (−0.47 eV) to a pre-existing vacancy (−0.55 eV). This will, however, come at an entropic cost if the total number of lattice sites (NPu) is large compared to the vacancy concentration. The total energy cost required to form the vacancy will also reduce the tendency for migration from interstitials to vacancies, however, this enthalpic cost can be reduced by allowing multiple H to bind in the vacancy, which again comes with an entropic cost. Formation of the H vacancy moiety becomes exothermic, with respect to gas phase H2, when 4H are bound in the vacancy. However, if the H source is H dissolved in interstitial sites, as in our case, formation of the 4H vacancy complex is endothermic. Moreover, increasing the H content in the vacancy cannot result in exothermic H vacancy moiety formation with respect to H dissolved in the pristine lattice. Therefore, there is no enthalpic driving force for SAV formation from dissolved H in Pu.
We now turn to the configurational entropy as a potential driving force for SAV formation. For low concentrations, the configurational entropy is written as the mixing entropy:
 | (10) |
 | (11) |
This entropic term drives vacancy formation despite the total energy/enthalpic cost associated with the process. The vacancy concentration is approximated as:
 | (12) |
For δ-Pu, the vacancy formation energy of 1.65 eV yields a vacancy concentration of 1.84 × 10−28 at 298 K. Similarly, the number of ways of placing NH,int. H atoms in NPu octahedral holes is:
 | (13) |
 | (14) |
The degeneracy of the binding sites in the vacancy has been ignored. Including 6 sites, for a single H binding will increase the computed vacancy concentrations by a factor of ten, which is irrelevant for our estimates.
With the configurational entropy, we rewrite the free energy:
 | (15) |
To examine the super saturated case, where H concentrations are above those needed for PuH2 precipitation, we want to understand how H will partition at fixed concentration. Assuming fixed total content of dissolved H, NH = NVH + NH,int, we write the free energy as:
 | (16) |
 | (17) |
To determine the likelihood of additional kinetic traps we include a climbing image nudged elastic band calculation.34,35 We compute an activation energy of 0.9 eV using the climbing image nudged elastic band calculation. In conjunction with the low adsorption energy of H in vacancies relative to interstitial sites we do not expect additional kinetic traps. With single occupations of vacancies, the maximum Pu vacancy concentration is 1 × 10−27 for H concentrations below 10 at%. Comparing to the H-free vacancy concentration of 2 × 10−28, we see that dissolved H can increase vacancy concentration, albeit marginally. The preceding result differs substantially from what is found if the configurational entropy of dissolved H is ignored and gas-phase H2 is the hydrogen source. Dissolved H is mobile, so the vacancy H complexes compete with interstitial H, which will allow interstitial H to equilibrate with H trapped in vacancies. Thus, we rescale the vacancy formation energy as:
 | (18) |
Increasing the H content in vacancies does not increase the predicted vacancy concentrations. This should be expected from the data in Table 1: increasing the H concentration in a vacancy decreases its adsorption energy. We can illustrate this behavior using occupancies of 4H or 6H in the vacancies. Doing so allows the vacancy concentrations to reach maxima of 5 × 10−28 and 3 × 10−29 when configurational entropy is included, respectively. As before, ignoring the configurational entropy contribution of dissolved H slightly alters the predictions.
Using the total energies alone we can rescale the vacancy concentrations as:
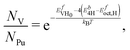 | (19) |
 | (20) |
The predicted 4H vacancy cluster concentration increases by several orders of magnitude when the configurational entropy of H is ignored, and the 8H vacancy cluster concentration decreases by an order of magnitude when configuration entropy of H is ignored. While these changes are irrelevant for our overall analysis, they reflect the source of stabilization. The adsorption of H in the 4H vacancy cluster is marginally more exothermic than the interstitial H, so 4H vacancy cluster formation is driven by enthalpy. Conversely, the adsorption energy H in the 8H vacancy cluster is less than that of interstitial H, so 8H vacancy cluster formation is driven by the configurational entropy increase associated with placing a small amount of H in vacancies. In other words, placing 8H atoms in the vacancy increases the effective vacancy formation energy when those H atoms are equilibrated with interstitial H, while placing 4H atoms in a vacancy decreases the effective vacancy formation energy.
Note that in all the examined cases, the vacancy concentration remains closer to the 10−27 found for the H-free thermal vacancy concentration than the concentrations required for SAVs. This behavior is driven primarily by the small total energy differences between interstitial H and H in vacancies. Thus, using the appropriate thermodynamic reservoir of H shows SAV formation will not occur at 298 K for the magnetic state and defect used in this study.
3.2 Model 2
We now compute the equilibrium vacancy concentrations at room temperature in H2 gas by considering the configurational entropy of dissolved H, thermal vacancies, and H trapped in vacancies. We will start with the chemical potential of dissolved H: | (21) |
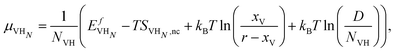 | (22) |
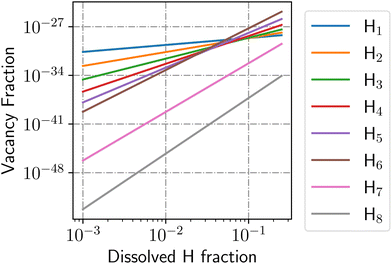
This value is shown in Fig. 6 for the case of degenerate H adsorption in the vacancy for 1 ≤ NVH ≤ 8. Higher NVH were not plotted for the sake of readability, but they sit below the lower level plotted here. Assuming the H induced, and thermal vacancy concentrations are independent, we find that below 5 at% dissolved H content, H will not induce vacancy formation above the level of normal thermal vacancies.
From Fig. 6, increasing the dissolved H content increases the concentration of H-induced vacancies as a power law as long as the dissolved H concentration remain low:
| ln(xV) = NVHln(xH) + bNVH, | (23) |
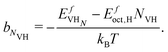 | (24) |
This expression is valid for low concentrations of vacancies and dissolved H. From this power law relationship, however, the vacancy concentration will remain low when the dissolved H content is below 25% and that the vacancy-1H complex will be the most populated because of the bNVH term.
Equating eqn (21) and (22), we can see the vacancy concentration reaches only 10−28 for the vacancy-1H complex at PuH0.25, which is far above the solubility limit.36 Increasing the number of H atoms in the vacancy reduces the vacancy concentration because the heat of adsorption cannot offset the entropic penalty. The vacancy-3H complex has a concentration of only 10−30 at PuH0.25. At PuH0.25 we expect H will be distributed across interstitial sites with 10−28 of the H content trapped in vacancies. This gives a total vacancy concentration of 10−26 at PuH0.25. While H induces vacancy formation already at 0.25 at% dissolved H, the vacancy concentration and total H stored in vacancies both remain negligible. Moreover, 0.25 at% may be above the solubility limit of H in Pu at 298 K, which we will now explore.14
3.3 Model 3
We connect to the gas phase chemical potential to address the vacancy concentration under fixed H2 pressure by simply equating chemical potentials: | (25) |
Zero-point energy corrections are more likely to become important when comparing to a gas-phase reservoir. These were implicitly ignored in the preceding analysis, which is reasonable if the change in zero-point energy between dissolved H and H in vacancies is small, but this needs to be tested explicitly in the future. From experimental measurements of PuH2 and PuD2 it appears the zero-point energy is quenched in the solid; the difference in the heats of formation of PuH2 and PuD2 is equal to the differences in gas-phase zero point energies of H2 and D2.32 Curiously, however, DFT gives values of 0.17 eV and 0.18 eV for the zero-point energy of H in the octahedral holes of Pu and the tetrahedral holes of PuH2.37 While the two values are nearly identical, supporting our assumption that the zero-point energy in the solid will not change between sites, both values are larger relative to the zero-point energy of  (0.135 eV). An increase of H zero-point energy in the solid will reduce the predicted H-induced vacancy concentration and is at odds with experiment, so we will continue to assume the zero-point energy is quenched for H in the solid. For the gas-phase, however, we have:
(0.135 eV). An increase of H zero-point energy in the solid will reduce the predicted H-induced vacancy concentration and is at odds with experiment, so we will continue to assume the zero-point energy is quenched for H in the solid. For the gas-phase, however, we have:
 | (26) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) H2 (298 K, 1 atm) = −0.32 eV and
H2 (298 K, 1 atm) = −0.32 eV and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) D2 (298 K, 1 atm) = −0.36 eV, is the enthalpic and entropic correction to the total energy at 298 K.4 ZPT is the experimental zero-point energy of H2 (0.27 eV) and D2 (0.19 eV).25 The
D2 (298 K, 1 atm) = −0.36 eV, is the enthalpic and entropic correction to the total energy at 298 K.4 ZPT is the experimental zero-point energy of H2 (0.27 eV) and D2 (0.19 eV).25 The  term accounts for changes in pressure assuming H2 behaves as an ideal gas, where p0 is standard pressure. This approach is shown schematically in Fig. 7, where gas-phase H2 fixes the H chemical potential.
term accounts for changes in pressure assuming H2 behaves as an ideal gas, where p0 is standard pressure. This approach is shown schematically in Fig. 7, where gas-phase H2 fixes the H chemical potential.
If we ignore changes in entropic effects in the solid phases, the allowed range of chemical potential for H dissolved in Pu will be bound by the heat of formation of PuH2. That is, the decomposition pressure of PuH2 is fixed by:
| μH2,gas(298 K, pH2) ≈ ΔHPuH2, | (27) |
• Experimental ΔH of PuH2:32
• Theoretical ΔH computed with DFT:
• Pressure extrapolated from the measured decomposition temperature:32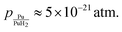
The choice to use several approaches is motivated by the possibility that using the DFT result will give error cancellation with the computed H adsorption energies. However, as capturing the structure of the dihydride and metallic forms of plutonium require different approximate Hamiltonians in DFT, it is unclear such error cancellation will occur. Thus, we include the measured heat of formation. Finally, extrapolation of the decomposition pressure to 298 K offers the most direct route, but relies on extrapolating from temperatures all of which are above 673 K. The resulting H-induced vacancy concentrations are summarized in Table 2 and can be seen to vary by up to 4 orders of magnitude but remain below the thermal vacancy concentration of 2.7 × 10−27 at 298 K. Table 2 also shows the maximum concentration of dissolved H is predicted to be 10−7 to 10−4 at 298 K, which is above the 10−9 extrapolated from experiment but below the 10−3 predicted from a DFT parameterized lattice gas model.37
 ) computed at the decomposition pressures of PuH2 at 298 K under different assumptions: DFT ΔH uses heat of formation of PuH2 from DFT; Exp ΔH for PuH2 is from Mullen;32 Extrapolated decomposition pressure uses decomposition pressure extrapolated from high T data.32 The 6-fold degeneracy for H adsorption into octahedral vacancies has been included. Note the 3Q structure predicts a thermal vacancy concentration of 7 × 10−27 and was computed at the experimental lattice constant with
) computed at the decomposition pressures of PuH2 at 298 K under different assumptions: DFT ΔH uses heat of formation of PuH2 from DFT; Exp ΔH for PuH2 is from Mullen;32 Extrapolated decomposition pressure uses decomposition pressure extrapolated from high T data.32 The 6-fold degeneracy for H adsorption into octahedral vacancies has been included. Note the 3Q structure predicts a thermal vacancy concentration of 7 × 10−27 and was computed at the experimental lattice constant with 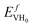 = 1.65 eV
= 1.65 eV
| DFT ΔH | Exp. ΔH | Extrap. decomp. | |
|---|---|---|---|
| Vac.-H1 complex | 9 × 10−19 | 1 × 10−21 | 2 × 10−18 |
| Dissolved H | 4 × 10−4 | 6 × 10−7 | 8 × 10−4 |
| Vac.-D1 complex | 9 × 10−19 | 6 × 10−21 | 6 × 10−18 |
| Dissolved D | 4 × 10−4 | 3 × 10−6 | 3 × 10−4 |
| Vac.-H1 complex (3Q) | 7 × 10−35 | 6 × 10−34 | 7 × 10−31 |
| Dissolved H (3Q) | 2 × 10−7 | 2 × 10−6 | 2 × 10−3 |
Below pressures where dihydride forms the H-vacancy complexes reach a concentration of 10−35–10−30, depending on what decomposition pressure is employed. This behavior is shown in Fig. 8, where the vertical lines show the different possible dihydride decomposition pressures, and the horizontal line shows the H-free thermal vacancy concentration. In all cases, the total concentration of H-vacancy complexes is less than the concentration of thermal vacancies, suggesting no SAV formation occurs. A 10−3 at% vacancy concentration would require quasi-equilibration with 4 × 10−11 atm H2, which would yield a stoichiometry of PuH0.99 assuming the energetics from Table 1. The model presented here will not be valid under those conditions and there is no evidence supporting such supersaturation of Pu metal with H can occur. Thus, SAVs will not form under equilibration with gas-phase H2 at 298 K.
 | ||
| Fig. 8 Vacancy concentration vs. gas phase H2 pressure at 298 K. Zero-point energies of the solid are taken as zero, while the experimental value of the zero-point energy for gas-phase H2 was employed. The dashed vertical line shows the decomposition pressure of PuH2 found from the experimental heat of formation of PuH2 (μH2,gas = ΔHPuH2), the dotted line is the decomposition pressure of PuH2 found from the DFT heat of formation of PuH2 (μH2,gas = ΔHDFT), and the dashed-dotted line is the decomposition pressure extrapolated from experimental decomposition pressures.37 | ||
It is worth considering the DFT error in energy required to reach a 10−3 at% vacancy concentration for the vacancy complex with one H atom at 298 K. This is the limiting error, and it could be in the vacancy formation energy, the adsorption energy of H at a vacancy, or a combination of the two. It will depend on the method used to compute the dihydride dissociation energy and runs from 0.76 eV to 0.90 eV. That is, the vacancy formation energy must be overestimated by 0.76 eV to 0.90 eV, or the adsorption energy of H must be underestimated by 0.76 eV to 0.90 eV, or a combination of overestimated vacancy formation energy and underestimated H trapping energy must total 0.76 eV to 0.90 eV. Considering that the computed heat of formation of PuH2 differs from the measured value by 0.05 eV per H atom, an error above 0.76 eV per atom is unlikely. This value also exceeds the MAE found for energies computed with the PBE functional.38–40 As a more robust measurement of the error, we include the 95% confidence interval for the heat of formation to our analysis which yields 0.17 eV per atom.26 The combination of the shift in the vacancy formation energy and the resultant change of the dissociation pressure is insufficient to obtain the vacancy concentrations associated with SAVs.
The absence of SAVs in δ-Pu is in line with expectations, where unlike in the case of metal hydrides, metals tend not to form SAVs as metal–metal bonding is typically stronger than the metal–hydrogen bonding found in the hydrides. As a demonstration, we consider PuH2 in the 3Q magnetic state. The magnetism of PuH2 and related materials is a matter of debate with ferromagnetism, collinear antiferromagnetism and noncollinear magnetism being actively discussed.15,41–44 An in-depth study of the magnetism of PuH2 is beyond the scope of this study, but warrants further investigation. Consistent with this view, the Pu vacancy formation energy in PuH2 in the 3Q magnetic state is 0.21 eV, significantly lower than the 1.65 eV found in δ-Pu, and with a thermal vacancy concentration on the order of 10−4, the bulk PuH2 hydride falls much closer to the SAV regime.
4 Conclusions
Super abundant vacancies (SAVs) have been suggested to form in δ-Pu under a low-pressure hydrogen environment. In this report, we presented DFT results for δ-Pu in the noncollinear 3Q magnetic state to study the formation of SAVs. With publicly available experimental data, we provide further constraints on the physical conditions needed to thermodynamically stabilize SAVs in δ-Pu. In developing several thermodynamic models, we estimate the vacancy concentrations in δ-Pu and discuss the limits of hydrogen driven formation of vacancies. We find that, when hydrogen in the lattice is equilibrated with gaseous H2, the formation of SAVs in δ-Pu is unlikely and any excess vacancy concentration beyond thermal vacancies would need to occur by a different mechanism. Without H, the room temperature vacancy concentration is predicted to be 2.7 × 10−27. Under conditions where PuH2 forms the maximum vacancy concentration may reach 10−25 in δ-Pu due to H incorporation. In all other cases, H incorporation does not increase the vacancy concentration at room temperature.Predicted maximum concentrations of dissolved H at 298 K range between 10−7 to 10−4 at% and these lower pressures will have fewer H induced vacancies. While this range is large, it is within the bounds reported based on experimental extrapolation (10−9) and lattice gas model results (10−3).37 However, our analysis of metastable phases showed that even if dissolved H concentrations reach above 2 at%, an SAV phase will not form in δ-Pu. In summary, there is no evidence that vacancies are a non-negligible source of stored H in δ-Pu, and H does not induce significant vacancy formation in the metal at 298 K. However, other defect structures with noncollinear magnetism may be able to push the metal closer to the SAV regime.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the LDRD project number 20230202DR. This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under Contract No. 89233218CNA000001.Notes and references
- Y. Fukai and N. Okuma, Phys. Rev. Lett., 1994, 73, 1640–1643 CrossRef CAS PubMed.
- Y. Fukai, Phys. Scr., 2003, 11 CrossRef CAS.
- Y. Fukai, M. Mizutani, S. Yokota, M. Kanazawa, Y. Miura and T. Watanabe, J. Alloys Compd., 2003, 270–273 CrossRef CAS.
- C. Zhang and A. Alavi, J. Am. Chem. Soc., 2005, 127, 9808–9817 CrossRef CAS PubMed.
- Y. Fukai, J. Alloys Compd., 1995, 231, 35–40 CrossRef CAS.
- Plutonium Handbook, ed. D. L. Clark, D. A. Gleeson and R. J. H. Jr., American Nuclear Society, 2nd edn, 2019, vol. 2 Search PubMed.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- D. Schwartz, S. Richmond, C. Taylor, A. Smith and A. Pugmire, Plutonium Futures-The Science, 2014.
- D. S. Schwartz, S. Richmond, A. I. Smith, A. Costello and C. D. Taylor, MRS Online Proc. Libr., 2012, 1444, 183–188 Search PubMed.
- R. O. Simmons and R. W. Balluffi, Phys. Rev., 1960, 117, 52–61 CrossRef CAS.
- C. Colmenares, R. Howell, D. Ancheta, T. Cowan, H. Hanafee and P. Sterne, First positron annihilation lifetime measurement of Pu, Lawrence livermore National Laboratory, Technical Report, 1996.
- R. Howell, L. Summers, D. Ancheta, T. Cowan, J. Hanafee and P. Sterne, Positron annihilation study of age-induced defect structures in Plutonium, Lawrence Livermore National Laboratory, Technical Report, 1997.
- P. A. Sterne and J. E. Pask, AIP Conf. Proc., 2003, 673, 205–206 CrossRef CAS.
- T. H. Allen, The solubility of hydrogen in plutonium in the temperature range 475 to 825 degrees centigrade, Rocky flats, Inc., technical report, 1991.
- J. W. Kim, E. D. Mun, J. P. Baiardo, A. I. Smith, S. Richmond, J. Mitchell, D. Schwartz, V. S. Zapf and C. H. Mielke, J. Appl. Phys., 2015, 117, 053905 CrossRef.
- C. D. Taylor, M. F. Francis and D. S. Schwartz, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 214114 CrossRef.
- S. C. Hernandez, F. J. Freibert, R. G. Hoagland, B. P. Uberuaga and J. M. Wills, Phys. Rev. Mater., 2018, 2, 085005 CrossRef CAS.
- S. P. Rudin, J. Nucl. Mater., 2022, 570, 153954 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- F. H. Ellinger, JOM, 1956, 8, 1256–1259 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed.
- K. K. Irikura, J. Phys. Chem. Ref. Data, 2007, 36, 389–397 CrossRef CAS.
- B. Ruscic, Int. J. Quantum Chem., 2014, 114, 1097–1101 CrossRef CAS.
- B. Medasani, M. Haranczyk, A. Canning and M. Asta, Comput. Mater. Sci., 2015, 101, 96–107 CrossRef CAS.
- M. Huda and A. Ray, Phys. B, 2004, 352, 5–17 CrossRef CAS.
- M. T. Curnan and J. R. Kitchin, J. Phys. Chem. C, 2014, 118, 28776–28790 CrossRef CAS.
- C. D. Taylor, S. C. Hernandez, M. F. Francis, D. S. Schwartz and A. K. Ray, J. Phys.: Condens. Matter, 2013, 25, 265001 CrossRef PubMed.
- R. Nazarov, T. Hickel and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 144108 CrossRef.
- R. N. R. Mulford and G. E. Sturdy, J. Am. Chem. Soc., 1955, 77, 3449–3452 CrossRef CAS.
- R. G. Mullen and N. Goldman, J. Chem. Phys., 2021, 155, 234702 CrossRef CAS PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- S. Richmond, J. S. Bridgewater, J. W. Ward and T. H. Allen, IOP Conf. Ser.: Mater. Sci. Eng., 2010, 9, 012036 Search PubMed.
- R. G. Mullen and N. Goldman, J. Phys. Chem. C, 2020, 124, 20881–20888 CrossRef CAS.
- J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44 CrossRef CAS.
- L. Vega, J. Ruvireta, F. Viñes and F. Illas, J. Chem. Theory Comput., 2018, 14, 395–403 CrossRef CAS PubMed.
- P. Janthon, S. M. Kozlov, F. Viñes, J. Limtrakul and F. Illas, J. Chem. Theory Comput., 2013, 9, 1631–1640 CrossRef CAS PubMed.
- J. T. Pegg, A. E. Shields, M. T. Storr, A. S. Wills, D. O. Scanlon and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2018, 20, 20943–20951 RSC.
- T. Smith, S. Moxon, D. J. Cooke, L. J. Gillie, R. M. Harker, M. T. Storr, E. L. da Silva and M. Molinari, Crystals, 2022, 12, 1499–1512 CrossRef CAS.
- S. Li, Y. Guo, X. Ye, T. Gao and B. Ao, Int. J. Hydrogen Energy, 2017, 42, 30727–30737 CrossRef CAS.
- T. Muromura, T. Yahata, K. Ouchi and M. Iseki, J. Inorg. Nucl. Chem., 1972, 34, 171–173 CrossRef CAS.
| This journal is © the Owner Societies 2024 |