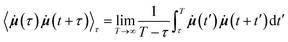Molecular dynamics simulations reliably identify vibrational modes in far-IR spectra of phospholipids

Abstract

The properties of self-assembled phospholipid membranes are of essential importance in biochemistry and physical chemistry, providing a platform for many cellular life functions. Far-infrared (far-IR) vibrational spectroscopy, on the other hand, is a highly information-rich method to characterize intermolecular interactions and collective behaviour of lipids that can help explain, e.g., chain packing, thermodynamic phase behaviour, and sequestration. However, reliable interpretation of the far-IR spectra is still lacking. Here we present a molecular dynamics (MD) based approach to simulate vibrational modes of individual lipids and in an ensemble. The results are a good match to synchrotron far-IR measurements and enable identification of the molecular motions corresponding to each vibrational mode, thus allowing the correct interpretation of membrane spectra with high accuracy and resolving the longstanding ambiguities in the literature in this regard. Our results demonstrate the feasibility of using MD simulations for interpreting far-IR spectra broadly, opening new avenues for practical use of this powerful method.

---

Introduction

Mechanical vibrations of specific groups of atoms in organic molecules are characteristic of each of these moieties. Shifts in the eigenfrequency of a specific vibrational mode indirectly reveal us about their chemical environment. Consistent identification of bond vibrations in the infrared (IR) energy range is a routine spectroscopy method with a sophisticated empirical and theoretical tool-base to interpret the spectra.¹ However, the reliability of the assignments suffers a fast break-down at the low energy end of the spectrum: interpretation of the modes in the far-IR, also known as terahertz, range is ambiguous.² This is in spite of the feature richness of this region, and the tacit understanding that far-IR spectroscopy contains highly valuable information about large chemical moieties, packing and ensemble effects.^3–5 Of particular interest in the far-IR range is the detection of part or all-molecule vibrations that involve an ensemble of atoms and bonds, and which in turn are very sensitive to conformational and intermolecular interactions. Far-IR spectra can also reveal the ensemble molecular structures and carry information about the packing of adjacent molecules.⁵ However, the identification of these modes is increasingly difficult with increasing complexity in the low energy end of the spectra. Far-IR has been applied successfully to characterize a range of organic macromolecules, e.g. various polymers,⁶ but in many cases the peak assignment is largely speculative. The information richness of far-IR spectra is generally acknowledged but most efforts have failed thus far to extract this information.

An attractive feature of far-IR spectroscopy is the sensitivity of its vibration modes to conformation and intermolecular interactions that could provide unparalleled insights into the properties of self-assembled systems.⁷ A prominent example for multiple disciplines is the plasma membrane.^5,8,9 The key enabler of life as we know it, the plasma membrane separates the biochemical life processes of cells from the external world, regulating transfer, metabolism, and signalling.¹⁰ The core of the plasma membrane is a phospholipid bilayer. Extensively studied from the physicochemical point of view, some fundamental properties of phospholipid bilayers such as the intermolecular interactions governing their phase transitions, packing and sequestration in the presence of ions or proteins, and the localization of cholesterol in a lipid ensemble still elude detection.¹¹ Importantly, far-IR spectroscopy of phospholipid membranes and membrane–protein interactions is of interest in biochemistry and physical chemistry. Several works have noted the feature richness of the far-IR spectra of phospholipid membranes, suggesting that they carry the answer to a range of open questions.⁵ However, attempts to assign vibrational modes in this range has resulted in broadly divergent predictions that appear to be little more than guesswork.^8,9,12–19 In Table 1, reported data on various lipids are included, i.e. phospholipids as well as fatty acids where acyl modes are expected to be similar if not identical, providing an overview as well as comparison and cross referencing. It is apparent that the same features are often ascribed to different effects: for example, the mode at ∼50 cm⁻¹ may be from headgroup vibrations or van der Waals effects, whereas the band at 150–190 cm⁻¹ is assigned to either CH₂ chain torsion or hydrogen bonds. Considering the broad nature of peaks in this part of the spectrum and their sensitivity to environmental conditions, peak positions reported by different authors with 5–10 cm⁻¹ difference are likely the same feature. Thus, there is no consensus on peak assignment in the far-IR spectra of lipids in contrast to the peak assignment in the high energy region. And this is a major hindrance towards using far-IR spectroscopy to assess membrane interactions with biochemical agents.

Table 1 Summary of peak assignments from the spectroscopy literature on phospholipids. Peaks are grouped into bands with suspected similar origins

Band	Freq. [cm^−1]	Assignment(s)	Ref.
#
I	50, 50–60	van der Waals, head group vibrations	9 and 13
II	70	van der Waals	9
III	88, 89	Water hydrogen bond stretch, van der Waals	9 and 14
IV	110, 113, 116	C–CH3	9 and 15
V	130, 136	Water hydrogen bond stretch, van der Waals	9 and 14
V	155, 150–165, 150–190	van der Waals, Hydrogen bonds, CH2 chain torsion	8, 9 and 16
V	186, 189, 191, 195	C–CH2 chain torsion, CH2 chain torsion, C–CH2 chain torsion, Water hydrogen bond stretch	8, 9 and 14
VI	225	C–C–C deformation	18
VII	235, 240	Hydrogen bonds, C–C–C deformation	17 and 18
VII	247, 250, 251	Hydrogen bonds, C–CH3 torsion, Water hydrogen bond stretch	8, 14 and 17
VII	254, 260	C–C–C deformation, C–CH3 torsion	9 and 19
VII	275	C–CH3 torsion	18
VII	328	C=O vibrations	17
VII	363, 368	C–C–C deformation, C–C–N torsion	8 and 18
VII	378	C=O vibrations	17
VIII	425–490	Libration of headgroup and rotation of top of the chain	13
VIII	428	C–C–O deformation (unclear which O is this in nonanoic–COOH), C–C–C deformation	18 and 19
VIII	438	C–C–O deformation (which O is this in oleic–COOH?)	19
IX	475, 480	C–C–O and C–C–C deformations	18 and 19
X	505	O–P–O deformation	8
X	518, 520	C–C–O torsion and C–C–C deformation, Headgroup libration	13 and 19
X	526, 528, 531	C–C–O torsion and C–C–C deformation, O–P=O deformation, C–C–C deformation and C=C–C torsion	8, 18 and 19
XI	543, 547	O–P–O deformation, C–C–O and C–C–C and C–O–P deformations	12 and 20
XII	575	CN + (CH3)3 deformation	8
XII	617, 673	O–PO2–O deformation	12
XII	685, 690	C–O–O deformation, O–C=O deformation	12 and 18

---

The challenges of experimental data analysis of IR spectra necessitate a computational approach. For the near and mid-IR range computational quantum chemistry methods are routinely used.^21–24 Density–functional theory (DFT) calculations can reliably model bond vibrations in isolated small molecules, amino acids, nucleic acid bases, peptides and even single phospholipids.^{12,22,24–30} However, their predictive power breaks down when folding, hydrogen bonding or dispersion forces are involved. In particular, it is not suited to model molecular ensembles. Hence the predictive power of DFT breaks down exactly where modelling is needed the most: in the far-IR where ensemble effects are believed to dominate.

While it is seldomly used to calculate the vibrational modes of molecular ensembles, classical molecular dynamics (MD) calculations have been employed to study various properties of the lipid bilayer membrane.^31–36 The far-IR spectrum of liquid water has been satisfactorily reproduced using classical MD simulations via the Fourier transform of time-correlation function of the total dipole moment with considerations for the dipole-induced mechanism and correction for quantum effects.³⁷ Temperature dependence of the water vibrational spectrum has also been investigated using classical MD simulations.³⁸ By incorporating the effects of Fermi resonance into a polarizable model of methanol, the complex C–H stretching region of the methyl group in IR, Raman and sum frequency generation spectra was successfully reproduced by classical MD simulations.³⁹Ab initio MD (AIMD) simulations, where the electronic structure is taken into account, were used in the calculations of IR spectra for four organic molecules including methanol whereby the modulation of the spectrum by inter-molecular interactions was demonstrated.⁴⁰ IR absorption spectra of small model peptides have also been calculated using classical MD as well as quantum mechanical/molecular mechanics (QM/MM) methods, with the latter having better agreement with experiments.⁴¹ Use of a polarizable force-field to extract IR spectra from classical MD simulations of small peptide analogues and a helical peptide showed comparable accuracy to various quantum chemistry methods.⁴² Thus although there is precedence for the capability of the MD approach to model molecular vibrations, the technique has only been applied to a few model systems to date. IR vibrational spectra of phospholipids have not been calculated using either AIMD, QM/MM or classical MD simulations.

In this manuscript, we compare the experimental far-IR spectra of dipalmitoyl phosphatidylcholine (DPPC) and dimyristoyl phosphatidylcholine (DMPC), two saturated phospholipids that only differ in acyl chain length, to the calculated spectra from classical MD simulations. Good agreement between the peaks from the experimental and calculated far-IR spectra was obtained. By observing how the calculated spectra change as we include different groups of atoms on the phospholipids, we have attempted to assign peaks to molecular vibrations of different functional groups and compared to literature assignments that were based on experiment or quantum chemistry calculations. This integrated experimental–computational approach allows us to better understand the far-IR spectra of phospholipids, as computations can help interpret which functional groups on the lipid contribute to peaks in the resultant far-IR spectrum.

Methods

Experimental methods

The experiments were carried out on the THz/far-IR Beamline at the Australian synchrotron. This beamline is equipped with a temperature-controlled ATR consisting of a diamond prism and 45° incident beam angle, a Bruker IFS 125/HR Fourier transform spectrometer and a silicon bolometer. A thermal stage was fitted to the ATR unit and a thermocouple was placed next to the diamond crystal. The temperature of the sample was controlled to ±0.5 °C. Environmental humidity was controlled using an enclosure over the ATR unit. 20–50 μL of lipid sample was dropcast onto the diamond crystal from chloroform solution until the absorption was strong enough to give a signal to noise ratio of approximately 1 : 10 for the clear distinction of absorbance peaks from artefacts. The sample was then hydrated and that facilitated self-assembly into multiple bilayers with either a drop (2–5 μL) of deionized water or increasing the relative humidity to 70% and monitoring the spectrum until it stabilised, such as the reduction of the bulk water feature below 150 cm⁻¹. Spectra are averages of 100 scans. Raw single channel data was recorded with separate background scans collected at regular intervals to eliminate any fluctuations in the synchrotron beam intensity. Data analysis, including ATR correction, was carried out with OPUS 8.0 software. The useable frequency range was 70–640 cm⁻¹.

Computational methods

Molecular dynamics simulation of phospholipids in bilayer and in water. An atomistic model of a bilayer of 320 DPPC (or DMPC or DPPE) phospholipids is generated using the Membrane Builder module of the CHARMM-GUI webserver, together with simulation parameter files and set-up files for simulations using GROMACS.^43–47 The bilayer was placed in a simulation box of size 10 nm × 10 nm × 8.5 nm with periodic boundary conditions in all three directions, and the top and bottom of the bilayer was solvated with TIP3P water molecules. The CHARMM36 all-atom force–field was used to describe inter-atomic interactions and all simulations were performed with the GROMACS v2020 MD package.^48,49 First, energy minimization was performed with the steepest descent method with positional restraints on the lipid phosphate atom in the Z-direction. This is followed by a series of five dynamics simulations with restraints being progressively reduced: first three simulations of 125 ps at a time-step of 1 fs, followed by another two simulations of 500 ps at a time-step of 2 fs. Bonds involving hydrogen atoms are constrained using the LINCS algorithm. The system temperature was maintained at 323 K or 50 °C (above the gel–fluid transition temperature of DPPC lipid of 315 K,⁵⁰ following a previous simulation study³²) with the Berendsen method with a time constant of 1 ps. Pressure control at 1 bar with the Berendsen method was turned on from the third simulation, with a time constant of 1 ps and compressibility of 4.5 × 10⁻⁵ bar⁻¹. Positional restraints are turned off in the sixth simulation for 500 ps at a time-step of 2 fs. Lastly, a production simulation was carried out for 30 ns at a time-step of 2 fs to equilibrate the lipid bilayer at 323 K with the Nose–Hoover method and at 1 bar with the Parrinello–Rahman method using the same time constants as above. The van der Waals forces between atoms are smoothly switched to zero between 1.0 and 1.2 nm. Electrostatic forces between atoms are calculated with the Fast smooth Particle–Mesh Ewald method with a cutoff of 1.2 nm for the real-space calculation. A similar protocol was used for simulations of DMPC or DPPE lipids in a bilayer, with a temperature of 313 K or 40 °C maintained for DMPC in fluid phase and temperatures of 323 K or 350 K were maintained for DPPE in the gel or fluid phase respectively. The equilibrium area per lipid (area/lipid) of DPPC and DMPC in the fluid phase is 0.63 nm² and 0.58 nm², respectively. The value for DPPC is similar to what was reported in previous simulations with the all-atom CHARMM force–field,³² though the value for DMPC is slightly smaller than reported and also smaller than DPPC as observed.³² The equilibrium area/lipid of DPPE in fluid and gel phases are 0.58 nm² and 0.45 nm², respectively, with the gel phase value very close to that reported for the gel phase DPPE simulated with the CHARMM36 force–field.⁵¹

For simulations of a single lipid in water, a single DPPC lipid is extracted from the 30 ns configuration of the lipid bilayer. It is then placed in the centre of a cubic box of side 4 nm which is then filled with TIP3P water molecules. Energy minimization using the steepest descent method is followed by 10 ps of dynamics simulation with the temperature maintained at 323 K with the Nose–Hoover method, and then 200 ps of dynamics simulation at a time-step of 1 fs (bonds involving hydrogen atoms are unconstrained) with the temperature of 323 K and pressure of 1 bar maintained with the Parrinello–Rahman method.

Calculation of IR vibrational spectra of phospholipids in water and in the bilayer. For calculation of the IR vibrational spectrum for a phospholipid in water, 200 ps trajectory data were saved every 1 fs and no constraints were placed on bonds involving hydrogen atoms to capture C–H stretching vibrations. For the case of phospholipids in the lipid bilayer, the simulation was performed for 200 ps after 30 ns of equilibration with trajectory data saved every 10 fs, with C–H bonds constrained to allow for the larger 2 fs simulation time-step. The trajectory was first least-squares-fitted to remove rigid body rotational and translational motions. The IR intensity is given by the Fourier Transform of a time correlation function involving dipole moments,⁴⁰
where [small mu, Greek, dot above](t) is the time derivative of the total dipole moment, defined as where eZ_j is the fixed atomic charge on atom j and R_j(t) is the position vector of atom j at time t taken from the MD simulation. The IR intensity may also be written using the dipole moment rather than its time derivative.³⁸ Working with the time derivatives has the advantage of insensitivity to the choice of reference coordinates. The term in angle brackets denotes a time correlation function involving time derivatives of the total dipole moment, an ensemble averaged over different starting time τ. By invoking the ergodic hypothesis, we may replace the ensemble average by a time average over different starting times,
in which it is understood that the maximum value of t + t′ cannot exceed the maximum time-step of the trajectory, T, and that τ ≤ T. The algorithm was implemented in Python using NumPy and SciPy numerical libraries. The computed frequencies ω in Hz are then converted to inverse wavenumbers in cm⁻¹ by dividing by 30 × 10⁹ Hz or 30 GHz, which is the frequency of an electromagnetic wave with a wavelength of 1 cm in free space. By changing the sampling time-interval in the calculation of the autocorrelation function, we were able to calculate the spectrum over different wavenumber ranges.

Principal component analysis of phospholipid trajectories. Covariance analysis, also known as principal component analysis (PCA) or essential dynamics, could identify collective motions from MD simulations.^52,53 PCA was performed on the MD trajectories of the DPPC lipid fatty acid tail in water and in lipid bilayers using GROMACS tools to identify collective motions.⁵⁴ First, a covariance matrix C of atomic positions is constructed,
where M is a diagonal matrix containing the masses of the atoms (mass-weighted analysis) or unit matrix (non-mass weighted analysis, which is our case as only carbon atoms are used). This covariance matrix is diagonalized by GROMACS “gmx covar” tool via orthonormal transformation to obtain eigenvalues and eigenvectors, , where 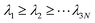. The columns of R are the eigenvectors, also called principal modes. The eigenvectors define a new orthogonal coordinate set. Typically, the eigenvectors are ranked by their corresponding eigenvalues, with the first few eigenvectors representing global, collective motions of the molecule concerned. Specifically, the original trajectory is “decomposed” into a superposition of “component” trajectories which are projections of the original trajectory (a 3N dimensional vector for N atoms) onto the principal modes to obtain the principal components (PCs): . The original trajectory can then be filtered along one (or more) principal modes, e.g. for mode i the filtered trajectory is 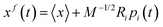. The filtered trajectories exhibit bending or twisting motions as the dominant collective motions present in the original trajectory.

Calculation of the order parameter of phospholipids in bilayers. The packing of lipids in the bilayer was quantified using the order parameter S_CD defined as |〈3 cos² θ − 1〉/2|, where the straight brackets represent taking the absolute value, the angle brackets represent averaging over lipids and simulation time (20 to 30 ns), and θ is the angle of the CH vector of the acyl chain carbons with respect to the bilayer normal.³² The order parameters were calculated using the GROMACS “gmx order” tool.

Results and discussion

Experimental far-IR vibrational spectra

Fig. 1 shows the attenuated total reflectance (ATR) spectrum of hydrated multiple DPPC bilayers at 45 °C and DMPC bilayers at 30 °C. It should be noted that these lipids are largely identical, differing in the acyl chain length only; to ensure they are both in the same thermodynamic (fluid) phase the measurement temperatures are different, just above the chain melting temperatures for each, respectively. The chain melting temperature for DMPC is ∼23–24 °C whereas for DPPC ∼41–42 °C. Fig. 1 shows that temperature has little to no effect on peak shape.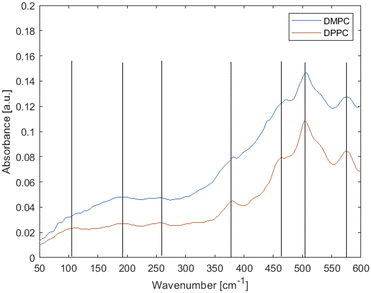

Fig. 1 Experimental far-IR spectra of fluid-phase phospholipid membranes made up of saturated lipids DMPC (at 30 °C) and DPPC (at 45 °C). Lines are added as a guidance.

Neglecting the smaller and ambiguous peaks, the main features of the spectra are three weak peaks at low wavenumbers and an increasing background and stronger peaks feature above ∼300 cm⁻¹. As per Table 1, the peaks at 575 and 505 cm⁻¹ have usually been attributed to vibrations from the head group, peaks at 460, 380 and 250 cm⁻¹ have been tentatively attributed to torsional modes in the hydrocarbon chains and peaks at ∼190 and ∼100 cm⁻¹ have simply been called “hydrogen bonding features”.⁵⁵

Inconsistencies notwithstanding, according to literature assignments (Table 1), there should be several acyl chain vibration modes in the 460–250 cm⁻¹ range, hence differences would be expected between the lipids with the varying acyl chain lengths. Yet there is little to no difference in the observed spectra, with one small shift observed at ∼475 cm⁻¹. Thus, the experimental data suggest that the modes observed here originate predominantly from headgroups and/or collective effects.

Computational spectra from molecular dynamics simulation and data analysis

The computational approach is outlined in Fig. S1 (ESI†). Molecular dynamics simulations allow for the sampling of atomic-level vibrations of various functional groups in a phospholipid within a bilayer membrane as a function of time. The absorption spectrum can then be calculated as the Fourier transform of the time-correlation function of time derivatives of the dipole moments (Fig. S1, ESI†). In the following sections, we present validation of the calculated spectrum for lipid fatty acid chains with the analogous polyethylene spectrum and investigate the effect of the environment (water or bilayer) on the spectrum for fatty acid tails (Fig. 2). The complete far-IR spectrum with all functional groups (lipid head and tail) was then calculated and found to be in good agreement with the experimental spectrum (Fig. 3), and thus it is possible to proceed with the assignment of peaks to the vibrations of lipid functional groups, i.e., a comprehensive interpretation of the far-IR spectrum.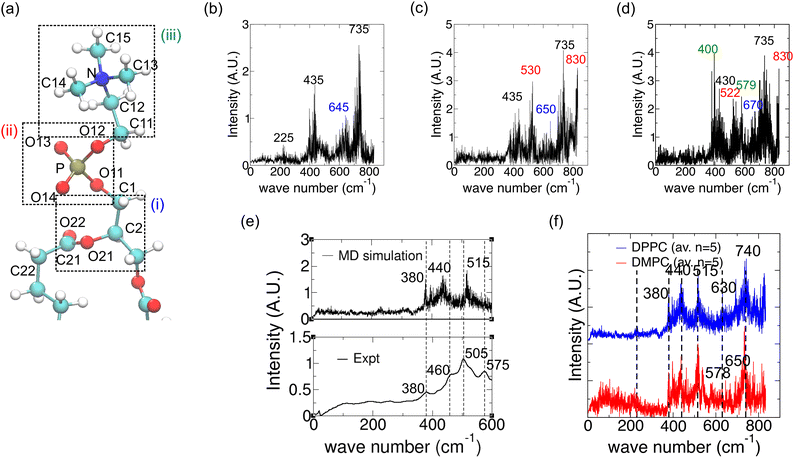

Fig. 2 Calculation of the IR spectrum of one or more CH₂ groups along a phospholipid fatty acid tail. (a) (top) 3D atomic structure of DPPC, a fully saturated phospholipid. Atoms are colored as follows: carbons in cyan, hydrogens in white, oxygens in red, phosphorous in dark green, and nitrogen in blue. Selected carbon atoms along one of the fatty acid tails are labelled. (Middle) Representative snapshot of DPPC lipid in water (shown as lines). (Bottom) Representative snapshot of DPPC lipid in a bilayer (surrounding lipids shown as lines). (b)–(e) Calculated IR spectra of different numbers of CH₂ groups along one of the two saturated fatty acid tails of the DPPC phospholipid from a 200 ps molecular dynamics simulation of a DPPC lipid in water. The wavenumbers of the peaks are labelled in the plots. The experimental IR spectrum of polyethylene is overlaid in (e) which is an analogue of the multiple CH₂ groups along the fatty acid tail. (f) Schematics of the inter-atomic vibrations contributing to peaks at the mid to high wavenumbers. (g) and (h) Spectra for the DPPC lipid in water calculated over lower wavenumbers. (i) and (j) Spectra for the DPPC lipid in the bilayer calculated over lower wavenumbers. Simulation times are 200 ps for both systems.

Fig. 3 The effect of including phospholipid head-group atoms on the calculated IR spectrum for a DPPC lipid in a bilayer and comparison with an experimental spectrum. (a) 3D atomic structure of DPPC with the glycerol backbone (i), phosphate (ii) and choline (iii) atoms highlighted using dashed boxes from bottom to top. (b) Spectrum calculated using a DPPC fatty acid tail and glycerol backbone atoms, with a new peak compared to Fig. 2j labelled in blue. (c) Spectrum with phosphate atoms included, with new peaks labelled in red. (d) Spectrum with choline atoms included (i.e. tail + complete head-group), with new peaks labelled in green. (e) (top) Averaged calculated spectrum (over 5 spectra). (Bottom) Experimental spectrum. Dashed lines are shown for ease of comparison of the respective peak locations. (f) Comparison of averaged calculated spectra for DMPC (blue) and DPPC (red). The major peak positions on DMPC are shown with dashed lines for ease of comparison with DPPC spectra.

Vibrations of the acyl chains

We have performed molecular dynamics simulations of the DPPC phospholipid in water and in a bilayer and computed the corresponding IR vibrational spectra (Fig. 2). Movies from 200 ps of MD simulations showing molecular vibrations of a single DPPC lipid molecule in water and in a lipid bilayer are included in the ESI.† The spectra for a DPPC lipid in water computed with an increasing number of CH₂ groups along one of its fatty acid tails (Fig. 2a) are presented in Fig. 2b–e. The IR spectrum for a single CH₂ group (Fig. 2b) shows a peak at 3000 cm⁻¹ attributed to the C–H stretching vibration, and the peaks at 1340 and 1430 cm⁻¹ are attributed to C–H bending vibrations (e.g. scissoring or rocking) known for alkanes.^39,56 The cartoons depicting stretching, scissoring and rocking vibrations are shown in Fig. 2f, where scissoring is the opening/closing of the H–C–H angle and rocking is the side-to-side movement of the whole CH₂ group about an axis centered on the carbon atom and pointing out of the plane of the figure. Note that real simulation snapshots are used in Fig. 2f, hence C–H stretching could occur concurrently with the bending vibrations.

As more CH₂ groups were included in the calculation of the molecular dipole moment, the peaks attributed to C–H bending vibrations shift to lower wavenumbers likely due to an increase in the effective mass contributed to these vibrational modes (Fig. 2c–e). Furthermore, a peak around 720 cm⁻¹ appears as we included more than one CH₂ group, becoming stronger as we progressively include more CH₂ groups. This peak is regularly attributed to long chain methyl rocking.⁵⁶ For comparison with experimental data, the IR spectrum for polyethylene (adapted from ref. 57) is overlaid on the spectrum processed using 15 CH₂ groups in Fig. 2e, which shows generally good agreement especially the peaks at 1410 and 720 cm⁻¹. The peak at 3000 cm⁻¹ from our calculated spectrum for the DPPC C22–C216 chain is at a slightly higher wavenumber compared to polyethylene which may be due to inter-acyl chain interactions which make the C22–C216 chain stiffer than a single polyethylene chain.

To determine how inclusion of CH₂ groups contribute to the vibrational spectrum at lower wavenumbers, we have obtained spectra by including one to five CH₂ groups in the total dipole moment in the spectra calculations. For wavenumbers below 1800 cm⁻¹ in the range of bending vibrations and collective modes (Fig. S2, ESI†), we changed the sampling time-interval in the calculation of the autocorrelation function: 10 fs for wavenumbers up to 1800 cm⁻¹ and 20 fs for wavenumbers up to 900 cm⁻¹. The spectra up to 1800 cm⁻¹ (Fig. S2a, ESI†) show a similar trend in terms of the growth of the 720 cm⁻¹ peak as those spectra shown in Fig. 2b–e. The peak at about 1300 cm⁻¹ (C–H rock) also shifts to lower wavenumbers as more CH₂ groups are included in the total dipole moment, whereas the peak at about 1410 cm⁻¹ (C–H scissoring) does not shift. Hence the C–H rock motion seems to be affected by a hitherto unknown collective motion, which we speculate to be coupled motions via dihedral angle restraints. The spectra up to 900 cm⁻¹ (Fig. S2b, ESI†) reveal peaks at 240–250 cm⁻¹ and 334–440 cm⁻¹ (currently unassigned and absent from experimental spectra of lipids or alkanes). Whereby the former peak remains at about 250 cm⁻¹ after 2 or more CH₂ groups are included, and the latter peak increases from 334 to 440 cm⁻¹ as we include more CH₂ groups. What accounts for this shift towards larger wavenumbers is unclear.

The effect of the environment

The effect of the environment on the vibrational spectra was examined by comparing the vibrational spectrum for a DPPC lipid in water with that in a lipid bilayer consisting of 320 lipids (Fig. 2a). As the surroundings of the lipid are more likely to affect collective motions than individual bond vibrations, we have focused on lower wavenumber (up to 1800 cm⁻¹) spectra as shown in Fig. 2g–j. The two spectra for lipids in water (Fig. 2g and h) and two spectra for lipids in a bilayer (Fig. 2i and j) are obtained using different sampling time-intervals in the calculation of the autocorrelation function (see the methods section).

We found that the IR vibration spectra for a single lipid tail in water vs. a lipid tail in a bilayer (where it can be affected by inter-molecular interactions) are similar for the mid-range of wavenumbers from 0 to 1800 cm⁻¹ (Fig. 2g and i). But the calculated spectra for the lower range of wavenumbers from 0 to 900 cm⁻¹ (far-IR) showed more significant differences, in particular the shifting of the peak at 255 cm⁻¹ to 225 cm⁻¹ (Fig. 2h and j). This is likely the result of inter-molecular dispersion interactions between fatty acid tails that restrains free movement of neighbouring lipid tails enforcing a collective motion. Lipid tails in water have more conformational freedom and are surrounded by hydration shells formed by H-bonded water molecules thus the tails are separated in a high dielectric environment. In contrast, lipid tails in a bilayer are in a low dielectric environment and can interact via dispersion interactions.

Vibrations of the polar moieties

We next studied how the glycerol backbone, phosphate group and other head-group atoms contribute to the vibrational spectrum. Fig. 3a shows the atomic structure of DPPC with a glycerol backbone. Comparing Fig. 3b with Fig. 2j, inclusion of the glycerol backbone (Fig. 3a(i)) resulted in a new peak at 645 cm⁻¹ (Fig. 3b). Further inclusion of phosphate (Fig. 3a(ii)) resulted in new peaks at 530 and 830 cm⁻¹, and the disappearance of the peak at 225 cm⁻¹ (Fig. 3c). The 645 cm⁻¹ peak in Fig. 3b shifted to 650 cm⁻¹ due to a change in the chemical environment. Lastly, inclusion of choline in the head-group (Fig. 3a(iii)) gave rise to peaks at 400 cm⁻¹ and 579 cm⁻¹ (Fig. 3d). These peaks may be attributed to C–C–N torsion and choline deformation, respectively (see Table 2). Spectra for four other lipids well separated on the bilayer were then computed and all five spectra were averaged as shown in the top panel of Fig. 3e. The experimental spectrum for DPPC in the fluid phase is shown in the bottom panel of Fig. 3e. Both spectra are up to 600 cm⁻¹ as the quality of the near-IR data beyond that in our experiment is lower. The corresponding peaks between the calculated and experimental spectra are labelled, showing reasonably good agreement between the two other than acceptable shifts in the wavenumbers of corresponding peaks. However, the 579 cm⁻¹ peak is missing in the averaged spectrum (Fig. 3e). The five individual spectra contributing to the average are shown in Fig. S3 (ESI†), where only the first spectrum has a clear 579 cm⁻¹ peak. Close inspection of the corresponding simulation trajectories reveals different degrees of residual rigid body motion of choline after removal of whole lipid rigid body motion. Recalculating the spectra after fitting the trajectories onto only N and C12 atoms more effectively removed the rigid body motion of choline and enhanced the peak at 574 to 580 cm⁻¹, possibly attributed to choline deformation modes (Fig. S3d, ESI†). Lastly, Fig. 3f shows that the averaged spectrum for DMPC is broadly similar to that of DPPC, as observed in our experimental spectra (Fig. 1). However, a peak at 578 cm⁻¹ appears in the averaged spectrum for DMPC, in agreement with the experimental spectrum in Fig. 1. The individual DMPC spectra seem to show more peaks near 575 cm⁻¹ (Fig. S4, ESI†). The presence of peaks close to 575 cm⁻¹ might be correlated with a low to moderate residual rigid body motion of choline with more of these peaks for DMPC (Table S1, ESI†).

Table 2 Summary of peak assignments from our calculation for DPPC/DMPC/DPPE in bilayers

Frequency [cm^−1]	Reference frequencies from Table 1	Possible assignment	Atoms involved
230 (DPPC), 237 (DPPE)	225, 235, 240	C–C–C deformation	Fatty acid tail
380 (DPPC, DMPC, DPPE)	368	C–C–N torsion	Head-group choline/amine
440 (DPPC, DMPC), 447 (DPPE)	428, 480	C–C–C deformation	Fatty acid tail
515 (DPPC, DMPC, DPPE)	505, 528, 543	O–P–O deformation	Head-group phosphate
578 (DMPC)	575	CN + (CH3)3 deformation	Head-group choline
630 (DPPC), 650 (DMPC, DPPE)	690	O–C=O deformation	Glycerol backbone
740 (DPPC, DMPC), 760 (DPPE)	N.A.	Long chain methyl rock	Fatty acid tail

---

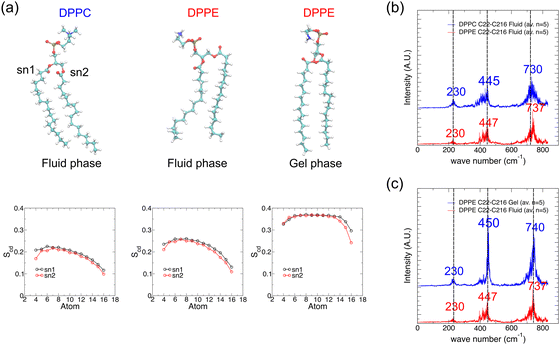
To investigate the effect of different phospholipid head-groups on the resultant IR vibrational spectra, we carried out MD simulation of the 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine (DPPE) bilayer following the same protocol as used for the DPPC bilayer. The simulation temperature was raised to 350 K, above the gel-to-fluid transition temperature of 337 K for the fluid phase DPPE bilayer.⁵⁰ DPPE and DPPC differ in their head-group, while the head-group of PC lipids is N–(CH₃)₃, that of PE lipids is NH₃ which is more polar in nature. The effects of the head group (labelled (iii) in Fig. 4a) are studied using a similar analysis as that in Fig. 3 and the results are presented in Fig. 4b–d. The amine head-group in DPPE yielded several new peaks in the vibrational spectrum (Fig. 4d), distinct from those from the choline head-group in DPPC (Fig. 3d). After averaging over five spectra, peaks at wavenumbers lower than 400 cm⁻¹ appear more prominent for DPPE as compared to DPPC, as well as a stronger peak at 650 cm⁻¹ for DPPE versus a weak peak at 630 cm⁻¹ for DPPC (Fig. 4e). The peaks at 237 and 300 cm⁻¹ (DPPC shows very weak peaks at 230 and 320 cm⁻¹) may reflect stronger collective motions of the PE head-group in contrast to the PC head-group due to H-bonding between the PE and phosphate groups. The prominent peak at 440 cm⁻¹ in the DPPC spectrum becomes more diffused in the case of DPPE (Fig. 4e). Lastly, the peak assigned to the long chain methyl rock slightly shifted from 740 cm⁻¹ for DPPC to 760 cm⁻¹ for DPPE (Fig. 4e), possibly reflecting a more packed environment for the lipid tail (Fig. 6a shows the lipid tail order parameters). The peak assignments from the averaged spectra of DPPC, DMPC and DPPE (Fig. 3f and 4e) are summarized in Table 2. Since the analysis presented herein clearly and unambiguously identifies specific vibrational patterns of key moieties and atomic groups, the results allow us to resolve the conflicting assignments that hitherto prevailed in the literature as summarized in Table 1 above. Our results in Table 2 thus supersede the information collected in Table 1, providing the first ever theoretically confirmed peak assignment of vibrational spectra of lipid membranes in the terahertz range.

Fig. 4 The effect of including phospholipid head-group atoms on the calculated IR spectrum for a DPPE lipid in a bilayer and comparison with the DPPC spectrum. (a) 3D atomic structure of DPPE with the glycerol backbone (i), phosphate (ii) and choline (iii) atoms highlighted using dashed boxes from bottom to top. (b) Spectrum calculated using a DPPE fatty acid tail and glycerol backbone atoms, with new peaks compared to Fig. 3j labelled in blue. (c) Spectrum with phosphate atoms included, with new peaks labelled in red. (d) Spectrum with amine atoms included (i.e. tail + complete head-group), with new peaks labelled in green. (e) Overlay of DPPE and DPPC spectra with major peaks labelled. The baseline of the DPPC spectrum has been shifted upwards for ease of comparison.

Peak assignment to molecular motions

To gain insights into the vibrational modes that contribute to the peaks in the spectrum, we carried out principal component analysis (PCA) on the molecular movement trajectories for a lipid fatty acid tail in water and in a bilayer, as shown in Fig. 5. PCA provides the orthogonal directions (eigenvectors) in the high dimensional space of molecular motion that reveal low frequency, collective motions. The details of PCA are given in Methods. The first few principal components (PCs) with the largest eigenvalues (variance of the motion along the first few eigenvectors) are identified. The first two PCs for lipid in water are shown in Fig. 5a whereas those for lipid in a bilayer are shown in Fig. 5b, whereby the simulation trajectories have been projected onto each eigenvector and the extreme projections are shown to indicate the range of motions for each PC. In both cases, the first mode is related to bending of the chain and the second mode is related to twisting of the chain. Subsequent modes are all twisting modes. However, the eigenvalues for the first four PCs in the bilayer are lower than those in water (Fig. 5c), especially for the first PC corresponding to bending of the chain. This agrees with the simulation trajectory of a lipid in water where the tails can easily bend compared to the bilayer environment whereby tail motions are more restricted due to tail–tail packing via hydrophobic interaction (Fig. 2a). Movies of the original trajectory filtered onto the first three principal modes (see Methods) are presented in the ESI.† Despite the lack of direct correspondence of PC modes to the peaks in the IR vibrational spectrum, it is probable that the lowest wavenumber peaks correspond to one or more of the first few PC modes.

Fig. 5 Principal component analysis of conformational changes to a DPPC lipid tail (a) in water and (b) in a bilayer. Extreme projections of the simulation trajectory onto the first two principal component eigenvectors showing bending modes for the first principal component (PC1) and twisting modes for the second principal component (PC2). Double-headed arrows indicate back-and-forth transitions between the extreme projections. Only carbon atom positions are included in the analysis. (c) Principal component eigenvalues for lipids in water and in the bilayer.

As the chemical nature of the lipid head-group as well as the lipid phase (driven by temperature) affects the packing of lipids in the bilayer, their respective IR vibrational spectrum may reflect these different states. The top panels in Fig. 6a show representative snapshots of DPPC and DPPE lipids in both fluid (disordered) and gel (ordered) phases. The PE head-group could form H-bonds with water or with a neighboring PE head or phosphate groups. This enhances lipid–lipid packing as shown by the order parameters (measures the degree of alignment of acyl chains to the bilayer normal, see the methods section) as presented in the bottom panels in Fig. 6a. The order parameter close to the glycerol group for DPPC is about 0.2, close to values reported using MD simulations in the literature.^32,58 The order parameters profile suggests that the acyl tails are reasonably ordered close to the headgroup and become more conformationally disordered towards the center of the bilayer. Order parameters are slightly higher values for DPPE compared to DPPC in agreement with the literature.^32,35,59 However, the vibrational spectra for DPPC and DPPE lipid tails in the fluid phase overlap very well, except for a very slight shift to a higher wavenumber in the DPPE spectrum for the peak at 730 cm⁻¹ attributed to long chain methyl rocking (Fig. 6b). Since the gel-to-fluid transition temperature for DPPC is about 315 K and that of DPPE is about 337 K,⁵⁰ DPPC lipids in our simulations at 323 K are in the fluid phase, whereas DPPE lipids at the same temperature are in the gel phase. In the gel phase, the lipid tail packing becomes highly ordered and the order parameter values are thus higher, with a higher (and wider) plateau value of about 0.37 in the gel phase vs. 0.27 in the fluid phase at 350 K. In terms of the resulting vibrational spectra, the set of major peaks again overlap well except that the peaks for the gel phase lipids appear sharper (Fig. 6c). Note that results for DPPC lipids in the gel phase are not available as simulating DPPC bilayers at temperatures below the transition temperature resulted in a phase more resembling the ripple phase rather than the gel phase.¹¹

Fig. 6 Effect of lipid head-group type and lipid phase on the IR vibrational spectrum of lipid tails. (a) Representative simulation snapshots of DPPC and DPPE lipids extracted from lipid bilayers simulated for 30 ns at 323 K (DPPC fluid phase and DPPE gel phase) and at 350 K (DPPE fluid phase). Lipid order parameters of lipid tails (denoted sn1 and sn2) averaged over the last 10 ns of simulation and over all lipids in the bilayer for each of the three systems are shown at the bottom of each simulation snapshot. (b) IR vibrational spectra for fatty acid tail atoms of DPPC and DPPE lipids in the fluid phase, averaged over spectra from five lipids, for wavenumbers less than 900 cm⁻¹. (c) Similar to (b) but for DPPE lipids in the fluid or gel phase.

Conclusions

Self-assembly of lipid molecules into superstructures such as the plasma membrane underpins a plethora of phenomena and applications in chemistry, biochemistry, and biology, making life itself possible. Understanding the properties of lipid assemblies at the molecular level is essential to reveal their structures and functionalities. Far-IR spectroscopy is a powerful tool to characterize the intermolecular interactions and collective behaviour of lipid ensembles. However, due to the complexity of membrane behaviour, interpretation of the far-IR spectra remains a major challenge. In this study, we have addressed this challenge by using a molecular dynamics-based approach to reveal the vibrational modes of phospholipid molecules in separation and in an ensemble. The method is validated by demonstrating a good match to known high frequency IR bond vibrational modes. Our results also show good agreements between the peaks from the MD simulations and those from synchrotron far-IR measurements. For the far-IR spectra, our method allows for the identification of molecular motions responsible for each vibrational mode, thus underpinning the correct interpretation of membrane spectra with high accuracy and resolving the longstanding ambiguities that have hitherto prevailed in the literature. Our results demonstrate the feasibility of using MD simulations for interpreting far-IR spectra more broadly, opening new avenues for future use of this powerful method.

Author contributions

A. M. and K. J. H. conceptualized the work. C.-P. C. created the computational models and analysed the data, and A. D. carried out the experimental investigation. C.-P. C., A. M. and A. D. wrote the original draft. K. J. H. and A. M. reviewed and edited the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

K. J. H. acknowledges the financial support from the Ministry of Education, Singapore under its Academic Research Fund Tier 3 (Grant MOE-MOET32022-0002). The experiments were undertaken on the THz–Far infrared beamline at the Australian Synchrotron, part of the Australian Nuclear Science and Technology Organisation (ANSTO). A. D. and A. M. would like to acknowledge assistance from Dominique Appadoo, a beamline scientist of the THz beamline at the Australian Synchrotron.

References

1. K. B. Beć, J. Grabska and C. W. Huck, Biomolecular and bioanalytical applications of infrared spectroscopy – A review, Anal. Chim. Acta, 2020, 1133, 150–177.
2. S. S. Dhillon, M. S. Vitiello, E. H. Linfield, A. G. Davies, M. C. Hoffmann, J. Booske, C. Paoloni, M. Gensch, P. Weightman, G. P. Williams, E. Castro-Camus, D. R. S. Cumming, F. Simoens, I. Escorcia-Carranza, J. Grant, S. Lucyszyn, M. Kuwata-Gonokami, K. Konishi, M. Koch, C. A. Schmuttenmaer, T. L. Cocker, R. Huber, A. G. Markelz, Z. D. Taylor, V. P. Wallace, J. Axel Zeitler, J. Sibik, T. M. Korter, B. Ellison, S. Rea, P. Goldsmith, K. B. Cooper, R. Appleby, D. Pardo, P. G. Huggard, V. Krozer, H. Shams, M. Fice, C. Renaud, A. Seeds, A. Stöhr, M. Naftaly, N. Ridler, R. Clarke, J. E. Cunningham and M. B. Johnston, The 2017 terahertz science and technology roadmap, J. Phys. D: Appl. Phys., 2017, 50, 043001.
3. A. G. Davies, A. D. Burnett, W. Fan, E. H. Linfield and J. E. Cunningham, Terahertz spectroscopy of explosives and drugs, Mater. Today, 2008, 11, 18–26.
4. R. J. Falconer and A. G. Markelz, Terahertz spectroscopic analysis of peptides and proteins, J. Infrared, Millimeter, Terahertz Waves, 2012, 33, 973–988.
5. A. Hornemann, D. M. Eichert, A. Hoehl, B. Tiersch, G. Ulm, M. G. Ryadnov and B. Beckhoff, Investigating Membrane-Mediated Antimicrobial Peptide Interactions with Synchrotron Radiation Far-Infrared Spectroscopy, ChemPhysChem, 2022, 23, e2021008.
6. V. A. Bershtein and V. A. Ryzhov, Far infrared spectroscopy of polymers, Adv. Polym. Sci., 1994, 114, 42–121.
7. K. Müller-Dethlefs and P. Hobza, Noncovalent Interactions: A Challenge for Experiment and Theory, Chem. Rev., 2000, 100, 143–167.
8. R. Hielscher and P. Hellwig, The temperature-dependent hydrogen-bonding signature of lipids monitored in the far-infrared domain, ChemPhysChem, 2010, 11, 435–441.
9. G. D’Angelo, V. Conti Nibali, C. Crupi, S. Rifici, U. Wanderlingh, A. Paciaroni, F. Sacchetti and C. Branca, Probing Intermolecular Interactions in Phospholipid Bilayers by Far-Infrared Spectroscopy, J. Phys. Chem. B, 2017, 121, 1204–1210.
10. D. Lingwood and K. Simons, Lipid rafts as a membrane-organizing principle, Science, 2010, 327, 46–50.
11. I. Y. Hasan and A. Mechler, Analytical approaches to study domain formation in biomimetic membranes, Analyst, 2017, 142, 3062–3078.
12. S. Krishnamurty, M. Stefanov, T. Mineva, S. Bégu, J. M. Devoisselle, A. Goursot, R. Zhu and D. R. Salahub, Density functional theory-based conformational analysis of a phospholipid molecule (dimyristoyl phosphatidylcholine), J. Phys. Chem. B, 2008, 112, 13433–13442.
13. J. Yang, C. Calero and J. Martí, Diffusion and spectroscopy of water and lipids in fully hydrated dimyristoylphosphatidylcholine bilayer membranes, J. Chem. Phys., 2014, 140, 104901.
14. J. B. Brubach, A. Mermet, A. Filabozzi, A. Gerschel and P. Roy, Signatures of the hydrogen bonding in the infrared bands of water, J. Chem. Phys., 2005, 122, 184509.
15. M. C. Rheinstädter, C. Ollinger, G. Fragneto, F. Demmel and T. Salditt, Collective Dynamics of Lipid Membranes Studied by Inelastic Neutron Scattering, Phys. Rev. Lett., 2004, 93, 108107.
16. L. I. Maklakov and S. V. Aksakova, Low-frequency vibrational spectroscopy of amides and urethanes, Russ. Chem. Rev., 1997, 66, 375–388.
17. F. L. Jiang, I. Ikeda, Y. Ogawa and Y. Endo, Terahertz absorption spectra of fatty acids and their analogues, J. Oleo Sci., 2011, 60, 339–343.
18. C. Vogel-Weill and A. Gruger, Etude de la conformation des acides n-nonanoïque, Z et E-9 octadécénoïques à 90 K par spectromètrie infrarouge et Raman. Partie 1. Etude par spectromètrie de vibration de la conformation de l’acide n-nonanoïque à 90 K, Spectrochim. Acta, Part A, 1996, 52, 1297–1310.
19. C. Vogel-Weill and A. Gruger, Etude de la conformation des acides n-nonanoique, Z et E-9 octadecenoiques à 90 K par spectrométries infrarouge et Raman II – Etude de la conformation des chaines hydrocarbonées des acides Z et E-9 octadecenoiques à 90 K par spectrométrie infrarouge et Ra, Spectrochim. Acta, Part A, 1996, 52, 1737–1755.
20. K. Leberle, I. Kempf and G. Zundel, An intramolecular hydrogen bond with large proton polarizability within the head group of phosphatidylserine. An infrared investigation, Biophys. J., 1989, 55, 637–648.
21. Y. Choi, K. D. Jordan, Y. H. Paik, W. Chang and P. Dowd, Ab Initio Calculations of the Geometries and IR Spectra of Two Derivatives of Tetramethyleneethane, J. Am. Chem. Soc., 1988, 110, 7575–7576.
22. M. M. El-Nahass, M. A. Kamel, A. F. El-Deeb, A. A. Atta and S. Y. Huthaily, Ab initio HF, DFT and experimental (FT-IR) investigation of vibrational spectroscopy of P-N,N-dimethylaminobenzylidenemalononitrile (DBM), Spectrochim. Acta, Part A, 2011, 79, 443–450.
23. G. R. Medders and F. Paesani, Infrared and Raman spectroscopy of liquid water through ‘first-principles’ many-body molecular dynamics, J. Chem. Theory Comput., 2015, 11, 1145–1154.
24. M. A. Palafox, Computational chemistry applied to vibrational spectroscopy: a tool for characterization of nucleic acid bases and some of their 5-substituted derivatives, Phys. Sci. Rev., 2017, 2, 1–21.
25. T. D. Jaeger, D. Van Heijnsbergen, S. J. Klippenstein, G. Von Helden, G. Meijer and M. A. Duncan, Vibrational spectroscopy and density functional theory of transition-metal ion – Benzene and dibenzene complexes in the gas phase, J. Am. Chem. Soc., 2004, 126, 10981–10991.
26. J. Kubelka and T. A. Keiderling, Differentiation of β-sheet-forming structures: ab initio-based simulations of IR absorption and vibrational CD for model peptide and protein β-sheets, J. Am. Chem. Soc., 2001, 123, 12048–12058.
27. J. Clarkson and W. E. Smith, A DFT analysis of the vibrational spectra of nitrobenzene, J. Mol. Struct., 2003, 655, 413–422.
28. M. Karabacak, M. Cinar, Z. Unal and M. Kurt, FT-IR, UV spectroscopic and DFT quantum chemical study on the molecular conformation, vibrational and electronic transitions of 2-aminoterephthalic acid, J. Mol. Struct., 2010, 982, 22–27.
29. X. Wang and L. Andrews, Quantum-chemical calculations and IR spectra of the (F2)MF 2 molecules (M = B, Al, Ga, In, Tl) in solid matrices: a new class of very high electron affinity neutral molecules, J. Am. Chem. Soc., 2011, 133, 3768–3771.
30. A. Boukaoud, Y. Chiba and D. Sebbar, A periodic DFT study of IR spectra of amino acids: an approach toward a better understanding of the N–H and O–H stretching regions, Vib. Spectrosc., 2021, 116, 103280.
31. A. S. Reddy, D. T. Warshaviak and M. Chachisvilis, Effect of membrane tension on the physical properties of DOPC lipid bilayer membrane, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 2271–2281.
32. R. M. Venable, F. L. H. Brown and R. W. Pastor, Mechanical properties of lipid bilayers from molecular dynamics simulation, Chem. Phys. Lipids, 2015, 192, 60–74.
33. G. Shahane, W. Ding, M. Palaiokostas and M. Orsi, Physical properties of model biological lipid bilayers: insights from all-atom molecular dynamics simulations, J. Mol. Model., 2019, 25, 1–13.
34. S. O. Yesylevskyy, T. Rivel and C. Ramseyer, The influence of curvature on the properties of the plasma membrane. Insights from atomistic molecular dynamics simulations, Sci. Rep., 2017, 7, 16078.
35. C. P. Chng, Y. Sadovsky, K. J. Hsia and C. Huang, Curvature-regulated lipid membrane softening of nano-vesicles, Extrem. Mech. Lett., 2021, 43, 101174.
36. C. P. Chng, Y. Sadovsky, K. J. Hsia and C. Huang, Site-specific peroxidation modulates lipid bilayer mechanics, Extrem. Mech. Lett., 2021, 42, 101148.
37. B. Guillot, A molecular dynamics study of the far infrared spectrum of liquid water, J. Chem. Phys., 1991, 95, 1543–1551.
38. M. Praprotnik, D. Janežič and J. Mavri, Temperature dependence of water vibrational spectrum: a molecular dynamics simulation study, J. Phys. Chem. A, 2004, 108, 11056–11062.
39. T. Ishiyama, V. V. Sokolov and A. Morita, Molecular dynamics simulation of liquid methanol. I. Molecular modeling including C–H vibration and Fermi resonance, J. Chem. Phys., 2011, 134, 024509.
40. M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Computing vibrational spectra from ab initio molecular dynamics, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622.
41. J. Jeon, S. Yang, J. H. O. Choi and M. Cho, Computational vibrational spectroscopy of peptides and proteins in one and two dimensions, Acc. Chem. Res., 2009, 42, 1280–1289.
42. D. Semrouni, A. Sharma, J. P. Dognon, G. Ohanessian and C. Clavaguéra, Finite temperature infrared spectra from polarizable molecular dynamics simulations, J. Chem. Theory Comput., 2014, 10, 3190–3199.
43. S. Jo, T. Kim, V. G. Iyer and W. Im, CHARMM-GUI: a web-based graphical user Interface for CHARMM, J. Comput. Chem., 2008, 29, 1859–1865.
44. S. Jo, T. Kim and W. Im, Automated builder and database of protein/membrane complexes for molecular dynamics simulations, PLoS One, 2007, 2, e880.
45. S. Jo, J. B. Lim, J. B. Klauda and W. Im, CHARMM-GUI membrane builder for mixed bilayers and its application to yeast membranes, Biophys. J., 2009, 97, 50–58.
46. E. L. Wu, X. Cheng, S. Jo, H. Rui, K. C. Song, E. M. Dávila-Contreras, Y. Qi, J. Lee, V. Monje-Galvan, R. M. Venable, J. B. Klauda and W. Im, CHARMM-GUI membrane builder toward realistic biological membrane simulations, J. Comput. Chem., 2014, 35, 1997–2004.
47. J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong, Y. Qi, S. Jo, V. S. Pande, D. A. Case, C. L. Brooks, A. D. MacKerell, J. B. Klauda and W. Im, CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field, J. Chem. Theory Comput., 2016, 12, 405–413.
48. J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O’Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell and R. W. Pastor, Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types, J. Phys. Chem. B, 2010, 114, 7830–7843.
49. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1, 19–25.
50. A. G. Petrov, K. Gawrisch, G. Brezesinski, G. Klose and A. Mops, Optical detection of phase transitions in simple and mixed lipid–water phases, Biochim. Biophys. Acta, 1982, 690, 1–7.
51. K. Uppulury, P. S. Coppock and J. T. Kindt, Molecular Simulation of the DPPE Lipid Bilayer Gel Phase: Coupling between Molecular Packing Order and Tail Tilt Angle, J. Phys. Chem. B, 2015, 119, 8725–8733.
52. A. Amadei, A. B. M. Linssen and H. J. C. Berendsen, Essential dynamics of proteins, Proteins Struct. Funct. Bioinform., 1993, 17, 412–425.
53. A. Kitao, Principal component analysis and related methods for investigating the dynamics of biological macromolecules, J: Multidiscip. Sci. J., 2022, 5, 298–317.
54. Gromacs reference manual – Covariance analysis, https://manual.gromacs.org/2023.1/reference-manual/analysis/covariance-analysis.html, (accessed 26 November 2023).
55. R. Hielscher and P. Hellwig, Specific far infrared spectroscopic properties of phospholipids, Spectrosc., 2012, 27, 525–532.
56. IR spectroscopy tutorial: Alkanes, https://orgchemboulder.com/Spectroscopy/irtutor/alkanesir.shtml, (accessed 4 July 2023).
57. The infrared spectra of polymers, part I: Introduction, https://www.spectroscopyonline.com/view/the-infrared-spectra-of-polymers-part-i-introduction, (accessed 12 July 2023).
58. M. Patra, M. Karttunen, M. T. Hyvönen, E. Falck, P. Lindqvist and I. Vattulainen, Molecular dynamics simulations of lipid bilayers: major artifacts due to truncating electrostatic interactions, Biophys. J., 2003, 84, 3636–3645.
59. S. Leekumjorn and A. K. Sum, Molecular simulation study of structural and dynamic properties of mixed DPPC/DPPE bilayers, Biophys. J., 2006, 90, 3951–3965.

---

Footnote

† Electronic supplementary information (ESI) available: Workflow for calculation of the IR absorption spectrum of phospholipids from atomistic MD simulations. Calculated spectra showing the effect of increasing numbers of methyl groups on the DPPC lipid acyl chain. Calculated spectra from five DPPC or DMPC lipids in the bilayer to highlight the presence of the choline deformation peak. Table showing the effect of choline rigid body motion on the presence of the choline deformation peak. Movies showing molecular vibrations of a single DPPC lipid in water and in the bilayer taken from our MD simulations. Movies showing the trajectory of the DPPC lipid in water and in the bilayer filtered along the first three principal modes. See DOI: https://doi.org/10.1039/d4cp00521j

---