Big data benchmarking: how do DFT methods across the rungs of Jacob's ladder perform for a dataset of 122k CCSD(T) total atomization energies?†
Amir
Karton

School of Science and Technology, University of New England, Armidale, NSW 2351, Australia. E-mail: amir.karton@une.edu.au
First published on 13th May 2024
Abstract
Total atomization energies (TAEs) are a central quantity in density functional theory (DFT) benchmark studies. However, so far TAE databases obtained from experiment or high-level ab initio wavefunction theory included up to hundreds of TAEs. Here, we use the GDB-9 database of 133k CCSD(T) TAEs generated by Curtiss and co-workers [B. Narayanan, P. C. Redfern, R. S. Assary and L. A. Curtiss, Chem. Sci., 2019, 10, 7449] to evaluate the performance of 14 representative DFT methods across the rungs of Jacob's ladder (namely, PBE, BLYP, B97-D, M06-L, τ-HCTH, PBE0, B3LYP, B3PW91, ωB97X-D, τ-HCTHh, PW6B95, M06, M06-2X, and MN15). We first use the A25[PBE] diagnostic for nondynamical correlation to eliminate systems that potentially include significant multireference effects, for which the CCSD(T) TAEs might not be sufficiently reliable. The resulting database (denoted by GDB9-nonMR) includes 122k species. Of the considered functionals, B3LYP attains the best performance relative to the G4(MP2) reference TAEs, with a mean absolute deviation (MAD) of 4.09 kcal mol−1. This first-generation hybrid functional, in which the three mixing coefficients were fitted against a small set of TAEs, is one of the few functionals that are not systematically biased towards overestimating the G4(MP2) TAEs, as demonstrated by a mean-signed deviation (MSD) of 0.45 kcal mol−1. The relatively good performance of B3LYP is followed by the heavily parameterized M06-L meta-GGA functional, which attains a MAD of 6.24 kcal mol−1. The PW6B95, M06, M06-2X, and MN15 functionals tend to systematically overestimate the G4(MP2) TAEs and attain MADs ranging between 18.69 (M06) and 28.54 (MN15) kcal mol−1. However, PW6B95 and M06-2X exhibit particularly narrow error distributions. Thus, scaling their TAEs by an empirical scaling factor reduces their MADs to merely 3.38 (PW6B95) and 2.85 (M06-2X) kcal mol−1. Empirical dispersion corrections (e.g., D3 and D4) are attractive, and therefore, their inclusion worsens the performance of methods that systematically overestimate the TAEs.
Introduction
The total atomization energy (TAE) is the most fundamental thermodynamic property of a molecule, which captures the energetics of the molecular system. The calculation of TAEs is a major challenge for density functional theory (DFT) methods since it involves simultaneously breaking all the bonds in the molecule. Whereas typical bond dissociation energies (BDEs) range between 200–400 kcal mol−1, the TAEs for medium-sized species with ∼10 nonhydrogen atoms are typically one order of magnitude higher. Thus, whereas a 0.5% error in the BDE translates to 1–2 kcal mol−1, a 0.5% error in the TAE translates to 10–20 kcal mol−1. Consequently, TAEs are among the most challenging tests for approximate electronic structure methods.1–9 It should be mentioned that a successful approach for calculating TAEs using relatively low levels of theory is via thermochemical cycles in which the parent molecule is broken down into smaller fragments for which accurate TAEs are available from theory or experiment.10–19A number of databases of highly accurate theoretical TAEs have been generated over the past decade, for example, the W4-08,20 W4-11,21 and W4-1722 databases of TAEs calculated at the full configuration interaction (FCI) complete basis-set limit (CBS) via the Weizmann-n (Wn) composite ab initio methods.23–26 The most recent of these databases (W4-17) includes 200 TAEs for molecules with up to eight non-hydrogen atoms, which cover a broad spectrum of bonding situations, electronic states, and multireference character. However, a collection of a few hundred small molecules cannot possibly represent the chemical space of small organic and inorganic species. For example, although the W4-17 database includes alkenes, alkynes, haloalkenes, haloalkynes, arenes, aromatic heterocycles, nonaromatic heterocycles, alcohols, aldehydes, ketones, anhydrides, carboxylic acids, amines, imines, and nitriles; many of these classes include only 2–3 prototypical examples. In addition, there are only a few examples of (i) molecules combining several of these functional groups in the same molecule or (ii) complex chemical functionalities such as conjugation, hyperconjugation, aromaticity, and ring strain.
In a landmark study, Ramakrishnan et al.27 considered the GDB-9 subset of over 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules with up to nine nonhydrogen first-row atoms (i.e., composed of H, C, N, O, and F) from the much larger GDB-17 database with 166 billion organic molecules.36 All the structures in the GDB-9 database were fully optimized at the B3LYP/6-31G(2df,p) level of theory.28–30 Importantly, all structures were verified to be equilibrium structures on the potential energy surface (PES) by confirming they have all real harmonic frequencies. It should be noted that the B3LYP functional has been found to provide excellent performance for calculating equilibrium structures of organic molecules.31 Accordingly, B3LYP is used for optimizing the geometries in many high-level composite ab initio procedures, including the Gn, ccCA, and low-level Wn thermochemical protocols.32–34 A comprehensive overview of composite ab initio methods, including the Wn and Gn methods (n = 1–4), is given in ref. 1, 2, 32, and 33. Overall, this exhaustive database covers a significant portion of the chemical space of small drug-like molecules with up to nine first-row atoms.27 This work also refined the energies for a subset of 6095 C7H10O2 isomers using the G4(MP2) composite ab initio method.35,36
000 molecules with up to nine nonhydrogen first-row atoms (i.e., composed of H, C, N, O, and F) from the much larger GDB-17 database with 166 billion organic molecules.36 All the structures in the GDB-9 database were fully optimized at the B3LYP/6-31G(2df,p) level of theory.28–30 Importantly, all structures were verified to be equilibrium structures on the potential energy surface (PES) by confirming they have all real harmonic frequencies. It should be noted that the B3LYP functional has been found to provide excellent performance for calculating equilibrium structures of organic molecules.31 Accordingly, B3LYP is used for optimizing the geometries in many high-level composite ab initio procedures, including the Gn, ccCA, and low-level Wn thermochemical protocols.32–34 A comprehensive overview of composite ab initio methods, including the Wn and Gn methods (n = 1–4), is given in ref. 1, 2, 32, and 33. Overall, this exhaustive database covers a significant portion of the chemical space of small drug-like molecules with up to nine first-row atoms.27 This work also refined the energies for a subset of 6095 C7H10O2 isomers using the G4(MP2) composite ab initio method.35,36
In a tour de force follow-up study, Narayanan et al.37 calculated G4(MP2) energies for the species of the GDB-9 database. The G4(MP2) method is a computationally efficient composite ab initio procedure for obtaining highly accurate thermochemical properties for organic systems at the CCSD(T) level (coupled cluster with singles, doubles, and quasiperturbative triple excitations).38,39 Even for challenging thermochemical properties such as total atomization energies, the deviations between the CCSD(T) and full configuration interaction (FCI) method are typically below ∼1 kcal mol−1 for systems that are not dominated by strong multireference effects.1,2,33 G4(MP2) theory has been found to produce gas-phase thermochemical properties (such as reaction energies, bond dissociation energies, and enthalpies of formation) with a mean absolute deviation (MAD) of 1.0 kcal mol−1 from the experimental energies of the G3/05 test set.35 In addition, G4(MP2) theory has been found to produce accurate theoretical thermochemical properties with MADs below or around the threshold of chemical accuracy (i.e., ∼1.0 kcal mol−1), including bond dissociation, atomization, isomerization energies, and reaction barrier heights involving species which are not characterized by strong multireference effects.10,21,22,40–46 It should be emphasized that G4(MP2) theory is a computationally economical CCSD(T)-based composite ab initio method that calculates the CCSD(T) energy in conjunction with the small 6-31G(d) basis set and uses ΔE(MP2) and ΔE(HF) basis set correction terms calculated using triple-ζ and quadruple-ζ quality basis sets, respectively.32,35 As such G4(MP2) is applicable to systems as large as C60.47 However, to compensate for systematic deficiencies in the theoretical model (e.g., basis set incompleteness and core-valence corrections), G4(MP2) theory employs an empirical higher-level correction (HLC) term. Therefore, the G4(MP2) theory is not as robust as nonempirical CCSD(T)-based composite ab initio procedures such as W1 and W1-F12 theories,23,25 which are computationally more demanding (for recent reviews of composite ab initio procedures, see ref. 1, 2, 32, and 33).
The combination of the works of Ramakrishnan et al.27 and Narayanan et al.37 has generated an invaluable database of over 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CCSD(T) TAEs that could be used for the evaluation of approximate theoretical procedures and, in particular, DFT methods. As mentioned above, the largest databases of TAEs that have been used for this purpose in the past included only hundreds of TAEs,20–22,48 which cannot represent the same chemical space represented by over 130
000 CCSD(T) TAEs that could be used for the evaluation of approximate theoretical procedures and, in particular, DFT methods. As mentioned above, the largest databases of TAEs that have been used for this purpose in the past included only hundreds of TAEs,20–22,48 which cannot represent the same chemical space represented by over 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 species (for a comprehensive discussion of the chemical composition of the GDB-9 database, see ref. 27, 37, and 49). In the present work, we evaluate the performance of a representative set of DFT methods across rungs 2–4 of Jacob's ladder for their ability to reproduce the G4(MP2) total atomization energies in the GDB-9 database. This will enable us to provide insights into the following aspects of the benchmarking and performance of DFT methods:
000 species (for a comprehensive discussion of the chemical composition of the GDB-9 database, see ref. 27, 37, and 49). In the present work, we evaluate the performance of a representative set of DFT methods across rungs 2–4 of Jacob's ladder for their ability to reproduce the G4(MP2) total atomization energies in the GDB-9 database. This will enable us to provide insights into the following aspects of the benchmarking and performance of DFT methods:
• The performance of DFT methods for an extensive database of CCSD(T) TAEs that covers a large segment of the chemical space of small molecules.
• Does the performance of the considered DFT methods improve in the order GGA → MGGA → HGGA → HMGGA.
• Does the size of the database matter? The W4-17 database contains 200 TAEs (i.e., ∼0.15% of the number of species in the GDB-9 database). Can this small database capture the same trends as a database that covers a larger segment of the complete chemical space?
• How do empirical dispersion corrections (D3, D3BJ, and D4) affect the performance of the DFT methods for TAEs across a large database of organic molecules?
Computational details
We calculate the TAEs for the extensive set of molecules in the GDB-9 database with 14 representative DFT methods from rungs 2–4 of Jacob's ladder.50 All the DFT single-point energy (SPE) calculations were carried out in conjunction with the 6-31G(2df,p) basis set. Since the evaluation of each DFT method requires 122k SPE calculations (vide infra), we were only able to consider a handful of DFT methods. We, therefore, carefully choose the set of exchange–correlation (XC) functionals to be considered, including DFT methods that have been found to give relatively good performance for the TAEs in the W4-11 database.21 In particular, we consider the following XC functionals:• Rung 2: the generalized gradient approximation (GGA) methods BLYP,30,51 PBE,52 and B97-D53
• Rung 3: the meta-GGAs τ-HCTH54 and M06-L55
• Rung 3.5: the global hybrid GGAs B3LYP,28–30 B3PW91,28,56 PBE0,57 and the range-separated hybrid GGA ωB97X-D58
• Rung 4: the global hybrid-meta GGAs τ-HCTHh,54 PW6B95,59 M06,60 M06-2X,60 and MN1561
We note that we have confirmed that our B3LYP TAEs are consistent with the B3LYP/6-31G(2df,p) TAEs from ref. 27, e.g., the MAD between the two sets of TAEs amounts to 0.007 kcal mol−1, with no significant outliers.
DFT functionals from the fifth rung of Jacob's ladder are not considered since the G4(MP2) reference TAEs are not deemed sufficiently accurate for evaluating the performance of double-hybrid DFT methods.62 Empirical D3 and D4 dispersion corrections are also considered, where the D3 corrections are included using the finite Becke–Johnson (denoted by D3BJ) and zero damping (denoted by D3) potentials.63–68 All the DFT calculations were carried out with the Gaussian16 program suite.69 The default convergence criterion of 10−8 a.u. for the self-consistent field (SCF) iterations was used in conjunction with an ultrafine integration grid. For the atomic calculations, the unrestricted Kohn–Sham framework was used.
Results and discussion
Multireference considerations
It is well established that the CCSD(T) method cannot achieve chemical accuracy for TAEs of multireference systems.1–5,21,22,25,33 For example, for species characterized by moderate-to-severe multireference effects, the difference between the CCSD(T) and FCI TAE at the CBS limit amounts to 1.1 (ClF5, NO2), 1.2 (S3), 1.3 (N2O4), 1.4 (B2, ClNO), 1.7 (linear-C7), and 1.8 (F2O2, cis-HO3) kcal mol−1.1 Whereas for pathologically multireference systems, the CCSD(T)–FCI difference can exceed 2.0 kcal mol−1, for example, it is 2.4 (S4), 2.9 (O3), 3.0 (FO2), and 3.5 (ClO2) kcal mol−1.1 Therefore, before using reference CCSD(T) TAEs for benchmarking DFT methods, it is instructive to remove any potentially multireference systems from the data set. For this purpose, we use the TAE-based multireference diagnostic A25[PBE], which is readily calculated from our DFT computations as A25[PBE] = (1 − TAE[PBE0]/TAE[PBE])/0.25, where the factor 0.25 corresponds to the 25% of HF exchange involved in the PBE0 XC functional.70 The A25[PBE] diagnostic correlates well with the more robust %TAE[(T)] multireference diagnostic, which is the percentage of the TAE accounted for by parenthetical connected triple excitations.21,24,34,70,71 In addition, the A25[PBE] diagnostic has been found to provide a better correlation with the magnitude of post-CCSD(T) contributions than the popular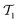 diagnostic.70 It has been shown that A25[PBE] values of 0.10% (or lower) indicate systems dominated by dynamical correlation effects; A25[PBE] values of about 0.15% indicate systems with mild nondynamical correlation effects; and A25[PBE] values of about 0.30% indicate moderate nondynamical correlation effects. Table S1 of the ESI† gives the A25[PBE] values for the species in the GDB-9 database. For half of the systems (49.8%), we obtain A25[PBE] < 0.10%, indicating that these systems are dominated by dynamical correlation effects. For another 42.1% of the species, we obtain A25[PBE] values between 0.10–0.15%, indicating mild nondynamical correlation effects. For 8.1% of the species, we obtain A25[PBE] values between 0.15–0.30%, and values above 0.3% are obtained for merely 0.03% of the species. These results indicate that the GDB-9 database is dominated by species with mild nondynamical correlation effects. To be on the safe side, however, we remove all systems with A25[PBE] > 0.15%. Importantly, only ∼8% of the species are removed, leaving us with a subset of species that is likely to include mostly non-multireference species but is still sufficiently large and diverse. The resulting database (denoted as GDB9-nonMR) includes 122
diagnostic.70 It has been shown that A25[PBE] values of 0.10% (or lower) indicate systems dominated by dynamical correlation effects; A25[PBE] values of about 0.15% indicate systems with mild nondynamical correlation effects; and A25[PBE] values of about 0.30% indicate moderate nondynamical correlation effects. Table S1 of the ESI† gives the A25[PBE] values for the species in the GDB-9 database. For half of the systems (49.8%), we obtain A25[PBE] < 0.10%, indicating that these systems are dominated by dynamical correlation effects. For another 42.1% of the species, we obtain A25[PBE] values between 0.10–0.15%, indicating mild nondynamical correlation effects. For 8.1% of the species, we obtain A25[PBE] values between 0.15–0.30%, and values above 0.3% are obtained for merely 0.03% of the species. These results indicate that the GDB-9 database is dominated by species with mild nondynamical correlation effects. To be on the safe side, however, we remove all systems with A25[PBE] > 0.15%. Importantly, only ∼8% of the species are removed, leaving us with a subset of species that is likely to include mostly non-multireference species but is still sufficiently large and diverse. The resulting database (denoted as GDB9-nonMR) includes 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 476 species. This extensive database is used to evaluate the performance of a representative set of DFT exchange–correlation functionals in predicting G4(MP2) total atomization energies.
476 species. This extensive database is used to evaluate the performance of a representative set of DFT exchange–correlation functionals in predicting G4(MP2) total atomization energies.
Statistical analysis
Both the mean absolute deviation (MAD) and root-mean-square deviation (RMSD) have been extensively used for gauging the accuracy of DFT methods and other approximate quantum chemical methods. Each of these error statistics has its own strengths and weaknesses. The MAD is a simple and robust measure of the average absolute difference between predictions and reference values. However, it can downplay large errors, potentially masking significant discrepancies. As noted by Ruscic,72 for a normal distribution, the MAD is smaller than the 95% confidence interval by a factor of 2.5–3.5 depending on the distribution. The RMSD, on the other hand, amplifies larger errors, providing a more sensitive measure of outliers. However, the sensitivity of the RMSD to outliers can also be misleading since a few large outliers can result in an RMSD that significantly overestimates the average deviations. Therefore, in this work, we report both the MAD and RMSD. We note that in the present work, using either the MAD or the RMSD leads to a very similar ranking of the best and worst DFT functionals.Another useful statistical measure is the MAD/RMSD ratio.21 For a normal distribution, with no systematic errors, this ratio is 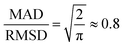 .73,74 Thus, when this ratio approaches 0.8, it indicates a small systematic error for a purely Gaussian error distribution. However, error distributions for which this ratio approaches unity are expected to have a large systematic error across the dataset. Finally, the mean-signed deviation (MSD) is also a very useful statistical measure for detecting systematic bias, i.e., whether the predicted values are consistently overestimating or underestimating the reference values. In particular, MSD ≈ MAD indicates systematic overestimation, whilst MSD ≈ −1 × MAD indicates systematic underestimation. However, it should be emphasized that while MSD ≈ ±1 × MAD confirms the presence of a systematic bias, a near-zero MSD does not necessarily imply that systematic errors do not exist. Therefore, it is useful to consider both the MSD and the MAD/RMSD ratio for identifying systematic biases.
.73,74 Thus, when this ratio approaches 0.8, it indicates a small systematic error for a purely Gaussian error distribution. However, error distributions for which this ratio approaches unity are expected to have a large systematic error across the dataset. Finally, the mean-signed deviation (MSD) is also a very useful statistical measure for detecting systematic bias, i.e., whether the predicted values are consistently overestimating or underestimating the reference values. In particular, MSD ≈ MAD indicates systematic overestimation, whilst MSD ≈ −1 × MAD indicates systematic underestimation. However, it should be emphasized that while MSD ≈ ±1 × MAD confirms the presence of a systematic bias, a near-zero MSD does not necessarily imply that systematic errors do not exist. Therefore, it is useful to consider both the MSD and the MAD/RMSD ratio for identifying systematic biases.
Overview of the CCSD(T) reference TAEs in the GDB9-nonMR database
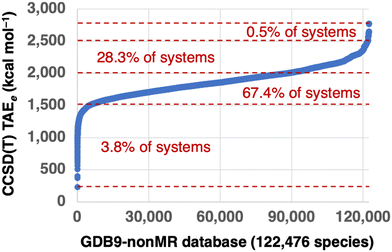
All the G4(MP2) reference TAEs are taken from ref. 37. To ensure we are comparing apples to apples, we will compare bottom-of-the-well CCSD(T) TAEs (TAEe) from G4(MP2) theory with TAEe values obtained for the various DFT methods. Therefore, zero-point vibrational energies (ZPVEs) are not included in the G4(MP2) reference values. Fig. 1 gives an overview of the electronic G4(MP2) TAEs. The G4(MP2) TAEs exhibit a logit-shaped distribution, with sharper variations in the TAEs of the most and least energetic species and a very shallow region in between with much smaller variations in the TAEs. Only 3.8% of the molecules in the GDB-9 database are associated with TAEs below 1500 kcal mol−1. The species associated with the lowest TAEs are small molecules such as water, hydrogen cyanide, formaldehyde, acetylene, carbon tetrafluoride, cyanogen, and methanol. The lion's share of the molecules in the GDB9-nonMR database (95.7%) are associated with TAEs between 1500.0 and 2500.0 kcal mol−1. Whereas 0.5% of the systems are associated with TAEs between 2500.0 and 2777.8 kcal mol−1. For comparison, the W4-17 database of 200 TAEs includes mostly TAEs below 1000 kcal mol−1, with only 11 TAEs ranging between 1000–1600 kcal mol−1.22Table 1 gives an overview of the molecular size and elemental distribution in the GDB9-nonMR database. Inspection of these results reveals that practically all species contain at least one carbon atom, 59% of the species contain at least one nitrogen, 85% of the species contain at least one oxygen, and 0.9% of the species contain at least one fluorine atom. The species in the GDB9-nonMR database contain up to 9 carbon, 5 nitrogen, 4 oxygen, and 3 fluorine atoms. As might be expected, the largest TAEs in the database correspond to saturated aliphatic hydrocarbons. Of these, the C9H20 alkanes are associated with the largest TAEs ranging between 2770.9 (3-ethyl-2,4-dimethylpentane) and 2777.8 (2,2,5-trimethylhexane) kcal mol−1. Then there is a gap of 116.4 kcal mol−1 in the TAEs, which is visible in the top right corner of Fig. 1. This gap is followed by the TAEs of C9H18 monocyclic saturated hydrocarbons, which range between 2620.9 (2-tert-butyl,1,3-dimethylcyclopropane) and 2654.5 (1,3,5-trimethylcyclohexane) kcal mol−1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 476 species in the GDB9-nonMR dataset. The tabulated values are the number of species containing a certain number of each element; for example, the second column provides the number of species with 1–9 carbon atoms
476 species in the GDB9-nonMR dataset. The tabulated values are the number of species containing a certain number of each element; for example, the second column provides the number of species with 1–9 carbon atoms
| # of atoms | C | N | O | F |
|---|---|---|---|---|
| 1 | 4 | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 907 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 898 898 |
713 |
| 2 | 19 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 143 143 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 068 068 |
69 |
| 3 | 285 | 6878 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 322 322 |
330 |
| 4 | 3405 | 1504 | 829 | 0 |
| 5 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 808 808 |
145 | 0 | 0 |
| 6 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 136 136 |
0 | 0 | 0 |
| 7 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 079 079 |
0 | 0 | 0 |
| 8 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 010 010 |
0 | 0 | 0 |
| 9 | 3729 | 0 | 0 | 0 |
Performance of DFT methods for describing the TAEs in the GDB9-nonMR database (122k species)
Table 2 summarizes the error statistics for a representative set of DFT methods across rungs 2–4 of Jacob's ladder. Namely, BLYP, PBE, and B97-D (rung 2), τ-HCTH and M06-L (rung 3), B3LYP, B3PW91, PBE0, and ωB97X-D (rung 3.5), and τ-HCTHhyb, PW6B95, M06, M06-2X, and MN15 (rung 4). Before proceeding to a detailed discussion of the performance of the DFT methods, we note the following general observations:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 476 total atomization energies in the GDB9-nonMR dataset (error statistics are given in kcal mol−1)a
476 total atomization energies in the GDB9-nonMR dataset (error statistics are given in kcal mol−1)a
| RMSD | MAD | MSD | MAD/RMSD | SD | #ND (LND) | #PD (LPD) | #LPD | |
|---|---|---|---|---|---|---|---|---|
| a RMSD = root-mean-square deviation, MAD = mean-absolute deviation, MSD = mean-signed deviation, SD = standard deviation, #ND = total number of negative deviations, LND = largest negative deviation in parentheses, #PD = total number of positive deviations, LPD = largest positive deviation in parentheses, #LPD = number of positive deviations exceeding the MAD. | ||||||||
| PBE | 79.70 | 79.22 | 79.22 | 0.99 | 8.80 | 1 (−2.30) | 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 475 (106.94) 475 (106.94) |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815 815 |
| BLYP | 11.89 | 9.59 | 2.52 | 0.81 | 11.62 | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085 (−30.03) 085 (−30.03) |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 391 (38.99) 391 (38.99) |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 485 |
| B97-D | 9.05 | 8.03 | 7.86 | 0.89 | 4.48 | 5453 (−16.56) | 117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 023 (29.53) 023 (29.53) |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 270 |
| M06-L | 7.62 | 6.24 | 4.99 | 0.82 | 5.76 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972 (−18.64) 972 (−18.64) |
98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 (35.30) 504 (35.30) |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 317 317 |
| τ-HCTH | 8.56 | 7.29 | 6.87 | 0.85 | 5.09 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288 (−16.36) 288 (−16.36) |
112![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 188 (38.05) 188 (38.05) |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 270 |
| PBE0 | 32.29 | 31.79 | 31.79 | 0.98 | 5.66 | 4 (−8.86) | 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472 (50.82) 472 (50.82) |
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 595 595 |
| B3LYP | 5.16 | 4.09 | 0.45 | 0.79 | 5.14 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 (−27.73) 780 (−27.73) |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 696 (21.48) 696 (21.48) |
51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 629 629 |
| B3PW91 | 17.43 | 16.94 | 16.94 | 0.97 | 4.10 | 9 (−6.87) | 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 (30.18) 467 (30.18) |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185 185 |
| ωB97X-D | 15.87 | 15.31 | 15.30 | 0.96 | 4.24 | 323 (−15.16) | 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 153 (27.15) 153 (27.15) |
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 896 896 |
| τ-HCTHh | 11.11 | 9.87 | 9.81 | 0.89 | 5.22 | 2561 (−8.16) | 119![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 915 (32.88) 915 (32.88) |
69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 679 679 |
| PW6B95 | 22.67 | 22.34 | 22.34 | 0.99 | 3.83 | 2 (−6.00) | 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 474 (35.37) 474 (35.37) |
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 961 961 |
| M06 | 19.20 | 18.69 | 18.69 | 0.97 | 4.39 | 13 (−6.77) | 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 463 (39.22) 463 (39.22) |
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 918 918 |
| M06-2X | 19.68 | 19.41 | 19.41 | 0.99 | 3.24 | 6 (−14.20) | 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 470 (34.84) 470 (34.84) |
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 881 881 |
| MN15 | 29.08 | 28.54 | 28.54 | 0.98 | 5.59 | 3 (−3.62) | 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 473 (49.13) 473 (49.13) |
62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 819 819 |
• The RMSDs and MADs spread over a very wide energetic window. Namely, the RMSDs range between 5.16 (B3LYP) and 79.70 (PBE), and the MADs range between 4.09 (B3LYP) and 79.22 (PBE)
• Most of the functionals tend to systematically overestimate the CCSD(T) TAEs, as indicated by MSD ≈ MAD. Notable exceptions are BLYP, M06-L, and B3LYP.
• Hybrid GGA methods (B3LYP and PBE0) outperform their GGA counterparts (BLYP and PBE). However, surprisingly, the considered HMGGA functionals show poor performance relative to their counterparts from the lower rungs (e.g., M06 and M06-2X relative to M06-L and τ-HCTHh relative to τ-HCTH)
Let us begin by examining the performance of the GGA methods BLYP, PBE, and B97-D. Of these, the moderately parameterized, dispersion-corrected B97-D functional gives the best performance with an RMSD of 9.05 and a MAD of 8.03 kcal mol−1. Consistent with previous benchmark studies for TAEs,20,21,75,76 the nonempirical PBE functional shows exceptionally poor performance with RMSD ≈ MAD ≈ 80 kcal mol−1. Table 2 lists the total number of positive and negative deviations – for PBE, all deviations but one are positive. Table 2 also lists the number of deviations that are larger than the MAD (denoted by #LPD). For PBE, there are as many as 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815 such deviations. Thus, PBE systematically and severely overestimates the TAEs, as also evidenced by MSD = MAD = 79.22 kcal mol−1 and MAD/RMSD = 0.99. This systematic and severe overbending is already apparent from examining much smaller and less diverse databases. For example, for the set of linear and branched alkanes with up to eight carbon atoms,40 PBE attains an RMSD of 13.7 and a MAD = MSD = 12.7 kcal mol−1. For the 140 TAEs in the W4-11 database,21 PBE attains similar error statistics, namely, RMSD = 16.9 kcal mol−1, MAD = 13.8, and MSD = 12.5 kcal mol−1. However, the increase of these RMSDs and MADs by nearly an order of magnitude for the GDB9-nonMR database is indeed unexpected. These results demonstrate the dramatic changes in the results obtained for some DFT methods (vide infra) when benchmarking against small databases with dozens or hundreds of TAEs compared with a database with over 120
815 such deviations. Thus, PBE systematically and severely overestimates the TAEs, as also evidenced by MSD = MAD = 79.22 kcal mol−1 and MAD/RMSD = 0.99. This systematic and severe overbending is already apparent from examining much smaller and less diverse databases. For example, for the set of linear and branched alkanes with up to eight carbon atoms,40 PBE attains an RMSD of 13.7 and a MAD = MSD = 12.7 kcal mol−1. For the 140 TAEs in the W4-11 database,21 PBE attains similar error statistics, namely, RMSD = 16.9 kcal mol−1, MAD = 13.8, and MSD = 12.5 kcal mol−1. However, the increase of these RMSDs and MADs by nearly an order of magnitude for the GDB9-nonMR database is indeed unexpected. These results demonstrate the dramatic changes in the results obtained for some DFT methods (vide infra) when benchmarking against small databases with dozens or hundreds of TAEs compared with a database with over 120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 TAEs that covers a larger segment of the chemical space. The lightly empirical GGA BLYP functional performs much better than PBE, with an RMSD = 11.89 and MAD = 9.59 kcal mol−1. Notably, BLYP is one of the few functionals that does not systematically overestimate the CCSD(T) TAEs, for example, the MSD of 2.52 kcal mol−1 is smaller than the MAD (9.59 kcal mol−1). BLYP has ∼53
000 TAEs that covers a larger segment of the chemical space. The lightly empirical GGA BLYP functional performs much better than PBE, with an RMSD = 11.89 and MAD = 9.59 kcal mol−1. Notably, BLYP is one of the few functionals that does not systematically overestimate the CCSD(T) TAEs, for example, the MSD of 2.52 kcal mol−1 is smaller than the MAD (9.59 kcal mol−1). BLYP has ∼53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 negative deviations vs. ∼69
000 negative deviations vs. ∼69![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 positive deviations. In addition, an RMSD/MAD ratio of 0.81 suggests a reasonable Gaussian distribution of the deviations. The number of positive deviations larger than the MAD (33
000 positive deviations. In addition, an RMSD/MAD ratio of 0.81 suggests a reasonable Gaussian distribution of the deviations. The number of positive deviations larger than the MAD (33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485) is much smaller than for PBE (62
485) is much smaller than for PBE (62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185) and B97-D (61
185) and B97-D (61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270). Similarly to the number of positive deviations larger than the MAD, we can calculate the number of negative deviations that are smaller than −1 × MAD. For BLYP, there are as many as 19
270). Similarly to the number of positive deviations larger than the MAD, we can calculate the number of negative deviations that are smaller than −1 × MAD. For BLYP, there are as many as 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 255 such deviations. These results are illustrated in the error distribution depicted in Fig. 2. It is also apparent that BLYP exhibits a very wide error distribution with a standard deviation of 11.62 kcal mol−1, compared with 8.80 (PBE) and 4.48 (B97-D) kcal mol−1.
255 such deviations. These results are illustrated in the error distribution depicted in Fig. 2. It is also apparent that BLYP exhibits a very wide error distribution with a standard deviation of 11.62 kcal mol−1, compared with 8.80 (PBE) and 4.48 (B97-D) kcal mol−1.
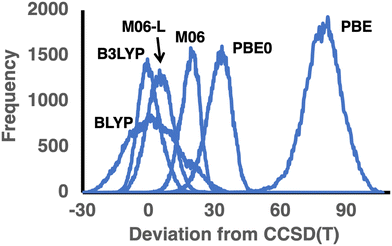 | ||
| Fig. 2 Distribution of deviations between the DFT and CCSD(T) TAEs (in kcal mol−1) in the GDB9-nonMR database for three functional pairs BLYP/B3LYP, PBE/PBE0, and M06-L/M06 (see Table 2 for error statistics; for the error distribution of all functionals, see Fig. S1 of the ESI†). | ||
Let us move on to the hybrid GGA counterparts of PBE and BLYP. The inclusion of exact exchange in the functional form reduces the RMSDs and MADs by ∼60% for both functionals. Adding 25% of exact exchange in PBE0 reduces the RMSD from 79.7 to 32.29 kcal mol−1, and a similar reduction is observed for the MAD. The inclusion of 20% exact exchange in B3LYP results in an equally dramatic reduction in the RMSD from 11.89 to 5.16 kcal mol−1 and a similar reduction in the MAD from 9.59 to 4.09 kcal mol−1. However, whilst PBE0 still severely and systematically overestimates the TAEs, as evidenced by practically no negative deviations and MAD = MSD = 31.79 kcal mol−1, B3LYP shows a balanced performance with a near-zero MSD and a near-perfect MAD/RMSD ratio for a Gaussian distribution of 0.79 (see Table 2 and Fig. 2). Furthermore, B3LYP is the only functional that exhibits nearly equal amounts of ∼61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 positive and negative deviations (Table 2).
000 positive and negative deviations (Table 2).
Overall, B3LYP is the best-performing DFT functional considered here. To put the MAD = 4.09 and RMSD = 5.16 kcal mol−1 into perspective, the average TAE in the GDB9-nonMR database is 1878.9 kcal mol−1 (with TAEs reaching up to 2777.8 kcal mol−1, Fig. 1). Thus, a MAD of 4.09 kcal mol−1 represents an error of merely 0.2% of the average TAE. This result illustrates that this first-generation HGGA functional, which includes only three mixing coefficients fitted against a small set of atomization energies, ionization potentials, and proton affinities, can outperform next-generation functionals. Most of the more modern HGGA and HMGGA employ more parameters and were parameterized against broader datasets covering thermochemistry, kinetics, and noncovalent interactions. Replacing the LYP correlation functional in B3LYP with PW91 results in a significant deterioration in performance and a severe tendency for overbinding, as demonstrated by MAD = MSD = 16.94 kcal mol−1. This is also demonstrated by the remarkable drop in the number of negative deviations from 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 780 (B3LYP) to 9 (B3PW91). These results confirm the important role that the LYP correlation functional, which is rooted in the Colle–Salvetti correlation-energy formula,77 for obtaining good overall performance for thermochemistry.20,78
780 (B3LYP) to 9 (B3PW91). These results confirm the important role that the LYP correlation functional, which is rooted in the Colle–Salvetti correlation-energy formula,77 for obtaining good overall performance for thermochemistry.20,78
Even though B3LYP turns out to be the best performer overall relative to the G4(MP2) TAEs in the GDB9-nonMR database, it still has its share of problems, documented in the literature,10,20,21,24,79,80 but also visible in our results. It is therefore important to highlight some of the challenges that B3LYP experiences for specific categories of TAEs. B3LYP has been found to perform poorly for TAEs of pseudo-hypervalent and polarly bound systems (mostly containing both first- and second-row elements).20,21 For example, deviations larger than 16 kcal mol−1 have been observed for TAEs obtained from W4 theory24 for systems such as HClO4, SF6, PF5, SiF4, and SO3. Purely first-row systems with significant deviations ranging between 6–10 kcal mol−1 include perfluoro compounds such as BF4 and CF4,20,21 as well as fluorine oxides.79 It was also found that B3LYP tends to underbind the TAEs of linear alkanes,80 however, this deficiency is partly remedied by the inclusion of an empirical dispersion correction.40 Yet, even with the inclusion of the empirical D3BJ dispersion correction B3LYP-D3BJ performs poorly for TAEs of strained (CH)n polycyclic hydrocarbon cages (e.g., tetrahedrane, triprismane, cubane, pentaprismane, octahedrane, and dodecahedrane), see ref. 10 for further details. Examining the error statistics for subsets of the GDB9-nonMR database, we can identify an increase in the RMSD for saturated hydrocarbons with an increasing number of cyclic rings. For example, we obtain the following RMSDs for saturated hydrocarbons with nine carbons 1.9 (one ring), 3.1 (two rings), 5.5 (three rings), and 8.2 (four rings) kcal mol−1. Furthermore, as is the case of other functionals (vide infra), B3LYP attains poor performance for the subset of 145 TAEs involving five nitrogens (RMSD = 17.5) and 330 TAEs involving three fluorine atoms (RMSD = 28.8 kcal mol−1).
We also consider here the long-range corrected ωB97X-D method, which includes about 22% of exact exchange for the short-range and 100% exact exchange for long-range interactions. ωB97X-D performs better than the global hybrids PBE0 and B3PW91. However, all three functionals suffer from a systematic tendency to overbind, as demonstrated by MAD = MSD and MAD/RMSD ratios of 0.96–0.98 (Table 2). Similarly to PBE0 and B3PW91, ωB97X-D has practically no negative deviations. Thus, the only hybrid functional that does not suffer from systematic overbinding is B3LYP.
Let us examine the performance of the two meta-GGA methods, which include the kinetic energy density – τ-HCTH and M06-L. These empirical XC functionals can be considered moderately and heavily parameterized, respectively. M06-L includes 39 empirical parameters and was parameterized against an extensive set of energetic data covering main-group thermochemistry, thermochemical kinetics, transition-metal chemistry, and noncovalent interactions. The thermochemistry subset included 109 TAEs for main-group compounds.81 τ-HCTH includes 16 empirical parameters, which were parameterized against an extensive set of thermochemical data, including atomic energies, TAEs of neutral and charged species, ionization potentials, electron affinities, and hydrogen bond energies. Both M06-L and τ-HCTH show relatively good performance for the 122k TAEs in the GDB9-nonMR database. Both methods tend to systematically overestimate the CCSD(T) TAEs, however, not as severely as the GGA methods PBE and B97-D. This is evidenced by MSD < MAD and MAD/RMSD ratios of 0.82 (M06-L) and 0.85 (τ-HCTH), and a nonnegligible number of negative deviations 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972 (M06-L) and 10
972 (M06-L) and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288 (τ-HCTH) (Table 2). Overall, both methods result in respectable RMSDs of 7.62 (M06-L) and 8.56 (τ-HCTH) kcal mol−1, and MADs of 6.24 (M06-L) and 7.29 (τ-HCTH) kcal mol−1. Thus, the heavily parameterized M06-L method has a visible edge over τ-HCTH.
288 (τ-HCTH) (Table 2). Overall, both methods result in respectable RMSDs of 7.62 (M06-L) and 8.56 (τ-HCTH) kcal mol−1, and MADs of 6.24 (M06-L) and 7.29 (τ-HCTH) kcal mol−1. Thus, the heavily parameterized M06-L method has a visible edge over τ-HCTH.
Somewhat surprisingly, moving from the meta-GGAs M06-L and τ-HCTH to their hybrid-meta GGA counterparts, M06 and τ-HCTHhyb, results in a deterioration in performance and an enhanced tendency for overbinding. The deterioration in performance is much more pronounced for M06 than for τ-HCTHhyb. The RMSD and MAD for M06 are 19.20 and 18.69 kcal mol−1, respectively. These values are nearly three times higher than for M06-L. The deterioration in performance for τ-HCTHh relative to τ-HCTH is not as significant, but still visible (Table 2). We note that for both M06 and τ-HCTHh we obtain MAD ≈ MSD and MAD/RMSD ratios that indicate systematic errors across the dataset. However, while M06 has practically no negative deviations, τ-HCTHh has ∼2% (or 2561) negative deviations. The deteriorated performance of M06 relative to τ-HCTHh could be related to the significantly higher percentage of exact exchange included in M06 (27%) relative to τ-HCTHh (15%). However, moving from M06 to M06-2X with 54% of exact exchange leads only to a small deterioration in performance relative to M06. Namely, M06-2X attains RMSD and MAD of 19.68 and 19.41 kcal mol−1, respectively.
We also consider here the lightly parametrized PW6B95 hybrid-meta-GGA method with 28% of exact exchange and the heavily parameterized MN15 with 44% of exact exchange. We note that PW6B95 shows good performance for the 121 TAEs in the W4-11-nonMR database (namely, RMSD and MAD of 2.5 and 1.8 kcal mol−1, respectively). Nevertheless, PW6B95 results in rather disappointing RMSD and MAD values for the much larger GDB9-nonMR database that are nearly an order of magnitude larger (Table 2). MN15 results in the worst performance of the considered hybrid-meta-GGAs with MAD, RMSD, and MSD of ∼29.0 kcal mol−1. All the Minnesota functionals (M06, M06-2X, and MN15) and PW6B95 suffer from systematic overbinding as demonstrated from MAD = RMSD and positive deviations reaching up to 49.13 kcal mol−1 for MN15 (Table 2). Overall, τ-HCTHh shows better performance than the other HMGGA functionals (PW6B95, M06, M06-2X, and MN15). This could be attributed to the former being paramatrized against the HCTH/407 dataset, which is dominated by thermochemical properties. In contrast, PW6B95, M06, M06-2X, and MN15 were trained using more diverse databases, including thermochemistry, transition-metal chemistry, thermochemical kinetics, and noncovalent interactions.
Inspection of the standard deviations in Table 2 reveals that although PW6B95 and M06-2X tend to systematically overestimate the G4(MP2) TAEs, they exhibit particularly low standard deviations of 3.83 and 3.24 kcal mol−1, respectively. For comparison, the standard deviation for B3LYP is 5.14 kcal mol−1. Therefore, it is worthwhile exploring the possibility of eliminating the systematic bias of PW6B95 and M06-2X by empirical scaling. Scaling the PW6B95 and M06-2X TAEs by a single empirical scaling factor optimized to minimize the RMSDs, reduces the RMSD for PW6B95 from 22.67 to 4.20 and for M06-2X from 19.68 to merely 3.60 kcal mol−1. The optimal scaling factors are 0.9884 (PW6B95) and 0.9899 (M06-2X).
Basis set effects
It is well established that TAEs exhibit a significant basis set dependency.21,22,26,75 The error statistics reported in Table 2 reflect the performance of the DFT methods in conjunction with the relatively small 6-31G(2df,p) basis set. Considering the size of the GDB9-nonMR database, evaluating the performance of the DFT methods in conjunction with a larger basis set is beyond the computational resources currently available to us. However, it is of interest to examine the basis set effect for the smaller W4-17* database. The W4-17* dataset is simply the original W4-17 set without the highly multireference and second-row systems (a more comprehensive description of the W4-17* dataset is provided in the next section). These multireference and second-row systems are eliminated to enable a more straightforward comparison to the GDB9-nonMR dataset. Table S2 of the ESI† gives the error statistics for the W4-17* database for the considered DFT functionals calculated in conjunction with the 6-31G(2df,p) and aug′-pc3 basis sets.82 The later basis set is a large quadruple-ζ-quality basis set, which was optimized for DFT calculations (we have chosen this basis set since it was used for evaluating the performance of the DFT methods for the W4-11 database).21 Inspection of Table S2 (ESI†) reveals that the performance of all functionals deteriorates when moving from the aug′-pc3 basis set to the smaller 6-31G(2df,p) basis set. However, the degree of deterioration can change drastically between different functionals. Particularly large deteriorations in performance where the RMSD for the W4-17* database nearly triples when moving from the aug′-pc3 to the 6-31G(2df,p) basis set are observed for PW6B95, M06-2X, and ωB97X-D. Cases where the RMSD doubles include MN15, M06, B3PW91, PBE0, τ-HCTH, B97-D, and τ-HCTHhyb. It is reasonable to assume that the basis set effect will become more pronounced for the much larger GDB9-nonMR database, which includes larger and more complex systems with more demanding basis set requirements. Thus, the large RMSDs obtained for these functionals in Table 2 are partly attributed to their stronger basis set dependency. This is particularly important for the three functionals that exhibit the strongest basis set dependencies (PW6B95, M06-2X, and ωB97X-D). On the other hand, PBE, BLYP, B3LYP, and M06-L exhibit a less pronounced basis set dependency; namely, the RMSD increases by a factor of 1.1–1.2 when moving from the aug′-pc3 to the 6-31G(2df,p) basis set.Comparing the performance of DFT for the TAEs in the GDB9-nonMR and W4-17* databases
There has been a discussion in the literature around the ability of relatively small databases to represent larger ones.83–85 In the context of the present work, it is important to highlight that the W4-17* database includes a range of organic species with up to six non-hydrogen atoms; however, it is not a derivative of the GDB9-nonMR database.22 To ensure the comparison between the performance of DFT methods for the GDB9-nonMR and W4-17 databases is made on an even keel, we consider a modified version of the W4-17 database in which multireference and second-row species have been removed. This results in a subset of 121 TAEs for first-row systems, which are listed in Table S3 of the ESI† (we will denote this subset of the W4-17 database as W4-17*). The systems in the W4-17* database cover a broad spectrum of bonding situations and functional groups (for a comprehensive description of all the species in the W4-17* database, see ref. 22 and 31). However, the W4-17* database contains smaller and less diverse systems than the GDB9-nonMR database. Finally, we note that the reference TAEs in the W4-17* database are zero-point exclusive, all-electron, nonrelativistic, clamped-nuclei TAEs calculated close to the FCI/CBS limit.22 Thus, these two databases represent two extreme cases: the W4-17* database is highly accurate but small (i.e., 121 TAEs of small systems obtained at the FCI/CBS level of theory via W4 theory) and the GDB9-nonMR database is moderately accurate but exceptionally large and diverse (i.e., 122k TAEs of medium-sized systems obtained at the CCSD(T)/TZ level of theory via G4(MP2) theory).Table 3 summarizes the error statistics for the considered DFT methods for the W4-17* database. The GGA methods PBE and BLYP perform poorly for the W4-17* database with RMSDs of 29.59 and 14.36 kcal mol−1, respectively. As expected and consistent with the results for the GDB9-nonMR database, the inclusion of exact exchange significantly improves the performance. Namely, the PBE0 and B3LYP methods attain RMSDs of 9.17 and 4.84 kcal mol−1, respectively. Again, consistent with the results for the GDB9-nonMR database, replacing the LYP correlation functional in B3LYP with PW91 results in deteriorated performance with an RMSD of 6.73 kcal mol−1. The meta-GGA methods perform significantly better than the GGA methods. Of the hybrid-meta GGA methods, M06-2X shows the best performance with an RMSD of 6.80 kcal mol−1. Followed by τ-HCTHh and PW6B95 with RMSDs of ∼8 kcal mol−1. This is in contrast to the results for the GDB9-nonMR database in which τ-HCTHh outperforms the other hybrid-meta GGA methods.
| RMSD | MAD | MSD | MAD/RMSD | #ND (LND) | #PD (LPD) | #LPD | |
|---|---|---|---|---|---|---|---|
| a The reference values are obtained at the FCI/CBS level of theory from W4 (or higher) theory. RMSD = root-mean-square deviation, MAD = mean-absolute deviation, MSD = mean-signed deviation, #ND = total number of negative deviations, LND = largest negative deviation in parentheses, #PD = total number of positive deviations, LPD = largest positive deviation in parentheses, #LPD = number of positive deviations exceeding the MAD. | |||||||
| PBE | 29.59 | 24.77 | 24.51 | 0.84 | 5 (−4.52) | 116 (99.8) | 55 |
| BLYP | 14.36 | 10.29 | 8.99 | 0.72 | 28 (−10.36) | 93 (64.4) | 46 |
| B97-D | 9.11 | 6.80 | 6.26 | 0.75 | 11 (−12.86) | 110 (39.24) | 44 |
| M06-L | 6.10 | 4.52 | 0.88 | 0.74 | 57 (−11.15) | 64 (26.9) | 29 |
| τ-HCTH | 11.72 | 7.81 | 5.94 | 0.67 | 23 (−39.43) | 98 (47.8) | 35 |
| PBE0 | 9.17 | 6.81 | 5.45 | 0.74 | 28 (−9.49) | 93 (29.8) | 41 |
| B3LYP | 4.84 | 3.71 | 2.85 | 0.77 | 23 (−7.25) | 98 (16.7) | 47 |
| B3PW91 | 6.73 | 5.25 | 4.27 | 0.78 | 25 (−7.52) | 96 (21.9) | 47 |
| ωB97X-D | 5.26 | 3.88 | 2.65 | 0.74 | 30 (−8.08) | 91 (22.5) | 42 |
| τ-HCTHh | 8.43 | 5.58 | 4.14 | 0.66 | 36 (−14.43) | 85 (38.4) | 39 |
| PW6B95 | 8.04 | 6.15 | 5.48 | 0.76 | 18 (−6.71) | 103 (29.4) | 47 |
| M06 | 8.82 | 5.90 | 4.61 | 0.67 | 32 (−10.66) | 89 (42.57) | 40 |
| M06-2X | 6.80 | 4.60 | 3.46 | 0.68 | 35 (−6.26) | 86 (32.7) | 43 |
| MN15 | 11.03 | 8.03 | 7.48 | 0.73 | 15 (−5.61) | 106 (50.1) | 42 |
Inspection of the MADs and RMSDs in Tables 2 and 3 reveals that for both the GDB9-nonMR and W4-17* databases, PBE ranks as the worst-performing functional, and B3LYP ranks as the best-performing functional. It should also be noted that M06-L ranks highly for both databases, i.e., it ranks as the second-best functional for the GDB9-nonMR database and the third-best functional for the W4-17* database. Similarly, MN15 ranks as one of the worst-performing functionals for both databases. Whilst there are some differences in the ranking of the medial functionals, overall, there seems to be a reasonable degree of qualitative agreement between the performance of the DFT methods for the two databases. The main exception to this is ωB97X-D, which ranks second-best for the W4-17* database but seventh-best for the GDB9-nonMR database.
It is also instructive to examine the qualitative agreement between the performance of the functionals for both databases. Table 4 depicts the differences in RMSD and MAD obtained for the GDB9-nonMR and W4-17* databases, i.e., ΔMAD = MAD(GDB9-nonMR) − MAD(W4-17*); ΔRMSD = RMSD(GDB9-nonMR) − RMSD(W4-17*). However, it is important to stress that since the GDB9-nonMR database is dominated by larger and more challenging species than the W4-17* database, the error statistics for the former are expected to be larger. Accordingly, in nearly all cases, the performance deteriorates when moving from the small W4-17* database to the GDB9-nonMR database. Nevertheless, the magnitude of the ΔMAD and ΔRMSD values can vary significantly between different functionals. In particular, for some functionals, the RMSD and MAD change drastically between the two databases (most notably for PBE and PBE0), whilst for others, the performance remains relatively unchanged (most notably BLYP, B3LYP, and τ-HCTH). For two methods (BLYP and τ-HCTH), the overall performance for the GDB9-nonMR database is better than that for the W4-17* database. For the B3LYP functional, the RMSD and MAD obtained for the W4-17* database are similar to those obtained for the GDB9-nonMR database (i.e., ΔMAD = 0.38 and ΔRMSD = 0.32 kcal mol−1). BLYP, B97-D, M06-L, and τ-HCTH also exhibit relatively small variations in performance between the two databases, with ΔMADs below 1.7 and ΔRMSDs below 3.1 kcal mol−1 (in absolute values). In contrast, B3PW91 and ωB97X-D exhibit deterioration in performance in the ΔRMSDs and ΔMADs of ∼10 kcal mol−1. Similarly, the hybrid-meta GGA methods M06-2X and PW6B95 methods exhibit deterioration in performance in the ΔRMSDs and ΔMADs of ∼12 kcal mol−1.
| ΔMAD | ΔRMSD | |
|---|---|---|
| a The tabulated values are ΔRMSD = RMSD(GDB9-nonMR) − RMSD(W4-17*) and ΔMAD = MAD(GDB9-nonMR) − MAD(W4-17*). Negative ΔRMSD and ΔMAD values indicate that the performance for the GDB9-nonMR database is better than that for the much smaller W4-17* database. b It should be noted that since the GDB9-nonMR database is dominated by larger species (and arguably more challenging) than the W4-17* database, the error statistics for the former are expected to be larger. | ||
| PBE | 54.45 | 50.11 |
| BLYP | −0.70 | −2.47 |
| B97-D | 1.23 | −0.06 |
| M06-L | 1.72 | 1.52 |
| τ-HCTH | −0.52 | −3.16 |
| PBE0 | 24.98 | 23.12 |
| B3LYP | 0.38 | 0.32 |
| B3PW91 | 11.69 | 10.70 |
| ωB97X-D | 11.43 | 10.61 |
| M06 | 12.79 | 10.38 |
| M06-2X | 14.81 | 12.88 |
| τ-HCTHh | 4.29 | 2.68 |
| PW6B95 | 16.19 | 14.63 |
| MN15 | 18.05 | 20.51 |
Overall, the ΔMADs and ΔRMSDs in Table 4 show that five functionals (B3LYP, M06-L, BLYP, τ-HCTH, and B97-D) exhibit similar performance for the two databases with ΔMADs ranging between −0.7 (BLYP) and 1.72 (M06-L) kcal mol−1. While eight functionals (ωB97X-D, B3PW91, M06, M06-2X, MN15, PW6B95, PBE0, and PBE) exhibit significant deterioration in performance when moving from the W4-17* to the GDB9-nonMR database with ΔMADs ranging between 11.43 (ωB97X-D) and 54.45 (PBE) kcal mol−1. τ-HCTHh exhibits intermediate deterioration in performance with ΔMAD = 4.29 kcal mol−1. Excluding PBE and PBE0, which are not expected to perform well for TAEs in the first place, it seems that functionals from the higher rungs of Jacob's ladder tend to exhibit larger variations in performance between the two databases.
Ref. 37 evaluated the performance of three functionals (B3LYP, M06-2X, ωB97X-D) for the 459 heats of formation in the Pedley test set, which contains 175 hydrocarbons and 284 first-row substituted hydrocarbons. The MADs for the Pedley test set are 3.99 (B3LYP), 2.71 (M06-2X), and 1.85 (ωB97X-D) kcal mol−1. The MAD for B3LYP is similar to that obtained for the larger GDB9-nonMR database (4.09 kcal mol−1). In both studies, B3LYP is evaluated in conjunction with the 6-31G(2df,p) basis set. The performance of the M06-2X and ωB97X-D functionals was evaluated in ref. 37 in conjunction with the larger 6-311+G(3df,2p) basis set. Thus, the differences between the MADs obtained for the Pedley and GDB9-nonMR databases might partly be attributed to the use of the larger 6-311+G(3df,2p) basis set for the evaluation of the M06-2X and ωB97X-D methods (vide supra). Having said that, it is of interest to inspect the largest errors for the M06-2X and ωB97X-D methods for the GDB9-nonMR database. Inspection of the largest errors for both M06-2X and ωB97X-D reveals that they are dominated by systems that combine several challenging functional groups in one molecule. For example, a CF3 group, at least one highly strained ring (e.g., cyclopropane, oxirane, aziridine, cyclobutene, oxetane, or azetidine), and at least one oxygen-containing functional group (e.g., alcohol, ether, or carbonyl). A useful subset to examine, which is dominated by challenging multifunctional-group compounds, is the group of 268 molecules containing CF3 and at least one heteroatom. The RMSDs over this challenging subset are 29.0 (M06-2X), 22.3 (ωB97X-D), and 11.6 (B3LYP) kcal mol−1. Another subset of molecules that appears to be more challenging for M06-2X and ωB97X-D than for B3LYP is the subset of saturated hydrocarbons containing three rings. This subset can be isolated by considering all H14C9 structures containing only C–C bonds longer than 1.48 Å. There are 541 such hydrocarbons in the GDB9-nonMR database. The RMSDs over this challenging subset are 20.9 (M06-2X and ωB97X-D) and 5.5 (B3LYP) kcal mol−1. Similarly, for the subset of 190 H12C9 saturated hydrocarbons with four rings, we obtain RMSDs of 21.2 (M06-2X), 19.3 (ωB97X-D), and 8.2 (B3LYP) kcal mol−1. Since such systems are not represented in the Pedley test set, these results partly explain the appreciably larger MADs obtained for the M06-2X and ωB97X-D functionals for the GDB9-nonMR database relative to the Pedley test set.
As mentioned above, the difference in RMSD for PBE between the W4-17* and GDB9-nonMR database is very significant. Inspection of the deviations obtained for PBE for the GDB9-nonMR database reveals that there are 584 deviations above 100 kcal mol−1. A closer look at these 584 deviations reveals that they include a significant population of species (mostly cyclic) containing multiple nitrogen atoms. In particular, 76 species contain five nitrogens, 194 species contain four nitrogens, 248 species contain three nitrogens, 56 species contain two nitrogens, and 10 species contain one nitrogen. Thus, 89% of the species with deviations above 100 kcal mol−1 contain at least three nitrogen atoms, and 46% of the species with deviations above 100 kcal mol−1 contain at least four nitrogens. In addition, 177 of the species containing three nitrogens also contain at least one oxygen. For as many as 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 329 species, PBE overestimates the G4(MP2) TAE by amounts ranging between 90–100 kcal mol−1. This set of molecules is much more diverse. However, it still has an appreciable number of 4408 (or 36%) of systems with 3–5 nitrogen atoms. Therefore, the increase in the RMSD, MAD, and MSD when moving from the W4-17* to the GDB9-nonMR database is partly attributed to the presence of heterocycles with 3–5 nitrogen atoms. This class of molecules is not represented in the W4-17* database.
329 species, PBE overestimates the G4(MP2) TAE by amounts ranging between 90–100 kcal mol−1. This set of molecules is much more diverse. However, it still has an appreciable number of 4408 (or 36%) of systems with 3–5 nitrogen atoms. Therefore, the increase in the RMSD, MAD, and MSD when moving from the W4-17* to the GDB9-nonMR database is partly attributed to the presence of heterocycles with 3–5 nitrogen atoms. This class of molecules is not represented in the W4-17* database.
Finally, we have to consider the possibility that the difference in the performance of the DFT functionals for the two databases is partly a result of the accuracy of the reference values used (i.e., W4 theory vs. G4(MP2) theory). Namely, the W4-17* database uses CCSDT(Q)/CBS, CCSDTQ5/CBS, and CCSDTQ56/CBS TAEs from W4, W4.n, and W4lite theories, whereas the GDB9-nonMR database uses CCSD(T) TAEs from G4(MP2) theory. One way to examine this, is by replacing the reference values in the W4-17* database with G4(MP2) TAEs and see how this affects the ΔMAD and ΔRMSD values in Table 4. Table S4 of the ESI† reports the ΔMAD and ΔRMSD values in Table 4, but with using G4(MP2) rather than W4 reference TAEs in the W4-17* database. Indeed, lowering the quality of the reference values in the W4-17* database changes the ΔMAD and ΔRMSD values in Table 4, however, the changes are relatively small. Interestingly, upon changing the reference values in the W4-17* database, all the ΔRMSD values are reduced by a relatively constant amount of ∼1.0 kcal mol−1, and all the ΔMAD values are reduced by a relatively constant amount of ∼0.8 kcal mol−1. However, these systematic changes do not change the conclusions in the previous sections. The relatively small and systematic changes in the ΔMAD and ΔRMSD values when moving from using FCI/CBS to G4(MP2) reference TAEs in the W4-17* database are largely attributed to the fact that this subset does not include strongly multireference systems and second-row systems with which G4(MP2) theory would generally struggle (e.g., highly polar and pseudohypervalent systems like SF6, PF5, ClF5, AlF3, PF3, HClO4, HClO3, ClO3, and SO3).
Empirical dispersion effects
We have seen above that, by and large, the considered dispersion-uncorrected DFT methods tend to overbind the TAEs. Some XC functionals such as PBE, PBE0, B3PW91, and PW6B95 overestimate the CCSD(T) TAEs systematically and severely, whereas others such as BLYP and B3LYP are less biased toward overestimation of the TAEs. Dispersion corrections are attractive, and therefore they are expected to increase the errors further for methods that already systematically overestimate the TAEs. It is, nevertheless, of interest to consider the effects of dispersion on the performance of DFT for the 122k TAEs in the GDB9-nonMR dataset. Table 5 lists the RMSDs, MADs, MSDs, and MAD/RMSD ratios for a subset of dispersion-corrected functionals (we focus here on the functionals that do not account for dispersion interactions in the functional parameterization). As expected, the inclusion of an empirical dispersion correction results in an overall deterioration in performance across the board. The deterioration in performance is more pronounced with the more recent D3BJ and D4 dispersion corrections since the zero-damping function in the original D3 procedure leads to less attractive interatomic forces at short distances.64–66 In particular, the inclusion of the D3 dispersion correction increases the RMSDs by ∼5 kcal mol−1 for the functionals considered (with the exception of B3PW91 for which the RMSD is increased by 9.79 kcal mol−1). For comparison, the inclusion of the D3BJ or D4 dispersion correction increases the RMSDs by larger amounts ranging from about 9–18 kcal mol−1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 476 total atomization energies in the GDB9-nonMR dataset (error statistics are given in kcal mol−1)a
476 total atomization energies in the GDB9-nonMR dataset (error statistics are given in kcal mol−1)a
| RMSD | MAD | MSD | MAD/RMSD | ||
|---|---|---|---|---|---|
| a RMSD = root-mean-square deviation, MAD = mean-absolute deviation, MSD = mean-signed deviation. | |||||
| PBE | No disp. | 79.70 | 79.22 | 79.22 | 0.99 |
| D3 | 84.68 | 84.27 | 84.27 | 1.00 | |
| D3BJ | 90.39 | 89.99 | 89.99 | 1.00 | |
| D4 | 90.36 | 89.94 | 89.94 | 1.00 | |
| BLYP | No disp. | 11.89 | 9.59 | 2.52 | 0.81 |
| D3 | 16.72 | 14.01 | 13.47 | 0.84 | |
| D3BJ | 26.35 | 24.67 | 24.67 | 0.94 | |
| D4 | 27.68 | 26.08 | 26.08 | 0.94 | |
| PBE0 | No disp. | 32.29 | 31.79 | 31.79 | 0.98 |
| D3 | 37.54 | 37.08 | 37.08 | 0.99 | |
| D3BJ | 41.55 | 41.06 | 41.06 | 0.99 | |
| D4 | 41.38 | 40.88 | 40.88 | 0.99 | |
| B3LYP | No disp. | 5.16 | 4.09 | 0.45 | 0.79 |
| D3 | 10.38 | 9.27 | 9.18 | 0.89 | |
| D3BJ | 19.10 | 18.48 | 18.48 | 0.97 | |
| D4 | 18.03 | 17.39 | 17.39 | 0.96 | |
| B3PW91 | No disp. | 17.43 | 16.94 | 16.94 | 0.97 |
| D3 | 27.22 | 26.89 | 26.89 | 0.99 | |
| D3BJ | 35.60 | 35.23 | 35.23 | 0.99 | |
| D4 | 33.45 | 33.06 | 33.06 | 0.99 | |
Limitations and scope for future work
Finally, it is important to highlight some limitations that are, by necessity, inherent to a ‘big data’ benchmark study considering 122k molecules with up to nine non-hydrogen atoms and to point out prospects for future work. The performance of the DFT methods in the present work is benchmarked relative to CCSD(T) reference TAEs obtained from G4(MP2) theory. It would be desirable to use reference TAEs from a higher-level CCSD(T)-based composite ab initio method such as W1 or W1-F12 theory.1,2,21,23,25Fig. 3 depicts a typical system in the GDB9-nonMR database, which involves 64 electrons (H7C7NO, dsgdb9nsd_133885). A W1-F12 calculation for this system would require 10.9 hours running on 16 Intel Xeon Cascade Lake CPUs using 180 GB of RAM and 400 GB of fast SSD scratch disk. Thus, running W1-F12 calculations for the entire GDB9-nonMR database of 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 476 structures is expected to take about one year on a machine with 160 cores and 2 TB of RAM. Clearly, this is a very significant investment in terms of computer time.
476 structures is expected to take about one year on a machine with 160 cores and 2 TB of RAM. Clearly, this is a very significant investment in terms of computer time.
Another limitation of the present work is the use of the 6-31G(2df,p) basis set in the evaluation of the DFT functionals. A PW6B95/6-31G(2df,p) calculation for the molecule in Fig. 3 runs for 0.40 of a minute on a node with 16 cores. This translates to over a month's worth of computer time for running the entire GDB9-nonMR database on a single node just for this one DFT functional. In the present work, we have considered 14 DFT functionals across the rungs of Jacob's ladder. Considering the availability of more cores, the different computational scaling of functionals from different rungs of Jacob's ladder, and the optimization of the number of cores used per calculation makes the 6-31G(2df,p) calculations performed here achievable within a realistic timeframe. However, moving to the large aug′-pc3 quadruple-ζ basis set, which was considered here for the W4-17* database, increases the above wall time by two orders of magnitude to 42.4 minutes. We note that even with the smaller triple-ζ-quality aug′-pc2 basis set, this calculation requires 3.3 minutes, i.e., an increase by nearly one order of magnitude in computer time relative to the 6-31G(2df,p) basis set. Thus, repeating the DFT calculations for the entire GDB9-nonMR database using a sufficiently large basis set would require a significant investment in terms of computer time. As noted in a previous subsection, the results for the W4-17* database indicate that employing a much larger basis set is likely to improve the performance for functionals that exhibit strong basis set dependencies for TAEs, such as PW6B95, M06-2X, and ωB97X-D.
Finally, we note that consistent with previous benchmark studies,7–10,20–22,40,79 we have used the same geometries for the evaluation of all the DFT functionals (optimized at the B3LYP/6-31G(2df,p) level of theory). Reoptimizing the geometries with the DFT functional being evaluated would require nearly two million geometry optimizations across the 14 functionals. Further explorations along these directions considering the GDB9-nonMR database (or similarly sized databases) would be desirable.
Conclusions
Total atomization energies (TAEs) are among the most challenging thermochemical tests for electronic structure methods and, therefore, serve as a central quantity in benchmark studies. So far, TAE databases used in DFT benchmark studies included a few hundred of TAEs. Here, we use the GDB9-nonMR database of 122k CCSD(T) TAEs calculated at the G4(MP2) level to evaluate the performance of 14 representative DFT methods across the rungs of Jacob's ladder (namely, PBE, BLYP, B97-D, M06-L, τ-HCTH, PBE0, B3LYP, B3PW91, ωB97X-D, τ-HCTHhyb, PW6B95, M06, M06-2X, and MN15). Importantly, we used the A25[PBE] diagnostic for nondynamical correlation to confirm that the GDB9-nonMR database does not include species with moderate-to-severe multireference effects, for which the CCSD(T) TAEs might not be sufficiently reliable. With respect to the performance of the considered DFT methods for the TAEs in the GDB9-nonMR database, we draw the following conclusions:• With the main exception of B3LYP and BLYP, all XC functionals tend to systematically overbind the species in the GDB9-nonMR database. The most prominent examples are PBE, PBE0, B3PW91, ωB97X-D, τ-HCTHhyb, PW6B95, M06, M06-2X, and MN15.
• Overall, the lightly parameterized B3LYP functional, in which the three mixing parameters were fitted against a set of atomization energies, ionization potentials, and proton affinities, shows the best overall performance with RMSD = 5.16 and MAD = 4.09 kcal mol−1. B3LYP is one of the few XC functionals that are not systematically biased towards overbinding as demonstrated by MSD = 0.45 kcal mol−1 and nearly equal amounts of ∼61k negative deviations and ∼62k positive deviations.
• The relatively good performance of B3LYP is followed by that of the heavily parameterized meta GGA M06-L (RMSD = 7.62 and MAD = 6.24) and the moderately parameterized meta GGA τ-HCTH (RMSD = 8.56 and MAD = 7.29 kcal mol−1).
• None of the considered hybrid-meta GGA functionals outperform B3LYP, M06-L, and τ-HCTH. Of the considered hybrid-meta GGAs, τ-HCTHh shows the best performance with RMSD = 11.11 and MAD = 9.87 kcal mol−1.
• Whilst PW6B95 and M06-2X systematically overestimate the G4(MP2) TAEs, they exhibit particularly low standard deviations of 3.83 and 3.24 kcal mol−1, respectively. Thus, scaling the PW6B95 and M06-2X TAEs by a single empirical scaling factor optimized to minimize the RMSDs results in RMSDs of 4.20 (PW6B95) and 3.60 (M06-2X) kcal mol−1.
• A comparison between the performance of the XC functionals for the GDB9-nonMR and the much smaller W4-17* database (121 TAEs) reveals that for some functionals (e.g., B3LYP, M06-L, BLYP, τ-HCTH and B97-D) the RMSDs and MADs for the two databases are similar. While other functionals (e.g., ωB97X-D, B3PW91, M06, M06-2X, MN15, PW6B95, PBE0, and PBE) exhibit the expected deterioration in performance when moving from the W4-17* to the GDB9-nonMR database.
• Empirical dispersion corrections are attractive, and therefore, their inclusion worsens the performance of methods that already systematically overestimate the TAEs. In such cases, the less attractive D3 dispersion correction performs better than the more attractive D3BJ and D4 corrections.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The present work was undertaken with the assistance of resources from the National Computational Infrastructure (NCI), which is supported by the Australian Government. We gratefully acknowledge the system administration support provided by the Faculty of Science, Agriculture, Business and Law at the University of New England to the Linux cluster of the Karton group. We would also like to thank the reviewers of the manuscript for their valuable comments and suggestions.References
- A. Karton, Annu. Rep. Comput. Chem., 2022, 18, 123 CrossRef.
- A. Karton, Benchmark Accuracy in Thermochemistry, Kinetics, and Noncovalent Interactions, in Comprehensive Computational Chemistry, ed. R. J. Boyd and M. Yanez, Elsevier, 1st edn, 2023, vol. 1, pp. 47–68, ISBN 9780128232569 Search PubMed.
- D. Feller, K. A. Peterson and B. Ruscic, Theor. Chem. Acc., 2013, 133, 1407 Search PubMed.
- K. A. Peterson, D. Feller and D. A. Dixon, Theor. Chem. Acc., 2012, 131, 1079 Search PubMed.
- D. Feller, K. A. Peterson and D. A. Dixon, J. Chem. Phys., 2008, 129, 204105 CrossRef.
- J. M. L. Martin and S. Parthiban, “W1 and W2 theory and their variants: Thermochemistry in the kJ/mol accuracy range”, in Quantum-Mechanical Prediction of Thermochemical Data, Understanding Chemical Reactivity, ed. J. Cioslowski, Kluwer, Dordrecht, 2001, vol. 22, pp. 31–65 Search PubMed.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670 RSC.
- N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315 CrossRef CAS.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184 RSC.
- A. Karton, P. R. Schreiner and J. M. L. Martin, J. Comput. Chem., 2016, 37, 49 CrossRef CAS PubMed.
- S. E. Wheeler, K. N. Houk, P. V. R. Schleyer and W. D. Allen, J. Am. Chem. Soc., 2009, 131, 2547 CrossRef CAS PubMed.
- S. E. Wheeler, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 204 CAS.
- M. D. Wodrich, C. Corminboeuf and S. E. Wheeler, J. Phys. Chem. A, 2012, 116, 3436 CrossRef CAS PubMed.
- R. O. Ramabhadran and K. Raghavachari, J. Chem. Theory Comput., 2011, 7, 2094 CrossRef CAS PubMed.
- R. O. Ramabhadran and K. Raghavachari, J. Phys. Chem. A, 2012, 116, 7531 CrossRef CAS PubMed.
- S. Grimme, Angew. Chem., Int. Ed., 2006, 45, 4460 CrossRef CAS PubMed.
- M. D. Wodrich, C. Corminboeuf and P. V. R. Schleyer, Org. Lett., 2006, 8, 3631 CrossRef CAS PubMed.
- M. D. Wodrich, C. Corminboeuf, P. R. Schreiner, A. A. Fokin and P. V. R. Schleyer, Org. Lett., 2006, 9, 1851 CrossRef PubMed.
- P. R. Schreiner, Angew. Chem., Int. Ed., 2007, 46, 4217 CrossRef CAS PubMed.
- A. Karton, A. Tarnopolsky, J.-F. Lamère, G. C. Schatz and J. M. L. Martin, J. Phys. Chem. A, 2008, 112, 12868 CrossRef CAS PubMed.
- A. Karton, S. Daon and J. M. L. Martin, Chem. Phys. Lett., 2011, 510, 165 CrossRef CAS.
- A. Karton, N. Sylvetsky and J. M. L. Martin, J. Comput. Chem., 2017, 38, 2063 CrossRef CAS PubMed.
- J. M. L. Martin and G. de Oliveira, J. Chem. Phys., 1999, 111, 1843 CrossRef CAS.
- A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108 CrossRef PubMed.
- A. Karton and J. M. L. Martin, J. Chem. Phys., 2012, 136, 124114 CrossRef PubMed.
- N. Sylvetsky, K. A. Peterson, A. Karton and J. M. L. Martin, J. Chem. Phys., 2016, 144, 214101 CrossRef PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 140022 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- A. Karton and P. R. Spackman, J. Comput. Chem., 2021, 42, 1590 CrossRef CAS PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 810 CAS.
- N. DeYonker, T. R. Cundari and A. K. Wilson, Progress in Theoretical Chemistry and Physics, Springer, Dordrecht, The Netherlands, 2009, vol. 19, pp. 197–224 Search PubMed.
- A. Karton, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 292 CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 127, 124105 CrossRef PubMed.
- L. Ruddigkeit, R. van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864 CrossRef CAS PubMed.
- B. Narayanan, P. C. Redfern, R. S. Assary and L. A. Curtiss, Chem. Sci., 2019, 10, 7449 RSC.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- K. Raghavachari, Chem. Phys. Lett., 2013, 589, 35 CrossRef CAS.
- A. Karton, D. Gruzman and J. M. L. Martin, J. Phys. Chem. A, 2009, 113, 8434 CrossRef CAS PubMed.
- A. Karton and J. M. L. Martin, Mol. Phys., 2012, 110, 2477 CrossRef CAS.
- R. J. O’Reilly, A. Karton and L. Radom, Int. J. Quantum Chem., 2012, 112, 1862 CrossRef.
- A. Karton, R. J. O’Reilly and L. Radom, J. Phys. Chem. A, 2012, 116, 4211 CrossRef CAS PubMed.
- L.-J. Yu and A. Karton, Chem. Phys., 2014, 441, 166 CrossRef CAS.
- A. Karton and L. Goerigk, J. Comput. Chem., 2015, 36, 622 CrossRef CAS PubMed.
- L.-J. Yu, F. Sarrami, R. J. O’Reilly and A. Karton, Chem. Phys., 2015, 458, 1 CrossRef CAS.
- W. Wan and A. Karton, Chem. Phys. Lett., 2016, 643, 34 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2005, 123, 124107 CrossRef PubMed.
- B. Huang and O. A. von Lilienfeld, Chem. Rev., 2021, 121, 10001 CrossRef CAS PubMed.
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2000, 577, 1 CrossRef.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- A. D. Boese and N. C. Handy, J. Chem. Phys., 2002, 116, 9559 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032 RSC.
- J. M. L. Martin and G. Santra, Isr. J. Chem., 2020, 60, 787 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 024101 CrossRef.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154112 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- U. R. Fogueri, S. Kozuch, A. Karton and J. M. L. Martin, Theor. Chem. Acc., 2013, 132, 1291 Search PubMed.
- M. K. Sprague and K. K. Irikura, Theor. Chem. Acc., 2014, 133, 1544 Search PubMed.
- B. Ruscic, Int. J. Quantum Chem., 2014, 114, 1097 CrossRef CAS.
- R. C. Geary, Biometrika, 1933, 27, 310 CrossRef.
- R. C. Geary, Biometrika, 1936, 28, 295 CrossRef.
- A. D. Boese, J. M. L. Martin and N. C. Handy, J. Chem. Phys., 2003, 119, 3005 CrossRef CAS.
- S. Lehtola and M. A. L. Marques, J. Chem. Theory Comput., 2021, 17, 943 CrossRef CAS PubMed.
- R. Colle and O. Salvetti, Theor. Chim. Acta, 1975, 37, 329 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- A. Karton, S. Parthiban and J. M. L. Martin, J. Phys. Chem. A, 2009, 113, 4802 CrossRef CAS PubMed.
- P. C. Redfern, P. Zapol, L. A. Curtiss and K. Raghavachari, J. Phys. Chem. A, 2000, 104, 5850 CrossRef CAS.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364 CrossRef PubMed.
- F. Jensen, J. Chem. Phys., 2001, 115, 9113 CrossRef CAS.
- B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 8996 CrossRef CAS.
- T. Gould, Phys. Chem. Chem. Phys., 2018, 20, 27735 RSC.
- B. Chan, J. Chem. Theory Comput., 2018, 14, 4254 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: A25[PBE] values for the species in the GDB-9 database (Table S1); error statistics for the W4-17* database for the considered DFT functionals calculated in conjunction with the aug′-pc3+d and 6-31G(2df,p) basis sets (Table S2); species in the W4-17* database (Table S3); ΔMAD and ΔRMSD values reported in Table 4 calculated using G4(MP2) reference TAEs rather than Wn reference TAEs (Table S4); DFT TAEs for the GDB9-nonMR database (Table S5); individual deviations and error statistics for the W4-11-nonMR, W4-17-nonMR, and W4-17* databases (Tables S6–S9); error distribution for the DFT functionals that are not included in Fig. 2 (Fig. S1). See DOI: https://doi.org/10.1039/d4cp00387j |
| This journal is © the Owner Societies 2024 |