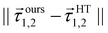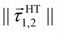A diabatization method based upon integrating the diabatic potential gradient difference†
Fengyi
Li
ab,
Xiaoxi
Liu
ab,
Haitao
Ma
 *a and
Wensheng
Bian
*a and
Wensheng
Bian
 *ab
*ab
aBeijing National Laboratory for Molecular Sciences, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China. E-mail: mht@iccas.ac.cn; bian@iccas.ac.cn
bUniversity of Chinese Academy of Sciences, Beijing, 100049, China
First published on 11th April 2024
Abstract
In this work we develop a new scheme to construct a diabatic potential energy matrix (DPEM). We propose a diabatization method which is based on integrating the diabatic potential gradient difference to diabatize adiabatic ab initio energies. This method is capable of performing high-precision adiabatic-to-diabatic transformations, with a unique advantage in effectively handling the significant fluctuations in derivative-couplings caused by conical intersection (CI) seams. The above scheme is applied to the DPEM construction of the Na(3p) + H2 → NaH + H reaction. The fitting data including adiabatic energies, energy gradients and derivative-couplings obtained from a previous benchmark DPEM are diabatized and fitted using a general neural network fitting procedure to generate the DPEM. The produced DPEM can effectively describe nonadiabatic processes involving different electronic states. We further perform quantum dynamical calculations on the new DPEM and the previous benchmark DPEM, and the obtained results demonstrate the effectiveness of our scheme.
1 Introduction
Within the Born–Oppenheimer (BO) approximation, various electronic structure methods are employed to solve the electronic Schrödinger equation. This process yields adiabatic potential energy surfaces (APESs) which are commonly used in reaction dynamics studies. However, the BO approximation may not be adequate for chemical reactions that involve nonadiabatic processes, which are known to be very important in many fields such as DNA photodamage, photocatalysis and astrochemistry.1–5 Therefore, the reaction dynamics studies of nonadiabatic processes involving potential energy surface intersections have attracted great research interest.6–9 In theoretical studies, the nonadiabatic reaction dynamics calculations can be carried out in either the adiabatic or diabatic representation. However, the DPEM construction remains a challenge nowadays.Due to the non-uniqueness of the diabatic representation, there are various methods of diabatization.10–25 According to the type of information used, these methods of diabatization can be grouped into a few categories: ansatz, property-based and derivative-coupling-based diabatization.21,22,26 The adiabatic electronic structure data are reproduced very well by fitting a predetermined physical model in the ansatz method, which is a widely used diabatization scheme using the block-diagonalization algorithm.19,22 One of the great advantages of the ansatz method is that it expands the adiabatic wave functions into only a low order of Taylor expansion in the normal coordinates around a reference geometry. The property-based diabatization is appealing due to its simplicity and widely used since almost every Hermitian operator can be used to generate a diabatic representation, such as orbitals, projection of dipoles, the entire dipole matrix, quadrupoles and angular momenta.13,22 Based on orbital transformations, the threefold- and fourfold-way direct diabatization schemes were popular for yielding diabatic molecular orbitals. The third type of diabatization uses the derivative-coupling information and it is in principle the most accurate method,27,28 as the derivative-couplings are directly used to diabatize the electronic states. The shortcoming of the derivative-coupling method is that it is only implemented in a limited number of quantum chemistry programs, which limits its application to larger systems. However, this kind of method has been quite successfully applied to a series of reactive systems.29–33 The fitting of derivative-couplings via least-squares minimizes the residual-couplings, providing a reliable diabatic energy matrix representation for simulating nonadiabatic processes, which was first introduced in the Zhu–Yarkony diabatization strategy.26 The rigorous diabatic representation does not exist for polyatomic (including tri-atomic) molecules due to the fact that the rigorous diabatic electronic wave functions could not be obtained with limited calculations and methods,6,7,34–36 hence it is referred to as quasi-diabatic in the rest of this work. Very recently, Truhlar and co-workers achieved DPEM smoothness by combining the deep neural network architecture with diabatization procedures.5,22 Achieving accurate diabatization through machine learning frequently necessitates a significant volume of data, while the ab initio computations involved in processing this data can be time-consuming.
In this work, we propose a hybrid scheme that combines a diabatization approach based on the diabatic potential gradient difference with the neural network (NN) technique for the construction of DPEMs. The ab initio derived DPEMs are of paramount importance in quantum dynamics, particularly for an accurate description of non-adiabatic processes, which has long been a primary objective in the field. We apply our scheme to the development of DPEMs for the two lowest electronic states of NaH2 to illustrate the accuracy and effectiveness of our new diabatization method. The Na(3p) + H2 → NaH + H reaction serves as a prototype for the study of the collisional quenching of electronically excited alkali and alkaline earth atoms.10,37–41 This reaction is also representative of a fundamental class of nonadiabatic processes occurring through an excited-state potential energy well that intersects with the ground electronic state conically, and such processes are of particular interest in both experimental and theoretical studies.42,43 In this work, we construct an analytical 2 × 2 DPEM for the two lowest-lying 1,22A′ states of the title system using our scheme, which generates coupled quasi-diabatic potentials over a wide range of geometries. The organization of the present article is as follows. Section 2 introduces our theoretical approach for constructing a DPEM. The properties of the DPEM and further time-dependent wave packet calculations are presented and discussed in detail in Section 3. Finally, a brief summary is given in Section 4.
2 Theoretical approach
Derivative-coupling-based methods are in principle the most accurate ones for constructing quasi-diabatic states.14,44,45 In most derivative-coupling-based diabatization,46–49 the interstate couplings are obtained by![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) = = ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2(Ea2 − Ea1) 1,2(Ea2 − Ea1) | (1) |
![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2 is the derivative-coupling vector between the two adiabatic states, which is a vector with 3 × N elements, where N is the number of atoms. In the two-state coupling model, the nonadiabatic coupling matrix τ has a very simple form:
1,2 is the derivative-coupling vector between the two adiabatic states, which is a vector with 3 × N elements, where N is the number of atoms. In the two-state coupling model, the nonadiabatic coupling matrix τ has a very simple form: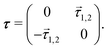 | (2) |
The corresponding adiabatic-to-diabatic transformation (ADT) matrix A for the two-state model is a real orthogonal matrix of dimension 2 × 2, and it can be presented in the form:
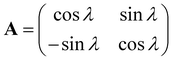 | (3) |
∇λ + ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2 = 0 1,2 = 0 | (4) |
Ignoring the sign of ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2, we get the key equation in ADT:
1,2, we get the key equation in ADT:
∇λ = ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2 1,2 | (5) |
The ADT equation is:
| Ed = A†EaA | (6) |
Ed1,1 = Ea1cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ + Ea2sin2 λ + Ea2sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ λ | (7) |
Ed2,2 = Ea2cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ + Ea1sin2 λ + Ea1sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ λ | (8) |
Ed1,2 = (Ea1 − Ea2)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λcos λcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) λ λ | (9) |
As shown in eqn (5), simply integrating ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2 in all directions could be one of the most direct ways to obtain the mixing angle, and then the diabatic energies are transformed from the adiabatic energies via the ADT matrix. However, the fluctuations of the values of
1,2 in all directions could be one of the most direct ways to obtain the mixing angle, and then the diabatic energies are transformed from the adiabatic energies via the ADT matrix. However, the fluctuations of the values of ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2 would lead to the inaccuracy of the result of numerical integration, especially when a point in the grid incidentally has an extremely large value of
1,2 would lead to the inaccuracy of the result of numerical integration, especially when a point in the grid incidentally has an extremely large value of ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2. An alternative is to fit
1,2. An alternative is to fit ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2 with an appropriate function so that the result of the indefinite integral of this function could be used as the mixing angle. The numerical integration in a shorter step length for the functions that could not give an indefinite integral would also lead to a much more accurate result than integrating
1,2 with an appropriate function so that the result of the indefinite integral of this function could be used as the mixing angle. The numerical integration in a shorter step length for the functions that could not give an indefinite integral would also lead to a much more accurate result than integrating ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2 directly. However, it is very difficult to find such a function to fit
1,2 directly. However, it is very difficult to find such a function to fit ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2 because of the fluctuations of the values. In our test using a feedforward neural network50,51 with 3 hidden layers and 3 × 20 hidden neurons, the least root-mean-square error (RMSE) fitting error of
1,2 because of the fluctuations of the values. In our test using a feedforward neural network50,51 with 3 hidden layers and 3 × 20 hidden neurons, the least root-mean-square error (RMSE) fitting error of ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2 is about 0.1 bohr−1.
1,2 is about 0.1 bohr−1.
In some derivative-coupling-based diabatization methods,6,7,31,32 the interstate couplings were fitted instead. Due to the approximate negative correlation between (Ea2 − Ea1) and ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2, the interstate coupling becomes a much smoother function than the derivative-coupling; however, the existence of protrusions caused by singularities still hinders the fitting. So it is not recommended to fit the derivative or interstate couplings directly, because of the divergence problem in the conical intersection regions. Recently, a smart approach25 was proposed in which a so-called modified derivative-coupling term, rather than the derivative or interstate coupling, is incorporated in the quasi-diabatic Hamiltonian. This modified term behaves similarly to the original derivative-coupling in regions where the two states have different energies, but effectively avoids singularities when degeneracy occurs, thereby preserving the essential characteristics of the derivative-coupling.
1,2, the interstate coupling becomes a much smoother function than the derivative-coupling; however, the existence of protrusions caused by singularities still hinders the fitting. So it is not recommended to fit the derivative or interstate couplings directly, because of the divergence problem in the conical intersection regions. Recently, a smart approach25 was proposed in which a so-called modified derivative-coupling term, rather than the derivative or interstate coupling, is incorporated in the quasi-diabatic Hamiltonian. This modified term behaves similarly to the original derivative-coupling in regions where the two states have different energies, but effectively avoids singularities when degeneracy occurs, thereby preserving the essential characteristics of the derivative-coupling.
2.1 Diabatization by integrating the diabatic potential gradient difference
Integrating the derivative couplings or interstate couplings would introduce the risk of imprecision in determining the mixing angle and, consequently, the electronic state energies. Here, we propose to use a new integrand in our diabatization method, defined as ∇(Ed1,1 − Ed2,2), representing the diabatic potential gradient difference, and it could be obtained in the following way. Eqn (7) directly subtracting by eqn (8) results in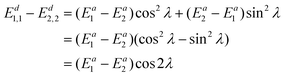 | (10) |
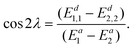 | (11) |
Now we differentiate both sides of eqn (10):
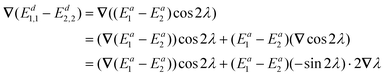 | (12) |
Substituting ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2 = ∇λ into eqn (12), we obtain
1,2 = ∇λ into eqn (12), we obtain
∇(Ed1,1 − Ed2,2) = (∇Ea1 − ∇Ea2)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2λ − 2 2λ − 2![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2(Ea1 − Ea2)sin 1,2(Ea1 − Ea2)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2λ 2λ | (13) |
To simplify eqn (13), we can use vector ![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) provided by eqn (1) and
provided by eqn (1) and ![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) defined as the gradient difference in the following form,
defined as the gradient difference in the following form,
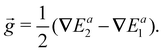 | (14) |
Then we have
∇(Ed1,1 − Ed2,2) = −2![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) ·cos ·cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2λ + 2 2λ + 2![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) ·sin ·sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2λ 2λ | (15) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2λ can be replaced by
2λ can be replaced by 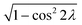 in the
in the  region,
region,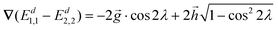 | (16) |
Substituting eqn (11) into eqn (16), we obtain
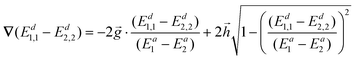 | (17) |
Vectors ![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) and
and ![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) could be obtained using an ab initio package, such as Columbus. It is essential to use the original vectors rather than the orthogonalized ones. That is because only the original ones are the direct reflection of the adiabatic gradient difference and the derivative couplings, the orthogonalized ones cannot be defined using eqn (1) and (14). An alternative is to calculate them using Ea, ∇Ea and
could be obtained using an ab initio package, such as Columbus. It is essential to use the original vectors rather than the orthogonalized ones. That is because only the original ones are the direct reflection of the adiabatic gradient difference and the derivative couplings, the orthogonalized ones cannot be defined using eqn (1) and (14). An alternative is to calculate them using Ea, ∇Ea and ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2 which are obtained during ab initio simulations.
1,2 which are obtained during ab initio simulations.
Now the diabatic energy difference (Ed1,1 − Ed2,2) could be calculated by solving eqn (17). To provide the diabatic energy of the two states, respectively, the sum of diabatic energy (Ed1,1 + Ed2,2) is needed, so we add eqn (7) and (8) and get
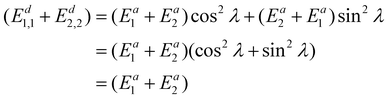 | (18) |
The diabatic energy can now be obtained using
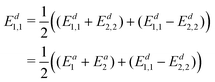 | (19) |
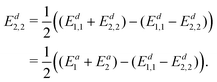 | (20) |
The diabatic coupling term between the two states is also needed in non-adiabatic dynamics, which is provided below:
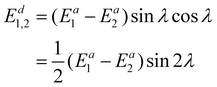 | (21) |
To avoid using the mixing angle λ, we again replace sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2λ with
2λ with 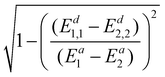 and get
and get
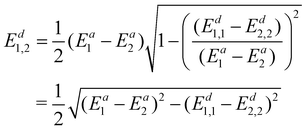 | (22) |
Combining Ed1,1, Ed2,2 and Ed1,2, we get the final DPEM Ed, with the form:
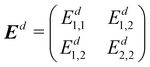 | (23) |
In our ADT method, the integration of ∇(Ed1,1 − Ed2,2), which solely relies on the derivative-couplings, offers a foundation for constructing DPEMs. This construction is achieved without encountering singularities and without resorting to any approximation.
This method can be extended to study systems involving multiple electronic states, since the diabatization of each pair of states could be done using the same method as described above. Here we take a 3-state coupling system as an example, for which the ADT matrix can be written as a product of three 2-in-3-state ADT matrices,34 made up of the functions of 3 mixing angles λ1,2, λ1,3 and λ2,3. Although the mixing angle is avoided to be used directly in the scheme described above, it can still be obtained easily after diabatization using the following formula:
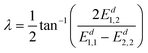 | (24) |
Then the diabatic energy matrix could be calculated viaeqn (6) using the obtained 3-state ADT matrix. To demonstrate the diabatization process, we conducted tests on a simple model system which involves multiple electronic states. As can be seen from Fig. S4 (ESI†), the obtained diabatic potentials are reasonable and smooth, and the continuity of the diabatic state PES can be ensured. The details are given in the ESI.†
2.2 The neural network fitting
In the above diabatization procedure, the residual-couplings were nearly eliminated. Then we used the feedforward NN method to fit the obtained diabatic surfaces. The inverse of three cartesian coordinates of the system was used as the input of the NN. The NN structure we used to fit diabatic potentials Ed1,1 and Ed2,2 is 3-8-15-10-3, which has 3 hidden layers and 338 parameters. And the NN structure for Ed1,2 is 3-8-10-1, which has 2 hidden layers and 133 parameters. The sizes of our NNs are quite small owing to the smoothness of all the DPEM elements, which are enough to give satisfactory results. The transfer functions of the neurons in the input and output layers are linear functions, and those in the hidden layers were chosen to be hyperbolic tangent functions. The functional form of a sampled NN with the structure of 3-8-10-1 can be written as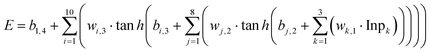 | (25) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h is the hyperbolic tangent function, wi,j and bi,j are the weights and bias for the ith neuron of the jth layer, respectively, and E is the output energy or coupling. The weights and bias were optimized using the Levenberg–Marquardt (LM) algorithm in each fitting to minimize the error. The “early stopping” method was used to avoid over fitting, with 70% of the data points randomly picked as the training set, 50% of the rest as the validating set, and the others as the testing set. Thus, the fitting procedure was stopped in such conditions:
h is the hyperbolic tangent function, wi,j and bi,j are the weights and bias for the ith neuron of the jth layer, respectively, and E is the output energy or coupling. The weights and bias were optimized using the Levenberg–Marquardt (LM) algorithm in each fitting to minimize the error. The “early stopping” method was used to avoid over fitting, with 70% of the data points randomly picked as the training set, 50% of the rest as the validating set, and the others as the testing set. Thus, the fitting procedure was stopped in such conditions:
(a) The mean-square error gradient of each epoch is smaller than 10−10 kcal per mol per epoch.
(b) The damping factor μ in the LM algorithm is larger than 1010.
(c) The RMSE of validating set keeps growing for 10 epochs.
The quality of the fitting NN was measured by RMSE, and 6 best NN fits were averaged over to further reduce the fitting error.
3 Method application: the benchmark NaH2 reaction system
The purpose of this work is to demonstrate the effectiveness of the developed method in constructing a quasi-diabatic representation. Therefore, instead of performing extensive actual ab initio calculations, we generate the fitting data from the available benchmark DPEM39 of Hack and Truhlar (HT).The Jacobi coordinates R (distance of Na from the center of HH mass), r (bond distance of HH) and γ (the angle between R and r) are used as coordinates to generate the fitting data and for the following dynamical calculations. The grid of points is defined by the following values of R, r and γ:
R ∈ [1.00, 2.00, 3.00, 3.20, 3.30, 3.35, 3.40, 3.45, 3.50, 3.55, 3.60, 3.65, 3.70, 3.80, 3.90, 3.95, 4.00, 5.00, 6.00, 7.00, 8.00, 9.00, 10.00, 12.00, 15.0, 30.0] bohr;
r ∈ [1.00, 1.35, 1.40, 1.45, 1.50, 1.60, 1.70, 1.80, 1.90, 2.00, 2.10, 2.20, 2.50, 3.00, 4.00, 5.00, 6.00, 7.00, 10.00, 15.00, 30.0] bohr;
γ ∈ [0.00, 0.01, 0.02, 0.03, 0.04, 0.05, 0.07, 0.10, 0.20, 0.30, 0.40, 0.42, 0.45, 0.46, 0.47, 0.48, 0.49, 0.50] π;
The geometries with energies greater than 13.0 eV are excluded from the surface construction. The additional geometries around extrema including the potential energy well and the lowest minimum energy crossing point (MEX) are also included. A total of 7318 geometries are assembled, which also include 256 points near the MEX. When the geometry closely approaches the MEX, the relative values of derivative-coupling tend to go to infinitely large. In the construction of our DPEM using the new diabatization method, it is unnecessary to incorporate these geometries very near to the MEX, as they may bring numerical challenges. Therefore, the maximum value of derivative-coupling does not exceed 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bohr−1. This grid offers detailed information of the potential energies and the interstate couplings as ab initio data to construct surfaces, and provides a good description of dynamically relevant regions and is sufficient to generate a satisfactory DPEM.
000 bohr−1. This grid offers detailed information of the potential energies and the interstate couplings as ab initio data to construct surfaces, and provides a good description of dynamically relevant regions and is sufficient to generate a satisfactory DPEM.
3.1 Features of the DPEM
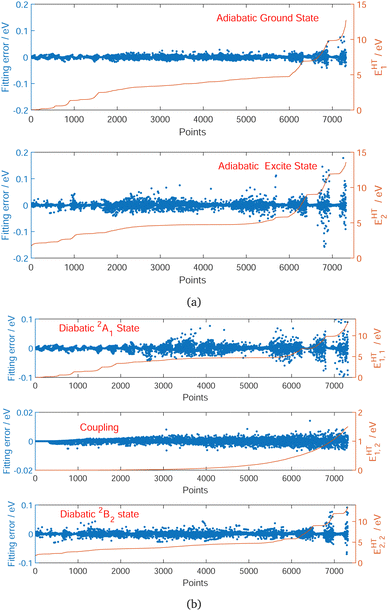
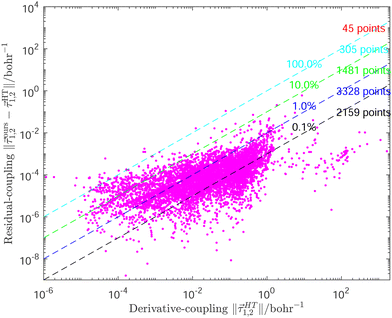
In the construction of potential energy surfaces for the molecules experiencing significant motion, the relevant group in the Schrödinger equation is the complete nuclear permutation and inversion group, as introduced by Longuet–Higgins.52 While electronic energies, energy gradients and derivative-couplings are invariant under group operations, the eigenfunctions are only guaranteed to carry irreducible representations of that group.18,53 In this work, the fitting coordinates are the functions based on nuclear distances, designed to be invariant under certain pair(s) of C2v permutation operation. The distributions of the fitting errors for the first two-state 12A′ and 22A′ energies, gradients and derivative-couplings between them are shown in Fig. 1 to illustrate the fitting quality, in which most of the energy fitting errors larger than 0.025 eV are localized in the relative energies higher than 10.0 eV and the rest of them are scattered over the CI seam in the energy region (2.0,5.0) eV. The largest gradients fitting error is 0.0141 eV. The gradients and their fitting errors for the first 306 points are zero due to the fact that they are determined by C2v symmetry in the processes of diabatization.A more careful analysis for the fitting of derivative-couplings is provided by Fig. 2 which plots the residual-coupling norm against HT DPEM determined derivative-coupling norm for fitting. The magnitude of the residual-coupling norm, 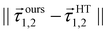 , is used to assess the quality of the diabatization so that the quality of diabatization is strictly under control in this work. Despite the fact that a log scale is required to represent a wide range of fitting data, the significant agreement for derivative-coupling fitting in the range of order of 10−2 is evident. The small norm of the residual-coupling represents a well quasi-diabatic character of the representation. The residual-coupling cannot disappear completely because the Hamiltonian, Hd, does not contain the non-removable part of the derivative-coupling. A large absolute percentage fitting error means a large difference between HT DPEM and Hd determined derivative-couplings, however, it does not indicate a significant problem for the small values of derivative-couplings. There are 45 fitting points with the percentage error exceeding 100.0%, which represents around 0.6% of the total points. The geometries of these 45 points are far away from the surface intersection seam in Fig. 3; therefore, the corresponding values of derivative-couplings are small and have insignificant effect on diabatization. Instead, the fitting for these points, close to the surface intersection seam, with large derivative-coupling values is very good. The number of points with percentage errors ranging from 0.1% to 1.0%, from 1.0% to 10.0% are 2159 and 3328, respectively, which significantly dominates the total points. The fitting errors are quite small compared to the large absolute values for the derivative coupling vector
, is used to assess the quality of the diabatization so that the quality of diabatization is strictly under control in this work. Despite the fact that a log scale is required to represent a wide range of fitting data, the significant agreement for derivative-coupling fitting in the range of order of 10−2 is evident. The small norm of the residual-coupling represents a well quasi-diabatic character of the representation. The residual-coupling cannot disappear completely because the Hamiltonian, Hd, does not contain the non-removable part of the derivative-coupling. A large absolute percentage fitting error means a large difference between HT DPEM and Hd determined derivative-couplings, however, it does not indicate a significant problem for the small values of derivative-couplings. There are 45 fitting points with the percentage error exceeding 100.0%, which represents around 0.6% of the total points. The geometries of these 45 points are far away from the surface intersection seam in Fig. 3; therefore, the corresponding values of derivative-couplings are small and have insignificant effect on diabatization. Instead, the fitting for these points, close to the surface intersection seam, with large derivative-coupling values is very good. The number of points with percentage errors ranging from 0.1% to 1.0%, from 1.0% to 10.0% are 2159 and 3328, respectively, which significantly dominates the total points. The fitting errors are quite small compared to the large absolute values for the derivative coupling vector ![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2. It reflects the small difference in the Hd and HT DPEM determined values for the geometries close to the surface intersection seam in Fig. 3.
1,2. It reflects the small difference in the Hd and HT DPEM determined values for the geometries close to the surface intersection seam in Fig. 3.
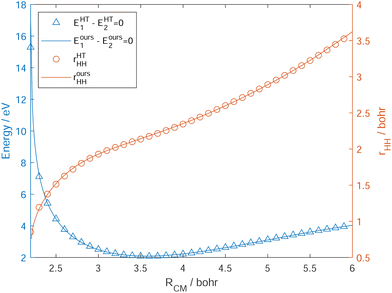
The fitting results of the ground state 12A′ and the excited state 22A′ are listed in Table 1. The root-mean-square errors (RMSEs) of energies in this fitting are converged to around 0.01 eV, and are found to be 0.0097 eV and 0.0059 eV for 12A′ and 22A′ states, respectively, in the energy range under 10.0 eV. It should be noted that 80 percent fitting errors of energies are less than 0.0089 eV and 0.0063 eV, respectively. The RMSEs of the diabatic energies on WYYC DPEM for the Na + H2 reactive system, constructed using property-based diabatization, are 0.010 eV, 0.020 eV, and 0.009 eV, respectively.54 It is noteworthy that the RMSEs for the adiabatic energies in our DPEM constructions are lower than those for the diabatic energies. Moreover, our new DPEM in this work is expected to give an accurate description of the first two states 12A′ (2B2) and 22A′ (2A1) coupled by CI in the quasi-diabatic representation. This reaction starts at the adiabatic 2B2 surface and then intersects the adiabatic 2A1 surface to enter into the product channel. The two extrema play an important role in the field of diabatic reaction dynamics, one is an excited-state potential energy well (exciplex) located near RCM = 3.92 bohr and rHH = 1.50 bohr, and the other is the MEX located near RCM = 3.59 bohr and rHH = 2.17 bohr. The properties of the MEX and exciplex from our DPEM and HT DPEM are collected in Table 2. The geometries and the relative energies of the two extrema on our new DPEM agree well with those on the HT DPEM.
| Point range | ||||
|---|---|---|---|---|
| Energya | <3.0 | [3.0, 5.0) | [5.0, 10.0) | ≥10.0 |
a Energies in eV. Zero of energy is at Na infinitely far from H2 on the ground surface.
b RMSE for the energies of ground state 12A′ (E1) and excited states 22A′ (E2) in eV.
c RMSE for the energy gradients of ground state 12A′ (∇E1) and excited states 22A′ (∇E2) in eV bohr−1.
d RMSE for the interstate couplings vector ![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) in eV bohr−1. in eV bohr−1.
|
||||
| Point number | 1845 | 3983 | 1217 | 273 |
| RMSE (E1)b | 0.0043 | 0.0099 | 0.0141 | 0.0131 |
| RMSE (E2)b | 0.0064 | 0.0055 | 0.0063 | 0.0201 |
| RMSE (∇E1)c | 0.0113 | 0.0242 | 0.0331 | 0.0762 |
| RMSE (∇E2)c | 0.0085 | 0.0201 | 0.0296 | 0.0842 |
RMSE (![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) )d )d |
0.0025 | 0.0042 | 0.0373 | 0.1966 |
| Our | Truhlar's | |||
|---|---|---|---|---|
| DPEM | HTb | DPEM-5Gc | ||
| a r HH is the H2 bond distance in bohr, RCM is the distance of Na from the center of HH mass in bohr, and γ is the angle between RCM and rHH. b Ref. 39 NaH2 surface set 6. c Ref. 39,40 NaH2 surface set 5G. d Zero of energy in eV is at Na infinitely far from H2 on the ground surface. | ||||
| MEX | Energyd | 2.064 | 2.064 | 1.622 |
| R CM | 3.59 | 3.59 | 3.68 | |
| r HH | 2.17 | 2.17 | 1.98 | |
| γ | π/2 | π/2 | π/2 | |
| Exciplex | Energyd | 1.700 | 1.698 | 1.620 |
| R CM | 3.92 | 3.93 | 3.70 | |
| r HH | 1.50 | 1.49 | 1.93 | |
| γ | π/2 | π/2 | π/2 | |
Table 2 and Fig. 3 indicate that the results from our new diabatization method based on integrating the diabatic potential gradient difference could reproduce the geometries and energies from the HT DPEM accurately in the intersection seam region. Compared to the property-based diabatization, which is an efficient approach applicable to nearly every Hermitian operator for generating diabatic representations, our new diabatization technique has some advantages in the constructions of the DPEM coupled by CIs. Although the property-based diabatization schemes, using different choices of properties, are appealing in their simplicity, there are subtle difficulties in these methods for diabatization.22 In practice, it is possible that the selected properties confound one another, which makes the diabatization process problematic. Although derived from the same ab initio calculations, the geometries of conical intersections (CIs) may exhibit significant variation. For example, at the MEX point on the DK DPEM for the O + H2 reaction system,13 the OH bond distance derived from the configuration coefficients is 3.16 bohr, while it is only 3.04 bohr when determined from the angular momenta. Similarly, the HH bond distance at the MEX, derived from the configuration coefficients, is 2.36 bohr, whereas it is only 2.12 bohr when calculated based on the angular momenta. Moreover, another general problem is that the signs of the diabatic couplings produced by property-based diabatization are not unique.22 These findings underscore the advantages of our new DPEM, which is constructed using the diabatic potential gradient difference method.
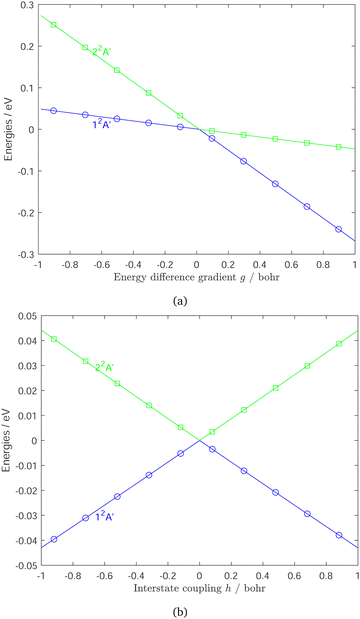
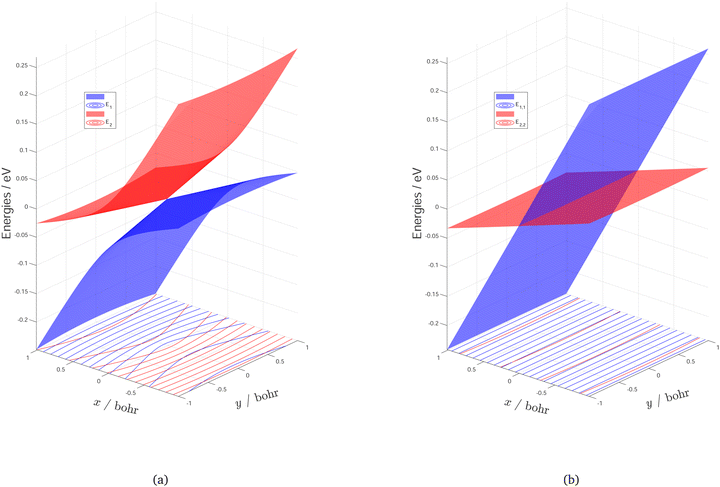
The normalized interstate coupling vector and gradient difference vector, and the energies along these vectors are represented in Fig. 4 and Fig. 5, respectively. In terms of atom centered displacements, the interstate coupling vector ![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) breaks the C2v symmetry, while the potential gradient difference vector
breaks the C2v symmetry, while the potential gradient difference vector ![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) is a symmetry preserving mode. The energy surfaces along the interstate coupling vector
is a symmetry preserving mode. The energy surfaces along the interstate coupling vector ![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) and the potential gradient difference vector
and the potential gradient difference vector ![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) are, respectively, symmetric and non-symmetric. The energy surface crossing point is a CI point. There are protrusions in the adiabatic energy curves along the interstate coupling vector
are, respectively, symmetric and non-symmetric. The energy surface crossing point is a CI point. There are protrusions in the adiabatic energy curves along the interstate coupling vector ![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) , which would bring numerical issues in fitting. However, the diabatic energy changes monotonically and smoothly, which makes the fitting much easier. A modified Newton–Raphson method is used in the optimization of CI seam in the present work, to reduce the energy differences to 10−4 cm−1 and the geometry errors to less than 10−6 bohr.
, which would bring numerical issues in fitting. However, the diabatic energy changes monotonically and smoothly, which makes the fitting much easier. A modified Newton–Raphson method is used in the optimization of CI seam in the present work, to reduce the energy differences to 10−4 cm−1 and the geometry errors to less than 10−6 bohr.
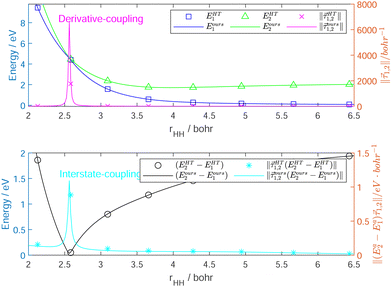
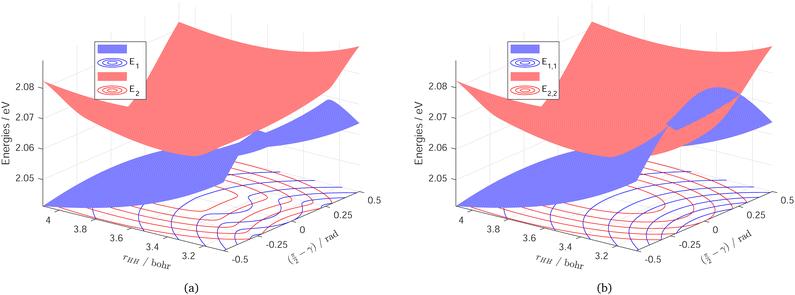
Fig. 6 shows the fitting accuracy of the constructed Hd near the seam along the surface conical intersection. Adiabatic (E1 and E2) and diabatic (E1,1 and E2,2) potential energy curves with the norm of the derivative-coupling vector (![[small tau, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1ca.gif) 1,2) are plotted against rHH near the MEX. The curves are not crossing through the MEX, because otherwise nothing could be seen but an extremely large singularity of the coupling, and no difference between the diabatic and adiabatic energies would appear around the MEX. The errors of the interstate coupling near the MEX region cannot vanish completely because the derivative-couplings are not the real gradients of the mixing angle, and not completely removed by the transformation and the corresponding quasi-diabatic electronic states have a weak dependence on the nuclear coordinates.
1,2) are plotted against rHH near the MEX. The curves are not crossing through the MEX, because otherwise nothing could be seen but an extremely large singularity of the coupling, and no difference between the diabatic and adiabatic energies would appear around the MEX. The errors of the interstate coupling near the MEX region cannot vanish completely because the derivative-couplings are not the real gradients of the mixing angle, and not completely removed by the transformation and the corresponding quasi-diabatic electronic states have a weak dependence on the nuclear coordinates.
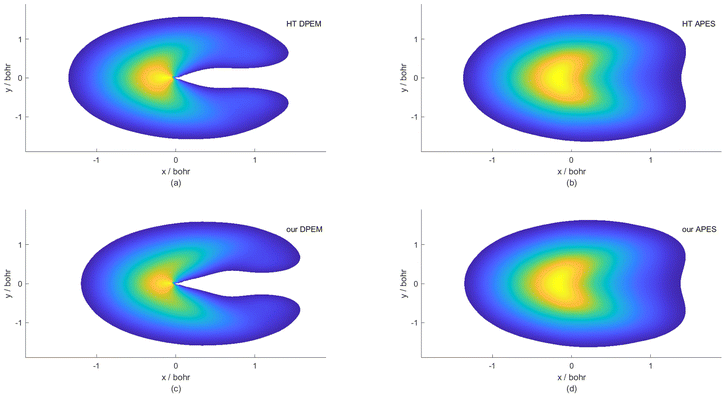
The final DPEM and APESs are represented in Fig. 7 and Fig. 8. Fig. 7 shows the first two surfaces of NaH2 and their conical intersection in both adiabatic and diabatic representation in the g–h plane. The opposite cones could be seen in the adiabatic energy surfaces, while they merge and disappear in the diabatic representation to form two crossing smooth surfaces. Fig. 8 shows the first two surfaces of NaH2 in adiabatic and diabatic representation in the Jacobi coordinates with the distance of Na from the center of HH mass fixed at 3.0 bohr. In this perspective, the CI seams could be well described in the adiabatic energy surfaces, while it is transformed to an ordinary intersection in the diabatic representation. It is important to note that the energy hyper-surfaces are smoothed in both 3 dimensions of the reactive system in the diabatic representation, which are much easier to fit than the adiabatic energy surfaces.
3.2 Dynamics on the DPEM
In this work, the non-adiabatic coupling effect of the CI between the two states is carefully considered to perform the adiabatic–diabatic transformation by integrating the diabatic potential gradient difference fitting procedure. Accurate quantum dynamic calculations serve as a powerful tool for exploring and comparing the features of potential energy surfaces.50,55 To demonstrate the qualities of the diabatization and NN fitting, we conducted quantum dynamic calculations that provided accurate results on the surfaces. These calculations are performed on both the benchmark and our DPEMs, respectively. The numerical parameters for the quantum time-dependent wave packet calculations56,57 are shown in Table 3. The initial wave packet was placed on the excited electronic state with H2 in its ground ro-vibrational state.| Grid range and size | R ∈ [0.8, 13.6] | N R = 256 |
| Rotational basis size | r ∈ [0.8, 13.6] | N r = 256 |
| j min = 0 | N j = 64 | |
| j max = 130 | ||
| Initial wave packet | E 0 = 1.0 eV | R 0 = 13.0 |
| ΔR = 0.01 | ||
| Dividing plane | r = 3.0 | |
| Total propagation | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.0 iterations 000.0 iterations |
|
| Time step | 20.0 attoseconds | |
| Energy step | 0.0001 | |
| Highest J | 100 |
In the vicinity of a CI, electronic states strongly interact with each other through derivative-couplings, which the BO approximation neglects.58,59 It has been pointed out that conducting dynamic studies in the adiabatic representation without considering the geometric phase (GP) factor may yield qualitatively inaccurate outcomes.59–61 In Fig. 9, the wave functions of the two lowest-lying states obtained in the g–h plane are compared in the diabatic and adiabatic representations, respectively, in the quantum mechanical framework. The time-dependent wave packet calculations on HT and our DPEMs reveal a node on the right side (x > 0) in Fig. 9(a) and (c), respectively, demonstrating that the non-adiabatic interactions around the CI region interfere. The GP makes parts of a nuclear wave packet traveling on different sides from the CI point to acquire the opposite phases. In the adiabatic representation, on the other hand, such a node is absent in Fig. 9(b) and (d) due to the fact that the geometry-dependent phase factor is missing. These conclusions are consistent with the recent work of Izmaylov and co-workers,62–64 which explored the GP effects on nuclear dynamics of the isolated subsystem. It should be noted that there is a slight disparity in the magnitude of the wave functions obtained from HT and our DPEMs. This difference may be due to the fact that the fitted relative values of derivative-coupling for geometries near the MEX on our DPEM are not as large as those on the HT DPEM.
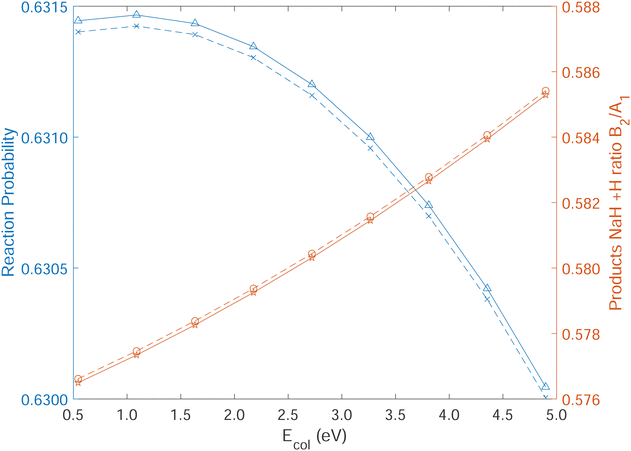
In Fig. 10, the reaction probabilities for the Na(3p) + H2 (ν = 0, j = 0) → NaH(ν ≤ 5, j ≤ 100) + H reaction are calculated using the time-dependent wave packet approach. The initial wave packet is placed on the excited electronic state with H2 in its ground ro-vibrational state to simulate the electronically nonadiabatic reaction involving CI. Despite the very slight difference for population ratio (B2/A1), the original DPEM and our newly constructed one yield almost identical product population ratios over a wide energy range, which validates our new diabatization method and NN fitting procedures.
4 Summary and conclusions
In this work, a new scheme for the construction of a quasi-diabatic representation is proposed. By integrating ∇(Ed1,1 − Ed2,2), this method is capable of performing high-precision ADT transformations, with a unique advantage in effectively handling the significant fluctuations in derivative-couplings caused by CI seams. The above scheme is applied to the DPEM construction of the Na(3p) + H2 → NaH + H reaction, including the exciplex and the MEX properly. The produced DPEM can effectively describe nonadiabatic processes involving different electronic states. Quantum dynamical calculations were performed on the new DPEM and the previous benchmark DPEM, and the obtained results demonstrate the effectiveness of our scheme. This approach is expected to be extended to larger molecular systems, and would be helpful for dynamics simulations of nonadiabatic processes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (no. 22133003, 22320102004) and the Beijing Municipal Natural Science Foundation (no. 8212043). We thank Professor David R. Yarkony for the valuable discussions on the derivative-coupling based fitting procedure. We thank Professor Burkhard Schmidt and Professor Ulf Lorenz for providing the codes for time-dependent wave packets and many discussions on the QD calculations.References
- C. Petrongolo, G. Hirsch and R. J. Buenker, Mol. Phys., 1990, 70, 825–834 CrossRef CAS.
- C. R. Evenhuis and M. A. Collins, J. Chem. Phys., 2004, 121, 2515–2527 CrossRef CAS PubMed.
- S. Nangia and D. G. Truhlar, J. Chem. Phys., 2006, 124, 124309 CrossRef PubMed.
- Y. Guan, D. H. Zhang, H. Guo and D. R. Yarkony, Phys. Chem. Chem. Phys., 2019, 21, 14205–14213 RSC.
- Y. Shu and D. G. Truhlar, J. Chem. Theory Comput., 2020, 16, 6456–6464 CrossRef CAS PubMed.
- C. L. Malbon, B. Zhao, H. Guo and D. R. Yarkony, Phys. Chem. Chem. Phys., 2020, 22, 13516–13527 RSC.
- Y. Shen and D. R. Yarkony, J. Phys. Chem. A, 2020, 124, 4539–4548 CrossRef CAS PubMed.
- Y. Liu, H. Song, D. Xie, J. Li and H. Guo, J. Am. Chem. Soc., 2020, 142, 3331–3335 CrossRef CAS PubMed.
- Y. Liu and J. Li, J. Phys. Chem. Lett., 2022, 13, 4729–4738 CrossRef CAS PubMed.
- P. Botschwina, W. Meyer, I. V. Hertel and W. Reiland, J. Chem. Phys., 1981, 75, 5438–5448 CrossRef CAS.
- H. Werner and W. Meyer, J. Chem. Phys., 1981, 74, 5802–5807 CrossRef CAS.
- L. S. Cederbaum, J. Schirmer and H. D. Meyer, J. Phys. A: Math. Gen., 1989, 22, 2427 CrossRef.
- A. J. Dobbyn and P. J. Knowles, Mol. Phys., 1997, 91, 1107–1124 CAS.
- W. Domcke, D. R. Yarkony and H. Koppel, Conical Intersections, World Scientific, 2004 Search PubMed.
- H. Köuppel, W. Domcke and L. S. Cederbaum, Multimode Molecular Dynamics Beyond the Born-Oppenheimer Approximation, John Wiley Sons, Ltd, 2007, pp. 59–246 Search PubMed.
- M. Boggio-Pasqua, A. I. Voronin, P. Halvick, J.-C. Rayez and A. J. C. Varandas, Mol. Phys., 2010, 98, 1925–1938 CrossRef.
- V. C. Mota, P. J. S. B. Caridade and A. J. C. Varandas, Int. J. Quantum Chem., 2011, 111, 3776–3785 CrossRef CAS.
- D. Opalka and W. Domcke, J. Chem. Phys., 2013, 138, 224103 CrossRef PubMed.
- D. M. G. Williams and W. Eisfeld, J. Chem. Phys., 2018, 149, 204106 CrossRef PubMed.
- F. G. D. Xavier and A. J. C. Varandas, Mol. Phys., 2021, 119, e1904157 CrossRef.
- Y. Guan, D. R. Yarkony and D. H. Zhang, J. Chem. Phys., 2022, 157, 014110 CrossRef CAS PubMed.
- Y. Shu, Z. Varga, S. Kanchanakungwankul, L. Zhang and D. G. Truhlar, J. Phys. Chem. A, 2022, 126, 992–1018 CrossRef CAS PubMed.
- J. Chen, H. Zhang, L. Zhou, X. Hu and D. Xie, Phys. Chem. Chem. Phys., 2023, 25, 26032–26042 RSC.
- J. Wang, F. An, J. Chen, X. Hu, H. Guo and D. Xie, J. Chem. Theory Comput., 2023, 19, 2929–2938 CrossRef CAS PubMed.
- Y. Hong, Z. Yin, Y. Guan, Z. Zhang, B. Fu and D. H. Zhang, J. Phys. Chem. Lett., 2020, 11, 7552–7558 CrossRef CAS PubMed.
- X. Zhu, Dissertation: The Quasi-Diabatic Hamiltonian Approach to Accurate and Efficient Nonadiabatic Dynamics with Correct Treatment of Conical Intersection Seams, Johns Hopkins University, Baltimore, Maryland, 2014 Search PubMed.
- D. R. Yarkony, J. Chem. Phys., 1996, 104, 2932–2939 CrossRef CAS.
- D. Yarkony, Rev. Mod. Phys., 1996, 68, 985–1013 CrossRef CAS.
- D. R. Yarkony, J. Chem. Phys., 2004, 121, 628–631 CrossRef CAS PubMed.
- M. S. Schuurman and D. R. Yarkony, J. Chem. Phys., 2007, 127, 094104 CrossRef PubMed.
- X. Zhu and D. R. Yarkony, J. Chem. Phys., 2012, 136, 174110 CrossRef PubMed.
- X. Zhu and D. R. Yarkony, J. Phys. Chem. A, 2015, 119, 12383–12391 CrossRef CAS PubMed.
- Y. Wang and D. R. Yarkony, J. Chem. Phys., 2018, 149, 154108 CrossRef PubMed.
- M. Baer, Beyond Born–Oppenheimer: Conical Intersections and Electronic Nonadiabatic Coupling Terms, John Wiley & Sons, Inc., 2006 Search PubMed.
- M. A. Collins, O. Godsi, S. Liu and D. H. Zhang, J. Chem. Phys., 2011, 135, 234307 CrossRef PubMed.
- Z. Yin, B. J. Braams, Y. Guan, B. Fu and D. H. Zhang, Phys. Chem. Chem. Phys., 2021, 23, 1082–1091 RSC.
- I. V. Hertel, Collisional Energy-Transfer Spectroscopy with Laser-Excited Atoms in Crossed Atom Beams: A New Method for Investigating the Quenching of Electronically Excited Atoms by Molecules, John Wiley and Sons, Ltd, 1981, pp. 341–398 Search PubMed.
- D. R. Yarkony, J. Chem. Phys., 1986, 84, 3206–3211 CrossRef CAS.
- M. D. Hack and D. G. Truhlar, J. Chem. Phys., 1999, 110, 4315–4337 CrossRef CAS.
- D. W. Schwenke, S. L. Mielke, G. J. Tawa, R. S. Friedman, P. Halvick and D. G. Truhlar, Chem. Phys. Lett., 1993, 203, 565–572 CrossRef CAS.
- W. T. Zemke, R. E. Olson, K. K. Verma, W. C. Stwalley and B. Liu, J. Chem. Phys., 1984, 80, 356–364 CrossRef CAS.
- J. A. Silver, N. C. Blais and G. H. Kwei, J. Chem. Phys., 1979, 71, 3412–3427 CrossRef CAS.
- E. Gislason, A. Kleyn and J. Los, Chem. Phys., 1981, 59, 91–109 CrossRef CAS.
- A. Thiel and H. Koppel, J. Chem. Phys., 1999, 110, 9371–9383 CrossRef CAS.
- D. R. Yarkony, J. Chem. Phys., 1996, 105, 10456–10461 CrossRef CAS.
- C. L. Malbon, X. Zhu, H. Guo and D. R. Yarkony, J. Chem. Phys., 2016, 145, 234111 CrossRef PubMed.
- C. L. Malbon and D. R. Yarkony, J. Chem. Phys., 2017, 146, 134302 CrossRef PubMed.
- Y. Wang, Y. Guan and D. R. Yarkony, J. Phys. Chem. A, 2019, 123, 9874–9880 CrossRef CAS PubMed.
- Y. Guan and D. R. Yarkony, J. Phys. Chem. Lett., 2020, 11, 1848–1858 CrossRef CAS PubMed.
- F. Li, X. Yang, X. Liu, J. Cao and W. Bian, ACS Omega, 2023, 8, 17296–17303 CrossRef CAS PubMed.
- F. Li, X. Liu, X. Yang, J. Cao and W. Bian, Chin. J. Chem. Phys., 2023, 36, 545–552 CrossRef CAS.
- H. Longuet-Higgins, Mol. Phys., 1963, 6, 445–460 CrossRef CAS.
- O. Godsi, C. R. Evenhuis and M. A. Collins, J. Chem. Phys., 2006, 125, 104105 CrossRef PubMed.
- S. Wang, Z. Yang, J. Yuan and M. Chen, Sci. Rep., 2018, 8, 17960 CrossRef CAS PubMed.
- J. Luo, J. Cao, H. Liu and W. Bian, Chin. J. Chem. Phys., 2022, 35, 185–192 CrossRef CAS.
- B. Schmidt and U. Lorenz, Comput. Phys. Commun., 2017, 213, 223–234 CrossRef CAS.
- B. Schmidt and C. Hartmann, Comput. Phys. Commun., 2018, 228, 229–244 CrossRef CAS.
- X. Liu, W. Bian, X. Zhao and X. Tao, J. Chem. Phys., 2006, 125, 074306 CrossRef PubMed.
- Y. Wu, C. Zhang and H. Ma, RSC Adv., 2017, 7, 12074–12084 RSC.
- H. von Busch, V. Dev, H.-A. Eckel, S. Kasahara, J. Wang, W. Demtröder, P. Sebald and W. Meyer, Phys. Rev. Lett., 1998, 81, 4584–4587 CrossRef CAS.
- M. Keil, H.-G. Kramer, A. Kudell, M. Baig, J. Zhu, W. Demtroder and W. Meyer, J. Chem. Phys., 2000, 113, 7414–7431 CrossRef CAS.
- I. G. Ryabinkin and A. F. Izmaylov, Phys. Rev. Lett., 2013, 111, 220406 CrossRef PubMed.
- L. Joubert-Doriol, I. G. Ryabinkin and A. F. Izmaylov, J. Chem. Phys., 2013, 139, 234103 CrossRef PubMed.
- A. F. Izmaylov, J. Li and L. Joubert-Doriol, J. Chem. Theory Comput., 2016, 12, 5278–5283 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00375f |
| This journal is © the Owner Societies 2024 |