Monitoring the state of charge of vanadium redox flow batteries with an EPR-on-a-Chip dipstick sensor

Abstract

The vanadium redox flow battery (VRFB) is considered a promising candidate for large-scale energy storage in the transition from fossil fuels to renewable energy sources. VRFBs store energy by electrochemical reactions of different electroactive species dissolved in electrolyte solutions. The redox couples of VRFBs are VO²⁺/VO₂⁺ and V²⁺/V³⁺, the ratio of which to the total vanadium content determines the state of charge (SOC). V(IV) and V(II) are paramagnetic half-integer spin species detectable and quantifiable with electron paramagnetic resonance spectroscopy (EPR). Common commercial EPR spectrometers, however, employ microwave cavity resonators which necessitate the use of large electromagnets, limiting their application to dedicated laboratories. For an SOC monitoring device for VRFBs, a small, cost-effective submersible EPR spectrometer, preferably with a permanent magnet, is desirable. The EPR-on-a-Chip (EPRoC) spectrometer miniaturises the complete EPR spectrometer onto a single microchip by utilising the coil of a voltage-controlled oscillator as both microwave source and detector. It is capable of sweeping the frequency while the magnetic field is held constant enabling the use of small permanent magnets. This drastically reduces the experimental complexity of EPR. Hence, the EPRoC fulfils the requirements for an SOC sensor. We, therefore, evaluate the potential for utilisation of an EPRoC dipstick spectrometer as an operando and continuously online monitor for the SOC of VRFBs. Herein, we present quantitative proof-of-principle submersible EPRoC experiments on variably charged vanadium electrolyte solutions. EPR data obtained with a commercial EPR spectrometer are in good agreement with the EPRoC data.

---

1 Introduction

The climate crisis is one of the major challenges humanity faces today. To mitigate its impacts, anthropogenic greenhouse gas emissions need to be net neutral or even negative as soon as possible. To this end, a transition from a fossil fuel-based economy to one based on renewable power sources such as wind power and photovoltaics is necessary and paramount to success. Due to the intermittent nature of these renewable energies, both energy generation and storage solutions play a vital role in this transition. Hitherto, pumped hydroelectric storage utilising the gravitational potential has been most widely used for the latter purpose. The high cost of construction and the special geographical requirement, however, limit the adoption of this technology on a larger scale. Therefore, the demand for alternative storage solutions is vast. Among other techniques, redox flow batteries (RFB) are considered promising candidates as a storage of chemical energy due to their scalability, flexibility, fast response, relatively low capital cost and other features.^1–3

The energy conversion in an RFB takes place in an electrochemical cell consisting of anode and cathode half-cells filled with anolyte (negative electrolyte) and catholyte (positive electrolyte) solutions, respectively, separated by an ion-exchange membrane.⁴ The electrodes are typically comprised of porous graphite-felt materials to enhance the surface area, the ion-exchange membrane is typically Nafion, and the internal current collectors, often called bipolar plates, are made from graphite composite materials while the external current collectors are most often made from copper.^4,5 In the case of the vanadium redox flow battery² (VRFB), four major oxidation states of vanadium are utilized to store the energy. The respective redox coupes are: V²⁺/V³⁺ and VO²⁺/VO₂⁺, with corresponding oxidation states V(II)/V(III) and V(IV)/(V). More specifically, the redox couple of the anolyte is V²⁺/V³⁺ with the electrochemical reaction given by

V³⁺ + e⁻ ↔ V²⁺; E_anode = −0.255 V (1)

and the redox couple of the catholyte is VO²⁺/VO₂⁺ with the electrochemical reaction given by

VO²⁺ + H₂O − e⁻ ↔ VO₂⁺ + 2H⁺; E_cathode = 1.004 V. (2)

During charge, trivalent (V³⁺) ions are reduced to bivalent (V²⁺) ions at the anode (eqn (1)), while tetravalent vanadium (VO²⁺) ions are oxidized to pentavalent vanadium (VO₂⁺) at the cathode (eqn (2)). In the case of a cation-exchange membrane, positively charged hydronium ions (H₃O⁺) move through the selective membrane to ensure electrical neutrality of the electrolytes. During discharge, the processes are reversed. The vanadium reactions are typically performed in mid-concentrated aqueous sulfuric acid (≈2 mol l⁻¹), resulting in a 1.5–1.8 mol l⁻¹ vanadium solution, maximizing solubility of vanadium under these conditions and resulting in theoretical capacities¹ of around 20–25 W h l⁻¹.

In an ideal charging/discharging process, the amount of oxidised and reduced species remains constant during subsequent battery cycles so that the electrolytes remain balanced, i.e., the amount of VO²⁺ and V³⁺ as well as VO₂⁺ and V²⁺ in the electrolytes is equal, respectively. Both the ratios of VO²⁺ and V²⁺ to the total vanadium concentration define the state of charge (SOC) of the VRFB. This carries the unique advantage of utilizing the same element (V) in both half cells relative to other RFB technologies, greatly reducing problems associated with cross-contamination, such as loss of active material or undesirable chemical reactions,⁶ and thereby extending the effective lifetime of the electrolyte solutions.⁴ Still, electrolyte imbalance is the main driver for performance degradation and capacity loss. While concentration imbalances caused by, e.g., water crossover through the membrane,⁷ differential transfer of vanadium ions or volumetric transfer of electrolyte between half cells may be corrected by periodic electrolyte remixing,⁸ imbalances due to oxidation of the V²⁺ ions in the negative half-cell caused by, e.g., gassing due to impurities or hydrogen evolution⁹ as well as due to the reduction of VO₂⁺ caused by, e.g., corrosion of battery materials or precipitation of VO₂⁺ at higher temperatures, require more rigorous processes such as electrochemical rebalancing.^3,8 Electrolyte remixing is not sufficient in this case, since an additional oxidation or reduction process is necessary to restore the equilibria of VO²⁺ and V³⁺ as well as VO₂⁺ and V²⁺, respectively.^8,9

These problems may be mitigated if detected early. Therefore, several methods have been developed to monitor SOC, such as open cell potential,^10–13 conductivity,^4,8,14 UV-vis absorption^8,15 and transmission,¹⁶ IR absorption,¹⁷ viscosity,¹⁸ hydraulic pressure monitoring¹⁹ or a combination thereof. Grossmith et al. demonstrated that the application of Beer's Law to vanadium electrolyte systems is only valid up to 0.04 mol l⁻¹, preventing UV-vis absorption techniques from being applied directly at the high vanadium concentrations present in the VRFB half cells.^4,15 Skyllas-Kazacos et al. patented the first independent SOC measurement system based on conductivity, allowing the SOC of each half-cell to be measured independently, replacing the previously dominant open-circuit potential measurements.^4,10 Other monitoring methods that utilize conductivity, potential, and current measurements have been proposed; however, they require significant modelling due to indirect measurements of vanadium and electrolyte concentrations.^11–14 Additionally, a rather creative system was proposed to monitor and manipulate hydraulic pressures in the half cells by regulation of gas pressure; however, expanding this method to include viscosity considerations required the use of complex computations and a neural network for optimization.^18,19 Most measurements suffer from indirectly measured variables (viscosity, conductivity, density), which can greatly change if the flux of water is considered. Potentiometric measurements with reference electrodes on the other hand have the problem of required periodic maintenance, which makes long-duration measurements in a remote battery relatively challenging and unreliable. Therefore, a direct quantification of vanadium species in the electrolyte is highly desirable.

Alternative methods utilizing electron paramagnetic resonance (EPR) have been proposed recently as a direct measurement of vanadium (VO²⁺, V(IV)) concentration to monitor SOC as well as ion diffusion into the Nafion membrane.^20,21 EPR is a quantitative spectroscopic method to detect paramagnetic species and is a frequently used tool in physics, chemistry, biology, and materials science to investigate transition metal ions.^22,23 Though monitoring methods utilising EPR have only been explored so far for the VO²⁺ (S = 1/2)/VO₂⁺ (S = 0) cycle, it has been shown previously that V²⁺ (S = 1/2 or 3/2) and V³⁺ (S = 1) may also be monitored by EPR; however, in many cases, these methods employ high frequencies and high magnetic fields that are not easily amenable to in situ operation.^24,25 Like the studies of the VO²⁺ system, V³⁺ has been shown in mixed-valence systems using parallel mode EPR at X-band.²⁶ In a study of the reactions of vanadyl N and C capped trisphenolate complexes, Soshnikov et al. demonstrated the ability to differentiate between VO²⁺ and V²⁺ in the reaction mixtures by using standard X-band, perpendicular mode EPR.²⁷ The many investigations by Lawton et al. on the interactions of vanadium with the Nafion membrane and the electrolyte solution using EPR demonstrate the wealth of information obtainable.^20,28–30 It is, in theory, possible to monitor V²⁺, V³⁺, and VO²⁺ concentrations, the mobility of the VO²⁺ ions both in solution and in the membrane, and the diffusion of V²⁺, V³⁺, and VO²⁺ across the membrane directly using only EPR spectroscopy. These unique features render EPR spectroscopy optimal for monitoring the SOC of VRFBs. For a commercial application of EPR as an online monitoring tool for the SOC of VRFBs, a small, robust, and cost-effective EPR sensor with a time resolution relevant to the charge/discharge cycling time and submersible in the V electrolyte solutions is preferable.

Commercially available EPR spectrometers usually employ microwave (MW) cavity resonators with large quality factors, Q, providing spatially separated electric and magnetic components of the MW. The size of these MW resonators is determined by the employed MW frequency, and for the X-band (9.8 GHz) is of the order of a few cm. To avoid non-resonant absorption of the electric field component, the sample volume is typically confined by a sample tube with a diameter of a few millimetres (in case of polar solvents only a few μm), which is then inserted in the centre of the resonator or is flowed through the centre of the resonator as in, e.g., ref. 28, where the electric component of the MW is at a minimum and the magnetic component of the MW is maximal. The response of the sample is detected via the reflected MW using a MW bridge. To obtain the EPR resonance condition, an external magnetic field perpendicular to the magnetic field of the MW is swept using an electromagnet, while the MW frequency is kept constant. For these reasons, current commercial EPR spectrometers are relatively bulky, with typical dimensions from several tens of centimetres for benchtop X-band spectrometers to several meters for high-end research spectrometers. In addition, the prices of these spectrometers are relatively high, ranging from 50 000 € for small benchtop spectrometers to over 1 000 000 € for high-sensitivity spectrometers, limiting their use to research laboratories. Therefore, a complete redesign of the EPR spectrometer is necessary to achieve the goal of a small, cost-effective submersible EPR spectrometer.

To this end, several miniaturized EPR spectrometers have been developed over the years, such as a handheld EPR spectrometer for transcutaneous oximetry,³¹ an EPR “dipstick” spectrometer,³² the EPR mobile-universal-surface-explorer (EPR-MOUSE)³³ and a compact EPR spectrometer based on a marginal oscillator for monitoring automobile lubricant degradation.³⁴ Yet, most of these designs still require a microwave bridge to which they are interfaced, limiting their application to research laboratories. Significant progress in semiconductor fabrication technology has propelled the design of new EPR spectrometers that are fully integrated into a single silicon microchip, so-called EPR-on-a-Chip (EPRoC) devices.^35–39 These EPRoC devices either integrate a conventional microwave bridge or variants thereof in a single integrated circuit^37,39 and use a fixed-frequency oscillator^35,36 or a voltage-controlled oscillator (VCO)³⁸ to detect the EPR signal. In the latter approach, a miniaturized coil with a diameter of a few hundred micrometres is part of a voltage-controlled LC oscillator circuit and serves as both microwave source and EPR detector. The idea of using a VCO instead of a microwave bridge to excite and detect the nuclear magnetic resonance (NMR) signal was first proposed in 1950.⁴⁰ Importantly, this approach circumvents the classical trade-off between resonator Q and detection sensitivity,⁴¹ enabling frequency-swept EPR over wide bandwidths with near-constant sensitivity. This allows the use of permanent magnets for smaller, cost-effective, battery-driven spectrometers, as recently demonstrated.^38,42–44 Building on the success of VCO-based EPR spectrometers, we herein present proof-of-principle quantitative EPRoC fluid-submersible “dipstick” experiments on V electrolyte solutions with different SOCs still using an electromagnet, which are then compared with spectra obtained using a commercial resonator-based EPR spectrometer. The quantitation of the data obtained with the EPRoC and with the commercial EPR spectrometer yields similar results showing the possibility to utilise EPRoC as an online SOC monitoring sensor for VRFBs.

2 Results

2.1 EPRoC FM spectrum

With the EPRoC both dispersion-like^35,36,45 (frequency-modulated, FM) and absorption-like^46,47 (amplitude-modulated, AM) signals may be detected, while with resonator-based EPR usually only a field-modulated absorption EPR signal is measured. In this work, we only analyse the FM spectra as they benefit from the VCO-array concept, which will be discussed in Section 3 below. EPRoC FM-detected field-swept spectra of V electrolyte solutions with different states of charge corresponding to different concentrations of vanadyl ions (VO²⁺ (S = 1/2)) are shown in Fig. 1(a). The spectra of the samples between 0% and 79% SOC exhibit eight EPR lines with different amplitudes as expected for VO²⁺-containing samples,²⁸ while the sample with 97% SOC does not show an EPR signal due to low amount of VO²⁺ present. The spectra of the samples with an SOC of 0% to 60% show a strong exchange broadened behaviour due to the high concentration of VO²⁺ of up to 1.58 mol l⁻¹, in which the linewidth of each of the eight lines is so broad that they are overlapping, while the sample with an SOC of 79% shows only slight exchange broadening due to the lower VO²⁺ concentration (∼0.33 mol l⁻¹). To improve the SNR, the spectra were obtained using a modulation amplitude larger than would be optimal for a high-resolution spectroscopic investigation. This, however, has no negative impact on spin concentration quantification.⁴⁸ The acquisition time to obtain each full spectrum was about 3:15 hours (t_exp), which is mainly due to the time required for the settling of the magnetic field for the electromagnet and power supply used in these experiments. From the effective measurement time, t_eff = 3N_points·N_avg·τ_LIA ≈ 4593 s = 85 min, the duty cycle of the experiment may be calculated, which is about 40% (t_eff/t_exp). N_points is the number of points of the spectrum, N_avg is the number of averages, and τ_LIA is the time constant of the lock-in amplifier. The factor of 3 was introduced in the effective measurement time to account for the response time of the lock-in amplifier.

Fig. 1 Field-swept EPR spectra of V electrolyte solutions with varying states of charge (0%, 21%, 40%, 60%, 79% and 97%) corresponding to different concentrations of vanadyl ions (VO²⁺). (a) EPRoC FM spectra. The vertical lines at 400.6 and 492.8 mT show the values that are used for the two-point quantitation. The measurement time for each spectrum was 3:15 h, while the effective measurement time was 1:25 h (b) EPRoC absorption spectra obtained via Kramers–Kronig relations from the recorded FM spectra. (c) EPR absorption spectra as obtained with the X-band spectrometer. All spectra are shifted vertically such that they do not overlap. The measurement time for each X-band spectrum was 60 s.

Generally, dispersion(-like) spectra have wider wings compared to their absorption(-like) counterpart, which may lead to an apparent asymmetry. This, however, is a mere consequence of dispersion(-like) spectra such as the FM spectra shown in Fig. 1(a). Because the Kramers–Kronig relation is utilised to convert the FM-detected dispersion(-like) to absorption(-like) spectra, the apparent asymmetry is “removed” as seen in Fig. 1(b).

2.2 Comparison to resonator-based EPR

Absorption EPR spectra of the samples with SOC from 0% to 97% obtained at X-band using a commercial cavity resonator-based EPR spectrometer are shown in Fig. 1(c). For a direct comparison of these with the FM detected EPRoC, the FM signal is Hilbert transformed using the Kramers–Kronig relation; the result of which is displayed in Fig. 1(b). This method may only be invoked if the investigated spin system is unsaturated with respect to microwave power.⁴⁹ The relaxation times of the V electrolyte solutions are relatively short due to the very high VO²⁺ concentrations because of increased dipolar interactions,⁵⁰ saturation therefore is unlikely at the concentrations investigated. A saturation analysis of these samples at X-band showed only minor saturation for the highest available MW power (see Fig. S6 in ESI†) of 100 mW (B₁ ≈ 40 μT), such that no spectral distortions resulting from the Hilbert transformation are observed. The lineshape of the V electrolytes for all SOCs are well reproduced with the EPRoC and all eight lines exhibit a similar ratio of intensities when compared to the absorption spectra obtained at X-band.

In the spectra measured in a conventional X-band spectrometer, the 97% SOC sample shows a small EPR signal as expected due to the much lower VO²⁺ concentration in the sample of approximately 0.04 mol l⁻¹ compared to the samples with lower SOC, which is, however, not observed in the EPRoC spectrum.

A more rigorous analysis was performed by simulation of the FM and absorption spectra of the V-containing electrolyte solutions. Since the VO²⁺ is in solution, the spectrum exhibits an isotropic and fast-motional regime lineshape, which is confirmed by simulation using the function garlic of the EasySpin software package.⁵¹ For the simulation, a sample with an SOC of 90%, and, therefore, a lower concentration (0.16 mol l⁻¹), was used since the exchange broadened spectra of 0% to 79% SOC cannot be easily simulated and any simulation attempts lead to erroneous results.

To perform an analysis representative for the native lineshape observed at lower concentrations, the modulation amplitude was substantially decreased such that the spectrum is not broadened (cf. Section 2.1). The g- and A-tensors were determined from the simulation of a resonator-based X-band spectrum recorded at a temperature of T = 100 K as shown in Fig. 2(a), for which the spectrum is in the rigid limit and the g- and A-tensor may be directly observed from the recorded spectrum. These values are listed in Table 1 and are comparable to literature values obtained for similar V electrolyte samples.²⁰ For the simulations at room temperature as shown in Fig. 2(b) (X-band EPR) and (c) (EPRoC), the only free parameter is the rotational correlation time, τ_R, with no additional convolutional broadening. The rotational correlation time at X-band, τ_R,X, and EPRoC, τ_R,EPRoC, are similar and in good agreement. Both simulations show a good agreement with the experimental data, as seen by the residuals plotted in Fig. 2.

Fig. 2 Experimental field-swept spectra (black solid line), simulation (blue dashed line) and residual (subtraction of experimental and simulated spectrum; green solid line) of the V electrolyte with 90% SOC corresponding to 0.16 mol l⁻¹ VO²⁺ investigated with (a) resonator-based X-band EPR at 100 K, (b) resonator-based X-band EPR at room temperature and (c) EPRoC FM at room temperature. A frequency-swept spectrum (orange solid line denoted with f-sweep) with a sweep width of ∼1 GHz around the centre MW frequency of 14.34 GHz and recorded with the same experimental settings as the field-swept spectrum covering the first two transitions is plotted on the g-axis at the bottom and is vertically shifted by −0.4 kHz for better visibility. (Please note, the g-axis only applies to (c) and the magnetic field axis does not apply to the frequency-swept spectrum orange solid line).

Table 1 Parameters of the spin system of the V electrolyte SOC 90%. Please note that the convolutional Gaussian broadening was applied to the resonator-based X-band spectrum at 100 K only

Quantity	Value	Standard deviation
g ⊥	1.9798	0.0001
g ‖	1.9349	0.0001
A ⊥/MHz	206.9	0.1
A ‖/MHz	544.6	0.3
τ R,EPRoC/ns	0.15	0.01
τ R,X/ns	0.13	0.01
ΔBG/mT	1.76	0.01

---

In addition, a frequency-swept FM EPRoC spectrum of the same sample recorded with the same experimental settings as the field-swept FM EPRoC spectrum with a sweep width of ∼1 GHz around the centre MW frequency of f = 13.44 GHz at a fixed magnetic field of B₀ = 480.6 mT is shown in Fig. 2(c). To compare field- and frequency-swept spectra, both are plotted against a g-axis shown below the magnetic field axis in Fig. 2(c). The g-axis is calculated by g = hf/μ_BB₀, which is a reformulation of the resonance condition, where h is Planck's constant and μ_B is the Bohr magneton. Due to the limited frequency sweep width of the EPRoC, only two of the eight transitions may be recorded in a single scan. While the signal shape is the same for both spectra, demonstrating the equivalence of the two, the noise of the frequency-swept spectrum is slightly higher than that of the field-swept spectrum. The duty cycle of the frequency sweep is >90%, effectively improving the duty cycle by more than a factor of 2.

The absolute SNRs of the resonator-based EPR spectra are much higher (160–3100) than that of the EPRoC FM spectra (40–80) (cf.Fig. 1). Considering the different measurement times to acquire a spectrum using the two different instruments (resonator-based EPR: 60 s, EPRoC: 4593 s) it becomes clear that the SNR per second is between 20 and 400 for resonator-based EPR and about 1 for EPRoC, respectively. The sample volume used in the resonator-based EPR spectrometer measurements is about 50 μl, which is about 5 × 10⁴ larger than the active volume of the EPRoC⁵² (∼1 nl). Therefore, it can be concluded that the EPRoC shows an approximate 100–470 times (cf.Table 2) better absolute sensitivity than resonator-based EPR. This finding agrees well with estimations of the theoretical spin sensitivities of this EPRoC sensor⁴⁵ of approximately 2 × 10⁸ spins (cf. calculation in the ESI:† S2) and of the resonator-based EPR spectrometer operating at X-band of approx. 10¹¹ spins.⁵³

Table 2 Comparison of the SNR and sample volumes of the EPRoC FM and the resonator-based X-band spectra

SOC %	SNREPRoC s^−1 μl^−1	SNRX s^−1 μl^−1	SNREPRoC/SNRX 1
−0.19	660	2.0	320
20.53	720	2.0	360
40.09	1040	2.2	470
60.01	810	3.9	210
79.03	790	8.0	100
97.28	NA	0.4	NA

---

For the X-band measurement, the actual measurement time rather than the effective measurement time was used for comparison as the X-band spectrometer which has a duty cycle approaching 100%.

2.3 Quantitation

2.3.1 Estimations of SOC using the entire spectrum. The quantitation of the EPRoC FM data and the X-band EPR absorption data is shown in Fig. 3(a). The EPR signal intensity for the X-band data was determined by double integration. Since the FM spectra are dispersion-like, the double integration results in zero intensity because the dispersion is an odd function with symmetry about the resonance field/frequency, assuming a Lorentzian lineshape, of which the integral (area under the curve) is always zero. To avoid this problem, instead of the FM spectra, the Hilbert transform shown in Fig. 1(b) was used for double integration (cf. Fig. S5 in ESI†). For a comparison of the EPR absorption and the EPRoC signal intensities, all data are normalised to the maximum values obtained within each dataset, respectively. The signal intensity decreases with increasing SOC (decreasing VO²⁺ concentration) as expected from earlier reports on the dependence of the signal intensity.²⁸ Linear regressions of the datasets show that their slopes are similar (−0.0103) for the X-band EPR absorption and the Hilbert transformed, doubly integrated EPRoC data (−0.0104).

Fig. 3 Quantitation of the V electrolyte solution VO²⁺. (a) EPR signal intensity obtained by double integration of the complete X-band EPR spectra and of the complete Hilbert transformed doubly integrated (DI) EPRoC FM spectra. The error bars show the standard error. (b) Signal amplitude from a two-point measurement via on- and off-resonance data collection (denoted as “Two-point truncation”) at field values of 492.8 and 400.6 mT, respectively. The same data points were extracted from the full spectra shown in Fig. 1 and are denoted as “Full spectrum”. The actual and effective measurement time of the two-point measurement were similar and approximately 10 minutes. The error bars are calculated from the standard deviation of the baseline regions of the spectra for the full spectrum analysis and from the standard error of the experimental data from the two-point truncation experiment as described in Section 5.4.

2.3.2 Estimations of SOC using a two-point measurement. To drastically reduce the measurement time for quantitation of the SOC, a simplified method based on only two measurement points was evaluated. Rather than using the complete EPRoC spectrum for quantitation of the SOC, the signal amplitude (y-distance between the two points) is instead used as an indication of the SOC. In principle, the signal amplitude may also be obtained at one fixed magnetic field and microwave frequency, i.e., a single point instead of two if the spectrometer and overall environment are sufficiently stable. However, since the oscillation frequency of the VCO is temperature-dependent, a slight temperature shift would yield false or otherwise inaccurate SOC measurements. Temperature shifts could be mitigated with a temperature control loop that can in principle be integrated into a sensor device; however, it was not available for these experiments. Therefore, the experiment was performed with two field points: one off-resonance point and one on-resonance point, which took about 10 minutes in total to acquire, leading to a reduction of the experimental time by a factor of ∼180 compared to recording the entire spectrum. To quantify the SOC in a device, a calibration curve mapping the SOC to each signal amplitude is required and is depicted in Fig. 3(b). The field values for this experiment were 400.6 mT (off-resonance) and 492.8 mT (slightly right of the 2nd transition in the spectrum as indicated in Fig. 1(a)). The data are strictly monotonically decreasing and are therefore suited for the determination of the SOC. The monotonic decrease is not linearly correlated due to spin-dependent broadening at high VO²⁺ concentrations (low SOC). In principle, for samples with a low concentration of paramagnetic species for which no concentration broadening occurs, the calibration curve is expected to be linear as seen in ref. 28 where electrolyte solutions with a much lower concentration of VO²⁺ (∼100× less) were investigated. Generally, many field points fulfil the requirement of being strictly monotonically decreasing with increasing SOC and the value of 492.8 mT was arbitrarily chosen for this proof-of-principle experiment.

3 Discussion

Summarising the main results of this work, it was found that the quantitation of the field-swept EPRoC FM spectra of differentially charged catholyte solutions of a VRFB yields a linear relationship of the EPR signal intensity with respect to the SOC with a slope similar to data obtained with a resonator-based X-band spectrometer. In addition, it was shown that the SOC may also be monitored using only two magnetic field points of the spectrum due to the strictly monotonically decreasing behaviour of the signal amplitude as a function of the SOC. In general, a single-point measurement without any sweep, i.e., at a fixed MW frequency and fixed magnetic field, would also suffice if the monitoring setup were properly calibrated and the environment sufficiently stable.

Furthermore, both, spectra obtained with an X-band spectrometer and EPRoC of a 90% SOC catholyte solution could successfully be simulated and the spin system parameters obtained are comparable to literature values of similar V electrolyte samples.²⁰ The same spectral shape as for the field-swept EPRoC spectrum was found for a frequency-swept spectrum with a sweep width of 1 GHz of the same sample.

These experiments, though performed with unoptimized laboratory equipment, show the potential for applying the EPRoC as an online SOC sensor for VRFBs.

The most important parameter of an SOC sensor is the measurement time required to meet the necessary time resolution for monitoring the SOC of the VRFB. The required time resolution depends on the charge/discharge time, which is defined by the capacity and power rating. For a high-power battery, the time resolution needs to be higher than for a low-power battery with the same capacity, as the charge/discharge time of the former is shorter than for the latter. Typical charge/discharge times, t_c, of the largest commercial VRFBs range between 1 and 10 hours.⁵⁴ Therefore, to obtain an accuracy of the determined SOC of <1%, the maximum acquisition time per SOC under full load should be between approximately 36 s (t_c = 1 hour) and 360 s (t_c = 10 hours). This is the time it takes to charge/discharge the battery by 1 percentage point at the maximum power.

While the time resolution of X-band EPR spectrometer to obtain spectra with sufficient SNR for quantitation is in the order of tens of seconds, the sales prices of these devices of >50 000 € do not allow a widespread implementation in VRFBs. The full field-swept EPRoC spectra, on the other hand, required approximately 3 : 15 h. However, these experiments were performed to adequately define the spectra obtained at the SOCs investigated and required a duty cycle of approximately 40%, which can mainly be attributed to the time required for the settling of the magnetic field for the electromagnet and power supply used within these experiments. EPRoC spectra with much lower SNR in combination with suitable post-processing could be sufficient to accurately predict the SOC, lowering the acquisition time. In addition, the duty cycle of the EPRoC can be increased with frequency sweeps to about 90%, effectively improving the time resolution by a factor of ∼2, while preserving the spectral shape. In these experiments, the electromagnet was held at a constant field value, allowing for a drastic reduction in the complexity of the EPRoC sensor should a permanent magnet be used. Development and evaluations of suitable permanent magnets for use with EPRoC devices are described in ref. 55.

The most profound reduction of the acquisition time is achieved by reducing the spectral width for quantitation as we have shown via quantitation of the EPRoC signal amplitude at only two magnetic field points, which reduced the acquisition time to approximately 10 minutes, already approaching the required time resolution for SOC monitoring. Frequency stepping, fractional integration, or even a single-point measurement with a fixed MW frequency and magnetic field as mentioned above could further reduce the acquisition time, enabling calibration and measurement procedures to be tailored to real-world applications with varying t_c and monitoring requirements.

Furthermore, the acquisition time could be lowered by an improved sensitivity of the SOC sensor. Here, the simplest solution would be to average the signal from several individual EPRoC sensors placed at different locations in the battery to increase the effective sensitive volume of the EPRoC sensor. In addition to the improved SNR from the spatial averaging of multiple EPRoC sensors, an average SOC across the entire electrolyte tank is obtained. To improve the sensitivity of each individual EPRoC sensor, multiple EPRoC VCOs could also be injection-locked to form an EPRoC array sensor.⁵⁶ The injection-locking reduces the phase noise of the FM signal by n^1/2, where n is the number of EPRoC VCOs in the array. This improvement of the phase noise can directly be translated to a reduction of measurement time. For the samples used in this report, the measurement time with, e.g., a 14-VCO array EPRoC as presented in ref. 57 may be reduced by a factor of 14^1/2 ∼ 3.7. Even with this improvement, the acquisition time could be reduced to about 3 minutes, approaching the required time resolution for t_c = 10 hour. Further improvements can be achieved by increasing the sensitive volume of the individual VCO tank inductors by using the segmented coil approach presented in ref. 58.

4 Conclusions and outlook

In conclusion, we have shown quantitative room-temperature EPR-on-a-Chip experiments on paramagnetic vanadium electrolyte solutions serving as proof-of-principle experiments for a submersible dipstick EPRoC sensor stable in a harsh and corrosive, strongly acidic environment. Our experiments demonstrate a linear dependence of the EPRoC FM signal intensity on the SOC of a V electrolyte solution, reproducing the quantitative EPR results from commercial EPR spectrometers. Therefore, the results suggest that EPRoC may be utilised as an SOC sensor for VRFBs. In addition, the experiments utilising the signal amplitude calculated from only two data points showed a strictly monotonically decreasing behaviour with the SOC. Thus, this experiment allows for the monitoring of the SOC with the EPRoC on a drastically reduced measurement timescale. Furthermore, the equivalence of field and frequency sweeps of the EPRoC has been demonstrated, allowing the usage of permanent magnets, which will lower the experimental complexity.

We used the monitoring of the SOC of VRFB electrolyte solutions as a proof-of-principle experiment in a very harsh environment, but the submersible dipstick EPRoC may be used for other battery types such as tempol RFBs⁵⁹ or more generally, for detection of radicals in solution in chemistry, biology or the life sciences. Here, a paradigm shift enabling the utilisation of EPR for quantitation of radicals in solution is imaginable with a submersible battery-operated handheld frequency-swept EPRoC-based device in combination with a permanent magnet.

5 Materials and methods

5.1 EPR-on-a-chip

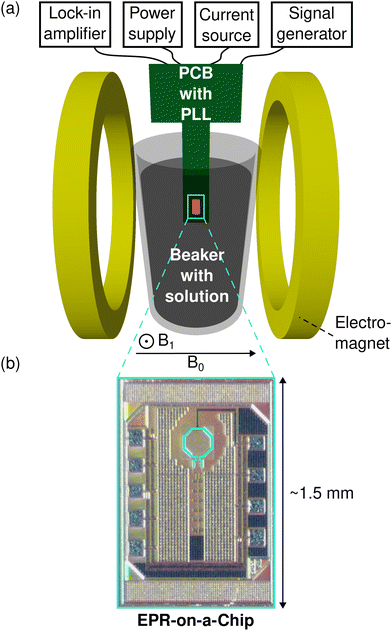
The experimental configuration of the EPR-on-a-Chip dipstick experiment is depicted in Fig. 4(a). The EPRoC sensor is located on a printed circuit board (PCB), which is submersed in the aqueous sample solution in a beaker placed between the poles of an electromagnet (Bruker B-E 25). The EPRoC is comprised of an octagonally-shaped coil embedded inside a VCO, which act as both the microwave source and detector simultaneously. In this design, the MW hardware used in the MW bridge of commercial EPR spectrometers, such as a MW source, a circulator and a diode detector, is not required. The VCO can be described as an RLC resonator combined with a cross-coupled transistor pair⁶⁰ with a negative differential resistance that serves to replenish the energy dissipated in the RLC resonator. The frequency of the VCO may be adjusted by changing the tuning voltage applied to the varactors, which in turn enables sweeping of the frequency instead of the magnetic field and will allow the use of a permanent magnet instead of an electromagnet. Therefore, this oscillator-based design enables the construction of a completely miniaturised EPRoC spectrometer with a permanent magnet in a single, standalone device. In this prototype, the EPRoC is embedded in a phased-locked loop (PLL) with a bandwidth of about 10 MHz to control the MW frequency of the dipstick EPRoC in combination with a radio frequency (RF) generator (Rohde & Schwarz, SMB100B) as the PLL frequency reference. The FM signal is recorded as a change of the tuning voltage, which is proportional to the change of the oscillation frequency due to EPR. On the EPRoC, a 32-divider/multiplier is placed such that the reference frequency for the PLL (448 MHz) results in an oscillator operating frequency of 14.34 GHz. To improve the SNR of the EPRoC signal, sinusoidal frequency modulation is applied to the reference frequency, which effectively modulates the MW carrier wave with a modulation rate, f_mod, and a peak-to-peak modulation amplitude, Δf_mod. The EPRoC signal is detected with a dual-phase lock-in amplifier (Anfatec, eLockIn 203).

Fig. 4 (a) Depiction of the EPRoC as utilised in this report. The EPRoC is located on the PCB, which is inserted between the poles of the electromagnet. It is connected to an RF generator, a current source, a power supply and a lock-in amplifier (LIA). The directions of the static B₀ field and B₁ MW field are indicated by the arrows. (b) Close-up of the EPRoC with the octagonally-shaped coil.

To protect the EPRoC from short circuit events due to the aqueous environment, the entire sensor-containing PCB is coated with a 10–12-μm thick layer of parylene C, such that the PCB and the EPRoC can directly be put into contact with the vanadium electrolyte.

5.2 Preparation of the vanadium electrolyte solutions

To prepare the electrolyte samples with well-defined SOC, a commercial VRFB electrolyte (Gesellschaft für Elektrometallurgie mbH) with a total concentration of 1.6 mol l⁻¹ has been charged in a cell to the respective SOC. For the charging, a test cell assembly as described in detail in ref. 61 with both half cells separated by an anion-exchange membrane (Fumasept FAP 450) was used. Graphite bipolar plates (FU-4369, Schunk Kohlenstofftechnik, Germany) and graphite felts (GFA 5, SGL Carbon, Germany, thermally activated at 400 °C for 1 h) were used. The geometric area of the cell was 40 cm².

Prior to charging, the concentration of the pristine commercial electrolyte was determined by cerimetric titration. The electrolyte for the cell tests had a composition of 49.85% V³⁺ and 50.15% V⁴⁺, with a total concentration of 1.58 mol l⁻¹. Accordingly, 1600 ml anolyte and 1609.63 ml catholyte were charged to SOC 0% by galvanostatic charging with 1 A (25 mA cm⁻²) until a calculated charge of 33.9787 Ah was reached. For the next steps, the amount of electrolyte was equal on both sides. For every SOC step from 20%, 40%, 60% and 80%, galvanostatic charging with 1 A (25 mA cm⁻²) was used until the calculated charge was reached. For SOC 100%, I–V-charging with a voltage of 1.625 V was used until the calculated charge was reached. All sample concentrations were then determined by cerimetric titration from which the SOC was calculated (cf.Table 2).

5.3 Data acquisition

For the EPRoC measurements, 10 ml of each electrolyte solution was placed in a glass beaker, into which the EPRoC was submersed. The field-swept EPRoC FM spectra of the samples with 0%, 21%, 40%, 60%, 79%, and 97% SOC were recorded at room temperature with a fixed microwave frequency of 14.34 GHz at a bias current to the EPRoC of 4 mA with frequency modulation (f_mod = 90 kHz, Δf_mod = 25.6 MHz (equivalent to 0.91 mT field modulation)). For phase-sensitive detection, the time constant of the lock-in amplifier was set to 100 ms with a roll-off of 24 dB oct⁻¹. Nine spectra were averaged to improve SNR.

The field and frequency-swept spectra of the 90% SOC sample were recorded at room temperature at a fixed microwave frequency of 14.34 GHz and a fixed magnetic field of 480.6 mT, respectively, at a bias current to the EPRoC of 4 mA with frequency modulation (f_mod = 90 kHz, Δf_mod = 9.6 MHz (equivalent to 0.34 mT field modulation)). The settings of the lock-in amplifier were the same as above. In total, 40 spectra were averaged to improve SNR. As the EPRoC has a MW frequency-dependent baseline, a frequency-swept off-resonance spectrum recorded at a field of 200.6 mT was subtracted from the on-resonance spectrum obtained at 480.6 mT. The EPR induced frequency shift of the EPRoC was calculated from the measured signal voltage and the VCO tuning curve⁶² recorded off-resonantly. All EPRoC spectra were baseline-corrected with a 2nd-order polynomial and subsequently smoothed with a 2nd-order Savitzky–Golay filter such that the spectrum is not broadened by the filtering procedure.

The central MW frequency, bias current, frequency modulation (f_mod = 90 kHz, Δf_mod = 25.6 MHz (equivalent to 0.91 mT field modulation)) and lock-in detection were the same for the two-point measurements. In total, 1000 averages were recorded in the following procedure: the field was stepped between baseline (400.6 mT) and resonance (492.8 mT) 100 times. At each point, the lock-in reading was averaged 10 times.

For X-band measurements, the solutions were placed in open-ended capillary tubes (1.02 mm ID, Hirschmann ringcaps 50 μl), sealed with capillary tube sealant (Critoseal) at both ends and placed in a capillary guidance tube for reproducible sample placement in the Magnettech MS5000 spectrometer. The room temperature resonator-based EPR spectra at X-band were obtained at a B₁ of 12 μT (10 mW with a conversion factor of 0.12 mT W^−1/2), modulation frequency of 100 kHz, and modulation amplitude of 0.4 mT. The g- and A-tensors of the 90% SOC electrolyte solution were determined from a spectrum recorded at 100 K using the same operating conditions.

The magnetic field of the MS5000 spectrometer was calibrated using N@C₆₀ powder sample.

The X-band EPR spectra were linearly baseline-corrected and subsequently smoothed with a 2nd-order Savitzky–Golay filter such that the spectrum is not broadened by the filtering procedure.

5.4 Quantitation and error estimation

The EPR signal intensity of the X-band data was obtained by double integration of the spectrum with baseline corrections of 1st and 5th order for the as-recorded and singly integrated spectra, respectively. The values displayed in Fig. 3(a) are the values obtained after double integration at the highest field value of each spectrum. To estimate the error for the X-band quantitation, the double integration with the previously described baseline-correction process was performed on 100 individual spectra. The mean and standard error of the signal intensities are displayed in Fig. 3(a).

The quantitation of the FM EPRoC data is similar to the “standard” quantitation used in the resonator-based EPR described above. Here, the FM spectra were transformed to synthetic absorption-like spectra by means of the Kramers–Kronig relation (Hilbert transformation) and were then integrated twice. Both the synthetic absorption spectra shown in Fig. S5b (ESI†) and the singly integrated spectra shown in Fig. S5c (ESI†) were baseline corrected with a 3rd and 5th order polynomial, respectively. The intensity values used in Fig. 3(a) were obtained as the last value from each doubly integrated spectrum shown in the ESI† in Fig. S5d.

To obtain the quantitation error for the EPRoC measurements, a tempol sample was investigated due to the low SNR of the single spectra of the vanadium solutions and the long measurement times required to obtain a similar number of individual spectra previously employed for statistical analysis. Therefore, the quantitation error of the EPRoC system was determined using a 10 mmol l⁻¹ aqueous tempol solution. Similar to the X-band EPR data, 100 EPRoC FM spectra were obtained with this sample with the same settings as for the electrolyte solutions, which were quantified using the two methods described above. The relative error of the signal intensity was determined from the mean and the standard error of the signal intensities, which was then used for the EPRoC FM quantitation of the electrolyte solutions.

For the two-point measurement data obtained from the full EPRoC FM spectra, the mean signal observed below 435.6 mT was subtracted from the signal amplitude at 492.8 mT (slightly right of the second transition of the spectrum as indicated in Fig. 1(a)). The error was estimated from the standard deviation of the same region.

The experimental two-point truncation measurement was analysed as follows. For each average, the signal amplitude was calculated as the difference of the two data points. The mean and standard error of the signal amplitudes is plotted in in Fig. 3(b).

In the error analyses, only the statistical error was considered, while the systematic error introduced by the possible combinations of different baseline corrections was ignored. This approach is justified by the fact that the same systematic error will be present in all analyses in the same way and may therefore be ignored.

5.5 Spectral simulations

The spectral simulations were performed with the EasySpin software package⁵¹ (version 6.0.0-dev.53). The g- and A-tensors were determined from the simulation of an X-band EPR absorption spectrum recorded at 100 K using the function pepper for solid state powder samples. The total electron spin of VO²⁺ is s = 1/2 containing naturally abundant V (99.75% ⁵¹V, I = 7/2).⁶³ The starting parameters of the g- and A-tensors for the least-square fit of the simulation were taken from literature.²⁰ In addition, a convolutional Gaussian line broadening was included to improve the fitting of the simulation to the recorded spectrum. The resulting g- and A-tensors were subsequently used for the simulation of the room temperature X-band absorption and EPRoC FM spectra. For these simulations, the function garlic for samples in the isotropic, fast-motion regime was utilised. Here, the rotational correlation time was the only free fit parameter, with no additional convolutional broadening included.

The simulations using EasySpin most commonly return the absorption spectra as is typically recorded with commercial EPR spectrometers. To obtain simulated dispersion spectra, or a mixture of absorption/dispersion, the MW phase may be explicitly defined in the simulation. Since the EPRoC FM signal is dispersion-like, the MW phase was set to π/2 accordingly in the simulation for these data.

Author contributions

SK, JEM, BN, PF, JA and KL defined the goals of the research and designed the experiments. PF provided the vanadium electrolyte samples and provided expertise about VRFBs. AC, MK, PF and SK investigated suitable coatings for the EPRoC. AC, MK and JA designed the dipstick EPR-on-a-Chip spectrometer. SK performed all of the EPR experiments, data processing, and simulations. SK, JEM, BN and KL evaluated and discussed the results of the experiments. SK, JEM and BN wrote the manuscript. KPD advised the authors at all stages of the research and authoring of the manuscript. The article was revised by all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to Diener Electronics for coating the EPR-on-a-Chip sensor with Parylene C and to Dr Tobias Gerber for the preparation of the vanadium electrolyte samples. SK acknowledges the beneficial discussions with Ekaterina Shabratova, Elizaveta Kobeleva, Gianluca Marcozzi and Michele Segantini as well as field calibration data provided by Elizaveta Kobeleva.

This work has been supported by the Bundesministerium für Bildung und Forschung under contract number 01186916/1 (EPRoC), by the HEMF (Helmholtz Energy Materials Foundry) infrastructure funded by the Helmholtz Association (HGF), and by the DFG priority program INtegrated TERahErtz sySTems Enabling Novel Functionality (INTEREST) (SPP 2314). B. N. acknowledges the financial support from the Deutsche Forschungsgemeinschaft (project numbers 410866378 and 410866565).

References

1. K. Lourenssen, J. Williams, F. Ahmadpour, R. Clemmer and S. Tasnim, J. Energy Storage, 2019, 25, 100844.
2. X.-Z. Yuan, C. Song, A. Platt, N. Zhao, H. Wang, H. Li, K. Fatih and D. Jang, Int. J. Energy Res., 2019, 43, 6599–6638.
3. N. Poli, M. Schäffer, A. Trovò, J. Noack, M. Guarnieri and P. Fischer, Chem. Eng. J., 2021, 405, 126583.
4. M. Skyllas-Kazacos, L. Cao, M. Kazacos, N. Kausar and A. Mousa, ChemSusChem, 2016, 9, 1521–1543.
5. Y. Shi, C. Eze, B. Xiong, W. He, H. Zhang, T. M. Lim, A. Ukil and J. Zhao, Appl. Energy, 2019, 238, 202–224.
6. D. Schulte, J. Drillkens, B. Schulte and D. U. Sauer, J. Electrochem. Soc., 2010, 157, A989.
7. K. Oh, M. Moazzam, G. Gwak and H. Ju, Electrochim. Acta, 2019, 297, 101–111.
8. M. Skyllas-Kazacos and M. Kazacos, J. Power Sources, 2011, 196, 8822–8827.
9. C.-N. Sun, F. M. Delnick, L. Baggetto, G. M. Veith and T. A. Zawodzinski, J. Power Sources, 2014, 248, 560–564.
10. World Intellectual Property Organization, U.S. Pat., WO1990003666A1, 1990.
11. B. Xiong, J. Zhao, Z. Wei and M. Skyllas-Kazacos, J. Power Sources, 2014, 262, 50–61.
12. Z. Wei, T. M. Lim, M. Skyllas-Kazacos, N. Wai and K. J. Tseng, Appl. Energy, 2016, 172, 169–179.
13. M. R. Mohamed, H. Ahmad and M. N. A. Seman, Elektron. Elektrotech., 2013, 19, 37–42.
14. S. Corcuera and M. Skyllas-Kazacos, Eur. Chem. Bull., 2012, 1, 511–519.
15. F. Grossmith, P. Llewellyn, A. G. Fane and M. Skyllas-Kazacos, in Stationary Energy Storage: Load Leveling and Remote Applications, ed. A. R. Landgrebe, S. L. Van Voorhees, D. J. Rand and R. K. Sen, 1988.
16. L. Liu, J. Xi, Z. Wu, W. Zhang, H. Zhou, W. Li and X. Qiu, J. Appl. Electrochem., 2012, 42, 1025–1031.
17. S. Rudolph, U. Schröder, I. M. Bayanov, K. Blenke and D. Hage, J. Electroanal. Chem., 2013, 694, 17–22.
18. X. Li, J. Xiong, A. Tang, Y. Qin, J. Liu and C. Yan, Appl. Energy, 2018, 211, 1050–1059.
19. B. Li, Q. Luo, X. Wei, Z. Nie, E. Thomsen, B. Chen, V. Sprenkle and W. Wang, ChemSusChem, 2014, 7, 577–584.
20. J. S. Lawton, S. M. Tiano, D. J. Donnelly, S. P. Flanagan and T. M. Arruda, Batteries, 2018, 4, 40.
21. W. S. Chace, S. M. Tiano, T. M. Arruda and J. S. Lawton, Batteries, 2020, 6, 49.
22. J. R. Pilbrow, Transition Ion Electron Paramagnetic Resonance, Clarendon Press, 1990.
23. M. Brustolon and E. Giamello, Electron Paramagnetic Resonance: A Practitioners Toolkit, John Wiley & Sons, 2009.
24. T. A. Jackson, J. Krzystek, A. Ozarowski, G. B. Wijeratne, B. F. Wicker, D. J. Mindiola and J. Telser, Organometallics, 2012, 31, 8265–8274.
25. J. Krzystek, A. Ozarowski, J. Telser and D. C. Crans, Coord. Chem. Rev., 2015, 301–302, 123–133.
26. C. Li, M. Shen, X. Lou and B. Hu, J. Phys. Chem. C, 2018, 122, 27224–27232.
27. I. E. Soshnikov, N. V. Semikolenova, K. P. Bryliakov, V. A. Zakharov, C. Redshaw and E. P. Talsi, J. Mol. Catal. Chem., 2009, 303, 23–29.
28. J. S. Lawton, A. Jones and T. Zawodzinski, J. Electrochem. Soc., 2013, 160, A697–A702.
29. J. S. Lawton, D. S. Aaron, Z. Tang and T. A. Zawodzinski, J. Membr. Sci., 2013, 428, 38–45.
30. J. S. Lawton, D. S. Aaron, Z. Tang and T. A. Zawodzinski, ECS Trans., 2012, 41, 53.
31. H. Wolfson, R. Ahmad, Y. Twig, A. Blank and P. Kuppusamy, in Medical Imaging 2015: Biomedical Applications in Molecular, Structural, and Functional Imaging, ed. B. Gimi and R. C. Molthen, International Society for Optics and Photonics, Orlando, Florida, United States, 2015, vol. 9417, p. 941706.
32. O. Zgadzai, Y. Twig, H. Wolfson, R. Ahmad, P. Kuppusamy and A. Blank, Anal. Chem., 2018, 90, 7830–7836.
33. L. E. Switala, B. E. Black, C. A. Mercovich, A. Seshadri and J. P. Hornak, J. Magn. Reson., 2017, 285, 18–25.
34. F. Cheng, T. Shibata, Y. Aoki and H. Hirata, J. Magn. Reson., 2021, 332, 107081.
35. T. Yalçin and G. Boero, Rev. Sci. Instrum., 2008, 79, 094105.
36. J. Anders, A. Angerhofer and G. Boero, J. Magn. Reson., 2012, 217, 19–26.
37. X. Yang and A. Babakhani, IEEE Trans. Microwave Theory Tech., 2015, 63, 3727–3735.
38. J. Handwerker, B. Schlecker, U. Wachter, P. Radermacher, M. Ortmanns and J. Anders, in 2016 IEEE International Solid-State Circuits Conference (ISSCC), IEEE, San Francisco, CA, USA, 2016, pp. 476–477.
39. L. Zhang and A. M. Niknejad, IEEE Microw. Wirel. Compon. Lett., 2021, 1.
40. R. V. Pound and W. D. Knight, Rev. Sci. Instrum., 1950, 21, 219–225.
41. J. S. Hyde, R. A. Strangeway, T. G. Camenisch, J. J. Ratke and W. Froncisz, J. Magn. Reson., 2010, 205, 93–101.
42. B. Schlecker, A. Chu, J. Handwerker, S. Künstner, M. Ortmanns, K. Lips and J. Anders, 2017 IEEE SENSORS, IEEE, Glasgow, 2017, p. 1.
43. B. Schlecker, A. Chu, J. Handwerker, S. Künstner, M. Ortmanns, K. Lips and J. Anders, 017 IEEE SENSORS, IEEE, Glasgow, 2017, pp. 1–3.
44. J. Anders and K. Lips, J. Magn. Reson., 2019, 306, 118–123.
45. J. Anders, Studies in systems, decision and control, Springer International Publishing, 2017, pp. 57–87.
46. A. Chu, B. Schlecker, M. Kern, J. L. Goodsell, A. Angerhofer, K. Lips and J. Anders, Magn. Reson., 2021, 2, 699–713.
47. S. Künstner, A. Chu, K.-P. Dinse, A. Schnegg, J. E. McPeak, B. Naydenov, J. Anders and K. Lips, Magn. Reson., 2021, 2, 673–687.
48. G. R. Eaton, S. S. Eaton, D. P. Barr and R. T. Weber, Quantitative EPR, Springer, Vienna, Vienna, Austria, 2010.
49. A. M. Portis, Phys. Rev., 1953, 91, 1071–1078.
50. S. S. Eaton and G. R. Eaton, in eMagRes, ed. R. Wasylishen, John Wiley & Sons, Ltd., 2016, pp. 1543–1556.
51. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
52. S. Künstner, J. E. McPeak, A. Chu, M. Kern, M. Wick, K.-P. Dinse, J. Anders, B. Naydenov and K. Lips, Small Methods, under review.
53. J. A. Weil and J. R. Bolton, Electron Paramagnetic Resonance: Elementary Theory and Practical Applications, 2nd edn, John Wiley & Sons, Inc., 2007.
54. DOE Global Energy Storage Database, https://gesdb.sandia.gov/, (accessed November 9, 2023).
55. M. A. Hassan, M. Kern, A. Chu, G. Kalra, E. Shabratova, A. Tsarapkin, N. MacKinnon, K. Lips, C. Teutloff, R. Bittl, J. G. Korvink and J. Anders, Frequenz, 2022, 76, 699–717.
56. A. Chu, B. Schlecker, K. Lips, M. Ortmanns and J. Anders, in 2018 IEEE International Solid-State Circuits Conference – (ISSCC), IEEE, San Francisco, CA, USA, 2018, pp. 354–356.
57. M. A. Hassan, T. Elrifai, A. Sakr, M. Kern, K. Lips and J. Anders, 2021 IEEE Sensors, 2021, pp. 1–4.
58. A. Chu, M. Kern, K. Khan, K. Lips and J. Anders, in 2023 IEEE International Solid-State Circuits Conference (ISSCC), 2023, pp. 20–22.
59. X. Wei, W. Xu, M. Vijayakumar, L. Cosimbescu, T. Liu, V. Sprenkle and W. Wang, Adv. Mater., 2014, 26, 7649–7653.
60. B. Razavi, IEEE Solid-State Circuits Mag., 2014, 6, 7–10.
61. J. Noack and J. Tübke, ECS Trans., 2010, 25, 235.
62. B. Schlecker, A. Hoffmann, A. Chu, M. Ortmanns, K. Lips and J. Anders, IEEE Sens. J., 2018, 1.
63. National Nuclear Data Center, information extracted from the NuDat database, https://www.nndc.bnl.gov/nudat/.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00373j

---