Isomer-specific photofragmentation of C₃H₃⁺ at the carbon K-edge

Abstract

Individual fingerprints of different isomers of C₃H₃⁺ cations have been identified by studying photoionization, photoexcitation, and photofragmentation of C₃H₃⁺ near the carbon K-edge. The experiment was performed employing the photon-ion merged-beams technique at the photon-ion spectrometer at PETRA III (PIPE). This technique is a variant of near-edge X-ray absorption fine-structure spectroscopy, which is particularly sensitive to the 1s → π* excitation. The C₃H₃⁺ primary ions were generated by an electron cyclotron resonance ion source. C₃H_n²⁺ product ions with n = 0, 1, 2, and 3 were observed for photon energies in the range of 279.0 eV to 295.2 eV. The experimental spectra are interpreted with the aid of theoretical calculations within the framework of time-dependent density functional theory. To this end, absorption spectra have been calculated for three different constitutional isomers of C₃H₃⁺. We find that our experimental approach offers a new possibility to study at the same time details of the electronic structure and of the geometry of molecular ions such as C₃H₃⁺.

---

1 Introduction

During the last decades, an increasing number of molecular species has been discovered in the interstellar medium (ISM) and in planetary atmospheres.¹ These findings include a variety of carbon-containing and organic molecules ranging from small ones such as the formyl radical, HCO,² cyclopropenylidene, c-C₃H₂,³ or benzene, c-C₆H₆,^4,5 to fullerenes.

Small molecules such as C₃H₃ are interesting candidates as precursors or intermediates for the formation of c-C₆H₆^6,7 and further to polyaromatic hydrocarbons (PAHs). The corresponding cation C₃H₃⁺ has different constitutional isomers, which cannot be distinguished with a mass spectrometer, but the constitutional isomeric form is important for further reactions. The cyclopropenyl cation, c-C₃H₃⁺, was previously detected by the Cassini mission using a mass spectrometer⁸ in the atmosphere of Titan, the largest moon of Saturn. The linear H₂C–C–CH⁺ was found in the interstellar medium through radio astronomy.⁹ Missing information about the structure and the associated reactivity leads to significant problems in understanding subsequent ion–neutral–molecule reactions,^10–12 which in turn are important to model the formation of chemical compounds in space and in the atmospheres of celestial bodies.¹³

c-C₃H₃⁺ is the structurally simplest aromatic molecule. Due to the high chemical importance of aromatic molecules, computer models simulating the aromaticity are steadily improving, which leads to the development of aromatic systems that are adapted to certain applications.^14,15 A possible application for c-C₃H₃⁺ could be the integration into hybrid halide perovskite architectures, which may be used as a photovoltaic material.¹⁶ C₃H₃⁺ is difficult to study in isolation due to its charge. Solutions to the problem are to investigate the ion in an ion trap or a free ion beam moving in a vacuum with a kinetic energy of several keV and selecting it by mass-spectrometric techniques. In order to identify the constitutional isomers and specifically their geometry, a further examination method is required.

Since c-C₃H₃⁺ does not have a dipole moment, its detection by infrared spectroscopy is very difficult and could not be accomplished yet.⁷ Therefore, the dissociation of C₃H₃⁺, attached with various inert ligands has been studied by infrared spectroscopy utilizing vibrational states of molecular bonds in order to determine the C₃H₃⁺ geometrical structure.^7,17–21 The neutral C₃H_x (x = 0–3) species were investigated by photoelectron spectroscopy.^22,23 It can be assumed that the spectroscopic properties of the molecular ions differ significantly from the properties of the corresponding neutral molecules. This has been shown, e.g., for the neutral c-C₆H₆ and the singly charged c-C₆H₆⁺ molecules.²⁴ In the present study, near-edge X-ray absorption fine-structure spectroscopy (NEXAFS) at the C 1s edge is applied. NEXAFS has the advantage to be site- and element-specific. It is particularly sensitive to double bonds as well as aromaticity as shown, e.g., by Kolczewski et al.²⁵

A powerful technique to study molecular ions with soft X-rays is the merged-beams technique, in which an ion beam is merged with a photon beam over a certain distance.^26–28 Using this technique the electronic structure of the unoccupied states can be studied.^29–32 Moreover, it allows one to measure fast dynamic dissociation processes, which take place on a time scale of a few femtoseconds.³¹

In this paper, we present the X-ray absorption spectra of a mixture of three different C₃H₃⁺ isomers at the C 1s edge by measuring the ion yield of selected photofragmentation channels using the merged-beams technique. The experimental spectra are compared to TDDFT calculations to disentangle the contributions of the three isomers.

2 Experiment

The experiment was performed using the photon-ion end-station at the synchrotron radiation source PETRA III (PIPE).^33,34 The setup is a permanently installed instrument at the soft X-ray beamline P04 at DESY in Hamburg, Germany.³⁵ It allows one to measure cross sections in a wide range of eight orders of magnitude from (2 ± 1)b³⁶ up to several hundred Mb³⁷ or even Gb³⁸ with the merged-beams technique. The beamline was operated using a 400 lines mm⁻¹ grating and an exit-slit opening of 500 μm. With this exit-slit width a photon-energy spread of 0.65 eV and a photon flux of 3 × 10¹³ s⁻¹ at 280 eV photon energy were obtained. During the measurement, the photon flux was permanently monitored by a calibrated photodiode. The photon-energy scale was calibrated by a CO photoabsorption measurement at the C 1s → 2pπ* resonance. The photon-energy axis has been shifted such that the resonance lies at the literature value of (287.31 ± 0.05) eV.³⁹

The ions for the experiment were generated from butane gas in the hot plasma of a 10 GHz electron cyclotron resonance ion source.⁴⁰ The pressure inside the ion source was 3 × 10⁻² Pa. Due to this rather low pressure, only fragmentation products were generated from the neutral target gas in the plasma and reactive collisions or cooling of the molecular ions can be neglected. The ions were extracted by an applied voltage of 6 kV between the ion source and the puller electrode. The ion beam was focused by electrostatic lenses and a specific mass-over-charge ratio was selected by the proper setting of a dipole magnet. A specific constitutional isomer of the molecular ions could not be selected by the dipole magnet. The ion beam, which contained several energetically favorable constitutional isomers, was steered onto the axis of the photon beam by using electrostatic deflectors. The length of the mutual overlap of the photon beam with the ion beam was 1.7 m. In order to ensure a low background from ion-residual-gas collisions, the pressure in the ion-beam and photon-beam merging area was kept at 5 × 10⁻⁸ Pa. Using a second double-focusing dipole magnet with a bending radius of 0.6 m, the photoionization products were selected by a 90° deflection from the primary ion beam and other ionic products. In order to further reduce the background, for example generated from stray electrons, the photoions were deflected out of the collision plane by a 180° electrostatic deflector and then counted with a single-particle detector using a channeltron.^41,42 The dark-count rate of the channeltron was 20 mHz. To improve the overlap of the merged beams, apertures on the entry side and on the exit side of the interaction area were adjusted to match the ion-beam size to the photon-beam size. The primary ion current was permanently monitored using a large Faraday cup inside the demerging magnet. A current of about 11 nA was obtained for the C₃H₃⁺ cations. The background resulting from ion-residual-gas collisions was determined by measuring the count rate without the photon beam using a photon-beam shutter. Relative cross sections were obtained by dividing the difference between the count rates with photons and without photons by the photon flux, which was recorded by a calibrated photodiode.

In our experiment, we have measured the doubly charged fragments C₃H_n²⁺. Following a resonant C 1s excitation, the C₃H₃⁺ core-excited molecule decays via the Auger–Meitner process. This mainly produces the dication C₃H₃²⁺, as the probability for a double Auger process is only on the order of 3%.⁴³ The dication can fragment by neutral-hydrogen elimination, which produces the observed C₃H_n²⁺ fragments. In the case of positively charged hydrogen elimination (H⁺ or H₂⁺), the C₃H_n photofragments will only be singly charged or even neutral and cannot be detected in our setup. Following an unlikely double ionization, a doubly charged fragment might be formed together with a charged hydrogen ion. This would result in a Coulomb repulsion and the C₃H_n²⁺ ion would acquire a kinetic energy on the order of 0.76 eV. This small additional kinetic energy does not affect the detection efficiency for the heavy fragment. The acceptance of the detector is sufficiently large for the detection of ions with such a small additional (or reduced) kinetic energy. Thus, we conclude that practically all produced dicationic fragments were recorded in our experimental setup with equal detection probability.

3 Computations

The calculated photoabsorption spectra were computed using time-dependent density functional theory (TDDFT). The calculations were performed with the quantum-chemistry program ORCA^44,45 (version 5.0.3). The first three lowest-energy conformers as determined by Cameron et al.⁴⁶ were selected as possible geometries. In addition to the singlet cyclopropenyl, c-C₃H₃⁺, these are the singlet propargylium cation, [H₂C–C–CH]⁺, and the triplet 1-propenyl cation, [H₃C–C–C]⁺. The Becke '88 exchange and Perdew '86 correlation (BP86)⁴⁷ functionals were applied together with the def2-TZVP(-f) basis set.^48,49 Other local and gradient-corrected functionals such as Becke '88 exchange and Lee–Yang–Parr correlation (BLYP) or Perdew–Burke–Erzerhoff GGA (PBE) were also tried and very similar results were obtained. Hence, we decided to use the Becke '88 exchange and Perdew '86 correlation (BP86)⁴⁷ functionals. In order to get a more accurate description, 10 s- and 10 p-type functions per atom according to the procedure described by Kaufmann et al.⁵⁰ were added to the set of basis functions. For the calculation of the transition states between c-C₃H₃⁺ and [H₂C–C–CH]⁺ in Fig. 5, the nudged elastic band with transition state (NEB-TS) optimization was used.⁵¹

In the cyclic geometry, all carbon atoms are equivalent, i.e., it makes no difference which C 1s electron is excited. In order to generate the energetic degeneracy of the three C 1s orbitals for the localized C 1s core excitation, the function ‘XASLoc’ of ORCA^44,45 was applied in the calculation. The calculated photoabsorption spectra were convoluted with a Voigt function consisting of a Lorentzian contribution with a full width at half maximum (FWHM) of 0.08 eV and a Gaussian contribution with a FWHM of 0.65 eV to take into account the core–hole lifetime and the experimental broadening, respectively. The calculated energies were shifted by E_shift = 15.83 eV such that the computed energy of the 1s → π* resonance of the c-C₃H₃⁺ ions agrees with the measured one. This resonance corresponds to the transition from the C 1s level to the lowest unoccupied molecular orbital (LUMO). For the triplet state a slightly different shift of E_shift = 15.6 eV was used, such that the measured peak C in Fig. 1(a) matches the computed resonance 3.3 in Fig. 1(d). The used functional gives a slightly too large energy spread of the resonant C 1s structures. For a better comparison with the experimental data we have slightly compressed the calculated spectra centered at resonance 1 of the c-C₃H₃⁺ spectrum by:

E_compressed = f_compression(E_abinitio + E_shift − E_res.1) + E_res.1 (1)

E_abinitio represents the energy calculated using ORCA. E_res.1 is the energy of resonance 1 in Fig. 1(b). The compression factor f_compression was 0.86 and 0.77 for the singlet and triplet initial states, respectively. This compression corresponds to a mean energy change of the calculated resonance positions on the order of 300 meV relative to the reference resonance 1.

Fig. 1 The ionization channels C₃H₃⁺ → C₃H_n²⁺ with n = 0–3 are shown in panel (a). In panel (b), the calculated spectrum for the cyclic isomer is shown. Since all carbon atoms are equal in this geometry, the summed spectrum for the identical atoms is provided. The theoretical resonance feature 1 is due to the excitation into the LUMO. Panel (c) shows the individual and the summed carbon spectra for the [H₂C–C–CH]⁺ singlet geometry, which energetically lies 1.1 eV above the cyclic geometry (see Fig. 3(b)). Panel (d) displays the spectra for the [H₃C–C–C]⁺ triplet geometry, which energetically lies 4.7 eV above the cyclic geometry [see Fig. 3(b)]. Since the three carbon atoms of the linear geometries are distinguishable, the absorption spectra for each carbon atom are shown individually in panels (c) and (d). The first digit of the resonance labels describes the atom and the second the excited orbital [see also Fig. 3]. In order to line up the theoretical with the experimental resonance structures, the theoretical energy scales in panels (b)–(d) have been adjusted as described in Section 3.

4 Results

In Fig. 1(a), the sum of all recorded photon-energy-dependent ion yields is depicted. The sum has been obtained by adding the measured ion yield channels C₃H₃⁺ → C₃H_n²⁺ with n = 0–3 shown in Fig. 2. The spectrum is dominated by the single ionization C₃H₃⁺ → C₃H₃²⁺ channel. The C₃H₃⁺ → C₃H₂²⁺ channel with single hydrogen loss is smaller by a factor of two compared to direct single ionization. The channels with double or triple hydrogen loss are smaller by at least one order of magnitude. The spectrum in Fig. 1(a) consists of three resonance features, A, B, and C at 282.9 eV, 285.7 eV, and 287.1 eV, respectively. Another broad structure is observed around 292 eV. Peak A at 282.9 eV photon energy has an asymmetric shape, which is an indication that it is a blend resulting from several individual resonance transitions. The main peak B at 285.7 eV photon energy exhibts an asymmetric shape. It is about a factor of three larger than peak A and partially overlaps with the smaller peak C.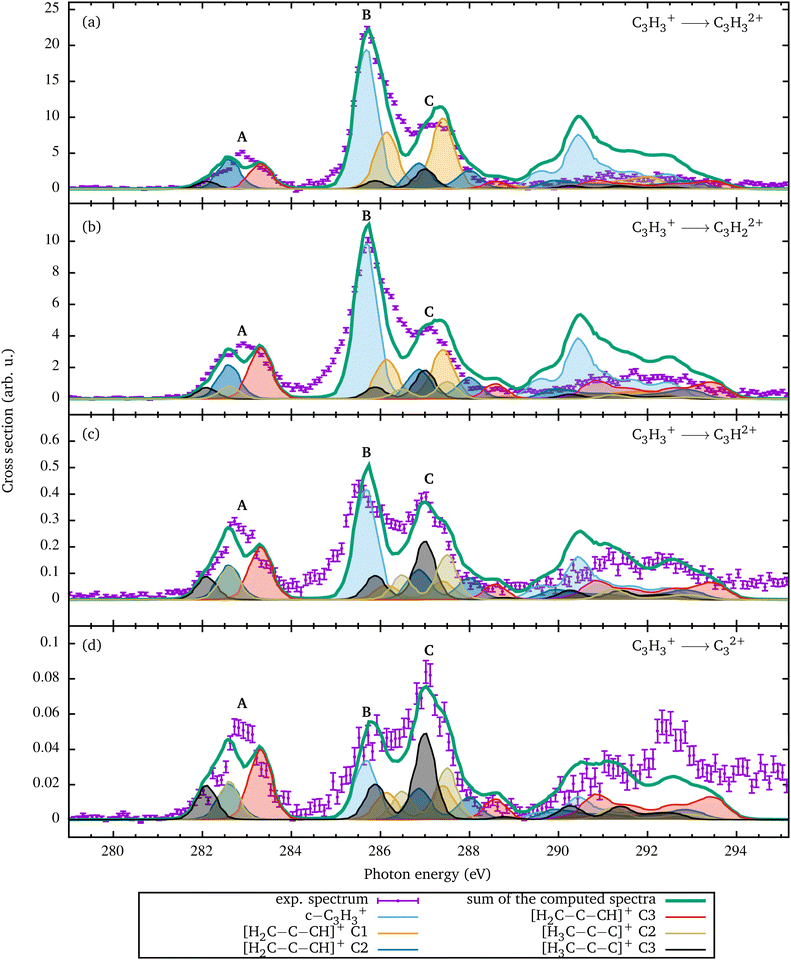

Fig. 2 Relative cross sections for single ionization of C₃H₃⁺ [panel (a)] and for fragmentation leading to the formation of C₃H₂²⁺ [panel (b)], C₃H²⁺ [panel (c)], and C₃²⁺ [panel (d)]. Since the experimental spectra contain contributions from different geometries, these relative contributions were determined by a fit of the coefficients a_i of eqn (2). The renormalized individual contributions are shown by the colored curves with shading. Their sum is the thick green curve. Since the [H₃C–C–C]⁺ C1 conformation does not show any resonance in this energy range, it is not included in the fit. The relative contributions resulting from the fit are shown in Fig. 4.

The ion yields resulting from single ionization and from the loss of up to three hydrogen atoms are shown individually in Fig. 2. These reaction channels can be described as

C₃H₃⁺ + hν → C₃H_n²⁺ + (3 − n)H + e⁻, (2)

where n ranges from 0 to 3. The fragmentation channels leading to singly charged fragments were not measured, because they had a very strong background contribution from collisions with the residual gas in the merged-beams interaction region. As a result, the difference in the normalized count rate with and without photons was small and had very large uncertainties. Besides the lower ion yield of the hydrogen-loss channels compared to the C₃H₃²⁺ single-ionization channel, further differences are immediately apparent. In the single-ionization spectrum displayed in Fig. 2(a), the main peak B is very distinct and is dominating the spectrum. Peak B is significantly smaller for the fragmentation channels. Its intensity is decreasing with the number of H atoms lost. Furthermore, peak A differs significantly in shape when comparing the different measured spectra. In the photon-energy range above 288 eV, a significant increase of the ion yield relative to peak B is found with an increasing number of H atoms lost.

To analyze the experimental spectra, the C 1s absorption spectra for the three constitutional isomers of C₃H₃⁺ were calculated using the computational methods described above. The results are depicted in Fig. 1(b)–(d). In addition, the resonant excitation energies to the singly occupied molecular orbitals (SOMOs) and the first LUMO(+k) (k = 0–2) orbitals are provided in Table 1. Since the two SOMOs of the triplet H₃C–C–C⁺ are energetically degenerate, we do not distinguish between them. The SOMO and all depicted LUMO(+k) orbitals have a π*-like character (see Table 2). The calculated spectrum for the c-C₃H₃⁺ ion is shown in Fig. 1(b). For the [H₃C–C–C]⁺ isomer, the triplet geometry was chosen because this state is closer by 1.5 eV to the cyclic geometry than the singlet geometry. The c-C₃H₃⁺ cation has the largest binding energy and the two isomers have lower binding energies, lower by 1.1 eV for the [H₂C–C–CH]⁺ singlet geometry and about 4.7 eV for the [H₃C–C–C]⁺ triplet geometry as depicted in Fig. 3(b).

Table 1 The calculated 1s → π* resonance energies for the three C₃H₃⁺ constitutional isomers under consideration. The energetic positions of the resonances are shifted according to the description in Section 3

Geometry	Resonance	Energy (eV)	Excited orbital
c-C3H3^+	1	285.6	LUMO
	2	290.5	σ*
[H2C–C–CH]^+	1.1	281.7	LUMO
	1.2	286.0	LUMO+1
	1.3	287.5	LUMO+2
	2.1	282.7	LUMO
	2.2	287.0	LUMO+1
	2.3	288.1	LUMO+2
	3.1	283.4	LUMO
	3.2	287.4	LUMO+1
	3.3	288.7	LUMO+2
[H3C–C–C]^+	1.1	280.7	SOMO
	1.2	289.0	σ*
	2.1	282.5	SOMO
	2.2	286.4	LUMO
	2.3	287.4	β LUMO
	3.1	282.0	SOMO
	3.2	285.8	LUMO
	3.3	286.9	β LUMO

---

Table 2 Visualization of the excited orbitals of the 1s → π* resonances for the different isomers. All shown excited states extend over the whole molecule and are π* orbitals. The excited molecular orbitals were visualized with the program Iboview.⁵³ In the cyclic geometry, the LUMO+1 and the LUMO+2 are unoccupied σ* orbitals not relevant for the discussed resonance structures and are not shown here. The triplet state has two degenerate SOMO orbitals, which are rotated relative to each other by 90° on the the molecular axis. Therefore, only one SOMO orbital is shown

Excited state	c-C3H3^+		[H2C–C–CH]^+	[H3C–C–C]^+
SOMO	—		—
LUMO
LUMO+1	—			—
LUMO+2	—			—

---

Fig. 3 Panel (a) shows the orbital energies calculated with TDDFT for the different constitutional isomers. The arrows visualize the different excitation pathways. The intensity or transition probability is not displayed by the arrows. 1s₁, 1s₂, and 1s₃ represent the respective orbital energies of the different C 1s orbitals of the molecular ions. Panel (b) depicts the total energies calculated by TDDFT for the constitutional isomers relative to the cyclic ground state.

The equivalence of the carbon atoms in the cyclic geometry of the C₃H₃⁺ ion results in almost identical transitions for the three C atoms in the c-C₃H₃⁺ ion [Fig. 3(a)]. Yet, the calculations show a small difference in the C 1s orbital energies. This small difference is due to the antisymmetric C 1s based wave function of the three identical carbon atoms in c-C₃H₃⁺ and results in a small splitting of the three corresponding C 1s energy levels. One C 1s eigenstate has a 60 meV higher binding energy than the other. This is equivalent to the gerade–ungerade splitting of the N₂ 1s energy levels.⁵² This difference has a negligible effect on the calculated spectrum as can be seen in the stick spectrum at the resonance labeled with 1 in Fig. 1(b). The low-energy C 1s based state is due to a state with no node and two degenerate 1e′ states with one node. The LUMO state has an e′′ symmetry. Hence, the excitation from the to the e′′ state is much weaker because the molecular orbitals do not have the same symmetry. In addition to the main resonance, there is a much smaller contribution to peak 1, which is associated with this small difference. With this, the main peak B in Fig. 1(a) can be assigned to an excitation of a C 1s electron to the c-C₃H₃⁺ π* LUMO. The group of resonances around 290 eV can be assigned to σ* core-excited energy levels.

Fig. 1(c) shows the spectrum for the linear isomer [H₂C–C–CH]⁺ whose binding energy is smaller by 1.1 eV than that of the c-C₃H₃⁺ isomer. In contrast to the cyclic geometry, the three C 1s orbitals have substantially different binding energies. This results in site-specific C 1s excitation energies as depicted in Fig. 3(a). The TDDFT calculation permits us to disentangle the contributions by each of the three C 1s orbitals. The transitions are designated as X.Y with X being the number of the carbon atom and Y the excited LUMO–(Y−1) orbital.

In principle, there are 9 possible transitions for [H₂C–C–CH]⁺ in the experimental energy range. Fig. 1(c) clearly shows that the present experimental resolving power permits us to discriminate between the different site-specific resonance positions. The TDDFT calculation shows that transitions 1.1 and 3.2 are extremely weak. Therefore, they are missing, and the two resonances near 283 eV in Fig. 3(a) can be assigned to an excitation of a C 1s electron originating from the C atoms 2 and 3 into the LUMO. The excitations from the carbon atom 1 appear at higher photon energies of 285.9 eV and 287.4 eV, which correspond to excitations into the LUMO+1 and LUMO+2 states, respectively.

Fig. 1(d) depicts the spectrum for the constitutional isomer [H₃C–C–C]⁺. Again 9 transitions are possible [see Fig. 3(a)]. For the carbon atom C1, only the 1.1 excitation into the SOMO is visible. The excitations to the LUMOs cannot be seen in the calculated spectrum, since the associated cross sections are too small. Resonance 1.2 is most likely a resonance structure from excitations into σ*-like non-bonding states with a much larger width and therefore not visible. The C2 and C3 atoms show very similar spectra, which are shifted with respect to the C1 spectrum according to the differences in the binding energies of the C 1s orbitals.

5 Discussion

From the comparison of the experimental with the calculated spectra of the three C₃H₃⁺ isomers, it is obvious that the experimental spectra cannot originate from just a single isomer. Due to the rather high temperature of the plasma in the electron cyclotron resonance ion source, C₃H₃⁺ cations with different geometries were likely produced simultaneously. After passing the approximately 10 m distance from the source region to the merged-beams interaction region within a flight time of 58 μs, the ions were in the electronic ground states of the respective isomers. Vibrationally excited states of the C₃H₃⁺ ions can survive the flight time for this distance and, thus, the ions in the interaction region were not necessarily in the vibrational ground state.

The high intensity of the main peak B in Fig. 1(a) is reproduced by the calculation. From the calculation it follows that due to the almost degenerate C 1s electrons in c-C₃H₃⁺, the excitation into the LUMO, which is associated with the very prominent resonance labeled 1 at 285.6 eV, is 2–3 times larger than the excitation features from [H₂C–C–CH]⁺ in Fig. 1(c) and [H₃C–C–C]⁺ in Fig. 1(d).

To disentangle the contributions of the three isomers in the experimental spectra, the calculated isomer spectra have been superimposed using a linear combination, i.e.,

The relative contributions a_i of the different spectra were determined by fitting the weighted sum of the individual theoretical cross sections to the experimental data in the energy range from 281 to 288 eV. This energy range has been chosen since it covers all 1s → π* excitation features. It can be assumed that the fragmentation of the molecules at the 1s → π* excitations is less likely than the fragmentation at the 1s → 3p* excitations, which are energetically above 288 eV. Since the [H₃C–C–C]⁺ C1 spectrum only shows the small 1.1 resonance in this region and 1.2 is considered as a broad resonance structure with excitation to σ* orbitals, which usually have non-bonding energy surfaces, the spectrum was not taken into account in the fit. The [H₃C–C–C]⁺ C2 and C3 spectra were combined in the analysis due to their similarity. Above 288 eV, the relative ion yield is significantly smaller than below. As already mentioned, the measured relative ion yield in the energy range above 288 eV significantly increases with increasing hydrogen loss. For example, for the channel C₃H₃⁺ → C₃²⁺ in Fig. 2(d), the measured ion yield in the range above 288 eV is higher than the fitted calculated cross section.

In order to make statements about the compositions of the different photoion channels, the coefficients a_i from the fit for each individual fragmentation channel are normalized such that the sum of the normalized coefficients amounts to one in each fragmentation channel. These normalized coefficients are visualized in Fig. 4 and detailed in Table 3. The c-C₃H₃⁺ isomer is more stable against H loss following a C 1s → π* excitation than the linear isomers, which can be related to the rather stable aromatic state. Due to the binding character of the core-excited π* state in c-C₃H₃⁺ also vibrational states can be excited. This is also suggested by the asymmetry of the main resonance B and is similar to what was observed earlier for benzene.²⁵

Fig. 4 Relative contributions of the different constitutional isomers to the observed fragmentation channels as resulting from the fit shown in Fig. 2. The error bars show the uncertainties from the fits. Potential uncertainties from the TDDFT calculations were not taken into account.

Table 3 Normalized coefficients a_i [eqn (2)] for the different photoionization channels. The errors given in parentheses were determined from the corresponding fits. A graphical illustration of the values is shown in Fig. 4

Geometry	C3H3^2+	C3H2^2+	C3H^2+	C3^2+
c-C3H3^+	0.44(2)	0.42(3)	0.32(3)	0.16(3)
[H2C–C–CH]^+ C1	0.26(3)	0.15(5)	0.06(6)	0.11(5)
[H2C–C–CH]^+ C2	0.15(4)	0.15(6)	0.16(7)	0.16(6)
[H2C–C–CH]^+ C3	0.10(2)	0.17(3)	0.18(3)	0.23(3)
[H3C–C–C]^+ C2	0.05(2)	0.06(3)	0.13(3)	0.18(3)
[H3C–C–C]^+ C3	0.003(4)	0.05(5)	0.15(7)	0.16(6)

---

For the linear [H₃C–C–C]⁺ triplet geometry with the lowest electronic ground-state binding energy the trend is opposite. Following an excitation of C2 or C3 the relative cross section of [H₃C–C–C]⁺ increases with the number of H atoms lost. The relative contributions from C₃H²⁺ and C₃²⁺ are significantly larger than the relative contributions from C₃H₃²⁺ and C₃H₂²⁺. This trend can also be seen in the changing of resonance C in Fig. 2. The C1 contribution of the linear [H₃C–C–C]⁺ isomer corresponds to a CH₃ methyl group. An excitation into the π* orbitals between C2 and C3 is unlikely. This can be clearly seen from the calculated LUMO orbital, which is very similar to the β LUMO orbital. The notation β orbital was chosen for the corresponding β spin function, which is a down electron eigenfunction. The LUMO orbital shows an electron density located at the C1 atom. It can be assumed that the generated charge is transferred to the methyl group, which finally leads to the fragmentation.

The second linear isomer [H₂C–C–CH]⁺ shows an increasing probability for H atom losses following a C 1s excitation at atoms C2 or C3 compared to the [H₃C–C–C]⁺ isomer. However, for C1 the distribution is somewhat different. Here, ionization without fragmentation is slightly favored over ionization with fragmentation, and the H loss channels have identical probabilities within the error bars.

The increase in H losses can be seen already from the resonance A in Fig. 2(b). The resonance shape changes in comparison to the resonance A in Fig. 2(a). Obviously, the two C₃H₃⁺ linear isomers are significantly less stable against H losses subsequent to a 1s → π* excitation than the cyclic isomer.

From the coefficients a_i in eqn (2), the portions of the three isomer fragments in the ion beam in the merged-beams region can be estimated as (43 ± 2)% c-C₃H₃⁺, (49 ± 11)% [H₂C–C–CH]⁺, and (8 ± 7)% [H₃C–C–C]⁺. In a rough approximation, these values represent the composition of the ion beam from the electron cyclotron resonance ion source. This approximation is limited to the measured ionization and fragmentation channels. The ratios might change slightly when all possible channels were analyzed. From this composition and the total energies of the three isomers (see Fig. 3), a plasma temperature T of about 31 kK (E_thermal = 3/2k_BT = 4 eV) is obtained via the Maxwell–Boltzmann distribution, which is in very good agreement with the conditions for the production of different iron ions with the same source.⁵⁴ However, the molecules should cool down rather quickly, which can be estimated by assuming that cooling proceeds by the emission of black-body radiation. With a c-C₃H₃⁺ radius of R ≅ 1.66 Å the surface of the molecule is estimated as A = 4πR². The temperature change dT during a short time dt is given by

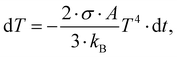with σ and k_B the Stefan–Boltzmann and the Boltzmann constants, respectively. Since the ambient temperature is much lower, it was neglected in this model. Using this very crude approximation, the molecules have a temperature below 7 kK (0.9 eV) after 1 ns and about 3 kK (0.4 eV) after 10 ns, hence, when they have just left the ion source.

To analyze whether the metastable, linear [CH₂–C–CH]⁺ isomer can decay into the c-C₃H₃⁺ isomer, we have also calculated the energy barrier between the two singlet states in Fig. 5, the nudged elastic band with transition state (NEB-TS) optimization was used.⁵¹ A change of the electron spin is unlikely, hence the transition from the [H₃C–C–C]⁺ triplet state was not included. The result of the calculation is depicted in Fig. 5. The energy barrier of 2.28 eV suggests that within the electron cyclotron resonance ion source both isomers are produced and right after leaving the ion source a transition between the two isomers is no longer possible. The prop-2-en-1-yl-3-ylidine cation ([CH₂–CH–C]⁺), which is formed during the transition, has a very low energy barrier of approximately 8 meV to the c-C₃H₃⁺ isomer. Due to this very low barrier, the ion can easily relax into the c-C₃H₃⁺ isomer. Liu et al. have calculated a similar energy barrier of 2.15 eV for the pathway from [H₂C–C–CH]⁺ to c-C₃H₃⁺via [H₂C–CH–C]⁺.⁵⁵ The small difference to our value shows that the chosen basis set as well as the functional describes the C₃H₃⁺ isomers equally well as the approach of Liu et al. They report a second transition path with a higher barrier of 3.85 eV,⁵⁵ which is not relevant for our results.

Fig. 5 The minimum energy pathway from the [H₂C–C–CH]⁺ to the c-C₃H₃⁺ isomer calculated with the NEB-TS method.⁵¹ The height of the energy barrier between the two states is 2.28 eV. The transition proceeds via the prop-2-en-1-yl-3-ylidine cation.

6 Conclusions and outlook

Using the photon-ion merged-beams technique, inner-shell excitation in the soft X-ray range was applied for analyzing the photoionization and photofragmentation of C₃H₃⁺ hydrocarbon ions. Employing TDDFT, the cross sections for different carbon atoms of the three constitutional isomers were calculated. With the help of the calculated absorption spectra, the measured NEXAFS spectra could be analyzed and the relative contributions of the different carbon atoms to the observed spectra could be determined. The cyclic c-C₃H₃⁺ isomer undergoes considerably less fragmentation than the two linear isomers. The linear [H₂C–C–CH]⁺ isomer, which lies energetically 1.1 eV above the cyclic ground state, manifests itself in the spectra with enhanced hydrogen elimination. Additionally, we find indications for an 8% contribution of the isomer [CH₃–C–C]⁺ in a triplet state, which lies 4.7 eV above the cyclic singlet ground state.

Using NEXAFS spectroscopy, the different constitutional isomers can be distinguished very well. The formation of the isomers strongly depends on the plasma temperature, or, more precisely, on the electron energy. Marimuthu et al. describe a beam of C₃H₃⁺ ions consisting of 81% c-C₃H₃⁺ and 19% [H₂C–C–CH]⁺.²⁰ This distribution would correspond to a temperature of 5.9 kK (0.76 eV). At this temperature, the fraction of the linear triplet [H₃C–C–C]⁺ isomer would be 0.02%. In our measurements, the plasma of the electron cyclotron resonance ion source had a temperature of 31 kK (4 eV). At this source temperature, the two singlet isomers were present in almost equal proportions in the ion beam and the linear triplet contribution is estimated to be ≈8%.

The ratio between the cyclic and linear C₃H₃⁺ isomers can be important for reactivity and chemical reactions, e.g., in space and planetary atmospheres, where larger molecular aggregates are formed such as benzene, C₆H₆. Due to the generally exothermic formation process of molecular ions, such as C₃H₃⁺ by collisions in the planetary ionospheres, they may have a thermal energy in the range up to a few electron volts shortly after the collision process, and the different isomers can be created. The ground-state cyclic isomer, as the smallest aromatic molecule, is more stable and has a lower reactivity, because a reaction will typically be associated with a ring opening. This process is not required for the linear isomers and a step-wise growth by an addition reaction, e.g., with methane, might be favored. Clearly, the relative contributions of the different isomers in space are important for the probability of producing larger molecules. Using NEXAFS spectroscopy, we can distinguish these isomers from each other, which is a challenge in infrared spectroscopy due to the vanishing dipole moment of c-C₃H₃⁺.⁹

From our results we are encouraged to anticipate that different ion sources can be optimized for the production of a specific constitutional isomer mixture. This would allow for experiments on ion–neutral–gas reactions of the different isomers to understand the role of the isomer in planetary atmospheres. Time-resolved NEXAFS spectroscopy at the C 1s edge will be the ideal tool to investigate the dynamics of the isomerization process as depicted in Fig. 5.

Author contributions

S. R. and M. M. conceived the beam time. S. R., P. C., T. B., A. P.-S., S. S., A. M., F. T., and M. M. carried out the experiments. S. R. performed the data analysis and the calculations using ORCA. S. R. and M. M. interpreted the results. S. R. wrote the manuscript with input from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at PETRA III and we would like to thank M. Hoesch, J. Buck, F. Scholz, K. Bagschik, and J. Seltmann for assistance in using beamline P04. Beamtime was allocated for proposal I-20191440. This project was funded by the Bundesministerium für Bildung und Forschung (BMBF, Federal Ministry of Education and Research) funding scheme (Projects no. 05K10RG1, no. 05K10GUB, no. 05K16RG1, no. 05K16GUC, no. 05K19GU4, and no. 15K22GUC), and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation – Projects no. 245652604, no. 389115454, and no. 201267377). F. T. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project 509471550, Emmy Noether Programme.

Notes and references

1. B. A. McGuire, Astrophys. J., Suppl. Ser., 2022, 259, 30.
2. L. E. Snyder, M. S. Schenewerk and J. M. Hollis, Astrophys. J., 1985, 298, 360.
3. C. A. Nixon, A. E. Thelen, M. A. Cordiner, Z. Kisiel, S. B. Charnley, E. M. Molter, J. Serigano, P. G. J. Irwin, N. A. Teanby and Y.-J. Kuan, Astron. J., 2020, 160, 205.
4. V. Vuitton, R. V. Yelle and J. Cui, J. Geophys. Res., 2008, 113, E05007.
5. J. H. Waite, Jr., D. T. Young, T. E. Cravens, A. J. Coates, F. J. Crary, B. Magee and J. Westlake, Science, 2007, 316, 870–875.
6. V. Vuitton, R. V. Yelle and P. Lavvas, Philos. Trans. R. Soc., A, 2008, 367, 729–741.
7. D. Zhao, K. D. Doney and H. Linnartz, Astrophys. J., 2014, 791, L28.
8. T. E. Cravens, I. P. Robertson, J. H. Waite, Jr., R. V. Yelle, W. T. Kasprzak, C. N. Keller, S. A. Ledvina, H. B. Niemann, J. G. Luhmann, R. L. McNutt, W.-H. Ip, V. De La Haye, I. Mueller-Wodarg, J.-E. Wahlund, V. G. Anicich and V. Vuitton, Geophys. Res. Lett., 2006, 33, L07105.
9. W. G. D. P. Silva, J. Cernicharo, S. Schlemmer, N. Marcelino, J.-C. Loison, M. Agúndez, D. Gupta, V. Wakelam, S. Thorwirth, C. Cabezas, B. Tercero, J. L. Doménech, R. Fuentetaja, W.-J. Kim, P. de Vicente and O. Asvany, Astron. Astrophys., 2023, 676, L1.
10. D. Gerlich and S. Horning, Chem. Rev., 1992, 92, 1509–1539.
11. J. S. Brodbelt, Mass Spectrom. Rev., 1997, 16, 91–110.
12. R. Wester, Phys. Chem. Chem. Phys., 2014, 16, 396–405.
13. D. J. Hollenbach and A. G. G. M. Tielens, Rev. Mod. Phys., 1999, 71, 173.
14. A. Stanger, Chem. Commun., 2009, 1939–1947.
15. Aromaticity: Modern Computational Methods and Applications, ed. I. Fernandez, Elsevier, 2021.
16. T. W. Kasel, A. T. Murray and C. H. Hendon, J. Phys. Chem. C, 2018, 122, 2041–2045.
17. O. Dopfer, D. Roth and J. P. Maier, J. Am. Chem. Soc., 2002, 124, 494–502.
18. O. Dopfer, D. Roth and J. P. Maier, Int. J. Mass Spectrom., 2002, 218, 281–297.
19. D. Roth and O. Dopfer, Phys. Chem. Chem. Phys., 2002, 4, 4855–4865.
20. A. N. Marimuthu, D. Sundelin, S. Thorwirth, B. Redlich, W. D. Geppert and S. Brünken, J. Mol. Spectrosc., 2020, 374, 111377.
21. W. G. D. P. Silva, D. Gupta, E. Plaar, J. L. Doménech, S. Schlemmer and O. Asvany, Mol. Phys., 2023, e2296613.
22. G. A. Garcia, B. Gans, J. Krüger, F. Holzmeier, A. Röder, A. Lopes, C. Fittschen, C. Alcaraz and J.-C. Loison, Phys. Chem. Chem. Phys., 2018, 20, 8707–8718.
23. H. Gao, Z. Lu, L. Yang, J. Zhou and C. Y. Ng, J. Chem. Phys., 2012, 137, 161101.
24. M. Epshtein, V. Scutelnic, Z. Yang, T. Xue, M. L. Vidal, A. I. Krylov, S. Coriani and S. R. Leone, J. Phys. Chem. A, 2020, 124, 9524–9531.
25. C. Kolczewski, R. Püttner, M. Martins, A. S. Schlachter, G. Snell, M. M. Sant’Anna, K. Hermann and G. Kaindl, J. Chem. Phys., 2006, 124, 034302.
26. I. C. Lyon, B. Peart, J. B. West and K. Dolder, J. Phys. B: At. Mol. Phys., 1986, 19, 4137.
27. H. Kjeldsen, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, R325.
28. S. Schippers, A. L. D. Kilcoyne, R. A. Phaneuf and A. Müller, Contemp. Phys., 2016, 57, 215–229.
29. J.-P. Mosnier, E. T. Kennedy, P. van Kampen, D. Cubaynes, S. Guilbaud, N. Sisourat, A. Puglisi, S. Carniato and J.-M. Bizau, Phys. Rev. A, 2016, 93, 061401(R).
30. S. Carniato, J.-M. Bizau, D. Cubaynes, E. T. Kennedy, S. Guilbaud, E. Sokell, B. McLaughlin and J.-P. Mosnier, Atoms, 2020, 8, 67.
31. M. Martins, S. Reinwardt, J. O. Schunck, J. Schwarz, K. Baev, A. Müller, T. Buhr, A. Perry-Sassmannshausen, S. Klumpp and S. Schippers, J. Phys. Chem. Lett., 2021, 12, 1390–1395.
32. S. Schippers, P.-M. Hillenbrand, A. Perry-Sassmannshausen, T. Buhr, S. Fuchs, S. Reinwardt, F. Trinter, A. Müller and M. Martins, ChemPhysChem, 2023, 24, e202300061.
33. S. Schippers, S. Ricz, T. Buhr, A. Borovik, Jr., J. Hellhund, K. Holste, K. Huber, H.-J. Schäfer, D. Schury, S. Klumpp, K. Mertens, M. Martins, R. Flesch, G. Ulrich, E. Rühl, T. Jahnke, J. Lower, D. Metz, L. P. H. Schmidt, M. Schöffler, J. B. Williams, L. Glaser, F. Scholz, J. Seltmann, J. Viefhaus, A. Dorn, A. Wolf, J. Ullrich and A. Müller, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 115602.
34. S. Schippers, A. Borovik, Jr., T. Buhr, J. Hellhund, K. Holste, A. L. D. Kilcoyne, S. Klumpp, M. Martins, A. Müller, S. Ricz and S. Fritzsche, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 144003.
35. J. Viefhaus, F. Scholz, S. Deinert, L. Glaser, M. Ilchen, J. Seltmann, P. Walter and F. Siewert, Nucl. Instrum. Methods Phys. Res., Sect. A, 2013, 710, 151–154.
36. A. Müller, M. Martins, A. Borovik, Jr., T. Buhr, A. Perry-Sassmannshausen, S. Reinwardt, F. Trinter, S. Schippers, S. Fritzsche and A. S. Kheifets, Phys. Rev. A, 2021, 104, 033105.
37. A. Müller, A. Borovik, Jr., S. Bari, T. Buhr, K. Holste, M. Martins, A. Perry-Saßmannshausen, R. A. Phaneuf, S. Reinwardt, S. Ricz, K. Schubert and S. Schippers, Phys. Rev. Lett., 2018, 120, 133202.
38. A. Müller, E. Lindroth, S. Bari, A. Borovik, Jr., P.-M. Hillenbrand, K. Holste, P. Indelicato, A. L. D. Kilcoyne, S. Klumpp, M. Martins, J. Viefhaus, P. Wilhelm and S. Schippers, Phys. Rev. A, 2018, 98, 033416.
39. A. P. Hitchcock and C. E. Brion, J. Electron Spectrosc. Relat. Phenom., 1980, 18, 1–21.
40. M. Schlapp, R. Trassl, E. Salzborn, R. W. McCullough, T. K. McLaughlin and H. B. Gilbody, Nucl. Instrum. Methods Phys. Res., Sect. B, 1995, 98, 525–527.
41. J. Fricke, A. Müller and E. Salzborn, Nucl. Instrum. Methods, 1980, 175, 379–384.
42. K. Rinn, A. Müller, H. Eichenauer and E. Salzborn, Rev. Sci. Instrum., 1982, 53, 829–837.
43. A. Müller, A. Borovik, Jr., T. Buhr, J. Hellhund, K. Holste, A. L. D. Kilcoyne, S. Klumpp, M. Martins, S. Ricz, J. Viefhaus and S. Schippers, Phys. Rev. A, 2018, 97, 013409.
44. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
45. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
46. A. Cameron, J. Leszczynski, M. C. Zerner and B. Weiner, J. Phys. Chem., 1989, 93, 139–144.
47. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822(R).
48. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
49. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
50. K. Kaufmann, W. Baumeister and M. Jungen, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, 2223.
51. V. Ásgeirsson, B. O. Birgisson, R. Bjornsson, U. Becker, F. Neese, C. Riplinger and H. Jónsson, J. Chem. Theory Comput., 2021, 17, 4929–4945.
52. U. Hergenhahn, O. Kugeler, A. Rüdel, E. E. Rennie and A. M. Bradshaw, J. Phys. Chem. A, 2001, 105, 5704–5708.
53. G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843.
54. S. Schippers, R. Beerwerth, S. Bari, T. Buhr, K. Holste, A. L. D. Kilcoyne, A. Perry-Sassmannshausen, R. A. Phaneuf, S. Reinwardt, D. W. Savin, K. Schubert, S. Fritzsche, M. Martins and A. Müller, Astrophys. J., 2021, 908, 52.
55. G.-x. Liu, Z.-s. Li, Y.-h. Ding, Q. Fu, X.-r. Huang, C.-c. Sun and A.-c. Tang, J. Phys. Chem. A, 2002, 106, 10415–10422.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00370e

---