Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Shell-dependent photofragmentation dynamics of a heavy-atom-containing bifunctional nitroimidazole radiosensitizer†
Lassi
Pihlava
 *a,
Pamela H. W.
Svensson
*a,
Pamela H. W.
Svensson
 b,
Edwin
Kukk
b,
Edwin
Kukk
 a,
Kuno
Kooser
a,
Kuno
Kooser
 c,
Emiliano
De Santis
c,
Emiliano
De Santis
 d,
Arvo
Tõnisoo
c,
Tanel
Käämbre
d,
Arvo
Tõnisoo
c,
Tanel
Käämbre
 c,
Tomas
André
b,
Tomoko
Akiyama
b,
Lisa
Hessenthaler
b,
Flavia
Giehr
b,
Olle
Björneholm
b,
Carl
Caleman
c,
Tomas
André
b,
Tomoko
Akiyama
b,
Lisa
Hessenthaler
b,
Flavia
Giehr
b,
Olle
Björneholm
b,
Carl
Caleman
 be and
Marta
Berholts
be and
Marta
Berholts
 *c
*c
aDepartment of Physics and Astronomy, University of Turku, FI-20014 Turku, Finland. E-mail: leapih@utu.fi
bDepartment of Physics and Astronomy, University of Uppsala, SE-75120 Uppsala, Sweden
cInstitute of Physics, University of Tartu, W. Ostwald 1, EST-50411, Tartu, Estonia. E-mail: marta.berholts@gmail.com
dDepartment of Chemistry – BMC, University of Uppsala, SE-75123 Uppsala, Sweden
eCenter for Free-Electron Laser Science, DESY, DE-22607 Hamburg, Germany
First published on 21st February 2024
Abstract
Radiation therapy uses ionizing radiation to break chemical bonds in cancer cells, thereby causing DNA damage and leading to cell death. The therapeutic effectiveness can be further increased by making the tumor cells more sensitive to radiation. Here, we investigate the role of the initial halogen atom core hole on the photofragmentation dynamics of 2-bromo-5-iodo-4-nitroimidazole, a potential bifunctional radiosensitizer. Bromine and iodine atoms were included in the molecule to increase the photoionization cross-section of the radiosensitizer at higher photon energies. The fragmentation dynamics of the molecule was studied experimentally in the gas phase using photoelectron–photoion–photoion coincidence spectroscopy and computationally using Born–Oppenheimer molecular dynamics. We observed significant changes between shallow core (I 4d, Br 3d) and deep core (I 3d) ionization in fragment formation and their kinetic energies. Despite the fact, that the ions ejected after deep core ionization have higher kinetic energies, we show that in a cellular environment, the ion spread is not much larger, keeping the damage well-localized.
1 Introduction
Radiosensitizers are agents that enhance the efficacy of radiotherapy by making cancer cells more sensitive to ionizing radiation.1,2 Among them, electron-affinic nitroimidazole derivatives – so-called oxygen mimetics – are particularly promising due to their ability to accumulate in radioresistant hypoxic tumors.3–6 However, the underlying mechanisms of how these compounds interact with radiation and/or secondary particles generated in the cells and induce sensitization remain poorly understood.The oxygen fixation hypothesis suggests that molecular oxygen attaching to a DNA can make single and double DNA strand breaks permanent, leading to irreparable cell damage.7 Nitroimidazoles activated by radiation or by ion/electron collisions can also interfere with DNA repair processes. The increased damage enables lowering the radiation doses and reducing the side effects of radiotherapy. Molecular radiosensitizers require radiation activation before their sensitizing effects can occur,7,8 and understanding the nature of these activation processes is crucial in comprehending how radiosensitizers function. Previous molecular studies have aimed to provide a fundamental understanding of the activation by probing the interactions between radiosensitizers and ionizing radiation/secondary particles (ions, electrons) in the gas phase.9–23 These fragmentation-oriented studies provided valuable insight into the occurring rearrangement reactions and the fragment formation upon dissociation of various nitroimidazole-based radiosensitizers – predominantly in the photon energy region ≈60–670 eV. Notably, the efficiency of the radiosensitizers was suggested to be correlated with the quantity of produced ions/radicals originating from the nitro group. Radiosensitizers that demonstrated higher efficacy in a clinical trial were observed to generate increased quantities of such products following fragmentation in the gas phase.15,16 It is important to emphasize that nitro group constituent, NO, serves as a more effective radiosensitizer than oxygen,24,25 while NO2 has strong oxidizing properties relevant for the fixation of radiation-induced damage.26
An alternative sensitization mechanism involves incorporating high atomic number elements or materials such as Au, Pt, Gd, and halogens into the tumor cells.27–31 The heavy element functions as an X-ray “antenna”, having higher photo and electron absorption cross-sections at higher photon energies compared to common cellular elements such as H, C, N, and O. Consequently, this leads to an intensified and localized release of secondary X-rays and electrons from the radiosensitizers after their initial interaction with X-rays. Significant quantities of low-energy electrons (LEEs) – including photo-, Compton, Auger–Meitner, intermolecular/interatomic coulombic decay (ICD),32–34 and electron transfer-mediated decay (ETMD)35 electrons – are generated with energies below 30 eV. LEEs are highly efficient not only at ionizing water molecules,36 which then produce harmful radicals that cause breaks in DNA strands,37,38 but also at directly attacking DNA.39 However, the DNA breakages can be repaired rather efficiently40,41 unless an irreversible reaction occurs at the site of the DNA radical. Therefore, in hypoxic environments, oxygen mimetics are required to interfere with the DNA repair processes. Bifunctional compounds, wherein a halogen atom is attached to a nitroimidazole moiety, offer a potential approach for low-energy photon radiotherapy.42,43 Above 33.2 keV photon energy, the ionization cross-section of iodine is significantly higher than that of lighter elements resulting in enhanced absorption of X-rays, reaching a maximum dose enhancement ratio around 50 keV.44 Moreover, it was shown in vitro on human colonic adenocarcinoma cells that iodinated nitroimidazoles have higher radiosensitizing efficiency than non-halogenated compounds at 50 keV.45
In this work, we present a detailed description of the photodissociation dynamics in a model radiosensitizer compound 2-bromo-5-iodo-4-nitroimidazole (henceforth referred to as BrINim). The structure of the molecule is shown in Fig. 1.
The molecule combines two distinct sensitization mechanisms characteristic of both heavy elements and nitroimidazoles. The fragmentation of the protonated version of this molecule was recently studied using near-edge X-ray absorption mass spectrometry,23 and building on this we examine here the fragmentation behavior of the non-protonated molecule upon core-ionization at the I 4d, Br 3d, and I 3d edges using multiparticle coincidence spectroscopy in the gas phase and Born–Oppenheimer-based molecular dynamics. The primary objective is to quantify the resulting fragments and their kinetic energies aiming to find clues regarding the better radiosensitivity of halogenated nitroimidazoles from the perspective of molecular fragmentation. Furthermore, we simulate the behavior of the oxygen ions in a water box to estimate the spread of ions in a cellular environment after the molecule's fragmentation depending on the ions' initial kinetic energy and therefore make predictions regarding the damage localization.
2 Experiment
The photoelectron–photoion–photoion coincidence spectroscopy (PEPIPICO) experiment was carried out at the gas-phase endstation46 of the Finnish–Estonian beamline (FinEstBeAMS)47,48 at the MAX IV synchrotron radiation facility. The beamline uses an SX700 monochromator (FMB Feinwerk-und-Messtech GmbH) and receives radiation from an Apple II type undulator. We used horizontally polarized light in the experiment. The photoelectron–photoion–photoion coincidence (PEPIPICO) setup consists of a modified Wiley–McLaren ion time-of-flight (TOF) spectrometer, equipped with a Roentdek 80 mm MCP and a HEX-anode detector, and a modified Scienta R4000 hemispherical electron analyzer, which is equipped with a 40 mm microchannel plate and a resistive anode position-sensitive detector (Quantar Inc.).The BrINim powder sample (C3HBrIN3O2, BLD Pharmatech, stated purity 97%) was evaporated from an MBE-Komponenten effusion cell at a temperature of 120 °C into the interaction region, where the molecular beam crossed with the monochromatized synchrotron radiation beam. We ionized the I 4d, Br 3d and I 3d core orbitals using photon energies of 85 eV, 115 eV, and 670 eV, respectively.
Detection of the targeted photoelectrons provided triggers for ion extraction voltage pulses. The combined coincidence data consists of ion flight times, ion hit positions and electron hit positions per trigger. Additionally, the extraction voltages were also triggered by non-coincident “random” triggers, which were obtained from a pulse generator and interleaved with the coincident electron triggers to be later used in a statistical false coincidence background removal.
For I 4d and Br 3d measurements, the electron analyzer was operated under a pass energy of 100 eV with a curved entrance slit of 2.5 mm, resulting in an energy resolution of 625 meV. In the I 3d measurement, the pass energy of 200 eV was used with a straight entrance slit of 4 mm with an energy resolution of 2 eV. The following TOF voltages were used for all measurements: extraction ±150 V, MCP 2300 V, drift tube 900 V, ion lens 100 V, and anode 250 V.
2.1 Data analysis
Some level of ion loss is inevitable in mass spectrometric experiments. For instance, ions hitting the detector could remain undetected due to detector efficiency and dead time effects. Here, the same TOF spectrometer voltages were used in all three experiments. However, I 3d ionization produced fragments with much higher kinetic energy (particularly the N+ and O+ ions). These ions were missing the detector if they obtained a high enough initial velocity component in the perpendicular direction against the TOF central axis during dissociation. Therefore, the I 3d experiment involved more ion loss than the other two experiments.To correct for the ion loss in coincident TOF mass spectra, we extracted the three-dimensional momentum vector for each ion using the flight time and the hit position on the detector. We then projected the momenta onto the pyz plane, divided the projection into sectors, and counted the number of ions in each sector. By assuming an isotropic momentum distribution and that all ions in the most populated sector were detected, we estimated ion transmission. Distortions of the isotropic distribution may occur due to e.g. intramolecular scattering, introducing minor systematic errors to the procedure. This method allowed us to correct the ion loss of all ionic fragments except for those containing bromine, due to the overlapping of the two isotopes in TOF spectra. More details about the correction procedure and its results can be found in ESI† (see Table SI).
3 Theory
To complement the experimental data, we used density functional theory (DFT) calculations to simulate the fragmentation dynamics occurring within femtoseconds after photoionization and subsequent Auger–Meitner decay. We used the Siesta code,49 which employs Born–Oppenheimer-based molecular dynamics in conjunction with pseudo-potential DFT. The wave functions were modeled using the default double-zeta+ polarization basis sets as implemented in Siesta, the core regions were described using norm-conserving pseudo-potentials, and all unknown exchange and correlation effects were included in the PBE-GGA functional.50The BrINim molecule was first allowed to relax to its geometrical ground state, followed by a 2 ps presimulation using the Verlet algorithm. For charge states q = +2 and q = +4 (henceforth all charges are given in units e), 77 and 83 independent snapshots, respectively, of the geometry were sampled from the presimulation and used as starting configurations in the fragmentation simulations. This eliminates artifacts arising from the initial conditions. The ionization is assumed to be sudden and the core hole lifetimes are approximated to be much shorter than the movement of the nuclei, thus the fragmentation simulation starts with the charge of the molecule delocalized across the valence orbitals.
The simulations corresponding to shallow core ionization (I 4d, Br 3d) are initiated at charge state q = +2, while deeper core ionization (I 3d) simulations are initiated at charge state q = +4. To account for the rapidly increasing electronic temperature due to the loss of Auger–Meitner electrons, the electronic temperature was set to 5000 K for the +2-system and to 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K for the +4-system, resulting in increased energy in the molecule by ≈5 and 15 eV, respectively. The dissociation of BrINim2+ and BrINim4+ were thereafter observed for 1 ps duration with time-steps of 0.5 fs. We estimated the breakage of covalent bonds and the regulation of the different possible fragmentation pathways using the bond integrity parameter
000 K for the +4-system, resulting in increased energy in the molecule by ≈5 and 15 eV, respectively. The dissociation of BrINim2+ and BrINim4+ were thereafter observed for 1 ps duration with time-steps of 0.5 fs. We estimated the breakage of covalent bonds and the regulation of the different possible fragmentation pathways using the bond integrity parameter 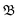 , as defined by Grånäs et al.,51 which was calculated for each bond at each timestep t,
, as defined by Grånäs et al.,51 which was calculated for each bond at each timestep t,
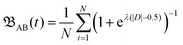 | (1) |
| D = diAB(t) − μ(dTAB(t)) − σ(dTAB(t)). |
It incorporates the distance dAB(t) between atoms A and B, the mean distance μ and standard deviation σ between A and B from the presimulation, and a smearing parameter λ. 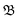 stretches from 1 (intact bond) to 0 (broken bond).
stretches from 1 (intact bond) to 0 (broken bond).
To study the charges on the fragments recorded at the final time step we have performed Mulliken charge analysis using post-Hartree–Fock theory as implemented in the Orca software.52 We have used the RI approximation with MP2 correlation integrals,53 cc-PVTZ basis set for C, N, O, H, and Br atoms,54 and SARC-ZORA-TZVP basis set for I.55
In addition to the DFT calculations, we conducted classical molecular dynamics simulations using GROMACS (version 2018.8)56,57 to investigate the temperature dependence of the displacement of an O+ ion within a 5 × 5 × 5 nm3 water box until reaching thermal equilibrium. We performed presimulations with the ions at an average kinetic energy of 2.90 eV, 3.45 eV, and 7.96 eV (corresponding to 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653 K, 40
653 K, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 035 K, and 92
035 K, and 92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 372 K) for 1 ps, using a simulation time step of 0.05 fs, and saving data frames every 10 fs. From each frame of these presimulations, the velocities of the ions are extracted and ions are subsequently positioned at the center of a previously equilibrated 300 K water box. Following this, a total of 100 simulations, each lasting for 1 ps, were executed for each of the three ion temperatures. During these simulations, water molecules were coupled to a 300 K thermal bath using the velocity rescaling thermostat,58 while the ion remained decoupled. The TIP3P water model59 was employed for the water molecules, whereas the ion underwent an ad hoc parametrization using Gaussian,60 Antechamber,61 and ACPYPE62 tools. From the simulations, we calculated the ions' radius of gyration63 as a measure of their geometrical spread.
372 K) for 1 ps, using a simulation time step of 0.05 fs, and saving data frames every 10 fs. From each frame of these presimulations, the velocities of the ions are extracted and ions are subsequently positioned at the center of a previously equilibrated 300 K water box. Following this, a total of 100 simulations, each lasting for 1 ps, were executed for each of the three ion temperatures. During these simulations, water molecules were coupled to a 300 K thermal bath using the velocity rescaling thermostat,58 while the ion remained decoupled. The TIP3P water model59 was employed for the water molecules, whereas the ion underwent an ad hoc parametrization using Gaussian,60 Antechamber,61 and ACPYPE62 tools. From the simulations, we calculated the ions' radius of gyration63 as a measure of their geometrical spread.
4 Results
4.1 Electron–ion–ion coincident mass spectra
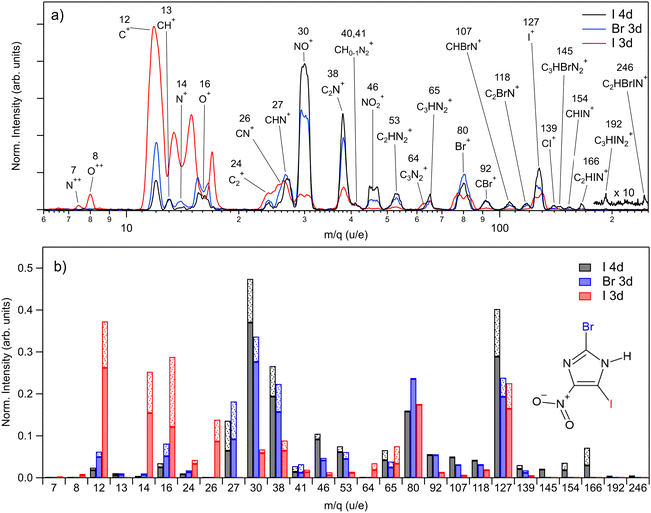
The PEPIPICO experiments were run upon ionizing the molecule with 85 eV, 115 eV, and 670 eV photons, i.e. just above iodine 4d, bromine 3d, and iodine 3d ionization thresholds, respectively. We measured the following binding energies for BrINim: I 4d5/2 – 57.56 eV, I 4d3/2 – 59.28 eV, Br 3d5/2 – 77.32 eV, Br 3d3/2 – 78.35 eV, I 3d5/2 – 639.26 eV, and I 3d3/2 – 650.42 eV. For I 4d and Br 3d, the standard deviation is 0.01 eV, while for I 3d it is 0.02 eV. The photoelectron spectra extracted from the PEPIPICO datasets are included in the ESI† (see Fig. S1–S3).In Fig. 2(a), we present three mass spectra, converted from the time-of-flight scale, that coincide with the I 4d, Br 3d, and I 3d photoelectrons. Peak areas from the TOF spectra, normalized as ion counts per electron trigger for each m/q ratio, are given in Fig. 2(b) by solid bars. The shaded fractions of the bars show the addition of the estimated lost-ion fraction to the detected peak areas. Statistical errors for the normalized peak areas were calculated from the Poisson statistics of the ion counts and are negligibly small compared to the variations in Fig. 2(b). The lost-ion correction is another, systematic source of error, which is however difficult to characterize. We do not assign specific numeric error-bar values that take into account the lost-ion corrections but estimate them to dominate over the statistical error. As related to the observed differences in Fig. 2(b), we can say on the example of the fragment at m/q 127 (from here on given in u/e units), that we consider the difference between I 4d and Br 3d ionizations to be significant, while the difference between the Br 3d and I 3d ionization is not.
Ionization of shallow and deep core levels leads via Auger–Meitner decay in one or two steps to a distribution of dissociative multiply charged states. We approximate the charge state distribution of the molecule after I 4d, Br 3d, and I 3d photoionization to the known charge state distributions of the neighboring rare gas elements Xe 4d,64 Kr 3d,65 and Xe 3d,66 correspondingly. Thus, the approximated charge distribution for I 4d is 81% 2+ and 19% 3+, for Br 3d 70% 2+ and 30% 3+, and for I 3d 0.3% 2+, 4% 3+, 39% 4+, 32% 5+, 20% 6+, 4% 7+, 0.5% 8+. Consequently, the shallow core ionization (I 4d, Br 3d) mostly results in a doubly charged molecule. The deeper I 3d photoionization leads to more highly charged states, predominantly +4, +5, and +6.
For shallow core levels, the most abundant ionic fragment is NO+, followed by I+ for the I 4d edge and Br+ for the Br 3d edge. Additionally, C2N+ fragment at m/q 38 is strongly present in both spectra. However, notable differences can be observed when comparing the ions of higher masses. In I 4d mass spectrum, heavier ions such as C3HBrN2+, CHIN+, C2HIN+, C3HIN2+, and C2HBrIN+ are observed. Conversely, with higher photon energy in the Br 3d spectrum, these ions are missing, and the ion distribution shifts towards lighter masses. The intensities of small atomic fragments, C+, N+, and O+, noticeably increase mostly at the expense of heavier fragments such as NO+, C2N+, and NO2+. Interestingly, the intensity of the intact ring ion C3HN2+ at m/q 65 does not change significantly for all three measured edges. Furthermore, it even shows an increase for the I 3d edge, when also including the fragment at m/q 64 – the ring that has lost its hydrogen.
The I 3d mass spectrum is characterized by the increased amount of atomic ions that form above 70% from all fragments created. Accounting for the correction, the C+ ions dominate the spectrum followed by O+, N+, I+, and Br+ ions. Note that the actual production of Br+ should be higher than shown in Fig. 2(b) since the ion loss correction could not be applied to it. Nevertheless, it is clear that the ionization of a deep core level results in a more vigorous fragmentation than the ionization of the shallow core levels. This is explained by the creation of a highly charged final state that results in a more energetic Coulomb explosion. Indeed, in the I 3d experiment, N++ and O++ dications are detected unlike upon shallow-core ionization, indicating a higher charge state of the parent. The magnitude of the Coulomb explosion is reflected in the widths of the ion peaks: in the I 3d mass spectrum, the widening of the peaks is observed for the fragments such as C+, N+, O+, NO+ Br+, and I+. Note that N+ and O+ ions are partly overlapping at around m/q 15 in Fig. 2(a), but in Fig. 2(b) the contribution of each ion was accounted for. Generally, the multiatomic ions become much weaker or disappear completely except for m/q 24, 26, 64, and 65. In comparison with the I 4d spectrum, there is a significant decrease by 67%, 86%, and 87% in the production of C2N+, NO+, and NO2+ fragments, correspondingly.
4.2 Fragmentation simulations and charge analysis
Yields of various fragments were also investigated by Born–Oppenheimer-based molecular dynamics simulations for two chosen charge states of the parent molecule: q = +2 and q = +4 approximating, respectively, a shallow inner-shell ionization followed by a one-step Auger decay and a deeper inner-shell ionization followed by a multi-step Auger decay. All fragments that were present at the end of all simulated trajectories are listed in Table 1 and their occurrence probabilities are also summarized by Fig. 3. The fragments that were also detected in the experiment are highlighted in bold. A direct comparison with the three coincidence measurements shown in Fig. 2(b) is, however, not possible since the simulations do not reproduce the localization of the unit charges to the fragments. We have computed the average partial charges of the fragments using Mulliken charge analysis as an approximate indicator, showing what fraction of each fragment in the simulated trajectories would carry a positive charge and therefore be directly comparable with the experimental results. High positive partial charges in Table 1 suggest that likely an ionic fragment is produced.![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) q=+2 and
q=+2 and ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) q=+4. Fragments observed in the experimental mass spectra are indicated in bold
q=+4. Fragments observed in the experimental mass spectra are indicated in bold
| m (u) | Fragments | q = +2 (%) |
![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) q=+2 (e)
q=+2 (e) |
q = +4 (%) |
![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) q=+4 (e)
q=+4 (e) |
|---|---|---|---|---|---|
| 1 | H | 11.7 | 0.35 ± 0.08 | 54.2 | 0.33 ± 0.07 |
| 12 | C | 15.6 | 0.29 ± 0.11 | 73.5 | 0.23 ± 0.11 |
| 14 | N | 3.9 | 0.12 ± 0.23 | 73.5 | 0.08 ± 0.15 |
| 15 | NH | — | — | 16.8 | 0.29 ± 0.06 |
| 16 | O | 48.0 | −0.21 ± 0.08 | 96.4 | 0.11 ± 0.15 |
| 24 | C 2 | 1.3 | 0.28 | 33.7 | 0.38 ± 0.06 |
| 26 | CN | 9.1 | 0.21 ± 0.06 | 57.8 | 0.20 ± 0.15 |
| 27 | CHN | 15.6 | 0.28 ± 0.12 | 24.1 | 0.38 ± 0.10 |
| 30 | NO | 42.9 | 0.27 ± 0.11 | 84.3 | 0.58 ± 0.10 |
| 38 | C 2 N | 5.2 | 0.40 ± 0.09 | 4.8 | 0.32 ± 0.03 |
| 39 | C2HN | 1.3 | 0.67 | 4.8 | 0.68 ± 0.06 |
| 42 | CNO | 1.3 | 0.67 | — | — |
| 46 | NO 2 | 46.7 | 0.09 ± 0.17 | 3.6 | 0.74 ± 0.08 |
| 52 | C2N2 | 2.6 | 0.05 ± 0.01 | — | — |
| 53 | C 2 HN 2 | 2.6 | 0.39 ± 0.08 | — | — |
| 64 | C 3 N 2 | 2.6 | 0.49 ± 0.01 | — | — |
| 65 | C 3 HN 2 | 9.1 | 0.78 ± 0.07 | — | — |
| 69 | C2HN2O | 1.3 | 0.99 | — | — |
| 80 | Br | 26.0 | 0.43 ± 0.06 | 100 | 0.94 ± 0.12 |
| 92 | CBr | 6.5 | 0.64 ± 0.11 | — | — |
| 106 | CBrN | 13.0 | 0.59 | — | — |
| 107 | CHBrN | 6.5 | 0.99 ± 0.27 | — | — |
| 118 | C 2 BrN | 5.2 | 0.87 ± 0.05 | — | — |
| 127 | I | 63.6 | 0.76 ± 0.11 | 100 | 1.45 ± 0.14 |
| 144 | C3N2Br | 1.3 | 0.79 | — | — |
| 145 | C 3 HBrN 2 | 20.8 | 1.21 ± 0.10 | — | — |
| 153 | CIN | 2.6 | 0.59 ± 0.01 | — | — |
| 154 | CHIN | 7.8 | 1.03 ± 0.06 | — | — |
| 165 | C2IN | 5.2 | 1.22 ± 0.28 | — | — |
| 175 | C3HBrN3O | 1.3 | 1.64 | — | — |
| 191 | C3HBrN3O2 | 2.6 | 1.35 ± 0.05 | — | — |
| 192 | C 3 HIN 2 | 2.6 | 1.53 ± 0.06 | — | — |
| 272 | C3HBrIN2 | 14.3 | 2.08 ± 0.42 | — | — |
| 318 | Parent | 2.6 | 2.00 ± 0.00 | — | — |
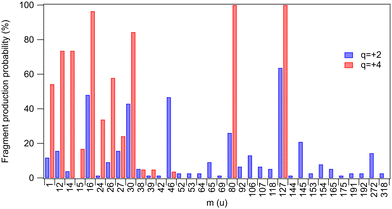 | ||
| Fig. 3 Probabilities by which a fragment was observed at the end of the simulated trajectories for charge states q = +2 and q = +4 (taken from Table 1). The probabilities do not differentiate between neutral and ionic fragments. | ||
One first notes that the ring fragments heavier than the nitro-group fragment (m = 46 u) are only produced in dicationic trajectories. These include ring segments with iodine or bromine (CHIN, CHIN2, CHBrN, C3HBrN2). Such fragments are also observed experimentally in shallow inner-shell ionization of I 4d. The quadruply-charged trajectories are, in contrast, dominated by a high degree of atomization: 68% of all fragments are atomic for q = +4, as compared to 42% for q = +2. This trend with charge increase is only expected and is observed also in the experiment (Fig. 2(b)), where 71% of fragments are atomic following the I 3d ionization, as compared to 30% in I 4d. The most dramatic change occurs in the atomic N yield, which increases 57 times going from the I 4d to I 3d ionization, and 18 times going from q = +2 to q = +4 in the simulations. A significant gain in the H yield is predicted by simulations, reaching over 50% at q = +4. Hydrogen ions were not detected in the experiment due to the high-voltage ion extraction pulses that created a disturbance in the low-mass region.
Breakage of the carbon–halogen bond is a very common event in the simulations, with atomic halogen fragments comprising 27% (q = +4) and 22% (q = +2) of the total – notably, the C–I and C–Br bonds are broken in all q = +4 trajectories. The predicted yields compare well with the experiment, where halogen ions comprise 21% (I 3d) and 27% (I 4d) of all charged fragments. The halogen atoms in the simulations also have strongly positive fractional charges, suggesting positive charge localization and thus detection in the ion mass spectra. However, the simulations and the experiment show opposing trends for the halogen atoms. The simulations predict an increased yield when the charge state of the system increases while the experiment shows a decrease. Note that in the analysis the ion loss correction was not extended to Br+ but we estimate the amount of lost Br+ to be comparable with the amount of lost I+ (see Fig. 2). In the simulations, the yield of bromine increases fourfold, and the ion losses may therefore only account for the discrepancy partially.
Overall, the decreased yield of halogen ions in the experiment between shallow core and deep core ionization is an intriguing phenomenon. As a potential explanation here, the deep core ionization may lead to a wide internal energy distribution for the quadruply-charged state. With higher internal energy, more competing dissociation pathways become available. For example, the number of bonds broken and the atomic fragments released may increase, as indeed observed. The system would then have more dissociation pathways to choose from leading to the decreased yield of the halogen atoms. The internal energies used in the simulations may not correctly capture this behavior.
Other discrepancies arise between the experiment and simulations e.g. in the mass range of 27–38 u (CHN, NO, C2N). The simulations show an increase of fragment yield for the q = +4 charge state (Fig. 3), while these fragments are suppressed in the deep core-hole (I 3d) measurement that yields the highest charge states (Fig. 2(b)). At the same time, a comparison of the two figures also shows that with deep inner shell ionization, the light atomic fragment yield increases even more than in the simulations (q = +4). This suggests that the discrepancies in both regions are explained if, in the higher-charge states, the CHN+, NO+, and C2N+ fragments would start to be depleted by secondary time-delayed dissociation events. A significant fraction of these events can be cut off in the simulated trajectories due to the limited integration time of 1 ps. The time scale of the secondary dissociation is also strongly dependent on the available internal energy67 and its distribution is only very approximatively represented by the simulations. There are also several fragments predicted by the simulation that are missing in the experiments (see Table 1). It can be due to two main reasons: the fragments could be released as neutral, experimentally undetected species, and as discussed above, the simulation time can be insufficient to represent the further dissociation steps.
The nitro-group fragment NO2 and its possible secondary dissociation products NO, N and O deserve special attention due to their relevance as oxygen mimetic agents.24–26 In the simulations – as in the experiment – we see the yield of NO2 almost vanishing as the charge increases to q = +4 (Fig. 3), indicating that most likely it is now dissociating further, either as a second-step or a concerted process. Indeed, we also see an expected corresponding increase in the production of the NO and O fragments. There is also some increase in the yield of atomic nitrogen, which can also originate from the ring break-up. A closer inspection of the trajectories shows that almost all of the atomic nitrogen fragments originate from the ring in the simulations.
As was mentioned above, the NO2+ yield is strongly depleted for the deeper I 3d core ionization (Fig. 2(b)) in agreement with the simulation. However, so is the yield of NO+, whereas the yield of NO increased in the high-charge simulation. Furthermore, the I 3d experiment shows a more dramatic enhancement of the N+ and O+ yields than the high-charge simulation (even though the neutral N and O yield is not observable). As mentioned above, these findings and discrepancies are likely explained by the continuing secondary dissociation depleting the NO fragments in deep core ionization. In the simulations, we assume instant ionization and electronic relaxation, and these approximations are likely the reasons that the secondary dissociation is not described accurately enough to capture the production of some of the fragments seen in the experiment.
4.3 Photoelectron–photoion–photoion coincidence maps
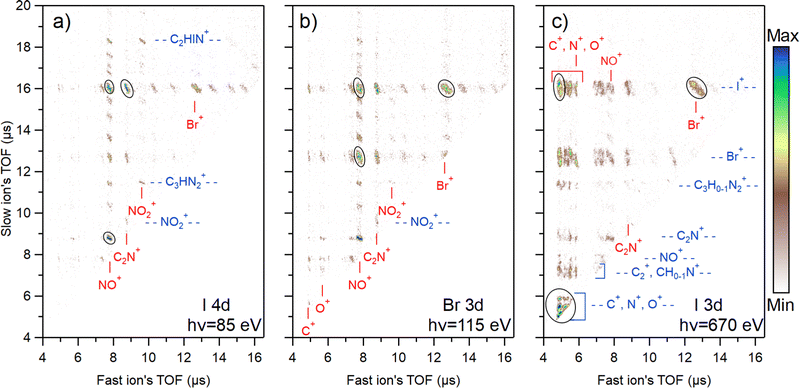
The photoion–photoion coincidence (PIPICO) maps in Fig. 4 present the ion pairs (i.e., the two-ion coincidences) detected together with the I 4d, Br 3d, and I 3d photoelectrons. These maps provide a more detailed insight into the photodissociation dynamics. The x-axis of the map represents the flight time of the faster ion, while the y-axis shows the flight time of the slower one. Conservation of momentum results in the correlation of the velocities of the two ions that form a coincident pair, therefore tilted patterns emerge. In the I 3d experiment, the TOF spreads of the patterns are longer, indicating higher dissociation energies of the ions. Due to the ion losses, many patterns in the I 3d experiment are missing their central region, where the flight time of ions is not strongly affected by their initial velocity. This region is populated by ion pairs with initial velocity vectors in the off-axis direction. When the initial velocity is too high for the applied voltage settings, these ions may miss the detector, causing the region to appear empty. On the other hand, ion pairs with initial velocity vectors in the axial direction populate the two ends of a pattern. The ion losses were estimated for the mass spectra presented in Fig. 2, and here we do not estimate the loss for each ion pair separately.Each map shows the three most abundant ion pairs with black ovals. In the I 3d map, these are the single atom coincidences C+ & N+ & O+ (overlapped region), C+ & I+, and I+ & Br+ that form about 38% of all ion pairs produced. For Br 3d, these are Br+ & I+, NO+ & I+, NO+ & Br+ which is about 22% of all ion pairs. For I 4d, these are NO+ & I+, C2N+ & I+, and NO+ & C2N+ that form about 27% of all ion pairs created. In total, 62 different ion pairs were detected following shallow core ionization and 32 pairs following the I 3d ionization. The lower number of different ion pairs in the I 3d experiment is explained by the higher level of atomization and therefore the disappearance of coincidences with heavier fragments.
Fig. 4 reveals a strong ionization-site-dependent trend: as the photon energy increases, the ion pair distribution on the maps shifts towards the lower-left quadrant. This region corresponds to ions with faster flight time and therefore lighter mass. The trend can be attributed to the growing amount of internal energy available for dissociation going from shallow core levels to deeper ones.
States created by ionizing I 4d and Br 3d are energetically the most similar out of the three studied cases (primarily dicationic states vs. more highly charged states). Yet, there are major distinctions in their dissociation dynamics. For I 4d, there is a multitude of ion pair patterns involving I+ (see the slow ion time of flight at about 16 μs). In contrast, the majority of Br+ ions can be found in just three predominant patterns coincident with NO+, C2N+, and I+. Meanwhile, Br 3d ionization both increases the release of Br+ (as seen in Fig. 2) and the number of Br+-producing fragmentation pathways. Even though the I+ release is reduced in comparison with I 4d ionization, there are still multiple clear patterns containing I+. The most significant factor influencing the observed differences in fragmentation dynamics is the charge states produced following corresponding ionization. As was mentioned in Section 4.1, the fraction of tricationic states after Auger–Meitner decay is higher for Br 3d than for I 4d (30% vs. 19%).64,65 This explains the stronger fragmentation after Br 3d ionization. The Auger–Meitner decay of the I 4d and Br 3d core holes may also populate the dicationic final states differently, leading to a different internal energy distribution. In addition, the dicationic dissociation landscape could be affected by the original position of the initial core hole. The retained “memory” of the core hole site can indicate nuclear relaxation dynamics during the core hole lifetime.
There is a multitude of strong patterns involving NO+ ion in the case of I 4d and Br 3d ionization (see fast ion axis at about 8 μs in Fig. 4(a) and (b)), forming 43% and 39% of all ion pairs created, respectively. In the I 3d experiment, however, there are only three strong patterns with the NO+ in coincidence with Br+, I+, and C2N+. Adding also weak patterns with NO+, we get about 8% from all ion pairs produced. This aspect is interesting from the viewpoint of radiosensitization as high production of NO+ ions is generally correlated with better efficiency of nitroimidazole radiosensitizers. Here, we see that upon deep core ionization, the NO+ production is highly suppressed and replaced by N+ and O+.
The N+ ions observed in the experiment can originate either from the ring break-up or the nitro group. A more detailed analysis of the PIPICO patterns, ion momentum vectors, and triple ion coincidences sheds light on the origin of these ions. Firstly, it is seen from the PIPICO map in Fig. 4(c) that it forms the strongest pattern with Br+, but also with I+. Indeed, further data analysis shows that there is a significant amount of (N+, Br+, I+) triple coincidences. The same is true for the O+ ions and the (O+, Br+, I+) triple coincidences that are even more abundant. Next, the ion momentum correlations were investigated. We found that the momentum of the majority of N+ ions is approximately 2.2 times less than the momentum of I+, and the momentum of O+ is about 1.8 times less. This would be consistent with the secondary dissociation sequence, where there is a strong Coulomb interaction between the I+ and NO+ fragments in the first step and the acquired momentum is divided in the secondary dissociation step between the N and O atoms in the ratio of 14/16. For a triply charged parent, for example:
| C3HBrIN3O23+ → C3HN2 + Br+ + I+ + NO+ + O; |
| NO+ → (N + O)+, |
4.4 Calculation of fragmentation pathways
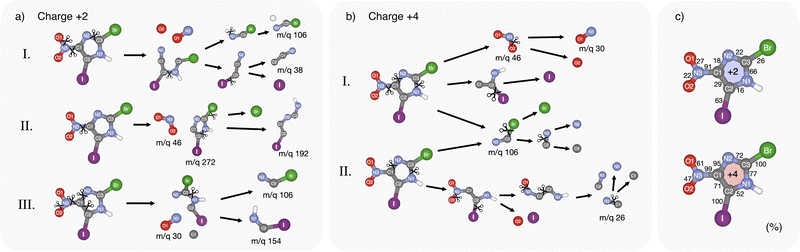
The Born–Oppenheimer-based molecular dynamics simulations revealed a rich, highly charge-dependent fragmentation landscape. Some of the modeled pathways are illustrated in Fig. 5(a) and (b) for charges q = +2 and q = +4. Fig. 5(c) shows the calculated probability of bond breaking during dissociation for each bond in the molecule at the specific charge state.Shallow core ionization leads to a variety of bond-breaking dynamics and outcomes. Three of them are shown in Fig. 5(a). According to the calculations, the C1–N3 bond between the ring and the nitro group is most frequently broken, occurring approximately nine times out of ten. The release of the nitro group is often followed by the release of iodine and ring-opening at C3–N1 (see path (a) I, Fig. 5). In some simulations, interestingly, we observed a semi-stable m/q 272 fragment, see path (a) II. Upon longer simulation runs, this fragment resulted in the creation of a single Br ion and a fragment with m/q 192, which is also visible in the experimental mass spectrum (Fig. 2). In path (a) III the C1–N3 bond is broken, but instabilities in this path cause the NO2 group to lose an O atom and trigger the breaking of the ring at three sites leading to halogenated fragments at m/q 106 and 154. In summary, single atom ions are mostly observed in paths aI and aII, while path (a) III shows different combinations of fragmentation leading to heavier fragments, often in the shape of open ring strands, with or without halogen atoms. For more possible dissociation pathways see Fig. S4 in ESI.†
At photon energies reaching I 3d ionization, more energy is dispatched into the molecular system, causing the breaking of the weakest bonds first. This is apparent in Fig. 5(b) where the two most probable fragmentation pathways are shown. We can observe a direct domino effect caused by the initial bond breaking which leads to the production of single atom fragments. In fragmentation path (b) I, the C1–N3 bond breaks a few femtoseconds after photoionization, similarly as in the case of the doubly charged system, causing an almost instantaneous degradation of the ring with broken covalent bonds at C1–N2 and C3–N1. Subsequently, the Br and I atoms are broken off at very short time scales, while O fragments are produced from the NO2 group. This pathway shares similarities with the previously discussed experimental ((N,O)+, Br+, I+) tricationic pathway based on the momentum considerations but differs in the timing of the fragmentation steps. In path (b) II, single I, Br, and O atoms are produced while maintaining the C1–N3 bond intact. In both paths bI and bII, the majority of the single Br atoms are produced via the short-lived intermediate fragment m/q 106 while coincidently producing single C and N atoms originating from the imidazole ring region closest to the Br atom. Furthermore, in path (b) II, the dissociation of single N and C atoms originates from the region close to the NO2-group. CN fragments consisting of N1 and C2 atoms seem to be particularly stable and can be observed in the experiment at m/q 26.
4.5 Average kinetic energies of the ions and their spread in aqueous environment
To better understand the differences in fragmentation dynamics upon shallow and deep core ionization of halogen-containing nitroimidazole, we examined the kinetic energies of the produced ions. Table 2 displays the average kinetic energy of various ions in each core ionization case. The average kinetic energies were obtained from a momentum vector magnitude histogram using a Gaussian fit. The results indicate that the kinetic energy of the ions tends to increase going from I 4d to Br 3d to I 3d. The O+ has the highest kinetic energy across all three ionization cases. Moreover, we note that atomic ions – C+, N+, O+, and I+ – gain significant kinetic energy upon I 3d core ionization in comparison to I 4d and Br 3d ionization. N+ and O+ ions, in particular, are faster than the others.| Ion | I 4d | Br 3d | I 3d | |||
|---|---|---|---|---|---|---|
| E k | FWHM | E k | FWHM | E k | FWHM | |
| N++ | — | — | — | — | 5.02 | 1.41 |
| O++ | — | — | — | — | 1.73 | 0.55 |
| C+ | 1.19 | 1.02 | 1.54 | 1.34 | 3.07 | 1.48 |
| CH+ | 1.08 | 0.82 | 1.23 | 1.09 | — | — |
| N+ | 1.68 | 1.40 | 2.25 | 1.39 | 5.85 | 2.95 |
| O+ | 2.90 | 0.81 | 3.45 | 0.99 | 7.96 | 1.66 |
| C2+ | 1.34 | 0.94 | 1.58 | 1.29 | 2.63 | 1.11 |
| CN+ | — | — | — | — | 3.23 | 1.46 |
| CHN+ | 1.61 | 1.15 | 1.66 | 1.39 | — | — |
| NO+ | 2.59 | 0.61 | 2.77 | 0.83 | 3.90 | 1.43 |
| C2N+ | 1.21 | 1.27 | 1.26 | 1.47 | 2.21 | 1.80 |
| CHN2+ | 1.97 | 2.03 | 2.38 | 2.51 | 2.99 | 1.10 |
| NO2+ | 2.66 | 0.39 | 2.65 | 0.68 | 3.59 | 1.95 |
| C2HN2+ | 1.87 | 1.44 | 2.01 | 1.87 | 2.53 | 1.51 |
| C3N2+ | — | — | — | — | 2.30 | 1.26 |
| C3HN2+ | 0.54 | 0.91 | 0.40 | 1.48 | 2.10 | 1.79 |
| I+ | 1.67 | 0.57 | 1.79 | 0.92 | 3.30 | 0.73 |
| CI+ | 0.88 | 0.95 | 1.09 | 1.70 | — | — |
| CHIN+ | 0.52 | 0.54 | — | — | — | — |
| C2HIN+ | 0.08 | 0.17 | — | — | — | — |
To estimate the role of the radiosensitizer in a cellular environment based on the spread of produced ions due to the different kinetic energies acquired after ionization, we performed molecular dynamics simulations of an oxygen ion in a box of water (see Section 3 for details on the simulations). We calculate Rgyr at the point in time when the average kinetic energy of the ion is the same as that of the surrounding water molecules. The results are listed in Table 3, and we can conclude that the ions with the highest kinetic energy (7.96 eV) do not travel much further than the ions with lower kinetic energy (Rgyr = 3.00 Å vs. Rgyr = 4.75 Å). The number of different water molecules that the ion interacts with before reaching thermal equilibrium increases with the ion's kinetic energy, going from 10.33 to 13.77 (2.9 eV vs. 7.96 eV). The number of collisions was averaged over 100 simulations per kinetic energy. A collision was counted each time the distance between the ion and a water molecule decreased to 2.5 Å.
| E k [eV] | 2.90 | 3.45 | 7.96 |
| R gyr [Å] | 3.00 | 3.35 | 4.75 |
| N | 10.33 | 11.15 | 13.77 |
5 Discussion
In low-energy photon radiotherapy, the I 1s photoionization channel becomes dominant for the iodine-containing radiosensitizer, given the iodine's high absorption cross-section above the I 1s edge.44 The 1s−1 state decays mostly via fluorescence to the 2p−1 state,68 which decays further primarily via Auger cascade, creating larger charge build-up in the molecule.69 This suggests that the molecule will undergo an even more energetic Coulomb explosion than observed in our I 3d ionization experiment. In this case, it is expected that the dissociation would lead primarily to the release of atomic ions with varying charge states. The stronger Coulomb repulsion in the molecule will lead to a further increase in the kinetic energies of the formed ions.In a cellular environment, it is expected that the ions will quickly lose their initial kinetic energy by colliding with surrounding water molecules. Our simulations of oxygen ion at its highest kinetic energy (determined experimentally in I 3d experiment) in a water box show that even if the initial kinetic energy after fragmentation is relatively high (around 8 eV), this energy is absorbed by the surrounding water already within 1 ps, and the ion radius of gyration, used here to estimate the ion spread, is below 5 Å. For the sake of comparison, the width of a DNA double-strand is approximately 2 nm and the size of human cells is in the order of micrometers. This indicates that the sensitization effect with halogenated molecules would be highly localized.
Charged atomic ions are chemically very reactive, resulting in a radiation damage “hot spot” that could lead directly to DNA damage. Moreover, the ions could react with water, an abundant molecule within cells, and our simulations indicate that the released ionic fragments would interact with multiple water molecules before stopping. Ionization of water leads to the generation of reactive oxygen species that then damage DNA contributing to extensive local damage.70,71
It is important to note that water can influence the fragmentation process of the radiosensitizer in several ways. For example, it can alter the electronic and geometric structure of the molecule in its ground state and impede the fragmentation process by affecting nuclear motion. In a solute–solvent environment, the additional relaxation channels such as intermolecular coulombic decay and electron/proton transfer-mediated decay also could affect the fragmentation outcome.72–75 Hence, further research is needed to explore the role of water in the fragmentation process of halogenated nitroimidazoles. For example, this could be achieved with nitroimidazoles embedded in water clusters.
6 Conclusions
We investigated the gas-phase photodissociation of 2-bromo-5-iodo-4-nitroimidazole by targeting three different electron shells in its absorption hot spots, the Br and I atoms. Consequently, we were able to compare the fragmentation dynamics between low-charge (+2, +3 at I 4d and Br 3d) and high-charge states (+4, +5 at I 3d), mimicking the interactions of the radiosensitizer with low energy secondary particles and high energy photons.From the molecular dissociation perspective, we discovered that deep core ionization leads to the suppression of NO+ and NO2+ release and to the formation of energetic atomic ions (C+, N+, O+, Br+, I+) in large quantities (above 70%). Particularly, N+ and O+ ions gain significant kinetic energy upon dissociation. Note that this effect is expected to get stronger at I 1s ionization due to a larger charge build-up via Auger–Meitner cascades that lead to the emission of a larger number of electrons. The fast ions are produced in 29% of cases and could potentially play an important role in damaging DNA, depositing more energy to their immediate surroundings than slow ions. Simulations of oxygen ions in the water box revealed that following I 3d core ionization, the ions do not travel further than about 5 Å from the emitter, which makes the halogenated nitroimidazoles highly selective to cancer cells.
In conclusion, the presence of a heavy halogen atom in the molecular structure of nitroimidazoles contributes to the release of energetic, highly reactive atomic fragments upon deep core ionization that could interfere with DNA repair processes. These fragments can directly damage DNA or indirectly harm it by ionizing surrounding water molecules, which then produce harmful radicals and electrons. From the perspective of molecular fragmentation, these factors could contribute to better radiosensitivity of halogen-containing nitroimidazole radiosensitizers.
Author contributions
Experiments, LP, MB, OB, EK, KK, PHWS, AT, TK, TA, TA, LH, FG; computation and software, PHWS, EDS, CC; experimental data analysis, MB, LP, EK; calculations analysis, PHWS, EDS, CC; writing of the manuscript, LP, MB; review and editing, OB, EK, KK, CC, PHWS, AT, TK, TA, TA, LH, FG; funding acquisition, MB. All authors have read and agreed to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Estonian Research Council grant MOBTP1013. LP acknowledges funding from the Vilho, Yrjö, and Kalle Väisälä Foundation. TK acknowledges the financial support provided by the European Regional Development Fund (grant no. MAX-TEENUS 2014-2020.4.01.20-0278 to the University of Tartu). EDS and CC acknowledge support from a Röntgen Ångström Cluster grant provided by the Swedish Research Council and the Bundesministerium für Bildung und Forschung (2021-05988) and by project grants from the Swedish Research Council (2018-00740). CC further acknowledges the Helmholtz Association through the Center for Free-Electron Laser Science at DESY for financial support. OB acknowledges support from the Swedish Research Council through project 2023-04346. We acknowledge MAX IV Laboratory for time on Beamline FinEstBeAMS under Proposal 20220337. Research conducted at MAX IV, a Swedish national user facility, is supported by the Swedish Research Council under contract 2018-07152, the Swedish Governmental Agency for Innovation Systems under contract 2018-04969, and Formas under contract 2019-02496.References
- P. Wardman, Clin. Oncol., 2007, 19, 397–417 CrossRef CAS PubMed.
- H. Wang, X. Mu, H. He and X.-D. Zhang, Trends Pharmacol. Sci., 2018, 39, 24–48 CrossRef CAS PubMed.
- A. Nunn, K. Linder and H. W. Strauss, Eur J Nucl Med, 1995, 22, 265–280 CrossRef CAS PubMed.
- Y. Masaki, Y. Shimizu, T. Yoshioka, Y. Tanaka, K.-I. Nishijima, S. Zhao, K. Higashino, S. Sakamoto, Y. Numata, Y. Yamaguchi, N. Tamaki and Y. Kuge, Sci. Rep., 2015, 5, 16802 CrossRef CAS PubMed.
- Y. Masaki, Y. Shimizu, T. Yoshioka, F. Feng, S. Zhao, K. Higashino, Y. Numata and Y. Kuge, PLoS One, 2016, 11, e0161639 CrossRef PubMed.
- F. B. Rashed, D. Diaz-Dussan, F. Mashayekhi, D. Macdonald, P. N. Nation, X.-H. Yang, S. Sokhi, A. C. Stoica, H. El-Saidi, C. Ricardo, R. Narain, I. H. Ismail, L. I. Wiebe, P. Kumar and M. Weinfeld, Redox Biol., 2022, 52, 102300 CrossRef CAS.
- P. Alexander, Trans. N. Y. Acad. Sci., 1962, 24, 966–978 CrossRef CAS PubMed.
- M. A. Shenoy, J. C. Asquith, G. E. Adams, B. D. Micheal and M. E. Watts, Radiat. Res., 1975, 62, 498–512 CrossRef CAS PubMed.
- R. Meißner, J. Kočišek, L. Feketeová, J. Fedor, M. Fárník, P. Limão-Vieira, E. Illenberger and S. Denifl, Nat. Commun., 2019, 10, 2388 CrossRef PubMed.
- R. Flammang, J. Elguero, H. Thanh Le, P. Gerbaux and M. Tho Nguyen, Chem. Phys. Lett., 2002, 356, 259–266 CrossRef CAS.
- A. Cartoni, A. R. Casavola, P. Bolognesi, M. C. Castrovilli, D. Catone, J. Chiarinelli, R. Richter and L. Avaldi, J. Phys. Chem. A, 2018, 122, 4031–4041 CrossRef CAS PubMed.
- M. Satta, A. R. Casavola, A. Cartoni, M. C. Castrovilli, D. Catone, J. Chiarinelli, S. Borocci, L. Avaldi and P. Bolognesi, ChemPhysChem, 2021, 22, 2387–2391 CrossRef CAS.
- L. Feketeová, J. Postler, A. Zavras, P. Scheier, S. Denifl and R. A. J. O'Hair, Phys. Chem. Chem. Phys., 2015, 17, 12598–12607 RSC.
- J. Chiarinelli, A. R. Casavola, M. C. Castrovilli, P. Bolognesi, A. Cartoni, F. Wang, R. Richter, D. Catone, S. Tosic, B. P. Marinkovic and L. Avaldi, Front. Chem., 2019, 7, 1–14 CrossRef PubMed.
- P. Bolognesi, A. R. Casavola, A. Cartoni, R. Richter, P. Markus, S. Borocci, J. Chiarinelli, S. Tošić, H. Saadeh, M. Masič, B. Marinković, K. Prince and L. Avaldi, J. Chem. Phys., 2016, 145, 191102 CrossRef CAS PubMed.
- E. Itälä, K. Tanzer, S. Granroth, K. Kooser, S. Denifl and E. Kukk, J. Mass Spectrom., 2017, 52, 770–776 CrossRef PubMed.
- E. Itälä, H. Myllynen, J. Niskanen, J. González-Vázquez, Y. Wang, D. T. Ha, S. Denifl and E. Kukk, J. Phys. Chem. A, 2019, 123, 3074–3079 CrossRef PubMed.
- E. Itälä, J. Niskanen, L. Pihlava and E. Kukk, J. Phys. Chem. A, 2020, 124, 5555–5562 CrossRef PubMed.
- S. Pandeti, L. Feketeová, T. J. Reddy, H. Abdoul-Carime, B. Farizon, M. Farizon and T. D. Märk, RSC Adv., 2017, 7, 45211–45221 RSC.
- R. Meißner, L. Feketeová, A. Bayer, P. Limão-Vieira and S. Denifl, J. Chem. Phys., 2021, 154, 074306 CrossRef PubMed.
- K. Tanzer, L. Feketeová, B. Puschnigg, P. Scheier, E. Illenberger and S. Denifl, Angew. Chem., Int. Ed., 2014, 53, 12240–12243 CrossRef CAS PubMed.
- L. Pihlava, M. Berholts, J. Niskanen, A. Vladyka, K. Kooser, C. Stråhlman, P. Eng-Johnsson, A. Kivimäki and E. Kukk, Phys. Chem. Chem. Phys., 2023, 25, 13004–13011 RSC.
- P. H. W. Svensson, L. Schwob, O. Grånäs, I. Unger, O. Björneholm, N. Timneanu, R. Lindblad, A.-L. Vieli, V. Zamudio-Bayer, M. Timm, K. Hirsch, C. Caleman and M. Berholts, Phys. Chem. Chem. Phys., 2024, 26, 770–779 RSC.
- J. Scicinski, B. Oronsky, S. Ning, S. Knox, D. Peehl, M. M. Kim, P. Langecker and G. Fanger, Redox Biol., 2015, 6, 1–8 CrossRef CAS PubMed.
- E. Hays and B. Bonavida, Antioxidants, 2019, 8, 407 CrossRef PubMed.
- B. T. Oronsky, S. J. Knox and J. J. Scicinski, Transl. Oncol., 2012, 5, 66–71 CrossRef PubMed.
- K. Kobayashi, N. Usami, E. Porcel, S. Lacombe and C. Le Sech, Mutat. Res., Rev. Mutat. Res., 2010, 704, 123–131 CrossRef CAS.
- Nanotechnology-Based Precision Tools for the Detection and Treatment of Cancer, ed. C. Mirkin, T. J. Meade, S. H. Petrosko and A. H. Stegh, Springer International Publishing, 2015 Search PubMed.
- A. G. Denkova, H. Liu, Y. Men and R. Eelkema, Adv. Ther., 2020, 3, 1900177 CrossRef.
- C. Verry, S. Dufort, B. Lemasson, S. Grand, J. Pietras, I. Troprès, Y. Crémillieux, F. Lux, S. Mériaux, B. Larrat, J. Balosso, G. Le Duc, E. L. Barbier and O. Tillement, Sci. Adv., 2020, 6, eaay5279 CrossRef CAS PubMed.
- C. Verry, S. Dufort, J. Villa, M. Gavard, C. Iriart, S. Grand, J. Charles, B. Chovelon, J.-L. Cracowski, J.-L. Quesada, C. Mendoza, L. Sancey, A. Lehmann, F. Jover, J.-Y. Giraud, F. Lux, Y. Crémillieux, S. McMahon, P. J. Pauwels, D. Cagney, R. Berbeco, A. Aizer, E. Deutsch, M. Loeffler, G. Le Duc, O. Tillement and J. Balosso, Radiother. Oncol., 2021, 160, 159–165 CrossRef CAS PubMed.
- P. OKeeffe, E. Ripani, P. Bolognesi, M. Coreno, M. Devetta, C. Callegari, M. Di Fraia, K. C. Prince, R. Richter, M. Alagia, A. Kivimäki and L. Avaldi, J. Phys. Chem. Lett., 2013, 4, 1797–1801 CrossRef CAS PubMed.
- K. Gokhberg, P. Kolorenč, A. I. Kuleff and L. S. Cederbaum, Nature, 2014, 505, 661–663 CrossRef CAS PubMed.
- F. Trinter, M. S. Schöffler, H.-K. Kim, F. P. Sturm, K. Cole, N. Neumann, A. Vredenborg, J. Williams, I. Bocharova, R. Guillemin, M. Simon, A. Belkacem, A. L. Landers, T. Weber, H. Schmidt-Böcking, R. Dörner and T. Jahnke, Nature, 2014, 505, 664–666 CrossRef CAS PubMed.
- I. Unger, R. Seidel, S. Thürmer, M. N. Pohl, E. F. Aziz, L. S. Cederbaum, E. Muchová, P. Slavíček, B. Winter and N. V. Kryzhevoi, Nat. Chem., 2017, 9, 708–714 CrossRef CAS PubMed.
- B. C. Garrett, D. A. Dixon, D. M. Camaioni, D. M. Chipman, M. A. Johnson, C. D. Jonah, G. A. Kimmel, J. H. Miller, T. N. Rescigno, P. J. Rossky, S. S. Xantheas, S. D. Colson, A. H. Laufer, D. Ray, P. F. Barbara, D. M. Bartels, K. H. Becker, K. H. J. Bowen, S. E. Bradforth, I. Carmichael, J. V. Coe, L. R. Corrales, J. P. Cowin, M. Dupuis, K. B. Eisenthal, J. A. Franz, M. S. Gutowski, K. D. Jordan, B. D. Kay, J. A. LaVerne, S. V. Lymar, T. E. Madey, C. W. McCurdy, D. Meisel, S. Mukamel, A. R. Nilsson, T. M. Orlando, N. G. Petrik, S. M. Pimblott, J. R. Rustad, G. K. Schenter, S. J. Singer, A. Tokmakoff, L.-S. Wang and T. S. Zwier, Chem. Rev., 2005, 105, 355–390 CrossRef CAS PubMed.
- B. Boudaïffa, P. Cloutier, D. Hunting, M. A. Huels and L. Sanche, Science, 2000, 287, 1658–1660 CrossRef PubMed.
- Radiation Damage in Biomolecular Systems, ed. G. G. Gómez-Tejedor and M. C. Fuss, Springer, 2012th edn, 2014 Search PubMed.
- L. Sanche, Nature, 2009, 461, 358–359 CrossRef CAS PubMed.
- P. Jeggo and M. Löbrich, Radiat. Prot. Dosim., 2006, 122, 124–127 CrossRef PubMed.
- W. L. Santivasi and F. Xia, Antioxid. Redox Signaling, 2014, 21, 251–259 CrossRef CAS.
- R. Vinit, R. Amit, S. Saurabh, M. Raghvendra, M. Ravindra, P. Piyush, G. Ankur and S. Mahendra, J. Anal. Pharm. Res., 2018, 7, 175–180 Search PubMed.
- S. McGregor, J. Minni and D. Herold, J. Clin. Aesthetic Dermatol., 2015, 8, 12–14 Search PubMed.
- S. J. Karnas, E. Yu, R. C. McGarry and J. J. Battista, Phys. Med. Biol., 1999, 44, 2537 CrossRef CAS PubMed.
- W. Krause, A. Jordan, R. Scholz and J.-L. M. Jimenez, Anticancer Res., 2005, 25, 2145–2151 CAS.
- K. Kooser, A. Kivimäki, P. Turunen, R. Pärna, L. Reisberg, M. Kirm, M. Valden, M. Huttula and E. Kukk, J. Synchrotron Radiat., 2020, 27, 1080–1091 CrossRef CAS PubMed.
- R. Pärna, R. Sankari, E. Kukk, E. Nõmmiste, M. Valden, M. Lastusaari, K. Kooser, K. Kokko, M. Hirsimäki, S. Urpelainen, P. Turunen, A. Kivimäki, V. Pankratov, L. Reisberg, F. Hennies, H. Tarawneh, R. Nyholm and M. Huttula, Nucl. Instrum. Methods Phys. Res., Sect. A, 2017, 859, 83–89 CrossRef.
- K. Chernenko, A. Kivimäki, R. Pärna, W. Wang, R. Sankari, M. Leandersson, H. Tarawneh, V. Pankratov, M. Kook, E. Kukk, L. Reisberg, S. Urpelainen, T. Käämbre, F. Siewert, G. Gwalt, A. Sokolov, S. Lemke, S. Alimov, J. Knedel, O. Kutz, T. Seliger, M. Valden, M. Hirsimäki, M. Kirm and M. Huttula, J. Synchrotron Radiat., 2021, 28, 1620–1630 CrossRef CAS PubMed.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- O. Grånäs, N. Timneanu, I. Eliah Dawod, D. Ragazzon, S. Trygg, P. Souvatzis, T. Edvinsson and C. Caleman, J. Chem. Phys., 2019, 151, 144307 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- M. Feyereisen, G. Fitzgerald and A. Komornicki, Chem. Phys. Lett., 1993, 208, 359–363 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- J. D. Rolfes, F. Neese and D. A. Pantazis, J. Comput. Chem., 2020, 41, 1842–1849 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- M. Abraham, D. van der Spoel, E. Lindahl, B. Hess and the GROMACS development team, GROMACS User Manual version 2018, 2018 Search PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, 2016, Gaussian Inc., Wallingford, CT Search PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graphics Modell., 2006, 25, 247–260 CrossRef CAS.
- A. W. Sousa da Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, 1–8 CrossRef.
- M. Fixman, J. Chem. Phys., 1962, 36, 306–310 CrossRef CAS.
- T. Luhmann, C. Gerth, M. Groen, M. Martins, B. Obst, M. Richter and P. Zimmermann, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 282–291 CrossRef CAS.
- S. Brünken, C. Gerth, B. Kanngießer, T. Luhmann, M. Richter and P. Zimmermann, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 042708 CrossRef.
- Y. Tamenori, K. Okada, S. Nagaoka, T. Ibuki, S. Tanimoto, Y. Shimizu, A. Fujii, Y. Haga, H. Yoshida, H. Ohashi and I. H. Suzuki, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, 2799 CrossRef CAS.
- E. Kukk, L. Pihlava, K. Kooser, C. Stråhlman, S. Maclot and A. Kivimäki, Phys. Chem. Chem. Phys., 2023, 25, 5795–5807 RSC.
- M. O. Krause, J. Phys. Chem. Ref. Data, 1979, 8, 307–327 CrossRef CAS.
- P. J. Ho, D. Ray, C. S. Lehmann, A. E. A. Fouda, R. W. Dunford, E. P. Kanter, G. Doumy, L. Young, D. A. Walko, X. Zheng, L. Cheng and S. H. Southworth, J. Chem. Phys., 2023, 158, 134304 CrossRef CAS PubMed.
- G. Gopakumar, I. Unger, P. Slavíček, U. Hergenhahn, G. Öhrwall, S. Malerz, D. Céolin, F. Trinter, B. Winter, I. Wilkinson, C. Caleman, E. Muchová and O. Björneholm, Nat. Chem., 2023, 15, 1408–1414 CrossRef CAS PubMed.
- V. Stumpf, K. Gokhberg and L. S. Cederbaum, Nat. Chem., 2016, 8, 237–241 CrossRef CAS PubMed.
- E. Pelimanni, A. Hans, E. Heikura, M. Huttula and M. Patanen, Phys. Chem. Chem. Phys., 2022, 24, 11646–11653 RSC.
- A. Hans, P. Schmidt, C. Küstner-Wetekam, F. Trinter, S. Deinert, D. Bloß, J. H. Viehmann, R. Schaf, M. Gerstel, C. M. Saak, J. Buck, S. Klumpp, G. Hartmann, L. S. Cederbaum, N. V. Kryzhevoi and A. Knie, J. Phys. Chem. Lett., 2021, 12, 7146–7150 CrossRef CAS PubMed.
- M. Johny, C. A. Schouder, A. Al-Refaie, L. He, J. Wiese, H. Stapelfeldt, S. Trippel and J. Küpper, Molecular sunscreen: water protects pyrrole from radiation damage, arXiv, 2020, preprint, arXiv:2010.00453 [physics.chem-ph] DOI:10.48550/arXiv.2010.00453.
- J. Kočišek, A. Pysanenko, M. Fárník and J. Fedor, J. Phys. Chem. Lett., 2016, 7, 3401–3405 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00367e |
| This journal is © the Owner Societies 2024 |