Open Access Article
Open Access ArticleSearching for stable copper borozene complexes in CuB7− and CuB8−†
Wei-Jia
Chen‡
 a,
Anton S.
Pozdeev‡
b,
Hyun Wook
Choi
a,
Alexander I.
Boldyrev
a,
Anton S.
Pozdeev‡
b,
Hyun Wook
Choi
a,
Alexander I.
Boldyrev
 c,
Dao-Fu
Yuan
c,
Dao-Fu
Yuan
 *ad,
Ivan A.
Popov
*b and
Lai-Sheng
Wang
*ad,
Ivan A.
Popov
*b and
Lai-Sheng
Wang
 *a
*a
aDepartment of Chemistry, Brown University, Providence, Rhode Island 02912, USA. E-mail: lai-sheng_wang@brown.edu
bDepartment of Chemistry, The University of Akron, Akron, Ohio 44325, USA. E-mail: ipopov@uakron.edu
cDepartment of Chemistry and Biochemistry, Utah State University, Logan, Utah 84322, USA
dHefei National Research Center for Physical Sciences at the Microscale, University of Science and Technology of China, Hefei 230026, China. E-mail: ydfu@ustc.edu.cn
First published on 4th March 2024
Abstract
Copper has been shown to be an important substrate for the growth of borophenes. Copper–boron binary clusters are ideal platforms to study the interactions between copper and boron, which may provide insight about the underlying growth mechanisms of borophene on copper substrates. Here we report a joint photoelectron spectroscopy and theoretical study on two copper-doped boron clusters, CuB7− and CuB8−. Well resolved photoelectron spectra are obtained for the two clusters at different wavelengths and are used to understand the structures and bonding properties of the two CuBn− clusters. We find that CuB8− is a highly stable borozene complex, which possesses a half-sandwich structure with a Cu+ species interacting with the doubly aromatic η8-B82− borozene. The CuB7− cluster is found to consist of a terminal copper atom bonded to a double-chain B7 motif, but it has a low-lying isomer composed of a half-sandwich structure with a Cu+ species interacting with an open-shell η7-B72− borozene. Both ionic and covalent interactions are found to be possible in the binary Cu–B clusters, resulting in different structures.
1 Introduction
The electron deficiency of boron gives rise to a variety of bulk allotropes with cage structures.1–3 Boron-based nanotubes with a triangular boron layer were also proposed after the discovery of carbon nanotubes.4,5 However, a triangular boron layer is too electron-rich, which results in out-of-plane distortions.6,7 Theoretical calculations suggested that a triangular boron lattice with hexagonal vacancies could be perfectly planar.8,9 Combined experimental and theoretical studies have revealed the structures of various boron clusters.10–19 Different from bulk boron materials, finite boron clusters have been found predominantly to possess two-dimensional (2D) structures consisting of B3 triangles decorated with vacancies of different shapes, where the 2D structures are stabilized by delocalized σ and π bonds throughout the cluster plane.20,21 The C6v planar B36 cluster with a central hexagonal vacancy provided the first experimental evidence for the viability of a graphene-like planar boron sheet (a.k.a. borophene).22 The B35− cluster was also found to contain a planar structure with a double hexagonal vacancy, providing a more flexible building block for borophenes.23 Borophenes have been successfully realized on various metal substrates,24,25 becoming a new class of 2D materials.26,27 The discovery of the B40 cage marks the first all-boron fullerene (borospherene).28 The B48− cluster was confirmed to be the first bilayer boron cluster,29,30 suggesting the possibility of bilayer borophenes that have also been successfully prepared on coinage metal substrates.31,32 Theoretical analyses for the formation of bilayer borophenes on the copper substrate suggested that electron transfers from the metal substrate to the first layer of boron play an important role in the growth of the bilayer borophene.31 To fully understand the growth mechanisms of borophenes, it is important to study the interactions between boron and the underlying metal substrates at the atomic level. Metal–boron binary clusters provide ideal model systems.Significant amounts of work have been done on metal-doped boron clusters over the past two decades.18,33,34 The study on transition-metal-doped boron clusters has uncovered various novel structures including metal-centered molecular wheels,35–37 metallo-boron nanotubes38–40 and metallo-borophenes.33,41,42 The B7−, B8− and B9− clusters were among the first few boron clusters jointly studied by photoelectron spectroscopy (PES) and computational chemistry.12,43 B9− was found to possess a perfect D8h structure with σ and π double aromaticity. The closed-shell B73− and B82−, possessing similar double aromaticity, were first found in the AlB7, PrB7, and LiB8− clusters.44–46 During a recent study on a series of LnB8− clusters (Ln = La, Pr, Tb, Tm, Yb), the similarity between the π bonding in B73−, B82− and B9− and that in the series of prototypical hydrocarbons, C5H5−, C6H6 and C7H7+, was recognized and the name “borozene” was proposed for the series of doubly aromatic boron motifs.47 Several B73− and B82− borozene complexes have been realized recently in multiple metal-doped boron clusters, even in a boron oxide cluster.48–50
Copper–boron binary clusters (CuxBy−) are ideal systems to study the interactions between copper and boron atoms at the atomic levels, which may help develop a better understanding of the growth of borophenes on copper substrates. Our recent study on Cu2B8− revealed a Cu2+–[B82−] borozene complex,51 in which the charge transfer from the copper atoms to the boron motif is similar to what was suggested in the growth of bilayer borophenes on copper substrates.31 Smaller di-copper-doped boron clusters Cu2Bn− (n = 3–7) were also studied recently, revealing competitions between covalent and ionic interactions in determining the cluster structures.52,53 In this article, we report a combined experimental and computational study on two mono-copper-doped boron clusters, CuB7− and CuB8−, to probe the Cu–boron bonding and search for stable copper borozene complexes. Well-resolved photoelectron spectra are obtained for the two clusters at different wavelengths and are combined with theoretical calculations to understand the structures and bonding of the two CuBn− clusters. CuB8− is found to be a highly stable metal borozene complex, which possesses a half-sandwich structure with a Cu+ species coordinated by the η8-B82− borozene. On the other hand, CuB7− is found to consist of a terminal copper atom bonded to a double-chain B7 motif with strong covalent Cu–B covalent bonding, while the borozene complex consisting of the open-shell η7-B72−, is a low-lying isomer present in the experiment as a minor species. We have also found strong electron correlation effects in the two clusters and a multi-reference method was required to calculate their electron detachment energies.
2 Experimental and theoretical methods
2.1. Experimental methods
The experiments were conducted using a PES apparatus consisting of a laser vaporization cluster source, a time-of-flight (TOF) mass spectrometer, and a 3.5-meter-long magnetic bottle photoelectron analyzer. Details of the experimental apparatus can be found elsewhere.17 The CuB7− and CuB8− clusters were formed by laser vaporization of a hot-pressed Cu/11B disk target prepared using a natural isotope Cu powder and a 11B-enriched (97%) boron powder. The laser-induced plasma was quenched by a helium carrier gas pulse seeded with 5% argon. Clusters formed inside the nozzle were mixed with the carrier gas and underwent a supersonic expansion to create a cold cluster beam. After passing a skimmer, anionic clusters from the collimated beam were extracted perpendicularly into the TOF mass spectrometer. The CuB7− and CuB8− clusters were mass-selected and decelerated before photodetachment. Three different photon energies were used in the current study, including 355 nm (3.496 eV) and 266 nm (4.661 eV) from a Nd:YAG laser, and 193 nm (6.424 eV) from an ArF excimer laser. Photoelectrons were collimated by the magnetic bottle with >90% collecting efficiency and analyzed in the 3.5-meter-long electron TOF tube. The photoelectron kinetic energies were calibrated using the known transitions of the Bi− atomic anion. The kinetic energy (Ek) resolution (ΔEk/Ek) of the apparatus was around 2.5%, which was around 25 meV for 1 eV electrons.2.2. Theoretical methods
We utilized the Coalescence Kick (CK) algorithm54 for the global minimum (GM) search. The CK algorithm randomly generated numerous structures that coalesced to the center of mass based on a predetermined parameter derived from the covalent radii of the involved atoms. In the first step, the generated structures of CuB7/CuB7− and CuB8/CuB8− were optimized to local minima in their respective lower (singlet/doublet) and higher (triplet/quartet) spin states at the MN15/def2-SVP level.55,56 Large populations of the initial structures were considered for each stoichiometry, spin state, and charge states (Table S1, ESI†). The slightly larger population sizes for the anions were due to their greater tendency for dissociation. Calculations at this step were performed using the Gaussian16 suite.57In the second step, the non-dissociated structures found by the CK procedure in the first step were re-optimized and harmonic frequencies were calculated at the PBE0/def2-TZVPD level,58–62 applying the UKS formalism for all cases regardless of the studied multiplicity. Additionally, the RIJCOSX approximation63 with the universal def2/J auxiliary basis set64,65 was used to accelerate the calculations, achieving SCF convergence with VeryTight criterion (TolE = 1e-9). For geometry optimization, we used the default NORMALOPT criterion. Isomers within 15 kcal mol−1 from the lowest energy structure were evaluated at the CCSD(T)/aug-cc-pVQZ level,66–69 with zero-point energy (ZPE) corrections at the PBE0/def2-TZVPD level. The wave functions for all GM structures and low-lying isomers were examined by the wave function stability test to ensure that the calculations converged to the ground states.70 Unstable structures were re-converged towards the broken-symmetry solution, and their geometries were subsequently re-optimized. The first vertical detachment energy (VDE1) was calculated at the PBE0/def2-TZVPD and CCSD(T)/aug-cc-pVQZ levels as the energy difference between the anion and the corresponding neutral species, both at the geometry of the anion. Higher VDEs were calculated employing PBE0/def2-TZVPD (time-dependent density functional theory, TD-DFT71) and the multireference NEVPT272,73/aug-cc-pVTZ66–69 approach for both clusters and an additional reference approach IP-EOM-CCSD74/aug-cc-pVQZ for CuB8−, in all cases at the geometry of the corresponding anion. Due to the large number of MOs, the domain-based local pair natural orbital [DLPNO-CCSD(T) and DLPNO-CCSD] approximation75–77 was applied with “TightPNO” settings to obtain an accurate energy. Quasi-restricted orbitals78 (QROs) obtained from the UHF reference wavefunctions were applied to eliminate the influence of possible spin-contamination. The adiabatic detachment energy (ADE) was calculated as the energy difference between the anion and the corresponding neutral structure at their respective reoptimized geometries. Chemical bonding of the GM and selected isomers was analyzed employing the adaptive natural density partitioning (AdNDP) algorithm,79 as implemented in the Multiwfn software.80 The described calculations were performed via the ORCA 5.04 suite.81,82 All ORCA computations were performed with the “defgrid3” settings for integration grids and C1 point group symmetry. Visualization of molecular structures and the AdNDP results was performed using ChemCraft.83
3 Experimental results
Photoelectron spectra of CuB7− and CuB8− taken at three different wavelengths are presented in Fig. 1 and 2, respectively. For each cluster, the observed PES bands are labeled with letters (X, A, B…) and the measured VDEs are given in Tables 1 and 2, respectively, where they are compared with the theoretical results. The label X′ in Fig. 1 refers to potential contributions from a low-lying isomer of CuB7−. Band X in each spectrum represents the electron detachment transition from the ground state of the anion to that of the corresponding neutral, while bands A, B, C,… indicate detachment transitions to excited neutral states. The ADEs are determined by drawing a straight line at the leading edge of the ground state detachment transition and then adding the instrumental resolution, as given in Table 3, where they are also compared with the theoretical results. The ADE is equivalent to the electron affinity (EA) of the corresponding neutral cluster.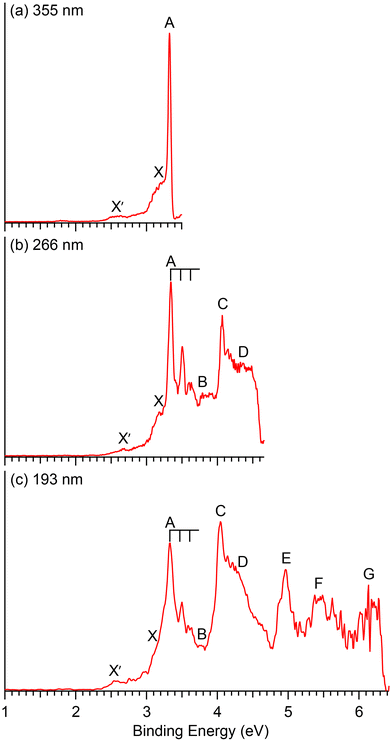 | ||
| Fig. 1 Photoelectron spectra of CuB7− at (a) 355 nm (3.496 eV), (b) 266 nm (4.661 eV) and (c) 193 nm (6.424 eV). | ||
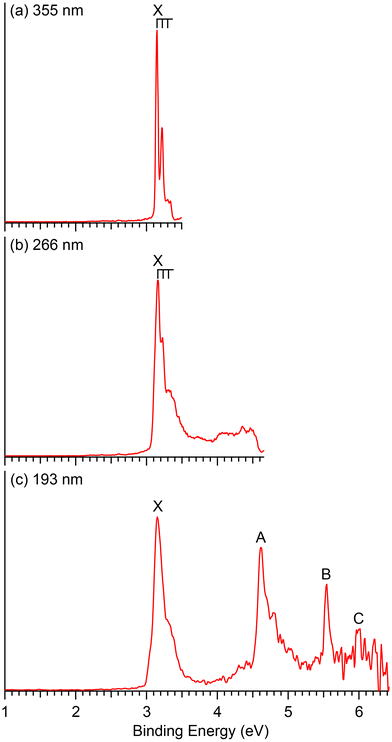 | ||
| Fig. 2 Photoelectron spectra of CuB8− at (a) 355 nm (3.496 eV), (b) 266 nm (4.661 eV) and (c) 193 nm (6.424 eV). | ||
| Final state and electron configuration | VDE (exp)a | VDE (theo) | |
|---|---|---|---|
| a The experimental uncertainty is ±0.02 eV. | |||
| X | 1A′{…(22a′)2(5a′′)2(23a′)2(24a′)2(25a′)2(26a′)2(6a′′)2(27a′)0} | 3.17 | 3.26 |
| A | 3A′′{…(22a′)2(5a′′)2(23a′)2(24a′)2(25a′)2(26a′)2(6a′′)1(27a′)1} | 3.34 | 3.46 |
| B | 1A′′{…(22a′)2(5a′′)2(23a′)2(24a′)2(25a′)2(26a′)2(6a′′)1(27a′)1} | 3.79 | 3.68 |
| C | 3A′{…(22a′)2(5a′′)2(23a′)2(24a′)2(25a′)2(26a′)1(6a′′)2(27a′)1} | 4.07 | 3.99 |
| 1A′{…(22a′)2(5a′′)2(23a′)2(24a′)2(25a′)2(26a′)1(6a′′)2(27a′)1} | 4.21 | ||
| D | 3A′{…(22a′)2(5a′′)2(23a′)2(24a′)2(25a′)1(26a′)2(6a′′)2(27a′)1} | ∼4.4 | 4.39 |
| 3A′′{…(22a′)2(5a′′)1(23a′)2(24a′)2(25a′)2(26a′)2(6a′′)2(27a′)1} | 4.56 | ||
| E | 1A′{…(22a′)2(5a′′)2(23a′)2(24a′)2(25a′)1(26a′)2(6a′′)2(27a′)1} | 4.97 | 4.97 |
| 3A′{…(22a′)2(5a′′)2(23a′)2(24a′)1(25a′)2(26a′)2(6a′′)2(27a′)1} | 5.04 | ||
| F | 1A′{…(22a′)2(5a′′)2(23a′)2(24a′)1(25a′)2(26a′)2(6a′′)2(27a′)1} | ∼5.5 | 5.49 |
| 1A′′{…(22a′)2(5a′′)1(23a′)2(24a′)2(25a′)2(26a′)2(6a′′)2(27a′)1} | 5.56 | ||
| 3A′{…(22a′)1(5a′′)2(23a′)2(24a′)2(25a′)2(26a′)2(6a′′)2(27a′)1} | 5.59 | ||
| 1A′{…(22a′)1(5a′′)2(23a′)2(24a′)2(25a′)2(26a′)2(6a′′)2(27a′)1} | 5.62 | ||
| 3A′{…(22a′)2(5a′′)2(23a′)1(24a′)2(25a′)2(26a′)2(6a′′)2(27a′)1} | 5.72 | ||
| G | nA′{…(22a′)2(5a′′)2(23a′)1(24a′)2(25a′)2(26a′)2(6a′′)2(27a′)1} | ∼6.1 | 5.92 |
| Final state and electron configuration | VDE (exp)a | VDE (theo) | |
|---|---|---|---|
| a The experimental uncertainty is ±0.02 eV. | |||
| X | 2E1{…(3e2)4(2e3)4(11a1)2(6e1)4(7e1)3} | 3.15 | 3.07 |
| A | 2E1{…(3e2)4(2e3)4(11a1)2(6e1)3(7e1)4} | 4.62 | 4.63 |
| B | 2nA1{…(3e2)4(2e3)4(11a1)1(6e1)4(7e1)4} | 5.54 | 5.65 |
| C | 2E3{…(3e2)4(2e3)3(11a1)2(6e1)4(7e1)4} | ∼6 | 6.02 |
| 2E2{… (3e2)3(2e3)4(11a1)2(6e1)4(7e1)4} | 6.15 | ||
3.1. CuB7−
The photoelectron spectra of CuB7− are complicated due to its open-shell nature (Fig. 1). The first PES band X is relatively weak and broad, yielding a VDE1 of 3.17 eV and an estimated ADE of 2.98 eV. An intense and sharp peak is observed near the detachment threshold at 355 nm (Fig. 1a), which represents the 0–0 transition for band A, for which a short vibrational progression is resolved in the 266 nm spectrum (Fig. 1b). The VDE of band A is measured to be 3.34 eV and the vibrational spacing is ∼1150 cm−1. A weak band B is discernable at 3.79 eV. A sharp and intense feature C is observed at 4.07 eV, followed by a congested broad feature around ∼4.4 eV designated as D. In the 193 nm spectrum, a well-defined band E is observed at 4.97 eV, whereas two broad features F and G can be tentatively identified at ∼5.5 eV and ∼6.1 eV, respectively. A weak broad feature X′ is also observed on the low binding energy side at ∼2.6 eV, which is likely due to the presence of a low-lying isomer.3.2. CuB8−
The photoelectron spectra of CuB8− appear very simple with only four well-separated detachment transitions (Fig. 2), suggesting a highly symmetric and closed-shell cluster. A short vibrational progression is observed for the ground state transition (band X) with a spacing of ∼600 cm−1. The VDE, defined by the sharp 0–0 transition, is 3.15 eV, while the ADE is estimated from its leading edge to be 3.13 eV to account for possible unresolved low-frequency vibrations. The sharp and short vibrational progression for the ground state transition indicates a small geometry change between the ground state of the anion and that of the neutral CuB8. No more major detachment transitions are observed in the 266 nm spectrum (Fig. 2b), except some weak and broad signals above 4 eV, which may be due to contributions from impurities. The masses of both Cu2B2− (m/z = 148–152) and B14− (m/z = 154) are close to that of CuB8− (m/z = 151–153) and they could be candidates for the weak signals.13 At 193 nm (Fig. 2c), two strong and sharp bands A and B are clearly observed at VDEs of 4.62 eV and 5.54 eV, respectively. A relatively weak band C is also discernible at a VDE around 6 eV on the high binding energy side with poor signal-to-noise ratios.4 Theoretical results
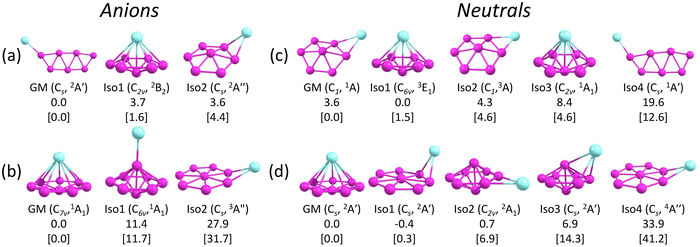
Fig. 3 presents the GM structures of CuB7− and CuB8− and their neutral counterparts with several low-lying isomers arranged by the relative energies at the CCSD(T) level of theory. Additional low-lying structures are shown in Fig. S1 and S2 (ESI†) for the anions and neutrals, respectively. Recently, the structures of the neutral CuB7 and CuB8 species were examined at the DFT level of theory.84 While some of the previously reported structures agree with the current CCSD(T) relative energy ordering, several of them are substantially different, highlighting the importance of employing more accurate methods along with experimental verification. The coordinates of the GM of CuB7− and CuB8− and low-lying isomers of CuB7− and the corresponding neutrals are provided in the xyz format as an additional zip file in the ESI.†4.1. CuB7− and CuB7
Several low-lying isomers are identified for CuB7−, as shown in Fig. 3a. The GM structure (Cs, 2A′) features a planar double-chain B7 motif with the Cu atom bonded to one of the two apex boron atoms. The electronic stability of this structure can be glimpsed by its large SOMO–LUMO gap (alpha electrons) of 3.12 eV at the PBE0/def2-TZVPD level. The first low-lying isomer, Iso1 (C2v, 2B2), which is only 1.6 kcal mol−1 above the GM structure at CCSD(T), adopts a half-sandwich structure, with the Cu atom located above a hexagonal B7 motif. Similar half-sandwich architectures were previously found in other complexes involving the η7-B73− borozene motif.44,45,50 However, Iso1 of CuB7− (C2v, 2B2) is one electron short of a B73− borozene configuration, which is why it is not the GM. The B7 motif in Iso1 is similar to the first low-lying isomer of the bare B7− cluster.43 The second low-lying isomer, Iso2 (Cs, 2A′′), which is 4.4 kcal mol−1 above the GM structure, is another derivative of the distorted hexagonal B7 motif, where the Cu atom is bonded to its edge bridging two boron atoms. All other isomers are at least 11.0 kcal mol−1 higher in energy than the GM structure (Fig. S1A, ESI†). Electron detachment from CuB7− leads to significant destabilization of the double chain structure, making it energetically less stable by 12.6 kcal mol−1 than the GM structure of neutral CuB7 at CCSD(T) (Fig. 3c). The GM and the first three low-lying isomers of neutral CuB7 all feature the hexagonal B7 motif, differing in the position of the Cu atom and in the spin states, as shown in Fig. 3c.4.2. CuB8− and CuB8
The GM of CuB8− (C7v, 1A1) adopts a half-sandwich structure (Fig. 3b), in which the B8 motif is quasi-planar with the central B atom slightly moving out of the B7 plane by 0.35 Å away from the Cu atom relative to the planar bare B8.12 The large HOMO–LUMO gap of 3.05 eV indicates the high electronic stability of the CuB8− GM. In contrast to CuB7−, the closest low-lying isomer of CuB8−, Iso1, is 11.7 kcal mol−1 higher in energy than the GM at the CCSD(T) level. The high stability of the C7v CuB8− GM is related to the high stability of the B82− borozene.47 Iso1 of CuB8− (C6v, 1A1) has a 3D bipyramidal boron framework bonded to Cu at the top, which is reminiscent of the umbrella structure of B9O− [B8(BO)−].50 In the next isomer, Iso2 (Cs, 3A′′), which is 31.7 kcal mol−1 higher than the GM, the Cu atom is bonded to the edge of the planar B8 moiety, similar to the GM of AuB8−.49 More high energy isomers for CuB8− are given in Fig. S1B (ESI†). Electron detachment from the GM of CuB8− leads to a minor geometry reorganization, reducing its symmetry from C7v to Cs in the GM of the open-shell CuB8 (2A′) (Fig. 3d). However, Iso1 of CuB8 (Cs, 2A′) is almost degenerate with the GM, where the Cu atom is bonded to the edge of the planar B8 motif. Iso2 of CuB8 (C2v, 2A1), which is 6.9 kcal mol−1 above the GM, consists of a bipyramidal B8 motif with the Cu atom bonded to its equator. The potential energy surface of neutral CuB8 is much flatter in comparison with that of the anion.5 Discussion
5.1. Comparison between experiment and theory
The GM structures of CuB7− and CuB8− are verified by comparison with the experimental PES data. The computed ADE and VDE1 values at both the PBE0/def2-TZVPD and CCSD(T)/aug-cc-pVQZ levels of theory for the GM structures of CuB7− and CuB8− and the two low-lying isomers of CuB7− are compared with the experimental data in Table 3.We first applied the accurate IP-EOM-CCSD/aug-cc-pVQZ approach74 for the closed-shell CuB8− as a reference method and found that it gave excellent results in comparison with the experiment (Fig. S8, ESI†). However, the IP-EOM-CCSD method cannot be used for the open-shell CuB7−. We next examined the multi-reference method, NEVPT2(17,12),68,69 for CuB8− and found that it also gave excellent results similar to those using the IP-EOM-CCSD method (Fig. S8, ESI†). Finally, we used the NEVPT2(14,12) method to compute higher VDEs for CuB7− (Fig. S7, ESI†). For consistency and accuracy, we will use the multi-reference NEVPT2 results to compare with the PE spectra of CuB7− and CuB8−, as shown in Fig. 4. The calculated VDEs for higher detachment channels of the GM structures at the NEVPT2/aug-cc-pVTZ level of theory are compared with the experimental results in Tables 1 and 2 for CuB7− and CuB8−, respectively.
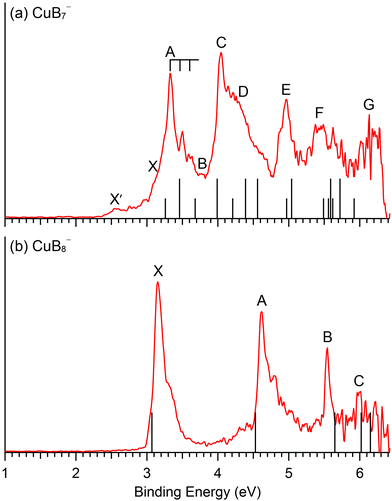 | ||
| Fig. 4 Comparison between the 193 nm PE spectra and the computed VDEs (vertical bars) for the GM of (a) CuB7− and (b) CuB8−. In (a), the short bars correspond to singlet final states and the longer bars correspond to triplet final states. See Fig. S11 (ESI†) delineating potential contributions of the low-lying isomers of CuB7− to the weak X′ signals. | ||
Electron detachment from the HOMO (6a′′) yields a triplet and singlet final state with computed VDEs of 3.46 and 3.68 eV, respectively, in good accord with the observed A and B bands at 3.34 and 3.79 eV (Table 1). The HOMO of CuB7− is a π orbital in the B7 motif (Fig. S3, ESI†). Electron detachment from this orbital is expected to induce in-plane B–B stretching vibrations. While we could not compute the vibrational frequencies for the triplet excited state of the corresponding neutral CuB7, the computed B–B stretching frequencies for the ground state, ranging from 1313 cm−1 (ν3) to 1054 cm−1 (ν5) (Fig. S10, ESI†), are consistent with the observed frequency of ∼1150 cm−1 for band A. Detachment from the HOMO−1 (26a′) gives rise to a computed VDE of 3.99 eV for the triplet final state, in good agreement with the measured VDE of 4.07 eV for band C. The calculated VDE for the singlet final state from detachment of the HOMO−1 (4.21 eV) and those for the triplet final states from detachment from the HOMO−2 (25a′) (4.39 eV) and HOMO−5 (5a′′) (4.56 eV) are close to band C and to each other, consistent with the broad overlapping band D. The computed VDE for the singlet final state from detachment from the HOMO−2 (4.97 eV) and that for the triplet final state from detachment from the HOMO−3 (24a′) (5.04 eV) are close to each other and are in excellent agreement with the well-resolved band E at 4.97 eV. A dense manifold of detachment channels is found in the higher binding energy side, consistent with the congested bands F and G. The overall computed VDEs match well with the complex experimental PES pattern (Fig. 4a), providing considerable credence to the double chain GM structure of CuB7−. It should be noted that the PE spectral pattern of CuB7− displays some resemblance to that of Cu2B7−,52 which is closed-shell with a similar double chain structure and gives much better resolved PE spectra because each occupied MOs only result in one double final state.
The computed ADE/VDE1 values for Iso1 (C2v, 2B2) of 2.37/2.46 eV agree with the observed values of 2.41/2.63 eV for the minor X′ band (Table 3), suggesting its presence experimentally due to its close energy relative to the GM (Fig. 3a). Higher VDEs of Iso1 would be masked by the dominant signals of the Cs GM. Iso2 (Cs, 2A′′) can be ruled out because no PES signals were observed near its calculated ADE/VDE1 at 2.15/2.43 eV. The observation of Iso1 provides further evidence for the identified GM for CuB7−.
The second detachment channel for CuB8− is from the HOMO−1 (6e1) with a computed VDE of 4.63 eV, in excellent agreement with band A at 4.62 eV. There are unresolved vibrational features for band A. The third detachment channel is from the HOMO−2 (11a1) with a computed VDE of 5.65 eV, agreeing well with the observed VDE of band B at 5.54 eV. Band B is an extremely sharp peak without any discernible vibrational feature, in agreement with the nondegenerate 11a1 HOMO−2, which is mainly a σ bonding MO on the B7 ring of the B8 motif with a small contribution from the Cu 3dz2 orbital (Fig. S6, ESI†). The fourth and fifth detachment channels from the HOMO−3 (2e3) and HOMO−4 (3e2) give similar computed VDEs of 6.02 eV and 6.16 eV, respectively, in good agreement with the weak band C at ∼6 eV. The excellent agreement between the simple spectral pattern observed for CuB8− and the computed VDEs (Fig. 4b) provides unequivocal evidence for the C7v GM structure of CuB8−.
5.2. Borozenes and the chemical bonding in the CuB7− and CuB8− clusters
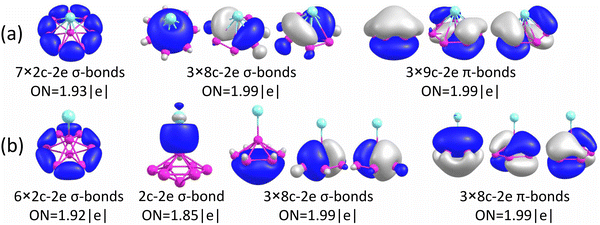
The chemical bonding for the GM and Iso1 structures of CuB7− and CuB8− is analyzed using the AdNDP method, as shown in Fig. 5 and 6, respectively. In all cases, the Cu 3d electrons are found primarily as five 3d lone pairs, i.e., one-center two electron (1c–2e) AdNDP elements, and they are omitted from the figures for clarity. The occupation numbers (ONs) for the Cu 3d electron pairs are found to be in the range of 2.00–1.91|e|, consistent with the fact that they are essentially non-bonding localized electron pairs on the Cu atom in each cluster.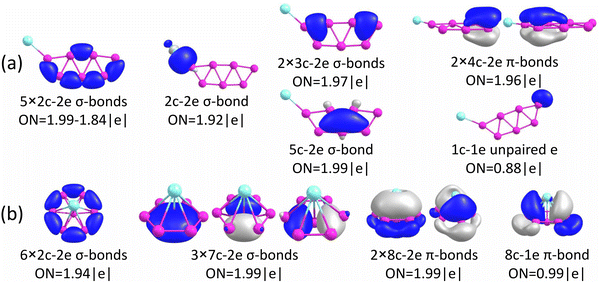 | ||
| Fig. 5 Results from AdNDP bonding analyses for (a) the GM of CuB7− (Cs, 2A′) and (b) Iso1 of CuB7− (C2v, 2B2). | ||
 | ||
| Fig. 6 Results from AdNDP bonding analyses for (a) the GM of CuB8− (C7v, 1A1) and (b) Iso1 of CuB8− (C6v, 1A1). | ||
Iso1 of CuB7− possesses a half-sandwich structure, which is only 1.6 kcal mol−1 higher in energy than the double chain GM (Fig. 3a) and can be viewed as Cu coordinated by the hexagonal B7−. The GM of B7− has a C6v structure with a triplet ground state.43 As shown recently, adding two electrons to B7− leads to the closed-shell doubly aromatic B73− borozene with six delocalized σ and six delocalized π electrons.47 The B73− closed-shell electron configuration was first realized in the C6v PrB7, i.e., [Pr3+][ B73−] with a half-sandwich structure.45 However, Cu can only contribute one valence electron to B7−, resulting in the doublet state for Iso1 of CuB7− with one partially filled π orbital (Fig. S4, ESI†). The ensuing Jahn–Teller distortion in the open shell Iso1 would lead to the C2v symmetry. The AdNDP results reveal precisely this bonding picture, as shown in Fig. 5b. In addition to the six peripheral 2c–2e B–B σ-bonds on the B7 motif, we observe three delocalized 7c–2e σ bonds, two 8c–2e π bonds, and one 8c–1e π bond. Hence, the half-sandwich Iso1 of CuB7− can be viewed as [Cu+][B72−], which is one electron short of the closed-shell B73− borozene configuration. Clearly, ionic interactions are dominant between Cu and the B7 motif in Iso1, whereas in the double chain GM of CuB7− the Cu−B covalent interaction dominates. The NPA charge of Cu in the double chain GM of CuB7− is only +0.29|e|, consistent with more covalent interactions, in comparison to a value of +1.00|e| in the ionic Iso1 of CuB7−. The missing π electron in the [Cu+][B72−] open-shell borozene complex is the reason why Iso1 has slightly lower stability compared to the double chain GM structure.
As shown above for the CuB7− cluster and other Cu–B clusters,51–53 Cu can interact with boron clusters both covalently and ionically. We have found that in CuB8− the position of the Cu atom around the B82− borozene molecular wheel dictates the degree of covalent interactions between the Cu atom and the borozene framework. For example, the shift of the Cu atom from the center position to the edge, and ultimately to the side in a planar structure, results in a decrease of the NPA charge on the Cu atom from +1.00|e| to +0.76|e|, and finally to +0.67|e| (Fig. S14A, ESI†). Thus, just like that in the case of Iso1 of CuB7− discussed above, the half-sandwich structure facilitates the most significant charge transfer from Cu to the B8 motif and leads to the formation of the stable closed-shell C7v [Cu+][B82−] borozene complex. Previously, it was found that the LiB8− cluster also had the C7v [Li+][B82−] structure,46 and all the LnB8− clusters had similar C7v [Ln+][B82−] structures.47
Interestingly, the GM of AuB8− is known to consist of the B8 wheel with the Au atom bonded at the side,49 due to the fact that Au tends to engage in strong covalent bonding as a result of the strong relativistic effects.87,88 The C7v AuB8− structure, which has the strongest ionic interactions, is not even a minimum on the potential energy surface with two imaginary frequencies (Fig. S14B, ESI†). The GM of AuB8− exhibits the lowest charge transfer, i.e., the strongest covalent interaction between Au and B, as shown in Fig. S14B (ESI†) and also previously.49 Furthermore, unlike transition metal doped boron clusters,35–37 the Cu©B8− molecular wheel structure is disfavored, less stable than the GM by 45.3 kcal mol−1 (Fig. S1B, ESI†), owing to the lacking of d–p covalent interactions between Cu and the B8 ring.89
The chemical bonding of the umbrella-shaped low-lying Iso1 of CuB8− is also very interesting. It is identical to that found in the umbrella-shaped B9O− cluster, i.e., [B8–BO]−,50 by replacing the BO unit with the Cu atom. The central B atom can be viewed as forming a covalent bond with the Cu atom, while sharing its three valence electrons with the hexagonal B7 unit to fulfill the B73− borozene configuration. Thus, both the GM and the low-lying isomer of CuB8− involve the borozene motifs, the B82− borozene in the GM and the B73− borozene in Iso1. These results provide further confirmation of the high stability of the borozenes B73− and B82−.
6 Conclusions
We report a joint photoelectron spectroscopy and theoretical study of two Cu-doped boron clusters CuB7− and CuB8−. Well-resolved photoelectron spectra are obtained for the two clusters and are combined with theoretical calculations to understand their structures and bonding. The global minimum of CuB7− consists of a double-chain B7 boron motif with a copper atom covalently bonded to one of its two apex boron atoms, whereas the low-lying isomer of CuB7− is found to be a half-sandwich structure involving the open-shell B72− borozene. The global minimum of CuB8− reveals a highly stable copper–borozene complex with a copper atom coordinated by the η8-B82− borozene. The current results provide not only new examples of borozene complexes, but also further insight about the interactions between copper and boron atoms and the competition between covalent and ionic interactions. The strong electron correlation effects found in the CuB7− and CuB8− clusters will also have implications for understanding the electronic structure of other copper–boron systems.Data availability
The data that supports the findings of this study is available from the corresponding authors upon reasonable request.Author contributions
L. S. W., I. A. P., and A. I. B. designed the project. W. J. C. and H. W. C. with help from D. F. Y. performed the experiment. A. S. P. performed the theoretical calculations and bonding analyses. W. J. C., A. S. P., I. A. P., and L. S. W. wrote and edited the manuscript. All authors helped to analyze the experimental and theoretical results.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The experiment done at Brown University was supported by the National Science Foundation (CHE-2053541). Computational resources from the ARCC HPC cluster of the University of Akron are gratefully acknowledged. I.A.P. acknowledges the start-up funding from the University of Akron.References
- B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668 CrossRef CAS PubMed.
- E. D. Jemmis and D. L. V. K. Prasad, J. Solid State Chem., 2006, 179, 2768–2774 CrossRef CAS.
- A. R. Oganov, J. Chen, C. Gatti, Y. Ma, Y. Ma, C. W. Glass, Z. Liu, T. Yu, O. O. Kurakevych and V. L. Solozhenko, Nature, 2009, 457, 863–867 CrossRef CAS PubMed.
- A. Gindulyte, W. N. Lipscomb and N. L. Massa, Inorg. Chem., 1998, 37, 6544–6545 CrossRef CAS PubMed.
- I. Boustani and A. Quandt, Europhys. Lett., 1997, 39, 527–532 CrossRef CAS.
- I. Boustani, A. Quandt, E. Hernandez and A. Rubio, J. Chem. Phys., 1999, 110, 3176–3185 CrossRef CAS.
- M. H. Evans, J. D. Joannopoulos and S. T. Pantelides, Phys. Rev. B, 2005, 72, 045434 CrossRef.
- H. Tang and S. Ismail-Beigi, Phys. Rev. Lett., 2007, 99, 115501 CrossRef PubMed.
- X. Yang, Y. Ding and J. Ni, Phys. Rev. B, 2008, 77, 041402 CrossRef.
- H. J. Zhai, L. S. Wang, A. N. Alexandrova and A. I. Boldyrev, J. Chem. Phys., 2002, 117, 7917–7924 CrossRef CAS.
- A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai, L. S. Wang, E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2003, 107, 1359–1369 CrossRef CAS.
- H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2003, 42, 6004–6008 CrossRef CAS PubMed.
- H. J. Zhai, B. Kiran, J. Li and L. S. Wang, Nat. Mater., 2003, 2, 827–833 CrossRef CAS PubMed.
- A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, Coord. Chem. Rev., 2006, 250, 2811–2866 CrossRef CAS.
- E. Oger, N. R. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503–8506 CrossRef CAS PubMed.
- A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W. L. Li, C. Romanescu, L. S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349–1358 CrossRef CAS PubMed.
- L. S. Wang, Int. Rev. Phys. Chem., 2016, 35, 69–142 Search PubMed.
- T. Jian, X. Chen, S. D. Li, A. I. Boldyrev, J. Li and L. S. Wang, Chem. Soc. Rev., 2019, 48, 3550–3591 RSC.
- S. Pan, J. Barroso, S. Jalife, T. Heine, K. R. Asmis and G. Merino, Acc. Chem. Res., 2019, 52, 2732–2744 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, J. Comput. Chem., 2007, 28, 251–268 CrossRef CAS PubMed.
- A. I. Boldyrev and L. S. Wang, Phys. Chem. Chem. Phys., 2016, 18, 11589–11605 RSC.
- Z. A. Piazza, H. S. Hu, W. L. Li, Y. F. Zhao, J. Li and L. S. Wang, Nat. Commun., 2014, 5, 3113 CrossRef PubMed.
- W. L. Li, Q. Chen, W. J. Tian, H. Bai, Y. F. Zhao, H. S. Hu, J. Li, H. J. Zhai, S. D. Li and L. S. Wang, J. Am. Chem. Soc., 2014, 136, 12257–12260 CrossRef CAS PubMed.
- A. J. Mannix, X. F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago and J. R. Guest, et al. , Science, 2015, 350, 1513–1516 CrossRef CAS PubMed.
- B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563–568 CrossRef CAS PubMed.
- S. Y. Xie, Y. Wang and X. B. Li, Adv. Mater., 2019, 31, 1900392 CrossRef PubMed.
- Y. V. Kaneti, D. P. Benu, X. Xu, B. Yuliarto, Y. Yamauchi and D. Golberg, Chem. Rev., 2022, 111, 1000–1052 CrossRef PubMed.
- H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727–731 CrossRef CAS PubMed.
- W. J. Chen, Y. Y. Ma, T. T. Chen, M. Z. Ao, D. F. Yuan, Q. Chen, X. X. Tian, Y. W. Mu, S. D. Li and L. S. Wang, Nanoscale, 2021, 13, 3868–3876 RSC.
- L. Sai, X. Wu, N. Gao, J. Zhao and R. B. King, Nanoscale, 2017, 9, 13905–13909 RSC.
- C. Chen, H. Lv, P. Zhang, Z. Zhuo, Y. Wang, C. Ma, W. Li, X. Wang, B. Feng, P. Cheng, X. Wu, K. Wu and L. Chen, Nat. Chem., 2022, 14, 25–31 CrossRef CAS PubMed.
- X. Liu, Q. Li, Q. Ruan, M. S. Rahn, B. I. Yakobson and M. C. Hersam, Nat. Mater., 2022, 21, 35–40 CrossRef CAS PubMed.
- W. L. Li, X. Chen, T. Jian, T. T. Chen, J. Li and L. S. Wang, Nat. Rev. Chem., 2017, 1, 0071 CrossRef CAS.
- J. Barroso, S. Pan and G. Merino, Chem. Soc. Rev., 2022, 51, 1098–1123 RSC.
- C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2011, 50, 9334–9337 CrossRef CAS PubMed.
- T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2012, 51, 2101–2105 CrossRef CAS PubMed.
- C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Acc. Chem. Res., 2013, 46, 350–358 CrossRef CAS PubMed.
- I. A. Popov, T. Jian, G. V. Lopez, A. I. Boldyrev and L. S. Wang, Nat. Commun., 2015, 6, 8654 CrossRef CAS PubMed.
- T. Jian, W. L. Li, I. A. Popov, G. V. Lopez, X. Chen, A. I. Boldyrev, J. Li and L. S. Wang, J. Chem. Phys., 2016, 144, 154310 CrossRef PubMed.
- W. L. Li, T. Jian, X. Chen, H. R. Li, T. T. Chen, X. M. Luo, S. D. Li, J. Li and L. S. Wang, Chem. Commun., 2017, 53, 1587–1590 RSC.
- W. L. Li, T. Jian, X. Chen, T. T. Chen, G. V. Lopez, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2016, 55, 7358–7363 CrossRef CAS PubMed.
- T. Jian, W. L. Li, X. Chen, T. T. Chen, G. V. Lopez, J. Li and L. S. Wang, Chem. Sci., 2016, 7, 7020–7027 RSC.
- A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, J. Phys. Chem. A, 2004, 108, 3509–3517 CrossRef CAS.
- T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, J. Chem. Phys., 2011, 135, 104301 CrossRef PubMed.
- T. T. Chen, W. L. Li, T. Jian, X. Chen, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2017, 56, 6916–6920 CrossRef CAS PubMed.
- A. N. Alexandrova, H. J. Zhai, L. S. Wang and A. I. Boldyrev, Inorg. Chem., 2004, 43, 3552–3554 CrossRef CAS PubMed.
- W. L. Li, T. T. Chen, W. J. Chen, J. Li and L. S. Wang, Nat. Commun., 2021, 12, 6467 CrossRef CAS PubMed.
- W. J. Chen, M. Kulichenko, H. W. Choi, J. Cavanagh, D. F. Yuan, A. I. Boldyrev and L. S. Wang, J. Phys. Chem. A, 2021, 125, 6751–6760 CrossRef CAS PubMed.
- W. J. Chen, Y. Y. Zhang, W. L. Li, H. W. Choi, J. Li and L. S. Wang, Chem. Commun., 2022, 58, 3134–3137 RSC.
- W. J. Tian, W. J. Chen, M. Yan, R. Li, Z. H. Wei, T. T. Chen, Q. Chen, H. J. Zhai, S. D. Li and L. S. Wang, Chem. Sci., 2021, 12, 8157–8164 RSC.
- M. Kulichenko, W. J. Chen, H. W. Choi, D. F. Yuan, A. I. Boldyrev and L. S. Wang, J. Vac. Sci. Technol., 2022, 40, 042201 CrossRef CAS.
- A. S. Pozdeev, W. J. Chen, M. Kulichenko, H. W. Choi, A. I. Boldyrev and L. S. Wang, Solid State Sci., 2023, 142, 107248 CrossRef CAS.
- A. S. Pozdeev, W. J. Chen, H. W. Choi, M. Kulichenko, D. F. Yuan, A. I. Boldyrev and L. S. Wang, J. Phys. Chem. A, 2023, 127, 4888–4896 CrossRef CAS PubMed.
- A. P. Sergeeva, B. B. Averkiev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2011, 134, 224304 CrossRef PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. J. Frisch, et al., Gaussian 16, revision A.03, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef CAS.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- H. J. Monkhorst, Int. J. Quantum Chem., 2009, 12, 421–432 CrossRef.
- N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107 CrossRef PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, J. Chem. Phys., 1996, 104, 9047–9052 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- F. Neese, J. Am. Chem. Soc., 2006, 128, 10213–10222 CrossRef CAS PubMed.
- D. Yu Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207 RSC.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- F. Neese, WIREs Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- F. Neese, WIREs Comput. Mol. Sci., 2018, 8, 1327 CrossRef.
- G. A. Zhurko, Chemcraft - Graphical Software for Visualization of Quantum Chemistry Computations. Ivanovo, Russia, 2005, https://www.chemcraftprog.com Search PubMed.
- P. L. Rodríguez-Kessler, A. Vasquez-Espinal and A. Munoz-Castro, Polyhedron, 2023, 243, 116538 CrossRef.
- H. J. Zhai, L. S. Wang, D. Y. Zubarev and A. I. Boldyrev, J. Phys. Chem. A, 2006, 110, 1689–1693 CrossRef CAS PubMed.
- W. L. Li, C. Romanescu, T. Jian and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 13228–13231 CrossRef CAS PubMed.
- P. Pyykkö, Chem. Rev., 1988, 88, 563–594 CrossRef.
- L. S. Wang, Phys. Chem. Chem. Phys., 2010, 12, 8694–8705 RSC.
- C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2013, 138, 134315 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00296b |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2024 |