The nature of metallophilic interactions in closed-shell d⁸–d⁸ metal complexes

Abstract

We have quantum chemically analyzed the closed-shell d⁸–d⁸ metallophilic interaction in dimers of square planar [M(CO)₂X₂] complexes (M = Ni, Pd, Pt; X = Cl, Br, I) using dispersion-corrected density functional theory at ZORA-BLYP-D3(BJ)/TZ2P level of theory. Our purpose is to reveal the nature of the [X₂(CO)₂M]⋯[M(CO)₂X₂] bonding mechanism by analyzing trends upon variations in M and X. Our analyses reveal that the formation of the [M(CO)₂X₂]₂ dimers is favored by an increasingly stabilizing electrostatic interaction when the M increases in size and by more stabilizing dispersion interactions promoted by the larger X. In addition, there is an overlooked covalent component stemming from metal–metal and ligand–ligand donor–acceptor interactions. Thus, at variance with the currently accepted picture, the d⁸–d⁸ metallophilicity is attractive, and the formation of [M(CO)₂X₂]₂ dimers is not a purely dispersion-driven phenomenon.

---

1. Introduction

Metallophilicity is the manifestation of a net attractive intra- or intermolecular interaction between metal centers (M), yielding metal–metal-bonded complexes.¹ This metal–metal interaction causes the spontaneous association, i.e., self-assembly, of metal complexes forming aggregates with luminescence properties² and medicinal applications.³ Earlier work by Hoffman et al. showed that the closed-shell metallophilic interactions between linear d¹⁰ metal complexes are covalent due to the donor–acceptor interactions between the filled nd_Z²-type HOMO on one M and the (n + 1)s-type LUMO on the other M.⁴ However, Brands et al. showed that the donor–acceptor interactions cannot overcome the destabilizing steric Pauli repulsion between the two metal centers, and the metallophilic interactions are only attractive due to the additional stabilizing electrostatic interactions.⁵ In general, the closed-shell d¹⁰–d¹⁰ metalllophilic interactions have a similar mechanistic picture to other well-known intermolecular interactions, such as hydrogen bonds.⁶

Nonetheless, alternative models have been used to explain metallophilicity. For example, Pyykkö and coworkers concluded that the d¹⁰–d¹⁰ Au⁺⋯Au⁺ attraction in staggered dimers of linear AuPH₃Cl complexes is a dispersion-driven phenomenon, whereas the ligand–ligand repulsion hampers the formation of parallel dimers.⁷ This has been further supported by Chen et al. who found that π–π interactions between face-to-face, eclipsed ligands are repulsive.⁸ On the other hand, Che et al. attributed the formation of d⁸–d⁸ and d¹⁰–d¹⁰ metal-complexes dimers to stabilizing ligand–ligand dispersion interactions.⁹

In the present study, we have quantum chemically investigated the bonding mechanism of eclipsed closed-shell d⁸–d⁸ metal complexes, using [M(CO)₂X₂]₂ dimers (M = Ni, Pd, Pt; X = Cl, Br, I) as model systems (Scheme 1). As will become clear in the following sections, our bonding analyses reveal that the stability of the [M(CO)₂X₂]₂ dimers stems from significantly attractive electrostatic interactions, on top of dispersion interactions promoted by the ligands. This closed-shell d⁸–d⁸ metal–metal interaction is, therefore, similar to that between d¹⁰ metal centers, that is, it is also partially covalent in nature and, thus, not a pure dispersion-driven phenomenon.

Scheme 1 The studied [M(CO)₂X₂]₂ dimers.

2. Computational methods

2.1. Computational details

All calculations were carried out using the Amsterdam Modeling Suite (AMS) 2020.101 program.¹⁰ All stationary points and energies were obtained using relativistic, dispersion-corrected density functional theory at ZORA-BLYP-D3(BJ)/TZ2P. This approach has been benchmarked in previous work for bond energies of metal–metal complexes using CCSD(T)/CBS with mean absolute error of 0.7 kcal mol⁻¹.⁵ This approach comprises the BLYP level of the generalized gradient approximation (GGA); exchange functional developed by Becke (B), and the GGA correlation functional developed by Lee, Yang, and Parr (LYP)¹¹ (see Tables S4 and S5 in the ESI,† for the Cartesian coordinates). The DFT-D3(BJ) method developed by Grimme and coworkers,¹² which contains the damping function proposed by Becke and Johnson,¹³ is used to describe non-local dispersion interactions. Scalar relativistic effects are accounted for using the zeroth-order regular approximation (ZORA).¹⁴ Molecular orbitals (MO) were expanded in a large, uncontracted set of Slater-type orbitals (STOs) containing diffuse functions: TZ2P.¹⁵ The basis set is of triple-ζ quality augmented with polarization functions, i.e., one 3d and one 4f set on C, O, Cl; one 4d and one 4f set on Br; one 5d and one 4f set on I; one 4f set on Ni; one 5p and one 4f set on Pd; one 6p and one 5f set on Pt. All electrons were included in the variational process, i.e., no frozen core approximation was applied. The accuracies of both the fitting scheme and the integration grid (Becke grid) were set to ‘EXCELLENT’. The formation of trans-[M(CO)₂X₂] monomers and trans-[M(CO)₂X₂]₂ dimers (M = Ni, Pd, Pt; X = Cl, Br, I) is, in most cases, more favorable than the formation of cis-[M(CO)₂X₂] monomers and cis-[M(CO)₂X₂]₂ dimers (see Table S3 and Fig. S4 for bond energies and geometries, ESI†). The [Ni(CO)₂Br₂], [Ni(CO)₂I₂], and [Pd(CO)₂I₂] monomers, and their respective dimers, are the only exceptions in which the cis forms are more favorable (Table S3, ESI†). Thus, in this study, we always refer to the trans-[M(CO)₂X₂]₂ dimers. We have found here that the global-minimum structures of the [M(CO)₂X₂]₂ dimers are in the staggered conformation by performing a fully relaxed rotation around the M⋯M bond, in which the X–M⋯M–X dihedral angle is varied from 0° to 90° (see Fig. S5 and S6 in the ESI†). All optimized structures were confirmed to be true minima through vibrational analysis (no imaginary frequencies).

2.2. Bond analyses

Insight into the bonding mechanism is obtained by analyzing the potential energy curves for the formation of the [M(CO)₂X₂]₂ dimers (M = Ni, Pd, Pt; X = Cl, Br, I). The analyses are done by varying the M⋯M bond distance within the range of 2.5 Å to 4.5 Å, starting from the equilibrium geometry of the complex (r_M⋯M,eq) while keeping all other geometrical parameters frozen.

The interaction between [X₂(CO)₂M] and [M(CO)₂X₂] is analyzed using the activation strain model,¹⁶ which is a fragment-based approach to understanding the energy profile associated with a chemical process in terms of the original reactants. Thus, the total bond energy ΔE is decomposed along the M⋯M bond distance r_M⋯M (or just at one point along r_M⋯M) into the strain energy ΔE_strain(r_M⋯M), which is associated with the geometrical deformation of the individual reactants as the process takes place, plus the actual interaction energy ΔE_int(r_M⋯M) between the deformed reactants [eqn (1)].

ΔE(r_M⋯M) = ΔE_strain(r_M⋯M) + ΔE_int(r_M⋯M) (1)

In the equilibrium geometry, that is, for r_M⋯M = r_M⋯M,eq, this yields an expression for the bond energy ΔE(r_M⋯M,eq) = ΔE = ΔE_strain + ΔE_int. The interaction energy ΔE_int(r_M⋯M) between the deformed reactants is further analyzed in the conceptual framework provided by the quantitative Kohn–Sham MO model.¹⁷ To this end, it is decomposed into physically meaningful terms [eqn (2)] using a quantitative energy decomposition analysis (EDA) as implemented in ADF.¹⁷

ΔE_int(r_M⋯M) = ΔV_elstat(r_M⋯M) + ΔE_Pauli(r_M⋯M) + ΔE_oi(r_M⋯M) + ΔE_disp(r_M⋯M) (2)

The usually attractive term ΔV_elstat corresponds to the classical Coulomb interaction between the unperturbed charge distributions of the deformed reactants and has four components: (i) the electron–electron repulsion between the electron densities of [X₂(CO)₂M] and [M(CO)₂X₂]; (ii) the nuclei–electron attraction between the nuclei of [X₂(CO)₂M] and the electron density of [M(CO)₂X₂]; (iii) the electron–nuclei attraction between the electron density of [X₂(CO)₂M] and the nuclei of [M(CO)₂X₂]; and (iv) the nuclei–nuclei repulsion between the nuclei of [X₂(CO)₂M] and [M(CO)₂X₂].¹⁷

The Pauli repulsion energy (ΔE_Pauli) comprises the destabilizing interactions between the fully occupied orbitals on either fragment and arises from the antisymmetrization of the Hartree wavefunction due to the Pauli principle. The orbital-interaction energy (ΔE_oi) accounts for charge transfer, that is, the interaction between occupied orbitals of one fragment with unoccupied orbitals of the other fragment, including the interactions of the highest occupied and lowest unoccupied MOs (HOMO–LUMO), and polarization, that is, empty–occupied orbital mixing on one fragment, due to the presence of another fragment. The dispersion energy ΔE_disp accounts for the dispersion corrections as introduced by Grimme et al.¹² To facilitate the analyses, the ASM and EDA were performed using the PyFrag 2019 program.¹⁸

3. Results and discussion

3.1. Bond strength and structure

Equilibrium geometries, dimerization energies (ΔE), and the M⋯M bond distances (r_M⋯M) of the stable C_S symmetrical [M(CO)₂X₂]₂ dimers (M = Ni, Pd, Pt; X = Cl, Br, I) calculated at the ZORA-BLYP-D3(BJ)/TZ2P level of theory are shown in Fig. 1. Upon the formation of the studied dimers, we have identified two main features: (i) the stability of the dimers significantly increases, and the M⋯M bond distance slightly shortens for heavier M; and (ii) the dimers are only slightly stronger but longer for heavier X ligands. For example, along the series from [Ni(CO)₂Br₂]₂ to [Pt(CO)₂Br₂]₂, ΔE becomes more stabilizing from −13.1 kcal mol⁻¹ to −17.6 kcal mol⁻¹ and r_M⋯M decreases from 3.269 Å to 3.192 Å (Fig. 1). Along the series from [Pd(CO)₂Cl₂]₂ to [Pd(CO)₂I₂]₂, ΔE varies only from −15.8 kcal mol⁻¹ to −16.6 kcal mol⁻¹ and r_M⋯M increases from 3.117 Å to 3.220 Å (Fig. 1).

Fig. 1 Equilibrium geometries (in Å) and electronic bond energies (in kcal mol⁻¹) of the [M(CO)₂X₂]₂ dimers (M = Ni, Pd, Pt; X = Cl, Br, I). Computed at ZORA-BLYP-D3(BJ)/TZ2P.

Next, we performed our activation strain analysis¹⁶ (ASA) to decompose the bond energies (ΔE) into the strain (ΔE_strain) and interaction (ΔE_int) energies (see Computational methods), and the results are shown in Table 1. The trends in the stability of the [M(CO)₂X₂]₂ dimers along M = Ni, Pd, Pt and X = Cl, Br, I are dominated by the stronger ΔE_int, whereas the weaker ΔE_strain varies only slightly along the same series. For example, along the series from [Ni(CO)₂Br₂]₂ to [Pt(CO)₂Br₂]₂, ΔE_int becomes more stabilizing from −14.0 kcal mol⁻¹ to −18.9 kcal mol⁻¹ and ΔE_strain becomes slightly more destabilizing from 0.9 kcal mol⁻¹ to 1.3 kcal mol⁻¹ (Table 1). Along the series from [Pd(CO)₂Cl₂]₂ to [Pd(CO)₂I₂]₂, ΔE_int becomes more stabilizing from −16.6 kcal mol⁻¹ to −17.9 kcal mol⁻¹ and ΔE_strain becomes slightly more destabilizing from 0.8 kcal mol⁻¹ to 1.3 kcal mol⁻¹ (Table 1). Note that the impact on ΔE_int and, thus, on the stability of the [M(CO)₂X₂]₂ dimers when varying M is larger than when varying X. As will become clear in the next sections, this is because of the difference in nature between the metal–metal interactions and those involving the ligands. This conclusion emerges from understanding the physical nature behind the observed trends in ΔE_int when the metal center M varies along Ni, Pd, and Pt and the ligands X vary along Cl, Br, and I.

Table 1 Activation strain and energy decomposition analyses (in kcal mol⁻¹) for the formation of the [M(CO)₂X₂] dimers (M = Ni, Pd, Pt; X = Cl, Br, I) in their equilibrium geometries (in Å). Computed at ZORA-BLYP-D3(BJ)/TZ2P

M	X	r M⋯M	ΔE	ΔEstrain	ΔEint	ΔVelstat	ΔEPauli	ΔEoi	ΔEdisp
Ni	Cl	3.199	−12.6	0.6	−13.2	−12.3	20.3	−7.6	−13.6
	Br	3.269	−13.1	0.9	−14.0	−14.8	21.3	−8.0	−15.4
	I	3.371	−13.8	0.9	−14.7	−11.6	22.7	−7.7	−18.1
Pd	Cl	3.117	−15.8	0.8	−16.6	−24.1	34.8	−11.4	−15.8
	Br	3.160	−15.9	1.3	−17.2	−23.1	35.8	−12.0	−17.9
	I	3.220	−16.6	1.3	−17.9	−22.3	37.1	−12.0	−20.8
Pt	Cl	3.157	−17.1	0.9	−18.0	−28.0	39.5	−12.9	−16.6
	Br	3.192	−17.6	1.3	−18.9	−27.3	41.0	−13.8	−18.9
	I	3.239	−18.3	1.8	−20.1	−26.8	43.2	−14.2	−22.1

---

3.2. Variation of M

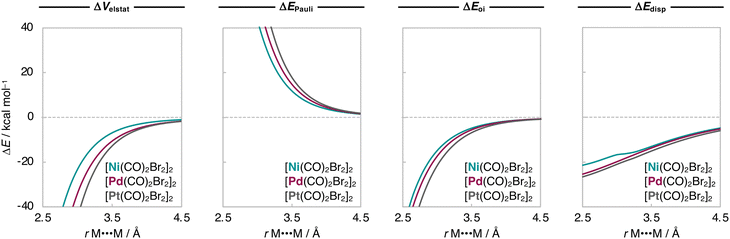
To understand the origin of the increased stabilization of the [M(CO)₂X₂]₂ dimers upon varying M along Ni, Pd, and Pt, we further decomposed the ΔE_int into physically meaningful terms, namely the electrostatic interactions (ΔV_elstat), steric Pauli repulsion (ΔE_Pauli), orbital interactions (ΔE_oi), and dispersion energy (ΔE_disp) using our energy decomposition analysis¹⁷ (EDA; see Computational methods), and the results are shown in Table 1. Our analyses reveal that, for the smaller Ni, we find that ΔE_disp is the largest attractive term in [X₂(CO)₂M]⋯[M(CO)₂X₂]. However, as M increases in size, ΔV_elstat and ΔE_oi become significantly more stabilizing whereas ΔE_disp varies much less, which causes ΔV_elstat to dominate and become the most attractive term for Pd and Pt. For example, from [Ni(CO)₂Br₂]₂ to [Pt(CO)₂Br₂]₂, ΔE_disp varies only from −15.4 kcal mol⁻¹ to −18.9 kcal mol⁻¹, whereas ΔV_elstat and ΔE_oi become significantly more stabilizing from −14.8 kcal mol⁻¹ to −27.3 kcal mol⁻¹ and from −8.0 kcal mol⁻¹ to −13.8 kcal mol⁻¹, respectively (Table 1).

For a consistent comparison, we extend our analysis to the entire reaction coordinate, as a function of the M⋯M bond distance (r_M⋯M). Since ΔE_strain is small and the ΔE is dominated by ΔE_int, the analyses were done while the geometries of the fragments were kept frozen to that of the equilibrium geometries of the [M(CO)₂X₂]₂ dimers. The resulting interaction energy curves ΔE_int(r_M⋯M) for the representative [Ni(CO)₂Br₂]₂, [Pd(CO)₂Br₂]₂, and [Pt(CO)₂Br₂]₂ series are graphically shown in Fig. 2. Herein, the ΔE_int(r_M⋯M) curves also become more stabilizing and the energy minimum is shifted towards shorter r_M⋯M as M varies along Ni, Pd, and Pt.

Fig. 2 Interaction energies (in kcal mol⁻¹) as a function of the M⋯M distance (in Å) starting from the equilibrium geometries of the representative [M(CO)₂Br₂]₂ dimers (M = Ni, Pd, Pt), while the geometry of the monomers is kept frozen. Computed at ZORA-BLYP-D3(BJ)/TZ2P.

Next, we analyze the EDA terms as a function of r_M⋯M and the resulting diagrams for the representative [Ni(CO)₂Br₂]₂, [Pd(CO)₂Br₂]₂, and [Pt(CO)₂Br₂]₂ series are graphically shown in Fig. 3. Our findings show that the increased stability of the [M(CO)₂Br₂]₂ dimers as M varies along Ni, Pd, Pt is due to a greater electrostatic attraction between the monomers, as the electrostatic interaction curves ΔV_elstat(r_M⋯M) become significantly more stabilizing along the same series (Fig. 3). This is because the [X₂(CO)₂M]⋯[M(CO)₂X₂] electrostatic attraction is largely affected by the charge distributions around the metal centers within the monomers. In essence, there is a more effective electron–nuclei overlap as the electron density (ρ) of [M(CO)₂Br₂]₂ becomes more diffuse, and the nucleus of the metal center increases in size (i.e., has more protons) along the same series. For example, at the same point of the reaction coordinate, e.g., r_M⋯M = 3.5 Å, the negatively charged ρ of one fragment is more diffuse around the metal center and extends further towards the nucleus of the metal center of the other fragment, which becomes more positively charged as M varies along Ni, Pd, and Pt (see Fig. 4). As the two monomers approach each other, this attractive electron–nuclei overlap more quickly increases for heavier M and, consequently, the slope of the descending ΔV_elstat(r_M⋯M) curves increases along Ni, Pd, and Pt, shifting the equilibrium geometries of the [M(CO)₂Br₂]₂ dimers to a shorter r_M⋯M as M varies along the same series.

Fig. 3 Energy decomposition analysis (in kcal mol⁻¹) as a function of the M⋯M distance (in Å) for the representative [M(CO)₂Br₂]₂ dimers (M = Ni, Pd, Pt), while the geometry of the monomers is kept frozen. Computed at ZORA-BLYP-D3(BJ)/TZ2P.

Fig. 4 Attractive overlap between the negatively charged electron densities and the positively charged nuclei (density contours from 0.0001 to 0.5000 a.u.) for the representative [M(CO)₂Br₂]₂ dimers (M = Ni, Pd, Pt) at a consistent M⋯M bond distance (r_M⋯M = 3.5 Å). Computed at ZORA-BLYP-D3(BJ)/TZ2P.

Together with ΔV_elstat(r_M⋯M), the orbital interactions ΔE_oi(r_M⋯M) and the dispersion energy curves ΔE_disp(r_M⋯M) follow the same trend as ΔE_int(r_M⋯M) and become more stabilizing along M = Ni, Pd, Pt (Fig. 3). This effect is more pronounced in ΔE_oi(r_M⋯M) which arises, in part, from the donation of charge from the metal d_Z²-type HOMO of one M(CO)₂X₂ monomer into the metal s-type LUMO of the other monomer and will be explained in detail later (see Scheme 2). The ΔE_oi(r_M⋯M) curves are weakly attractive at longer r_M⋯M and, as soon as the d_Z²-HOMO and s-LUMO start to overlap at shorter r_M⋯M, they become significantly stabilizing (Fig. 3). The ΔE_disp(r_M⋯M) curves, on the other hand, are relatively strong already at longer r_M⋯M, but neither become much more stabilizing at shorter r_M⋯M nor significantly vary along M = Ni, Pd, Pt. In other words, the ΔE_disp term significantly contributes to the stability of the [M(CO)₂X₂]₂ dimers but is almost insensitive to variations of the metal centers.

Scheme 2 Schematic molecular orbital diagram of the metal–metal donor–acceptor interactions in [M(CO)₂X₂]₂ dimers. The DFT orbitals are shown in Fig. S3 of the ESI.†

3.3. Variation of X

To understand why the ΔE_int, and thus the [M(CO)₂X₂]₂ dimers, becomes slightly more stable upon varying X along Cl, Br, and I, we first analyze the EDA terms at the equilibrium geometries. Contrary to the variation along M = Ni, Pd, Pt, our analyses reveal that ΔE_disp becomes more stabilizing, whereas ΔV_elstat and ΔE_oi do not significantly change when X varies along Cl, Br, and I. For example, from [Pd(CO)₂Cl₂]₂ to [Pd(CO)₂I₂]₂, ΔE_disp becomes more stabilizing from −15.8 kcal mol⁻¹ to −20.8 kcal mol⁻¹, whereas ΔV_elstat and ΔE_oi vary from −24.1 kcal mol⁻¹ to −22.3 kcal mol⁻¹ and −11.4 kcal mol⁻¹ to −12.0 kcal mol⁻¹, respectively (Table 1).

Next, we analyze the ΔE_int and the EDA terms as a function of r_M⋯M, and the resulting diagrams for the representative [Pd(CO)₂Cl₂]₂, [Pd(CO)₂Br₂]₂, and [Pd(CO)₂I₂]₂ series are graphically shown in Fig. 5 and 6. The ΔE_int(r_M⋯M) curves also become more stabilizing, and the energy minimum is shifted towards longer r_M⋯M as X varies along Cl, Br, and I. Our analyses show that the increased stability of the [Pd(CO)₂X₂]₂ dimers as X varies along Cl, Br, and I is due to a greater attractive dispersion interaction promoted by the ligands as they increase in size along the same series. Note that the ΔE_disp(r_M⋯M) curves become significantly more stabilizing along [Pd(CO)₂Cl₂]₂, [Pd(CO)₂Br₂]₂, and [Pd(CO)₂I₂]₂ (Fig. 6). Nevertheless, the equilibrium r_M⋯M slightly expands because the Pauli repulsion curves ΔE_Pauli(r_M⋯M) are steeper than the ΔE_disp(r_M⋯M) curves and push the equilibrium r_M⋯M to longer values as X varies along Cl, Br, and I (Fig. 6).

Fig. 5 Interaction energies (in kcal mol⁻¹) as a function of the M⋯M distance (in Å) starting from the equilibrium geometries of the representative [Pd(CO)₂X₂]₂ dimers (X = Cl, Br, I), while the geometry of the monomers is kept frozen. Computed at ZORA-BLYP-D3(BJ)/TZ2P.

Fig. 6 Energy decomposition analysis (in kcal mol⁻¹) as a function of the M⋯M distance (in Å) for the representative [Pd(CO)₂X₂]₂ dimers (X = Cl, Br, I), while the geometry of the monomers is kept frozen. Computed at ZORA-BLYP-D3(BJ)/TZ2P.

The ΔV_elstat(r_M⋯M) curves are almost insensitive to variations of X in the [Pd(CO)₂X₂]₂ dimers and become only slightly more stabilizing along X = Cl, Br, I (Fig. 6). This is because, as aforementioned, the attractive electron–nuclei overlap occurs mainly at the M⋯M bond region and does not significantly change as the X ligands increase in size along X = Cl, Br, I. Instead, the increased size of X causes the ρ of the monomers to extend further along the CO⋯X region, where there is not a pronounced electron–nuclei overlap (see Fig. S1, ESI†). Consequently, the electrostatic attraction between the monomers in the [M(CO)₂X₂]₂ only marginally increases when X varies along Cl, Br, and I.

Our analyses along variations of M and X have revealed two important interactions for the bonding mechanism and, thus, stability of the [M(CO)₂X₂]₂ dimers. On the one hand, there are electrostatic interactions that increase in relevance as the metal becomes bigger. On the other hand, there are attractive dispersion interactions stemming from the ligands. Despite this difference in nature between the metal–metal and ligand–ligand interactions, they also share some similarities. Similar to the trend upon varying M along Ni, Pd, and Pt, the ΔE_oi(r_M⋯M) curves also become more stabilizing when X varies along Cl, Br, and I in the [Pd(CO)₂X₂]₂ dimers (Fig. 6). This is due to the stabilizing ligand–ligand donor–acceptor interaction of the C=O π*-type (π*_CO) LUMO of one monomer with the X lone-pair-type (LP_X) HOMO of the other monomer (see Scheme 3). In the following section, we explain why the ΔE_oi(r_M⋯M) curves become more stabilizing along M = Ni, Pd, Pt and X = Cl, Br, I in the [M(CO)₂X₂]₂ dimers.

Scheme 3 Schematic molecular orbital diagram of the ligand–ligand donor–acceptor interactions in [M(CO)₂X₂]₂ dimers. The DFT orbitals are shown in Fig. S3 of the ESI.†

3.4. Metal–metal versus ligand–ligand donor–acceptor interactions

In previous sections, we showed that the stability of the [M(CO)₂X₂]₂ dimers is mainly governed by the electrostatic attraction, which becomes more important for larger M and dispersive interactions promoted by the ligands. However, both metal–metal and ligand–ligand interactions have a covalent component stemming from donor–acceptor interactions that has been hitherto overlooked. Note that the ΔE_oi between the monomers in [M(CO)₂X₂]₂ dimers, which accounts for donor–acceptor interactions, becomes more stabilizing along M = Ni, Pd, Pt and X = Cl, Br, I (vide supra). Next, we explain the physical nature behind these trends.

The donor–acceptor interactions in the [M(CO)₂X₂]₂ dimers comprise of two main components, namely, the metal–metal d_Z²-HOMO–s-LUMO and the ligand–ligand π*_CO-LUMO–LP_X-HOMO interactions (see Schemes 2 and 3). The relevance of a donor–acceptor interaction can be estimated by the magnitude of its orbital stabilization, which is proportional to its HOMO–LUMO overlap squared (S²) divided by its respective orbital energy gap (Δε) [see eqn (3)]. For a consistent comparison, we report these values for the metal–metal and ligand–ligand donor–acceptor interactions at r_M⋯M = 3.5 for all [M(CO)₂X₂]₂ dimers in Table 2.

ΔE_oi ∝ S²/Δε (3)

Table 2 Orbital interaction energies (in kcal mol⁻¹), orbital overlap, energy gap (Δε, in eV), and orbital stabilization for the metal–metal and ligand–ligand donor–acceptor interactions in the [M(CO)₂X₂]₂ dimers (M = Ni, Pd, Pt; X = Cl, Br, I) at a consistent M⋯M bond distance (r_M⋯M = 3.5 Å). Computed at ZORA-BLYP-D3(BJ)/TZ2P

M	X	ΔEoi	Metal–metal				Ligand–ligand
			S	Δε^a	10^3×S^2/Δε	%^b	S	Δε^a	10^3×S^2/Δε	%^b
a See HOMO and LUMO energies in Tables S1 and S2 (ESI). b Contribution of the associated orbital stabilization to the total metal–metal + ligand–ligand orbital stabilization.
Ni	Cl	−3.8	0.11	8.2	1.5	53	0.07	3.8	1.3	47
	Br	−4.9	0.09	7.8	1.0	36	0.08	3.5	1.8	64
	I	−5.8	0.08	7.3	0.9	25	0.09	3.1	2.6	75
Pd	Cl	−4.7	0.18	8.4	3.9	67	0.08	3.4	1.9	33
	Br	−5.6	0.17	8.1	3.6	58	0.09	3.1	2.6	42
	I	−6.5	0.16	7.7	3.3	47	0.10	2.7	3.7	53
Pt	Cl	−5.8	0.20	8.2	4.9	67	0.09	3.3	2.5	33
	Br	−6.8	0.18	8.1	4.0	55	0.10	3.0	3.3	45
	I	−8.0	0.17	7.8	3.7	44	0.11	2.6	4.7	56

---

The ΔE_oi(r_M⋯M) curves for the [M(CO)₂X₂]₂ dimers become more stabilizing along M = Ni, Pd, Pt because the metal–metal donor–acceptor interactions between the d_Z²-type HOMO of one monomer and the s-type LUMO of the other monomer are strengthened along the same series. When the metal center increases in size along Ni, Pd, and Pt, the bond overlap S between the d_Z²-HOMO and the s-LUMO increases as both orbitals become more diffuse, resulting in larger orbital stabilization and, thus, stronger donor–acceptor interactions along the same series. For example, in the series of [Ni(CO)₂Br₂]₂, [Pd(CO)₂Br₂]₂, and [Pt(CO)₂Br₂]₂ at r_M⋯M = 3.5, S increases from 0.09 to 0.17 to 0.18, as both the d_Z²-HOMO and the s-LUMO further extend towards the other metal center (see Fig. 7a, but also the overlap densities in Fig. S2a, ESI†). Consequently, S²/Δε times 10³ increases from 1.0 to 3.6 to 4.0 along the same series (Table 2).

Fig. 7 Stabilizing HOMO–LUMO energy gap (in eV) and orbital overlap for (a) the metal–metal and (b) ligand–ligand donor–acceptor interactions for the representative [M(CO)₂Br₂]₂ (M = Ni, Pd, Pt) and [Pd(CO)₂X₂]₂ (X = Cl, Br, I) dimers at a consistent M⋯M bond distance (r_M⋯M = 3.5 Å; contour plots from 0.9 to 0.04 a.u.). Computed at ZORA-BLYP-D3(BJ)/TZ2P.

The ΔE_oi term in the [M(CO)₂X₂]₂ dimers is not fully dominated by the metal–metal donor–acceptor interactions and is, in part, made by ligand–ligand donor–acceptor interactions. This is confirmed by the trends in the ΔE_oi(r_M⋯M) curves that also become more stabilizing along X = Cl, Br, I (Fig. 6). The bond overlap S for the π*_CO-LUMO–LP_X-HOMO interaction is, in general, significantly smaller than that of the metal–metal donor–acceptor interactions (Table 2). However, as the X ligands become larger and less electronegative along Cl, Br, and I, the LP_X-HOMO extends further towards the π*_CO-LUMO and becomes higher in energy (see Fig. S2b and Table S2 for the orbital energies, ESI†). This results in a larger S and a smaller Δε between the π*_CO-LUMO and the LP_X-HOMO. For example, in the series of [Pd(CO)₂Cl₂]₂, [Pd(CO)₂Br₂]₂, and [Pd(CO)₂I₂]₂ at r_M⋯M = 3.5, S increases from 0.08 to 0.09 to 0.10 and Δε decreases from 3.4 eV to 3.1 eV to 2.7 eV. Consequently, S²/Δε times 10³ increases from 1.9 to 2.6 to 3.7 along the same series (Table 2).

Since the ΔE_oi term is not made of one single component, our analyses show that there is an interplay between the metal–metal and ligand–ligand donor–acceptor interactions in the [M(CO)₂X₂]₂ dimers along M = Ni, Pd, Pt and along X = Cl, Br, I. Therefore, to understand the relative importance of the metal–metal and ligand–ligand interactions, we computed the magnitude of their orbital stabilization according to eqn (3) and estimated their relative contribution to the total orbital stabilization (metal–metal + ligand–ligand). The results are collected in Table 2.

When the metal centers are large and the ligands are small and more electronegative, the donor–acceptor metal–metal interactions are strengthened and dominate over the weakened ligand–ligand interactions. For example, for [Pt(CO)₂Cl₂]₂ at r_M⋯M = 3.5 Å, the metal–metal interactions are up to 67% of the total orbital stabilization. On the other hand, the ligand–ligand donor–acceptor interactions only dominate when the metal center is small and the ligands are large and less electronegative, like in the [Ni(CO)₂I₂]₂ dimer, in which the ligand–ligand donor–acceptor interactions are up to 75% of the total orbital stabilization at r_M⋯M = 3.5 Å (Table 2).

4. Conclusions

The stability of square planar [X₂(CO)₂M]⋯[M(CO)₂X₂] dimers increases as the metal centers M vary along Ni, Pd, and Pt, and the X ligands vary along Cl, Br, and I. Our quantum chemical bonding analyses show that the dimers are formed due to stabilizing electrostatic interactions on top of stabilizing dispersion interactions promoted by the ligands. Both interactions become more stabilizing as M and X increase in size. In addition, our analyses revealed an overlooked covalent component stemming from metal–metal and ligand–ligand donor–acceptor interactions. These findings emerge from our quantitative Kohn–Sham molecular orbital analyses using dispersion-corrected relativistic density functional theory.

The stability of the studied [M(CO)₂X₂]₂ dimers increases as M varies along Ni, Pd, and Pt as the electron density of one monomer becomes more diffuse around M and more effectively interpenetrates towards the nucleus of M on the other monomer, resulting in a stronger electron–nuclei electrostatic attraction. Larger X ligands further increase the stability of [M(CO)₂X₂]₂ due to a greater dispersion interaction as X increases in size along Cl, Br, and I. The dispersion component in [X₂(CO)₂M]⋯[M(CO)₂X₂], which is almost insensitive to variations in the metal center, only dominates when M is small, and X is large.

The overlooked covalent component in [X₂(CO)₂M]⋯[M(CO)₂X₂] comprises the metal–metal donor–acceptor interaction of the nd_z²-type HOMOs of one monomer with (n + 1)s-type LUMOs of the other monomer as well as the ligand–ligand donor–acceptor interaction of the C=O π*-type LUMO on one monomer with the X lone-pair-type HOMO on the other monomer. The metal–metal donor–acceptor interaction dominates when M is large, resulting in a larger stabilizing nd_z²-HOMO–(n + 1)s-LUMO overlap. On the other hand, the ligand–ligand donor–acceptor interactions dominate when M is small and X becomes less electronegative. In this situation, the metal–metal donor–acceptor interaction is weakened, and the ligand–ligand donor–acceptor interaction is favored due to a smaller π*_CO-LUMO–LP_X-HOMO energy gap.

Data availability

The data that support the findings of this study are available in the ESI,† of this article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Netherlands Organization for Scientific Research (NWO) for its support. This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative.

References

1. (a) H. Schmidbaur and A. Schier, Angew. Chem., Int. Ed., 2015, 54, 746; (b) H. Schmidbaur and A. Schier, Organometallics, 2015, 34, 2048; (c) N. Zhou, C. Zou, S. Suo, Y. Liu, J. Lin, X. Zhang, M. Shi, X. Chang and W. Lu, Dalton Trans., 2023, 52, 550; (d) E. Priola, G. Mahmoudi, J. Andreo and A. Frontera, Chem. Commun., 2021, 57, 7268; (e) J. Lin, M. Xie, X. Zhang, Q. Gao, X. Chang, C. Zou and W. Lu, Chem. Commun., 2021, 57, 1627.
2. (a) J. Nitsch, F. Lacemon, A. Lorbach, A. Eichhorn, F. Cisnetti and A. Steffen, Chem. Commun., 2016, 52, 2932; (b) M. El Sayed Moussa, S. Evariste, H. L. Wong, L. Le Bras, C. Roiland, L. Le Polles, B. Le Guennic, K. Costuas, V. W.-W. Yam and C. Lescop, Chem. Commun., 2016, 52, 11370; (c) Y. Zhang, J. Miao, J. Xiong, K. Li and C. Yang, Angew. Chem., Int. Ed., 2022, 61, e202113718; (d) Q. Hu, C. Zhang, X. Wu, G. Liang, L. Wang, X. Niu, Z. Wang, W.-D. Si, Y. Han, R. Huang, J. Xiao and D. Sun, Angew. Chem., Int. Ed., 2023, 62, e202217784; (e) R. Kobayashi, T. Yumura, H. Imoto and K. Naka, Chem. Commun., 2021, 57, 5382.
3. (a) E. Barreiro, J. S. Casas, M. D. Couce, A. Laguna, J. M. López-de-Luzuriaga, M. Monge, A. Sánchez, J. Sordo, J. M. Varela and E. M. V. A. López, Eur. J. Inorg. Chem., 2011, 1322; (b) E. Barreiro, J. S. Casas, M. D. Couce, A. Sánchez, A. Sánchez-González, J. Sordo, J. M. Varela and E. M. Vázquez López, J. Inorg. Biochem., 2010, 104, 551.
4. (a) P. K. Mehrotra and R. Hoffmann, Inorg. Chem., 1978, 17, 2187; (b) A. Dedieu and R. Hoffmann, J. Am. Chem. Soc., 1978, 100, 2074; (c) Y. Jiang, S. Alvarez and R. Hoffmann, Inorg. Chem., 1985, 24, 749.
5. M. B. Brands, J. Nitsch and C. Fonseca Guerra, Inorg. Chem., 2018, 57, 2603.
6. L. de Azevedo Santos, T. C. Ramalho, T. A. Hamlin and F. M. Bickelhaupt, Chem. – Eur. J., 2023, 29, e202203791.
7. (a) P. Pyykkö and Y. F. Zhao, Angew. Chem., Int. Ed. Engl., 1991, 30, 604; (b) J. Li and P. Pyykkö, Chem. Phys. Lett., 1992, 197, 586; (c) P. Pyykkö, J. Li and N. Runeberg, Chem. Phys. Lett., 1994, 218, 133; (d) P. Pyykkö, N. Runeberg and F. Mendizabal, Chem. – Eur. J., 1997, 3, 1451; (e) P. Pyykkö, Chem. Rev., 1997, 97, 597.
8. J.-P. Zhang, Y.-B. Wang, X.-C. Huang, Y.-Y. Lin and X.-M. Chen, Chem. – Eur. J., 2005, 11, 552.
9. Q. Wan, J. Yang, W.-P. To and C.-M. Che, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2019265118.
10. (a) AMS2020.101, SCM Theoretical Chemistry, Vrije Universiteit Amsterdam, The Netherlands, https://www.scm.com; (b) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931.
11. (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
12. (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
13. E. R. Johnson and A. D. Becke, J. Chem. Phys., 2005, 123, 024101.
14. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783.
15. E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142.
16. (a) P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Chem. Commun., 2021, 57, 5880; (b) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649.
17. (a) F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86; (b) T. A. Hamlin, P. Vermeeren, C. Fonseca Guerra and F. M. Bickelhaupt, in Complementary Bonding Analysis, ed. S. Grabowski, De Gruyter, Berlin, 2021, pp. 199–212.
18. (a) X. Sun, T. M. Soini, L. P. Wolters, W.-J. van Zeist, C. Fonseca Guerra, T. A. Hamlin and F. M. Bickelhaupt, PyFrag, Vrije Universiteit Amsterdam, The Netherlands, 2019; (b) X. Sun, T. M. Soini, J. Poater, T. A. Hamlin and F. M. Bickelhaupt, J. Comput. Chem., 2019, 40, 2227.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00250d

‡ L. A. S and T. W. contributed equally to this work.

---