Open Access Article
Open Access ArticleA computational study of the negative LiIn modified anode and its interaction with β-Li3PS4 solid–electrolyte for battery applications†
Naiara Leticia
Marana
 a,
Fabrizio
Silveri
ab,
Eduardo
de Oliveira Gomes
c,
Lorenzo
Donà
a,
Fabrizio
Silveri
ab,
Eduardo
de Oliveira Gomes
c,
Lorenzo
Donà
 a,
Maddalena
D'Amore
a,
Maddalena
D'Amore
 a,
Eleonora
Ascrizzi
a,
Eleonora
Ascrizzi
 a,
Mauro Francesco
Sgroi
a,
Lorenzo
Maschio
a,
Mauro Francesco
Sgroi
a,
Lorenzo
Maschio
 a and
Anna Maria
Ferrari
a and
Anna Maria
Ferrari
 *a
*a
aChemistry Department, University of Torino, via P.Giuria 5, 10125 Torino, Italy. E-mail: anna.ferrari@unito.it
bGemmate Technologies s.r.l., Buttigliera Alta, Torino 10090, Italy
cDepartment of Analytical and Physical Chemistry, Universitat Jaume I, 12071 Castelló, Spain
First published on 14th May 2024
Abstract
All-solid-state lithium batteries (ASSLBs) have sparked interest due to their far superior energy density compared to current commercial material, but the heightened reactivity of the negative Li electrode can compromise the long-term cyclability of the cell, calling for the introduction of passivating layers or alloy anodes. In this article, we aim to explain the outstanding stability of LiIn alloy-based anodes over extended cycling by comparing its bulk and interface properties to Li-metal. Using density functional theory, we conducted an in-depth analysis of the LiIn surfaces' formation and subsequent structural stability in interfaces with the solid electrolyte β-Li3PS4. Several LiIn facets are shown to possess sufficient structural stability, with the (110) surface being the most stable. The stable interfaces established with the β-Li3PS4(100) surface featured favorable adhesion energy, low strain energy, and little reconstruction. By comparing these interface properties with the bulk properties of Li-metal and LiIn, we highlighted the influence of the cohesion energy, Fermi energy level, and band position of the two materials in the long-term stability of their anodes under battery conditions.
1. Introduction
Lithium-ion batteries are quickly becoming the most widely used energy storage unit for a wide variety of applications, ranging from portable electronic devices to road transport.1 However, current commercial batteries make use of liquid electrolytes, which pose safety risks due to their thermal instability and high flammability. Lithium-ion batteries with solid electrolytes, or all-solid-state lithium batteries (ASSLBs), are gaining traction as a safer alternative, and much research is focused on their improvement.2,3 Most commonly, the anode of ASSLBs is composed of metallic lithium, which provides a high theoretical capacity to the battery, but can also chemically decompose the solid electrolyte due to its very low reducing potential (around −3.04 V vs the standard hydrogen electrode), causing the formation of dendrites and secondary interface compounds.4In our previous ASSLBs computational investigations,5,6 we performed a detailed analysis of the Li3PS4 (LPS) solid electrolyte and its interface with Li-metal. These studies confirmed the promising potential of LPS as a solid electrolyte and provided insights into the morphology of electrolyte microparticles. However, a severe instability of the direct Li/LPS interface was observed. Li-metal induced a barrierless reduction of LPS at the interface, resulting in the formation of a mixed layer of Li3P and Li2S. Therefore, the direct use of Li-metal as an ASSLB anode imposes a buffer layer composed of a passivating material to stabilize the interface. This buffer layer aims to mitigate the instability observed at the Li/LPS interface, particularly the barrierless reduction that leads to the formation of by-product layers, but with the disadvantage of increasing resistance to lithium transport.
As a possible alternative, LixM alloys (in which M is a metal or semimetal) have been proposed as replacements for the pure Li-metal anode, with the objective of trading off a smaller operating electrochemical potential window for improved electrochemical stability under prolonged cycling.7 Among the variety of lithium alloys proposed for this application,8,9 the indium lithium (LiIn) system has sparked considerable interest in recent years due to a relatively wide electrochemical window and much-improved cycling stability.10 Due to the presence of a two-phase region in the LixIn diagram at 300 K for 0 < x < 1,11–13 the electrochemically active species of the LixIn system for all alloys with Li content below about 50% is Li1In, providing a stable 0.6 V vs. Li +/Li potential during charging.11 Even more importantly, the LiIn alloy has been linked with much-improved cycling stability than Li-metal, providing stable electrochemical performances for almost 1000 cycles under real battery conditions.14 This stability opens the way to the use of LiIn alloy anodes in commercial applications, but little characterization of the LiIn system at a molecular level has been reported.
To understand the physical and chemical properties of the LiIn alloy leading to its reported outstanding cycling capabilities, in this paper, we present an ab initio computational investigation of the bulk and surface properties of the material, followed by an analysis of its interface formed with the LPS solid electrolyte. Although the models outlined in this work describe the LiIn/LPS interfaces in “as-synthesized” conditions – i.e. without explicitly accounting for the operative conditions of the battery – we were still able to extract qualitative data on the stability of the interfaces through the comparison of characteristics and interface chemistry of LiIn with our previous results on the Li-metal anode, providing insight into the origin of the outstanding electrochemical performances reported for the alloy.
2. Computational approach
The simulations were conducted by applying the density functional theory (DFT) with PBE0 hybrid functional15,16 and all-electron basis sets 6-1117 contracted to [1s,2sp], 8-6311-1 contracted to [1s,4sp,1d],18 8-521-1 to [1s,3sp,1d],19 and 9-763111-63120 to [1s,6sp,3d], for Li, S, P, and In atoms, respectively. Such combination of functional and basis sets for Li, S, and P provided accurate results in our previous works on similar systems;5,6 In basis set has been successfully used for In alloys and In sulfide studies.20–22 All the calculations were performed using the most recent version of the CRYSTAL program.23 To better estimate noncovalent interactions involved in the interface formation, energy estimates have been performed by using Minnesota hybrid functional (MN15)24 by computing single-point energy calculations on the PBE0 optimized structures. In addition, energy estimates have been also performed by using the meta-GGA r2SCAN functional, recently proved to be safe and robust and recommended for general materials discovery.25The five thresholds used to control the accuracy of the truncation criteria for the bi-electronic integrals were [7, 7, 7, 7, 14]. The shrinking factor in reciprocal space and for a denser k-point net were set to 12 and 24, respectively, for the surface simulations, and 6 and 12, for the interfaces, which correspond to 49 and 20 independent k-points in the irreducible part of the Brillouin zone for the surfaces and interfaces, respectively. For metallic systems, the Fermi Dirac smearing procedure was adopted with a value of 0.01 Hartree in order to facilitate SCF convergence. The basis set superposition error (BSSE) was estimated a posteriori, by applying the standard counterpoise method.26
In the CRYSTAL code surfaces are periodic slab models with two infinite dimensions (x and y) and a finite thickness along the z direction. LiIn surfaces were optimized keeping the lattice parameter fixed at bulk values and the same procedure was adopted for the heterostructure optimization.
The structural stability of the surfaces was evaluated according to the surface energy (Esurf), calculated as:
 | (1) |
The cohesive energy (Ecoh) was used to evaluate the energetic cost for each atom to detach from the corresponding bulk structure and the LiIn bulk. Ecoh (per atom in the unit cell) was calculated as:
| Ecoh = EbulkLiIn − n(EatomLi + EatomIn) | (2) |
The LPS/LiIn interfaces were modeled taking into account the most stable (100)LPS5 surface, and the LiIn surfaces. The structural stability of these interfaces was estimated by considering the corresponding adhesion energy (per surface unit), Eadh, computed as:
 | (3) |
 | (4) |
During the optimization of the interface, 4–5 layers of the LiIn substrates have been kept fixed at the bulk values. The same reference has been used for ELiIn in eqn (3).
The work function (Φ), was computed, as routinely done, as the energy of an electron at infinity minus the Fermi energy, E(∞) − EF. However, there are some considerations to take into account when performing the work function calculation with the CRYSTAL code. Firstly, calculating E(∞) requires computing the electrostatic potential in a vacuum, V(∞). When employing Gaussian-type orbitals, this process becomes highly dependent on the chosen basis set, as it would require very diffuse exponents, leading to numerical instability. To overcome this issue, two layers of ghost sp orbital functions (αsp = 0.1) were added above and below each structure at a distance of 2.0 Å along the z-axis, following the procedure outlined in ref. 27.
In addition, for slab models, the CRYSTAL code automatically sets the electrostatic potential V in such a way that:27
| V(∞) = −V(−∞) | (5) |
Following the work of Trasatti29 and its many applications to the ab initio formalism, it is possible to convert work function values into electrochemical potentials using the relationship:
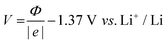 | (6) |
3. Results and discussion
3.1 LiIn surfaces
The LiIn bulk structure was obtained from the cubic indium bulk structure (space group Im3m) and had 50% of its atoms substituted by Li atoms, forming the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 LiIn structure. Geometry optimization led to a lattice parameter of 6.74 Å, with Li–In bond distances of 2.87 Å, which is in good agreement with experimental and computational results available in the literature.12,30,31
1 LiIn structure. Geometry optimization led to a lattice parameter of 6.74 Å, with Li–In bond distances of 2.87 Å, which is in good agreement with experimental and computational results available in the literature.12,30,31
LiIn(001), (110), (111), and (112) surfaces were modeled by considering slabs of increasing thickness (from 6 to 24 layers). The resulting structures were characterized according to their Li–In bond length (both in the center and on the uppermost layer of the slab) and their surface energy. Results are reported in Table 1 for two slabs of different z-thickness for each surface, alongside those for similar Li-metal slabs for comparison. 12-layer slabs for each LiIn surface are also represented in Fig. 1.
| LiIn | n layer | n Li–In | Li–In | Li–Inouter | z-thickness | E surf | E F |
|---|---|---|---|---|---|---|---|
| (001) | 6 | 3 | 2.91 | 2.87 | 8.63 | 56.09 | −3.40 |
| (001) | 12 | 6 | 2.92 | 2.87 | 18.45 | 57.77 | −3.37 |
| (110) | 4 | 4 | 2.97 | 2.97 | 8.46 | 43.20 | −3.59 |
| (110) | 8 | 8 | 2.95 | 2.97 | 18.18 | 45.15 | −3.69 |
| (111) | 8 | 4 | 2.89 | 2.86 | 6.74 | 55.49 | −3.41 |
| (111) | 20 | 10 | 2.89 | 2.86 | 18.27 | 55.01 | −3.43 |
| (112) | 8 | 8 | 2.87 | 2.90 | 9.01 | 53.53 | −3.81 |
| (112) | 14 | 14 | 2.88 | 2.89 | 17.22 | 51.34 | −3.83 |
| Li | n layer | n Li–Li | Li–Li | Li–Liouter | z-thickness | E surf | E F |
|---|---|---|---|---|---|---|---|
| (001) | 6 | 6 | 2.99 | 3.03 | 11.20 | 29.16 | −2.99 |
| (110) | 6 | 6 | 3.01 | 2.88 | 11.94 | 32.65 | −2.93 |
| (111) | 14 | 14 | 2.99 | 2.89 | 12.94 | 34.23 | −2.47 |
As can be seen in Fig. 1, the (001) and (111) surfaces are stoichiometric but not symmetrical, and the relative surface energies are an average of the two terminations. The optimized LiIn surfaces have Li–In bond length values close to that of the bulk structure (2.87 Å), mainly for the (111) and (112) surfaces. For all surfaces, Li atoms on the uppermost layer tend to be slightly displaced upwards during optimization, placing themselves above the respective In atoms along the z-direction. This behavior is particularly evident on the (110) surface where, after optimization, the Li–In bonds of the uppermost layer are elongated by ∼0.10 Å with respect to bulk LiIn and the other surfaces. Following this relatively larger reconstruction, the (110) surface has the lowest Esurf, which indicates that it is the most structurally stable. However, the difference with the Esurf of the other three facets is small, less than 15 meV Å−2, indicating that all LiIn surfaces are structurally stable and could be experimentally relevant.
As expected, all the surfaces kept the metallic behavior of LiIn, and the projected density of states (PDOS, reported in Fig. S1, ESI†) shows that Li and In atoms do not exhibit any significant difference, presenting almost the same behavior along all of the energy range, which suggests that the atoms are strongly bonded. Moreover, states close to the Fermi level are almost equally distributed between In and Li.
In order to build the interface systems, 4–5 layers of the LiIn surfaces were fixed to represent the bulk, to reduce the vertical size needed for the slab relaxation. However, the (001) surface, for which no coincidence cell with LPS of tractable size could be found, is not included in the following discussion.
According to Goodenough and co-worker,32,33 a way to analyze and predict the stability of a solid electrolyte against an anode is by verifying the alignment of the energy levels of the electrolyte conduction (CB) and the valence bands (VB) with the chemical potential of the anode (the Fermi level): a chemical potential of the anode above the electrolyte LUMO reduces the electrolyte.
Furthermore, the prediction of interfacial stability can also be analyzed through the work function of the metallic surfaces, and the corresponding electrode potentials, predicted through the Trasatti formula reported in eqn (6). Similar results are obtained for all these three descriptors, consistently predicting higher stability for the symmetric and In-terminated slabs, with respect to both the LiIn (111)–Li surface and Li-metal surfaces. The energy differences ΔE for these four surfaces are schematically represented in Fig. 3(a)–(d). When compared to ΔE values for Li/LPS interfaces, with a corresponding value of about 0.9 eV,6 this descriptor suggests that a higher thermodynamic barrier to LPS reduction is present in LiIn surfaces, though this effect is far less present when the outermost layer of the LiIn surface consists of Li atoms.
Table S3 (ESI†) reports Φ and V values for LiIn and Li surfaces. LiIn(110), (112), and (111)-In have computed Φ values of 3.80 eV, 3.71 eV, and 3.91 eV respectively, contrasting with the value of 2.80 eV for LiIn(111)–Li, and a 2.47–2.99 eV range for Li slabs. This different behavior of (111)-Li surface is more apparent by considering the electrode potential. Although the average value computed for all the surfaces is 0.53 V vs. Li+/Li, very close to the experimental value (0.6 V vs. Li+/Li,11), the electrode potential of (110), (112) and (111)-In is about 2.3 V significant different from the (111)-Li case whose value, 1.43 V is very close the corresponding average value computed for pure Li surfaces (1.4 V).
Collectively, these results predict a lower reducing power for the LiIn alloy with respect to Li-metal when the (110), (112), and (111)-In facets are considered, and a strong effect of Li-termination of the electronic properties of the (111)-Li surface. This discrepancy is probably caused by the presence of a topmost layer of pure Li atoms, which affects the position of its Φ value. Its influence on the reactivity of the surface, however, is unclear. In addition, the analysis of the valence and conduction band energy levels (HOMO and LUMO), as well as the Fermi energy of the separated materials are not sufficient to describe the stability of the interface in the face of redox reactions or to predict the potential electrochemical reaction, as discussed by Peljo and Girault.34 Therefore, the stability of the interface can only be investigated in more detail through the construction of explicit interface models.
3.2 LiIn/LPS interfaces
The construction of heterostructures between different materials must satisfy two important requirements. The first concerns chemical compatibility and requires a certain degree of pseudomorphicity with the formation of new chemical bonds at the interface that can stabilize the structure. The second is a mechanical issue that concerns the match between the lattice parameters of the substrate, fixed at the values of the bulk (LiIn in this case) and those of the overlayer (LPS); if the difference is too large, the mismatch may generate enough strain to destabilize the structure. In this regard, it is necessary to identify a coincidence cell between the two components that maximizes mechanical compatibility, minimizes strain energy, and can at the same time guarantee a good chemical adhesion.Here we want to combine the most stable termination of LPS, the (100) surface, with the previously investigated surfaces of LiIn. We found three matches that satisfy the requirements listed above and nominally the combination between LPS with (110)LiIn, to form the (110)LiIn/(100)LPS heterostructure; with (111)LiIn to form (111)-Li LiIn/(100)LPS and (111)-In LiIn/(100)LPS, because of the two terminations of the (111)LiIn surface; and with (112)LiIn to give the (112)LiIn/(100)LPS interface. Details on the coincidence cells selected for each heterostructure and related mismatch are reported in Table S1 of ESI.† From Table S1 (ESI†) we note that excluding the (110)LiIn/(100)LPS structure which presents a significant mismatch along the lattice parameters a and b (−5.57% and −15.59% for a and b, respectively), in all other cases the mismatch is almost negligible, in that, it does not exceed 6% along both the lattice parameters of the coincidence cell.
The four optimized interfaces are reported in Fig. 2 and their main energetic and electronic properties are in Table 2. Inspection of the figure shows the structural integrity of the two sub-units: appreciable deformations of the structures are observed only near the interface mainly due to the formation of Li–In bonds, with average bond length of ∼2.96 Å, very close to the value for LiIn bulk (see Table 1), and Li–S bonds, with average length of ∼2.43 Å, again very close to the value found in LPS, 2.41–2.49 Å.5
 | ||
| Fig. 2 Optimized interfaces (a) (110)LiIn/(100)LPS, (b) (112)LiIn/(100)LPS, (c) (111)-In LiIn/(100)LPS, and (d) (111)-Li LiIn/(100)LPS. | ||
 | ||
| Fig. 3 Band aligment for (a)–(d) LPS and LiIn isolated surfaces and (e)–(h) LPS/LiIn interfaces. The band alignment was made according to the zero energy level assigned by the CRYSTAL code. | ||
| Functional | LiIn surface | E adh | E strain | E BSSE | E cadh | E F | CT | Φ LPS/LiIn(ΔΦad) |
|---|---|---|---|---|---|---|---|---|
| PBE0 | (110) | −22.94 | +17.31 | +10.84 | −12.09 | −3.87 | 6.16 | 3.85 (0.05) |
| PBE0 | (112) | −32.04 | +4.58 | +14.12 | −17.91 | −3.78 | 10.01 | 3.81 (0.10) |
| PBE0 | (111)-In | −33.58 | +0.03 | +16.59 | −16.99 | −3.58 | 5.65 | 3.88 (−0.03) |
| PBE0 | (111)-Li | −28.04 | +0.03 | +14.11 | −13.91 | −3.83 | 3.51 | 3.60 (0.80) |
Analysis of the PDOS reported in Fig. S4 (ESI†) confirms this behavior. In fact, it is observed that the valence band and the conduction band are substantially unchanged in isolated LPS and in the heterostructure. Furthermore, in the valence band, in the energy region between −6 and −9 eV, the formation of new bonds involving sulfur, indium, and lithium can be appreciated.
E cadh offer insights into the attractive forces between LiIn and (100)LPS surfaces. Using the PBE0 density functional, the (112) surfaces exhibit relatively stronger adhesion energy, −17.91 meV Å−2, followed by (111)-In with a Ecadh value of −16.99 meV Å−2. In comparison, the (111)-Li and 110 surfaces show a slightly weaker adhesion, −13.91 and −12.09 meV Å−2, respectively. Ecadh computed at the MN15//PBE0 and r2SCAN levels follow the same trend as PBE0 values; r2SCAN values are quite close to PBE0 ones (they range from −15 to −23 meV Å−2), MN15 energy values are significantly larger (they range from −23 to −30 meV Å−2) even if the order of stability of the heterostructures computed by the three functionals is the same, compare Tables S3 and S5 (ESI†); thus, in the attempt to describe noncovalent interactions, MN15 functional may offer a more accurate description of energetics, particularly in scenarios where these contributions play a crucial role, such as in interfaces involving metals and notably large atoms like In. Correlating charge transfer (CT) with adhesion energies reveals that higher CT values align with more negative Ecadh values, which is particularly evident in the (112) surface, which exhibits both higher adhesion and CT. This suggests a correlation between charge transfer, interface bond formation, and the strength of adhesion, underscoring the influence of charge redistribution (bond polarization) on the attractive forces between the surfaces.
Finally, considering the Estrain, that is the energy cost for the structural deformation required from LPS to match the lattice parameters of the substrate, we can notice a relatively small strain for the (112) interface Estrain = +4.58 meV Å−2 and actually negligible strain for (111)-In and (111)-Li with Estrain values of +0.03 meV Å−2. Only LPS in the (110) heterostructure undergoes a significant expansion mainly along the b lattice parameter (see Table S1, ESI†) with a significant Estrain value of +17.31 meV Å−2. This high value of Estrain does not necessarily indicate an instability of the interface as it has been reported several times in the literature35 that the intrinsic value of the interface energy is dominated by the chemical compatibility between the components rather than by mechanical issues. However, for a correct description of the heterostructure, the mechanical stress cannot be neglected, and the high Estrain value obtained for the (110)LiIn/(100)LPS interface indicates that the junction is very far from ideality.
Thus, the adhesion energies presented in Table 2 for the LiIn/LPS interfaces all indicate a good adhesion between LiIn and LPS at the anode/solid–electrolyte interface, despite the absence of any major reconstruction of the interfaces. When compared to our previous investigation of the Li-metal/LPS interface,6 which presents adhesion energy over one order of magnitude larger, an interesting correlation can be drawn with the reported experimental characteristics of the two anodes and their computed bulk properties. The very large Eadh of the Li-metal/LPS interface is due to the reduction of P5+ to P−3, which causes a dramatic reconstruction of the interface, creating a mixed layer of Li2S and Li3P between the two surfaces, which contrasts with the relatively minor rearrangement presented here for all LiIn/LPS interfaces.
This result is consistent with our previous evaluation of work function and band alignment data (Fig. 3), which predicted the stability of the LiIn/LPS interfaces. Furthermore, we can now observe that the (111)-Li surface presents similar adhesion properties than all other LiIn surfaces, despite the aforementioned electronic properties. Even though the outermost layer of Li atoms on the LiIn surface is partially extracted towards LPS, consistently with the lower work function and ΔE calculated for that model, the structural change is far less dramatic compared to that found on Li/LPS interfaces: no reduction of the solid electrolyte is identified and the movement of Li atoms is limited to 0.67 Å over the original LiIn surface, without the formation of Li2S and Li3P interphase layers. This is likely due to the lack of a pure Li reservoir in the metallic slab and the far higher cohesion energy found for the LiIn alloy compared to Li metal (see Table S2, ESI†): the stronger Li–In bonds prevent the partial dissolution of the LiIn alloy even with more reductant potentials, and the lower reductant power of the alloy, calculated in terms of work function and ΔE, helps protect the surface.
Furthermore, the change in work function upon interface formation (ΔΦad, see Table 2) also suggests higher stability for all LiIn surfaces; for the (110) and (112) surfaces, the work function increases slightly; for the (111)-In, the change in work function is negligible; but for the less stable (111)-Li surface, the formation of the interface and its reconstruction lead to a much deeper Fermi energy (as highlighted in Fig. 3h), increasing its work function and ΔE (see Table 2 and Fig. 3).
Following these results, it is possible to rationalize the outstanding results reported for the LiIn anode cyclability in terms of the stability of the LiIn alloy: its higher cohesion compared to Li-metal could prevent undesirable mobility of Li atoms at the interface, while its deeper Fermi level with respect to LPS conduction band provide increased stability towards LPS reduction, preventing Li3P formation. Taken together, these physical characteristics of LiIn bulk and surface structures provide a rationale for both the higher stability of LiIn/LPS presented in this paper and the improved cyclability of LiIn-based anodes reported by previous experimental papers.
It is important to note, however, that these results have been obtained at 0 K, with no applied voltage, and without the extensive sampling of the phase possible with AIMD or AIMC simulations: these results are crucial in rationalizing the experimentally proven LiIn stability when compared to pure Li alloys, but are not sufficient to predict the stability of LiIn anodes by themselves, an incredibly complex task that we reserve for future investigations.
4. Conclusions
In this work, we have studied computationally, within a DFT approach, the LiIn alloy (with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Li
1 Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) In ratio) to investigate the physical and chemical properties of LiIn as a negative electrode replacement for metallic Li in solid-state batteries. Four low-index LiIn surfaces, (110), (112), (111), and (001), have been carefully characterized and have been found to be of comparable stability, since corresponding Esurf differs by less than 15 meV Å−2. LiIn anode has been coupled with the LPS solid–electrolyte identifying four feasible heterostructures: (112)LiIn/(100)LPS, (111)-In LiIn/(100)LPS, (111)-Li LiIn/(100)LPS and (110)-LiIn/(100)LPS. The calculated PBE0 Ecadh for LPS/LiIn heterojunctions are in the 13–18 meV Å−2 range, whereas MN15 values, which more accurately consider non-covalent interactions, are predicted to be in the 23–30 meV Å−2 range, confirming the importance of those interactions are important heterojunctions involving metals. However, regardless of the applied functional, the Ecadh trend is the same and all investigated LiIn/LPS junctions are chemically stable and characterized by only minor rearrangements involving the interface atomic layers, which stimulate the formation of new Li–S, Li–In, and In–S bonds. This behavior is in stark contrast to that reported for Li-metal/LPS heterostructures, where the contact with Li promotes the reduction of P5+ to P−3, causing the decomposition of the interface and the formation of a mixed layer of Li2S and Li3P. The remarkable difference in the behavior between Li and LiIn anodes can be correlated to two main reasons: (i) a deeper Fermi energy for the LiIn alloy with respect to Li (computed as 0.7 eV, consistent with the value of 0.6 V reported experimentally for the electrochemical potential difference), inhibiting electron transfer to the conduction band of Li3PS4 and preventing electrolyte reduction; (ii) strengthened cohesive energy in LiIn alloy with respect to Li metal, which further stabilizes the electrode material; (iii) the lack of a pure Li reservoir at the interface between metal and solid electrolyte. By considering all these three phenomena it is possible to qualitatively correlate the bulk and surface properties of LiIn with its improved performance as a battery anode.
In ratio) to investigate the physical and chemical properties of LiIn as a negative electrode replacement for metallic Li in solid-state batteries. Four low-index LiIn surfaces, (110), (112), (111), and (001), have been carefully characterized and have been found to be of comparable stability, since corresponding Esurf differs by less than 15 meV Å−2. LiIn anode has been coupled with the LPS solid–electrolyte identifying four feasible heterostructures: (112)LiIn/(100)LPS, (111)-In LiIn/(100)LPS, (111)-Li LiIn/(100)LPS and (110)-LiIn/(100)LPS. The calculated PBE0 Ecadh for LPS/LiIn heterojunctions are in the 13–18 meV Å−2 range, whereas MN15 values, which more accurately consider non-covalent interactions, are predicted to be in the 23–30 meV Å−2 range, confirming the importance of those interactions are important heterojunctions involving metals. However, regardless of the applied functional, the Ecadh trend is the same and all investigated LiIn/LPS junctions are chemically stable and characterized by only minor rearrangements involving the interface atomic layers, which stimulate the formation of new Li–S, Li–In, and In–S bonds. This behavior is in stark contrast to that reported for Li-metal/LPS heterostructures, where the contact with Li promotes the reduction of P5+ to P−3, causing the decomposition of the interface and the formation of a mixed layer of Li2S and Li3P. The remarkable difference in the behavior between Li and LiIn anodes can be correlated to two main reasons: (i) a deeper Fermi energy for the LiIn alloy with respect to Li (computed as 0.7 eV, consistent with the value of 0.6 V reported experimentally for the electrochemical potential difference), inhibiting electron transfer to the conduction band of Li3PS4 and preventing electrolyte reduction; (ii) strengthened cohesive energy in LiIn alloy with respect to Li metal, which further stabilizes the electrode material; (iii) the lack of a pure Li reservoir at the interface between metal and solid electrolyte. By considering all these three phenomena it is possible to qualitatively correlate the bulk and surface properties of LiIn with its improved performance as a battery anode.
Author contributions
Conceptualization, N. L. Marana, A. M. Ferrari, and F. Silveri; methodology, N. L. Marana and A. M. Ferrari; software, L. Donà; validation, N. L. Marana, A. M. Ferrari, and F. Silveri; formal analysis, N. L. Marana and A. M. Ferrari; investigation, N. L. Marana and A. M. Ferrari; data curation, N. L. Marana; writing—original draft preparation, N. L. Marana, A. M. Ferrari, and F. Silveri; writing—review and editing, E. Oliveira, L. Donà, M. D’Amore, E. Ascrizzi, M. Sgroi, L. Maschio; supervision, A. M. Ferrari; project administration, A. M. Ferrari; funding acquisition, L. Maschio.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support by the MODALIS2 project, grant agreement no. 875193 of the European Union Horizon 2020 research and innovation program, is gratefully acknowledged. We acknowledge support from Project CH4.0 under the MUR program “Dipartimenti di Eccellenza 2023–2027” (CUP: D13C22003520001). The access to the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk) is also is gratefully acknowledged.References
- J. Xu, X. Cai, S. Cai, Y. Shao, C. Hu, S. Lu and S. Ding, High-Energy Lithium-Ion Batteries: Recent Progress and a Promising Future in Applications, Energy Environ. Mater., 2023, 6, e12450 CrossRef CAS.
- C. Bubulinca, N. E. Kazantseva, V. Pechancova, N. Joseph, H. Fei, M. Venher, A. Ivanichenko and P. Saha, Development of All-Solid-State Li-Ion Batteries: From Key Technical Areas to Commercial Use, Batteries, 2023, 9, 157 CrossRef CAS.
- M. Du, K. Liao, Q. Lu and Z. Shao, Recent advances in the interface engineering of solid-state Li-ion batteries with artificial buffer layers: challenges, materials, construction, and characterization, Energy Environ. Sci., 2019, 12, 1780 RSC.
- X.-B. Cheng, R. Zhang, C.-Z. Zhao, F. Wei, J.-G. Zhang, Q. Zhang, X. B. Cheng, R. Zhang, C. Z. Zhao, F. Wei, Q. Zhang and J.-G. Zhang, A Review of Solid Electrolyte Interphases on Lithium Metal Anode, Adv. Sci., 2016, 3, 1500213 CrossRef PubMed.
- N. L. Marana, M. F. Sgroi, L. Maschio, A. M. Ferrari, M. D’Amore and S. Casassa, Computational Characterization of β-Li3PS4 Solid Electrolyte: From Bulk and Surfaces to Nanocrystals, Nanomaterials, 2022, 12, 2795 CrossRef CAS PubMed.
- N. L. Marana, S. Casassa, M. F. Sgroi, L. Maschio, F. Silveri, M. D’Amore and A. M. Ferrari, Stability and Formation of the Li3PS4/Li, Li3PS4/Li2S, and Li2S/Li Interfaces: A Theoretical Study, Langmuir, 2023, 39, 18797 CrossRef CAS PubMed.
- Y. Lu, C. Z. Zhao, R. Zhang, H. Yuan, L. P. Hou, Z. H. Fu, X. Chen, J. Q. Huang and Q. Zhang, The carrier transition from Li atoms to Li vacancies in solid-state lithium alloy anodes, Sci. Adv., 2021, 7, eabi5520 CrossRef CAS PubMed.
- C. Yang, H. Xie, W. Ping, K. Fu, B. Liu, J. Rao, J. Dai, C. Wang, G. Pastel, L. Hu, C. Yang, H. Xie, W. Ping, K. Fu, B. Liu, J. Dai, C. Wang, G. Pastel, L. Hu and J. Rao, An Electron/Ion Dual-Conductive Alloy Framework for High-Rate and High-Capacity Solid-State Lithium-Metal Batteries, Adv. Mater., 2019, 31, 1804815 CrossRef PubMed.
- Y. Huang, B. Shao and F. Han, Li alloy anodes for high-rate and high-areal-capacity solid-state batteries, J. Mater. Chem. A, 2022, 10, 12350–12358 RSC.
- Y. Chen, X. Xu, L. Gao, G. Yu, O. O. Kapitanova, S. Xiong, V. S. Volkov, Z. Song and Y. Liu, Two Birds with One Stone: Using Indium Oxide Surficial Modification to Tune Inner Helmholtz Plane and Regulate Nucleation for Dendrite-free Lithium Anode, Small Methods, 2022, 6, 2200113 CrossRef CAS PubMed.
- A. L. Santhosha, L. Medenbach, J. R. Buchheim and P. Adelhelm, The Indium–Lithium Electrode in Solid-State Lithium-Ion Batteries: Phase Formation, Redox Potentials, and Interface Stability, Batteries Supercaps, 2019, 2, 524–529 CrossRef CAS.
- W. A. Alexander, L. D. Calvert, R. H. Gamble and K. Schinzel, The lithium–indium system, Can. J. Chem., 2011, 54, 1052–1060, DOI:10.1139/v76-150.
- X. Zhou, F. Zhang, S. Liu, Y. Du and B. Jin, Phase equilibria and thermodynamic investigation of the In–Li system, Calphad, 2020, 70, 101779 CrossRef CAS.
- S. Luo, Z. Wang, X. Li, X. Liu, H. Wang, W. Ma, L. Zhang, L. Zhu and X. Zhang, Growth of lithium-indium dendrites in all-solid-state lithium-based batteries with sulfide electrolytes, Nat. Commun., 2021, 12, 1–10 CrossRef PubMed.
- J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef PubMed.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- L. Ojamäe, K. Hermansson, C. Pisani, M. Causà and C. Roetti, Structural, vibrational and electronic properties of a crystalline hydrate from ab initio periodic Hartree–Fock calculations, Acta Crystallogr., Sect. B, 1994, 50, 268–279 CrossRef.
- A. Lichanot, E. Aprà and R. Dovesi, Quantum Mechnical Hartree-Fock Study of the Elastic Properties of Li2S and Na2S, Phys. Status Solidi, 1993, 177, 157–163 CrossRef CAS.
- C. M. Zicovich-Wilson, A. Bert, C. Roetti, R. Dovesi and V. R. Saunders, Characterization of the electronic structure of crystalline compounds through their localized Wannier functions, J. Chem. Phys., 2001, 116, 1120 CrossRef.
- J. Rothballer, F. Bachhuber, S. M. Rommel, T. Söhnel and R. Weihrich, Origin and effect of In–Sn ordering in InSnCo3S2: a neutron diffraction and DFT study, RSC Adv., 2014, 4, 42183–42189 RSC.
- J. Rothballer, F. Bachhuber, F. Pielnhofer, F. M. Schappacher, R. Pöttgen and R. Weihrich, Effect of In–Sn Ordering on Semiconducting Properties in InSnCo3S2 – X-ray, 119Sn Mößbauer Spectroscopy, and DFT Studies, Eur. J. Inorg. Chem., 2013, 248–255 CrossRef CAS.
- F. Pielnhofer, J. Rothballer, P. Peter, W. Yan, F. M. Schappacher, R. Pöttgen and R. Weihrich, Half Antiperovskites VI: On the Substitution Effects in Shandites InxSn2–xCo3S2, Z. Anorg. Allg. Chem., 2014, 640, 286–294 CrossRef CAS.
- A. Erba, J. Desmarais, S. Casassa, B. Civalleri, L. Donà, I. Bush, B. Searle, L. Maschio, L. E. Daga, A. Cossard, C. Ribaldone, E. Ascrizzi, N. Marana, J.-P. Flament and B. Kirtman, CRYSTAL23: A Program for Computational Solid State Physics and Chemistry, J. Chem. Theory Comput., 2023, 19, 6891 CrossRef CAS PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions, Chem. Sci., 2016, 7, 5032–5051 RSC.
- M. Kothakonda, A. D. Kaplan, E. B. Isaacs, C. J. Bartel, J. W. Furness, J. Ning, C. Wolverton, J. P. Perdew and J. Sun, Testing the r2SCAN Density Functional for the Thermodynamic Stability of Solids with and without a van der Waals Correction, ACS Mater. Au, 2023, 3, 102–111 CrossRef CAS PubMed.
- F. B. Van Duijneveldt, J. G. C. M. Van Duijneveldt-Van De Rijdt and J. H. Van Lenthe, State of the Art in Counterpoise Theory, 1994, vol. 94 Search PubMed.
- K. Doll, Calculation of the work function with a local basis set, Surf. Sci., 2006, 600, L321–L325 CrossRef CAS.
- G. Heimel, L. Romaner, J. L. Brédas and E. Zojer, Interface energetics and level alignment at covalent metal-molecule junctions: π-conjugated thiols on gold, Phys. Rev. Lett., 2006, 96, 196806 CrossRef PubMed.
- S. Trasatti, The concept of absolute electrode potential an attempt at a calculation, J. Electroanal. Chem., 1974, 52, 313–329 CrossRef CAS.
- G. J. Lamprecht and P. Crowther, The systems sodium-indium and lithium-indium, J. Inorg. Nucl. Chem., 1969, 31, 925–931 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The materials project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 11002 CrossRef.
- J. B. Goodenough and K. S. Park, The Li-ion rechargeable battery: A perspective, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- K. Kim and D. J. Siegel, Predicting Wettability and the Electrochemical Window of Lithium-Metal/Solid Electrolyte Interfaces, ACS Appl. Mater. Interfaces, 2019, 11, 39940–39950 CrossRef CAS PubMed.
- P. Peljo and H. H. Girault, Electrochemical potential window of battery electrolytes: the HOMO–LUMO misconception, Energy Environ. Sci., 2018, 11, 2306–2309 RSC.
- A. Mahmoud, L. Maschio, M. F. Sgroi, D. Pullini and A. M. Ferrari, Ab Initio Simulation of ZnO/LaMnO3 Heterojunctions: Insights into Their Structural and Electronic Properties, J. Phys. Chem. C, 2017, 121, 25333–25341 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Projected density of states for the LiIn surfaces; LiIn and LPS surfaces and interfaces cell parameters and mismatch; and cohesive energies for Li and In atoms. See DOI: https://doi.org/10.1039/d4cp00102h |
| This journal is © the Owner Societies 2024 |