Mixture of hydrogen and methane under planetary interior conditions

Abstract

We employ first-principles molecular dynamics simulations to provide equation-of-state data, pair distribution functions (PDFs), diffusion coefficients, and band gaps of a mixture of hydrogen and methane under planetary interior conditions as relevant for Uranus, Neptune, and similar icy exoplanets. We test the linear mixing approximation, which is fulfilled within a few percent for the chosen P–T conditions. Evaluation of the PDFs reveals that methane molecules dissociate into carbon clusters and free hydrogen atoms at temperatures greater than 3000 K. At high temperatures, the clusters are found to be short-lived. Furthermore, we calculate the electrical conductivity from which we derive the non-metal-to-metal transition region of the mixture. We also calculate the electrical conductivity along the P–T profile of Uranus [N. Nettelmann et al., Planet. Space Sci., 2013, 77, 143–151] and observe the transition of the mixture from a molecular to an atomic fluid as a function of the radius of the planet. The density and temperature ranges chosen in our study can be achieved using dynamic shock compression experiments and seek to aid such future experiments. Our work also provides a relevant data set for a better understanding of the interior, evolution, luminosity, and magnetic field of the ice giants in our solar system and beyond.

---

1 Introduction

Hydrogen and carbon, the most and fourth most abundant elements in the universe,¹ are fundamental building blocks of organic compounds and, thus, the very essence of life that we know today, encompassing an astounding array of molecules that have captivated the attention of scientists across various disciplines. From astrophysics to astrobiology and materials science to quantum physics, researchers have focused on these elemental mixtures, seeking a deeper understanding of our observable universe.

Hydrogen, the first element in the periodic table, exhibits a rich tapestry of physical phenomena such as a first-order liquid–liquid phase transition, a pressure-induced atomic solid, and quantum rotational phases, see ref. 2–9 Additionally, under high temperature and pressure conditions, hydrogen not only reacts with other materials but also can produce van der Waals compounds.^10–13

Methane (CH₄), a molecule consisting of an sp³-hybridized carbon atom surrounded by four hydrogen atoms, is very important for planetary physics as it is one of the major constituents of ice-giant planets like Uranus and Neptune.^14,15 Hydrocarbons are, e.g., the reason for the distinct bluish hue of these planets as they absorb red light and reflect blue light.¹⁶ Space missions like Cassini¹⁷ and New Horizon¹⁸ revealed huge lakes and seas of liquid hydrocarbons and mountains covered with frozen methane on Titan and Pluto, respectively.

Therefore, many studies investigated the behavior of hydrocarbons under pressure and temperature conditions relevant to planetary interiors. Interestingly, early gas gun-driven shock wave experiments on methane found evidence of diamond formation under pressure and temperature conditions as relevant for the interior of Uranus and Neptune.^19–21 Since then, numerous high-pressure experiments using diamond anvil cells (DACs) have investigated the formation of diamond from compressed methane and hydrocarbons.^21–26 Note that more complex mixtures containing hydrogen, carbon, nitrogen, and oxygen were also studied.^27–29 In particular, evidence for diamond formation under conditions typical for the deep interior of Uranus has been found in laser-driven shock compression experiments on plastics like polystyrene.^28,30–32

Molecular dynamics (MD) simulations combined with density functional theory (DFT) were used to calculate the equation of state (EOS) and analyze the dissociation, polymerization into carbon chains, and chemical bonding properties of methane.^33–37 Although there are various EOSs for a pure methane fluid and solid^34,38–40 and for the mixture of methane with other compounds,^41,42 such as water and ammonia, the mixture of CH₄ and H₂ under these conditions remains an area of ongoing research. For instance, the stability of methane–hydrogen solid compounds exceeding 160 GPa was studied by⁴³ using XRD, DAC, and DFT techniques, which resulted in different structures depending on the concentration of hydrogen. However, in the liquid region, the database is extremely sparse.

The P–T conditions under study are relevant not only for the interior of ice-giant planets such as Uranus and Neptune but also for industrial purposes^44–50 and inertial confinement fusion (ICF).^51,52 Accordingly, further investigation of the EOS of methane and hydrocarbons and subsequent analysis of their behavior under high P–T conditions are important for modeling the interior, evolution, and magnetic field of ice-giant planets.^14,53–56

Given these important applications, we have assessed the behavior of hydrocarbons and performed extensive DFT-MD simulations to determine the EOS. We analyze the EOS data and assess the question of whether the linear mixing approximation (LMA), often used to model giant planets,^57,58 is applicable to hydrogen and methane or not and found it valid within 4%. We further analyze our hydrocarbon simulations by calculating the pair distribution function (PDF), coordination number and self-diffusion coefficient using the velocity autocorrelation function. This analysis supports the formation of hydrocarbon polymers after dissociation of the methane molecules. Finally, we provide the electrical conductivity calculated using the Kubo–Greenwood formula^59,60 and the band gap of mixtures of hydrogen and methane over a wide range of different densities and pressures relevant to the interiors of giant planets.

Our paper is organized as follows: Section 2 summarizes the details of the DFT-MD simulations. Sections 3.1 and 3.2 provide EOS data and check the validity of the LMA. Structural changes are discussed in Section 3.3 using the self-diffusion coefficient, PDF and coordination number. Section 3.4 discusses the band gaps and our schema for calculating the electrical conductivity. Finally, a summary of our work is presented in Section 4.

2 Computational methods

We use the Vienna ab initio simulation package (VASP)^61–65 for the DFT-MD simulations and derive the relevant data for the mixture of CH₄ and H₂. Use of the Born–Oppenheimer approximation allows us to ignore any kind of coupling between the movement of electrons and of the nuclei. The nuclei then undergo classical motion in an effective potential generated by their mutual Coulomb interaction and the interaction with the electronic charge distribution calculated with the Hellman–Feynman theorem. This procedure involves a combination of DFT and classical MD at finite temperatures.^66–69 The electronic interactions are evaluated using DFT. We use classical MD simulations and the Verlet algorithm to propagate the nuclei in time. Projector augmented wave (PAW) potentials,^70,71 implemented in VASP as PAW PBE H h 06Feb2004 and PAW PBE C h 06Feb2004, and the Perdew–Burke–Ernzerhof (PBE)⁷² exchange–correlation functional were used. The temperature of the ions is controlled by the Nosé–Hoover thermostat with a Nosé-mass of 10 fs.^73,74 Similar simulation approaches had been applied very successfully to warm dense matter, see ref. 34, 41 and 75.

We used a cubic periodic simulation box containing 54 CH₄ and 54 H₂ molecules and a plane-wave energy cutoff of 1100 eV to calculate the EOS for hydrogen and methane mixtures. The EOS for pure hydrogen is calculated using 256 atoms and a plane-wave cutoff energy of 1200 eV. The Brillouin zone is evaluated using the Baldereschi mean value point (BMVP).⁷⁶ This simulation parameter led to results that converged better than 1% in pressure and 0.05 kJ g⁻¹ in specific internal energy. All MD simulations were run for at least 8–12 ps using a time step of 0.25 fs. Neglecting the first 4000 time steps of our simulation allowed us to calculate the thermodynamic averages of the equilibrated system. For pure methane, we used the EOS provided by Bethkenhagen et al.⁴¹

3 Results

3.1 Equation of state

The EOS data are obtained from thermodynamic properties such as pressure P, energy U, and temperature T by averaging over the entire simulation time after equilibration. We have studied a density–temperature grid bounded by 0.74 g cm⁻³ ≤ ρ ≤ 3.70 g cm⁻³ and 700 K ≤ T ≤ 16 000 K. It is important to note that as carbon atoms can undergo various hybridization states, the simulations have to start with the same configuration in order to avoid bias towards certain structures.

Fig. 1 shows the EOS along various isochores. A very smooth behavior is observed for both the thermal (top) and caloric EOSs (bottom). The pressure increases systematically with increasing temperature. A small plateau at T = 3000 K for ρ = 1.32 g cm⁻³ at about 83 GPa indicates the onset of dissociation of methane molecules; the pressure rises again with temperature afterwards. As density increases we observe a more pronounced drop in pressure. This behavior indicates the onset of a phase transition from a molecular to a polymeric fluid consistent with previous works.^34,77 This feature has a resemblance to the behavior of pure molecular hydrogen. DFT-MD simulations for dense fluid hydrogen show that dissociation of molecules can lead to a region with (∂P/∂T)_V < 0 as hydrogen atoms can be packed more efficiently than molecules at high densities.^7,78,79 It is essential to note that hydrogen molecules undergo a dissociation process at a lower pressure than methane, which leads the hydrogen atoms to contribute to the process of methane dissociation.

Fig. 1 Caloric (top) and thermal (bottom) EOSs of the mixture of H₂ and CH₄ along the isochores.

3.2 Testing the linear mixing approximation

Models for giant planets employ EOS data for different materials and mix them linearly at constant pressure and temperature based on the work of DeMarcus and Peebles.^57,58 The LMA allows the density to be extracted,(eqn 1)and the specific internal energy,where ρ_j, u_j, and ξ_j are the density, specific internal energy, and mass fraction, respectively, of individual components j of the mixture composed of N components. The validity of the LMA has been tested using Monte Carlo simulations^80,81 and later extended to DFT studies.^82,83

Although several mixing rules exist in the case of the H–He mixtures, the additive volume rule at constant pressure and temperature performed the best.⁸⁴ The LMA was tested for the dilute limit of ternary mixtures of H–He for gas giants⁸⁵ with high Z elements such as C, N, O, Si, and Fe, as well as for C₂H₃ as a mixture of carbon and hydrogen.⁸⁶ The icy mixtures have been studied before with DFT-MD, e.g., for binary and ternary mixtures of CH₄–H₂O–NH₃.⁴¹

We define the deviations in density and specific internal energy between the linear (LM) and real mixtures as,

Δρ(P,T) = ρ_LM(P,T)/ρ_real(P,T) − 1 (3)

and

Δu(P,T) = u_LM(P,T) − u_real(P,T) (4)

The EOS obtained for pure hydrogen, pure methane and the mixture was interpolated onto a P–T grid, to interpolate the pressure values along the isotherm we used Akima splines, and temperatures were interpolated linearly. The deviation in energy varies between −4 kJ g⁻¹ and 3 kJ g⁻¹ and 4% for the density (see Fig. 2). The region of large deviations signals the presence of different phases. For instance, in the case of binary mixtures of CH₄ with H₂O and NH₃ as studied by Bethkenhagen et al.,⁴¹ the maximum deviation in energy was observed to lie between −4 kJ g⁻¹ and 2 kJ g⁻¹, which was due to the formation of superionic phases in water and ammonia,^87–89 where the energy was released by forming these lattices. In our case, it is mostly atomic hydrogen and polymeric chains of carbon that lead to such deviations as the bonds formed by the carbon atom release energy.

Fig. 2 Deviations of internal energy (top) and densities (bottom) of the real 1 : 1 hydrogen and water mixture from the LMA. Black dots denote the underlying data for the real binary mixture of methane and hydrogen.

It should be noted that our density deviation always remains positive, V_REAL > V_LMA. This suggests that the constituents occupy a larger phase space as long as the system remains fluid throughout the entire P–T space studied here. Although carbon polymerizes into long chains, free hydrogen atoms occupy the phase space. In the study of Bethkenhagen et al.,⁴¹ some regions in P–T space were observed where the atoms are more closely packed occupying less volume due to the formation of superionic lattices of nitrogen and oxygen.

3.3 Structural analysis

We have determined self-diffusion coefficients shown in Fig. 3 and PDFs displayed in Fig. 4. The self-diffusion coefficients were calculated via the velocity autocorrelation function,where α is the species, v_i(τ) is the velocity autocorrelation function, and N_α is the particle number.

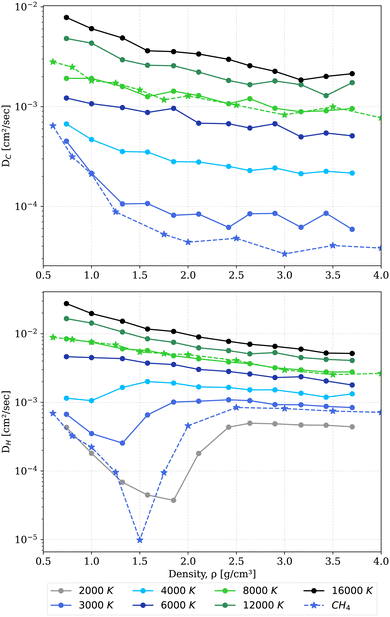Fig. 3 Diffusion coefficients of carbon (top) and hydrogen (bottom) in the mixture at temperatures between 2000 K and 16 000 K (color coded solid lines). Diffusion coefficients of carbon and hydrogen in pure methane⁴¹ (the star symbol with dotted lines).

Fig. 4 PDFs of the constituents in the hydrogen–methane 1 : 1 mixture at a constant density of 1.32 g cm⁻³ and temperatures of 2000, 3000, 4000, 6000 and 16 000 K. Left panel: Hydrogen–hydrogen interaction, middle panel: hydrogen–carbon interaction, and right panel: carbon–carbon interaction.

Diffusion coefficients of both species show a strong dependence on temperature and density, rising with increasing temperature. Interesting features, however, pop up with increasing density. The diffusion coefficients of hydrogen exhibit minima at 2000 K and 1.85 g cm⁻³, indicating the transition from a molecular to an atomic fluid. At a temperature of 3000 K the diffusion coefficient of hydrogen is shifted towards higher values compared to the diffusion coefficient of hydrogen in pure methane. This shift is attributed to the excess hydrogen and dissociation of methane giving rise to more hydrogen atoms in the box. The excess hydrogen also provides electrostatic repulsion to carbon atoms, making them more mobile and leading to a slightly higher carbon diffusion coefficient in the mixture. At higher temperature, due to thermal dissociation we do not see a huge difference between the diffusion coefficients of the mixture and of pure methane. The minima of the hydrogen diffusion coefficient shift to lower densities with increasing temperatures. This feature finally vanishes at 6000 K. The diffusion coefficients of carbon and hydrogen are almost constant at higher densities, as already obtained by Bethkenhagen et al.⁸⁷ for ammonia. Due to the formation of polymeric chains of carbon, it is difficult to calculate the diffusion coefficients with sufficient numerical accuracy. Especially, at high density and low temperatures for carbon, the thermal energy provided is not sufficient for the clusters to exhibit translational degrees of freedom. Therefore, coefficients smaller than 10⁻⁵ cm² s⁻¹ are considered to be zero.

To better understand the structural changes of the fluid with respect to temperature and density variations, we calculated PDFs. Exemplarily we show results for the 1.32 g cm⁻³ isochore for the temperature range considered here in Fig. 4. The system exhibits molecular properties at lower temperatures. The narrow peak of g_HC(r) occurs at an intermolecular distance of 1.09 Å under ambient conditions and the same for g_HH(r) where the peak occurs at 0.74 Å, followed by a minimum. Note that we see two peaks for the PDF of the hydrogen subsystem. The first maximum is due to the presence of hydrogen molecules and the second is due to hydrogen atoms in methane at 1.76 Å. Increasing temperatures results in a decrease in peak heights of the hydrogen–carbon and hydrogen–hydrogen PDFs. The peak of g_HH(r) is flattened as a consequence of the dissociation of hydrogen molecules and hydrogen from methane. For g_HC(r) the peak decreases to half of the value that it was at T = 2000 K. Higher temperatures result in a higher peak of g_CC(r) and a lower peak of g_HC(r) diminishes furthermore and at T = 4000 K a new peak of g_CC(r) occurs at 1.4 Å, indicating the appearance of longer carbon chains. This observation was also reported by Spanu et al.³⁵ when a distinct feature at 1600 cm⁻¹ in the vibrational density of states appeared, which can be attributed to threefold coordinated carbon atoms. In recent experimental work on shock-compressed methane,⁹¹ the observed changes in the Hugoniot shock velocity–particle velocity slope predict a polymeric region, which is consistent with our and previous DFT-MD simulations.^34,92 The peak of g_CC(r) suggests an sp²-hybridization between the carbon atoms, whereas in diamond all carbon atoms are single-bonded, i.e. sp³-hybridized with the nearest carbon atom located at 1.54 Å under ambient conditions. Finally, at 16 000 K the peak of g_CC(r) is reduced and broadened, indicating the short-lived and unstable nature of the molecules.

The coordination number is calculated to analyse the structural changes in carbon upon compression in more detail and shown in Fig. 5. This number is obtained by integrating the PDF under spherical symmetry consideration to the first minimum.

At temperatures of 1000 and 2000 K and densities below 2 g cm⁻³, the coordination number is greater than 8 due to the molecular nature of the system and many of methane molecules being in the first coordination sphere. Note that the occurrence of the first minima for g_CC(r) is found to be at a distance greater than 3 Å. At densities above 2 g cm⁻³, the dissociation of methane molecules starts and a new peak of g_CC(r) arises at 1.4 Å. This leads to a sharp drop in the coordination number. An increase in the coordination number of up to two indicates the gradual transition from the molecular to the polymeric regime. The increase in the coordination number becomes slower at the highest temperatures due to the tendency of shorter carbon chains.

Fig. 5 Coordination number of carbon–carbon as a function of density along the isotherms of 1000, 2000, 3000, 4000, 6000, 8000 and 16 000 K.

In Fig. 6, the PDFs of methane g^mixture_XY(r) and the hydrogen–methane mixture g^mixture_XY(r) at a temperature of 4000 K are presented at a comparable pressure. The first peak of g^mixture_HC(r) is lowered compared to pure hydrogen indicating dissociation. Additionally, a peak arises at r ≈ 1.34 Å for g^mixture_HC(r), indicating the presence of carbon chains. This change indicates that the onset of the formation of carbon clusters in the mixture takes place at a lower pressure than that in pure methane.

Fig. 6 PDFs of the constituents in the hydrogen–methane 1 : 1 mixture and pure methane⁴¹ (dotted lines) at T = 4000 K and P ≈ 40 GPa.

Despite experiments suggesting diamond formation^22,24,25,93 from various mixtures of C/H, we do not observe such a feature in our calculations. Due to the starting symmetry of our simulation box, it is impossible to distinguish between long carbon chains and the early stage of diamond nucleation, which is also aided by small system sizes.⁹³ Also, we do not rule out the possibility of observing demixing in our system even though it is not the goal of this work.

3.4 Electronic properties

In Fig. 7, we show the average electronic band gap along the 1.58 g cm⁻³ isochore as a function of the temperatures averaged over the MD trajectory after equilibration and compare with results on pure methane³⁴ and a mixture of water and methane.⁴² To calculate the band gap we use the technique developed by Preising and Redmer.⁹⁴ We observe our system to be in an insulating state with a band gap of more than 5 eV. With increasing temperature, the band gap decreases. At 3000 K the dissociation of the constituent leads to a polymeric state in carbon and additional hydrogen atoms so that the band gap closes. Compared to pure methane³⁴ and methane–water mixtures,⁴² it is clear that the presence of hydrogen molecules has a great impact on the electronic properties. The insulator-to-metal transition in hydrogen–methane mixtures is driven by disorder that dissociation introduces into the fluid. The mixture becomes metallic at lower temperatures compared with pure methane and methane–water mixtures.

Fig. 7 Average electronic band gap of the hydrogen–methane mixture along the 1.58 g cm⁻³ isochore as a function of the temperature (the blue line with symbols). The band gaps of pure methane given by Sherman et al.³⁴ (yellow) and of the methane–water mixture of Hu et al.⁴² (brown) are also shown.

To calculate the dynamic electronic electrical conductivity we used the Kubo–Greenwood formula:^{59,60,95–97}

where m is the mass, ω is the frequency, α is the sum of the average of contribution from the three spatial directions, e is the electronic charge and Ω is the volume of the simulation box. F(ε_i,k) and ε_i,k are the Fermi distribution functions describing the occupation of the Bloch state |ψ_i,k〉 having energy ε_i,k at k and the dipole matrix elements with the velocity operator 〈ψ_j,k|v|ψ_i,k〉 are calculated using optical routines of VASP.^61–65 As the simulation box is constrained by periodic boundary conditions, this leads to a discrete spectrum of eigenvalues; hence, the δ function has to be broadened to a finite width for which we use a Gaussian function. Brillouin zone summation is performed using special k-point sets with weighting factors.^75,97–99 Finally, the DC conductivity follows from the static limit:

We evaluated the formula (7) for 100 snapshots of equilibrated MD simulations chosen at equivalent time intervals using a Monkhorst–Pack k-point mesh of 2 × 2 × 2 to sample the Brillouin zone. Fig. 8 shows the calculated DC conductivities along the isotherms. At low temperature and pressure, the conductivity is very small and the system exhibits an insulating behavior. At 1000, 3000, and 4000 K the molecular-to-atomic transition can be seen as a sharp increase in the electrical conductivity. For isotherms at lower temperatures, the transition occurs at higher pressures. At 3000 K and a pressure of 181 GPa the value of the DC conductivity is 0.44 MS m⁻¹. Using a two-stage light-gas gun Nellis et al.²¹ determined the electrical conductivity of shock compressed methane at pressures between 20 and 60 GPa and temperatures in the range of 2000 to 4000 K, finding that conduction is predominantly caused by hydrogen from methane. Similarly, quantum molecular dynamic simulations performed by Li et al.⁷⁷ on shocked methane predicted that the conductivity is negligible up to 40 GPa, but at pressures above 55 GPa, the DC conductivity increased up to values of more than 0.1 MS m⁻¹, see Fig. 8. A similar behavior can be seen in our results, and the rise of the conductivity is attributed to the dissociation of methane and of hydrogen molecules as well. The dissociated constituents can only contribute to the magnetic field in the form of metallic hydrogen, and the radio waves are generated due to the trapping of such charged particles in the magnetic fields as the Voyager II flyby mission detected radio emissions from Uranus and Neptune.^90,100

Fig. 8 DC electrical conductivity of a dense hydrogen–methane 1 : 1 mixture as a function of pressure along five isotherms (color coded). For comparison, the theoretical results of Li et al.⁷⁷ (red crosses) and the experimental data of Nellis et al.²¹ (blue triangle up) for pure methane are also shown.

It should be noted that the conductivity does not rise forever. With increasing pressure and temperature, the scattering rate of electrons on ions increases as a result of the broadening of the Fermi function, and their mobility is reduced, a typical characteristic of metals. The effect of both processes almost cancels out and, therefore, the conductivity does not rise significantly at high pressure and temperature, see Fig. 8. A physical explanation was given by Mott¹⁰² and Ioffe et al.,¹⁰³ which states that any disordered system will remain metallic if the characteristic mean free path of charge carriers is greater than the average distance between the constituent ions. Based on these arguments, the minimum metallic conductivity was estimated to be 2000 Ω⁻¹ cm⁻¹ and 0.2 MS m⁻¹ in fluid hydrogen and expanded metallic fluids such as rubidium, cesium, and mercury. This criterion can also be applied to locate the metallization transition of nonmetallic chemical elements like oxygen and nitrogen when exposed to high temperatures and pressures.^77,104,105 By obtaining conductivity values beyond this minimum metallic conductivity for our system (see Fig. 8), we conclude that a nonmetal-to-metal transition occurred in our mixture of methane and hydrogen.

Finally, in Fig. 9, we calculate the electrical conductivity along the P–T profile of Uranus as proposed by Nettelmann et al.¹⁰¹ This model consists of a rocky core surrounded by two envelopes of hydrogen, helium and water with a constant mass ratio of 0.275 : 0.725 in the envelopes. The model predicts a density jump at ∼75% of the planet's radius.¹⁰¹ From our calculations we observe a metallic behaviour of the mixture at ∼60% of the planet's radius corresponding to a temperature of T ≈ 4176 K and a pressure of P ≈ 126 GPa, and a subsequent conductivity of σ ≈ 0.49 MS m⁻¹. Note that the PBE functional underestimates the band gap. Therefore, the metallisation pressures might be slightly low.

Fig. 9 DC electrical conductivity of a dense hydrogen–methane 1 : 1 mixture along the pressure and temperature profile of Uranus.¹⁰¹

The complete data set for DC electrical conductivities is provided in the ESI.†

4 Conclusion

We have calculated the EOS, structural properties, band gaps, and electrical conductivities of methane–hydrogen mixtures at temperatures between 700 K and 16 000 K and pressures between 12 GPa and 1300 GPa. We found that the dissociation of hydrogen molecules increases the disorder and aids in the process of decomposition of methane into carbon clusters and hydrogen atoms. As an example, we choose an isochore of 1.32 g cm⁻³ to demonstrate the evolution of the PDFs of the mixture from a molecular to an atomic phase as a function of temperature. However, contrary to experiments and theoretical prediction of Cheng et al.,⁹³ our simulations yield no nano-diamonds, which might be due to the symmetry of the simulation box, an insufficient number of carbon atoms to form diamond, or finite size effects with respect to the kinetics of diamond nucleation. Our work does not rule out the possibility of observing demixing and future work will be dedicated to this problem. Calculations of the band gap of the mixture show that it closes at lower temperatures than for pure methane. The metallic nature of the fluid is demonstrated by calculating the electrical conductivity and interpreted by using the physical assertions of Mott¹⁰² and Ioffe et al.¹⁰³ As an example we calculate the electrical conductivity along the P–T profile of Uranus¹⁰¹ and observe that the mixture turns metallic at ∼60% of the planet's radius. Testing the LMA yields a limit of 4% deviation in density and of 4 kJ g⁻¹ in specific energy for all P–T conditions considered. Accordingly, we find the LMA to be appropriate for applications such as planetary modeling. Interior models of Uranus and Neptune assume that the planet is made up of several layers: a rocky core in the center, an “icy” middle layer rich in water, ammonia, and methane, and an outer gaseous envelope rich in H₂ and He,^{15,56,101,106} albeit more rock-dominated structures are also possible.^14,107

The fact that the observed internal heat production of Neptune was twice the energy received from the Sun can be explained via gravitational sinking of crystalline, complex or amorphous carbon clusters precipitating towards the planetary center. Also, the lighter hydrocarbons such as ethane and propane formed due to the dissociation inside the planets cannot sink into the planetary core but levitate to the atmosphere by the convection process. This would explain the large amounts of hydrogen molecules in the atmosphere of both planets and for Neptune, the huge abundance of ethane in its atmosphere.^90,108 Although insight into the pure systems is of fundamental interest, planets are composed of a mixture of materials and their combined behavior determines the interior structure as well as the cooling and magnetic field generation. Crucial physical quantities for characterizing the internal structure and evolution of planets include the EOS and fundamental transport properties such as conductivity and diffusivity of the planetary materials.

Information on the EOS and on possible phase transitions of planetary materials helps to advance models for such planets. Furthermore, our findings will facilitate new experiments on the behavior of matter under extreme conditions, in particular at free-electron-laser facilities like LCLS, SACLA, and European XFEL.^26,28,30,32

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Martin Preising, Uwe Kleinschmidt, and Martin French for their helpful discussions and technical support. We also thank Roi Baer and Rebecca E. Hadad of the Hebrew University of Jerusalem for their useful notes. This work was supported by the ITMZ of the University of Rostock and the German Israel Foundation for Scientific Research and Development (GIF) within the Research Grant No. I-1486-303.7/2019. Armin Bergermann thanks the Evangelische Studienwerk e.V. for support.

References

1. H. E. Suess and H. C. Urey, Rev. Mod. Phys., 1956, 28, 53–74.
2. H.-K. Mao and R. J. Hemley, Rev. Mod. Phys., 1994, 66, 671–692.
3. R. T. Howie, C. L. Guillaume, T. Scheler, A. F. Goncharov and E. Gregoryanz, Phys. Rev. Lett., 2012, 108, 125501.
4. R. T. Howie, P. Dalladay-Simpson and E. Gregoryanz, Nat. Mater., 2015, 14, 495–499.
5. E. Gregoryanz, C. Ji, P. Dalladay-Simpson, B. Li, R. T. Howie and H.-K. Mao, Matter Radiat. Extremes, 2020, 5, 038101.
6. P. Loubeyre, F. Occelli and P. Dumas, Nature, 2020, 577, 631–635.
7. W. Lorenzen, B. Holst and R. Redmer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195107.
8. J. M. McMahon, M. A. Morales, C. Pierleoni and D. M. Ceperley, Rev. Mod. Phys., 2012, 84, 1607–1653.
9. R. Helled, G. Mazzola and R. Redmer, Nat. Rev. Phys., 2020, 2, 562–574.
10. P. Loubeyre, R. Letoullec and J.-P. Pinceaux, Phys. Rev. Lett., 1994, 72, 1360–1363.
11. T. A. Strobel, P. Ganesh, M. Somayazulu, P. R. C. Kent and R. J. Hemley, Phys. Rev. Lett., 2011, 107, 255503.
12. R. Turnbull, M.-E. Donnelly, M. Wang, M. Peña Alvarez, C. Ji, P. Dalladay-Simpson, H.-K. Mao, E. Gregoryanz and R. T. Howie, Phys. Rev. Lett., 2018, 121, 195702.
13. D. K. Spaulding, G. Weck, P. Loubeyre, F. Datchi, P. Dumas and M. Hanfland, Nat. Commun., 2014, 5, 5739.
14. R. Helled, N. Nettelmann and T. Guillot, Space Sci. Rev., 2020, 216, 1–26.
15. J. J. Fortney and N. Nettelmann, Space Sci. Rev., 2010, 152, 423–447.
16. P. G. Irwin, N. A. Teanby, L. N. Fletcher, D. Toledo, G. S. Orton, M. H. Wong, M. T. Roman, S. Pérez-Hoyos, A. James and J. Dobinson, J. Geophys. Res. Planets, 2022, 127, e2022JE007189.
17. M. Mastrogiuseppe, V. Poggiali, A. Hayes, J. Lunine, R. Seu, G. Mitri and R. Lorenz, Nat. Astron., 2019, 3, 535–542.
18. T. Bertrand, F. Forget, B. Schmitt, O. L. White and W. M. Grundy, Nat. Commun., 2020, 11, 5056.
19. M. Ross, Nature, 1981, 292, 435–436.
20. W. Nellis, F. Ree, M. Van Thiel and A. Mitchell, Chem. Phys., 1981, 75, 3055–3063.
21. W. Nellis, D. Hamilton and A. Mitchell, Chem. Phys., 2001, 115, 1015–1019.
22. H. Hirai, K. Konagai, T. Kawamura, Y. Yamamoto and T. Yagi, Phys. Earth Planet, 2009, 174, 242–246.
23. H. Radousky, A. Mitchell and W. Nellis, J. Chem. Phys., 1990, 93, 8235–8239.
24. L. R. Benedetti, J. H. Nguyen, W. A. Caldwell, H. Liu, M. Kruger and R. Jeanloz, Science, 1999, 286, 100–102.
25. S. S. Lobanov, P.-N. Chen, X.-J. Chen, C.-S. Zha, K. D. Litasov, H.-K. Mao and A. F. Goncharov, Nat. Commun., 2013, 4, 2446.
26. M. Frost, R. S. McWilliams, E. Bykova, M. Bykov, R. J. Husband, L. M. Andriambariarijaona, S. Khandarkhaeva, B. Massani, K. Appel, C. Baehtz, O. B. Ball, V. Cerantola, S. Chariton, J. Choi, H. Cynn, M. J. Duff, A. Dwivedi, E. Edmund, G. Fiquet, H. Graafsma, N. Jaisle, J. Kim, Z. Konopkova, T. Laurus, Y. Lee, H.-P. Liermann, J. D. McHardy, M. I. McMahon, G. Morard, M. Nakatsutsumi, L. A. Nguyen, S. Ninet, V. B. Prakapenka, C. Prescher, R. Redmer, S. Stern, C. Strohm, J. Sztuk-Dambietz, M. Turcato, Z. Wu, S. H. Glenzer and A. F. Goncharov, Nat. Astron., 2024, 8, 174–181.
27. M. C. Marshall, M. G. Gorman, D. N. Polsin, J. H. Eggert, M. K. Ginnane, J. R. Rygg, G. W. Collins and L. D. Leininger, J. Appl. Phys., 2022, 131, 085904.
28. Z. He, M. Rödel, J. Lütgert, A. Bergermann, M. Bethkenhagen, D. Chekrygina, T. E. Cowan, A. Descamps, M. French and E. Galtier, et al. , Sci. Adv., 2022, 8, eabo0617.
29. A. S. Naumova, S. V. Lepeshkin, P. V. Bushlanov and A. R. Oganov, J. Phys. Chem. A, 2021, 125, 3936–3942.
30. D. Kraus, J. Vorberger, A. Pak, N. Hartley, L. Fletcher, S. Frydrych, E. Galtier, E. Gamboa, D. O. Gericke and S. Glenzer, et al. , Nat. Astron, 2017, 1, 606–611.
31. D. Kraus, N. J. Hartley, S. Frydrych, A. K. Schuster, K. Rohatsch, M. Rödel, T. E. Cowan, S. Brown, E. Cunningham, T. van Driel, L. B. Fletcher, E. Galtier, E. J. Gamboa, A. Laso Garcia, D. O. Gericke, E. Granados, P. A. Heimann, H. J. Lee, M. J. MacDonald, A. J. MacKinnon, E. E. McBride, I. Nam, P. Neumayer, A. Pak, A. Pelka, I. Prencipe, A. Ravasio, R. Redmer, A. M. Saunders, M. Schölmerich, M. Schörner, P. Sun, S. J. Turner, A. Zettl, R. W. Falcone, S. H. Glenzer, T. Döppner and J. Vorberger, Phys. Plasmas, 2018, 25, 056313.
32. A. K. Schuster, N. J. Hartley, J. Vorberger, T. Döppner, T. van Driel, R. W. Falcone, L. B. Fletcher, S. Frydrych, E. Galtier, E. J. Gamboa, D. O. Gericke, S. H. Glenzer, E. Granados, M. J. MacDonald, A. J. MacKinnon, E. E. McBride, I. Nam, P. Neumayer, A. Pak, I. Prencipe, K. Voigt, A. M. Saunders, P. Sun and D. Kraus, Phys. Rev. B, 2020, 101, 054301.
33. F. Ancilotto, G. L. Chiarotti, S. Scandolo and E. Tosatti, Science, 1997, 275, 1288–1290.
34. B. L. Sherman, H. F. Wilson, D. Weeraratne and B. Militzer, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 224113.
35. L. Spanu, D. Donadio, D. Hohl, E. Schwegler and G. Galli, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6843–6846.
36. G. Gao, A. R. Oganov, Y. Ma, H. Wang, P. Li, Y. Li, T. Iitaka and G. Zou, Chem. Phys., 2010, 133, 144508.
37. D. Murayama, S. Ohmura, R. Kodama and N. Ozaki, J. Appl. Phys., 2023, 134, 095902.
38. G. Kerley, J. Appl. Phys., 1980, 51, 5368–5374.
39. U. Setzmann and W. Wagner, J. Phys. Chem. Ref. Data, 1991, 20, 1061–1155.
40. M. Bykov, E. Bykova, C. J. Pickard, M. Martinez-Canales, K. Glazyrin, J. S. Smith and A. F. Goncharov, Phys. Rev. B, 2021, 104, 184105.
41. M. Bethkenhagen, E. R. Meyer, S. Hamel, N. Nettelmann, M. French, L. Scheibe, C. Ticknor, L. A. Collins, J. D. Kress and J. J. Fortney, et al. , Astrophys. J., 2017, 848, 67.
42. R. Hu, Y. Li, C. Wang, Y. Hu and M. Lv, Phys. Rev. B, 2023, 107, 174108.
43. U. Ranieri, L. J. Conway, M.-E. Donnelly, H. Hu, M. Wang, P. Dalladay-Simpson, M. Peña-Alvarez, E. Gregoryanz, A. Hermann and R. T. Howie, Phys. Rev. Lett., 2022, 128, 215702.
44. M. Somayazulu, L. Finger, R. Hemley and H. Mao, Science, 1996, 271, 1400–1402.
45. W. L. Mao, V. V. Struzhkin, H.-K. Mao and R. J. Hemley, Chem. Phys. Lett., 2005, 402, 66–70.
46. Y. Liu, D. Duan, F. Tian, X. Huang, D. Li, Z. Zhao, X. Sha, B. Chu, H. Zhang and B. Liu, et al. , RSC Adv., 2014, 4, 37569–37574.
47. G. Saleh and A. R. Oganov, Sci. Rep., 2016, 6, 32486.
48. A. S. Naumova, S. V. Lepeshkin and A. R. Oganov, J. Phys. Chem. C, 2019, 123, 20497–20501.
49. W. Cui, T. Bi, J. Shi, Y. Li, H. Liu, E. Zurek and R. J. Hemley, Phys. Rev. B, 2020, 101, 134504.
50. A. F. Goncharov, E. Bykova, M. Bykov, X. Zhang, Y. Wang, S. Chariton, V. B. Prakapenka and J. S. Smith, J. Appl. Phys., 2022, 131, 025902.
51. A. B. Zylstra, A. L. Kritcher, O. A. Hurricane, D. A. Callahan, J. E. Ralph, D. T. Casey, A. Pak, O. L. Landen, B. Bachmann, K. L. Baker, L. Berzak Hopkins, S. D. Bhandarkar, J. Biener, R. M. Bionta, N. W. Birge, T. Braun, T. M. Briggs, P. M. Celliers, H. Chen, C. Choate, D. S. Clark, L. Divol, T. Döppner, D. Fittinghoff, M. J. Edwards, M. Gatu Johnson, N. Gharibyan, S. Haan, K. D. Hahn, E. Hartouni, D. E. Hinkel, D. D. Ho, M. Hohenberger, J. P. Holder, H. Huang, N. Izumi, J. Jeet, O. Jones, S. M. Kerr, S. F. Khan, H. Geppert Kleinrath, V. Geppert Kleinrath, C. Kong, K. M. Lamb, S. Le Pape, N. C. Lemos, J. D. Lindl, B. J. MacGowan, A. J. Mackinnon, A. G. MacPhee, E. V. Marley, K. Meaney, M. Millot, A. S. Moore, K. Newman, J.-M. G. Di Nicola, A. Nikroo, R. Nora, P. K. Patel, N. G. Rice, M. S. Rubery, J. Sater, D. J. Schlossberg, S. M. Sepke, K. Sequoia, S. J. Shin, M. Stadermann, S. Stoupin, D. J. Strozzi, C. A. Thomas, R. Tommasini, C. Trosseille, E. R. Tubman, P. L. Volegov, C. R. Weber, C. Wild, D. T. Woods, S. T. Yang and C. V. Young, Phys. Rev. E, 2022, 106, 025202.
52. A. B. Zylstra, O. A. Hurricane, D. A. Callahan, A. L. Kritcher, J. E. Ralph, H. F. Robey, J. S. Ross, C. V. Young, K. L. Baker, D. T. Casey, T. Döppner, L. Divol, M. Hohenberger, S. Le Pape, A. Pak, P. K. Patel, R. Tommasini, S. J. Ali, P. A. Amendt, L. J. Atherton, B. Bachmann, D. Bailey, L. R. Benedetti, L. Berzak Hopkins, R. Betti, S. D. Bhandarkar, J. Biener, R. M. Bionta, N. W. Birge, E. J. Bond, D. K. Bradley, T. Braun, T. M. Briggs, M. W. Bruhn, P. M. Celliers, B. Chang, T. Chapman, H. Chen, C. Choate, A. R. Christopherson, D. S. Clark, J. W. Crippen, E. L. Dewald, T. R. Dittrich, M. J. Edwards, W. A. Farmer, J. E. Field, D. Fittinghoff, J. Frenje, J. Gaffney, M. Gatu Johnson, S. H. Glenzer, G. P. Grim, S. Haan, K. D. Hahn, G. N. Hall, B. A. Hammel, J. Harte, E. Hartouni, J. E. Heebner, V. J. Hernandez, H. Herrmann, M. C. Herrmann, D. E. Hinkel, D. D. Ho, J. P. Holder, W. W. Hsing, H. Huang, K. D. Humbird, N. Izumi, L. C. Jarrott, J. Jeet, O. Jones, G. D. Kerbel, S. M. Kerr, S. F. Khan, J. Kilkenny, Y. Kim, H. Geppert Kleinrath, V. Geppert Kleinrath, C. Kong, J. M. Koning, J. J. Kroll, M. K. G. Kruse, B. Kustowski, O. L. Landen, S. Langer, D. Larson, N. C. Lemos, J. D. Lindl, T. Ma, M. J. MacDonald, B. J. MacGowan, A. J. Mackinnon, S. A. MacLaren, A. G. MacPhee, M. M. Marinak, D. A. Mariscal, E. V. Marley, L. Masse, K. Meaney, N. B. Meezan, P. A. Michel, M. Millot, J. L. Milovich, J. D. Moody, A. S. Moore, J. W. Morton, T. Murphy, K. Newman, J.-M. G. Di Nicola, A. Nikroo, R. Nora, M. V. Patel, L. J. Pelz, J. L. Peterson, Y. Ping, B. B. Pollock, M. Ratledge, N. G. Rice, H. Rinderknecht, M. Rosen, M. S. Rubery, J. D. Salmonson, J. Sater, S. Schiaffino, D. J. Schlossberg, M. B. Schneider, C. R. Schroeder, H. A. Scott, S. M. Sepke, K. Sequoia, M. W. Sherlock, S. Shin, V. A. Smalyuk, B. K. Spears, P. T. Springer, M. Stadermann, S. Stoupin, D. J. Strozzi, L. J. Suter, C. A. Thomas, R. P. J. Town, E. R. Tubman, C. Trosseille, P. L. Volegov, C. R. Weber, K. Widmann, C. Wild, C. H. Wilde, B. M. Van Wonterghem, D. T. Woods, B. N. Woodworth, M. Yamaguchi, S. T. Yang and G. B. Zimmerman, Nature, 2022, 601, 542–548.
53. M. Podolak, R. Helled and G. Schubert, Mon. Not. R. Astron. Soc., 2019, 487, 2653–2664.
54. R. Redmer, T. R. Mattsson, N. Nettelmann and M. French, Icarus, 2011, 211, 798–803.
55. L. Scheibe, N. Nettelmann and R. Redmer, Astron. Astrophys., 2019, 632, A70.
56. R. Helled, J. D. Anderson, M. Podolak and G. Schubert, Astrophys. J., 2010, 726, 15.
57. P. Peebles, Astrophys. J., 1964, 140, 328.
58. W. C. Demarcus, Astron. J., 1958, 63, 2.
59. R. Kubo, JPSJ, 1957, 12, 570–586.
60. D. Greenwood, Proc. Phys. Soc., 1958, 71, 585.
61. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
62. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
63. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
64. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
65. J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078.
66. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
67. N. D. Mermin, Phys. Rev., 1965, 137, A1441–A1443.
68. M. Weinert and J. W. Davenport, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13709–13712.
69. R. M. Wentzcovitch, J. L. Martins and P. B. Allen, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 11372–11374.
70. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
71. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
72. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
73. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
74. N. Shuichi, Prog. Theor. Phys., 1991, 103, 1–46.
75. B. Holst, R. Redmer and M. P. Desjarlais, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 184201.
76. A. Baldereschi, Phys. Rev. B: Condens. Matter Mater. Phys., 1973, 7, 5212–5215.
77. D. Li, P. Zhang and J. Yan, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 184204.
78. B. Militzer, W. B. Hubbard, J. Vorberger, I. Tamblyn and S. Bonev, Astrophys. J, 2008, 688, L45.
79. M. A. Morales, C. Pierleoni, E. Schwegler and D. M. Ceperley, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12799–12803.
80. W. Hubbard, Astrophys. J., 1972, 176, 525.
81. D. J. Stevenson, Phys. Rev. B: Condens. Matter Mater. Phys., 1975, 12, 3999–4007.
82. J. Vorberger, I. Tamblyn, B. Militzer and S. A. Bonev, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 024206.
83. C. Wang, X.-T. He and P. Zhang, Phys. Rev. E, 2013, 88, 033106.
84. F. Soubiran and B. Militzer, Astrophys. J, 2015, 806, 228.
85. F. Soubiran and B. Militzer, Astrophys. J, 2016, 829, 14.
86. J.-F. Danel and L. Kazandjian, Phys. Rev. E, 2015, 91, 013103.
87. M. Bethkenhagen, D. Cebulla, R. Redmer and S. Hamel, J. Phys. Chem. A, 2015, 119, 10582–10588.
88. B. Cheng, M. Bethkenhagen, C. J. Pickard and S. Hamel, Nat. Phys., 2021, 17, 1228–1232.
89. C. Cavazzoni, G. Chiarotti, S. Scandolo, E. Tosatti, M. Bernasconi and M. Parrinello, Science, 1999, 283, 44–46.
90. D. Richters and T. D. Kühne, JETP Lett., 2013, 97, 184–187.
91. G. Tabak, J. R. Rygg, M. Millot, Y.-J. Kim, S. Hamel, P. M. Celliers, D. E. Fratanduono, S. Ali, D. Erskine, T. R. Boehly, T.-A. Suer, N. Dasenbrock-Gammon, R. Dias, S. Zhang, S. X. Hu, L. E. Hansen, B. J. Henderson, M. Zaghoo, T. Ogawa, D. Murayama, K. Miyanishi, N. Ozaki, T. Sano, R. Jeanloz, D. G. Hicks, J. H. Eggert and G. W. Collins, Phys. Rev. B, 2024, 109, 064102.
92. S. Zhang, K. P. Driver, F. Soubiran and B. Militzer, Phys. Rev. E, 2017, 96, 013204.
93. B. Cheng, S. Hamel and M. Bethkenhagen, Nat. Commun., 2023, 14, 1104.
94. M. Preising and R. Redmer, Phys. Rev. B, 2020, 102, 224107.
95. M. French and R. Redmer, Phys. Plasmas, 2017, 24, 092306.
96. M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112.
97. B. Holst, M. French and R. Redmer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235120.
98. M. French, G. Röpke, M. Schörner, M. Bethkenhagen, M. P. Desjarlais and R. Redmer, Phys. Rev. E, 2022, 105, 065204.
99. D. Knyazev and P. Levashov, Comput. Mater. Sci., 2013, 79, 817–829.
100. J. W. Warwick, D. R. Evans, G. R. Peltzer, R. G. Peltzer, J. H. Romig, C. B. Sawyer, A. C. Riddle, A. E. Schweitzer, M. D. Desch and M. L. Kaiser, et al. , Science, 1989, 246, 1498–1501.
101. N. Nettelmann, R. Helled, J. Fortney and R. Redmer, Planet. Space Sci., 2013, 77, 143–151.
102. N. Mott, Metal-Insulator Transitions, Taylor and Francis, London, 2nd edn, 1990.
103. A. Ioffe and A. Regel, Non-crystalline, amorphous, and liquid electronic semiconductors: Progress in semiconductors, 1960, pp. 237–291.
104. W. Nellis, R. Chau, P. P. Edwards and R. Winter, Z. Phys. Chem., 2003, 217, 795–802.
105. W. Nellis, J. Condens. Matter Phys., 2004, 16, S923.
106. W. B. Hubbard and J. J. MacFarlane, J. Geophys. Res. Solid Earth, 1980, 85, 225–234.
107. N. Teanby, P. Irwin, J. Moses and R. Helled, Philos. Trans. R. Soc., A, 2020, 378, 20190489.
108. R. V. Yelle, F. Herbert, B. R. Sandel, R. J. Vervack and T. M. Wentzel, Icarus, 1993, 104, 38–59.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00058g

---