Kinetics of the reaction of OH with methyl nitrate (223–343 K)

Abstract

Rate coefficients (k₄) for the reaction of hydroxyl radicals (OH) with methyl nitrate (CH₃ONO₂) were measured over the temperature range 232–343 K using pulsed laser photolysis to generate OH and pulsed laser-induced fluorescence to detect it in real-time and under pseudo-first-order conditions. In order to optimize the accuracy of the rate coefficients obtained, the concentration of CH₃ONO₂ (the reactant in excess) was measured on-line by absorption spectroscopy at 213.86 nm for which the absorption cross-section was also measured (σ_213.86 = 1.65 ± 0.09 × 10⁻¹⁸ cm² molecule⁻¹). The temperature-dependent rate coefficient is described by k₄(T) = 7.5 × 10⁻¹³ exp[(−1034 ± 40)/T] cm³ molecule⁻¹ s⁻¹ with a room temperature rate coefficient of k₄(296 ± 2 K) = (2.32 ± 0.12) × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹ where the uncertainty includes the statistical error of 2σ and an estimation of the potential systematic bias of 5%. This new dataset helps to consolidate the database for this rate coefficient and to reduce uncertainty in the atmospheric lifetime of CH₃ONO₂. As part of this study, an approximate rate coefficient for the reaction of H-atoms with CH₃ONO₂ (k₉) was also derived at room temperature: k₉(298 K) = (1.68 ± 0.45) × 10⁻¹³ cm³ molecule⁻¹ s⁻¹.

---

1 Introduction

Organic nitrates are formed in the atmosphere during the degradation of hydrocarbons in the presence of nitrogen oxides.¹ The atmospheric lifetimes of organic nitrates can vary from seconds (e.g. for thermally unstable peroxy-nitrates such as CH₃OONO₂ at temperatures close to room temperature) to months (e.g. for α-carbonyl peroxy-nitrates such as CH₃C(O)OONO₂ at temperatures close to 220 K typical for the upper troposphere). In contrast to peroxy-nitrates, alkyl nitrates (such as CH₃ONO₂) are generally thermally stable at the temperatures of our atmosphere and can be transported over long distances before being oxidized via reaction with OH or photolyzed.^1–3 Following OH-induced oxidation of hydrocarbons, alkyl nitrates are formed in a usually minor (termolecular) channel of the reaction of organic peroxy radicals (RO₂) with NO:

RO₂ + NO → RO + NO₂ (R1a)

RO₂ + NO + M → RONO₂ + M (R1b)

Alternatively, RONO₂ can be formed in the NO₃-induced oxidation of unsaturated biogenic hydrocarbons in the presence of O₂, which involves electrophilic addition of NO₃ to a C=C double bond followed by further reaction of the nitro-peroxy radicals thus formed.⁴ The target molecule of this study, CH₃ONO₂ is formed in the lower atmosphere when CH₃O₂ radicals (e.g. from methane oxidation) react with NO. The formation of CH₃ONO₂via this reaction is inefficient, with a yield of <1% at room temperature,⁵ but with some evidence for an increase in the yield at lower temperatures, commensurate with its formation in a termolecular process:⁶

CH₃O₂ + NO → CH₃O + NO₂ (R2a)

CH₃O₂ + NO + M → CH₃ONO₂ + M (R2b)

In the lower atmosphere, the fate of CH₃O is dominated by reaction with O₂ to form HO₂ and HCHO. However, in the stratosphere, when O₂ concentrations are much lower, some CH₃O can react with NO₂⁷ and this represents a further source of CH₃ONO₂:

CH₃O + NO₂ + M → CH₃ONO₂ + M (R3)

The important chemical loss processes for CH₃ONO₂ in the atmosphere are photodissociation and reaction with OH, with thermal decomposition and reaction with O₃ or NO₃ insignificant.^1,8 Previous measurements indicate that R4 has a small rate coefficient, of the order of 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹ (see below). The photolysis of CH₃ONO₂ proceeds via O–N bond fission to form a methoxy radical and NO₂, whereas the slow reaction with OH (R4) proceeds via H-abstraction to form an unstable radical that dissociates to formaldehyde and NO₂(R5):

OH + CH₃ONO₂ → CH₂ONO₂ + H₂O (R4)

CH₂ONO₂ → HCHO + NO₂ (R5)

Both HCHO and CH₃O react much more rapidly with OH than does CH₃ONO₂ and secondary chemistry is a potential source of systematic bias in the determination of the rate coefficient (k₄) for the title reaction when using absolute rate methods. A further source of systematic bias in an absolute rate coefficient study of this slow reaction (R4) is the presence of reactive impurities in the CH₃ONO₂ sample. Such problems can be avoided by working at low OH concentrations (and thus low fractional conversion of CH₃ONO₂ to products) and by carefully purifying the CH₃ONO₂ sample, thus minimising the levels of reactive impurities (see Section 2).

The rate coefficient for reaction (R4) has been reported by Gaffney et al.,⁹ Nielsen et al.,¹⁰ Talukdar et al.,⁸ and Shallcross et al.,¹¹ but there are large differences in the rate coefficient at room temperature (a factor of 10) and its temperature dependence which is reported to be both positive and negative (see later). The goal of this study is to generate highly accurate rate coefficients for the title reaction at different (atmospherically relevant) temperatures and to resolve these differences in the literature and thus better constrain the lifetime of CH₃ONO₂ in the atmosphere.

2 Experimental

Rate coefficients for the reaction of OH with CH₃ONO₂ were determined using pulsed-laser-photolysis (PLP) pulsed-laser-induced fluorescence (PLIF) under pseudo-first-order conditions ([CH₃ONO₂] ≫ [OH]) in (mainly) N₂ and He bath gases. The concentration of methyl nitrate was measured in situ by optical absorption. The experimental setup has been described in detail elsewhere¹² and is only briefly described here.

2.1 PLP–PLIF technique

The reaction took place in a cylindrical, jacketed quartz reactor with a volume of approximately 300 cm³. The temperature inside the reactor was controlled by circulating a 60 : 40 ethylene glycol/water mixture (343–251 K) or ethanol (T < 251 K) through an outer-jacket. The gas mixture enters the reactor about 15 cm before the photolysis zone, ensuring thermal equilibrium with the walls of the reactor. The reaction temperature was measured by inserting a recently calibrated K-type thermocouple into the photolysis zone before each experiment at a different temperature. 100 and 1000 torr manometers were used to measure the pressure in the reactor.

OH was generated by excimer laser photolysis (Coherent COMPex 205 F or Pro 201 F, ∼20 ns width) of a precursor gas molecule, either H₂O₂ (248 nm), HONO (351 nm) or CH₃ONO₂ itself (248 nm) (see below).

OH radicals were excited at 281.997 nm (A²Σ(ν′ = 1) ← X²Π(ν′′ = 0), Q₁₁ (1) transition) using a Nd-YAG pumped (532 nm, ∼6 ns pulse width) and frequency-doubled dye laser (Quantel Brilliant B, Lambda Physik Scanmate/Scanmate UV with KPD crystal). The resulting fluorescence signal was detected by a photomultiplier tube screened by a long-pass filter (λ > 290 nm). The photolysis and excitation lasers were mainly operated at a repetition rate of 10 Hz using a pulse/delay generator (Stanford Research Systems DG 535), which was also used to control the delay between the photolysis and excitation laser pulses. Prior to the PLP pulse, 20 pulses of the PLIF laser were used to measure a background signal that includes scattered light from the excitation laser and electronic noise. The averaged background signal was subtracted before further processing of the measured data. Each datapoint was averaged between 10 and 40 times, depending on the measurement.

The total flow and pressure in the reactor were chosen such that an average, linear gas-velocity of ≈13–19 cm s⁻¹ was achieved, ensuring that the gas in the photolysis region was replenished between laser pulses. For measurements in helium, the linear velocity was 5 or 6.6 cm s⁻¹ and the laser repetition rate was reduced to 5 Hz, to ensure complete gas exchange.

2.2 In situ absorption spectroscopy: The absorption cross-section of CH₃ONO₂ at 213.86 nm

As the experiments were performed under pseudo first order conditions, accurate rate coefficients depend on accurate measurement of the concentration of the excess reactant. The concentration of methyl nitrate was therefore determined on-line, downstream of the reactor by optical absorption using a dual-beam absorption cell (path length 34.8 cm) equipped with a low-pressure Zn-lamp and interference filter (214 ± 5 nm) to isolate the 213.86 nm line. The temperature (close to room temperature) and pressure (a few percent lower than in the reactor) in the absorption cell were also measured and used to make corrections for gas-density differences in the reaction and absorption cell. Optical density (OD) due to CH₃ONO₂ was converted to a concentration using the Beer–Lambert expression (1) and an absorption cross-section that was determined as described below.

OD = ln (I₀/I) = σ_213.86l [CH₃ONO₂] (1)

σ _213.86 is the CH₃ONO₂ absorption cross-section (cm² molecule⁻¹), l is the absorption path-length and I₀ and I are the transmitted light intensity without and with absorber, respectively and [CH₃ONO₂] is the concentration of methyl-nitrate (molecule cm⁻³).

To measure the absorption cross-section, the absorption cell was first filled with N₂ to determine I₀. Subsequently, static samples of CH₃ONO₂ in N₂ at different pressures were introduced into the cell from a storage bulb and the optical absorption was recorded. Two different storage bulbs (0.482% and 0.728%) made up using samples of CH₃ONO₂ from two different syntheses (≈ one month apart in time) were used to check for reproducibility. The storage bulbs were prepared using standard manometric methods with 10 and 1000 torr capacitance manometers with quoted accuracies of better than 1‰.

Fig. 1 presents the results from 17 determinations of optical density at room-temperature. The slope of the weighted, linear regression gives an absorption cross-section of σ_213.86 = (1.65 ± 0.09) × 10⁻¹⁸ cm² molecule⁻¹, where the uncertainty is 2σ and includes as assessment of systematic bias (2%) which stems predominantly from uncertainty in the CH₃ONO₂ mixing ratio and thus [CH₃ONO₂]. In addition, minor contributions stem from uncertainty in the optical path-length (<1%) and in determination of the optical density (0.05–1.5%). As an interference filter with a finite FWHM was used to isolate the 213.86 nm Zn-line, our cross-section should strictly be regarded as an “effective” cross-section since weaker atomic lines may also be detected. Our cross-section is significantly larger than the value of 3.04 × 10⁻¹⁹ cm² molecule⁻¹ at 213.99 nm reported by Taylor et al.¹³ but is similar to a value of 2.16 × 10⁻¹⁸ cm² molecule⁻¹ at 214.01 nm measured by McMillan et al. and reported by Calvert and Pitts.¹⁴ More importantly, our value is in excellent agreement with the more recent determination of Talukdar et al.,¹⁵ who obtained σ_213.86 = (1.67 ± 0.08) × 10⁻¹⁸ cm² molecule⁻¹ using a Zn-lamp. We conclude that our cross-section is approriate for converting in situ optical density measurements to accurate concentrations of CH₃ONO₂.

Fig. 1 Optical density (OD) plotted against concentration of methyl nitrate (molecule cm⁻³) multiplied by path length l (cm). The slope of the corresponding, weighted linear regression yields an effective absorption cross-section of . The error is 2σ and includes an estimate of systematic uncertainty.

2.3 Determination of impurities in the CH₃ONO₂ sample

As the reaction between CH₃ONO₂ and OH is slow, the presence of reactive impurities can bias the rate coefficients obtained to higher values. Likely impurities are CH₃OH and HNO₃ which are involved in the synthesis of CH₃ONO₂ as well as NO₂ and HONO. Initial measurements revealed the presence of low levels of HNO₃ in the CH₃ONO₂ samples. In order to eliminate this (and other acidic gases) the sample flow was passed through ≈20 cm of PFA tubing containing nylon before entering the reactor. In some experiments (in which methyl nitrate itself was used as OH source) CaCO₃ was used to remove HNO₃.

Following each new synthesis of CH₃ONO₂, levels of HNO₃, HONO, CH₃OH and NO₂ were determined using a combination of IR and UV/Vis absorption spectroscopy. An FTIR (Bruker Vector 22) spectrometer coupled to an absorption cell of 45 cm pathlength¹⁶ and equipped with an external MCT detector was used to determine impurity levels of HNO₃ and CH₃OH in a flowing mixture of CH₃ONO₂ in N₂, as used in the kinetic experiments. Generally, 32 spectra at a resolution of 1 cm⁻¹ (acquisition time ≈ 1 min) were co-added to measure absorption in the 700–3750 cm⁻¹ range. HONO and NO₂ impurities were investigated using multi-pass (l = 880 cm) UV/Vis absorption spectroscopy (346–518 nm) using a H4-lamp light source coupled to a CCD detector (Andor DU420A-OE) and a 0.5 m monochromator (BM50) with 300 lines mm⁻¹ grating. The spectral resolution (FWHM of a Hg line from a low-pressure discharge lamp) was 0.5 nm.

The results of the impurity determinations (none were detected and upper limits were established) are summarized in Table 1, which shows that the rate coefficients obtained were not significantly influenced by impurities in the CH₃ONO₂ sample.

Table 1 Impurities and their contribution to the OH decay coefficient

Impurity	Fraction^a	k impurity	Contribution to k′ (%)
a Relative concentration of impurity (in %) of the CH3ONO2 concentration. b Rate coefficient (cm^3 molecule^−1 s^−1) at room temperature. c Calculated for a pressure of 135 torr.
HNO3	<0.01	1.5 × 10^−13	<0.06
CH3OH	<0.01	9.0 × 10^−13	<0.38
HONO	<0.03	6.0 × 10^−12	<6.80
NO2	<0.03	4.2 × 10^−12^c	<4.78

---

2.4 OH sources

During the course of this study, three different sources of OH were tested. The photolysis of HONO at 351 nm (R6) and the photolysis of H₂O₂ at 248 nm (R7) both generate OH in the ground vibrational state.¹⁷ The photolysis of CH₃ONO₂ at 248 nm is an indirect source of OH¹⁵via formation of H atoms (R8b) and (R9).

HONO + hν (351 nm) → OH + NO (R6)

H₂O₂ + hν (248 nm) → 2OH (R7)

CH₃ONO₂ + hν (248 nm) → CH₃O + NO₂ (R8a)

CH₃ONO₂ + hν (248 nm) → H + CH₂ONO₂ (R8b)

H + CH₃ONO₂ → OH + CH₃ONO (R9)

In Section 3.2 and 3.3, we describe how the OH-decays obtained using the 248 nm photolysis laser (i.e., (R7) or (R8b) and (R9)) are strongly influenced by secondary reactions involving CH₃O and NO₂ resulting from the photolysis of CH₃ONO₂. Only data obtained using the photolysis of HONO at 351 nm (a wavelength at which CH₃ONO₂ no longer absorbs significantly) were used to derive the rate coefficient for the title reaction.

2.5 Chemicals

The synthesis of CH₃ONO₂, the nitration of methanol with HNO₃, was carried out according to Black and Babers¹⁸ but with a modification of the purification step. ∼62 mL of Nitric acid (HNO₃; Sigma-Aldrich, ≥65%) was pre-cooled (ice bath) in a 250 ml Erlenmeyer flask. ∼31 mL of Methanol (CH₃OH; Sigma-Aldrich, ≥99.9%) was pre-cooled in a 100 mL Erlenmeyer flask. ∼62 mL of sulphuric acid (Roth, 98%) was added to the nitric acid. The remaining sulphuric acid was added to the methanol using a dropping funnel with vigorous stirring, whereby a temperature of 14 °C was not exceeded. The CH₃OH/H₂SO₄ mixture was then added. The temperature of the mixture increased to about 45 °C and was subsequently kept between 32 °C and 35 °C for about 15 minutes. The mixture was then rapidly cooled in an ice-water bath for 5 minutes and then transferred to a separating funnel. The aqueous phase and part of the organic phase were discarded.

The unwashed methyl nitrate was transferred to a bubbler and N₂ was bubbled through the liquid for about 15 min to remove any dissolved methanol. The liquid was then vacuum-distilled through a drying tube with CaCl₂ (Roth, ≥94%, dehydrated) before the transmitted gas was trapped in a cold-finger at liquid nitrogen temperature. The methyl nitrate was then subjected to repeated freeze–pump–thaw cycles at −196 °C. Nitrogen (N₂, Air-Liquide, 99.999%) and helium (He, Westfalen, 99.999%) were used as buffer gases in the experiments. HONO was prepared in situ by adding 5–10 drops of 0.1 M NaNO₂ solution (Roth, ≥98%) into a 20 wt% H₂SO₄ solution (Roth, 98%). Hydrogen peroxide (H₂O₂; AppliChem, 35%) was vacuum distilled to >90% purity.

3 Results and discussion

In all experiments, the methyl nitrate concentration was 5–6 orders of magnitude larger than that of OH (typically 1 × 10¹⁰ molecule cm⁻³) and pseudo-first order conditions prevailed. The decay of OH can therefore be described by

[OH]_t = [OH]₀exp(−k′t) (2)

where [OH]_t is the OH concentration at time t after the photolysis laser pulse, [OH]₀ is the initial OH concentration and k′ is the first-order decay coefficient. The latter is defined as:

k′ = k₄[CH₃ONO₂] + k_d (3)

where k₄ is the bimolecular rate coefficient (cm³ molecule⁻¹ s⁻¹) of the reaction of methyl nitrate with OH and k_d (s⁻¹) accounts for diffusion of OH from the detection zone and its reaction with H₂O₂ or HONO.

3.1 Generation of OH from HONO photolysis at 351 nm

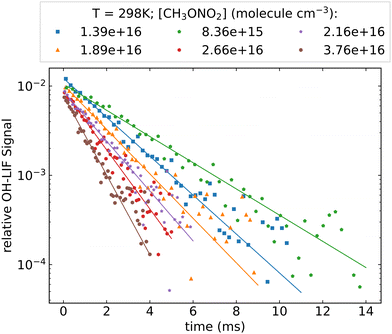
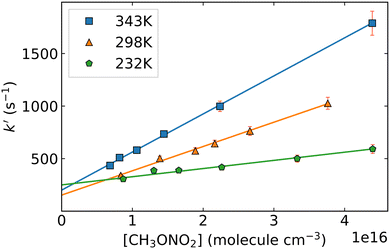
Fig. 2 shows an example of the OH fluorescence signal plotted against time after the excimer laser pulse. The typical HONO concentration in this experiment is approx. 1.5 × 10¹³ molecule cm⁻³, which results in an initial OH concentration of ∼1 × 10¹⁰ molecule cm⁻³. As expected (eqn (2)), the decay of OH is exponential (over 2 orders of magnitude). Decay coefficients (k′, s⁻¹), obtained by least-squares-fitting of eqn (2) to the OH-decays, are plotted against the respective concentration of CH₃ONO₂ in Fig. 3. A linear dependence of k’ on the CH₃ONO₂ concentration (eqn (3)) was observed under all experimental conditions, enabling derivation of k₄(T). Variability in the y-axis intercept of ∼200–250 s⁻¹ reflects slight changes in the HONO concentration between experiments at different temperatures. Prior experiments indicate that the contribution of diffusion to k′ is circa 50–100 s⁻¹, depending mainly on the pressure (or bath gas) and the flow rate. As the rate coefficient for the reaction between OH and HONO is 6.0 × 10⁻¹² cm³ molecule⁻¹ s⁻¹ (at room temperature), the approximate HONO concentration can be calculated to be < 4 × 10¹³ molecule cm⁻³. This is consistent with the concentration obtained using the weak absorption (OD < 1 × 10⁻³) observed at 213.86 nm (σ = 1.8 × 10⁻¹⁸ cm⁻³ molecule⁵) when adding HONO in the absence of CH₃ONO₂.

Fig. 2 OH-LIF signal (datapoints) with mono-exponential fits (solid lines) plotted against time after the photolysis laser pulse. Data were obtained using HONO as OH source at room temperature, the pressure was 134.0 torr (N₂ bath-gas).

Fig. 3 First-order OH decay-coefficient (k′) plotted against the corresponding methyl nitrate concentration [CH₃ONO₂] (data obtained using HONO as the OH precursor). The slope of the linear regression (orange: k(298 K) = (2.31 ± 0.15) × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹; green: k(232 K) = (7.78 ± 0.92) × 10⁻¹⁵ cm³ molecule⁻¹ s⁻¹; k(343 K) = (3.62 ± 0.22) × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹) is the rate coefficient k₄ under these experimental conditions. Error bars represent 2σ statistical uncertainty.

Within experimental uncertainty, variation of the pressure or bath-gas (N₂ or He) (for a given temperature) had no effect on the rate coefficient, which is thus independent of pressure or collision partner within the range of pressures (69–400 torr N₂, 100 torr He) investigated in this study. Variation of the excimer-laser fluence over a factor 30 also had no significant influence (±3%) on the OH decay coefficient, showing that reactions of OH with primary and secondary products of the title reaction do not contribute significantly to its loss. A complete list of the values of k₄ obtained under various experimental conditions is given in Table 2 and plotted in Arrhenius form in Fig. 4. The regression through the data points is described by k₄(T) = 7.5 × 10⁻¹³ exp[(−1034 ± 40)/T]. The average, room-temperature (296 ± 2) K rate coefficient is 2.32 × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹. The total uncertainty associated with the rate coefficients obtained (and derived from the Arrhenius expression), is dominated by uncertainty in the concentration of CH₃ONO₂ and is estimated to be ∼ 5% (see ESI,† Section S4).

Table 2 Experimental conditions and rate coefficients (k₄) for the reaction OH + CH₃ONO₂

T (K)	p (torr)	k 4 (10^−14 cm^3 molecule^−1 s^−1)	Δk4^a (10^−14 cm^3 molecule^−1 s^−1)	Bath gas
Notes: All rate coefficients were obtained using the 351 nm photolysis of HONO as OH-source.a Uncertainty is 2σ, statistical only.
223.3	101.2	0.84	0.07	He
231.7	134.6	0.78	0.09	N2
239.6	134.3	0.87	0.09	N2
247.3	135.7	1.05	0.10	N2
251.5	134.8	1.28	0.05	N2
259.7	127.0	1.42	0.07	N2
266.0	136.3	1.49	0.10	N2
268.7	135.2	1.56	0.10	N2
276.2	134.8	1.69	0.09	N2
282.2	135.1	1.86	0.12	N2
289.0	135.1	2.07	0.15	N2
294.2	101.6	2.28	0.11	He
294.5	135.5	2.21	0.20	N2
295.2	98.8	2.14	0.13	N2
295.8	133.5	2.39	0.08	N2
296.2	99.1	2.41	0.15	N2
296.7	201.0	2.48	0.15	N2
297.5	135.1	2.34	0.17	N2
297.7	400.4	2.12	0.30	N2
298.0	134.0	2.31	0.15	N2
298.2	68.5	2.23	0.18	N2
317.8	135.2	2.78	0.19	N2
342.7	135.4	3.62	0.22	N2

---

Fig. 4 Arrhenius plot of k₄versus inverse temperature. In blue: k₄ from generation of OH from HONO photolysis at 351 nm. In red, the exponential fit to the data with 2σ confidence limit. In green: k₄ from generation of OH from CH₃ONO₂ photolysis at 248 nm. In purple: k₄ from generation of OH from CH₃ONO₂ photolysis at 248 nm considering only data at t > 1.7 ms.

3.2 Generation of OH from CH₃ONO₂ or H₂O₂ photolysis at 248 nm (298 K)

As described above, the photolysis of methyl nitrate at 248 nm indirectly produces OH. Based on the CH₃ONO₂ concentration, the laser fluence and the photolysis quantum yields at 248 nm,¹⁵ between 8 × 10⁸ and 2 × 10⁹ molecule cm⁻³ of OH are generated via R8 and R9 when [CH₃ONO₂] is varied from 7.4 × 10¹⁵ to 2.1 × 10¹⁶ molecule cm⁻³. At the same time 1.4 × 10¹¹ to 3.9 × 10¹¹ molecule cm⁻³ of NO₂ and CH₃O are formed.

Fig. 5 displays OH time profiles from the photolysis of six different concentrations of CH₃ONO₂. The OH decays are bi-exponential, with well separated production and loss terms. The rapid production of OH (via R9) is followed by a slower decay as OH is lost (mainly) via R4. The solid lines are fits to the data according to:

where is the pseudo-first order term dominated by H-atom loss via its reactions with CH₃ONO₂(R9). In principle, values of k₄ and k₉ can be extracted from the data by plotting and versus the concentration of CH₃ONO₂ as displayed in Fig. 6. From the regression slopes we derive k₄(298 K) = (1.37 ± 0.19) × 10⁻¹⁴ and k₉(298 K) = (1.68 ± 0.45) × 10⁻¹³ cm³ molecule⁻¹ s⁻¹. The y-axis intercept of 75 ± 22 s⁻¹ for the plot of versus [CH₃ONO₂] is consistent with diffusive losses of OH. The much larger intercept for the plot of versus [CH₃ONO₂] stems from H-atom diffusion and possibly reaction of H atoms with O₂ present as impurity.

Fig. 5 OH formation and decay when different concentrations of CH₃ONO₂ were photolyzed at 248 nm.

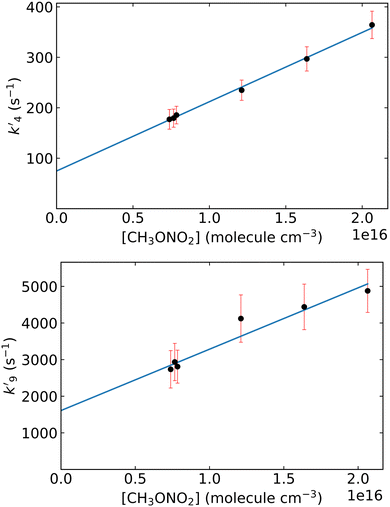Fig. 6 First-order rate coefficients k′ for OH generation and loss derived from the bi-exponential fits (eqn (4)) to OH profiles obtained by photolysis of CH₃ONO₂ at 248 nm and plotted against the corresponding methyl nitrate concentration [CH₃ONO₂] in molecule cm⁻³. Error bars represent 2σ statistical uncertainty. The solid lines are linear regressions where the slopes correspond to the rate coefficients k₄ (upper panel) and k₉ (lower panel).

The value of k₄ thus obtained is a factor ≈ 1.6 lower than the average room-temperature value (2.32 × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹) obtained in the experiments in which OH was generated by the 351 nm photolysis of HONO. A different data treatment, in which only the latter part of the bi-exponential profile (t > 1700 μs) was analysed (i.e. after all H atoms have been converted to OH via reaction with CH₃ONO₂) results in a rate coefficient of (1.65 ± 0.10) × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹, which is also lower (factor 1.4) than that obtained using HONO photolysis. As the photolysis of CH₃ONO₂ at 248 nm results mainly in the formation of CH₃O and NO₂ and OH reacts rapidly with both (k(OH + NO₂) = 3.6 × 10⁻¹² cm³ molecule⁻¹ s^−1 5 and k(OH + CH₃O) = 3 × 10⁻¹¹ cm³ molecule⁻¹ s^−1 19 at 298 K and 100 torr), the unavoidable presence of CH₃O and NO₂ would be expected to result in an overestimation of the rate coefficient via this method. In the ESI† we use numerical simulations to examine the impact of secondary reactions and the effect of simultaneous detection of both OH and CH₃O (resulting in “OH” profiles that are not perfectly bi-exponential). Clearly, the photolysis of CH₃ONO₂ with complex secondary chemistry does not lend itself to accurate measurement of the OH-rate coefficient. As shown in Fig. 6, the linear relationship between k’₉ and [CH₃ONO₂] enables us to derive an approximate rate coefficient (k₉) for the OH-forming reaction of H + CH₃ONO₂. Our result is k₉(298 K) = (1.68 ± 0.45) × 10⁻¹³ cm³ molecule⁻¹ s⁻¹, where the uncertainty is 2σ, statistical only. This result is in good agreement with that reported by Talukdar et al.¹⁵ using an almost identical method and similar analysis.

The photolysis of H₂O₂ is commonly used as a source of prompt OH radicals in PLP–PLIF experiments. The generation of OH via 248 nm photolysis of H₂O₂ in the presence of CH₃ONO₂ does however not result in exponential OH decays. The more complex behaviour compared to that observed when using HONO at 351 nm as OH precursor is related to the photolysis of CH₃ONO₂ at 248 nm (see above). Values of k′ obtained using this method were strongly dependent on the 248 nm pulse energy and no linear relationship with the concentration of methyl nitrate was found. Clearly, as described above for experiments in the absence of H₂O₂, the photolysis of methyl nitrate at 248 nm precludes a straightforward analysis of the OH-profiles thus obtained.

3.3 Comparison of k₄ with literature values and the CH₃ONO₂ atmospheric lifetime

The low rate coefficient for the reaction of OH with CH₃ONO₂ is consistent with the reaction proceeding via H-atom abstraction from the methyl group, with each C–H bond contributing about 1 × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹ to the rate coefficient at room temperature. Kinetic isotope effects⁸ confirm that H-atom abstraction is the only significant pathway for the title reaction in the temperature range representative of our atmosphere.

In order to compare our rate coefficients and their temperature dependence with literature values, we consider only our data measured using the photolysis of HONO at 351 nm, which are not biased by complex secondary processes involving photo-fragments of CH₃ONO₂. Table 3 and Fig. 7 compare the room temperature rate coefficients and Arrhenius expression obtained in this work with those reported in the literature.

Table 3 Comparison with previous determinations of k₄

Source	k 4 (cm^3 molcule^−1 s^−1)	T (K)	Method
PLP–PLIF = Pulsed laser photolysis/pulsed laser induced fluorescence; DF-RF = discharge flow/resonance fluorescence; PR-RA = pulse radiolysis/resonant absorption; RR = relative rate.
This work	(2.32 ± 0.04) × 10^−14	296 ± 2	PLP–PLIF
	7.5 × 10^−13 × exp[(−1034 ± 40)/T]	223–343
Gaffney et al.^9	(3.4 ± 0.4) × 10^−14	298	DF-RF
Nielsen et al.^22	(3.2 ± 0.5) × 10^−13	298 ± 2	PR-RA
	8.8 × 10^−15 × exp[(1050 ± 180)/T]	298–393
	(3.1 ± 0.7) × 10^−13	298 ± 2	RR
Talukdar et al.^8	(2.36 ± 0.16) × 10^−14	298	PLP–PLIF
	8.2 × 10^−13 × exp[(−1020 ± 60)/T]	221–414
Shallcross et al.^23	(4.7 ± 1.0) × 10^−14	298	DF-RF
	4.1 × 10^−13 × exp[(−604 ± 121)/T]	298–423
Kerr and Stocker^20	(3.8 ± 1.0) × 10^−13	303 ± 2	RR
Kakesu et al.^3	(3.0 ± 0.7) × 10^−14	307 ± 3	RR

---

Fig. 7 Arrhenius plot of k₄versus inverse temperature. The rate coefficients and experimental conditions of the present work can be found in Table 3.

Absolute rate coefficient measurements. When considering only those studies that used absolute methods, our room-temperature rate coefficient is essentially identical to that of Talukdar et al.,⁸ but factors of 13, 1.4 and 2 lower than those reported by Nielsen et al.,¹⁰ Gaffney et al.⁹ and Shallcross et al.,¹¹ respectively. For slow reactions such as OH + CH₃ONO₂, reactive impurities and secondary reactions of OH (e.g. with products or photo-fragments) can bias the rate coefficients derived from absolute methods to higher values. In the study of Nielsen et al. (the only one to report a negative dependence of k₄ on temperature), the pulse-radiolysis technique generated not only very high concentrations of OH (∼10¹³ molecule cm⁻³) but also would have caused substantial fragmentation of CH₃ONO₂ (e.g. to CH₃O and NO₂). This probably explains the very large rate coefficient and anomalous temperature dependence observed.

The other temperature-dependent studies report a positive dependence on temperature, with values of E/R (in K) varying from −1054 (this work) to −1020 (Talukdar et al.⁸) and −604 (Shallcross et al.¹¹). While the two studies using the “wall-free” method of PLP–PLIF agree extremely well, the flow tube study of Shallcross et al. has a substantially weaker dependence on temperature. Close examination of their data set (5 data points all at T > 298 K) reveals considerable scatter in k₄, which is also seen in their plots of k′ versus [CH₃ONO₂]. We speculate that the difference in slope reflects changes in the wall loss rates of OH, which were determined at room temperature only. As mentioned above, absolute rate studies of slow reactions require that very pure samples are used. In this study and that of Talukdar et al.,⁸ spectroscopic checks were made to exclude the presence of specific reactive impurities. In the studies of Gaffney et al.⁹ and Shallcross et al.,¹¹ the sample purity was determined to be > 99%, but no attempt was made to detect impurities such as HNO₃, NO₂ or CH₃OH. Perhaps more pertinent however, is the fact that the two studies that utilized in situ (optical absorption) measurement of CH₃ONO₂ are in excellent agreement. In situ measurement of the concentration of the excess reactant removes uncertainty associated with calculating [CH₃ONO₂] from partial flows, pressures and variations in the mixing-ratios in storage bulbs. The fact that both this work and Talukdar et al.⁸ measured absorption cross-sections for CH₃ONO₂ at 213.86 nm that are in almost perfect agreement strongly suggests that the excellent agreement in the values of k₄ reported by these two groups is not fortuitous, but a result of multi-diagnostics and careful execution of the experiments, leading to derivation of the true rate coefficient.

Relative rate coefficient measurements. In principle, the relative rate measurements (all close to room temperature) should not be biased by reactive impurities in the CH₃ONO₂ sample, yet the results of the three relative-rate studies are highly divergent. The very large rate coefficients measured by Nielsen et al.¹⁰ and Kerr and Stocker²⁰ can be traced back to an inappropriate choice of reference reactants, which ideally should react with rate coefficients that are similar to the target molecule. The use of 2-methylpropane (k_{OH+2-methylpropane} = 2.1 × 10⁻¹² cm³ molecule⁻¹ s^−1 5) and ethene (k_OH+ethene = 7.8 × 10⁻¹² cm³ molecule⁻¹ s⁻¹ at 1 bar⁵) by Nielsen et al.¹⁰ and Kerr and Stocker,²⁰ respectively, would have made relative depletion rates of the reference and target molecule difficult to measure and also prone to other loss processes of CH₃ONO₂. In the relative rate study of Kakesu et al.,³ the more slowly reacting reference trace-gases, methane (k_OH+methane = 6.4 × 10⁻¹⁵ cm³ molecule⁻¹ s^−1 5) and ethane (k_OH+ethane = 2.4 × 10⁻¹³ cm³ molecule⁻¹ s^−1 5) were used. Those authors derived a rate coefficient at 307 K of (3.0 ± 0.7) × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹. Within combined uncertainty, this value agrees with the absolute rate coefficient derived in the present study for the same temperature: of k₄(307 K) = (2.7 ± 0.4) × 10⁻¹⁴ cm³ molecule⁻¹ s⁻¹.

Atmospheric lifetime of CH₃ONO₂ with respect to reaction with OH. As the rate coefficient for the title reaction is independent of pressure under all conditions of the Earth's lower atmosphere (i.e. the troposphere and lower stratosphere) we use the Arrhenius expression derived from our experiments using HONO as OH source: k₄(T) = 7.5 × 10⁻¹³ exp(−1034/T) to calculate the lifetime of CH₃ONO₂ with respect to OH loss. For this we assume an altitude independent, global mean OH concentration of 1 × 10⁶ molecule cm⁻³.²¹ The lifetime of CH₃ONO₂ w.r.t. OH reaction at different altitudes is plotted in Fig. S5 (ESI†) and varies from circa 500 days at ground level to > 1000 days at 10 km. Photolysis rate coefficients for CH₃ONO₂ vary from ∼3 × 10⁻⁷ s⁻¹ to 5 × 10⁻⁷ s⁻¹ in the boundary layer and lower stratosphere,¹⁵ respectively, resulting in lifetimes with respect to photodissociation of close to 1 month. Our data thus confirms the conclusion of Talukdar et al.¹⁵ showing that reaction with OH is a minor sink of CH₃ONO₂ in the atmosphere. This is in contrast to the conclusions of Nielsen et al.¹⁰ and Kerr and Stocker²⁰ who (based on too-high rate coefficients) suggested that reaction with OH is important.

4 Conclusions

Motivated by greatly divergent reports of the rate coefficient for the reaction of OH with CH₃ONO₂, we have determined the rate coefficient using pulsed laser photolysis-laser induced fluorescence. High-quality kinetic data were obtained when measures were taken to avoid the photolysis of CH₃ONO₂. Our result, a positive dependence of the rate coefficient on temperature described by k₄(T) = 7.5 × 10⁻¹³ exp[(−1034 ± 40)/T], is in close agreement with that reported by Talukdar et al..⁸ Both studies used in situ measurement of [CH₃ONO₂] using independently determined absorption cross-sections that agreed with 1.2%. The divergent results obtained by other groups are rationalised in terms of choice of OH source or reference reactant and data corrections.

Author contributions

This work was carried out as part-fulfilment of CF's master's degree in chemistry at the Julius-Maximilians-University, Würzburg, Germany. CF and FB conducted the experiments, CF evaluated the data and prepared the manuscript. JC conceptualized the experiment, JC and JL contributed to writing the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Open Access funding provided by the Max Planck Society.

Notes and references

1. J. M. Roberts, Atmos. Environ., Part A, 1990, 24, 243.
2. E. Atlas, Nature, 1988, 331, 426.
3. M. Kakesu, H. Bandow, N. Takenaka, Y. Maeda and N. Washida, Int. J. Chem. Kinet., 1997, 29, 933.
4. N. L. Ng, S. S. Brown, A. T. Archibald, E. Atlas, R. C. Cohen, J. N. Crowley, D. A. Day, N. M. Donahue, J. L. Fry, H. Fuchs, R. J. Griffin, M. I. Guzman, H. Herrmann, A. Hodzic, Y. Iinuma, J. L. Jimenez, A. Kiendler-Scharr, B. H. Lee, D. J. Luecken, J. Mao, R. McLaren, A. Mutzel, H. D. Osthoff, B. Ouyang, B. Picquet-Varrault, U. Platt, H. O. T. Pye, Y. Rudich, R. H. Schwantes, M. Shiraiwa, J. Stutz, J. A. Thornton, A. Tilgner, B. J. Williams and R. A. Zaveri, Atmos. Chem. Phys., 2017, 17, 2103.
5. IUPAC, Task Group on Atmospheric Chemical Kinetic Data Evaluation, (Ammann, M., Cox, R.A., Crowley, J.N., Herrmann, H., Jenkin, M.E., McNeill, V.F., Mellouki, A., Rossi, M. J., Troe, J. and Wallington, T. J.). Last access Sept. 2023, (https://iupac.aeris-data.fr/).
6. N. Butkovskaya, A. Kukui and G. Le Bras, J. Phys. Chem. A, 2012, 116, 5972.
7. F. Flocke, E. Atlas, S. Madronich, S. M. Schauffler, K. Aikin, J. J. Margitan and T. P. Bui, Geophys. Res. Lett., 1998, 25, 1891.
8. R. K. Talukdar, S. C. Herndon, J. B. Burkholder, J. M. Roberts and A. R. Ravishankara, J. Chem. Soc., Faraday Trans., 1997, 93, 2787.
9. J. S. Gaffney, R. Fajer, G. I. Senum and J. H. Lee, Int. J. Chem. Kinet., 1986, 18, 399.
10. O. J. Nielsen, H. W. Sidebottom, M. Donlon and J. Treacy, Chem. Phys. Lett., 1991, 178, 163.
11. D. E. Shallcross, P. Biggs, C. E. Canosa-Mas, K. C. Clemitshaw, M. G. Harrison, M. Reyes López Alañón, J. A. Pyle, A. Vipond and R. P. Wayne, J. Chem. Soc., Faraday Trans., 1997, 93, 2807.
12. M. Wollenhaupt, S. A. Carl, A. Horowitz and J. N. Crowley, J. Phys. Chem., 2000, 104, 2695.
13. W. D. Taylor, T. D. Allston, M. J. Moscato, G. B. Fazekas, R. Kozlowski and G. A. Takacs, Int. J. Chem. Kinet., 1980, 12, 231.
14. J. G. Calvert and J. N. J. Pitts, Photochemistry, J. Wiley, New York, 1966.
15. K. R. Talukdar, J. B. Burkholder, M. Hunter, M. K. Gilles, J. M. Roberts and A. R. Ravishankara, J. Chem. Soc., Faraday Trans., 1997, 93, 2797.
16. C. B. M. Groß, T. J. Dillon, G. Schuster, J. Lelieveld and J. N. Crowley, J. Phys. Chem. A, 2014, 118, 974.
17. G. L. Vaghjiani and A. R. Ravishankara, J. Chem. Phys., 1990, 92, 996.
18. A. P. Black and F. H. Babers, Org. Synth., 1939, 19, 64.
19. W. Tsang and R. F. Hampson, J. Phys. Chem. Ref. Data, 1986, 15, 1087.
20. J. A. Kerr and D. W. Stocker, J. Atmos. Chem., 1986, 4, 253.
21. J. Lelieveld, S. Gromov, A. Pozzer and D. Taraborrelli, Atmos. Chem. Phys., 2016, 16, 12477.
22. O. J. Nielsen, H. W. Sidebottom, M. Donlon and J. Treacy, Chem. Phys. Lett., 1991, 178, 163.
23. D. Shallcross, C. Canosa-Mas, K. Clemitshaw, M. Harrison, J. Pyle and R. Wayne, J. Chem. Soc., Faraday Trans., 1997, 93, 2807.

---

Footnote

† Electronic supplementary information (ESI) available. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cp00054d

---