New insights into the photocyclization reaction of a popular diarylethene switch: a nonadiabatic molecular dynamics study†
Mikołaj
Martyka
 ab and
Joanna
Jankowska
ab and
Joanna
Jankowska
 *a
*a
aFaculty of Chemistry, University of Warsaw, Pasteura 1, Warsaw, 02-093, Poland. E-mail: jjankowska@chem.uw.edu.pl
bInterdisciplinary Doctoral School, University of Warsaw, Dobra 56/66, Warsaw, 00-312, Poland
First published on 9th April 2024
Abstract
Diarylethene (DAE) molecular switches have continued to attract the attention of researchers for over 20 years. Their remarkable photophysical properties endow them with countless applications in photonics and molecular technologies. However, despite extensive experimental and theoretical research, the mechanism of DAE photoswitching is not yet fully rationalized. In this work, we investigate the ring closure dynamics of a popular DAE switch, 1,2-bis(3-methyl-5-phenyl-2 thienyl)perfluorocyclopentene (PT), using nonadiabatic molecular dynamics (NAMD) simulations. Employing the fewest switches surface hopping protocol, along with the semi-empirical multireference ODM2/MRCI-SD method, we investigate possible reaction pathways for this photoprocess, as well as their timescales and resulting photoproducts. Furthermore, using a dynamic configuration-space sampling procedure, we elucidate the role of triplet states in the photocyclization of PT, supporting available experimental data for the closely related DMPT molecule, which indicate an ultrafast intersystem crossing (ISC) transition competing with the singlet-driven photoswitching reaction. Our findings not only corroborate experimental studies on DAE switches, but also provide new mechanistic insights into the potential use in the rational design of DAE switches tailored for specific technological applications.
1 Introduction
Diarylethenes (DAEs) are an outstanding family of molecular switches, with numerous applications in fundamental science and new technologies.1–5 They are known for their high thermal stability,6 fatigue resistance7–9 and ultra-fast response time.10–12 Furthermore, they can be synthesised with relative ease,13 and are reactive in a variety of environments, including a wide range of solvents, gels, crystals, and nanoparticles.14–16Upon exposure to light, DAE compounds undergo a 6π, thermally irreversible16,17 photocyclization/cycloreversion reaction, switching between an open-ring, hexatriene-based isomer (OF), and a closed-ring, cyclohexadiene-like form (CF). The UV-induced cyclization reaction can be reversed under excitation of the closed form in the visible range. The photoswitching cycle of DAEs is schematically shown in Fig. 1. For most DAE molecules, two ground-state conformers of the OF exist in equilibrium: a parallel (P) rotamer, with the two side-rings being mirror reflections of each other (Cs symmetry), and an anti-parallel (AP) rotamer, exhibiting C2 symmetry.18–20 Because of the Woodward–Hoffman rules,21,22 only the AP rotamer is reactive in the photoswitching process. Both the cyclization and cycloreversion processes are assumed to proceed through a common conical intersection, involving breaking/formation of the central C1–C6 bond between the reactive carbon atoms.11,23,24
Among numerous photoswitches belonging to the DAE family, 1,2-bis(3-methyl-5-phenyl-2 thienyl)perfluorocyclopentene, commonly referred to as PT, and closely related DMPT (1,2-bis(2,4dimethyl-5-phenyl-3-thienyl)perfluorocyclopentene) stand out as particularly interesting photoswitches from both, pure and applied science, points of view. The photoswitching cycle of these systems is particularly highly biased: a trait exhibited to a certain extent by all DAE systems, meaning that the quantum yield of the photocyclization process is much higher than that of photocycloreversion. This property, along with outstanding fatigue resistance,25 and a two-photon amplification of the cycloreversion quantum yield23,24 allowed PT and DMPT to make their way into many technological applications,26–28 as well as made them the object of numerous fundamental studies.14,23,29
Owing to its popularity, a rich set of dedicated experimental studies deliver high-quality data describing PT photochemistry and photophysics. The first absorption maximum of PT-OF is reported at 280 nm (4.42 eV) in n-hexane,30 while PT-CF typically absorbs at 575 nm (2.16 eV).14,23,31 The closed-form isomer of PT exhibits weak fluorescence, emitting at 780–800 nm, when irradiated with 580 nm light.23 Fluorescence of the OF is much stronger, with a maximum at around 425 nm, upon 300 nm excitation. However, this open-isomer emission is attributed solely to the unreactive P conformer.32 The total photocyclization quantum yield of PT, ΦOF→CF, is reported to be 59%,14 which, after taking into account the actual fraction of the AP conformer, assumed to be ca. 0.6–0.7,23 translates to a quantum yield of around 90% per reactive AP molecule. On the other hand, the photocycloreversion yield of PT is exceptionally low, given at 1.3%.14,23,33 The cycloreversion process occurs on a timescale of ca. 12 ps,23 while the cyclization reaction is known to be ultra-fast, with sub-picosecond timescales reported for numerous DAE compounds,34 including 300 fs for DMPT.35 Until recently, both, the cyclization and the cycloreversion processes, were assumed to take place only within the singlet manifold of states. However, Hamdi et al. in their 2016 paper raised questions about this, discovering an unexpected and fast intersystem crossing process during the cyclization dynamics of the AP conformer of DMPT-OF.36 Conversely, the unreactive P isomer is reported as phosphorescent, decaying at a microsecond timescale, after a fast (22 ps in DMPT) intersystem crossing from the S1 state.35,36
Despite numerous difficulties arising from the complexity of the discussed photoprocess, several theoretical investigations have provided high-level insights into DAE photoswitching. The pioneers in this field were Nakamura and Irie in 1988, discovering a connection between the energy difference of the OF and CF isomers and the thermal stability of the system, using the semi-empirical MNDO method.37 A couple of years later, Majumundar et al.38 used the TD-DFT methodology with the B3LYP functional to study the impact of the Franck–Condon (FC) vertical excitation energy difference between the two switching forms on the performance of DAE switches. Several later works, by Uchida et al.39 and Asano et al.,40 started utilizing the multireference methodology for the study of DAE systems. Relaxed complete active space self-consistent field (CASSCF) calculations, supplemented with single point complete active space perturbation theory of the second order (CASPT2) results, yielded an accurate description of the excited states participating in the cycloreversion reaction, at least in the vicinity of the closed-form Franck–Condon region. In 2013, a work by Perrier et al.41 highlighted the necessity of including both static and dynamic electronic correlations for a proper description of the S1 and S2 states. Recently, the photoswitching of DAE systems was studied at the TD-DFT,42 spin–flip TD-DFT,43 and semi-empirical44 levels of theory, with reported relaxed potential energy profile scans along the reaction coordinate. Several studies investigated this photo-reaction by means of molecular dynamics;45–47 however, due to the size and demanding nature of the system, they were only limited to model, truncated molecules. Recently, our group conducted the first study of a full-size DAE system using on-the-fly nonadiabatic molecular dynamics, which stood in good agreement with available experimental data.48
The aim of this investigation is to provide theoretical insights into the photocyclization reaction of PT at a previously unavailable dynamic level. To achieve this, we employ the cutting-edge ODM2/MRCI-SD semi-empirical methodology, coupled with the tried-and-true fewest switches surface hopping algorithm, to investigate the possible reaction pathways, and conical intersections through which they proceed, the timescales, as well as the formed photoproducts. Furthermore, an analysis of intersystem crossing effects is performed, using a dynamic configuration-space sampling procedure, allowing for the inclusion of vibronic effects, in order to provide comprehensive insights into the role of triplet states in the PT photocyclization process.
This manuscript is organised in the following order: the Computational details section outlines the employed computational methods and protocols, as well as their settings. Next, in the Results and discussion section, the results of the investigation are presented, including: (1) characterization of the ground-state minima, relevant in the photoswitching process; (2) NAMD simulations of the PT cyclization process; (3) photophysics of the unreactive PT-twist form, and its potential ISC mechanism to the triplet manifold of states. The findings are summarised in the Conclusions section.
2 Computational details
2.1 Electronic structure methods
In all ODM2/MRCI-SD calculations, the half-electron restricted open-shell Hartree–Fock formalism60 was applied for the initial SCF step, with two singly occupied orbitals: the HOMO and the LUMO. During the MRCI calculations, the SCF configuration (of singlet multiplicity for calculations within the singlet manifold of states, and triplet when the system is within the triplet manifold of states) was supplemented with two additional reference state functions: the closed shell HOMO–HOMO and doubly excited LUMO–LUMO configurations. The MRCI-SD procedure included all single and double electronic excitations from these references, restricted to electron transfers from and to orbitals included in the active space (AS). The AS consisted of 6 electrons in 8 orbitals in all semi-empirical calculations, and was previously tested by our group for closely related DAE systems.44 Contour plots of the AS orbitals can be found in Section S1 of the ESI,† while the Cartesian coordinates of all optimized minima, as well as minimum-energy conical intersection points, can be found in Section S7 of the ESI.† Through this study, we have chosen to keep the ODM2/MRCI-SD orbital active space equal in size between different forms of PT. Due to this fact, the chosen active space may not always conform to the approximate symmetry of the given PT isomer. However, this factor does not impact the geometrical conformation of PT in a substantial manner, as supporting DFT optimizations (discussed in Section 2.1.2) remain in very good agreement with the ODM2/MRCI-SD results.
The spin–orbit coupling matrix elements (SOC-MEs) were computed using the spin–orbit mean-field (SOMF) approximation,67–69 using ORCA, with the inclusion of one-electron terms, exact Coulomb terms, and exchange terms modelled by exact one-centre integrals including the spin–other orbit interaction (corresponding to the SOCFlags option set to 1,4,3,0). The magnitude of the SOC-ME reported throughout this manuscript is obtained by taking the module square of the coupling vector.
The structures of the studied S0 and S1 minima were benchmarked at the density functional theory level. For the ground-state minima, as well as in the excited-state TD-DFT calculations, structural reoptimizations were performed using the range-separated hybrid ωB97X-D functional,70 again combined with the cc-pVDZ basis set. The Tamm–Dancoff approximation (TDA)71 was used in all TD-DFT calculations. A detailed analysis of the DFT benchmark data can be found in Section S3 in the ESI,† along with the Cartesian coordinates of all the reoptimized molecular structures. Furthermore, the obtained agreement between DFT and semi-empirical optimizations in the geometrical parameters of PT may be used as a validation of the chosen AS in ODM2/MRCI-SD calculations.
2.2 Nonadiabatic molecular dynamics
For the propagation of the nonadiabatic molecular dynamics, Tully's fewest switches surface hopping (FSSH)72,73 algorithm was used, as implemented in the MNDO99 package, with orbital phase tracking between the consecutive dynamics steps. Initial conditions were sampled from a 4 ps microcanonical-ensemble molecular dynamics (MD), which was preceded by a 4 ps thermalization run within the canonical ensemble. Sampling initial conditions from the ground-state Born–Oppenheimer molecular dynamics (BOMD) allow for a straightforward inclusion of finite-temperature effects and anharmonic vibrational contributions into the initial conditions, making the BOMD the method of choice for a system like PT, expected to be heavily influenced by large-amplitude side-ring vibrations and rotations.A 298 K Nose–Hoover thermostat74 with a chain length of 10 and a characteristic time of 0.05 ps was used in the thermalization step. The time step for the nuclear motion was set to 0.5 fs in all dynamic simulations. In the initial conditions generation procedure, the starting points (molecular structures and atomic velocities) were filtered according to the optical transition probability, with an excitation energy window of 4.10 ± 0.15 eV, using the following equation:75
 | (1) |
Eventually, a set of 168 (125) NAMD trajectories were run in the PT-OF (PT-twist) dynamics. The maximum propagation times were set to 1800 fs and 2000 fs, respectively. All relevant properties, such as gradients and nonadiabatic coupling (NAC), were obtained analytically on-the-fly at the ODM2/MRCI-SD level. Electronic motion was propagated using the unitary propagator evaluated at the middle point,76 with electronic structure integration performed every 0.0025 fs. The adaptive time step algorithm77 was also employed, with an energy change threshold set to 0.01%, and a maximum number of step reductions of 10. Decoherence was accounted for using Shenvi–Subotnik's parameterless correction and the phase of the AS orbitals was tracked between subsequent NAMD steps.78 To ensure energy conservation, nuclear velocities were rescaled after hopping, along the direction of the NAC vector. Frustrated hops (with the nuclear velocity component along the NAC vector too small to compensate for the energy change due to surface switching) were rejected, and the velocity along the NAC vector was reversed.
To explicitly account for vibronic effects impact on the intersystem crossing during the PT photorelaxation, a procedure of dynamic configuration-space sampling was applied. From each of the 125 PT-twist NAMD trajectories, 30 snapshots were randomly selected and used for the evaluation of molecular properties. In this protocol, spin–orbit coupling matrix elements, as well as energies of the T1, S0, S1, and S2 states were determined at the QD-NEVPT2 level of theory in a single-point manner. From the total of 3750 sampled geometries, 1624 were discarded due to numerical errors, leaving 2126 samples available for analysis.
2.3 Data analysis
This work follows a two-letter convention for naming electron configurations appearing in the configuration interaction expansion: A–B denotes a configuration in which an electron was removed from orbital(s) A and placed on orbital B, with respect to the closed-shell HOMO–HOMO configuration. For example, H1–L1 is a configuration constructed by moving a single electron from the HOMO-1 orbital to the LUMO+1 orbital, and HH–LL is a doubly excited configuration, in which two electrons were moved from the HOMO to the LUMO.Molecular dynamics-averaged electronic absorption spectra were obtained using a Lorentzian broadening:
 | (2) |
The reaction quantum yields, ΦA→B, have been calculated as a fraction of trajectories relaxing to a given photoproduct (NB), to the total number of trajectories starting from A and relaxing to S0 (Ntraj):
 | (3) |
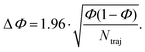 | (4) |
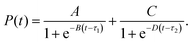 | (5) |
3 Results and discussion
3.1 Ground-state properties of PT
In the first step of the investigation, ground-state minima of PT, corresponding to the open- and closed-ring isomers, were optimized at the ODM2/MRCI-SD level. In line with previous findings regarding DAE systems,44 PT-OF proved to be the global minimum in S0, with the PT-CF form less stable by 0.28 eV. The C1–C6 distance, which can be interpreted as a leading reaction coordinate in the photocyclization/cycloreversion process, takes values of 1.54 Å in PT-CF and 3.50 Å in PT-OF. In the CF minimum, the DAE core of the molecule remains relatively flat, with the φ1 and φ2 angles of 5 and 8 degrees. Conversely, in the OF form, the thiophene moieties lay at an angle with respect to the perfluoro-pentane ring, with φ1 and φ2 angles equal to 50 and 53 degrees. The discussed structures were reoptimized using DFT, as described in Section 2.1.2. The global-minimum character of the OF is maintained in the DFT calculations, with PT-OF being stabilized by 0.49 eV with respect to PT-CF. The obtained geometric structures match the ODM2/MRCI-SD minima very well, with the same predicted C1–C6 distance, and very similar values of the φ1 and φ2 dihedral angles, differing by no more than 5 degrees from the ODM2/MRCI-SD results.The PT vertical absorption properties, computed at the semiempirical and ab initio levels of theory, are summarised in Table 1. For most diarylethene photoswitches, the first excited state is found bright, dominated by a H–L contribution. The second excited state is predicted to be dark, with contributions mainly from an H1–L configuration for PT-OF. For the closed-form, however, the S2 wavefunction is predicted to be distinctly multiconfigurational, dominated by a doubly-excited HH–LL determinant. Compared to experiment,30 for the OF isomer, both applied methods underestimate the absorption energy by ca. 0.3 eV (experimental value: 4.42 eV/280 nm), while a blue-shift of about 0.6 eV is observed for PT-CF at the semiempirical level, with ab initio yielding a fairly accurate value (2.16 eV/575 nm measured experimentally in n-hexane14,23,31). TD-DFT vertical excitation energies computed using DFT-optimized minima of PT predict PT-OF to absorb at ΔE = 4.37 eV (283 nm), which improves upon the ODM2/MRCI-SD and QD-NEVPT2 predictions; however, ΔE = 2.72 (456 nm) for PT-CF replicates the blue-shift obtained at the semi-empirical level.
| PT-OF | PT-CF | |||||
|---|---|---|---|---|---|---|
| ΔE | f | Orbs | ΔE | f | Orbs | |
| ODM2/MRCI-SD | ||||||
| S1 | 4.11 (B) | 0.1462 | H–L (92%) | 2.77 (B) | 0.2230 | H–L (92%) |
| S2 | 4.60 (A) | 0.0640 | H1–L (88%) | 3.68 (A) | 0.0033 | HH–LL (50%) |
| H1–L (22%), H–L1 (21%) | ||||||
| QD-NEVPT2 | ||||||
| S1 | 4.07 (B) | 0.2152 | H–L (75%), H1–L (15%) | 2.16 (B) | 0.3871 | H–L (88%) |
| S2 | 4.57 (A) | 0.0857 | H1–L (72%), | 3.50 (A) | 0.0010 | HH–LL (48%) |
| H–L (15%) | H–L1 (18%) | |||||
| H1–L (15%) | ||||||
3.2 NAMD simulation of the PT photocyclization process
In the next step, nonadiabatic dynamics runs, simulating the relaxation of PT-OF after the optical excitation, were performed. First, the dynamic, MD-averaged electronic spectra were prepared, as plotted in Fig. 2, along with marked individual contributions from the S0 → Sx transitions. The overall shape of the absorption spectrum, as well as its secondary features, match the experimental data reasonably well with the previously indicated systematic energy shifts. | ||
| Fig. 3 Electronic state population evolution in the photo-cyclization dynamics of PT. The states S0, S1, and S2 have been marked respectively in black, red, and blue. | ||
Characteristic timescales of the nonradiative relaxation were extracted from the simulation data by fitting a double-sigmoid decay curve, given by eqn (5). The parameters A and C can be interpreted as the fraction of the excited state population relaxing with timescales of τ1 and τ2, respectively. From the fitted parameters’ values, given in Section S4 of the ESI,† along with their uncertainties, we can conclude that about 53% of the trajectories relax at a timescale of τ1 = 342 fs, and 41% with τ2 = 766 fs, while the remaining 6% remains primarily in the S1 state. The fitted timescales stand in good agreement with the experimental data, which report the cyclization process occurring on a sub-picosecond timescale in most diarylethene derivatives.12,34,35 Interestingly, the observed time interval between the two obtained timescales lies close to a characteristic excited-state DAE vibration (v = 67 cm−1; τ = 498 fs) involving anti-symmetric out-of-plane rocking of the thiophene rings about φ1 and φ2 which, in the vicinity of the S1/S0 conical intersection, has a strong impact on the S1/S0 energy gap.40,45
Of the 150 trajectories relaxing in the vicinity of MECI-CC, PT-OF and PT-CF are the only photoswitching products observed in the simulations. The closer inspection of trajectories relaxing viaMECI-PT reveals that 3 of 7 such trajectories form an alternative photoproduct in which the hydrogen atom is permanently bonded to the C5H6 ring, whilst the remainder recreates PT-OF. This alternative deactivation channel can be thought of as a side process, lowering the cyclization quantum yield of the studied DAE system. It should be noted that an unequivocal distinction between a proton-transfer or a hydrogen atom-transfer nature of the observed process is hard to make in the studied case, since the proton-donating and proton-accepting moieties are directly conjugated electronically. Moreover, the existence and role of this deactivation channel may be dependent on the solvent used; this effect, however, was not investigated in the present study. The Cartesian coordinates of the optimized S0 structure of this alternative photoproduct can be found in the ESI,† in Table S14. The S0 → S1 transition energy of this new form is found to be 4.08 eV, making it practically indistinguishable from PT-OF in a simple UV-Vis absorption experiment, while the adiabatic energy of its optimized structure is found to be 0.62 eV relative to PT-OF.
In Fig. 5, one can find the distribution of the final C1–C6 distances, i.e., distances measured in the last geometrical structure of every trajectory in the cyclization dynamics simulations. Taking C1–C6 < 2.00 Å as a fingerprint of the successful CF product formation and applying eqn (3), one can determine the total photocyclization quantum yield of Φ = 78 ± 6%. This value corresponds reasonably with available experimental data, typically reporting a quantum yield of 96% per reactive PT-OF (AP) molecule (46% overall).14,23 Moreover, if one excludes trajectories that relaxed to S0viaMECI-PT, the theoretically estimated Φ value increases to 83 ± 6%.
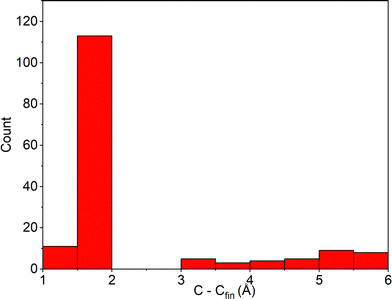 | ||
| Fig. 5 C1–C6 distance distribution of trajectories that underwent deactivation to S0, at the end of the photocyclization process of PT. | ||
We now turn to the unrelaxed portion of trajectories, which remained in the excited state in the PT-OF dynamics. Structural analysis reveals that most of them (8 out of 10 trajectories) adopt a twisted geometry, PT-twist, with the thiophene-phenyl moieties being oriented perpendicularly with respect to the central ring, as shown in Fig. 6, resulting in the new, potentially unreactive OF conformation. This seems to remain in line with experimentally observed slow decay proceeding via an unspecified conformational change, reported for several different DAE systems.81,82 Interestingly, a similar anti-parallel geometry was observed by Sotome et al. in an inverse DAE molecule with the same substituents (i.e., with phenyl at positions 5 in the thiophene ring), and was considered nonreactive.83 To determine the role of the PT-twist form in the PT-OF photodynamics, in the remaining part of the manuscript, we focus on the investigation of its possible relaxation pathways.
 | ||
| Fig. 6 A comparison of molecular structures of the newly found unreactive twisted form, PT-twist (a), and the reactive AP conformer of PT-OF (b). | ||
It should be kept in mind that the presented simulations are performed in the gas phase, while most experiments concerning the photophysics and photochemistry of DAE systems are performed in solution. This can have an impact on the possible relaxation pathways of the system, and the formed photoproducts. The viscosity of the solvent can hinder the conformational change from the PT-OF to PT-twist, decreasing the overall prevalence of this reaction channel. While the experimental data reporting fast ISC in DMPT was obtained in chloroform, which has a quite low viscosity, experiments conducted for different DAE switches81,82 in high viscosity solvents (cis- and trans-decalin) show that the solvent viscosity can have an impact on the deactivation pathways of DAE systems. Aside from this, the presence of a solvent could also impact the transition energies in the studied DAE molecule (so called solvent shifts). The S0 → S1 transition energies of all the ground-state and S1 minima found in this study, with the several different solvents accounted for under the conductor-like screening model (COSMO),84 are found in Table S8 of the ESI.† At this level of theory, the solvent has a negligible effect on the absorption properties of PT-CF; however, it adds an observable red-shift to the absorption maxima of the PT-OF and PT-twist, which increases with the dielectric constant of the solvent. At the same time, however, a parallel shift of the low-lying triplet state energies is observed. Eventually, it should be expected that, while the absolute transition energy values are sensitive to the environment, the proposed deactivation mechanism should be most likely prevalent in varying conditions, at least as long as they remain similar to the ones commonly chosen in DAE experiments.
3.3 Photophysics of the PT-twist
Single-point QD-NEVPT2 calculations performed at the optimized PT-twist S1-minimum reveal a small S1–T1 SOC-ME of 1.42 cm−1, unlikely to facilitate an ISC to the triplet manifold of states directly, with a singlet–triplet energy gap, ΔST, of 0.13 eV. Interestingly, the S1 and S2 states are near-degenerate at this point, separated by 0.22 eV, with the wavefunction of the former comprising mainly the H–L configuration, and the latter composed predominantly of the H1–L configuration. Here, the HOMO and HOMO-1 orbitals are of π character and are localised on either of the thiophene rings, while the LUMO is a π* orbital localised on the C3–C4 double bond. The QD-NEVPT2 optimized orbital contours can be found in the ESI,† in Fig. S8. Higher triplet states, T2 and T3, are found to be almost-degenerate, and energetically above S1 by about 0.2 eV. The SOC-ME between S1 and T2 and T3 are found to be 2.84 cm−1 and 7.75 cm−1.
A ground-state ODM2/MRCI-SD optimization starting from the PT-twist geometry reveals an additional S0 minimum corresponding to this form, which has not been identified before. Here, the thiophene rings are almost perpendicular to the cyclopentyl plane, with φ1 = 89 degrees and φ2 = 113 degrees, and the C1–C6 amounts to 4.84 Å. The S1 excitation energy at the S0-optimized structure is found to be 4.90 eV, with a moderate oscillator strength of f = 0.0504, leading to the H–L+1 orbital contribution. The S2 and S3 states are both bright, with oscillator strengths of f = 0.4041 and 0.3470, and with corresponding transition energies of 5.03 eV and 5.13 eV, respectively. Energetically, this new structure is almost degenerate with PT-OF: at the applied level of semi-empirical theory, it was found to lie even 0.04 eV lower. At the same time, it should be expected that the interaction between PT and typical solvents used in DAE experiments will stabilise the PT-OF form. Indeed, upon a single-point check performed at the ODM2/MRCI-SD level with the COSMO cyclohexane environment, the relative PT-twist form energy increases to +0.07 eV, remaining in line with the originally assumed global-minimum role of the PT-OF structure. Reoptimization at the DFT level yields a ground-state minimum of the PT-twist, with a relative energy of +0.28 eV with respect to the DFT-optimized PT-OF global minimum.
The observed photodynamics of the PT-twist can be compared with the experimental results by Hamdi et al., reporting an ISC of the AP form in a very similar DAE system to occur within just 1 ps. This, along with no reported evidence for fluorescence originating from the AP form of PT or DMPT, and the slow or nonexistent internal conversion process of the PT-twist observed in NAMD simulations, leaves a vibration-mediated deactivation pathway through the triplet states as the most plausible deactivation mechanism of the PT-twist, which we investigate in more detail below.
Due to the rather low energy gap between the S1 singlet state and T2 and T3 triplet states, it is possible that ISC could occur in other triplet states than T1. If a quantitative estimation of ISC time constants was to be performed, the effect of coupling between the S1 and T2 and T3 should be taken into account. However, the conducted study only aims at proving qualitatively the possibility of ISC during the cyclization reaction of PT (supporting available experimental data). Henceforth, we will only consider the ISC process from the S1 state to the lowest lying triplet state, T1.
First, focusing on the role of angles between the perfluoro-pentane ring and the thiophene moieties, φ1 and φ2 (Fig. 7a), one can notice that the magnitude of the SOC-ME peaks when one of the angles is equal to approximately 90 degrees, i.e., when the planes of the perfluoro-pentane and the thiophene rings are orthogonal to each other. This leads to a negligible overlap between molecular orbitals of the two sub-systems, breaking the π-electronic conjugation.
Second, one can take a look at the correlation between the length of the central C3–C4 bond and the SOC-ME value shown in panels (b) and (c) of Fig. 7, with ϕ1 and ϕ2 angles marked on the x axis, respectively. From these plots, it can be immediately observed that a shorter C3–C4 distance favours a higher value of SOC-ME. This effect is particularly synergistic with the φ angle rotation, with SOC-ME reaching values well over 10 cm−1 when both of these parameters align.
The C3–C4 distance can be used as an indicator of the central cyclohexatriene bond character: smaller values, of about 1.35–1.40 Å, indicate a double bond, with an sp2 hybridisation of C3 and C4, while larger values, of 1.45–1.55 Å, mean a single bond, with both the atoms sp3-hybridised. It is worth mentioning that a phenomenon similar to the one discussed here has been observed previously, experimentally and theoretically, for phenylthiophene compounds.85 Our findings are in line with the therein predicted increased quinoid-like character of the excited state (increase in the double-bond character of C3–C4), as well as the non-planarity of the excited state driving the intersystem crossing. The latter effect is known to impact spin–orbit coupling in other systems as well.86,87
Another key factor that needs to be take into account in order to estimate the rate of the intersystem crossing is the energy gap between the S1 and T1 states. In most cases, the ΔST value in the PT-twist dynamics is quite small, remaining below 0.50 eV. Moreover, sometimes the singlet–triplet energy difference even drops to a negative value, indicating a vibrationally induced Hund's rule violation. Color-coded heat maps, analogous to the SOC maps, illustrating the dependence of ΔST on the same geometric parameters are found in Fig. S11 in the ESI.† Overall, while the energy gap might be higher in some regions exhibiting particularly strong SOC, the PT system does not show a general correlation between ΔST and the magnitude of SOC-ME: in fact, there are plenty of sample points with SOC-ME well above 10 cm−1 and ΔST below 0.20 eV, as illustrated in Fig. 8.
 | ||
| Fig. 8 Correlation plot illustrating the magnitude of the SOC-ME and energy gap between the S1 and T1 states in the computed snapshots. | ||
The observed vibrationally induced increase of the SOC-ME and, hence, the expected enhanced ISC rate can also be interpreted in terms of El-Sayed's rules,88,89 stating that “the rate of intersystem crossing is relatively large if the radiationless transition involves a change of orbital type”.90 Here, the orbital type refers to its symmetry. In Fig. 9, one can find the QD-NEVPT2 orbital contours of an example sampling the snapshot with a high SOC-ME value. In this case, the T1 state's wavefunction is composed mainly of a H–L determinant, while S1 is of the H–L1 character. Both the HOMO and the LUMO+1 orbital are centred on the phenyl ring which tends to orient perpendicularly to the thiophene rings, while the LUMO is located on the thiophene moiety of the opposite aryl substituent. Thus, while the HOMO and LUMO+1 orbitals share the same plane of symmetry, the LUMO is symmetric with respect to an approximately orthogonal plane of the thiophene ring. As a result, a transition from the H–L+1 singlet state to the H–L triplet state involves a change of orbital symmetry and, following the El-Sayed rules, is predicted to provide an efficient pathway for the ISC process.
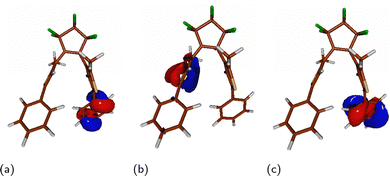 | ||
| Fig. 9 HOMO (a), LUMO (b), and LUMO+1 (c) orbital contours of the PT-twist optimized at a sample point exhibiting high spin–orbit coupling. | ||
Eventually, considering all the points discussed above, and taking into account the experimental evidence for ultrafast ISC in closely related DAE systems,36 we are inclined to assume the S1 → T1 ISC as the leading S1 decay mechanism for the PT-twist isomer.
Finally, to elucidate the fate of the system after the ISC process, an optimization of the T1 state was performed, at the ODM2/MRCI-SD level, starting from the S1 minimum of the PT-twist. The optimization yields a structure without major geometric rearrangements, with the only substantial difference being the increased piramidization of the C1 carbon atom. Here, the triplet state is of the H–L+1 character, with both orbitals delocalized over the entire phenylthiophene moiety, giving the potential T1 → S0 transition a local character. The Cartesian coordinates of the optimized triplet state, as well as the ODM2/MRCI-SD orbitals, can be found in the ESI,† in Table S15 and Fig. S5, respectively. The adiabatic energy of the T1 state is predicted to be 2.41 eV, with a T1/S0 energy gap of 1.35 eV (918 nm). This value seems to underestimate the phosphorescence energy by ca. 0.4 eV with respect to the experimentally reported, wide phosphorescence spectrum36 which, however, remains within the average accuracy of the ODM2/MRCI-SD method applied to DAE systems.
4 Conclusions
The ring-closure reaction of a popular diarylethene photoswitch, PT, was studied by means of the on-the-fly nonadiabatic molecular dynamics simulations. The conducted simulations allowed the available experimental results to be replicated with satisfactory accuracy as well as provided novel insights into the photo-relaxation mechanism of the open-ring PT form. Using a dynamic configuration-space sampling procedure, we identified the key forms and structural changes involved in the experimentally observed triplet deactivation pathway in dithienylethene molecules undergoing the photo-cyclization reaction. The spatial orientation of the thiophene rings as well as the character of the central bond in the hexatriene moiety were found to strongly influence the magnitude of the spin–orbit coupling. An additional singlet-mediated reaction pathway proceeding via proton/hydrogen atom transfer was identified and characterised. Our findings, on the one hand, support and rationalise the available experimental data on DAE photoswitches and, on the other hand, provide information that can guide the rational design of diarylethene systems for both fundamental research and technological applications.Author contributions
Mikołaj Martyka: writing – original draft, writing – review and editing, visualization, investigation, formal analysis, data curation, methodology, conceptualization, and software. Joanna Jankowska: writing – review and editing, validation, supervision, project administration, methodology, investigation, funding acquisition, and conceptualization.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the National Science Centre (Poland) for financial support through grant 2018/31/D/ST4/02219. The Polish high-performance computing infrastructure, PLGrid (HPC Centers: ACK Cyfronet AGH), is also gratefully acknowledged for providing computer facilities and support through computational grant no. PLG/2023/016751.Notes and references
- Y. Nakagawa, T. Hishida, K. Sumaru, K. Morishita, K. Kirito, S. Yokojima, Y. Sakamoto, S. Nakamura and K. Uchida, J. Med. Chem., 2023, 66, 5937–5949 CrossRef CAS PubMed.
- M. Yin, Q. Zhang, T. Fan, C. Fan, S. Pu, R. Krishna and F. Luo, Chem. Eng. J., 2023, 451, 139004 CrossRef CAS.
- L. Mao, H. Ding, X. Li, G. Liu and S. Pu, J. Photochem. Photobiol., A, 2022, 431, 114011 CrossRef CAS.
- Y. Chen, H. Wang, H. Chen, W. Zhang, S. Xu, M. Pätzel, C. Ma, C. Wang, I. McCulloch, S. Hecht and P. Samorì, Adv. Funct. Mater., 2023, 2305494 CrossRef CAS.
- Y.-Y. Tang, Y.-L. Zeng and R.-G. Xiong, J. Am. Chem. Soc., 2022, 144, 8633–8640 CrossRef CAS PubMed.
- S. Takami, S. Kobatake, T. Kawai and M. Irie, Chem. Lett., 2003, 32, 892–893 CrossRef CAS.
- H. Jean-Ruel, R. R. Cooney, M. Gao, C. Lu, M. A. Kochman, C. A. Morrison and R. J. D. Miller, J. Phys. Chem. A, 2011, 115, 13158–13168 CrossRef CAS PubMed.
- H. Jean-Ruel, M. Gao, M. A. Kochman, C. Lu, L. C. Liu, R. R. Cooney, C. A. Morrison and R. J. D. Miller, J. Phys. Chem. B, 2013, 117, 15894–15902 CrossRef CAS PubMed.
- K. Uno, M. L. Bossi, V. N. Belov, M. Irie and S. W. Hell, Chem. Commun., 2020, 56, 2198–2201 RSC.
- R. J. D. Miller, Science, 2014, 343, 1108–1116 CrossRef CAS PubMed.
- C. R. Honick, G. M. Peters, J. D. Young, J. D. Tovar and A. E. Bragg, Phys. Chem. Chem. Phys., 2020, 17–21 Search PubMed.
- M. Irie, T. Fukaminato, K. Matsuda and S. Kobatake, Chem. Rev., 2014, 114, 12174–12277 CrossRef CAS PubMed.
- Z. Li, J. Xia, J. Liang, J. Yuan, G. Jin, J. Yin, G. A. Yu and S. H. Liu, Dyes Pigm., 2011, 90, 290–296 CrossRef CAS.
- M. Irie, T. Lifka, S. Kobatake and N. Kato, J. Am. Chem. Soc., 2000, 122, 4871–4876 CrossRef CAS.
- K. Shibata, K. Muto, S. Kobatake and M. Irie, J. Phys. Chem. A, 2002, 106, 209–214 CrossRef CAS.
- M. Irie, Diarylethene molecular photoswitches concepts and functionalities, Wiley-VCH, Weinheim, 2021 Search PubMed.
- M. Hanazawa, R. Sumiya, Y. Horikawa and M. Irie, J. Chem. Soc., Chem. Commun., 1992, 206–207 RSC.
- A. J. Vazquez and N. S. Nudelman, J. Phys. Org. Chem., 2012, 25, 925–932 CrossRef CAS.
- Y. Ishibashi, M. Fujiwara, T. Umesato, H. Saito, S. Kobatake, M. Irie and H. Miyasaka, J. Phys. Chem. C, 2011, 115, 4265–4272 CrossRef CAS.
- Y. Ishibashi, T. Umesato, M. Fujiwara, K. Une, Y. Yoneda, H. Sotome, T. Katayama, S. Kobatake, T. Asahi, M. Irie and H. Miyasaka, J. Phys. Chem. C, 2016, 120, 1170–1177 CrossRef CAS.
- R. B. Woodward and R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 395–397 CrossRef CAS.
- R. B. Woodward and R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1969, 8, 781–853 CrossRef CAS.
- H. Sotome, T. Nagasaka, K. Une, S. Morikawa, T. Katayama, S. Kobatake, M. Irie and H. Miyasaka, J. Am. Chem. Soc., 2017, 139, 17159–17167 CrossRef CAS PubMed.
- H. Sotome, H. Okajima, T. Nagasaka, Y. Tachii, A. Sakamoto, S. Kobatake, M. Irie and H. Miyasaka, ChemPhysChem, 2020, 21, 1524–1530 CrossRef CAS PubMed.
- M. Herder, B. M. Schmidt, L. Grubert, M. Pätzel, J. Schwarz and S. Hecht, J. Am. Chem. Soc., 2015, 137, 2738–2747 CrossRef CAS PubMed.
- J. L. Butterfield, G. P. Penoncello, K. Dikshit and C. J. Bruns, ACS Appl. Nano Mater., 2022, 5, 13840–13844 CrossRef CAS.
- Y. Akaishi, A. D. Pramata, S. Tominaga, S. Kawashima, T. Fukaminato and T. Kida, Chem. Commun., 2019, 55, 8060–8063 RSC.
- K. Zheng, S. Han, X. Zeng, Y. Wu, S. Song, H. Zhang and X. Liu, Adv. Mater., 2018, 30, 1–5 Search PubMed.
- J. J. De Jong, W. R. Browne, M. Walko, L. N. Lucas, L. J. Barrett, J. J. McGarvey, J. H. Van Esch and B. L. Feringa, Org. Biomol. Chem., 2006, 4, 2387–2392 RSC.
- H. Shoji, D. Kitagawa and S. Kobatake, New J. Chem., 2014, 38, 933–941 RSC.
- D. Kitagawa, T. Nakahama, Y. Nakai and S. Kobatake, J. Mater. Chem. C, 2019, 7, 2865–2870 RSC.
- H. Sotome, K. Une, T. Nagasaka, S. Kobatake, M. Irie and H. Miyasaka, J. Chem. Phys., 2020, 152, 034301 CrossRef CAS PubMed.
- K. Morimitsu, S. Kobatake and M. Irie, Mol. Cryst. Liq. Cryst., 2005, 431, 451–454 CrossRef CAS.
- P. R. Hania, R. Telesca, L. N. Lucas, A. Pugzlys, J. van Esch, B. L. Feringa, J. G. Snijders and K. Duppen, J. Phys. Chem. A, 2002, 106, 8498–8507 CrossRef CAS.
- E. Pontecorvo, C. Ferrante, C. G. Elles and T. Scopigno, J. Phys. Chem. B, 2014, 118, 6915–6921 CrossRef CAS PubMed.
- I. Hamdi, G. Buntinx, A. Perrier, O. Devos, N. Jaïdane, S. Delbaere, A. K. Tiwari, J. Dubois, M. Takeshita, Y. Wada and S. Aloïse, Phys. Chem. Chem. Phys., 2016, 18, 28091–28100 RSC.
- S. Nakamura and M. Irie, J. Org. Chem., 1988, 53, 6136–6138 CrossRef CAS.
- D. Majumdar, H. M. Lee, J. Kim, K. S. Kim and B. J. Mhin, J. Chem. Phys., 1999, 111, 5866–5872 CrossRef CAS.
- K. Uchida, D. Guillaumont, E. Tsuchida, G. Mochizuki, M. Irie, A. Murakami and S. Nakamura, THEOCHEM, 2002, 579, 115–120 CrossRef CAS.
- Y. Asano, A. Murakami, T. Kobayashi, A. Goldberg, D. Guillaumont, S. Yabushita, M. Irie and S. Nakamura, J. Am. Chem. Soc., 2004, 126, 12112–12120 CrossRef CAS PubMed.
- A. Perrier, S. Aloise, M. Olivucci and D. Jacquemin, J. Phys. Chem. Lett., 2013, 4, 2190–2196 CrossRef CAS.
- M. G. Chiariello, U. Raucci, F. Coppola and N. Rega, Phys. Chem. Chem. Phys., 2019, 21, 3606–3614 RSC.
- E. Salazar, S. Reinink and S. Faraji, Phys. Chem. Chem. Phys., 2022, 24, 11592–11602 RSC.
- J. Jankowska, M. Martyka and M. Michalski, J. Chem. Phys., 2021, 154, 204305 CrossRef CAS PubMed.
- M. Boggio-Pasqua, M. Ravaglia, M. J. Bearpark, M. Garavelli and M. A. Robb, J. Phys. Chem. A, 2003, 107, 11139–11152 CrossRef CAS.
- C. Wiebeler and S. Schumacher, J. Phys. Chem. A, 2014, 118, 7816–7823 CrossRef CAS PubMed.
- A. Jarota, E. Pastorczak and H. Abramczyk, Phys. Chem. Chem. Phys., 2020, 22, 5408–5412 RSC.
- M. Martyka and J. Jankowska, J. Photochem. Photobiol., A, 2023, 438, 114513 CrossRef CAS.
- P. O. Dral, X. Wu, L. Spörkel, A. Koslowski, W. Weber, R. Steiger, M. Scholten and W. Thiel, J. Chem. Theory Comput., 2016, 12, 1082–1096 CrossRef CAS PubMed.
- A. Koslowski, M. E. Beck and W. Thiel, J. Comput. Chem., 2003, 24, 714–726 CrossRef CAS PubMed.
- W. Weber and W. Thiel, Theor. Chem. Acc., 2000, 103, 495–506 Search PubMed.
- P. O. Dral, X. Wu and W. Thiel, J. Chem. Theory Comput., 2019, 15, 1743–1760 CrossRef CAS PubMed.
- W. Thiel, MNDO99 v7.0 with upgrades, Max-Planck-Institut für Kohlenforschung, 2017 Search PubMed.
- M. R. Silva-Junior and W. Thiel, J. Chem. Theory Comput., 2010, 6, 1546–1564 CrossRef CAS PubMed.
- G. Cui and W. Thiel, Angew. Chem., Int. Ed., 2013, 52, 433–436 CrossRef CAS PubMed.
- Y.-J. Gao, X.-P. Chang, X.-Y. Liu, Q.-S. Li, G. Cui and W. Thiel, J. Phys. Chem. A, 2017, 121, 2572–2579 CrossRef CAS PubMed.
- Y. Lu, Z. Lan and W. Thiel, Angew. Chem., Int. Ed., 2011, 50, 6864–6867 CrossRef CAS PubMed.
- J. B. Schönborn, A. Koslowski, W. Thiel and B. Hartke, Phys. Chem. Chem. Phys., 2012, 14, 12193–12201 RSC.
- J. B. Schönborn and B. Hartke, Phys. Chem. Chem. Phys., 2014, 16, 2483–2490 RSC.
- M. J. S. Dewar, J. A. Hashmall and C. G. Venier, J. Am. Chem. Soc., 1968, 90, 1953–1957 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554–562 CrossRef CAS PubMed.
- B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef.
- J. Tatchen and C. M. Marian, Chem. Phys. Lett., 1999, 313, 351–357 CrossRef CAS.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- S. Hammes-Schiffer and J. C. Tully, J. Chem. Phys., 1994, 101, 4657–4667 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
- M. Barbatti, G. Granucci, M. Persico, M. Ruckenbauer, M. Vazdar, M. Eckert-Maksić and H. Lischka, J. Photochem. Photobiol., A, 2007, 190, 228–240 CrossRef CAS.
- E. Fabiano, T. Keal and W. Thiel, Chem. Phys., 2008, 349, 334–347 CrossRef CAS.
- L. Spörkel and W. Thiel, J. Chem. Phys., 2016, 144, 194108 CrossRef PubMed.
- J. E. Subotnik and N. Shenvi, J. Chem. Phys., 2011, 134, 024105 CrossRef PubMed.
- S. Wallis, J. Quant. Linguist., 2013, 20, 178–208 CrossRef.
- L. Spörkel, J. Jankowska and W. Thiel, J. Phys. Chem. B, 2015, 119, 2702–2710 CrossRef PubMed.
- H. Miyasaka, T. Nobuto, M. Murakami, A. Itaya, N. Tamai and M. Irie, J. Phys. Chem. A, 2002, 106, 8096–8102 CrossRef CAS.
- Y. Ishibashi, M. Fujiwara, T. Umesato, H. Saito, S. Kobatake, M. Irie and H. Miyasaka, J. Phys. Chem. C, 2011, 115, 4265–4272 CrossRef CAS.
- H. Sotome, D. Kitagawa, T. Nakahama, S. Ito, S. Kobatake, M. Irie and H. Miyasaka, Phys. Chem. Chem. Phys., 2019, 21, 8623–8632 RSC.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- I. L. Zheldakov, J. M. Wasylenko and C. G. Elles, Phys. Chem. Chem. Phys., 2012, 14, 6211 RSC.
- F. D. Lewis and X. Zuo, J. Am. Chem. Soc., 2003, 125, 8806–8813 CrossRef CAS PubMed.
- N. I. Nijegorodov and W. S. Downey, J. Phys. Chem., 1994, 98, 5639–5643 CrossRef CAS.
- M. A. El-Sayed, Acc. Chem. Res., 1968, 1, 8–16 CrossRef CAS.
- M. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- IUPAC, Compendium of Chemical Terminology, (the “Gold Book”), Blackwell Scientific Publications, 2nd edn, 1997 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06256b |
| This journal is © the Owner Societies 2024 |




