Photophysics of a nucleic acid–protein crosslinking model strongly depends on solvation dynamics: an experimental and theoretical study

Abstract

We present a combined experimental and theoretical study of the photophysics of 5-benzyluracil (5BU) in methanol, which is a model system for interactions between nucleic acids and proteins. A molecular dynamics study of 5BU in solution through efficient DFT-based hybrid ab initio potentials revealed a remarkable conformational flexibility – allowing the population of two main conformers – as well as specific solute–solvent interactions, which both appear as relevant factors for the observed 5BU optical absorption properties. The simulated absorption spectrum, calculated on such an ensemble, enabled a molecular interpretation of the experimental UV-Vis lowest energy band, which is also involved in the induced photo-reactivity upon irradiation. In particular, the first two excited states (mainly involving the uracil moiety) both contribute to the 5BU lowest energy absorption. Moreover, as a key finding, the nature and brightness of such electronic transitions are strongly influenced by 5BU conformation and the microsolvation of its heteroatoms.

---

1 Introduction

Interactions between nucleic acids and proteins on the molecular scale govern the most basic processes of life, from DNA replication and repair to protein expression and synthesis.^1–11 However, it is challenging to isolate nucleoprotein complexes with null or small perturbations, where these last ones in their turn might disrupt the very nature of these complexes. Moreover, very intricate, and indeed not fully understood, is the role of light (i.e. UV irradiation) with protein–nucleic acid complexes. Light can cause the crosslinking of the protein to the nucleic acid, resulting in a covalent modification that can drastically change (usually for the worst) the biological roles of such compounds.^12–15 Thus, it is very important to understand how light interacts with nucleoprotein complexes, starting from their optical properties and moving towards the study of the photo-induced crosslinking reaction mechanism.

The complete comprehension of protein–nucleic acid interactions and their interplay with light has been limited because, upon irradiation, extensive protein and nucleic acid damage is often observed and the involved reactions are not very efficient. Advanced spectroscopic techniques and model compounds have been developed (and sometimes combined together) to better study this matter. Nucleic acid–protein laser-based photo-crosslinking is, for example, a promising technique to isolate nucleoprotein complexes in their biological conformation. It employs UV femtosecond-stimulated lasers to induce in vivo the formation of covalent bonds – named crosslinks – between a nucleobase and an amino acid residue. In this way, it is easier to stabilize the biological conformation of the complex and allow it to survive the following isolation. In addition, the employment of ultra-short irradiation times minimizes side reactions and allows characterisation of even transient interactions.^16–21

The resulting complex reaction mixtures and conditions also make it difficult to identify specific aminoacid/base cross-links.^22,23 A common proposed strategy is to attach a pyrimidine base to tyrosine, phenylalanine, and tryptophan side chains, using a short linker to mimic the proximity and orientation in nucleoprotein complexes.²⁴ Furthermore, in this study, we focus on the photophysics of 5-benzyluracil (5BU, see Fig. 1). Such a compound is useful to investigate the photoinduced crosslinking reaction that leads to the formation of 1,2-indaneuracil, allowing to model the photo-addition of phenylalanine to thymine, with the additional advantage of having high reaction yields.²⁴ This reaction has been already shown to be possible in methanol, by photoexcitation between 254 and 266 nm,^24–26 corresponding to the maximum of the first band of the UV-Vis spectrum.

Fig. 1 Photo-cyclization of 5-benzyluracil to 1,2-indaneuracil.

This model compound has also been previously investigated theoretically via both wave-function and DFT based approaches, further proving that 5BU is a very good candidate as a model compound for studying the optical properties of nucleoprotein complexes and their photo-reactivity.^25,27,28 The 5BU photo-cyclization pathway appears to be influenced by multiple factors: Sun et al.²⁴ proposed a mechanism relying on electron transfer between the chromophores and proton exchange with the solvent; according to Valadan et al.,²⁶ the absorption involves exclusively the S₁ ← S₀ transition, but the following reactive pathway is determined by a strong coupling among low-lying states and the reciprocal orientation of the two aromatic rings.

However, the photophysics of such a model compound is still far from being fully understood. It is still debated which one of the low-lying excited states of 5BU is responsible for absorption preceding the photoreaction, given the different results of the previous theoretical studies, relying on minimum energy structures.^25–28 Indeed, gas-phase simulations^27,28 considered the S₂ ← S₀ transition to be the only bright one; on the contrary, in the methanol solution, the absorption is either attributed entirely to the S₁ ← S₀ transition,²⁶ or can involve different states depending on the level of theory.²⁸ These different findings reflect on the hypothesized evolution of the system in the excited state, where single and multiple crossings among electronic states can be predicted. Such results can be further influenced by the role of the solvent and how this one is modelled, as well as by the thermal effects, that are not fully taken into account when few minimum energy structures are analyzed.²⁹

In this work, we propose to accurately describe the optical absorption of 5BU in methanol solution at room temperature by including both the explicit solute–solvent interactions and the finite temperature effects with a combined computational and experimental approach. For this aim, we performed a complete study of both the conformational space accessible to the solute and the dynamics of the solute–solvent interactions. In such a way, we were able to have an exhaustive knowledge, gauging our prediction with the experiments, of the ground-state equilibrium of the system in solution at room temperature to provide molecular insights for the absorption spectrum. We collected a room temperature ab initio molecular dynamics (AIMD) trajectory using a hybrid explicit/implicit solvation scheme, combining quantum/molecular mechanics (QM/MM) and non-periodic boundary conditions (NPBCs).^30–33 Then, we simulated the optical absorption from configurations extracted from the AIMD²⁹ through linear response time-dependent DFT (LR TD-DFT).^34–36 This methodology, taking into account several conformations and solute–solvent interactions, allowed us to unveil the role of different excited states in the overall 5BU observed photophysical properties.

The article is organized as follows: in Sections 2.1 and 2.2, we describe the methodology of the S₀ QM/MM/continuum MD; in Sections 2.3 and 2.4, we detail, respectively, the experimental and computational setup for the study of the photophysics; Section 3.1 describes the photophysics of the system from minimum energy structures; in Section 3.2, we characterize the ground-state conformational and solvation equilibrium of the system; in Section 3.3, we describe the optical properties of 5BU as depicted by our experiment and AIMD analysis; in Section 4 we discuss these results.

2 Methods

Multilayered quantum/classical/continuum MD simulations are necessary to accurately describe the ensemble averages, microsolvation dynamics and absorption spectra of chromophores in solution.^{29,33,37–49} This is particularly true for 5BU in methanol because 5BU is a flexible solute with two interacting aromatic rings and four heteroatoms, while methanol is a flexible, polar and protic solvent: they thus require, at the same time, the accurate treatment of the solute degrees of freedom and the efficient description of the solvent viscosity and mobility; moreover, we have to take into account the specific, polarization and electrostatic solute–solvent interactions.^33,50–56

2.1 Multilayered ONIOM/NPBCs partition scheme

For the aforementioned reasons, the 5BU–methanol system was simulated by a multilayered QM/MM/implicit partition, combining the N-layered integrated molecular orbital and molecular mechanics (ONIOM)^57–59 extrapolative scheme with non-periodic boundary conditions.^{30–33,39,41,60–68} The solute, treated at the B3LYP^69–72/6-31G(d,p) level of theory, was put at the center of a spherical cavity with a radius of 20 Å, including 356 methanol molecules, described using the General AMBER Force Field (GAFF) model⁷³ (see Fig. S1 in the ESI†). Using DFT potentials appears in this context the method of choice because of their good compromise between cost and accuracy, for both organic/biological^33,74–86 and inorganic/materials systems.^29,87–106 The cavity radius was determined using the equilibration procedure detailed in Section 2.2. NPBCs were enforced on the cavity by the conductor-like polarizable continuum model (C-PCM) self-consistent reaction field^107–110 (via the ONIOM/PCM-X^111–113 formalism) and a dispersion–repulsion potential W_disp–rep,^{30–33,39,41,64,66–68} specifically designed by some of us for flexible solvents.

For a NVT ensemble, the constant-volume free energy A of the simulated system can be expressed as:

A(R) = E(P,R) + W(P,R) (1)

where E(P,R) is the potential energy of the explicit system in the nuclear configuration R, and W(P,R) is the “mean field” contribution accounting for the interactions with the implicit environment; the mutual polarization of the explicit and implicit systems is explicitly considered through the one-electron density matrix P. The mean field contribution W can be decomposed according to Ben–Naim's scheme of the solvation process:¹¹⁴

W(R) = W_disp–rep(R) + W_elec(R) + W_cav(R) (2)

where W_cav is the cavitation free energy (constant in our NVT model), W_elec accounts for long-range electrostatic interactions with the bulk solvent, included through the C-PCM self-consistent reaction field, W_disp–rep accounts for the short-range dispersion–repulsion interactions between explicit and bulk solvent molecules, allowing to maintain the correct solvent density and behaviour, while also serving as a confining potential. The dispersion–repulsion potential is a radial potential W_disp–rep(r) acting on the center of mass of each explicit solvent molecule and given by the sum of a set of N_g Gaussian functions, g_i, with r_i centers equally spaced along the radius of the spherical cavity:The height λ_i of each g_i(r) function is determined using an optimization procedure involving the experimental density of the solvent as a reference.^{30–33,64,66} This methodology has been developed and widely employed by some of us to model systems in both water^{30–32,39,41,64,66–68} and methanol solution.³³

The energy of the atomistic system – E(P,R) in eqn (1) – can be expressed, according to the ONIOM scheme, as:

E(P,R) = E^model,QM(P,R) + E^real,MM(R) − E^model,MM(R) (4)

where E^real,MM is the energy of the whole explicit system calculated at the MM level, while E^model is the energy of the so-called model system, treated at the quantum mechanical level. The electrostatic interaction between the two layers was treated by including the atomic charges of the MM layer into the hamiltonian of the model sub-system (electronic embedding).

The combination of ONIOM and NPBCs provides a well defined, single valued and differentiable potential to perform AIMD simulations in explicit solvents. Such a hybrid solute–solvent QM/MM approach offers a good compromise between accuracy and computational cost for the equilibrium and non-equilibrium simulation of medium-large size systems in solution, including specific solute–solvent interactions.^{33,75,101,115–123} In fact, a fully correlated, wavefunction-based QM approach for both solute and solvent, although giving in principle a more accurate modelling of solute–solvent hydrogen bonds compared to a QM/MM scheme, is, in practice, not feasible, due to the large dimensions of the simulated system (5BU solute in a solvent box of 356 methanol molecules).

2.2 AIMD simulation

As aforementioned, we collected a ground-state AIMD trajectory of 5BU in methanol at room temperature, with the hybrid ONIOM/NPBCs partition scheme described in Section 2.1, by using a development version of the Gaussian electronic structure software package.¹²⁴ We exploited the atom-centered density matrix propagation (ADMP)^125–129 formalism, which avoids the density matrix convergence at each step by propagating it alongside the nuclear degrees of freedom. A (fictitious) mass is required in the density matrix equation of motion. A tensorial mass weighting scheme was employed:¹²⁵ the mass of valence orbitals was set to 0.1 amu bohr², whereas core orbitals were weighted according to the scheme described in ref. 125. The ONIOM/ADMP/NPBCs MD was carried out for 20 ps, with a time step of 0.2 fs, in a NVT ensemble. A 298 K temperature was kept constant by rescaling velocity every 1 ps. A preliminary equilibration was carried out before production AIMD simulation. 5BU was placed into a cubic box of 9582 methanol molecules. A MM Langevin dynamics study was performed (using NAMD software¹³⁰) in the NpT ensemble (T = 298 K, p = 1 atm) with periodic boundary conditions, applying a Langevin piston to also keep the pressure constant.^131,132 GAFF was employed: GAFF atom types were assigned to solute atoms, as well as HF/6-31G(d) RESP charges. Solvent equilibration (with the solute coordinates fixed) was first performed for 10 ns. Then solute degrees of freedom were also allowed to propagate for 1 ns. Then, solvent molecules within 20 Å from the solute center of mass were selected. An AIMD equilibration of the selected system was performed with NPBCs in the NVT ensemble for 1 ps, applying velocity rescaling every 250 fs, using the same partition scheme and level of theory of the following production simulation.

2.3 Experimental details

5BU powder was purchased from Giotto Biotech S.r.l. Italia and it was dissolved in 99.9% HPLC grade methanol. A UV-Vis spectrophotometer was used to obtain an absorbance spectrum of the sample in a quartz cuvette with a 1 cm optical path length. The spectrum was acquired in the 200–700 nm range at a 5BU concentration of 10 μg mL⁻¹ (≈50 μM), where we had already verified its linear response.

2.4 UV-Vis spectrum simulation

The intensity of the electronic absorption spectrum L(ω) can be calculated (assuming a classical nuclear motion) as:^39,133where Q represents a set of nuclear coordinates and ρ_i(Q,T) is the density of states in the initial electronic state, which could be obtained by a MD trajectory on the V_i(Q) potential energy surface. Further approximating such density of states with a discrete set of N_p configurations Q_l extracted from the MD, the spectrum L(ω) features the highest intensity at frequencies ω such that ħω = |V_i(Q_l) − V_f(Q_l)|:where L_f(ω) represents the spectrum contribution by the adiabatic state f, N_p is the number of sampled configurations, Q_l is the l-th geometry, f_if(Q_l) is the oscillator strength of the i → f transition at that geometry, ΔV_if(Q_l) is the vertical transition energy, and w(ħω − ΔV_if(Q_l)) is a broadening function, peaked at ħω = ΔV_if, which is here a Gaussian broadening with a variance of s² = 0.001 eV²:

This approach is able to simulate absorption spectra of systems even of significant size including thermal broadening, but neglecting the vibronic fine structure.^39,133

In order to simulate the 5BU spectrum in the methanol solution, 2001 uncorrelated configurations were extracted from the AIMD trajectory at regular time intervals (10 fs). The latter was chosen as a compromise between the computational cost of excited states calculation and the accurate sampling of 5BU torsional degrees of freedom.²⁹ The first 8 excited states were calculated for each configuration through linear response time-dependent DFT.^34–36 An ONIOM hybrid scheme was used: 5BU and the four methanol molecules closest to the solvation sites (possibly forming hydrogen bonds) were modeled at the QM TD-CAM-B3LYP/6-31+G(d,p) level,^69–72,134 and the remaining ones were modeled at the MM level through the GAFF (see Fig. S2 in the ESI†). In this regard, the CAM-B3LYP functional appears suitable to describe the photophysics of pyrimidines (also substituted ones)^{25,28,135–138} and especially their charge-transfer states. Electrostatic interactions by the bulk solvent were treated using the C-PCM implicit solvent model, placed at the boundary of the spherical solvent box.

3 Results

3.1 Optical absorption data from minimum energy structures

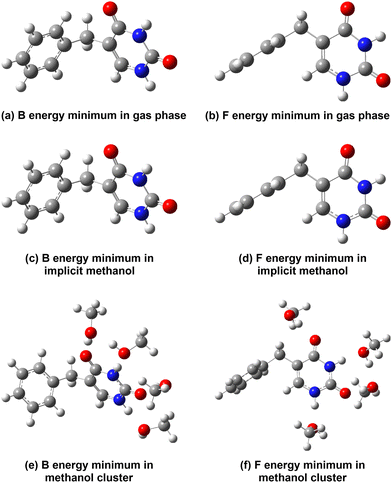
We first describe the optical properties of 5BU in methanol by adopting a static picture, i.e. by performing TD-DFT calculations on ground-state minimum energy structures, differing in 5BU geometries, solvation schemes and levels of theory. First, we chose two conformations that, according to the literature,²⁶ are adopted by the 5BU molecule: the former has the rings arranged in an approximately orthogonal manner (flag-like structure, shortened to “F”), while the latter has the rings approximately facing each other (butterfly-like structure, shortened to “B”) – see Fig. 3. It is expected that the relative orientation of the two rings could influence the amount of orbital interaction and so the excited states character. Moreover, to evaluate the role of solvent effects, three different solvation schemes were employed: first, we simulated the isolated molecule; then, we added the effect of the methanol bulk solvent by an implicit description (C-PCM potential); finally, we included both the implicit solvent and four explicit methanol molecules, each one interacting with a solute hydrogen-bond site. All the optimizations were performed at the B3LYP/6-31G(d,p) level of theory, also employed for AIMD simulations (see also the following discussion). Structures were also optimized at the CAM-B3LYP/6-31+G(d,p) level for comparison because this density functional was previously adopted in the literature for this system.^25,26 For each ground-state minimum energy structure, time-dependent calculations were performed at the TD-CAM-B3LYP/6-31+G(d,p) level, with the same solvation scheme used in the relative optimization. All calculations were performed using the Gaussian 16 software package.¹³⁹

The minimum energy structures optimized at the B3LYP/6-31G(d,p) level are shown in Fig. 3: the left and the right columns show the butterfly-like and the flag-like energy minima, respectively; the three rows show instead the structures optimized respectively in the gas phase (Fig. 3a and b), in the methanol treated implicitly (Fig. 3c and d), and in methanol described in a hybrid manner, i.e. by four methanol molecules and bulk implicit solvent (Fig. 3e and f). The two dihedral angles ϑ and φ mainly represent the 5BU conformation: the former is defined by the carbon atoms 5, 7, 8 and 9 and describes the rotation of the phenyl ring, while the latter is defined by the carbon atoms 6, 5, 7 and 8 and describes the rotation of the uracil ring (see Fig. 2). Their values for each B3LYP/6-31G(d,p) optimized structure are reported in Table 1. The structures optimized at the CAM-B3LYP/6-31+G(d,p) level are shown and described instead in the ESI† – please refer to Fig. S3 and Table S1.

Fig. 2 (a) The numbering adopted in the article. (b) The two rotations described by the dihedrals ϑ and φ.

Table 1 Values of the dihedral angles ϑ and φ (degrees) of 5BU minimum energy structures optimized at the B3LYP/6-31G(d,p) level, for B (on the right) and F (on the left) conformers, in gas phase (first row), implicit methanol (second row) and 5BU–methanol cluster (third row)

	B structure		F structure
	φ	ϑ	φ	ϑ
5BU	93.75	−102.98	0.02	−89.58
5BU/C-PCM	96.63	−95.78	0.01	−89.80
5BU + 4MeOH/C-PCM	107.75	−60.69	−21.57	−79.94

---

In the following discussion, we compare the results of optimization of the structures at the B3LYP/6-31G(d,p) level in different solvation schemes. We also compare the results with those obtained at the CAM-B3LYP/6-31+(d,p) level, and with those reported in the literature.

Two different ground-state energy minima were actually found for each solvation scheme, in accordance with the previous works.²⁶ The orthogonal (φ ≈ 0° and ϑ ≈ 90°, Table 1) arrangement of the two rings is retained by flag-like structures in almost all solvation models (Fig. 3b and d) and for both levels of theory (see Fig. S3b, S3d and S3f in the ESI†). A slight rotation of the uracil ring (φ = −21.57°) is observed for the B3LYP/6-31G(d,p) optimized F conformer in the methanol cluster (Fig. 3f).

Fig. 3 5BU structures optimized at the B3LYP/6-31G(d,p) level.

The butterfly-like conformer, on the other hand, displays a more symmetric arrangement of the two rings, with both dihedral angles at around 90° (Table 1). This is consistent with the gas-phase structures optimized at different levels of theory (such as M06/cc-pVTZ and SA-CASSCF(20,14)/DZP)^27,28 proposed in recent literature studies. In gas phase and implicit methanol, this symmetric arrangement is indeed highly preserved in the B3LYP/6-31G(d,p) optimized B conformer (Fig. 3a and c). However, the addition of explicit solvent molecules induces a slight phenyl ring rotation (ϑ = −60.69°, see Fig. 3e), a finding also confirmed by the CAM-B3LYP optimized B conformer with the same solvation scheme (ϑ = −56.96°, see Fig. S3e, ESI†).

We then discuss the main features of 5BU lowest energy excited states in solution, computed at the TD-CAM-B3LYP/6-31+G(d,p) level from B3LYP/6-31G(d,p) minimum energy structures. Their vertical excitation energies and oscillator strengths are reported in Table 2, while the natural transition orbital (NTO) pairs¹⁴⁰ describing the first two excitations are displayed in the ESI† (see Section SI-4 and Fig. S4–S9). Excited states from the CAM-B3LYP/6-31+G(d,p) optimized structures were also computed for further comparison and confirmation, and reported in the ESI† (Table S2).

Table 2 Vertical excitation energies (eV) and oscillator strengths of the first four electronic transitions of 5BU in methanol, calculated at the TD-CAM-B3LYP/6-31+G(d,p) level, for the two structures F (top) and B (bottom) optimized in the ground state at the B3LYP/6-31G(d,p) level, in gas phase (left), implicit methanol (center) and cluster (right)

Transition	V.E.E. (f)
	5BU	5BU/C-PCM	5BU + 4MeOH/C-PCM
F structure
S1 ← S0	5.12 (0.000)	5.16 (0.218)	5.04 (0.226)
S2 ← S0	5.26 (0.155)	5.31 (0.000)	5.39 (0.005)
S3 ← S0	5.41 (0.000)	5.42 (0.000)	5.45 (0.003)
S4 ← S0	5.99 (0.000)	6.04 (0.024)	5.98 (0.010)
B structure
S1 ← S0	5.10 (0.004)	5.09 (0.265)	5.04 (0.294)
S2 ← S0	5.14 (0.189)	5.28 (0.002)	5.38 (0.001)
S3 ← S0	5.38 (0.012)	5.39 (0.003)	5.43 (0.003)
S4 ← S0	5.74 (0.020)	5.84 (0.056)	5.87 (0.066)

---

For each conformer optimized in the gas phase, S₂ is the only low-lying bright state (f = 0.155 and f = 0.189 in F and B conformers, respectively, see Table 2) and is dominated by a uracil Uππ* transition. In the B conformer, such transition is mixed with a charge-transfer transition from a phenyl ring π orbital to a uracil π* orbital (PπUπ*) (see Fig. S5, ESI†). In contrast, for both conformers, S₁ has a dark uracil nπ* character, where the n orbital is localized on oxygen #4 (Fig. S4 ESI,† please refer to Fig. 2a for atoms labels). Interestingly, the inclusion of solvent effects (either implicitly or through cluster models) increases the energy of the dark Unπ* transition and stabilizes the bright Uππ* state. Therefore, in the methanol solution, the S₁ state has a main Uππ* character (Fig. S6 and S8, ESI†) and becomes the bright state (Table 2). Conversely, the S₂ state acquires a dark Unπ* character (including an implicit solvent model, Fig. S7, ESI†), or a dark Pππ* one with a minimal Unπ* contribution in a cluster/implicit solvent model (Fig. S9, ESI†), while the Unπ* character (S₁ in gas phase) is shown instead by the S₃ state (NTOs not shown).

In particular, specific solvation effects (included in the cluster/implicit solvent model) induce a relevant increase (0.24 eV for the B conformer) of the adiabatic S₂ state energy, while S₁ energy is slightly reduced. This results in an increase of the S₂–S₁ energy gap, as well as a decrease of the S₃–S₂ gap, both for the B3LYP/6-31G(d,p) and CAM-B3LYP/6-31+G(d,p) optimized structures.

For each solvation scheme, we also observe that the transitions from the B minimum are generally brighter and red-shifted with respect to the corresponding ones from the F minimum; the same conformational effect is observed for the CAM-B3LYP/6-31+G(d,p) structures.

Comparing transitions calculated on structures optimized at B3LYP/6-31G(d,p) and CAM-B3LYP/6-31+G(d,p) levels, we observe overall very similar features of the excited states, both in terms of energy and brightness. The former level of theory was also employed in ADMP/ONIOM/NPBCs ab initio molecular dynamics to sample the conformation space for the following excited states and spectrum simulations (Section 3.3).

3.2 Conformational and solvation equilibrium in the ground state

In order to better characterize and systematically explore 5BU conformational space and, in particular, other possible minimum energy structures, an energy scan in methanol with respect to ϑ and φ dihedral angles (defined in Section 3.1) was performed. In particular, the energy was evaluated in the whole domain ϑ,φ ∈ [−180° : 180°] at the B3LYP/6-31G(d,p)/C-PCM level of theory, starting the scan from the (−89.8, 0.01) optimized F conformer.

The total energy of the system, relative to the scan minimum energy (in the following referred to as “R.T.E”, for “relative total energy”), is reported in Fig. 4 as a function of the dihedrals ϑ and φ. Because of the C₂ symmetry of the phenyl ring, the scan can be divided into two congruent halves: the upper one, where ϑ > 0, and the lower one, where ϑ < 0; we can thus restrict our analysis of the scan to the region −180° < ϑ < 0°. Three wells (R.T.E. < 1 kcal mol⁻¹) can be recognized: (i) the well on the left, hereafter called “L”, lies approximately between −160° < ϑ < −50° and −120° < φ < −70° and its lowest point has ϑ = −89.8°, φ = −100.0° and R.T.E. = 0.118 kcal mol⁻¹; (ii) the well at the center, hereafter named “C”, ranges approximately between −130° < ϑ < −60° and −30° < φ < 50° and its lowest point has ϑ = −89.8°, φ = 0.0° and R.T.E. = 0 kcal mol⁻¹ (the absolute minimum of the scan); (iii) the well on the right, named “R”, lies approximately between −130° < ϑ < −10° and 70° < φ < 120° and its lowest point has ϑ = −89.8°, φ = 100.0° and R.T.E. = 0.118 kcal mol⁻¹.

Fig. 4 Color map of 5BU total energy (kcal mol⁻¹) at the B3LYP/6-31G(d,p)/C-PCM level, as a function of the dihedrals ϑ (vertical axis) and φ (horizontal axis) (degrees), relative to the scan minimum energy. Energy is reported using a color scale.

Conformers belonging to L and R wells are actually mirror images (enantiomers). Thus, the energy scan shows that 5BU in methanol has just two distinct conformers: the flag-like minimum energy structure (Fig. 3d), corresponding to the C well, and the butterfly-like minimum energy structure (Fig. 3c), located in the R (or L) well, both previously characterized in Section 3.1.

At the same time, the saddle point between the C and R wells (ϑ = −109.8°, φ = 60°) has a R.T.E. = 0.961 kcal mol⁻¹, suggesting a low activation barrier for the interconversion of the two conformers: the ground-state equilibrium of 5BU does not appear to be dominated by rigid structures, but rather by a plethora of energetically close configurations: a dynamical analysis is thus necessary to achieve a complete understanding of the excited states, overcoming the bias associated with the study of few minimum energy structures.

A conformational analysis of the solute from ADMP/ONIOM/NPBCs MD was performed to understand the 5BU conformations explored at the equilibrium. The (ϑ,φ) two-dimensional distribution from the AIMD is plotted in Fig. 5. We clearly distinguish two regions: one on the left, approximately located at −130° < ϑ < −30°, −60° < φ < 50°, the other one on the right, approximately at −170° < ϑ < −50°, 50° < φ < 130°. These two regions correspond, respectively, to the aforementioned C and R wells of the energy scan (Fig. 4) and so to the population of the flag-like and the butterfly-like conformers. Therefore, a sufficient sampling of both 5BU distinct conformers in methanol at room temperature is provided by the collected trajectory, as well as structural fluctuations within each conformer.

Fig. 5 (ϑ,φ) two-dimensional dihedral distribution from 5BU AIMD. The color map indicates the number of AIMD frames within 1° × 1° resolution, normalized with respect to the maximum. Hotter colours are used for more populated (ϑ,φ) values and white colour denotes frequencies less than 0.01.

Solvent structuring and 5BU microsolvation were then studied, through radial distribution functions (RDFs) between solvent oxygen atoms and 5BU solvation sites, i.e. uracil O2, O4 (as hydrogen bond acceptors) and N1, N3 (as hydrogen bond donors, please see Fig. 2a for atoms numbering). Clear 5BU–methanol specific interactions can be recognized. Looking at the O2 RDF (Fig. 6a), the first peak at 2.75 Å suggests a strong interaction with 1–2 methanol molecules (according to g(r) radial integral) in the first solvation shell. The second peak at 3.55 Å is instead actually due to the methanol molecules solvating the other three heteroatoms: the g(r) integral (between 2 and 3) is compatible with the coordination numbers of N1, N3 and O4. The O2 second solvation shell is represented by the peak at 7.25 Å, including, on an average, about 14 solvent molecules. A third shell at 11.45 Å is moreover recognized. While the O4 first solvation shell is located at the same distance as that of O2 (2.75 Å, Fig. 6b), it is instead less populated (between 0 and 1 methanol molecule). This effect can be explained by the steric hindrance of the benzyl group, closer to O4. Moreover, a reduced exchange between first and outer shells of O4 is observed, as suggested by g(r) minimum values between the peaks (0.338 for O4, 0.797 for O2), likely due to the lower exposure to the solvent. The two low peaks at 3.75 and 4.75 Å actually reflect O2, N1 and N3 solvation. The O4 second solvation shell (at 6.75 Å) includes, on average, 9–10 solvent molecules. The third shell is located instead at 11.55 Å. N1 and N3 first solvation shells are at the same average distance (2.85 Å, Fig. 6c and d, respectively) and show a comparable population (1 methanol molecule). Nevertheless, the first minimum in N3 RDF is much deeper and wider (0.295 and 0.580 g(r) minimum values for N3 and N1, respectively). This suggests that the number of solvent molecules moving between the first two shells of N3 is, on average, less than that of N1. This is likely due to the position of N3 between the two oxygen atoms, where the interplay of three solvation sites causes a stronger local structuring of the solvent. The intense second peaks at 4.95 Å include the methanol molecules solvating O2 (N1 RDF) or O2 and O4 (N3 RDF). The N3 second solvation shell is represented by the peak at 6.65 Å (Fig. 6d) and includes, on average, about 18 methanol molecules. The N1 RDF in the same region (Fig. 6c) instead appears to have already converged to 1, suggesting a lower structuration.

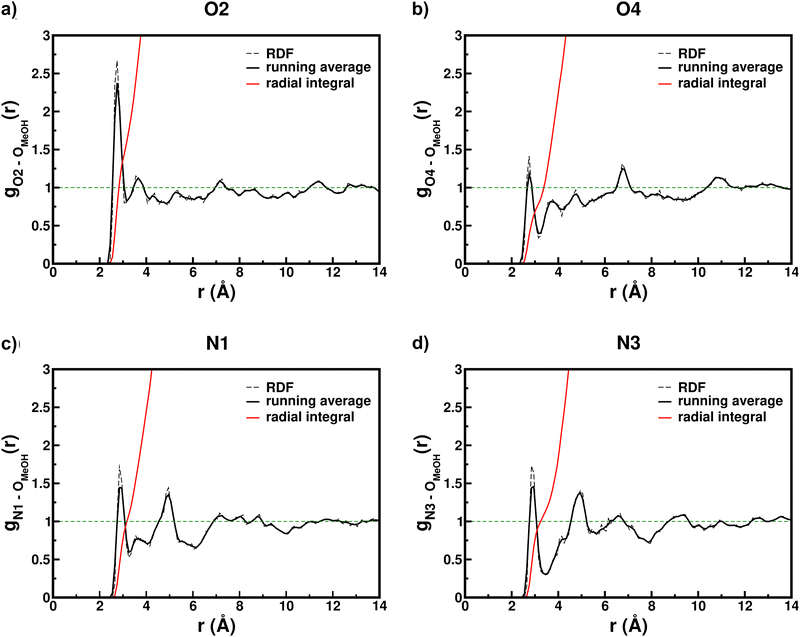Fig. 6 RDFs (dashed black) of methanol oxygen atoms – 5BU heteroatoms distances (please refer to Fig. 2a for atoms labels). The solid black line represents the 3-point g(r) running average and the red line represents its radial integral; the green dashed straight line is set to 1, the value of g(r) for a homogeneous distribution.

In addition to the average information provided by the RDFs, we further investigated the microsolvation of 5BU heteroatoms to observe the occurrence of strong hydrogen bonds. A structural criterion was employed (based on a donor–acceptor distance ≤4 Å and hydrogen-donor–acceptor angle ≤40°). For each heteroatom and for each AIMD frame, the distance from the oxygen of the closest methanol molecule having an orientation suitable for hydrogen bonding (i.e., verifying the angle criterion) was evaluated. Distributions of such distance from the AIMD for each heteroatom are shown in Fig. 7. These distributions reveal a mobile solvation equilibrium, exploring both fully solvated configurations and partially solvated ones. Indeed, we can consider a heteroatom unsolvated when the closest protic molecule with an adequate angle is too distant (>4 Å). Therefore, O4 and N1 appear unsolvated in a significant fraction of the configurations explored by the AIMD because their distributions (Fig. 7b and c, respectively) show a significant population of >4 Å distances.

Fig. 7 Distributions of the distance of each 5BU heteroatom from the closest solvent oxygen verifying H_MeOH–O_MeOH–O or H–N–O_MeOH < 40°. Such a criterion allows to select solvent molecules potentially able to participate in hydrogen bonds. Please refer to Fig. 2a for atoms labels.

According to the previous discussion, the collected 5BU ADMP/ONIOM/NPBCs MD simulation therefore provided a complete picture of both conformational and solvation equilibria in methanol at room temperature. Such an ensemble allowed a detailed prediction of 5BU excited states and absorption spectra under such conditions, as shown in the following section (Section 3.3).

3.3 Optical absorption spectrum: experimental and simulation results from AIMD sampling

The experimental UV-Vis absorption spectrum of 5BU in methanol was recorded according to the procedure detailed in Section 2.3. As shown in Fig. 8a, it exhibits two distinctive absorption bands, located at approximately 210 and 265 nm, corresponding to 5.90 and 4.68 eV, respectively. Our interest was to disentangle the main electronic transitions and the structural features determining the observed absorption. To this end, we simulated the optical absorption spectrum of 5BU in methanol by performing TD-DFT calculations on an ensemble of configurations extracted from the AIMD, according to the protocol detailed in Section 2.4. As shown in Fig. 8a, the band shape of the experimental spectrum is reproduced with a systematic blue shift, suggesting that the energy spacing among the excited states is correctly estimated. By recognizing the individual contributions of the different states, we attribute the lowest-energy band, which is the one excited during photo-cyclization,^25,26 mainly to the transition towards S₁, with contributions also from S₂ and S₃, the latter only found beyond the band maximum (see Fig. 8b).

Fig. 8 TD-CAM-B3LYP/6-31+G(d,p) calculated UV-Vis absorption spectrum of 5BU in methanol (black line). In plot (a), its 50-points running average (brown line) and the experimental spectrum (orange) are also reported; in plot (b), the contributions of the S₁ ← S₀ (red), S₂ ← S₀ (blue), S₃ ← S₀ (dark green), S₄ ← S₀ (magenta), S₅ ← S₀ (light green), S₆ ← S₀ (turquoise), S₇ ← S₀ (maroon) and S₈ ← S₀ (olive) transitions to the total spectrum are instead shown. The experimental spectrum is expressed as absorbance, while the simulated spectrum, its running average and states contributions are rescaled so that the (smoothed) calculated first band and the experimental one are comparable.

The different conformations and solvation states sampled by the QM/MM/NPBCs trajectory in methanol solution at room temperature (Section 3.2) suggest that the adiabatic S₁ and S₂ lowest-energy states may actually exchange their character based on such parameters. We thus investigated the character of the first two excitations (through a NTO analysis) on a small subset of representative configurations extracted from the QM/MM/NPBCs MD, differing in the conformation and solvation state (please refer to Fig. S10 in the ESI† for their structures). The features of S₁ and S₂ states calculated for such configurations are correlated to the structural parameters as shown in Table 3. NTO pairs isosurfaces can be instead found in Fig. S11–S15 in the ESI.†

Table 3 Analysis of S₁ and S₂ excited states at the TD-CAM-B3LYP/6-31+G(d,p) level for five representative configurations sampled from 5BU QM/MM/continuum MD in methanol solution (see Section SI-5 in the ESI). Columns 2–4: 5BU conformer and solvation state of O4 and N1 heteroatoms (please refer to Section 3.2 for the definition of the B and F conformers and to Fig. 2 for atoms numbering). Columns 5–8: S₁ and S₂ vertical excitation energies (eV), oscillator strengths and characters according to hole–electron NTO pairs

Configuration	Conformer	O4	N1	S1 ← S0		S2 ← S0
				V.E.E. (f)	Character	V.E.E. (f)	Character
α	B	H-bonded	H-bonded	4.92 (0.217)	Uππ*	5.25 (0.019)	Unπ* + PπUπ*
β	F	H-bonded	H-bonded	5.05 (0.179)	Uππ*	5.27 (0.017)	Unπ*
γ	B	Not H-bonded	H-bonded	4.83 (0.158)	Uππ* + PπUπ*	5.13 (0.054)	Unπ*
δ	F	Not H-bonded	H-bonded	5.12 (0.170)	Uππ*	5.30 (0.006)	Unπ*
ε	F	Not H-bonded	Not H-bonded	5.03 (0.024)	Unπ*	5.14 (0.102)	Uππ*

---

Consistently with the calculations on optimized structures with either implicit or explicit solvation (Section 3.1), S₁ is a bright Uππ* state, while S₂ has a dark Unπ* character (being the n orbital located on O4), due to specific methanol–5BU interactions (especially on N1). Interestingly, in the ε configuration, where neither of the two heteroatoms O4 and N1 are solvated, S₁ and S₂ characters are swapped: the former is therefore a dark Unπ* state, while the latter has instead a bright Uππ* character (see Fig. S15, ESI†). We also observe that S₁ and S₂ of the butterfly-like representative configurations (α and γ) also show a small PπUπ* charge-transfer character, which is absent in the corresponding transitions of flag-like configurations (see Fig. S11 and S12, ESI†).

We then compared the average values of energy and oscillator strength of the first four states from the AIMD (see Table 4) with the values calculated from the minimum energy structures optimized in the methanol cluster at the B3LYP/6-31G(d,p) level (i.e., the same level of the AIMD, see the third column of Table 2). This comparison revealed consistent energies and spacing, but fairly different oscillator strength values: S₁ is the brightest state from both static and dynamics calculations, but its oscillator strength calculated from AIMD frames is on average only 0.123, compared with the values of 0.294 and 0.226 from the minimum energy structures. S₂ and S₃, which from static calculations appeared to be completely dark states, instead exhibit an average oscillator strength of 0.042 and 0.013 respectively, based on AIMD frames. The S₂ state is therefore not completely dark because it acquires a Uππ* character in a reduced fraction of the sampled configurations. Besides S₁, S₂ is of particular interest since it contributes, together with S₁, to the first band, which is excited to induce 5BU photo-cyclization.^25,26

Table 4 Central column: oscillator-strength-weighted AIMD-averages of the vertical excitation energies of the first four transitions of 5BU in methanol; right column: AIMD-averaged oscillator strengths of the same transitions. Second-last row: average energy of the points composing the first band of the computed spectrum shown in Fig. 8, each one weighted for the respective intensity. Last row: energy of the maximum of the first band in the experimental spectrum

Transition	V.E.E. (eV)	f
S1 ← S0	5.01	0.123
S2 ← S0	5.20	0.042
S3 ← S0	5.34	0.013
S4 ← S0	5.82	0.050
Average of the first band	5.06
Experimental peak	4.68

---

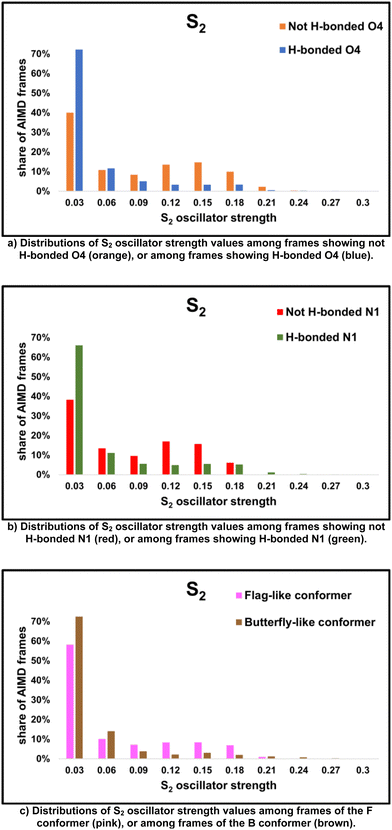
The swap of the character of the first two states depending on 5BU conformation and solvation can explain several trends in their brightness. Regarding the first excited state, the formation of a hydrogen bond between O4 and a solvent molecule appears to be an important feature. As discussed in Section 3.2, some of the sampled configurations have at least one solvent molecule with distance and orientation suitable for a hydrogen bond with O4, while in the other ones, O4 does not form hydrogen bonds (see Fig. 7b). In the former group, the average S₁ oscillator strength is 0.146 and its distribution peak lies between 0.15 and 0.18 (see the blue bars in Fig. 9a, please refer to Table 5 for average S₁ oscillator strength within each cluster of MD frames); in the latter group, instead, the average S₁ oscillator strength is 0.069 and its distribution peak lies between 0.00 and 0.03 (see the orange bars in Fig. 9a). Analogously to O4, N1 microsolvation (see Fig. 7c) also influences the brightness of S₁: S₁ is mostly a bright state when there is at least one solvent molecule with distance and orientation suitable for a hydrogen bond with N1, while it is darker when N1 does not form hydrogen bonds. In the former group, the average S₁ oscillator strength is 0.132 and its distribution peak lies between 0.15 and 0.18 (see the green bars in Fig. 9b); in the latter group, instead, the average S₁ oscillator strength is 0.059 and its distribution peak lies between 0.00 and 0.03 (see the red bars in Fig. 9b). Finally, the relative orientation of the uracil and phenyl rings also plays a role: when they are approximately orthogonal to each other (flag-like conformer, occupying the right half of the distribution in Fig. 5, see for instance Fig. 3b), S₁ oscillator strength has a bimodal distribution, with a dark peak between 0.00 and 0.03 and a bright peak between 0.15 and 0.18 (see the pink bars in Fig. 9c). When the rings face each other (butterfly-like conformer, occupying the left half of the distribution in Fig. 5, see for instance Fig. 3a), the distribution dark peak disappears and S₁ is mostly a bright state, with a distribution peak between 0.15 and 0.18 (see the brown bars in Fig. 9c).

Fig. 9 Distributions of S₁ oscillator strength values among groups of frames taken from the AIMD.

Table 5 Average S₁ oscillator strength for every considered cluster of AIMD frames

Cluster	Average f (S1)	Cluster	Average f (S1)
Not H-bonded O4	0.069	H-bonded O4	0.146
Not H-bonded N1	0.059	H-bonded N1	0.132
F conformer	0.123	B conformer	0.127

---

S₂ exhibits an opposite behaviour with respect to S₁, even if its variations are more subtle. Like S₁, indeed, its brightness mainly depends on the microsolvation of O4, but, contrarily to S₁, it is higher in the configurations where O4 does not form hydrogen bonds and decreases in those where a methanol molecule solvates O4. In the first group, S₂ oscillator strength has a bimodal distribution, with the highest peak between 0.00 and 0.03 and a lower peak (with a population half of the first one) between 0.15 and 0.18. In the second group instead, the distribution shows no bright peaks (see the blue bars in Fig. 10a) and the second excited state is mostly dark, with an average oscillator strength of 0.0308 (please refer to Table 6 for average S₂ oscillator strength within each cluster of MD frames). Again in contrast to the first state, the fraction of frames with a bright second excited state significantly increases when there are no nearby solvent molecules able to form a hydrogen bond with N1, while it is lower when N1 is solvated: in the first group, S₂ oscillator strength has a bimodal distribution, with the highest peak between 0.00 and 0.03 and a second one between 0.12 and 0.15, with a relative abundance half of the first one (see the red bars in Fig. 10b). The second group does not show this bright peak in the distribution, but a mostly dark second excited state, with an average oscillator strength of 0.039 (see the green bars in Fig. 10b). Finally, the effect of the two rings arrangement is also reversed with respect to S₁: the second excited state is brighter when the two rings are approximately orthogonal (flag-like conformer), while it is darker when they face each other (butterfly-like conformer) (see Fig. 10c).

Fig. 10 Distributions of S₂ oscillator strength values among groups of frames taken from the AIMD.

Table 6 Average S₂ oscillator strength for every considered cluster of AIMD frames

Cluster	Average f (S2)	Cluster	Average f (S2)
Not H-bonded O4	0.071	H-bonded O4	0.031
Not H-bonded N1	0.066	H-bonded N1	0.039
F conformer	0.042	B conformer	0.021

---

4 Conclusion

In this work, new features regarding the photophysics of 5BU in methanol solution at room temperature were found, using an accurate combined computational and experimental approach. From our analysis of the ground-state equilibrium and of the electronic layout of 5BU in methanol, an intricate and subtle correlation between the instantaneous configurations and the photophysics was found. The nature and brightness of the first two excited states were found to be dependent on the conformation of the solute and on the instantaneous microsolvation of its heteroatoms. Indeed, 5BU appears to have a soft conformational landscape, composed of a plethora of relevant conformations and microsolvation configurations at room temperature. As main results, we observed that the character and brightness of these two transitions can swap, depending on the reciprocal orientation of the aromatic rings and the instantaneous microsolvation of the heteroatoms O4 and N1. The dependence of absorption on the conformation and microsolvation may influence the successive photoreaction. The irradiation at different wavelengths may induce different reaction pathways by exciting different initial conformations and solute–solvent configurations, activating either S₁ or S₂ excited states. This may acquire even greater importance when applied to nucleoprotein complexes, where the involved residues are often blocked in a specific orientation and solvation state and may thus be susceptible or not to photo-crosslinking based on these features. This suggests that the description of the subsequent photorelaxation and photoreaction has to include a non-adiabatic treatment of both the first two excited states, already in its earliest stages. Moreover, given the significant role of the solvent in both the excitation and the photoreaction, excited state dynamics would benefit from the inclusion of an explicit treatment of the several solvent molecules to fully saturate the solvation sites. Our work will help in advancing such analysis, towards the comprehension of photophysics of DNA– and RNA–protein model complexes.

Author contributions

N. R. and C. A.: conceptualization, funding acquisition, project administration, supervision, writing – original draft. A. P.: formal analysis, methodology, supervision, writing – original draft, writing – review & editing. M. V.: data curation, formal analysis, methodology, investigation, supervision, writing – original draft. F. P.: formal analysis, methodology, software, validation, writing – original draft, writing – review & editing. G. I.: data curation, investigation, validation, visualization, writing – original draft, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

N. R. and A. P. gratefully acknowledge the Italian Ministry of University and Research (projects: PRIN 202082CE3T_002) for financial support. N. R. and A. P. acknowledge IBiSCo (Infrastructure for Big data and Scientific Computing) for HPC resources. N. R., A. P. and F. P. also acknowledge Gaussian Inc. for financial support. A. P. thanks the University of Napoli Federico II for financial support (project: FRA2022-CosmoHab CUP: E65F22000050001). G. I., F. P., A. P. and N. R. also thank Francesco Gambuli for his assistance and support.

References

1. R. Berisio, F. Schluenzen, J. Harms, A. Bashan, T. Auerbach, D. Baram and A. Yonath, Nat. Struct. Biol., 2003, 10, 366–370.
2. A. G. Matera, R. M. Terns and M. P. Terns, Nat. Rev. Mol. Cell Biol., 2007, 8, 209–220.
3. T. A. Steitz, Nat. Rev. Mol. Cell Biol., 2008, 9, 242–253.
4. T. Glisovic, J. L. Bachorik, J. Yong and G. Dreyfuss, FEBS Lett., 2008, 582, 1977–1986.
5. L. A. Yates, C. J. Norbury and R. J. Gilbert, Cell, 2013, 153, 516–519.
6. M. W. Hentze, A. Castello, T. Schwarzl and T. Preiss, Nat. Rev. Mol. Cell Biol., 2018, 19, 327–341.
7. G. L. Hager, C. Elbi and M. Becker, Curr. Opin. Genet. Dev., 2002, 12, 137–141.
8. D. J. Patel and Z. Wang, Annu. Rev. Biochem., 2013, 82, 81–118.
9. T. Siggers and R. Gordân, Nucleic Acids Res., 2014, 42, 2099–2111.
10. Q. Du, P. L. Luu, C. Stirzaker and S. J. Clark, Epigenomics, 2015, 7, 1051–1073.
11. C. D. Allis and T. Jenuwein, Nat. Rev. Genet., 2016, 17, 487–500.
12. K. Smith, B. Hodgkins and M. O'Leary, Biochim. Biophys. Acta, Nucleic Acids Protein Synth, 1966, 114, 1–15.
13. J. G. Peak and M. J. Peak, Mutat. Res., Fundam. Mol. Mech. Mutagen., 1991, 246, 187–191.
14. S. Barker, M. Weinfeld and D. Murray, Mutat. Res., Rev. Mutat. Res., 2005, 589, 111–135.
15. T. Nakano, X. Xu, A. M. Salem, M. I. Shoulkamy and H. Ide, Free Radical Biol. Med., 2017, 107, 136–145.
16. L. Zhang, K. Zhang, R. Prändl and F. Schöffl, Biochem. Biophys. Res. Commun., 2004, 322, 705–711.
17. C. Altucci, A. Nebbioso, R. Benedetti, R. Esposito, V. Carafa, M. Conte, M. Micciarelli, L. Altucci and R. Velotta, Laser Phys. Lett., 2012, 9, 234–239.
18. A. Nebbioso, R. Benedetti, M. Conte, V. Carafa, F. De Bellis, J. Shaik, F. Matarese, B. Della Ventura, F. Gesuele, R. Velotta, J. H. A. Martens, H. G. Stunnenberg, C. Altucci and L. Altucci, Sci. Rep., 2017, 7, 11725.
19. A. Reim, R. Ackermann, J. Font-Mateu, R. Kammel, M. Beato, S. Nolte, M. Mann, C. Russmann and M. Wierer, Nat. Commun., 2020, 11, 3019.
20. A. Stützer, L. M. Welp, M. Raabe, T. Sachsenberg, C. Kappert, A. Wulf, A. M. Lau, S. S. David, A. Chernev, K. Kramer, A. Politis, O. Kohlbacher, W. Fischle and H. Urlaub, Nat. Commun., 2020, 11, 5250.
21. A. Knörlein, C. P. Sarnowski, T. de Vries, M. Stoltz, M. Götze, R. Aebersold, F. H. Allain, A. Leitner and J. Hall, Nat. Commun., 2022, 13, 2719.
22. H. Morrison, Bioorganic photochemistry, J. Wiley and Sons, Ltd, New York, 1990.
23. M. Shetlar, Int. Congr. Ser., 1993, 67–72.
24. G. Sun, C. J. Fecko, R. B. Nicewonger, W. W. Webb and T. P. Begley, Org. Lett., 2006, 8, 681–683.
25. M. Micciarelli, M. Valadan, B. Della Ventura, G. Di Fabio, L. De Napoli, S. Bonella, U. Röthlisberger, I. Tavernelli, C. Altucci and R. Velotta, J. Phys. Chem. B, 2014, 118, 4983–4992.
26. M. Valadan, E. Pomarico, B. Della Ventura, F. Gesuele, R. Velotta, A. Amoresano, G. Pinto, M. Chergui, R. Improta and C. Altucci, Phys. Chem. Chem. Phys., 2019, 21, 26301–26310.
27. M. Micciarelli, C. Altucci, B. D. Ventura, R. Velotta, V. Tosa, A. B. G. Pérez, M. P. Rodríguez, A. R. de Lera and A. Bende, Phys. Chem. Chem. Phys., 2013, 15, 7161–7173.
28. M. Micciarelli, B. F. E. Curchod, S. Bonella, C. Altucci, M. Valadan, U. Rothlisberger and I. Tavernelli, J. Phys. Chem. A, 2017, 121, 3909–3917.
29. A. Petrone, F. Perrella, F. Coppola, L. Crisci, G. Donati, P. Cimino and N. Rega, Chem. Phys. Rev., 2022, 3, 021307.
30. N. Rega, G. Brancato and V. Barone, Chem. Phys. Lett., 2006, 422, 367–371.
31. G. Brancato, N. Rega and V. Barone, J. Chem. Phys., 2006, 125, 164515.
32. G. Brancato, N. Rega and V. Barone, J. Phys. Chem., 2008, 128, 144501.
33. U. Raucci, F. Perrella, G. Donati, M. Zoppi, A. Petrone and N. Rega, J. Comput. Chem., 2020, 41, 2228–2239.
34. M. E. Casida, in Recent Advances in Density Functional Methods (Part I), ed. D. P. Chong, World Scientific Publishing Co. Pte. Ltd., 1995, ch. 5, pp. 475–516.
35. R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224.
36. A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037.
37. R. Crespo-Otero and M. Barbatti, Theor. Chem. Acc., 2012, 131, 1237.
38. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2015, 119, 958–967.
39. A. Petrone, J. Cerezo, F. J. A. Ferrer, G. Donati, R. Improta, N. Rega and F. Santoro, J. Phys. Chem. A, 2015, 119, 5426–5438.
40. J. Cerezo, F. J. Avila Ferrer, G. Prampolini and F. Santoro, J. Chem. Theory Comput., 2015, 11, 5810–5825.
41. J. Cerezo, A. Petrone, F. J. Avila Ferrer, G. Donati, F. Santoro, R. Improta and N. Rega, Theor. Chem. Acc., 2016, 135, 263.
42. J. Cerezo, G. Mazzeo, G. Longhi, S. Abbate and F. Santoro, J. Phys. Chem. Lett., 2016, 7, 4891–4897.
43. D. Padula, J. Cerezo, G. Pescitelli and F. Santoro, Phys. Chem. Chem. Phys., 2017, 19, 32349–32360.
44. J. M. Milanese, M. R. Provorse, E. J. Alameda and C. M. Isborn, J. Chem. Theory Comput., 2017, 13, 2159–2171.
45. J. Cerezo, D. Aranda, F. J. Avila Ferrer, G. Prampolini, G. Mazzeo, G. Longhi, S. Abbate and F. Santoro, Chirality, 2018, 30, 730–743.
46. Y. Liu, J. Cerezo, N. Lin, X. Zhao, R. Improta and F. Santoro, Theor. Chem. Acc., 2018, 137, 40.
47. G. Donati, A. Petrone, P. Caruso and N. Rega, Chem. Sci., 2018, 9, 1126–1135.
48. S. V. Shedge, T. J. Zuehlsdorff, M. J. Servis, A. E. Clark and C. M. Isborn, J. Phys. Chem. A, 2019, 123, 6175–6184.
49. S. Del Galdo, M. Fusè and V. Barone, J. Chem. Theory Comput., 2020, 16, 3294–3306.
50. C. Reichardt, Chem. Rev., 1994, 94, 2319–2358.
51. K. M. Solntsev, D. Huppert, L. M. Tolbert and N. Agmon, J. Am. Chem. Soc., 1998, 120, 7981–7982.
52. K. M. Solntsev, D. Huppert and N. Agmon, J. Phys. Chem. A, 1999, 103, 6984–6997.
53. H. A. Frank, J. A. Bautista, J. Josue, Z. Pendon, R. G. Hiller, F. P. Sharples, D. Gosztola and M. R. Wasielewski, J. Phys. Chem. B, 2000, 104, 4569–4577.
54. C. Adamo, M. Cossi, N. Rega and V. Barone, in Theoretical Biochemistry, ed. L. A. Eriksson, Elsevier, Amsterdam, The Netherlands, 2001, vol. 9 of Theoretical and Computational Chemistry, pp. 467–538.
55. E. Krystkowiak, K. Dobek and A. Maciejewski, J. Photochem. Photobiol., A, 2006, 184, 250–264.
56. V. Barone, R. Improta and N. Rega, Acc. Chem. Res., 2008, 41, 605–616.
57. M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, J. Phys. Chem., 1996, 100, 19357–19363.
58. T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery Jr, K. Morokuma and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 815–826.
59. K. Morokuma, Q. Wang and T. Vreven, J. Chem. Theory Comput., 2006, 2, 1317–1324.
60. M. Berkowitz, C. L. Brooks and S. A. Adelman, J. Phys. Chem., 1980, 72, 3889–3898.
61. K. Kratky, J. Comput. Phys., 1980, 37, 205–217.
62. C. L. Brooks and M. Karplus, J. Phys. Chem., 1983, 79, 6312–6325.
63. D. Beglov and B. Roux, J. Chem. Phys., 1994, 100, 9050–9063.
64. G. Brancato, A. Di Nola, V. Barone and A. Amadei, J. Chem. Phys., 2005, 122, 154109.
65. E.-S. Riihimäki, J. M. Martínez and L. Kloo, THEOCHEM, 2006, 760, 91–98.
66. N. Rega, G. Brancato, A. Petrone, P. Caruso and V. Barone, J. Chem. Phys., 2011, 134, 074504.
67. A. Petrone, G. Donati, P. Caruso and N. Rega, J. Am. Chem. Soc., 2014, 136, 14866–14874.
68. M. G. Chiariello and N. Rega, J. Phys. Chem. A, 2018, 122, 2884–2893.
69. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
70. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
71. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206.
72. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
73. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
74. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215.
75. M. G. Chiariello, G. Donati, U. Raucci, F. Perrella and N. Rega, J. Phys. Chem. B, 2021, 125, 10273–10281.
76. J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 5287–5293.
77. F. Perrella, F. Coppola, A. Petrone, C. Platella, D. Montesarchio, A. Stringaro, G. Ravagnan, M. P. Fuggetta, N. Rega and D. Musumeci, Biomolecules, 2021, 11, 1048.
78. S. Grimme, J. Antony, T. Schwabe and C. Mück-Lichtenfeld, Org. Biomol. Chem., 2007, 5, 741–758.
79. F. Coppola, F. Perrella, A. Petrone, G. Donati and N. Rega, Front. Mol. Biosci., 2020, 7, 569990.
80. D. Jacquemin, V. Wathelet, E. A. Perpète and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420–2435.
81. C. A. Guido, D. Jacquemin, C. Adamo and B. Mennucci, J. Phys. Chem. A, 2010, 114, 13402–13410.
82. U. Raucci, M. G. Chiariello, F. Coppola, F. Perrella, M. Savarese, I. Ciofini and N. Rega, J. Comput. Chem., 2020, 41, 1835–1841.
83. C. A. Guido, S. Knecht, J. Kongsted and B. Mennucci, J. Chem. Theory Comput., 2013, 9, 2209–2220.
84. F. Perrella, U. Raucci, M. G. Chiariello, M. Chino, O. Maglio, A. Lombardi and N. Rega, Biopolymers, 2018, 109, e23225.
85. É. Brémond, M. Savarese, N. Q. Su, Á. J. Pérez-Jiménez, X. Xu, J. C. Sancho-García and C. Adamo, J. Chem. Theory Comput., 2016, 12, 459–465.
86. D. Jacquemin, E. A. Perpète, G. E. Scuseria, I. Ciofini and C. Adamo, J. Chem. Theory Comput., 2008, 4, 123–135.
87. M. Steinmetz and S. Grimme, ChemistryOpen, 2013, 2, 115–124.
88. F. Perrella, V. Langellotti, E. Buttarazzi, M. E. Cucciolito, M. Melchiorre, G. Pinto, V. Prokopenko, N. Rega, F. Ruffo, A. Petrone and R. Esposito, ChemCatChem, 2024, 16, e202300945.
89. T. Risthaus and S. Grimme, J. Chem. Theory Comput., 2013, 9, 1580–1591.
90. E. Buttarazzi, F. Perrella, N. Rega and A. Petrone, J. Chem. Theory Comput., 2023, 19, 8751–8766.
91. M. A. Iron and T. Janes, J. Phys. Chem. A, 2019, 123, 3761–3781.
92. F. Perrella, F. Coppola, N. Rega and A. Petrone, Molecules, 2023, 28, 3411.
93. D. Nazarian, P. Ganesh and D. S. Sholl, J. Mater. Chem. A, 2015, 3, 22432–22440.
94. F. Perrella, A. Petrone and N. Rega, J. Chem. Theory Comput., 2023, 19, 626–639.
95. M. M. Quintal, A. Karton, M. A. Iron, A. D. Boese and J. M. L. Martin, J. Phys. Chem. A, 2006, 110, 709–716.
96. F. Perrella, X. Li, A. Petrone and N. Rega, JACS Au, 2023, 3, 70–79.
97. C. Latouche, D. Skouteris, F. Palazzetti and V. Barone, J. Chem. Theory Comput., 2015, 11, 3281–3289.
98. F. Coppola, P. Cimino, F. Perrella, L. Crisci, A. Petrone and N. Rega, J. Phys. Chem. A, 2022, 126, 7179–7192.
99. Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2005, 1, 415–432.
100. M. P. Waller, H. Braun, N. Hojdis and M. Bühl, J. Chem. Theory Comput., 2007, 3, 2234–2242.
101. F. Perrella, A. Petrone and N. Rega, Phys. Chem. Chem. Phys., 2021, 23, 22885–22896.
102. A. Jain, Y. Shin and K. A. Persson, Nat. Rev. Mater., 2016, 1, 15004.
103. J. Hafner, C. Wolverton and G. Ceder, MRS Bull., 2006, 31, 659–668.
104. P. J. Hasnip, K. Refson, M. I. J. Probert, J. R. Yates, S. J. Clark and C. J. Pickard, Phil. Trans. R. Soc. A, 2014, 372, 20130270.
105. C. J. Cramer and D. G. Truhlar, Phys. Chem. Chem. Phys., 2009, 11, 10757–10816.
106. M. Bühl and H. Kabrede, J. Chem. Theory Comput., 2006, 2, 1282–1290.
107. S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.
108. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
109. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Chem. Phys., 2001, 114, 5691–5701.
110. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
111. T. Vreven, B. Mennucci, C. O. da Silva, K. Morokuma and J. Tomasi, J. Chem. Phys., 2001, 115, 62–72.
112. S. J. Mo, T. Vreven, B. Mennucci, K. Morokuma and J. Tomasi, Theor. Chem. Acc., 2004, 111, 154–161.
113. A. Petrone, P. Caruso, S. Tenuta and N. Rega, Phys. Chem. Chem. Phys., 2013, 15, 20536–20544.
114. A. Ben-Naim, Solvation Thermodynamics, Plenum, New York, 1987.
115. A. Nakayama, G. Arai, S. Yamazaki and T. Taketsugu, J. Chem. Phys., 2013, 139, 214304.
116. S. Komin, C. Gossens, I. Tavernelli, U. Rothlisberger and D. Sebastiani, J. Phys. Chem. B, 2007, 111, 5225–5232.
117. J. Gao and M. Freindorf, J. Phys. Chem. A, 1997, 101, 3182–3188.
118. M.-E. Moret, I. Tavernelli and U. Rothlisberger, J. Phys. Chem. B, 2009, 113, 7737–7744.
119. I. Tavernelli, B. F. Curchod and U. Rothlisberger, Chem. Phys., 2011, 391, 101–109.
120. M. Nonella, G. Mathias and P. Tavan, J. Phys. Chem. A, 2003, 107, 8638–8647.
121. V. Pham, I. Tavernelli, C. Milne, R. van der Veen, P. DAngelo, C. Bressler and M. Chergui, Chem. Phys., 2010, 371, 24–29.
122. R. M. Abolfath, P. K. Biswas, R. Rajnarayanam, T. Brabec, R. Kodym and L. Papiez, J. Phys. Chem. A, 2012, 116, 3940–3945.
123. J. Wen, S. Mai and L. González, J. Phys. Chem. A, 2023, 127, 9520–9529.
124. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, B. G. Janesko, F. Lipparini, G. Zheng, J. L. Sonnenberg, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, P. V. Parandekar, N. J. Mayhall, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian Development Version, Revision H.37+, Gaussian Inc., Wallingford CT, 2010.
125. S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291–10302.
126. H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758–9763.
127. H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694–8704.
128. S. S. Iyengar, H. B. Schlegel, G. A. Voth, J. M. Millam, G. E. Scuseria and M. J. Frisch, Isr. J. Chem., 2002, 42, 191–202.
129. N. Rega, S. S. Iyengar, G. A. Voth, H. B. Schlegel, T. Vreven and M. J. Frisch, J. Phys. Chem. B, 2004, 108, 4210–4220.
130. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
131. G. J. Martyna, D. J. Tobias and M. L. Klein, J. Phys. Chem., 1994, 101, 4177–4189.
132. S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, J. Phys. Chem., 1995, 103, 4613–4621.
133. A. Lami and F. Santoro, in Computational Strategies for Spectroscopy: From Small Molecules to Nano Systems, ed. V. Barone, John Wiley & Sons, Ltd, New York, NY, 2011, ch. 10, pp. 475–516.
134. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
135. R. Improta and V. Barone, Top. Curr. Chem., 2015, 355, 329–357.
136. R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540–3593.
137. A. J. Pepino, J. Segarra-Martí, A. Nenov, R. Improta and M. Garavelli, J. Phys. Chem. Lett., 2017, 8, 1777–1783.
138. A. J. Pepino, J. Segarra-Martí, A. Nenov, I. Rivalta, R. Improta and M. Garavelli, Phys. Chem. Chem. Phys., 2018, 20, 6877–6890.
139. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
140. R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06254f

---