Quantitative reaction monitoring using parahydrogen-enhanced benchtop NMR spectroscopy

Abstract

The parahydrogen-induced polarisation (PHIP) NMR signal enhancement technique is used to study H₂ addition to Vaska's complex (trans-[IrCl(CO)(PPh₃)₂]) with both standard high-field (9.4 T) NMR and benchtop (1 T) NMR detection. Accurate and repeatable rate constants of (0.84 ± 0.03) dm³ mol⁻¹ s⁻¹ and (0.89 ± 0.03) dm³ mol⁻¹ s⁻¹ were obtained for this model system using standard high-field and benchtop NMR, respectively. The high-field NMR approach is shown to be susceptible to systematic errors associated with interference from non-hyperpolarised signals, which can be overcome through a multiple-quantum filtered acquisition scheme. This challenge is avoided when using benchtop NMR detection because the non-hyperpolarised signals are much weaker due to the lower magnetic field, enabling the use of a simpler and more efficient single RF pulse detection scheme. Method validation against several experimental parameters (NMR relaxation, %pH₂ enrichment and temperature) demonstrates the robustness of the benchtop NMR approach but also highlights the need for sample temperature control throughout reaction monitoring. A simple temperature equilibration protocol, coupled with use of an insulated sample holder while manipulating the sample outside the spectrometer, is found to provide sufficient temperature stabilisation to ensure that accurate and repeatable rate constants are obtained. Finally, the benchtop NMR reaction monitoring protocol is applied to the analysis of a complex mixture, where multiple reaction products form simultaneously. H₂ addition to a mixture of three Vaska's complex derivatives was monitored, revealing the presence of competitive reaction pathways within the mixture.

---

1 Introduction

NMR spectroscopy is a powerful analytical technique that is well suited to reaction monitoring applications due to its non-destructive nature, the level of chemical resolution and the ability to obtain time-dependent quantitative information. However, reaction monitoring applications of NMR are limited in some cases by the large footprint and cost of the spectrometers, alongside the requirement for deuterated solvents for field locking.

Within the field of NMR, there has been a recent resurgence in the development and application of lower-field (1–2 T) benchtop NMR spectrometers.¹ These benchtop NMR spectrometers can achieve field homogeneities of <10 ppb giving linewidths below 0.5 Hz.^2–4 This movement towards cryogen-free spectrometers comes with significant advantages for affordability and portability.⁵ Furthermore, benchtop NMR spectrometers often contain external locking systems (usually to ²H or ¹⁹F) allowing the reaction to be performed with standard protonated solvents. Combined, these benefits allow for in situ reaction monitoring with the spectrometer situated close to the reaction vessel or even incorporated into a flow setup for continuous on-line monitoring.^6–11 These unique capabilities have resulted in a plethora of reaction monitoring applications. In synthesis, these spectrometers have been employed to monitor reaction completion,^12,13 investigate reaction pathways^10,14 and calculate reaction rate constants.^15,16 Further applications have been seen within the field of biochemistry,^17,18 especially for enzymatic biocatalysis,^19–21 and process control.^22–26 In recent years, continued methods development on benchtop NMR systems has enabled expansion into reaction monitoring using heteronuclear channels^27,28 and also using multidimensional NMR (both with standard^29,30 and ultra-fast^31,32 pulse sequences). Several studies have validated the use of benchtop NMR spectrometers for reaction monitoring through comparisons to other time-resolved techniques, such as high-field NMR, gas chromatography³³ and IR spectroscopy.³⁴ Similar studies have also highlighted the benefit of using benchtop NMR with complementary on-line reaction monitoring techniques, such as IR^35–37 and mass spectrometry,³⁸ in order to maximise the information gained about a reaction system.

The transition to a weaker magnetic field strength can lead to challenges both in terms of sensitivity and chemical shift dispersion. In terms of sensitivity, the signal-to-noise ratio (SNR) of an NMR spectrum scales approximately with B^3/2₀ and so there is an inherent reduction in sensitivity when using a weaker benchtop NMR magnet.³⁹ Furthermore, the chemical shift dispersion in Hz increases linearly with B₀ and so the chemical shift axis is compressed at lower fields. This can lead to spectral congestion, peak overlap and an increased potential for second order peak patterns due to strong coupling effects.⁴⁰ Overall, these two limitations can make the observation and resolution of low concentration chemical species challenging at weaker magnetic fields, limiting the potential reaction monitoring applications of benchtop NMR spectrometers.

An array of hyperpolarisation techniques have been developed to boost the sensitivity of NMR spectroscopy. The core principle governing hyperpolarisation is to drive overpopulation of one or more nuclear spin energy levels to enhance the population difference of the system and thus increase the observed NMR signal. Several robust hyperpolarisation methods have been developed for use with NMR including dynamic nuclear polarisation (DNP),^41,42 chemically induced DNP (CIDNP),^43,44 spin optical exchange pumping (SEOP)^45,46 and parahydrogen induced polarisation (PHIP).^47–49 Of these techniques, the versatility and affordability of PHIP make it a good candidate for use in low-field reaction monitoring NMR experiments.⁵⁰

The PHIP effect was originally predicted by Bowers and Weitekamp⁴⁹ in 1986, with experimental verification of the technique being provided the following year.⁵¹ Hydrogenation reaction studies by Eisenberg and co-workers in 1986⁴⁷ showed similar results which were originally attributed to CIDNP but were later rationalised using PHIP.⁴⁸ The PHIP effect involves the incorporation of parahydrogen (pH₂) into an unsaturated organic molecule or inorganic complex. Parahydrogen is the NMR silent, lowest energy nuclear spin isomer of H₂ that can be generated in >99% purity by passing a stream of H₂ gas over a paramagnetic catalyst at 28 K. Once the gas is no longer in contact with the catalyst, the gas can be heated to room temperature without loss of purity due to the spin-forbidden nature of the transition between the triplet (ortho) and singlet (para) spin states.⁵² To transform the spin order of pH₂ into hyperpolarisation, the symmetry of the molecule must be broken either chemically or magnetically. In PHIP, this is achieved through incorporation of the molecule into the target analyte to introduce asymmetry between the two ¹H nuclei. Upon breaking the symmetry, strongly enhanced NMR signals for the original pH₂ protons are observed. When performed within a strong magnetic field, this addition of pH₂ occurs under so-called PASADENA (parahydrogen and synthesis allow dramatically enhanced nuclear alignment) conditions.⁵¹ As opposed to standard NMR, PASADENA conditions result in the overpopulation of the αβ and βα spin states of the proton nuclei. As indicated by Fig. 1, this results in strongly enhanced signals that appear antiphase relative to the J_HH coupling between the pH₂-derived protons in the product.⁵³

Fig. 1 Illustration of the population of nuclear energy states for an AX-type spin system under (a) standard conditions and (b) under PASADENA conditions, highlighting the net transitions occurring from each energy level and the spectra that will be produced from them when J_HH is positive.

One challenge associated with incorporating hyperpolarisation into a reaction monitoring experiment is the quantification of the observed signals. In standard NMR, signals can be related directly to concentration as long as the requirement of sufficient relaxation time between spectra is met. However, with hyperpolarised signals the quantification of the concentration of species is more complex owing to the transient nature of the hyperpolarised signal and the need to account for the efficiency of the hyperpolarisation process. This fundamental difference means that there may not be a direct correlation between the observed signal and the amount of product present within the solution. Previous research using high-field NMR, from the research groups of both Eisenberg⁵⁴ and Bargon,⁵⁵ demonstrated that quantitative PHIP-hyperpolarised reaction monitoring was possible for catalytic systems through use of ROCHESTER-type pulse sequences (ROCHESTER = rates of catalytic hydrogenation estimated spectroscopically through enhanced resonances). Currently, the research into PHIP-hyperpolarised reaction monitoring on benchtop NMR spectrometers has focused on obtaining qualitative results. Recent studies from Jeong et al.⁵⁶ and Gołowicz et al.⁵⁷ have monitored hydrogenation reactions using pH₂ and in both cases product formation was successfully followed and reaction coordinates were obtained. However, neither study included quantitative analysis in order to obtain kinetic parameters for the observed systems.

In this article, we demonstrate the potential of quantitative low-field reaction monitoring using parahydrogen. Through development on a model reaction system involving oxidative addition of pH₂ to Vaska's complex, which has a well established kinetic profile, several experimental parameters including temperature gradients, hyperpolarisation lifetimes and the pH₂ enrichment level were explored. From these experiments, strategies were developed to ensure accurate and robust rate constants could be measured. Finally, these developments were applied to an equilibrium mixture of Vaska's complexes featuring various phosphine ligands to demonstrate the potential of this approach for quantitative reaction monitoring in a complex mixture.

2 Experimental

2.1 Synthesis and sample preparation

trans-[IrCl(CO)(PPh₃)₂] was synthesised according to the procedure reported by Collman et al.⁵⁸ The product was then purified through heating (100 °C) in vacuo overnight to remove oxygen adduct by-products. A final recrystalisation step was performed by dissolving the solid in warm chloroform (100 mL) under an N₂ atmosphere followed by precipitation using methanol (300 mL) to yield yellow crystals (1.08 g, 34.6%). ¹H NMR (400 MHz, C₆D₆) δ: 7.96 (m, 12H, o-Ph), 7.03 (m, 18H, m-Ph and p-Ph). ³¹P{¹H} NMR (162 MHz, C₆D₆) δ: 24.5. IR (ATR, cm⁻¹): 1949 (ν_CO).

The synthesis of trans-[IrCl(CO)(PBn₃)₂] was adapted from a procedure for the synthesis of Vaska's complex by Burk et al.⁵⁹ Under an N₂ atmosphere, a round-bottomed flask was charged with [IrCl(COD)]₂ (101 mg, 0.15 mmol), where COD = 1,5-cyclooctodiene, and tribenzylphosphine (183 mg, 0.60 mmol) dissolved in hexane/DCM (50 : 50 v/v, 20 mL). The solution was stirred for 10 minutes and then placed under a static pressure of CO (1 atm). After 1 hour of stirring, the solution was concentrated in vacuo and then filtered to give the product. The precipitate was washed with hexane (3 × 10 mL) and dried in vacuo to give a pale yellow powder (173 mg, 66.5%). ¹H NMR (400 MHz, C₆D₆) δ: 7.13 (m, 12H, o-Ph), 7.09 (m, 18H, m-Ph and p-pH), 3.48 (d, 6H, J = 3.5 Hz, CH), 3.47 (d, 6H, J = 3.5 Hz, CH). ³¹P{¹H} NMR (162 MHz, C₆D₆) δ: 12.7. IR (ATR, cm⁻¹): 1959 (ν_CO).

For reaction monitoring experiments, 0.43 mM of Vaska's complex was weighed out and then transferred into a glovebox under an N₂ atmosphere. The complex was then dissolved in C₆D₆ to form a bulk solution from which 0.6 mL aliquots were transferred into NMR tubes fitted with J Young taps. Samples were placed under vacuum through a freeze–pump–thaw method prior to experimentation: each sample was placed onto a high-vacuum line, frozen using liquid N₂ and then degassed. This process was repeated in triplicate.⁶⁰

2.2 Reaction monitoring procedure

All benchtop NMR reaction monitoring experiments were performed on a 1 T (43 MHz) Spinsolve Carbon spectrometer (Magritek, Germany). All high-field NMR experiments were performed using a 9.4 T (400 MHz) AVIII spectrometer (Bruker, USA). The pH₂ used was generated from a home-built pH₂ generator capable of producing >99% purity pH₂.⁵²

To perform each reaction monitoring experiment, the degassed sample is first placed into the spectrometer to thermally equilibrate for at least 10 minutes, during which time a ¹H spectrum is run to ensure starting material purity. Following this, the sample is removed from the spectrometer and placed under a pH₂ atmosphere (4 bar absolute). The sample is then shaken for 5 seconds and re-inserted back into the spectrometer, after which data acquisition is started.

During the experiment, a series of spectra are acquired using a pulse and acquire (PA) experiment with 45° excitation pulses (Fig. 2a). A consistent evolution delay (t) was used between successive pulses to ensure that reaction progress was probed at regular intervals. Unless otherwise stated, t = 5 s and n = 128, giving a total experiment time of 10.7 minutes. The pulse sequence generates a pseudo-2D dataset containing a stacked plot of 1D ¹H spectra along the reaction time coordinate (Fig. 2b).

Fig. 2 (a) Pulse sequence for the reaction monitoring experiment showing the acquisition delay, t, and number of loops, n, alongside (b) an example output pseudo-2D stacked spectrum.

2.3 Automated data processing

To enable rapid and consistent analysis of the experimental data, an automated data processing script was written using the coding language, Prospa, provided with the spectrometer. This script loads in the 2D dataset and extracts the second row (the first NMR spectrum with pure PASADENA character). Within this spectrum, peak picking of all hydride peaks is performed and an integration region is defined for each (further detail is given in the ESI†).

This information is used to integrate strips of the 2D dataset to produce the change in hydride peak integral over time. This dataset is then normalised and scaled to the final concentration of the system. This concentration is calculated from the initial concentration of Vaska's complex, the limiting reagent, using the knowledge that the reaction is irreversible and goes to completion over the timescale of the experiment. Data can then be fitted to a monoexponential recovery function to generate an observed rate constant (k_obs) for the reaction. Under the standard experimental conditions used (4 bar pH₂ and 0.43 mM Vaska's complex), there is a 27-fold excess of pH₂ and as such this reaction occurs under pseudo-first order conditions. This allows for calculation of the overall k₂ rate constant using eqn (1) and the known concentration of pH₂ (0.0118 M) - calculated using a pressure of 4 bar and a mole fraction of H₂ of 3.00 × 10⁻³ M atm⁻¹ at 28.5 °C.⁶¹ Within the equation, [Vaska], [Vaska(H₂)] and [H₂] correspond to the concentrations of the starting material, product, and hydrogen gas respectively.

3 Results and discussion

3.1 Initial reaction monitoring

The addition of parahydrogen to Vaska's complex (Fig. 3a) was chosen as a model system with which to probe the reaction monitoring capability of the benchtop NMR spectrometer. This selection was based upon the irreversible nature of the reaction at the temperature of the spectrometer (held at 28.5 °C for magnetic field homogeneity) and a reaction timescale of several minutes. Upon addition of pH₂, the formation of [Ir(H)₂Cl(CO)(PPh₃)₂] is observed under PASADENA conditions as a pair of triplets of antiphase doublets (at −6.7 and −17.5 ppm for the hydrides trans to CO and Cl, respectively).

Fig. 3 (a) Reaction scheme for the oxidative addition of pH₂ to Vaska's complex, highlighting the spontaneous formation of hyperpolarised product that subsequently relaxes according to R₁. (b) Hydride signal decay (grey) and product formation curve (red) for the oxidative addition of pH₂ (4 bar) to Vaska's complex (0.43 mM).

Following the procedure outlined in Section 2.2, reaction monitoring for this system was repeated in triplicate to give an average k₂ rate constant of (0.792 ± 0.008) dm³ mol⁻¹ s⁻¹ for the reaction. Fig. 3b shows an example reaction monitoring profile for these experiments, with the decay of PHIP activity over time highlighted in grey and the corresponding product formation curve in red. To benchmark this result, comparisons were made to previous studies on the system performed by Chock et al.⁶² that monitored the reaction kinetics through H₂ gas uptake. Through interpolation of a variable temperature study between 20–35 °C, the expected k₂ rate constant for this experiment at 28.5 °C was found to be (0.86 ± 0.03) dm³ mol⁻¹ s⁻¹ which is slightly higher than that observed here experimentally.

For comparison, an identical PHIP-hyperpolarised reaction monitoring methodology was followed on a high-field (9.4 T) NMR spectrometer. This gave a k₂ rate constant of (0.963 ± 0.013) dm³ mol⁻¹ s⁻¹ which was higher than both the low-field NMR and literature values. This overprediction originated from the build-up of thermally-polarised product molecules across the reaction coordinate. The growing in-phase signal from the non-hyperpolarised product destructively interferes with the anti-phase signals from the hyperpolarised product. This was confirmed experimentally through repetition of the reaction monitoring experiment with an OPSY (Only Parahydrogen SpectroscopY) pulse sequence replacing the 45° pulse within the spectral acquisition loop.⁶³ This multiple-quantum filter (pulse sequence given in the ESI†) selectively allows parahydrogen derived signals to pass through. This approach sacrifices sensitivity, as only a fraction of the hyperpolarised signal successfully passes through the filter, but ensures that all thermal magnetisation is dephased prior to observation. Using this method a k₂ rate constant of (0.84 ± 0.03) dm³ mol⁻¹ s⁻¹ was observed for the reaction, showing good agreement with the expected literature value of (0.86 ± 0.03) dm³ mol⁻¹ s⁻¹.⁶²

The deviation of the low-field rate constant from both the high-field NMR and literature values does not originate from the presence of background signal. This is because, unlike the high-field NMR spectra, there is no observable NMR signal from the non-hyperpolarised product once the reaction has reached completion due to the lower inherent sensitivity of the benchtop NMR system. As a result, the use of the OPSY sequence on the benchtop NMR spectrometer reduces the observed SNR without bringing any improvements in accuracy (a more comprehensive analysis can be found within the ESI†). Indeed the accuracy of the experiment decreases due to the reduction in the signal that passes through the OPSY filter. Therefore, in this case, the lower magnetic field of the benchtop NMR spectrometer is a benefit, because the absence of observable non-hyperpolarised signals from the product allows the simpler and more sensitive 45° pulse detection scheme to be used.

Following these initial comparisons, there is a clear discrepancy between the observed and expected kinetic parameters for the model system at low-field. To evaluate the source of this discrepancy, three reaction parameters were examined to establish the impact they may have on the effective rate constant: the lifetime of the hyperpolarised signal, the temperature of the sample and the pH₂ enrichment level used for the reaction.

3.2 Hyperpolarised signal lifetime

Upon product formation, the lifetime of the hyperpolarised signal has two potential routes through which it could impact the observed rate constant for the reaction. As shown in Fig. 3a, the hyperpolarised complex will relax after formation according to the hyperpolarised relaxation rate, R₁, of the species. If this relaxation process occurs prior to acquisition, then the observed signal will be reduced compared to the true number of molecules formed within this period. Conversely, if the relaxation rate is much slower than the repetition rate of the reaction monitoring experiment, signals from product formation in a previous sampling window could persist to contribute to subsequent observation windows. This can occur because the 45° pulse used for NMR detection has a theoretical maximum efficiency of 50% with the remaining magnetisation being preserved within NMR unobservable terms.⁶⁴ This remaining magnetisation could convert into observable NMR terms within the following acquisition window and so artificially inflate the integrals being observed.

To investigate if relaxation effects were affecting the observed rate constant, the NMR experiment was repeated using different evolution delays of t = 5, 2.5 and 1.25 seconds. Shorter delays between acquisition could affect how much leftover magnetisation from previous evolution periods persists and so a variation in k₂ with evolution delay would be present. However, the results of the experiment, shown in Table 1, show that the change in evolution delay had a negligible impact on the measured rate constant for the reaction. This indicates that relaxation effects do not significantly impact this model system.

Table 1 Calculated k₂ rate constants for the oxidative addition of pH₂ to Vaska's complex with a variable acquisition delay (t)

t/s	k 2/dm^3 mol^−1 s^−1
	1	2	3	Average
5.00	0.787	0.783	0.807	(0.792 ± 0.008)
2.50	0.763	0.783	0.806	(0.784 ± 0.012)
1.25	0.764	0.774	0.836	(0.79 ± 0.02)

---

To investigate under what conditions relaxation effects need to be accounted for, the oxidative addition reaction was simulated within MATLAB. To achieve this, the evolution of the system was controlled by eqn (2), where [1] and [2*] correspond to the concentrations of starting material and hyperpolarised product respectively, k_obs is the pseudo-first order rate constant and R₁ is the rate constant for the longitudinal relaxation of the hyperpolarised species. The starting state of the simulation is 100% of 1. The system is then moved forward in time by 0.01 seconds during which time 1 will be converted into the hyperpolarised product 2* according to k_obs while any residual 2* will relax according to R₁. As NMR acquisition acts to remove 2* from the system, upon detection an additional leftover magnetisation parameter is used to determine the proportion of 2* to be preserved into the next acquisition window in the system. Once collected the simulated data can be fitted to a monoexponential recovery function to calculate a value of k_obs that can be compared to the initial input value.

Within the simulation, different combinations of k_obs and R₁ values were applied to determine the possible impact on the obtained rate constant. Of interest was the impact of varying R₁ for a reaction with a k_obs of 0.01 s⁻¹ (the expected k_obs of the model reaction of Vaska's complex) and of 0.1 s⁻¹ (a system reacting on the second timescale). Values of R₁ between 15 s⁻¹ and 0.015 s⁻¹ were used to observe relaxation timescales that were fast or slow relative to k_obs. For all simulations a leftover term of 0.5 (simulating residual magnetisation following a 45° pulse) was utilised. Further details about the simulation and the data from these studies is given in the ESI.† Simulations performed using a k_obs of 0.01 s⁻¹ showed negligible variation of the calculated value of k_obs across all R₁ values (with a maximum deviation of <1%). This is consistent with the experimental studies performed using the model system of Vaska's complex where no relaxation dependency was observed.

The observed signal decay curves for simulations using different R₁ values with a k_obs of 0.1 s⁻¹ are given in Fig. 4. To highlight the difference in signal observed for each experiment, the data has been normalised to the fastest relaxing system (R₁ = 15 s⁻¹, Fig. 4a). Through these simulation studies, it was found that for the fast relaxing system (R₁ ≫ k_obs, Fig. 4a) an accurate reaction rate was obtained but this system suffered from having a low SNR. This low SNR resulted from only a small proportion of the hyperpolarised product contributing to the signal as only instantaneous hyperpolarisation formed directly prior to the acquisition pulse would persist long enough to be observed. As R₁ is increased, an optimal set of parameters is observed when R₁ > k_obs (Fig. 4b). Under these conditions, an increase in SNR is observed due to a build up of bulk hyperpolarised signal during the acquisition delay (as the slower relaxation of hyperpolarised products enables those formed earlier within the acquisition delay to contribute to the observed signal). Importantly, this additional signal has a short enough relaxation lifetime as to not persist into the following acquisition delay and so no deviation in the calculated rate constant is observed.

Fig. 4 Simulated signal detected during the reaction monitoring experiment with k_obs = 0.1 s⁻¹, t = 1.25 s, a leftover magnetisation term of 0.5 and an R₁ value of either (a) 15 s⁻¹, (b) 1.5 s⁻¹ or (c) 0.015 s⁻¹. Data is normalised to (a) to show the observed signal increasing across the series.

As R₁ is increased further, to a regime where R₁ <= k_obs (Fig. 4c), there is continued improvement to the SNR but the determined rate deviates to lower than expected values. This deviation is indicative of a breakdown of the analysis method which assumes the observed signal will adhere to a simple monoexponential recovery function. This is due to the persistence of hyperpolarised signal between acquisition windows which leads to the observed signal representing a complex interplay between R₁ and k_obs. Under these conditions, it is possible to mitigate the effect of this interplay through use of smaller acquisition delays. More frequent spectral acquisition reduces the contribution of the residual signal within each acquisition delay thus minimising the effect of relaxation upon the observed signal. Overall for a system where R₁ <= k_obs, care must be taken within any analysis performed as the observed rate constant can be dependent on both parameters.

3.3 Temperature gradients

Temperature is an important factor to keep consistent within reaction monitoring procedures as the presence of a temperature gradient could affect the observed rate constant. From the literature data for the Vaska's complex system,⁶² it was found that within the examined temperature range (20–35 °C) the reaction displays a linear dependence on temperature with a constant of proportionality of 0.06 dm³ mol⁻¹ s⁻¹ T⁻¹. Therefore, a change in temperature during the reaction monitoring has the potential to skew the observed rate constant away from the expected value. Understanding the impact of temperature variations in reaction monitoring is especially crucial for benchtop NMR spectrometers based on permanent magnets as the internal instrument temperature is fixed to ensure magnetic field stability.

Within the original reaction monitoring procedure, there were two potential routes through which a temperature gradient could form within a sample. The first was during the transportation of the sample to and from the pH₂ generator when the sample would be exposed to the external environment of the lab. The lab is temperature controlled at 18 °C (as opposed to the internal Spinsolve temperature of 28.5 °C) and as such any time the sample is removed from the spectrometer a change of temperature will be observed. The second route for temperature loss is during the addition of pH₂ into the headspace of a sample. This step adds a room temperature gas into a sample that is preheated and as such, when mixed, the internal temperature of the system will change over time as it returns back to the temperature of the spectrometer.

Quantification of the potential impact of temperature was achieved using a sample of pure methanol as an NMR thermometer, whereby the chemical shift difference between the OH and CH₃ peaks (Δδ) for the sample can be converted into a temperature using eqn (3).⁶⁵ This method is able to simulate the procedure effectively as the accuracy of these measurements is retained when the sample is placed under N₂ and O₂ and so the influence of an H₂ atmosphere is expected to be negligible.⁶⁶

T(K) = 409.0 − 36.54(Δδ) − 21.85(Δδ)² (3)

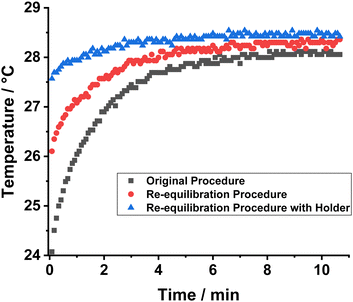
The combined impact of the two temperature factors described above is highlighted by the grey data set in Fig. 5, which shows the variation in the temperature of the NMR sample on the timescale of the reaction monitoring experiment. A large temperature range of 4.4 °C (between 24.1 and 28.5 °C) is observed which results in a substantial temperature gradient dominating the entire reaction monitoring experiment. To overcome the external temperature problem, an NMR tube sheath was manufactured to allow for the sample to be transported across the lab in a thermally insulated container. To address the internal temperature gradient caused by pH₂ addition, an additional re-equilibration step was added into the experimental protocol. Following pH₂ addition, the sample was reinserted into the spectrometer, without shaking, and left for 10 minutes to re-equilibrate to the internal temperature of the spectrometer. This step is made possible by the slow diffusion of pH₂ into the solution across the liquid–gas interface within the NMR tube. The reaction monitoring experiment was performed on the spectrometer during this re-equilibration step and no PHIP activity was observed during the 10 minute re-equilibration window. Upon shaking in the thermally insulated sheath, the pH₂ effectively mixes into the solution and initiates the reaction, which can be monitored using the previously described NMR acquisition procedure. Through combination of these two modifications, a large reduction in temperature gradient was observed over the timescale of the reaction monitoring experiment (the blue data set in Fig. 5) with the temperature range observed only spanning 0.9 °C (between 27.6 and 28.5 °C). Using this improved procedure, the average k₂ rate constant now increases to (0.89 ± 0.03) dm³ mol⁻¹ s⁻¹ which is in good agreement with the value expected from literature.⁶² The increased rate constant compared to prior studies is expected as the low initial temperatures of the original procedure would skew the observed rate constant to lower values.

Fig. 5 Observed temperature gradient when using a methanol thermometer to follow the original reaction monitoring procedure (grey) and the adapted procedure using a re-equilibration period (red) and a thermally-insulated holder (blue).

3.4 pH₂ enrichment

The final parameter investigated was the effect of changing the pH₂ enrichment level (%pH₂) on the observed rate constant. %pH₂ is defined as the proportion of H₂ that is in the para spin state based on the absolute populations of pH₂ (N_p) and oH₂ (N_o) in the mixture (eqn (4)).⁶⁷

For this reaction monitoring procedure to be robust, the rate constant must be independent of the precise %pH₂ used. This ensures that the approach can be used to determine kinetic information regardless of the parahydrogen generator being employed and the exact %pH₂ that is achievable - a crucial quality required of the technique to ensure results can be replicated across different experimental setups. To investigate this, the reaction monitoring experiment was repeated using variable %pH₂ enrichment levels. The different enrichment levels (between 99% and 60%) were created by changing the temperature of the pH₂ generator, using the procedure described by Richardson et al.⁶⁷ At each %pH₂ enrichment level, the reaction was repeated three times and the resulting k₂ rate constants are given in Table 2. The full dataset, along with the temperatures used to generate each %pH₂ enrichment level, are given within the ESI.†

Table 2 Averaged k₂ rate constants and initial SNRs for the oxidative addition of pH₂ to Vaska's complex with variable %pH₂ enrichment levels

%pH2	Initial SNR	Avg k2/dm^3 mol^−1 s^−1
99.04	65	0.901 ± 0.014
91.34	47	0.926 ± 0.003
80.13	44	0.88 ± 0.02
69.77	32	0.932 ± 0.008
59.78	28	1.00 ± 0.04

---

As observed from this data, there is a high level of consistency within the values obtained between 99% and 70%. This indicates that the %pH₂ enrichment level and the determined k₂ rate constant are independent of each other and thus the exact pH₂ generator used does not affect the observed kinetics. Of note is the reduction in average SNR observed within the first usable spectrum at each %pH₂ level. The decrease in SNR is due to the reduced proportion of pH₂ present at lower %pH₂ enrichment levels as this produces a comparatively lower proportion of hyperpolarised product complexes during each evolution delay. This will impact the number of data points able to be collected prior to loss of NMR signal into the spectral noise. This is highlighted by the increasing rate constant observed at 60% pH₂ where the signal is lost to noise sooner which implies total completion of the reaction at an earlier time, corresponding to a faster rate of reaction. Overall, this observation highlights that a key requirement for this technique is the presence of strong PHIP signal enhancements for the species being monitored.

The observation that the calculated rate is independent of %pH₂ enrichment levels suggests that there is no secondary relaxation pathway for %pH₂ within this system. The presence of a H₂ spin-state interconversion pathway would result in the reduction in %pH₂ enrichment over the course of the reaction. While the rate of reaction would be invariant to a decrease in %pH₂, due to the total concentration of H₂ remaining in excess, the observed rate of reaction would appear faster due to the reduction in the observed hyperpolarised signal levels throughout the time course of the reaction. Although the spontaneous interconversion of pH₂ is very slow,^68,69 this could potentially occur via nuclear spin initiated conversion through the reversible formation of the transition state between Vaska's complex and the dihydride product.⁷⁰ As no variation is observed as a function of %pH₂ enrichment for the system being investigated, this suggests that no interconversion is occurring on the timescale of the NMR experiment. However, the potential presence of a secondary relaxation pathway would need to be considered when observing other chemical systems.

Overall, the experimental parameter studies performed on this reaction monitoring procedure demonstrate that monitoring PHIP activity is a robust tool with which to determine rates of reactions using a benchtop NMR spectrometer. Key challenges with this approach lie with the effective mitigation of temperature gradients formed during the reaction monitoring procedure and with the SNR available from the combination of pH₂ generator and chemical system used. One further hardware limitation is the requirement to manually shake the sample prior to acquisition as the transfer times involved preclude this method from being applicable to systems that react on the millisecond-to-second timescales. One possible solution to this is to implement an in situ bubbling setup (such as that shown by Kiryutin et al.⁷¹) that would enable rapid spectral acquisition following initiation of the reaction.

3.5 Application to a complex mixture

To extend the applicability of this reaction monitoring approach, the method was used to follow simultaneous processes occurring within a mixture containing Vaska's complex derivatives formed through substitution of the PPh₃ ligand with PBn₃ (tribenzylphosphine, P(CH₂C₆H₅)₃).

As a previously unexplored system, reaction monitoring was performed on a pure sample of trans-[IrCl(CO)(PBn₃)₂] (5), from which a rate constant of k₂ = (0.83 ± 0.03) dm³ mol⁻¹ s⁻¹ was determined. The similar value of k₂ compared to Vaska's complex is supported by the similar activation energy parameters of the two complexes. These were examined through a variable temperature study, the details of which can be found in the ESI.† Therefore, both reactions are expected to occur on comparable timescales when observed simultaneously.

When trans-[IrCl(CO)(PPh₃)₂] and trans-[IrCl(CO)(PBn₃)₂] are mixed, an equilibrium mixture of trans-[IrCl(CO)(PPh₃)₂] (1), trans-[IrCl(CO)(PPh₃)(PBn₃)] (3), and trans-[IrCl(CO)(PBn₃)₂] (5) is formed within the solution (Fig. 6). This scrambling of PR₃-type ligands between iridium-centred square-planar complexes has been observed previously by Rominger et al.,⁷² who noted that this process occurs rapidly, with an equilibrium distribution of phosphine ligands being observed within minutes at −70 °C. Within the equilibrium mixture, each complex is able to react irreversibly with pH₂ to form three unique hyperpolarised dihydride complexes (shown in Fig. 7): [Ir(H)₂Cl(CO)(PPh₃)₂] (2*), [Ir(H)₂Cl(CO)(PPh₃)(PBn₃)] (4*), and [Ir(H)₂Cl(CO)(PBn₃)₂] (6*).

Fig. 6 Reaction scheme for the equilibrium established when trans-[IrCl(CO)(PPh₃)₂] (1) and trans-[IrCl(CO)(PBn₃)₂] (5) are mixed to form trans-[IrCl(CO)(PPh₃)(PBn₃)] (3).

Fig. 7 Schemes for the reaction of trans-[IrCl(CO)(PPh₃)₂] (1), trans-[IrCl(CO)(PPh₃)(PBn₃)] (3), and trans-[IrCl(CO)(PBn₃)₂] (5) with pH₂ to form hyperpolarised dihydride complexes 2*, 4* and 6*.

While all three species (2*, 4* and 6*) are well-resolved at 9.4 T (spectrum shown in the ESI†), slight overlap of the ¹H proton resonances is observed at 1 T (Fig. 8a). To account for this within the reaction monitoring experiment, hydride peaks are grouped by complex with any peaks showing overlap being grouped into a fourth discarded category. The remaining peaks for each complex can then be analysed as previously discussed for a single complex.

Fig. 8 (a) Hyperpolarised single-scan ¹H spectrum and (b) PHIP signal decays corresponding to the formation of 2*, 4* and 6* from the reaction between pH₂ and an equilibrium mixture of 1, 3 and 5 formed from an initial sample containing 1 (0.43 mM) and 5 (0.43 mM). All PHIP signal integrals are normalised to the maximum integral recorded for [Ir(H)₂Cl(CO)(PPh₃)(PBn₃)].

To perform reaction monitoring on a complex mixture, equimolar solutions containing 0.43 mM of both 1 and 5 were prepared and analysed (Fig. 8b). Prior to this experiment, reaction monitoring using 0.86 mM of 1 was performed to confirm that pseudo-first order conditions were still satisfied within the mixture. The reaction monitoring experiment was performed in triplicate on the mixture and gave k_exp rate constants of (0.98 ± 0.07), (1.07 ± 0.09) and (1.05 ± 0.07) dm³ mol⁻¹ s⁻¹ for the formation of 2*, 4*, and 6* respectively.

The observed k_exp rate constants appear faster than the k₂ rate constants obtained when monitoring each complex in isolation. We hypothesise that this deviation is present due to the complex interplay between two competing processes: the irreversible formation of hyperpolarised products and the rapid dynamic equilibrium between the different derivatives of Vaska's complex within the sample. Over the course of the reaction, there will be continual adjustments to the proportions of each of the starting complexes (1, 3 and 5) present in order to push the system back towards equilibrium.

To explore this hypothesis, we fit the experimental data to a differential model that contains the competing processes illustrated in Fig. 6 and 7. Within the model, we fix the rate of formation of 2* and 6* to the values measured for each complex in isolation, while the unknown rate of formation of 4* and the rates associated with the dynamic equilibrium (K₁ and K₂ in Fig. 6) are allowed to vary. The hyperpolarised integrals are scaled to the final distribution of the dihydride complexes in solution, as observed in a 400 MHz ¹H NMR spectrum of the sample following reaction completion. Full details of the model and the fitting parameters are provided in ESI.† The model was found to produce a very good fit to the experimental data with an average k₂ of (1.26 ± 0.16) dm³ mol⁻¹ s⁻¹ for the formation of 4* across three independent measurements. We note that this value has a much greater variability than the previously measured rate constants, likely due to the increased uncertainty within the measurements due to the starting material equilibrium. The k₂ rate constant for 4* is significantly faster than those measured for the formation of 2* and 6* in isolation. This provides a potential explanation for the higher fit rates for these two complexes within the mixture. As 3 is consumed faster than 1 and 5, the equilibrium within the system will be shifted towards formation of more of 3. This will lead to additional consumption of 1 and 5, resulting in a visibly faster decline in PHIP signal for 2* and 6*. This is taken into account by the dynamic equilibrium in our model, such that the experimental data can be effectively fit with the pH₂ addition rates for the formation of 2* and 6* fixed to the values determined for these complexes in isolation.

As noted above, the fitted rate of formation of 4*, (1.26 ± 0.16) dm³ mol⁻¹ s⁻¹, is significantly faster than the measured rates for formation of 2* and 6* in isolation, (0.89 ± 0.03) dm³ mol⁻¹ s⁻¹ and (0.83 ± 0.03) dm³ mol⁻¹ s⁻¹, respectively. The rate of reaction of Vaska's complex and its derivatives with H₂ links to the electron donating ability of the phosphine ligands and the steric reorganisation needed to reach the transition state for H₂ addition. We propose that the observation that 4* forms with the fastest rate is indicative of steric reorganisation reducing the rate of H₂ addition to electron-rich 5. Studies to further investigate this system and explore this hypothesis are a topic for future work.

The results here demonstrate that the reaction monitoring methodology is able to obtain kinetic information for multiple species formed simultaneously. While the apparent rate constants in this system were found to be faster than those measured for the complexes in isolation when a simple addition model was used, the inclusion of a competitive pathway equilibrating the starting complexes resulted in good experimental fits to the model. Importantly, as the rate of equilibration exceeds the rate of H₂ addition, these deviations would be observed regardless of the reaction monitoring method that is applied and were revealed here by the sensitivity boost provided by the pH₂ hyperpolarisation.

4 Conclusions

In this study, a PHIP hyperpolarised reaction monitoring procedure was developed. Through use of pH₂, the link between magnetic field strength and sensitivity was broken allowing for strong signals to be observed for micromolar concentration species over the course of a reaction on a 1 T benchtop NMR spectrometer. Using this method, complete reaction coordinates were able to be obtained for samples containing down to 0.1 mM of Vaska's complex derivative starting material. The methodology was validated against several experimental parameters (including hyperpolarisation lifetimes and %pH₂ enrichment levels) with only temperature being observed to have a significant impact on the rate of [Ir(H)₂Cl(CO)(PPh₃)₂] formation. This effect was mitigated through the introduction of a thermally-insulated holder and sample temperature equilibration within the spectrometer prior to reaction monitoring. Using this procedure, the higher k₂ for [Ir(H)₂Cl(CO)(PPh₃)₂] formation of (0.89 ± 0.03) dm³ mol⁻¹ s⁻¹ showed excellent agreement with the expected value of (0.86 ± 0.03) dm³ mol⁻¹ s⁻¹ from literature.⁶²

Through the studies performed, the lower sensitivity of the benchtop NMR spectrometer was observed to bring advantages as well as challenges. The reduced signal contribution from non-hyperpolarised product molecules enabled the collection of robust kinetic information without the application of more complex and less sensitive OPSY-type pulse sequences as were required when using standard high-field NMR. However, for low concentration hyperpolarised complexes or setups that use lower pH₂ enrichment levels, SNR issues can prevent full reaction coordinates from being obtained for the species of interest. The limit found with this experimental setup was that an initial SNR above 30 was required to allow for a sufficient decay in PHIP activity to be monitored for a chemical reaction.

Despite being simple, this reaction monitoring method was shown to be capable of monitoring the formation of multiple products within a single reaction mixture. This study involved taking an equimolar mixture containing trans-[IrCl(CO)(PPh₃)₂] and trans-[IrCl(CO)(PBn₃)₂] and exposing it to pH₂. Unexpected deviations from the rate constants measured for the materials in isolation were initially observed when a simple growth model was used to analyse the data. This difference revealed that the dynamic equilibrium resulting from the assumed bimolecular substitution pathway leading to the formation of trans-[IrCl(CO)(PPh₃)(PBn₃)] needed to be taken into account. With the dynamic equilibrium included in our model, a good fit to the experimental data was obtained using rate constants for the formation of 2* and 6* fixed to those measured in studies on the isolated complexes. Hence, we illustrate that this approach can successfully screen complex reactions using low field benchtop NMR through single rather than multiple time course experiments. However, there is a need to adequately assess all the resulting chemical equilibria that are established in solution. Further investigations are required to develop a better understanding of the chemical systems explored herein and are a topic for future work using this reaction monitoring protocol.

A route to further expand the applicability of this benchtop NMR reaction monitoring method would be to use a spectrometer with additional decoupling channels (in particular ³¹P and ¹⁹F). Being able to reduce the multiplicity of peaks within the NMR spectra will improve SNR and enable better resolution of each component at low-field, allowing for more facile analysis of the mixture spectra and for more complicated mixtures to be examined with this technique. An alternative approach could be to harness the power of principle component analysis to analyse the dataset.⁷³ As this approach is effective at analysing small variations between spectra and handling low-SNR signals, it may provide a route to include the overlapped peaks within the analysis through separating out the contributions of each species within these peaks.

An alternative route for expansion is to integrate a photochemical setup with the benchtop NMR spectrometer (as demonstrated in recent literature by Bramham et al.⁷⁴) which would allow for reaction monitoring of a photochemical system with a clearly defined start time for the reaction. Incorporation of an in situ light irradiation source would also open up the possibility to explore hyperpolarisation via other hyperpolarisation methods such as photo-CIDNP, which has been shown to achieve strong signal enhancements on a benchtop NMR spectrometer⁷⁵ and would increase the scope of reactions able to be monitored. Furthermore, previous research using high-field NMR has shown that powerful insights can be gained from monitoring PHIP-hyperpolarised photochemical systems, including both kinetic information about the chemical reaction⁷⁶ as well as the milli-to-microsecond evolution of the pH₂ spin-state following photoinitiation.⁷⁷

Author contributions

Alastair Robinson: data curation, formal analysis, investigation and writing – original draft and editing. Fraser Hill-Casey: methodology, resources, supervision. Simon Duckett: conceptualisation, funding acquisition, supervision, writing – review and editing. Meghan Halse: conceptualisation, funding acquisition, supervision, writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to V. Annis and F. Adwal for assistance with this research. Financial support from the University of York (A. D. R. PhD studentship) and EPSRC (EP/R028745/1 and EP/M020983/1) is gratefully acknowledged.

The data supporting this research, including all raw NMR data, is openly available for download from the York Research Database at DOI: 10.15124/a123b19a-3cb5-4673-a1ad-88bf9158074a.

References

1. B. Blümich, J. Magn. Reson., 2019, 306, 27–35.
2. K. Halbach, Nucl. Instrum. Methods, 1980, 169, 1–10.
3. H. Raich and P. Blümler, Concepts Magn. Reson., Part B, 2004, 23, 16–25.
4. A. J. Parker, W. Zia, C. W. Rehorn and B. Blümich, J. Magn. Reson., 2016, 265, 83–89.
5. K. Singh and B. Blümich, Trends Anal. Chem., 2016, 83, 12–26.
6. S. K. Küster, E. Danieli, B. Blümich and F. Casanova, Phys. Chem. Chem. Phys., 2011, 13, 13172–13176.
7. B. Blümich, G. K. M. Verzijl, V. M. Litvinov, E. Danieli, F. Casanova, A. L. L. Duchateau, J. Perlo, A. L. L. Duchateau, G. K. M. Verzijl, V. M. Litvinov, B. Blümich and F. Casanova, Chem. Phys. Chem., 2014, 15, 3060–3066.
8. M. V. Gomez and A. De La Hoz, Beilstein J. Org. Chem., 2017, 13, 285–300.
9. P. Giraudeau and F. X. Felpin, React. Chem. Eng., 2018, 3, 399–413.
10. M. V. Silva Elipe and R. R. Milburn, Magn. Reson. Chem., 2016, 54, 437–443.
11. L. Tadiello, H. J. Drexler and T. Beweries, Organometallics, 2022, 41, 2833–2843.
12. H. Kim, Y. Yonekura and J. I. Yoshida, Angew. Chem., Int. Ed., 2018, 57, 4063–4066.
13. M. Goldbach, E. Danieli, J. Perlo, B. Kaptein, V. M. Litvinov, B. Blümich, F. Casanova and A. L. Duchateau, Tetrahedron Lett., 2016, 57, 122–125.
14. S. T. Knox, S. Parkinson, R. Stone and N. J. Warren, Polym. Chem., 2019, 10, 4774–4778.
15. M. Leutzsch, A. J. Sederman, L. F. Gladden and M. D. Mantle, Magn. Reson. Imaging, 2019, 56, 138–143.
16. E. Danieli, J. Perlo, A. L. L. Duchateau, G. K. M. Verzijl, V. M. Litvinov, B. Blümich and F. Casanova, ChemPhysChem, 2014, 15, 3060–3066.
17. D. Bouillaud, J. Farjon, O. Gonçalves and P. Giraudeau, Magn. Reson. Chem., 2019, 57, 794–804.
18. M. H. Killner, Y. Garro Linck, E. Danieli, J. J. Rohwedder and B. Blümich, Fuel, 2015, 139, 240–247.
19. C. Claaßen, K. Mack and D. Rother, ChemCatChem, 2020, 12, 1190–1199.
20. K. E. Anderssen and E. R. McCarney, Food Control, 2020, 112, 107053.
21. A. Soyler, D. Bouillaud, J. Farjon, P. Giraudeau and M. H. Oztop, LWT, 2020, 118, 108832.
22. V. Sans, L. Porwol, V. Dragone and L. Cronin, Chem. Sci., 2015, 6, 1258–1264.
23. S. Kern, K. Meyer, S. Guhl, P. Gräßer, A. Paul, R. King and M. Maiwald, Anal. Bioanal. Chem., 2018, 410, 3349–3360.
24. P. Giraudeau, F.-X. Felpin, B. Picard, M. Penhoat, T. Lebleu, J. Maddaluno, B. Gouilleux, J. Legros and I. Chataigner, Angew. Chem., 2017, 56, 7568–7572.
25. C. M. Archambault and N. E. Leadbeater, RSC Adv., 2016, 6, 101171–101177.
26. P. Sagmeister, J. Poms, J. D. Williams and C. O. Kappe, React. Chem. Eng., 2020, 5, 677–684.
27. T. H. Rehm, C. Hofmann, D. Reinhard, H. J. Kost, P. Löb, M. Besold, K. Welzel, J. Barten, A. Didenko, D. V. Sevenard, B. Lix, A. R. Hillson and S. D. Riegel, React. Chem. Eng., 2017, 2, 315–323.
28. B. Musio, E. Gala and S. V. Ley, ACS Sustainable Chem. Eng., 2018, 6, 1489–1495.
29. B. Ahmed-Omer, E. Sliwinski, J. P. Cerroti and S. V. Ley, Org. Process Res. Dev., 2016, 20, 1603–1614.
30. A. Friebel, E. Von Harbou, K. Münnemann and H. Hasse, Ind. Eng. Chem. Res., 2019, 58, 18125–18133.
31. B. Gouilleux, B. Charrier, E. Danieli, J. N. Dumez, S. Akoka, F. X. Felpin, M. Rodriguez-Zubiri and P. Giraudeau, Analyst, 2015, 140, 7854–7858.
32. B. Charrier, B. Gouilleux, S. Akoka, M. Rodriguez-Zubiri, P. Giraudeau and F.-X. Felpin, TrAC, Trends Anal. Chem., 2016, 83, 65–75.
33. K. Singh, E. Danieli and B. Blümich, Anal. Bioanal. Chem., 2017, 409, 7223–7234.
34. W. G. Lee, M. T. Zell, T. Ouchi and M. J. Milton, Magn. Reson. Chem., 2020, 58, 1193–1202.
35. K. A. Farley, U. Reilly, D. P. Anderson, B. P. Boscoe, M. W. Bundesmann, D. A. Foley, M. S. Lall, C. Li, M. R. Reese and J. Yan, Magn. Reson. Chem., 2017, 55, 348–354.
36. Y. Chae, S. Min, E. Park, C. Lim, C. H. Cheon, K. Jeong, K. Kwak and M. Cho, Anal. Chem., 2021, 93, 2106–2113.
37. D. Galvan, L. M. de Aguiar, J. J. R. Rohwedder, D. Borsato and M. H. M. Killner, Fuel Process. Technol., 2020, 208, 106511.
38. L. Porwol, A. Henson, P. J. Kitson, D. L. Long and L. Cronin, Inorg. Chem. Front., 2016, 3, 919–923.
39. A. Webb, Anal. Chem., 2012, 84, 9–16.
40. J. F. Araneda, T. Mendonça Barbosa, P. Hui, M. C. Leclerc, J. Ma, A. F. Maier and S. D. Riegel, J. Chem. Educ., 2021, 98, 1227–1232.
41. M. Thaning, M. H. Lerche, B. Fridlund, K. Golman, L. Hansson, J. H. Ardenkjaer-Larsen, G. Hansson, R. Servin and A. Gram, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10158–10163.
42. A. Abragam and M. Goldman, Rep. Prog. Phys., 1978, 41, 395–467.
43. J. Bargon, U. Johnsen and H. Fischer, Z. Naturforsch., A: Phys. Sci., 1967, 22, 1551–1555.
44. M. Goez, Concepts Magn. Reson., 1995, 7, 69–86.
45. M. A. Bouchiat, T. R. Carver and C. M. Varnum, Phys. Rev. Lett., 1960, 5, 373–375.
46. T. G. Walker and W. Happer, Rev. Mod. Phys., 1997, 69, 629–642.
47. S. I. Hommeltoft, D. H. Berry and R. Eisenberg, J. Am. Chem. Soc., 1986, 108, 5345–5347.
48. T. C. Eisenschmid, R. U. Kirss, P. P. Deutsch, S. I. Hommeltoft, R. Eisenberg, J. Bargon, R. G. Lawler and A. L. Balch, J. Am. Chem. Soc., 1987, 109, 8089–8091.
49. C. R. Bowers and D. P. Weitekamp, Phys. Rev. Lett., 1986, 57, 2645–2648.
50. S. B. Duckett and R. E. Mewis, Acc. Chem. Res., 2012, 45, 1247–1257.
51. C. R. Bowers and D. P. Weitekamp, J. Am. Chem. Soc., 1987, 109, 5541–5542.
52. D. Blazina, S. B. Duckett, T. K. Halstead, C. M. Kozak, R. J. K. Taylor, M. S. Anwar, J. A. Jones and H. A. Carteret, Magn. Reson. Chem., 2005, 43, 200–208.
53. M. G. Pravica and D. P. Weitekamp, Chem. Phys. Lett., 1988, 145, 255–258.
54. M. S. Chinn and R. Eisenberg, J. Am. Chem. Soc., 1992, 114, 1908–1909.
55. P. Hübler, R. Giernoth, G. Kümmerle and J. Bargon, J. Am. Chem. Soc., 1999, 121, 5311–5318.
56. K. Jeong, S. Min, H. Chae and S. K. Namgoong, Magn. Reson. Chem., 2019, 57, 44–48.
57. D. Gołowicz, K. Kazimierczuk, M. Urbańczyk and T. Ratajczyk, ChemistryOpen, 2019, 8, 196–200.
58. J. P. Collman, C. T. Sears, M. Kubota, A. Davison, E. T. Shawl, J. R. Sowa and R. J. Angelici, in Inorganic Syntheses, ed. R. J. Angelici, John Wiley & Sons Ltd, New York, Vol. 28, 2007, pp. 92–94.
59. M. J. Burk and R. H. Crabtree, Inorg. Chem., 1986, 25, 931–932.
60. R. Shaver, S. Van Wallendael and D. P. Rillema, J. Chem. Educ., 1991, 68, 604.
61. C. L. Young, in IUPAC Solubility Data Series, ed. C. L. Young, Pergamon Press, Oxford, 1981, vol. 5/6, pp. 159–160.
62. P. B. Chock and J. Halpern, J. Am. Chem. Soc., 1966, 88, 3511–3514.
63. J. A. Aguilar, P. I. Elliott, J. López-Serrano, R. W. Adams and S. B. Duckett, Chem. Commun., 2007, 1183–1185.
64. J. Natterer and J. Bargon, Prog. Nucl. Magn. Reson. Spectrosc., 1997, 31, 293–315.
65. C. Ammann, P. Meier and A. E. Merbach, J. Magn. Reson., 1982, 46, 319–321.
66. A. L. Van Geet, Anal. Chem., 1970, 42, 679–680.
67. P. M. Richardson, R. O. John, A. J. Parrott, P. J. Rayner, W. Iali, A. Nordon, M. E. Halse and S. B. Duckett, Phys. Chem. Chem. Phys., 2018, 20, 26362–26371.
68. R. A. Green, R. W. Adams, S. B. Duckett, R. E. Mewis, D. C. Williamson and G. G. Green, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 67, 1–48.
69. A. J. Parrott, P. Dallin, J. Andrews, P. M. Richardson, O. Semenova, M. E. Halse, S. B. Duckett and A. Nordon, Appl. Spectrosc., 2019, 73, 88–97.
70. G. Buntkowsky, B. Walaszek, A. Adamczyk, Y. Xu, H. H. Limbach and B. Chaudret, Phys. Chem. Chem. Phys., 2006, 8, 1929–1935.
71. A. S. Kiryutin, A. V. Yurkovskaya, H. Zimmermann, H. M. Vieth and K. L. Ivanov, Magn. Reson. Chem., 2018, 56, 651–662.
72. R. L. Rominger, J. M. McFarland, J. R. Jeitler, J. S. Thompson and J. D. Atwood, J. Coord. Chem., 1994, 31, 7–18.
73. R. Stoyanova and T. R. Brown, NMR Biomed., 2001, 14, 271–277.
74. J. E. Bramham and A. P. Golovanov, Commun. Chem., 2022, 5, 1–10.
75. G. R. Stadler, T. F. Segawa, M. Bütikofer, V. Decker, S. Loss, B. Czarniecki, F. Torres and R. Riek, Angew. Chem., Int. Ed., 2023, 62, e20230869.
76. B. Procacci, P. M. Aguiar, M. E. Halse, R. N. Perutz and S. B. Duckett, Chem. Sci., 2016, 7, 7087–7093.
77. M. E. Halse, B. Procacci, S. L. Henshaw, R. N. Perutz and S. B. Duckett, J. Magn. Reson., 2017, 278, 25–38.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional experimental details, tables and figures. See DOI: https://doi.org/10.1039/d3cp06221j

‡ Present address: University of Cambridge, Cambridge, UK.

§ Present address: Gold Standard Phantoms Limited, Sheffield, UK

---