¹H and ¹³C chemical shift–structure effects in anhydrous β-caffeine and four caffeine–diacid cocrystals probed by solid-state NMR experiments and DFT calculations

Abstract

By using density functional theory (DFT) calculations, we refined the H atom positions in the structures of β-caffeine (C), α-oxalic acid (OA; (COOH)₂), α-(COOH)₂·2H₂O, β-malonic acid (MA), β-glutaric acid (GA), and I-maleic acid (ME), along with their corresponding cocrystals of 2 : 1 (2C–OA, 2C–MA) or 1 : 1 (C–GA, C–ME) stoichiometry. The corresponding ¹³C/¹H chemical shifts obtained by gauge including projector augmented wave (GIPAW) calculations agreed overall very well with results from magic-angle-spinning (MAS) nuclear magnetic resonance (NMR) spectroscopy experiments. Chemical-shift/structure trends of the precursors and cocrystals were examined, where good linear correlations resulted for all COO¹H sites against the H⋯O and/or H⋯N H-bond distance, whereas a general correlation was neither found for the aliphatic/caffeine-stemming ¹H sites nor any ¹³C chemical shift against either the intermolecular hydrogen- or tetrel-bond distance, except for the ¹³COOH sites of the 2C–OA, 2C–MA, and C–GA cocrystals, which are involved in a strong COOH⋯N bond with caffeine that is responsible for the main supramolecular stabilization of the cocrystal. We provide the first complete ¹³C NMR spectral assignment of the structurally disordered anhydrous β-caffeine polymorph. The results are discussed in relation to previous literature on the disordered α-caffeine polymorph and the ordered hydrated counterpart, along with recommendations for NMR experimentation that will secure sufficient ¹³C signal-resolution for reliable resonance/site assignments.

---

1 Introduction

Efficient administration of active pharmaceutical ingredients (APIs) is often challenging because the powders are either unstable or feature a low solubility in water/body fluids. One option for improving the solubility and/or other physical or chemical properties without recourse to ionic salts is the usage of a cocrystal, i.e., a supramolecular compound of an API and another molecular species (or even another API, a so-called drug–drug cocrystal).^1–3 Consequently, intense efforts have been spent during the past two decades to explore synthetic routes to cocrystal preparation as well as their structures and formation mechanisms.^2–5

One widely used API is the stimulant caffeine (1,3,7-trimethylpurine-2,6-dione), whose storage and precise quantitative (physiological) administration is complicated by its highly hygroscopic nature.^6–8 At room temperature (RT) in the absence of humidity, anhydrous caffeine exists as the low-temperature “β” modification, which at temperatures >150 °C converts into the metastable high-temperature “α” form, which transforms very slowly into β-caffeine at RT and dry air.⁹ Hence, commercial anhydrous caffeine powders often comprise a mixture of both modifications. Caffeine also exists in a monohydrate form, which unfortunately is very unstable at RT and converts either into phases with <1 water molecule/caffeine moiety or anhydrous β-caffeine (depending on the relative humidity).^7,9 Hence, large-scale storage, processing and other handling of caffeine powder with a well-defined stoichiometry is not trivial.

Yet, as demonstrated by Trask et al.,⁸ cocrystals of caffeine with diacids, such as oxalic acid (OA), malonic acid (MA), glutaric acid (GA), and maleic acid (ME), are stable across wide humidity ranges. Several studies are reported on their formation, stability, and physical properties.^8,10–14 The present investigation targeted the cocrystal structures obtained from β-caffeine (β-C) with each of OA, MA, GA, and ME, abbreviated as 2C–OA, 2C–MA, C–GA, and C–ME, respectively, according to the corresponding 2 : 1 and 1 : 1 caffeine : diacid stoichiometry. Although a fixed stoichiometry would be desirable, the C–ME cocrystal is metastable,¹⁰ while 2C–OA, 2C–MA, and C–GA cocrystals were hitherto not reported. Each X-ray diffraction (XRD) derived cocrystal structure is reported,⁸ encompassing the main caffeine–diacid motifs governing their supramolecular organization via hydrogen bonds (Section 3). The well-known limitation of XRD to locate precise H-atom positions, however, restricts its capacity of unveiling quantitative details on weak non-covalent interactions, such as H⋯O/N hydrogen and C⋯O/N tetrel bonds that account for the intermolecular interactions and structural organization of cocrystals, as well as numerous other supramolecular systems. Then, high-resolution magic-angle-spinning (MAS) ¹H and ¹³C nuclear magnetic resonance (NMR) spectroscopy offer valuable complementary structural insight,^15–20 in particular for structurally disordered (in)organic phases,^18,20,21 encompassing β-caffeine.^14,22–24

Herein, we present a comprehensive combined MAS NMR and density functional theory (DFT) study, reporting on DFT refinements of previous XRD-derived structures of each 2C–OA, 2C–MA, C–GA, and C–ME cocrystal⁸ together with each β-caffeine,⁹ α-OA,²⁵ α-OA·2H₂O,²⁶ β-MA,²⁷ β-GA,²⁸ and I-ME²⁹ precursor phase. ¹H and ¹³C isotropic chemical shifts calculated by the gauge including projector augmented wave (GIPAW) method^30–33 were contrasted with those from MAS NMR experiments, aiming at improved insight into the shift–structure trends, notably the hydrogen bond (HB)^34–46—and for the methyl moieties also tetrel bond (TB)^47–49—effects on the chemical shifts. While the complete sets of ¹³C chemical shifts/NMR-peak assignments of the 2C–MA and C–GA cocrystals were reported earlier by Vigilante and Mehta,⁵⁰ out of the four cocrystals considered herein, a majority of the ¹H chemical shifts are reported for the first time, along with nearly half of their ¹³C counterparts, such as those for 2C–OA and C–ME. We also present the first complete ¹³C NMR spectral assignment of the ten resonances from the eight unique ¹³C sites of the structurally disordered anhydrous β-caffeine polymorph. The results are discussed in relation to previous ¹³C MAS NMR reports on the ordered hydrated and anhydrous disordered α/β-caffeine and polymorphs, highlighting the role of the magnetic field for unambiguously discriminating between the α- and β-caffeine forms.

2 Materials and Methods

2.1 Cocrystal preparation

Anhydrous β-caffeine (98% purity), oxalic acid (98%), malonic acid (99%), glutaric acid (99%) and chloroform were obtained from Sigma-Aldrich along with maleic acid (99%) from Thermo Fisher. All cocrystals were prepared by solvent drop grinding,^8,13 using ball milling (Mixer Mill 500 Vario; Retsch) of the two precursor powders that were placed in a 25 mL stainless steel jar and ground with 7 mm stainless steel balls at a rate of 30 Hz for 90 min. All cocrystals were prepared from stoichiometric amounts of the precursors. The 2C–OA (space group P2₁/c) and 2C–MA (Fdd2) cocrystals⁸ with a 2 : 1 caffeine : diacid stoichiometry resulted by mixing 250 mg of β-caffeine with either 60 mg of α-OA or 70 mg of β-MA, respectively, along with 5 drops of chloroform. Likewise, the 1 : 1 stoichiometric C–GA (form II;⁸ space group P1̄) cocrystal was prepared by grinding 510 mg of β-caffeine with 350 mg of β-GA and a few drops of chloroform, and likewise for the C–ME (P2₁/n) counterpart (250 mg of β-MA and 150 mg of I-ME).⁸

2.2 Powder X-ray diffraction

Powder XRD (PXRD) patterns were collected from all cocrystals and precursors with a Bruker D8 Discover diffractometer equipped with a LYNXEYE position-sensitive detector, using Cu Kα_1,2 radiation (λ₁ = 154.06 pm; λ₂ = 154.44 pm) and a focusing Göbel mirror. Each powder was filled in a 0.7 mm borosilicate glass capillary. All diffractograms were collected at RT over a 2θ range of 5°–50°, employing a step size of 0.02° with either 0.25 s per step (for β-caffeine, OA, β-MA, β-GA, I-ME, 2C–MA, and C–ME) or 0.75 s per step (for 2C–OA and C–GA), giving total measurement times of around 10 and 30 min per sample, respectively. The XRD patterns of the precursors and cocrystals are shown in Fig. S1 and S2 (ESI†), respectively. Rietveld refinements and Pawley fits, performed with the TOPAS software,⁵¹ verified a near-100% purity of all specimens, except for the oxalic acid powder, which comprised a mixture of α-OA (96.1 wt%), α-OA·2H₂O (3.5%), and β-OA (0.39 wt%). The anhydrous β-caffeine purity was ≥99.6%, along with a (statistically unascertained) minute amount of α-caffeine (0.37 wt%). All refined unit cell parameters are listed in Table S1 (ESI†).

2.3 Solid-state NMR

All solid-state NMR experiments were performed at ambient temperature with a Bruker Avance-III spectrometer and a magnetic field (B₀) of 14.1 T, which provided the respective ¹H and ¹³C Larmor frequencies of −600.1 MHz and −150.9 MHz. ¹H and ¹³C chemical shifts are quoted relative to neat tetramethylsilane (TMS).

¹H→¹³C cross polarization (CP) MAS NMR (CPMAS) experimentation was performed with filled 4.0 mm zirconia rotors spinning at the MAS rate (ν_r) of 12.00 kHz, using contact periods (τ_CP) of 1.25 ms (except for β-MA; 833 μs and ν_r = 9.00 kHz), and the modified Hartmann–Hahn condition ν_H = ν_C + ν_r, where the ¹³C nutation frequency (ν_C) was ramped linearly⁵² by ±4.7 kHz around ν_C = 47 kHz. Throughout, the 90° ¹H pulse prior to CP operated at ν_H ≈ 100 kHz and SPINAL-64⁵³ proton decoupling at ν_H ≈ 78 kHz (6.4 μs pulses) was applied during signal detection. The relaxation delays (τ_relax) varied between 15 s and 30 s. The signal averaging involved 2048–3328 co-added signal transients, except for MA and GA (1024). Single-pulse (“Bloch decay”) ¹H MAS NMR spectra were recorded with 1.3 mm zirconia rotors undergoing fast MAS at 60.00 kHz with 90° rf pulses operating at the ¹H nutation frequency ν_H ≈ 80 kHz. 256–512 accumulated NMR-signal transients were recorded with τ_relax = 3 s. These relaxation delays were not sufficiently long to ensure NMR intensities that quantitatively reflect the relative H/C site populations in the structures but do not affect any conclusions from our analysis, which only concerned the chemical shifts. NMR spectral deconvolutions were performed with in-house developed software.⁵⁴

2.4 DFT/GIPAW calculations

DFT energy optimizations were performed on the following published PXRD-derived structures: β-caffeine;⁹ α-OA;²⁵ α-OA·2H₂O;²⁶ β-MA;²⁷ β-GA;²⁸ I-ME,²⁹ whereas all cocrystal structures were from ref. 8; see Table S2 (ESI†). The first-principle DFT energy minimizations were performed with the CASTEP software⁵⁵ (version 22.11) along current standard and well-developed protocols,^19,32,33 encompassing usage of the local density approximation (LDA) functional⁵⁶ with on-the-fly-generated ultrasoft pseudopotentials⁵⁷ and a plane-wave basis set.⁵⁸ The Tkatchenko and Scheffler method was employed for dispersion corrections.⁵⁹ All structures were initially optimized by solely adjusting the proton positions with fixed positions of all heavier atoms and unit-cell parameters. However, the agreement between the experimental and GIPAW-derived chemical shifts improved slightly for the β-caffeine structure by optimizing all cell parameters and atom positions (Table S2 and Section 4.3, ESI†). The ¹H and ¹³C magnetic shielding values were calculated with the GIPAW method^19,30–33 for all DFT-optimized structures. For both the DFT energy optimizations and the GIPAW shielding-parameter calculations, a Monkhorst–Pack k-point grid⁶⁰ was used with a maximum spacing of 0.05 Å⁻¹ in the reciprocal space, and a 1000 eV plane-wave energy cutoff to ensure convergence.

The DFT/GIPAW-derived principal values, {σ^Hj_xx, σ^Hj_yy, σ^Hj_zz} and {σ^Cj_xx, σ^Cj_yy, σ^Cj_zz}, of the respective second-rank magnetic shielding tensor of each unique ¹Hj and ¹³Cj site in the structure were converted into the corresponding chemical shift values, {δ^Sj_xx, δ^Sj_yy, δ^Sj_zz}, by the expression^19,32,33

δ^Sj_αα = σ^S_ref − σ^Sj_αα, with αα = {xx, yy, zz} and S = {¹H, ¹³C}. (1)

We employ a chemical shift scale throughout, where low (high) chemical shifts correspond to shielded (deshielded) nuclei, and the isotropic chemical shift is given by^61–63The shielding-to-shift conversion terms of eqn (1) were σ^H_ref = 29.034 ppm for ¹H and σ^C_ref = 169.837 ppm for ¹³C. The values were obtained by linear regressions that minimized the difference between the sets of calculated and experimental isotropic ¹H and ¹³C chemical shifts based on roughly half of each entire set of {δ^j_H} and {δ^j_C} values, and giving correlation coefficients (R²) of R² = 0.980 and R² = 0.999 when evaluated across each entire {δ^j_H} and {δ^j_C} ensemble, respectively.

3 Overview of cocrystals and their precursor structures

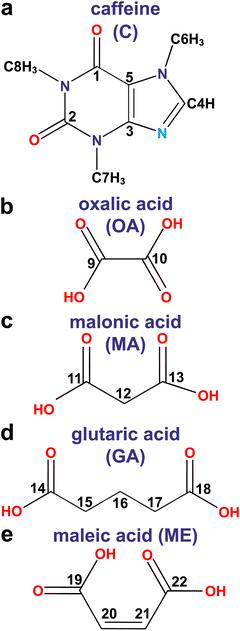
Fig. 1 shows the structures of caffeine and the four diacid molecules, where each number represents the ¹³C site index, giving the label “Cj” with 1 ≤ j ≤ 22, while all its directly bonded H, O, and N atoms carry the same index j. Note that although the C14/C18 sites are crystallographically equivalent in the β-GA structure, they are inequivalent in the C–GA cocrystal. For simplicity, we employ a strict C1–C22 labelling because all C/H sites are crystallographically distinct in either/both the diacid/cocrystal structure, except for C9/C10 (H9/H10), which remain equivalent in each α-OA, α-OA·2H₂O, and 2C–OA structure.

Fig. 1 Molecular structure with atom numbering of (a) caffeine, and the (b) oxalic, (c) malonic, (d) glutaric, and (e) maleic diacids. Each label/index j refers to carbon atom “Cj”, whose directly bonded O, N, and H atoms feature the same label (Oj, Nj, and Hj, respectively), except for the nitrogen atom of the imidazolium ring (cyan color) in (a), which is referred to simply as “N”.

Fragments from the by DFT energy-minimized crystal structures (Section 2.4) are shown in Fig. 2 for the diacids (a, b, d, f, h) and their respective cocrystals with caffeine (c, e, g, i). All pristine diacid structures involve strong intermolecular H bonds between the carboxy groups of neighboring molecules, except for I-ME, which besides one expected C19OOH⋯O22 contact also features a short intramolecular C22OOH⋯O19 HB (Fig. 2h), which remains intact also in the C–ME cocrystal shown in Fig. 2i, within a minute (2 pm) lengthening.

Fig. 2 Fragments from the DFT-refined crystal structures of (a) α-OA, (b) α-OA·2H₂O, (c) 2C–OA, (d) β-MA, (e) 2C–MA, (f) β-GA, (g) C–GA, (h) I-ME, and (i) C–ME. The dotted lines mark intermolecular H and tetrel bonds, with the accompanying number specifying the distance (in pm). The red and green lines/numbers distinguish tetrel bonds between caffeine–diacid and caffeine–caffeine molecules, respectively. Note that each methyl group undergoes a rapid rotation around the C–N bond and that only one H bond is indicated for each of the three equivalent protons.

As discussed by Trask et al.,⁸ both 2C–OA and 2C–MA cocrystals feature a heteromeric synthon where one diacid molecule is sandwiched between two caffeine units by a strong COOH⋯N hydrogen bond and a weaker C4H⋯OOC counterpart (Fig. 2c and e). The alternating caffeine–diacid–caffeine moieties of the supramolecular structure are stabilized primarily by those H bonds.⁸ The 1 : 1 caffeine : diacid stoichiometries of C–GA and C–ME, however, yield different intermolecular interactions. Owing to the intact intramolecular C22H⋯O19 bond in the C–ME cocrystal (Fig. 2i), its structure involves strictly alternating caffeine–ME interconnections, with a similar C4H⋯O19OC and C19OOH⋯N bond constellation as in the 2C–OA/MA cocrystals, yet with only one diacid-COOH group H-bonded to caffeine. Moreover, while the C–GA structure is also stabilized by two N⋯H14OOC and C4H⋯O14OC bonds between caffeine and one GA molecule (Fig. 2g), the C4H atom also involves another HB with O18 of a second diacid molecule, where moreover C18H is bonded to O14 of the first diacid unit. Hence, each caffeine molecule in C–GA features three different H bonds to two distinct GA molecules, both of which are additionally interlinked by a HB between their carboxy moieties, as in the parent GA structure.

Although the N⋯H bond between caffeine and a COOH group of a diacid unit constitutes the strongest intermolecular contact of the cocrystal,⁸ a further minor structure stabilization is arranged by H bonds between the CH₃ groups of caffeine with either diacid carboxy moieties or the O1/O2 atoms of neighboring caffeine molecules (Fig. 2c, e, g and i). The CH₃ moieties may furthermore form weak CH₃⋯O tetrel bonds^47–49 with the O1/O2 atoms of caffeine, or with the CO counterparts of the diacids, as marked in green and red color, respectively, in Fig. 2c, e, g and i (see Section 4.7). The methyl groups also form intermolecular tetrel and H bonds in the structurally disordered β-caffeine structure (Table S3, ESI†). We refer to ref. 9 and 22 for details about the anhydrous β-caffeine structure, whose unit cell comprises five inequivalent molecules, and thereby five NMR signal-contributions to each detected ¹³Cj and ¹Hj resonance.

4 Results and discussion

4.1. ¹³C MAS NMR spectra from cocrystal precursors

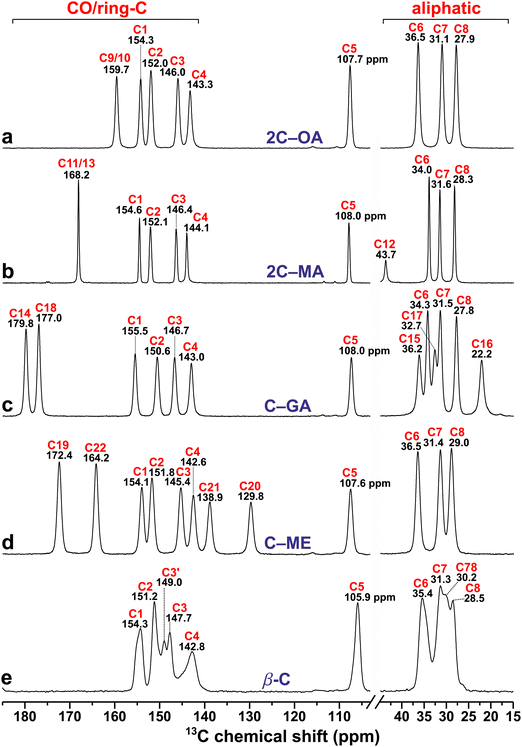
Because the chemical shift of a given ¹³C or ¹H nuclear site reflects its electronic environment in the structure, it is often a sensitive probe of the precise location of neighboring atoms in close vicinity. Fig. 3 displays the ¹³C CPMAS NMR spectra recorded from the diacids and β-caffeine cocrystal precursors. They involve resonances ranging from the most deshielded ¹³C nuclei (high chemical shifts) of carboxy groups with δ_C ≳ 160 ppm from the diacids (Fig. 3a–d) to the more shielded (lower shifts) aliphatic ¹³C sites with chemical shifts δ_C ≲ 40 ppm from β-MA, β-GA, and β-caffeine (Fig. 3b, c and e). The NMR spectral region intermediate of these extreme ¹³C shifts encompasses the comparatively deshielded ¹³C20 and ¹³C21 sites of I-ME (Fig. 3d), together with the ¹³C1–¹³C5 sites of β-caffeine resonating between 105–155 ppm (Fig. 3e).

Fig. 3 ¹³C CPMAS NMR spectra recorded at 14.1 T and a MAS rate of 12.00 kHz from (a) α-OA/α-OA·2H₂O mixture (“OA”), (b) malonic acid (β-MA), (c) glutaric acid (β-GA), (d) maleic acid (I-ME), and (e) anhydrous β-caffeine (β-C). Here and in other figures: NMR signals from the α-OA and α-OA·2H₂O phases are abbreviated by “OA” and “OAw”, respectively, whereas the red and black number above each NMR peak marks the C label of Fig. 1 and the chemical shift (in ppm) at the peak maximum, respectively. The inset of (b) is a zoom of the NMR spectral region marked by the dotted rectangle, and the asterisk marks a spinning sideband from the use of a lower MAS rate (9.00 kHz) for this experiment.

All cocrystal precursor powders (but OA) were phase pure, where the two crystallographically inequivalent ¹³COOH sites of MA and ME reveal chemical-shift differences of 0.4 ppm and 3.7 ppm, respectively, while both ¹³COOH sites of GA resonate at 181.5 ppm. In contrast, the two ¹³C NMR signals at 160.7 ppm and 163.1 ppm from OA derive from anhydrous α-OA and α-OA·2H₂O, respectively, each featuring one crystallographically unique ¹³COOH site.^25,26 From the integrated ¹³C NMR intensities of Fig. 3a, and confirmed by integrating the corresponding ¹H MAS NMR spectrum (Section 4.5.1), we estimated relative OA : OA·2H₂O amounts of approximately 0.7 : 1.0 in the oxalic acid mixture. (Although that estimate is only approximate, its precise value is immaterial for our subsequent analyses. The reason for the markedly higher OA·2H₂O content derived by NMR relative to PXRD is unknown but likely stems from a water uptake of the OA powder prior to the NMR experiments). The ¹³C chemical shifts obtained from Fig. 3 agree well with previous reports from α-OA,^36,64 α-OA·2H₂O,³⁶ MA,^14,65 GA,^36,65,66 and ME.^65–67

4.2. ¹³C NMR-peak assignments of anhydrous β-caffeine

Notwithstanding several ¹³C NMR publications on caffeine-based cocrystals,^{23,24,41,46,49,50} encompassing complete {δ_C} reports thereof,^23,50 ambiguities prevail about the precise set of ¹³C shifts and their assignments of the anhydrous β-caffeine structure itself, which produces two hitherto unassigned ¹³C resonances, none of which are present in MAS NMR spectra from either the structurally ordered caffeine monohydrate (henceforth referred to as C·H₂O) or disordered anhydrous α-caffeine modifications,²² each of which manifests one ¹³C resonance per C1–C8 site. Enright et al.²² presented ¹³C MAS NMR spectra from all α-/β-caffeine and C·H₂O forms, but precise chemical shifts were only reported for the latter.²² Likewise, δ_C values were not provided along with the ¹³C MAS NMR spectra from the anhydrous caffeine modifications studied in ref. 12, 24, 50 and 68. To the best of our knowledge, Table 1 presents the precise ¹³C chemical shifts and complete peak assignments for the anhydrous β-caffeine polymorph for the first time, where all further references herein to “α/β-caffeine” imply the anhydrous polymorphs. The ¹³C MAS NMR spectrum from β-caffeine of Fig. 3e appears to match very well that reported in ref. 22 while moreover our PXRD analysis confirmed a phase-pure specimen (Section 2.2). Notwithstanding that all eight {δⁿ_C} values of both α/β-caffeine modifications are (very) similar,²² the presence of two additional ¹³C NMR peaks at 149 ppm and 30 ppm in β-caffeine (Fig. 3e) distinguishes it from its “α” and C·H₂O counterparts, which Enright et al.²² attributed to ¹³C sites of crystallographically distinct molecules in the β-caffeine unit cell. That very plausible suggestion is confirmed below.

Table 1 NMR/DFT-derived ¹³C chemical shifts of β-caffeine^a

Site		δ ^jC[NMR] (ppm)	[small delta, Greek, macron] ^jC[NMR] (ppm)	[small delta, Greek, macron] ^jC[DFT] (ppm)		δ ^jC[DFT] (ppm)
a ^13C chemical shift at the NMR peak maximum, δ^jC[NMR], along with the center-of-gravity (average) chemical shift obtained by deconvolution of the MAS NMR spectrum (Fig. S3, ESI), [small delta, Greek, macron]^jC[NMR], or by DFT calculations, δ^jC[DFT]; the latter values are averages over the ^13C chemical shift values of five distinct caffeine molecules in the unit cell, each of which is given in the five rightmost columns. b The C3 sites produces two resonances at 149.0 ppm and 147.7 ppm, which are labelled by “C3′” and “C3” in Fig. 3e. c The “C78” ^13C resonance intensity at 30.2 ppm (Fig. 3e) involves equal contributions from the ^13C7 and ^13C8 sites.
C1		154.3	154.5 ± 0.2	153.0 ± 0.3		152.5	152.7	152.8	152.9	154.1
C2		151.2	150.8 ± 0.2	149.4 ± 0.3		148.3	148.9	149.5	149.7	150.5
C3^b		149.0/147.7	148.0 ± 0.2	147.5 ± 0.6		146.5	146.7	147.4	147.7	149.4
C4		142.8	143.5 ± 0.4	146.0 ± 1.3		142.9	143.9	145.0	148.9	149.3
C5		105.9	106.1 ± 0.2	107.8 ± 0.6		106.2	106.9	107.9	108.1	109.7
C6		35.4	35.0 ± 0.2	35.3 ± 0.6		33.7	34.8	35.4	35.7	36.7
C7^c		31.3/30.2	30.7 ± 0.2	29.6 ± 0.9		28.0	28.3	29.3	30.5	32.2
C8^c		30.2/28.5	29.6 ± 0.2	29.5 ± 0.6		27.7	28.6	29.2	29.9	32.0

---

Previous solid-state ¹³C NMR-peak assignments of all anhydrous and monohydrate caffeine polymorphs derive either from (i) employing DFT/GIPAW calculations of a caffeine-based cocrystal to assign its ¹³C sites of the caffeine moiety^23,24,50 or from (ii) the solution-NMR work of Sitkowski et al.,⁶⁹ which was exploited by Enright et al.²² for the ¹³C-site/NMR-peak identifications of the ordered C·H₂O modification in the solid state (which is greatly facilitated by its narrow ¹³C resonances). Those peak assignments were subsequently assumed in ref. 14 and 70. Although such straightforward ¹³C site/shift-mappings are also sufficiently reliable for application to α-caffeine, which involves one resonance per ¹³C site, the peak-assignment strategies (i) and (ii) are precluded for the two additional resonances at around 149/30 ppm from β-caffeine and labelled as C3′/C78 in Fig. 3e. To the best of our knowledge, both remain unidentified in current literature. Nonetheless, for each ¹³C1–¹³C8 resonance assignment of Fig. 3e, the DFT/GIPAW-derived ¹³C chemical shifts of Table 1 corroborate previously employed NMR-peak assignments made for both C·H₂O and α-caffeine modifications.^{14,22–24,70} The modeled chemical shifts, which were averaged over the 5 distinct caffeine molecules in the unit cell, reproduce the ¹³C NMR results from β-caffeine (very) well (Table 1), which for every asymmetric peakshape represents the center-of-gravity (CG) shift ([small delta, Greek, macron]^j_C) obtained from NMR-peak deconvolutions into two components (Fig. S3, ESI†) rather than the shift at the peak-maximum amplitude (δ^j_C). Note that (I) [small delta, Greek, macron]^j_C and δ^j_C represent the average and the most probable value over the chemical-shift distribution of ¹³Cj, respectively; (II) invoking CG shifts is only required for the structurally disordered β-caffeine structure, as opposed to those of any cocrystal or diacid precursor considered herein, for which [small delta, Greek, macron]^j_C = δ^j_C throughout.

Despite an overall good agreement between the experimental and modeled ¹³C chemical shifts of β-caffeine, the DFT/GIPAW calculations alone cannot uniquely identify the hitherto unassigned resonances at 149.0 ppm and 30.2 ppm (Fig. 3e). By spectral deconvolution, however, the integrated ¹³C NMR-peak intensities at around {154.3, 151.2, 149.0, 147.7} ppm were found to relate as 1.00 : 1.44 : 0.27 : 0.74 (Fig. S3, ESI†). That observation naturally attributes the resonance at 149.0 ppm to C3 (it is therefore referred to as C3′ in Fig. 3e), leading to [small delta, Greek, macron]^j_C values of {154.5(C1), 150.8(C2), 148.0(C3)} ppm with relative intensities 1.00 : 1.44 : 1.01. The deviations from the expected exact 1 : 1 : 1 ratios (where the discrepancy is only significant for C2) mainly reflect that integrated ¹³C NMR-peak intensities obtained by ¹H → ¹³C CPMAS NMR experiments do generally not exactly reproduce the corresponding ¹³C site populations in the structure. Likewise, the ¹³CH₃-associated resonance at δ^j_C = 30.2 ppm, which is labelled “C78” in Fig. 3e, was deduced to involve equal contributions from ¹³C7 and ¹³C8. Upon distributing half of the NMR-signal intensity at δ^j_C = 30.2 ppm to each of ¹³C7 (δ^j_C = 31.3 ppm) and ¹³C8 (δ^j_C = 28.5 ppm), the as-obtained relative integrated NMR-signal intensities of the C6 : C7 : C8 sites become 1.00 : 1.03 : 0.96, which is in excellent agreement with the expected 1 : 1 : 1 ratios (Fig. S3, ESI†).

Further support for the spectral-deconvolution-derived attribution of the “C3′” and “C78” NMR peaks to the ¹³C3 site and equal contributions to ¹³C7/¹³C8, respectively, is provided by the resulting very close {[small delta, Greek, macron]³_C, [small delta, Greek, macron]⁷_C, [small delta, Greek, macron]⁸_C} = {148.0, 30.7, 29.6} ppm values observed relative to the {δ³_C, δ⁷_C, δ⁸_C} = {147.8, 30.6, 29.0} ppm counterparts of the structurally ordered C·H₂O polymorph.²² The excellent agreement between the average ¹³C chemical shifts (i.e., [small delta, Greek, macron]^j_C) of the disordered β-caffeine structure obtained by “down-projecting” its 10 ¹³C NMR peaks to the unique 8 ¹³C resonance-mapping of the C·H₂O polymorph²² is very gratifying. Moreover, almost all [small delta, Greek, macron]^j_C/δ^j_C discrepancies between β-caffeine and C·H₂O are well within the experimental uncertainties. For instance, the {[small delta, Greek, macron]¹_C, [small delta, Greek, macron]⁵_C, [small delta, Greek, macron]⁶_C} values of Table 1 agree within 0.2 ppm with the {δ¹_C, δ⁵_C, δ⁶_C} counterparts of C·H₂O.²² Significant chemical-shift differences between the two polymorphs are only observed for the ¹³C2 and ¹³C4 carbonyl sites, both of which are ≈1.0 ppm higher for β-caffeine than those of C·H₂O, which is attributed to distinct HB scenarios between the two structures. DFT calculations (not shown) reveal that the crystallographically unique C4H site of C·H₂O involves one C4H⋯OH₂ HB (201 pm), whereas the five distinct H4 sites of β-caffeine feature a range of HB distances to the O1 (198; 235; 250 pm), O2 (212 pm), and N (236 pm) sites of neighboring molecules. They contribute strongly to the “local” disorder of the ¹³C4 environment, and thereby to its sizable fwhm value relative to any other ¹³Cj site of β-caffeine, while also explaining the accompanying larger [small delta, Greek, macron]⁴_C–δ⁴_C difference (Table 1).

4.3 NMR/GIPAW-derived ¹³C chemical shifts of cocrystals and precursors

Fig. 4 contrasts the ¹³C CPMAS NMR spectra recorded from β-caffeine and its four cocrystals. The successful completion of each cocrystal reaction is evidenced both from our PXRD analyses (Section 2.2) and by the unique ¹³Cj site/chemical-shift mapping resulting for all cocrystals, for which δ^j_C of each ¹³C1–¹³C22 site differs only slightly relative to that of its precursor phases (Table 2). In particular, each of the 8 caffeine-moiety-related ¹³C resonances is readily identified for each cocrystal, meaning that no cocrystal manifests NMR peaks traceable to either “C3′” or “C78” of Fig. 4e, thereby eliminating all NMR-peak assignment ambiguities of β-caffeine. Hence, all ¹³C resonance identifications for each cocrystal (Fig. 4) readily follow from those established for its parent phases (Fig. 3), as corroborated further by contrasting the experimental and DFT/GIPAW-generated {δ^j_C} values listed in Table 2.

Fig. 4 ¹³C CPMAS NMR spectra acquired at 14.1 T and 12.00 kHz MAS from cocrystals of β-caffeine and (a) oxalic acid (2C–OA), (b) malonic acid (2C–MA), (c) glutaric acid (C–GA), and (d) maleic acid (C–ME), along with the spectrum from (e) β-caffeine (β-C) for reference.

Table 2 NMR/DFT-derived ¹³C chemical shifts of cocrystals and precursors^a

Coformer	Site		Coformer δC (ppm)		2C–OA δC (ppm)	2C–MA δC (ppm)	C–GA δC (ppm)	C–ME δC (ppm)
a ^13C chemical shifts (δ^jC) for the ^13Cj site labels of Fig. 1, obtained either experimentally from the shift at the NMR-peak maximum, or by DFT/GIPAW calculations (values within parentheses). The δC uncertainties are around ±0.30 ppm (DFT/GIPAW) and ±0.15 ppm (NMR), except for β-caffeine (Table 1). b For β-caffeine (only), center-of-gravity ^13C chemical shifts ([small delta, Greek, macron]^jC) are reported rather than δ^jC. The experimental {[small delta, Greek, macron]^jC} data were obtained by deconvolution of the MAS NMR spectrum, while each DFT/GIPAW-derived [small delta, Greek, macron]^jC value is the average chemical shift over five crystallographically distinct sites/molecules (see Table 1).
β-Caffeine^b	C1		154.5(153.0)		154.3(153.1)	154.6(154.8)	155.5(154.5)	154.1(153.1)
	C2		150.8(149.4)		152.0(150.4)	152.1(150.1)	150.6(148.9)	151.8(150.5)
	C3		148.0(147.5)		146.0(147.0)	146.4(146.6)	146.7(148.5)	145.4(145.1)
	C4		143.5(146.0)		143.3(145.2)	144.1(146.6)	143.0(145.0)	142.6(143.2)
	C5		106.1(107.8)		107.7(110.9)	108.0(110.8)	107.4(110.6)	107.6(110.2)
	C6		35.0(35.3)		36.5(36.2)	34.0(33.0)	34.3(33.5)	36.5(36.6)
	C7		30.7(29.6)		31.1(28.5)	31.6(30.0)	31.5(29.1)	31.4(29.7)
	C8		29.6(29.5)		27.9(25.2)	28.3(25.8)	27.8(24.2)	29.0(27.4)
α-OA	C9/10		160.7(162.9)		159.7(162.2)
α-OA·2H2O	C9/10		163.1(164.5)		159.7(162.2)
β-MA	C11		175.1(179.0)			168.2(170.1)
	C12		40.8(39.7)			43.7(44.3)
	C13		174.7(175.4)			168.2(170.1)
β-GA	C14		181.5(186.6)				179.8(183.4)
	C15		33.8(33.8)				36.2(36.0)
	C16		18.7(16.5)				22.2(22.0)
	C17		33.8(33.8)				32.7(32.2)
	C18		181.5(186.6)				177.0(182.8)
I-ME	C19		172.9(173.4)					172.4(174.2)
	C20		133.1(141.4)					129.8(137.9)
	C21		140.1(148.1)					138.9(146.4)
	C22		169.2(168.5)					164.2(167.2)

---

While hitherto no report on any even partially complete set of {δ^j_C} data or ¹³C NMR-peak assignments appears to exist for the 2C–OA and C–ME cocrystals, very notable is the excellent agreement between the ¹³C chemical shifts obtained herein for 2C–MA and C–GA with those reported earlier by Vigilante and Mehta:⁵⁰ the truly marginal discrepancies of ≤0.2 ppm are well within the experimental uncertainties throughout, where systematic ¹³C MAS NMR shift-referencing errors often yield δ^j_C discrepancies exceeding 0.5 ppm between studies. For instance, the two ¹³C chemical shifts reported by Bryce and coworkers for the ¹³C4 (142.9 ppm)⁴⁶ and ¹³C8 (28.3 ppm)⁴⁹ sites of C–ME accord with those of Table 2 within 0.3 ppm and 0.7 ppm, respectively.

Table 2 reveals a typical agreement of 2–3 ppm between the experimental and modeled {δ^j_C} values across all diacid precursors and their corresponding cocrystals with caffeine, where deviations ≤1 ppm and ≤3 ppm result for 24 and 56 sites out of the entire ensemble of 68 sites/shifts, respectively. Out of the 12 ¹³Cj sites manifesting a >3.0 ppm δ^j_C discrepancy between the model and experiment, however, 8 sites concern the GA and ME diacid precursors and their cocrystals, where the GIPAW calculations of the GA-associated phases consistently overestimate the ¹³COOH shifts, whereas the ¹³CH₂ counterparts are in excellent agreement with experiments. That scenario is reversed for the ME/C–ME structures, for which the NMR/GIPAW-derived ¹³COOH chemical shifts accord well, whereas substantial deviations are observed for the ¹³CH sites (Table 2). Similar systematic errors—but of overall much smaller magnitudes—are observed for the 2C–OA and 2C–MA cocrystals and their OA, OA·2H₂O, and MA precursors, where the modeled {δ^j_C} values are consistently higher that their experimental counterparts. While Table 2 also reveals minor systematic discrepancies for the C1–C8 sites of the caffeine moiety in the cocrystals relative to β-caffeine, the GIPAW-derived {δ^j_C} values are typically lower than those from NMR, except for C4/C5 that conform to the more typical trend of overestimated δ^j_C values by the calculations.

Because most deviations between the NMR/GIPAW-derived ¹³C chemical shifts are systematic, they have little/no bearings on our analyses below that target the shift-difference between the cocrystals and precursors (Section 4.6). Nonetheless, the very significant discrepancies between a few experimental/modeled δ^j_C values for the GA and ME moieties in both precursor and cocrystal structures are reasons for concern. We remind that our δ^j_C values of Table 2 originated from DFT energy minimizations where only the H positions were adjusted, except for β-caffeine, for which all unit-cell parameters and atom coordinates were optimized (Table S2, ESI†). That significantly improved the chemical-shift predictions, as reflected in a root-mean-square deviation (rmsd) of 1.4 ppm relative to the experimental shifts, which may be contrasted with the rmsd(DFT/NMR) = 2.0 ppm outcome that resulted by only adjusting the H atom positions of β-caffeine, or with the corresponding rmsd(DFT/NMR) = 3.0 ppm obtained across the entire {δ^j_C} ensemble from all other phases (60 data points). Yet, there were no improvements by employing full-atom/cell optimizations of the {GA, C–GA} and {ME, C–ME} structures (which manifest the globally largest δ^j_C discrepancies), whose {δ^j_C} sets revealed an even larger rmsd(DFT/NMR) = 6.5 ppm relative to its experimental counterpart, which exceeded that of rmsd(DFT/NMR) = 4.5 ppm resulting by solely optimizing the H atom positions (Table 2). We have no satisfactory explanation for the large discrepancies (≳5 ppm) between the models and experiments for a few ¹³C sites of the GA/ME-related structures, which must originate from unaccounted structural effects.

4.4. Factors governing the ¹³C resonance widths

Here we discuss three factors expected to primarily govern the full width at half maximum (fwhm) height of the ¹³C signals observed from the cocrystals and their precursors (Table S4, ESI†), leading to some recommendations about the choice of external magnetic field (B₀) for arranging (sub)optimal ¹³C MAS NMR spectral resolution. The two primary spectral-resolution-limiting factors involve so-called “inhomogeneous broadening”,⁶¹i.e., ¹³C chemical-shift dispersions from either the anisotropic bulk magnetic susceptibility (ABMS)^24,71–74 or static structural disorder.^18,20,21 Both scale linearly with B₀ on a frequency scale (in Hz), which complicates their discrimination if only having a ¹³C (CP)MAS NMR spectrum available.^24,73,74 Yet, the ABMS-stemming broadening in ppm is shared among all nuclear sites in the structure, regardless of their nuclide type or structural origin, meaning that the ABMS remains constant for all {¹³Cj} and {¹Hj} sites in the sample,^24,71–74 in contrast to the local structural disorder that varies among crystallographically distinct ¹³Cj sites, and thereby giving variable ¹³C fwhm values (in ppm). Hence, contrasting the (lack of) variations within the {¹³Cj} fwhm set listed in Table S4 (ESI†) within each precursor/cocrystal helps gauging the potential presence of structural disorder.

Fig. 3 reveals that the ¹³C resonance widths vary markedly among the various well-ordered cocrystal precursors, which most likely reflects variable ABMS effects. The polycrystalline MA powder produces fwhm values of <30 Hz (≤0.2 ppm at 14.1 T; Table S4, ESI†), which are typical for organic molecules in well-ordered crystals with negligible ABMS broadening. In contrast, the OA, OA·2H₂O, and GA powders reveal 3–4 times broader ¹³C resonances than MA, whereas the ¹³C sites of the ME and β-caffeine specimens manifest substantially larger fwhm values of ≈240 Hz (≈1.6 ppm) and 200–435 Hz (1.3–2.9 ppm), respectively. Here, the near-constant peakwidths observed for ME suggests that ABMS broadening mainly limits its ¹³C NMR spectral resolution, whereas structural disorder is mainly degrading that for β-caffeine, notably so in the CH₃ region (Fig. 3e). Indeed, the markedly larger ¹³Cj fwhm values of β-caffeine relative to all other specimens (Fig. 3 and 4) primarily stems from a significant (static) structural disorder,^22,24 where the lowest fwhm value of 1.3 ppm observed for the ¹³C5 resonance sets an upper limit of the ABMS contribution to all peak widths.

Despite the larger supramolecular aggregate of the cocrystal units, their ¹³C peak widths remain consistently narrower than those of β-caffeine (Table S4, ESI†), which reflects a higher degree of local structural order of each cocrystal.^12,14,24 The relative ¹³C fwhm values increase along the series 2C–MA ≪ 2C–OA < C–GA ≲ C–ME, roughly following those of each respective pristine diacids (Table S4, ESI†) but with 1.2–6 times wider ¹³C resonances. Only the peakwidths from C–ME break that trend, where narrower peaks are observed relative to both the ME and β-caffeine crystallites for which ABMS and structural disorder primarily govern the respective ¹³C fwhm values, both apparently being reduced in the C–ME crystallites.

A third factor known to broaden ¹³C resonances from molecules featuring direct C–N bonds is the spin-1 ¹⁴N nuclide (99.6% natural abundance) that may induce additional NMR-peak splittings/broadenings of nearby ¹³C sites by ¹⁴N–¹³C dipolar interactions, whose effects are incompletely suppressed by MAS and scale as B₀⁻¹ (in Hz) and B₀⁻² (in ppm).^75,76 Indeed, while demonstrated to vastly dominate the ¹³C MAS NMR-peak widths and the spectral resolution from C·H₂O at a low magnetic field of 4.7 T but being negligible at B₀ = 21 T,²² we expect marginal signal broadenings for our experimentation at B₀ = 14.1 T, as was also concluded in ref. 50. The data of Table S4 (ESI†) confirm those expectations, suggesting a <30 Hz ¹³C resonance broadening from the ¹⁴N–¹³C dipolar interactions, as is also supported by the ¹³C NMR peak-width analysis of ref. 24 performed at B₀ = 11.7 T, at which one expects slightly larger effects from ¹⁴N–¹³C interactions. From the marginal dipolar broadening to the net ¹³C fwhm values, we conclude that inhomogeneous ABMS and structural-disorder stemming ¹³C chemical-shift distributions dominate the NMR peak-widths throughout all specimens considered herein, as also suggested by our ¹H NMR results (Section 4.5).

At least for anhydrous β-caffeine, however, ¹³C NMR experimentation at B₀ ≥ 14.1 T is advantageous for achieving sufficient resolution. Recalling the two additional C3′ and C78 NMR peaks (Section 4.2) of anhydrous β-caffeine relative to its α counterpart,²² a puzzling feature is their apparent absence in several ¹³C MAS NMR spectra reported from β-caffeine in the literature,^14,23,24 incidentally rendering those spectra closer to that observed from α-caffeine,²² encompassing some results from “anhydrous caffeine” of unspecified phase identity.^68,70 Yet all those NMR spectra were recorded at lower magnetic fields of either 9.4 T (ref. 14 and 23) or 11.7 T (ref. 24) relative to those acquired at 14.1 T herein (Fig. 4e) and in ref. 12 along with the high-field result by Enright et al.²² at B₀ = 21 T. Evidently, only MAS NMR spectra recorded at B₀ ≥ 14.1 T give discernible ¹³C resonances at ≈30 ppm (C78) and ≈149 ppm (C3′), whereas those signals apparently coalesce with those from ¹³C7/¹³C8 and ¹³C3, respectively, in NMR spectra obtained at B₀ < 14.1 T.^14,23,24 This effect must stem from the resolution-degradation associated with lower-B₀ experimentation alone and/or its accompanying emphasized ¹³C resonance broadening from ¹⁴N–¹³C interactions. Likewise, the ¹³C MAS NMR spectrum obtained from “anhydrous caffeine” at 9.4 T by Nonappa and Kolehmainen⁶⁸ appears very similar to those reported from β-caffeine in ref. 14, 23 and 24.

We conclude that “high-field” NMR experimentation is beneficial for enabling complete ¹³C site/NMR-peak assignments of anhydrous β-caffeine, where B₀ = 14.1 T appears to be the minimum magnetic field admitting resonance-discrimination between all crystallographically inequivalent ¹³C sites, potentially enabling ¹³C NMR quantifications of the α/β-caffeine contributions in a powder mixture without resorting to PXRD.

4.5. ¹H NMR and DFT/GIPAW results

4.5.1. ¹H MAS NMR spectra. Fig. 5 and 6 present the ¹H NMR spectra from the precursors and cocrystals, respectively, all recorded at B₀ = 14.1 T and fast MAS (60.0 kHz) to suppress the normally spectral-resolution-limiting homonuclear ¹H–¹H dipolar interactions.^15–18 Indeed, the relative ¹H NMR peak widths of the cocrystals match well those of the respective ¹³C NMR spectra (Fig. 4), further underscoring that the ¹H/¹³C resonance widths are governed primarily by chemical-shift dispersions stemming from variable ABMS^24,71–74 and structural disorder^18,20,21 effects among the specimens (Section 4.4). In the least ordered structure—i.e., that of β-caffeine—all C¹H₃-stemming ¹H resonances coalesce into a near-Gaussian peak, whereas the C6¹H₃ peak is discernible in all NMR spectra from the cocrystals (Fig. 6), despite a further overlap from C¹H₂ signals in those from 2C–MA and C–GA. All three ¹H6–¹H8 resonances are resolved from the most ordered cocrystal structure, i.e., 2C–MA (Fig. 6b). Notably, the present ¹H MAS NMR spectrum from β-caffeine is very similar to those of ref. 23 and 24 where the value of δ⁴_H = 7.6 ppm reported by Bordignon et al.²³ is identical to ours (Table 3), despite that all C¹H₃ resonances coalesced fully^23,24 (although, for unclear reasons, ref. 23 tabulated distinct ¹H6 and ¹H7/¹H8 shifts).

Fig. 5 ¹H MAS NMR spectra recorded at 14.1 T and 60.0 kHz MAS from the (a) α-OA (“OA”) and α-OA·2H₂O (“OAw”) mixture together with powders from the other (b) β-MA, (c) β-GA, and (d) I-ME diacids. The red traces in (b) are deconvolution results of the two overlapping OH11/OH13 resonances. The low-ppm resonance region marked by an asterisk in (a) and (d) reveal background signals from the NMR probehead, and the peak marked by “?” in (b) and (c) stems from an unknown impurity phase of the MA and GA precursors.

Fig. 6 ¹H MAS NMR spectra recorded at 14.1 T and 60.0 kHz MAS from the (a) 2C–OA, (b) 2C–MA, (c) C–GA, (d) C–ME cocrystals, and (e) anhydrous β-caffeine. The insets show vertically expanded zooms across the high-ppm spectral region. The red/green traces in (b) and (c) are deconvolution results of the overlapping C¹H₃ (red) and C¹H₂ (green) NMR signals. The vertical dotted line at δ_H = 4.1 ppm marks the approximate chemical shift of the C6¹H₃ resonance of the caffeine molecule for the C–GA, C–ME, and β-caffeine specimens in (c)–(e), which differ slightly from those of 2C–OA and 2C–MA in (a) and (b). The NMR peak marked by “?” in (c) stems from an unknown impurity of the GA precursor (see Fig. 5c).

Table 3 NMR/DFT-derived ¹H chemical shifts of cocrystals and precursors^a

Coformer	Site		Coformer δH/ppm		2C–OA δH/ppm	2C–MA δH/ppm	C–GA δH/ppm	C–ME δH/ppm
a ^1H chemical shifts (δ^jH) for the Cj^1H site labels of Fig. 1, obtained either experimentally from the shift at the NMR-peak maximum, or by DFT/GIPAW calculations (values within parentheses). The δH uncertainties are around ±0.30 ppm (GIPAW) and around ±0.15 ppm for the experimental values for all well-resolved NMR peaks (±0.5 ppm for those obtained by spectral deconvolution; Fig. 6). b All GIPAW-derived shifts for β-caffeine are averages of the five {δ^jH} values of the inequivalent molecules in the unit cell. c Owing to the complete overlap among the C6H3, C7H3, and C8H3 resonances in β-caffeine, only the average chemical-shift values are reported. However, the NMR spectra from the cocrystals admitted further site/signal-resolution by spectral deconvolution, yielding the following NMR-derived δ^jH (or average CG [small delta, Greek, macron]^jH chemical shifts), with the corresponding GIPAW-derived data given within parentheses: for 2C–OA, δ^6H = 4.5 (3.7) ppm; [small delta, Greek, macron]^7/8H = 2.9 (2.1) ppm; for 2C–MA, δ^6H = 4.4 (3.8) ppm; δ^7H =3.4 (2.8) ppm; δ^8H = 2.5 (1.8) ppm; for C–GA, δ^6H = 4.1 (3.5) ppm; [small delta, Greek, macron]^7/8H = 3.0 (2.3) ppm; for C–ME, δ^6H = 4.1 (3.2) ppm; [small delta, Greek, macron]^7/8H = 3.1 (2.3) ppm.
β-Caffeine^b	H4		7.6(8.4)		8.3(7.2)	8.3(7.6)	8.1(7.3)	8.0(6.7)
	H6/7/8^c		3.3(3.8)		3.3(2.6)	3.4(2.8)	3.3(2.7)	3.4(2.6)
α-OA	HO9/10		11.1(11.2)		14.8(15.0)
α-OA·2H2O	HO9/10		16.6(17.8)		14.8(15.0)
	H2O		5.6(5.6)
β-MA	HO11		12.7(13.7)			14.1(14.8)
	H12a/b		3.4(2.6)			2.7(1.7)
	HO13		12.3(13.4)			14.1(14.8)
β-GA	HO14		12.7(13.7)				13.5(14.0)
	H15/16/17		1.8(1.2)				1.9(1.0)
	HO18		12.7(13.7)				9.8(10.6)
I-ME	HO19		13.1(13.6)					18.9(20.2)
	H20/21		6.9(6.2)					6.0(4.9)
	HO22		15.8(16.2)					14.3(14.6)

---

Nonetheless, the reduced ¹H NMR spectral resolution in the aliphatic region, for which broadening from residual ¹H–¹H interactions is most pronounced, compromises accurate site-specific assessments of the ¹H chemical-shift alterations upon cocrystal formation. Table 3 collects the NMR and DFT/GIPAW derived ¹H chemical shifts, which constitute δ^j_H data for all well-resolved signals but CG shifts ([small delta, Greek, macron]^j_H) for all heavily overlapping resonances. Hence, in what follows, we focus on the ¹Hj resonances that are well resolved in the NMR spectra from both the precursors (Fig. 5) and their corresponding cocrystals (Fig. 6), namely COO¹H of the diacid molecules, C4¹H of caffeine, and the equivalent C¹H20/21 sites of ME.

4.5.2. ¹H chemical shifts of carboxy groups. Here, we discuss the set {δ^j_H} of COO¹H chemical shifts, assessed directly from the respective NMR-peak maximum shift values of Fig. 5 and 6 and assigned such that the highest/lowest chemical shift represents the Hj site with shortest/longest H⋯O distance in the diacid/cocrystal structure. These ¹Hj/δ^j_H assignments are further corroborated by the DFT/GIPAW calculations (Table 3). The herein observed COO¹H chemical shifts from the α-OA·2H₂O, β-MA, and ME powders agree within 0.3 ppm with the δ^j_H values reported by Harris et al.³⁴ by using CRAMPS (combined rotation and multiple-pulse spectroscopy) to suppress NMR-peak broadenings from ¹H–¹H interactions under slow-MAS conditions. This excellent agreement is well within the experimental uncertainties, while moreover δ⁹_H of α-OA·2H₂O (16.6 ppm) matches perfectly that reported earlier by Berglund and Vaughan⁷⁷ (16.5 ppm). Notably, the chemical shifts observed by us from MA and ME agree much better with those of Harris et al.³⁴ than with ref. 77 but the former study did not include α-OA. Although the experimental shift δ^9/10_H = 11.1 ppm (Table 3) is reproduced within 0.1 ppm by our GIPAW calculations, there is a significant deviation with that of 12.6 ppm reported in ref. 77 which is well outside of our experimental uncertainties. We believe that the herein reported δ^9/10_H = 11.1 ppm value of α-OA is the hitherto most accurate result.

The COO¹H chemical shifts of the pristine diacids presented in Fig. 5 correlate qualitatively well with the H⋯O distances of their crystal structures (Fig. 2): the two α-OA·2H₂O and α-OA structures reveal the highest (16.6 ppm) and lowest (11.1 ppm) chemical shifts, respectively, as expected from their corresponding shortest (146 pm) and longest (175 pm) HB lengths among all diacids (see caveat below). All COO¹H sites of MA and GA along with H19 of ME feature essentially identical H-bond distances of 162–165 ppm (Fig. 2), as is mirrored in very similar δ^j_H values between 12.3–13.1 ppm (Fig. 5). Notably, the ¹H NMR signals from the two crystallographically inequivalent OH11 and OH13 sites of MA are discernible in Fig. 5b, despite their very small chemical-shift separation of 0.4 ppm stemming from a minute H⋯O bond-length difference of 1 pm (Fig. 2d), as also reproduced near-perfectly by the GIPAW calculations (0.3 ppm shift-difference).

Within a consistent but minor overestimation of the DFT/GIPAW-derived ¹H chemical shift within typically ≲1 ppm (Table 3), the calculated {δ^j_H} values match the experimental counterparts very well for all COO¹H sites. Note that while all diacid structures feature H⋯O bonds, all cocrystals involve H⋯N contacts with the “N” atom of caffeine, except for the OH18⋯O14 bond in C–GA and OH22⋯O19 in C–ME (Fig. 2). Each NMR/GIPAW-derived {δ^j_H} dataset gave a good linear correlation with the shortest H⋯O or H⋯N distance, denoted r(H⋯O/N), throughout all COO¹H sites. Fig. 7 plots the experimental and calculated ¹H chemical shifts along with the corresponding best-fit results given by

δ^j_H[NMR]/ppm = 47.0 − 0.208r(H⋯O/N)/pm (R² = 0.912), (3)

δ^j_H[DFT]/ppm = 50.0 − 0.222r(H⋯O/N)/pm (R² = 0.919), (4)

both of which verify the expected trend^{34,35,39,40,42} of an increasing¹H chemical shift for decreasing HB length. Indeed, both the experimental and modeled {δ^j_H} sets are captured well by their very similar best-fit expressions and nearly equal correlation coefficients. Only the H22 site of ME breaks the trend, manifesting lower experimental and calculated shifts than those predicted from the very short intramolecular H⋯O distance of 145 pm within the diacid unit (vide supra).

Fig. 7 Experimental (black symbols) and DFT/GIPAW-generated (red) ¹H chemical shifts of the carboxy moieties of the pristine diacids (solid symbols) and the cocrystals (open) plotted against the H⋯O/H⋯N distance, r(H⋯O/N), given in Fig. 2. The number around each data-point represents the proton label of Fig. 1. The lines are best-fit results, eqn (3) and (4), obtained by omitting one outlier data point (δ²²_H) and yielding the as-indicated R² correlations coefficients. All chemical-shift uncertainties are within the symbol sizes.

4.5.3 COO¹H chemical-shift changes upon cocrystal formation. To monitor the ¹H chemical-shift alterations upon cocrystal formation, we define the difference between the chemical shift of site ¹Hj in the cocrystal, δ^j_H[C–X], relative to that in each pristine coformer, δ^j_H[X], where X represents β-caffeine or one of the {OA, OA·H₂O, MA, GA, ME} diacids,

Δ^j_H = δ^j_H[C–X] − δ^j_H[X], with 1 ≤ j ≤ 22, (5)

and the index j runs over all proton-bearing Cj sites of Fig. 1. The linear δ^j_H/r(H⋯O/N) trends of Fig. 7 readily rationalize the observed COO¹H chemical-shift alterations, whose values are presented in Table 4 along with those for the other C¹H_n sites (the latter are discussed in Section S1). Fig. S4 (ESI†) plots the NMR/DFT-derived Δ^j_H values against the difference between the shortest H⋯O/N distance of each cocrystal and precursor, which is denoted by Δr(H⋯O/N).

Table 4 ¹H Chemical-shift differences between cocrystals and precursors^a

Coformer	Site		2C–OA Δ^jH/ppm	2C–MA Δ^jH/ppm	C–GA Δ^jH/ppm	C–ME Δ^jH/ppm
a Chemical-shift differences (Δ^jH) defined by eqn (5) and calculated from δ^jH data with two decimals. b Average chemical-shift values over all C6H3, C7H3, and C8H3 sites of the caffeine moiety; see Table 3.
β-Caffeine	H4		0.6(−1.2)	0.7(−0.8)	0.5(−1.1)	0.4(−1.7)
	H6/7/8^b		0.0(−1.2)	0.1(−1.0)	0.0(−1.1)	0.1(−1.2)
α-OA	HO9/10		3.8(3.8)
α-OA·2H2O	HO9/10		−1.8(−2.8)
β-MA	HO11			1.3(1.1)
	H12a/b			−0.7(−0.9)
	HO13			1.8(1.4)
β-GA	HO14				0.8(0.3)
	H15/16/17				0.1(−0.2)
	HO18				−2.9(−3.1)
I-ME	HO19					5.8(6.6)
	H20/21					−0.9(−1.3)
	HO22					−1.5(−1.6)

---

For the COO¹H chemical-shift changes (Δ^j_H), Table 4 reveals an overall trend of higher δ^j_H values of the cocrystals (i.e., Δ^j_H > 0), as is witnessed by Fig. 7 and rationalized from the typically shorter H⋯O distance encountered in the cocrystal relative to that of the pristine diacid (Fig. 2). Such HB-length effects also account for the higher δ⁹_H value of 2C–OA relative to its α-OA counterpart, as well as for the increased δ¹¹_H and δ¹³_H values upon 2C–MA cocrystal formation. Likewise, the lower δ⁹_H value of 2C–OA relative to α-OA·2H₂O—along with the lower chemical shift of ¹H18 of C–GA compared to the identical values δ¹⁴_H = δ¹⁸_H of the crystallographically equivalent COO¹H sites of β-GA—are readily understood from the longer H⋯O distances in the cocrystals.

4.6. ¹³C chemical-shift changes upon cocrystal formation

In direct analogy with the ¹H chemical-shift difference between the cocrystal and its precursors [eqn (5)], we define

Δ^j_C = δ^j_C[C–X] − δ^j_C[X], with 1 ≤ j ≤ 22, and X = {β-C, OA, OA·2H₂O, MA, GA, ME}, (6)

as the corresponding δ^j_C alteration when each {2C–OA, 2C–MA, C–GA, C–ME} cocrystal is formed. Table 5 compiles the {Δ^j_C} data obtained either by NMR experiments or GIPAW calculations. However, as for the ¹H chemical-shift/structure correlations (except those for COO¹H), the δ^j_C and Δ^j_C data only admits qualitative discussions.

Table 5 ¹³C Chemical-shift differences between cocrystals and precursors^a

Coformer	Site		2C–OA Δ^jC/ppm	2C–MA Δ^jC/ppm	C–GA Δ^jC/ppm	C–ME Δ^jC/ppm
a Chemical-shift differences (Δ^jC) defined by eqn (6) and calculated from δ^jC data with two decimals.
β-Caffeine	C1		−0.2(0.1)	0.0(1.8)	1.0(1.5)	−0.5(0.1)
	C2		1.2(1.0)	1.3(0.7)	−0.2(−0.5)	1.0(1.1)
	C3		−2.0(−0.6)	−1.6(−0.9)	−1.3(1.0)	−2.7(−2.4)
	C4		−0.1(−0.8)	0.6(0.6)	−0.4(−1.0)	−0.9(−2.8)
	C5		1.7(3.2)	1.9(3.1)	1.4(2.8)	1.5(2.5)
	C6		1.4(0.9)	−1.0(−2.3)	−0.7(−1.7)	1.5(1.4)
	C7		0.4(−1.1)	0.9(0.3)	0.8(−0.6)	0.7(0.0)
	C8		−1.7(−4.3)	−1.3(−3.7)	−1.8(−5.3)	−0.7(−2.0)
α-OA	C9/10		−1.1(−0.7)
α-OA·2H2O	C9/10		−3.5(−2.3)
β-MA	C11			−6.9(−8.8)
	C12			2.9(4.6)
	C13			−6.5(−5.3)
β-GA	C14				−1.6(−3.3)
	C15				2.4(2.2)
	C16				3.4(5.5)
	C17				−1.1(−1.6)
	C18				−4.5(−3.9)
I-ME	C19					−0.4(0.7)
	C20					−3.3(−3.5)
	C21					−1.1(−1.7)
	C22					−5.0(−1.3)

---

In contrast with the ¹³CH₂ shifts of MA and GA, which deshield slightly by a few ppm, significantly decreased δ_C values are observed for the ¹³COOH diacid sites, whose adjacent O atom form an HB with protons of neighboring caffeine/diacid molecules, which along with COO⁻ → COOH conversions are well known to decrease the ¹³C shift in various molecular systems.^{37,38,78–81} However, that trend has remained qualitative without any firm quantitative relationship having thus far been established between the isotropic¹³C chemical shift and the ¹³COH⋯O or ¹³CO⋯HO distance (the principal value δ^j_yy of the chemical-shift tensor, however, correlates linearly with the HB distance/angle parameters^36–38). Indeed, the plot of δ^j_C against r(H⋯O/N) in Fig. 8 reveals a significant scatter for the diacid/cocrystal structures. Although a weak trend of ¹³COOH shift-reduction with a shortened COO⋯H distance is discernible, our data do not reveal any reasonable δ^j_C/r(H⋯O/N) or Δ^j_C/Δr(H⋯O/N) correlation for either the experimental or modeled data. The only exceptions are the ¹³COOH sites of the 2C–OA (δ⁹_C), 2C–MA (δ¹¹_C), and C–GA (δ¹⁴_C) cocrystals, all of which share the feature of a strong H⋯N bond to the N atom of the caffeine molecule (which is expected to constitute the primary stabilization of the supramolecular structure⁸): they establish an excellent linear δ_C/r(H⋯N) relationship (Fig. 8) for both the NMR and GIPAW-derived shifts but with the caveat that only three data points underlie the correlation.

Fig. 8 Experimental (black symbols) and DFT/GIPAW-generated (red) ¹³C chemical shifts of the carboxy moieties of the pristine diacids (solid symbols) and the cocrystals (open) plotted against the H⋯O or H⋯N distance, r(H⋯O/N), within each structure (Fig. 2). Each number represents the corresponding Cj label of Fig. 1. The symbols set in green and gray color for the NMR and DFT/GIPAW data, respectively, correspond to the results obtained from the 2C–OA (δ⁹_C), 2C–MA (δ¹¹_C), and C–GA (δ¹⁴_C) cocrystals, all of which are H-bonded to the “N” atom of caffeine. The corresponding lines are best-fit results to the expressions δ^j_C[NMR]/ppm = −185.6 + 2.1905r(H⋯N)/pm (R² = 0.990) and δ^j_C[DFT]/ppm = −206.5 + 2.336r(H⋯N)/pm (R² = 0.998), respectively. All chemical-shift uncertainties are within the symbol sizes.

Turning to the δ^j_C changes of the caffeine moiety in the cocrystals relative to β-caffeine, Table 5 reveals the overall largest observed |Δ^j_C| values for the {C3, C5, C8} sites upon cocrystal formation (and to a lesser extent, C2 and C6), thereby suggesting that those local ¹³C electronic environments alter the most by the intermolecular caffeine–coformer interactions in the cocrystals structure (Fig. 2) relative to the caffeine–caffeine contacts in β-caffeine. The C3 and C5 atoms constitute a C=C fragment between the pyriminedione and imidazolium rings (Fig. 1). We attribute the (globally largest) chemical-shift alteration of the C3 site of the caffeine molecule to its close proximity to the N atom, whose N⋯HOOC HB constitutes the primary intermolecular interaction in all cocrystal structures;⁸ see Section 3 and Fig. 2. However, while the ¹³C3 site shields upon cocrystal formation (Δ³_C < 0), ¹³C5 deshields (Δ⁵_C > 0) to a comparable extent, for unknown reasons when considering its remoteness to any atom of a neighboring molecule in either the β-caffeine or cocrystal structures. The ¹³CH₃ shift alterations are discussed in Section 4.7.

As commented in Section 4.5, the C4¹H chemical shift remains near-constant throughout all cocrystals, which is attributed to Δ⁴_C cancellation-effects from variable and complex H-bonding scenarios. Likewise, only minor chemical-shift alterations are observed for ¹³C4H, which besides being directly linked to the H-bonded “N” site of caffeine, additionally experiences weak H bonds to the CO atoms of the diacid carboxy groups upon cocrystal formation (Fig. 2). We speculate that the chemical-shift effects from those two competing H bonds might partially cancel each other. We remark that even slightly more negative Δ⁴_C values of {−1.3, −0.5, −1.6, −2.0} ppm apply if the respective {2C–OA, 2C–MA, C–GA, C–ME} cocrystals would be prepared from the ordered C·H₂O phase that features δ⁴_C = 144.6 ppm²² and one C4H⋯OH₂ bond.

4.7 Tetrel-bonding effects on methyl ¹³C/¹H chemical shifts

Besides the possibility of a weak HB, the electrophilic nature of methyl groups offer the option of a H₃C⋯O TB to a proximate electronegative and nucleophilic atom.^47–49 From our as-observed Δ^j_H/Δ^j_C data for the three ¹³CH₃ groups of the caffeine moiety upon cocrystal formation, we discuss the complex HB/TB interplay on their ¹³C/¹H chemical shifts in relation to current literature, which is both sparse and inconclusive. Likewise, our data may only be discussed qualitatively.

Both DFT calculations^48,49 and NMR experiments⁴⁹ suggest consistently larger δ_C than δ_H alterations when a TB is formed. Scheiner et al.⁴⁸ investigated the ¹³CH₃ and C¹H₃ chemical-shift displacements upon CH⋯O HB or HC⋯O TB formation by DFT calculations, inferring that both ¹H and ¹³C chemical shifts increase for either scenario, with the precise deshielding depending on the TB-length and N–C–O bond angle (θ_TB). The largest chemical-shift alterations occurred for a linear TB constellation, for which Δ^j_C ≤ 6 ppm was predicted, whereas the ¹H chemical shift only increased marginally (≲1 ppm).⁴⁸ Formation of a weak CH⋯O HB, however, is reported to produce a comparably larger ¹H deshielding than for ¹³C.^43,46,48 Currently no firm/general experimental correlation is reported of either the ¹H or ¹³C chemical shifts against the CH₃⋯O or H₃C⋯O distance. A recent compilation by Southern et al.⁴⁹ of experimental ¹³C/¹H chemical shifts from the literature along with GIPAW calculations, suggested very scattered ¹³C/¹H chemical-shift-structure correlations of CH₃ groups involved in tetrel bonds:⁴⁹ although experiments confirm that δ^j_C is often increased for decreasing HC⋯O distance, no significant dependence was observed versus θ_TB, nor of δ^j_H against either the TB distance or θ_TB. Moreover, when HB and TB bonds coexist for a CH₃ group, their effects on δ^j_C may either reinforce or counteract each other.⁴⁹

The ¹³C and ¹H chemical-shift data from the current cocrystals accord qualitatively with previous findings of a smaller δ^j_H than δ^j_C change when the TB scenario alters between β-caffeine and its cocrystals. The NMR-derived value Δ^6/7/8_H ≈ 0 apply throughout all cocrystals. Although the δ^j_H/TB distance-accuracy is compromised by the lack of NMR-signal discrimination among the ¹H6–¹H8 methyl resonances from β-caffeine, the near-constant ¹H chemical shift is also confirmed by the DFT calculations (within a constant shift-displacement of Δ^6/7/8_H ≈ −1 ppm), for which each δ^j_H and Δ^j_H value is readily determined (Table S5, ESI†). Consistently larger ¹³C chemical-shift displacements occur on cocrystal formation, where Table 2 reveals the largest changes for ¹³C8H₃, all of which are negative and conforming to the experimental range of −1.8 ≤ Δ⁸_C/ppm ≤ −1.3, whereas more negative values are predicted by the GIPAW calculations: −5.3 ≤ |Δ⁸_C|/ppm ≤ −2.0. Somewhat lower shift-differences (0.7–1.5 ppm) are observed for the ¹³C6H₃ sites, where 2C–OA and C–ME yield positive Δ⁶_C values, while those for 2C–MA and C–GA are negative (Table 5). Besides slightly larger magnitudes predicted by the GIPAW calculations, all positive/negative Δ⁶_C trends are reproduced, as well as the experimental finding that ¹³C7H₃ consistently manifests the smallest shift-change for each cocrystal.

Unfortunately, the Δ^j_C trends identified above for the three ¹³CH₃ sites of the caffeine moiety are for several reasons very difficult to rationalize: (i) δ^j_C is expected to depend on both H⋯O/N and C⋯O/N distance-changes between β-caffeine and each cocrystal, whose effects on the chemical shift may augment or cancel partially. (ii) Even if only each shortest HB/TB distance per ¹³CH₃ site of the cocrystal is considered (which is expected to be most influential on δ^j_C), the presence of five inequivalent molecules in the β-caffeine unit cell implies a complex reference scenario with a range of HB/TB lengths relative to the structurally ordered cocrystals. (iii) The current absence of any firm δ^j_C/r(CH_n⋯O) or δ^j_C/r(CH_n⋯O) correlation in conjunction with (i) and (ii), complicate the establishment of even semiquantitative Δ^j_C correlations with the HB/TB-distance alterations accompanying the {2C–OA, 2C–MA, C–GA, C–ME} formation.

The shortest HB and TB distances of the methyl groups in β-caffeine and the cocrystals are compiled in Table S3 (ESI†). We first consider the most pronounced ¹³C chemical-shift change upon cocrystal formation—i.e., Δ⁸_C, assuming that the HB effects are minor because the range of C8H₃⋯O1/O2 distances (236–294 pm) in β-caffeine span those of the cocrystals (and is thereby expected to give, on the average, a very similar [small delta, Greek, macron]⁸_C contribution as for the cocrystals). Hence, the corresponding TB-length alterations are expected to primarily govern Δ⁸_C. Notably, the TB distances are overall shorter in the cocrystals than in β-caffeine (except for 2C–OA). Then given that a TB contraction is expected to increase δ⁸_C,^48,49 positive values of Δ⁸_C are anticipated throughout all cocrystals, in stark contrast to the de facto observed experimental and modeled results. The lack of an even qualitative Δ_C/Δr(CH₃⋯O/N) correlation also applies to the ¹³C6H₃ site: again, the wide HB-distance range in β-caffeine (207–276 pm; Table S3, ESI†) relative to those of the cocrystals (223–249 pm) suggest minor effects on Δ⁶_C. Notably, however, the C6H₃⋯O bond-lengths in the β-caffeine structure is consistently shorter than those of any cocrystal, from which negative Δ⁶_C values are predicted throughout,^48,49 in clear contradiction to our NMR and DFT results. Moreover, no correlation was observed for the set of ¹³CH_n chemical shifts against the TB angle (data not shown), despite wide θ_TB ranges within 71°–90° (4 δ^j_C values) and 147°–178° (8 δ^j_C values).

Notwithstanding the uncertainties accompanying (i)–(iii) above, we believe that our ¹³C chemical-shift data suggest that a TB-length contraction may not necessarily produce an increased ¹³C chemical shift, along previous difficulties to establish a general δ^j_C/r(CH₃⋯O/N) correlation. Such a relationship is likely obscured for similar reasons as some inconclusive experimental δ^j_C/r(CH_n⋯O) correlations, for which ¹³C shift-alterations upon CH⋯O bond formation depend both on the precise molecular fragments involved and (longer-range) crystal-structure effects,^44,45 whose complex interplay may result in ¹³C deshielding,^44,46 shielding,⁴³ or either/both.^42,44

5 Conclusion

The present comprehensive NMR/DFT study encompassed altogether 68 distinct ¹³C sites and 33 unique ¹H resonances from altogether four caffeine-based cocrystals and their six precursor structures, with an overall very good agreement between the experimental and modeled chemical shifts. We believe that the results herein may serve as accurate benchmark values for further MAS NMR investigations, given the very good accordance with previous literature for the ¹H/¹³C chemical shifts—such as the δ_C data of 2C–MA and C–GA of ref. 50 along with both ¹H and ¹³C chemical shifts of the diacid precursors—and because a significant fraction of all δ_H/δ_C data are presented herein for the first time.

Despite our large ¹³C and ¹H chemical-shift ensembles and an encouraging NMR/DFT agreement, the herein established linear chemical-shift/distance correlations were confined to the COO¹H ⋯O/N diacid–diacid and diacid–caffeine hydrogen bonds, along with the COO¹H ⋯N counterparts, which nonetheless are those most instrumental for the supramolecular cocrystal organization. We also examined possible CH₃⋯O/N tetrel-bond effects on the ¹H/¹³C chemical shifts, which were overall uncertain and inconclusive but suggesting that previously reported (weak) chemical-shift correlations against tetrel-bond parameters might not hold in general, thereby underscoring the need for more research in this very sparsely investigated field. Further efforts towards better confining the H-atom positions of the caffeine–diacid cocrystals by direct ¹H–¹H and ¹H–¹³C internuclear-distance measurements are underway by employing a recent NMR crystallography method.^81,82

Except for the methylene groups of MA/GA and their cocrystals, the compromised ¹H NMR spectral resolution (and for β-caffeine also the ¹³C NMR counterpart) originates mainly from chemical-shift dispersions stemming from anisotropic bulk magnetic susceptibility and structural disorder rather than the often dominant peak-broadening from ¹H–¹H interactions. Hence, modest spectral resolution enhancements are expected from faster-MAS (>60 kHz) ¹H NMR experiments, and let alone by utilizing higher fields (B₀ > 14.1 T) because the shift-dispersion scales linearly with B₀. That sharply contrasts with the ¹³C NMR scenario, however, where B₀ ≥ 14.1 T experimentation appears mandatory for resolving all 10 resonances from the 8 distinct ¹³C sites of anhydrous β-caffeine, where the previously unassigned ¹³C NMR peaks at 30.2 ppm (C7/C8) and 149.0 ppm (C3) are spectral markers for discriminating the disordered anhydrous β-caffeine polymorph from both its disordered α-caffeine and ordered hydrated C·H₂O counterparts. This insight facilitates further α/β-phase quantifications of mixtures of both polymorphs by ¹³C MAS NMR alone, which has hitherto only proven possible by PXRD analyses.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Knut and Alice Wallenberg Foundation (project 2019.0124), and in part by the Swedish Research Council (project VR 2022-03652). The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS), partially funded by the Swedish Research Council through grant agreement no. 2022-06725. We thank an anonymous reviewer for helpful comments on NMR-peak broadening factors.

References

1. H. G. Brittain, Cocrystal systems of pharmaceutical interest: 2010, Cryst. Growth Des., 2012, 12, 1046–1054.
2. R. Shaikh, R. Singh, G. M. Walker and D. M. Croker, Pharmaceutical cocrystal drug products: an outlook on product development, Trends Pharmacol. Sci., 2018, 39, 1033–1048.
3. G. Bolla, B. Sarma and A. K. Nangia, Crystal engineering of pharmaceutical cocrystals in the discovery and development of improved drugs, Chem. Rev., 2022, 122, 11514–11603.
4. T. Friščić and W. Jones, Recent advances in understanding the mechanism of cocrystal formation via grinding, Cryst. Growth Des., 2009, 9, 1621–1637.
5. M. Rodrigues, B. Baptista, J. A. Lopes and M. C. Sarraguça, Pharmaceutical cocrystallization techniques. Advances and challenges, Int. J. Pharm., 2018, 547, 404–420.
6. U. J. Griesser and A. Burger, The effect of water vapor pressure on desolvation kinetics of caffeine 4/5-hydrate, Int. J. Pharm., 1995, 120, 83–93.
7. H. G. M. Edwards, E. Lawson, M. de Matas, L. Shields and P. York, Metamorphosis of caffeine hydrate and anhydrous caffeine, J. Chem. Soc., Perkin Trans., 1997, 2, 1985–1990.
8. A. V. Trask, W. D. S. Motherwell and W. Jones, Pharmaceutical cocrystallization: engineering a remedy for caffeine hydration, Cryst. Growth Des., 2005, 5, 1013–1021.
9. C. W. Lehmann and F. Stowasser, The crystal structure of anhydrous β-caffeine as determined from X-ray powder-diffraction data, Chem. – Eur. J., 2007, 13, 2908–2911.
10. K. Guo, G. Sadiq, C. Seaton, R. Davey and Q. Yin, Co-crystallization in the caffeine/maleic acid system: lessons from phase equilibria, Cryst. Growth Des., 2010, 10, 268–273.
11. T. Leyssens, G. Springuel, R. Montis, N. Candoni and S. Veesler, Importance of solvent selection for stoichiometrically diverse cocrystal systems: Caffeine/maleic acid 1 : 1 and 2 : 1 cocrystals, Cryst. Growth Des., 2012, 12, 1520–1530.
12. V. S. Mandala, S. J. Loewus and M. A. Mehta, Monitoring cocrystal formation via in situ solid-state NMR, J. Phys. Chem. Lett., 2014, 5, 3340–3344.
13. M. Mukaida, K. Sugano and K. Terada, Stability order of caffeine co-crystals determined by co-crystal former exchange reaction and its application for the validation of in silico models, Chem. Pharm. Bull., 2015, 63, 18–24.
14. K. P. Nartowski, Y. Z. Khimyak and D. J. Berry, Tuning the spontaneous formation kinetics of caffeine: malonic acid co-crystals, CrystEngComm, 2016, 18, 2617–2620.
15. S. P. Brown, Probing proton-proton proximities in the solid state, Prog. Nucl. Magn. Reson. Spectrosc., 2007, 50, 199–251.
16. T. Le Marchand, T. Schubeis, M. Bonaccorsi, P. Paluch, D. Lalli, A. J. Pell, L. B. Andreas, K. Jaudzems, J. Stanek and G. Pintacuda, ¹H-detected biomolecular NMR under fast magic-angle spinning, Chem. Rev., 2022, 122, 9943–10018.
17. M. K. Dudek, S. Kazmierski, M. Kostrzewa and M. J. Potrzebowski, Solid-state NMR studies of molecular crystals, Annu. Rep. NMR Spectrosc., 2018, 95, 1–81.
18. I. Schnell, Dipolar recoupling in fast-MAS solid-state NMR spectroscopy, Prog. Nucl. Magn. Reson. Spectrosc., 2004, 45, 145–207.
19. P. Hodgkinson, NMR crystallography of molecular organics, Prog. Nucl. Magn. Reson. Spectrosc., 2020, 118–119, 10–53.
20. M. Li, W. Xu and Y. Su, Solid-state NMR spectroscopy in pharmaceutical sciences, Trac., Trends Anal. Chem., 2021, 135, 116152.
21. M. Edén, Probing oxide-based glass structures by solid-state NMR: opportunities and limitations, J. Magn. Reson. Open, 2023, 16–17, 100112.
22. G. D. Enright, V. V. Terskikh, D. H. Brouwer and J. A. Ripmeester, The structure of two anhydrous polymorphs of caffeine from single-crystal diffraction and ultrahigh-field solid-state ¹³C NMR spectroscopy, Cryst. Growth Des., 2007, 7, 1406–1410.
23. S. Bordignon, P. C. Vioglio, E. Priola, D. Voinovich, R. Gobetto, Y. Nishiyama and M. R. Chierotti, Engineering codrug solid forms: mechanochemical synthesis of an indomethacin-caffeine system, Cryst. Growth Des., 2017, 17, 5744–5752.
24. H. E. Kerr, H. E. Mason, H. A. Sparkes and P. Hodgkinson, Testing the limits of NMR crystallography: the case of caffeine-citric acid hydrate, CrystEngComm, 2016, 18, 6700–6707.
25. S. Bhattacharya, Thermal expansion and dimensionality of a hydrogen bond network: a case study on dimorphic oxalic acid, CrystEngComm, 2020, 22, 7896–7902.
26. N. Casati, P. Macchi and A. Sironi, Hydrogen migration in oxalic acid di-hydrate at high pressure?, Chem. Commun., 2009, 2679–2681.
27. S. Bhattacharya, V. G. Saraswatula and B. K. Saha, Thermal expansion in alkane diacids—another property showing alternation in an odd–even series, Cryst. Growth Des., 2013, 13, 3651–3656.
28. V. R. Thalladi, M. Nüsse and R. Boese, The melting point alternation in α,ω-alkanedicarboxylic acids, J. Am. Chem. Soc., 2000, 122, 9227–9236.
29. D. Rychkov, S. Arkhipov and E. Boldyreva, Structure-forming units of amino acid maleates. Case study of L-valinium hydrogen maleate, Acta Crystallogr., 2016, B72, 160–163.
30. F. Mauri, B. G. Pfrommer and S. G. Louie, Ab initio theory of NMR chemical shifts in solids and liquids, Phys. Rev. Lett., 1996, 77, 5300–5303.
31. C. J. Pickard and F. Mauri, All-electron magnetic response with pseudopotentials: NMR chemical shifts, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
32. T. Charpentier, The PAW/GIPAW approach for computing NMR parameters: a new dimension added to NMR of solids, Solid State Nucl. Magn. Reson., 2011, 40, 1–20.
33. C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azaïs, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, First-principles calculation of NMR parameters using the gauge including projector augmented wave method: a chemist's point of view, Chem. Rev., 2012, 112, 5733–5779.
34. R. K. Harris, P. Jackson, L. H. Merwin, B. J. Say and G. Hägele, Perspectives in high-resolution solid-state nuclear magnetic resonance, with emphasis on combined rotation and multiple-pulse spectroscopy, J. Chem. Soc., Faraday Trans. 1, 1988, 84, 3649–3672.
35. U. Sternberg and E. Brunner, The influence of short-range geometry on the chemical shift of protons in hydrogen bonds, J. Magn. Reson., Ser. A, 1994, 108, 142–150.
36. N. R. Jagannathan, Carbon-13 chemical shielding tensors in alkanedicarboxylic acids. Influence of molecular geometry on the carboxyl carbon tensors in alkanedicarboxylic acids and related compounds, Magn. Reson. Chem., 1989, 27, 941–946.
37. Z. Gu and A. McDermott, Chemical shielding anisotropy of protonated and deprotonated carboxylates in amino acids, J. Am. Chem. Soc., 1993, 115, 4282–4285.
38. Z. Gu, R. Zambrano and A. McDermott, Hydrogen bonding of carboxyl groups in sold-state amino acids and peptides: comparison of chemical shielding, infrared frequencies, and structures, J. Am. Chem. Soc., 1994, 116, 6368–6372.
39. R. Gobetto, C. Nervi, M. R. Chierotti, D. Braga, L. Maini, F. Grepioni, R. K. Harris and P. Hodgkinson, Hydrogen bonding and dynamic behaviour in crystals and polymorphs of dicarboxylic-diamine adducts: a comparison between NMR parameters and x-ray diffraction studies, Chem. – Eur. J., 2005, 11, 7461–7471.
40. X. Xue and M. Kanzaki, Proton distributions and hydrogen bonding in crystalline and glassy hydrous silicates and related inorganic materials: insights from high-resolution solid-state nuclear magnetic resonance spectroscopy, J. Am. Ceram. Soc., 2009, 92, 2803–2830.
41. F. G. Vogt, J. S. Clawson, M. Strohmeier, A. J. Edwards, T. N. Pham and S. A. Watson, Solid-state NMR analysis of organic cocrystals and complexes, Cryst. Growth Des., 2009, 9, 2620–2626.
42. S. Scheiner, Identification of spectroscopic patterns of CH⋯O H-bonds in proteins, J. Phys. Chem. B, 2009, 113, 10421–10427.
43. J. R. Yates, T. N. Pham, C. J. Pickard, F. Mauri, A. M. Armado, A. M. Gil and S. P. Brown, An investigation of weak CH⋯O hydrogen bonds in maltose anomers by a combination of calculation and solid-state NMR spectroscopy, J. Am. Chem. Soc., 2005, 127, 10216–10220.
44. A.-C. Uldry, J. M. Griffin, J. R. Yates, M. Pérez-Torralba, M. D. Santa Maria, A. L. Webber, M. L. L. Beaumont, A. Samoson, R. M. Claramunt, C. J. Pickard and S. P. Brown, Quantifying weak hydrogen bonding in uracil and 4-cyano-4′-ethynylphenyl: a combined computational and experimental investigation of NMR chemical shifts in the solid state, J. Am. Chem. Soc., 2008, 130, 945–954.
45. K. Bouzková, M. Babinský, L. Novosadorá and R. Marek, Intermolecular interactions in crystalline theobromine as reflected in electron deformation density and ¹³C NMR chemical shift tensors, J. Chem. Theory Comput., 2013, 9, 2629–2638.
46. S. A. Southern and D. L. Bryce, To what extent do bond length and angle govern the ¹³C and ¹H NMR response to weak CH⋯O hydrogen bonds? A case study of caffeine and theophylline cocrystals, Solid State Nucl. Magn. Reson., 2022, 119, 101795.
47. A. Bauzá, T. J. Mooibroek and A. Frontera, Tetrel-bonding interaction: rediscovered supramolecular force?, Angew. Chem., Int. Ed., 2013, 52, 12317–12321.
48. S. Scheiner, Ability of IR and NMR spectral data to distinguish between a tetrel bond and a hydrogen bond, J. Phys. Chem. A, 2018, 122, 7852–7862.
49. S. A. Southern, M. S. West, M. J. Z. Bradshaw and D. L. Bryce, Experimental ¹³C and ¹H solid-state NMR response in weakly tetrel-bonded methyl groups, J. Phys. Chem. C, 2021, 125, 2111–2123.
50. N. J. Vigilante and M. A. Mehta, A ¹³C solid-state NMR investigation of four cocrystals of caffeine and theophylline, Acta Crystallogr., 2017, C73, 234–243.
51. A. Coelho, TOPAS-academic v6, Coelho Software, 2016.
52. G. Metz, X. L. Wu and S. O. Smith, Ramped-amplitude cross polarization in magic-angle-spinning NMR, J. Magn. Reson., Ser. A, 1994, 110, 219–227.
53. B. M. Fung, A. K. Khitrin and K. Ermolaev, An improved broadband decoupling sequence for liquid crystals and solids, J. Magn. Reson., 2000, 142, 97–101.
54. E. Leonova, A. S. Hakeem, K. Jansson, B. Stevensson, Z. Shen, J. Grins, S. Esmaeilzadeh and M. Edén, Nitrogen-rich La–Si–Al–O–N oxynitride glass structures probed by solid state NMR, J. Non-Cryst. Solids, 2008, 354, 49–60.
55. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr., 2005, 220, 567–570.
56. J. P. Perdew and A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
57. J. R. Yates, C. J. Pickard and F. Mauri, Calculation of NMR chemical shifts for extended systems using ultrasoft pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024401.
58. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients, Rev. Mod. Phys., 1992, 64, 1045–1097.
59. A. Tkatchenko and M. Scheffler, Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data, Phys. Rev. Lett., 2009, 102, 073005.
60. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
61. M. M. Maricq and J. S. Waugh, NMR in rotating solids, J. Chem. Phys., 1979, 70, 3300–3316.
62. U. Haeberlen, High Resolution NMR in Solids. Selective Averaging, Academic Press, New York, 1976.
63. J. Mason, Conventions for the reporting of nuclear magnetic shielding (or shift) tensors suggested by participants in the NATO ARW on NMR shielding constants at the University of Maryland, College Park, July 1992, Solid State Nucl. Magn. Reson., 1993, 2, 285–288.
64. C. López, R. Claramunt and J. Elguero, Oxalic acid/phenols and oxalic acid/cholesterol co-crystals: a solid state ¹³C CPMAS NMR study, ARKIVOC, 2008, 33–46.
65. E. Pindelska, A. Sokal, L. Szeleszczuk, D. M. Pisklak and W. Kolodziejski, Solid-state NMR studies of theophylline co-crystals with dicarboxylic acids, J. Pharm. Biomed. Anal., 2014, 100, 322–328.
66. J. Kastelic, Ž. Hodnik, P. Šket, J. Plavec, N. Lah, I. Leban, M. Pajk, O. Planinšek and D. Kikelj, Fluconazole cocrystals with dicarboxylic acids, Cryst. Growth Des., 2010, 10, 4943–4953.
67. M. Ilczyszyn, D. Godzisz and M. M. Ilczyszyn, Sarcosine-maleic acid (1 : 1) crystal: structure, ¹³C NMR and vibrational properties, protonation character, Spectrochim. Acta, Part A, 2003, 59, 1815–1828.
68. Nonappa and E. Kolehmainen, Caffeine as a gelator, Gels, 2016, 2, 9.
69. J. Sitkowski, L. Stefaniak, L. Nicol, M. L. Martin, G. J. Martin and G. A. Webb, Complete assignments of ¹H, ¹³C, and ¹⁵N NMR spectra of caffeine, Spectrochim. Acta, Part A, 1995, 51, 839–2841.
70. N. Liédana, A. Galve, C. Rubio, C. Téllez and J. Coronas, CAFZIF-8: one-step encapsulation of caffeine in MOF, ACS Appl. Mater. Interfaces, 2012, 4, 5016–5021.
71. D. L. VanderHart, W. L. Earl and A. N. Garroway, Resolution in ¹³C NMR of organic solids using high-power proton decoupling and magic-angle sample spinning, J. Magn. Reson., 1981, 44, 361–401.
72. M. Alla and E. Lippmaa, Resolution limits in magic-angle rotation NMR spectra of polycrystalline solids, Chem. Phys. Lett., 1982, 87, 30–33.
73. A. J. Robbins, W. T. K. Ng, D. Jochym, T. W. Keal, S. J. Clark, D. J. Tozer and P. Hodgkinson, Combining insights from solid-state NMR and first principles calculation: applications to the ¹⁹ F NMR of octafluoronaphthalene, Phys. Chem. Chem. Phys., 2007, 9, 2389–2396.
74. M. P. Hanrahan, A. Venkatesh, S. L. Carnahan, J. L. Calahan, J. W. Lubach, E. J. Munson and A. J. Rossini, Enhancing the resolution of ¹H and ¹³C solid-state NMR spectra by reduction of anisotropic bulk magnetic susceptibility broadening, Phys. Chem. Chem. Phys., 2017, 19, 28153–28162.
75. J. G. Hexem, M. H. Frey and S. J. Opella, Molecular and structural information from ¹⁴N–¹³C NMR spectra of solids, J. Chem. Phys., 1982, 77, 3847–3856.
76. A. C. Olivieri, L. Frydman and L. E. Diaz, A simple approach for relating molecular structural information to the dipolar coupling in ¹³C–¹⁴N CP MAS NMR, J. Magn. Reson., 1987, 75, 50–62.
77. B. Berglund and R. W. Vaughan, Correlations between proton chemical shift tensors, deuterium quadrupole couplings, and bond distances in solids, J. Chem. Phys., 1980, 73, 2037–2043.
78. R. G. Griffin and D. J. Ruben, Carbon-13 chemical shielding in ammonium hydrogen oxalate hemihydrate, J. Chem. Phys., 1975, 63, 1272–1275.
79. R. G. Griffin, A. Pines, S. Pausak and J. S. Waugh, ¹³C chemical shielding in oxalic acid, oxalic acid dihydrate, and diammonium oxalate, J. Chem. Phys., 1975, 63, 1267–1271.
80. C. Gardiennet-Doucet, X. Assfeld, B. Henry and P. Tekely, Revealing successive steps of deprotonation of L-phosphoserine through ¹³C and ³¹P chemical shielding tensor fingerprints, J. Phys. Chem. A, 2006, 110, 9137–9144.
81. R. Mathew, B. Stevensson and M. Edén, Refined structures of O-phospho-L-serine and its calcium salt by new multinuclear solid-state NMR crystallography methods, J. Phys. Chem. B, 2021, 125, 10985–11004.
82. Y. Yu, B. Stevensson, M. Pujari-Palmer, H. Guo, H. Engqvist and M. Edén, The monetite structure probed by advanced solid-state NMR experimentation at fast magic-angle spinning, Int. J. Mol. Sci., 2019, 20, 6356.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06197c

‡ Present address: Department of Chemistry, National Institute of Technology Tiruchirappalli, Tiruchirappalli-620015, Tamil Nadu, India.

---