Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cyclic ion mobility of doped [MAu24L18]2− superatoms and their fragments (M = Ni, Pd and Pt; L = alkynyl)†
Frank
Hennrich
ad,
Shun
Ito
b,
Patrick
Weis
 a,
Marco
Neumaier
a,
Marco
Neumaier
 ac,
Shinjiro
Takano
ac,
Shinjiro
Takano
 b,
Tatsuya
Tsukuda
b,
Tatsuya
Tsukuda
 b and
Manfred M.
Kappes
b and
Manfred M.
Kappes
 *acd
*acd
aInstitute of Physical Chemistry, Karlsruhe Institute of Technology, Fritz-Haber-Weg 2, Karlsruhe 76131, Germany. E-mail: manfred.kappes@kit.edu
bDepartment of Chemistry, Graduate School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan
cInstitute of Nanotechnology, Karlsruhe Institute of Technology, Hermann-von-Helmholtz-Platz 1, Eggenstein-Leopoldshafen 76344, Germany
dInstitute of Quantum Materials and Technologies, Karlsruhe Institute of Technology, Hermann-von-Helmholtz-Platz 1, Eggenstein-Leopoldshafen 76344, Germany
First published on 20th February 2024
Abstract
Collision-induced dissociation and high-resolution cyclic ion mobility mass spectrometry, along with quantum chemical calculations and trajectory simulations, were used to compare the structures of isolated [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2−, M = Ni, Pd, or Pt, and their associated fragment ions. The three different alkynyl ligand-stabilized (C
CR)18]2−, M = Ni, Pd, or Pt, and their associated fragment ions. The three different alkynyl ligand-stabilized (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR, R = 3,5-(CF3)2C6H3), transition metal-doped, gold cluster dianions showed mutually resolvable collision cross sections (CCS), which were ordered consistently with their molecular structures from X-ray crystallography. All three [MAu24(C
CR, R = 3,5-(CF3)2C6H3), transition metal-doped, gold cluster dianions showed mutually resolvable collision cross sections (CCS), which were ordered consistently with their molecular structures from X-ray crystallography. All three [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− species fragment by sequential diyne loss to form [MAu24(C
CR)18]2− species fragment by sequential diyne loss to form [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]2−, with n up to 12. The resultant fragment isomer distributions are significantly n- and M-dependent, and hint at a process involving concerted elimination of adjacent ligands. In particular [NiAu24(C
CR)18−n]2−, with n up to 12. The resultant fragment isomer distributions are significantly n- and M-dependent, and hint at a process involving concerted elimination of adjacent ligands. In particular [NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− also fragments to generate alkyne-oligomers, an inference supported by the parallel observation of precursor dianion isomerization as collision energy is increased.
CR)18]2− also fragments to generate alkyne-oligomers, an inference supported by the parallel observation of precursor dianion isomerization as collision energy is increased.
1. Introduction
Doped elemental clusters often form cage-like structures enclosing atomic or molecular dopants. Endohedrally doped fullerene carbon cages were among the first examples. Analogous centrally doped clusters are known for many other elements.1–4 For example, naked (i.e. ligand-free) gold clusters caging different transition metal atoms have been extensively studied in rarified molecular beam experiments and by quantum chemical calculations.5 It has also become possible to stabilize such transition metal doped gold clusters using a shell of organic ligands.6–9 In contrast to bare gold clusters, the “coating” with a finite number of ligands provides sufficient protection of the cluster cores to prevent them from coalescing. Consequently air-stable, ligand-stabilized, gold clusters centrally doped with transition metal atoms can be made in bulk quantities and studied at a level of detail going much beyond molecular beam experiments.The recently established “MAu24L18 series” (M = Ni, Pd and Pt) is a prototypical example of single-atom doped gold clusters stabilized by ligands L, such as thiolates (SR) and alkynyls (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR).10–17 The geometric structure of MAu24L18 clusters including the location of dopant M was determined by X-ray crystallography. The three [MAu24(C
CR).10–17 The geometric structure of MAu24L18 clusters including the location of dopant M was determined by X-ray crystallography. The three [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− dianions (M = Ni, Pd, Pt; R = 3,5-(CF3)2C6H3) share a common molecular structure as exemplified in Scheme 1 for M = Ni. The central heteroatom M (green) is surrounded by an icosahedral shell of 12 gold atoms (yellow). This icosahedron is protected by six staples each comprising discrete Au2(C
CR)18]2− dianions (M = Ni, Pd, Pt; R = 3,5-(CF3)2C6H3) share a common molecular structure as exemplified in Scheme 1 for M = Ni. The central heteroatom M (green) is surrounded by an icosahedral shell of 12 gold atoms (yellow). This icosahedron is protected by six staples each comprising discrete Au2(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)3 units (bronze Au atoms) which can be thought of as holding the core together against isomerization. There are small systematic changes in M–Au bond lengths as the dopant is varied – reflecting to first order the different sizes of the central heterometal atoms.
CR)3 units (bronze Au atoms) which can be thought of as holding the core together against isomerization. There are small systematic changes in M–Au bond lengths as the dopant is varied – reflecting to first order the different sizes of the central heterometal atoms.
 | ||
Scheme 1 [NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− structure as determined by X-ray crystallography (R = 3,5-(CF3)2C6H3 (3,5-bis(trifluoromethyl)phenyl)).12 The icosahedral NiAu12 cluster core with central heteroatom is surrounded by six Au2(C CR)18]2− structure as determined by X-ray crystallography (R = 3,5-(CF3)2C6H3 (3,5-bis(trifluoromethyl)phenyl)).12 The icosahedral NiAu12 cluster core with central heteroatom is surrounded by six Au2(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)3 staples one of which is highlighted. Each staple comprises three (C CR)3 staples one of which is highlighted. Each staple comprises three (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) ligands labelled A, B and C. Color coding: Au (yellow (icosahedral shell) and bronze (staples)), C (blue), H (pink), F (lime green) and Ni (green). [PdAu24(C CR) ligands labelled A, B and C. Color coding: Au (yellow (icosahedral shell) and bronze (staples)), C (blue), H (pink), F (lime green) and Ni (green). [PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− and [PtAu24(C CR)18]2− and [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− have the same molecular structure with slightly different bond lengths. CR)18]2− have the same molecular structure with slightly different bond lengths. | ||
The different [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− species, which from here on we will generally refer to as MAu24, also share a common electronic structure as inferred from DFT (density functional theory) calculations of the isolated dianions and from various experimental results. According to an interpretation based on the spherical jellium model of simple metal clusters,18–20 the isolated ground state species correspond to 8-electron superatoms with eight s1-electrons delocalized over the icosahedral core (counting rule: 24 (Au) + 0 (M) − 18 (L) + 2 (dianion) = 8, i.e. 1S2 + 1P6). Interestingly, in this counting of delocalized electrons, the group 10 metal atom at the center does not contribute to the number of delocalized valence electrons. In a cross section through the center of the positive jellium background this can be rationalized by raising the potential of the central region relative to the perimeter (two-step jellium model).21–24 This destabilizes the 1S shell relative to 1P and 1D shells, but not enough to change the 1S2 + 1P6 filling order.
CR)18]2− species, which from here on we will generally refer to as MAu24, also share a common electronic structure as inferred from DFT (density functional theory) calculations of the isolated dianions and from various experimental results. According to an interpretation based on the spherical jellium model of simple metal clusters,18–20 the isolated ground state species correspond to 8-electron superatoms with eight s1-electrons delocalized over the icosahedral core (counting rule: 24 (Au) + 0 (M) − 18 (L) + 2 (dianion) = 8, i.e. 1S2 + 1P6). Interestingly, in this counting of delocalized electrons, the group 10 metal atom at the center does not contribute to the number of delocalized valence electrons. In a cross section through the center of the positive jellium background this can be rationalized by raising the potential of the central region relative to the perimeter (two-step jellium model).21–24 This destabilizes the 1S shell relative to 1P and 1D shells, but not enough to change the 1S2 + 1P6 filling order.
The establishment of a synthesis route to ligand stabilized MAu24 clusters has been significantly aided by electrospray ionization (ESI) mass spectrometry. [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− dianions are the primary gold-containing species observed in the ESI mass spectra of a solution of [MAu24(C
CR)18]2− dianions are the primary gold-containing species observed in the ESI mass spectra of a solution of [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18](PPh4)2. It is interesting to consider whether these isolated dianions have the same molecular structures as the MAu24 clusters making up the single crystals. Perhaps there are structure changes upon solvation and electrospraying? Clusters in the crystalline solid may undergo structural relaxation due to interactions with solvent molecules, counterions and also other proximal clusters – which are missing under isolated conditions. On the other hand, highly charged ions can unravel dynamically in gas phase relative to their solution forms (in which localized excess charges are better shielded from each other by the surrounding dielectric medium).25
CR)18](PPh4)2. It is interesting to consider whether these isolated dianions have the same molecular structures as the MAu24 clusters making up the single crystals. Perhaps there are structure changes upon solvation and electrospraying? Clusters in the crystalline solid may undergo structural relaxation due to interactions with solvent molecules, counterions and also other proximal clusters – which are missing under isolated conditions. On the other hand, highly charged ions can unravel dynamically in gas phase relative to their solution forms (in which localized excess charges are better shielded from each other by the surrounding dielectric medium).25
Here we use ultrahigh resolution cyclic ion mobility spectrometry combined with mass spectrometry (cIMS-MS) to compare the solid-state structures with the gas phase collision cross sections (CCS) of precursor MAu24 dianions, M = Ni, Pd and Pt – the so far most highly resolved CCS measurements of ligand stabilized coinage metal clusters. In combination with DFT modelling and trajectory method simulations of the experimental CCS values we find that the “size” of the isolated dianions closely follows the M–Au bond length trend observed by X-ray crystallography in solid state.
Isolation of molecular ions in gas phase also offers the possibility to controllably excite them by collisions with an inert gas without accessing dissipative processes involving neighboring molecules (e.g. cluster–cluster reactions) as would occur upon thermal treatment in condensed phase environments. In this study, we have used this capability also to compare the structural stability of MAu24 towards isomerization and fragmentation as internal excitation levels are incrementally raised. Specifically, we have performed energy dependent CID (collision induced dissociation) measurements and have determined CCS values for precursor dianions and the resulting fragments using cIMS-MS. While, sequential diyne (RC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C
C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR) loss is the dominant common fragmentation channel for all M, we find E50 values (50% survival yield) and fragment CCS values to be M dependent. For M = Ni, collisional excitation also accesses significant ligand oligomer loss.
CR) loss is the dominant common fragmentation channel for all M, we find E50 values (50% survival yield) and fragment CCS values to be M dependent. For M = Ni, collisional excitation also accesses significant ligand oligomer loss.
Below we describe our results and provide first order structural rationalizations based on DFT and semiempirical calculations (of the electronic ground states) as well as ion trajectory simulations of the corresponding orientationally averaged collision cross sections.
2. Methods
2.1 Synthesis
Cluster samples were synthesized at U. Tokyo as described in detail in SI. [PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− and [PtAu24(C
CR)18]2− and [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− were synthesized by hydride-mediated transformation of presynthesized [PdAu8(PPh3)8]2+ and [PtAu8(PPh3)8]2+,11,26–28 respectively. In brief, [PdAu24(C
CR)18]2− were synthesized by hydride-mediated transformation of presynthesized [PdAu8(PPh3)8]2+ and [PtAu8(PPh3)8]2+,11,26–28 respectively. In brief, [PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− was obtained by the reaction of Au–C
CR)18]2− was obtained by the reaction of Au–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR polymer complexes and [PdHAu8(PPh3)8]+ generated by the reaction between [PdAu8(PPh3)8]2+ and NaBH4.11 The synthetic procedure for [PtAu24(C
CR polymer complexes and [PdHAu8(PPh3)8]+ generated by the reaction between [PdAu8(PPh3)8]2+ and NaBH4.11 The synthetic procedure for [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− was the same except for the use of [PtAu8(PPh3)8]2+ instead of [PdAu8(PPh3)8]2+. [NiAu24(C
CR)18]2− was the same except for the use of [PtAu8(PPh3)8]2+ instead of [PdAu8(PPh3)8]2+. [NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− was synthesized by the reaction of Au–C
CR)18]2− was synthesized by the reaction of Au–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR polymer complexes and crude [NiHAu8(PPh3)8]+.12 The samples of [MAu24(C
CR polymer complexes and crude [NiHAu8(PPh3)8]+.12 The samples of [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− (M = Ni, Pd and Pt) were obtained as PPh4+ salts in a pure form by reprecipitation procedure. The samples were characterized by mass spectrometry and UV-vis spectroscopy.
CR)18]2− (M = Ni, Pd and Pt) were obtained as PPh4+ salts in a pure form by reprecipitation procedure. The samples were characterized by mass spectrometry and UV-vis spectroscopy.
2.2 ESI-MS and cyclic IMS-MS.
Materials were dissolved in MeOH/acetonitrile (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) at typical concentrations of 0.1 mg mL−1 and electrosprayed into a Waters Select Series Cyclic IMS ion mobility mass spectrometer at KIT for further study. Gold containing charged species were only observed in the negative ion mode. By far the most dominant anions observed by high resolution mass spectrometry under standard analytical electrospray conditions were [MAu24(C
2) at typical concentrations of 0.1 mg mL−1 and electrosprayed into a Waters Select Series Cyclic IMS ion mobility mass spectrometer at KIT for further study. Gold containing charged species were only observed in the negative ion mode. By far the most dominant anions observed by high resolution mass spectrometry under standard analytical electrospray conditions were [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2−, M = Ni, Pd and Pt. In the following, we focus on these precursor ions and their anionic fragments as generated by collisional activation.
CR)18]2−, M = Ni, Pd and Pt. In the following, we focus on these precursor ions and their anionic fragments as generated by collisional activation.
The Waters Select Series Cyclic IMS ion mobility mass spectrometer can be run in several different standard modes. The setup and working principle of this apparatus which allows for CID, ultrahigh resolution cyclic ion mobility spectrometry cIMS and iterative CID-IMS (cIMSn) measurements each combined with high resolution mass spectrometry have been extensively described.29 Further details in particular of components and procedures relevant for this study are given in ESI.† Here we used the instrument for: (i) solution analytics by measuring high resolution ESI mass spectra under soft ionization conditions (achievable mass resolution, m/Δm of >100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) while bypassing the cyclic ion mobility separation device (cIM), (ii) collisional activation and fragment mass analysis as a function of collision energy (also bypassing the cIM), (iii) cIMS of mass-range selected precursor dianions to yield arrival time distributions (ATD's) upon one or more cIM cycles and (iv) collisional activation coupled with cIMS and m/z measurements as described. The collisional activation is performed in the ion trap located behind the quadrupole mass filter, the collision gas is nitrogen at a pressure of 2.6 × 10−2 mbar, i.e. multiple collision conditions.
000) while bypassing the cyclic ion mobility separation device (cIM), (ii) collisional activation and fragment mass analysis as a function of collision energy (also bypassing the cIM), (iii) cIMS of mass-range selected precursor dianions to yield arrival time distributions (ATD's) upon one or more cIM cycles and (iv) collisional activation coupled with cIMS and m/z measurements as described. The collisional activation is performed in the ion trap located behind the quadrupole mass filter, the collision gas is nitrogen at a pressure of 2.6 × 10−2 mbar, i.e. multiple collision conditions.
Cyclic-IMS is one of several commercially available instrumental variants coupling ion mobility spectrometry with high resolution mass spectrometry. In its simplest form IMS measures the drift time of an ion pulled by a static electric field through a finite length drift cell filled with an inert collision gas. This drift time is inversely proportional to the ions’ mobility which can be converted to a collision cross section using the Mason–Schamp equation30 (see ESI†). Such (orientationally averaged) CCS values provide first order structural information for the molecular ion of interest. State-of-the-art IMS instrumental platforms seek to achieve high sensitivities combined with highest mass and ion mobility resolutions. Some of us have previously used and extensively described trapped ion mobility spectrometry (tims) which offers CCS resolutions (CCS/ΔCCS) of up to ca. 200 as implemented in a Bruker timsTOFMS. In the present study we make use of a Waters Cyclic IMS which is a comparatively new addition to the arsenal of commercialized IMS methods and can provide significantly higher CCS resolution. cIMS uses travelling wave (TWIMS) excitation to push the ions to be analysed through a cyclic drift cell filled with molecular nitrogen. This allows to extend separation lengths relative to a linear TWIMS cell simply by cycling the ions multiple times. Concretely, in the Waters Cyclic IMS system ions are pulsed into the ca. 1 m length cIM device, undergo a selected number of cycles which can range up to more than 50 and are then pulse extracted from the drift tube for mass analysis to yield ATD's as a function of mass-to-charge ratio. The ATD's are then converted to calibrated collision cross sections using a procedure described in detail in ESI.† According to the IMS nomenclature convention they are denoted as twCCSN2 values. According to ref. 29 cIMS can achieve twCCSN2 resolutions of more than 750 as ultimately limited by self-diffusion and collisional broadening of the ion packets injected into the cIM. We will separately report on twCCSN2 calibration and dependence of resolution on TWIMS parameters in a future publication – including a comparison to timsCCSN2 values for a variety of substance classes and molecular ion charge states.31
For measurements of the high m/z monoanionic fragments generated upon CID of [NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− we used a Bruker compact ESI-MS optimized for high m/z detection (at U. Tokyo).
CR)18]2− we used a Bruker compact ESI-MS optimized for high m/z detection (at U. Tokyo).
2.3 Theory
Experimental twCCSN2 values were compared to predictions, theoCCSN2, from trajectory method simulations using the IMoS 1.09 package32,33 (see ESI† for further details). These simulations were based on model structures obtained from DFT calculations performed with TURBOMOLE 7.434 using the PBE functional35–38 with def2-SVP basis sets39 and accounting for dispersion interactions at the DFT-D3 bj level.40,41 To prevent SCF (self-consistent-field) convergence problems we used Fermi smearing as implemented in TURBOMOLE. For calculating partial charges of some model structures we also used semiempirical extended tight binding calculations, i.e. the GFN 1 xTB-method.42,43 For the three [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− precursor dianions, starting structures were taken as corresponding to the published X-ray crystal based DFT structure 0a44 of [PdAu24(C
CR)18]2− precursor dianions, starting structures were taken as corresponding to the published X-ray crystal based DFT structure 0a44 of [PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− (i.e. with central heteroatom surrounded by 12 gold atoms oriented in an icosahedral shell) and further geometry optimized with DFT without symmetry constraints. For [PtAu24(C
CR)18]2− (i.e. with central heteroatom surrounded by 12 gold atoms oriented in an icosahedral shell) and further geometry optimized with DFT without symmetry constraints. For [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− and [NiAu24(C
CR)18]2− and [NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− we swapped the central metal atom. The resulting relaxed structures share basically the same geometry as the X-ray structures, except for a small overall contraction (3–4% for [NiAu24(C
CR)18]2− we swapped the central metal atom. The resulting relaxed structures share basically the same geometry as the X-ray structures, except for a small overall contraction (3–4% for [NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2−, [PdAu24(C
CR)18]2−, [PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− and [PtAu24(C
CR)18]2− and [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2−). The contraction mainly occurs in the ligand shell reflecting minor changes in the ligand orientations and slightly shorter Au–C bonds upon geometry optimization. The root mean square deviation between the [MAu24(C
CR)18]2−). The contraction mainly occurs in the ligand shell reflecting minor changes in the ligand orientations and slightly shorter Au–C bonds upon geometry optimization. The root mean square deviation between the [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− X-ray structures11,12 and our DFT optimized structures of isolated [MAu24(C
CR)18]2− X-ray structures11,12 and our DFT optimized structures of isolated [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− is 0.92 Å (M = Ni), 0.81 Å (M = Pd) and 0.86 Å (M = Pt), respectively, as determined with Jmol45 and RMSD.46 Comparing only the MAu24 metal cores a deviation of 0.19 Å is determined for PdAu24 and PtAu24 and 0.20 Å for NiAu24, showing that most of the changes occur in the ligand shell and not in the metal core. To compare to experiment, relaxed DFT structures were translated into the corresponding theoCCSN2 values via trajectory calculations (see ESI†).
CR)18]2− is 0.92 Å (M = Ni), 0.81 Å (M = Pd) and 0.86 Å (M = Pt), respectively, as determined with Jmol45 and RMSD.46 Comparing only the MAu24 metal cores a deviation of 0.19 Å is determined for PdAu24 and PtAu24 and 0.20 Å for NiAu24, showing that most of the changes occur in the ligand shell and not in the metal core. To compare to experiment, relaxed DFT structures were translated into the corresponding theoCCSN2 values via trajectory calculations (see ESI†).
Selected fragments [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]2− were investigated by iteratively removing ligands from the corresponding [MAu24(C
CR)18−n]2− were investigated by iteratively removing ligands from the corresponding [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− DFT structure in a variety of different ways designed to simulate either statistical or non-statistical fragmentation behavior as described in detail below (and in ESI†). The theoCCSN2 of the resulting unrelaxed structures were then calculated with IMoS by using partial charges obtained from GFN 1 xTB calculations (see ESI†). Structures were visualized with VMD47 and Jmol.45
CR)18]2− DFT structure in a variety of different ways designed to simulate either statistical or non-statistical fragmentation behavior as described in detail below (and in ESI†). The theoCCSN2 of the resulting unrelaxed structures were then calculated with IMoS by using partial charges obtained from GFN 1 xTB calculations (see ESI†). Structures were visualized with VMD47 and Jmol.45
3. Results and discussion
3.1 Separating [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e002.gif) CR)18]2− precursor ions according to their ion mobility
CR)18]2− precursor ions according to their ion mobility
Assuming that the known crystal structures are essentially retained in gas phase we expected the three MAu24 precursor dianions to have very close lying twCCSN2, close to the instrumental resolution of our cIM. To minimize small perturbations due to temperature and pressure fluctuations in the cIM, we therefore explored their relative size using a mixture – i.e. essentially with an internal reference. For this all three dianions were softly injected into the cIM device together and then separated from each other in up to 50 cycles, pulse extracted from the cIM and subsequently mass analyzed (much as in a recirculating HPLC analysis with specific optical detection).48
Fig. 1 shows a partial mass spectrum of the mixture used – containing [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− with M = Ni, Pd and Pt in the relative ratios 2.7
CR)18]2− with M = Ni, Pd and Pt in the relative ratios 2.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.3
1.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Fig. 2 shows arrival time distributions obtained for this mixture at different numbers of separation cycles ranging from 1–50 as indicated (left – integrating over the full mass range from m/z = 4520–4600, i.e. encompassing all three precursor dianions; and right mass- and therefore M-selective arrival times for the case of a 50 cycle separation). With increasing numbers of cycles in Fig. 2 (left), three peaks begin to separate corresponding to the three different [MAu24(C
1. Fig. 2 shows arrival time distributions obtained for this mixture at different numbers of separation cycles ranging from 1–50 as indicated (left – integrating over the full mass range from m/z = 4520–4600, i.e. encompassing all three precursor dianions; and right mass- and therefore M-selective arrival times for the case of a 50 cycle separation). With increasing numbers of cycles in Fig. 2 (left), three peaks begin to separate corresponding to the three different [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− species contained in the mixture (as confirmed by relative ion intensities and concurrent m/z analysis). Note that 50 cycles correspond to an overall drift length of 50 m. The dianions arrive at the extraction point (equivalent to a column elution in chromatography) in the sequence Ni < Pd < Pt. Thus, the size trend seen in solid state is also retained in gas phase.
CR)18]2− species contained in the mixture (as confirmed by relative ion intensities and concurrent m/z analysis). Note that 50 cycles correspond to an overall drift length of 50 m. The dianions arrive at the extraction point (equivalent to a column elution in chromatography) in the sequence Ni < Pd < Pt. Thus, the size trend seen in solid state is also retained in gas phase.
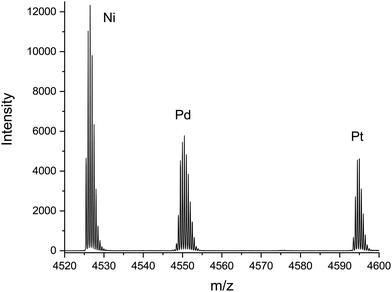 | ||
Fig. 1 Electrospray ionization mass spectrum obtained for the mixture of [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2−, M = Ni, Pd and Pt, which was used to obtain their orientally averaged collision cross sections in molecular nitrogen, twCCSN2, as shown in Fig. 2 and Table 1. See ESI† for comparison of resolved experimental isotope distributions to simulations for natural isotope abundances. CR)18]2−, M = Ni, Pd and Pt, which was used to obtain their orientally averaged collision cross sections in molecular nitrogen, twCCSN2, as shown in Fig. 2 and Table 1. See ESI† for comparison of resolved experimental isotope distributions to simulations for natural isotope abundances. | ||
 | ||
Fig. 2 Cyclic-IMS separations obtained for a mixture of [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2−, M = Ni, Pd and Pt (see Fig. 1). Left: Arrival time distributions (ATD's) for all [MAu24(C CR)18]2−, M = Ni, Pd and Pt (see Fig. 1). Left: Arrival time distributions (ATD's) for all [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− ions together obtained by integrating over the m/z = 4520–4600 range – as a function of the number of separation cycles from 1–50. Right – M-specific arrival time distributions for 50 separation cycles, i.e. recorded for the m/z range corresponding to the isotopologues of a specific [MAu24(C CR)18]2− ions together obtained by integrating over the m/z = 4520–4600 range – as a function of the number of separation cycles from 1–50. Right – M-specific arrival time distributions for 50 separation cycles, i.e. recorded for the m/z range corresponding to the isotopologues of a specific [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− and normalized to the respective ATD maxima. The ATD's can be converted to orientationally averaged collision cross sections, twCCSN2 of the three different gas phase dianions, see text. Note that the order of elution, Ni < Pd < Pt, is consistent with the size trend in condensed phase. CR)18]2− and normalized to the respective ATD maxima. The ATD's can be converted to orientationally averaged collision cross sections, twCCSN2 of the three different gas phase dianions, see text. Note that the order of elution, Ni < Pd < Pt, is consistent with the size trend in condensed phase. | ||
Note, that the 50 cycle separation shown in Fig. 2 corresponds to a CCS resolution of about 300. Even higher CCS resolutions could be obtained by cycling further. Achievable resolution is however ultimately limited by the finite cIM ring circumference of ∼1 m: eventually the lower CCS (and thus faster) ions begin to catch up to the higher CCS (and thus slower) ions. Note also, that under our conditions MAu24 ion intensity decays roughly by 3.7% per pass of the cIM device.
Based on multiple such 50 cycle measurements (on MAu24 mixtures probed under similar conditions on different days and calibrated against 50 cycle separations of Agilent Tunemix monoanions some of which also lie in the same m/z range) we determined absolute twCCSN2 values of 721.5, 723.3 and 724.9 Å2 for NiAu24, PdAu24 and PtAu24 with an error of ± 0.8 Å2 whereas the difference between peaks can be measured with higher precision and is 1.80 ± 0.1 Å2 between NiAu24 and PdAu24 and 1.63 ± 0.1 Å2 between PdAu24 and PtAu24. To analyze the data, Gaussian functions were fitted to the mass-resolved ATD's. The corresponding maxima were then converted to calibrated twCCSN2 values. Error bars reflect statistical fluctuations in the positions of the maxima of the Gaussians from one cIM injection to the next.
Table 1 compares experimental and theoretical CCS values (calculated starting from the X-ray based DFT structure of [PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− – see above) for the gas phase precursor dianions. With theoCCSN2 values of 730.5 Å2 (M = Pt), 730.4 Å2 (M = Pd) and 728.3 Å2 (M = Ni), the experimental twCCSN2 values are reproduced to within 1%. The standard error (i.e. the statistical uncertainty) of theoCCS was determined to ±0.3 Å2 from at least 10 different trajectory simulation runs (each with ca. 3 million trajectories with varying starting orientation, see ESI†). Additionally, in order to address sources of systematic error, we list theoCCSN2 of the DFT structures but using Mulliken partial charges from GFN1 xTB as we used this method for calculating theoCCS of the fragment isomers (see below). When using Mulliken charges from xTB, the theoCCS values agree even better with the experimental data (presumably due to error compensation as Mulliken results in unphysically negative partial charges for the central metal atom). The decreasing theoCCSN2 from Pt to Ni is well correlated with (the DFT computed) decreasing distances from the central atom M to the icosahedral Au atoms of 2.81 Å (Pt–Auico) and 2.76 Å (Ni–Auico). The theoCCSN2 of the Pt and Pd containing cluster are very similar as are the distances of 2.81 Å (Pt–Auico) and 2.80 Å (Pd–Auico). In general, agreement of theory and experiment to within 1% is surprisingly good for molecules of this size and complexity. In previous tims studies of related molecules in this size range we have typically achieved agreement to within 2%.49,50 This is a strong indicator, that in the MAu24 dianions, transfer into gas phase does not significantly change the bond connectivity or relative bond orientations.
CR)18]2− – see above) for the gas phase precursor dianions. With theoCCSN2 values of 730.5 Å2 (M = Pt), 730.4 Å2 (M = Pd) and 728.3 Å2 (M = Ni), the experimental twCCSN2 values are reproduced to within 1%. The standard error (i.e. the statistical uncertainty) of theoCCS was determined to ±0.3 Å2 from at least 10 different trajectory simulation runs (each with ca. 3 million trajectories with varying starting orientation, see ESI†). Additionally, in order to address sources of systematic error, we list theoCCSN2 of the DFT structures but using Mulliken partial charges from GFN1 xTB as we used this method for calculating theoCCS of the fragment isomers (see below). When using Mulliken charges from xTB, the theoCCS values agree even better with the experimental data (presumably due to error compensation as Mulliken results in unphysically negative partial charges for the central metal atom). The decreasing theoCCSN2 from Pt to Ni is well correlated with (the DFT computed) decreasing distances from the central atom M to the icosahedral Au atoms of 2.81 Å (Pt–Auico) and 2.76 Å (Ni–Auico). The theoCCSN2 of the Pt and Pd containing cluster are very similar as are the distances of 2.81 Å (Pt–Auico) and 2.80 Å (Pd–Auico). In general, agreement of theory and experiment to within 1% is surprisingly good for molecules of this size and complexity. In previous tims studies of related molecules in this size range we have typically achieved agreement to within 2%.49,50 This is a strong indicator, that in the MAu24 dianions, transfer into gas phase does not significantly change the bond connectivity or relative bond orientations.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− with calculated theoCCSN2 values (see text and Fig. S1, ESI)
CR)18]2− with calculated theoCCSN2 values (see text and Fig. S1, ESI)
| twCCSN2/Å2 | theoCCSN2/Å2 DFT structure/DFT charges | theoCCSN2/Å2 DFT structure/GFN1 xTB charges | Deviationa/% | |
|---|---|---|---|---|
| a Deviation between column 1 and 2 and column 1 and 3, respectively. | ||||
[PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− CR)18]2− |
724.9 ± 0.8 | 730.5 ± 0.4 | 724.0 ± 0.3 | 0.7, −0.13 |
[PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− CR)18]2− |
723.3 ± 0.8 | 730.4 ± 0.3 | 723.4 ± 0.4 | 1.0, 0.02 |
[NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− CR)18]2− |
721.5 ± 0.8 | 728.3 ± 0.4 | 721.0 ± 0.3 | 0.9, −0.07 |
3.2 Collision induced dissociation
The authors of ref. 10 inferred from their CID MS measurements and DFT calculations, that collisionally excited [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− and [PdAu24(C
CR)18]2− and [PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− (R = 3,5-(CF3)2C6H3) can sequentially eliminate neutral 1,3-diynes (RC
CR)18]2− (R = 3,5-(CF3)2C6H3) can sequentially eliminate neutral 1,3-diynes (RC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C
C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR), i.e. concerted loss of two C
CR), i.e. concerted loss of two C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR units at a time, to generate [MAu24(C
CR units at a time, to generate [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]2−, with even n = 2–12, reaction (1).
CR)18−n]2−, with even n = 2–12, reaction (1).[MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2−* → [MAu24(C CR)18]2−* → [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)16]2− + RC CR)16]2− + RC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR → [MAu24(C CR → [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)14]2− + RC CR)14]2− + RC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR→… CR→… | (1) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR molecule may sometimes also be lost – to generate [MAu24(C
CR molecule may sometimes also be lost – to generate [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR′)(C
CR′)(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)17−n]2−, (R′ = 3,5-(CF3)2C6H2) with overall odd numbered n = 1–11. Remarkably, dianions were found to be the dominant fragment charge state (only comparatively small amounts of monoanions were additionally detected) and these always retained an intact MAu24 metal cluster moiety – i.e. the cleaved/reacted ligands did not significantly carry away any excess charge or metal atoms.
CR)17−n]2−, (R′ = 3,5-(CF3)2C6H2) with overall odd numbered n = 1–11. Remarkably, dianions were found to be the dominant fragment charge state (only comparatively small amounts of monoanions were additionally detected) and these always retained an intact MAu24 metal cluster moiety – i.e. the cleaved/reacted ligands did not significantly carry away any excess charge or metal atoms.
In the present study, we have confirmed the [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− and [PdAu24(C
CR)18]2− and [PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− measurements of ref. 10 and have now also probed the corresponding CID phenomenology of [NiAu24(C
CR)18]2− measurements of ref. 10 and have now also probed the corresponding CID phenomenology of [NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− (see Fig. S3 and S4, ESI†). At intermediate to high collision energies, we find fragments analogous to those observed for M = Pt and Pd, i.e. [NiAu24(C
CR)18]2− (see Fig. S3 and S4, ESI†). At intermediate to high collision energies, we find fragments analogous to those observed for M = Pt and Pd, i.e. [NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]2− and [MAu24(C
CR)18−n]2− and [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR′)(C
CR′)(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)17−n]2−. There is however one interesting difference. Significant ligand oligomer monoanion formation is also seen (for odd n = 5–9: (C
CR)17−n]2−. There is however one interesting difference. Significant ligand oligomer monoanion formation is also seen (for odd n = 5–9: (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)n−; for even n = 4–10: (C
CR)n−; for even n = 4–10: (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)n− plus some [(C
CR)n− plus some [(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)n ± H]−) – already at low collision energies. While trace amounts of (C
CR)n ± H]−) – already at low collision energies. While trace amounts of (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)n− can also be seen upon collisional excitation of PtAu24 and PdAu24 (upon closer inspection), for NiAu24 the polymer intensity is at least two orders of magnitude larger and extends to a remarkably high n > 10. Note, that CID measurements on a Bruker compact ESI-MS platform optimized for the detection of high m/z species indicate that the complementary monoanionic molecular fragments comprise [NiAu24(C
CR)n− can also be seen upon collisional excitation of PtAu24 and PdAu24 (upon closer inspection), for NiAu24 the polymer intensity is at least two orders of magnitude larger and extends to a remarkably high n > 10. Note, that CID measurements on a Bruker compact ESI-MS platform optimized for the detection of high m/z species indicate that the complementary monoanionic molecular fragments comprise [NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]−, reaction (2) (see Fig. S5, ESI†).
CR)18−n]−, reaction (2) (see Fig. S5, ESI†).
[MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2−* → [MAu24(C CR)18]2−* → [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]− + (C CR)18−n]− + (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)n− CR)n− | (2) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)n− signals. In terms of RC
CR)n− signals. In terms of RC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C
C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR and HC
CR and HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR′ loss, NiAu24 behaves qualitatively the same as PdAu24 and PtAu24. However, the relative intensity of the minor HC
CR′ loss, NiAu24 behaves qualitatively the same as PdAu24 and PtAu24. However, the relative intensity of the minor HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR loss channel is higher for Ni than for Pd and Pt.
CR loss channel is higher for Ni than for Pd and Pt.
Fig. S6 (top) (ESI†) shows breakdown curves and fragment yields (on a logarithmic intensity scale) for all [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]2− as well as [MAu24(C
CR)18−n]2− as well as [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR′)(C
CR′)(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)17−n]2−versus collision energy (strictly speaking the applied collision voltage). Fig. S6 (bottom) (ESI†) shows the corresponding ligand oligomer monoanion yields in the case of NiAu24. E50 values (50% survival yield) are 68, 77 and 84 V for the breakdown curves of NiAu24, PdAu24 and PtAu24, respectively, i.e. M = Ni is the most labile of the three [MAu24(C
CR)17−n]2−versus collision energy (strictly speaking the applied collision voltage). Fig. S6 (bottom) (ESI†) shows the corresponding ligand oligomer monoanion yields in the case of NiAu24. E50 values (50% survival yield) are 68, 77 and 84 V for the breakdown curves of NiAu24, PdAu24 and PtAu24, respectively, i.e. M = Ni is the most labile of the three [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− species studied. Interestingly, the [MAu24(C
CR)18]2− species studied. Interestingly, the [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]2− fragment yields for n = 2 and 4 (and also n = 6 for Pd and Ni) show roughly the same dependence on increasing collision energy. Only after n = 6 is the collision energy required for further fragmentation observed to clearly increase (roughly linearly) with n. Perhaps some elimination of small neutral oligomers (n = 4) also occurs in the early fragmentation stages.
CR)18−n]2− fragment yields for n = 2 and 4 (and also n = 6 for Pd and Ni) show roughly the same dependence on increasing collision energy. Only after n = 6 is the collision energy required for further fragmentation observed to clearly increase (roughly linearly) with n. Perhaps some elimination of small neutral oligomers (n = 4) also occurs in the early fragmentation stages.
3.3 Structures of collisionally excited precursor and fragment ions
Additional cIMS measurements were carried out to further investigate the collisionally activated reactions described above, concentrating in particular on the reaction (1) cascade to form [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]2− which is the primary dissociation process under typical experimental conditions.
CR)18−n]2− which is the primary dissociation process under typical experimental conditions.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e002.gif) CR)18]2−*.
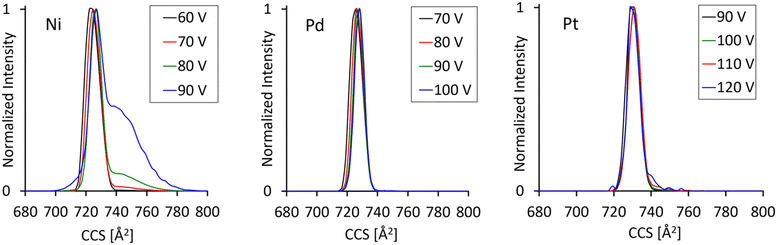
Fig. 3 compares arrival time distributions for all three MAu24 precursor dianions previously subjected to different levels of collisional excitation as achieved by injecting the ions into the ion trap upstream from the cIM at variable collision voltages from 60 to 100 V. As seen in the breakdown curves discussed previously, this energy range is associated with the onset of extensive fragmentation leading to a drop of precursor dianion intensity by several orders of magnitude. Nevertheless, the dynamic range of the machine is high enough to resolve a collision energy dependent change in the ATD's of the residual, vibrationally excited NiAu24. Whereas the measurements for M = Pd and Pt show only one, symmetric, feature throughout the injection voltage range probed, the ATD for M = Ni develops an initially weak but then clearly visible shoulder extending to longer arrival times. This feature, indicating the presence of at least one additional significantly larger structural isomer at the m/z being probed, becomes dominant as the collision energy is raised further – see Fig. 3. This special behavior of NiAu24 is likely related to its enhanced lability towards ligand oligomer anion loss as already mentioned in Section 3.2. We are exploring this further and will report in detail in a future study.51
CR)18]2−*.
Fig. 3 compares arrival time distributions for all three MAu24 precursor dianions previously subjected to different levels of collisional excitation as achieved by injecting the ions into the ion trap upstream from the cIM at variable collision voltages from 60 to 100 V. As seen in the breakdown curves discussed previously, this energy range is associated with the onset of extensive fragmentation leading to a drop of precursor dianion intensity by several orders of magnitude. Nevertheless, the dynamic range of the machine is high enough to resolve a collision energy dependent change in the ATD's of the residual, vibrationally excited NiAu24. Whereas the measurements for M = Pd and Pt show only one, symmetric, feature throughout the injection voltage range probed, the ATD for M = Ni develops an initially weak but then clearly visible shoulder extending to longer arrival times. This feature, indicating the presence of at least one additional significantly larger structural isomer at the m/z being probed, becomes dominant as the collision energy is raised further – see Fig. 3. This special behavior of NiAu24 is likely related to its enhanced lability towards ligand oligomer anion loss as already mentioned in Section 3.2. We are exploring this further and will report in detail in a future study.51
It is interesting to note ref. 52 in this context. The authors of the latter study observed collision induced isomerization of [Au25(2-PET)18]±, PET = phenylethyl thiolate, to form an isomer with a ca. 28% larger CCS than the initial gas phase structure. This was interpreted in terms of a concerted rearrangement of the entire cluster, which has an icosahedral core/shell + staple topology analogous to that of [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2−. Ab initio molecular dynamics (AIMD) simulations suggested that collision induced rearrangement of [Au25(2-PET)18]± begins with a correlated rotation of the triangular faces of the icosahedral shell about the central gold atom. As the staples remain attached to the same gold atoms in this internally rotating shell, their constituent PET ligands – much like sails – are torqued and “unfurled” resulting in an isomer with a significantly larger CCS. In contrast to the case of [Au25(2-PET)18]±, we interpret our observation of isomerization at high collisional excitation of [NiAu24(C
CR)18]2−. Ab initio molecular dynamics (AIMD) simulations suggested that collision induced rearrangement of [Au25(2-PET)18]± begins with a correlated rotation of the triangular faces of the icosahedral shell about the central gold atom. As the staples remain attached to the same gold atoms in this internally rotating shell, their constituent PET ligands – much like sails – are torqued and “unfurled” resulting in an isomer with a significantly larger CCS. In contrast to the case of [Au25(2-PET)18]±, we interpret our observation of isomerization at high collisional excitation of [NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− as due to reactions which change bond connectivity in the ligands. This seems plausible as extensive loss of neutral diynes and ligand polymer anions (both involving Au-bond breaking) occurs in parallel.
CR)18]2− as due to reactions which change bond connectivity in the ligands. This seems plausible as extensive loss of neutral diynes and ligand polymer anions (both involving Au-bond breaking) occurs in parallel.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e002.gif) CR)18−n]2− fragments.
CR)18−n]2− fragments.
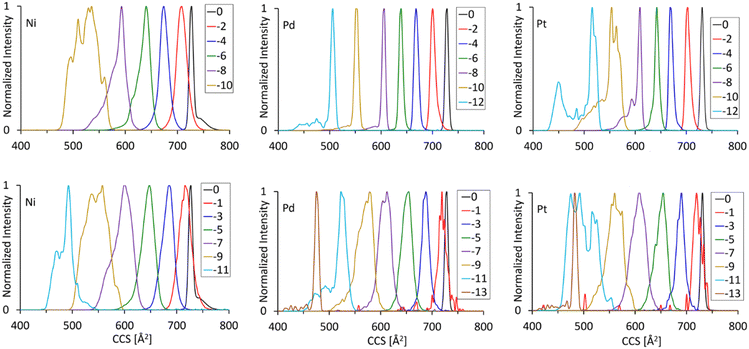
3.3.2.1 Single cycle separations. We performed single cycle separations to obtain a phenomenological overview of the structural changes associated with increasing fragmentation degree, n = 1–12 (for all [MAu24(C
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]2−, resp. [MAu24(C
CR)18−n]2−, resp. [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR′)(C
CR′)(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)17−n]2−). The corresponding ATD's, plotted on a twCCSN2 scale, are presented in Fig. 4.
CR)17−n]2−). The corresponding ATD's, plotted on a twCCSN2 scale, are presented in Fig. 4.
At the comparatively low resolution accessible by a single separation cycle, the collision cross sections decrease essentially monotonically with the number of ligands lost. Note again, that odd numbered n indicates the additional loss of one HC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR unit. Fig. 5 plots this trend (twCCSN2 against n, the number of ligands lost) for M = Pt. The experimental data for the other two M′s show a similar monotonic CCS dropoff with n (see Fig. S8, ESI†).
CR unit. Fig. 5 plots this trend (twCCSN2 against n, the number of ligands lost) for M = Pt. The experimental data for the other two M′s show a similar monotonic CCS dropoff with n (see Fig. S8, ESI†).
Remarkably (and in contrast to the isomerization of the [NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]2− precursor dianion discussed above), ATDmax values of specific [MAu24(C
CR)18−n]2− precursor dianion discussed above), ATDmax values of specific [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]2− fragments do not change significantly with collision energy – apart from the fact that higher collision energies are required for on average more extensive fragmentation. This suggests that an evaporative ensemble is being probed to first order.53 Nevertheless, ATD halfwidths are already visibly n and M dependent. In particular, the even numbered fragments appear on average to have significantly narrower ATD's than the odd numbered ones. Additionally, some ATD's show a reproducible (fine) structure, suggesting that the fragmentation cascade can form multiple coexisting isomers.
CR)18−n]2− fragments do not change significantly with collision energy – apart from the fact that higher collision energies are required for on average more extensive fragmentation. This suggests that an evaporative ensemble is being probed to first order.53 Nevertheless, ATD halfwidths are already visibly n and M dependent. In particular, the even numbered fragments appear on average to have significantly narrower ATD's than the odd numbered ones. Additionally, some ATD's show a reproducible (fine) structure, suggesting that the fragmentation cascade can form multiple coexisting isomers.
We attempted to model the global trend shown in Fig. 5 by sequentially removing the requisite numbers of ligands from the molecular structure (see also Fig. S9, ESI†). For this we used the converged DFT (m4 grid, PBE, def2-SVP, Disp3bj) structure of [PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− as a starting point and generated the correspondingly defected structures by removing ligand pairs (always ligand type A and B in Scheme 1) in an otherwise random sequence in the case of even n and one additional arbitrarily chosen type A ligand in case of odd n. With these unrelaxed “defected” structures we then performed single point calculations at the GFN1 xTB level to generate Mulliken partial charges necessary for the trajectory method simulations of the collision cross sections. We used Pd as GFN1 xTB shows convergency problems with Pt in some cases. Considering that theoCCSN2 of [PdAu24(C
CR)18]2− as a starting point and generated the correspondingly defected structures by removing ligand pairs (always ligand type A and B in Scheme 1) in an otherwise random sequence in the case of even n and one additional arbitrarily chosen type A ligand in case of odd n. With these unrelaxed “defected” structures we then performed single point calculations at the GFN1 xTB level to generate Mulliken partial charges necessary for the trajectory method simulations of the collision cross sections. We used Pd as GFN1 xTB shows convergency problems with Pt in some cases. Considering that theoCCSN2 of [PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− and [PtAu24(C
CR)18]2− and [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− agree within the error of the trajectory calculation and no geometry optimization of the fragment is performed, this approach seems reasonable. Fig. 5 shows the resulting theoCCSN2 predictions and schematics of the defect structures for n = 0–14. Apparently, the assumption of statistical ligand pair loss without further structural relaxation describes the global experimental observation – after one separation cycle – already surprisingly well.
CR)18]2− agree within the error of the trajectory calculation and no geometry optimization of the fragment is performed, this approach seems reasonable. Fig. 5 shows the resulting theoCCSN2 predictions and schematics of the defect structures for n = 0–14. Apparently, the assumption of statistical ligand pair loss without further structural relaxation describes the global experimental observation – after one separation cycle – already surprisingly well.
3.3.2.2 Multiple separation cycles. Additional cycles of separation can be used to explore the fragment isomer space in more detail. For example, one might question whether alkyne/diyne loss is in fact always sequential, completely statistical or whether sequential eliminations are to some degree spatially correlated. Generally, the numbers, relative intensities and twCCSN2 values of the isomers resolvable by a given number of separation cycles depend strongly on M and n. Selected measurements are shown in Fig. S7 (ESI†). Fig. 6 shows an extreme example for the n = 10 fragment of PtAu24, i.e. [PtAu24(C
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)8]2−. After six separation cycles, four fragment isomers can be (partially) resolved, superposed on a broad shoulder to shorter arrival times. From smallest to largest, these isomers differ in twCCSN2 by ca. 3%. They are formed roughly in the intensity ratio 5
CR)8]2−. After six separation cycles, four fragment isomers can be (partially) resolved, superposed on a broad shoulder to shorter arrival times. From smallest to largest, these isomers differ in twCCSN2 by ca. 3%. They are formed roughly in the intensity ratio 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3:2
3:2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
 | ||
Fig. 6 Example of resolved isomers formed upon CID of [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− for the n = 10 fragment, i.e. [PtAu24(C CR)18]2− for the n = 10 fragment, i.e. [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)8]2− after six cIM separation cycles. The vertical lines refer to theoCCSN2 values calculated for possible isomers as listed in Table S2 (ESI†). The red bars highlight largest, smallest and two intermediate sized structural models for which we show the structure. The corresponding defect structures are shown from the front and back side (see the caption of Fig. 5 for details on the schematic representation). Other defect model structures are shown in Fig. S10 (ESI†). CR)8]2− after six cIM separation cycles. The vertical lines refer to theoCCSN2 values calculated for possible isomers as listed in Table S2 (ESI†). The red bars highlight largest, smallest and two intermediate sized structural models for which we show the structure. The corresponding defect structures are shown from the front and back side (see the caption of Fig. 5 for details on the schematic representation). Other defect model structures are shown in Fig. S10 (ESI†). | ||
To put this observation into perspective it is important to remember that there are initially six Au2(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)3 “staples” (each with an Au2 unit and three C
CR)3 “staples” (each with an Au2 unit and three C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR ligands). After loss of 10 ligands and assuming no structural relaxation occurs, multiple [PtAu24(C
CR ligands). After loss of 10 ligands and assuming no structural relaxation occurs, multiple [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)8]2− isomer types can result which are distinguishable by the partitioning of their 8 remaining ligands over the cluster “surface” (in principle Au2 units can host 3, 2, 1 or 0 remaining ligands subject to the restriction that there are only 8 ligands left overall). Table S2 (ESI†) lists examples of the seven possible isomer types ordered according to number of ligands left on each of the six staples. Obviously, there are a large number of different combinatorial possibilities for each isomer type depending on whether ligand loss is completely random or somehow spatially correlated (the Au2(C
CR)8]2− isomer types can result which are distinguishable by the partitioning of their 8 remaining ligands over the cluster “surface” (in principle Au2 units can host 3, 2, 1 or 0 remaining ligands subject to the restriction that there are only 8 ligands left overall). Table S2 (ESI†) lists examples of the seven possible isomer types ordered according to number of ligands left on each of the six staples. Obviously, there are a large number of different combinatorial possibilities for each isomer type depending on whether ligand loss is completely random or somehow spatially correlated (the Au2(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)3 staples themselves are initially indistinguishable due to molecular symmetry). Many of these combinatorial possibilities will have distinguishable patches of ligand-free surface regions and corresponding CCS values. It goes beyond the scope of this study to consider all combinatorial possibilities but it is nevertheless of interest to compare the experimentally resolved CCS spread to the predictions for several different isomers resulting from various assumed fragmentation sequences – ranging from fully correlated in space (i.e. a sequence of A + B or B + C ligand losses (see Scheme 1) to form diynes progressing from staple to adjacent staple) to purely statistical (10 of 18 monomers are randomly removed regardless of which staple/position they originate from).
CR)3 staples themselves are initially indistinguishable due to molecular symmetry). Many of these combinatorial possibilities will have distinguishable patches of ligand-free surface regions and corresponding CCS values. It goes beyond the scope of this study to consider all combinatorial possibilities but it is nevertheless of interest to compare the experimentally resolved CCS spread to the predictions for several different isomers resulting from various assumed fragmentation sequences – ranging from fully correlated in space (i.e. a sequence of A + B or B + C ligand losses (see Scheme 1) to form diynes progressing from staple to adjacent staple) to purely statistical (10 of 18 monomers are randomly removed regardless of which staple/position they originate from).
For this, we calculated theoCCSN2 for nine possible [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)8]2− isomers generated by removing either three, two, one or zero C
CR)8]2− isomers generated by removing either three, two, one or zero C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR ligands from the staples – otherwise with the same method as already described above. Fig. 6 presents the theoCCSN2 values of the nine calculated isomers (see also Table S2 and Fig. S10 which shows schematics of the corresponding structures, ESI†). The smallest theoCCSN2 is found for isomer 9 (496.5 Å2) in which the ligands have been removed from one side of the cluster only in a non-statistical pattern. The largest isomer (isomer 1, 606.6 Å2) is obtained when 2 of the staples stay complete, one ligand is removed from a third staple and all ligands are removed from the remaining three staples. Doing the same, but with a spatially more correlated loss sequence, results in a theoCCSN2 of 551.3 Å2, i.e. 9% smaller (isomer 8). Interestingly, the experimental [PdAu24(C
CR ligands from the staples – otherwise with the same method as already described above. Fig. 6 presents the theoCCSN2 values of the nine calculated isomers (see also Table S2 and Fig. S10 which shows schematics of the corresponding structures, ESI†). The smallest theoCCSN2 is found for isomer 9 (496.5 Å2) in which the ligands have been removed from one side of the cluster only in a non-statistical pattern. The largest isomer (isomer 1, 606.6 Å2) is obtained when 2 of the staples stay complete, one ligand is removed from a third staple and all ligands are removed from the remaining three staples. Doing the same, but with a spatially more correlated loss sequence, results in a theoCCSN2 of 551.3 Å2, i.e. 9% smaller (isomer 8). Interestingly, the experimental [PdAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)8]2− isomer spread lies well between the limits of isomer 1 and isomer 9. Overall, it seems that the best agreement with the experiment is obtained when radical formation is minimized. In particular isomer 4 (five adjacent pairs of ligands are lost; 553.4 Å2) and isomer 7 (4 adjacent pairs and 2 singles are lost; 555.8 Å2) have theoCCSN2 which are very close to the most intense isomer found in the experiment.
CR)8]2− isomer spread lies well between the limits of isomer 1 and isomer 9. Overall, it seems that the best agreement with the experiment is obtained when radical formation is minimized. In particular isomer 4 (five adjacent pairs of ligands are lost; 553.4 Å2) and isomer 7 (4 adjacent pairs and 2 singles are lost; 555.8 Å2) have theoCCSN2 which are very close to the most intense isomer found in the experiment.
To summarize: we can rule out extensive fragmentation to form highly anisotropic [PtAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)8]2− structures. Furthermore, the observed isomer spread is inconsistent with random monomer loss and instead points to mainly diyne evolution by way of loss of pairs of adjacent ligands on a given staple. However, it remains unclear whether in the fragmentation sequence the next diyne loss is spatially correlated to the previous one. Further insight, also into relative isomer intensities and into the behavior at intermediate fragment sizes, requires much more extensive modelling which will be the subject of a future study.
CR)8]2− structures. Furthermore, the observed isomer spread is inconsistent with random monomer loss and instead points to mainly diyne evolution by way of loss of pairs of adjacent ligands on a given staple. However, it remains unclear whether in the fragmentation sequence the next diyne loss is spatially correlated to the previous one. Further insight, also into relative isomer intensities and into the behavior at intermediate fragment sizes, requires much more extensive modelling which will be the subject of a future study.
Summary and conclusions
Collision induced dissociation, high resolution cyclic ion mobility mass spectrometry and trajectory simulations based on quantum chemical calculations were used to compare the structures of isolated [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− (M = Ni, Pd and Pt) and of the associated fragment ions. The resolution of cIMS is high enough to allow differentiation of the three different transition metal doped precursor dianions on the basis of purely their collision cross sections. The size trend observed for the gas phase dianions is consistent with X-ray crystallography which shows that in the ionic solid (held together by PPh4+ countercations), the [MAu24(C
CR)18]2− (M = Ni, Pd and Pt) and of the associated fragment ions. The resolution of cIMS is high enough to allow differentiation of the three different transition metal doped precursor dianions on the basis of purely their collision cross sections. The size trend observed for the gas phase dianions is consistent with X-ray crystallography which shows that in the ionic solid (held together by PPh4+ countercations), the [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− molecules have a common geometry but slightly M-dependent M–Au bond distances.
CR)18]2− molecules have a common geometry but slightly M-dependent M–Au bond distances.
All three [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− dianions fragment to [MAu24(C
CR)18]2− dianions fragment to [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18−n]2− species – with even numbered n losses strongly favored. This and the dependence of fragmentation degree on collision energy argues for primarily sequential diyne loss. Up to 12 ligands, i.e. formally 6 RC
CR)18−n]2− species – with even numbered n losses strongly favored. This and the dependence of fragmentation degree on collision energy argues for primarily sequential diyne loss. Up to 12 ligands, i.e. formally 6 RC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C–C
C–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR diyne moieties can be eliminated in this fashion. Cyclic IMS measurements show that the resulting [MAu24(C
CR diyne moieties can be eliminated in this fashion. Cyclic IMS measurements show that the resulting [MAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18–n]2− isomer distributions are strongly n- and M-dependent. Preliminary analysis is consistent with an underlying process involving elimination from staples of pairs of neighbouring ligands. Future MD simulations will be required to help establish whether sequential ligand/diyne eliminations continue in a spatially correlated fashion.
CR)18–n]2− isomer distributions are strongly n- and M-dependent. Preliminary analysis is consistent with an underlying process involving elimination from staples of pairs of neighbouring ligands. Future MD simulations will be required to help establish whether sequential ligand/diyne eliminations continue in a spatially correlated fashion.
[NiAu24(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− also fragments significantly by loss of ligand oligomers, (C
CR)18]2− also fragments significantly by loss of ligand oligomers, (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)n− with n ranging up to 10. In parallel, it can undergo measurable isomerization to generate isobaric species with significantly larger collision cross sections (a process not observed for M = Pd and Pt). We will report further details in a future publication.
CR)n− with n ranging up to 10. In parallel, it can undergo measurable isomerization to generate isobaric species with significantly larger collision cross sections (a process not observed for M = Pd and Pt). We will report further details in a future publication.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
MK acknowledges support of this work by DFG under CRC 1441 “TrackAct”, project A2 and CRC 1573 “4f-for-future” projects C1 and C3. Additionally, MK and PW are grateful to KIT, Land B.-W. and DFG for the funding of a Waters Cyclic IMS system under Art. 91b GG without which this study would not have been possible. TT thanks JST, CREST (Grant No. JPMJCR20B2) for financial support of this work. SI acknowledges the financial support by JSPS KAKENHI (JP21J20631).References
- J. J. Zhao, Q. Y. Du, S. Zhou and V. Kumar, Endohedrally Doped Cage Clusters, Chem. Rev., 2020, 120(17), 9021–9163 CrossRef CAS PubMed.
- T. Weiske, D. K. Böhme, J. Hrusak, W. Krätschmer and H. Schwarz, Endohedral Cluster Compounds – Inclusion of Helium within C60+ and C70+ through Collision Experiments, Angew. Chem., Int. Ed. Engl., 1991, 30(7), 884–886 CrossRef.
- H. Shinohara, Endohedral metallofullerenes, Rep. Prog. Phys., 2000, 63(6), 843–892 CrossRef CAS.
- S. Furuse, K. Koyasu, J. Atobe and A. Nakajima, Experimental and theoretical characterization of MSi16−, MGe16−, MSn16−, and MPb16− (M = Ti, Zr, and Hf): The role of cage aromaticity, J. Chem. Phys., 2008, 129(6), 6 CrossRef PubMed.
- L. M. Wang, J. Bai, A. Lechtken, W. Huang, D. Schooss, M. M. Kappes, X. C. Zeng and L. S. Wang, Magnetic doping of the golden cage cluster M@Au16− (M = Fe,Co,Ni), Phys. Rev. B, 2009, 79(3), 4 CrossRef.
- C. A. Fields-Zinna, M. C. Crowe, A. Dass, J. E. F. Weaver and R. W. Murray, Mass Spectrometry of Small Bimetal Monolayer-Protected Clusters, Langmuir, 2009, 25(13), 7704–7710 CrossRef CAS PubMed.
- B. K. Teo, H. Zhang and X. B. Shi, Design, Synthesis, and Structure of the Largest Trimetallic Cluster, [(PH3P)10Au12Ag12PtCl7]Cl – The First Example of a Trimetallic Biicosahedral Supracluster and Its Implication for the Vertex-Sharing Polyicosahedral Growth of the Au/Ag/Pt Ternary Cluster System, J. Am. Chem. Soc., 1993, 115(18), 8489–8490 CrossRef CAS.
- J. J. Bour, R. P. F. Kanters, P. P. J. Schlebos and J. J. Steggerda, Mixed platinum-gold clusters – Synthesis, structure and properties of PtAu8(PPh3)8(NO3)2, Recl. Trav. Chim. Pays-Bas-J. Roy. Neth. Chem. Soc, 1988, 107(3), 211–215 CrossRef CAS.
- T. Kawawaki, Y. Imai, D. Suzuki, S. Kato, I. Kobayashi, T. Suzuki, R. Kaneko, S. Hossain and Y. Negishi, Atomically Precise Alloy Nanoclusters, Chem. – Eur. J., 2020, 26(69), 16150–16193 CrossRef CAS PubMed.
- S. Ito, K. Koyasu, S. Takano and T. Tsukuda, Collision-Induced Reductive Elimination of 1,3-Diynes from [MAu24(C
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CR)18]2− (M = Pd, Pt) Yielding Clusters of Superatoms, J. Phys. Chem. C, 2020, 124(35), 19119–19125 CrossRef CAS.
CR)18]2− (M = Pd, Pt) Yielding Clusters of Superatoms, J. Phys. Chem. C, 2020, 124(35), 19119–19125 CrossRef CAS. - S. Takano, S. Ito and T. Tsukuda, Efficient and Selective Conversion of Phosphine-Protected (MAu8)2+ (M = Pd, Pt) Superatoms to Thiolate-Protected (MAu12)6+ or Alkynyl-Protected (MAu12)4+ Superatoms via Hydride Doping, J. Am. Chem. Soc., 2019, 141(40), 15994–16002 CrossRef CAS PubMed.
- S. Takano, E. Ito, T. Nakamura and T. Tsukuda, Effect of Group-10 Element M (Ni, Pd, Pt) on Electronic Structure of Icosahedral M@Au12 Cores of MAu24L18 (L = Alkynyl, Thiolate), J. Phys. Chem. C, 2023, 7 Search PubMed.
- Y. Negishi, W. Kurashige, Y. Niihori, T. Iwasa and K. Nobusada, Isolation, structure, and stability of a dodecanethiolate-protected Pd1Au24 cluster, Phys. Chem. Chem. Phys., 2010, 12(23), 6219–6225 RSC.
- M. A. Tofanelli, T. W. Ni, B. D. Phillips and C. J. Ackerson, Crystal Structure of the PdAu24(SR)180 Superatom, Inorg. Chem., 2016, 55(3), 999–1001 CrossRef CAS PubMed.
- H. F. Qian, D. E. Jiang, G. Li, C. Gayathri, A. Das, R. R. Gil and R. C. Jin, Monoplatinum Doping of Gold Nanoclusters and Catalytic Application, J. Am. Chem. Soc., 2012, 134(39), 16159–16162 CrossRef CAS.
- S. B. Tian, L. W. Liao, J. Y. Yuan, C. H. Yao, J. S. Chen, J. L. Yang and Z. K. Wu, Structures and magnetism of mono-palladium and mono-platinum doped Au25(PET)18 nanoclusters, Chem. Commun., 2016, 52(64), 9873–9876 RSC.
- K. Kwak, Q. Tang, M. Kim, D. E. Jiang and D. Lee, Interconversion between Superatomic 6-Electron and 8-Electron Configurations of M@Au24(SR)18 Clusters (M = Pd, Pt), J. Am. Chem. Soc., 2015, 137(33), 10833–10840 CrossRef CAS PubMed.
- M. M. Kappes, R. W. Kunz and E. Schumacher, Production of large Sodium Clusters (Nax, x ≤ 65) by Seeded Beam Expansions, Chem. Phys. Lett., 1982, 91(6), 413–418 CrossRef CAS.
- W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Electronic Shell Structure and Abundances of Sodium Clusters, Phys. Rev. Lett., 1984, 52(24), 2141–2143 CrossRef CAS.
- M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Gronbeck and H. Häkkinen, A unified view of ligand-protected gold clusters as superatom complexes, Proc. Natl. Acad. Sci. U. S. A., 2008, 105(27), 9157–9162 CrossRef CAS PubMed.
- S. B. Zhang, M. L. Cohen and M. Y. Chou, Electronic shell structure of simple metal heteroclusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36(6), 3455–3458 CrossRef CAS PubMed.
- M. M. Kappes, P. Radi, M. Schar and E. Schumacher, Probes for electronic and geometrical shell structure effects in alkali-metal clusters – photoionization measurements on KxLi, KxMg and KxZn (x ≤ 25), Chem. Phys. Lett., 1985, 119(1), 11–16 CrossRef CAS.
- C. Baladron and J. A. Alonso, Stability and Magic Numbers of Hetero-Atomic Clusters of Simple Metals, Physica B, 1988, 154(1), 73–81 CrossRef CAS.
- E. Janssens, S. Neukermans and P. Lievens, Shells of electrons in metal doped simple metal clusters, Curr. Opin. Solid State Mat. Sci., 2004, 8(3–4), 185–193 CrossRef CAS.
- B. C. Bohrer, S. I. Mererbloom, S. L. Koeniger, A. E. Hilderbrand and D. E. Clemmer, Biomolecule Analysis by Ion Mobility Spectrometry, Annu. Rev. Anal. Chem., 2008, 1, 293–327 CrossRef CAS PubMed.
- B. J. Gregory and C. K. Ingold, Mechanism of Electrophilic Substitution at a Saturated Carbon Atom. Part XI. Bimolecular and Unimolecular Substitution of Mercury for Gold in Alkylgold Complexes, J. Chem. Soc. B, 1969, 276 RSC.
- M. C. Brandys, M. C. Jennings and R. J. Puddephatt, Luminescent gold(I) macrocycles with diphosphine and 4,4′-bipyridyl ligands, J. Chem. Soc., Dalton Trans., 2000, 24, 4601–4606 RSC.
- S. Takano, H. Hirai, S. Muramatsu and T. Tsukuda, Hydride-Mediated Controlled Growth of a Bimetallic (Pd@Au8)2+ Superatom to a Hydride-Doped (HPd@Au10)3+ Superatom, J. Am. Chem. Soc., 2018, 140(39), 12314–12317 CrossRef CAS PubMed.
- K. Giles, J. Ujma, J. Wildgoose, S. Pringle, K. Richardson, D. Langridge and M. Green, A Cyclic Ion Mobility-Mass Spectrometry System, Anal. Chem., 2019, 91(13), 8564–8573 CrossRef CAS PubMed.
- E. A. M. Mason and E. W. McDaniel, Transport Properties of Ions in Gases, Wiley, New York, Chichester, Brisbane, Toronto, Singapore, 1988 Search PubMed.
- P. Weis, L. Fercic and M. Kappes, to be published.
- C. Larriba and C. J. Hogan, Free molecular collision cross section calculation methods for nanoparticles and complex ions with energy accommodation, J. Comput. Phys., 2013, 251, 344–363 CrossRef CAS.
- C. Larriba-Andaluz and C. J. Hogan, Collision cross section calculations for polyatomic ions considering rotating diatomic/linear gas molecules, J. Chem. Phys., 2014, 141(19), 9 CrossRef PubMed.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Electronic-Structure calculations on Workstation Computers – The Program System Turbomole, Chem. Phys. Lett., 1989, 162(3), 165–169 CrossRef CAS.
- P. A. M. Dirac, The quantum theory of the electron, Proc. R. Soc. London, Ser. A, 1928, 117(778), 610–624 Search PubMed.
- J. C. Slater, A simplification of the Hartree-Fock method, Phys. Rev., 1951, 81(3), 385 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple (vol 77, pg 3865, 1996), Phys. Rev. Lett., 1997, 78(7), 1396 CrossRef CAS.
- J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(23), 13244 CrossRef PubMed.
- A. Hellweg and D. Rappoport, Development of new auxiliary basis functions of the Karlsruhe segmented contracted basis sets including diffuse basis functions (def2-SVPD, def2-TZVPPD, and def2-QVPPD) for RI-MP2 and RI-CC calculations, Phys. Chem. Chem. Phys., 2015, 17(2), 1010–1017 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu, J. Chem. Phys., 2010, 132(15), 19 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465 CrossRef CAS PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Extended tight-binding quantum chemistry methods, Wiley Interdiscip. Rev.-Comput. Mol. Sci., 2021, 11(2), 49 Search PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86), J. Chem. Theory Comput., 2017, 13(5), 1989–2009 CrossRef CAS PubMed.
- S. Ito, K. Koyasu, S. Takano and T. Tsukuda, Critical Role of CF3 Groups in the Electronic Stabilization of [PdAu24(C
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C6H3(CF3)2)18]2− as Revealed by Gas-Phase Anion Photoelectron Spectroscopy, J. Phys. Chem. Lett., 2021, 12(42), 10417–10421 CrossRef CAS PubMed.
C6H3(CF3)2)18]2− as Revealed by Gas-Phase Anion Photoelectron Spectroscopy, J. Phys. Chem. Lett., 2021, 12(42), 10417–10421 CrossRef CAS PubMed. - Jmol: an open-source Java viewer for chemical structures in 3D, https://www.jmol.org/.
- Calculate Root-mean-square deviation (RMSD) of Two Molecules Using Rotation, Github, https://github.com/charnley/rmsd, 1.5.1.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38 CrossRef CAS PubMed.
- Z. D. Xu, T. Nakane and H. Shinohara, Production and isolation of Ca@C-82 (I-IV) and Ca@C-84 (I,II) metallofullerenes, J. Am. Chem. Soc., 1996, 118(45), 11309–11310 CrossRef CAS.
- A. Baksi, E. K. Schneider, P. Weis, I. Chakraborty, O. Fuhr, S. Lebedkin, W. J. Parak and M. M. Kappes, Linear Size Contraction of Ligand Protected Ag-29 Clusters by Substituting Ag with Cu, ACS Nano, 2020, 14(11), 15064–15070 CrossRef CAS PubMed.
- Y. Zeng, S. Havenridge, M. Gharib, A. Baksi, K. Weerawardene, A. R. Ziefuss, C. Strelow, C. Rehbock, A. Mews, S. Barcikowski, M. M. Kappes, W. J. Parak, C. M. Aikens and I. Chakraborty, Impact of Ligands on Structural and Optical Properties of Ag29 Nanoclusters, J. Am. Chem. Soc., 2021, 143(25), 9405–9414 CrossRef CAS PubMed.
- F. Hennrich, S. Ito, P. Weis, M. Neumaier, S. Takano, T. Tsukuda and M. M. Kappes, to be published.
- E. Kalenius, S. Malola, M. F. Matus, R. Kazan, T. Bürgi and H. Häkkinen, Experimental Confirmation of a Topological Isomer of the Ubiquitous Au25(SR)18 Cluster in the Gas Phase, J. Am. Chem. Soc., 2021, 143(3), 1273–1277 CrossRef CAS PubMed.
- C. E. Klots, Temperatures of Evaporating Clusters, Nature, 1987, 327(6119), 222–223 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06192b |
| This journal is © the Owner Societies 2024 |