 Open Access Article
Open Access ArticleInsights into ultrafast decay dynamics of electronically excited pyridine-N-oxide†
Baihui
Feng
abc,
Wenping
Wu
ac,
Shuaikang
Yang
ad,
Zhigang
He
a,
Benjie
Fang
b,
Dongyuan
Yang
 *a,
Guorong
Wu
*a,
Guorong
Wu
 *a and
Xueming
Yang
*a and
Xueming
Yang
 ae
ae
aState Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, 457 Zhongshan Road, Dalian, Liaoning 116023, China. E-mail: yangdy@dicp.ac.cn; wugr@dicp.ac.cn
bKey Laboratory of Chemical Lasers, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, 457 Zhongshan Road, Dalian, Liaoning 116023, China
cUniversity of Chinese Academy of Sciences, Beijing 100049, China
dDepartment of Chemical Physics, University of Science and Technology of China, Hefei, Anhui 230026, China
eDepartment of Chemistry, College of Science, Southern University of Science and Technology, Shenzhen 518055, China
First published on 12th February 2024
Abstract
The ultrafast decay dynamics of pyridine-N-oxide upon excitation in the near-ultraviolet range of 340.2–217.6 nm is investigated using the femtosecond time-resolved photoelectron imaging technique. The time-resolved photoelectron spectra and photoelectron angular distributions at all pump wavelengths are carefully analyzed and the following view is derived: at the longest pump wavelengths (340.2 and 325.6 nm), pyridine-N-oxide is excited to the S1(1ππ*) state with different vibrational levels. The depopulation rate of the S1 state shows a marked dependence on vibrational energy and mode, and the lifetime is in the range of 1.4–160 ps. At 289.8 and 280.5 nm, both the second 1ππ* state and the S1 state are initially prepared. The former has an extremely short lifetime of ∼60 fs, which indicates that the ultrafast deactivation pathway such as a rapid internal conversion to one close-lying state is its dominant decay channel, while the latter is at high levels of vibrational excitation and decays within the range of 380–520 fs. At the shortest pump wavelengths (227.3 and 217.6 nm), another excited state of Rydberg character is mostly excited. We assign this state to the 3s Rydberg state which has a lifetime of 0.55–2.2 ps. This study provides a comprehensive picture of the ultrafast excited-state decay dynamics of the photoexcited pyridine-N-oxide molecule.
I. Introduction
The photochemistry and photophysics of small aromatic heterocyclic molecules have become a hot topic over the past few decades. This offers an ideal prototype for understanding photoinduced processes of complex biomolecules found in nature, such as aromatic amino acids1 and nucleobases.2–7 Pyridine is one of the six-membered heteroaromatic molecules containing the nitrogen heteroatom. The ultraviolet (UV) photostability of it8–15 and its substituted derivatives8,16–21 has attracted a great deal of interest from many theoretical and experimental chemists since the pyridine ring occurs in a series of important organic compounds. In recent years, we have investigated the ultrafast and radiationless electronic excited state decay dynamics of several substituted pyridines, such as 2-hydroxypyridine,22 2-aminopyridine and 3-aminopyridine,23 highlighting that the substitution effects are sensitive to the different substitution positions. In this article, we continue our efforts on this same topic and focus solely on one specific substituted pyridine, namely pyridine-N-oxide (hereafter termed simply PyNO), with special interest in exploring the pump wavelength-dependent decay dynamics of electronically excited PyNO.The near UV absorption spectrum of PyNO in the gas phase has been studied by numerous researchers since the 1950s and 1960s24,25 and three electronic transitions (the first, second and third transitions) have been widely reported for this molecule. It has been evidenced that the first 1B2 ← 1A1 electronic transition is π* ← π rather than π* ← n in the case of PyNO.26–31 Later on, the vibrational structure of this electronic transition to the first singlet excited state of PyNO has been analyzed.31–33 In these works, the more exact 0-0 band origin of the S1 ← S0 electronic transition was found to be ∼341 nm. The second absorption band with the peak position of around 280 nm has been assigned to the 1A1 ← 1A1 (π* ← π) electronic transition.26,31 The analysis of the vibronic structure of the second electronic transition was performed and the 0-0 transition was suggested to be ∼290 nm.34 The 0–0 band origin of the third electronic transition was measured to be ∼228 nm.35,36 Recently, Palmer et al. performed ab initio configuration interaction computations to calculate both Rydberg and valence state vertical excitation energies and oscillator strengths, which were correlated with the experimentally identified states in their measured photoabsorption spectrum.37
Although there have been a variety of previous spectroscopic studies which focused on the UV or vacuum ultraviolet (VUV) absorption of PyNO, to the best of our knowledge, there has not yet been a direct time-resolved study on the excited-state dynamics of the isolated PyNO molecule. Herein we present a femtosecond time-resolved photoelectron imaging (fs-TRPEI) study of the ultrafast decay dynamics of electronically excited PyNO in a broad UV pump wavelength range of 340.2–217.6 nm. The excitation of PyNO at each pump wavelength is successfully assigned to specific singlet electronic excited state(s) based on the characterizations of the time-resolved photoelectron spectroscopy (TRPES) spectra and the photoelectron angular distributions (PADs). Our assignments are also strongly supported by the previous assignments of the four lowest absorption bands of the absorption spectrum and calculations of the adiabatic singlet excited state structures and energies.37 In addition, the clear pump wavelength dependence of the decay dynamics of photoexcited PyNO is analyzed and discussed in detail.
II. Experimental section
The fs-TRPEI experiment was carried out on a velocity map imaging (VMI) spectrometer38 and the experimental methods have been described in our earlier publications.39–42 Here, only a brief description of the key features will be given. A solid sample of PyNO was purchased commercially with a purity of ≥97% and used directly without further purification. The PyNO sample was heated to about 80–90 °C and mixed with 2–3 bar of helium carrier gas and expanded supersonically into a high vacuum source chamber via a pulsed Even-Lavie valve operating at 1 kHz. The seeded PyNO molecular beam entered into the interaction chamber of the VMI spectrometer through a 1 mm skimmer (Beam Dynamics Inc., Model 1) located 40 mm downstream from the nozzle orifice.The wavelength-tunable UV laser pulses were generated using two commercial optical parametric amplifiers (OPA, Coherent, OPerA Solo), each pumped by a fraction (1.1 mJ per pulse) of the fundamental output of the fully integrated Ti: Sapphire oscillator-regenerative amplifier (Coherent, Libra-HE, 1 kHz, 800 nm). Six different pump wavelengths in the range of 340.2–217.6 nm were employed. The spectra of the pump wavelengths are shown in Fig. S1 (see the ESI†). The wavelength of the probe laser was chosen at 239.2 nm because this wavelength corresponds to a minimum in the absorption spectrum (Fig. 1). The unwanted signals from the probe–pump dynamics processes, which complicate the analysis of the transients around the time-zero, can be minimized. The pump laser pulses, 340.2, 325.6, 289.8 and 280.5 nm (0.4–0.9 μJ per pulse, 249–525 cm−1 at full width at half-maximum (FWHM)), were directly produced from one of the OPAs. For pump laser pulses at 227.3 and 217.6 nm (0.2–0.3 μJ per pulse, 190–232 cm−1), the outputs of this OPA at about 526.6 and 477.3 nm were mixed with a 400 nm laser beam using a 0.1 mm β-barium borate (β-BBO) crystal, respectively, which itself was the doubling of a fraction of the amplifier fundamental 800 nm output using another 0.1 mm β-BBO crystal. The probe laser pulses of 239.2 nm (1.1–1.9 μJ per pulse, ∽161 cm−1 (FWHM)) were obtained by doubling the output of the second OPA at 478.4 nm using a 0.15 mm β-BBO crystal. The two laser pulses were combined collinearly on a dichroic mirror without further compression, and then focused using a calcium fluoride lens (f = 300 mm) into the interaction region of the VMI spectrometer to intersect the seeded PyNO molecular beam. Both the pump and probe pulses were linearly polarized and the polarization direction was parallel to the micro-channel plate (MCP)/phosphor screen detector.
 | ||
| Fig. 1 The UV absorption cross section for PyNO vapor measured at 55 °C as adapted from ref. 37 (the data were obtained from www.uv-vis-spectral-atlas-mainz.org). The inset shows the absorption spectrum in the range of 233–215 nm. | ||
The pump–probe time delay was precisely controlled using a linear translation stage (Newport, M-ILS250HA) located at the upstream of the second OPA. A fine delay step of 50 fs (30 fs for the range of 0–600 fs) was only taken up to 1 ps. From 1 ps beyond, delay steps were larger and larger with a maximum delay of 1 ns employed. The 2D photoelectron images at different time delays were recorded using a computer-controlled camera and transferred to 3D distributions using the pBasex Abel inversion method.43 The time-dependent photoelectron 3D distributions were integrated along the recoiling angle to derive the photoelectron kinetic energy distributions, i.e., TRPES. Additionally, the angular distributions of the emitted photoelectron, i.e., PADs, can be derived by integrating the 3D photoelectron distributions over a desired kinetic energy range and further analyzed in detail.44,45
The two-color nonresonant ionization of NO molecules served to measure the time-zero and cross-correlation (i.e., instrumental response function (IRF)) between the pump and the probe laser pulse. For the pump wavelengths of 289.8 and 280.5 nm, the (1 + 1′) IRF was measured to be 140 ± 15 fs (FWHM) based on the approximation that both pump and probe laser pulses possessed a Gaussian profile. At pump wavelengths of 340.2 and 325.6 nm, the (1 + 1′) two-photon energy is insufficient for the photoionization of NO. Therefore, the value of 140 fs was used as an approximation of the (1 + 1’) cross-correlation at these pump wavelengths and varied in a small range to find the best fit. The (1 + 1′) IRF was 160 ± 15 fs (FWHM) for the pump wavelengths of 227.3 and 217.6 nm. The uncertainties of the time-zero and IRF in their own range also make a contribution to the error bars of the derived time constants during the fits.
III. Results and discussion
UV absorption spectrum of PyNO
The high-resolution absorption spectrum of PyNO in the near UV region has been previously reported37 and is shown in Fig. 1 based on the open-access data from the MPI-Mainz UV/VIS Spectral Atlas.46 The main features of this spectrum are four absorption bands for wavelengths above 200 nm. As mentioned in the Introduction, the first weak absorption band of PyNO corresponding to the π* ← π electronic transition and the valence state, 1B2(3b12a2*),37 is initially prepared starting from the excitation wavelength of ∼341 nm. Overall, the second absorption band is strong and has a peak position of ∼280 nm, while the third one starting from ∼228 nm is much weaker and has a clear vibrational structure. The second broad UV band between 4 and 5 eV (310–248 nm) is probably related to several electronic states and the main contribution is from the excitation of the second 1ππ* state, 1A1(3b14b1*).37 The third band is ascribed to one specific Rydberg state, the 1B1(3b13s) state.37 Furthermore, the fourth absorption band between ∼217 and 200 nm is more complicated. So far, the discussion about this band is rare and its assignment is less clear-cut. The excitation in this shorter wavelength region seems to be associated with several higher-lying valence and Rydberg states. The valence state, which is mainly involved in the fourth absorption band, is suggested to be one of the higher-lying 1ππ* states, the 1A1(3b15b1*) state.35,37The analysis of each TRPES spectrum
In Fig. 2(a) and (b), the TRPES spectra for PyNO at pump wavelengths of 340.2 and 325.6 nm are shown, respectively. The white dash lines indicate the photoelectron kinetic energy limits for two-color (1 + 1′) ionization to the ground state (D0) of the PyNO cation, which are calculated using an experimental adiabatic ionization potential of 8.39 eV.37 The raw photoelectron images at 1 ps pump–probe delay are also presented. By visual inspection, the dynamics becomes shorter as the pump wavelength decreases from 340.2 to 325.6 nm. In order to derive more detailed information, a 2D global least-squares method is employed to simultaneously fit the TRPES data at all time delays and photoelectron kinetic energies. The model used here can be expressed as the following equation: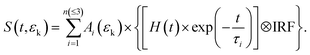 | (1) |
Here, S(t,εk) represents the 2D TRPES spectrum, while t and εk are the pump–probe time delay and the kinetic energy of the emitted photoelectron, respectively. Ai(εk) × exp(−t/τi) is the contribution with a lifetime τi and amplitude Ai(εk). H(t) is the Heaviside step function. The IRF is the (1 + 1′) cross-correlation between the pump and probe laser pulses, which is measured independently and described by a Gaussian function. It should be mentioned that a numerical convolution of this Gaussian cross-correlation function and H(t) × exp(−t/τi) is used instead of analytical convolution solutions. When employing our convolution algorithm, the simulated transients ([H(t) × exp(−t/τi)] ⊗ IRF) generated from the numerical convolution approach are not normalized. Therefore, for a given FWHM value of the IRF and a given value of the time constant (τi), the intensity of a simulated transient describes the detection efficiency of the excited state with a specific lifetime (τi) in a given experimental pump–probe measurement.
An overall very satisfactory fit to the 2D TRPES spectra is achieved. The fitting results including the derived time constants and the photoelectron kinetic energy-dependent amplitudes of each component are shown in Fig. 2(c) and (d). In Fig. 2(e) and (f), a cut of the 2D global least-squares fit over the photoelectron kinetic energy range below the corresponding energetic limit is presented. Three different time constants, 160 ± 20, 10.6 ± 0.8 and 1.6 ± 0.4 ps for PyNO at 340.2 nm are derived from the 2D global fit. At 325.6 nm, two time constants of 7.1 ± 0.6 and 1.2 ± 0.2 ps are obtained.
The TRPES spectra for PyNO at 289.8 and 280.5 nm are shown in Fig. 3(a) and (b), respectively. Both spectra share large similarities, such as the dynamics becomes obviously much shorter and the photoelectron kinetic energy distribution extends to higher kinetic energies below the energetic limit associated with D0(3b1−1). An identical 2D global least-squares fit using eqn (1) is performed and the results are shown in Fig. 3(c) and (d). The photoelectron kinetic energy limits for two-color (1 + 1′) ionization to the ground state (D0) and the first excited state (D1) of the PyNO cation, calculated using the experimental adiabatic ionization potentials of 8.39 and 9.18 eV,37 are indicated by the black and red dash lines, respectively. A satisfactory fit is achieved and consists of three components. The derived time constants are 60 ± 30, 520 ± 60 fs, ≫1 ns for 289.8 nm and 60 ± 30, 380 ± 60 fs, ≫1 ns for 280.5 nm. The component of ≫1 ns (labeled as ∞ in Fig. 3(c) and (d)) shows no decay within the experimental scanning range (a maximum delay of 1 ns was employed in our measurements) and has a very small amplitude and diffuse photoelectron kinetic energy distribution. This contribution is most likely to be from the multiphoton ionization of the metastable intermediate products or the final products associated with both pump and probe laser pulses. This component is out of the scope of the current study which focuses on two-color (1 + 1′) photoionization of PyNO itself and no further discussion will be provided. Therefore, only two time constants are assigned to the excited-state lifetimes at 289.8 and 280.5 nm. The component of 60 ± 30 fs has a diffuse distribution over the whole photoelectron kinetic energy range, while the component of hundreds of femtoseconds appears at lower kinetic energies. Herein, the relative detection sensitivity for two different components must be taken into account when one of the time constants is close to the time resolution of a time-resolved pump–probe experiment. The influences of excited-state lifetime and laser pulse duration on effective relative detection efficiency in photoionization-based pump–probe molecular spectroscopy have been discussed in detail in a previous study by Townsend and coworkers.47 In particular, for these two components of 60 and 520/380 fs, the difference of the relative detection efficiency for a given FWHM value (140 fs) of the IRF is large enough, with the value of the former being down by a factor of ∼2.5/2.3 compared with that of the latter. This factor is obtained from the comparison of the intensities of [H(t) × exp(−t/τi)] ⊗ IRF using a numerical convolution algorithm. That is to say, although the signals associated with photoelectrons of higher kinetic energies (>0.6 eV) seem to be minor in the TRPES spectra shown in Fig. 3(a) and (b), when considering the excitation step, the contribution of the former 60 fs component is not so small compared with that of the other component at lower kinetic energies. The contributions of each component are clearly shown in Fig. 3(c) and (d). It should be noted that the photoelectron kinetic energy-dependent amplitudes of each component (Ai(εk)) are not influenced by the detection efficiency since this effect has been mathematically described by [H(t) × exp(−t/τi)] ⊗ IRF in eqn (1) when employing our fitting model. The cuts of the 2D global least-squares fit over the higher and lower photoelectron kinetic energy range are shown in Fig. 4. The contributions of each component derived from the least-squares fit are also included.
At 227.3 and 217.6 nm, the TRPES spectra (Fig. 5(a) and (b)) show different features compared with those at longer pump wavelengths. The main feature observed in these TRPES spectra is a dominated component with a strong and narrow peak centered at ∼2.24 eV, showing a few picoseconds decay dynamics. The raw photoelectron images at 500 fs pump–probe delay are also presented. In Fig. 4(c) and (d), the photoelectron kinetic energy distributions derived by integrating the TRPES spectra over a delay range of −0.5 to 10 ps are shown. An analogous 2D global least-squares fit was performed, but using eqn (2). Here A0 × IRF describes the contribution from the nonresonant two-color (1 + 1′) photoionization signal.
 | (2) |
The derived time constants and the photoelectron kinetic energy-dependent amplitudes of each component are shown in Fig. 6(a) and (d). The cuts of the 2D global least-squares fit over the higher and lower photoelectron kinetic energy range are shown in Fig. 6(b) and (c) for 227.3 nm (Fig. 6(e) and (f) for 217.6 nm). The IRF component makes a minor contribution, but it could not be neglected due to the relatively weak and narrow absorption features, especially for 227.3 nm (see Fig. 1). Besides the contribution of the nonresonant two-color signal around time zero, a probe–pump signal associated with the photoexcited dynamics of PyNO at 239.2 nm also appears at lower kinetic energies. This probe–pump signal, which is too weak to record reliable photoelectron kinetic energy distributions and transients, will not be further discussed and is beyond the scope of the current study. For the pump–probe signal, only one time constant, 2.2 ± 0.2 ps, is derived at 227.3 nm. For 217.6 nm, two time constants, 2.2 ± 0.2 ps and 550 ± 50 fs, are derived.
The analysis of PADs
For the TRPES spectrum at each pump wavelength, a selected raw image at specific delay is included as an inset. By visual inspection, the isotropic feature of PADs provides no additional information about the electronic character(s) of the excited state(s) involved at 340.2–280.5 nm, whereas the PADs deserve to be further analyzed for the 2.24 eV feature of the TRPES spectra at 227.3 and 217.6 nm, which show a visible anisotropic distribution with a relatively sharp-ring feature, as presented in Fig. 5(a) and (b).The TRPAD can be expressed as a function of the electron kinetic energy εk and the pump–probe time delay t in terms of the well-known anisotropy parameters, β2 and β4, using the following equation for the (1 + 1′) two-photon ionization process with parallel linear polarizations.48,49
 | (3) |
Here, Pn(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) terms are the nth-order Legendre polynomials, σ(εk,t) is the time-dependent electron kinetic energy distribution and θ is the angle between the polarization direction of the pump and probe laser pulses and the recoil direction of the photoelectrons.
θ) terms are the nth-order Legendre polynomials, σ(εk,t) is the time-dependent electron kinetic energy distribution and θ is the angle between the polarization direction of the pump and probe laser pulses and the recoil direction of the photoelectrons.
At 227.3 and 217.6 nm, the PADs associated with the 2.24 eV feature are derived by integrating the deconvoluted images over the photoelectron kinetic energy range of 2.08–2.40 eV. Satisfactory fits to the PADs are achieved using eqn (3) and the derived anisotropy parameters, β2 and β4, as a function of pump–probe time delays are shown in Fig. 7(a) and (b). The derived β2 value for the 2.24 eV feature varies around the time-zero due to the contribution of the IRF component (as illustrated in Fig. 6(b) and (e)) and does not change at larger time delays with an average value of about 1.0 for pump wavelengths of 227.3 nm and 0.9 for 217.6 nm. The derived β4 value for the 2.24 eV feature is always close to zero for both 227.3 and 217.6 nm. The interpretation of the derived anisotropy parameters will be given in the discussion of the assignment of the 2.24 eV feature.
The assignments of the time constants
The pump wavelength of 340.2 nm matches the excitation energy of the S1 ← S0 (π* ← π, 2a2* ← 3b1) band origin of PyNO (∼341 nm, as mentioned above) due to the intrinsic broad spectral bandwidth of the femtosecond laser pulses. At 340.2 nm, the v′ = 0 and a series of low-energy vibrational states of the S1 state, which are covered by the bandwidth of the pump laser, are expected to be excited. At 325.6 nm, slightly higher vibrational levels of the S1 state are prepared. Therefore, it is straightforward to assign all the derived time constants at 340.2 and 325.6 nm to the lifetimes of different vibrational states of the S1 state. The small difference in the photoelectron kinetic energy distribution of each component results from the Franck–Condon (FC) factors associated with the S1 vibrational states and the PyNO cation in the ionization step.At 289.8 and 280.5 nm, the v′ = 0 and/or a few vibrational states of the second bright singlet ππ* state, which correspond to 4b1* ← 3b1 electronic transition, should be initially excited. It is therefore straightforward to assign the time constant of 60 ± 30 fs to the lifetime of the second 1ππ* state. As mentioned previously, the excitation energies and oscillator strengths of the low-lying valence states have been calculated using the multi-reference multi-root doubles and singles CI method (MRD-CI).37 The vertical and adiabatic excitation energies of the S1(3b12a2*) state were calculated to be 4.32 and 3.65 eV, respectively. As a consequence, highly excited vibrational states of the S1 state may also make a contribution to the second absorption band. Therefore, the time constants of 520 ± 60 fs at 289.8 nm and 380 ± 60 fs at 280.5 nm are ascribed to the lifetimes of some highly excited vibrational states of the S1 state.
As pointed out previously, the first Rydberg state excitation corresponds to the 3s ← 3b1 electronic transition. The vertical excitation energy of this 3s Rydberg state was calculated to be 5.50 eV37 and its experimental 0–0 vibronic band origin was around 228 nm.36,37 It is therefore straightforward to assign the time constant of 2.2 ± 0.2 ps at 227.3 nm to the lifetime of the 3s state (v′ = 0). For 217.6 nm, the time constants of 2.2 ± 0.2 ps and 550 ± 50 fs are assigned to the lifetimes of a few vibrational states of the 3s state. Note that the photoelectron kinetic energy-dependent amplitudes of these time constants have a peak position of 2.24 ± 0.01 eV here. We can take advantage of the relatively sharp photoelectron kinetic energy distribution of the 3s state and its peak position invariance with the change of the pump wavelength (the photoionization process should be dominated by diagonal FC factors (Δv = 0) for a pure Rydberg state). The adiabatic ionization potential of PyNO can be calculated using the following relationship:
| εk = hvprobe − (IPa − AEE) | (4) |
However, it can be recognized that there exist photoelectron signals at lower kinetic energies for both 227.3 and 217.6 nm. The photoelectron transients of lower kinetic energies can be fitted well using the nearly same time constant derived from the fit to the 2.24 eV feature. It can be rationalized in simple terms of the existence of vibrational coupling between the 1B1(3b13s) Rydberg state and two close-lying valence states, the 11B1(8b22a2*) and 21B1(3b117a1*) states.37 These two valence states have much smaller oscillator strengths compared with the 3s Rydberg state. The other higher-lying 1B1 states, such as the 3b115a1* and 1a29b2* states, may also be involved. Because some of these 1B1 valence states prefer to yield an ionic excited state, D1(8b2−1) or D2(1a2−1), the photoelectron signals occur at lower kinetic energies, as presented in Fig. 4(c) and (d). The somewhat mixed character of the 3s state of PyNO also reasonably explains why the derived β2 value for the 2.24 eV feature is less than the limiting value of 2.0 for a pure 3s Rydberg state,44 with a value of about 1.0 for 227.3 nm. It seems that the vibronic mixing between the 3s state and other valence states is stronger at 217.6 nm than that at 227.3 nm, evidenced by a smaller average β2 value of 0.9 for 217.6 nm.
In summary, the features of the TRPES spectra and PADs vary with the pump wavelength. On the basis of the detailed analysis of all TRPES spectra and PADs mentioned above, the initially prepared excited state(s) at each pump wavelength employed herein can be successfully assigned. The achieved assignments show consistency with the previous assignment of each UV absorption band.
Decay dynamics of the electronic excited states of PyNO
At the S1 state origin of PyNO, the excited-state lifetime is measured to be vibrational-state dependent (see Fig. 2) and the decay channel of intersystem crossing (ISC) to the lower-lying triplet state is possibly in operation.25 Unfortunately, the triplet state(s) of PyNO could not be one-photon effectively detected when employing the 239.2 nm UV probe laser here. Therefore, there is no evidence in our TRPES data that it really happens for some low-energy vibrational states of the S1 state. We prefer to propose that the internal conversion (IC) along ring deformation coordinates to the S0 state through the S1/S0 conical intersection (CI) is the dominant decay channel of the S1 state. Herein, the lifetime of the S1 state is in the range of 1.4–160 ps, which can be rationalized in terms of a low-energy barrier between the FC region and the S1/S0 CI. The time-resolved UV pump-VUV probe experiment is in the planning in our laboratory and may provide direct experimental evidence to support the above proposed decay mechanism.As the pump wavelength further decreases, both the highly excited vibrational states of the S1(1ππ*) state and the second 1ππ* state are excited at 289.8 and 280.5 nm, respectively. We still suggest that the main deactivation channel of the former is IC to the S0 state with a fast decay of 380–520 fs. The lifetime of the second 1ππ* state is measured to be 60 ± 30 fs. We propose that there exists an ultrafast decay pathway of IC from the second 1ππ* state to a potentially close-lying 1nπ* state within tens of femtoseconds. For the second 1ππ* state, the energetically nearby 1nπ* state is the 11A2(8b24b1*) state,37 which is about 0.3 eV lower in the FC region and optically forbidden for one-photon absorption. If there is a strong coupling between the 11A2(8b24b1*) state and the second 1ππ* state (also termed 1A1(3b14b1*)) in the FC region, this can provide a possible explanation why the lifetime is 60 ± 30 fs for the latter and why the photoelectron kinetic energy distribution of the 60 ± 30 fs component partly appears at the photoelectron kinetic energy limit associated with D1(8b2−1). However, the above interpretation is tentative due to the limited time resolution of the current experiment and needs further experimental and theoretical evidence. The 1nπ* state may be undetectable when employing the 239.2 nm probe laser. For example, at the pump wavelength of 289.8 nm, if the subsequently populated 1nπ* state contains more than 0.3 eV vibrational excess energy,37 it should not preferentially ionize to D1 (v = 0) in the cation and is not likely to be effectively detected here. Therefore, we do not assign the component of 380–520 fs to the photoelectron signals generated from the ionization of the 1nπ* state since the distribution of this component extends to a higher kinetic energy range above the adiabatic energetic limit of D1. As mentioned above, we prefer to assign the time constant of 380–520 fs to the lifetime of the S1 vibrational states. Additionally, it is worth mentioning that there is another possibility for the decay dynamics of the second 1ππ* state. Upon excitation at 289.8 and 280.5 nm, the S1 vibrational states are suggested to be subsequently populated by a multistep sequential decay process within 60 ± 30 fs. However, based on the analysis of the current (1 + 1′) TRPES spectra (Fig. 3(a) and (b)) in this work, there is no clear evidence to provide strong support for this assumption. This is perhaps due to the overlap of the photoelectron signals from the S1 state and the second 1ππ* state.
At 227.3 and 217.6 nm, the PyNO molecules are excited to a superposition of a mixture of Rydberg and valence characters, which is mostly like the 3s Rydberg state revealed by the 2.24 eV feature and the corresponding PADs. The initially prepared wavepacket decays with a lifetime of 2.2 ± 0.2 ps or 550 ± 50 fs. At these high excitation energies, the N–O dissociation channel is in operation25 and may be the dominant channel. At high levels of vibrational excitation in the 3s state, it is inferred that the initial wavepacket is facilitated to evolve along appropriate coordinates for some vibrational modes, resulting in a shorter predissociation lifetime of 550 ± 50 fs rather than that of 2.2 ± 0.2 ps for the vibrational ground state (v′ = 0) and other ineffective vibrational states of the 3s Rydberg state.
Herein, the pump wavelength-dependent excited-state lifetimes of isolated PyNO are experimentally measured for the first time and the obtained information is quantitative. However, the proposed deactivation mechanism of PyNO at each excitation wavelength is somewhat tentative. In order to make the interpretation of these current experimental results to be more convinced and elucidate some debates, the mixed quantum-classical surface hopping molecular dynamics simulations of photoexcited PyNO is expected to be achieved by theoretical chemists in the future for providing more valuable insights on the UV photoinduced dynamics of PyNO. The picture of the excited-state decay dynamics of PyNO is far from complete.
IV. Conclusions
In conclusion, we investigated the ultrafast decay dynamics of PyNO following femtosecond pulses excitation in a pump wavelength range of 340.2–217.6 nm using the fs-TRPEI technique. The S1(1ππ*) state lifetime is vibrational-state dependent at vibrational levels slightly above the S1 state origin and shows a rapid decrease with the further increase of the vibrational excess energy. The second 1ππ* state has an ultrashort lifetime of 60 ± 30 fs. The 3s Rydberg state (v′ = 0) has a lifetime of 2.2 ± 0.2 ps and is mixed with some nearby valence states. For vibrational states of this 3s Rydberg state, the decay dynamics is suggested to be vibrational-state dependent, revealed by two different lifetimes of 2.2 ± 0.2 ps and 550 ± 50 fs. This gas-phase photochemical study on the isolated PyNO molecule over a broad UV pump wavelength range provides very detailed information on the ultrafast decay dynamics of electronically excited PyNO, highlighting the different deactivation rates of low-lying electronic excited states and the influence of vibrational excess energy on the excited-state dynamics of heteroaromatic molecules.Author contributions
Conceptualization, supervision and funding acquisition: D. Y., G. W. and X. Y.; experiments and data analysis: B. F., W. W. and D. Y.; writing: D. Y. and G. W.; discussion: all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (No. 22203095, 22103087, 21833003, and 22288201) and the Key Technology Team of the Chinese Academy of Sciences (GJJSTD20220001). The authors also gratefully acknowledge the support from the Dalian Coherent Light Source (DCLS).References
- S. Soorkia, C. Jouvet and G. Grégoire, Chem. Rev., 2020, 120, 3296–3327 CrossRef CAS PubMed.
- C. E. Crespo-Hernández, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2019 CrossRef PubMed.
- C. Canuel, M. Mons, F. Piuzzi, B. Tardivel, I. Dimicoli and M. Elhanine, J. Chem. Phys., 2005, 122, 074316 CrossRef PubMed.
- Z. Lan, E. Fabiano and W. Thiel, J. Phys. Chem. B, 2009, 113, 3548–3555 CrossRef CAS PubMed.
- R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540–3593 CrossRef CAS PubMed.
- B. Marchetti, T. N. V. Karsili, M. N. R. Ashfold and W. Domcke, Phys. Chem. Chem. Phys., 2016, 18, 20007–20027 RSC.
- X. Mu, M. Zhang, J. Feng, H. Yang, N. Medvedev, X. Liu, L. Yang, Z. Wu, H. Xu and Z. Li, Ultrafast Sci., 2023, 3, 0015 CrossRef.
- I. Yamazaki, K. Sushida and H. Baba, J. Chem. Phys., 1979, 71, 381–387 CrossRef CAS.
- J. I. Selco, P. L. Holt and R. B. Weisman, J. Chem. Phys., 1983, 79, 3269–3278 CrossRef CAS.
- E. Villa, A. Amirav and E. C. Lim, J. Phys. Chem., 1988, 92, 5393–5397 CrossRef CAS.
- M. Chachisvilis and A. H. Zewail, J. Phys. Chem. A, 1999, 103, 7408–7418 CrossRef CAS.
- Z. L. Cai and J. R. Reimers, J. Phys. Chem. A, 2000, 104, 8389–8408 CrossRef CAS.
- H. Wang, C. Y. Zhu, J. G. Yu and S. H. Lin, J. Phys. Chem. A, 2009, 113, 14407–14414 CrossRef CAS PubMed.
- P. C. Varras, P. S. Gritzapis and K. C. Fylaktakidou, Mol. Phys., 2018, 116, 154–170 CrossRef CAS.
- J. Yang, X. Zhu, J. P. F. Nunes, J. K. Yu, R. M. Parrish, T. J. A. Wolf, M. Centurion, M. Gühr, R. Li, Y. Liu, B. Moore, M. Niebuhr, S. Park, X. Shen, S. Weathersby, T. Weinacht, T. J. Martinez and X. Wang, Science, 2020, 368, 885–889 CrossRef CAS PubMed.
- J. Cao, Q. Fang and W.-H. Fang, J. Chem. Phys., 2011, 134, 044307 CrossRef PubMed.
- A. L. Sobolewski and L. Adamowicz, J. Phys. Chem., 1996, 100, 3933–3941 CrossRef CAS.
- D. R. Borst, J. R. Roscioli and D. W. Pratt, J. Phys. Chem. A, 2002, 106, 4022–4027 CrossRef CAS.
- L. Poisson, D. Nandi, B. Soep, M. Hochlaf, M. Boggio-Pasqua and J. M. Mestdagh, Phys. Chem. Chem. Phys., 2014, 16, 581–587 RSC.
- E. Samoylova, V. R. Smith, H. H. Ritze, W. Radloff, M. Kabelac and T. Schultz, J. Am. Chem. Soc., 2006, 128, 15652–15656 CrossRef CAS PubMed.
- F. Zhang, Y. J. Ai, Y. Luo and W. H. Fang, J. Chem. Phys., 2009, 130, 144315 CrossRef PubMed.
- Y. Min, W. Yuan, D. Yang, D. Dai, S. Yu, G. Wu and X. Yang, Chin. J. Chem. Phys., 2022, 35, 242–248 CrossRef CAS.
- B. Feng, D. Yang, Y. Min, Q. Gao, B. Fang, G. Wu and X. Yang, Phys. Chem. Chem. Phys., 2023, 25, 17403–17409 RSC.
- M. Ito and W. Mizushima, J. Chem. Phys., 1956, 24, 495–500 CrossRef CAS.
- N. Hata and I. Tanaka, J. Chem. Phys., 1962, 36, 2072–2077 CrossRef.
- E. M. Evleth, Theoret. Chim. Acta, 1968, 11, 145–155 CrossRef CAS.
- K. Seibold, G. Wagniere and H. Labhart, Helv. Chim. Acta, 1969, 52, 789–796 CrossRef CAS.
- R. M. Hochstra. and D. A. Wiersma, J. Chem. Phys., 1971, 55, 5339–5343 CrossRef.
- J. C. D. Brand and K. T. Tang, J. Mol. Spectrosc., 1971, 39, 171–174 CrossRef CAS.
- R. D. Peacock and B. Samori, J. Chem. Soc., Faraday Trans. 2, 1975, 71, 1909–1911 RSC.
- H. D. Bist, J. S. Parihar and J. C. D. Brand, J. Mol. Spectrosc., 1976, 59, 435–441 CrossRef CAS.
- H. D. Bist, J. S. Parihar and J. C. D. Brand, J. Mol. Spectrosc., 1977, 64, 211–216 CrossRef CAS.
- Y. Nakagawa, I. Suzuka and M. Ito, Chem. Phys. Lett., 1993, 208, 453–459 CrossRef CAS.
- K. V. Berezin and L. M. Babkov, J. Struct. Chem., 1995, 36, 314–318 CrossRef.
- K. V. Berezin, L. M. Babkov and V. M. Bulanov, J. Struct. Chem., 1995, 36, 309–313 CrossRef.
- K. V. Berezm and L. M. Babkov, J. Struct. Chem., 1997, 38, 287–291 CrossRef.
- M. H. Palmer, S. V. Hoffmann, N. C. Jones, E. R. Smith and D. L. Lichtenberger, J. Chem. Phys., 2013, 138, 214317 CrossRef PubMed.
- Z. He, Z. Chen, D. Yang, D. Dai, G. Wu and X. Yang, Chin. J. Chem. Phys., 2017, 30, 247–252 CrossRef CAS.
- D. Yang, Z. Chen, Z. He, H. Wang, Y. Min, K. Yuan, D. Dai, G. Wu and X. Yang, Phys. Chem. Chem. Phys., 2017, 19, 29146–29152 RSC.
- D. Yang, Y. Min, Z. Chen, Z. He, K. Yuan, D. Dai, X. Yang and G. Wu, Phys. Chem. Chem. Phys., 2018, 20, 15015–15021 RSC.
- D. Yang, Y. Min, B. Feng, X. Yang and G. Wu, Phys. Chem. Chem. Phys., 2022, 24, 22710–22715 RSC.
- B. Feng, D. Yang, Z. He, B. Fang, G. Wu and X. Yang, J. Phys. Chem. A, 2023, 127, 10139–10146 CrossRef CAS PubMed.
- G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996 CrossRef CAS.
- W. Yuan, B. Feng, D. Yang, Y. Min, S. Yu, G. Wu and X. Yang, Chin. J. Chem. Phys., 2021, 34, 386–392 CrossRef CAS.
- W. Yuan, D. Yang, B. Feng, Y. Min, Z. Chen, S. Yu, G. Wu and X. Yang, Phys. Chem. Chem. Phys., 2021, 23, 17625–17633 RSC.
- H. Keller-Rudek, G. K. Moortgat, R. Sander and R. Sörensen, Earth Syst. Sci. Data, 2013, 5, 365–373 CrossRef.
- N. Kotsina and D. Townsend, Phys. Chem. Chem. Phys., 2017, 19, 29409–29417 RSC.
- K. L. Reid, Annu. Rev. Phys. Chem., 2003, 54, 397–424 CrossRef CAS PubMed.
- T. Suzuki, Annu. Rev. Phys. Chem., 2006, 57, 555–592 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Spectra of the pump wavelengths. See DOI: https://doi.org/10.1039/d2cp06187f |
| This journal is © the Owner Societies 2024 |






