Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational predictions of interfacial tension, surface tension, and surfactant adsorption isotherms†
Jing
Li
a,
Carlos
Amador
b and
Mark R.
Wilson
 *a
*a
aDepartment of Chemistry, Durham University, Stockton Road, Durham, DH1 3LE, UK. E-mail: mark.wilson@durham.ac.uk
bNewcastle Innovation Centre, Procter & Gamble Ltd, Newcastle Upon Tyne, NE12 9BZ, UK
First published on 27th March 2024
Abstract
All-atom (AA) molecular dynamics (MD) simulations are employed to predict interfacial tensions (IFT) and surface tensions (ST) of both ionic and non-ionic surfactants. The general AMBER force field (GAFF) and variants are examined in terms of their performance in predicting accurate IFT/ST, γ, values for chosen water models, together with the hydration free energy, ΔGhyd, and density, ρ, predictions for organic bulk phases. A strong correlation is observed between the quality of ρ and γ predictions. Based on the results, the GAFF-LIPID force field, which provides improved ρ predictions is selected for simulating surfactant tail groups. Good γ predictions are obtained with GAFF/GAFF-LIPID parameters and the TIP3P water model for IFT simulations at a water–triolein interface, and for GAFF/GAFF-LIPID parameters together with the OPC4 water model for ST simulations at a water–vacuum interface. Using a combined molecular dynamics-molecular thermodynamics theory (MD-MTT) framework, a mole fraction of C12E6 molecule of 1.477 × 10−6 (from the experimental critical micelle concentration, CMC) gives a simulated surface excess concentration, ΓMAX, of 76 C12E6 molecules at a 36 nm2 water–vacuum surface (3.5 × 10−10 mol cm−2), which corresponds to a simulated ST of 35 mN m−1. The results compare favourably with an experimental ΓMAX of C12E6 of 3.7 × 10−10 mol cm−2 (80 surfactants for a 36 nm2 surface) and experimental ST of C12E6 of 32 mN m−1 at the CMC.
1 Introduction
Surface active agents, or surfactants, are some of the most versatile chemicals used today.1–3 Surfactants are employed in a range of applications including washing products,4,5 pharmaceuticals,6,7 and petroleum recovery.8,9 The presence of both hydrophilic and hydrophobic parts enables surfactants to lower interfacial tension (IFT), γ, between two phases (where one phase is usually water or an aqueous phase).10,11 IFT reduction, (or in the case of a water–air interface – surface tension (ST) reduction), is one of the crucial factors in reflecting the capability of surfactant molecules in real-world applications.12For an air–water interface, the surface reaches a maximum surface coverage of surfactant, ΓMAX, at the critical micelle concentration (CMC).13–17 Below this concentration, additional surfactant molecules added to the interface help reduce γ. Therefore, the value of the CMC and the form of the surface adsorption isotherm, together with the inherent ability of certain surfactants to reduce γ more than others, are crucial factors in choosing surfactants for “real-world” applications.18
Computer simulation has become a powerful technique for studying and making quantitative predictions of natural phenomena.19 Several previous studies have calculated γ for surfactants at both water–oil and water–vacuum interfaces using all-atom (AA) molecular dynamics (MD),20–23 and the impact of both ionic and non-ionic surfactants on lowering water–oil IFT or water–vacuum ST has been investigated. In these studies, previous oil phases have included toluene, nonane, decane, and dodecane.24–33 While experimental techniques used for γ measurements (e.g. pendant drop tensiometry) provide γ with changing bulk concentration, C,34–37 simulations provide γ measurement based on controlling the number of surfactants at the interface, i.e. a controlled surface concentration (Γ).18 This difference adds difficulty in providing quantitative comparisons between simulation and experimental results. Nevertheless, the comparison can still be made by evaluating adsorption isotherms Γ(C) experimentally by various methods including colorimetry, chemical and radiochemical techniques, spectroscopic techniques,38,39 and by employing the Gibbs adsorption isotherm equation40
 | (1) |
A key component of all AA MD studies is provided by the molecular force field employed within the simulation. While some literature studies focus on the simulation of γ for one category of surfactants at the interface by employing a specific force field (e.g. SDK force field for polyethylene glycol alkyl ethers),41–44 developments of force fields for predicting γ of various categories of surfactants remain an active research area in high-throughput screening of surfactant formulations, where lower γ at CMC (γCMC) and lower CMC are targeted for higher efficiency and lower cost.45
In the current study, we test the performance of general AMBER force field (GAFF), and variants thereof, in the prediction of γ for different surfactants at interfaces.20 We show that the performance of the force field in predicting γ at a water–air interface is very sensitive to the water model used, and also to the ability of the force field to predict the correct molecular flexibility and density (ρ) for hydrocarbon chains. We show that the relatively new OPC446 (4-point, rigid optimal point charge) water model works well in combination with the GAFF/GAFF-LIPID in predicting ST for realistic ΓMAX values, and we show that GAFF/GAFF-LIPID works well in combination with a TIP3P (transferable intermolecular potential 3 points) water model for predicting the IFT for a (typical “real world” interface) water–triolein system.
2 Computational methods
2.1 Simulation details
In this study, the GAFF parameter sets20 and semi-empirical with bond charge correction (AM1-BCC) charge model47,48 were employed for the AA MD simulations, using the simple harmonic functional form shown in eqn (2), | (2) |
Force fields were generated for the structures shown in Fig. 1. The triolein molecule, which is found in naturally occurring products such as olive oil, was chosen as a typical “oil molecule”. The sodium dodecyl sulphate (SDS), sodium 4-dodecylbenzene sulfonate (SDBS), sodium 4-(dodecan-2-yl)benzene sulfonate (SD2BS) and sodium laureth-3 sulfate (SLE3S) were chosen as typical ionic surfactants, and polyethylene glycol alkyl ethers (C12E3, C12E5 and C15E7) were chosen as non-ionic surfactants.
 | ||
| Fig. 1 Chemical structures of (a) triolein, (b) SDS, (c) SDBS, (d) SD2BS, (e) SLE3S, (f) C12E3, (g) C12E5, (h) C15E7 and (i) C12E6. | ||
The generated GAFF topology and coordinate files were converted to GROMACS format by the ACPYPE script.52 The TIP3P model was used as a compatible water model to be used with GAFF parameter sets.53 We note that GAFF parameters and the TIP3P water model were successfully employed previously by Wilson and co-workers to study self-assembly within several lyotropic systems, e.g. Sunset Yellow (SSY),54 and a number of ionic cyanine dyes,55–58 and this force field combination therefore provides a suitable starting point for this study. In addition, (as described below – see Section 3), alternative 3-site and 4-site water models were also used and the GAFF force was amended/enhanced for some calculations. Finally, the OPLS-AA force field was used for some of the test calculations, to calibrate and understand the influence of different force field factors on IFT. OPLSA-AA force fields were generated using the LigGenPar server,59–61 with the 1.14*CM1A charge model.60
Simulations and analysis of results made use of the GROMACS 2021.1 package.62 Molecular structures and positions were viewed in Visual Molecular Dynamics (VMD).63 A leap-frog integrator was used for all simulations64 using a time step of 2 fs, and the Linear Constraints Solver (LINCS) constraint algorithm65 was applied to all molecular bonds in both equilibration and production runs. Long-range electrostatic interactions were modified by the Particle Mesh Ewald (PME) method,66 and the long-range dispersion corrections for energy and pressure were applied to long-range van der Waals interactions, having applied a cutoff distance of 1.2 nm for short-range interactions.
2.2 Interfacial tension
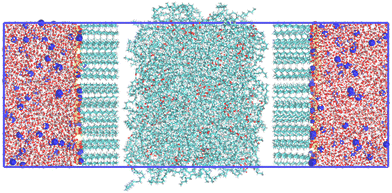
For IFT measurements, a simulation box was constructed as follows: water molecules were randomly inserted into a 6 nm × 6 nm × 3 nm box; oil molecules were randomly inserted into a 6 nm × 6 nm × 6 nm box (the number of molecules was chosen according to their experimental ρ); and surfactant molecules (number of molecules ranging from 10 to 100) were inserted into a 6 nm × 6 nm × 3 nm box such that x, y positions were chosen randomly but they were orientated with their principal axis along the z-axis of the simulation box. These “sub boxes” were combined (in a sandwich geometry) along the z direction, with the order of water sub box + oil sub box + water sub box, or water sub box + surfactants sub box + oil sub box + surfactants sub box + water sub box, depending on whether surfactants were required. It should be noted that the head groups of the surfactants were always arranged to point towards the water box, as demonstrated in the initial configuration snapshot of Fig. 2.After energy minimization, with a steepest descent algorithm,67 a 200 ps NPNAT pre-equilibration was carried out with a V-rescale thermostat and a Berendsen barostat,68,69 followed by a 50 ns NPNAT equilibration run with a Nosé–Hoover thermostat and a Parrinello–Rahman barostat.70–72 A further production run was carried by for 200 ns as a NPNAT ensemble simulation using a Nosé–Hoover thermostat (with a time constant of 1.0 ps) and a Parrinello–Rahman barostat (with a time constant of 2.0 ps). Here, PN and A are normal pressure and surface area of x–y plane respectively. In both the equilibration and production runs, a temperature of 298.15 K and a pressure of 1 bar were maintained.
The NPNAT ensemble runs in GROMACS were carried out using a semi-isotropic pressure coupling scheme, with a reference pressure of 1.0 bar and compressibilities set to 0 bar−1 in the x–y plane and to 4.5 × 10−5 bar−1 in z direction respectively. IFT, γ, was calculated from the pressure tensor elements (PXX, PYY and PZZ) using the equation73
 | (3) |
We note in passing that to obtain reproducible surface tensions we always use the procedure of producing an initial surfactant layer with head groups pointing towards the water. Following the equilibration steps described above leads to a liquid layer of surfactant with considerable liquid disorder. In principle, this procedure is not mandatory, i.e. we could use a random arrangement of surfactants in a layer or start from surfactants dissolved initially in the aqueous phase. However, although both of these cases tend toward a configuration with the surfactant head groups pointing towards the water, equilibration is very slow (on the time scales used for atomistic simulation). So, from a practical point of view, the procedure outlined above is necessary.
2.3 Surface tension
Two 6 nm × 6 nm × 6 nm vacuum sub-boxes, two surfactant sub-boxes and a 6 nm × 6 nm × 6 nm water sub-box were combined in z direction (with the order of vacuum + surfactants + water + surfactants + vacuum box) to form the initial simulation box. After minimisation, a 200 ps NVT pre-equilibration was run with the V-rescale thermostat, followed by a 50 ns NVT equilibration with the Nosé–Hoover thermostat. The production run was carried out by a 200 ns NVT ensemble simulation with the Nosé–Hoover thermostat (with a time constant of 1.0 ps). In both the equilibration and production runs, a temperature of 298.15 K was maintained. Data analysis for ST simulations employed the same procedure described in Section 2.2.2.4 Density of bulk phases
We calculate the bulk density for several systems: methanol, 1,2-dimethoxyethane (DME), dodecane, pentadecane and C12E5. For these simulations, molecules were randomly inserted into a 7 nm × 7 nm × 7 nm box according to its experimental ρ.74 Long-range electrostatic interactions were modified by the Particle Mesh Ewald (PME) method, and the long-range dispersion corrections for energy and pressure were applied to long-range van der Waals interactions, both with a cut-off distance of 1.2 nm. After energy minimisation, a 100 ps NVT equilibration was run with the V-rescale thermostat, followed by a 1 ns NPT equilibration with the V-rescale thermostat and Berendsen barostat. The MD production run was carried out using a 10 ns NPT ensemble simulation with a Nosé–Hoover thermostat (with a time constant of 1.0 ps) and a Parrinello–Rahman barostat (with a time constant of 2.0 ps). In both equilibration and production runs, a temperature of 298.15 K and a pressure of 1 bar were maintained.2.5 Free energy of hydration
The target molecule was inserted into a rhombic dodecahedron box with a distance between the solute and the box edge of 1.2 nm, followed by a solvation step using explicit water molecules in the box. After energy minimisation and equilibration, the production run was carried by a 5 ns NPT ensemble simulation at each of 14 λ states. The λ values were 0.0, 0.1, 0.2, 0.3, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.8, 0.9 and 1.0 (λ = 0 for the decoupled state and λ = 1 for the fully coupled state). Here, both van der Waals and electrostatic interactions were turned off when λ = 0 (soft core interactions were applied to avoid singularities, where soft core-α = 1.0, soft-core-σ = 0.3 and soft core power = 1),75 and all interactions were turned on when λ = 1. At each stage, both van der Waals and electrostatic interactions were gradually turned on together. In both the equilibration and production runs, a temperature of 298.15 K and a pressure of 1 bar were maintained, if applicable. In addition, an SD-integrator (a leap-frog stochastic dynamics integrator) was used with a time step of 2 fs in MD simulations, and the LINCS constraint algorithm was applied to all molecular bonds in both the equilibration and production run. The free energy of each λ state was calculated using the Bennett acceptance ratio (BAR) method,76 and the final free energy of hydration (ΔGhyd) was calculated by the difference of free energy obtained between the states λ = 0 and λ = 1 states.2.6 Free energy of adsorption
A 6 nm × 6 nm × 6 nm vacuum sub box and a 6 nm × 6 nm × 6 nm water sub box (with a surfactant molecule) were combined along the z-direction to form the initial simulation box. After energy minimisation, a 200 ps NVT pre-equilibration was performed with the V-rescale thermostat, followed by a 50 ns NVT equilibration with the Nosé–Hoover thermostat. In equilibration, a temperature of 298.15 K was maintained.To obtain the free energy of adsorption (ΔGads), umbrella sampling was employed to calculate the potential of mean force (UPMF). UPMF is compiled from average forces calculated as a function of the intermolecular coordinate between two interacting species using
 | (4) |
We employed centre-of-mass (COM) pulling,79 between the centre of mass of a surfactant molecule and the centre of mass of a water slab. COM windows were selected with a neighbouring distance of 0.15 nm between them (25 windows in total). Each window was equilibrated for 1 ns followed by a 10 ns production run to obtain a range of configurations in which the COM of the pulling species was constrained.
To plot UPMF as a function of full and continuous intermolecular coordinates, the energy values in adjacent windows were reassembled to produce a continuous function using a weighted histogram analysis method (WHAM).79 The value of ΔGads was calculated by the difference between the highest and lowest values in the UPMF curve. The statistical error raised from the WHAM, due to limited counting (i.e. finite time steps in simulations), was conveniently calculated by bootstrap analysis.80
3 Results and discussion
3.1 Initial testing and validation of force fields of surfactants at water–oil interfaces
In initial tests, the IFT of a water–triolein interface shows a simulated value of 34.03 ± 0.93 mN m−1 using GAFF parameters and the TIP3P water model, which compares well with the experimental value of 32 mN m−1.88This interface was then used in initial test simulations to evaluate the IFT of the surfactants (i.e. SDS, SDBS, SD2BS, SLE3S, C12E3, C12E5 and C15E7) as a function of the number of surfactant molecules at the water–triolein interface within the symmetrical slab geometry shown in Fig. 2. The results are presented in Fig. 3, where initially both triolein and surfactant molecules are simulated with GAFF parameters.
We note that at high Γ the interface starts to distort from the planar geometry as it becomes oversaturated with surfactant. This leads to an “apparent rise” in IFT, as the increase in the area of the interface is not being accounted for. Hence, to make a comparison with experimental results, we, where available, compare the calculated IFT with the experimental value of IFT measured at ΓMAX.
Unexpectedly high IFT values were obtained from simulations at high Γ for both ionic and non-ionic surfactants at the water–triolein interface in Fig. 3. For example, the simulated IFTs of 70 SDS and 80 C12E5 molecules at a 36 nm2 cross-section water–triolein interface (approximate values expected at ΓMAX) show values of 21.12 ± 0.92 mN m−1 and 17.26 ± 1.27 mN m−1 respectively, whereas the experimental IFTCMC of ionic and non-ionic surfactants at a water–oil interface can approach 5 mN m−1 in the case where the oils are triglycerides with similar structure to triolein34,82,83,89–94 (noting that the experimental values of ΓMAX of SDS and C12E5 are 3.2 × 10−10 mol cm−2 and 3.6 × 10−10 mol cm−2, respectively).95 Thus, further optimisation and validation of the GAFF force field for the calculation of IFTs is required.
3.2 Improving predictions of IFT in GAFF
Here, C12E5 (Fig. 1), a non-ionic alcohol ethoxylate was chosen to perform the initial tests and improvements of the GAFF parameter set in combination with the TIP3P water model. The three key parts of alcohol ethoxylates consist of a hydrophobic hydrocarbon tail group, together with a head group composed of a terminal hydrophilic alcohol and an extended ethylene oxide (EO) chain. It is reasonable to consider how well the force field performs in reproducing experimental data of each of these constituent parts using typical force field validation approaches.96–98 Accordingly, we consider the performance of GAFF for representative fragment molecules: methanol, 1,2-dimethoxyethane (DME) and dodecane.42,86,99,100It is known already that GAFF underestimates ΔGhyd of alcohol and DME, with a simulated ΔGhyd for methanol of −3.49 ± 0.02 kcal mol−1 (experimental data of −5.10 ± 0.60 kcal mol−1), and a simulated ΔGhyd for DME of −3.10 ± 0.03 kcal mol−1 (experimental data of −4.84 ± 0.60 kcal mol−1).75,86 Also, GAFF is known to provide relatively poor predictions of ρ for long hydrocarbon chains. Here, long hydrocarbon chains are slightly too stiff in GAFF and, consequently, ρ values are too high with GAFF parameters from bulk phase simulations.100 The ρ of dodecane molecules simulated with GAFF shows a value of 824 kg m−3,98 compared to the experimental value of 750 kg m−3.87
Here, it is interesting to compare the results from tests of the OPLS-AA force field. According to Akinshina et al.,99 OPLS-AA parameters successfully reproduced the hydration of the short EO chains of the chromonic amphiphile 2,3,6,7,10,11-hexa-(1,4,7-trioxa-octyl)-triphenylene (TP6EO2M) in aqueous solution, and hence the chromonic aggregation behaviour of TP6EO2M molecules in bulk water (i.e. single molecule-cross section stacks). In contrast, GAFF parameters underestimate the hydration of EO chains, resulting in a high aggregation free energy for TP6EO2M molecules and compact disordered clusters. Calculation of ΔGhyd of DME with GAFF and OPLS-AA parameters using the methodology of Section 2.5 shows that the OPLS-AA parameters estimate enhanced hydration of DME with a value of −23.31 kJ mol−1, compared to GAFF parameters with a value of −15.97 kJ mol−1 (experimental value −20.25 kJ mol−1).75
IFT simulations were performed (with GAFF and OPLS-AA parameters) for a water–octane interface system and a water–octane interface system with 80 C12E5 molecules at each of the two 36 nm2 interfaces (Table 1),35 in order to test the relationship between ΔGhyd and calculated IFTs. OPLS-AA parameters estimate a much lower IFT for the 36 nm2 water-80 C12E5–octane system (with both TIP3P and SPC/E water models) compared to the GAFF parameters, noting that the OPLS-AA and GAFF parameters simulate similar IFTs arising from the pure water–octane interface. It could reasonably be hypothesised that the force field, which simulates a more negative ΔGhyd for the head groups of surfactants, would estimate a lower IFT for those surfactants at a water–oil interface.101 However, OPLS-AA parameters are not capable of reducing the IFT of the water–70 SDS–octane system to a much lower value than GAFF parameters: a value of 25.00 ± 0.54 mN m−1 is obtained from GAFF and a value of 25.71 ± 0.47 mN m−1 is obtained for OPLS-AA with the SPC/E water model.
| Force fields | Water–octane IFT/mN m−1 | Water-80 C12E5–octane IFT/mN m−1 | Water-70 SDS-octane IFT/mN m−1 |
|---|---|---|---|
| a IFTCMC of water–C12E4–hexadecane interface at a ΓMAX of 3.6 × 10−10 mol cm−2.82 C12E4 surfactant shows a same experimental ΓMAX as C12E5, both with a value of 3.6 × 10−10 mol cm−2 (i.e. 80 surfactants at a 36 nm2 interface).82 In addition, the water–hexadecane interface shows a similar experimental IFT to the water–octane interface, where the IFT of the water–hexadecane interface is 55.2 mN m−1 and the IFT of the water–octane interface is 52.5 mN m−1.81 | |||
| GAFF + TIP3P | 45.46 ± 0.26 | 25.67 ± 0.72 | 22.28 ± 0.59 |
| GAFF + SPC/E | 54.73 ± 0.30 | 25.21 ± 0.80 | 25.00 ± 0.54 |
| OPLS-AA + TIP3P | 44.66 ± 0.32 | −3.76 ± 0.49 | 18.61 ± 0.31 |
| OPLS-AA + SPC/E | 53.45 ± 0.34 | −3.50 ± 0.60 | 25.71 ± 0.47 |
| Experimental | 52.581 | 3.1a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82 82 |
9.783 |
| Simulation Γ | 2.22 nm−2 | 1.94 nm−2 | |
| Experimental ΓMAX | 2.22 nm−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82 82 |
1.99 nm−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 83 83 |
|
| Experimental CMC | 6.4 × 10−5 M84 | 8.2 × 10−3 M85 | |
Although ΔGhyd might be one important factor influencing the accurate determination of IFTs in the MD, further validations are still needed. GAFF and OPLS-AA have different functional forms and parameter sets.20,22 The difference between the two force fields might not provide a clear conclusion about the relationship between ΔGhyd and IFT. However, it is possible to investigate the relationship between ΔGhyd and IFT by careful modification of the GAFF force field.
Here, three separate modifications of GAFF parameters are performed (Table 2). First, following the approach of Fennell et al., the partial atomic charge of the EO chains in GAFF is scaled by a factor of 1.1 to correctly calculate ΔGhyd of DME.86 Second, following Boyd,74 the ε of “atomtype os” (ether oxygen of EO chains) in GAFF is changed from 0.71128 kJ mol−1 to 1.60656 kJ mol−1, which improves the calculations of ΔGhyd for DME. Third, GAFF-DC parameters are applied to the alcohol functional group to correctly simulate ΔGhyd of methanol.86
| Force fields | Modification 1 (q-scaling) | Modification 2 (ε modification) | Modification 3 (GAFF-DC) | |||
|---|---|---|---|---|---|---|
| ΔGhyd/kJ mol−1 (DME) | IFT/mN m−1 | ΔGhyd/kJ mol−1 (DME) | IFT/mN m−1 | ΔGhyd/kJ mol−1 (methanol) | IFT/mN m−1 | |
| a IFTCMC of water-C12E4-hexadecane interface. | ||||||
| GAFF | −16.05 ± 0.22 | 25.21 ± 0.80 | −16.05 ± 0.22 | 25.21 ± 0.80 | −12.52 ± 0.37 | 25.21 ± 0.80 |
| (25.67 ± 0.72) | (25.67 ± 0.72) | (25.67 ± 0.72) | ||||
| Modified GAFF | −20.87 ± 0.08 | 22.10 ± 0.56 | −20.17 ± 0.15 | 48.22 ± 0.55 | −23.34 ± 0.20 | 29.31 ± 0.51 |
| (18.88 ± 0.64) | (45.27 ± 0.82) | (26.18 ± 0.59) | ||||
| Experimental | −20.2575 | 3.1a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82 82 |
−20.2575 | 3.1a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82 82 |
−21.3486 | 3.1a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82 82 |
It was initially hypothesised that a modified GAFF, which simulates correctly ΔGhyd of either DME or methanol, would estimate a lower IFT for the water–C12E5–octane interface.44,101 However, both the second and third modifications of GAFF parameters surprisingly lead to the prediction of higher IFTs (Table 2). As a result, we additionally determined the influence of force field modifications on both ρ and ΔGhyd for methanol, DME and dodecane (Table 3). OPLS-AA parameters simulate enhanced hydration for DME, compared to GAFF parameters, although both OPLS-AA and GAFF underestimate ΔGhyd of methanol (i.e. alcohol head group of non-ionic surfactant). However, the results indicate that the lower IFT value of the 36 nm2 water-80 C12E5–octane system obtained from OPLS-AA is probably correlated with the lower ρ of methanol and DME predicted with OPLS-AA. GAFF-DC, which simulates a higher ρ for methanol, produces a higher IFT for the 36 nm2 water-80 C12E5–octane compared to GAFF parameters. In addition, it should be noted that both GAFF and OPLS-AA simulate a ρ for dodecane that is too high compared to the experimental values, as has been noted elsewhere.100,102
| Force fields | Methanol | DME | Dodecane | |||
|---|---|---|---|---|---|---|
| ρ/kg m−3 | ΔGhyd/kJ mol−1 | ρ/kg m−3 | ΔGhyd/kJ mol−1 | ρ/kg m−3 | ΔGhyd/kJ mol−1 | |
| GAFF | 785.76 ± 0.42 | −12.52 ± 0.37 | 913.90 ± 1.10 | −15.97 ± 0.15 | 824.00 ± 1.00 | 15.07 ± 0.17 |
| OPLS-AA | 737.54 ± 0.46 | −13.36 ± 0.08 | 886.64 ± 0.91 | −23.31 ± 0.40 | 838.45 ± 0.39 | 14.39 ± 0.31 |
| GAFF-DC | 787.76 ± 0.68 | −23.34 ± 0.24 | ||||
| Experimental | 79287 | −21.3486 | 86887 | −20.2575 | 75087 | 15.0775 |
3.3 IFT predictions using a combination of GAFF and GAFF-LIPID force fields
From the above, correctly capturing ρ for pure components plays a key role in predicting IFT simulations successfully. This relationship between γ and ρ has been suggested from previous theories and simulations, emphasising that IFT can be defined as the stress transmitted across a unit width strip that is normal to a Gibbs dividing surface (according to the mechanical definition).30,42,73,103–105 Thus, GAFF-LIPID,100 which makes better predictions for ρ, the heat of vaporisation and the isothermal compressibility of long carbon chain compounds, can be suggested for the tail group parameters of surfactants in the IFT simulation. In addition, Lennard-Jones parameters (σ and ε) of “atomtype c3” described in GAFF-LIPID are utilised in the PEO chains of non-ionic surfactants (C12E3, C12E5 and C15E7) to simulate a reduced ρ for the heads. However, the use of GAFF-LIPID “atomtype c3” for SLE3S PEO chains does not result in a significant difference compared to the original GAFF, which could be due to the existence of the sulfate group. Therefore, we chose the original GAFF parameters to simulate PEO chains for SLE3S (see ESI,† for details). GAFF-LIPID parameters are also tested to describe the acyl chains in the triolein molecule. For the phenyl and sulfonate functional groups involved in the SDBS and SD2BS molecules, GAFF parameters are capable of simulating the correct intercolumn distances and free energies of binding of a molecule to a stack of Sunset Yellow54 and a thiacyanine dye,55 a system consisting of aromatic rings and sulfonate functional groups. Thus, the original GAFF parameters are applied directly to ionic surfactant head groups. As discussed below, this combination of GAFF/GAFF-LIPID parameters provides improved IFT predictions for surfactants at the water–triolein interface (Fig. 4).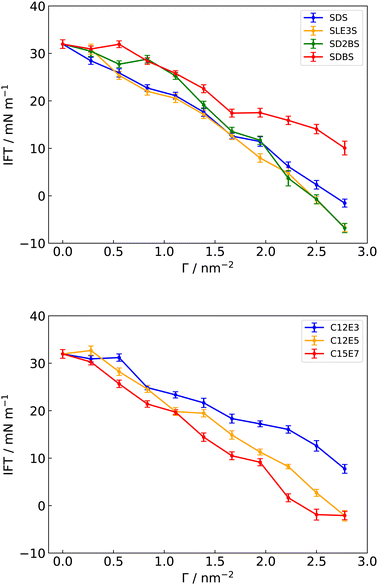 | ||
| Fig. 4 Simulated interfacial tensions (IFT) of different surfactants at a water–triolein interface, with GAFF/GAFF-LIPID parameters and TIP3P water model. | ||
Because of the lack of experimental data for some surfactants at the water–triolein interface, a water–surfactant–octane system is also employed for validation purposes. IFT simulation of a 36 nm2 water-80 C12E5–octane interface shows a value of 8.83 ± 0.35 mN m−1, with GAFF-LIPID for both C12E5 tail group and head group with the SPC/E water model, compared to a value of 25.21 ± 0.80 mN m−1 simulated from GAFF and SPC/E (experimental value of water–C12E4–hexadecane interface of 3.1 mN m−1).82 IFT calculations for the 36 nm2 water–70 SDS–octane system shows a value of 18.45 ± 0.48 mN m−1, when GAFF-LIPID is used for SDS tail groups with the SPC/E water model, compared to a value of 25.00 ± 0.54 mN m−1 simulated from GAFF and SPC/E (experimental value of 9.7 mN m−1).83
It should be noted that the SPC/E water model with GAFF parameters provides a more accurate IFT for the water–octane interface than the TIP3P water model (Table 1). In contrast (see Section 3.4), the TIP3P water model with GAFF/GAFF LIPID parameters is best for the water–triolein interface (Table 4). The reason why different oil interfaces require different water models for optimal IFT results is yet to be fully understood. However, it has been previously noted that subtle changes to water models can have a significant effect in both structural and dynamic properties.106
| Water models | IFT/mN m−1 |
|---|---|
| TIP3P | 31.96 ± 0.92 |
| SPC/E | 36.70 ± 0.56 |
| TIP4P | 29.03 ± 0.67 |
| TIP4P/2005 | 34.44 ± 0.87 |
| OPC4 | 42.48 ± 0.87 |
| Experimental | 3288 |
3.4 IFT predictions with GAFF/GAFF-LIPID for different water models
Different water models (SPC/E, TIP4P, TIP4P/2005, OPC4 in addition to TIP3P) are tested with GAFF/GAFF-LIPID parameters at the water–triolein interface (Table 4). The results suggest that the TIP3P water model gives a better performance in combination with this force field compared to the other tested water models. The combination of GAFF/GAFF-LIPID and TIP3P provides a value of 31.96 ± 0.92 mN m−1 (experimental value of 32 mN m−1).88 Noting that this is in line with a good performance from GAFF-derived parameters with the TIP3P water model in simulating IFT for the water–toluene interface.107Calculations for pentadecane in combination with different water models again show that IFT and ΔGhyd predictions are not strongly correlated (Table 5). Here, the IFT values for the water–pentadecane interface decrease from 71.07 ± 0.83 mN m−1 (GAFF and SPC/E) to 55.05 ± 0.44 mN m−1 (GAFF-LIPID and SPC/E) using the more flexible GAFF-LIPID chains (experimental value of 54.9 mN m−1);81 noting that for the same systems the values of ΔGhyd increase from 22.48 ± 0.58 kJ mol−1 to 30.13 ± 0.78 kJ mol−1 (experimental value 17.30 kJ mol−1).75 GAFF-LIPID also simulates reasonably good values for IFT of a 36 nm2 water-80 C12E5–octane interface and ρ for the surfactant molecule C12E5 (Table 6). Here, however ΔGhyd for C12E5 is underestimated. The contradiction between IFT and ΔGhyd from simulations might suggest a future reparametrisation of this force field may be necessary to study surfactant aggregation and micellization of surfactants in bulk water, as suggested by other work.99,108–110
| Force fields | IFT/mN m−1 | ρ/kg m−3 | ΔGhyd/kJ mol−1 |
|---|---|---|---|
| GAFF(TIP3P) | 76.26 ± 0.61 | 794.02 ± 0.28 | 17.24 ± 0.65 |
| GAFF-LIPID(TIP3P) | 45.86 ± 0.40 | 760.59 ± 0.33 | 24.12 ± 0.31 |
| GAFF(SPC/E) | 71.07 ± 0.83 | 794.02 ± 0.28 | 22.48 ± 0.58 |
| GAFF-LIPID(SPC/E) | 55.05 ± 0.44 | 760.59 ± 0.33 | 30.13 ± 0.78 |
| Experimental | 54.981 | 769100 | 17.3075 |
| Force fields | IFT/mN m−1 | ρ/kg m−3 | ΔGhyd/kJ mol−1 |
|---|---|---|---|
| a IFTCMC of water–C12E4–hexadecane interface. | |||
| GAFF | 25.21 ± 0.80 | 976.38 ± 0.43 | −49.37 ± 1.65 |
| GAFF/GAFF-LIPID | 8.83 ± 0.35 | 943.07 ± 0.30 | −41.58 ± 1.02 |
| Modified GAFF (q) | 22.10 ± 0.56 | 980.90 ± 0.79 | −60.06 ± 1.25 |
| Modified GAFF (ε) | 48.22 ± 0.55 | 1008.24 ± 0.47 | −56.86 ± 1.09 |
| GAFF-DC | 29.31 ± 0.51 | 973.82 ± 0.12 | −58.13 ± 1.78 |
| Experimental | 3.1a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82 82 |
96344 | −66.344 |
Finally, it is worth noting that, through visualization of dense surfactant layers at the interface, it is evident that GAFF parameters give significantly stiffer surfactant tails in comparison to GAFF-LIPID, resulting in lower areas per surfactant and higher order parameters in comparison to experiments;100 and, consequently, higher simulated IFT values are obtained for the same Γ. In these cases, using GAFF chains, more surfactant molecules can “fit” at a crowded interface because of closer molecular packing. For example, in simulations of water–surfactants–triolein interfaces, “frozen islands” of surfactants and holes in the surfactant layer interface have been observed with GAFF parameters, whereas a liquid state of surfactants at the interface is always observed with GAFF-LIPID chains (Fig. 6).
3.5 Surfactants at a water–vacuum interface
Despite the excellent performance of TIP3P for water–triolein IFTs, TIP3P water is found to provide poor predictions for ST at a water–vacuum interface. We see this when a variety of different water models are tested (Table 7), with several models failing to correctly predict the ST of pure water or the reduction in ST arising from surfactants. However, the 4-point rigid optimal point charge (OPC4) water model, which is designed to provide a better description of the electrostatic potential around a water molecule,46 is found to dramatically improve ST predictions using GAFF-derived force fields (Fig. 5). As noted above, the reason why different interfaces require different water models for optimal IFT results or ST results is yet to be fully understood. We have also included the ST simulated from C12E6 (Fig. 1) for prediction of the adsorption isotherm in Section 3.7. ST results for the water–vacuum interface with the OPC4 water model show a value of 70.66 ± 0.20 mN m−1 (experimental value of 72 mN m−1),111 and for a 36 nm2 water–100 SDS–vacuum shows a value of 34.51 ± 0.43 mN m−1 (experimental value of 39.5 mN m−1).112A further comparison is carried out between the simulated and experimental STs of the non-ionic surfactant C12E3 at a water–vacuum interface using the promising OPC4 water model. The experimental STCMC is approximately 30 mN m−1 and ΓMAX is 4.5 × 10−10 mol cm−2,113 compared to a simulated ST of 33.32 ± 0.37 mN m−1 at this ΓMAX, which corresponds to approximately 100 molecules of C12E3 at a 36 nm2 interface.
3.6 Maximum packing of surfactants
Good predictions of ΓMAX from simulation would ideally play an important role in screening new surfactants before synthesis. However, it should be noticed that within the framework of atomistic simulations, it is relatively easy for surfactants to become overpacked at the interface and the surface layer in the simulation box to become metastable, compared to multibody dissipative particle dynamics (M-DPD) simulations.114 Surfactants prefer to stay at an interface in AA MD even when the number of molecules leads to ΓMAX being exceeded. The experimental ΓMAX will occur at the CMC, when the chemical potential of the monomers at the interface is the same as that in solution and micelles. However, we have no good way to determine this equilibrium within AA simulations. However, we expect AA simulations to offer some information about ΓMAX, arising from packing considerations at the interface.Head group (i.e. –SO4−) density graphs of four surface concentrations of SDS molecules (i.e. 50 SDS, 70 SDS, 80 SDS and 130 SDS) at a 36 nm2 water–triolein interface are presented in Fig. 6. For the maximum packing of 70 SDS molecules, consistent heights are observed for surfactant head groups at the two interfaces. However, above this packing, variations from these smooth distributions start to be seen, eventually leading to major distortions of the surfactant layer. This suggests that it might be reasonable to estimate ΓMAX of surfactants from qualitative observation of a flat monolayer of surfactants. For example, it is straightforward to visualise that the monolayer of 70 SDS molecules at a 36 nm2 interface is relatively flat compared to 80 SDS molecules. However, this visualisation can be difficult to achieve in practice for many systems.
 | ||
| Fig. 6 Head group density graphs and head groups VMD captures of 50, 70, 80 and 130 SDS molecules at 36 nm2 water–triolein interface, simulated with GAFF/GAFF-LIPID parameters and TIP3P water model. | ||
We note that for 130 molecules of SDS (bottom frame in Fig. 6), which is well above ΓMAX, major distortions of the interface occur, with the system essentially creating additional interface to adjust to a large number of surfactants. In this case, the calculation of γ viaeqn (3) immediately fails because additional interfacial area has been created.
Interestingly, by applying qualitative observation of the monolayer of surfactants, the simulated ΓMAX and IFT at this ΓMAX of SDBS at the water–triolein interface are 100 molecules at a 36 nm2 interface and 10.06 ± 1.45 mN m−1 respectively, whereas the simulated ΓMAX and IFT at this ΓMAX of SD2BS are 80 molecules at a 36 nm2 interface and 3.69 ± 1.61 mN m−1 respectively. The difference between these two molecules might be explained by the lower density of dodecan-2-yl chains at the interface, compared to dodecyl.115,116 This observation is consistent with experimental value where experimental ΓMAX and STCMC of SD2BS at water–air interface (“hard river” water, 303.15 K) are 4.16 × 10−10 mol cm−2 and 36.4 mN m−1 respectively, experimental ΓMAX and STCMC of SD4BS (“hard river” water, 303.15 K) are 3.44 × 10−10 mol cm−2 and 28.2 mN m−1 respectively and experimental ΓMAX and STCMC of SD6BS (“hard river” water, 303.15 K) are 3.15 × 10−10 mol cm−2 and 27.5 mN m−1 respectively.117
3.7 Adsorption isotherms of surfactants
Using an MD-MTT framework (a combination of MD and molecular thermodynamics theory),41,118 it is, in principle, feasible to fully determine adsorption isotherms for non-ionic surfactants at a water–vacuum interface by simulation. AA MD determines three parameters: (i) the radius r of the surfactant, (ii) the second virial coefficient B for the interaction of surfactants at the interface and (iii) the free energy of adsorption ΔGads of the surfactant. By fitting the ST graph of C12E6 molecules at a water–vacuum interface, parameters r and B can be deduced. The relationship between surface pressure and surface concentration of non-ionic surfactants follows the equation41,118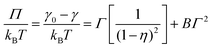 | (5) |
 | (6) |
Here, GAFF/GAFF-LIPID parameters with the OPC4 water model, and the OPLS-AA parameters with the SPC/E water model (as used by Sresht et al.)41 are used to simulate the ST of the C12E6 molecules at the water–vacuum interface. The fitted data from the GAFF/GAFF-LIPID and OPC4 model provides a r value of 0.279 nm and B value of 0 nm2, and the OPLS-AA and SPC/E model provides a r value of 0.272 nm and B value of −0.364 nm2 (Fig. 7). We note that neither graph in Fig. 7 exactly followed the theoretical functional form suggested. However, the start and end points at Γ = 0 nm−2 and Γ = ΓMAX are quite close and the fitted curve for the OPLS-AA and SPC/E model quite closely follows the simulation data. It should be noticed that the fitting data assumes a prior knowledge of an experimental ΓMAX of surfactants (i.e. 2.22 nm−2 for C12E6),119 and simulated IFT values that exceed ΓMAX are discarded. To fully predict the parameters r and B from the simulations, qualitative observations of a surfactant monolayer (Fig. 6) could be used to determine an approximate ΓMAX of C12E6 surfactants from simulations. Then, a calculated ΓMAX could be determined from the adsorption isotherm (Fig. 10) and compared with the previous ΓMAX value. If they are found to be different, then the fitting procedure in Fig. 7 could be iterated to calculate a new ΓMAX.
As part of an MD-MTT framework, it is necessary to know the change in the free energy for a molecule that is transferred from bulk water to the water–vacuum interface. The free energy curves for GAFF/GAFF-LIPID and OPC4, and GAFF/GAFF-LIPID and SPC/E are shown in Fig. 8 in the form of potentials of mean force, and the calculated ΔGads for different force fields and water model combinations are shown in Table 8. Interestingly, the results in Table 8 suggest that GAFF/GAFF-LIPID parameters (for surfactants) with the SPC/E water model reproduce the experimental ΔGads most closely. This is even though the combination of GAFF-LIPID and the SPC/E water produces a ΔGhyd for pentadecane that is more positive than the experiment, worse than GAFF and SPC/E, and worse than the excellent prediction for GAFF and TIP3P (Table 5). Here, of course, ΔGhyd is not the only contribution to ΔGads, and most of the experimental ΔGads arises from a lowering of the ST.40,95 This explains why GAFF/GAFF-LIPID parameters, which we see can provide accurate predictions of the lowering of ST, provide good agreement with the experimental ΔGads.
Based on simulation results from Fig. 7 and Table 8, r, B and ΔGads of C12E6 molecule (Table 9) are obtained with GAFF/GAFF-LIPID parameters and the OPC4 water model (for r and B) and the SPC/E water model (for ΔGads). As discussed in Section 3.3, the reasons why different physical measurements perform better with different optional water models are yet to be fully explored. Though we know that even small changes in the water models (charge and shape etc.) can lead to measurable differences in radial distribution functions and this is likely to have an effect on surface properties.106
| r/nm | B/nm2 | ΔGads/kJ mol−1 |
|---|---|---|
| 0.279 | 0 | −44.05 |
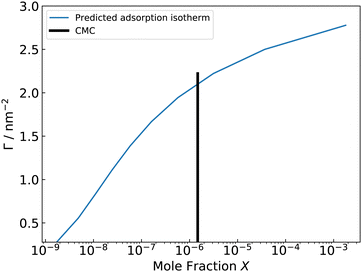
From the calculated adsorption isotherm graph (Fig. 9), the experimental mole fraction of C12E6 of 1.477 × 10−6 gives a simulated ΓMAX of 76 C12E6 molecules at a 36 nm2 water–vacuum interface, which corresponds to a simulated ST of 35 mN m−1 (Fig. 10). The results agree well with the experimental ΓMAX of 3.7 × 10−10 mol cm−2 (80 surfactants at 36 nm2) and experimental STCMC of 32 mN m−1.118–120 The agreement between the simulation data and the experimental data also validates the use of GAFF-LIPID “atomtype c3” for non-ionic surfactant PEO chains.
With further validation, the MD-MTT framework could be extended to predict both ionic surfactants and non-ionic surfactants at the water–oil and water–vacuum interface, with the help of the force fields refined in this paper.121,122 In combination with CMCs calculated directly from dissipative particle dynamics (DPD) simulations,123–127 or slightly more expensive approaches such as many-body dissipative particle dynamics (M-DPD)114 or coarse-grained molecular dynamics,128 this provides a way to fully predict ΓMAX, γCMC, CMC and the adsorption isotherm of surfactants directly from simulation.
Based on the simulations presented in this study, we summarise the most suitable force field combinations in Table 10 for each AA MD simulation system mentioned above.
| Simulation systems | Force fields and (or) water models |
|---|---|
| IFT for water–triolein | GAFF/GAFF-LIPID + TIP3P |
| IFT for water–octane | GAFF + SPC/E |
| IFT for water–pentadecane | GAFF-LIPID + SPC/E |
| ΔGhyd of pentadecane | GAFF + TIP3P |
| ST for water–vacuum | OPC4 |
| ΔGads from water–vacuum | SPC/E |
4 Conclusions
AA MD simulations have been used to predict accurately the value of γ and the reduction of γ due to surfactants at the water–triolein and water–vacuum interfaces. In this study, we tested the performance of GAFF, and variants thereof, in the prediction of γ for different surfactants at interfaces.20 Correct predictions of ρ for pure components are important to ensure accurate prediction of γ. Thus, GAFF-LIPID,100 which makes better predictions for ρ and isothermal compressibility of long carbon chain compounds, provides much better predictions for γ, in most systems, than GAFF. Based on the results from this study we highlight recommended force field/water model combinations for predictions of IFT, ST, ΔGhyd and ΔGads from AA MD simulation systems as summarised in Table 10.The TIP3P water model was used to provide good IFT predictions for water with a series of oils and was found to be compatible with GAFF and GAFF-derived parameter sets.53 However, TIP3P water provides poor predictions for ST of water–vacuum interfaces. A variety of different water models were tested to improve these predictions, with several models failing to correctly predict the ST of pure water or the reduction in ST arising from different surfactants. However, the 4-point rigid optimal point charge (OPC4) water model, which provides a better description of the electrostatic potential around a water molecule, is found to dramatically improve ST predictions using GAFF-derived force fields.46
A major issue related to AA MD predictions of γ values arises from difficulties in predicting the maximum surface concentration, ΓMAX, to find the maximum reduction in ST for a given surfactant. With the help of a MD-MTT framework and an experimental CMC, simulations successfully predict a STCMC for C12E6 of 35 mN m−1 at ΓMAX with GAFF/GAFF-LIPID parameters, which compares favourably to the experimental value of 32 mN m−1.118–120
Finally, it is worth highlighting some of the slightly unsatisfactory findings arising from this work. TIP3P, the best water model for the water–triolein interface (with the GAFF/GAFF LIPID force field), was much poorer than OPC4 in predicting surface tensions at the water–vacuum interface. Moreover, the various water models have differing performance in relation to the predictions of ΔGads and ΔGhyd. Here, it is worth recalling that all these water models are effective two-body potentials, in which higher body terms have been combined into the effective pair potential. Although this is reasonable as an approximation for bulk water, the interactions vary at an interface or when the dielectric environment changes. Hence, it is difficult to predict which water model will behave best in combination with different oil and surfactant force fields at different interfaces. An interesting extension to the current work may arise from the use of polarisable force fields,129 where the ability of the force field to adjust to changes in the molecular environment and relative permittivity potentially provide a way to address these issues.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from the UK research council, EPSRC, through the ANTENNA Prosperity Partnership (Grant No. EP/V056891/1). The authors thank Durham University for providing computer time on its high performance computer (HPC) system, Hamilton. This work also made use of the HPC system, Bede, at the N8 Centre of Excellence in Computationally Intensive Research (N8 CIR) provided and funded by the N8 research partnership and EPSRC (Grant No. EP/T022167/1). The Centre is co-ordinated by the Universities of Durham, Manchester, and York. J. L. thanks Procter and Gamble for providing partial studentship funding.Notes and references
- J. Zhao, X. Liu, Y. Wu, D.-S. Li and Q. Zhang, Coord. Chem. Rev., 2019, 391, 30–43 CrossRef CAS.
- M. Palmer and H. Hatley, Water Res., 2018, 147, 60–72 CrossRef CAS PubMed.
- D. B. Tripathy, A. Mishra, J. Clark and T. Farmer, Comptes Rendus Chim., 2018, 21, 112–130 CrossRef CAS.
- M. Zambianchi, M. Durso, A. Liscio, E. Treossi, C. Bettini, M. L. Capobianco, A. Aluigi, A. Kovtun, G. Ruani, F. Corticelli, M. Brucale, V. Palermo, M. L. Navacchia and M. Melucci, Chem. Eng. J., 2017, 326, 130–140 CrossRef CAS.
- A. Seweryn, Adv. Colloid Interface Sci., 2018, 256, 242–255 CrossRef CAS PubMed.
- S. P. Callender, J. A. Mathews, K. Kobernyk and S. D. Wettig, Int. J. Pharm., 2017, 526, 425–442 CrossRef CAS PubMed.
- H. Rostamabadi, S. R. Falsafi and S. M. Jafari, J. Controlled Release, 2019, 298, 38–67 CrossRef CAS PubMed.
- A. A. Umar, I. B. M. Saaid, A. A. Sulaimon and R. B. M. Pilus, J. Pet. Sci. Eng., 2018, 165, 673–690 CrossRef CAS.
- S. J. Geetha, I. M. Banat and S. J. Joshi, Biocatal. Agric. Biotechnol., 2018, 14, 23–32 CrossRef.
- R. E. Pattle, Nature, 1955, 175, 1125–1126 CrossRef CAS PubMed.
- M. A. Bos and T. van Vliet, Adv. Colloid Interface Sci., 2001, 91, 437–471 CrossRef CAS PubMed.
- J. J. Scheibel, J. Surfactants Deterg., 2004, 7, 319–328 CrossRef CAS.
- C.-H. Chang and E. I. Franses, Colloids Surf., A, 1995, 100, 1–45 CrossRef CAS.
- L. Peltonen, J. Hirvonen and J. Yliruusi, J. Colloid Interface Sci., 2001, 240, 272–276 CrossRef CAS PubMed.
- S. Paria and K. C. Khilar, Adv. Colloid Interface Sci., 2004, 110, 75–95 CrossRef CAS PubMed.
- T. P. Golub, L. K. Koopal and M. P. Sidorova, Colloid J., 2004, 66, 38–43 CrossRef CAS.
- T. P. Golub and L. K. Koopal, Colloid J., 2004, 66, 44–47 CrossRef CAS.
- B. Smit, A. G. Schlijper, L. A. M. Rupert and N. M. Van Os, J. Phys. Chem., 1990, 94, 6933–6935 CrossRef CAS.
- D. Frenkel, Eur. Phys. J. Plus, 2013, 128, 10 CrossRef.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- C. Oostenbrink, A. Villa, A. E. Mark and W. F. V. Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, J. Comput. Chem., 2010, 31, 671–690 CrossRef CAS PubMed.
- C. Jian, Q. Liu, H. Zeng and T. Tang, Energy Fuels, 2018, 32, 3225–3231 CrossRef CAS.
- Z.-Y. Liu, C. Wang, H. Zhou, Y. Wang, L. Zhang, L. Zhang and S. Zhao, J. Mol. Model., 2017, 23, 112 CrossRef PubMed.
- S. S. Jang, S.-T. Lin, P. K. Maiti, M. Blanco, W. A. Goddard, P. Shuler and Y. Tang, J. Phys. Chem. B, 2004, 108, 12130–12140 CrossRef CAS.
- G. Alonso, P. Gamallo, A. Mejía and R. Sayós, J. Mol. Liq., 2020, 299, 112223 CrossRef CAS.
- J. Xu, Y. Zhang, H. Chen, P. Wang, Z. Xie, Y. Yao, Y. Yan and J. Zhang, J. Mol. Struct., 2013, 1052, 50–56 CrossRef CAS.
- J. D. Berry, M. J. Neeson, R. R. Dagastine, D. Y. C. Chan and R. F. Tabor, J. Colloid Interface Sci., 2015, 454, 226–237 CrossRef CAS PubMed.
- R. E. Isele-Holder and A. E. Ismail, J. Phys. Chem. B, 2014, 118, 9284–9297 CrossRef CAS PubMed.
- T. Cheng, Q. Chen, F. Li and H. Sun, J. Phys. Chem. B, 2010, 114, 13736–13744 CrossRef CAS PubMed.
- X. Tang, K. J. Huston and R. G. Larson, J. Phys. Chem. B, 2014, 118, 12907–12918 CrossRef CAS PubMed.
- C. Jian, M. R. Poopari, Q. Liu, N. Zerpa, H. Zeng and T. Tang, J. Phys. Chem. B, 2016, 120, 5646–5654 CrossRef CAS PubMed.
- N. R. Biswal, N. Rangera and J. K. Singh, J. Phys. Chem. B, 2016, 120, 7265–7274 CrossRef CAS PubMed.
- S. Zeppieri, J. Rodríguez and A. L. López de Ramos, J. Chem. Eng. Data, 2001, 46, 1086–1088 CrossRef CAS.
- K. J. Mysels, Langmuir, 1986, 2, 423–428 CrossRef CAS.
- D. Hu, A. Mafi and K. C. Chou, J. Phys. Chem. B, 2016, 120, 2257–2261 CrossRef CAS PubMed.
- A. P. Dudgeon, PhD thesis, Durham University, 2017.
- T. F. Trados, Surfactants, Academic Press, London, 1984 Search PubMed.
- G. Barnes and I. Gentle, Interfacial Science: An Introduction, OUP, Oxford, 2011 Search PubMed.
- V. Sresht, E. P. Lewandowski, D. Blankschtein and A. Jusufi, Langmuir, 2017, 33, 8319–8329 CrossRef CAS PubMed.
- W. Shinoda, R. DeVane and M. L. Klein, Mol. Simul., 2007, 33, 27–36 CrossRef CAS.
- K. J. Huston and R. G. Larson, Langmuir, 2015, 31, 7503–7511 CrossRef CAS PubMed.
- Z. Shen and H. Sun, J. Phys. Chem. B, 2015, 119, 15623–15630 CrossRef CAS PubMed.
- D. Seddon, E. A. Müller and J. T. Cabral, J. Colloid Interface Sci., 2022, 625, 328–339 CrossRef CAS PubMed.
- S. Izadi, R. Anandakrishnan and A. V. Onufriev, J. Phys. Chem. Lett., 2014, 5, 3863–3871 CrossRef CAS PubMed.
- A. Jakalian, B. L. Bush, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2000, 21, 132–146 CrossRef CAS.
- A. Jakalian, D. B. Jack and C. I. Bayly, J. Comput. Chem., 2002, 23, 1623–1641 CrossRef CAS PubMed.
- J. Wang, W. Wang, P. A. Kollman and D. A. Case, J. Mol. Graph. Model., 2006, 25, 247–260 CrossRef CAS PubMed.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CAS.
- D. A. Case, T. E. Cheatham III, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr., A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688 CrossRef CAS PubMed.
- A. W. Sousa da Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, 367 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- F. Chami and M. R. Wilson, J. Am. Chem. Soc., 2010, 132, 7794–7802 CrossRef CAS PubMed.
- R. Thind, M. Walker and M. R. Wilson, Adv. Theory Simul., 2018, 1, 1800088 CrossRef.
- G. Yu, M. Walker and M. R. Wilson, Phys. Chem. Chem. Phys., 2021, 23, 6408–6421 RSC.
- G. Yu and M. R. Wilson, J. Mol. Liq., 2022, 345, 118210 CrossRef CAS.
- G. Yu and M. R. Wilson, Soft Matter, 2022, 18, 3087–3096 RSC.
- W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670 CrossRef CAS PubMed.
- L. S. Dodda, J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2017, 121, 3864–3870 CrossRef CAS PubMed.
- L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336 CrossRef CAS PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- W. F. Van Gunsteren and H. J. C. Berendsen, Mol. Simul., 1988, 1, 173–185 CrossRef.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- E. J. Haug, J. S. Arora and K. Matsui, J. Optim. Theory Appl., 1976, 19, 401–424 CrossRef.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1949, 17, 338–343 CrossRef CAS.
- N. J. Boyd, PhD thesis, Durham University, 2017.
- D. L. Mobley and J. P. Guthrie, J. Comput.-Aided Mol. Des., 2014, 28, 711–720 CrossRef CAS PubMed.
- C. H. Bennett, J. Comput. Phys., 1976, 22, 245–268 CrossRef.
- R. Zangi, H. Kovacs, W. F. van Gunsteren, J. Johansson and A. E. Mark, Protein Struct. Funct. Genet., 2001, 43, 395–402 CrossRef CAS PubMed.
- F. Fraternali and W. F. Van Gunsteren, Biopolymers, 1994, 34, 347–355 CrossRef CAS.
- J. A. Lemkul and D. R. Bevan, J. Phys. Chem. B, 2010, 114, 1652–1660 CrossRef CAS PubMed.
- J. S. Hub, B. L. de Groot and D. van der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720 CrossRef CAS.
- A. Goebel and K. Lunkenheimer, Langmuir, 1997, 13, 369–372 CrossRef CAS.
- M. J. Rosen and D. S. Murphy, Langmuir, 1991, 7, 2630–2635 CrossRef CAS.
- S. J. Rehfeld, J. Phys. Chem., 1967, 71, 738–745 CrossRef CAS.
- M. J. Rosen, A. W. Cohen, M. Dahanayake and X. Y. Hua, J. Phys. Chem., 1982, 86, 541–545 CrossRef CAS.
- P. H. Elworthy and K. J. Mysels, J. Colloid Interface Sci., 1966, 21, 331–347 CrossRef CAS.
- C. J. Fennell, K. L. Wymer and D. L. Mobley, J. Phys. Chem. B, 2014, 118, 6438–6446 CrossRef CAS PubMed.
- W. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 2016 Search PubMed.
- L. Wang, D. Atkinson and D. M. Small, J. Biol. Chem., 2005, 280, 4154–4165 CrossRef CAS PubMed.
- J. P. R. Day, P. D. A. Pudney and C. D. Bain, Phys. Chem. Chem. Phys., 2010, 12, 4590 RSC.
- F. Mori, J. Lim, O. Raney, C. Elsik and C. Miller, Colloids Surf., 1989, 40, 323–345 CrossRef CAS.
- D. S. Murphy and M. J. Rosen, J. Phys. Chem., 1988, 92, 2870–2873 CrossRef CAS.
- D. Dittmar, R. Eggers, H. Kahl and S. Enders, Chem. Eng. Sci., 2002, 57, 355–363 CrossRef CAS.
- T. T. Phan, J. H. Harwell and D. A. Sabatini, J. Surfactants Deterg., 2010, 13, 189–194 CrossRef CAS.
- T. T. Phan, C. Attaphong and D. A. Sabatini, J. Am. Oil Chem. Soc., 2011, 88, 1223–1228 CrossRef CAS.
- M. Rosen and J. Kunjappu, Surfactants and Interfacial Phenomena, Wiley, 2012 Search PubMed.
- C. Caleman, P. J. van Maaren, M. Hong, J. S. Hub, L. T. Costa and D. van der Spoel, J. Chem. Theory Comput., 2012, 8, 61–74 CrossRef CAS PubMed.
- N. J. Boyd and M. R. Wilson, Phys. Chem. Chem. Phys., 2015, 17, 24851–24865 RSC.
- N. J. Boyd and M. R. Wilson, Phys. Chem. Chem. Phys., 2018, 20, 1485–1496 RSC.
- A. Akinshina, M. Walker, M. R. Wilson, G. J. T. Tiddy, A. J. Masters and P. Carbone, Soft Matter, 2015, 11, 680–691 RSC.
- C. J. Dickson, L. Rosso, R. M. Betz, R. C. Walker and I. R. Gould, Soft Matter, 2012, 8, 9617–9627 RSC.
- A. A. Freitas, F. H. Quina and F. A. Carroll, J. Phys. Chem. B, 1997, 101, 7488–7493 CrossRef CAS.
- S. W. I. Siu, K. Pluhackova and R. A. Böckmann, J. Chem. Theory Comput., 2012, 8, 1459–1470 CrossRef CAS PubMed.
- D. B. Macleod, Trans. Faraday Soc., 1923, 19, 38–41 RSC.
- J. Escobedo and G. A. Mansoori, AIChE J., 1996, 42, 1425–1433 CrossRef CAS.
- M. Kunieda, K. Nakaoka, Y. Liang, C. R. Miranda, A. Ueda, S. Takahashi, H. Okabe and T. Matsuoka, J. Am. Chem. Soc., 2010, 132, 18281–18286 CrossRef CAS PubMed.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- K. D. Papavasileiou, O. A. Moultos and I. G. Economou, Fluid Ph. Equilib., 2018, 476, 30–38 CrossRef CAS.
- B. C. Stephenson, K. A. Stafford, K. J. Beers and D. Blankschtein, J. Phys. Chem. B, 2008, 112, 1634–1640 CrossRef CAS PubMed.
- B. C. Stephenson, K. A. Stafford, K. J. Beers and D. Blankschtein, J. Phys. Chem. B, 2008, 112, 1641–1656 CrossRef CAS PubMed.
- J. Iyer, J. D. Mendenhall and D. Blankschtein, J. Phys. Chem. B, 2013, 117, 6430–6442 CrossRef CAS PubMed.
- C. Vega and E. de Miguel, J. Chem. Phys., 2007, 126, 154707 CrossRef CAS PubMed.
- M. Dahanayake, A. W. Cohen and M. J. Rosen, J. Phys. Chem., 1986, 90, 2413–2418 CrossRef CAS.
- J. R. Lu, E. M. Lee, R. K. Thomas, J. Penfold and S. L. Flitsch, Langmuir, 1993, 9, 1352–1360 CrossRef CAS.
- R. L. Hendrikse, C. Amador and M. R. Wilson, Soft Matter, 2023, 19, 3590–3604 RSC.
- J. Yang, W. Qiao, Z. Li and L. Cheng, Fuel, 2005, 84, 1607–1611 CAS.
- P. H. Doe, W. H. Wade and R. S. Schechter, J. Colloid Interface Sci., 1977, 59, 525–531 CrossRef CAS.
- Y.-P. Zhu, M. J. Rosen, S. W. Morrall and J. Tolls, J. Surfactants Deterg., 1998, 1, 187–193 CrossRef CAS.
- Y. J. Nikas, S. Puvvada and D. Blankschtein, Langmuir, 1992, 8, 2680–2689 CrossRef CAS.
- J. E. Carless, R. A. Challis and B. A. Mulley, J. Colloid Sci., 1964, 19, 201–212 CrossRef CAS.
- J. M. Corkill, J. F. Goodman and S. P. Harrold, Trans. Faraday Soc., 1964, 60, 202 RSC.
- M. Mulqueen and D. Blankschtein, Langmuir, 1999, 15, 8832–8848 CrossRef CAS.
- M. Mulqueen and D. Blankschtein, Langmuir, 2002, 18, 365–376 CrossRef CAS.
- W. C. Swope, M. A. Johnston, A. I. Duff, J. L. McDonagh, R. L. Anderson, G. Alva, A. T. Tek and A. P. Maschino, J. Phys. Chem. B, 2019, 123, 1696–1707 CrossRef CAS PubMed.
- M. A. Johnston, A. I. Duff, R. L. Anderson and W. C. Swope, J. Phys. Chem. B, 2020, 124, 9701–9721 CrossRef CAS PubMed.
- A. Del Regno, P. B. Warren, D. J. Bray and R. L. Anderson, J. Phys. Chem. B, 2021, 125, 5983–5990 CrossRef CAS PubMed.
- R. L. Hendrikse, A. E. Bayly and P. K. Jimack, J. Phys. Chem. B, 2022, 126, 8058–8071 CrossRef CAS PubMed.
- S. J. Gray, M. Walker, R. Hendrikse and M. R. Wilson, Soft Matter, 2023, 19, 3092–3103 RSC.
- S. D. Anogiannakis, P. C. Petris and D. N. Theodorou, J. Phys. Chem. B, 2020, 124, 556–567 CrossRef CAS PubMed.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. J. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06170a |
| This journal is © the Owner Societies 2024 |