Tuning the low-temperature phase behavior of aqueous ionic liquids

Abstract

Water's anomalous behavior is often explained using a two-liquid model, where two types of water, high-density liquid (HDL) and low-density liquid (LDL), can be separated via a liquid–liquid phase transition (LLPT) at low temperature. Mixtures of water and the ionic liquid hydrazinium trifluoroacetate were suggested to also show an LLPT but with the advantage that there is no rapid ice crystallization hampering its observation. It remains controversial whether these solutions exhibit an LLPT or are instead associated with complex phase separation phenomena. We here show detailed low-temperature calorimetry and diffraction experiments on aqueous solutions containing hydrazinium trifluoroacetate and other similar ionic liquids, all at a solute mole fraction of x = 0.175. Hydrazinium trifluoroacetate, ammonium trifluoroacetate, ethylammonium trifluoroacetate and hydrazinium pentafluoropropionate all boast exothermic transitions unrelated to crystallization as well as remarkable structural changes upon cooling into the glassy state. We propose a model inspired by micelle formation and decomposition in surfactant solutions, which is complemented by MD simulations and allows rationalizing the rich phase behavior of our mixtures during cooling. The fundamental aspect of the model is the hydrophobic nature of fluorinated anions that enables aggregation, which is reversed upon cooling and culminates in the remarkable exothermic first-order transition observed at low temperature. That is, we assign the first-order transition not to an LLPT but to phase-separations similar to the ones when falling below the Krafft temperature. All other solutions merely show simple vitrification behavior. Still, they exhibit distinct differences in liquid fragility, which is decreased continuously with decreasing hydrophobicity of the anions. This might enable the systematic tuning of ionic liquids with the goal of designing aqueous solutions of specific fragility.

---

Introduction

Water is a simple, yet fascinating liquid with a range of unique physical and chemical properties that make it essential for life as we know it.¹ Despite the huge amount of research dedicated to elucidating its nature, there are still many aspects of water's behavior that remain poorly understood. This includes numerous anomalies,^2,3 especially the apparently diverging behavior of the isobaric heat capacity, isothermal compressibility and expansion coefficient of the liquid upon supercooling, which puzzled researchers for decades.⁴ In order to explain this peculiar behavior, different models have been suggested, including the Speedy stability limit conjecture,⁵ the liquid–liquid critical point (LLCP) scenario,⁶ the singularity-free scenario⁷ and the critical-point-free scenario.⁸ Especially in recent years, many pieces of evidence were gathered in favor of the LLCP scenario, both from the experimental and computational side.⁹ In essence, the scenario introduces a second critical point in the “no man's land”, the temperature-pressure window in which supercooled water rapidly crystallizes to ice.¹⁰ This critical point is analogous to the one involving liquid and vapor, and hence tied to a phase transition from one fluid to another. In the case of this second critical point however, it does not comprise liquid and gas but a so-called liquid–liquid phase transition (LLPT) between a low- (LDL) and a high-density liquid (HDL).¹¹

In simulations, ice crystallization usually poses no issue and consequently, this scenario could be proven for classical full-atomistic water models such as ST2, TIP4P/2005 and TIP4P/Ice.^12,13 The LLCP scenario most likely also applies to many other water models,^14–18 although definitive proof is still sought. On the other hand, direct experimental evidence is difficult to gather as many traits exclusive to the LLCP scenario are hidden in the no man's land, behind the curtain of crystallization. In particular, observation of the elusive LLPT is a necessity for the LLCP hypothesis.¹⁹ Here, a common experimental approach is to start from low- (LDA) and high-density amorphous ice (HDA), which represent the glassy proxies of the two liquids in this scenario.^20,21 The liquids are then accessed by heating the glasses above their glass transition temperatures^22–27 where the LLPT could be induced through de-/compression. Still, also these liquids tend to crystallize rather rapidly,²⁸ thereby hampering the observation of the LLPT with conventional experimental techniques. In 2011, Winkel et al. demonstrated the LLPT at 140 K upon decompression by showing that the first-order transition takes place in the deeply supercooled, ultraviscous regime, above both glass transition temperatures related to HDL and LDL.²⁹ Later on, when employing sophisticated pump–probe techniques, a first-order transition that could be related to the LLPT was also observed at higher temperatures and shorter time scales.^30,31 However, these studies are not straightforward and require not only an elaborate experimental setup (including accurate pressure and temperature control) but also extensive data analysis.

As a result, alternative approaches exist that usually aim at unveiling the LLPT by suppressing ice crystallization, e.g., using confinement³² or aqueous solutions.³³ Notably, in the field of aqueous solutions, observation of the LLPT was reported in binary mixtures containing either glycerol,³⁴ the ionic liquid hydrazinium trifluoroacetate (N₂H₅⁺TFA⁻),^35,36 trehalose³⁷ or LiCl.³⁸ In these cases, the LLPT was observed through cooling/heating at ambient pressure conditions, though, without the need of pressurization during any point of the experiment. The LLPT claims are however not free from controversy.^39–45 For LiCl solutions, the transition does not take place in chemical equilibrium at ambient pressure, but only in the direction to lower chemical potential, from HDL to LDL, and not backwards. In the case of water–glycerol, it is difficult to differentiate the potential LLPT from crystallization of small ice crystallites.^40,41,45 Water–N₂H₅⁺TFA⁻ solutions on the other hand, are especially puzzling because they experience an unprecedented first-order transition involving latent heat upon cooling, that is reversible and without ice crystallization.^35,36,46 This could possibly imply chemical equilibrium, where the high-pressure situation is reached at ambient conditions through electrostrictive forces of ions. This transition is accompanied by a strengthening of hydrogen bonding³⁶ and an increase in tetrahedrality.⁴⁶ In addition, it shifts significantly to lower temperatures upon H/D isotope substitution.⁴⁷ Although this would be consistent with the LLPT related to water,⁴⁸ it is missing other signature traits known from the pure water case. Specifically, the halo peak pertaining to low-density solution (LDL-/LDA-like) in XRD diffraction and the pressure-induced polyamorphic transition back to high-density solution (HDL-/HDA-like) are lacking.⁴⁴ Based on a recent molecular dynamics study, Zanetti-Polzi et al. proposed that the transition is coupled to a cooling-induced phase separation, where ionic liquid segregates on the nanoscale.⁴⁹ Simultaneously, water rearranges from predominantly high-density states in the mixed phase to low-density states in the unmixed phase. Nanosegregation itself is not a well defined term and used for a plethora of phenomena related to structural heterogeneity: in concentrated sorbitol solutions, water segregates from sorbitol on the nanoscale by filling up voids within the solute matrix.⁵⁰ In many room temperature ionic liquids, polar and apolar chains separate from each other even without the addition of water.⁵¹ Eutectic LiCl–water and LiSCN–water solutions exhibit a nanophase separation upon cooling that one could mistake for an LLPT.^52,53 All these cases of nanosegregation – while mechanistically different from each other – have in common that (i) there is structural inhomogeneity that is not macroscopic (on the order of few nanometer or below), and (ii) they are not associated with a substantial release of latent heat. To the best of our knowledge, the “Angell mix” (H₂O + N₂H₅⁺TFA⁻ with solute mole fraction x ≈ 0.15–0.20) is the first and only example where such segregation is accompanied by an exothermic first-order-like transition. This would justify calling the nanophase separation a liquid–liquid transition (LLT). The LLPT however is associated with the one-component system water, where, composition changes cannot occur by definition. Hence, we will refrain from using the expression “LLPT” and instead use the more general “LLT” in this work, bearing in mind possible composition changes due to (nano)segregation.

The unprecedented LLT in the Angell mix suggests that aqueous ionic liquids are promising candidates for discovering intriguing low-temperature phase behavior. In that regard, one of their key advantages for experimentalists is tunability, which allows their physicochemical properties to be customized by modifying the cation and anion components.⁵⁴ In the present work, we use this tunability to prepare selected aqueous ionic liquids, in which either the cation or the anion of N₂H₅⁺TFA⁻ is replaced with compounds similar in chemical structure (see Fig. 1). Similarity is achieved by keeping the core functional group of the respective ions, i.e., the NH₃⁺ in hydrazinium and the COO⁻ in trifluoroacetate, and only altering the side chains. That is, we use cations R₁–NH₃⁺ where R₁ = NH₂ (hydrazinium), H (ammonium), CH₃ (methylammonium), C₂H₅ (ethylammonium), and anions R₂–COO⁻ where R₂ = CF₃ (trifluoroacetate), CCl₃ (trichloroacetate), CHCl₂ (dichloroacetate), CH₃ (acetate), C₂F₅ (pentafluoropropionate). This difference in chemical nature has an impact on hydrogen-bonding ability and hydrophobicity of the solute. We probe the low-temperature phase behavior of the aqueous solutions at a constant solute mole fraction x = 0.175 (equating to 4.71 water molecules per molecule of ionic liquid) employing differential scanning calorimetry (DSC). Solutions exhibiting extraordinary phase behavior are further investigated using X-ray diffraction (XRD). Additional mechanistic insights are gained via molecular dynamics (MD) simulations.

Fig. 1 Cations (red box) and anions (blue box) employed in this work. The reference solute hydrazinium trifluoroacetate is shown at the top. One set of ionic liquids is designed by exchanging the H₂N-group of hydrazinium (red circle) with H (ammonium), CH₃ (methylammonium) or C₂H₅ (ethylammonium) while keeping the NH₃⁺ group and the TFA⁻ anion. In the other set, the CF₃-group of trifluoroacetate (blue circle) is replaced by CCl₃ (trichloroacetate), CHCl₂ (dichloroacetate), CH₃ (acetate) or C₂F₅ (pentafluoropropionate) while keeping the COO⁻ group and the hydrazinium cation.

Materials and methods

Solutions of N₂H₅⁺TFA⁻ and water were prepared through a simple acid/base neutralization reaction. Hydrazine-monohydrate N₂H₄·H₂O and trifluoroacetic acid TFA were purchased from Sigma Aldrich and used without further purification. First, the sample vial was flushed with argon and placed in an ice bath. Then, stochiometric amounts of TFA were carefully added to the aqueous hydrazine. Finally, water was added until the composition of solution was at a solute mole fraction of x = 0.175 (considering also water from N₂H₄·H₂O). All other aqueous solutions with x = 0.175 were prepared in a similar fashion using commercially available educts and following the neutralization reactions shown below:

Methylamine CH₃NH₂ + TFA → CH₃NH₃⁺TFA⁻

Ethylamine C₂H₅NH₂ + TFA → C₂H₅NH₃⁺TFA⁻

N₂H₄ + trichloroacetic acid TCA → N₂H₅⁺TCA⁻

N₂H₄ + dichloroacetic acid DCA → N₂H₅⁺DCA⁻

N₂H₄ + acetic acid HOAc → N₂H₅⁺OAc⁻

N₂H₄ + pentafluoroproprionic acid PFP → N₂H₅⁺PFP⁻

The only exception is ammonium trifluoroacetate NH₄⁺TFA⁻, which is available directly from Sigma Aldrich and was simply dissolved in water.

Thermal behavior of solutions was studied using a DSC8000 by PerkinElmer calibrated for low temperatures with indium, adamantane and cyclopentane.⁵⁵ About 10 μL of each solution (corresponding to roughly 10–15 mg of sample, depending on the density of solution) were weighed in aluminum crucibles, sealed airtight and loaded into the instrument. Each sample was subjected to 6 freeze-and-thaw cycles. We used different rates Q_cool for the cooling scans (100, 50, 30, 10, 5 and 2 K min⁻¹) but the same heating rate Q_heat = 30 K min⁻¹ for the heating scans. This protocol was performed at least twice for each solution to ensure reproducibility.

Diffraction experiments were carried out on a D8 Bruker Advance X-ray diffractometer using a CuKα X-ray source (λ = 0.154178 nm) including parallel beam optics, and a LynxEye XE-T array detector. The sample holder is made of nickel-plated copper and can be cooled to ∼15 K using our FMB Oxford chamber and helium cryostat. Diffractograms of liquids were recorded at 300 K, after pipetting 200 μL of solution onto the sample holder. Diffraction data of glasses were collected at 80 K, after quenching in liquid nitrogen (Q_cool ≈ 100–1000 K min⁻¹), grinding the transparent product to a fine powder and transferring it onto the precooled sample holder.

MD simulations of N₂H₅⁺TFA⁻ solution are performed at 300 K and 1 bar using a solute molar fraction x = 0.16, which is very close to the mole fraction used in experiments. In the initial configuration the ions are placed at the interface with water, resulting in an initially unmixed solution. The TIP5P model⁵⁶ is used for water. OPLS-AA force field parameters, generated with the LigParGen tool⁵⁷ are used for N₂H₅⁺ and TFA⁻ ions apart from the atomic partial charges that were computed using a series of optimized N₂H₅⁺TFA⁻ ion pairs and then using a scaling factor of 0.9.⁵⁸ MD simulations are performed with the GROMACS package (version 5.1.2)⁵⁹ in the NPT ensemble using a rectangular simulation box, the velocity rescaling temperature coupling⁶⁰ and the Parrinello–Rahman barostat⁶¹ with 2 ps relaxation times. Periodic boundary conditions are used, and the long-range electrostatic interactions are treated with the particle mesh Ewald method⁶² with a real space cutoff of 0.9 nm. The Lennard-Jones potential is truncated at 0.9 nm. The LINCS algorithm⁶³ is used to constrain bond lengths along with a 2 fs time step. Additionally, the popular density-based clustering algorithm DBSCAN is used to detect possible phase separation.^64,65 DBSCAN starts from a query point and expands clusters around it. To do that, it uses a cutoff distance (ε) and a threshold number of neighbors (minPts, also including the query point). In other words, the N points (with N ≥ minPts) within a radius ε belong to the same cluster. The point that is surrounded by N − 1 other points within ε is the core point. If one of the other N − 1 points is also surrounded by N ≥ minPts−1 points within ε, it becomes a core point itself, and the cluster gets bigger.

Results

Thermal analysis

Fig. 2 shows differential scanning calorimetry (DSC) traces for a number of aqueous solutions of x = 0.175. In the top panel, cations are exchanged where trifluoroacetate is always the anion. In the bottom panel, anions are exchanged, where hydrazinium serves as the cation. Left panels show the initial cooling scans, and the right panels show the subsequent heating scan. Additionally, the behavior of the simple glass-forming molecular liquid glycerol is depicted as dashed grey line in all panels for comparison. Upon cooling, glycerol experiences merely a glass transition with a glass transition temperature T_g ≈ 197 K.⁶⁶ This is manifested as a typical step-like change in heat capacity, or here, heat flow. Upon heating, the glassy glycerol exhibits the reverse glass-to-liquid transition with a typical heat capacity overshoot.⁶⁷ Overshoots are well known phenomenona in glass physics⁶⁸ and further explained in the ESI.† Our second reference is the Angell mix (N₂H₅⁺TFA⁻), which serves as benchmark for an LLT with similarities to the LLPT. That is, it involves latent heat release (rather than just a step in heat capacity), as indicated by a pronounced exotherm at ≈190 K upon cooling (Fig. 2a and c). Similarly, it involves latent heat uptake upon reheating, where the peak area of the endotherm at ≈195 K (Fig. 2b and d) is quite similar to the peak area of the exotherm upon cooling (Fig. 2a and c). We note that both the latent heat and the hysteresis in transformation temperature are definition criteria for first-order transitions.

Fig. 2 DSC traces of aqueous ionic liquids with x = 0.175. (a) Cooling scans and (b) reheating scans of trifluoroacetate solutions with various cations. (c) Cooling scans and (d) reheating scans of hydrazinium solutions with various anions. All traces were recorded with cooling/heating rates of 30 K min⁻¹. The full heating scans showing cold-crystallization events and melting as well as scans with other cooling rates are found in the ESI.† A scan of the benchmark glass-former glycerol is included as a reference (grey dashed line).

It is not yet clear what is at the origin of this transition, though Woutersen et al. were able to rule out first-order transitions such as crystallization/melting based on spectroscopy experiments.³⁶ We emphasize that the first-order transition is in fact coupled to a glass transition where the step-like change in heat flow is masked by the pronounced exo-/endotherm.^35,36 In our data, this can be seen by the remarkable difference in baseline after the transition (Δc_p, marked by brackets in Fig. 2a and c). This adds the necessity to consider the transition either as an LLT followed by a glass transition or a liquid–glass transition.

Now, we move on to trifluoroacetate solutions with different cations (Fig. 2a and b). For ammoniumtrifluoroacetate NH₄⁺TFA⁻ (red curves), we observe transitions very similar to the ones in the Angell mix upon cooling, i.e., an exotherm around the same temperature (≈190 K) and a pronounced difference in baseline afterwards. First and foremost, this demonstrates that an LLT is not an exclusive feature of the Angell mix. Interestingly, this LLT appears to develop already slowly at higher temperatures (≈210 K), making the transition significantly broader. Upon reheating, we would expect the endothermic reverse transition but instead, we find an asymmetric peak that appears to consist of a glass transition and an endothermic bump. Using methylammonium CH₃NH₃⁺ as cation (green curves) changes the phenomenology dramatically. There is no longer an LLT during cooling and only a simple glass transition with T_g = 171 K remains. Also when reheating the glass, we infer only a glass transition including the typical overshoot, just like, e.g., in glycerol. Surprisingly, changing the cation to ethylammonium C₂H₅NH₃⁺ (blue curves) again leads to the observation of an exotherm at ≈190 K upon cooling. This LLT is less broad than for the NH₄⁺TFA⁻ and N₂H₅⁺TFA⁻ case and furthermore, followed by a step in heat flow starting at ≈180 K indicating a glass transition. In other words, first-order transition and glass transition seem to be separated in this case. Reheating the solution reveals an even more complex phase behavior with four distinct calorimetric traits: first, the solution experiences the reverse glass transition at ≈175 K, directly followed by a weak exotherm at ≈190 K that is related to cold-crystallization of ice. The cold-crystallization event is superseded by yet another endotherm at ≈200 K before the solution again crystallizes at ≈210 K.

In the case of hydrazinium solutions with different anions (Fig. 2c and d), already replacing fluorine atoms by chlorine atoms, i.e., the switch from TFA⁻ to TCA⁻ (cyan curves), leads to disappearance of the LLT upon cooling. Only a tiny exothermic drift is observed before the glass transition at T_g = 186 K. The reheating scan also lacks the endotherm and only reveals a glass transition with overshoot. Replacing some chlorine atoms with hydrogen atoms retains the simple glass-forming behavior as is evident from Fig. 2c for both dichloroacetate (cyan curves) with T_g = 183 K and acetate (dark yellow curves) with T_g = 173 K. Adding fluorine atoms by using PFP⁻ (orange curves) on the other hand again produces an intense exotherm upon cooling, albeit at significantly higher temperatures (≈210 K). The transition is succeeded by a very broad step between 200 and 180 K, and a tiny but reproducible exotherm at ≈160 K. Reheating the solution does not yield any endotherm that would signify a reverse LLT, but two broad steps possibly related to a double glass transition before cold-crystallization sets in.

Upon closer inspection of all the DSC heating scans in Fig. 2b and d, one might notice that all solutions except for N₂H₅⁺PFP⁻ generate similar warm-up traces, regardless of which type of transitions occurred during cooling. The first calorimetric feature is always a glass-to-liquid transition with heat capacity overshoot, just like in the reference glycerol glass. Even the endotherm in the Angell mix could be described as a glass transition with a very pronounced overshoot. The shape of the overshoot is highly dependent on the cooling rate: High Q_cool will lead to a small overshoot and low Q_cool to a large overshoot – provided the glasses are warmed with the same heating rate. To our surprise, even the Angell mix obeys this principle, at least between 100 and 2 K min⁻¹ (Fig. 3a). This phenomenology is very typical of glasses and was studied in depth, e.g., by Moynihan et al.⁶⁹ From the changing overshoot at the glass transition it is possible to extract fragilities for the supercooled liquids thermodynamically connected to the glasses. Specifically, the steepness index m⁷⁰ can be extracted as a measure of fragility. From the cooling rate dependence of the overshoot, it is furthermore possible to extract the activation energy of relaxation times.⁷¹ The paramter m is defined as the slope of relaxation times at T_g and used as a measure of fragility, i.e., how much the relaxation behavior deviates from Arrhenius behavior.⁶⁷ A straightforward way of evaluation was promoted by Angell and co-workers^72,73 using an enthalpy differencing procedure. This procedure is summarized in great detail in the ESI.† One key advantage of the method is that only the glass transition is used whereas any possibly overlapping first-order transitions are removed in the evaluation. We utilize this method to estimate m for all our solutions except for N₂H₅⁺PFP⁻. Here, the model fails because of the overlapping double glass transition. Results for TFA⁻ mixtures with different cations are shown in Fig. 3b and for N₂H₅⁺ solutions with different anions in Fig. 3c. The Angell mix and pure glycerol (for reference) are included in both panels. Glycerol exhibits a fragility index of m = 59, making it a perfect example of a rather fragile liquid. Please note that the small discrepancy to the literature value of m = 51⁷³ is most likely due to differing water content. We obtain m = 44 for the Angell mix, which points towards stronger, more Arrhenius-like relaxation behavior. This is consistent with the increase in tetrahedrality when approaching the LLT and consequently, the glass transition during cooling.^36,46 However, the solution is still significantly more fragile than pure water LDL (m ≈ 14) or HDL (m ≈ 20–25), the strongest liquids known thus far.²⁶ Replacing N₂H₅⁺ increases liquid fragility slightly for NH₄⁺ (m = 58) yet substantially for CH₃NH₃⁺ (m = 125) and C₂H₅⁺ (m = 146). This is remarkable because fragility indices m > 100 are typically encountered for the most fragile molecular liquids and long-chained polymers, signifying a very complex relaxation behavior, as well as dynamic heterogeneity.^74–76 Also replacing TFA⁻ leads to a more fragile mixture for all anions employed, albeit none of them cross the m = 100 mark (see Fig. 3c). This suggests that exchanging either cations or anions not only leads to the observation of different thermal signatures but also to pronounced differences in relaxation behavior. Here, an obvious question is whether all these remarkable traits have a common structural origin, which can be probed using XRD.

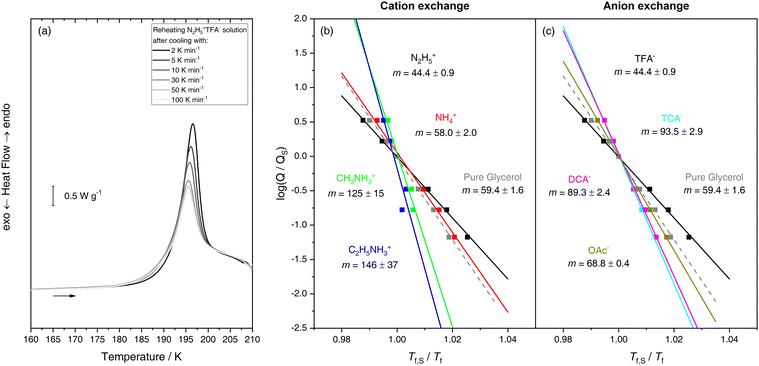Fig. 3 (a) DSC heating traces highlighting the impact of previous cooling rate on the heat capacity overshoot of the glass transition in the Angell mix. (b and c) Scaled Arrhenius plots of cooling rate vs. estimated fictive temperature for aqueous ionic liquids (x = 0.175) containing either (b) TFA⁻ or (c) N₂H₅⁺. Glycerol is included as reference. Cooling rates and temperatures have been scaled with the values obtained from a standard cooling scan (30 K min⁻¹). Steepness indices m are calculated using an Arrhenius fit (depicted as lines in these plots) and errors are given from the standard deviation of the fits. For further details please see ref. 73 and the ESI.†

X-ray diffraction

Fig. 4 shows X-ray diffractograms of aqueous mixtures with N₂H₅⁺TFA⁻, NH₄⁺TFA⁻, C₂H₅NH₃⁺TFA⁻, N₂H₅⁺OAc⁻ and N₂H₅⁺PFP⁻ in the liquid phase (panel a) and in the glassy state at 80 K (panel b). Solutions were selected based on their thermal behavior (see Fig. 2), i.e., all solutions that exhibit an exotherm upon cooling and one that does not (N₂H₅⁺OAc⁻) were chosen. This allows examining the structural changes accompanying the cooling-induced LLT. Most importantly, no signs of sharp Bragg peaks stemming from crystal phases are found in all diffractograms, excluding the possibility that the exotherms in DSC during cooling are linked to crystallization. The Angell mix (black) at 300 K is characterized by a broad feature exhibiting a double halo peak with maxima at 2θ = 23.6° and 33.1° (see also the ESI in ref. 44). This suggests structural heterogeneity and two preferred geometries, one of lower density (low diffraction angles) and one of higher density (high diffraction angles). In the glassy state at 80 K, we observe changes in relative peak intensities and a shift of the two halo peaks to 2θ = 26.3° and 32.7°, indicating a rearrangement of molecules. The most interesting feature however, is the emergence of another feeble halo peak at 2θ = 15.6° that was shown to evolve into a set of Bragg peaks pertaining to TFA tetrahydrate at higher temperatures.⁴⁴ That is, the LLT is connected to a structural change from two domains in the liquid phase to three domains in the glassy state.

Fig. 4 Diffractograms of selected aqueous solutions in (a) the liquid state at 300 K and (b) the glassy state after quenching to 80 K. Halo peak maximum positions obtained via Gaussian fits are labelled in the scans. Intensities are normalized using the most intense halo peak of each scan.

A similar picture for the liquid is presented for NH₄⁺TFA⁻ solution (red) with halo peaks at 2θ = 24.0° and 34.2°. In the glassy state, a new peak emerges at 2θ = 14.9° and the first halo shifts to higher angles. In stark contrast to the Angell mix however, the new halo peak is very pronounced whereas the halo at 2θ = 34.2° has transitioned into a broad shoulder. This could signify that mostly molecules from denser geometries transform in the course of the LLT. The arguably most peculiar diffraction patterns are observed for C₂H₅NH₃⁺TFA⁻ solution (blue). Here, we find a halo peak maximum at 2θ = 21.9° accompanied by a broad shoulder at high angles (2θ ≈ 32.9°) and another shoulder at low angles (2θ = 14.3°) in the liquid state. Upon quenching into the glass state, none of the aforementioned halos remain. Instead, there is a broad amorphous band with a maximum that could only be anticipated around 2θ = 27.3°. In contrast, the water–N₂H₅⁺OAc⁻ mixture (dark yellow) shows a simple glass-forming behavior just as inferred from Fig. 2. That is, there is a broad halo with a maximum at 2θ = 27.8° in the liquid, which is hardly affected by the vitrification process. This exemplifies the widely accepted notion that glasses represent immobilized liquids. Lastly, solutions containing N₂H₅⁺PFP⁻ feature yet another diffraction pattern. At 300 K, it is quite similar to N₂H₅⁺TFA⁻ and NH₄⁺TFA⁻ solutions: we again observe a double halo peak at 2θ = 19.1° and 34.3°. Notably, for this solution the double halo peak is more separated in the liquid state when compared to N₂H₅⁺TFA⁻ and NH₄⁺TFA⁻. This indicates that the two preferred geometries are more pronounced. At 80 K, the two maxima approach each other, resulting in peaks at 2θ = 21.1° and 33.9°. Instead of a separate halo peak there appears a broad shoulder at the lower angle side in the glass state.

Molecular dynamics simulations

Computer simulations are a powerful tool for shedding light on the molecular structures underlying experimentally observed diffraction peaks.^77,78 Similarly, our MD simulation of N₂H₅⁺TFA⁻ solution at 300 K allows disentangling the microscopic origin of the peculiar double halo peaks observed in our X-ray diffractograms. More specifically, we recognize small TFA⁻ aggregates in which CF₃ groups are in contact with each other while the COO⁻ groups are exposed to surrounding solution (Fig. 5). The observation of aggregation is bolstered by density-based clustering analysis when considering as points the C atoms of the CF₃ group using minPts = 3 and ε = 0.44 nm (i.e., the peak in the C–C radial distribution function). These small aggregates composed of 3–4 TFA⁻ ions make up ≈25% of the total of TFA⁻ molecules (Table 1). In order to extend our cluster analysis to water molecules beyond the first hydration shell, we consider as points the O atoms of the water molecules using minPts = 13 and ε = 0.45 nm (i.e., the second peak in the O_water–O_water radial distribution function). It is revealed that one third of water molecules is found in pools comprising 25 molecules on average, i.e., more than one hydration shell (Table 1).

Fig. 5 Snapshot of N₂H₅⁺TFA⁻ solution at 300 K. Transient TFA⁻ clusters are highlighted by yellow circles. Color code: blue, nitrogen; red, oxygen; pink, fluorine; cyan, carbon; white, hydrogen.

Table 1 Characterization of TFA⁻ and water clusters in the course of the MD simulation using the average number of clusters per frame 〈N_c〉, the average fraction 〈f〉 of molecules involved in clusters and the average number of molecules in each cluster 〈N_m〉 (i.e., the dimension of the cluster). Clusters have been identified using the DBSCAN method

	TFA aggregates	Water aggregates
〈Nc〉	14	14
〈f〉	0.27	0.35
〈Nm〉	3.7	25

---

These findings allow a tentative assignment of the two halo peaks found in the diffractograms at 300 K: the 23.6° peak, corresponding to a distance of ≈0.4 nm, is due to the aggregation of CF₃ groups. This assignment is in reasonable agreement with the peak at 0.44 nm of the pair radial distribution function, g(r), for the C⋯C contacts of the CF₃ groups as obtained from the MD simulation (see ESI†). The broad peak at ≈33° on the other hand arises from hydrated TFA⁻ and N₂H₅⁺ molecules, as well as from their interaction. This peak corresponds to a distance of ≈0.26–0.28 nm, i.e., to a typical HB distance. The interaction between the COO⁻ groups and water is typically stronger than the one among water molecules, resulting in slightly shorter hydrogen bond distances.⁷⁹ This feature is also observed in the MD simulation as is demonstrated by both the pair radial distribution functions and the average hydrogen bond distances (see ESI†). Our MD simulation hence aids in revealing the molecular origin of the double-halo feature in X-ray diffractograms. It is clearly tied to the nature of the solutes involved, specifically the TFA⁻ anions. These solutes give rise to a multitude of possible interactions, as is evident from analysis of the HB population (see ESI†).

Discussion

We identify an array of mixtures that exhibit low-temperature exotherms upon cooling (Fig. 2a and c). These transitions cannot be associated with crystallization, because no sharp Bragg peaks appear in any of the diffractograms (Fig. 4b). Such transitions could possibly involve a liquid–liquid phase transition (LLPT) in water itself, without change in composition. Alternatively, they could also involve a liquid–liquid transition (LLT), in which the composition changes at the transition. On the contrary, solutions with non-fluorinated anions (TCA⁻, DCA⁻ or OAc⁻) show no exothermic transitions (Fig. 2c). They merely display glass-forming behavior where the glass transition temperature and fragility gradually decrease when going from TCA⁻ (T_g = 186 K, m = 94) to DCA⁻ (T_g = 183 K, m = 89) and OAc⁻ (T_g = 173 K, m = 69). This suggests that the glass-forming behavior can easily be tuned by varying the chemical nature of the anion. Reversely, this signifies that potential LLTs are limited to fluorinated ionic liquids. The solutions containing those anions studied here (i.e., TFA⁻ and PFP⁻) exhibit at least two halo peaks in the liquid at 300 K. This is rather uncommon as only one broad halo peak is observed in water and most of its solutions at room temperature (see for instance N₂H₅⁺OAc⁻ in Fig. 4a). It shows that while these solutions represent globally disordered liquids, there are two preferred structural motifs. Supported by MD simulations, we argue that this is because the anion itself is amphiphilic, containing a hydrophilic (COO⁻) and an extremely hydrophobic (CF₃, C₂F₅) part. Consequently, hydrogen-bonding is possible only with the COO⁻ functional group of the anion but not with the fluorocarbon skeleton.⁸⁰ This is known to drive water molecules from hydrophobic to hydrophilic solute parts, where they then form small water pools.⁸¹ In turn, the depletion of water molecules around hydrophobic parts leads to clustering of the latter through hydrophobic interaction.

Interestingly, such structural inhomogeneities typical for fluorinated aqueous ionic liquids are known under the general term “nanosegregation” in literature.⁸¹ We point out that this nanosegregation very much resembles micellization as observed in many surfactant solutions. In fact, some fluorinated ionic liquids were shown to form self-assembled micellar aggregates in water.⁸² Thus, we also suggest to associate the aggregation behavior of aqueous ionic liquids from the present work with the formation and dissociation of micelle-like structures. For simplicity, we call these aggregates “micelles”, albeit they consist only of 3–4 molecules.

In general, the formation of micelles is a process governed by thermodynamics. For micellization to occur, the difference of Gibbs energy consisting of both enthalpic and entropic contributions needs to be negative. Given that micellization is found to be an endothermic process at room temperature for most surfactants, it must be tied to an increase in entropy.⁸³ This increase is achieved by breaking the cage-like structures that water needs to form around hydrophobic groups.⁸⁴ Due to the fact that water no longer hydrates the hydrophobic parts, they aggregate. This state is schematically illustrated in the left panel of Fig. 6 using the Angell mix as an example. Specifically, the fluorinated tails of TFA⁻ are aggregated (red sphere) whereas the hydrophilic COO⁻ groups are integrated into a disordered H-bond network made of water and hydrazinium (blue). Upon lowering temperature, the contribution of entropy to the Gibbs energy decreases, which makes enthalpy the decisive factor. Consequently, at a certain temperature the Gibbs energy for micellization will become positive and this leads to (exothermic) decomposition of micelles (“LLT”) followed immediately by the glass transition. A possible depiction of the resulting vitrified state is shown in the right panel of Fig. 6.

Fig. 6 Schematic representation of N₂H₅⁺TFA⁻ solution at 300 K (left) and after quenching to 80 K (right). Water is shown implicitly in blue color and H-bonds of TFA⁻ are marked by dotted lines. At 300 K, trifluoroacetate ions are encountered in micellic structures (red sphere) that are bonded to the surrounding H-bond network consisting of water and hydrazinium. At 80 K, micellic structures have broken down through an exothermic transition, possibly resulting in the TFA dimeric structures that are present in the tetrahydrate. Notably, this necessitates that protons are withdrawn from hydrazinium and shared between the carboxylate groups of two TFA⁻ molecules each.

We conjecture that TFA⁻ is not encountered as individually hydrated ion but rather as [H(CF₃COO)₂]⁻ dimers (green ellipses). This is based on the same arrangement found in the hemiclathrate TFA tetrahydrate⁸⁵ to which the glassy solution crystallizes upon reheating.⁴⁴ It is largely consistent with the X-ray pattern at 80 K that can be interpreted as nanocrystalline TFA·4H₂O where peak broadening due to small crystal size leads to halo peaks instead of sharp Bragg peaks. So, in a sense, the transition can be interpreted as falling below the Krafft temperature⁸⁶ where the solution phase-separates but the surfactant does not crystallize fully to its tetrahydrate and forms frustrated clusters instead. We argue that frustration of crystallization is enhanced by the cation since similar observations were made for specific cations in aluminate solutions.⁸⁷ Interestingly, there is a proton in the [H(CF₃COO)₂]⁻ dimer that can only come from the H-bond network or more specifically, from hydrazinium. This suggests that the pH of the solution changes, i.e., becomes more basic upon vitrification. In addition to pH changes, demicellization is coupled to a loss of hydrogen bonding sites and more exposed hydrophobic groups. The latter cannot form hydrogen bonds and must be accommodated by cage-like water structures⁸⁴ that have close resemblance to the ordered LDA network.³⁶ Such ordered tetrahedral states are at the heart of the rather low fragility index determined at the glass transition.

We now use the same concept to understand the phase behavior upon cooling of all aqueous ionic liquids studied here. For NH₄⁺TFA⁻, we observe a similar exothermic demicellization at nearly identical Krafft temperatures because the responsible anion TFA⁻ remains unchanged. Similarly, the phase-separated vitrified state bears resemblance to TFA·4H₂O nanocrystals encountered for the Angell mix. Still, the change of cation may alter the surrounding H-bond network slightly. Compared to N₂H₅⁺, the switch to NH₄⁺ could affect the nature of the frustrated TFA hydrate clusters because of the ions’ differences in acidity and hydrogen-bonding ability. This is also reflected in the X-ray data with a more pronounced low-angle halo peak at 2θ = 14.9° but no dedicated shoulder at 2θ > 30°. For aqueous N₂H₅⁺PFP⁻, exothermic demicellization is also found but at slightly higher temperatures. The increase in Krafft temperature is due to higher hydrophobicity of PFP⁻ compared to TFA⁻ consistent with literature on other perfluoroalkane carboxylates.⁸⁸ We cannot determine from our X-ray data whether frustrated PFP⁻ clusters form similar dimeric structures as TFA⁻. However, the cooling behavior with a pronounced shoulder following the demicellization exotherm observed in calorimetry scans indicates a more complex arrangement of molecules in the vitrified state.

Using amines instead of N₂H₅⁺ or NH₄⁺ as cations adds yet another layer of complexity. This is because the hydrocarbon group represents a part, which is more hydrophobic than the NH₃⁺ and COO⁻ groups but less hydrophobic than fluorinated carbons. In pure fluorinated ionic liquids, such hydrocarbon chains can even induce nanosegregation into three distinct domains instead of two.⁸⁹ In other words, there could be two different types of micellic arrangements in aqueous solution instead of one. In fact, C₂H₅NH₃⁺TFA⁻ mixtures exhibit two low-angle halo peaks at 300 K, which might correspond to these two arrangements. At 80 K, both halo peaks disappear indicating complete demicellization. During cooling we observe two exothermic events, a pronounced peak followed by a broad shoulder, which we attribute to demicellization of fluorocarbon micelles and hydrocarbon micelles, respectively. That is, we expect the mixture to be multi-phase-separated into two solute-rich components at 80 K, one component comprising mostly TFA⁻ and the other mostly C₂H₅NH₃⁺.

Surprisingly, merely simple vitrification behavior is observed for aqueous CH₃NH₃⁺TFA⁻ (see Fig. 2a), despite being the “intermediate” compound between NH₄⁺TFA⁻ and C₂H₅⁺TFA⁻. We speculate that CH₃NH₃⁺ is not hydrated fully (as suggested for the cation in the Angell mix) but is also not found in micelles (as suggested for the cation in C₂H₅⁺TFA⁻). Hydration is impeded by the hydrophobicity of the hydrocarbon and micelle formation is inhibited by insufficient chain length. In other words, the cation is too hydrophobic for hydration but too hydrophilic for micellization. We imagine that this results in a structurally partially arrested mixture where the exothermic demicellization of TFA⁻ is no longer possible. This might also explain why the glass transition temperature is shifted to lower temperatures than observed for N₂H₅⁺TFA⁻ and NH₄⁺TFA⁻ solutions.

The first trait upon reheating each of these phase-separated glassy solutions is a glass transition into the corresponding supercooled liquid (Fig. 2b and d). In the supercooled liquid, ion and molecular mobility are enhanced substantially and now the solutions could either (i) form micelles again via an endothermic apparent first-order transition, or (ii) crystallize fully via exothermic first-order transition(s). For N₂H₅⁺TFA⁻ solutions, scenario (i) is supported by an abrupt change in local hydrogen-bond structure³⁶ and a pronounced endotherm (Fig. 2b).³⁵ However, hardly any structural changes were inferred upon reheating when using X-ray diffraction^44,46 and we here reveal that the endotherm can in fact also be explained by the heat capacity overshoot of a glass transition rather than latent heat uptake (Fig. 3a). That is, it is not possible to exclude either scenario based on current experimental findings. The same dilemma persists for NH₄⁺TFA⁻ mixtures, with the notable difference that here, we observe a two-step feature in the form of a glass transition with an endothermic bump instead of one single endotherm (Fig. 2b). Both features are affected by the rate of the preceding cooling (see ESI†), which suggests that they are related to glass transitions. This is an important piece of evidence against scenario (i) and raises the question whether an abrupt change in local hydrogen-bond structure could be of a different, still unknown origin.

For aqueous C₂H₅⁺TFA⁻, we observe four distinct calorimetric features before the solution crystallizes entirely (Fig. 2b). Consistent with our claim of multi-phase separation during cooling, we assign the first glass transition to devitrification of only one solute-rich part of the mixture. The enhanced mobility of molecules allows for the growth of some ice crystals nucleated during cooling, resulting in the first exotherm. Then, the second part of the mixture devitrifies and might even start to form micelles again, producing the endothermic signal. However, the micellization is interrupted as soon as the steadily increasing mobility of molecules enables full crystallization. That is, we argue that hypothesis (i) of micelle (re-)formation provides the best explanation for this aqueous ionic liquid. Lastly, in N₂H₅⁺PFP⁻ solutions, we find two broad overlapping steps, which we attribute to step-wise devitrification of the complex phase-separated solution. We find no sign of re-micellization due to preemptive cold-crystallization. However, we emphasize that different cooling rates have a significant impact on the warm-up phase behavior (see ESI†).

Summary and outlook

We have conducted a low-temperature calorimetric study on the controversially discussed Angell mix and related aqueous ionic liquids, all with the same solute mole fraction of x = 0.175. This allows us to assess the role each ion plays in triggering phase transitions. Information on structural changes is further gained via X-ray diffraction experiments. Our results highlight the fact that the complex chemical nature of ionic liquids allows for many possible interactions between solute and water molecules. This is arguably shown most impressively by the rich calorigrams of C₂H₅⁺TFA⁻ and N₂H₅⁺PFP⁻ solutions. Most notably, we find that the anion largely determines which transformations are encountered. For all ionic liquids with fluorinated anions except CH₃NH₃⁺TFA⁻, we observe exothermic first-order transitions (Fig. 2) that are not associated with ice crystallization upon cooling as is usually the case in most aqueous solutions. They are accompanied by pronounced structural changes (Fig. 3), which we believe to be indicative of phase separation and frustrated crystallization. The phase separations are rationalized using ideas associated with the formation and decomposition of micelles (see Fig. 6). This model aligns with earlier observations suggesting the presence of water patches in a phase-separated state at lower temperatures.⁴⁹ A straightforward way to further probe this hypothesis is to determine the surface tension upon increasing solute concentration. In the case of micelle formation, surface tension is expected to drop gradually until it reaches a plateau at a certain concentration (in analogy to the critical micelle concentration). Alternatively, isothermal titration calorimetry (ITC) allows for a straightforward thermodynamic characterization of interactions during the aggregation process.⁹⁰ Yet another possibility would be to apply sophisticated small-angle scattering techniques, which enable to capture the formation or dissociation of such micellic arrangements.

By employing solutions with non-fluorinated anions, the first-order transition vanishes, leading to simple vitrification behavior. Here, the fragility of the liquid can be tuned by the chemical nature of anions. Specifically, the fragility parameter m almost linearly decreases from TCA⁻ to OAc⁻ upon stepwise replacement of chlorine atoms with hydrogen atoms, i.e., m decreases by gradually reducing hydrophobicity. This opens the door for the design of model aqueous systems with adjustable fragility, yet another branch where ionic liquids as solute shine through their versatility, on top of their multitude of applications in chemical industry.⁹¹ Disentangling the structural changes in the hydrogen-bond network of these solutions both upon cooling and heating is a promising premise for future studies. This would allow addressing the especially interesting role of water in the observed transformations.

Author contributions

J. B. and T. L. designed the study. J. B. measured the data. I. D., and L. Z.-P. performed MD simulations. J. B. and T. L. wrote the manuscript with valuable input from I. D. and L. Z.-P.

Conflicts of interest

There are not conflicts to declare.

Acknowledgements

We thank Sander Woutersen and Federico Caporaletti for fruitful discussion about the nature of the phase transitions. Furthermore, we thank Herwig Schottenberger for informing us about the special position held by fluorinated compounds in ionic liquid chemistry. J. B. is a recipient of a DOC fellowship of the Austrian Academy of Sciences (ÖAW). I. D. acknowledges support by the European Union - NextGenerationEU under the Italian Ministry of University and Research (MUR) project PRIN2022-P2022MC742PNRR, CUP E53D23018440001. I. D. and L. Z. P. acknowledge the CINECA award under the ISCRA initiative, for the availability of high-performance computing resources and thank Sara del Galdo for sharing a customized version of the DBSCAN algorithm.

References

1. P. Ball, Water as an Active Constituent in Cell Biology, Chem. Rev., 2008, 108(1), 74.
2. F. Caupin, Escaping the no man's land: Recent experiments on metastable liquid water, J. Non-Cryst. Solids, 2015, 407, 441.
3. M. Chaplin, Water Structure and Science, London Southbank University, 2023, https://water.lsbu.ac.uk/water/, accessed Dec. 2023.
4. P. G. Debenedetti, Supercooled and glassy water, J. Phys.: Condens. Matter, 2003, 15(45), R1669.
5. R. J. Speedy, Stability-limit conjecture. An interpretation of the properties of water, J. Phys. Chem., 1982, 86(6), 982.
6. P. H. Poole, F. Sciortino, U. Essmann and H. E. Stanley, Phase behaviour of metastable water, Nature, 1992, 360(6402), 324.
7. S. Sastry, P. G. Debenedetti, F. Sciortino and H. E. Stanley, Singularity-free interpretation of the thermodynamics of supercooled water, Phys. Rev. Lett. E, 1996, 53(6), 6144.
8. P. H. Poole, F. Sciortino, T. Grande, H. E. Stanley and C. A. Angell, Effect of hydrogen bonds on the thermodynamic behavior of liquid water, Phys. Rev. Lett., 1994, 73(12), 1632.
9. P. Gallo, J. Bachler, L. E. Bove, R. Böhmer, G. Camisasca, L. E. Coronas, H. R. Corti, I. de Almeida Ribeiro, M. de Koning and G. Franzese, et al., Advances in the study of supercooled water, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44(11), 143.
10. P. H. Handle, T. Loerting and F. Sciortino, Supercooled and glassy water: Metastable liquid(s), amorphous solid(s), and a no-man's land, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(51), 13336.
11. P. Gallo, K. Amann-Winkel, C. A. Angell, M. A. Anisimov, F. Caupin, C. Chakravarty, E. Lascaris, T. Loerting, A. Z. Panagiotopoulos and J. Russo, et al., Water: A Tale of Two Liquids, Chem. Rev., 2016, 116(13), 7463.
12. J. C. Palmer, P. H. Poole, F. Sciortino and P. G. Debenedetti, Advances in Computational Studies of the Liquid-Liquid Transition in Water and Water-Like Models, Chem. Rev., 2018, 118(18), 9129.
13. P. G. Debenedetti, F. Sciortino and G. H. Zerze, Second critical point in two realistic models of water, Science, 2020, 369(6501), 289.
14. D. Paschek, How the liquid-liquid transition affects hydrophobic hydration in deeply supercooled water, Phys. Rev. Lett., 2005, 94(21), 217802.
15. D. Paschek, A. Rüppert and A. Geiger, Thermodynamic and structural characterization of the transformation from a metastable low-density to a very high-density form of supercooled TIP4P-Ew model water, ChemPhysChem, 2008, 9(18), 2737.
16. M. Yamada, S. Mossa, H. E. Stanley and F. Sciortino, Interplay between time-temperature transformation and the liquid-liquid phase transition in water, Phys. Rev. Lett., 2002, 88(19), 195701.
17. D. Corradini, M. Rovere and P. Gallo, A route to explain water anomalies from results on an aqueous solution of salt, J. Chem. Phys., 2010, 132(13), 134508.
18. Y. Ni and J. L. Skinner, Evidence for a liquid-liquid critical point in supercooled water within the E3B3 model and a possible interpretation of the kink in the homogeneous nucleation line, J. Chem. Phys., 2016, 144, 214501.
19. H. Tanaka, Liquid-liquid transition and polyamorphism, J. Chem. Phys., 2020, 153(13), 130901.
20. O. Mishima and Y. Suzuki, Vitrification of emulsified liquid water under pressure, J. Chem. Phys., 2001, 115(9), 4199.
21. J. Bachler, J. Giebelmann and T. Loerting, Experimental evidence for glass polymorphism in vitrified water droplets, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(30), e2108194118.
22. O. Mishima, The glass-to-liquid transition of the emulsified high-density amorphous ice made by pressure-induced amorphization, J. Chem. Phys., 2004, 121(7), 3161.
23. I. Kohl, L. Bachmann, A. Hallbrucker, E. Mayer and T. Loerting, Liquid-like relaxation in hyperquenched water at < or = 140 K, Phys. Chem. Chem. Phys., 2005, 7(17), 3210.
24. O. Andersson, Glass–liquid transition of water at high pressure, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(27), 11013.
25. M. Seidl, M. S. Elsaesser, K. Winkel, G. Zifferer, E. Mayer and T. Loerting, Volumetric study consistent with a glass-to-liquid transition in amorphous ices under pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(10), 100201(R).
26. K. Amann-Winkel, C. Gainaru, P. H. Handle, M. Seidl, H. Nelson, R. Böhmer and T. Loerting, Water's second glass transition, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(44), 17720.
27. J. Bachler, J. Giebelmann, K. Amann-Winkel and T. Loerting, Pressure-annealed high-density amorphous ice made from vitrified water droplets: A systematic calorimetry study on water’s second glass transition, J. Chem. Phys., 2022, 157(6), 064502.
28. C. M. Tonauer, L.-R. Fidler, J. Giebelmann, K. Yamashita and T. Loerting, Nucleation and growth of crystalline ices from amorphous ices, J. Chem. Phys., 2023, 158(14), 141001.
29. K. Winkel, E. Mayer and T. Loerting, Equilibrated high-density amorphous ice and its first-order transition to the low-density form, J. Phys. Chem. B, 2011, 115(48), 14141.
30. K. H. Kim, K. Amann-Winkel, N. Giovambattista, A. Späh, F. Perakis, H. Pathak, M. L. Parada, C. Yang, D. Mariedahl and T. Eklund, et al., Experimental observation of the liquid-liquid transition in bulk supercooled water under pressure, Science, 2020, 370(6519), 978.
31. K. Amann-Winkel, K. H. Kim, N. Giovambattista, M. Ladd-Parada, A. Späh, F. Perakis, H. Pathak, C. Yang, T. Eklund and T. J. Lane, et al., Liquid-liquid phase separation in supercooled water from ultrafast heating of low-density amorphous ice, Nat. Commun., 2023, 14(1), 442.
32. S. Cerveny, F. Mallamace, J. Swenson, M. Vogel and L. Xu, Confined Water as Model of Supercooled Water, Chem. Rev., 2016, 116(13), 7608.
33. J. Bachler, P. H. Handle, N. Giovambattista and T. Loerting, Glass polymorphism and liquid-liquid phase transition in aqueous solutions: experiments and computer simulations, Phys. Chem. Chem. Phys., 2019, 21(42), 23238.
34. K.-i Murata and H. Tanaka, Liquid-liquid transition without macroscopic phase separation in a water-glycerol mixture, Nat. Mater., 2012, 11(5), 436.
35. Z. Zhao and C. A. Angell, Apparent First-Order Liquid-Liquid Transition with Pre-transition Density Anomaly, in Water-Rich Ideal Solutions, Angew. Chem., Int. Ed., 2016, 55(7), 2474.
36. S. Woutersen, B. Ensing, M. Hilbers, Z. Zhao and C. A. Angell, A liquid-liquid transition in supercooled aqueous solution related to the HDA-LDA transition, Science, 2018, 359(6380), 1127.
37. Y. Suzuki, Direct observation of reversible liquid–liquid transition in a trehalose aqueous solution, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(5), e2113411119.
38. J. Giebelmann, J. Bachler and T. Loerting, Glass Polymorphism in Hyperquenched Aqueous LiCl Solutions, J. Phys. Chem. B, 2023, 127(15), 3463.
39. Y. Suzuki and O. Mishima, Experimentally proven liquid-liquid critical point of dilute glycerol-water solution at 150 K, J. Chem. Phys., 2014, 141(9), 094505.
40. I. Popov, A. Greenbaum Gutina, A. P. Sokolov and Y. Feldman, The puzzling first-order phase transition in water-glycerol mixtures, Phys. Chem. Chem. Phys., 2015, 17(27), 18063.
41. L.-S. Zhao, Z.-X. Cao and Q. Wang, Glass transition of aqueous solutions involving annealing-induced ice recrystallization resolves liquid-liquid transition puzzle of water, Sci. Rep., 2015, 5, 15714.
42. J. Bachler, V. Fuentes-Landete, D. A. Jahn, J. Wong, N. Giovambattista and T. Loerting, Glass polymorphism in glycerol-water mixtures: II. Experimental studies, Phys. Chem. Chem. Phys., 2016, 18(16), 11058.
43. J. R. Bruijn, T. H. van der Loop and S. Woutersen, Changing Hydrogen-Bond Structure during an Aqueous Liquid-Liquid Transition Investigated with Time-Resolved and Two-Dimensional Vibrational Spectroscopy, J. Phys. Chem. Lett., 2016, 7(5), 795.
44. J. Bachler, L.-R. Fidler and T. Loerting, Absence of the liquid-liquid phase transition in aqueous ionic liquids, Phys. Rev. Lett. E, 2020, 102(6), 060601.
45. C. Alba-Simionesco, P. Judeinstein, S. Longeville, O. Osta, F. Porcher, F. Caupin and G. Tarjus, Interplay of vitrification and ice formation in a cryoprotectant aqueous solution at low temperature, Proc. Natl. Acad. Sci. U. S. A., 2022, 119(12), e2112248119.
46. K. Yoshida, S. Nishimoto and T. Yamaguchi, Structural analysis of hydrazinium trifluoroacetate aqueous solution by X-ray diffraction and empirical potential structure refinement modeling in the temperature range of 25 to −125 °C, J. Mol. Liq., 2022, 353, 118802.
47. M. R. Bittermann, C. López-Bueno, M. Hilbers, F. Rivadulla, F. Caporaletti, G. Wegdam, D. Bonn and S. Woutersen, Austen in Amsterdam: Isotope effect in a liquid-liquid transition in supercooled aqueous solution, J. Non-Cryst. Solids X, 2022, 13, 100077.
48. K. H. Kim, A. Späh, H. Pathak, F. Perakis, D. Mariedahl, K. Amann-Winkel, J. A. Sellberg, J. H. Lee, S. Kim and J. Park, et al., Maxima in the thermodynamic response and correlation functions of deeply supercooled water, Science, 2017, 358(6370), 1589.
49. L. Zanetti-Polzi, A. Amadei and I. Daidone, Segregation on the nanoscale coupled to liquid water polyamorphism in supercooled aqueous ionic-liquid solution, J. Chem. Phys., 2021, 155(10), 104502.
50. S. G. Chou, A. K. Soper, S. Khodadadi, J. E. Curtis, S. Krueger, M. T. Cicerone, A. N. Fitch and E. Y. Shalaev, Pronounced Microheterogeneity in a Sorbitol–Water Mixture Observed through Variable Temperature Neutron Scattering, J. Phys. Chem. B, 2012, 116(15), 4439.
51. O. Russina, A. Triolo, L. Gontrani and R. Caminiti, Mesoscopic Structural Heterogeneities in Room-Temperature Ionic Liquids, J. Phys. Chem. Lett., 2012, 3(1), 27.
52. L. E. Bove, C. Dreyfus, R. Torre and R. M. Pick, Observation of nanophase segregation in LiCl aqueous solutions from transient grating experiments, J. Chem. Phys., 2013, 139(4), 044501.
53. P. D. Lane, J. Reichenbach, A. J. Farrell, L. A. I. Ramakers, K. Adamczyk, N. T. Hunt and K. Wynne, Experimental observation of nanophase segregation in aqueous salt solutions around the predicted liquid-liquid transition in water, Phys. Chem. Chem. Phys., 2020, 22(17), 9438.
54. S. Mallakpour and M. Dinari, in Green Solvents II: Properties and Applications of Ionic Liquids, ed. A. Mohammad and D. Inamuddin, Springer, Netherlands, Dordrecht, 2012.
55. G. W. H. Höhne; W. F. Hemminger and H.-J. FlammersheimDifferential Scanning Calorimetry, Springer Berlin: Heidelberg, 2003.
56. M. W. Mahoney and W. L. Jorgensen, A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions, J. Chem. Phys., 2000, 112(20), 8910.
57. L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, LigParGen web server: an automatic OPLS-AA parameter generator for organic ligands, Nucleic Acids Res., 2017, 45(W1), W331.
58. B. Doherty, X. Zhong, S. Gathiaka, B. Li and O. Acevedo, Revisiting OPLS Force Field Parameters for Ionic Liquid Simulations, J. Chem. Theory Comput., 2017, 13(12), 6131.
59. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19.
60. G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126(1), 014101.
61. M. Parrinello and A. Rahman, Crystal Structure and Pair Potentials: A Molecular-Dynamics Study, Phys. Rev. Lett., 1980, 45(14), 1196.
62. T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98(12), 10089.
63. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, LINCS: A linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18(12), 1463.
64. M. Ester, H.-P. Kriegel, J. Sander and X. Xu, KDD, 1996, p. 226.
65. A. Semmeq, S. Del Galdo, M. Chiarini, I. Daidone and C. Casieri, Macromolecular vs. molecular crowding in aqueous solutions: A comparative study of PEG400 and ethylene glycol, J. Mol. Liq., 2024, 394, 123713.
66. D. H. Rasmussen and A. P. MacKenzie, Glass transition in amorphous water. Application of the measurements to problems arising in cryobiology, J. Phys. Chem., 1971, 75(7), 967.
67. C. A. Angell, Liquid Fragility and the Glass Transition in Water and Aqueous Solutions, Chem. Rev., 2002, 102(8), 2627.
68. C. T. Moynihan, Correlation between the Width of the Glass Transition Region and the Temperature Dependence of the Viscosity of High-Tg Glasses, J. Am. Ceram. Soc., 1993, 76(5), 1081.
69. C. T. Moynihan, A. J. Easteal, J. Wilder and J. Tucker, Dependence of the glass transition temperature on heating and cooling rate, J. Phys. Chem., 1974, 78(26), 2673.
70. K. J. Crowley and G. Zografi, The use of thermal methods for predicting glass-former fragility, Thermochim. Acta, 2001, 380(2), 79.
71. C. T. Moynihan, A. J. Easteal, M. A. De Bolt and J. Tucker, Dependence of the Fictive Temperature of Glass on Cooling Rate, J. Am. Ceram. Soc., 1976, 59(1–2), 12.
72. V. Velikov, S. Borick and C. A. Angell, Molecular Glasses with High Fictive Temperatures for Energy Landscape Evaluations, J. Phys. Chem. B, 2002, 106(5), 1069.
73. L.-M. Wang, V. Velikov and C. A. Angell, Direct determination of kinetic fragility indices of glassforming liquids by differential scanning calorimetry: Kinetic versus thermodynamic fragilities, J. Chem. Phys., 2002, 117(22), 10184.
74. R. Böhmer, K. L. Ngai, C. A. Angell and D. J. Plazek, Nonexponential relaxations in strong and fragile glass formers, J. Chem. Phys., 1993, 99(5), 4201.
75. D. Huang and G. B. McKenna, New insights into the fragility dilemma in liquids, J. Chem. Phys., 2001, 114(13), 5621.
76. A. P. Sokolov, V. N. Novikov and Y. Ding, Why many polymers are so fragile, J. Phys.: Condens. Matter, 2007, 19(20), 205116.
77. R. Shi and H. Tanaka, Distinct signature of local tetrahedral ordering in the scattering function of covalent liquids and glasses, Sci. Adv., 2019, 5(3), eaav3194.
78. R. Shi and H. Tanaka, Direct Evidence in the Scattering Function for the Coexistence of Two Types of Local Structures in Liquid Water, J. Am. Chem. Soc., 2020, 142(6), 2868.
79. K. R. Leopold, Hydrated acid clusters, Annu. Rev. Phys. Chem., 2011, 62, 327.
80. V. H. Dalvi and P. J. Rossky, Molecular origins of fluorocarbon hydrophobicity, Proc. Natl. Acad. Sci. U. S. A., 2010, 107(31), 13603.
81. J. C. Bastos, S. F. Carvalho, T. Welton, J. N. Canongia Lopes, L. P. N. Rebelo, K. Shimizu, J. M. M. Araújo and A. B. Pereiro, Design of task-specific fluorinated ionic liquids: nanosegregation versus hydrogen-bonding ability in aqueous solutions, Chem. Commun., 2018, 54(28), 3524.
82. A. B. Pereiro, J. M. M. Araújo, F. S. Teixeira, I. M. Marrucho, M. M. Piñeiro and L. P. N. Rebelo, Aggregation Behavior and Total Miscibility of Fluorinated Ionic Liquids in Water, Langmuir, 2015, 31(4), 1283.
83. S. Paula, W. Sues, J. Tuchtenhagen and A. Blume, Thermodynamics of micelle formation as a function of temperature: a high sensitivity titration calorimetry study, J. Phys. Chem., 1995, 99(30), 11742.
84. E. D. Sloan Jr and C. A. KohClathrate hydrates of natural gases, CRC Press, 2007.
85. D. Mootz and M. Schilling, Fluorides and fluoro acids. 30. Crystal structures of acid hydrates and oxonium salts. 34. Trifluoroacetic acid tetrahydrate: a unique change from an ionic to a molecular crystal structure on deuteration, J. Am. Chem. Soc., 1992, 114(19), 7435.
86. K. Holmberg, B. Jönsson, B. Kronberg and B. Lindman, Polymers in aqueous solution, Wiley-Blackwell, 2002.
87. H.-W. Wang, T. R. Graham, E. Mamontov, K. Page, A. G. Stack and C. I. Pearce, Countercations Control Local Specific Bonding Interactions and Nucleation Mechanisms in Concentrated Water-in-Salt Solutions, J. Phys. Chem. Lett., 2019, 10(12), 3318.
88. H. Kunieda and K. Shinoda, Krafft points, critical micelle concentrations, surface tension, and solubilizing power of aqueous solutions of fluorinated surfactants, J. Phys. Chem., 1976, 80(22), 2468.
89. M. L. Ferreira, M. J. Pastoriza-Gallego, J. M. M. Araújo, J. N. Canongia Lopes, L. P. N. Rebelo, M. Piñeiro, K. Shimizu and A. B. Pereiro, Influence of Nanosegregation on the Phase Behavior of Fluorinated Ionic Liquids, J. Phys. Chem. C, 2017, 121(9), 5415.
90. V. Domínguez-Arca, J. Sabín, P. Taboada, L. García-Río and G. Prieto, Micellization thermodynamic behavior of gemini cationic surfactants. Modeling its adsorption at air/water interface, J. Mol. Liq., 2020, 308, 113100.
91. N. V. Plechkova and K. R. Seddon, Applications of ionic liquids in the chemical industry, Chem. Soc. Rev., 2008, 37(1), 123.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06101a

---