Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hemicellulose pyrolysis: mechanism and kinetics of functionalized xylopyranose†
Leandro
Ayarde-Henríquez
 *ab,
Jacopo
Lupi
*ab,
Jacopo
Lupi
 ab and
Stephen
Dooley
*ab
ab and
Stephen
Dooley
*ab
aSchool of Physics, Trinity College Dublin, Dublin 2, Ireland. E-mail: leandro.ayarde@tcd.ie; stephen.dooley@tcd.ie
bAMBER, Advanced Materials and BioEngineering Research Centre, Dublin 2, Ireland
First published on 4th April 2024
Abstract
This work analyzes the thermochemical kinetic influence of the most prominent functionalizations of the β-D-xylopyranose motif, specifically 4-methoxy, 5-carboxyl, and 2-O-acetyl, regarding the pyrolytic depolymerization mechanism. The gas-phase potential energy surface of the initial unimolecular decomposition reactions is computed with M06-2X/6-311++G(d,p), following which energies are refined using the G4 and CBS-QB3 composite methods. Rate constants are computed using the transition state theory. The energies are integrated within the atomization method to assess for the first time the standard enthalpy of formation of β-D-xylopyranose, 4-methoxy-5-carboxy-β-D-xylopyranose, and 2-O-acetyl-β-D-xylopyranose: −218.2, −263.1, and −300.0 kcal mol−1, respectively. For all isomers, the activation enthalpies of ring-opening are considerably lower, 43.8–47.5 kcal mol−1, than the ring-contraction and elimination processes, which show higher values ranging from 61.0–81.1 kcal mol−1. The functional groups exert a notable influence, lowering the barrier of discrete elementary reactions by 1.9–8.3 kcal mol−1, increasing thus the reaction rate constant by 0–4 orders of magnitude relative to unsubstituted species. Regardless of the functionalization, the ring-opening process appears to be the most kinetically favored, characterized by a rate constant on the order 101 s−1, exceeding significantly the values associated with ring-contraction and elimination, which fall in the range 10−4–10−10 s−1. This analysis shows the decomposition kinetics are contingent on the functionalization specificities and the relative orientation of reacting centers. A relatively simple chemical reactivity and bonding analysis partially support the elaborated thermokinetic approach. These insights hold significance as they imply that many alternative decomposition routes can be quickly, yet accurately, informed in forthcoming explorations of potential energy surfaces of diverse hemicellulose motifs under pyrolysis conditions.
Introduction
In contemporary global economic scenarios, predominant reliance persists on non-renewable energy resources, including coal, natural gas, and petroleum.1,2 Recent assessments underscore that worldwide energy consumption has reached a staggering 412 exajoules per year (EJ per year),1 displaying an upward trajectory for the past ten decades, barring any economic recessions. This escalating demand stresses the importance of identifying and harnessing alternative, sustainable fuel sources.3 Fortunately, biomass emerges as a plentiful and renewable reservoir of sustainable carbon and hydrogen with the potential to provide up to 147 EJ in 2030.1,2 Biomass broadly encompasses organic matter of plants and animals;4,5 however, this term is usually restricted to the referring of botanical constituents. Plant biomass is a composite of diverse organic compounds, including lipids, sugars, and lignocellulose, the latter being the fundamental structural material of plants. The inherent complexity of lignocellulosic plant matter is illustrated through the relative proportions of its principal components: cellulose 40–60%, hemicellulose 15–30%, and lignin 10–25%.4,6 Cellulose, the most abundant saccharide on Earth,7–10 is an ordered polymeric structure of glucose (C6H12O6). Frequently, cellulose is represented in terms of its basic unit, namely, the degree of polymerization (n), highlighting its polysaccharide nature, i.e., (C6H10O5)n.4,7 This renewable and biodegradable polymer has found wide-ranging applications across diverse food, textile, and plastics industries.7 In contrast, hemicellulose is not a homopolysaccharide since it is formed by shorter chains, including mainly hexoses (C6H12O6) and pentoses (C5H10O5).11,12 Conversely, lignin presents an amorphous polymeric structure of aromatic ether rings attached to a three-carbon propene tail,13–15 as presented in Scheme 1.The degradation of biomass to valuable chemicals and fuels through thermochemical processes, such as pyrolysis, gasification, hydrothermal liquefaction, and others, has captured the attention of the Industry, Government, and Academia.3,4,6,16 Among all methods for degrading biomass, the so-called fast pyrolysis (FP) is considered the most attractive.1,17,18 Under FP conditions, biomass is thermally decomposed (≈400–600 °C, ≈103 °C) under an inert atmosphere, i.e., without oxygen.1,19,20 Fast pyrolysis is regarded as a leading technology due to its technical and economic performance. In the context of the FP regime, it is essential to note that cellulose, hemicellulose, and lignin bio-oil yields exhibit characteristic values of approximately 70, 60, and 40%, respectively. However, these values are notably sensitive to variations in temperature. This means that an increase or drop in the temperature will cause the system to deviate from these thermal operation conditions, thus impacting these yields.21,22 Currently, the bio-oil produced falls short in quality and cost-effectiveness compared to its petroleum-derived crude oil counterparts. This discrepancy is primarily attributed to several issues that must be surmounted before the commercial-scale utilization of bio-products can be achieved:1,4,5,17,23 (i) the chemical structural complexity and high variability of main biomass components, (ii) challenges posed by the scale and multiscale problems, (iii) the imperative development of effective technologies for characterizing biomass products, and (iv) the pressing need for accurate and unified kinetic models to predict the type and relative abundance of bioproducts. From our perspective, it is crucial to conduct systematic theoretical studies that account for the influence of both metals and substituents due to the current experimental limitations. This rigorous approach is needed for elucidating fundamental molecular physical knowledge underpinning the thermal depolymerization of biomass, facilitating the transition towards a bio-based and circular economy.
Recently, our research group has been actively immersed in developing a detailed kinetic model for the pyrolysis of hemicellulose and lignin. This model is poised for further refinement through the Machine Learned Optimization of Chemical Kinetics (MLOCK) coded algorithm.24 MLOCK optimizes kinetic models to target data (e.g., experimental measurements) through the generation and evaluation of sets of solutions by simultaneous perturbation of Arrhenius parameters. Machine learning and data-analysis techniques are employed to direct the search algorithm toward the ideal set of solutions that results in a kinetic model of high fidelity to the optimization targets. Furthermore, it is well known that a minor content of minerals is present within the plant tissues in the form of cations, oxides, salts, phosphates, and sulfates.1,17 This inorganic material encompasses a variety of minerals such as potassium (K), magnesium (Mg), sodium (Na), calcium (Ca), cobalt (Co), and copper (Cu).1,17 These elements significantly impact the depolymerization processes, although the content is typically low, ranging from 2–25% of the total mass.1 In addition, the presence of O-acetyl groups in hard and soft wood hemicellulose is well-documented.25–27 The precise positions of such groups, C2 and/or C3, were determined by combining nuclear magnetic resonance (NMR), thermogravimetric analysis (TGA), and chemical analysis. Separate experimental investigations have successfully isolated 4-methoxy-5-carboxy-β-D-xylopyranose (henceforth referred to as 4-O-methyl-D-glucuronic acid) from different hemicellulose plant sources.28,29
It should be emphasized that considerable research efforts have been dedicated to investigating the thermal degradation mechanism of cellulose, leading to comparatively fewer studies on the other two primary biomass components.27 In the existing literature, investigations addressing the depolymerization impact of substituents on the thermokinetic features of pyrolytic processes are scarce. Wang and co-workers30 identified some products resulting from the breakage of O-acetyl groups and 4-O-methyl-D-glucuronic acid units from xylan by combining thermogravimetric and Fourier-transform infrared spectroscopy techniques. Huang et al.31 proposed some pyrolytic reaction pathways for products of 2-O-acetyl-β-D-xylopyranose (hereafter termed 2-O-acetyl-xylose). However, to the best of our knowledge, there is a conspicuous absence of prior studies concerning the systematic assessment of the influence of functional groups on hemicellulose depolymerization, even though some studies show that the amount of O-acetyl groups could significantly impact the product yields and condition bio-oils acidity.18,32–34 Consequently, this work aims to discuss to what extent functional groups affect the pyrolytic degradation of the hemicellulose motif, β-D-xylopyranose (hereafter referred to as xylose), from both thermodynamic and kinetic viewpoints. Subsequent systematic studies will address other biomass components (e.g., lignin), the organic–inorganic interaction, and the transferring of all these insights to our kinetic model.
The manuscript is organized as follows: first, the computational methods employed are outlined. Subsequent sections discuss the thermochemical and kinetics results for the initial pyrolysis steps of xylose, 2-O-acetyl-xylose, and 4-O-methyl-D-glucuronic acid. Additionally, the insights derived from the analysis of electron-density-based descriptors are discussed. The last section summarizes the main findings and delineates potential directions for future research.
Computational methods
Geometry optimizations were performed at the M06-2X/6-311++G(d,p) level of theory using the Gaussian 16 code.35 This global hybrid functional is parametrized for non-metal elements and has been recommended for main-group thermochemistry and kinetic investigations.36 For all cases, the intrinsic reaction coordinate (IRC)37 was followed to ensure the transition state (TS) connects the correct reactant and product(s). As a standard procedure, the stationary points on the IRC were characterized as minima (i.e., reactants and products) and first-order saddle points (TSs) based on the vibrational frequency signs. The adequacy of our single-reference-based methodology was assessed via the![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 diagnostic38 for key species along the pathways. The static correlation is insignificant for the investigated systems, meaning multireference methods are not required since
1 diagnostic38 for key species along the pathways. The static correlation is insignificant for the investigated systems, meaning multireference methods are not required since ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 < 0.02. See the ESI† for further details.
1 < 0.02. See the ESI† for further details.
Conformational analysis for critical species (e.g., minima and TSs) along the IRC was conducted using the CREST program.39 This software combines semiempirical tight-binding methods with meta-dynamics to generate conformers thermodynamic ensembles within a relatively narrow energy window of 4.87 kcal mol−1. This set of structures was further optimized at the M06-2X/6-311++G(d,p) level and compared with those observed in scattering experiments to ensure the study of the correct enantiomer.
In order to obtain accurate thermochemistry values at both absolute zero and 298 K, composite model chemistry methods such as the complete basis set (CBS)40,41 and Gaussian-4 (G4)42 were employed. In these approaches, geometry optimizations and frequency calculations are performed using relatively simple and cost-effective methods, adding higher levels of theory in a stepwise manner.
Calculations of thermodynamic properties such as the Gibbs free energy (ΔG) and heat capacities (Cp and Cv) at various temperatures were conducted in the rigid-rotor harmonic oscillator (RRHO) approximation using the Shermo 2.3.5 suite.43 This is a pretty flexible code that allows the explicit consideration of scaling factors of vibrational frequencies for several quantities, including the zero-point vibrational energy (ZPE), for determining thermochemical values and automatically treating the low frequencies via Grimme's44 entropy interpolation between harmonic and free-rotor approximations on an ideal gas behavior assumption. It is worth mentioning that Lu and Chen43 showed that applying quasi-RRHO (QRRHO) schemes for treating hindered internal rotors in relatively flexible molecules moderately impacts entropy (S). Based on harmonic approximation, the Cp is computed as follows:
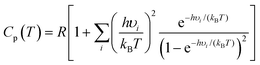 | (1) |
The standard enthalpy of formation, ΔH0f at 298 K, of chemical species was computed using Rogers et al.'s methodology.45 This procedure combines experimental46,47 and computed thermochemistry data to accurately derive the values of ΔH0f by using the reaction enthalpy, ΔH0r, as a proxy. Let us exemplify this algorithm by considering the formation of one molecule of water from its constituents (atoms) in their standard state:
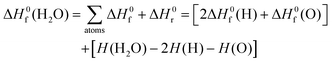 | (2) |
The rate constant, k(T), of each elementary step is determined through canonical transition state theory (TST):
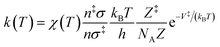 | (3) |
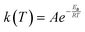 | (4) |
The chemical reactivity assessment was conducted by calculating the electronic chemical potential, μ,49 and Fukui's functions (f+, f−, and f0).50 The parameter μ measures the global tendency of electrons to escape from a ground-state system.49,51 Conversely, the f indices describe the local response of the molecule to nucleophilic (f+), electrophilic (f−), and neutral/radical (f0) attacks.50,52–54 Additionally, the bonding analysis was performed using the electron localization function (ELF).55,56 ELF is frequently interpreted as a local measure of electrons’ kinetic energy excess due to Pauli's exclusion principle;57,58 thus, high values of this function (>0.5) correspond to a spatial position with high electron localization.59,60 The nullity condition applied to the ELF gradient yields a partition of the molecular space into basins of attractors, empirically associated with Lewis’ bonding elements, including valence bonds, lone pairs, and atomic cores.61–63 The numerical computation of the chemical reactivity and bonding analysis was carried out using the Multiwfn packages.64
Results and discussion
Thermochemical insights
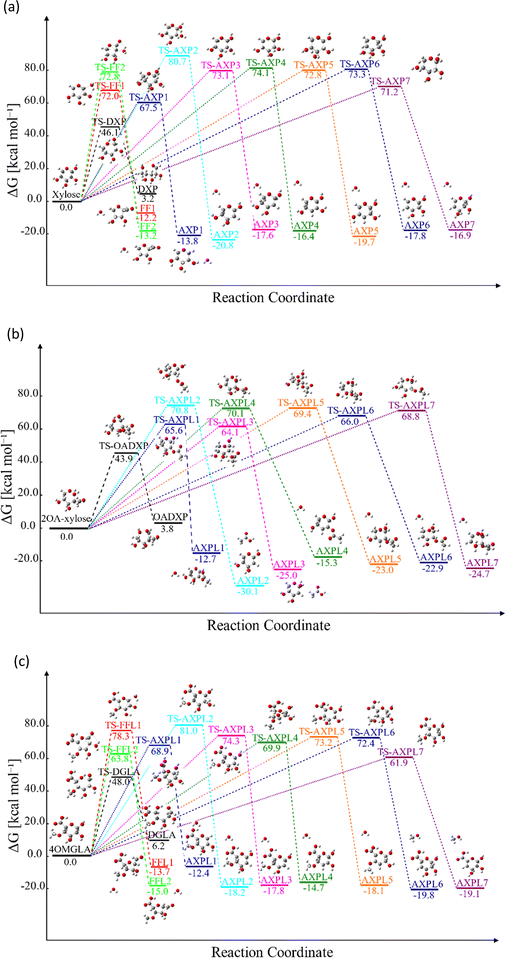
Various structural motifs have been used to investigate the depolymerization of hemicellulose under different experimental setups.5 Lu et al.65 extensively studied the pyrolytic mechanism of xylose, 1,4-β-D-xylobiose, and xylan by combining experimental and computational methodologies. They employed a gas-chromatograph (GC) coupled to a mass spectrometer (MS) to analyze and identify the products generated upon pyrolysis of these hemicellulose motifs. Next, a detailed reaction network comprising about 50 processes was proposed to elucidate the depolymerization mechanism of xylose, including three elemental initial steps: ring-opening, ring-contraction, and elimination. Consequently, this system is chosen as a prototypical structure for modeling hemicellulose in this study. Our goal is to assess the impact of substituents through the use of functionalized species such as 2-O-acetyl-xylose and 4-O-methyl-D-glucuronic acid undergoing the same initial reactions, as illustrated in Scheme 2. This strategic approach provides a systematic basis for hierarchically ordering subsequent steps along the decomposition channels. The ring-opening leads to an acyclic product via the bond scission between the pyran-ring oxygen (O) and the carbon at position 1 (C1). Conversely, furfural (FF) and furfural-like (FFL) compounds result from the ring-contraction process through both carbon–carbon (CC) and carbon–oxygen (CO) breakages. At last, reacting species undergo eliminations at positions 1, 2, 3, and 4 upon the bond cleavage of carbons at these sites and the oxygen atom of hydroxyl, methoxy, and O-acetyl groups. This process leads to the formation of anhydroxylopyranose (AXP), anhydroxylopyranose-like (AXPL), acetic acid (AA), and methanol. The simplest system yields AXP, whereas the other three form upon the initial pyrolytic reactions of substituted reactants. The ring-contraction and elimination entail the transfer of the proton situated at neighboring positions to the cleaving CO bond, which emphasizes the intricacies of such elementary steps.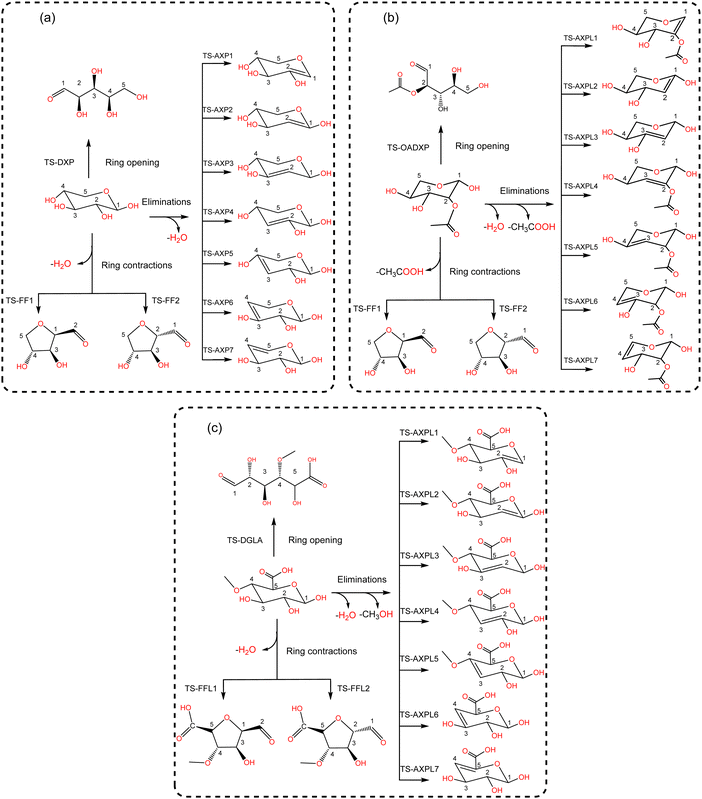 | ||
| Scheme 2 Lewis-like structures illustrating a simple kinetic model comprising key initial depolymerization reactions65 of xylose (panel a). Functionalized chemical species 2-O-acetyl-xylose (panel b) and 4-O-methyl-D-glucuronic acid (panel c) undergo the same reactions to systematically assess the influence of substituents. For all systems, the ring-opening process comprises the C1–O bond cleavage leading to an acyclic form, the ring-contraction involves the transformation of the pyran ring to a five-membered ring, and anhydroxylopyranose forms through elimination. | ||
Table 1 shows the relative enthalpy of activation, ΔH‡, at both 0 and 298 K of substituted and unsubstituted species concerning the ring opening/contraction and elimination processes at three levels of theory: M06-2X/6-311++G(d,p), CBS-QB3, and G4. The performance of G4, the highest level, in predicting activation barriers has been extensively documented for reacting systems in the gas phase. Curtiss and co-workers66 reported a mean unsigned deviation of 1.36 kcal mol−1 between predicted and experimentally derived barriers (both forward and reverse) across thirty-eight hydrogen and non-hydrogen transfer reactions. Sun and McKee67 investigated the initial steps of diborane pyrolysis, noting a deviation of 0.35 kcal mol−1 in the activation energy from experimental values regarding both uni- and bi-molecular paths. Additionally, Houk and collaborators68 computed barriers for 1,3-dipolar cycloadditions of ozone with low-molecular-weight hydrocarbons, demonstrating good agreement with the referential level CCSD(T)/aug-cc-pVXZ//CCSD(T)/cc-pVTZ, where X = T, Q, 5. Using reliable data, Karton and Goerigk69 benchmarked twenty-six pericyclic reactions, including electrocyclic, sigmatropic shift, cycloreversion, and cycloaddition subclasses, reporting a mean absolute deviation equal to 0.6 kcal mol−1. These studies evidence the suitability of G4 in generating accurate thermodynamic properties, particularly activation enthalpies.
| Elementary reaction | T = 0 K | T = 298 K | ||||
|---|---|---|---|---|---|---|
| ΔH‡DFT | ΔH‡CBS | ΔH‡G4 | ΔH‡DFT | ΔH‡CBS | ΔH‡G4 | |
| DFT stands for M06-2X/6-311++G(d,p).CBS stands for CBS-QB3.a Indicates relaxed convergence criteria. | ||||||
| Xylose → D-xylose | 49.68 | 38.19 | 45.55 | 45.54 | 37.30 | 45.54 |
| Xylose → FF1 + H2O | 76.21 | 71.20a | 71.41 | 72.84 | 71.30a | 71.47 |
| Xylose → FF2 + H2O | 73.19 | 57.55 | 65.07 | 70.25 | 56.68 | 65.09 |
| Xylose → AXP1 + H2O | 75.55 | 62.02 | 69.11 | 70.56 | 61.64 | 69.65 |
| Xylose → AXP2 + H2O | 87.20 | 73.70 | 80.73 | 82.00 | 73.27 | 81.08 |
| Xylose → AXP3 + H2O | 79.73 | 66.27 | 73.49 | 74.55 | 65.69 | 73.76 |
| Xylose → AXP4 + H2O | 81.45 | 67.78 | 74.86 | 76.08 | 67.40 | 75.20 |
| Xylose → AXP5 + H2O | 80.08 | 66.41 | 74.05 | 74.78 | 65.96 | 74.39 |
| Xylose → AXP6 + H2O | 81.68 | 67.01 | 74.38 | 76.07 | 66.46 | 74.85 |
| Xylose → AXP7 + H2O | 77.19 | 64.26 | 71.49 | 71.81 | 63.48 | 71.56 |
| 2-O-Acetyl-xylose → OADXP | 46.56 | 43.99 | 43.91 | 42.65 | 43.89 | 43.79 |
| 2-O-Acetyl-xylose → FFL1 + CH3COOH | — | — | — | — | — | — |
| 2-O-Acetyl-xylose → FFL2 + CH3COOH | 71.64a | 65.49 | 65.27 | 68.44a | 65.61 | 65.35 |
| 2-O-Acetyl-xylose → AXPL1 + H2O | 70.71 | 68.04 | 67.72 | 66.07 | 68.33 | 67.94 |
| 2-O-Acetyl-xylose → AXPL2 + CH3COOH | 79.37 | 73.76 | 73.28 | 74.39 | 74.32 | 73.80 |
| 2-O-Acetyl-xylose → AXPL3 + CH3COOH | 70.94 | 65.25 | 65.14 | 65.77 | 65.55 | 65.43 |
| 2-O-Acetyl-xylose → AXPL4 + H2O | 75.77 | 72.43 | 71.94 | 70.84 | 72.72 | 72.19 |
| 2-O-Acetyl-xylose → AXPL5 + H2O | 77.76 | 71.49 | 71.32 | 72.57 | 71.63 | 71.43 |
| 2-O-Acetyl-xylose → AXPL6 + H2O | 76.33 | 73.10 | 72.38 | 71.16 | 73.58 | 72.79 |
| 2-O-Acetyl-xylose → AXPL7 + H2O | 75.25 | 70.38 | 69.78 | 69.60 | 70.49 | 69.87 |
| 4-O-Methyl-D-glucuronic acid → DGLA | 51.87 | 47.77 | 47.66 | 47.36 | 47.76 | 47.62 |
| 4-O-Methyl-D-glucuronic acid → FFL1 + H2O | 82.85 | 76.77a | 76.70a | 79.21 | 77.02a | 76.99a |
| 4-O-Methyl-D-glucuronic acid → FFL2 + H2O | 67.34 | 60.91 | 61.01 | 64.66 | 60.94 | 61.03 |
| 4-O-Methyl-D-glucuronic acid → AXPL1 + H2O | 75.64 | 70.19 | 68.79 | 70.49 | 70.62 | 69.27 |
| 4-O-Methyl-D-glucuronic acid → AXPL2 + H2O | 85.70 | 75.67 | 75.28 | 81.37 | 75.53 | 75.10 |
| 4-O-Methyl-D-glucuronic acid → AXPL3 + H2O | 80.77 | 74.82 | 74.29 | 75.62 | 75.19 | 74.60 |
| 4-O-Methyl-D-glucuronic acid → AXPL4 + H2O | 73.24 | 69.40 | 68.89 | 68.71 | 69.38 | 68.78 |
| 4-O-Methyl-D-glucuronic acid → AXPL5 + H2O | 78.65 | 73.87 | 73.51 | 73.68 | 74.23 | 73.84 |
| 4-O-Methyl-D-glucuronic acid → AXPL6 + CH3OH | 79.67 | 72.23 | 72.28 | 74.73 | 72.85 | 72.92 |
| 4-O-Methyl-D-glucuronic acid → AXPL7 + CH3OH | 66.35 | 63.95 | 63.53 | 62.58 | 64.08 | 63.70 |
It is worth noting that the transition states (TSs) of reactions comprising the conversion from the pyran to FF configuration, TS-FFL1, failed to converge for 2-O-acetyl-xylose at the DFT level regardless of utilizing Gaussian 16 algorithms such as synchronous transit-guided quasi-Newton (STQN) and scan. Attempts to explore the PES using the nudged elastic band (NEB) and NEB-TS algorithms implemented in ORCA 5.070 proved unsuccessful in providing a reliable guess for this TS. In this context, the TS-FFL2 was finally located upon relaxing the convergence criteria by adjusting the Gaussian ConvF threshold, i.e., ConvF = N × 10−6, where N = 3.0 × 105. This approach was also adopted for xylose (CBS-QB3) and 4-O-methyl-D-glucuronic acid (CBS-QB3 and G4), using N = 1.2 × 104 and N = 3.0 × 105, respectively. These values have been indicated by an asterisk (see Table 1) and are excluded from our analysis.
Interestingly, the barrier description provided by G4 and CBS-QB3 differs substantially across functionalized and unfunctionalized species. This proves fundamental differences in the state-of-the-art levels of theory integrated within these composite models, particularly in their capabilities to describe correlation effects. The electronic energy accuracy provided by CCSD(T) and QCSD(T) plays a significant role in this discrepancy. In the case of the single-functionalized species, CBS-QB3 yields a significant difference of 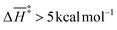 for most steps relative to the simplest system. Contrary to the results obtained with G4. This Gaussian-family method reveals that the presence of the O-acetyl group at C2 significantly lowers the activation enthalpy (≈7–8 kcal mol−1) of processes directly involving the substituent, specifically TS-AXPL2 and TS-AXPL3. Similarly, this trend is observed when comparing xylose and 4-O-methyl-D-glucuronic acid results, as evidenced by the relatively high difference in ΔH‡ for the elimination comprising the methoxy group (undergone via TS-AXPL7). This is expected for TSs involving such a group; however, we found other dehydrations where ΔH‡ > 5 kcal mol−1 at the G4 level, exemplified by the reactions associated with TS-AXPL2 and TS-AXPL4. Therefore, conducting an in-depth examination of the steric and regioselectivity effects is pertinent to elucidate the underlying mechanisms influencing the apparent favorable direction.
for most steps relative to the simplest system. Contrary to the results obtained with G4. This Gaussian-family method reveals that the presence of the O-acetyl group at C2 significantly lowers the activation enthalpy (≈7–8 kcal mol−1) of processes directly involving the substituent, specifically TS-AXPL2 and TS-AXPL3. Similarly, this trend is observed when comparing xylose and 4-O-methyl-D-glucuronic acid results, as evidenced by the relatively high difference in ΔH‡ for the elimination comprising the methoxy group (undergone via TS-AXPL7). This is expected for TSs involving such a group; however, we found other dehydrations where ΔH‡ > 5 kcal mol−1 at the G4 level, exemplified by the reactions associated with TS-AXPL2 and TS-AXPL4. Therefore, conducting an in-depth examination of the steric and regioselectivity effects is pertinent to elucidate the underlying mechanisms influencing the apparent favorable direction.
The standard enthalpy of formation, ΔH0f(298 K), of atoms and molecules is an essential thermodynamic quantity in the analysis of gas-phase processes employing detailed kinetic models. This quantity is determined through different methodologies, including isodesmotic71,72 and connectivity-based hierarchy (CBH)44,73 schemes. In our study, we determined ΔH0f(298 K) for reactants and products resulting from the initial elementary steps through the atomization scheme outlined by Rogers and collaborators.45 This procedure combines experimental46,47 and atomization thermochemistry data generated via computational algorithms to calculate ΔH0f by considering the reaction enthalpy of various isodesmic74 and homodesmotic74 reactions. Although less prone to error cancellations, the atomization approach was adopted due to its easy applicability and reasonable accuracy.45,75 The evaluation of water, methanol, and acetic acid (AA) in the gas phase reveals discrepancies not surpassing 0.50 kcal mol−1 between the experimental and computed values when corrections for spin–orbit couplings (SOC)76,77 of carbon and oxygen atoms are integrated a posteriori within the atomization scheme to fine-tune ΔH0f, as presented in Table 2. Notably, the absolute error decreases by 0.16, 0.20, and 0.50 kcal mol−1 for the corresponding species when such a correction is considered; these values are presented in parentheses in Table 2. This trend indicates the potential significant influence of SOC effects on the accuracy of the predicted ΔH0f, particularly for moieties characterized by a relatively high molecular weight.
| Species | ΔH0f | Formula | Species | ΔH0f | Formula | Species | ΔH0f | Formula |
|---|---|---|---|---|---|---|---|---|
| a The experimental value is equal to (−57.80 ± 0.02) kcal mol−1. See Ruscic et al.46 b The experimental value is equal to (−103.41 ± 0.36) kcal mol−1. See Ruscic et al.46 c The experimental value is equal to (−48.07 ± 0.15) kcal mol−1. See Ruscic et al.46 | ||||||||
| Xylose | −218.15 (−216.91) | C5H10O5 | 2-O-Acetyl-xylose | −263.08 (−261.51) | C7H12O6 | 4OMGLA | −299.99 (−298.26) | C7H12O7 |
| DXP | −209.65 (−208.41) | C5H10O5 | OADXP | −253.62 (−252.05) | C7H12O6 | DGLA | −291.27 (−289.54) | C7H12O7 |
| FF1 | −145.27 (−144.20) | C5H8O4 | FFL1 | −145.28 (−144.20) | C5H8O4 | FFL1 | −229.11 (−227.55) | C7H10O6 |
| FF2 | −145.96 (−144.88) | C5H8O4 | FFL2 | −146.06 (−144.99) | C5H8O4 | FFL2 | −230.49 (−228.92) | C7H10O6 |
| AXP1 | −145.78 (−144.71) | C5H8O4 | AXPL1 | −189.18 (−187.77) | C7H10O5 | AXPL1 | −226.61 (−225.05) | C6H8O6 |
| AXP2 | −152.76 (−151.69) | C5H8O4 | AXPL2 | −152.77 (−151.69) | C7H10O5 | AXPL2 | −232.26 (−230.69) | C6H8O6 |
| AXP3 | −150.87 (−149.80) | C5H8O4 | AXPL3 | −148.49 (−147.41) | C7H10O5 | AXPL3 | −233.14 (−231.57) | C7H10O6 |
| AXP4 | −149.52 (−148.44) | C5H8O4 | AXPL4 | −190.48 (−189.08) | C7H10O5 | AXPL4 | −228.63 (−227.07) | C7H10O6 |
| AXP5 | −152.56 (−151.49) | C5H8O4 | AXPL5 | −199.94 (−198.54) | C5H8O4 | AXPL5 | −233.80 (−232.23) | C7H10O6 |
| AXP6 | −150.47 (−149.40) | C5H8O4 | AXPL6 | −200.34 (−198.93) | C5H8O4 | AXPL6 | −238.97 (−237.49) | C7H10O6 |
| AXP7 | −149.79 (−148.72) | C5H8O4 | AXPL7 | −202.59 (−201.19) | C7H10O5 | AXPL7 | −237.89 (−236.41) | C7H10O6 |
| H2O | −57.46a (−57.30) | H2O | AA | −102.95b (−102.46) | C2H4O2 | Methanol | −48.12c (−47.87) | CH4O |
The heat capacity of materials is a relevant quantity in thermodynamics, aiding in the precise calculation of thermal requirements and optimal processing temperatures. Furthermore, it serves as a discriminative parameter in distinguishing between two distinct polymeric composites based on their thermal characteristics.78 In this context, the heat capacities at constant volume (Cv) and pressure (Cp), as well as the entropy, were computed for all the species in the gas phase. The low values of Cp increase with rising temperatures for all species. As anticipated, the pyran-ring structures have lower values than their corresponding acyclic form since the latter molecular configuration is less rigid, which favors the contribution of additional vibrational degrees of freedom. The influence of functional groups is evident since larger structures, in terms of the number of atoms, are characterized by higher Cp. For instance, at 200 K and 1.0 atm, the heat capacity of 2-O-acetyl-xylose and 4-O-methyl-D-gluguronic acid are 22.9 and 27.7% higher, respectively, than that of xylose. Such percentages slightly decrease as the absolute temperature increases.
At a temperature of 381.20 K and under 1.0 atm of pressure, calorimetric experiments conducted by McCullough and co-workers79 give a value of 0.0088 kcal mol−1 K−1 for the water vapor, characterized by an expected uncertainty not greater than ±0.2%. Notably, our calculations yield 0.0082 kcal mol−1 K−1 at 400 K, showing a close agreement with the experimental data. However, they applied statistical procedures to compensate for deviations driven by gas imperfections since the apparent heat capacity decreased as the temperature increased. This observation contrasts with our computational findings, which do not display such a trend, as evidenced in Table 3.
| Species | T/K 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
|---|---|---|---|---|---|---|---|---|---|
| The experiment-derived values of water, acetic acid, and methanol are provided in round brackets. See Stull et al.80 | |||||||||
| Xylose | 0.02935 | 0.04030 | 0.05075 | 0.05989 | 0.06740 | 0.07349 | 0.07851 | 0.08270 | 0.08626 |
| DXP | 0.03244 | 0.04277 | 0.05263 | 0.06126 | 0.06839 | 0.07421 | 0.07904 | 0.08310 | 0.08657 |
| FF1 | 0.02567 | 0.03435 | 0.04308 | 0.05081 | 0.05721 | 0.06245 | 0.06677 | 0.07038 | 0.07345 |
| FF2 | 0.02591 | 0.03446 | 0.04312 | 0.05082 | 0.05722 | 0.06245 | 0.06678 | 0.07040 | 0.07346 |
| AXP1 | 0.02544 | 0.03494 | 0.04385 | 0.05153 | 0.05780 | 0.06287 | 0.06704 | 0.07053 | 0.07348 |
| AXP2 | 0.02539 | 0.03492 | 0.04389 | 0.05160 | 0.05787 | 0.06294 | 0.06709 | 0.07057 | 0.07351 |
| AXP3 | 0.02481 | 0.03445 | 0.04352 | 0.05130 | 0.05763 | 0.06276 | 0.06696 | 0.07047 | 0.07345 |
| AXP4 | 0.02507 | 0.03464 | 0.04364 | 0.05137 | 0.05768 | 0.06280 | 0.06699 | 0.07050 | 0.07346 |
| AXP5 | 0.02495 | 0.03463 | 0.04365 | 0.05139 | 0.05770 | 0.06281 | 0.06701 | 0.07051 | 0.07348 |
| AXP6 | 0.02531 | 0.03481 | 0.04376 | 0.05146 | 0.05776 | 0.06286 | 0.06705 | 0.07054 | 0.07351 |
| AXP7 | 0.02526 | 0.03480 | 0.04385 | 0.05161 | 0.05792 | 0.06300 | 0.06716 | 0.07063 | 0.07357 |
| H2O | 0.00795 | 0.00800 | 0.00816 | 0.00839 | 0.00864 | 0.00890 | 0.00916 | 0.00943 | 0.00969 |
| (0.00803) | (0.00819) | (0.00842) | (0.00868) | (0.00895) | (0.00925) | (0.00955) | (0.00985) | ||
| 2-O-Acetyl-xylose | 0.03806 | 0.05136 | 0.06441 | 0.07588 | 0.08534 | 0.09305 | 0.09942 | 0.10475 | 0.10927 |
| OADXP | 0.04135 | 0.05416 | 0.06649 | 0.07735 | 0.08639 | 0.09383 | 0.10001 | 0.10522 | 0.10966 |
| FFL1 | 0.02556 | 0.03428 | 0.04303 | 0.05078 | 0.05719 | 0.06243 | 0.06676 | 0.07038 | 0.07344 |
| FFL2 | 0.02578 | 0.03441 | 0.04314 | 0.05088 | 0.05727 | 0.06250 | 0.06681 | 0.07042 | 0.07348 |
| AXPL1 | 0.03416 | 0.04604 | 0.05748 | 0.06746 | 0.07569 | 0.08241 | 0.08796 | 0.09261 | 0.09654 |
| AXPL2 | 0.02537 | 0.03491 | 0.04389 | 0.05159 | 0.05787 | 0.06294 | 0.06710 | 0.07057 | 0.07351 |
| AXPL3 | 0.02469 | 0.03442 | 0.04358 | 0.05139 | 0.05772 | 0.06283 | 0.06701 | 0.07050 | 0.07345 |
| AXPL4 | 0.03437 | 0.04607 | 0.05747 | 0.06745 | 0.07568 | 0.08242 | 0.08797 | 0.09262 | 0.09656 |
| AXPL5 | 0.03388 | 0.04578 | 0.05732 | 0.06736 | 0.07562 | 0.08235 | 0.08791 | 0.09256 | 0.09650 |
| AXPL6 | 0.03345 | 0.04548 | 0.05713 | 0.06723 | 0.07552 | 0.08229 | 0.08786 | 0.09252 | 0.09646 |
| AXPL7 | 0.03257 | 0.04490 | 0.05683 | 0.06711 | 0.07549 | 0.08228 | 0.08786 | 0.09251 | 0.09644 |
| AA | 0.01268 | 0.01625 | 0.01977 | 0.02286 | 0.02546 | 0.02763 | 0.02946 | 0.03103 | 0.03239 |
| (0.01597) | (0.01952) | (0.02260) | (0.02515) | (0.02735) | (0.02908) | (0.03060) | (0.03199) | ||
| 4OMGLA | 0.04061 | 0.05469 | 0.06822 | 0.08008 | 0.08986 | 0.09783 | 0.10439 | 0.10987 | 0.11450 |
| DGLA | 0.04207 | 0.05623 | 0.06953 | 0.08107 | 0.09059 | 0.09837 | 0.10480 | 0.11019 | 0.11477 |
| FFL1 | 0.03624 | 0.04838 | 0.06033 | 0.07085 | 0.07957 | 0.08671 | 0.09259 | 0.09750 | 0.10165 |
| FFL2 | 0.03648 | 0.04849 | 0.06037 | 0.07086 | 0.07958 | 0.08671 | 0.09260 | 0.09752 | 0.10167 |
| AXPL1 | 0.03629 | 0.04916 | 0.06124 | 0.07167 | 0.08023 | 0.08719 | 0.09291 | 0.09768 | 0.10171 |
| AXPL2 | 0.03645 | 0.04930 | 0.06141 | 0.07185 | 0.08039 | 0.08733 | 0.09303 | 0.09778 | 0.10179 |
| AXPL3 | 0.03556 | 0.04855 | 0.06081 | 0.07137 | 0.08001 | 0.08703 | 0.09279 | 0.09760 | 0.10165 |
| AXPL4 | 0.03662 | 0.04928 | 0.06130 | 0.07172 | 0.08028 | 0.08724 | 0.09297 | 0.09774 | 0.10177 |
| AXPL5 | 0.03580 | 0.04882 | 0.06102 | 0.07153 | 0.08014 | 0.08713 | 0.09286 | 0.09765 | 0.10168 |
| AXPL6 | 0.03234 | 0.04440 | 0.05525 | 0.06432 | 0.07159 | 0.07740 | 0.08212 | 0.08601 | 0.08929 |
| AXPL7 | 0.03308 | 0.04491 | 0.05559 | 0.06456 | 0.07177 | 0.07754 | 0.08221 | 0.08608 | 0.08934 |
| Methanol | 0.00946 | 0.01079 | 0.01270 | 0.01470 | 0.01653 | 0.01815 | 0.01956 | 0.02081 | 0.02191 |
| (0.01052) | (0.01229) | (0.01422) | (0.01602) | (0.01762) | (0.01904) | (0.02029) | (0.02138) | ||
In a separate study, Stull and collaborators80 compiled a thermochemical dataset spanning over several decades, comprising 741 pure organic compounds in the gas phase. This type of collection of experimental values was previously obtained by combining thermal and spectroscopic direct measurements. For water, the computed Cp in the range of 300 to 1000 K deviates by 1.6% at most from the corresponding experimental value. Furthermore, this remarkable trend is also observed for acetic acid (AA) and methanol; see Table 3.
Goldberg and collaborators81 performed rigorous combustion calorimetric measurements on the crystalline alpha anomer of xylose, specifically α-D-xylopyranose. Their investigation covered a wide temperature range from 1.9 to 305 K and used an isoperibol static bomb calorimeter. They reported an experimental value equal to Cp = (0.04254 ± 0.00180) kcal mol−1 K−1 at 298.15 K, which deviates 3.21% from other measures obtained through similar experimental setups.82,83 Surprisingly, the Cp provided by Goldberg closely approximates the computed one for the beta isomer in the gas phase at 300 K. In contrast, the Cp = (0.06716 ± 0.002) kcal mol−1 K−1 of the α configuration in the aqueous phase at 303 K found by Kawaizumi et al.83 is about 60% higher. Additional details concerning computed values of Cv and S for all species in the gas phase can be found in the ESI.†
Reactive potential energy surfaces of the three investigated systems are reported in Fig. 1.
Kinetic findings
The analysis of the Gibbs free energy, ΔG, reveals distinct thermodynamic behaviors among the species studied. For xylose, the ring-opening step becomes favorable only at temperatures exceeding 800 K. In contrast, ΔG > 0 for both substituted systems in the temperature interval of 400 to 1000 K indicates the thermodynamic non-favorability of this reaction. All the other processes proceed in the forward direction across this temperature range for the simplest reactant and 4-O-methyl-D-glucuronic acid. However, the elimination process leading to the AXPL1 product is unfavorable at the lowest temperature for the single-substituted system, as shown in Table 4. It is worth noting that 400 K falls completely outside the FP domain.| Reaction | T/K 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
|---|---|---|---|---|---|---|---|
| Xylose | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| D-Xylose | 2.01 | 1.49 | 0.99 | 0.49 | 0.01 | −0.45 | −0.90 |
| FF1 + H2O | −1.72 | −5.80 | −9.84 | −13.84 | −17.79 | −21.70 | −25.56 |
| FF2 + H2O | −2.71 | −6.82 | −10.89 | −14.91 | −18.89 | −22.82 | −26.70 |
| AXP1 + H2O | −0.87 | −4.83 | −8.79 | −12.74 | −16.66 | −20.56 | −24.43 |
| AXP2 + H2O | −7.83 | −11.84 | −15.85 | −19.86 | −23.83 | −27.79 | −31.71 |
| AXP3 + H2O | −5.72 | −9.58 | −13.44 | −17.27 | −21.08 | −24.85 | −28.60 |
| AXP4 + H2O | −4.26 | −8.16 | −12.05 | −15.93 | −19.77 | −23.59 | −27.38 |
| AXP5 + H2O | −6.67 | −10.60 | −14.53 | −18.44 | −22.33 | −26.20 | −30.03 |
| AXP6 + H2O | −5.13 | −9.06 | −12.99 | −16.89 | −20.77 | −24.63 | −28.45 |
| AXP7 + H2O | −3.05 | −7.05 | −11.04 | −15.01 | −18.96 | −22.88 | −26.77 |
| 2-O-Acetyl-xylose | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| OADXP | 4.32 | 3.73 | 3.13 | 2.53 | 1.94 | 1.34 | 0.75 |
| FFL1 + CH3COOH | −3.89 | −8.82 | −13.74 | −18.65 | −23.55 | −28.42 | −33.29 |
| FFL2 + CH3COOH | −5.06 | −9.99 | −14.92 | −19.84 | −24.74 | −29.62 | −34.49 |
| AXPL1 + H2O | 1.43 | −2.58 | −6.60 | −10.61 | −14.59 | −18.56 | −22.50 |
| AXPL2 + CH3COOH | −15.11 | −19.92 | −24.75 | −29.60 | −34.44 | −39.28 | −44.11 |
| AXPL3 + CH3COOH | −11.49 | −16.21 | −20.94 | −25.67 | −30.38 | −35.08 | −39.76 |
| AXPL4 + H2O | −0.73 | −4.87 | −9.01 | −13.14 | −17.25 | −21.34 | −25.40 |
| AXPL5 + H2O | −9.44 | −13.42 | −17.40 | −21.36 | −25.30 | −29.22 | −33.10 |
| AXPL6 + H2O | −9.64 | −13.56 | −17.47 | −21.38 | −25.27 | −29.12 | −32.95 |
| AXPL7 + H2O | −10.00 | −13.84 | −17.68 | −21.52 | −25.35 | −29.15 | −32.93 |
| 4OMGLA | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| DGLA | 2.19 | 1.98 | 1.77 | 1.57 | 1.36 | 1.17 | 0.97 |
| FFL1 + H2O | −4.34 | −8.41 | −12.46 | −16.46 | −20.43 | −24.35 | −28.24 |
| FFL2 + H2O | −5.81 | −9.92 | −14.00 | −18.04 | −22.04 | −26.00 | −29.92 |
| AXPL1 + H2O | −0.05 | −4.02 | −7.99 | −11.95 | −15.89 | −19.80 | −23.68 |
| AXPL2 + H2O | −5.23 | −9.30 | −13.37 | −17.44 | −21.49 | −25.52 | −29.51 |
| AXPL3 + H2O | −6.76 | −10.72 | −14.68 | −18.62 | −22.54 | −26.43 | −30.29 |
| AXPL4 + H2O | −2.52 | −6.62 | −10.71 | −14.78 | −18.83 | −22.86 | −26.85 |
| AXPL5 + H2O | −5.58 | −9.58 | −13.58 | −17.58 | −21.56 | −25.52 | −29.45 |
| AXPL6 + CH3OH | −7.34 | −11.88 | −16.41 | −20.93 | −25.44 | −29.92 | −34.38 |
| AXPL7 + CH3OH | −6.92 | −11.58 | −16.25 | −20.91 | −25.55 | −30.17 | −34.77 |
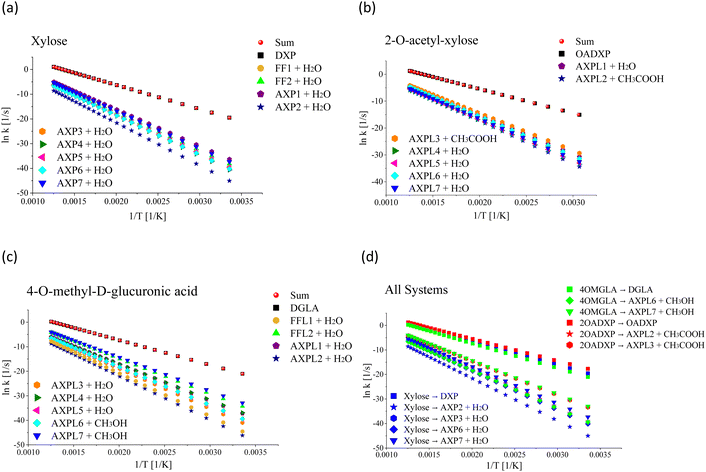
From a kinetic perspective, the ring-opening reaction exhibits the highest rate for all species; see Fig. 2, panels a–c. However, the presence of substituents induces some qualitative and quantitative changes. Among all processes, the ring-opening shows the least sensitivity to temperature changes, evidenced by the lowest tilt of its rate line. The functional groups close the competing gap as the temperature increases, which is more evident for the moiety characterized by the highest number of substituent groups, i.e., 4-O-methyl-D-glucuronic acid. For xylose, the water elimination at C1 undergone through TS-AXP1, the dehydration at C4 associated with TS-AXP7, and the ring-contraction linked to TS-FF2 are the second, third, and fourth fastest processes, respectively; in contrast, this ranking shifts to TS-AXPL7, TS-FFL2, and TS-AXPL1 for the double-substituted species. In the case of 2-O-acetyl-xylose, one of the reactions involving the substituent (TS-AXPL3) will still lie within the three fastest depolymerization events, even assuming that both elementary reactions associated with TS-FFL1 and TS-FFL2 could be faster. Surprisingly, the other elimination involving the functional group (TS-AXPL2) is the lowest reaction. These kinetics further support our previous thermodynamic findings regarding the relevant role of proton-transfer directionality (see Fig. 2, panel d), thereby underscoring the need for an in-depth assessment of selectivity and steric effects. Regardless of the relatively high vibrational frequency of TSs associated with ring-opening and eliminations, the Eckart tunneling effects are extremely weak because temperatures characterizing the FP regimen greatly surpass the cross-over temperature (≈92–458 K). Consequently, the tunneling is shallow and points out that rate constants can be computed using the classical rate theory.84,85
Table 5 presents a detailed overview of the frequency factor (A) and activation energy (Ea) values derived from fitting the thermal rate constant data depicted in Fig. 2, panels a–c, to a two-parameter Arrhenius model. In the case of the simplest system, the highest values of A correspond to the ring-contractions FF1 and FF2. In contrast, for the O-acetyl functionalized species, the A maximum value corresponds to one of the elementary reactions involving the substituent, i.e., TS-AXPL2. As expected, the same trend is observed in the case of the double-functionalized system. This shows the consistency between the thermodynamic and kinetic findings that substituents indeed exert a catalytic-like effect in both functionalized species. However, the extent of this effect is contingent upon the relative spatial arrangement of the reacting centers, particularly the specific side of the proton attack. More importantly, while discernible, the influence of functional groups is insufficient to substantially bridge the competition gap between the ring-opening reaction and the other elementary steps within the FP regime.
| Elementary reaction | A [s−1] | E a [kcal mol−1] | k [s−1] | k/ksum [%] |
|---|---|---|---|---|
| Xylose → D-xylose | 1.68 × 1013 | 44.68 | 4.11 | 100.00 |
| Xylose → FF1 + H2O | 8.79 × 1013 | 72.71 | 2.63 × 10−7 | 6.40 × 10−6 |
| Xylose → FF2 + H2O | 7.44 × 1013 | 64.62 | 4.28 × 10−5 | 1.04 × 10−3 |
| Xylose → AXP1 + H2O | 3.79 × 1013 | 68.06 | 2.33 × 10−6 | 5.70 × 10−5 |
| Xylose → AXP2 + H2O | 1.17 × 1013 | 79.31 | 4.80 × 10−10 | 1.17 × 10−8 |
| Xylose → AXP3 + H2O | 3.17 × 1013 | 72.39 | 1.17 × 10−7 | 2.85 × 10−6 |
| Xylose → AXP4 + H2O | 5.06 × 1013 | 74.17 | 5.86 × 10−8 | 1.42 × 10−6 |
| Xylose → AXP5 + H2O | 2.46 × 1013 | 72.26 | 9.86 × 10−8 | 2.40 × 10−6 |
| Xylose → AXP6 + H2O | 3.26 × 1013 | 73.28 | 6.74 × 10−8 | 1.64 × 10−6 |
| Xylose → AXP7 + H2O | 1.69 × 1013 | 70.12 | 2.72 × 10−7 | 6.62 × 10−6 |
| 2-O-Acetyl-xylose → OADXP | 3.23 × 1012 | 41.87 | 4.90 | 100.00 |
| 2-O-Acetyl-xylose → FFL1 + CH3COOH | — | — | — | — |
| 2-O-Acetyl-xylose → FFL2 + CH3COOH | — | — | — | — |
| 2-O-Acetyl-xylose → AXPL1 + H2O | 3.95 × 1013 | 66.27 | 7.77 × 10−6 | 1.58 × 10−4 |
| 2-O-Acetyl-xylose → AXPL2 + CH3COOH | 5.03 × 1014 | 73.31 | 1.02 × 10−6 | 2.08 × 10−5 |
| 2-O-Acetyl-xylose → AXPL3 + CH3COOH | 1.84 × 1013 | 63.64 | 2.00 × 10−5 | 4.08 × 10−4 |
| 2-O-Acetyl-xylose → AXPL4 + H2O | 3.94 × 1013 | 69.62 | 8.78 × 10−7 | 1.79 × 10−5 |
| 2-O-Acetyl-xylose → AXPL5 + H2O | 8.61 × 1013 | 70.33 | 1.21 × 10−6 | 2.47 × 10−5 |
| 2-O-Acetyl-xylose → AXPL6 + H2O | 2.43 × 1013 | 68.66 | 1.01 × 10−6 | 2.06 × 10−5 |
| 2-O-Acetyl-xylose → AXPL7 + H2O | 3.97 × 1013 | 69.62 | 8.85 × 10−7 | 1.81 × 10−5 |
| 4-O-Methyl-D-glucuronic acid → DGLA | 8.39 × 1012 | 46.41 | 6.66 × 10−1 | 99.95 |
| 4-O-Methyl-D-glucuronic acid → FFL1 + H2O | 1.45 × 1014 | 80.14 | 3.48 × 10−9 | 5.22 × 10−7 |
| 4-O-Methyl-D-glucuronic acid → FFL2 + H2O | 1.23 × 1013 | 62.20 | 3.41 × 10−5 | 5.12 × 10−3 |
| 4-O-Methyl-D-glucuronic acid → AXPL1 + H2O | 3.38 × 1012 | 67.94 | 2.25 × 10−7 | 3.38 × 10−5 |
| 4-O-Methyl-D-glucuronic acid → AXPL2 + H2O | 1.77 × 1012 | 76.56 | 4.34 × 10−10 | 6.51 × 10−8 |
| 4-O-Methyl-D-glucuronic acid → AXPL3 + H2O | 5.39 × 1013 | 74.64 | 4.60 × 10−8 | 6.90 × 10−6 |
| 4-O-Methyl-D-glucuronic acid → AXPL4 + H2O | 1.19 × 1012 | 66.99 | 1.47 × 10−7 | 2.21 × 10−5 |
| 4-O-Methyl-D-glucuronic acid → AXPL5 + H2O | 8.93 × 1013 | 71.50 | 5.87 × 10−7 | 8.81 × 10−5 |
| 4-O-Methyl-D-glucuronic acid → AXPL6 + CH3OH | 1.04 × 1013 | 71.53 | 6.70 × 10−8 | 1.01 × 10−5 |
| 4-O-Methyl-D-glucuronic acid → AXPL7 + CH3OH | 1.80 × 1014 | 63.04 | 2.89 × 10−4 | 4.34 × 10−2 |
Chemical reactivity and bonding analysis
Macro thermodynamic variables, such as heat capacity, originate from micro-level features. The kinetics of particles (e.g., vibrational and translational velocities) serve as the physical basis of an intensive state variable we call temperature. This emphasizes the significance of delving into the molecular physics underpinning the thermal conversion of biomass into a wide variety of bioproducts as a critical step before integrating sustainable materials into practical applications. The valence-shell electron-pair repulsion theory (VSEPR)86 leverages electrostatic considerations to accurately predict the molecular geometry of a wide variety of systems ranging from organic to inorganic compounds. Given the fundamental relationship between geometry, properties, and applications, our approach involves computing the electron population of each reactant as an initial step. This calculation constitutes a building block for establishing the intricate link between macro-level thermodynamics and micro-level molecular interactions through chemical bonding analysis of ELF. This kind of methodical approach has been broadly applied in both the solid-state and gas-phase to deepen our understanding across different covalent bonding situations,87,88 proton transfer reactions,89 C–H bonds activation,90 phase transition of the 14 group elements,91 cycloadditions,92–99 hemiaminals formation,100,101 photoreactions,99,102,103 arynes production,104 computing local and global properties of solids,105 and deducing linear models for predicting activation enthalpies of organic and organometallic reacting systems.106As expected, ELF disynaptic basins associated with the substituent positions show the most substantial variations in population (≈0.1 e), specifically V(C2,O2) and V(C4,O4). Nonetheless, the O-acetyl group exerts a discernible influence on nearby basins, as evidenced by the decrease of approximately 0.1 e in the V(C1,O1) population. While electron populations along the pyran ring maintain near-constant levels, the most relevant changes (±0.03 e) are observed over V(C1,O), the bonding region featuring the ring-opening process. The relatively low population of V(C1,O), V(C1,O1), V(C2,O2), V(C3,O3), and V(C4,O4) provides insights into the significance attributed to ring opening/contraction and eliminations as these classes of reactions comprise such basins, as detailed in Table 6.
| ELF basina | Xylose | 2-O-Acetyl-xylose | 4-O-Methyl-D-glucuronic acid |
|---|---|---|---|
| a The labeling of oxygen matches the pattern delineated by the Ci–Oi bonding notation. | |||
| V(C1,O) | 1.35 | 1.38 | 1.33 |
| V(C1,C2) | 2.08 | 2.08 | 2.07 |
| V(C2,C3) | 2.02 | 2.01 | 2.02 |
| V(C3,C4) | 2.02 | 2.02 | 2.02 |
| V(C4,C5) | 2.01 | 2.01 | 1.99 |
| V(C5,O) | 1.29 | 1.29 | 1.29 |
| V(C1,O1) | 1.41 | 1.36 | 1.42 |
| V(C2,O2) | 1.29 | 1.39 | 1.29 |
| V(C3,O3) | 1.28 | 1.28 | 1.29 |
| V(C4,O4) | 1.27 | 1.27 | 1.32 |
Both the global and local chemical reactivity indices51,52,107 leverage electron density as a foundational parameter to extract meaningful chemical information. This physical-observable-based approach streamlines the correlation of theoretical insights with experimental observations, thereby providing depth to the analysis in the context of thermokinetic discussions. Over recent decades, Fukui's functions have become a subject of increasing interest in both biomass materials and biomass pyrolysis fields, with diverse and impactful applications. López and co-workers108 identified the most reactive sites of two lignin precursors in reactions involving radicals. Benguerba et al.109 proposed agricultural olive cake waste as a low-cost material for absorbing acids. Muñiz and collaborators110 developed a methodology to predict the performance of carbon-based electrode materials for energy storage by assessing the reaction mechanism of various lignocellulosic components resulting from the pyrolysis of Agave angustifolia leaves. Yáñez et al.111 studied the influence of a solvent-water mixture used to extract lignin (from Eucalyptus nitens) on its structural features and content of functional groups. Very recently, Xia and co-workers112 prepared graft-modified fibbers from starch polymers as alternative adhesives.
The electronic chemical potential, μ, reveals that the O-acetyl functionalized species is the most reactive (−4.80 eV), whereas the double substituted reactant displays the lowest reactivity (−4.62 eV). In contrast, xylose's susceptibility to exchanging electron density falls between these two values (i.e., μ = −4.75 eV). The relatively high global reactivity of 2-O-acetyl-xylose might be indicative of the moderate thermodynamic stability of the functional group since they can be straightforwardly dissociated through acetic acid, as observed in experiments.27,30
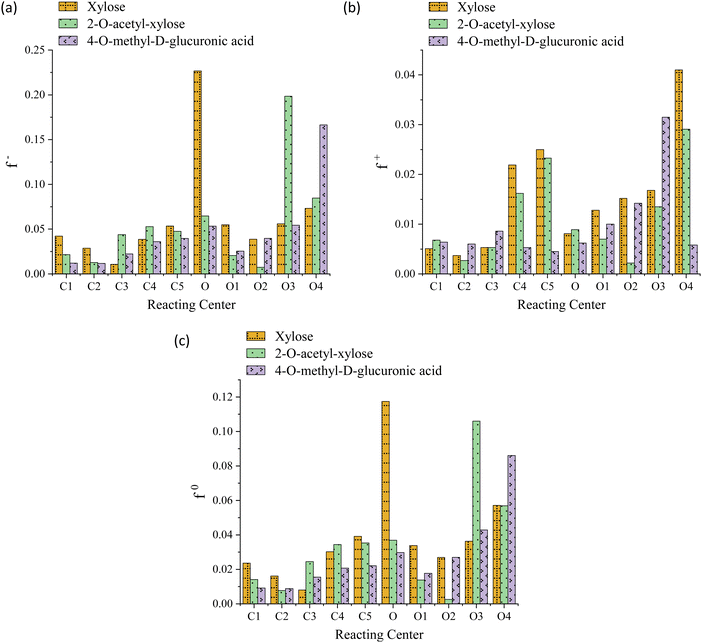
The striking low values of Fukui's functions f+, f−, and f0 reveal the extremely weak local reactivity of the investigated chemical species and justify the need for FP conditions. Moreover, this suggests the implausibility of the investigated processes being reversible, aligning with their thermodynamically favorable nature. Both the O-acetyl and methoxy functional groups consistently modulate the propensity of the system toward electrophilic attacks near C2 and C4, respectively; in contrast, while the latter significantly increases this probability at O4, the former lowers it in the locality of O2, as evidenced in Fig. 3, panel a. The value of f+ drops at the C2, C4, O2, and O4 centers, indicating that the substituents lower the propensity to a nucleophilic attack in their vicinity, see Fig. 3, panel b. The C2, C4, and O2 regions are less prone to a neutral (or radical) attack, while the probability notably increases at O4, see Fig. 3, panel c. For xylose, the preeminent reactivity of the pyran-ring oxygen might potentially support the notion that the ring-opening is the fastest reaction, as indicated by the highest values of f− and f0. Similarly, 4-O-methyl-D-glucuronic acid exhibits peak values for these functions for the methoxy oxygen (O4), possibly justifying the barrier reduction and the relatively high rate observed in one of the processes involving this functional group, namely, the elimination associated with TS-AXPL7. Intriguingly, in the case of 2-O-acetyl-xylose, all Fukui's functions are minimized at both C2 and O2, whereas f− and f0 are maximized at the C3 and O3 atoms. This signifies that O-acetyl diminishes the centers reactivity at the substituent position, while significantly favors it at the neighboring reacting center, C3. Nonetheless, these observations closely match the thermokinetic findings since the elimination undergone via TS-AXPL3 involving C3 is the reaction with the lowest barrier and highest rate, excluding ring-opening. For functionalized species, none of these local functions exhibit a notable peak at the pyran-ring oxygen, which contradicts the results derived from the thermokinetic analysis. Thus, these outcomes fall short of elucidating the thermokinetic observations across all structural motifs consistently.
Although Fig. 3 suggests that Fukui's functions might contribute to the learning of molecular thermodynamic properties of large and complex biomass systems, as demonstrated for other materials and processes, further work is needed. Therefore, forthcoming studies will focus on formulating this qualitative nexus into a predictive tool. A systematic assessment of alternative electron-density-based descriptors will be conducted to test their appropriateness. The integration of well-established theories, such as the Quantum Theory of Atoms in Molecules (QTAIM),113 will be considered as well.
Conclusions
In this study, we have analyzed the thermodynamic and kinetic effects of functional groups on the pyrolytic depolymerization of β-D-xylopyranose, a hemicellulose motif. Two distinct moieties, namely, 2-O-acetyl-β-D-xylopyranose and 4-methoxy-5-carboxy-β-D-xylopyranose, have been carefully selected to conduct this investigation as they have been experimentally isolated from various types of hemicellulose plant matter, a biomass main component relatively less studied compared to cellulose. Through state-of-the-art density functionals, composite chemistry methods, and transition state theory, we here reported quite complete thermochemical data for these carbohydrates for the first time to aid in developing reliable kinetic models. This dataset includes activation barriers, standard enthalpies of formation, Gibbs free energies, heat capacities, and rate constants at various temperatures for three initial reaction classes understood to decompose carbohydrates under pyrolysis conditions: ring-opening, ring-contraction, and elimination. The results demonstrated high reliability, as evidenced by the close agreement (i.e., below 0.5 kcal mol−1) between computed and experimental enthalpies of formation for pyrolytic products of elimination reactions: water, acetic acid, and methanol. In this vein, the predicted standard enthalpy of formation of β-D-xylopyranose, 4-methoxy-5-carboxy-β-D-xylopyranose, and 2-O-acetyl-β-D-xylopyranose are determined to be −218.2, −263.1, and −300.0 kcal mol−1, respectively. Across all examined species, the ring-opening barrier fell approximately within 43.8–47.5 kcal mol−1, in contrast to the higher activation enthalpies observed for ring-contraction and elimination, ranging from 61.0 to 81.1 kcal mol−1. Regardless of the functionalization, the pathway leading to acyclic products was the fastest, featuring a rate constant in the order of 10 s−1, significantly superior to the rate characterizing the other reaction types, which ranged from 10−10 and 10−4 s−1 for the other reaction types. Curiously, the most reactive elementary step is the only thermodynamically unfavorable reaction within the Fast Pyrolysis regime. The thermochemical and kinetic analyses consistently showed that introducing functional groups lowers the barrier by 1.9 to 8.3 kcal mol−1. Consequently, the rate constant increased by 0 to 4 orders of magnitude concerning the unfunctionalized system. However, this catalytic-like effect strongly depends on the relative spatial rearrangements of reacting centers and proved insufficient to effectively bridge the competition between processes, evidencing the significant role of steric effects and regioselectivity. In light of these quantitative outcomes, it seems reasonable that, although the transition states associated with the reaction channels leading to the decomposition of 2-O-acetyl-β-D-xylopyranose into five-membered ring structures could not be found, such processes are not expected to compete with the ring-opening, as the latter would still lay more than 10 kcal mol−1 below and be ten times kinetically faster in the most favorable scenario. Furthermore, our study underscores the importance of conformational analysis, which should be considered more frequently given the geometric flexibility observed in biomass main components. It is quite promising that a straightforward chemical reactivity and bonding analysis offer partial corroboration for the thermokinetic findings. These insights notably simplify the exploration of potential energy surfaces of hemicelluloses pyrolysis by offering to circumvent numerous alternative depolymerization pathways.Author contributions
L. A.-H., S. D.: project supervision, conceptualization, data analysis, and manuscript writing; L. A.-H., J. L.: calculations, reaction paths, and characterization. All authors reviewed and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication has emanated from research conducted with philanthropic financial support of the Ryanair Sustainable Aviation Research Centre at Trinity College Dublin, the European Union through the European Research Council, Mod-L-T, action number 101002649, and the Science Foundation Ireland (SFI) under grant number 12/RC/2278_2. This publication is also co-funded under the European Regional Development Fund under the AMBER award. The authors wish to acknowledge the Irish Centre for High-End Computing (ICHEC) for the provision of computational facilities and support. The authors thank Dr. Bernardo Ballotta, Mr. Liam Mannion, and Dr. Mark Kelly for significantly enriching this work through insightful discussions.References
- M. Brennan Pecha, J. I. M. Arbelaez, M. Garcia-Perez, F. Chejne and P. N. Ciesielski, Green Chem., 2019, 21, 2868–2898 RSC.
- J. N. Chheda, G. W. Huber and J. A. Dumesic, Liquid-phase catalytic processing of biomass-derived oxygenated hydrocarbons to fuels and chemicals, Angew. Chem., Int. Ed., 2007, 46, 7164–7183 CrossRef CAS PubMed.
- M. K. Ghosh, M. S. Howard, K. Dussan and S. Dooley, Mechanism and theory of d-glucopyranose homogeneous acid catalysis in the aqueous solution phase, Phys. Chem. Chem. Phys., 2019, 21, 17993–18011 RSC.
- S. Wang, G. Dai, H. Yang and Z. Luo, Prog. Energy Combust. Sci., 2017, 62, 33–86 CrossRef.
- B. Hu, B. Zhang, W. L. Xie, X. Y. Jiang, J. Liu and Q. Lu, Recent Progress in Quantum Chemistry Modeling on the Pyrolysis Mechanisms of Lignocellulosic Biomass, Energy Fuels, 2020, 34, 10384–10440 CrossRef CAS.
- K. Dussan, S. Dooley and R. Monaghan, Integrating compositional features in model compounds for a kinetic mechanism of hemicellulose pyrolysis, J. Chem. Eng., 2017, 328, 943–961 CrossRef CAS.
- D. N. S. Hon, Cellulose: a random walk along its historical path, Cellulose, 1994, 1, 1–25 CrossRef CAS.
- A. G. McDonald and L. A. Donaldson, Encyclopedia of Materials: Science and Technology, 2001, pp. 9612–9616 Search PubMed.
- R. T. Olsson, L. Fogelström, M. Martínez-Sanz and M. Henriksson, Multifunctional and Nanoreinforced Polymers for Food Packaging, Elsevier, 2011, pp. 86–107 Search PubMed.
- E. Rudnik, Handbook of Biopolymers and Biodegradable Plastics: Properties, Processing and Applications, Elsevier Inc., 2013, pp. 189–211 Search PubMed.
- O. Benaimeche, N. T. Seghir, Ł. Sadowski and M. Mellas, Encyclopedia of Renewable and Sustainable Materials, Elsevier Ltd, 2020, pp. 649–662 Search PubMed.
- R. A. Hussein and A. A. El-Anssary, in Herbal Medicine, ed. P. Builders, IntechOpen, 2019, pp. 11–30 Search PubMed.
- A. J. Yanez, W. Li, R. Mabon and L. J. Broadbelt, A Stochastic Method to Generate Libraries of Structural Representations of Lignin, Energy Fuels, 2016, 30, 5835–5845 CrossRef CAS.
- M. Abu-Ghalia and Y. Dahman, Lignocellulosic Fibre and Biomass-Based Composite Materials: Processing, Properties and Applications, Elsevier Inc., 2017, pp. 313–345 Search PubMed.
- C. Chio, M. Sain and W. Qin, Lignin utilization: A review of lignin depolymerization from various aspects, Renewable Sustainable Energy Rev., 2019, 107, 232–249 CrossRef CAS.
- M. K. Ghosh, M. S. Howard, Y. Zhang, K. Djebbi, G. Capriolo, A. Farooq, H. J. Curran and S. Dooley, The combustion kinetics of the lignocellulosic biofuel, ethyl levulinate, Combust. Flame, 2018, 193, 157–169 CrossRef CAS.
- M. S. Mettler, D. G. Vlachos and P. J. Dauenhauer, Energy Environ. Sci., 2012, 5, 7797–7809 RSC.
- X. Zhou, W. Li, R. Mabon and L. J. Broadbelt, A critical review on hemicellulose pyrolysis, Energy Technol., 2017, 5, 52–79 CrossRef CAS.
- R. Vinu and L. J. Broadbelt, A mechanistic model of fast pyrolysis of glucose-based carbohydrates to predict bio-oil composition, Energy Environ. Sci., 2012, 5, 9808–9826 RSC.
- E. Ranzi, P. E. A. Debiagi and A. Frassoldati, Mathematical Modeling of Fast Biomass Pyrolysis and Bio-Oil Formation. Note I: Kinetic Mechanism of Biomass Pyrolysis, ACS Sustainable Chem. Eng., 2017, 5, 2867–2881 CrossRef CAS.
- Z. Dong, Z. Liu, X. Zhang, H. Yang, J. Li, S. Xia, Y. Chen and H. Chen, Pyrolytic characteristics of hemicellulose, cellulose and lignin under CO2 atmosphere, Fuel, 2019, 256, 115890 CrossRef CAS.
- D. Chen, K. Cen, X. Zhuang, Z. Gan, J. Zhou, Y. Zhang and H. Zhang, Insight into biomass pyrolysis mechanism based on cellulose, hemicellulose, and lignin: Evolution of volatiles and kinetics, elucidation of reaction pathways, and characterization of gas, biochar and bio-oil, Combust. Flame, 2022, 242, 112142 CrossRef CAS.
- K. Dussan, S. Dooley and R. Monaghan, Integrating compositional features in model compounds for a kinetic mechanism of hemicellulose pyrolysis, Chem. Eng. J., 2017, 328, 943–961 CrossRef CAS.
- M. Kelly, M. Fortune, G. Bourque and S. Dooley, Machine learned compact kinetic models for methane combustion, Combust. Flame, 2023, 253, 112755 CrossRef CAS.
- P. Capek and J. Alfo, An acetylated galactoglucomannan from Picea abies L. Karst, Carbohydr. Res., 2002, 337, 1033–1037 CrossRef CAS PubMed.
- A. Teleman, M. Tenkanen, A. Jacobs and O. Dahlman, Characterization of O-acetyl-(4-O-methylglucurono)xylan isolated from birch and beech, Carbohydr. Res., 2002, 337, 373–377 CrossRef CAS PubMed.
- S. Wang, B. Ru, H. Lin and W. Sun, Pyrolysis behaviors of four O-acetyl-preserved hemicelluloses isolated from hardwoods and softwoods, Fuel, 2015, 150, 243–251 CrossRef CAS.
- K. Shimizu, M. Hashi and K. Sakurai, Isolation from a Softwood Xylan of Oligosaccharides Containing two 4-O-Methyl-D-Glucuronic Acid Residues, Carbohydr. Res., 1978, 62, 117–126 CrossRef CAS.
- S. Sakamoto, K. Yoshida, S. Sugihara and N. Mitsuda, Development of a new high-throughput method to determine the composition of ten monosaccharides including 4-O-methyl glucuronic acid from plant cell walls using ultra-performance liquid chromatography, Plant Biotechnol., 2015, 32, 55–63 CrossRef CAS.
- S. Wang, B. Ru, H. Lin and Z. Luo, Degradation mechanism of monosaccharides and xylan under pyrolytic conditions with theoretic modeling on the energy profiles, Bioresour. Technol., 2013, 143, 378–383 CrossRef CAS PubMed.
- J. B. Huang, C. Liu, H. Tong, W. M. Li and D. Wu, Theoretical studies on pyrolysis mechanism of O-acetyl-xylopyranose, J. Fuel Chem. Technol., 2013, 41, 285–293 CrossRef CAS.
- D. K. Shen, S. Gu and A. V. Bridgwater, Study on the pyrolytic behaviour of xylan-based hemicellulose using TG-FTIR and Py-GC-FTIR, J. Anal. Appl. Pyrolysis, 2010, 87, 199–206 CrossRef CAS.
- B. Ru, S. Wang, G. Dai and L. Zhang, Effect of Torrefaction on Biomass Physicochemical Characteristics and the Resulting Pyrolysis Behavior, EnergyFuels, 2015, 29, 5865–5874 CrossRef CAS.
- S. Wang, G. Dai, B. Ru, Y. Zhao, X. Wang, J. Zhou, Z. Luo and K. Cen, Effects of torrefaction on hemicellulose structural characteristics and pyrolysis behaviors, Bioresour. Technol., 2016, 218, 1106–1114 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinhe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, E. J. J. Heyd, N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, J. R. Cammi, W. Ochterski, R. L. Martin, K. Morokuma, Ö. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, 2016 Search PubMed.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- K. Fukui, A formulation of the reaction coordinate, J. Phys. Chem., 1970, 74, 4161 CrossRef CAS.
- T. J. Lee and P. R. Taylor, A Diagnostic for Determining the Quality of Single-Reference Electron Correlation Methods, Int. J. Quantum Chem., Quantum Chem. Symp., 1989, 23, 199–207 CAS.
- P. Pracht, F. Bohle and S. Grimme, Automated exploration of the low-energy chemical space with fast quantum chemical methods, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, A complete basis set model chemistry. VI. Use of density functional geometries and frequencies, J. Chem. Phys., 1999, 110, 2822–2827 CrossRef CAS.
- J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, A complete basis set model chemistry. VII. Use of the minimum population localization method, J. Chem. Phys., 2000, 112, 6532–6542 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, Gaussian-4 theory, J. Chem. Phys., 2007, 126, 1–12 CrossRef PubMed.
- T. Lu and Q. Chen, Shermo: A general code for calculating molecular thermochemistry properties, Comput. Theor. Chem., 2021, 1200, 113249 CrossRef CAS.
- R. O. Ramabhadran and K. Raghavachari, Connectivity-Based Hierarchy for theoretical thermochemistry: Assessment using wave function-based methods, J. Phys. Chem. A, 2012, 116, 7531–7537 CrossRef CAS PubMed.
- D. W. Rogers, A. A. Zavitsas and N. Matsunaga, Determination of enthalpies (‘Heats’) of formation, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 21–36 CAS.
- B. Ruscic, R. E. Pinzon, M. L. Morton, G. Von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, Introduction to active thermochemical tables: Several ‘Key’ enthalpies of formation revisited, J. Phys. Chem. A, 2004, 108, 9979–9997 CrossRef CAS.
- B. Ruscic, R. E. Pinzon, G. Von Laszewski, D. Kodeboyina, A. Burcat, D. Leahy, D. Montoy and A. F. Wagner, Active Thermochemical Tables: Thermochemistry for the 21st century, J. Phys.: Conf. Ser., 2005, 16, 561–570 CrossRef CAS.
- S. Canneaux, F. Bohr and E. Henon, KiSThelP: A program to predict thermodynamic properties and rate constants from quantum chemistry results, J. Comput. Chem., 2014, 35, 82–93 CrossRef CAS PubMed.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, Electronegativity: The density functional viewpoint, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- R. G. Parr and W. Yang, Theory of Orientation and Steroselection, Annu. Rev. Phys. Chem., 1984, 106, 4050–4051 Search PubMed.
- P. Geerlings, F. De Proft and W. Langenaeker, Conceptual density functional theory, Chem. Rev., 2003, 103, 1793–1873 CrossRef CAS PubMed.
- L. Shubin, Conceptual Density Functional Theory and Some Recent Developments, Acta Phys. Chim. Sin., 2009, 25, 590–600 Search PubMed.
- F. De, P. W. Ayers and P. Geerlings, in The Chemical Bond, ed. G. Frenkin and S. Shaik, Wiley-VCH, Weinheim, 2014, pp. 233–269 Search PubMed.
- F. De Profit, in Conceptual Density Functional Theory: Towards a New Chemical Reactivity Theory, ed. S. Liu, Wiley-VCH, Weinheim, 1st edn, 2022, pp. 17–46 Search PubMed.
- A. D. Becke and K. E. Edgecombe, A simple measure of electron localization in atomic and molecular systems, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- M. Kohout and A. Silvi, Atomic Shell Structure and Electron Numbers, Int. J. Quantum Chem., 1996, 60, 875–882 CrossRef CAS.
- J. Andrés, P. Gonz and V. S. Safont, Unraveling Reaction Mechanisms by Means of Quantum Chemical Topology Analysis, Int. J. Quantum Chem., 2014, 114, 1239–1252 CrossRef.
- P. Fuentealba, E. Chamorro and J. C. Santos, in Theoretical and Computational Chemistry, ed. A. Toro-Labbe, Elsevier, 1st edn, 2007, pp. 57–85 Search PubMed.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, ELF: The electron localization function, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- A. Savin, A. D. Becke, J. Flad, R. Nesper, H. Preuss and H. G. von Schnering, A New Look at Electron Localization, Angew. Chem., Int. Ed. Engl., 1991, 30, 409–412 CrossRef.
- B. Silvi, The synaptic order: A key concept to understand multicenter bonding, J. Mol. Struct., 2002, 614, 3–10 CrossRef CAS.
- A. Savin, B. Silvi and F. Colonna, Topological analysis of the electron localization function applied to delocalized bonds, Can. J. Chem., 1996, 74, 1088–1096 CrossRef CAS.
- L. Ayarde-Henríquez, C. Guerra, M. Duque-Noreña and E. Chamorro, Unraveling the role of the electron-pair density symmetry in reaction mechanism patterns: the Newman-Kwart rearrangement, New J. Chem., 2022, 46, 12002–12009 RSC.
- T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- B. Hu, Q. Lu, Z. X. Zhang, Y. T. Wu, K. Li, C. Q. Dong and Y. P. Yang, Mechanism insight into the fast pyrolysis of xylose, xylobiose and xylan by combined theoretical and experimental approaches, Combust. Flame, 2019, 206, 177–188 CrossRef CAS.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, Assessment of Gaussian-4 theory for energy barriers, Chem. Phys. Lett., 2010, 499, 168–172 CrossRef CAS.
- B. Sun and M. L. McKee, Computational study of the initial stage of diborane pyrolysis, Inorg. Chem., 2013, 52, 5962–5969 CrossRef CAS PubMed.
- S. E. Wheeler, D. H. Ess and K. N. Houk, Thinking out of the black box: Accurate barrier heights of 1,3-dipolar cycloadditions of ozone with acetylene and ethylene, J. Phys. Chem. A, 2008, 112, 1798–1807 CrossRef CAS PubMed.
- A. Karton and L. Goerigk, Accurate reaction barrier heights of pericyclic reactions: Surprisingly large deviations for the CBS-QB3 composite method and their consequences in DFT benchmark studies, J. Comput. Chem., 2015, 36, 622–632 CrossRef CAS PubMed.
- F. Neese, Software update: The ORCA program system—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, 1–15 Search PubMed.
- L. Radom, W. J. Hehre and J. A. Pople, Molecular Orbital Theory of the Electronic Structure of Organic Compounds. VII. A Systematic Study of Energies, Conformations, and Bond Interactions, J. Am. Chem. Soc., 1971, 93, 289–300 CrossRef.
- W. J. Hehre, R. Ditchfield, L. Radom and J. A. Pople, Molecular Orbital Theory of the Electronic Structure of Organic Compounds. V. Molecular Theory of Bond Separation, J. Am. Chem. Soc., 1970, 92, 4796–4801 CrossRef CAS.
- R. O. Ramabhadran and K. Raghavachari, Theoretical thermochemistry for organic molecules: Development of the generalized connectivity-based hierarchy, J. Chem. Theory Comput., 2011, 7, 2094–2103 CrossRef CAS PubMed.
- S. E. Wheeler, K. N. Houk, P. V. R. Schleyer and W. D. Allen, A Hierarchy of homodesmotic reactions for thermochemistry, J. Am. Chem. Soc., 2009, 131, 2547–2560 CrossRef CAS PubMed.
- M. K. Ghosh, M. S. Howard and S. Dooley, Accurate and standard thermochemistry for oxygenated hydrocarbons: A case study of ethyl levulinate, Proc. Combust. Inst., 2019, 37, 337–346 CrossRef CAS.
- C. E. Moore, Atomic Energy Levels, Circular of the National Bureau of Standards, Washington, 1949, vol. I.
- W. C. Martin, Table of Spin-Orbit Energies for p-Electrons in Neutral Atomic (core) np Configurations, J. Res. Natl. Bur. Stand., Sect. A, 1970, 75A, 109–111 CrossRef PubMed.
- A. Shrivastava, Introduction to Plastics Engineering, Elsevier, 2018, pp. 49–110 Search PubMed.
- J. P. McCullough, R. E. Pennington and G. Waddington, A Calorimetric Determination of the Vapor Heat Capacity and Gas Imperfection of Water, J. Am. Chem. Soc., 1952, 74, 4439–4442 CrossRef CAS.
- D. R. Stull, E. F. Westrum and G. C. Sinke, The Chemical Thermodynamics of Organic Compounds, Wiley, New York, 1969 Search PubMed.
- M. A. V. Ribeiro Da Silva, M. D. M. C. Ribeiro Da Silva, A. I. M. C. Lobo Ferreira, Q. Shi, B. F. Woodfield and R. N. Goldberg, Thermochemistry of α-D-xylose(cr), J. Chem. Thermodyn., 2013, 58, 20–28 CrossRef CAS.
- R. V. Jasra and J. C. Ahluwalia, Enthalpies of Solution, Partial Molal Heat Capacities and Apparent Molal Volumes of Sugars and Polyols in Water, J. Solution Chem., 1982, 11, 325–338 CrossRef CAS.
- F. Kawaizumi, S. Kushida and Y. Miyahara, Determination of the Specific Heat Capacities of Aqueous Solutions of Pentose, Bull. Chem. Soc. Jpn., 1981, 54, 2282–2285 CrossRef CAS.
- P. Hanggi, H. Grabert, G. L. Ingold and U. Weiss, Quantum theory of activated events in presence of long-time memory, Phys. Rev. Lett., 1985, 55, 761–764 CrossRef CAS PubMed.
- M. J. Gillan, Quantum-classical crossover of the transition rate in the damped double well, J. Phys. C: Solid State Phys., 1987, 20, 3621–3641 CrossRef.
- R. J. Gillespie and R. S. Nyholm, A simple electrostatic theory: The arrangement of electron pairs in valency shells, Q. Rev., Chem. Soc., 1957, 11, 339–380 RSC.
- X. Krokidis, S. Noury and B. Silvi, Characterization of elementary chemical processes by catastrophe theory, J. Phys. Chem. A, 1997, 101, 7277–7282 CrossRef CAS.
- L. Ayarde-Henríquez, C. Guerra, M. Duque-Noreña and E. Chamorro, Revisiting the bonding evolution theory: a fresh perspective on the ammonia pyramidal inversion and bond dissociations in ethane and borazane, Phys. Chem. Chem. Phys., 2023, 25, 27394–27408 RSC.
- I. Viciano, P. González-Navarrete, J. Andrés and S. Martí, Joint Use of bonding evolution theory and QM/MM hybrid method for understanding the hydrogen abstraction mechanism via cytochrome P450 aromatase, J. Chem. Theory Comput., 2015, 11, 1470–1480 CrossRef CAS PubMed.
- A. S. Nizovtsev, Activation of C-H bond in methane by Pd atom from the bonding evolution theory perspective, J. Comput. Chem., 2013, 34, 1917–1924 CrossRef CAS PubMed.
- O. Matthies, Y. Grin and M. Kohout, Absent Diamond-to-β-Sn Phase Transition for Carbon: Quantum Chemical Topology Approach, ChemistrySelect, 2017, 2, 7659–7669 CrossRef CAS.
- V. Polo, J. Andrés, S. Berski, L. R. Domingo and B. Silvi, Understanding reaction mechanisms in organic chemistry from catastrophe theory applied to the electron localization function topology, J. Phys. Chem. A, 2008, 112, 7128–7136 CrossRef CAS PubMed.
- P. González-Navarrete, L. R. Domingo, J. Andres, S. Berski and B. Silvi, Electronic fluxes during Diels-Alder reactions involving 1,2-benzoquinones: Mechanistic insights from the analysis of electron localization function and catastrophe theory, J. Comput. Chem., 2012, 33, 2400–2411 CrossRef PubMed.
- A. I. Adjieufack, V. Liégeois, I. N. Mboumbouo, M. J. Ketcha and B. Champagne, Intramolecular [3+2] Cycloaddition Reactions of Unsaturated Nitrile Oxides. A Study from the Perspective of Bond Evolution Theory (BET), J. Phys. Chem. A, 2018, 122, 7472–7481 CrossRef CAS PubMed.
- M. Ríos-Gutiérrez, P. Pérez and L. R. Domingo, A bonding evolution theory study of the mechanism of [3+2] cycloaddition reactions of nitrones with electron-deficient ethylenes, RSC Adv., 2015, 5, 58464–58477 RSC.
- P. Merino, T. Tejero, I. Delso and R. Matute, New mechanistic interpretations for nitrone reactivity, Org. Biomol. Chem., 2017, 15, 3364–3375 RSC.
- A. I. Adjieufack, I. M. Ndassa, I. Patouossa, J. K. Mbadcam, V. S. Safont, M. Oliva and J. Andrés, On the outside looking in: rethinking the molecular mechanism of 1,3- dipolar cycloadditions from the perspective of bonding evolution theory. The reaction between cyclic nitrones and ethyl acrylate, Phys. Chem. Chem. Phys., 2017, 19, 18288–18302 RSC.
- L. Ayarde-Henríquez, C. Guerra, M. Duque-Noreña, E. Rincón, P. Pérez and E. Chamorro, On the Notation of Catastrophes in the Framework of Bonding Evolution Theory: the Case of Normal and Inverse Electron Demand Diels-Alder Reactions, Chem. Phys. Chem., 2022, 23, e202200343 CrossRef PubMed.
- E. Chamorro, C. Guerra, L. Ayarde-Henríquez, M. Duque-Noreña, P. Pérez and E. Rincón, in Chemical Reactivity: Theories and Principles, ed. S. Kayas, L. von Szentpály, G. Serdaroglu and L. Guo, Elsevier, 2023, vol. 1, pp. 465–481 Search PubMed.
- S. Berski and L. Z. Ciunik, The mechanism of the formation of the hemiaminal and Schiff base from the benzaldehyde and triazole studied by means of the topological analysis of electron localisation function and catastrophe theory, Mol. Phys., 2015, 113, 765–781 CrossRef CAS.
- A. Ćmikiewicz, A. J. Gordon and S. Berski, Characterisation of the reaction mechanism between ammonia and formaldehyde from the topological analysis of ELF and catastrophe theory perspective, Struct. Chem., 2018, 29, 243–255 CrossRef.
- C. Guerra, L. Ayarde-Henríquez, E. Chamorro and A. Ensuncho, Uncovering Triradicaloid Structures in S1 Benzene Photochemistry, ChemPhotoChem, 2023, 7, e202200263 CrossRef CAS.
- C. Guerra, L. Ayarde-Henríquez, Y. A. Rodríguez-Núñez, A. Ensuncho and E. Chamorro, Elucidating the N–N and C–N Bond-breaking Mechanism in the Photoinduced Formation of Nitrile Imine, Chem. Phys. Chem., 2023, 24, e202200867 CrossRef CAS PubMed.
- C. Guerra, L. Ayarde-Henríquez, Y. A. Rodriguez-Nuñez, E. Chamorro and A. E. Ensuncho, Mechanistic insights into benzyne formation via 1,2-di-iodobenzene photolysis, New J. Chem., 2023, 47, 21270–21275 RSC.
- J. Contreras-García, A. Martín Pendás, J. M. Recio and B. Silvi, Computation of local and global properties of the electron localization function topology in crystals, J. Chem. Theory Comput., 2009, 5, 164–173 CrossRef PubMed.
- L. Ayarde-Henríquez, C. Guerra, M. Duque-Noreña and E. Chamorro, A simple topology-based model for predicting the activation barriers of reactive processes at 0 K, Phys. Chem. Chem. Phys., 2023, 25, 14274–14284 RSC.
- R. K. Roy and S. Saha, Annu. Rep. Prog. Chem. C, 2010, 106, 118–162 RSC.
- C. Martinez, J. L. Rivera, R. Herrera, J. L. Rico, N. Flores, J. G. Rutiaga and P. López, Evaluation of the chemical reactivity in lignin precursors using the Fukui function, J. Mol. Model., 2008, 14, 77–81 CrossRef CAS PubMed.
- K. H. Toumi, M. Bergaoui, M. Khalfaoui, Y. Benguerba, A. Erto, G. L. Dotto, A. Amrane, S. Nacef and B. Ernst, Computational study of acid blue 80 dye adsorption on low cost agricultural Algerian olive cake waste: Statistical mechanics and molecular dynamic simulations, J. Mol. Liq., 2018, 271, 40–50 CrossRef CAS.
- J. Muñiz, N. D. Espinosa-Torres, A. Guillén-López, A. Longoria, A. K. Cuentas-Gallegos and M. Robles, Insights into the design of carbon electrodes coming from lignocellulosic components pyrolysis with potential application in energy storage devices: A combined in silico and experimental study, J. Anal. Appl. Pyrolysis, 2019, 139, 131–144 CrossRef.
- R. Rozas, N. Aspée, C. Negrete-Vergara, D. Venegas-Yazigi, M. Gutiérrez-Cutiño, S. A. Moya, C. Zúñiga, P. Cantero-López, J. Luengo, R. Gonzalez, J. Romero and M. Yáñez-S, Solvent effects on the molecular structure of isolated lignins of Eucalyptus nitens wood and oxidative depolymerization to phenolic chemicals, Polym. Degrad. Stab., 2022, 201, 109973 CrossRef CAS.
- H. Yu, Y. Xia, X. Liu, H. Chen, Z. Jin and Z. Wang, Preparation of reed fibers reinforced graft-modified starch-based adhesives based on quantum mechanical simulation and molecular dynamics simulation, Int. J. Biol. Macromol., 2024, 262, 129802 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in molecules. A Quantum theory, Clarendon Press, Oxford, 1st edn, 1994 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06094b |
| This journal is © the Owner Societies 2024 |