Understanding the infrared spectrum of the protic ionic liquid [DEMA][TfO] by atomistic simulations

Abstract

Polymer-electrolyte fuel cells operating at a temperature above 100 °C would markedly reduce issues associated with water management in the cell and allow for a simplified system design. Available electrolytes such as fluoropolymers grafted with sulfonic acid groups or phosphoric acid either rely on the presence of water or they suffer from sluggish kinetics of the oxygen reduction reaction. Here, with experiments and atomistic simulations, we analysed vibrational spectra of the protic ionic liquid diethylmethylammonium triflate ([DEMA][TfO]) as an alternative electrolyte, with the aim to understand the statistical distribution of cations and anions in the electrolyte and the interaction of the H-bond with the surroundings. We present a comprehensive analysis of the infrared (IR) spectrum of [DEMA][TfO]. Special attention is given to understanding the high-frequency modes above 2500 cm⁻¹, which exhibit a double peak feature in the experiment. While this feature can generally be attributed to the N–H vibrations of the cation, the precise mechanism behind the double peak was unclear. In this manuscript we managed to explain the nature of the double distribution, being influenced by different orientations between the DEMAs and TFOs. The correct assignment of observed vibrational modes is enabled by simulations of the ionic liquid as an infinitely extended fluid.

---

1. Introduction

The efficient storage of electrical energy from renewables has emerged as a critical challenge which necessitates the exploration of various energy storage modalities. Amongst these, hydrogen production via electrolysis is nowadays considered the most compelling approach.¹ Hydrogen (H₂) is a chemical energy carrier that offers the advantage of storage in either large underground repositories or, for portable applications, in high-pressure tanks.² Subsequent re-conversion of stored hydrogen into electrical energy requires the utilization of efficient devices, i.e., fuel cells.

State-of-the-art polymer-electrolyte fuel cells (PEFCs) employ sulfonated fluoropolymer membranes.³ The proton conductivity of these materials (e.g. NAFION® or AQUIVION®) critically depends on the presence of liquid water.⁴ Therefore, at the ambient pressure the operating temperature is limited to a maximum of 80 °C. PEFCs based on sulfonated fluoropolymer membranes have achieved mature levels of performance and durability. However, cost reduction remains an issue. An effective way of reducing system costs would be to increase the operating temperature above 100 °C, which would enable a simplified cell design. A non-aqueous protic electrolyte does not require active water management, with a higher temperature enabling a more effective cooling and utilization of waste heat. Moreover, there is lower sensitivity against feed gas impurities.^5,6

High-temperature PEFCs (HT-PEFCs) based on phosphoric acid-doped polybenzimidazole (PBI) membranes are operated in a temperature range of 160–180 °C.⁷ Unfortunately, their poor performance, primarily due to the sluggish ORR kinetics caused by a poisoning of the platinum catalysts by (anionic) phosphoric acid species, impedes their commercialization.⁸ A doubling of Pt catalyst loading would raise the power density of an H₃PO₄/PBI-based HT-PEFC to only about half the density of a conventional NAFION®-based (low temperature) cell.⁹ An “intermediate temperature” PEFC, operating at about 120–160 °C, would be an intriguing innovation, particularly for automotive applications. The challenge is to develop non-aqueous proton-conducting electrolytes that meet the performance and durability requirements, under almost water-free conditions.

There is, therefore, a need for new protic, but non-aqueous electrolytes. Promising candidates for non-aqueous electrolytes are protic ionic liquids (PILs) that are immobilized in a host polymer. Ionic liquids are essentially salt melts consisting of bulky organic cations and anions of superacids, resulting in a low lattice energy and therefore a low melting point (<100 °C).¹⁰ PILs have attracted attention in the scientific community for possible electrochemical applications due to their wide electrochemical windows, high chemical and thermal stability, good conductivity, small vapour pressures, and therefore low flammability.¹¹ A PIL is an ionic liquid with a proton-carrying Brø nstedt acidic cation or anion. PILs with Brø nstedt acidic cations of the type [BH][A] can be prepared by protonating an (organic) base (B) with a strong acid (HA),

B + HA → BH⁺ + A⁻.

PILs are intrinsic proton conductors.¹² However, a prerequisite for their technical application is a detailed understanding of proton transport and electrochemical kinetics of relevant electrode processes, i.e., ORR and HOR. Due to the absence of a dielectric solvent, interactions between cations and anions in an ionic liquid are much stronger compared to an aqueous electrolyte, as ionic charges are not screened by solvent molecules. In the case of PILs, directed interactions between the cation BH⁺ and the anion A⁻ by means of H bonds are present. This will result in electrode–electrolyte interface structure that fundamentally differs from aqueous electrolyte systems.^13,14 Vibrational spectroscopy (IR/Raman) and spectro-electrochemical methods can be used to elucidate the microscopic structural arrangements, the underlying transport and electrochemical mechanisms. This requires detailed understanding of the origin of all vibrational modes of the new electrolytes.

Amongst possible ionic liquids, we focus on room-temperature ionic liquids (RTILs).^15,16

The PIL diethylmethylammonium triflate has been investigated in many studies with respect to its electrochemical and bulk properties. Lee et al. have reported that [DEMA][TfO] is well-suited for fuel cell applications, exhibiting beneficial properties, both ionically and mechanically,¹⁷ and having high levels of activity at the electrodes.^18,19

Infrared spectroscopy is routinely used to obtain information on the bulk and interfacial structure of an electrolyte.²⁰ With respect to the investigated PIL [DEMA][TfO], Mori et al.²¹ used a combination of IR spectroscopy and atomistic simulations to analyze the N–H vibration-related double peak at 3000 cm⁻¹. Their experiments with deuterated [DEMA][TfO] allowed for the unambiguous assignment of spectral features to N–H vibrations and excluded any significant C–H vibrational influence. With the aid of classical molecular dynamics simulations, they explained the double peak feature in terms of the formations of ion triplet in the bulk phase and the resulting symmetrical and asymmetrical stretching. However, the peak-to-peak splitting of 40 cm⁻¹ computed with density functional theory (DFT) in the mentioned paper, for a triplet configuration, is roughly an order of magnitude smaller than the measured splitting of 268 cm⁻¹. Because the measured splitting is comparable to the splitting of the two peaks seen for N–H₂ groups in the relevant frequency range,²² where the symmetrical–antisymmetrical stretching modes are expected to be much stronger than in the case of a triplet, we suspect that the explanation of Mori et al.²¹ might be incomplete, warranting further investigations of the IR spectrum of this PIL with different simulation methods.

Another study of Watanabe et al.²³ showed the same broad double peak feature in the high frequency IR spectrum of the [DEMA][TfO] PIL. However, they assigned only the higher frequency peak to the N–H stretching and provided no explanation for the lower frequency part.

Here, we present a vibrational analysis of the measured IR spectra of [DEMA][TfO] performed with with the help of DFT as well as classical molecular dynamics (CMD) and ab initio molecular dynamics (AIMD) simulations. We focus specifically on understanding the N–H bond vibrations.

2. Methods

2.1. Classical molecular dynamics simulations

CMD simulations were performed using the LAMMPS package.²⁴ The OPLS all-atom force field was employed using the parameters of Nasrabadi and Gelb.²⁵ Simulations were performed using periodic boundary conditions in the NVT (constant particle number, volume and temperature) ensemble. The volume of the ionic liquid was adjusted according to the density obtained from simulations at constant pressure.²⁶ The simulation timestep was 1 fs. In order to determine which conformations featured the highest occurrence in the bulk, liquid phase simulations with 200 [DEMA][TfO] ion pairs were performed. A production run of 5 ns was analysed and the conformations of the cation were identified using the dihedral angles of the ethyl chains with respect to the methyl group as descriptors. The frequency of occurrence of different conformations during the 5 ns trajectory was used as a criterion to select ionic configurations for single-point calculations. For details of considered conformations, please see ESI,† Section S2.

Simulation with a smaller system size aimed to produce starting configurations for follow-up single point DFT calculations involved four ion pairs (eight molecules). 10 ns-long trajectories were simulated with 1000 time steps in a periodic supercell cubic box of 10.6 Å length. From the obtained MD trajectory, ten snapshots were selected according to their probability of occurrence, observed in the 5 ns trajectory of the above-mentioned CMD simulation of 200 ion pairs.

2.2. Static density functional theory calculations

As follow-up, density functional theory calculations of the ten selected snapshots were performed with the Quantum-ESPRESSO (QE) package²⁷ using the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional²⁸ with energy cut-off for plane waves of 30 Ry²⁹ and ultrasoft pseudopotentials to represent core electrons.³⁰ The liquid ionic configurations were relaxed to obtain ground state configurations suitable for computation of vibrational spectra. The density functional perturbation theory (DFPT) calculations of vibrational modes and infrared (IR) spectra were performed in the quasi harmonic approximation using the PHonon tool of the Quantum-ESPRESSO package. The relatively small system of 112 atoms was imposed by the computational intensiveness of DFPT calculations. Visualization software “Avogadro”³¹ and “JMol”³² were used to identify and assign the vibrational modes.

2.3. Ab initio molecular dynamics simulations

The AIMD simulations were carried out with CP2K software.³³ For evaluating the forces, we applied the Becke–Lee–Yang–Parr (BLYP) exchange–correlation functional with van der Waals corrections³⁴ and employed the basis set DZVP-MOLOPT-SR-GTH.³⁵ To analyze the resulting AIMD trajectories and compute the IR spectra, the TRAVIS software was applied.³⁶ This package computes the IR spectrum from the Fourier transform of the dipole moment autocorrelation function.³⁷ AIMD simulations were performed for a system containing 10 ion pairs (20 molecules) and 280 atoms in total, for a 40 ps-long trajectory, which was sufficient to obtain converged spectra.

2.4. Analysis of the phonon spectrum

To further study the high frequency (HF) region of the spectrum (between ∼2800 cm⁻¹ and ∼3400 cm⁻¹), the vibrational phonon density of state of the shared hydrogen atoms was computed according to the Wiener–Khinchin theorem.³⁸ The shared hydrogen atom is the one bonded to the nitrogen atom of the DEMA cation, which is involved in the hydrogen bond with the triflate. Following this scheme, we first computed the velocity autocorrelation function. Then, the vibrational phonon density of states was obtained by means of the fast Fourier transform (FFT) of the resulting velocity autocorrelation function.

2.5. Experimental setup

Experimental Fourier-transformed infrared (FTIR) spectra were obtained in attenuated total reflection (ATR) mode using a GladiATR reflection unit (PIKE, Madison, USA) in conjunction with a Nicolet iS20 device (Thermo-Fisher Scientific, Waltham, USA). The protic ionic liquid [DEMA][TfO] (IoliTec – Ionic Liquids Technologies GmbH, Heilbronn, Germany) was deposited as a droplet on the diamond ATR crystal immediately before measurement in order to avoid water uptake.

3. Results and discussion

3.1. Analysis with the IR spectra of isolated ions

In the first step of the analysis of the structure of bulk [DEMA][TfO], we computed the IR spectra of single [DEMA] and [TfO] molecules. The comparison between the computed spectra and the experimental data is shown in Fig. 1. The measured spectrum of the PIL agrees in several features with the spectra of isolated species, allowing for straightforward peak assignment and interpretation. The low-frequency segment of the PIL spectrum is produced by the vibrational modes of the [TfO] anion, mainly by vibrations at 990 cm⁻¹, 1040 cm⁻¹, and 1230 cm⁻¹. Instead, the high-frequency components originate from the vibrational modes of the [DEMA] cation at 2980 cm⁻¹ and 3030 cm⁻¹. However, although the overall shape of the measured spectrum qualitatively matches the computed spectra of isolated ions, there is no clear correspondence between computed and measured peaks, with a significant mismatch for the high-frequency features seen around 3000 cm⁻¹.

Fig. 1 Comparison of the experimental ATR spectrum of [DEMA][TfO] with the computed IR spectra of single DEMA and TfO molecules. The computed spectra were obtained with the DFPT method. The unit of the intensity is an arbitrary unit (a.u.).

The computed high-frequency peaks have been analyzed with the aid of molecule visualization software, which enabled the attribution of this feature to the vibration of N–H and methyl groups. This was expected, as vibrations associated with the motion of light hydrogen atoms occur in this high-frequency range.³⁹ Nevertheless, the spectra of isolated ions are not sufficient for the quantitative analysis of the measured spectrum of the PIL. Hence, we can conclude that liquid phase effects and the continuum nature of the liquid medium cannot be neglected, as they significantly affect the structure and resulting IR spectral signature of the PIL.

3.2. Conformation analysis

We performed CMD simulations of two hundred ion pairs in a periodic simulation cell to assess the structure of the liquid phase of the PIL and select a set of configurations for the DFPT calculations of IR spectra. As the DEMA cation is a complex molecule, it can adopt different conformations, which can influence the molecular vibrations. As is illustrated in Fig. 2, the ethyl groups connected to the central nitrogen atom can be oriented in three different directions labelled trans (t), gauche1 (g₁), and gauche2 (g₂), which results in nine different conformations. Due to the symmetry of the molecule, some of these conformations are equivalent, and only six distinguishable conformations must be considered (for details see the ESI†).

Fig. 2 (a) Structural formula of the [DEMA]⁺ cation. The arrow shows the point of view while labelling the different conformations. Because we have three possible conformations on each side, we refer to two different gauche conformations. The reference groups are the methyl group on the side of the observer (C₄H₃) and the ethyl group on the other side. (b) Gauche1 (g₁) conformation considering C₂H₅ as a reference, it forms with the ethyl group at an angle of ∼ −60°. (c) Gauche2 (g₂) conformation considering C₂H₅ as a reference, it forms with the ethyl group at an angle of ∼ +60°. (d) Trans (t) conformation considering C₂H₅ as a reference, it forms with the ethyl group at an angle of ∼180°.

Fig. 3 shows the occurrence of the conformations of the DEMA cation as obtained in the CMD simulation. Nearly half of the cations adopt the g₁t conformation. The second most frequent conformation is the tt, which occurs with a probability of ∼20%, followed by the less common g₂t, g₂g₁, and g₁g₁ conformations. We noted that the g₂g₂ conformation occurred very rarely.

Fig. 3 Occurrence of conformations obtained with the CMD simulation of a system containing 200 ion pairs (see Section 2.1 for details).

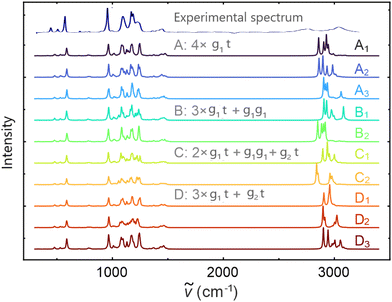
In order to select a set of configurations for DFPT calculations, we performed a 10 ns long CMD simulation on a smaller system of four ion pairs. From this trajectory, we extracted a set of ten snapshots that represent the statistical distribution of different cation conformations observed in simulations with 200 ion pairs (Fig. 3). We then computed the IR spectra for these snapshots. The snapshots were labeled according to the cation conformations: A_i when the four cations are in g₁t conformation, B_i when three cations are in g₁t conformation and one is in g₁g₁, C_i when two cations are in g₁t conformation, one is in g₁g₁, and one in g₂t, D_i when three cations are in g₁t conformation and one is in g₂t (Fig. 4). Different subscripts indicates different configurations of the same conformation.

Fig. 4 Infrared spectra calculated for the bulk structures of four ion pairs in representative conformations. The spectra have been computed with DFPT applying the quasi harmonic approximation (see Section 2.2). The unit used for the intensity is arbitrary units (a.u.). For comparison, the experimental spectrum is displayed on the top.

3.3. Simulated spectrum of ionic liquid

Fig. 4 shows the comparison between the computed spectra of different sets of conformations and the measured one. The first reported spectrum is experimental. When comparing the two spectra, we see that our calculations over-predict the intensities of the peaks, while still being able to correctly match peak position.

Then, from top to bottom, the first three spectra belong to the configuration in which all of the cations are in g₁t conformation; in the following two spectra, one of the cations is in g₁g₁ and so on, depending on what is reported on the plot. The spectra corresponding to the same letter have the same set of conformations as the cations. From analyzing each of the spectra corresponding to different configurations and conformations of [DEMA][TfO] in Fig. 4, we notice that in the low-frequency region (below 1500 cm⁻¹), there are only minor differences and all of the main features observed in the measured spectrum are well-reproduced. We also notice that the low-frequency component is not significantly influenced by the different conformations of the cation. However, for the high-frequency part of around 3000 cm⁻¹, we observe substantial differences in the number of the peaks and their positions. Nevertheless, we can identify four main peaks, which occur at different frequencies for each conformation and they arise due to N–H stretching in the [DEMA] cations. Interestingly, these observed differences are even present between spectra representing the same set of conformations (e.g., when the cations are all in the g₁t state, then a difference of ∼150 cm⁻¹ is observed). This indicates that the differences between the high-frequency parts of different spectra do not depend on the different structures of the cations. Because the measured spectrum represents a statistical mix of different conformations, we averaged the ten different computed infrared spectra shown in Fig. 3, excluding the measured one. The resulting spectrum is shown in Fig. 5a.

Fig. 5 Average IR spectrum of bulk [DEMA][TfO] obtained with single point DFT calculation from 10 snapshots with four ion pairs each (see Section 2.2 for details). The unit used for the intensity is an a.u. (a) The total IR spectrum was obtained by averaging the results from Fig. 4 with a comparison to the experimental spectrum; (b) IR spectrum in the low-frequency region with an illustration of the main vibrations.

The procedure resulted in a broader feature in the high-frequency region, bringing it closer in width and position to the measured one. This indicates that the hydrogen bond-driven high-frequency IR absorption is caused by a complex interplay of different configurations and conformations in the PIL. However, the double peak shape observed experimentally could not be reproduced. In the low-frequency region, the simulated spectrum matches the measured spectrum well, allowing for an assignment of the molecular group vibrations to the observed peaks, as is illustrated in Fig. 5b. The main peaks at ∼480 cm⁻¹ and ∼ 530 cm⁻¹ are assigned to the [TfO] modes, whereas the lower intensity peaks at ∼657 cm⁻¹ and ∼843 cm⁻¹ are due to the interactions between the cations and anions and belong to the [DEMA] vibrational modes. The same occurs with the low intensity peak at ∼1012 cm⁻¹, which belongs to the cation vibrational mode. The higher intensity peaks at ∼980 cm⁻¹, ∼1080 cm⁻¹, and ∼1245 cm⁻¹ are vibrational modes belonging to the [TfO] anion. To complete the description of the low-frequency region, the peaks occurring at ∼1339 cm⁻¹ and ∼1446 cm⁻¹ are given to the [DEMA] vibrational modes.

Table 1 presents the assignments of vibrational modes to peaks in the measured spectrum. The value of the wavenumber is obtained as explained in paragraph 2.2 using the software Quantum-ESPRESSO. To define which peak corresponds to which methyl or ethyl group, the labels in Fig. 2 are used as a reference. Avogadro molecule visualizer was used to define which peak corresponds to which methyl or ethyl group. The obtained assignment is reported in the table. As it will be explained in the next section, the vibrations occurring in the high-frequency region are influenced by the local structural arrangements inside the liquid.

Table 1 Dema⁺ vibrational modes computed from the simulations of four ion pairs in the bulk phase. The label “nitrogen” indicates that the vibrational mode is related to the methyl group bonded to the nitrogen atom and the carbon atom labeled C3 in Fig. 2

Bonds	w.n. (cm^−1)	Modes
C–N–C	248	Wagging
C–N–C	391	Rocking
C–N–C	657	Asym stretching
CH3 (nitrogen)	843	Wagging
CH3	843	Wagging
CH3 (nitrogen)	1012	Rocking
CH3	1012	Rocking
CH2	1339	Scissoring
CH3 (nitrogen)	1446	Rocking
CH3	1446	Rocking
CH3	2974	Sym stretching
CH2	2974	Sym stretching
CH3	3050	Asym stretching
CH2	3050	Asym stretching
N–H	3321	Stretching

---

3.4. Decoding the high-frequency IR feature

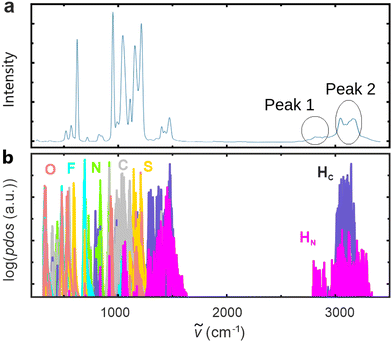
With the aid of classical molecular dynamics and DFT simulations, Mori et al.²¹ concluded that the formation of [DEMA]-[TfO]-[DEMA] triplets and associated symmetrical–antisymmetrical stretching is responsible for the broad “double” peak feature observed in the high-frequency region of the PIL-IR spectrum. To evaluate this claim, we analyzed the output of our CMD simulation of 200 ion pairs. Interestingly, we only found 25 [DEMA]-[TfO]-[DEMA] arrangements that could be classified as ion triplets. This fraction is too low to be responsible for such a distinct spectral feature (see the ESI†). Nevertheless, we further investigated the possible influence of ion triplets by means of experimental methods. As the probability for the formation of ion triplets should decrease with increasing temperatures, we performed FTIR measurements in a temperature range from room temperature up to 120 °C, but did not observe a significant change in the shape of the spectrum. As a further test, we diluted [DEMA][TfO] with deuterated water and dimethyl sulfoxide, expecting to detect a decreasing quantity of ion triplets. However, we did not observe the expected conversion of the “double” peak feature into a “single” one. This result strongly indicates that the presence of ion triplets cannot be singled out as the main reason for the characteristic shape of the high-frequency spectrum (for a detailed discussion, see the ESI†).

Independently of the above analysis, simple reasoning and the DFT calculations of Mori et al.²¹ as well as ours invalidate the ion triplet scenario. The observed separation of the double peak of ∼260 cm⁻¹ corresponds to the separation of vibrational modes of an NH₂ group.⁴⁰ In the case of a triplet, the symmetrical and antisymmetrical vibrations, as well as the splitting, should be much weaker. This is because the two vibrating hydrogen atoms in the triplet are much less strongly associated compared to those in an NH₂ groups. Indeed, DFT calculations of the triplet by Mori et al.²¹ exhibit peak splitting of just 40 cm⁻¹. We obtained a similarly small value of 32 cm⁻¹ in our DFT calculations. Based on our CMD and static DFT simulations, we can thus exclude the formation of [DEMA]-[TfO]-[DEMA] triplet as the cause of the high-frequency double-peak feature observed in the IR spectrum of the PIL. The results presented in Fig. 4 indicate that the surrounding of the DEMA cation has a large influence on the N–H vibration. As the surrounding liquid changes continuously over time due to the movement of molecules, we simulated the IR spectrum with the aid of AIMD by tracing the time evolution of the dipole moment.³⁷Fig. 6a displays the IR spectrum obtained with ab initio molecular dynamics (Section 2.3) for a box containing 10 ion pairs.

Fig. 6 AIMD simulation of the IR spectrum of [DEMA][TfO]. The unit used for the intensity was an a.u. (see Section 2.3 for details). (a) Spectrum of 10 ion pairs simulated for 40 ps; (b) phonon density of states of all simulated molecules in a time range of 7 ps. Circles in panel (a) indicate the features constituting two parts of the “double” peak. H_N and H_C in panel (b) indicate hydrogen atom bounded to N and C atoms, respectivelly.

Similarly to static DFT results, the low-frequency region, obtained with the Fourier transform of the dipole moment autocorrelation function,³⁷ matches the experimental spectrum well (see also Fig. 5). With respect to the high-frequency region, the match between computed and measured spectra has improved significantly. The “double” peak-like feature can now be clearly discerned. “Peak 1” is the one observed at ∼2800 cm⁻¹ as highlighted in Fig. 6(a). The second peak we refer to is labelled as “peak 2” in Fig. 6(a) and represents a broader feature at ∼3200 cm⁻¹. It consists of two minor “peaks”, because of the contribution of H_c atoms, intensity of which is severally overestimated by AIMD,⁴¹ and the reduced size of the system. Although quantitative differences between experimental and simulated spectra continue to exist, AIMD simulations reproduce the observed broad distribution in the range of wavenumbers from 2800 to 3200 cm⁻¹. In order to understand the origin of this feature, we performed a time-dependent analysis of the phonon density of states (PDOS). Fig. 6b displays the PDOS extracted from the first seven ps of the production run. Two types of hydrogen vibrations were detected, namely: C–H and N–H modes. C–H vibrations are confined in a range from 3000 top 3200 cm⁻¹, whereas N–H vibrations are found in the range from 2600 to 3400 cm⁻¹. However, our static DFT simulations as well as experiments of Mori et al.²¹ reveal that the IR intensity of the C–H mode is negligible with respect to the N–H mode. This was also visible in the measured spectrum of deuterated [DEMA][TfO] of Mori et al.²¹

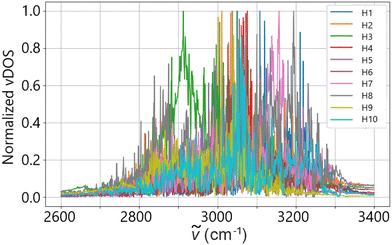
Fig. 7 reports the PDOS obtained for single hydrogen atoms at the N–H position of the cation computed from the full 40 ps long trajectory. It can be clearly seen that vibrations of the shared hydrogen atoms exhibit a broad frequency distribution without clearly discernible pattern.

Fig. 7 Vibrational density of states (vDOS) of the 10 hydrogen atoms over 40 ps.

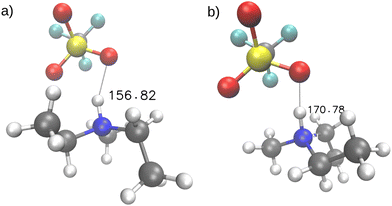
To better understand the origin of the double peak, we followed one of the hydrogen atoms along its trajectory. We analyzed short time frames of 200 femtoseconds to capture individual vibrations of the hydrogen atom. In Fig. 8 evaluation of hydrogen atom motion in four of these intervals are shown. In the applied procedure, we fixed the nitrogen atom at the origin and aligned the methyl and ethyl groups along the x and y axes, respectively. We then plotted the subsequent positions of the triflate to illustrate the pattern responsible for the broad, double-peaked distribution of vibrations in the high-frequency region. The analysis reveals that vibrations occur at frequencies >3000 cm⁻¹ when the hydrogen vibrates between two oxygen atoms of the triflate, forming an N–H–O angle of approximately 156° as shown in Fig. 9(a). In contrast, Fig. 9(b) shows the case for vibrations at frequencies <3000 cm⁻¹, where the hydrogen vibrates between the oxygen of the anion and the nitrogen of the cation, forming an angle of approximately 168°.

Fig. 8 The vibrational density of states (vDOS) for a single shared hydrogen atom (red points). Each plot corresponds to a 200 femtosecond time window at different times of the simulation. The lines represent cubic splie fit to the data points and are presented here for better visibility. Blue and green lines highlight vibrations at ∼3200 cm⁻¹ and ∼2800 cm⁻¹, respectivelly.

Fig. 9 A visual representation highlighting the difference between vibrations of the shared hydrogen atom at ∼2800 cm⁻¹ and at ∼3200 cm⁻¹. (a) shows it is vibrating constrained between two oxygen atoms of the triflate anion (TfO). (b) shows it vibrating in line with an oxygen atom of the triflate and the nitrogen of the DEMA.

Fig. 10 shows an asymmetric distribution of N–H–O angles. We fitted this distribution with two Gaussian functions, as shown in Fig. 10. The peaks of each distribution match the values we obtained when analyzing the respective orientations of the hydrogen bond, as illustrated in Fig. 9(a) and (b). Comparing the areas under the two curves, we observe a broader distribution for higher frequency mode and a narrower distribution for lower frequency mode, which is consistent with broadening of the two peaks indicated in Fig. 6.

Fig. 10 Histogram of the N–H–O angle distribution over the full trajectory. The nitrogen and hydrogen atoms are part of the DEMA cation, while the oxygen atom belongs to the TfO anion. The angles were calculated at each time step by identifying the closest oxygen atom to the shared hydrogen atom. The distribution is fitted with two Gaussian curves, representing vibrations with frequencies lower and higher than 3000 cm⁻¹.

4. Conclusions

The aim of this study was to computationally- and experimentally-analyze the infrared spectrum of the protic ionic liquid (PIL) diethylmethylammonium triflate [DEMA][TfO], proposed as potential electrolyte in polymerelectrolyte fuel cells (PEFCs). We conducted an in-depth analysis of the infrared (IR) spectrum of the protic ionic liquid diethylmethylammonium triflate ([DEMA][TfO]) using a combination of experimental techniques and atomistic simulations. Our results shed light on both the high-frequency and low-frequency regions of the spectrum, providing a comprehensive understanding of the vibrational modes within this system.

In the frequency region below 1500 cm⁻¹, our analysis revealed that the main vibrational contributions originate from the triflate anions, with peaks attributed to their distinct vibrational modes, such as those at 480 cm⁻¹, 530 cm⁻¹, and 1245 cm⁻¹. Interactions between cations and anions, particularly the influence of hydrogen bonding on these vibrational modes, were found to play a critical role in determining the spectral features. Our simulations closely matched the experimental data in this region, confirming the correct assignment of these modes and illustrating the complex interplay between cation and anion dynamics in the liquid phase.

For the high-frequency region, we resolved the previously unclear double-peak feature associated with N–H stretching vibrations. Contrary to earlier hypotheses that linked this feature to ion triplets,²¹ our computational results demonstrate that these high-frequency modes are strongly influenced by the dynamic restructuring of the liquid. This finding is corroborated by the observation of shifts over a range of ∼400 cm⁻¹ in the vibrations of the shared hydrogen atom. The continuous shifting of the shared hydrogen atoms' vibrational frequencies over time is caused by a dynamically changing environment around the N–H group. This dynamic environment prevents the IR spectrum's high-frequency region from showing two narrow peaks, which would typically be expected for the N–H stretching mode in two distinct environments. Instead, there is a broadening into two peak-like features at approximately 2800 cm⁻¹ and 3200 cm⁻¹. The broadening arises from distributions of local different environments with different configurations between DEMA and TfO. The frequency distribution around 2800 cm⁻¹ arises when the hydrogen vibrates in line between the nitrogen and one of the oxygen atoms of the triflate. In contrast, vibrations around 3200 cm⁻¹ are associated with the vibration of the shared hydrogen atom constrained between two neighboring oxygen atoms of the triflate, which is influenced by the partial rotation of the triflate along the trajectory.

The computational methodology employed in this study has proven instrumental in analyzing the complex vibrational characteristics of the PIL. The data supporting this article have been included as part of the ESI.† The studies provide a robust framework for future studies aiming to illuminate the complex interactions and behaviors of ionic liquids in electrochemical applications. Future research could leverage these computational techniques to investigate other ionic liquids with varying cation–anion combinations, potentially leading to breakthroughs in electrolyte optimization for fuel cells.

Author contributions

FP performed AIMD and DFT calculations together with the post process analysis. CR, PMK, FP and CK conceived the paper and structured the initial draft. CR and YC performed the CMD simulations and conducted IR measurements. PMK supervised DFT part of the studies and provided related computational methodologies. CR, FP, PMK and CK performed analysis of the data. All authors edited the final version of the paper.

Data availability

All the data are included in the paper and the data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge having access to JARA-CSD partition (projects jara0037 and JIEK61) and the financial support from the HiTEC graduate school for doctoral candidates at Forschungszentrum Jülich. We acknowledge Mr Wood for proofreading the manuscript.

Notes and references

1. J. Chi and H. Yu, Chin. J. Catal., 2018, 39, 390–394.
2. A. Züttel, Naturwissenschaften, 2004, 91, 157–172.
3. J. Chen, M. Asano, Y. Maekawa and M. Yoshida, J. Membr. Sci., 2006, 277, 249–257.
4. T. Li, J. Shen, G. Chen, S. Guo and G. Xie, ACS Omega, 2020, 5, 17628–17636.
5. Q. Li, R. He, J. Jensen and N. Bjerrum, Chem. Mater., 2003, 15, 4896.
6. S. Peighambardoust, S. Rowshanzamir and M. Amjadi, Int. J. Hydrogen Energy, 2010, 35, 9349.
7. C. Wannek, I. Konradi, J. Mergel and W. Lehnert, Int. J. Hydrogen Energy, 2009, 34, 9479–9485.
8. K. Wippermann and C. Korte, Curr. Opin. Electrochem., 2022, 32, 100894.
9. Z. Qi and A. Kaufman, J. Power Sources, 2003, 113, 37–43.
10. T. Endo, K. Sunada, H. Sumida and Y. Kimura, Chem. Sci., 2022, 13, 7560–7565.
11. A. Noda, M. A. B. Hasan Susan, K. Kudo, S. Mitsushima, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2003, 107, 4024–4033.
12. K.-D. Kreuer, Chem. Mater., 1996, 8, 610–641.
13. G.-R. Zhang and B. J. Etzold, J. Energy Chem., 2016, 25, 199–207.
14. W. Silva, M. Zanatta, A. S. Ferreira, M. C. Corvo and E. J. Cabrita, Int. J. Mol. Sci., 2020, 21, 20.
15. S. T. Handy, Curr. Org. Chem., 2005, 9, 959–988.
16. D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232–250.
17. T. Welton, Chem. Rev., 1999, 99, 2071–2084.
18. S.-Y. Lee, A. Ogawa, M. Kanno, H. Nakamoto, T. Yasuda and M. Watanabe, J. Am. Chem. Soc., 2010, 132, 9764–9773.
19. H. Nakamoto and M. Watanabe, Chem. Commun., 2007, 2539–2541.
20. J. Coates, Encyclopedia of Analytical Chemistry, John Wiley & Sons Ltd, Chichester, 2000, pp. 10815–10837.
21. K. Mori, S. Hashimoto, T. Yuzuri and K. Sakakibara, Bull. Chem. Soc. Jpn., 2010, 83, 328–334.
22. S.-T. King, J. Phys. Chem., 1971, 75, 405–410.
23. M. S. Miran, T. Yasuda, M. A. B. H. Susan, K. Dokko and M. Watanabe, RSC Adv., 2013, 3, 4141–4144.
24. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
25. A. T. Nasrabadi and L. D. Gelb, J. Phys. Chem. B, 2017, 121, 1908–1921.
26. C. Rodenbücher, Y. Chen, K. Wippermann, P. M. Kowalski, M. Giesen, D. Mayer, F. Hausen and C. Korte, Int. J. Mol. Sci., 2021, 22, 12653.
27. H. Blom and G. Björk, Appl. Opt., 2009, 48, 6050–6058.
28. G. K. H. Madsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195108.
29. D. S. Sholl and J. A. Steckel, Density functional theory: a practical introduction, John Wiley & Sons, 2022.
30. K. Laasonen, R. Car, C. Lee and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 6796.
31. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17.
32. Jmol Development Team, Jmol: An open-source Java viewer for chemical structures in 3D, https://jmol.sourceforge.net/.
33. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
34. I.-C. Lin, A. P. Seitsonen, I. Tavernelli and U. Rothlisberger, J. Chem. Theory Comput., 2012, 8, 3902–3910.
35. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 11.
36. M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152, 164105.
37. S. Jahn and P. M. Kowalski, Rev. Mineral. Geochem., 2014, 78, 691.
38. A. Koyama, D. A. Nicholson, M. Andreev, G. C. Rutledge, K. Fukao and T. Yamamoto, Phys. Rev. E, 2020, 102, 063302.
39. B. L. Mojet, S. D. Ebbesen and L. Lefferts, Chem. Soc. Rev., 2010, 39, 4643–4655.
40. B. Cain, J. Freeman and T. Henshall, Can. J. Chem., 1969, 47, 2947–2952.
41. N. Sundaraganesan, H. Saleem, S. Mohan, M. Ramalingam and V. Sethuraman, Spectrochim. Acta, Part A, 2005, 62, 740–751.

---

Footnote

† Electronic supplementary information (ESI) available: They are uploaded together with the paper. See DOI: https://doi.org/10.1039/d3cp06047k

---