Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemical engineering of cationic distribution in spinel ferrite nanoparticles: the effect on the magnetic properties†
Miran
Baričić‡
 *a,
Pierfrancesco
Maltoni
*a,
Pierfrancesco
Maltoni
 *b,
Gianni
Barucca
*b,
Gianni
Barucca
 c,
Nader
Yaacoub
d,
Alexander
Omelyanchik
c,
Nader
Yaacoub
d,
Alexander
Omelyanchik
 ae,
Fabio
Canepa
ae,
Fabio
Canepa
 a,
Roland
Mathieu
a,
Roland
Mathieu
 b and
Davide
Peddis
b and
Davide
Peddis
 *ae
*ae
aDipartimento di Chimica e Chimica Industriale & INSTM, nM2-Lab, Università degli Studi di Genova, Via Dodecaneso 31, Genova, 1-16146, Italy. E-mail: miranbaricic@yahoo.com; davide.peddis@unige.it
bDepartment of Materials Science and Engineering, Uppsala University, Box 35, Uppsala, 751 03, Sweden. E-mail: pierfrancesco.maltoni@angstrom.uu.se
cDipartimento di Scienze e Ingegneria della Materia, Dell’ambiente ed Urbanistica, Università Politecnica delle Marche, via Brecce Bianche 12, Ancona, Italy
dInstitut des Molécules et Mateŕiaux du Mans, CNRS UMR-6283, Le Mans Université, F-72085 Le Mans, France
eInstitute of Structure of Matter (ISM), nM2-Lab, National Research Council (CNR), Via Salaria, Km 29,300 00015 Monterotondo Scalo, Roma, Italy
First published on 20th January 2024
Abstract
A set of ∼9 nm CoFe2O4 nanoparticles substituted with Zn2+ and Ni2+ was prepared by thermal decomposition of metallic acetylacetonate precursors to correlate the effects of replacement of Co2+ with the resulting magnetic properties. Due to the distinct selectivity of these cations for the spinel ferrite crystal sites, we show that it is possible to tailor the magnetic anisotropy, saturation magnetization, and interparticle interactions of the nanoparticles during the synthesis stage. This approach unlocks new possibilities for enhancing the performance of spinel ferrite nanoparticles in specific applications. Particularly, our study shows that the replacement of Co2+ by 48% of Zn2+ ions led to an increase in saturation magnetization of approximately 40% from ∼103 A m2 kg−1 to ∼143 A m2 kg−1, whereas the addition of Ni2+ at a similar percentage led to an ∼30% decrease in saturation magnetization to 68–72 A m2 kg−1. The results of calculations based on the two-sublattice Néel model of magnetization match the experimental findings, demonstrating the model's effectiveness in the strategic design of spinel ferrite nanoparticles with targeted magnetic properties through doping/inversion degree engineering.
Introduction
Spinel ferrites are materials with stoichiometry M2+Fe2O4 (M2+ = Co2+, Zn2+, Ni2+, Fe2+) that have been intensely studied for their chemical flexibility, enabling the inclusion of a wide range of transition metal cations, thus providing an easy way to tune their magnetic properties. For these reasons, spinel ferrite nanoparticles (NPs) are suitable for many applications such as MRI contrast agents,1–3 molecular detection and separation, drug delivery systems and hyperthermic therapy,4,5 and design of rare-earth-free permanent magnets.6–11The spinel ferrite structure consists of a cubic close-packed (ccp) arrangement of oxygen atoms with tetrahedral (Td) and octahedral [Oh] sites.12–14 The cationic distribution is often reported as (M1−δ2+Feδ3+)Td[Mδ2+Fe2−δ3+]OhO4, with δ as the inversion degree, with a value between 0 (in normal spinel and 1 (in inverse spinel). The magnetization of spinel ferrites can be described by Néel's model for antiferro- and ferrimagnetic materials,12,13,15 where the total magnetic moment is the vectorial sum of the magnetic sublattice's magnetizations, corresponding to Oh and Td sites in spinel ferrites:  .
.
Since the metallic cations have different magnetic properties and site selectivity within the lattice, such spinel structures offer the possibility to easily modify the saturation magnetization (Ms), magneto-crystalline anisotropy, and interparticle magnetic interactions. Specifically, cobalt ferrite is a relatively highly anisotropic material with δ values in the range of 0.66 to 0.8;13,16–19 its large magneto-crystalline anisotropy (K1 = 290 kJ m−3 at room temperature20) is due to the strong single-ion anisotropy of Co2+ in Oh-sites, arising from its non-quenched spin–orbit coupling.21 Ni2+ and Zn2+ exhibit lower anisotropy in comparison to Co2+, yet—owing to their different single-ion properties and site selectivity—they yield opposite effects on saturation magnetization, providing interesting perspectives. Ni2+ tends to occupy the Oh sites, while Zn2+ prefers Td sites.11,22,23 The selectivity for different sites leads to a change in the inversion degree of the spinel structure.
When Ni2+ substitutes Co2+, the inversion degree increases (i.e., the stoichiometric NiFe2O4 is the totally inverted spinel with δ = 1) while Zn2+ substitution leads to a lower value of δ.24 This ability to control the inversion degree by chemical engineering provides an additional degree of freedom in designing the magnetic properties of spinel ferrite NPs.
At the nanoscale, the magnetic structure of spinel ferrites is due to the complex interplay between cationic distribution and surface magnetic disorder (i.e., spin canting25) as well as it is related to the particle size and synthesis method.24 For example, Mameli et al.26 studied the magnetic properties of ∼7 nm Zn-substituted CoFe2O4 NPs and reported a reduction of inversion degree to ∼0.4 when the Zn2+ content was ∼0.5. This led to a significant enhancement in saturation magnetisation up to 157 ± 3 A m2 kg−1, which is higher than the value measured for pure CoFe2O4. Andersen et al.27 found metastable cation distributions in hydrothermally prepared Zn-substituted CoFe2O4 NPs leading to increased Ms in Zn-rich samples, which decreased after annealing to the thermodynamic distribution.
On the other hand, nanocrystals of NiFe2O4 and CoFe2O4 may exhibit weak interdependence between particle size and inversion degree. For example, in their study, Carta et al.16 demonstrated that 6–9 nm NPs (including cobalt and nickel ferrites) prepared by the sol–gel method show the same inversion degree values as bulk analogues (0.68 and 1.0, respectively). On the other hand, Muscas et al.28 reported values of ∼0.74, ∼0.78, and ∼0.44 for CoFe2O4, Ni0.5Co0.5Fe2O4, and NiFe2O4 NPs of ∼4.5 nm, respectively, significantly different from bulk.
In this framework, comparative studies of nanostructure spinel ferrites, which go beyond the effect of synthesis methods and morpho structural features, appear to be very important. To the best of our knowledge, no prior studies have directly compared Zn- and Ni-substituted CoFe2O4 NPs synthesized by the same method and with comparable morpho-structural features.
This study focuses on the comparative study of magnetic properties of MxCo1−xFe2O4 (M2+ = Ni2+, Zn2+) NPs with increasing Ni2+/Zn2+ content. The thermal decomposition of metallic acetylacetonates in high-temperature boiling solvent (TD) synthesis29 has been used to have a fine control on morpho-structural features of NPs and the high value of Ms (see Fig. S1, ESI†). Furthermore, to the best of our knowledge, a few studies of the low-temperature magnetic properties of MxCo1−xFe2O4 are available in the literature28,30,31 (see Fig. S1a, ESI†).32–34 We prepared two sets of samples (hereafter referred to as “Ni-series” and “Zn-series”) which have an increasing M2+ substitution with respect to the cobalt-ferrite reference sample. The NPs have comparable size and shape distributions, thus avoiding any possible size effects on the magnetic properties owing to changes in the inversion degree.19 Therefore, this system can be considered as a model that allows us to establish direct correlations between the magnetic structure (i.e., cationic distribution) and magnetic properties. Herein, we present a thorough investigation, conducted at both low temperature and room temperature, on the magnetic anisotropy, saturation magnetization, and interparticle interactions. Inversion/doping content maps of the low temperature Ms were plotted by considering a spin-only two-sublattice Néel model of magnetization. The usefulness of the maps is demonstrated by predicting Ms for 2 samples for the Ni- and Zn-series with known composition and cationic distribution from in-field Mössbauer spectrometry. The potential interest of this study is related to the possibility of controlling the magnetic structure at the nanoscale, opening interesting perspectives to improve materials’ performance for targeted technological applications.
Experimental methods
Synthesis
For the synthesis of ∼9 nm CoFe2O4 NPs, Fe(acac)3 (2 mmol), Co(acac)2 (1 mmol), oleic acid (OLAC, 6 mmol), oleylamine (OLAM, 6 mmol), 1,2-hexadecanediol (HDD, 10 mmol) and dibenzylether (DBE, 20 mL) were employed according to the method described by Sun et al.29 All chemicals were stirred under an inert nitrogen atmosphere at 200 °C for 2 h, and then at 300 °C for 1 h (heating rates 5 °C min−1); at the end of the thermal program, the product was cooled at room temperature by removing the heating mantle. Eventually, the sample was washed in ethanol using a centrifuge (10 min, 4000 rpm) three times, and stored in a few mL of toluene. To synthesize MxCo1−xFe2O4 (M2+ = Ni2+, Zn2+), Co(acac)2 was partially substituted with Ni(acac)2 or Zn(acac)2, so that the sum of all Co2+ and M2+ acetylacetonates is kept to 1 mmol. The resulting stoichiometries in the final product were analysed by inductively coupled plasma atomic emission spectroscopy (ICP-AES), and each sample was named after its M2+ stoichiometric coefficient, x (e.g., Zn19 or Ni63). The samples were all compared with a reference no-substituted sample, CoRef. See the used acronyms of samples in Table 1.| Sample | Stoichiometry | 〈d〉XRPD, nm | 〈d〉TEM, nm |
|---|---|---|---|
| CoRef | Co0.85Fe2.15O4 | 8.3(4) | 9.0(1) |
| Ni22 | Ni0.22Co0.71Fe2.07O4 | 8.0(4) | 8.1(1) |
| Ni39 | Ni0.39Co0.45Fe2.16O4 | 8.3(5) | 8.5(1) |
| Ni63 | Ni0.63Co0.23Fe2.14O4 | 8.3(5) | 10.0(1) |
| Zn19 | Zn0.19Co0.70Fe2.11O4 | 9.3(4) | 8.4(2) |
| Zn32 | Zn0.32Co0.47Fe2.22O4 | 9.0(1) | 8.7(1) |
| Zn48 | Zn0.48Co0.26Fe2.26O4 | 8.6(5) | 9.3(2) |
Characterization techniques
X-ray powder diffraction (XRPD) was performed on NP powders using a Bruker D8 Advance diffractometer (solid state LynxEye detector, Cu Kα radiation, Bragg Brentano geometry, DIFFRACT plus software). The average sizes of crystallites were calculated using the Scherrer equation.35 Transmission Electron Microscopy (TEM) images were acquired using a Philips CM200 microscope operating at 200 kV and equipped with a LaB6 filament. The statistical analysis of particles’ sizes was performed using the ImageJ software.28 Inductively Coupled Plasma – Atomic Emission Spectroscopy (ICP-AES) measurements were performed using an iCAP 6300 DUP ICP-AES spectrometer (ThermoScientific) to check the composition of each sample. Thermo-gravimetric Analysis (TGA) was performed on a LabsysEvo 1600 DTA/TGA (Setaram): a few mg of powder was placed in an alumina crucible and heated from 30 to 1000 °C at 10 °C min−1 under an O2 atmosphere (20 mL min−1). The magnetization was normalized considering the weight loss measured by TGA, due to decomposition of the organic part.DC magnetization measurements were performed using a SQUID magnetometer (Quantum Design MPMS XL). The field dependence of magnetization loops was measured at 5 and 300 K in the range of ±5 T. The saturation magnetization (Ms) of each sample was obtained by fitting the high field values with the Law of Approach to Saturation (LAS) M(H) = Ms(1 − a/H − b/H2) where a and b are free-fitting parameters, and H is the applied field.36 The temperature dependence of magnetization has been investigated using Zero Field Cooled (ZFC) and Field Cooled (FC) protocols under 2.5 mT fields from 5 to 300 K, and Tmax and Tb were estimated by following the procedure reported in ref. 37. Remanent magnetization was measured by means of Isothermal Remanent Magnetization (IRM) and Direct Current Demagnetization (DCD) protocols.38,39 IRM curves are obtained starting from a demagnetized sample at μ0H = 0 T and measuring the remanence corresponding to increasing fields μ0H > 0; DCD curves are obtained in the same manner, but the measurement starts from μ0H = 0 with a sample previously being saturated at μ0H = −5 T. 57Fe Mössbauer spectra were obtained at 12 K in an externally applied field of 8 T oriented parallel to the γ-beam using a 57Co/Rh γ-ray source mounted on an electromagnetic transducer with a triangular velocity form. The hyperfine structure was modelled by a least-squares fitting procedure involving Zeeman sextets composed of Lorentzian lines using MOSSFIT (made-home software). The isomer shift values δ are referred to those of α-Fe at 300 K.
Results and discussions
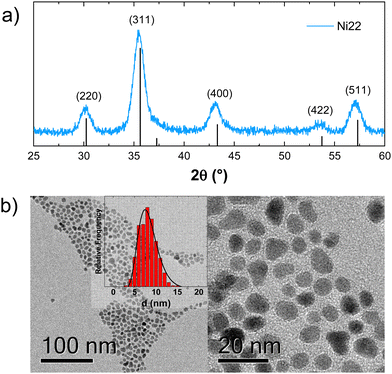
The XRPD patterns show the typical reflections of the spinel Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m cubic phase for all the samples, without any secondary phase (Fig. 1 and Fig. S2, ESI†). The crystallite size obtained by the Scherrer equation and estimated from the analysis of the TEM pictures were found in agreement (Table 1), suggesting the high crystallinity of the samples. TEM images confirm the spherical morphology and the low polydispersity of the particles (ESI,† Section S3; Table 1). It should be emphasized that the size is constant within experimental errors of different samples, allowing the investigation of magnetic properties beyond the effect of NPs’ size.40
m cubic phase for all the samples, without any secondary phase (Fig. 1 and Fig. S2, ESI†). The crystallite size obtained by the Scherrer equation and estimated from the analysis of the TEM pictures were found in agreement (Table 1), suggesting the high crystallinity of the samples. TEM images confirm the spherical morphology and the low polydispersity of the particles (ESI,† Section S3; Table 1). It should be emphasized that the size is constant within experimental errors of different samples, allowing the investigation of magnetic properties beyond the effect of NPs’ size.40
TGA was performed to determine the organic content (ESI,† Section S4) and the magnetization measurements were normalised considering only the inorganic content. The ICP analysis revealed an excess of iron with respect to the stoichiometric Co![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe 1
Fe 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio (Table 1 and ESI,† Section S5) expected for cobalt ferrite. This phenomenon was already observed for CoFe2O4 particles by Gyergyek et al.41 made with the same approach, putting forward the lack of Co2+ as a consequence of the higher stability of Co2+-oleate, compared to Fe3+-oleate, and attributed the iron excess to the presence of Fe2+. This agrees with other studies, that do not exclude the formation of Fe2+29,42. We left out the possibility that the Fe2+/3+ excess formed oxide impurities, as we did not identify any, neither structurally nor magnetically, as also observed by Mössbauer spectrometry. Note that, based on the mean value of isomer shift, the recorded spectra on all studied samples do not provide evidence for the presence of Fe2+ ions (Table S4 and Fig. S10, ESI†).
2 ratio (Table 1 and ESI,† Section S5) expected for cobalt ferrite. This phenomenon was already observed for CoFe2O4 particles by Gyergyek et al.41 made with the same approach, putting forward the lack of Co2+ as a consequence of the higher stability of Co2+-oleate, compared to Fe3+-oleate, and attributed the iron excess to the presence of Fe2+. This agrees with other studies, that do not exclude the formation of Fe2+29,42. We left out the possibility that the Fe2+/3+ excess formed oxide impurities, as we did not identify any, neither structurally nor magnetically, as also observed by Mössbauer spectrometry. Note that, based on the mean value of isomer shift, the recorded spectra on all studied samples do not provide evidence for the presence of Fe2+ ions (Table S4 and Fig. S10, ESI†).
The temperature dependence of magnetization recorded by ZFC/FC protocols (Fig. S6, ESI†) shows a clear dependence: the average blocking temperature and temperature of MZFC maximum (i.e., Tb and Tmax) decrease with an increase in Ni2+ and Zn2+ contents, suggesting a dominating effect of the magnetic anisotropy, even if an effect due to interparticle interactions can be present (ESI,† Section S6 and Table 2).11
| Sample | T b, K | T max, K | μ 0 H sw (5 K), T | M s (5 K), A m2 kg−1 | M s (300 K), A m2 kg−1 | M r /M s (5 K) | μ 0 H c (5 K), T | K a, 10−5 J m−3 |
|---|---|---|---|---|---|---|---|---|
| CoRef | 199(1) | 289(1) | 1.25(1) | 103(2) | 85(2) | 0.60(3) | 1.06(5) | 11 |
| Ni22 | 166(1) | 252(1) | 1.0(1) | 73(1) | 58(1) | 0.67(1) | 0.95(5) | 5.7 |
| Ni39 | 166(1) | 228(1) | 0.9(1) | 68(3) | 58(2) | 0.68(4) | 0.85(4) | 4.5 |
| Ni63 | 107(1) | 157(1) | 0.6(1) | 72(2) | 56(2) | 0.64(2) | 0.51(3) | 3.1 |
| Zn19 | 207(1) | 285(1) | 0.8(1) | 104(3) | 80(2) | 0.56(3) | 0.67(3) | 7.1 |
| Zn32 | 166(1) | 228(1) | 0.6(1) | 114(4) | 80(3) | 0.56(4) | 0.47(2) | 5.3 |
| Zn48 | 132(1) | 201(1) | 0.3(1) | 143(5) | 93(3) | 0.49(4) | 0.27(1) | 4.3 |
Magnetic anisotropy
The decrease in magnetic anisotropy is also confirmed by the shift in the maximum irreversible susceptibility obtained by the differentiated DCD curves at 5 K (χirr = dMDCD/dH) (Fig. 2), which is directly correlated with the distribution of coercive fields (i.e., switching fields distribution, SFD). All the SFDs have a single peak shape, indicating a homogeneous magnetization reversal. Both Ni2+ and Zn2+ have the same qualitative effect on the SFD, lowering their maximum position (μ0Hsw) as shown in Table 2. The effect is more marked for Zn2+, since twice more Ni2+ is needed to have μ0Hsw dropping to 0.6 T; the same applies to the width of the SFDs, showing that the substitution with Zn2+ narrows down the SFD more significantly than that with Ni2+. | ||
| Fig. 2 (a) and (b) DCD remanence plots and (c) and (d) switching field distributions (SFD) for the Zn and the Ni-series. | ||
Further evidence can be found in hysteresis loops at 5 K (Fig. 4), where the coercivity, μ0Hc, monotonically decreases as the Zn2+/Ni2+ content increases; the μ0Hc values of both series are similar to the corresponding μ0Hsw. (Table 2). An estimation of the NPs’ magnetic anisotropy was obtained by:43
 | (1) |
Spinel ferrites have a cubic magneto-crystalline anisotropy with an expected reduced remanent magnetization (Mr/Ms) of ∼ 0.83–0.87,46 but this feature is usually suppressed in small NPs by the surface and shape contributions, resulting in a uniaxial effective anisotropy; this is confirmed by the low Mr/Ms value of ∼0.5, characteristic for uniaxial anisotropy.40,42 In our case, the undoped cobalt ferrite sample CoRef possesses a Mr/Ms value of approximately 0.6, confirming the presence of competing uniaxial and cubic anisotropy contributions. Interestingly, the substitution with Ni2+ cations, with lower single-ion anisotropy, compared to Co2+ initially leads to an increase in Mr/Ms, while one would expect a reduction due to the decrease in a cubic magneto-crystalline term. This can be attributed to the change in cationic distribution. In fact, the inversion degree for nickel ferrite is expected to be higher than that for cobalt ferrite;13 that can result in an increase in cobalt occupying octahedral sites where it significantly contributes to anisotropy.47 Alternatively, Ni2+ cations may lower the surface anisotropy term, thereby reducing this source of uniaxial anisotropy. At the same time, as expected, the introduction of Zn2+ led to the formation of a pronounced uniaxial anisotropy, with Mr/Ms tending to be 0.5.42
Magnetic interparticle interactions
To study NPs’ magnetic interparticle interactions, normalized IRM and DCD magnetizations can be compared by means of the Kelly equation, providing the so-called δm-plot:48,49| δm = mDCD(H) − 1 + 2mIRM(H) | (2) |
A semi-quantitative estimation of the magnetic dipolar interactions can be obtained by calculating the dipolar energy.53 In general, a system of randomly distributed NPs with average magnetic moment μ and average separation d, the dipole–dipole interaction energy among particles can be expressed as follows:
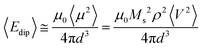 | (3) |
 | ||
| Fig. 3 (a) and (b) interaction δm plots of Ni-series and Zn-series, and (c) and (d) interaction dipolar energy values compared with δm profile depth. | ||
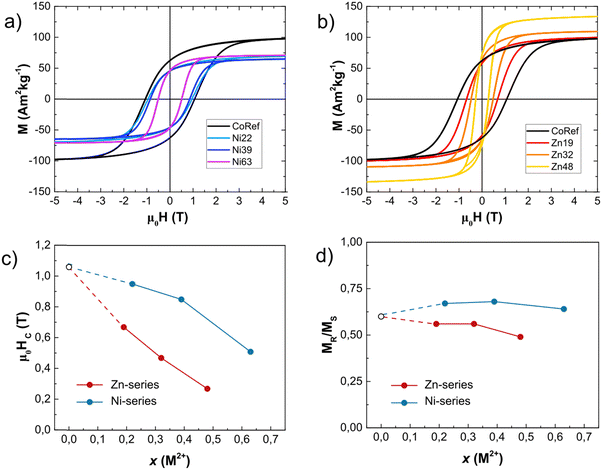 | ||
| Fig. 4 (a) and (b) 5 K isothermal magnetization plots for Ni and Zn-series; (c) coercivity and (d) reduced remanent magnetization (Mr/Ms) for all samples. | ||
Saturation magnetization
Finally, it is quite interesting to discuss the trend of Ms with respect to the chemical composition of the samples (ESI,† Section S7). In the case of the Ni-series, Ni2+ induces a steep decrease in Ms followed by an almost constant trend, leaving little room for property tuning (Fig. 4 and Table 2). The Ni2+ spin-only magnetic moment of 2μB is the lowest of all ions, and its selectivity drives it to Oh-sites, decreasing the term and explaining our observations. The moderate entity of the effect is in accordance with the literature.28,32,56,57
term and explaining our observations. The moderate entity of the effect is in accordance with the literature.28,32,56,57
Increasing Zn2+, instead, reveals a monotonic increase in Ms at 5 K, inducing an increase in Ms from ∼103 A m2 kg−1 for x = 0 to ∼143 A m2 kg−1 for x = 0.48 (Fig. 4 and Table 2). The Zn2+ diamagnetism and the selectivity for Td-sites27,58 make it decrease the term 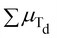 , unbalancing the sum of the moments and increasing saturation. However, the increase in saturation with Zn2+ content is limited to Zn2+ ∼ 0.5:26,42 due to its diamagnetic nature, it cannot participate in super-exchange interactions, interrupting the magnetic superexchange coupling and weakening the magnetic structure of the material. Above this threshold, the magnetic behaviour converges to that of ZnFe2O4,59,60 a normal antiferromagnetic spinel (TN = 10 K),13 and thus Ms decreases. Our results are in qualitative agreement with this explanation and with other results obtained by TD.26,42
, unbalancing the sum of the moments and increasing saturation. However, the increase in saturation with Zn2+ content is limited to Zn2+ ∼ 0.5:26,42 due to its diamagnetic nature, it cannot participate in super-exchange interactions, interrupting the magnetic superexchange coupling and weakening the magnetic structure of the material. Above this threshold, the magnetic behaviour converges to that of ZnFe2O4,59,60 a normal antiferromagnetic spinel (TN = 10 K),13 and thus Ms decreases. Our results are in qualitative agreement with this explanation and with other results obtained by TD.26,42
The Ms values can be estimated using the two-sublattice Néel model, considering the well-known ion site selectivity of Ni2+ for Oh-sites56 and of Zn2+ for Td-sites27 and the spin-only magnetic moment of our metal cations (Zn2+ = 0μB, Co2+ = 3μB, Ni2+ = 2μB, Fe3+ = 5μB).12 For both series, an equation was written to express Ms as a function of the stoichiometric coefficient of M2+ (x) and the one of Co2+ in Oh-sites (y, corresponding to δ). For the Ni-series, the expression of the Bohr magneton magnetization per formula unit is (ESI,† Section S7)
| μNifu(x,y) = 7 − 5x − 4y, | (4) |
| μZnfu(x,y) = 7 + 3x − 4y | (5) |
 | ||
| Fig. 5 (a) and (b) Low temperature magnetization maps calculated as a function of M2+ stoichiometric coefficient (x) and Co2+ inversion degree (y) for (a) Ni- and (b) Zn-series. Black dots represent the experimental saturations from hysteresis loops, while red dots represent Ms obtained from two additional samples with known composition and cationic distribution (Mössbauer spectroscopy data, see the ESI†). The black arrow indicates the verse of increasing magnetization. The (c) and (d) graphs compare the experimental and calculated magnetizations with respect to the composition for Ni- and Zn-series. Triangles indicate the maximal Ms value possible for two compositions with low Ms, as indicated on the map. | ||
Considering CoRef, cobalt ferrite is a partially inverted spinel, meaning that a fraction of Co2+ is still in Td-sites; far from the intention of giving an exact value of the cation distribution, the position of the point in the graph suggests y ∼ 0.66, which is close to literature values.13,16–18
The calculation explains a small change in magnetic saturation for the Ni-series after Ni22, with the points arranged between two iso-composition lines. The common Oh-site selectivity of Co2+ and Ni2+ implies that with increasing substitution, if Ni2+ simply replaces Co2+ at Oh sites, the magnetization will reduce slowly due to the small difference in spin-only magnetic moment between the two cations.
Turning now to the Zn series, Zn19 lies almost on the same iso-magnetization line of CoRef, thus suggesting an increase in the relative cobalt fraction in Oh-sites (y ∼ 0.8). This is consistent with the almost identical saturation of CoRef and Zn19, and it is in accordance with the fact that Zn2+ being Td-site selective, should occupy the fraction of Td-sites which would be filled by Co2+ in CoFe2O4. Zn32 and Zn48 experimental values are lower than the value predicted for their composition, lying on the composition limit line. This discrepancy may reflect spin canting, size effects, and a small Zn2+ quantity in Oh-sites. Compared to other synthetic methods,14,59–62 TD gives nanoparticles among those with the highest Ms values.63,64 The differences are certainly related to the cationic distribution,41 size distribution, spin canting and surface layer.65
To confirm the usefulness of the Ms(x,y) maps, the cationic distribution of samples of similar composition (Ni31 and Zn38) has been determined by Mössbauer spectrometry at 12 K and under an intense magnetic field of 8 T (ESI,† Section S8), yielding y = 0.54 and 0.62, respectively.
Combining x and y values yields Ms which is found to be close to the expected values (see ESI†). Yet, the obtained values are smaller, as mentioned earlier. This stems from structural features (defects, surface contributions) and the possible effect of the ligand on the magnetic moments on the surface.65
Furthermore, by examining Fig. S1 (ESI†), we note that only the samples obtained by this TD synthesis come close to the spin-only Ms, while other synthesis methods provide Ms much lower than any values predicted by the map, regardless of the particle size. As shown in Fig. S1 (ESI†), Ms depends greatly on the synthesis methods for a given x. Ms(x,y) maps may be used to give a quick graphical estimate of whether these differences stem from different δ and thus providing a simple way to compare synthetic methods.
Conclusions
The magnetic properties of two sets of Ni2+ and Zn2+ doped cobalt ferrite NPs with equal size of ∼9 nm were investigated to evaluate the influence of cation distribution over chemical composition on the saturation magnetization, magnetic anisotropy and interparticle interactions. Specifically, we observed up to 40% enhancement of saturation magnetization and decreased magnetic anisotropy in samples with greater Zn2+ content. The highest value of saturation magnetisation of 143 ± 5 A m2 kg−1 at 5 K, which is 40% higher than in the CoRef sample, was found for a sample with the composition Zn0.48Co0.26Fe2.26O4. In contrast, Ni2+ substitution resulted in a decrease in both magnetization by ∼30% and anisotropy by ∼70% for the higher concentration of nickel.A strong correlation was found between the results from the δm plot and the calculated dipolar energy. The obtained results suggest that Zn2+ substitution strongly affects the dipolar interparticle interaction intensity due to the increasing saturation magnetization and decreasing magnetocrystalline anisotropy.
Moreover, the inversion/doping content maps developed in this study provide a simple method to both visualize substitution impacts and predict Ms values from knowledge of only cation distributions or compositions. Our demonstration of accurate modelling of experimental data highlights the utility of these maps for the rational design of spinel ferrite nanoparticles tailored to further application needs.
Author contributions
The paper and ESI were written based on the contributions of all authors. P. M., D. P., F. C. and R. M. designed the experiments; R. M., A. O. and D. P. coordinated the data analysis and discussion. M. B. and P. M. synthesized the nanoparticles and characterized them by XRPD and magnetometry techniques. G. B. performed structural characterisation by TEM. N. Y. performed Mössbauer spectrometry. All authors contributed to the results discussion and revision of the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. M. and R. M. thank the Swedish Energy Agency (project number 46561-1) and the Swedish Research Council (VR). D. P. acknowledges project code PE0000021, Concession Decree No. 1561 of 11.10.2022 adopted by the “Ministero dell’Università e della Ricerca (MUR)”, according to attachment E of Decree No. 1561/2022, Project title “Network 4 Energy Sustainable Transition-NEST” in the frame of study of surface wettability properties, and REMAP, which has received funding from the European Commission PathFinder open programme under grant agreement No. 101046909.Notes and references
- N. Lee, D. Yoo, D. Ling, M. H. Cho, T. Hyeon and J. Cheon, Iron Oxide Based Nanoparticles for Multimodal Imaging and Magnetoresponsive Therapy, Chem. Rev., 2015, 115, 10637–10689 CrossRef CAS PubMed.
- J. Jang, H. Nah, J.-H. Lee, S. H. Moon, M. G. Kim and J. Cheon, Critical Enhancements of MRI Contrast and Hyperthermic Effects by Dopant-Controlled Magnetic Nanoparticles, Angew. Chem., Int. Ed., 2009, 48, 1234–1238 CrossRef CAS PubMed.
- S. H. Koenig and K. E. Kellar, Theory of 1/T 1 and 1/T 2 NMRD profiles of solutions of magnetic nanoparticles, Magn. Reson. Med., 1995, 34, 227–233 CrossRef CAS PubMed.
- M. Colombo, S. Carregal-Romero, M. F. Casula, L. Gutiérrez, M. P. Morales, I. B. Böhm, J. T. Heverhagen, D. Prosperi and W. J. Parak, Biological applications of magnetic nanoparticles, Chem. Soc. Rev., 2012, 41, 4306–4334 RSC.
- N. Sanpo, C. C. Berndt, C. Wen and J. Wang, Transition metal-substituted cobalt ferrite nanoparticles for biomedical applications, Acta Biomater., 2013, 9, 5830–5837 CrossRef CAS PubMed.
- P. Maltoni, T. Sarkar, G. Barucca, G. Varvaro, D. Peddis and R. Mathieu, Exploring the magnetic properties and magnetic coupling in SrFe12O19/Co1−xZnxFe2O4 nanocomposites, J. Magn. Magn. Mater., 2021, 535, 168095 CrossRef CAS.
- M. Estrader, A. López-Ortega, S. Estradé, I. V. Golosovsky, G. Salazar-Alvarez, M. Vasilakaki, K. N. Trohidou, M. Varela, D. C. Stanley, M. Sinko, M. J. Pechan, D. J. Keavney, F. Peiró, S. Suriñach, M. D. Baró and J. Nogués, Robust antiferromagnetic coupling in hard-soft bi-magnetic core/shell nanoparticles, Nat. Commun., 2013, 4, 2960 CrossRef CAS PubMed.
- P. Shyam, M. Mørch, A. Z. Eikeland, J. Ahlburg, A. Mamakhel, M. Saura-Múzquiz and M. Christensen, Combined characterization approaches to investigate magnetostructural effects in exchange-spring ferrite nanocomposite magnets, Mater. Chem. Front., 2022, 6, 2422–2437 RSC.
- B. Muzzi, M. Albino, M. Petrecca, C. Innocenti, C. de, J. Fernández, G. Bertoni, C. Marquina, M. R. Ibarra and C. Sangregorio, 3d Metal Doping of Core@Shell Wüstite@ferrite Nanoparticles as a Promising Route toward Room Temperature Exchange Bias Magnets, Small, 2022, 18, 1–11 CrossRef PubMed.
- R. Sharma, P. Thakur, P. Sharma and V. Sharma, Ferrimagnetic Ni2+ doped Mg-Zn spinel ferrite nanoparticles for high density information storage, J. Alloys Compd., 2017, 704, 7–17 CrossRef CAS.
- P. Maltoni, M. Baričić, G. Barucca, M. C. Spadaro, J. Arbiol, N. Yaacoub, D. Peddis and R. Mathieu, Tunable particle-agglomeration and magnetic coupling in bi-magnetic nanocomposites, Phys. Chem. Chem. Phys., 2023, 25, 27817–27828 RSC.
- B. D. Cullity and C. D. Graham, Introduction to Magnetic Materials, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2008 Search PubMed.
- F. G. da Silva, J. Depeyrot, A. F. C. Campos, R. Aquino, D. Fiorani and D. Peddis, Structural and Magnetic Properties of Spinel Ferrite Nanoparticles, J. Nanosci. Nanotechnol., 2019, 19, 4888–4902 CrossRef CAS PubMed.
- S. S. Jadhav, S. E. Shirsath, S. M. Patange and K. M. Jadhav, Effect of Zn substitution on magnetic properties of nanocrystalline cobalt ferrite, J. Appl. Phys., 2010, 108, 093920 CrossRef.
- A. Feirweather, F. F. Roberts and A. J. E. Welch, Ferrites, Rep. Prog. Phys., 1952, 15, 142–172 CrossRef.
- D. Carta, M. F. Casula, A. Falqui, D. Loche, G. Mountjoy, C. Sangregorio and A. Corrias, A Structural and Magnetic Investigation of the Inversion Degree in Ferrite Nanocrystals MFe2O4 (M = Mn, Co, Ni), J. Phys. Chem. C, 2009, 113, 8606–8615 CrossRef CAS.
- A. S. Vaingankar, B. V. Khasbardar and R. N. Patil, X-ray spectroscopic study of cobalt ferrite, J. Phys. F: Met. Phys., 1980, 10, 1615–1619 CrossRef CAS.
- D. Carta, G. Mountjoy, G. Navarra, M. F. Casula, D. Loche, S. Marras and A. Corrias, X-ray Absorption Investigation of the Formation of Cobalt Ferrite Nanoparticles in an Aerogel Silica Matrix, J. Phys. Chem. C, 2008, 112, 19791 CrossRef CAS.
- H. L. Andersen, M. Saura-Múzquiz, C. Granados-Miralles, E. Canévet, N. Lock and M. Christensen, Crystalline and magnetic structure-property relationship in spinel ferrite nanoparticles, Nanoscale, 2018, 10, 14902–14914 RSC.
- J. M. D. Coey, Magnetism and Magnetic Materials, Cambridge University Press, Cambridge, 2010 Search PubMed.
- S. Chikazumi and C. D. Graham, Magnetocrystalline anisotropy, Physics of Ferromagnetism, International series of monographs on physics, Oxford University Press, New York, 2nd edn, 1997, ch. 12, pp. 270–272 Search PubMed.
- G. Varvaro, A. Omelyanchik and D. Peddis, Tailored Functional Oxide Nanomaterials, Wiley, 2022, pp. 405–437 Search PubMed.
- G. F. Dionne, Magnetic Oxides, Springer US, Boston, MA, 2009, vol. 8 Search PubMed.
- K. R. Sanchez-Lievanos, J. L. Stair and K. E. Knowles, Cation Distribution in Spinel Ferrite Nanocrystals: Characterization, Impact on their Physical Properties, and Opportunities for Synthetic Control, Inorg. Chem., 2021, 60, 4291–4305 CrossRef CAS PubMed.
- D. Peddis, in Magnetic Nanoparticle Assemblies, ed. K. N. Trohidou, Pan Stanford, Singapore, 2014, vol. 7, pp. 159–198 Search PubMed.
- V. Mameli, A. Musinu, A. Ardu, G. Ennas, D. Peddis, D. Niznansky, C. Sangregorio, C. Innocenti, N. T. K. Thanh and C. Cannas, Studying the effect of Zn-substitution on the magnetic and hyperthermic properties of cobalt ferrite nanoparticles, Nanoscale, 2016, 8, 10124–10137 RSC.
- H. L. Andersen, C. Granados-Miralles, M. Saura-Múzquiz, M. Stingaciu, J. Larsen, F. Søndergaard-Pedersen, J. V. Ahlburg, L. Keller, C. Frandsen and M. Christensen, Enhanced intrinsic saturation magnetization of ZnxCo1−xFe2O4 nanocrystallites with metastable spinel inversion, Mater. Chem. Front., 2019, 3, 668–679 RSC.
- G. Muscas, N. Yaacoub, G. Concas, F. Sayed, R. Sayed Hassan, J. M. Greneche, C. Cannas, A. Musinu, V. Foglietti, S. Casciardi, C. Sangregorio and D. Peddis, Evolution of the magnetic structure with chemical composition in spinel iron oxide nanoparticles, Nanoscale, 2015, 7, 13576–13585 RSC.
- S. Sun, H. Zeng, D. B. Robinson, S. Raoux, P. M. Rice, S. X. Wang and G. Li, Monodisperse MFe2O4 (M = Fe, Co, Mn) Nanoparticles, J. Am. Chem. Soc., 2004, 126, 273–279 CrossRef CAS PubMed.
- U. B. Sontu, N. G. Rao, F. C. Chou and V. M. Ramana Reddy, Temperature dependent and applied field strength dependent magnetic study of cobalt nickel ferrite nano particles: Synthesized by an environmentally benign method, J. Magn. Magn. Mater., 2018, 452, 398–406 CrossRef CAS.
- N. B. Velhal, N. D. Patil, A. R. Shelke, N. G. Deshpande and V. R. Puri, Structural, dielectric and magnetic properties of nickel substituted cobalt ferrite nanoparticles: Effect of nickel concentration, AIP Adv., 2015, 5, 097166 CrossRef.
- T. Orlando, M. Albino, F. Orsini, C. Innocenti, M. Basini, P. Arosio, C. Sangregorio, M. Corti and A. Lascialfari, On the magnetic anisotropy and nuclear relaxivity effects of Co and Ni doping in iron oxide nanoparticles, J. Appl. Phys., 2016, 119, 134301 CrossRef.
- A. B. Nawale, N. S. Kanhe, S. A. Raut, S. V. Bhoraskar, A. K. Das and V. L. Mathe, Investigation of structural, optical and magnetic properties of thermal plasma synthesized Ni-Co spinel ferrite nanoparticles, Ceram. Int., 2017, 43, 6637–6647 CrossRef CAS.
- G. Datt, M. Sen Bishwas, M. Manivel Raja and A. C. Abhyankar, Observation of magnetic anomalies in one-step solvothermally synthesized nickel-cobalt ferrite nanoparticles, Nanoscale, 2016, 8, 5200–5213 RSC.
- J. I. Langford and A. J. C. Wilson, Scherrer after sixty years: A survey and some new results in the determination of crystallite size, J. Appl. Crystallogr., 2016, 11, 1536–1545 Search PubMed.
- A. H. Morrish, The Physical Principles of Magnetism, IEEE Press, Piscataway, 1965, vol. 1 Search PubMed.
- G. Concas, F. Congiu, G. Muscas and D. Peddis, Determination of Blocking Temperature in Magnetization and Mössbauer Time Scale: A Functional Form Approach, J. Phys. Chem. C, 2017, 121, 16541–16548 CrossRef CAS.
- D. Peddis, P. E. Jönsson, S. Laureti and G. Varvaro, in Frontiers of Nanoscience, ed. C. Binns, Elsevier B.V, Oxford, UK, 2014, vol. 6, pp. 129–188 Search PubMed.
- E. P. Wohlfarth, Relations between Different Modes of Acquisition of the Remanent Magnetization of Ferromagnetic Particles, J. Appl. Phys., 1958, 29, 595–596 CrossRef.
- D. Peddis, C. Cannas, A. Musinu, A. Ardu, F. Orru, D. Fiorani, S. Laureti, D. Rinaldi, G. Muscas, G. Concas, G. Piccaluga, F. Orrù, D. Fiorani, S. Laureti, D. Rinaldi, G. Muscas, G. Concas and G. Piccaluga, Beyond the Effect of Particle Size: Influence of CoFe2O4 Nanoparticle Arrangements on Magnetic Properties, Chem. Mater., 2013, 25, 2005–2013 CrossRef CAS.
- S. Gyergyek, D. Makovec, A. Kodre, I. Arčon, M. Jagodič and M. Drofenik, Influence of synthesis method on structural and magnetic properties of cobalt ferrite nanoparticles, J. Nanopart. Res., 2010, 12, 1263–1273 CrossRef CAS.
- M. Albino, E. Fantechi, C. Innocenti, A. López-Ortega, V. Bonanni, G. Campo, F. Pineider, M. Gurioli, P. Arosio, T. Orlando, G. Bertoni, C. de Julián Fernández, A. Lascialfari and C. Sangregorio, Role of Zn2+ Substitution on the Magnetic, Hyperthermic, and Relaxometric Properties of Cobalt Ferrite Nanoparticles, J. Phys. Chem. C, 2019, 123, 6148–6157 CrossRef CAS.
- S. Mørup, M. F. Hansen and C. Fradsen, Magnetic Nanoparticles, Amsterdam, 2011 Search PubMed.
- R. H. Kodama, A. E. Berkowitz, E. J. McNiff and S. Foner, Surface spin disorder in ferrite nanoparticles, Phys. Rev. Lett., 1996, 77, 394–397 CrossRef CAS PubMed.
- D. Peddis, F. Orrù, A. Ardu, C. Cannas, A. Musinu and G. Piccaluga, Interparticle Interactions and Magnetic Anisotropy in Cobalt Ferrite Nanoparticles: Influence of Molecular Coating, Chem. Mater., 2012, 24, 1062–1071 CrossRef CAS.
- S. E. Peschany and N. A. Usov, Theoretical hysteresis loops for single-domain particles with cubic anisotropy, J. Magn. Magn. Mater., 1997, 174, 247–260 CrossRef.
- M. Tachiki, Origin of the Magnetic Anisotropy Energy of Cobalt Ferrite, Prog. Theor. Phys., 1960, 23, 1055–1072 CrossRef CAS.
- P. E. Kelly, K. O’Grady, P. I. Mayo and R. W. Chantrell, Switching mechanisms in cobalt-phosphorus thin films, IEEE Trans. Magn., 1989, 25, 3881–3883 CrossRef CAS.
- J. García-Otero, M. Porto and J. Rivas, Henkel plots of single-domain ferromagnetic particles, J. Appl. Phys., 2000, 87, 7376–7381 CrossRef.
- C. Binns, Nanomagnetism: Fundamentals and Applications, Elsevier, 2014 Search PubMed.
- J. A. De Toro, M. Vasilakaki, S. S. Lee, M. S. Andersson, P. S. Normile, N. Yaacoub, P. Murray, E. H. Sánchez, P. Muñiz, D. Peddis, R. Mathieu, K. Liu, J. Geshev, K. N. Trohidou and J. Nogués, Remanence Plots as a Probe of Spin Disorder in Magnetic Nanoparticles, Chem. Mater., 2017, 29, 8258–8268 CrossRef CAS.
- A. Omelyanchik, S. Villa, M. Vasilakaki, G. Singh, A. M. Ferretti, A. Ponti, F. Canepa, G. Margaris, K. N. Trohidou and D. Peddis, Interplay between inter- and intraparticle interactions in bi-magnetic core/shell nanoparticles, Nanoscale Adv., 2021, 3, 6912–6924 RSC.
- A. V. Ambarov, V. S. Zverev and E. A. Elfimova, Influence of field amplitude and dipolar interactions on the dynamic response of immobilized magnetic nanoparticles: Perpendicular mutual alignment of an alternating magnetic field and the easy axes, Phys. Rev. E, 2023, 107, 24601 CrossRef CAS PubMed.
- G. Muscas, M. Cobianchi, A. Lascialfari, C. Cannas, A. Musinu, A. Omelyanchik, V. Rodionova, D. Fiorani, V. Mameli and D. Peddis, Magnetic Interactions Versus Magnetic Anisotropy in Spinel Ferrite Nanoparticles, IEEE Magn. Lett., 2019, 10, 1–5 Search PubMed.
- E. H. Sánchez, M. Vasilakaki, S. S. Lee, P. S. Normile, M. S. Andersson, R. Mathieu, A. López-Ortega, B. P. Pichon, D. Peddis, C. Binns, P. Nordblad, K. Trohidou, J. Nogués and J. A. De Toro, Crossover From Individual to Collective Magnetism in Dense Nanoparticle Systems: Local Anisotropy Versus Dipolar Interactions, Small, 2022, 18, 2106762 CrossRef PubMed.
- C. Yang, Y. Hu, X. Li, J. Li, L. Wang and H. Li, Tuning of magnetic properties and hyperfine interaction by the substitution of Ni2+ for cobalt ferrite nanoparticles, J. Mater. Sci.: Mater. Electron., 2019, 30, 19647–19653 CrossRef CAS.
- A. Omelyanchik, G. Singh, M. Volochaev, A. Sokolov, V. Rodionova and D. Peddis, Tunable magnetic properties of Ni-doped CoFe2O4 nanoparticles prepared by the sol–gel citrate self-combustion method, J. Magn. Magn. Mater., 2019, 476, 387–391 CrossRef CAS.
- S. Amiri and H. Shokrollahi, The role of cobalt ferrite magnetic nanoparticles in medical science, Mater. Sci. Eng., C, 2013, 33, 1–8 CrossRef CAS PubMed.
- G. Barrera, M. Coisson, F. Celegato, S. Raghuvanshi, F. Mazaleyrat, S. N. Kane and P. Tiberto, Cation distribution effect on static and dynamic magnetic properties of Co1-xZnxFe2O4 ferrite powders, J. Magn. Magn. Mater., 2018, 456, 372–380 CrossRef CAS.
- A. Omelyanchik, K. Levada, S. Pshenichnikov, M. Abdolrahim, M. Baricic, A. Kapitunova, A. Galieva, S. Sukhikh, L. Astakhova, S. Antipov, B. Fabiano, D. Peddis and V. Rodionova, Green Synthesis of Co-Zn Spinel Ferrite Nanoparticles: Magnetic and Intrinsic Antimicrobial Properties, Materials, 2020, 13, 5014 CrossRef CAS PubMed.
- D. D. Andhare, S. R. Patade, J. S. Kounsalye and K. M. Jadhav, Effect of Zn doping on structural, magnetic and optical properties of cobalt ferrite nanoparticles synthesized via. Co-precipitation method, Phys. B, 2020, 583, 412051 CrossRef CAS.
- M. Stefanescu, M. Bozdog, C. Muntean, O. Stefanescu and T. Vlase, Synthesis and magnetic properties of Co1−xZnxFe2O4 (x = 0 ÷ 1) nanopowders by thermal decomposition of Co(II), Zn(II) and Fe(III) carboxylates, J. Magn. Magn. Mater., 2015, 393, 92–98 CrossRef CAS.
- G. Muscas, S. Jovanović, M. Vukomanović, M. Spreitzer and D. Peddis, Zn-doped cobalt ferrite: Tuning the interactions by chemical composition, J. Alloys Compd., 2019, 796, 203–209 CrossRef CAS.
- R. Topkaya, A. Baykal and A. Demir, Yafet–Kittel-type magnetic order in Zn-substituted cobalt ferrite nanoparticles with uniaxial anisotropy, J. Nanopart. Res., 2013, 15, 1359 CrossRef.
- C. R. Vestal and Z. J. Zhang, Effects of Surface Coordination Chemistry on the Magnetic Properties of MnFe2O4 Spinel Ferrite Nanoparticles, J. Am. Chem. Soc., 2003, 125, 9828–9833 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06029b |
| ‡ Present affiliations: Laboratoire Interfaces Traitements Organisation et Dynamique des Systèmes, Université Paris Cité, CNRS UMR-7886, Rue Jean Antoine de Baïf, 75013 Paris, France and Dipartimento di Scienze, Università degli Studi Roma TRE, Via della Vasca Navale, 84-00146 Roma, Italy. |
| This journal is © the Owner Societies 2024 |