Multilevel quantum mechanical calculations show the role of promoter molecules in the dehydration of methanol to dimethyl ether in H-ZSM-5

Abstract

Methyl carboxylate esters promote the formation of dimethyl ether (DME) from the dehydration of methanol in H-ZSM-5 zeolite. We employ a multilevel quantum method to explore the possible associative and dissociative mechanisms in the presence, and absence, of six methyl ester promoters. This hybrid method combines density functional theory, with dispersion corrections (DFT-D3), for the full periodic system, with second-order Møller–Plesset perturbation theory (MP2) for small clusters representing the reaction site, and coupled cluster with single, double, and perturbative triple substitution (CCSD(T)) for the reacting molecules. The calculated adsorption enthalpy of methanol, and reaction enthalpies of the dehydration of methanol to DME within H-ZSM-5, agree with experiment to within chemical accuracy (∼4 kJ mol⁻¹). For the promoters, a reaction pathway via an associative mechanism gives lower overall reaction enthalpies and barriers compared to the reaction with methanol only. Each stage of this mechanism is explored and related to experimental data. We provide evidence that suggests the promoter's adsorption to the Brønsted acid site is the most important factor dictating its efficiency.

---

Introduction

Sustainable materials providing alternative, lower energy, greener routes to useful hydrocarbons have an increasingly important role to play in reducing emissions of carbon dioxide. There is recent significant interest in dimethyl ether (DME) due to its potential as a renewable liquefied petroleum gas (LPG) replacement.^1–4 It can be made via green methanol; which can be produced from many sources of carbon, including carbon dioxide.^1,5–9 Relatively high reaction temperatures (275–350 °C) are required to effectively produce DME commercially using solid catalysts. However, zeolites offer a lower temperature route (110–150 °C) as they are very active and selective for making DME under these conditions where methanol-to-gasoline (MTG) and methanol-to-olefin (MTO) chemistry can be largely avoided.

Zeolites, crystalline aluminosilicate porous materials, are among the most commercially important classes of heterogenous catalysts, with large-scale applications in the petrochemical industry and environmental catalysis.^10,11 They are formed from corner-sharing (SiO₄) and (AlO₄)⁻ tetrahedral units, assembled into ordered porous frameworks with large internal surface areas. Interactions at these internal interfaces confine and stabilise reactants and transition states; this well-known confinement effect is a key factor in zeolite catalysis.^12–14 Acidic protons at catalytic centres, the Brønsted acid sites (BAS), i.e. bridging Si(OH)Al hydroxyl groups, initiate many well-established reactions in zeolites. The acid-catalysed dehydration of methanol produces dimethyl ether (DME), a commercially important intermediate in MTG and MTO chemistry.^15–23

Two distinct mechanisms have been proposed for the dehydration of methanol to DME, associative (concerted) or dissociative (stepwise), as illustrated in Scheme 1 and debated in the literature.^24–28 Both mechanisms involve the adsorption of one methanol molecule at a BAS. The dissociative mechanism involves the formation of a surface methoxy species [Si(OMe)Al], followed by reaction with a second methanol molecule to form DME and water. In contrast, in the associative mechanism, a second methanol molecular is adsorbed adjacent to the BAS and a dimer species is formed before conversion to DME and water. A recent combined kinetic data²⁴ and density functional theory (DFT) study²⁵ indicates that the associative mechanism dominates^26,27 except at low methanol pressures.^28,29

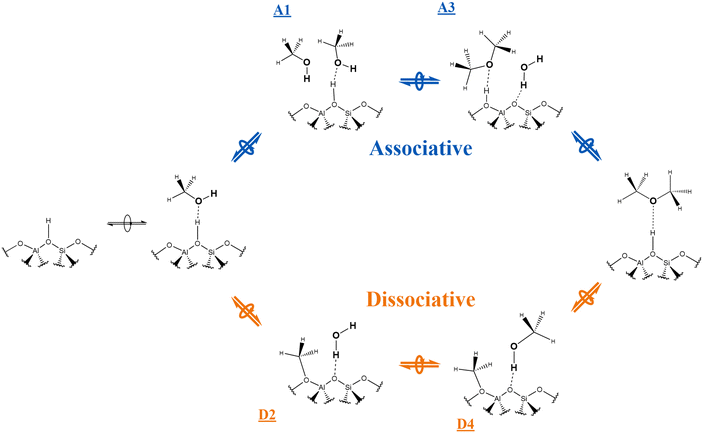Scheme 1 The associative and dissociative mechanisms, top path and bottom path, respectively, for the dehydration of methanol to DME reaction. Labels A̲1̲, A̲3̲, D̲2̲, and D̲4̲ refer to structures in Fig. 3 and 4 (energy minima).

Recently, it has been shown^30–32 that methyl esters (Fig. 1) can act as potent promoters for the low-temperature (110–150 °C) dehydration of methanol to DME. Preliminary kinetic and spectroscopic studies suggest a mechanism in which the promoters react with methanol to form DME via an associative mechanism,^30,32,33 except possibly for methyl formate which partially dissociates into formic acid and a surface methoxy species.³² FT-IR studies show that these promoters rapidly adsorb at BASs through the carbonyl group, binding more strongly than methanol;³² while both species are adsorbed to the BAS through hydrogen bonds, the promoters are further stabilised by van der Waals interactions with the pore walls. As the chain length increases, so too does this increased stabilisation. The shortest alkyl chain length promoter, methyl formate, is the only promoter for which surface methoxy species are observed experimentally, in low-temperature NMR studies by Yang et al.³² These findings suggest that the promotion of DME formation does not necessarily require promoter dissociation into methoxy species. Instead, a bimolecular associative mechanism, which we outline later, has been suggested by some of us to dominate DME formation.³⁰ We use multi-level quantum mechanical methods to explore more fully the proposed reaction pathway and mechanism.

Fig. 1 Impact of co-feeding a series of linear methyl ester promoters on the formation of DME from methanol dehydration, from left to right with colours indicating different promoters; none (methanol only); methyl formate; methyl acetate; methyl propionate; methyl n-butyrate; methyl n-pentanoate; and methyl n-hexanoate. The units g kg⁻¹ h⁻¹ refer to the grams of product produced from the kilograms of catalyst per hour. Conditions: 423 K, methanol WHSV 17.1 h⁻¹, methanol partial pressure 110 kPa, methyl ester partial pressure 5.5 kPa. STY refers to the space-time-yield, i.e., the efficiency of a chemical reaction.

An atomistic understanding of catalyst performance requires comprehensive information regarding active sites and elementary reaction steps. This is challenging through experiment alone as complex reaction pathways with multiple chemical transformations are likely. Application of computational methods is constrained by the size and complexity of the systems and the accuracy of the methods themselves presents challenges. While DFT is a powerful tool, it is not a systematically improvable method, and its predictions vary in accuracy depending on the approximate treatment of correlation and dispersion.^34–39 Higher-level methods, such as MP2, can be employed to combat these deficiencies, but at a computational cost; calculations on systems as large as the zeolites in this paper are unfeasible. Furthermore, the “Gold-standard” in quantum chemistry, coupled cluster with single, double, and perturbative triple excitations (CCSD(T)), provides accurate bond energies and molecular properties^40–45 but is limited to small molecules and clusters and cannot be applied to periodic systems such as zeolites.³⁴ Thus, quantum embedding (QE) methods have been developed which divide up a system into smaller subsystems that can be modelled at different levels of theory.⁴⁶ Here, the different subsystems consist of the periodic zeolite framework, the reaction site, and the reacting molecules.

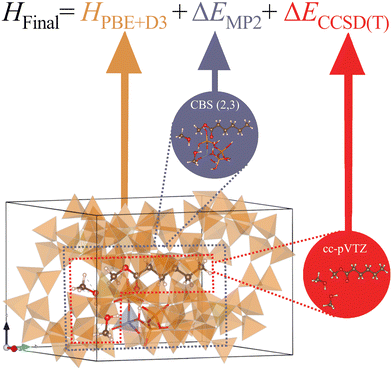
In this work, we apply a hybrid multilevel quantum method to investigate the conversion of methanol to DME in H-ZSM-5 with and without the addition of six promoter molecules. We model the zeolite framework with periodic DFT-D3, the reaction site with MP2, and the reacting molecules with CCSD(T). Specifically, we identify the key elementary steps and analyse how this leads to increased methanol conversion to DME.

Methodology

Zeolite structure and periodic DFT calculations

The MFI structure, shown on the left in Fig. 2, was obtained from the database of the international zeolite association (IZA),⁴⁷ with orthorhombic unit cell parameters a = 20.09 Å, b = 19.74 Å and c = 13.14 Å. There are twelve symmetry-inequivalent T sites, i.e., metal (Al/Si) atom positions, in the unit cell. The BAS incorporated is the so-called Al1–O1(H)–Si5 site:^48–51 an aluminium occupies the T1 position, silicon T5, and a proton is attached to the oxygen at the O1 position which links the Al to a neighbouring Si, this is consistent with previous work from collaborators.³³ This BAS lies at the intersection of the straight and zig-zag pores, and was chosen as it maximises the dispersion interactions between the promoter molecule and the pore wall.⁵²

Fig. 2 The levels of QM theory applied to each system. Bottom left: System used in the periodic plane wave DFT calculations consisting of a unit cell of H-ZSM-5 zeolite structure, a promoter, and two methanol molecules. The polyhedra represent the periodic zeolite, the stick model shows the cluster used in later calculations and the ball-and-stick representations show the reacting molecules. Bottom middle: System used to obtain the MP2 corrections. The ball-and-stick representation shows the reacting molecules and the stick model represents the 4T cluster model. Bottom right: The system chosen to obtain the CCSD(T) corrections. The ball-and-stick model represents the reacting atoms only. Colour key: orange tetrahedra = silicon; red = oxygen; purple = aluminium; brown = carbon; pink = hydrogen. The arrows illustrate how the levels of theory applied to each system contribute to the overall final energy shown in the equation.

Periodic plane-wave density functional theory (DFT) calculations were performed on one unit cell of approximately 300 atoms, as implemented in the Vienna ab initio simulation package (VASP) version 5.4.4,^53–56 with PAW pseudopotentials⁵⁷ and the PBE exchange–correlation functional.⁵⁸ Dispersion energies were calculated with Grimme's D3 dispersion term including Becke and Johnson damping (D3BJ).^59,60 The plane-wave basis set kinetic energy cutoff was 520 eV and the SCF energy convergence criterion 10⁻⁶ eV. Structural optimisations of reactants and products were considered converged when the maximum atomic force is less than 0.05 eV Å⁻¹.

VASPKIT⁶¹ was used to compute vibrational frequencies (within the harmonic approximation) to calculate the zero-point vibrational energies, ΔE_ZPVE, and vibrational contributions to thermal energies⁶² at 423 K, ΔE_therm. The enthalpy at 423 K is given by:

H_PBE+D3 = ΔE_elec + ΔE_ZPVE + ΔE_therm + pΔV, (1)

where ΔE_elec is the electronic energy, p the pressure, and ΔV the volume change. For the reaction studied here, the pΔV term equals −RT for adsorption enthalpies and zero for intrinsic enthalpy barriers.

Zeolites are flexible materials. Metastable states, involving multiple local minima separated by low barriers in the energy landscape, are associated with minor structural changes. The associated energy change to these structural rearrangements has been calculated with periodic DFT and found to be as large as 156 kJ mol⁻¹ for the functional and system size used in this work.⁶³ To avoid problems associated with structural reorganisation,⁶³ we optimised the zeolite framework using the sequential three-step geometry optimisation methodology of Hoffman et al.:⁶³ (i) initial DFT optimisation of both unit cell parameters and all basis atom positions of the bare zeolite obtained from the IZA, (ii) a second full optimisation with methyl n-hexanoate, the largest promoter, as an absorbate, and (iii) a final full optimisation of the zeolite after removal of the absorbate. After the methyl n-hexanoate was removed, the zeolite did not optimise back to the original structure, but to a restructured framework calculated to be 39 kJ mol⁻¹ lower in energy. The reduction in energy associated with the restructuring is consistent with the findings of Hoffman et al.,⁶³ and this structure was used in all subsequent calculations.

To sample the reaction paths, the nudged elastic band (NEB)^64,65 method with a minimum of four intermediate images was used with a force convergence criterion of 0.2 eV Å⁻¹. The climbing image algorithm⁶⁶ was applied to identify transition states and convergence set to 0.1 eV Å⁻¹. All minima and transition state structures were confirmed by their vibrational frequencies. During optimisation of the transition states, the reacting molecules and four TO₄ tetrahedra, i.e., the BAS and neighbouring framework atoms, were allowed to relax, while the rest of the zeolite framework was frozen.

Molecular clusters

For the systematically improvable calculations at higher levels of theory, we use Gaussian⁶⁷ on the systems shown in the middle and right of Fig. 2. We use the hierarchical approach employed by Sauer et al.^{41–44,52,68–81} as shown in eqn (2):

H_Final = H_PBE+D3 + ΔE_MP2 + ΔE_CCSD(T). (2)

This involves a scheme of wavefunction-based electron correlation method corrections, which can be capable of obtaining reaction energies and barriers to within chemical accuracy (∼4 kJ mol⁻¹), applied to the periodic DFT calculations.

The system used for the Møller–Plesset perturbation theory (MP2) corrections is shown in the top middle of Fig. 2 and highlighted in purple. It consists of a promoter, two methanol molecules, and a 4T cluster model of the zeolite. The cluster model extracted from the periodic calculations creates dangling bonds which we saturate with hydrogen atoms with O–H bond lengths of 95.3 pm and the same angle as the previous bond (O–Si). Single point energies were obtained at both lower and higher levels of theory, and the difference between the energies is the correction applied. We employ DFT+D3 with the Def2-TZVP basis set for the lower level of theory. The higher level of theory consisted of MP2 energies extrapolated to the complete basis set (CBS) limit using a two-point extrapolation scheme, with cc-pVXZ basis sets (X = D,T).^82,83 Previous work by Sauer et al.⁷¹ has compared different extrapolation schemes with varying cardinal numbers and found CBS/CPC(3,4) yielded energy barriers and adsorption energies within 1 kJ mol⁻¹ of their best estimate for the complete basis set limit values. However, due to the number of calculations needed and the associated computational cost, we employ CBS/CPC(2,3) which yields results very close to the CBS limit. These corrections aim to combat the key deficiency of periodic DFT calculations, the self-interaction error (SIE).^{68,71,72,84,85} Uncorrected, SIE results in the systematic underprediction of energy barriers, particularly for charge transfer reactions, such as the proton transfer steps important in zeolite catalysis.^71,72,84 For example, Goncalves et al. found that zwitterion intermediates in the MTH reaction, formed by protonation steps at active sites,⁸⁶ were too low in energy by as much as 40 kJ mol⁻¹. For the CCSD(T) corrections we extract the reacting atoms only shown on the right of Fig. 2 and highlighted red, i.e., the two methanol molecules, the BAS hydrogen, and the promoter. Single-point energy calculations were performed using the cc-pVTZ basis set^87,88 at the MP2 and CCSD(T) levels of theory, where the difference is the correction applied. Of course, such models only take into consideration a portion of the zeolite framework and there are associated complications due to edge effects and lack of proper account of the environment. The counterpoise method was used in both corrections to account for basis set superposition error.⁸⁹

Reaction mechanisms

Within the zeolite, complex reaction mixtures form containing different ratios of methanol, water, DME, and promoters. Experimental kinetic data show dependence on methanol and methyl n-hexanoate partial pressure, with the reaction becoming zero order in methanol at a methanol partial pressure of 1.1 bar and a methyl n-hexanoate partial pressure of 0.11 bar.³⁰ Overall, these kinetic studies reveal the dependence of both methanol and methyl ester partial pressures on the yield of DME. This behaviour is consistent with a bimolecular reaction mechanism involving both methanol and methyl ester adsorbed at the catalyst's active site. Spectroscopic analysis demonstrates ester molecules interact with BAS via the carbonyl group.^30,90 Furthermore, recent FT-IR studies involving one of us show that methyl n-hexanoate is rapidly adsorbed at BAS,³² binds more strongly than methanol, and remains adsorbed at the BAS during the reaction. Thus, instead of methanol molecules reacting to form DME at a BAS, the promoter is adsorbed at a BAS. The conformation adopted by the adsorbed promoter involves hydrogen bonding between the carbonyl group and the BAS, with the alkyl chain on the carboxylate carbon pointing along the straight channel,³⁰ as shown in Fig. 2, and the methoxy group of the promoter sitting in a pore intersection. Previous experimental work of some of us has suggested the dehydration of methanol to form dimethyl ether proceeds via an extended catalytic cycle in the presence of a promoter.³⁰

There are two possible mechanisms. In the first, the associative mechanism, protonation of the promoter is followed by nucleophilic attack of methanol on the methoxy group, forming DME. A subsequent reaction involving methanol reforms the promoter. The full associative mechanism is illustrated in Scheme 2.

Scheme 2 Reaction scheme for the associative mechanism of the formation of DME in H-ZSM-5 with methanol(s) and a promoter. The promoter is coloured purple and the reaction steps labelled in orange are those listed in Table 1.

In the alternative dissociative mechanism, the promoter first rotates 90° about the carbonyl bond, allowing the formation of a surface methoxy species. Another methanol molecule reacts with this species forming DME and water. NMR studies by some of us observed that methyl formate more easily dissociated to form surface methoxy species compared to the longer alkyl chain promoters. Therefore, a bimolecular associative mechanism plays an important role in the methyl ester promoted methanol dehydration to DME. However, at low methanol coverages, and for the methyl formate promoted reaction, we do not rule out the dissociative mechanism.³²

All elementary steps for both associative and dissociative mechanisms in the presence and absence of promoters are listed in Table 1. It is worth noting the competing nature of the mechanisms, i.e., the surface methoxy species formed in the dissociative mechanism deactivates that catalytic site until a second methanol molecule reacts with the surface methoxy species forming DME.

Table 1 Elementary steps for the associative and dissociative mechanism for the methanol dehydration to DME with and without a promoter, lines between rows separate different mechanisms. Steps M1 and P1 involve the adsorption to the BAS of methanol and a promoter, respectively. The dissociative and associative mechanisms involving methanol only involve steps M2–M3 and M4–M5, respectively. The dissociative mechanism involving a promoter is steps P2–M3, it is worth noting step M3 is the same with and without a promoter in the dissociative mechanism. The associative mechanism involving the promoter is seen in steps P3–P4

Adsorption	CH3OH(g) + H–Z ↔ CH3OH⋯H–Z	(M1)
	ROOCH3(g) + H–Z + 2CH3OH ↔ ROOCH3⋯H–Z + 2CH3OH	(P1)
Dissociative mechanism (methanol)	CH3OH⋯H–Z ↔ H2O + CH3–Z	(M2)
	CH3OH(g) + CH3–Z ↔ CH3OCH3⋯H–Z	(M3)
Associative mechanism (methanol)	CH3OH(g) + CH3OH⋯H–Z ↔ CH3OH⋯CH3OH⋯H–Z	(M4)
	CH3OH⋯CH3OH⋯H–Z ↔ CH3OCH3⋯H2O⋯H–Z	(M5)
Dissociative mechanism (promoter)	ROOCH3⋯H–Z ↔ ROOH + CH3–Z	(P2)
	CH3OH(g) + CH3–Z ↔ CH3OCH3⋯H–Z	(M3)
Associative mechanism (promoter)	CH3OH⋯CH3OH⋯ROOCH3⋯H–Z ↔ CH3OH⋯CH3OCH3⋯ROOH⋯Z–H	(P3)
	CH3OH⋯CH3OH⋯ROOH⋯Z–H ↔ ROOCH3⋯H–Z⋯CH3OH⋯H2O	(P4)

---

The full description of each mechanism requires the localization of stationary points on the potential energy surface. The adsorption enthalpy of a promoter molecule is given by:

H_ads = H_R-a − H_R (4)

where H_R is the enthalpy of the reactants (unloaded zeolite plus methanol molecules and promoter molecules in the gas phase) and H_R-a is the enthalpy of the adsorbed complex. Intrinsic enthalpy barriers are defined by:

H^‡_intr = H_TS − H_R-a (5)

where H_TS is the enthalpy of the transition state.

Results and discussion

Methanol dehydration to dimethyl ether

The calculated energetics and full reaction pathways for both the associative and dissociative mechanisms for the dehydration of methanol to DME in the absence of promoters are illustrated in Fig. 3. The structures involved in each pathway are displayed in Fig. 4. The calculated reaction enthalpy is −28 kJ mol⁻¹.

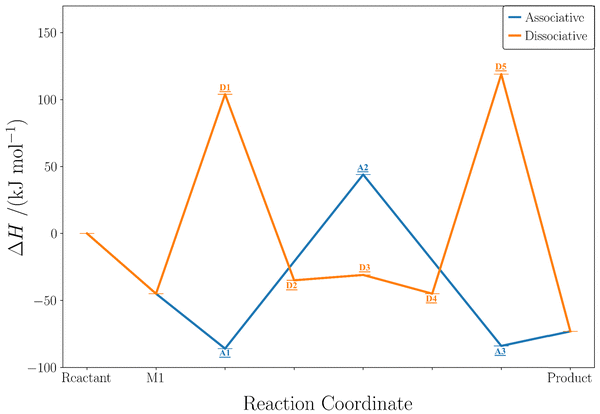Fig. 3 Reaction coordinate diagram showing the enthalpies (ΔH; kJ mol⁻¹) calculated with the hybrid QM method, for the dehydration of methanol to DME in the competing associative and dissociative mechanisms. Since the reaction pathway differs for each mechanism only Reactant, M1, and Product are labelled on the x-axis, axis and individual labels can be found on the diagram. Labels refer to reaction coordinate structures in Fig. 4.

Fig. 4 Structures involved in the reaction coordinate for each mechanism, labels in each box refer to their corresponding enthalpy in Fig. 3, A1, A3, D2, and D4 are minima shown also in Scheme 1, the others are transition states. Colour key for boxes: blue = associative; orange = dissociative. Colour key for structures: red = oxygen; brown= carbon; pink = hydrogen. Structures made using VESTA.⁹¹

In both mechanisms, the first stage involves the adsorption of a methanol molecule to the BAS with an enthalpy of −45 kJ mol⁻¹. This value is ∼40 kJ mol⁻¹ less negative than others have reported in the literature using similar methodologies;^{44,84,92–94} this is a consequence of taking account of the structural rearrangement discussed above and following the methodology of Hoffman et al.⁶³ Our zeolite framework is 39 kJ mol⁻¹ lower in energy compared to those typically used in the earlier literature. In the associative mechanism, a methanol dimer is formed at the BAS with an enthalpy of −86 kJ mol⁻¹. The rate-determining step—in the associative mechanism—involves DME formation from the protonated dimer intermediate with an intrinsic barrier of 130 kJ mol⁻¹. After desorption of the water by-product, the overall reaction enthalpy is −28 kJ mol⁻¹ and the formation enthalpy is −73 kJ mol⁻¹. In the dissociative mechanism, methylation of the zeolite surface takes place. The barrier height is 149 kJ mol⁻¹ and the reaction enthalpy 10 kJ mol⁻¹. Subsequently, water desorbs and a new methanol molecule is adsorbed. The final step is the methylation of methanol forming DME with a barrier of 164 kJ mol⁻¹. Our barrier for the associative mechanism is lower than those in the dissociative mechanism.

Our calculated intrinsic barriers using PBE+D3 alone give similar results to those calculated in the literature.^94,95 For example, using PBE+D3 we calculate an intrinsic barrier of 128 kJ mol⁻¹ for the formation of a surface methoxy species, Smith et al. calculates an intrinsic barrier of 143 kJ mol⁻¹,⁹⁵ whilst Kilburn et al. calculates an intrinsic barrier of 119 kJ mol⁻¹.⁹⁶

Di Iorio et al. have investigated the same dehydration reaction in a different zeolite,²⁵ CHA. They report results for mechanisms involving an S_N2 like step involving concerted backside attack. We have also modelled the associative and dissociative mechanisms in ZSM-5 with this geometry. The results can be found in the ESI.† The calculated intrinsic enthalpy barriers for the formation of the surface methoxy species in the dissociative and associative mechanisms are 154 kJ mol⁻¹ and 214 kJ mol⁻¹ respectively, values considerably higher than those for our proposed mechanisms. The structures for the transition states we propose above are similar to those reported for ZSM-5 by Nastase et al.⁹⁷ on the basis of QM/MM calculations.

Tables 2 and 3 show the importance of our hybrid multilevel QM correction scheme in analysing the mechanisms for methanol dehydration to DME. All the transition states contain charged species, which are over-stabilised by SIE – inherent in DFT+D3 only. In the absence of this QM scheme, every transition state is considerably more stable and lower in energy. However, the corrections applied to the transition states in the dissociative mechanism are much larger than those in the associative mechanism due to increased charge polarisation, since an extra water molecule stabilises the charge polarisation in the associative pathway.

Table 2 Enthalpies (H) and enthalpy differences (ΔH) (kJ mol⁻¹) of intermediates and transition states involved in the dissociative mechanism of methanol dehydration to DME, calculated with the hybrid multilevel QM scheme relative to the enthalpy of the reactants

Dissociative	Reactant	M1	TS1	M2	Int	M3	TS2	Product
ΔHFinal	0	−45	104	−35	−31	−45	119	−73
ΔHPBE+D3	0	−41	87	−7	7	−9	100	−61
ΔEMP2	0	0	33	−11	−19	−12	41	−5
ΔECCSD(T)	0	−4	−16	−17	−19	−24	−22	−7

---

Table 3 Enthalpies (H) and enthalpy differences (ΔH) (kJ mol⁻¹) of intermediates and transition states involved in the associative mechanism of methanol dehydration to DME, calculated with the hybrid multilevel QM scheme relative to the enthalpy of the reactants

Associative	Reactant	M1	M4	TS	M5	Product
ΔHFinal	0	−45	−86	44	−84	−73
ΔHPBE+D3	0	−41	−65	38	−74	−61
ΔEMP2	0	0	−18	21	−7	−5
ΔECCSD(T)	0	−4	−3	−15	−3	−7

---

Experimental enthalpies of methanol adsorption and dehydration to DME in H-ZSM-5 reported in the literature vary widely due to the varying methods employed, the zeolite structure, and the coverage of molecules at the BAS. For example, enthalpies of adsorption of −115 and −45 kJ mol⁻¹ have been reported respectively by Lee et al.⁹⁸ in 1997 and by Ortega et al. in 2021.⁹⁹ In Table 4 we compare our results for the associative mechanism with those from a recent experimental study.⁹⁹

Table 4 Experimental methanol adsorption enthalpy in H-ZSM-5 and methanol dehydration to DME reaction enthalpy compared with our calculated values

Methanol adsorption (kJ mol^−1)	Reaction enthalpy (kJ mol^−1)	Ref.
−45	−28	This study
−44.5 ± 0.7	−24	Ortega et al. Expt.^99

---

Our results for methanol adsorption and reaction enthalpies agree with those in Table 4 within the threshold of chemical accuracy (∼4 kJ mol⁻¹), although we caution that any such direct comparison with experiment is problematic for several reasons including the variation of adsorption enthalpies with coverage at active sites.⁹⁹ Experimental heats of desorption of methanol from ZSM-5 catalysts range from 47–107 kJ mol⁻¹ depending on the coverage and experimental method.^100–102

Methyl formate: associative vs. dissociative mechanisms

Experimentally, the promoters are added after several hours of methanol feed and competitively adsorb to the BAS. The full reaction pathways, for both the associative and dissociative mechanisms for the dehydration of methanol to DME in the presence of methyl formate are reported in Tables 5 and 6 and illustrated in Fig. 5. The structures along the reaction coordinate in the dissociative mechanism are displayed in Fig. 4 (but the methanol molecule in step D̲1̲ is now methyl formate) and in the associative mechanism in Fig. 6. The higher-order corrections can be found in the ESI.† The addition of a promoter molecule reveals a new reaction pathway via the associative mechanism. Instead of DME being formed from two methanol molecules, the methyl group of the promoter undergoes nucleophilic attack from one methanol molecule whilst another methanol molecule acts as a proton shuttler. As we have seen, the first stage of both mechanisms involves the adsorption of a methanol molecule to the BAS, with an adsorption enthalpy of 45 kJ mol⁻¹. The formation reaction enthalpies for the associative and dissociative mechanisms are −92 kJ mol⁻¹ and −85 kJ mol⁻¹, respectively; these are not the same because the promoter is left adsorbed to the BAS in the associative mechanism, whereas DME is left adsorbed in the dissociative mechanism.

Table 5 Enthalpies (H) and enthalpy differences (ΔH) (kJ mol⁻¹) of intermediates and transition states involved in the dissociative mechanism of methanol dehydration too DME with methyl formate, calculated with the hybrid multilevel QM scheme relative to the enthalpy of the reactants

Dissociative mechanism	Reaction coordinate
	Reactant	P1	PD1^‡	PD3	D3	D4	D5	Product
ΔHfinal	0	−30	192	−59	−22	−42	113	−85

---

Table 6 Enthalpies (H) and enthalpy differences (ΔH) (kJ mol⁻¹) of intermediates and transition states involved in the associative mechanism of methanol dehydration too DME with methyl formate, calculated with the hybrid multilevel QM scheme relative to the enthalpy of the reactants

Associative mechanism	Reaction coordinate
	Adsorption		Reaction 1				Reaction 2				Product
	Reactant	P1	P1^‡	P1*	P1*^‡	P3	P4	P4^‡	P5*	P5*^‡
ΔHfinal	0	−73	−6	−55	−28	−90	−104	−49	−90	−22	−92

---

Fig. 5 Reaction coordinate diagram, ΔH (kJ mol⁻¹), involving intermediates and transition states involved in methanol dehydration to DME in the presence of methyl formate in the competing associative and dissociative mechanisms. Note that the reaction coordinate is different for each mechanism so only Reactant, M1, P1, and Product are shown on the x-axis and individual labels can be found on the diagram. Structures for the dissociative mechanism are displayed in Fig. 4, while the structures for the associative are shown in Fig. 6.

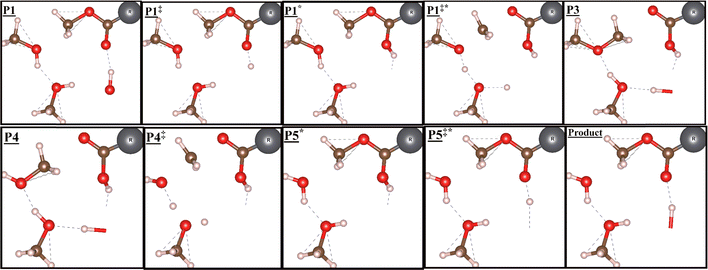Fig. 6 Structures involved in the reaction coordinate for the associative mechanism with a promoter, labels in each box refer to their corresponding reaction coordinate in Fig. 5 and 8. Reaction coordinate P̲1̲—P̲3̲ describes reaction (1), whereas reaction (2) describes reaction coordinate P̲4̲—Product. Colour key for structures: red = oxygen; brown = carbon; pink = hydrogen; grey = R (which refers to the alkyl chain in the promoter molecule). Structures made using VESTA.⁹¹

In the associative mechanism, the promoter points along the straight pore with an adsorption enthalpy of −73 kJ mol⁻¹ to the BAS, a value larger than that of methanol itself. This is consistent with the experimental observation that the promoter displaces methanol from the BAS. The promoter is then protonated from the BAS with an intrinsic barrier and reaction enthalpy of 67 and 18 kJ mol⁻¹, respectively. Subsequent nucleophilic attack by one of the methanol molecules on the methyl group of the promoter produces DME, formic acid, and water; the intrinsic barrier and reaction enthalpy are 27 and −35 kJ mol⁻¹, respectively. The protonation of the promoter is the rate-determining step. Once the water has desorbed and methanol has adsorbed to the reaction site, a second reaction takes place. Re-esterification of the promoter occurs, with an intrinsic barrier of 55 kJ mol⁻¹, and deprotonation of the promoters to re-form the BAS with an intrinsic barrier of 68 kJ mol⁻¹ and a calculated reaction enthalpy of −19 kJ mol⁻¹.

In the dissociative mechanism, to form the surface methoxy species the promoter must first rotate 90° about the carbonyl bond (Fig. 7) after adsorption to the BAS, since the methyl group of the promoter must be aligned to the zeolitic surface oxygen to allow dissociation. This rotation is accompanied by a decrease in the magnitude of the adsorption enthalpy by 43 kJ mol⁻¹; strikingly in this conformation the promoter adsorbs more weakly than methanol. Subsequent dissociation produces a surface methoxy species and formic acid, with a barrier and reaction enthalpy of 222 and −29 kJ mol⁻¹, respectively. Formic acid is then desorbed and methanol adsorbed once more. From this point on, the dissociative mechanism proceeds as in the absence of the promoter.

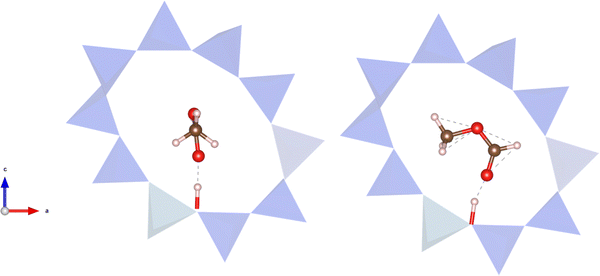Fig. 7 Left: Conformation of adsorbed methyl formate necessary for the associative mechanism. Right: Conformation of adsorbed methyl formate necessary for the dissociative mechanism. The BAS is at the bottom of the 10-ring zeolite structure below methyl formate. Colour key for structures: red = oxygen; brown= carbon; pink = hydrogen; blue polyhedral = TO₄ tetrahedra. Structures made using VESTA.⁹¹

Although more barriers exist in the associative pathway, they are much smaller than those in the dissociative pathway; 67, 27, 55, 68 kJ mol⁻¹ in the associative vs. 222 and 155 kJ mol⁻¹ in the dissociative. Nevertheless, the possibility of some dissociation is consistent with the experimental observation of surface methoxy species. The higher-order corrections listed in the ESI,† are similar to the corresponding values in the mechanisms with methanol only. Specifically, the corrections applied to the transition state energies in the dissociative mechanism are much greater than those applied in the associative.

Larger promoters: the associative mechanism

The full reaction pathways for the associative mechanism for the remaining promoters are illustrated in Fig. 8 with corresponding values reported in Table 7, and structures for each step of the reaction coordinate are displayed in Fig. 6.

Fig. 8 Reaction coordinate diagram (ΔH; kJ mol⁻¹), involving intermediates and transition states involved in methanol dehydration to DME with each promoter for the associative mechanism. ‡ signifies a transition state, * signifies an activated species, in this case, a protonated species.

Table 7 Enthalpies (H) and enthalpy differences (ΔH) (kJ mol⁻¹) of intermediates and transition states involved in the associative mechanism of methanol dehydration too DME with each promoter, calculated with the hybrid multilevel QM scheme relative to the enthalpy of the reactants

Promoter	Reaction coordinate
	Adsorption		Reaction 1				Reaction 2				Product
	Reactant	P1	P1^‡	P1*	P1*^‡	P3	P4	P4^‡	P5*	P5*^‡
Methyl acetate	0	−82	−33	−99	−50	−100	−114	−64	−119	−48	−120
Methyl propionate	0	−94	−48	−123	−58	−124	−131	−87	−132	−71	−138
Methyl n-butyrate	0	−104	−60	−132	−72	−130	−136	−95	−137	−84	−147
Methyl n-pentanoate	0	−109	−66	−137	−76	−136	−148	−104	−150	−97	−152
Methyl n-hexanoate	0	−119	−71	−145	−80	−144	−156	−118	−161	−106	−166

---

The formation reaction enthalpies, i.e., relative to the reactants, and calculated reaction enthalpies, i.e., relative to the adsorbed promoter, are listed in Table 8, where methyl formate is also included for completeness. There is a significant correlation between the formation reaction enthalpies for the promoters via the associative mechanism and their experimental DME STY (Fig. 1). This is not so for the calculated reaction enthalpies. This suggests the enthalpy of reaction is highly dependent on the adsorption of the promoter. In a PBE+D3 calculation alone, a protonated species is the lowest in enthalpy, whereas the hybrid multilevel method shows the lowest enthalpy structure is the final product itself, revealing the thermodynamic driving force toward the overall product.

Table 8 Formation reaction enthalpies and calculated reaction enthalpies (kJ mol⁻¹) for the associative mechanism for each promoter obtained by the hybrid multilevel QM method

Promoter	Methyl formate	Methyl acetate	Methyl propionate	Methyl n-butyrate	Methyl n-pentanoate	Methyl n-hexanoate
Formation reaction enthalpy	−92	−120	−138	−147	−152	−166
Calculated reaction enthalpy	−19	−38	−44	−43	−43	−47

---

(i) Adsorption of the promoter molecule. The calculated adsorption enthalpies, H_ads, are listed in Table 9, which also includes methyl formate for completeness. This step results in the greatest enthalpic change across the whole reaction pathway and occurs with no barrier. Every promoter adsorbs more strongly than methanol, this is consistent with previous experimental and modelling studies.^30,32 The adsorption enthalpy therefore has a significant effect on the overall reaction enthalpy.

Table 9 Adsorption enthalpies (kJ mol⁻¹) for each promoter at the T1 site obtained by the hybrid multilevel QM method

	Methyl formate	Methyl acetate	Methyl propionate	Methyl n-butyrate	Methyl n-pentanoate	Methyl n-hexanoate
H ads	−73	−82	−94	−104	−109	−119

---

Every promoter adsorbs to the BAS through a strong hydrogen bond interaction at a length of 1.49 Å between its carbonyl group and the BAS proton. The adsorption enthalpies increase with alkyl chain length due to attractive dispersion interactions between the chain and the zeolite pore walls. An extra –CH₂ group in the chain increases the adsorption enthalpy by approximately 10 kJ mol⁻¹, except between methyl n-butyrate and methyl n-pentanoate. We speculate that here, the extra –CH₂ group lies in an adjacent pore intersection unlike the other promoters, so it does not receive the same stabilisation from the pore walls. This effect in turn disappears with a further –CH₂ group in the chain, as with methyl n-hexanoate, because the increased chain length is now sufficiently long for attractive dispersion interactions with the pore wall after the intersection. We note this provides a static view of the most stable conformation of the adsorbed molecule rather one based on the temperature-dependent spatial distribution of adsorbed molecules. Molecular dynamics sampling of MP2 quality adsorption enthalpies could be achieved using parameterisation from MP2: DFT-D potential energy surfaces, as was done recently by Berger, Rybicki, and Sauer but is beyond the scope of this work.⁷³ The PBE+D3 functional by itself systematically predicts too strong adsorption. This is consistent with the work of Goncalves et al.⁸⁶ and Sauer et al.⁷⁷ on the adsorption energies of a wide range of molecules.

The correlation between the formation reaction enthalpy and promoter adsorption enthalpy highlights the importance of binding. The bound conformation is crucial for protonation of the promoter, i.e., the initial stage of the reaction, and promoters that adsorb more strongly to the BAS are less susceptible to inhibition of the catalytic site from by-products.

(ii) Reaction one – protonation of promoter and DME formation. Reaction (1) in Fig. 7 and Table 7 involves two steps; (i) the protonation of the promoter molecule, (ii) DME formation via nucleophilic attack of methanol on the methoxy group of the adsorbed promoter molecule, and simultaneous proton transfer to another methanol molecule. The structures involved in these steps are displayed in Fig. 6, and their calculated intrinsic enthalpy barriers and reaction enthalpies given in Table 10.

Table 10 Proton affinities, calculated enthalpy barriers, and calculated reaction enthalpies for (i) protonation of all promoters, and (ii) the formation of DME from methanol for all promoters. Data are in kJ mol⁻¹

Promoter	Proton affinity	(i) Protonation		(ii) DME formation
		H ^‡intr	Reaction enthalpy	H ^‡intr	Reaction enthalpy
Methyl acetate	822^103	49	−17	49	−14
Methyl propionate	830,^103 832^104	46	−29	65	−9
Methyl n-butyrate	836^103	44	−28	60	−4
Methyl n-pentanoate	839,^103 839^104	43	−28	61	−10
Methyl n-hexanoate	840^104	48	−26	65	−8

---

The transition states for both reactions are shown in Fig. 9 and relevant bond distances between labelled atoms are given in the ESI.† During protonation of the promoter molecule, O1–H1, and H1–O2 distances are ∼1.39 Å, and ∼1.26 Å, respectively, for all promoters. The proton is not equidistant between O1 and O2 but instead lies closer to the promoter molecule. Even though these bond distances do not change, the barrier and reaction enthalpy for protonation are significantly different for methyl acetate from the remaining promoters, due to the different proton affinities of the promoters (Table 10).

Fig. 9 The transition state found for (i) protonation of the promoter molecule, and (ii) formation of DME. The atoms involved in these steps are labelled and referred to in the ESI.† Colour key for structures: red = oxygen; brown = carbon; pink = hydrogen; grey = alkyl chain; blue polyhedral = TO₄ tetrahedra. Figure made using VESTA.⁹¹

While our results support the widely accepted notion that a variety of molecules readily deprotonate the BAS, we calculate much higher barriers—up to 49 kJ mol⁻¹—than other previous computational studies of reactions in zeolites.^105–109 The difference is likely due to SIE in DFT which causes the artificial stabilisation of charged structures. We find that barriers are underpredicted by up to 26 kJ mol⁻¹ without the higher-level corrections. This is consistent with the findings of Sauer et al.⁷¹ who found that proton exchange barriers for alkanes in H-ZSM-5 were underpredicted by 36–40 kJ mol⁻¹ by DFT-D alone. Accurate calculations of proton attachment energies are crucial when modelling reactions in zeolites. A comparison of the methods and the corrections for each promoter can be found in the ESI.†

The formation of DME is exothermic for every promoter and every transition state involves multiple molecules in a cyclic transition state involving proton shuttling and hydrogen bonding. Initially, a nucleophilic attack of methanol on the methoxy group of the protonated promoter molecule occurs; subsequent proton transfer from DME to another methanol molecule takes place with no barrier.

(iii) Reaction two – re-esterification and deprotonation of the promoters. Reaction two involves two steps; (i) the re-esterification of the promoter molecule and simultaneous proton transfer to form water, (ii) deprotonation of the promoter molecule by the BAS. Results are presented in Table 11.

Table 11 Enthalpy barriers and reaction enthalpies for (i) re-esterification of all promoters from methanol, and (ii) deprotonation of all promoters from the BAS. Data are in kJ mol⁻¹

Promoter	(i) Re-esterification		(ii) Deprotonation
	H ^‡intr	Reaction enthalpy	H ^‡intr	Reaction enthalpy
Methyl acetate	50	−5	71	−2
Methyl propionate	44	−6	61	−6
Methyl n-butyrate	41	−1	53	−10
Methyl n-pentanoate	44	−2	53	−2
Methyl n-hexanoate	38	−5	55	−5

---

The re-esterification of the promoter molecule involves a cyclic, concerted, transition state with three molecules; it is exothermic for each promoter. Umbrella inversion occurs as the –CH₃ group of the methanol molecule undergoes nucleophilic attack from the oxygen atom of the promoter. Simultaneous proton transfer, from the protonated methanol to the transient hydroxide, takes place and maintains charge neutrality. Table 11 shows that the intrinsic barriers decrease as the length of the alkyl chain in the promoter increases. These data are consistent with the earlier discussion of proton affinities reported in Table 10.

Conclusions

We have employed a hybrid multilevel quantum method to explore the competing associative and dissociative mechanisms underpinning the formation of DME from methanol in H-ZSM-5 in the presence, and absence, of six methyl ester promoters. For the dehydration of methanol to DME in the absence of promoters, most of our results are in agreement with experimental values to within chemical accuracy (∼4 kJ mol⁻¹). We show a reaction mechanism (not previously modelled) involving a promoter and two methanol molecules reacting to form DME. The promoters provide a more exothermic route to DME formation because the promoter is left adsorbed at the BAS, the intrinsic activation enthalpy barriers are also reduced. Highlighted in this work are the inaccuracies prevalent in common theoretical methodologies employed to investigate zeolite catalysis. Specifically, SIE over-stabilises polar species leading to inaccuracies in the calculation of reaction barriers within key steps of pathways, especially protonation steps. The results demonstrate the importance of high level (ab initio) calculations for drawing quantitative mechanistic conclusions, to overcome limitations of DFT. We show a thermodynamic driving force toward the final product by revealing the lowest enthalpy structure is the final product – a conclusion that would not be possible without employing the hybrid multilevel QM methodology. Overall, our results show why the promoter molecules increase the formation of DME from methanol, in H-ZSM-5, in agreement with experiment and rationalise the extent of promotion with promoter size. The promoter's adsorption to the BAS is a key factor, associated with lower overall reaction enthalpies (compared to methanol only) and lower barriers along the reaction pathway.

Data availability

All structure files can be found online (https://doi.org/10.5281/zenodo.10261595; https://doi.org/10.5281/zenodo.10260386) and are provided as open-source material.

Conflicts of interest

The ester promoters described in this manuscript are the subject of two patent filings (WO2019/037764 and WO2019037768) by BP plc and BP (China) Holdings Limited. There are no other conflicts to declare.

References

1. M. Tomatis, A. Mahmud Parvez, M. T. Afzal, S. Mareta, T. Wu, J. He and T. He, Fuel, 2019, 254, 115627.
2. M. Marchionna, R. Patrini, D. Sanfilippo and G. Migliavacca, Fuel Process. Technol., 2008, 89, 1255–1261.
3. R. Anggarani, M. Muchar, C. S. Wibowo and R. Sukaraharja, Energy Proc., 2015, 65, 274–281.
4. M. Himabindu and R. V. Ravikrishna, J. Renewable Sustainable Energy, 2010, 2, 52701.
5. M. Martín, J. CO₂ Utilization, 2016, 13, 105–113.
6. R. G. Santiago, J. A. Coelho, S. M. P. de Lucena, A. P. S. Musse, M. de, F. Portilho, E. Rodriguez-Castellón, D. C. S. de Azevedo and M. Bastos-Neto, Front. Chem., 2022, 10, 1–11.
7. S. P. Naik, T. Ryu, V. Bui, J. D. Miller, N. B. Drinnan and W. Zmierczak, Chem. Eng. J., 2011, 167, 362–368.
8. S. Le Goff, Electric Hybrid Rail Technol., 2022, 2021, 36–37.
9. F. Pontzen, W. Liebner, V. Gronemann, M. Rothaemel and B. Ahlers, Catal. Today, 2011, 171, 242–250.
10. S. Ernst, Angew. Chem., Int. Ed., 2011, 50, 5425–5426.
11. J. Liang, Z. Liang, R. Zou and Y. Zhao, Adv. Mater., 2017, 29, 1701139.
12. G. Sastre and A. Corma, J. Mol. Catal. A: Chem., 2009, 305, 3–7.
13. A. B. Grommet, M. Feller and R. Klajn, Nat. Nanotechnol., 2020, 15, 256–271.
14. E. Grifoni, G. M. Piccini, J. A. Lercher, V. A. Glezakou, R. Rousseau and M. Parrinello, Nat. Commun., 2021, 12, 2630.
15. J. F. Haw, W. Song, D. M. Marcus and J. B. Nicholas, Acc. Chem. Res., 2003, 36, 317–326.
16. M. Stöcker, Microporous Mesoporous Mater., 1999, 29, 3–48.
17. U. Olsbye, S. Svelle, K. P. Lillerud, Z. H. Wei, Y. Y. Chen, J. F. Li, J. G. Wang and W. B. Fan, Chem. Soc. Rev., 2015, 44, 7155–7176.
18. B. E. Langner, Appl. Catal., 1982, 2, 289–302.
19. A. D. Chowdhury, A. L. Paioni, K. Houben, G. T. Whiting, M. Baldus and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2018, 57, 8095–8099.
20. T. Mole, G. Bett and D. Seddon, J. Catal., 1983, 84, 435–445.
21. I. Lezcano-Gonzalez, E. Campbell, A. E. J. Hoffman, M. Bocus, I. V. Sazanovich, M. Towrie, M. Agote-Aran, E. K. Gibson, A. Greenaway, K. De Wispelaere, V. Van Speybroeck and A. M. Beale, Nat. Mater., 2020, 19, 1081–1087.
22. I. M. Dahl and S. Kolboe, Catal. Lett., 1993, 20, 329–336.
23. S. Kolboe, Stud. Surf. Sci. Catal., 1988, 36, 189–193.
24. A. J. Jones, S. I. Zones and E. Iglesia, J. Phys. Chem. C, 2014, 118, 17787–17800.
25. J. R. Di Iorio, A. J. Hoffman, C. T. Nimlos, S. Nystrom, D. Hibbitts and R. Gounder, J. Catal., 2019, 380, 161–177.
26. R. T. Carr, M. Neurock and E. Iglesia, J. Catal., 2011, 278, 78–93.
27. A. Ghorbanpour, J. D. Rimer and L. C. Grabow, ACS Catal., 2016, 6, 2287–2298.
28. A. J. Jones and E. Iglesia, Angew. Chem., Int. Ed., 2014, 53, 12177–12181.
29. J. Park, J. Cho, M. J. Park and W. B. Lee, Catal. Today, 2021, 375, 314–323.
30. B. J. Dennis-Smither, Z. Yang, C. Buda, X. Liu, N. Sainty, X. Tan and G. J. Sunley, Chem. Commun., 2019, 55, 13804–13807.
31. J. Crossley-Lewis, J. Dunn, C. Buda, G. J. Sunley, A. M. Elena, I. T. Todorov, C. W. Yong, D. R. Glowacki, A. J. Mulholland and N. L. Allan, J. Mol. Graph. Model., 2023, 125, 108606.
32. Z. Yang, B. J. Dennis-Smither, Z. Xu, Z. Zhao, M. Guo, N. Sainty, G. Hou, X. Liu and G. J. Sunley, Chemistry, 2023, 5, 511–525.
33. Z. Yang, B. J. Dennis-smither, C. Buda, A. Easey, F. Jackson, G. A. Price, N. Sainty, X. Tan, Z. Xu and G. J. Sunley, Catal. Sci. Technol., 2023, 13, 3590–3605.
34. F. Neese, A. Hansen, F. Wennmohs and S. Grimme, Acc. Chem. Res., 2009, 42, 641–648.
35. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667.
36. S. Mallikarjun Sharada, T. Bligaard, A. C. Luntz, G. J. Kroes and J. K. Nørskov, J. Phys. Chem. C, 2017, 121, 19807–19815.
37. E. Ruiz, D. R. Salahub and A. Vela, J. Phys. Chem., 1996, 100, 12265–12276.
38. J. Klime, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–29.
39. B. Vlaisavljevich, J. Huck, Z. Hulvey, K. Lee, J. A. Mason, J. B. Neaton, J. R. Long, C. M. Brown, D. Alfè, A. Michaelides and B. Smit, J. Phys. Chem. A, 2017, 121, 4139–4151.
40. F. Claeyssens, J. N. Harvey, F. R. Manby, R. A. Mata, A. J. Mulholland, K. E. Ranaghan, M. Schütz, S. Thiel, W. Thiel and H.-J. Werner, Angew. Chem., Int. Ed., 2006, 45, 6856–6859.
41. J. Sauer, Acc. Chem. Res., 2019, 52, 3502–3510.
42. P. Nachtigall and J. Sauer, Stud. Surf. Sci. Catal., 2007, 168, 701–736.
43. G. Piccini, M. Alessio and J. Sauer, Angew. Chem., Int. Ed., 2016, 55, 5235–5237.
44. G. Piccini, M. Alessio and J. Sauer, Phys. Chem. Chem. Phys., 2018, 20, 19664–19670.
45. K. E. Ranaghan, D. Shchepanovska, S. J. Bennie, N. Lawan, S. J. Macrae, J. Zurek, F. R. Manby and A. J. Mulholland, J. Chem. Inf. Model., 2019, 59, 2063–2078.
46. L. O. Jones, M. A. Mosquera, G. C. Schatz and M. A. Ratner, J. Am. Chem. Soc., 2020, 142, 3281–3295.
47. Database of Zeolite Structures, https://www.iza-structure.org/databases/, (accessed October 2022).
48. R. Grau-Crespo, A. G. Peralta, A. R. Ruiz-Salvador, A. Gómez and R. López-Cordero, Phys. Chem. Chem. Phys., 2000, 2, 5716–5722.
49. A. Palčić and V. Valtchev, Appl. Catal., A, 2020, 606, 117795.
50. M. Trachta, O. Bludský, J. Vaculík, R. Bulánek and M. Rubeš, Sci. Rep., 2023, 13, 12380.
51. M. Boronat and A. Corma, ACS Catal., 2019, 9, 1539–1548.
52. H. Windeck, F. Berger and J. Sauer, Angew. Chem., Int. Ed., 2023, 62, e202303204.
53. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
54. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
55. G. Kresse and D. Joubert, J. Phys. Chem. A, 2020, 124, 4053–4061.
56. J. Kresse and G. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11184.
57. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
58. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
59. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
60. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
61. V. Wang, N. Xu, J. C. Liu, G. Tang and W. T. Geng, Comput. Phys. Commun., 2021, 267, 108033.
62. C. J. Cramer, Essentials of Computational Chemistry: Second Edition, J Wiley, New York, 2004.
63. A. Hoffman, M. Deluca and D. Hibbitts, J. Phys. Chem. C, 2019, 123, 6572–6585.
64. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
65. H. Jonsson, G. Mills and K. W. Jacobsen, Classical and Quantum Dynamics in Condensed Phase Simulations, World Scientific, Singapore, 1998.
66. G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904.
67. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (Revision A.03), Gaussian Inc., Pittsburgh, PA, 2016.
68. F. Berger, M. Rybicki and J. Sauer, J. Catal., 2021, 395, 117–128.
69. F. Berger and J. Sauer, Angew. Chem., Int. Ed., 2021, 60, 3529–3533.
70. G. Piccini and J. Sauer, J. Chem. Theory Comput., 2014, 10, 2479–2487.
71. M. Rybicki and J. Sauer, J. Am. Chem. Soc., 2018, 140, 18151–18161.
72. C. Tuma and J. Sauer, Chem. Phys. Lett., 2004, 387, 388–394.
73. F. Berger, M. Rybicki and J. Sauer, ACS Catal., 2023, 13, 2011–2024.
74. U. Eichler, C. M. Kölmel and J. Sauer, J. Comput. Chem., 1997, 18, 463–477.
75. S. Svelle, C. Tuma, X. Rozanska, T. Kerber and J. Sauer, J. Am. Chem. Soc., 2009, 131, 816–825.
76. K. P. Schröder, J. Sauer, M. Leslie, C. Richard and C. R. A. Catlow, Zeolites, 1992, 12, 20–23.
77. N. Hansen, T. Kerber, J. Sauer, A. T. Bell and F. J. Keil, J. Am. Chem. Soc., 2010, 132, 11525–11538.
78. K. P. Schröder, J. Sauer, M. Leslie, C. Richard, C. R. A. Catlow and J. M. Thomas, Chem. Phys. Lett., 1992, 188, 320–325.
79. G. Piccini, M. Alessio, J. Sauer, Y. Zhi, Y. Liu, R. Kolvenbach, A. Jentys and J. A. Lercher, J. Phys. Chem. C, 2015, 119, 6128–6137.
80. C. Campbell, R. Van Santen, M. Stamatakis, N. Collis, H. J. Freund, C. Plaisance, J. Sauer, B. Garrett, E. Gross, A. Kotarba, B. Weckhuysen, W. Ueda, C. Reece, C. R. A Catlow, A. Trunschke, L. Briquet, T. Ho, I. Panas, D. Willock, C. Friend, M. Bowker, N. Robinson, A. Bruix, S. Gupta, B. Gates, A. Corma, R. Madix, D. Manganas, A. Roldan, A. O’malley, J. Staszak-Jirkovsky and J. Jirkovsky, Faraday Discuss., 2016, 188, 279–307.
81. P. Selvam, J. Sauer, B. Garrett, C. Campbell, R. Van Santen, P. Davies, A. L. Miller, M. Bowker, G. Hutchings, D. Wotton, H.-J. Freund, M. Howard, M. Feaviour, R. Burch, A. Maria, R. Galletti, E. Gross, F. Ivars Barcelo, A. Kotarba, S. Kondrat, B. Weckhuysen, B. Majumdar, A. Bruix, N. Fischer, B. Gates, J. Moulijn, A. Roldan, N. Novak Tusar, T. Jakubek, D. Willock, M. Craven, K. Sethu, C. R. A. Catlow, R. Madix, H. Manyar, C. Friend, A. Corma, P. Wells, W. Ueda, A. Trunschke and R. Palmer, Faraday Discuss., 2016, 188, 131.
82. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
83. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
84. S. Svelle, C. Tuma, X. Rozanska, T. Kerber and J. Sauer, J. Am. Chem. Soc., 2009, 131, 816–825.
85. P. N. Plessow and F. Studt, J. Phys. Chem. Lett., 2020, 11, 4305–4310.
86. T. J. Goncalves, P. N. Plessow and F. Studt, ChemCatChem, 2019, 11, 4368–4376.
87. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
88. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371.
89. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
90. O. Mowla, E. Kennedy and M. Stockenhuber, Fuel, 2018, 232, 12–26.
91. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
92. J. Van Der Mynsbrugge, K. Hemelsoet, M. Vandichel, M. Waroquier and V. Van Speybroeck, J. Phys. Chem. C, 2012, 116, 5499–5508.
93. L. Kilburn, M. DeLuca, A. J. Hoffman, S. Patel and D. Hibbitts, J. Catal., 2021, 400, 124–139.
94. A. Ghorbanpour, J. D. Rimer and L. C. Grabow, Catal. Commun., 2014, 52, 98–102.
95. A. T. Smith, P. N. Plessow and F. Studt, J. Phys. Chem. C, 2021, 125, 20373–20379.
96. L. Kilburn, M. DeLuca, A. J. Hoffman, S. Patel and D. Hibbitts, J. Catal., 2021, 400, 124–139.
97. S. A. F. Nastase, C. R. A. Catlow and A. J. Logsdail, Phys. Chem. Chem. Phys., 2021, 23, 2088–2096.
98. C. C. Lee, R. J. Gorte and W. E. Farneth, J. Phys. Chem. B, 1997, 101, 3811–3817.
99. C. Ortega, M. Rezaei, V. Hessel and G. Kolb, Chem. Eng. J., 2018, 347, 741–753.
100. T. Omojola, N. Cherkasov, A. I. McNab, D. B. Lukyanov, J. A. Anderson, E. V. Rebrov and A. C. van Veen, Catal. Lett., 2018, 148, 474–488.
101. G. Mirth, J. A. Lercher, M. W. Anderson and J. Klinowski, J. Chem. Soc., Faraday Trans., 1990, 86, 3039–3044.
102. C. G. Pope, J. Chem. Soc., Faraday Trans., 1993, 89, 1139–1141.
103. S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin and W. G. Mallard, J. Phys. Chem. Ref. Data, 1988, 17, 1–861.
104. J. L. Holmes, N. A. van Huizen and P. C. Burgers, Eur. J. Mass Spectrosc., 2017, 23, 341–350.
105. P. Liu and D. Mei, J. Phys. Chem. C, 2020, 124, 22568–22576.
106. N. S. Gould, S. Li, H. J. Cho, H. Landfield, S. Caratzoulas, D. Vlachos, P. Bai and B. Xu, Nat. Commun., 2020, 11, 1–13.
107. P. Liu, Z. Yan and D. Mei, Phys. Chem. Chem. Phys., 2021, 23, 10395–10401.
108. J. H. Hack, J. P. Dombrowski, X. Ma, Y. Chen, N. H. C. Lewis, W. B. Carpenter, C. Li, G. A. Voth, H. H. Kung and A. Tokmakoff, J. Am. Chem. Soc., 2021, 143, 10203–10213.
109. P. Deshlahra and E. Iglesia, Chem. Commun., 2020, 56, 7371–7398.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05987a

---