 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Vibrational dynamics and spectroscopy of water at porous g-C3N4 and C2N surfaces
Deepak
Ojha
 ,
Christopher
Penschke
,
Christopher
Penschke
 and
Peter
Saalfrank
and
Peter
Saalfrank
 *
*
Theoretische Chemie, Institut für Chemie, Universität Potsdam, Karl-Liebknecht-Strasse 24-25, D-14476 Potsdam-Golm, Germany. E-mail: peter.saalfrank@uni-potsdam.de
First published on 18th March 2024
Abstract
Porous graphitic materials containing nitrogen are promising catalysts for photo(electro)chemical reactions, notably water splitting, but can also serve as “molecular sieves”. Nitrogen increases the hydrophilicity of the graphite parent material, among other effects. A deeper understanding of how water interacts with C- and N-containing layered materials, if and which differences exist between materials with different N content and pore size, and what the role of water dynamics is – a prerequsite for catalysis and sieving – is largely absent, however. Vibrational spectroscopy can answer some of these questions. In this work, the vibrational dynamics and spectroscopy of deuterated water molecules (D2O) mimicking dense water layers at room temperature on the surfaces of two different C/N-based materials with different N content and pore size, namely graphitic C3N4 (g-C3N4) and C2N, are studied using ab initio molecular dynamics (AIMD). In particular, time-dependent vibrational sum frequency generation (TD-vSFG) spectra of the OD modes and also time-averaged vSFG spectra and OD frequency distributions are computed. This allows us to distinguish “free” (dangling) OD bonds from OD bonds that are bound in a H-bonded water network or at the surface – with subtle differences between the two surfaces and also to a pure water/air interface. It is found that the temporal decay of OD modes is very similar on both surfaces with a correlation time near 4 ps. In contrast, TD-vSFG spectra reveal that the interconversion time from “bonded” to “free” OD bonds is about 8 ps for water on C2N and thus twice as long as for g-C3N4, demonstrating a propensity of the former material to stabilize bonded OD bonds.
1 Introduction
Water at interfaces and on surfaces is of immense significance for it plays a role as a solvent and as a catalyst in many chemical processes.1–3 In biology, interfacial water at lipid bilayers and proteins contributes to the overall biological activity and selectivity.4 Water on semiconductor surfaces offers an alternative to conventional energy sources by means of electro- or photo-catalytic water splitting. Many photo(electro)catalysts contain metals that are expensive and sometimes hazardous.5–7 In contrast, recently synthesized organic materials like graphitic carbon nitride (g-C3N4)8–10 and C2N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11,12 have not only demonstrated their propensity to facilitate water-splitting, but they are also easy to synthesize and non-hazardous to the environment. These quasi-two-dimensional, porous, layered materials offer a large surface area, and their properties can be tuned by the C/N ratio and the size of the pores. Nitrogen is particularly important in these materials, notably for uptake of water, as it considerably increases the hydrophilicity of the material w.r.t. graphite or graphene.12,13 This makes these materials also interesting in a non-catalytic context, e.g., as sieves to separate liquids when acting as water-selective membranes.
11,12 have not only demonstrated their propensity to facilitate water-splitting, but they are also easy to synthesize and non-hazardous to the environment. These quasi-two-dimensional, porous, layered materials offer a large surface area, and their properties can be tuned by the C/N ratio and the size of the pores. Nitrogen is particularly important in these materials, notably for uptake of water, as it considerably increases the hydrophilicity of the material w.r.t. graphite or graphene.12,13 This makes these materials also interesting in a non-catalytic context, e.g., as sieves to separate liquids when acting as water-selective membranes.
Both for catalytic and non-catalytic purposes, like selective adsorption and separation, a precise understanding of the interaction of water with C/N-containing porous materials is desirable. Several theoretical studies have been performed that explored the geometric and electronic structure of these carbon-based materials and how the latter is modified by water adsorption.12,13,15–18 Often (but not always) single- or few-layer models were studied, and low coverages were studied using stationary models. For example, in a first-principles density functional theory (DFT) study including van der Waals corrections and employing a (3 × 3) periodic supercell model, it was found that a single water molecule preferentially adsorbs in a triangular pore of the g-C3N4 surface, with an adsorption energy between −0.55 and −0.62 eV depending on the functional.18 The water molecule lies almost flat in the pore of the buckled g-C3N4 surface, forming two hydrogen bonds with acceptor N atoms of the cavity. Also, cluster models using highly correlated wavefunction methods support these results.13,14 (Note that with smaller (1 × 1) unit cells, the surface is falsely predicted to be flat and other adsorption geometries are more stable.16) In ref. 18, other (metastable) adsorption sites for water were also found using a potential energy surface (PES) scan, and barriers for lateral diffusion of water to these sites were determined, which were in the order of 0.2 eV. In ref. 17, in an attempt to go to higher-coverage situations, multi-layer systems and dynamical behaviour relevant for water-selective membranes and “molecular sieves”, the diffusion of water (and ethanol) through pristine and modified g-C3N4 sheets was studied using classical molecular dynamics simulations based on empirical forcefields. An inverse correlation between the diffusion coefficient of water and the lifetime of intermolecular hydrogen bonds (HBs) was found, i.e., short lifetimes caused larger diffusion coefficients (and vice versa). Diffusion coefficients (for water) on/between g-C3N4 were also found to be smaller than for bulk water, and the HB-lifetime was correspondingly larger for water at/in g-C3N4 compared to bulk water.17
In the case of C2N, which consists of flat layers under ideal conditions and with hexagonal-shaped pores slightly larger than those of g-C3N4, both periodic DFT and cluster calculations predict a similar adsorption energy for a single H2O molecule on a C2N monolayer as for g-C3N4. In this case, however, the water resides above the (center of the) pore, but still forming two H-bonds to two adjacent, basic N atoms.12,13 Beyond single-layer models for C2N and after loading with larger amounts of water, according to the combined experimental–theoretical work in ref. 12, water molecules reside between the layers, forming H-bonds with N atoms of C2N that are stronger than the H-bonds between different water molecules in bulk water. The adsorption energy decreases with increasing water load.
In order to understand the interaction with and adsorption of liquid water on 2D C/N-containing materials better, it is necessary to consider high coverages, finite temperatures, and dynamical behaviour that will naturally arise at a finite temperature. (In the studies mentioned above, this was only done within the classical MD work reported in ref. 17.) Our goal here is to unravel the differences of the C/N material/water systems compared to bulk water or water/air interfaces, and also the differences between various C/N materials. This is, in the end, a prerequisite to fully understanding the performance of N-containing graphitic materials for water splitting or as sieves, and their rational design. Another motivation for our work is the mentioned observation that the H-network, and also the transport and chemical behaviours of water, in confined spaces/at surfaces can be very different from what is observed in the bulk (see also ref. 19 and 20).
Appropriate “fingerprints” are needed by which differences between various systems and general effects of a confining surface can be accessed. In this context, we note that the spectral signature peaks for the concerted intermolecular motion of hydrogen-bonded water molecules, as well as the intramolecular fluctuations of the OH (or OD) modes of water molecules, can be seen in vibrational spectra, such as the infrared (IR) spectrum. In particular, the IR spectrum provides a fingerprint region to decipher the hydrogen-bond dynamics in aqueous solutions and at interfaces.3 Nevertheless, conventional vibrational spectroscopy cannot disseminate the contribution of interfacial molecules from the bulk. Vibrational sum frequency generation spectroscopy (vSFG) enables us to selectively study the structure, hydrogen-bond network and orientational profile of interfaces and surfaces.21–28 Moreover, the temporal evolution of the interfacial molecules can be explored using time-dependent vSFG (TD-vSFG).29–31
Existing theoretical studies have not explored the vibrational dynamics of water molecules on two-dimensional, N-containing graphitic materials. In the present work, we have investigated the vibrational dynamics and vSFG spectra of interfacial water on g-C3N4 and C2N surfaces using ab initio molecular dynamics. We concentrate on surfaces in this work, using single-layer models for the 2D material, and leaving investigations of the effects of other layers and the bulk to future work. We will consider thin layers of D2O molecules (rather than H2O, for practical reasons) adsorbed on one side of the 2D layer, and analyze OD vibrations in detail. Fluctuations in the vibrational frequency of OD modes were obtained using the wavelet transform of the time-series analysis and the surface-specific velocity–velocity autocorrelation function (ssVVAF) approach32 was used to calculate the vSFG and TD-vSFG spectra of interfacial water molecules.
The paper is organized as follows. In the following Section 2, we briefly outline theoretical methods and computational models. In Section 3, we study the vibrational dynamics, time-averaged vibrational spectroscopy and time-resolved vibrational spectroscopy. Section 4 summarizes and concludes our work.
2 Computational details and models
2.1 Models
We performed AIMD simulations for D2O molecules adsorbed either on C2N or g-C3N4 monolayers, using periodic supercell models. For g-C3N4, a supercell of dimensions (20.4 × 20.4 × 24.0) Å with 126 atoms (C54N72) was employed representing a (3 × 3) 2D trigonal elementary cell to model the wave-like reconstruction found elsewhere13,18 (see Fig. 1(a) in ref. 13 for a pictorial representation). We then adsorbed 60 D2O molecules on one side (the surface) of the monolayer. A snapshot resulting from an AIMD simulation (see below), is shown in Fig. 1(a). As a result, about 14 Å of vacuum separate different periodic images along the z-axis (perpendicular to the surface).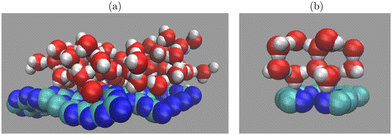 | ||
| Fig. 1 Snapshots of water (D2O) molecules simulated on (a) a C3N4 (3 × 3) monolayer and (b) a C2N monolayer. The employed unit cells are shown in side-views, with C: green, N: blue, O: red, D: white. | ||
C2N was modelled using a primitive unit cell of dimensions (8.32 × 8.32 × 20.0) Å with 18 atoms (composition C12N6), corresponding to a 2D trigonal elementary cell, (see Fig. 1(c) in ref. 13). On one side of this layer, 12 D2O molecules were added, as shown in the form of an AIMD snapshot in Fig. 1(b). This way, a vacuum gap of around 12 Å remained between the water-covered layers.
2.2 AIMD simulations
First-principles simulations of water molecules on the g-C3N4 and C2N surfaces were performed using the Vienna Ab initio Simulation Package33,34 (VASP, version 5.4). The inner core electrons were represented by projector augmented-wave (PAW) pseudopotentials35,36 and valence electrons using the Perdew–Becke–Ernzerhof (PBE) exchange correlation functional37 together with Grimme's D3 dispersion correction.38,39 (For a general assessment of DFT for water, see ref. 40.) The plane-wave kinetic energy cutoff was set to 400 eV for both systems. For C2N/water, a 3 × 3 × 1 k-point grid was used for Brillouin zone sampling; for g-C3N4/water, only the Γ-point was included.Simulations were performed in the NVT ensemble using the Nosé–Hoover thermostat41 at 300 K with deuterium masses for hydrogen and a time step of 1 fs for integrating the equations of motion. The vibrational spectra were sampled by using single, long NVT trajectories of 45 ps length (C3N4/D2O) and 55 ps (C2N/D2O). D2O instead of H2O was used in order to allow for longer time steps and total propagation times in AIMD, hence better statistics, and also to inspire experiments that are often done with deuterated water.42
2.3 Frequency distributions
A (time-dependent) distribution of vibrational frequencies of OD modes of water molecules on g-C3N4 and C2N surfaces was determined using the wavelet transform of a time-series analysis. The method is well documented43 and is based on the principle that a time-dependent function (f(t)) can be expressed in terms of basis functions obtained by the translations and dilations of a mother wavelet | (1) |
 | (2) |
 | (3) |
 the time-window narrows for high frequency (small a) and widens for low frequency (large a). The value of parameter a that maximizes the modulus of the wavelet transform of time series f at time t = b is used to calculate the most important frequency component for the given interval.
the time-window narrows for high frequency (small a) and widens for low frequency (large a). The value of parameter a that maximizes the modulus of the wavelet transform of time series f at time t = b is used to calculate the most important frequency component for the given interval.
The time series of interest in this work, f(t), is constructed as a complex function with its real and imaginary parts corresponding to fluctuations of the bond length and momentum of an OD mode projected along the OD bond, namely (possible unit factors omitted)
| f(t) = δrOD(t) + iδpOD(t). | (4) |
| δq(t) = q(t) − 〈q〉, | (5) |
![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) OD(t)| where
OD(t)| where ![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) OD(t) =
OD(t) = ![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) O −
O − ![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) D is the OD bond vector for a given OD bond, obtained from atomic position vectors. Furthermore, the momentum projected along the OD mode is given as
D is the OD bond vector for a given OD bond, obtained from atomic position vectors. Furthermore, the momentum projected along the OD mode is given as | (6) |
![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) O,
O, ![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) D are atom velocities, and
D are atom velocities, and 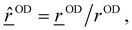 the unit vector along the OD bond. This method is then applied to all the OD modes present in a given system. For further details and recent applications of the method within AIMD, see ref. 43–46.
the unit vector along the OD bond. This method is then applied to all the OD modes present in a given system. For further details and recent applications of the method within AIMD, see ref. 43–46.
3 Results
3.1 Vibrational frequency distribution and dynamics
The time-averaged vibrational frequency distribution of OD modes of the interfacial water on the g-C3N4 surface was found to be a distribution ranging from about 2000 cm−1 to about 2900 cm−1 with a mean at 2496 cm−1, as shown in Fig. 2(a). The distribution is similar to a distribution found for bulk water at 300 K using a similar methodology (see Fig. 2(a) of ref. 46, for example), however, with two differences. First, the distribution in our Fig. 2(a) is slightly broader, and, more importantly, a clear shoulder peak now appears in the high-frequency region around 2750 cm−1, which is absent in bulk water. Closer analysis shows that this shoulder corresponds to the free or dangling OD modes, i.e., OD bonds that are not part of a H-bond network and not bound to the surface and stick out into vacuum instead. Similarly, the average vibrational frequency of OD modes on the C2N surface is 2487 cm−1 (Fig. 2(b)), and the whole time-averaged distribution is similar to the other surface. Also for C2N, a shoulder peak in the high-frequency region around 2750 cm−1 is found, again mainly due to the free/dangling OD modes of the interfacial water. Due to the non-centrosymmetric environment at the surface, the tetrahedral hydrogen-bond network is distorted for both surfaces and thus the population of free OD modes shows an overall increment. The high-frequency shoulder is more prominently observable for g-C3N4, which implies a comparatively higher population of free/dangling OD modes. Interestingly, high-frequency shoulders are also a characteristic feature of vSFG (vibrational sum frequency generation) spectra of other systems with interfacial water.24–26,42,47
| P(ω3,t2,ω1) = 〈δ(ω(t2) − ω3)·δ(ω(0) − ω1)〉. | (7) |
In Fig. 3, we have plotted the distributions for the waiting times t2 = 10, 100, 750 and 3500 fs for OD modes of water molecules on the g-C3N4 surface. For small waiting times, i.e., t2 = 10 fs, the distribution is predominantly a straight line aligned along the diagonal ω1 = ω3, indicating that the OD modes keep close to their initial vibrational frequency. However, for the longer waiting times, the distribution eventually gets elongated and evolves into a spherical distribution, which implies that the OD modes undergo vibrational spectral diffusion due to hydrogen-bond rearrangement. Moreover, within 3.5 ps the OD modes have sampled all accessible vibrational states/frequencies (cf.Fig. 2(a)). A key observation in the time-resolved frequency distributions is that the high-frequency shoulder is evidently observable at low as well as long waiting times. Furthermore, the vibrational dephasing of the modes corresponding to the shoulder peak is seen progressing as a vertical slab along 2750 cm−1.
 | ||
| Fig. 3 Joint probability frequency distribution P(ω3,t2,ω1) of OD modes of water molecules on the g-C3N4 surface for waiting times t2 = (a) 10, (b) 100, (c) 750 and (d) 3500 fs. | ||
A similar analysis for the water molecules on the C2N surface corresponding to the waiting times of t2 = 10, 100, 750 and 3500 fs is shown in Fig. 4. The vibrational dephasing follows a similar pattern, and overall differences between both surfaces seem small.
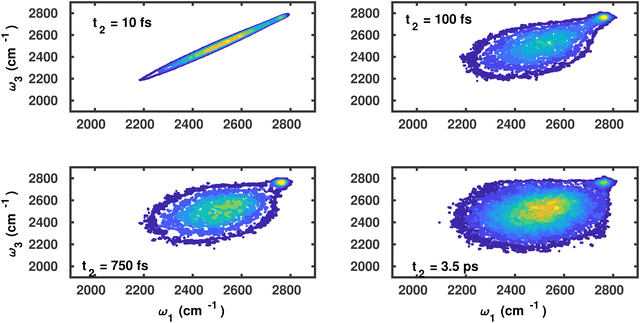 | ||
| Fig. 4 Joint probability frequency distribution P(ω3,t2,ω1) of OD modes of water molecules on the C2N surface for waiting times t2 = 0, 100, 750 and 3500 fs. | ||
To more quantitatively address this point, the temporal dynamics of the OD modes of water molecules on the g-C3N4 and C2N surfaces is also analyzed using a frequency time correlation function (FTCF), which is given as
 | (8) |
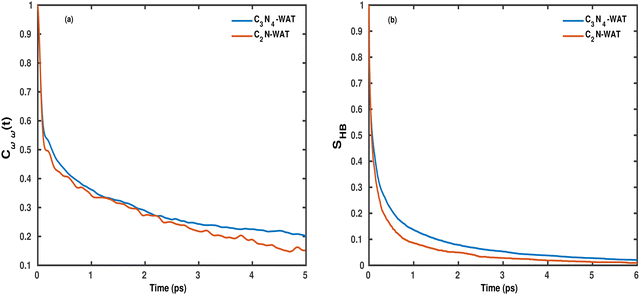 | ||
| Fig. 5 (a) Frequency correlation function Cωω(t) and (b) hydrogen bond correlation function SHB(t) for OD modes of water molecules on the g-C3N4 and C2N surfaces. | ||
Evidently, the decay is biphasic with a short time regime that extends up to 100 fs and is governed by the ultrafast librational dynamics or concerted collective motion of water molecules,48 whereas the long time decay extends up to a few picoseconds and is mainly attributed to the hydrogen bond rearrangement dynamics. The timescale of vibrational dephasing was determined by using a bi-exponential fitting function,
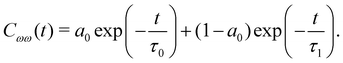 | (9) |
Since frequency fluctuations of the OD modes are associated with the rearrangement of the local hydrogen bond network, we have also calculated a “hydrogen bond lifetime” using a continuous HB correlation function given as
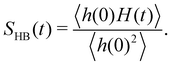 | (10) |
3.2 Vibrational sum frequency generation (vSFG) spectra
Further insight into the water dynamics on the studied 2D materials, more directly accessible by experiment, comes from vibrational spectroscopy. Here we concentrate on vibrational SFG as a particularly surface-sensitive method. | (11) |
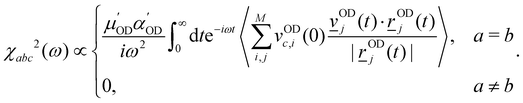 | (12) |
![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) ODi is the coordinate vector of an OD bond (i) as defined earlier (there are M = 2·N OD bonds for N water molecules),
ODi is the coordinate vector of an OD bond (i) as defined earlier (there are M = 2·N OD bonds for N water molecules), ![[v with combining low line]](https://www.rsc.org/images/entities/i_char_0076_0332.gif) ODi = d
ODi = d![[r with combining low line]](https://www.rsc.org/images/entities/i_char_0072_0332.gif) ODi/dt is the corresponding velocity, vODc,i is its c-component, and
ODi/dt is the corresponding velocity, vODc,i is its c-component, and  and
and  are the derivatives of the dipole moments and polarizabilities, respectively. A few things are worth mentioning: the ssVVAF expression (12) is approximate in the sense that only O–D stretching vibrations are considered. Furthermore, we also use a parameterized (linear) version of the dipole moments and polarizabilities without explicitly calculating them – in fact we also do not include the frequency dependence of
are the derivatives of the dipole moments and polarizabilities, respectively. A few things are worth mentioning: the ssVVAF expression (12) is approximate in the sense that only O–D stretching vibrations are considered. Furthermore, we also use a parameterized (linear) version of the dipole moments and polarizabilities without explicitly calculating them – in fact we also do not include the frequency dependence of 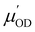 and
and  and set them as constants. Finally, a sometimes used “quantum correction factor” Q(ω)
and set them as constants. Finally, a sometimes used “quantum correction factor” Q(ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 is also neglected. Still, the approach followed here will give insight into the O–D dynamics and in particular into the dynamics of the interfacial H-bond network. The method has been shown to give for the O–H stretch region of a water/air interface quite similar vSFG spectra compared to a non-parameterized procedure with calculated dipole moments and polarizabilities.28
32 is also neglected. Still, the approach followed here will give insight into the O–D dynamics and in particular into the dynamics of the interfacial H-bond network. The method has been shown to give for the O–H stretch region of a water/air interface quite similar vSFG spectra compared to a non-parameterized procedure with calculated dipole moments and polarizabilities.28
In Fig. 6, we show the real and imaginary parts of χxxz2 for D2O at g-C3N4 (a) and C2N, respectively, again in the frequency range of the O–D stretching vibrations. To gain information on the orientation of the OD bonds, we focus on the imaginary part of χxxz2. (The real part of the vSFG spectrum is similar to a conventional infrared spectrum and provides information about the frequency required to excite vibrations of the adsorbed molecules.) For D2O/g-C3N4, the imaginary part of the susceptibility is characterized by a broad, (mostly) negative peak for the frequency domain of 2400–2700 cm−1, which refers to the OD modes that are hydrogen-bonded with the other water molecules or with the g-C3N4 surface (Fig. 6(a)). We also note a sharp positive peak for the frequency domain of 2700–2800 cm−1, referring to free, dangling, or weakly bound OD units (with D2O not having four D-bonded neighbours), which are orientated away from the surface. For example, OD bonds pointing into vacuum are of this type. Note that positive intensities refer to dominantly “upward” and negative intensities dominantly to “downward” orientations of OD bonds. We also note that the intensity of this peak remains unchanged relative to the (unsupported) pure water/air interface computed in ref. 30 (Fig. 2 there), while the intensity of bonded, red-shifted OD modes is relatively reduced compared to this reference. This may imply an overall reduction of contributing bonded OD bonds, relative to the free/non-bonded ones, in the case of water on C/N surfaces compared to the water/air interface. This is in agreement with the frequency distribution of water molecules on g-C3N4, as shown in Fig. 1(a), where the population of free/dangling OD modes is clearly visible as a high-frequency shoulder.
 | ||
| Fig. 6 Real and imaginary parts of χxxz2 for D2O at (a) g-C3N4 and (b) C2N surfaces. The y-axis is in arbitrary units, with the largest positive intensity of imaginary or real parts normalized to 1. | ||
Furthermore, in Fig. 6(b) the second-order susceptibility of the water molecules on the C2N surface is shown. The imaginary part of the second-order susceptibility for this system is more similar to the pure water–air interface.30 Namely, similar to the latter, the negative-intensity peak covering the spectral domain of 2200–2700 cm−1 for the water/C2N system is broader and of larger intensity (comparable to the high-frequency peak) compared to the water/g-C3N4 surface. (Note that in ref. 28 and 30, non-deuterated water was considered so absolute oxygen–hydrogen frequencies are different).
To summarize, the vSFG spectra of OD modes on the g-C3N4 and C2N surfaces have similar features for the high-frequency region around 2700–2800 cm−1. But for the frequency region of 2200–2700 cm−1, the spectral intensity is depleted in the case of g-C3N4, while it is not for water/C2N, which behaves similar to the water–air interface.28 We attribute this behaviour to a propensity of the C2N material to stabilize bonded OD bonds.
 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(2)(ω; Tw) (actually, Im
χ(2)(ω; Tw) (actually, Im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ(2)(ωIR; Tw, ωpump)).
χ(2)(ωIR; Tw, ωpump)).
To calculate the TD-vSFG spectra of the hydrogen-bonded OD modes, we have applied a broadband IR pump pulse corresponding to the frequency domain of 2200–2700 cm−1. Technically, this was done by computing the susceptibilities of the water molecules based on their vibrational excitation frequency within this frequency range. The imaginary parts of the second-order susceptibility of the hydrogen-bonded OD modes of the interfacial water molecules on g-C3N4 corresponding to the waiting times Tw = 0, 400, 2000, 3000 and 4000 fs are shown in Fig. 7(a). The spectrum for the waiting time Tw = 0 fs, the “impulsive limit”, is dominated by a peak with negative intensity centered around 2600 cm−1. With increasing waiting times, e.g. for Tw = 400 fs, we see a formerly shallow shoulder in the high-frequency region around 2750 cm−1 growing, corresponding to the free/dangling OD modes. In addition, within 4.0 ps, the peak has attained the maximum intensity and becomes saturated. The figure demonstrates the interconversion from hydrogen/surface-bonded (“bound”) OD modes to free OD modes taking place on this timescale.
Similarly, we have calculated spectra of free/dangling OD modes of g-C3N4 for waiting times Tw = 0, 200, 1000 and 2000 fs in Fig. 7(b). Here we applied a narrowband IR pump pulse in the range of 2700–2900 cm−1. The spectrum for Tw = 0 fs is a single, positive peak centered around 2750 cm−1. With increasing waiting times of Tw = 200, 1000, and 2000 fs, the frequency domain between 2200 and 2700 cm−1 corresponding to the H-bonded region shows finite-valued, negative intensity, while at the same time the high-frequency, positive peak loses intensity. This indicates interconversion of free OD modes to (H-)bound OD modes. Closer inspection shows, as can also be seen from the shorter timescale shown in Fig. 7(b), that the free → bound interconversion proceeds faster (within about 2 ps) in (b) than the bound → free interconversion (about 4 ps) in (a). This is due to the free OD modes having a strong propensity to form hydrogen bonds and stabilize. When compared to the pure water/air interface,30,31 it is found that the hydrogen-bond interconversion dynamics for the bonded OD modes are overall slowed down, whereas for the free OD, the timescale remains relatively unchanged in the presence of the g-C3N4 surface.
Along the same lines, we have also obtained the spectra of the bonded and dangling/free OD bonds of water on the C2N surface, as shown in Fig. 7(c) and (d). The spectra of the bonded OD modes are shown for waiting times of Tw = 0, 400, 2000, 5000 and 8000 fs. While the spectral features as seen in the TD-vSFG spectra are similar to previous calculations for the water/air interface,30 a key difference is a very slow temporal evolution of the peak for the free OD modes, which extends up to nearly 8 ps.
The spectra of dangling/free OD modes are shown for waiting times of Tw = 0, 200, 1000, 2000 and 5000 fs. Again, the free OD modes have a strong propensity to form hydrogen bonds due to which the spectral domain corresponding to the bonded OD modes proceeds mostly within 2 ps. The spectra of free OD modes of interfacial water molecules are interestingly independent of the surface, i.e., g-C3N4 or C2N.
To summarize, we note that although the overall vibrational dynamics of OD modes on g-C3N4 and C2N are similar according to the frequency correlation function, Fig. 5(a) (with a tendency of faster H-bond dynamics for C2N), the interconversion rates of free and bonded OD modes can still be significantly different (and of other order). This refers in particular to the bound → free interconversion of OD bonds, where D2O/C2N exhibits a significantly longer (∼8 ps) timescale than D2O/g-C3N4 (∼4 ps). Here we want to emphasize that the time-resolved vSFG spectra of hydrogen-bonded OD modes on the g-C3N4/C2N gives a comparative perspective of stabilization of the OD modes on two surfaces. The observed differences in the interconversion rates for the two systems imply that g-C3N4 could be more suitable for catalyzing interfacial reactions involving water, e.g., water dissociation because the OD modes have a relatively higher propensity to break the hydrogen bonds (∼4 ps). In contrast, C2N may be more suited for processes like desalination or sieving, which require stabilization of water by the surface with an average interconversion rate of nearly 8 ps.
The key differences between both systems is that the g-C3N4 has a buckled surface whereas C2N is flat. Moreover, from the stoichiometric perspective, g-C3N4 has a higher percentage of nitrogen compared to C2N. These factors obviously affect the HB dynamics of adsorbed water. Finally, we note that the present inferences are drawn based on the TD-vSFG spectra of water molecules on a single monolayer of g-C3N4 or C2N. The role of a multi-layered surface as well as the density of water molecules corresponding to a liquid phase in the simulation, may bring more insight into the catalytic properties of the two materials. Work along these lines is in progress in our laboratory.
4 Summary
To summarize, we have studied the vibrational dynamics and (time-dependent) vSFG spectra of deuterated water molecules at g-C3N4 and C2N surfaces, respectively, using DFT-based AIMD simulations. The most important results are as follows.• The time-averaged frequency distribution for the OD modes of water molecules on both surfaces shows a high-frequency peak corresponding to free OD modes. The “bound” OD bonds, either engaged in the intermolecular H-bond network or interacting with the C/N surface, are usually weakened and therefore red-shifted w.r.t. the high-frequency peak.
• The time-dependent decay of the OD frequency (measured using a frequency correlation function) is quite similar for both surfaces with a timescale of about 4 ps, which is considerably slower than that of the bulk liquid (deuterated) water. Similar trends for the two studied C/N surfaces arise when analyzing the H-bond network via a H-bond measure, SHB(t), which implies a slightly longer timescale for g-C3N4 than for C2N.
• Time-independent vSFG spectra (measured using χxxz2), indicate that the dangling OD bonds pointing upward and away from the water/vacuum interface are dominant features in the spectra and are characterized by positive imaginary parts of χxxz2 at high frequencies. “Bound” OD modes are usually of lower intensity, have negative imaginary parts of χ2 and are red-shifted. As a difference between the two surfaces, the spectral domain around 2000–2600 cm−1 of the vSFG spectrum for D2O/C2N is marked by a stronger negative intensity peak compared to g-C3N4.
• Detailed insight into OD bond dynamics is provided by TD-vSFG spectra, with interesting trends for the two surfaces. Although the vibrational frequency correlation functions are similar, the time-resolved vSFG of bonded OD modes saturates within about 4 ps for g-C3N4, whereas the same process takes nearly 8 ps for the C2N surface. The “free” → “bound” interconversion is faster (∼2 ps) and more similar for both surfaces. Thus we can infer on the basis of slower interconversion rates for the bonded to free OD state that the C2N surface has a propensity to stabilize bonded OD moieties.
All of these observations imply different performance of porous C/N-containing materials in either catalysis or sieving. That key factors like pore size, C/N ratio, or the three-dimensional structure of the materials (e.g., flat or buckled) influence the vibrational dynamics of adsorbed water has been demonstrated; however, how these factors act in detail is a matter of further research.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. S. acknowledges support by the Deutsche Forschungsgemeinschaft (DFG), through project Sa 547-18, and Ch. P. by Deutsche Forschungsgemeinschaft within Germany’s Excellence Strategy – EXC 2008/1-390540038, UniSysCat. The authors thank the Paderborn Center for Parallel Computing (PC2) for computation time on supercomputer “Noctua 2”.References
- O. Björneholm, M. H. Hansen, A. Hodgson, L.-M. Liu, D. T. Limmer, A. Michaelides, P. Pedevilla, J. Rossmeisl, H. Shen, G. Tocci, E. Tyrode, M.-M. Walz, J. Werner and H. Bluhm, Chem. Rev., 2016, 116, 7698–7726 CrossRef PubMed.
- Y. Jung and R. A. Marcus, J. Am. Chem. Soc., 2007, 129, 5492–5502 CrossRef CAS PubMed.
- J. L. Skinner, P. A. Pieniazek and S. M. Gruenbaum, Acc. Chem. Res., 2012, 45, 93–100 CrossRef CAS PubMed.
- P. Jungwirth, J. Phys. Chem. Lett., 2015, 6, 2449–2451 CrossRef CAS PubMed.
- G. Gonella, et al. , Nat. Rev. Chem., 2021, 5, 466–485 CrossRef CAS PubMed.
- J. Zhu, et al. , Angew. Chem., Int. Ed., 2015, 54, 9111–9114 CrossRef CAS PubMed.
- N. G. Hörrmann, Z. Guo, F. Ambrosio, O. Andreussi, A. Pasquarello and N. Marzari, npj Comput. Mater., 2019, 5, 100–105 CrossRef.
- X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80 CrossRef CAS PubMed.
- Y. Wang, X. Wang and M. Antonietti, Angew. Chem., Int. Ed., 2012, 51, 68–89 CrossRef CAS PubMed.
- X. Wang, S. Blechert and M. Antonietti, ACS Catal., 2012, 2, 1596–1606 CrossRef CAS.
- R. Walczak, B. Kurpil, A. Savateev, T. Heil, J. Schmidt, Q. Qin, M. Antonietti and M. Oschatz, Angew. Chem., Int. Ed., 2018, 57, 10765–10770 CrossRef CAS PubMed.
- J. Heske, R. Walczak, J. D. Epping, S. Youk, S. K. Sahoo, M. Antonietti, T. D. Kühne and M. Oschatz, J. Mater. Chem. A, 2021, 9, 22563–22572 RSC.
- C. Penschke, A. Zehle, N. Jahn, R. E. von Zander, R. Neumann, A. Beqiraj and P. Saalfrank, Phys. Chem. Chem. Phys., 2022, 24, 14709–14726 RSC.
- T. Schäfer, A. Gallo, A. Irmler, F. Hummel and A. Grüneis, J. Chem. Phys., 2021, 155, 244103 CrossRef PubMed.
- H.-Z. Wu, L.-M. Liu and S.-J. Zhao, Phys. Chem. Chem. Phys., 2014, 16, 3299–3304 RSC.
- S. M. Aspera, M. David and H. Kasai, Jpn. J. Appl. Phys., 2010, 49, 115703 CrossRef.
- X. Zou, M. Li, S. Zhou, Ch Chen, J. Zhong, A. Xue, Y. Zhang and Y. Zhao, J. Membr. Sci., 2019, 585, 81–89 CrossRef CAS.
- J. Wirth, R. Neumann, M. Antonietti and P. Saalfrank, Phys. Chem. Chem. Phys., 2014, 16, 15917–15926 RSC.
- I.-C. Yeh and G. Hummer, J. Phys. Chem. B, 2004, 108, 15873–15879 CrossRef CAS.
- N. Kavokine, R. R. Netz and L. Bocquet, Annu. Rev. Fluid Mech., 2021, 53, 377–410 CrossRef.
- Q. Du, R. Superfine, E. Freysz and Y. R. Shen, Phys. Rev. Lett., 1993, 70, 2313–2316 CrossRef CAS PubMed.
- Y. R. Shen and V. Ostroverkhov, Chem. Rev., 2006, 106, 1140–1154 CrossRef CAS PubMed.
- V. Ostroverkhov, G. A. Waychunas and Y. R. Shen, Phys. Rev. Lett., 2005, 94, 046102 CrossRef PubMed.
- A. Morita and J. T. Hynes, Chem. Phys., 2000, 258, 371–390 CrossRef CAS.
- A. Morita and J. T. Hynes, J. Phys. Chem. B, 2002, 106, 673–685 CrossRef CAS.
- T. Ishiyama, T. Imamura and A. Morita, Chem. Rev., 2014, 114, 8447–8470 CrossRef CAS PubMed.
- A. Morita, Theory of Sum Frequency Generation Spectroscopy, Springer, Singapore, 2018 Search PubMed.
- D. Ojha and T. D. Kühne, Molecules, 2020, 25, 3939 CrossRef CAS PubMed.
- E. H. G. Backus, J. D. Cyran, M. Grechko, Y. Nagata and M. Bonn, J. Phys. Chem. A, 2018, 122, 2401–2410 CrossRef CAS PubMed.
- D. Ojha, N. K. Kaliannan and T. D. Kühne, Commun. Chem., 2019, 2, 116 CrossRef.
- D. Ojha and T. D. Kühne, Sci. Rep., 2021, 11, 2456 CrossRef CAS PubMed.
- T. Ohto, K. Usui, T. Hasegawa, M. Bonn and Y. Nagata, J. Chem. Phys., 2015, 143, 124702 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. J. Gillan, D. Alfè and A. Michaelides, J. Chem. Phys., 2016, 144, 130901 CrossRef PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- G. Melani, Y. Nagata, R. K. Campen and P. Saalfrank, J. Chem. Phys., 2019, 150, 244701 CrossRef PubMed.
- A. Semparithi and S. Keshavamurthy, Phys. Chem. Chem. Phys., 2003, 5, 5051–5062 RSC.
- D. Ojha, A. Henao and T. D. Kühne, J. Chem. Phys., 2018, 148, 102328 CrossRef PubMed.
- D. Ojha, K. Karhan and T. D. Kühne, Sci. Rep., 2018, 8, 16888 CrossRef PubMed.
- D. Ojha and T. D. Kühne, Phys. Chem. Chem. Phys., 2023, 25, 13442 RSC.
- G. Melani, Y. Nagata, J. Wirth and P. Saalfrank, J. Chem. Phys., 2018, 149, 014707 CrossRef PubMed.
- M. Heyden, J. Sun, S. Funkner, G. Mathias, H. Forbert, M. Havenith and D. Marx, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12068–12073 CrossRef CAS PubMed.
- D. Ojha and A. Chandra, Chem. Phys. Lett., 2020, 751, 137493 CrossRef CAS.
- J. R. Choudhuri and A. Chandra, J. Chem. Phys., 2014, 141, 194705 CrossRef PubMed.
| This journal is © the Owner Societies 2024 |


