Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic origin of negative thermal expansion in samarium hexaboride revealed by X-ray diffraction and total scattering†
Li
Li
 a,
Martin T.
Dove
a,
Martin T.
Dove
 *bcd,
Zhongsheng
Wei
*bcd,
Zhongsheng
Wei
 d,
Anthony E.
Phillips
d,
Anthony E.
Phillips
 d and
Dean S.
Keeble
d and
Dean S.
Keeble
 e
e
aCollege of Science, Civil Aviation Flight University of China, 46 Nanchang Road, Guanghan, 618307, Sichuan, China
bInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu, 610065, Sichuan, China. E-mail: martin.dove@icloud.com
cSchool of Mechanical Engineering, Dongguan University of Technology, 1st Daxue Road, Songshan Lake, Dongguan, 523000, Guangdong, China
dSchool of Physical and Chemical Sciences, Queen Mary University of London, Mile End Road, London, E1 4NS, UK
eDiamond Light Source Ltd, Harwell Science and Innovation Campus, Didcot, Oxfordshire OX11 0DE, UK
First published on 14th February 2024
Abstract
Samarium hexaboride, SmB6, is a negative thermal expansion (NTE) material whose structure is similar to other known NTE materials such as the family of Prussian blues. In the Prussian blues, NTE is due to a phonon mechanism, but we recently showed from DFT calculations that this is unlikely in SmB6 (Li et al., Phys. Chem. Chem. Phys. 2023, 25, 10749). We now report experimental X-ray diffraction and pair distribution function analysis of this material in the temperature range 20–300 K. The interatomic distances shown by both methods are consistent with the NTE instead arising from an electronic effect, by which the samarium atoms lose electrons and thus have a smaller ionic radius as the temperature increases.
1 Introduction
Samarium hexaboride, SmB6, has a very simple cubic crystal structure1,2 (Fig. 1, space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), which consists of B6 octahedra whose corners are linked together with B–B bonds, and with the samarium atoms lying in the large cavities of m
m), which consists of B6 octahedra whose corners are linked together with B–B bonds, and with the samarium atoms lying in the large cavities of m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m point symmetry. SmB6 has many interesting features,5 including as a topological Kondo insulator with strongly correlated electrons and a narrow band gap.6–12 However, here we are primarily interested in its anomalous property of showing negative thermal expansion (NTE).
m point symmetry. SmB6 has many interesting features,5 including as a topological Kondo insulator with strongly correlated electrons and a narrow band gap.6–12 However, here we are primarily interested in its anomalous property of showing negative thermal expansion (NTE).
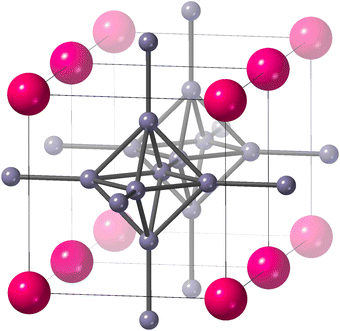 | ||
Fig. 1 The crystal structure of SmB6 (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m),1,2 reproduced from our earlier paper.3 Samarium atoms are the larger pink atoms at the corners of the unit cell, and boron atoms are the small grey spheres connected by rods to represent chemical bonds. We show two unit cells to highlight the connectivity of B6 octahedra. The figure was drawn using CrystalMaker®.4 m),1,2 reproduced from our earlier paper.3 Samarium atoms are the larger pink atoms at the corners of the unit cell, and boron atoms are the small grey spheres connected by rods to represent chemical bonds. We show two unit cells to highlight the connectivity of B6 octahedra. The figure was drawn using CrystalMaker®.4 | ||
NTE was first observed in SmB6 in 1999,1 and is confirmed in the present study. Whilst most materials show positive thermal expansion (PTE) at all temperatures, there is a growing number of materials that show NTE.13,14 For many of these, the NTE is isotropic, as in SmB6. Most NTE materials have crystal structures composed of linked structural polyhedra. Examples of isotropic NTE materials include ZrW2O8,15 ZnV2O7,16 CuO,17 ScF3,18 several zeolites,19–21 Zn(CN)2,22 Si(NCN)2,23 and the family of Prussian blue analogue materials.24 Whilst many of these have corner-sharing polyhedra, the last three have a small molecular ion providing the linkage between polyhedra. Several recent reviews discuss NTE materials and the underlying mechanisms.13,14,25–27
The common mechanism for NTE in network materials is the tension effect.25 In the case of a material as simple as ScF3, this is realised in an intuitive way,28,29 as we now explain. ScF3 has a simple cubic crystal structure consisting of corner-sharing ScF6 octahedra with linear Sc–F–Sc bonds. Because the Sc–F bonds are quite strong, transverse motions of the F atoms pull the connected Sc atoms together rather than stretch the Sc–F bonds. Since the amplitude of this motion increases with temperature, the inward pull grows with heating, and hence NTE emerges naturally. Moving from this simple idea into a robust explanation has been discussed recently, based on total scattering data analysed with the Reverse Monte Carlo method, molecular dynamics with simplified models, and ab initio phonon calculations,28,29 with a focus on the role of Rigid Unit Modes (RUMS) and quasi-RUMs.30,31
The signature of the operation of the tension effect is a difference between the behaviour of the average crystal structure, as given by the Bragg diffraction, and that of the local atomic structure as seen in measurements of the pair distribution function (PDF). For example, in ScF3 the average structure has the distances between the mean positions of neighbouring Sc and F atoms (equal to half the cubic lattice parameter, a/2) shrinking on heating, but the mean instantaneous Sc–F distance seen in the PDF shows normal PTE.28 Similarly the instantaneous F–F distances within the ScF6 octahedra from the PDF also show PTE whereas the corresponding distances between the mean positions of the fluorine atoms in the crystal structure (equal to 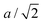 ) show NTE. On the other hand, the mean instantaneous Sc–Sc distance from the PDF also shows NTE, because the transverse displacements of the F atoms are pulling the two connected Sc atoms together along the common connecting line. Thus if NTE is caused by a tension effect we expect to see some of the changes in the local structure to be the opposite of those of the average structure, whereas if the behaviour of the local structure of an NTE material mirrors that of its average structure it is probable that the NTE arises from a reason other than the operation of a tension effect.
) show NTE. On the other hand, the mean instantaneous Sc–Sc distance from the PDF also shows NTE, because the transverse displacements of the F atoms are pulling the two connected Sc atoms together along the common connecting line. Thus if NTE is caused by a tension effect we expect to see some of the changes in the local structure to be the opposite of those of the average structure, whereas if the behaviour of the local structure of an NTE material mirrors that of its average structure it is probable that the NTE arises from a reason other than the operation of a tension effect.
There is a close analogy of the crystal structure of SmB6 with that of Prussian blue,24 representing another family of NTE materials. Because of this we had considered that there might be a tension effect giving rise to the NTE in SmB6. If so, it could involve the large number of potential RUMs in this structure type.32 We anticipated that the B6 octahedra might be relatively rigid, and that the linkage B–B bonds will be stiff, but that the network might be able to flex sufficiently through bending the angles between the B6 octahedra and the B–B linkages connecting neighbouring octahedra, as in the family of Prussian blue materials. We recently explored this by calculating the lattice dynamics of SmB6 and some alkali-earth hexaborides using Density Functional Theory (DFT).3 We found that the RUMs are actually of relatively high frequency, and that too few phonons will support NTE. Thus we concluded that NTE in SmB6 does not arise from a phonon-based tension-effect mechanism.
Because there is no magnetic order in SmB6,33 we do not believe that NTE can arise from magnetic interactions.21 This leaves only an electronic origin for NTE in SmB6via a charge-transfer mechanism.34 With an increasing temperature there might be a transfer of electrons from the samarium atom to the boron network, meaning that the samarium atom effectively becomes smaller on heating. The NTE caused by the atomic radius becoming smaller will dominate over the normal PTE caused by the phonons until higher temperatures. Examples of this occurring in Sm-containing compounds are samarium fulleride, Sm2.75C60,35 and Y-doped SmS,36 both studied using X-ray diffraction.
The purpose of this paper is to explore the electronic mechanism for NTE in SmB6, using a combination of X-ray powder diffraction, with Rietveld refinement of the crystal structure, and X-ray total scattering measurements which give the PDF. From the crystal structure we can obtain the distances between the average positions of pairs of atoms, and from the PDF we can obtain the average instantaneous separations between some of these.‡ As discussed above with the example of ScF3, we would expect to see differences in the distances between average positions of neighbouring atoms and their mean instantaneous separation if the NTE in SmB6 arises from a tension effect mechanism. Our recent study of the metal hexaborides using DFT methods3 showed that increasing the size of the metal atom leads to increases in the sizes of the B6 octahedra and of the length of the inter-octahedral B–B bonds. In this paper, we have extracted relevant interatomic distances from analysis of our diffraction data and from the positions of peaks in the PDF (see comments below regarding the B–B distances in the PDF). Anticipating later discussion, we will show that there is very little difference between how the average and local structures change with temperature, confirming the likelihood that NTE in SmB6 does not arise from a tension mechanism. Instead, the results are consistent with the samarium atoms becoming smaller on heating as a result of electron transfer from the samarium atoms to the boron network.
2 Methods
The sample of SmB6 was kindly given to us by Prof Geetha Balakrishnan (University of Warwick).33 It was sealed within a thin-walled silica-glass capillary tube of inner diameter 0.3 mm.The X-ray scattering experiments were performed on the XPDF (I15-1) beam-line at the Diamond Light Source (UK), with X-ray wavelength of 0.161669 Å. At the time of running the experiment, the instrument was operating with a single area detector, PerkinElmer XRD1621 EN, containing 4096 × 4096 square pixels, each with 100 μm edge length.§ For the total scattering measurements, the detector was placed at a position 214 mm from the sample, with data collection times of 600 s. For the diffraction measurements, the detector was placed at a position 827 mm from the sample, with data collection times of 10 s.
The data were extracted from the raw two-dimensional detector pixel data using Diamond's in-house Dawn software.37 The calibrations of scattering angle for both positions of the detector were performed by measuring the diffraction pattern from a NIST standard sample of silicon powder, calibrating on the Debye–Scherrer rings of the two-dimensional data. For the high-resolution setting for Rietveld analysis, a subsequent calibration was performed on the reduced one-dimensional data using the same silicon standard.
The temperature of the sample was controlled using a Oxford Cryosystems Helix open-flow helium system. The cold gas stream was collinear with the axis of the sample capillary. The Helix system was positioned so as to place the capillary as close as possible to the centre of the beryllium shield. The temperature calibration was performed using X-ray diffraction measurements of lead powder. This sample was chosen because lead still has an appreciable thermal expansion at the low temperatures demanded by this experiment. Since the procedure for temperature calibration defined the sample position using the location of the primary X-ray beam, and alignment along the beam direction was performed as a matter of course to ensure the validity of the scattering geometry calibration, any sample misalignment effects in the calibration would have been mitigated. Furthermore, since this procedure used the X-ray measurement for performing the temperature calibration, it also includes some corrections for the impact of X-ray heating of the sample. Total scattering and diffraction data were collected for the range of temperatures 20–300 K in steps of 10 K.
Rietveld refinement was performed using Topas. We used neutral-atom X-ray scattering factors in the Rietveld refinements, as we also did in our correction of the total scattering data (discussed below). In light of our argument from the data presented in this paper that the samarium atoms lose electrons on heating, it is important to understand whether this can be seen in the X-ray scattering factors. From comparison of the scattering factors for Sm3+ and neutral samarium – comparing the two extreme cases – it is found that the significant differences in the scattering functions only exist at low values of Q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ, for Q < 2 Å−1. The effect only being seen at low values of Q comes from the fact that the change in electron density only occurs at the outer radius of the atom. The value for Q = 2 Å−1 corresponds to a scattering angle 2θ = 3°. There is only a single Bragg peak below this scattering angle, at 2θ = 2.24°. At the corresponding value of Q the difference in scattering factors between Sm3+ and neutral samarium is only 1.2%, and, as we noted, this is the extreme limit of the effect of electron transfer, and the actual difference in SmB6 is likely to be much lower.
θ/λ, for Q < 2 Å−1. The effect only being seen at low values of Q comes from the fact that the change in electron density only occurs at the outer radius of the atom. The value for Q = 2 Å−1 corresponds to a scattering angle 2θ = 3°. There is only a single Bragg peak below this scattering angle, at 2θ = 2.24°. At the corresponding value of Q the difference in scattering factors between Sm3+ and neutral samarium is only 1.2%, and, as we noted, this is the extreme limit of the effect of electron transfer, and the actual difference in SmB6 is likely to be much lower.
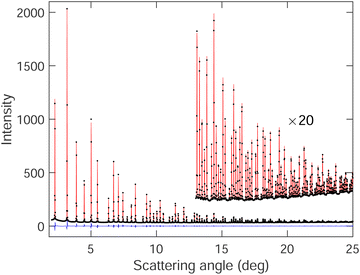
The graph of one of the fitted diffraction patterns is shown in Fig. 2, showing the quality of fit that was achieved.
Total scattering data were corrected for effects such as beam attenuation, background scattering, fluorescence and Compton scattering, and normalised, using GudrunX.38,39 This process required measurements of the empty instrument and empty silica glass tube. This gave the scattering function i(Q),40–42 obtained by subtraction of the self-scattering term from the total scattering, together with normalisation by the mean-square scattering factor 〈f2(Q)〉 to (approximately) deconvolve out the effects of atom size on the resultant PDF.
We can define two overall PDF functions, D(r) and T(r), in terms of the partial PDFs gmn(r):40–42
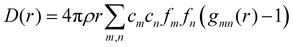 | (1) |
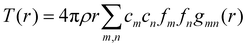 | (2) |
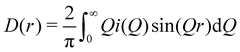 | (3) |
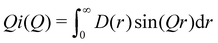 | (4) |
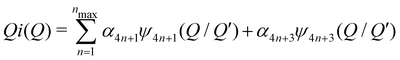 | (5) |
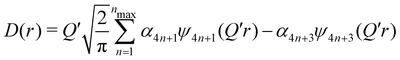 | (6) |
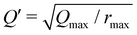 (Qmax and rmax are the maximum limits in the scattering data and PDF respectively), and nmax ≃ Qmaxrmax.44 The coefficients αm are obtained by fitting eqn (5) to the experimental data for Qi(Q). The PDF follows by recombining the Hermite functions with the fitted coefficients, eqn (6).
(Qmax and rmax are the maximum limits in the scattering data and PDF respectively), and nmax ≃ Qmaxrmax.44 The coefficients αm are obtained by fitting eqn (5) to the experimental data for Qi(Q). The PDF follows by recombining the Hermite functions with the fitted coefficients, eqn (6).
We used the Lorch modification function46,47 to remove the termination ripples in the Fourier transform, by modifying eqn (3) as
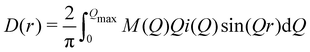 | (7) |
| M(Q) = sin(πQ/Qmax)/(πQ/Qmax) | (8) |
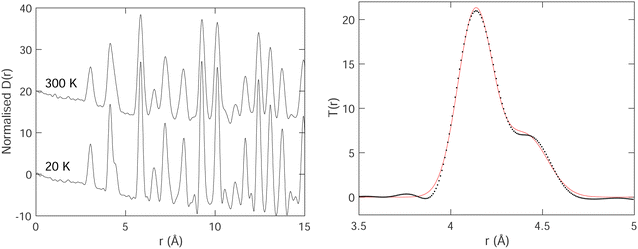
The PDFs for two temperatures, 20 K and 300 K, are shown in Fig. 3. In the PDFs, we cannot recognize B–B peaks, even though a prior simulation48 had shown that it might be possible to see such peaks, particularly the first intra-octahedral peak at around 1.75 Å. Thus we see only Sm–B and Sm–Sm peaks. The first peak at around 3 Å is the shortest Sm–B distance. The second feature at around 4.15 Å is a strong peak for the first Sm–Sm distance with a shoulder corresponding to the second Sm–B distance (around 4.4 Å).
We fitted T(r) (eqn (2)) using Gaussian functions to describe the peaks. The first peak (Sm–B) is a single Gaussian, and the second peak is a doublet of Sm–Sm (lattice repeat) and the second Sm–B peak. One of the examples of the fitting is shown in Fig. 3, which indicates that the fitting is very good.
3 Results
3.1 Results from X-ray powder diffraction and Rietveld refinement
Results from the Rietveld refinements for all temperatures are given in Table 1. These include the key parameters for the crystal structure and some interatomic distances derived from the crystal structure. Corresponding CIF files are given in the ESI.† The table also gives corresponding distances from analysis of the PDF (discussed later). The crystal structure parameters are in excellent agreement with two previous crystal structure refinements, one from neutron powder diffraction1 and the other from single-crystal X-ray diffraction,49 but whereas these two studies report only 3 or 4 temperatures, and one is only for temperatures of 100–300 K, our data are for a wide range of temperatures with much finer intervals (Section 2).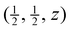 and those related to this position by the symmetry of the space group (Pm
and those related to this position by the symmetry of the space group (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). The Sm–B and B–B distances are derived from the crystallographic data,a and Sm–B and Sm–Sm distances are obtained directly from the PDFs. The final two columns give the isotropic APD for samarium and the weighed profile R factor. Estimated standard deviations on the last significant digits are given in brackets
m). The Sm–B and B–B distances are derived from the crystallographic data,a and Sm–B and Sm–Sm distances are obtained directly from the PDFs. The final two columns give the isotropic APD for samarium and the weighed profile R factor. Estimated standard deviations on the last significant digits are given in brackets
| T (K) | a (Å) | Sm–Sm from PDF (Å) | B z | Inter-B6 B–B (Å) | Intra-B6 B–B (Å) | 1st Sm–B (Å) | 1st Sm–B from PDF (Å) | Sm Uiso × 103 (Å2) | R wp (%) |
|---|---|---|---|---|---|---|---|---|---|
a Distances from the crystallographic data are obtained as 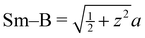 , inter-octahedral B–B = 2za, and intra-octahedral , inter-octahedral B–B = 2za, and intra-octahedral 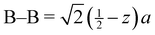 . .
|
|||||||||
| 20 | 4.134048 (11) | 4.1370 (5) | 0.2007 (7) | 1.661 (6) | 1.749 (4) | 3.0388 (5) | 3.0397 (6) | 1.50 (5) | 3.57 |
| 30 | 4.133853 (11) | 4.1370 (5) | 0.2009 (7) | 1.662 (6) | 1.748 (4) | 3.0389 (5) | 3.0399 (6) | 1.60 (5) | 3.60 |
| 40 | 4.133671 (11) | 4.1368 (5) | 0.2008 (7) | 1.661 (6) | 1.748 (4) | 3.0387 (6) | 3.0398 (6) | 1.74 (6) | 3.55 |
| 50 | 4.133459 (11) | 4.1363 (5) | 0.2010 (7) | 1.663 (6) | 1.747 (4) | 3.0387 (6) | 3.0397 (6) | 1.92 (6) | 3.55 |
| 60 | 4.133254 (12) | 4.1359 (5) | 0.2006 (7) | 1.659 (6) | 1.749 (4) | 3.0381 (6) | 3.0394 (6) | 2.15 (6) | 3.53 |
| 70 | 4.133054 (12) | 4.1357 (5) | 0.2004 (7) | 1.657 (6) | 1.751 (4) | 3.0377 (6) | 3.0395 (6) | 2.40 (6) | 3.52 |
| 80 | 4.132938 (12) | 4.1354 (5) | 0.2001 (7) | 1.655 (6) | 1.752 (4) | 3.0373 (6) | 3.0393 (6) | 2.61 (6) | 3.51 |
| 90 | 4.132830 (12) | 4.1351 (5) | 0.1991 (7) | 1.647 (6) | 1.758 (4) | 3.0361 (6) | 3.0392 (6) | 2.86 (6) | 3.47 |
| 100 | 4.132736 (12) | 4.1348 (5) | 0.2000 (7) | 1.654 (6) | 1.752 (4) | 3.0371 (6) | 3.0390 (6) | 3.10 (6) | 3.48 |
| 110 | 4.132690 (12) | 4.1344 (5) | 0.2003 (7) | 1.657 (6) | 1.751 (4) | 3.0374 (6) | 3.0389 (6) | 3.30 (6) | 3.46 |
| 120 | 4.132648 (12) | 4.1344 (5) | 0.2000 (7) | 1.654 (6) | 1.753 (4) | 3.0370 (6) | 3.0391 (6) | 3.52 (6) | 3.45 |
| 130 | 4.132647 (12) | 4.1341 (5) | 0.1993 (7) | 1.649 (6) | 1.756 (4) | 3.0363 (6) | 3.0388 (6) | 3.75 (7) | 3.42 |
| 140 | 4.132657 (12) | 4.1345 (5) | 0.1999 (7) | 1.654 (6) | 1.753 (4) | 3.0370 (6) | 3.0390 (6) | 4.01 (7) | 3.42 |
| 150 | 4.132704 (12) | 4.1343 (5) | 0.1997 (7) | 1.652 (6) | 1.754 (4) | 3.0368 (6) | 3.0388 (6) | 4.20 (7) | 3.42 |
| 160 | 4.132745 (12) | 4.1347 (5) | 0.1988 (7) | 1.645 (6) | 1.759 (4) | 3.0358 (6) | 3.0387 (6) | 4.45 (7) | 3.37 |
| 170 | 4.132808 (12) | 4.1346 (5) | 0.1990 (7) | 1.646 (6) | 1.758 (4) | 3.0360 (6) | 3.0386 (6) | 4.64 (7) | 3.37 |
| 180 | 4.132873 (12) | 4.1346 (5) | 0.1986 (7) | 1.644 (6) | 1.760 (4) | 3.0358 (6) | 3.0386 (6) | 4.87 (7) | 3.38 |
| 190 | 4.132954 (12) | 4.1345 (5) | 0.1991 (7) | 1.647 (6) | 1.758 (4) | 3.0363 (6) | 3.0384 (6) | 5.10 (7) | 3.35 |
| 200 | 4.133027 (13) | 4.1343 (5) | 0.1988 (7) | 1.645 (6) | 1.759 (4) | 3.0361 (6) | 3.0380 (6) | 5.32 (7) | 3.34 |
| 210 | 4.133116 (13) | 4.1343 (5) | 0.1990 (7) | 1.647 (6) | 1.758 (4) | 3.0363 (6) | 3.0385 (6) | 5.53 (8) | 3.32 |
| 220 | 4.133207 (13) | 4.1346 (5) | 0.1988 (7) | 1.645 (6) | 1.759 (4) | 3.0362 (6) | 3.0387 (6) | 5.77 (8) | 3.32 |
| 230 | 4.133311 (13) | 4.1346 (5) | 0.1986 (7) | 1.644 (6) | 1.760 (4) | 3.0361 (6) | 3.0383 (6) | 5.96 (8) | 3.31 |
| 240 | 4.133426 (13) | 4.1352 (5) | 0.1988 (7) | 1.646 (6) | 1.759 (4) | 3.0364 (6) | 3.0385 (6) | 6.18 (8) | 3.29 |
| 250 | 4.133542 (13) | 4.1350 (5) | 0.1988 (8) | 1.645 (6) | 1.759 (4) | 3.0364 (6) | 3.0383 (6) | 6.39 (8) | 3.28 |
| 260 | 4.133671 (13) | 4.1353 (5) | 0.1989 (8) | 1.646 (6) | 1.759 (4) | 3.0366 (6) | 3.0377 (6) | 6.60 (8) | 3.28 |
| 270 | 4.133793 (13) | 4.1355 (5) | 0.1989 (8) | 1.647 (6) | 1.759 (4) | 3.0368 (6) | 3.0382 (6) | 6.81 (8) | 3.28 |
| 280 | 4.133928 (13) | 4.1360 (5) | 0.1987 (8) | 1.645 (6) | 1.760 (4) | 3.0366 (6) | 3.0384 (6) | 7.01 (8) | 3.26 |
| 290 | 4.133715 (14) | 4.1359 (5) | 0.1988 (8) | 1.645 (6) | 1.760 (4) | 3.0365 (6) | 3.0386 (6) | 7.25 (9) | 3.52 |
| 300 | 4.134057 (13) | 4.1354 (5) | 0.1987 (8) | 1.645 (6) | 1.760 (4) | 3.0367 (6) | 3.0387 (6) | 7.49 (9) | 3.28 |
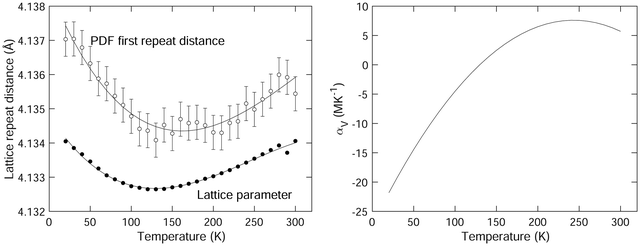
The variation of the lattice parameter with temperature is plotted in Fig. 4. This is in agreement with previous data,1 but our new data set contains a much larger number of individual points. We note that the NTE exists up to a temperature of around 130 K, with a maximum negative volume expansivity (at the lower temperatures) of αV ≈ −20 MK−1. The variation of αV with temperature as obtained from our diffraction data is shown in Fig. 4. This was extracted from differentiation of the trend-line fitted to the lattice parameter data shown in Fig. 4. The slight decrease in the value of αV appears to be robust in our analysis.
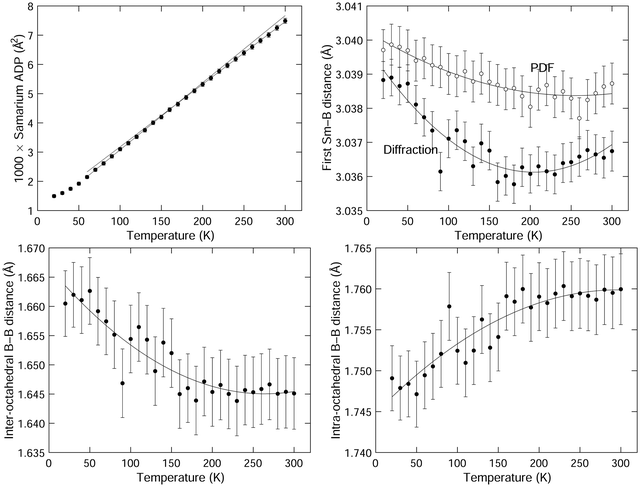
The isotropic ADP for samarium is shown in Fig. 5. The variation with temperature is in excellent quantitative agreement with the previous neutron and X-ray single crystal diffraction data.1,49 On the other hand, we found that our data have a low degree of sensitivity to the boron ADPs, and accordingly we do not report these values here. Several different models we investigated, including both isotropic and anisotropic ADPs refined freely, and ADPs constrained to have the same ratios as given by the prior studies, gave values of weighted profile Rwp factors that differed only by 0.01%, with an absolute value of around 3.3% (Table 1). They also had relatively high errors. This insensitivity, which is quite striking compared to the consistency of the values of the samarium ADP with prior studies,1,49 is presumably due to the low weighting of boron in the diffraction due to its much lower atomic number. That said, our refined values in each model we use are not very different from the prior results, and in particular they consistently reproduced the curious finding of the previous work that the boron ADPs have much weaker variation with temperature than the samarium ADPs.1,49
We want to draw attention to the existence of an interesting feature of the samarium APDs, which is that the gradient ∂〈u2〉/∂T is slightly higher at the lower temperatures than at the higher temperatures. This is highlighted in Fig. 5 by plotting linear fits to the two regions of the graph, and extending the extrapolated fitted lines over both regions. We will comment on this below.
Values of the Sm–B and B–B nearest-neighbour distances extracted from the refined crystal structures for all temperatures are listed in Table 1. and their variation with temperature is shown in Fig. 5. The first Sm–B nearest-neighbour distances show negative expansion at lower temperatures, up to a temperature of around 200 K. This is higher than the temperature at which NTE switches to PTE.
The nearest-neighbour B–B distances – for both intra-octahedral and inter-octahedral neighbours – are also shown in Fig. 5. The inter-octahedral B–B distance shows contraction on heating, with the minimum value at a temperature between 250–300 K. The intra-octahedral B–B bond length shows a small PTE, which saturates at the same temperature at which the inter-octahedral B–B bond length reaches its minimum.
3.2 Results from X-ray total scattering and the pair distribution function
The values of the mean instantaneous Sm–Sm distances obtained from the PDF are given in Table 1 with the crystal structure data, and are plotted as a function of temperature in Fig. 4 with the lattice parameter. This distance corresponds to two samarium atoms separated by a lattice spacing, but it is not necessary for this distance to be exactly equal to the lattice parameter since the distance may be affected by short-range correlations in the motions of the two atoms. There is a small offset in the data for the lattice parameter and Sm–Sm peak position given in Fig. 4 of around 0.07%; this difference can easily be accounted for by calibration errors.The mean instantaneous Sm–Sm distance in the PDF shows a reduction on heating, corresponding to NTE. The minimum in the data appears to be at a temperature about 30 K above the minimum in the lattice parameter, and the net contraction of the Sm–Sm distance is about twice that of the lattice parameter. However, the effects are very small compared to the width of the peak in the PDF (as seen in Fig. 3). The existence of the shoulder from the second Sm–B peak makes the exact position of the peak very susceptible to small effects in the fitting.
The data for the first Sm–B distance as a function of temperature are plotted in Fig. 5, and listed in Table 1 with the corresponding data from the Rietveld refinement. The first Sm–B distance shows NTE similar to that for the Sm–Sm distance (Fig. 4), with a minimum in the distance at about 50 K higher than the corresponding distance from diffraction. The temperatures of the minima in the distances from diffraction and PDF are both higher than the temperature of the minimum in the lattice parameter and the Sm–Sm distance respectively. There is an offset between the PDF and diffraction data of about 0.03% in the data for the first Sm–B distance, which could be due to very small calibration errors, or simply reflect the very small changes compared to the size of the peak width.
The PDFs for each temperature are given in the ESI.†
4 Discussion
We plot the two B–B distances from the crystal structure as a function of the Sm–B distance in Fig. 6, separating the data in the NTE region from the data in the PTE region, with our results giving a wider range of data in the NTE region. For comparison with results from our recent DFT study,3Fig. 3 from that paper is reproduced in Fig. 6 for convenience. This shows how the two B–B distances vary with the size of the metal atom M in MB6 for several different elements, with the M–B distances characterising the changing size of the M atom. The range of M–B distances in Fig. 6 is of course much wider than the range of Sm–B distances over a range of temperatures.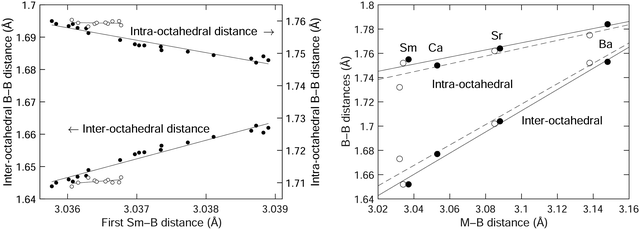 | ||
| Fig. 6 (left) Comparison of the inter-octahedral and intra-octahedral B–B distances as functions of the Sm–B distance, with data taken from the crystal structure obtained from Rietveld refinement of the diffraction data (Table 1). Data for T ≤ 200 K (the NTE region) are shown as filled circles, and data for T > 200 K (the PTE region) are shown as open circles. (right) The corresponding B–B distances as functions of the metal-boride distance for the cases of SmB6, CaB6, SrB6 and BaB6 obtained from experiment50 (filled circles) and our previous DFT calculations3 (open circles). The solid curves in each case are straight lines fitted to the data (in the case of the left plot, fitted to temperatures from 20–200 K), and are given as guides to the eye. | ||
The expansion rate of the inter-octahedral distance with the metal–boride (M–B) distance is Δ(B–B)/Δ(M–B) ≃ 0.9 from the crystal structure and DFT data. In the case of the diffraction data for SmB6 we actually see that ratio Δ(B–B)/Δ(Sm–B) is more than 6 times larger. The more significant (perhaps) difference is that the intramolecular B–B distance decreases with increasing Sm–B distance in the diffraction data, but increases in the crystal structure and DFT data with increasing M size. These differences might be accounted for by the intrinsic (Grüneisen) effects of temperature on thermal expansion. After all, we are not quite comparing like-for-like in Fig. 6 in that we are looking for the effects on changing size of the samarium atom but without eliminating effects of normal thermal expansion arising from the lattice dynamics with the standard Grüneisen mechanism. However, it may be that at the smaller end of the size of the M cation we cannot completely generalise from the trend, as we now discuss.
The point to make from the MB6 data from our previous study3 as reproduced in Fig. 6 is that increasing the size of the M cation leads to an increase in the intra-octahedral B–B distances as it forces the B6 octahedra further apart, and this is accompanied by a smaller increase in the size of the B6 octahedra, perhaps because the B3 triangle facing the metal atom needs to expand slightly. Thus if the samarium atom is also squeezed into its site, it too will force a slight increase in the intra-octahedral B–B distance. From the DFT calculations of phonon dispersion curves and elasticity it does not appear that the samarium atom is smaller, so as the samarium atom decreases in size on heating as it loses electrons this will be reflected in a decrease in the size of the inter-octahedral B–B distance. This appears to be the case.
On the other hand the intra-octahedral B–B distance appears to increase in size with decreasing size of the samarium atom, but this probably reflects the normal PTE of the intra-octahedral B–B bonds. If the samarium atom is small enough, it is possible that it exerts less lateral stress on the facing B3 triangle.
The picture from the diffraction and PDF data is that the decreasing size of the samarium atom with temperature as it loses electrons on heating is the origin of the NTE. There is no evidence from the comparison of PDF and diffraction data for a significant tension effect25 of the type seen in other systems, particular as recently evaluated in ScF3.28,29 This is consistent with the lattice dynamics calculations3 and with the effect seen in other systems.34–36
We emphasise the point by comparing, in Fig. 7, the way in which the shortest separation measured by the PDF varies with the corresponding distance measured by diffraction in both SmB6 and ScF3.28 In both cases, we use the data up to the point where the NTE changes to PTE. Ideally, we might have been able to compare the B–B distances in the case of SmB6, but as we noted these are not observed in the PDF. Therefore, we compare the shortest Sm–B distances in SmB6, and the neighbouring Sc–F distances in ScF3. In SmB6 the local structure shows the same NTE as the average structure, but in ScF3, the local structure shows PTE whereas the average structure shows NTE, this difference being highlighted by the different signs of the slopes on the two graphs. The relationship between the local structure and average structure in both cases emphasises the fact that in ScF3 the NTE arises from the tension effect, whereas in SmB6 it arises from an electronic effect.
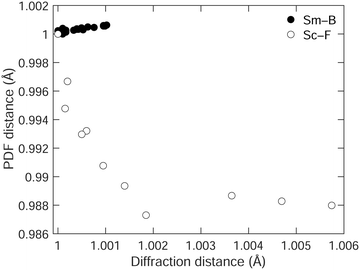 | ||
| Fig. 7 Comparison of the shortest distances in SmB6 (filled circles,) and ScF3 (open circles, data from our own earlier study28), measured by diffraction, and from the PDF, scaled such that the minimum distance in the diffraction data is equal to 1, and so that the corresponding PDF separation is also equal to 1. | ||
Finally we comment on the variation with temperatures of the samarium ADPs, and the fact that the gradient of the value of the ADP with temperature is higher at low temperature. We remarked in the methods section that the transfer of electrons from the samarium atoms is unlikely to be noticed in the X-ray atomic scattering factors. However, there is one other way in which the change in the number of electrons will have an effect, and that is on the vibrational force constants. This will then affect the atomic displacement parameters, which are inversely proportional to the square of the mode frequencies and hence inversely proportional to the force constants. Electron transfer will affect the force constants in two ways. First, a smaller ionic radius will change the short-range repulsion, and secondly the charge transfer will change – enhance – the Coulomb interactions. It is not straightforward to predict the impact on the frequencies and hence on the ADPs, but the change in the variation of the samarium ADPs with temperature may well be an additional signature of the charge transfer seen in the atomic structure and invoked here to explain the NTE in SmB6. It is interesting that the change in the behaviour of the ADPs occurs at around the same temperature that the NTE switches to PTE, but we are not in a position to develop the discussion further at this point,
Should a tension effect exist, we would expect to see an effect in the anisotropic ADPs for boron, namely the existence of large transverse vibrations for the apical atoms in the B6 octahedra. A small effect of this sort, but with significantly reduced variation with temperature compared to the ADPs of the samarium atoms, was seen in the prior neutron powder diffraction and single-crystal X-ray diffraction studies1,49 (as we remarked, our data do not appear to be sensitive enough to draw our own conclusions). The transverse ADP is, on average for both prior data sets, around 1.5 times larger than the longitudinal ADP. Compared to, say, ScF3, where the ratio between the two ADPs is 4.5,18 this is not a large effect.
5 Conclusion
We had previously anticipated, but ruled out, the possibility of a phonon mechanism for NTE in SmB6, based on the existence of RUMs providing a tension effect.3 Given the lack of a magnetic ordering in SmB6,33 the mostly likely origin of NTE in SmB6 is an electronic effect. This is clearly possible given the evidence of such an effect leading to NTE in other systems containing samarium.34–36 The crystal structure and PDF data presented in this paper are consistent with the samarium atom becoming smaller on heating as a result of charge transfer, leading to a contraction of the inter-octahedral B–B distance.While our methods are not directly sensitive to electron transfer, the evidence from the diffraction and PDF data presented here is that the Sm–B distance is acting as an indicator for a reduction in the size of the samarium atom on heating. Thus we are confident in being able to explain the NTE in SmB6 as having an electronic origin.
Author contributions
Li Li: investigation, formal analysis, validation, funding acquisition and writing (original draft). Martin T. Dove: conceptualisation, investigation, methodology, software, validation, formal analysis, resources, visualisation, supervision, funding acquisition and writing (original draft). Zhongshen Wei: investigation, formal analysis. Anthony E. Phillips: formal analysis, writing (review & editing). Dean S. Keeble: investigation.Data availability
All data reported in this paper are available on reasonable request to the corresponding author.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Prof. Geetha Balakrishnan (University of Warwick) for donation of the sample. We acknowledge the financial support from National Natural Science Foundation of China, grant number 12174274 (MTD) and the financial support from Civil Aviation Flight University of China, grant number 2023210 (LL). We appreciate the award of beam-time on the XPDF (I15-1) instrument at Diamond. We thank Prof. Paul Attfield (University of Edinburgh) for discussion.References
- V. A. Trounov, A. L. Malyshev, D. Y. Chernyshov, M. M. Korsukova, V. N. Gurin and L. A. Aslanov, et al., Temperature dependences of the parameters of atoms in the crystal structure of the intermediate-valence semiconductor SmB6: investigation by highresolution powder neutron diffraction, J. Phys.: Condens. Matter, 1999, 5, 2479–2488, DOI:10.1088/0953-8984/5/16/007.
- C. H. Chen, T. Aizawa, N. Iyi, A. Sato and S. Otani, Structural refinement and thermal expansion of hexaborides, J. Alloys Compd., 2004, 366, L6–L8, DOI:10.1016/S0925-8388(03)00735-7.
- L. Li, K. Refson and M. T. Dove, The contribution of phonons to the thermal expansion of some simple cubic hexaboride structures: SmB6, CaB6, SrB6 and BaB6, Phys. Chem. Chem. Phys., 2023, 25, 10749–10758, 10.1039/D3CP01306E.
- D. C. Palmer, Visualization and analysis of crystal structures using CrystalMaker software, Z. Kristallogr. – Cryst. Mater., 2015, 230, 559–572, DOI:10.1515/zkri-2015-1869.
- L. Li, K. Sun, C. Kurdak and J. W. Allen, Emergent mystery in the Kondo insulator samarium hexaboride, Nat. Rev. Phys., 2020, 2, 463–479, DOI:10.1038/s42254-020-0210-8.
- J. C. Cooley, M. C. Aronson, A. Lacerda, P. C. Canfield, Z. Fisk and R. P. Guertin, Magnetic field dependence of the correlation gap in SmB6, Phys. B, 1995, 206–207, 377–379, DOI:10.1016/0921-4526(94)00464-7.
- P. Nyhus, S. L. Cooper, Z. Fisk and J. Sarrao, Low-energy excitations of the correlationgap insulator SmB6: A light-scattering study, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 12488–12496, DOI:10.1103/PhysRevB.55.12488.
- M. Dzero, K. Sun, V. Galitski and P. Coleman, Topological Kondo insulators, Phys. Rev. Lett., 2010, 104, 106408, DOI:10.1103/PhysRevLett.104.106408.
- F. Lu, J. Zhao, H. Weng, Z. Fang and X. Dai, Correlated Topological Insulators with Mixed Valence, Phys. Rev. Lett., 2013, 110, 096401–096405, DOI:10.1103/PhysRevLett.110.096401.
- N. Xu, X. Shi, P. K. Biswas, C. E. Matt, R. S. Dhaka and Y. Huang, et al., Surface and bulk electronic structure of the strongly correlated system SmB6 and implications for a topological Kondo insulator, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 121102, DOI:10.1103/PhysRevB.88.121102.
- I. Batko and M. Batkova, SmB6: Topological insulator or semiconductor with valence-fluctuation induced hopping transport?, Solid State Commun., 2014, 196, 18–23, DOI:10.1016/j.ssc.2014.07.014.
- B. S. Tan, Y. T. Hsu, B. Zeng, M. C. Hatnean, N. Harrison and Z. Zhu, et al., Unconventional Fermi surface in an insulating state, Science, 2015, 349, 287–290, DOI:10.1126/science.aaa7974.
- J. Chen, L. Hu, J. Deng and X. Xing, Negative thermal expansion in functional materials: controllable thermal expansion by chemical modifications, Chem. Soc. Rev., 2015, 44, 3522–3567, 10.1039/C4CS00461B.
- N. Shi, Y. Song, X. Xing and J. Chen, Negative thermal expansion in framework structure materials, Coord. Chem. Rev., 2021, 449, 214204, DOI:10.1016/j.ccr.2021.214204.
- T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Negative thermal expansion from 0.3 to 1050 Kelvin in ZrW2O8, Science, 1996, 272, 90–92, DOI:10.1126/science.272.5258.90.
- V. Korthuis, N. Khosrovani, A. W. Sleight, N. Roberts, R. Dupree and W. W. J. Warren, Negative thermal expansion and phase transitions in the ZrV2−xPxO7 series, Chem. Mater., 1995, 7, 412–417, DOI:10.1021/cm00050a028.
- M. Dapiaggi, W. Tiano, G. Artioli, A. Sanson and P. Fornasini, The thermal behaviour of cuprite: An XRD–EXAFS combined approach, Nucl. Instrum. Methods Phys. Res., Sect. B, 2003, 200, 231–236, DOI:10.1016/s0168-583x(02)01682-8.
- B. K. Greve, K. L. Martin, P. L. Lee, P. J. Chupas, K. W. Chapman and A. P. Wilkinson, Pronounced negative thermal expansion from a simple structure: Cubic ScF3, J. Am. Chem. Soc., 2010, 132, 15496–15498, DOI:10.1021/ja106711v.
- J. W. Couves, R. H. Jones, S. C. Parker, P. Tschaufeser and C. R. A. Catlow, Experimental verification of a predicted negative thermal expansivity of crystalline zeolites, J. Phys.: Condens. Matter, 1993, 5, L329–L332, DOI:10.1088/0953-8984/5/27/001.
- S. H. Park, R. W. G. Kunstleve, H. Graetsch and H. Gies, The thermal expansion of the zeolites MFI, AFI, DOH, DDR, and MTN in their calcined and as synthesized forms, vol. 105 of Progress in Zeolite and Microporous Materials, Proceedings of the 11th International Zeolite Conference, Elsevier, 1997, pp. 1989–1994.
- M. P. Attfield and A. W. Sleight, Strong negative thermal expansion in siliceous faujasite, Chem. Commun., 1998, 601–602, 10.1039/a707141h.
- A. L. Goodwin, B. J. Kennedy and C. J. Kepert, Thermal expansion matching via framework flexibility in zinc dicyanometallates, J. Am. Chem. Soc., 2009, 131, 6334–6335, DOI:10.1021/ja901355b.
- P. Kroll, M. Andrade, X. Yan, E. Ionescu, G. Miehe and R. Riedel, Isotropic negative thermal expansion in β-Si(NCN)2 and its origin, J. Phys. Chem. C, 2012, 116, 526–531, DOI:10.1021/jp2106583.
- S. Adak, L. L. Daemen, M. Hartl, D. Williams, J. Summerhill and H. Nakotte, Thermal expansion in 3d-metal Prussian blue analogs – A survey study, J. Solid State Chem., 2011, 184, 2854–2861, DOI:10.1016/j.jssc.2011.08.030.
- M. T. Dove and H. Fang, Negative thermal expansion and associated anomalous physical properties: review of the lattice dynamics theoretical foundation, Rep. Prog. Phys., 2016, 79, 066503, DOI:10.1088/0034-4885/79/6/066503.
- R. Mittal, M. K. Gupta and S. L. Chaplot, Phonons and anomalous thermal expansion behaviour in crystalline solids, Prog. Mater. Sci., 2018, 92, 360–445, DOI:10.1016/j.pmatsci.2017.10.002.
- J. P. Attfield, Mechanisms and Materials for NTE, Front. Chem., 2018, 6, 14441–14446, DOI:10.3389/fchem.2018.00371.
- M. T. Dove, J. Du, Z. Wei, D. A. Keen, M. G. Tucker and A. E. Phillips, Quantitative understanding of negative thermal expansion in scandium trifluoride from neutron total scattering measurements, Phys. Rev. B, 2020, 102, 094105, DOI:10.1103/physrevb.102.094105.
- M. T. Dove, Z. Wei, A. E. Phillips, D. A. Keen and K. Refson, Which phonons contribute most to negative thermal expansion in ScF3?, APL Mater., 2023, 11, 041130, DOI:10.1063/5.0147610.
- M. T. Dove, Flexibility of network materials and the Rigid Unit Mode model: a personal perspective, Philos. Trans. R. Soc., A, 2019, 377, 20180222, DOI:10.1098/rsta.2018.0222.
- L. Tan, V. Heine, G. Li and M. T. Dove, The Rigid Unit Mode model: review of ideas and applications, Rep. Prog. Phys., 2023 DOI:10.1088/1361-6633/acc7b7.
- A. L. Goodwin, Rigid unit modes and intrinsic flexibility in linearly bridged framework structures, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 134302, DOI:10.1103/PhysRevB.74.134302.
- P. K. Biswas, Z. Salman, T. Neupert, E. Morenzoni, E. Pomjakushina and F. von Rohr, et al., Low-temperature magnetic fluctuations in the Kondo insulator SmB6, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(16), 155, DOI:10.1103/PhysRevB.89.161107.
- M. Azuma, K. Oka and K. Nabetani, Negative thermal expansion induced by intermetallic charge transfer, Sci. Technol. Adv. Mater., 2015, 16, 034904, DOI:10.1088/1468-6996/16/3/034904.
- J. Arvanitidis, K. Papagelis, S. Margadonna, K. Prassides and A. N. Fitch, Temperatureinduced valence transition and associated lattice collapse in samarium fulleride, Nature, 2003, 425, 599–602, DOI:10.1038/nature01994.
- K. Takenaka, D. Asai, R. Kaizu, Y. Mizuno, Y. Yokoyama and Y. Okamoto, et al., Giant isotropic negative thermal expansion in Y-doped samarium monosulfides by intraatomic charge transfer, Sci. Rep., 2019, 9, 122, DOI:10.1038/s41598-018-36568-w.
- J. Filik, A. W. Ashton, P. C. Y. Chang, P. A. Chater, S. J. Day and M. Drakopoulos, et al., Processing two-dimensional X-ray diffraction and small-angle scattering data in DAWN 2, J. Appl. Crystallogr., 2017, 50, 959–966, DOI:10.1107/S1600576717004708.
- A. K. Soper and E. R. Barney, Extracting the pair distribution function from white-beam X-ray total scattering data, J. Appl. Crystallogr., 2011, 44, 1–13, DOI:10.1107/s0021889811021455.
- A. K. Soper, N. Gudrun and X. Gudrun, Programs for correcting raw neutron and X-ray diffraction data to differential scattering cross section, Rutherford Appleton Laboratory, RAL-TR-2011-013, 2011 Search PubMed.
- D. A. Keen, A comparison of various commonly used correlation functions for describing total scattering, J. Appl. Crystallogr., 2001, 34, 172–177, DOI:10.1107/S0021889800019993.
- D. A. Keen, Total scattering and the pair distribution function in crystallography, Crystallogr. Rev., 2020, 26, 141–199, DOI:10.1080/0889311x.2020.1797708.
- M. T. Dove and G. Li, Review: Pair distribution functions from neutron total scattering for the study of local structure in disordered materials, Nucl. Anal., 2022, 1, 100037, DOI:10.1016/j.nucana.2022.100037.
- A. S. Krylov and A. V. Vvedenskii, Software package for radial distribution function calculation, J. Non-Cryst. Solids, 1995, 192–193, 683–687, DOI:10.1016/0022-3093(95)00424-6.
- M. Gao, Y. Qin, S. Wang, S. Zhang, S. Zhang and L. Tan, et al., Accounting for instrument resolution in the pair distribution functions obtained from neutron time-of-flight total scattering data using Hermite functions 1. Principles, 2023, in preparation.
- E. Celeghini, M. Gadella and M. A. del Olmo, Hermite Functions and Fourier Series, Symmetry, 2021, 13, 853, DOI:10.3390/sym13050853.
- E. Lorch, Neutron diffraction by germania, silica and radiation-damaged silica glasses, J. Phys. C-Solid State Phys., 1969, 2, 229–237, DOI:10.1088/0022-3719/2/2/305.
- E. Lorch, Conventional and elastic neutron diffraction from vitreous silica, J. Phys. C-Solid State Phys., 1970, 3, 1314–1322, DOI:10.1088/0022-3719/3/6/012.
- E. R. Cope and M. T. Dove, Pair distribution functions calculated from interatomic potential models using the General Utility Lattice Program, J. Appl. Crystallogr., 2007, 40, 589–594, DOI:10.1107/S0021889807016032.
- S. Funahashi, K. Tanaka and F. Iga, X-ray atomic orbital analysis of 4f and 5d electron configuration of SmB6 at 100, 165, 230 and 298 K, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 292–306, DOI:10.1107/S0108768110009250.
- K. Schmitt, C. Stückl, H. Ripplinger and B. Albert, Crystal and electronic structure of BaB6 in comparison with CaB6 and molecular [B6H6]2−, Solid State Sci., 2001, 3, 321–327, DOI:10.1016/S1293-2558(00)01091-8.
Footnotes |
| † Electronic supplementary information (ESI) available: It contains two compressed folders, one of which contains the crystallographic CIF files for all temperatures, and the other which contains the PDFs for all temperatures. See DOI: https://doi.org/10.1039/d3cp05954e |
| ‡ There are two reasons why we may not be able to obtain distances between all pairs. Firstly, there may be too great an overlap of peaks in the PDF, which is a one-dimensional function. Secondly, the weighting of the peaks in the PDF may be too weak for some pairs of atoms, as found in this study. |
| § Usually XPDF has two area detectors, one for total scattering and one for diffraction. The second detector was out of service at the time the experiment was performed. |
| This journal is © the Owner Societies 2024 |