Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coincidence measurements of photodouble ionization of benzene and thiophene
Nicholas L.
Wong
 *a,
Jason
Howard
a,
Ben
Delaney
*a,
Jason
Howard
a,
Ben
Delaney
 a,
Emma
Sokell
a,
Emma
Sokell
 a,
Paola
Bolognesi
a,
Paola
Bolognesi
 b and
Lorenzo
Avaldi
b and
Lorenzo
Avaldi
 b
b
aSchool of Physics, Science Centre North, University College Dublin, Belfield Dublin 4, Ireland. E-mail: nicholas.wong1@ucdconnect.ie
bCNR-Istituto di Struttura della Materia, Area della Ricerca di Roma 1, 00015 Monterontondo Scalo, Italy
First published on 19th March 2024
Abstract
Photodouble ionization (PDI) triple-differential cross sections (TDCSs) of benzene and thiophene have been measured in electron–electron coincidence experiments under 10–10 eV and 20–20 eV equal energy sharing conditions. A multi-Gaussian fit method has been employed to characterize the TDCSs. The trends and features observed for benzene and thiophene do highlight differences with helium most likely from molecular PDI contributions to the TDCS. A comparison with the well-known helium PDI TDCS for equal energy sharing conditions [Avaldi and Huetz J. Phys. B: At. Mol. Opt. Phys., 2005, 38, S861–S891] supported the validity of the multi-Gaussian fitting method and contextualized the benzene and thiophene fits. The molecular targets and energy sharing conditions were chosen to provide insight into the unexpected resonances observed in aromatic hydrocarbons but not aromatic heterocyclic molecules [Wehlitz et al., Phys. Rev. Lett., 2012, 109, 193001]. Contrary to the work of [Wehlitz et al., Phys. Rev. Lett., 2012, 109, 193001], no significant differences between benzene and thiophene were found.
1 Introduction
Photodouble ionization (PDI) is the ionization of an atom or molecule with one photon, yielding two electrons. Direct PDI processes occur when the two electrons are ionized without any intermediate states, while indirect processes involve an excited intermediate that is quickly ionized again.1 Measurement of coincidence electrons from PDI enables the investigation of PDI mechanisms, the correlation between the two electrons, and atomic or molecular structure. Aromatic hydrocarbons are of particular interest to be studied with coincidence PDI measurements, since electrons in the blended π orbitals characteristic of aromaticity are delocalized and freely moving over the molecule.2 Additionally, the stability of aromatic hydrocarbons lends to the molecules' importance in a variety of processes, for example: larger polycyclic aromatic hydrocarbons in astrochemistry3,4 and aromatic hydrocarbons' relevance to superconductivity2,5The PDI of aromatic hydrocarbons and aromatic heterocyclic molecules has been investigated by other groups.2,6,7 Aromatic heterocyclic molecules differ from aromatic hydrocarbons, by having one C atom of the cyclic ring replaced with another atom, like S. The free electrons of the C replacing atom maintain the aromaticity of the molecule. For the aromatic hydrocarbons, Wehlitz et al. found resonances in the ratio of doubly charged ions to the total number of parent molecules, after subtracting the contribution from the direct PDI process.6 The resonance in aromatic hydrocarbons began at excess energies between 30 eV and 40 eV, while the aromatic heterocyclic molecules only had an approximately linear increase starting at 42 eV excess energies.6 Furthermore, the photoelectron spectra of two aromatic hydrocarbons revealed corroborating resonances after subtraction of the expected direct process continuum, but the resonances were not observed for aromatic heterocyclic molecules.6 Wehlitz et al. suggested the mechanism for the resonance involves the emission of a Cooper pair which breaks up into two electrons, based on similar resonance enhancement observations in C60.6 In the C60 observations, the enhancements occurred at energies corresponding to de Broglie wavelengths of electrons equal to the specific C to C spacing within C60.8 For the aromatic hydrocarbons, the same matching was only achieved with a de Broglie wavelength from a particle of twice the mass of an electron.6 Then, assuming a de Broglie wavelength equal to the distance between carbons in the aromatic hydrocarbons, the particle has an energy of 38.3 eV, which is the energy where the resonances begin to appear.6 Jänkälä et al. performed coincidence measurements and separately observed the resonance enhancements; but the analysis of the energy sharing among the two photoelectrons did not support the proposed Cooper pair mechanism.7 The mechanism is still not well understood, but measurements of the triple-differential cross section (TDCS) of these PDI processes might provide further insight.
Helium gas was one of the first PDI targets given the simplicity of the atom resulting in the direct PDI process being dominant.1 Theoretical TDCS models developed for helium have also been extensively experimentally verified,1,9–11 and the helium TDCS for coincidence electrons in equal energy sharing conditions (E1 = E2) can be described as
| σ3 = |ag(E/2, E/2, θ12)|2[cos(θ1) + cos(θ2)]2, | (1) |
|ag|2 = a(E)·exp[−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2)(π − θ12)2/(θFWHM)2], ln(2)(π − θ12)2/(θFWHM)2], | (2) |
The measurements were performed at the GasPhase beamline of the Elettra Synchrotron in Trieste, Italy, selecting the case of equal energy sharing electrons. The resonances observed by Wehlitz et al.6 appear around total excess energies of 40 eV, so electrons in equal energy sharing conditions of 10 eV and 20 eV (denoted 10–10 and 20–20, respectively) were selected to measure both off- and on-resonance. Additionally, since the resonance was seen for aromatic hydrocarbons but not for aromatic heterocyclic molecules,6 benzene (C6H6) and thiophene (C4H4S) were selected as targets.
Section 2 first describes the experimental apparatus and procedures and second the TDCS fitting method employed for the benzene and thiophene data. The experimentally measured PDI TDCS with fits are presented in Section 3, with the analysis of the data in comparison with helium PDI TDCS. Finally, concluding remarks are contained in Section 4.
2 Experimental
2.1 Apparatus and setup
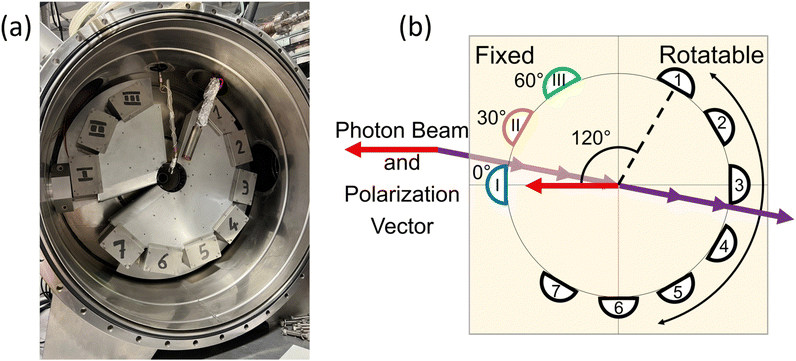
The Elettra Synchrotron in Trieste, Italy provided the ionizing radiation for the PDI experiments. The present measurements were taken during operation with beam energies of 2 and 2.4 GeV, and the electrons were stored in the ring in a multi-bunch mode. The dark gap between the two ends of the multi-bunch electron train was measured as 73.9 ns. As stated previously, the measurements were carried out at the GasPhase beamline of Elettra, which utilizes linearly polarized undulator radiation. A multi-coincidence angularly resolved electron spectrometer detected the PDI electrons.The spectrometer consists of 10 hemispherical analyzers mounted on two frames. Fig. 1(a) shows the actual spectrometer at the GasPhase beamline of Elettra, along with a schematic diagram of the spectrometer in Fig. 1(b). Three analyzers are mounted on a fixed frame at angles of 0°, 30°, and 60°, where 0° is the direction of the polarization vector of the linearly polarized light. These analyzers are kept stationary and are labeled M1, M2, and M3. The 7 other analyzers are mounted 30° apart on a rotatable frame and are labeled A1 through A7; although, A7 was not functioning for these experiments.
During data acquisition, each M analyzer records counts separately; thus, three sets of coincidence measurements are recorded at the same time, between each M analyzer and any of the A analyzers. Bolognesi et al.13 describe the data acquisition, data processing, and spectrometer in more detail. For the present data, both frames were in the plane perpendicular to the propagation direction of the ionizing radiation, and the position of the rotatable frame was changed to allow measurements from 113° to 291°. The hemispherical analyzers were then set to record electrons under 10–10 or 20–20 equal energy sharing conditions. The energy resolution and the angular acceptance in the dispersion plane of the spectrometers were ΔE1, ΔE2 ≅ 0.3 and 0.6 eV at 10 and 20 eV kinetic energy, respectively, and Δθ1, Δθ2 ≅ 4°.
This experimental end-station has been specifically designed to perform the angular resolved photoelectron–photoelectron coincidence experiments to study TDCS.13 The hemispherical analyzers can be equipped with entrance/exit slits of different size and shape to improve either the energy resolution or the count rate. The angular resolution is on the order of a few degrees, the energy resolution is about 3% of the hemispherical analyzers’ pass energy, and different target sources (gas jets, heated oven) can be hosted in the chamber.
A different approach to multiangle detection for PDI studies has been proposed by Reddish et al.,14 which used two toroidal analyzers to cover an angular range similar to the setup used here. The range of the kinetic energy of photoelectrons in this spectrometer has been limited to 30 eV.15 Setups with multi-angle and energy detection like the cold target recoil ion momentum spectroscopy (COLTRIMS) setup offer a more efficient data collection, but in the case of PDI studies COLTRIMS setups definitely have a lower angular resolution (in most cases the TDCSs are integrated over 20°10) and energy resolution comparable to the multi-angle spectrometer used here. Moreover, COLTRIMS setups use cold targets produced by supersonic jets, which increases the experimental complexity, and their use in the PDI studies has been limited to He atoms and H2 molecules.16 Magnetic bottle spectrometers17 have also been used to study double and multiple photoionization. This type of analyzer, which is based on the measurement of the time-of-flight of the photoelectrons, provides highly efficient detection of several electrons in coincidence and is characterized by high resolution. Magnetic bottle spectrometers have been extensively used to study the energy spectra of dications17 and to produce photoproduct coincidence maps, which inform molecular fragmentation and dissociation pathways17–19 but provide no information on the angular distribution.
Here, liquid benzene and thiophene samples were used. Before being connected to the experimental chamber, a process of freeze–pump–thawing the samples ensured the purity of benzene and thiophene. A sensitive leak valve permitted control of the flow of the gas sample. For measurements, the flow rate was adjusted until the vacuum chamber pressure was stable at a pressure at least an order of magnitude larger than the sample free pressures, which were on the order of 10−7 mbar.
One more step before measuring the PDI TDCS is determining the appropriate photon energy. Double ionization energy spectra from the literature act as starting points. Linusson et al.20 and Eland21 and Tarantelli et al.22 provide the double ionization energy for benzene and thiophene around, 24.6 eV and 24.7 eV respectively. The target photon energy is then derived from equal energy sharing condition electrons of either 10 eV or 20 eV kinetic energy and E1 + E2 = hν + ID, where hν is the photon energy and ID is the double ionization energy of the molecule. Next, a binding energy spectrum is measured around the calculated target photon energy to maximize the coincidence count rates of the spectrometer. The scans resulted in photon energies of 45.75 eV and 65 eV for benzene at 10–10 and 20–20 and energies of 46.5 eV and 66 eV for the thiophene at 10–10 and 20–20. A similar experiment on Ne, whose double ionized states produce well isolated features, allowed the accurate calibration of the kinetic energy of the photoelectrons. From this experiment, we derived that in both benzene and thiophene we have investigated dication states with a binding energy of about 25 eV. At this binding energy, the expected dication states to contribute to the measured PDI TDCS are 3A2g, 1E2g, and 1A1g for benzene21,22 and 3B2, 1B2, and 1A1 for thiophene.20
Additional angular distribution measurements of a well-known process enabled the relative calibration of the hemispherical analyzers to each other. Here, the photoionization of the 2p electron of Ne was the process, and electrons with 10 eV and 20 eV kinetic energy were measured. A photoelectron spectrum (PES) was measured at each position of the rotatable frame the coincidence measurements were taken at. A Gaussian fit to each PES provided counts at each angle, yielding an angular distribution. Comparing the experimental angular distribution to the known angular distribution for 2p Ne electrons23–25 gave scaling calibration coefficients for each analyzer at each position. When applying the scaling calibration coefficient, each coincidence measurement needed to account for both the A and M analyzer angular efficiency, so two scaling coefficients were applied to the final data to account for both the A and M analyzers. The angular calibration of the M analyzers allows the three TDCSs to be set on the same relative scale.
After measurement, the subtraction of the contribution of random coincidences to the time coincidence spectra is required. Two types of background contributions were considered. The first type was purely random coincidences resulting in a flat background contribution. The second type arises because the 73.9 ns dark gap in the electron train leads to a pulsed light source. Synchrotron radiation of this type has a known triangular shaped background coincidence count contribution centered on the region of true coincidence counts.26 However, including the synchrotron contributions in the background resulted in overfitting the data and the loss of most coincidence counts. The purely random and synchrotron background contributions were compared. Across the benzene and thiophene data, the mean percent contribution of the synchrotron background counts to the total background was 11.9 ± 0.6%. In some cases, the synchrotron background counts were within the uncertainties of the flat background contribution, but no clear trend was observed. Based on the low contribution of the synchrotron background, a flat background was assumed here.
2.2 TDCS fitting
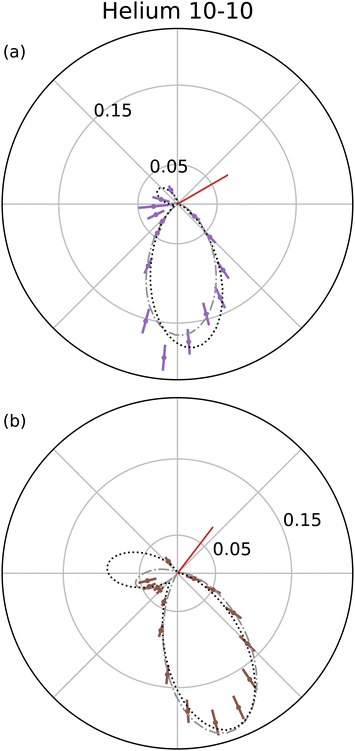
As mentioned previously, models of PDI TDCS give insight into the PDI mechanism and electron angular correlation of the ionized target. Works containing theoretical models for the TDCS of H2O,27 CO2,28 Mg,29 and various noble gases13 have been published; however, current reported theoretical studies have not yet been extended to molecules as complex as benzene and thiophene. Several models1,30–32 that fit PDI TDCS similar in shape to the following results were attempted to gain some quantitative comparison, but the lack of a strong physical basis and the poor fits lead to a different method for quantitative comparison.An examination of helium TDCS provides the basis for the new method. Helium PDI TDCS at 10–10 equal energy sharing conditions from Schwarzkopf and Schmidt9 are shown in Fig. 2 for fixed analyzer angles of 30° and 52.5°, marked by red lines. In Fig. 2, 0° corresponds to the ionizing radiation's polarization vector. The lobes of the TDCS can be described by Gaussian functions, as demonstrated by eqn (2) and highlighted by Fig. 2. Thus, a multi-Gaussian function was fit to each TDCS. Each Gaussian corresponded to a different lobe and was fit as
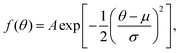 | (3) |
 | ||
| Fig. 2 TDCS for helium at 10–10 eV equal energy sharing conditions from Schwarzkopf and Schmidt9 with fixed analyzer angles of 30° and 52.5° (red lines in a and b, respectively). Here, 0° is the direction of the ionizing radiation's polarization vector, and the experimental TDCS are the purple and brown points for the 30° and 52.5° data. Multi-Gaussian fits (black dotted curves) and He fits from eqn (1) (grey dash-dotted curve) are also shown. | ||
The multi-Gaussian fit procedure utilized for benzene and thiophene (described below) was applied to published He data for PDI at equal energy sharing with 10 eV9,10 and 20 eV.11 The results of the fit not only provide multi-Gaussian parameters for comparison, but also act as a validity check of the multi-Gaussian fit when compared to the well tested He TDCS given by eqn (1) and (2), referred to here as the He fit to distinguish from the multi-Gaussian fits.
Fig. 2 shows both the multi-Gaussian and He fits are in good agreement, supporting the validity of the multi-Gaussian fit for PDI TDCS. Notably, the small secondary lobes observed in the He data and He fit, around θ = 180° in Fig. 2(a) and (b), are partially described by the multi-Gaussian fit through the symmetric lobe. The multi-Gaussian fit σs for He can also be scaled to reported θFWHM values, as described in Section 3.2, and the agreement between the scaled θFWHMs and the reported values provides further support for the multi-Gaussian fit. Additional comparisons with ratios of the molecular data and scaled He fits discussed in Section 3.2 and shown in Fig. 6 lend extra support to the validity of the multi-Gaussian fit for the molecular targets.
Limits were established for all three fitting parameters. The lower and upper limits for σ had the largest consequence on the fits, and the values used were 0.25 radians or 14.3° and π/2 radians or 90°, respectively. The lower limit is non-zero, because the multi-Gaussian fitting can easily overfit the data with many narrow Gaussians, since the expected number of lobes is unknown. 0.25 radians comes from the smallest lobe width obtained from fitting He TDCS from Dörner et al.10 in the 10–10 energy sharing case where the narrowest lobes are expected due to a smaller θFWHM. A comparison of the σ = 0.25 radian lobe to the known He PDI TDCS confirmed the validity of the limit on the lobe width. Meanwhile, the π/2 limit was chosen based on being slightly larger than the largest fit σ values which reasonably fit lobes. For the fitting, one group of three TDCSs for a molecule at a particular kinetic energy can have as many as 27 different fitting parameters if each coincidence data set just has three lobes. However, several factors constrain the parameters and reduces the amount of free variables.
First, the Gaussian description of each lobe can be thought of similarly to the He PDI TDCS model; thus the scaling parameters A in part contains the kinematic contributions, while the Gaussian contains the dynamic contributions. As a consequence, the widths, σ, should be the same across the three TDCSs for a given molecule at a given kinetic energy. Thus, as long as the three TDCSs are fit simultaneously a single σ parameter is employed in the fit. Second, since the coincidence electrons are measured under equal energy sharing conditions, the emission direction of the electrons is assumed to be symmetric about the axis of the first electron's emission angle and the back-to-back emission angle, which corresponds to two lobes whose positions, μ, are equidistant from the back-to-back emission angle. Here, the back-to-back emission angle is taken as the reference angle. Third, since electrons detected at M1 are in the direction of the polarization vector, there is a kinematic emission symmetry around the axis of the first electron's emission angle and back-to-back emission angle for M1 TDCSs. The kinematic symmetry restricts symmetric lobe pairs to have the same variable A parameter, since A accounts for the kinematic contributions in the fitting approach adopted here. Fourth, only lobes in the observed angular range are included in the fit to avoid unreasonable lobes fitting the tails of the data; thus, only lobes whose μ are within the data range contribute to the final multi-Gaussian fit. These constraints are summarized as:
(i) The three TDCSs for a given molecule and kinetic energy are fit simultaneously with one σ parameter;
(ii) Lobe positions (μ) should have symmetric partners around the back-to-back emission angle;
(iii) Symmetric lobes in M1 TDCSs share the same A parameter;
(iv) Lobes with μ values outside the data range do not contribute to the final fit.
With the restrictions (i)–(iv), the same multi-Gaussian fitting procedure was applied to each data set enabling a consistent comparison. For each molecule and at each kinetic energy, the TDCSs from the three M analyzers were fit simultaneously with one σ parameter. An initial fit swept through the parameter space for three allowable lobe pairs and a back-to-back emission lobe. Since the angular range of the A analyzers is not centered about the back-to-back emission angle, only one lobe out of a symmetric pair may be observed in the data set. Thus, fitting without some lobe parameters was carried out until a reasonable result with a χ2 value and overall shape consistent with the smallest achievable χ2 fit was obtained.
With this procedure, the multi-Gaussian fits only reflect the final summation of contributions. Randazzo et al. show the different final state contributions from theoretical water PDI TDCS have complex overlapping lobe structures;33 thus, the multi-Gaussian fit would not necessarily accurately predict the individual contributions of each PDI channel. Measures such as additional Gaussians or relaxed fitting constraints could enable more accurate final state contribution modeling, but overfitting the data and multiple fit solutions to the final TDCS fit are concerns. Without theoretical support, the more cautious approach for multi-Gaussian fitting described above was the chosen method to facilitate comparison of the molecular TDCS data sets.
3 Results and discussion
3.1 Benzene and thiophene
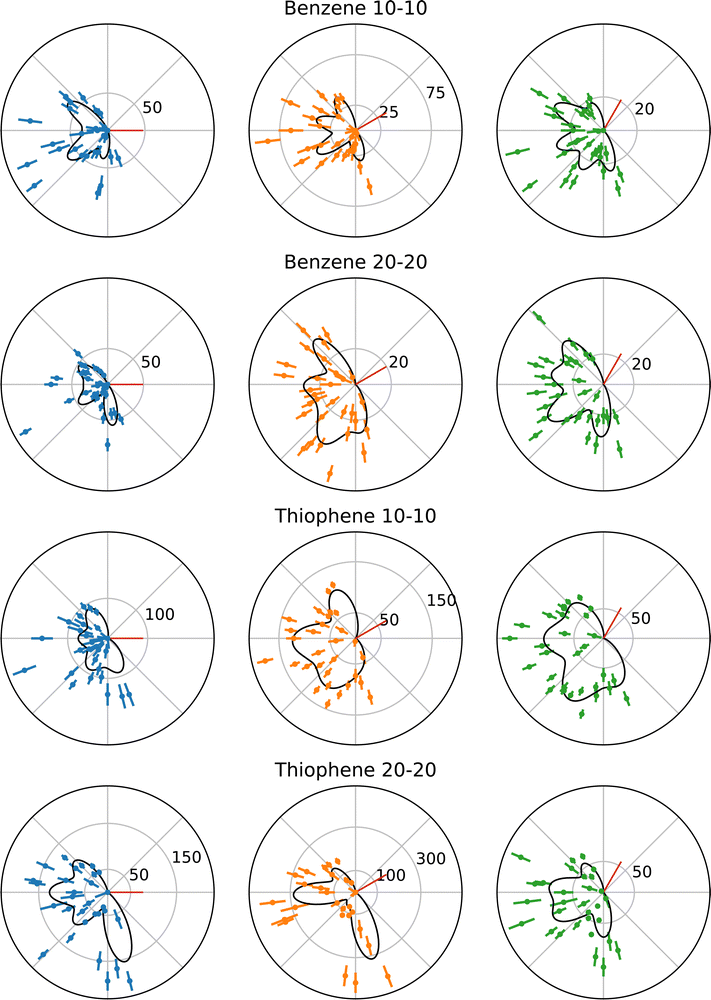
The following benzene and thiophene TDCS are three-point smoothed for clarity. Negative counts in the smoothed plots were artificially set to zero. The multi-Gaussian fits shown in the plots were calculated using the unsmoothed data. Fig. 3 shows the TDCS for benzene and thiophene at 10–10 and 20–20 energy sharing conditions, where 0° is the angle of the ionizing radiation's polarization vector. Each radial plot in Fig. 3 also depicts the multi-Gaussian fit as solid black curves. The parameters of each fit are stated in Table 1, as well the reduced chi-square fit statistic, χν2, for comparison. Since the symmetric lobe μ is calculated based on an input lobe position, uncertainties are omitted for the symmetric partner μs. Further, as mentioned in Section 2.2, some symmetric partner lobes were omitted and are marked with a “–“ in Table 1. Back-to-back emission lobes necessarily do not have symmetric partners, which is represented as “N/A” in Table 1. Moreover, back-to-back lobes here have a precisely set μ (fixed analyzer angle +180°), so no uncertainty is given for the back-to-back positions.| Target | Energy sharing | χ ν 2 | σ [deg] | Fixed analyzer [deg] | μ [deg] | A [counts] | Symmetric μ [deg] | Symmetric A [counts] |
|---|---|---|---|---|---|---|---|---|
| a Gaussian lobe parameters were fixed to obtain uncertainties for the rest of the fit. See text for further details. | ||||||||
| Benzene | 10–10 | 8.05 | 14 ± 3 | 0 | 144 ± 5 | 63 ± 14 | 216 | 63 ± 14 |
| 261 ± 8 | 38 ± 14 | — | — | |||||
| 180 | 29 ± 27 | N/A | N/A | |||||
| 30 | 120 ± 23 | 37 ± 40 | — | — | ||||
| 164 ± 14 | 39 ± 22 | 256 | 13 ± 16 | |||||
| 283 ± 16 | 28 ± 16 | 137 | 7.5 × 10−3 ± 61 | |||||
| 210 | 43 ± 14 | N/A | N/A | |||||
| 60 | 153 ± 7 | 32 ± 10 | — | — | ||||
| 113 ± 18 | 17 ± 9 | — | — | |||||
| 281 ± 6 | 24 ± 8 | 199 | 29 ± 9 | |||||
| 240 | 26 ± 8 | N/A | N/A | |||||
| Benzene | 20–20 | 7.49 | 15 ± 2 | 0 | 145 ± 4 | 46 ± 9 | 215 | 46 ± 9 |
| 277 ± 4 | 57 ± 12 | — | — | |||||
| 180 | 28 ± 18 | N/A | N/A | |||||
| 30 | 132 ± 21 | 34 ± 76 | 288 | 4.0 × 10−6 ± 152 | ||||
| 142 ± 51 | 5.4 × 10−11 ± 87 | 278 | 25 ± 128 | |||||
| 179 ± 9 | 26 ± 9 | 241 | 35 ± 10 | |||||
| 210 | 18 ± 15 | N/A | N/A | |||||
| 60 | 131 ± 6 | 37 ± 9 | — | — | ||||
| 169 ± 8 | 33 ± 9 | — | — | |||||
| 211 ± 6 | 41 ± 9 | 269 | 33 ± 8 | |||||
| 240 | 8 ± 19 | N/A | N/A | |||||
| Thiophene | 10–10 | 8.00 | 20 ± 3 | 0 | 122 ± 6 | 86 ± 16 | 238 | 86 ± 16 |
| 291a | 86.58a | — | — | |||||
| 180 | 70 ± 34 | N/A | N/A | |||||
| 30 | 113a | 100.04a | — | — | ||||
| 139 ± 21 | 4 ± 21 | 281 | 49 ± 26 | |||||
| 179 ± 14 | 110 ± 42 | 241 | 92 ± 33 | |||||
| 210 | 31 ± 110 | N/A | N/A | |||||
| 60 | 130 ± 8 | 73 ± 16 | — | — | ||||
| 180 ± 53 | 82 ± 428 | — | — | |||||
| 189 ± 16 | 15 ± 472 | 291 | 78 ± 29 | |||||
| 240 | 113 ± 17 | N/A | N/A | |||||
| Thiophene | 20–20 | 11.68 | 16 ± 2 | 0 | 136 ± 3 | 96 ± 15 | 224 | 96 ± 15 |
| 284 ± 6 | 156 ± 45 | — | — | |||||
| 180 | 123 ± 38 | N/A | N/A | |||||
| 30 | 129 ± 151 | 41 ± 981 | — | — | ||||
| 136 ± 6 | 108 ± 1046 | 284 | 315 ± 98 | |||||
| 183 ± 10 | 284 ± 105 | 237 | 67 ± 45 | |||||
| 210 | 2.0 × 10−6 ± 282 | N/A | N/A | |||||
| 60 | 125 ± 6 | 56 ± 12 | — | — | ||||
| 172 ± 10 | 81 ± 27 | — | — | |||||
| 208 ± 7 | 82 ± 25 | 272 | 70 ± 18 | |||||
| 240 | 20 ± 28 | N/A | N/A | |||||
While the fitting procedure described in Section 2.2 enabled the fitting of benzene at both kinetic energies and thiophene at 20 eV kinetic energy, the 10–10 TDCS for thiophene required further conditions to obtain uncertainties on the parameters. The issue for the 10–10 thiophene TDCS was data points at the angular ends of the data drove lobes in those regions to large and unreasonable values, since most of the lobes were in an angular region without data points to fit. However, during the fitting procedure, these lobes would not become unreasonable when constrained to the angular range of the observed data, constraint (iv), and the μ and A values obtained from the initial fit were utilized as fixed parameters in the secondary fit, yielding uncertainty values for the rest of the parameters. Specifically, the lobes at μ = 113° and 291° had fixed μ and A values reported in Table 1.
Comparison of the fitting parameters between the four scenarios provides some information. Scale parameters (A) approaching zero may indicate the suppression of a lobe due to kinematic restraints, like the cos(θ1) + cos(θ2) term in eqn (1). Additionally, since the lower limit of the A parameter is 0, the uncertainties are orders of magnitude larger than the A values. Aside from zero approaching A parameters, the uncertainty on most parameters is reasonable across the data sets, but several examples of uncertainties larger than the value exist, mostly for A parameters and especially in the thiophene data sets.
The most obvious explanation for the large uncertainties is the current multi-Gaussian fit does not accurately model the actual TDCS, despite the reasonable characterization the multi-Gaussian fit provides for the other data sets. However, until more in depth theoretical models exist for PDI of benzene and thiophene, it is difficult to confirm or deny the validity of the multi-Gaussian fit further. Another possible explanation is that different combinations of Gaussians can sum to the presented multi-Gaussian fits, including combinations where lobes are suppressed due to kinematic restraints. Without deeper theoretical understanding of the PDI process in benzene and thiophene, performing such fits lack a strong physical basis and could easily overfit the data. A consequence of the use of the more conservative constraints is the occasional discrepancy of minima in the multi-Gaussian fits but observed maxima in the experimental TDCS, for example in the 30° TDCS for benzene at 10–10 energy sharing in Fig. 3. Instead of possibly overfitting the data, He was maintained as a known and reasonable reference point for the multi-Gaussian fits, namely as the origin of the σ minimum limit described in Section 2.2. However, despite these minima-maxima discrepancies, the overall agreement in the χν2 between the data sets supports the multi-Gaussian approach.
One experimental reason exists for the additional constraints required for the 10–10 thiophene TDCSs. The M1 analyzer for the thiophene at 10–10 energy sharing experiments had much lower counts with respect to M2 and M3, when compared to other experimental conditions, which could account for the increased difficulty in fitting the data. The σ values for the different molecules at each kinetic energy may also be compared. One aspect of note is the consistency of σ values across the data sets, and the second important note is the benzene 10–10 TDCS σ is at the minimum value of 0.25 radians or 14.3°.
3.2 Helium comparison
As in the case of the multi-Gaussian fits, the He data at each kinetic energy was fit simultaneously by the He fit for the different fixed analyzer angles, yielding θFWHM values for the 10 eV and 20 eV He TDCSs. Since the He 10 eV data came from two sources and the TDCSs were not internormalized, another scaling factor was included to account for the difference in data sets. The He fit for the 10 eV electrons yielded θFWHM = 94 ± 4°. For comparison, Schwarzkopf and Schmidt reported a value of 90.9 ± 2°9 and Dörner et al. reported a value of 91.6 ± 2°.10 Likewise, the 20 eV electrons had a θFWHM = 99 ± 2° from the He fit, and Cvejanovic et al. give a θFWHM of 103 ± 2°.11 Additionally, multi-Gaussian fit σ values for helium were calibrated to their respective reported θFWHM values, with θFWHM at 10–10 being the average of Schwarkopf and Schmidt's9 and Dörner et al.'s10 values. The calibrated values using a common factor are θFWHM = 90 ± 7° and 105 ± 8° for the 10–10 and 20–20 σ values, respectively. The θFWHM agreement with the He fit performed here and the published results9–11 give support to the multi-Gaussian fit method. Thus, a comparison of the multi-Gaussian fit parameters can be done.Starting with the lobe widths, σ, Table 2 contains the σ values for helium, benzene, and thiophene at both energy sharing conditions and the helium calibrated θFWHM values. The σ values are directly compared and act as an indicator of electron correlation. Considering benzene and thiophene, only the 10–10 thiophene σ is significantly different, perhaps being larger than the other molecular cases. No clear differences are observed between benzene and thiophene, with σ values for the remaining three cases being within the uncertainties of each other. Comparing to helium, the molecular σs are smaller than both helium values.
| Target | Energy sharing | σ [deg] | θ FWHM [deg] |
|---|---|---|---|
| Helium | 10–10 | 24 ± 2 | 90 ± 7 |
| Helium | 20–20 | 28 ± 2 | 105 ± 8 |
| Benzene | 10–10 | 14 ± 3 | — |
| Benzene | 20–20 | 15 ± 2 | — |
| Thiophene | 10–10 | 20 ± 3 | — |
| Thiophene | 20–20 | 16 ± 2 | — |
A smaller σ (and therefore θFWHM) than He is reasonable. Kheifets and Bray showed the θFWHM is related to the momentum profile widths, which are determined from momentum space radial wave functions of the singly ionized PDI targets.34 Heavier atoms with similar valence electronic structures to He had smaller momentum widths and smaller θFWHMs following an established power law.34 Further, Kheifets and Bray also showed that the momentum width for molecular hydrogen, H2, is smaller than the He's ground state width.35 So, thiophene and benzene could be expected to have smaller momentum profile widths and consequently smaller θFWHMs.
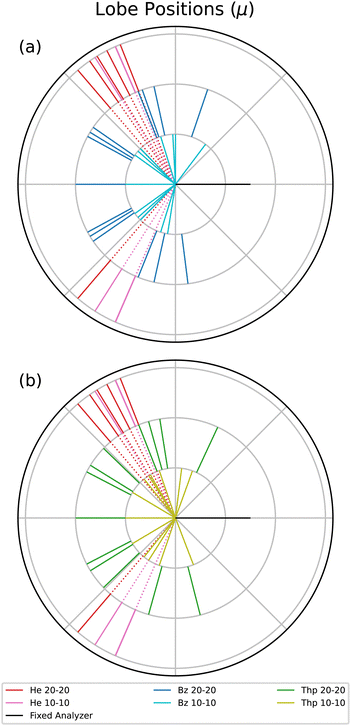
Next, the lobe position, μ, values are displayed in a radial plot form in Fig. 4. The magnitude of the lines in Fig. 4 are arbitrary to focus on the angular position of each lobe. For a reasonable comparison between different fixed analyzer angles, the angles in Fig. 4 are the mutual angle between the fixed analyzer angle and the lobe angle. He is plotted in both radial plots to provide an atomic comparison, and the benzene and thiophene lines are plotted separately in Fig. 4(a) and (b), respectively.
The He μ values highlight the kinematic restriction suppressing back-to-back emission.1 However, back-to-back emission is observed for the two molecules. The shape of the angular distribution in PDI is determined by the combination of the Coulomb repulsion of the two electrons in the continuum and the symmetry of the wave function of the electron pair, defined by the dipole selection rule and the initial state wave function. The symmetry of the electron pair determines the node, or absence of a lobe, in the back-to-back emission. For atoms, the node occurs when the electron pair does not have all even or odd quantum numbers, as in the case of helium where the electron pair wavefunction is 1Po. For randomly oriented molecules, besides the symmetry of the electron pair, the molecular contribution described by Reddish and Feagin32 can fill the node in the back-to-back direction. Thus, if different dication states contribute to the measured TDCS, then it may be possible the cross sections of the states varies with the excess energy, and therefore the filling of the back-to-back node is different at 10–10 and 20–20 energy sharing conditions.
Table 1 indicates that only the 30° fixed analyzer TDCS for thiophene under 20–20 energy sharing conditions has a suppressed back-to-back lobe. Aside from the back-to-back lobe though, the 20–20 μ values for both molecules have more lobes closer to back-to-back emission compared to the 10–10 data, which may indicate an energy dependent TDCS contribution common to both benzene and thiophene.
Although the molecular TDCSs are not expected to be similar to the He TDCS, the μ values for He provide a well understood atomic point of reference. Benzene at both 10–10 and 20–20 energy sharing do not have any features at the same mutual angle as He; only some μ values close to the He angles. For thiophene only the 10–10 energy sharing has lobes directed in the same angular region as helium. One possible explanation for the 10–10 thiophene lobes in the helium directions comes from the sulfur in the molecule. The PDI dication state targeted for thiophene consists of the outermost out-of-plane orbitals, namely the sulfur p subshell and the carbon ring.20 Further, PDI TDCS studies of argon show ionization lobes from 3p subshell into residual ion states of both 3Pe and 1Se yield lobes in similar directions to He PDI.13,36 Two factors do not support such a difference for the 10–10 thiophene μ values. First, the issue again of the difficult fitting of the 10–10 thiophene TDCS necessitates a reserved approach to observed differences. Second, the p subshell explanation does not explain the lack of such a lobe for 20–20 thiophene. Therefore, while the thiophene PDI TDCS at lower kinetic energies may suggest more atomic-like contributions to the TDCS, further support for such a difference is required.
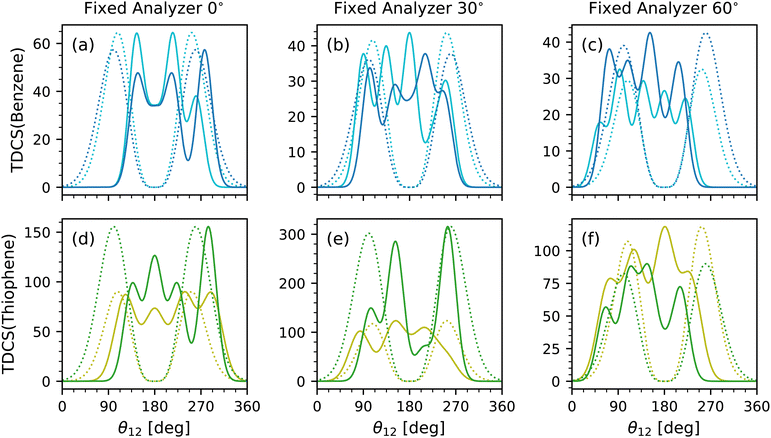
Lastly is the scaling parameter, A; however, a comparison of the scaling parameter did not reveal any clear insight. Instead, the full multi-Gaussian fits were compared to each other and the helium TDCS model. Fig. 5 shows the multi-Gaussian fits for each fixed analyzer for benzene at both equal energy sharing conditions in Fig. 5(a)–(c) and for both energy sharing conditions of thiophene in Fig. 5(d)–(f). Along with each multi-Gaussian fit is a He fit generated using eqn (1) with known θFWHM values of 91.25° (average from ref. 9 and 10) and 103°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 for 10–10 and 20–20 energy sharing, respectively. The He fits were then scaled to the maximum value of each TDCS.
11 for 10–10 and 20–20 energy sharing, respectively. The He fits were then scaled to the maximum value of each TDCS.
The data sets were not internormalized, hence the difference in counts for each TDCS fit. Rather, Fig. 5 emphasizes the relative scale and quantity of lobes for each data set. Broad similarities are observed such as similar number of lobes for the same fixed analyzer and molecule. A difference among the data is the strength of the back-to-back lobe. In benzene, the back-to-back lobe is similar in relative magnitude for both 10–10 and 20–20 energy sharing at the 0° fixed analyzer as evident in Fig. 5 and confirmed with Table 1, but for the 30° and 60° fixed analyzer the 10–10 energy sharing has a more dominant back-to-back lobe than the 20–20 multi-Gaussian fits. A similar trend is present for thiophene, with even the back-to-back lobe for the 20–20 fit for the 30° fixed analyzer TDCS approaching an A of zero.
Feagin,37 Reddish and Feagin,32 and Bolognesi et al.38 examined the ratio of their molecular target TDCSs, D232,37 and N2,38 and He TDCSs. For the ratios both experimental and fitted TDCSs were compared.32,37,38 The TDCS ratios highlighted not only how the molecular targets differ from He, especially at back-to-back emission, but also how the models compare to the data.32,37,38 Here, the ratios of the experimental TDCS with the He fit TDCS and the ratios of the multi-Gaussian fit with the He fit TDCS for benzene and thiophene are presented in Fig. 6 against the mutual angle θ12. For the ratio of the experimental TDCS, the He fits were scaled to the maximum of the experimental data, as for Fig. 5.
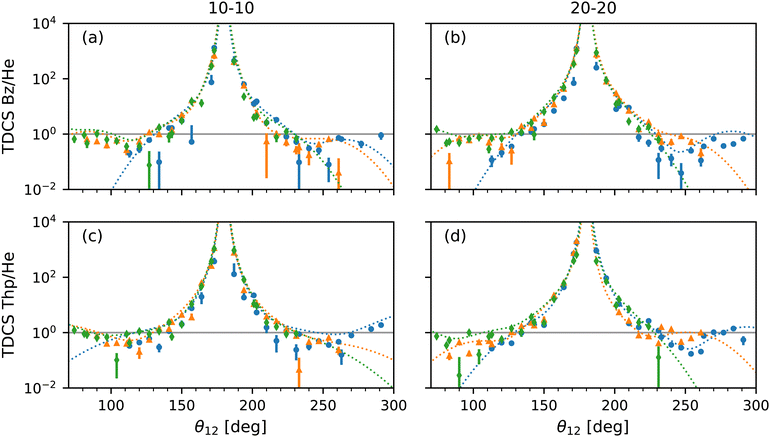 | ||
| Fig. 6 Plots of the ratio of TDCSs and multi-Gaussian fit by the He fits shown in Fig. 5 for benzene at 10–10 (a) and 20–20 (b) energy sharing and thiophene at 10–10 (c) and 20–20 (d) energy sharing against mutual angle, θ12. The ratio from TDCSs of fixed analyzer angles of 0° (blue dotted curves), 30° (orange dotted curves) and 60° (green dotted curves) are displayed with experimental values of the same color but different markers (circle, triangle and diamond, respectively) for comparison. Large uncertainties due to the semi-log scale are omitted for clarity. A ratio of 1 (solid grey horizontal line) highlights where the most helium-like the multi-Gaussian fits are in all plots. | ||
Focusing on the acceptable data range, the multi-Gaussian fit ratios match the experimental TDCS ratios well as expected, further confirming the validity of the fit method. Furthermore, the molecular behaviour of a large back-to-back emission peak observed by Feagin,37 Reddish and Feagin,32 and Bolognesi et al.38 is also present for thiophene and benzene. Both the multi-Gaussian fit ratios as well as the experimental TDCS ratios for thiophene appear to be more helium-like at both 10–10 and 20–20 energy sharing compared to benzene at θ12 > 180°. Fig. 6(a) and (b) show at θ12 > 180° the benzene TDCS ratios deviate more from the helium-like ratio, with the multi-Gaussian fit curves for benzene also moving away from helium-like (a value of 1). The difference could be due to the sulfur atom within thiophene with similar reasoning described previously for the thiophene 10–10 lobe μ values, where PDI originates from molecular orbitals comprised partly of the sulfur's p subshell.
A qualifying aspect to the TDCS ratios is the number of lobes in the molecular TDCS and multi-Gaussian fits, beyond the two lobes observed for helium. Since so many lobes have been used to fit the data and overlap within the region of the helium lobes as shown in Fig. 5, the TDCS ratios in Fig. 6 exhibit several humps around the ratio value of 1, which is most helium-like. The benzene 10–10 TDCS at the 60° fixed analyzer angle displays this behaviour most clearly in Fig. 6, where the three lobes below θ12 = 180° are visible as two humps and one shoulder. Without theoretical support, it is unclear whether or not the lobes in the helium angular region for benzene and thiophene are caused by helium-like atomic PDI contributions or a molecular contribution.
4 Conclusions
In summary, the PDI TDCS for benzene and thiophene at 10–10 and 20–20 equal energy sharing conditions have been presented. Despite the lack of a theoretical model, the TDCSs have been characterized via a multi-Gaussian fitting method. A comparison with the PDI of helium has not only validated the multi-Gaussian fits but also contextualized the benzene and thiophene TDCSs. No difference between the molecules was found for the σ value of the multi-Gaussian fits, which is an indication of the electron angular correlation; however, benzene and thiophene did have smaller σs than helium. A comparison of the multi-Gaussian fit μ values showed a slight similarity for benzene and thiophene at 20–20 energy sharing conditions, which contained more lobes closer to back-to-back emission than the 10–10 data. Further, the 10–10 thiophene μs were the only data to have lobes directly in the angular region of the helium lobes. The difference for thiophene may be due to PDI contributions from the sulfur p subshell, but this difference may also be due to the challenge in fitting the 10–10 thiophene TDCS. Finally, a comparison of the multi-Gaussian fits and the well-known He fit TDCS at equal energy sharing showed an overall greater contribution from the back-to-back emission for the 10–10 energy sharing conditions over the 20–20 for both molecules. Furthermore, examining the ratio of the TDCSs with the He fit TDCS, indicated thiophene had a more helium-like characteristic than benzene at mutual angles, θ12, greater than 180°. The difference is qualified by the fact that benzene and thiophene have multiple lobes which lie within the angular range of the helium lobes, and the source of these contributions cannot be determined without more theoretical support, which is needed to progress understanding of the experimental molecular TDCSs further.Even without the support yet, the multi-Gaussian characterization of the benzene and thiophene PDI TDCS gives some insight into the resonances observed by Wehlitz et al. for aromatic hydrocarbons but not for aromatic heterocyclic molecules.6 First, looking at the Gaussian fit parameters provides some information. The obtained σ values broadly showed no difference between benzene and thiophene, especially given the larger value for 10–10 thiophene may be due to poor counts. Generally, the trends in μ values for benzene and thiophene were similar, with the one difference again in 10–10 thiophene. Trends in the full multi-Gaussian fit and TDCS comparison with the He fit were also quite similar, with the one difference observed in the TDCS ratios of thiophene's more helium-like TDCS requiring more evidence. Thus according to the fit parameters, the present results do not show strong evidence of a reason for the resonance enhancement for benzene at 40 eV excess energy observed by Wehlitz et al.6 and Jänkälä et al.7 Second, examining the shape of each multi-Gaussian fit in Fig. 3 shows another facet of the TDCS. Between benzene at 10–10 and 20–20 energy sharing conditions the lobes at 20–20 appear to be broader at the fixed analyzer angles of 30° and 60°, as shown in Fig. 3. Then, comparing benzene and thiophene at 20–20 energy sharing, some visual differences appear as well. The differences observed in the fits are not well captured by the multi-Gaussian fit parameters; however, the fits do highlight differences among the PDI TDCS. Whether and how these qualitative differences may be attributed to an effect of the observed resonances6,7 is not straightforward.
Theoretical support which would help to understand the shapes of the measured TDCSs and the differences between benzene and thiophene should provide first of all an analysis of the contributions to the TDCS from the different ionization channels and second the TDCSs' variation with excess energy. The latter would also provide useful information on the active PDI mechanisms. This could lend further insight into the unexplained resonance observed by Wehlitz et al.6 and Jänkälä et al.7 A more robust TDCS model based on theory would provide a more grounded comparison with the multi-Gaussian fits and help to extract the parameterization information on the electron correlation in the case of these two polyatomic molecules, which then can be used for comparison with other molecules.
Author contributions
Conceptualization: ES, PB, LA; data curation: NLW, JH, BD, PB; formal analysis: NLW; funding acquisition: ES; investigation: NLW, JH, BD, ES, PB, LA; methodology: ES, PB, LA; project administration: ES; resources: ES, PB, LA; software: NLW, JH; supervision: ES, LA; validation: NLW, JH, BD, ES, PB, LA; visualization: NLW; writing – original draft preparation: NLW; writing – review & editing: NLW, JH, BD, ES, PB, LA;Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the assistance of Luigi Stebel in ensuring our data acquisition software continued to work in the last beamtime. This work was supported by Science Foundation Ireland through the Frontiers for the Future Programme 19/FFP/6795.Notes and references
- L. Avaldi and A. Huetz, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, S861–S891 CrossRef CAS.
- R. Wehlitz, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 222004 CrossRef.
- A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337 CrossRef CAS.
- R. K. Anand, S. Rastogi and B. Kumar, J. Astrophys. Astron., 2023, 44, 47 CrossRef CAS.
- Y. Kubozono, H. Goto, T. Jabuchi, T. Yokoya, T. Kambe, Y. Sakai, M. Izumi, L. Zheng, S. Hamao, H. L. T. Nguyen, M. Sakata, T. Kagayama and K. Shimizu, Phys. C, 2015, 514, 199–205 CrossRef CAS.
- R. Wehlitz, P. N. Juranić, K. Collins, B. Reilly, E. Makoutz, T. Hartman, N. Appathurai and S. B. Whitfield, Phys. Rev. Lett., 2012, 109, 193001 CrossRef CAS PubMed.
- K. Jänkälä, P. Lablanquie, F. Penent, J. Palaudoux, L. Andric and M. Huttula, Phys. Rev. Lett., 2014, 112, 143005 CrossRef PubMed.
- P. N. Juranić, D. Lukić, K. Barger and R. Wehlitz, Phys. Rev. Lett., 2006, 96, 023001 CrossRef PubMed.
- O. Schwarzkopf and V. Schmidt, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2847–2862 CrossRef CAS.
- R. Dörner, H. Bräuning, J. M. Feagin, V. Mergel, O. Jagutzki, L. Spielberger, T. Vogt, H. Khemliche, M. H. Prior, J. Ullrich, C. L. Cocke and H. Schmidt-Böcking, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 1074–1090 CrossRef.
- S. Cvejanovic, J. P. Wightman, T. J. Reddish, F. Maulbetsch, M. A. MacDonald, A. S. Kheifets and I. Bray, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, 265–283 CrossRef CAS.
- A. Huetz, P. Selles, D. Waymel and J. Mazeau, J. Phys. B: At., Mol. Opt. Phys., 1991, 24, 1917–1933 CrossRef CAS.
- P. Bolognesi, M. Coreno, G. Alberti, R. Richter, R. Sankari and L. Avaldi, J. Electron Spectrosc. Relat. Phenom., 2004, 141, 105–119 CrossRef CAS.
- T. J. Reddish, G. Richmond, G. W. Bagley, J. P. Wightman and S. CvejanoviÄ, Rev. Sci. Instrum., 1997, 68, 2685–2692 CrossRef CAS.
- C. Dawson, S. Cvejanovic, D. P. Seccombe, T. J. Reddish, F. Maulbetsch, A. Huetz, J. Mazeau and A. S. Kheifets, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, L525–L533 CrossRef CAS.
- T. Weber, A. Czasch, O. Jagutzki, A. Müller, V. Mergel, A. Kheifets, J. M. Feagin, E. Rotenberg, G. Meigs, M. H. Prior, S. Daveau, A. L. Landers, C. L. Cocke, T. Osipov, H. Schmidt-Böcking and R. Dörner, Phys. Rev. Lett., 2004, 92, 163001 CrossRef PubMed.
- J. H. D. Eland and R. Feifel, Chem. Phys., 2006, 327, 85–90 CrossRef CAS.
- R. Dörner, V. Mergel, O. Jagutzki, L. Spielberger, J. Ullrich, R. Moshammer and H. Schmidt-Böcking, Phys. Rep., 2000, 330, 95–192 CrossRef.
- I. Ismail, M. A. Khalal, M. Huttula, K. Jänkälä, J.-M. Bizau, D. Cubaynes, Y. Hikosaka, K. Bučar, M. Žitnik, L. Andric, P. Lablanquie, J. Palaudoux and F. Penent, Phys. Chem. Chem. Phys., 2022, 24, 20219–20227 RSC.
- P. Linusson, L. Storchi, F. Heijkenskjöld, E. Andersson, M. Elshakre, B. Pfeifer, M. Colombet, J. H. D. Eland, L. Karlsson, J. E. Rubensson, F. Tarantelli and R. Feifel, J. Chem. Phys., 2008, 129, 234303 CrossRef CAS PubMed.
- J. H. D. Eland, Chem. Phys., 2008, 345, 82–86 CrossRef CAS.
- F. Tarantelli, A. Sgamellotti, L. S. Cederbaum and J. Schirmer, J. Chem. Phys., 1987, 86, 2201–2206 CrossRef CAS.
- J. Cooper and R. N. Zare, J. Chem. Phys., 1968, 48, 942–943 CrossRef CAS.
- K. Codling, R. G. Houlgate, J. B. West and P. R. Woodruff, J. Phys. B: At., Mol. Opt. Phys., 1976, 9, L83–L86 CrossRef CAS.
- A. W. Bray, F. Naseem and A. S. Kheifets, Phys. Rev. A, 2018, 97, 063404 CrossRef CAS.
- P. Calicchia, S. Lagomarsino, F. Scarinci, C. Martinelli and V. Formoso, Rev. Sci. Instrum., 1999, 70, 3529–3536 CrossRef CAS.
- P. Bolognesi, J. M. Randazzo, G. Turri, J. Mathis, C. Penson, L. U. Ancarani and L. Avaldi, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 34002 CrossRef CAS.
- O. Alwan, O. Chuluunbaatar, X. Assfeld and B. B. Joulakian, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 185203 CrossRef.
- E. Sokell, P. Bolognesi, A. Kheifets, I. Bray, S. Safgren and L. Avaldi, Phys. Rev. Lett., 2013, 110, 083001 CrossRef CAS PubMed.
- L. Malegat, P. Selles and A. Huetz, J. Phys. B: At., Mol. Opt. Phys., 1997, 30, 251–261 CrossRef CAS.
- J. Mazeau, P. Lablanquie, P. Selles, L. Malegat and A. Huetz, J. Phys. B: At., Mol. Opt. Phys., 1997, 30, L293–L299 CrossRef CAS.
- T. J. Reddish and J. M. Feagin, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, 2473–2486 CrossRef CAS.
- J. M. Randazzo, G. Turri, P. Bolognesi, J. Mathis, L. U. Ancarani and L. Avaldi, Phys. Rev. A, 2020, 101, 033407 CrossRef CAS.
- A. S. Kheifets and I. Bray, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 75, 042703 CrossRef.
- A. S. Kheifets and I. Bray, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 020708 CrossRef.
- P. Bolognesi, M. Zitnik, L. Malegat, P. Selles, G. Turri, M. Coreno, R. Camilloni and L. Avaldi, J. Phys. B: At., Mol. Opt. Phys., 2004, 37, 2285 CrossRef CAS.
- J. M. Feagin, J. Phys. B: At., Mol. Opt. Phys., 1998, 31, L729 CrossRef CAS.
- P. Bolognesi, B. Joulakian, A. A. Bulychev, O. Chuluunbaatar and L. Avaldi, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 053405 CrossRef.
| This journal is © the Owner Societies 2024 |